Decoding the magnetic bit positioning error in a ferrimagnetic racetrack

Abstract

Current-driven motion of magnetic domain walls is one of the key technologies for developing storage class memory devices. Extensive studies have revealed a variety of material systems that exhibit high-speed and/or lower power propagation of the domain walls driven by electric current. However, few studies have assessed the reliability of the operations of the memory technology. Here, we decode the errors associated with writing and shifting domain walls using nanosecond current pulses in a ~5-micrometer-wide wire composed of a Pt/GdFeCo bilayer. We find that writing a domain wall at the edge of the wire causes a bit positioning error of ~0.3 micrometers, whereas the shifting process induces an error of ~0.1 micrometers per a 2-nanosecond-long current pulse. The error correlation among successive shifting is negligible when the current drive is sufficiently large. These features allow reliable operation of highly packed domain walls in a ferrimagnetic racetrack.

Bit positioning error of current-driven domain walls in a ferrimagnet racetrack is revealed.

INTRODUCTION

The discovery of spin transfer torque (STT) led to the development of magnetic random-access memory (MRAM) technologies (1–3). MRAM consists of arrays of magnetic tunnel junctions, in which information is coded in the magnetization direction of a magnetic layer that is part of the junction. Because the state of the magnetic bits can be maintained without power, MRAM is often referred to as a nonvolatile memory. In MRAM, binary operation of magnetic bits is performed using nanosecond current pulses to reverse the magnetization direction via STT. The recording density is defined by the footprint of the magnetic tunnel junctions, while the operation speed and power consumption are set, respectively, by the time and power required to switch the magnetization direction.

In contrast to random-access memories, hard disk drives (HDDs) and solid-state memories (primarily NAND-flash memories) can store information in orders of magnitude larger density (4), but with a cost of longer data access time. In addition, HDD has mechanically moving parts that restrict its durability while solid-state memories require erasing a block of data before storing information, causing additional power and limiting the operation speed.

Storage class memory refers to a class of memory-storage device that bridges the technology gap between random-access memories and storage devices (5). The data access time and read/write speed are substantially faster than those of storage devices while the recording density surpasses that of random-access memories. Such memories can be used in the cache, as an embedded memory in logic chips, and potentially as stand-alone universal memories (6). Because of the emergence of applications based on machine learning and artificial intelligence, demand to develop high-performance storage class memories is rapidly growing (7).

Racetrack memory has been proposed as a nonvolatile storage class memory (8–11). Information is encoded in the magnetization direction of the magnetic domains formed in a magnetic nanowire. The recording media takes a similar form with the HDD. However, there are no mechanical moving parts in racetrack memory: The magnetic domains are moved along the nanowire using current pulses. Current-driven domain wall motion, enabled by STT (12–16) or spin orbit torque (SOT) (17–20), is therefore the core technology for developing racetrack memory. The data access time is primarily defined by the speed at which the domain walls move with current while the recording density is set by the minimum stable domain size. Substantial efforts have been placed to explore material systems that exhibit fast current-driven motion of domain walls. Domain walls in antiferromagnets are expected to move at high speed due to their strong exchange interaction (21–23). Recent studies have indeed shown that the domain wall velocity of synthetic antiferromagnets and ferrimagnets is more than an order of magnitude larger than that of ferromagnets (24–31). In contrast, few studies have addressed the reliability of current-driven domain walls, i.e., the error associated with positioning domain walls to intended area. Variation of current-driven domain wall velocity can cause reading errors because sensors, such as magnetic tunnel junctions, are placed in fixed positions along the nanowire to read out the information. As we expect the errors to accumulate when domain walls are driven along the nanowire using current pulses, it is of interest, both scientifically and technologically, to understand how the error accumulation grows with the distance the domain walls travel. With regard to the memory operation, one must also verify whether writing domain walls into the nanowire introduce any positioning errors. It is therefore essential to develop a process to assess positioning errors and address the reliability issues.

Here, we show a protocol to determine the bit positioning error of domain walls driven by nanosecond-long electrical current pulses using a ferrimagnetic racetrack as an example. Bilayers composed of a GdFeCo alloy, a rare earth-transition metal ferrimagnet, and a heavy metal (Pt) are used as a model material system in which fast current-induced motion of domain walls has been reported (25, 29, 32). Thousands of Kerr microscopy images are acquired to characterize the bit positioning error of the domain walls in a ~5-μm-wide wire. Using a model developed to analyze the errors from the images, the bit positioning errors associated with bit writing and shifting processes are determined. We find that error correlation among successive shifting processes is negligible when the shifting pulse amplitude is sufficiently large, and that the positioning error shows little dependence on the bit size in the range studied. We show that these features of a ferrimagnetic racetrack allow reliable motion of highly packed domain walls.

RESULTS

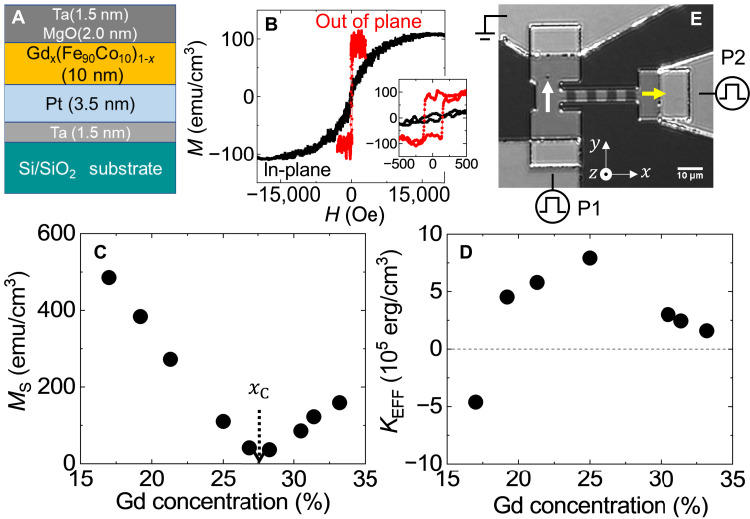
Figure 1A shows a schematic illustration of the film structure. Sub./Ta(1.5 nm)/Pt(3.5 nm)/Gd_x(Fe₉₀Co₁₀)_1−x(10 nm)/MgO(2.0 nm)/Ta(1.5 nm) films are deposited on 200-mm-diameter thermally oxidized silicon wafers using a mass-production magnetron sputtering apparatus (Canon Anelva C-7100) at room temperature. Gd_x(Fe₉₀Co₁₀)_1−x (referred to as GdFeCo hereafter) is deposited by cosputtering Gd, Fe, and Co targets. The sputtering power of each target is adjusted to form the alloy with a given concentration. X-ray fluorescence measurements are used to determine the composition of the alloy.

Fig. 1. Magnetic properties of Pt/GdFeCo thin films.

(A) Schematic illustration of the film structure. (B) Representative hysteresis loop of the film with x = 30.5%. The black and red lines show the magnetization M as a function of in-plane and out-of-plane magnetic field, respectively. The inset shows an expanded view of the main panel. (C and D) Gd concentration (𝑥) dependence of the saturation magnetization M_S (C) and the effective magnetic anisotropy energy density K_eff (D). x_C in (C) indicates the Gd concentration required for magnetic compensation. (E) Kerr microscope image of a representative device and schematic illustration of the experimental setup. P1 and P2 represent the pulse generators used to apply current to the vertical and horizontal lines, respectively. The white and yellow arrows indicate the current flow directions when a positive (negative) voltage pulse is applied from pulse generator P1 (P2). Definition of the coordinate axis is presented at the bottom of the image.

Vibrating sample magnetometry is used to study the magnetic properties of the films. Representative hysteresis loops of the film with x ~ 30.5% are shown in Fig. 1B. The black and red lines show loops when the magnetic field is swept along film plane and film normal, respectively. The coercive field of the easy axis loop (i.e., field along the film normal) is ~135 Oe. Figure 1C shows the Gd concentration (x) dependence of the saturation magnetization M_S. M_S reaches a minimum at the so-called magnetization compensation point (x_C), which is found to be x_C ~ 27.5%. The magnetic anisotropy energy density K_eff, estimated from the hard axis saturation field, is plotted against x in Fig. 1D. Positive K_eff indicates that the magnetic easy axis points along the film normal. The magnetic easy axis of the films points along the film normal in a wide range of x above ~20% that spans x ~ x_C. The average value of the domain wall pinning potential depth V is equal to the product of the average domain wall propagation field H_P and M_S. We assume that H_P is equal to the coercive field of the film hysteresis loop. For the film with x_C ~ 30.5%, we estimate V = H_PM_S ~ 1.5 × 10⁴ erg/cm³. Films are patterned into micrometer-scale devices using optical lithography and Ar ion milling. Here, we show representative data from films consisting of GdFeCo alloy with x ≳ x_C. Unless noted otherwise, data from x ~ 30.5% are shown below.

Figure 1E shows a Kerr microscope image of the patterned device, a rotated T-shaped wire, together with a schematic illustration of the experimental setup and definition of the coordinate axis. The bright and dark areas in the wire corresponds to magnetic domains with magnetic moments oriented along +z and −z, respectively. Note that there are no prepatterned pinning sites along the wire. Bit writing is performed by applying current pulses to the vertical line of the rotated T-shaped wire by pulse generator P1 (Tektronix, PSPL 10300B) via SOT magnetization switching. To promote deterministic magnetization switching, an in-plane magnetic field H_y = ± 500 Oe is applied along the y axis. Bit shifting is achieved by applying current pulses to the track (horizontal line) using pulse generator P2 (Avtech Electrosystems Ltd., AVP-AV-HV3-B-PN). Positive current is defined as current that flows along +x and +y in the horizontal and vertical lines, respectively.

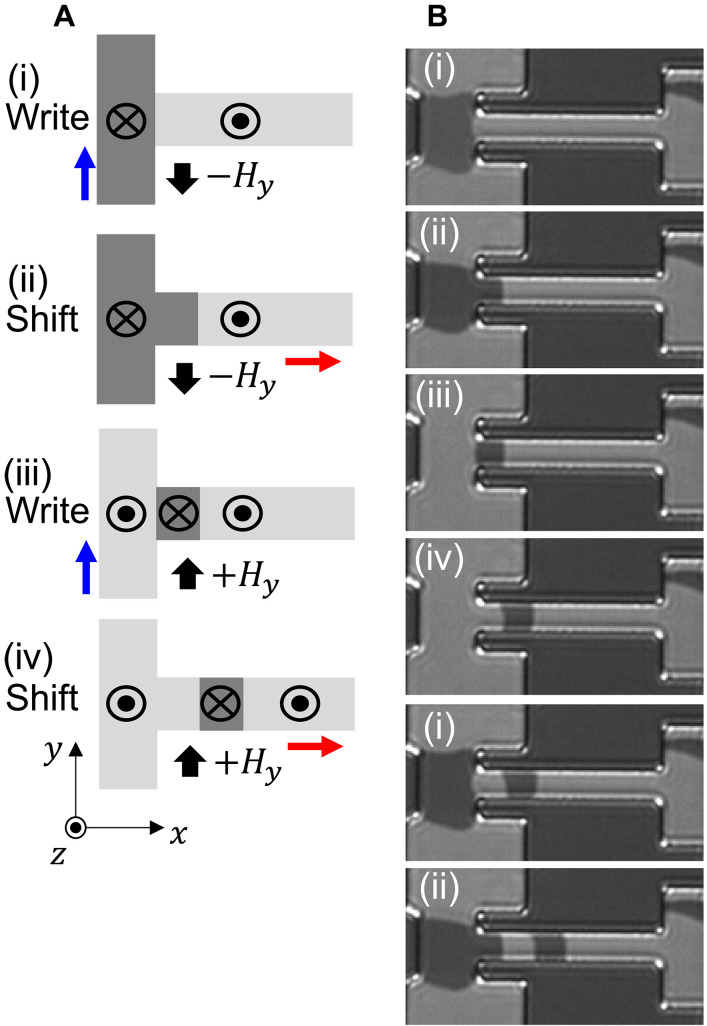
Figure 2A schematically describes the sequence of bit writing and shifting. The following processes (i) to (iv) are conducted in order: (i) A positive current pulse (pulse amplitude: V_w, pulse length: t_w) is applied to the vertical line under H_y = −500 Oe to induce SOT switching of the vertical line. (ii) A train of positive current pulses (pulse amplitude: V, pulse length: t, number of pulses: n, interval between the pulses: 10 ms) is applied to the horizontal line. A domain wall at the intersection of the horizontal and vertical lines moves into the track (along +x). Note that H_y is maintained at −500 Oe during this process. (iii) H_y is reversed to +500 Oe and the same positive current pulse with (i) (pulse amplitude: V_w, pulse length: t_w) is applied to the vertical line. Consequently, the magnetization in the vertical line reverses its direction. (iv) A train of positive current pulses, identical to that used in (ii), is applied to the horizontal line to move the domain walls in the track. H_y of +500 Oe is applied during this process. This sequence [from (i) to (iv)] is repeated N/2 times (the writing and shifting operations are conducted N times). We do not find a significant difference (18) in the domain wall velocity along the track when the direction of H_y is reversed. We infer that this is an advantage of ferrimagnets, which are less susceptible to external magnetic fields. For the writing processes (i) and (iii), one may fix the direction of H_y and reverse the current flow direction along the vertical line. Technically, our experimental setup does not allow this procedure.

Fig. 2. Demonstration of bit writing and shifting operations.

(A) Schematic illustration of the experimental sequences (i) to (iv) used to write and shift the magnetic bits in a ferrimagnetic racetrack and (B) the corresponding Kerr microscope images. In (A), sequences (i) to (iv) indicate the following: (i) A positive voltage pulse is applied from pulse generator P1 to reverse the magnetization direction of the vertical line via SOT switching. Bias magnetic field H_y is applied to promote the switching. A domain wall is created at the intersection of the vertical and horizontal line. (ii) A negative voltage pulse from pulse generator P2 is applied to the horizontal line to move the domain wall to the right. H_y is turned on during this process. (iii) Process (i) is carried out under a reversed H_y. A new domain wall is created at the intersection. (iv) Process (ii) is performed to move the domain walls in the horizontal line. Processes (i) to (iv) are repeated to obtain statistics. In (B), the bright and dark contrasts represent the magnetization direction of the GdFeCo oriented along +z and −z, respectively. Processes (i) and (ii) are repeated for clarity.

A Kerr microscope image is captured after each step of operations (i) to (iv): Exemplary images are presented in Fig. 2B. The acquired images are analyzed to study the position of the domain walls, which encode information of the magnetic bits. In the following, we present results where V_w and t_w are fixed to 28 V and 2 ns, respectively. The amplitude V and number n of the current pulses applied along the track are varied while its length t is fixed to 2 ns.

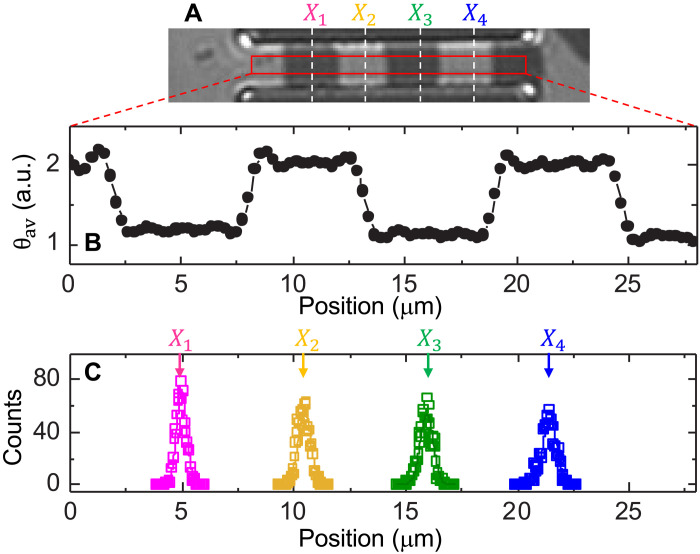
Figure 3A shows a typical Kerr microscope image of a multibit state in the track. We use a fixed area, as defined by the red box in Fig. 3A, to process the images. The Kerr image is digitized and averaged over the width of the wire to obtain the magnetization line profile, θ_av versus x, along the track. The average line profile along the track for the image shown in Fig. 3A is presented in Fig. 3B. θ_av at around 2.0 a.u. (1.0 a.u.) corresponds to the bright area (dark area) in Fig. 3A. The positions of domain walls are obtained from the peaks and valleys of the spatial derivative of θ_av, i.e., $\frac{{\mathrm{\partial \theta }}_{\text{av}}}{\partial x}$ . The center of the ith magnetic bit (X_i) is defined as the average position of the adjacent peak and valley of $\frac{{\mathrm{\partial \theta }}_{\text{av}}}{\partial x}$ . The bit information of the left and right edges of the track cannot be obtained as there can be no domain wall at the edges of the wire. We thus count the magnetic bit (i = 1, 2, …) as shown in Fig. 3A. X_i is obtained for each image acquired.

Fig. 3. Histograms of bit positions defined by current pulses.

(A) Exemplary Kerr microscope image of a multibit state in the track. The red box indicates the region used to analyze positions of the magnetic bits. The vertical dashed lines schematically show the position of the ith bit X_i. (B) Line profile of the Kerr signal θ_av along the track, averaged across the width, for the region defined by red box shown in (A). (C) Histograms of X_i (i = 1,2,3,4) obtained from experiments with shift pulse amplitude V = 14 V, pulse length t = 2 ns, total trial number N = 1000, and Gd concentration x = 30.5%. The lines, which represent Gaussian fitting to the data, are a guide to the eye.

Figure 3 shows exemplary histograms of X_i (i = 1,2,3,4) obtained from experiments with N = 1000. The bit writing and shifting conditions are described in the caption to Fig. 3. We do not find notable discretization of the histograms, suggesting that the domain walls are positioned in accordance with the current pulse length and amplitude. This also indicates that the pinning sites are uniformly distributed along the wire: the length scale of the distribution is below the spatial resolution of the Kerr microscopy imaging.

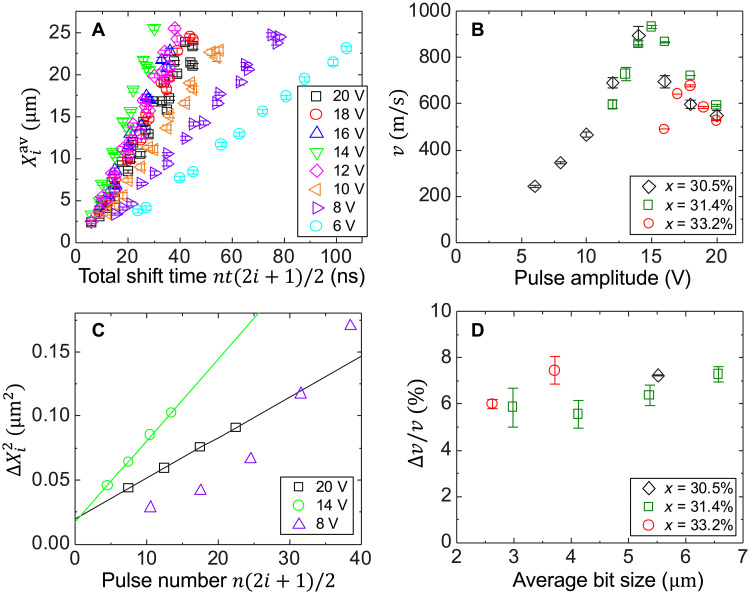
We first show in Fig. 4A the mean value of X_i ( $X_i^{\text{av}}$ ) obtained from experiments with N = 100 against the total duration of the pulses applied. The pulse amplitude V and the number of pulses n per one shift operation are varied. For a fixed n, the total shift duration is calculated as the following. Starting from the intersection of the vertical and horizontal lines, ni and n(i + 1) current pulses are required for a domain wall to reach the left and right edges of the ith bit, respectively, and the average pulse number is n(2i + 1)/2. The total shift duration to form a bit at position X_i is thus nt(2i + 1)/2 (the pulse length is fixed to t = 2 ns here). As evident from Fig. 4A, the relation between X_i and nt(2i + 1)/2 is linear. Fitting a linear function to the data, we obtain the domain wall velocity from its slope.

Fig. 4. Pulse amplitude and average bit size dependence of bit positioning error.

(A) Dependence of the average bit position $X_i^{\text{av}}$ on the total shift time nt(2i + 1)/2 under application of different shift pulse amplitudes (pulse length t = 2 ns, total trial number N = 100). The corresponding pulse amplitudes are shown in the legend. Results are obtained using the film with x = 30.5%. (B) Pulse amplitude V dependence of the domain wall velocity v estimated from the linear fitting of the data presented in (A). Symbols indicate results from films with different Gd concentrations. (C) The variance of bit position $∆{X_i}^2$ as a function of the average pulse number n(2i + 1)/2. N is fixed to 1000 and t = 2 ns. The shift pulse amplitudes V are shown in the legend. Results are obtained using the film with x = 30.5%. Lines show linear fits to the data for V = 14 V and 20 V. (D) The average bit size dependence of ∆v/v (V = 20 V, t = 2 ns, and N = 1000). Symbols indicate results from films with different Gd concentrations.

The open diamonds in Fig. 4B show the domain wall velocity v plotted as a function of pulse amplitude. v increases with pulse amplitude and then starts decreasing once it peaks. As reported previously, such change in v can be attributed to current-induced Joule heating (25, 29, 33). For SOT-driven domain wall motion in compensated ferrimagnets, v takes a maximum when the device temperature approaches the so-called spin angular momentum compensation temperature T_A (25, 32, 34–36). We infer that T_A is higher than room temperature because the alloy composition (x = 30.5%) is slightly rare earth (Gd) rich compared to the magnetization compensation point. Appropriate amount of current-induced Joule heating (33) can cause the device temperature to approach T_A, resulting in the maximum velocity. For a pulse amplitude of ~14 V (and a pulse width of 2 ns), the domain wall velocity reaches ~900 m/s.

We next study the variance of X_i ( ${\mathrm{\Delta }X}_i^2$ ) of the ith bit position.

$${\mathrm{\Delta }X}_i^2=\frac{1}{N}{\displaystyle \sum _{j=1}^N}{(X_{i,j}-X_i^{\text{av}})}^2$$ (1)

where X_{i, j} is the center position of the ith bit for the jth trial and $X_i^{\text{av}}$ is its average value among N trials. Here, we analyze data obtained from pulse amplitudes of 8, 14, and 20 V with N = 1000. We adjust the pulse number n such that the distance the domain walls move per one shift operation [processes (ii) and (iv)] becomes nearly the same for all amplitudes. This allows one to study the pulse amplitude dependence of the bit positioning error while keeping the bit size nearly the same. Here, the bit size is set close to 5 μm. Figure 4C shows the variance ${\mathrm{\Delta }X}_i^2$ plotted as a function of the average pulse number n(2i + 1)/2 . ${\mathrm{\Delta }X}_i^2$ increases linearly with n(2i + 1)/2 when V = 20 and 14 V, whereas it shows a nonlinear increase for V = 8 V.

First, we discuss the relation between ${\mathrm{\Delta }X}_i^2$ and the average pulse number. We consider ${\mathrm{\Delta }X}_i^2$ is caused by the writing and shifting processes. In the writing process, variation in the position of a domain wall, created by SOT-induced magnetization switching of the vertical line, contributes to ${\mathrm{\Delta }X}_i^2$ . For the shifting process, each current drive adds to ${\mathrm{\Delta }X}_i^2$ . Let us assume that the errors associated with the writing and shifting, including all successive drives, are uncorrelated. Under such assumption, the variance ${\mathrm{\Delta }X}_i^2$ of the ith bit position due to writing and shifting is given as

$${\mathrm{\Delta }X}_{\mathrm{i}}^2=\frac{{{\mathrm{\Delta }x}_{\mathrm{w}}}^2}{4}+\frac{n(2i+1)}{4}{(\mathrm{\Delta }\mathit{vt})}^2$$ (2)

where Δx_w is the variation in the domain wall position after the writing process and Δv is the variation in the domain wall velocity. See Materials and Methods for the details of the derivation of ${\mathrm{\Delta }X}_i^2$ . Equation 2 shows that, with no error correlation, ${\mathrm{\Delta }X}_i^2$ scales linearly with the average pulse number (2i + 1)n/2. We thus fit the experimental data, for the case of V = 20 and 14 V, with a linear function. The results, shown by the solid lines in Fig. 4C, agree well with the experimental data. This, in turn, shows that the error correlation among the writing and successive shifting processes are negligible for the stronger drives (V = 20 and 14 V). The slope and the y-axis intercept of the linear line are proportional to (Δvt)²/2 and ${{\mathrm{\Delta }x}_{\mathrm{w}}}^2$ , respectively. From the fitting, we obtain tΔv ~ 0.080 μm (0.11 μm) and Δx_w ~ 0.28 μm (0.26 μm) for V = 20 V (V = 14 V). We find that Δx_w is a few times larger than tΔv, suggesting that the positioning error caused by the writing is larger than that of the shifting error. Note that Δx_w should not depend on the shift pulse amplitude V. Δx_w shows similar values for the data obtained with V = 20 V and V = 14 V (and for V = 8 V if one extrapolates ${\mathrm{\Delta }X}_i^2$ to zero pulse number). The variation in bit position $\frac{t\text{∆}v}{\mathit{tv}}$ , which is equal to the variation in the velocity $\frac{\text{∆}v}{v}$ , is ~7.2% (6.2%) when V = 20 V (V = 14 V). $\frac{\text{∆}v}{v}$ does not show a significant change in this pulse amplitude range. When the shift pulse amplitude (V) is lowered to 8 V, ${\mathrm{\Delta }X}_i^2$ varies with the pulse number in a nonlinear fashion. Incidentally, the trend can be accounted for if error correlation among successive drives is considered. In Materials and Methods, the model on error analyses is extended to describe the case when the bit positioning errors are maximally correlated. Under such circumstance, ${\mathrm{\Delta }X}_i^2$ scales with the square of the average pulse number, consistent with the results obtained with V = 8 V. Fitting the data ( ${\mathrm{\Delta }X}_i^2$ ) with a parabolic function of the average pulse number, we obtain $\frac{\text{∆}{v}_{\mathrm{m}}}{v}~3.1\%$ , where ∆v_m is the variation of v when the errors are maximally correlated. $\frac{\text{∆}{v}_{\mathrm{m}}}{v}$ is smaller than $\frac{\text{∆}v}{v}$ obtained with larger pulse amplitude. The difference is intuitively expected for the two extreme cases (no error correlation versus maximum error correlation). However, further study is required to clarify the reason behind the difference and why the error correlation changes with the pulse amplitude. We infer that the latter is related to the change in the relative strength between the driving force and the pinning.

We next discuss the bit size dependence of ∆v/v. We fix the pulse amplitude to 20 V and varied the number of current pulses n. The average bit size is estimated using the Kerr microscopy images acquired. The average bit size dependence of ∆v/v is presented in Fig. 4D. Here, we include results from samples with different Gd concentrations (x = 30.5%, 31.4%, and 33.2%). The pulse amplitude dependence of the domain wall velocity for films with x = 31.4% and x = 33.2% is shown in Fig. 4B using green squares and red circles, respectively. The results show that ∆v/v is ~6% to 8% and does not change with the average bit size down to ~2.5 μm (the wire width is ~5 μm). Previous studies have shown that magnetic interaction among domain walls in ferromagnetic wires can cause inadvertent positioning error due to magnetic dipole interaction (37–39). In contrast, we infer that the small saturation magnetization and the weak stray field of the nearly compensated GdCoFe alloy allow little variation in ∆v/v against the average bit size.

Last, reliable motion of highly packed domain walls is essential for the operation of racetrack memory based on current-driven motion of domain walls. To this end, we show in the Supplementary Materials operations of a prototype racetrack memory using the devices formed in this study. The Kerr images obtained after bit writing and shifting operations are combined to create a movie. The results demonstrate reliable and highly reproducible operation of the memory device.

DISCUSSION

To develop a viable device, however, the bit positioning error must be substantially reduced. The error during the writing process can be mitigated by engineering the device structure. The SOT switching of the vertical line likely involves domain nucleation and domain wall propagation due to its large volume. As such process is typically stochastic, the position of the nucleated domain wall can vary from trial to trial. Removing the ferrimagnetic material from the arm of the vertical line may help improve the writing error as the switching process can be more deterministic for smaller size devices (40). We also note that during the writing process, a shunt current flows into the horizontal line. Assuming that SOT switching is fast and takes place within the duration of the current pulse, the position of the nucleated domain wall then depends on how fast magnetization reversal takes place as the remainder of the current pulse acts as a driving force to move the domain wall along the track (14, 37). If SOT-induced switching involves thermal activation, the time it takes to reverse the magnetization can vary from trial to trial, which can subsequently cause variation in the position of the nucleated domain walls and increase the bit positioning error. Minimizing current shunting into the track by engineering the circuitry of the device may help reduce the error.

For the shifting process, identifying the mechanism of domain wall pinning is important to lower the error. Structural inhomogeneity due to edge roughness and bulk defects as well as magnetic inhomogeneity induced by spatial variation of the Dzyaloshinskii-Moriya interaction (41) and magnetic anisotropy (42) may contribute to the pinning and become the source of bit positioning error. Engineering the film stacking is essential in addressing these issues. Further studies are required to clarify the relation between the bit positioning error and the pinning potential, including its depth and form (structural versus magnetic).

With regard to scaling of the bit positioning error, we note that the domain wall width of GdFeCo, estimated to be ~25 to 60 nm assuming an exchange stiffness constant reported in similar systems (43–45), is larger than that of typical ferromagnets. There are several factors that need to be considered for systems with a large domain wall width. The edge roughness of the wire can become an issue once the wire width is reduced to a length scale comparable to the domain wall width. In ferromagnetic materials, current-induced domain wall motion was observed in wires down to sub–100-nm width (15). It remains to be seen whether the edge roughness plays any role in defining the bit positioning error. Similarly, the nature of interaction among neighboring domain walls may change once the distance between them is reduced close to the domain wall width. Whether the bit positioning error shows little dependence on the average bit size, even for such highly packed exchange coupled systems, is an issue that needs to be clarified.

In summary, we have studied the bit positioning error in a ferrimagnetic racetrack composed of Pt/GdFeCo bilayers. The positioning error of the domain walls is estimated using thousands of Kerr microscope images. In a ~5-μm wide wire, we find that the writing process, the SOT-induced magnetization switching, causes a positioning error of ~0.3 μm whereas the shifting process using a 2-ns-long current pulse induces a positioning error of ~0.1 μm per pulse: The corresponding variation in the domain wall velocity is ~6 to 8%. Variation in the velocity is independent of the magnetic bit size down to ~2.5 μm. We find that the error correlation among successive shifting processes is negligible when the current drive is sufficiently large. These features allow reliable motion of highly packed domain walls in a ferrimagnetic racetrack, laying the foundation for developing storage class memory devices.

MATERIALS AND METHODS

Estimation of current density

The current density that flows in the wire is calculated from the pulse amplitude and the device resistance. Here, we assume all current flows into the Pt layer. The actual current density is smaller because a fraction of current flows into the other conducting layers. For the current that flows along the horizontal line, a pulse amplitude of V = 20 V corresponds to J = 4 × 10⁸ A/cm². Similarly, a pulse amplitude of V_w = 28 V gives J_w = 5.5 × 10⁸ A/cm² when the pulse is applied along the vertical line. In calculating J_w, we do not take into account current shunting into the horizontal line. As the resistance of the horizontal line is roughly five times larger than that of half the vertical line, approximately one-sixth of the current flows into the horizontal line when a current pulse is applied to the vertical line.

Image analyses

We use a 20× objective lens with a charge-coupled device camera to capture Kerr images. The camera (imi-tech, IMB-15FT) records data in a 12-bit image format (4096 tones) with 1032 × 776 pixels. Through a 20× objective lens, the area captured by the camera is ~271 × 204 mm². One image pixel therefore corresponds to an area of ~0.26 × 0.26 μm². We use image recognition tools to extract the wire from the entire image. The position of a domain wall is determined using the extracted image. We take the line profile of the Kerr signal along the wire. The line profile is averaged across the width of the wire. To avoid having topographical contributions from the edges of the wire on the Kerr signal, the averaging is taken for roughly 50% of the wire width, which corresponds to 8 to 9 pixels. We take the space derivative of the averaged line profile, in which a domain wall appears as a peak or dip. The position where the maximum (for the peaks) or the minimum (for the dips) Kerr signal is found is assigned as the center of a domain wall.

It must be noted that the sample stage slightly drifts during the measurements, primarily due to thermal effects (e.g., slight change in the room temperature). In addition, application of a magnetic field (H_y) to the sample causes shifting of the image due to magnetic components in the objective lens and other parts of the setup. (H_y ~ + 500 Oe and H_y ~ −500 Oe are applied alternately in the writing process, see Fig. 2.) Although these effects are small, the origin of the image, defined by the image extraction process, can vary from image to image within one pixel. To accurately determine the position of the domain walls, we attempt to remove these effects by subtracting long-term drifts and alternating shifts of the origin. We first separate the images into even and odd trial groups, where each group represents states under writing with H_y ~ + 500 Oe and H_y ~ −500 Oe, respectively. Within each group, we plot the domain wall position over the trial number. The domain wall position varies over time due to thermal drift of the sample stage (the overall change is smaller than one pixel). In many cases, the drift causes linear change in the domain wall position against the trial number. We thus fit a linear line to subtract the drift effect. The variance of the domain wall position is calculated using the background subtracted data. This process is carried out for both even and odd trial groups and their variance ( $\mathrm{\Delta }{X}_{i,\text{even}}^2$ and $\mathrm{\Delta }{X}_{i,\text{odd}}^2$ ) are added, that is, $\mathrm{\Delta }{X}_i^2=\mathrm{\Delta }{X}_{i,\text{even}}^2+\mathrm{\Delta }{X}_{i,\text{odd}}^2$.

Error analyses: No error correlation

The SD of the position of the ith bit is given as

$$∆X_i=\sqrt{\frac{1}{N}{\displaystyle \sum _{j=1}^N}{[\frac{1}{2}(x_{i,j}+x_{i+1,j})-\frac{1}{2}({\overline{x}}_i+{\overline{x}}_{i+1})]}^2}$$ (3)

where x_{i, j} and x_i+1,j are the position of the domain walls that form the ith magnetic bit. As described in Fig. 2, we first apply a current pulse along the vertical line to create a domain wall (say, an up-down domain wall) at the intersection of the horizontal and vertical lines. We denote its position as x_w1,j. Subsequently, current pulses of width t are applied along the horizontal line for ni times to move the domain wall into the track. Next, a current pulse is passed along the vertical line and a domain wall (here, a down-up domain wall) is created at the intersection of the horizontal and vertical lines, which we label as x_w2,j. Again, current pulses of width t are applied along the horizontal line for ni times. We define the positions of the first domain wall (the up-down domain wall) and the second domain wall (the down-up domain wall) as x_{i + 1,j} and x_i,j, respectively, because they experienced n(i + 1) and ni current pulses. The index j represents the trial number, which runs from 1 to N. ${\overline{x}}_i$ [ ${\overline{x}}_{w1(2)}$ ] is the average value of x_i,j [x_w1(2),j] for all the N trials. We define the domain wall velocity of the lth current pulse at the jth trial as v_l,j and the average of the N trials as ${\overline{v}}_l$ . x_{i + 1,j}, x_i,j, ${\overline{x}}_{i+1}$ , and ${\overline{x}}_i$ can be expressed as

$$x_{i+1,j}=x_{\mathrm{w}1,j}+{\displaystyle \sum _{l=1}^{n(i+1)}}t{v}_{l,j}, {\overline{x}}_{i+1}={\overline{x}}_{\mathrm{w}1}+{\displaystyle \sum _{l=1}^{n(i+1)}}t{\overline{v}}_l$$ (4)

$$x_{i,j}=x_{\mathrm{w}2,j}+{\displaystyle \sum _{l=1}^{\mathit{ni}}}t{v}_{l,j},{\overline{x}}_i={\overline{x}}_{\mathrm{w}2}+{\displaystyle \sum _{l=1}^{\mathit{ni}}}t{\overline{v}}_l$$ (5)

Substituting Eqs. 4 and 5 into Eq. 3, we obtain

$$∆X_i=\sqrt{\frac{1}{N}{\displaystyle \sum _{j=1}^N}{\left[\frac{1}{2}\left\{(x_{\mathrm{w}1,j}-{\overline{x}}_{\mathrm{w}1})+(x_{\mathrm{w}2,j}-{\overline{x}}_{\mathrm{w}2})+t{\displaystyle \sum _{l=1}^{\mathit{ni}}}(v_{l,\mathrm{j}}-{\overline{v}}_l)+t{\displaystyle \sum _{l=1}^{n(i+1)}}(v_{l,j}-{\overline{v}}_l)\right\}\right]}^2}$$ (6)

We may assume

$${\displaystyle \sum _{j=1}^N}(v_{l,j}-{\overline{v}}_l)(x_{\mathrm{w}1,j}-{\overline{x}}_{\mathrm{w}1})=0$$ (7)

$${\displaystyle \sum _{j=1}^N}(v_{l,j}-{\overline{v}}_l)(x_{\mathrm{w}2,j}-{\overline{x}}_{\mathrm{w}1})=0$$ (8)

if there is no error correlation among current-induced domain wall motion and SOT-induced magnetic reversal, and

$${\displaystyle \sum _{j=1}^N}(x_{\mathrm{w}1,j}-{\overline{x}}_{\mathrm{w}1})(x_{\mathrm{w}2,j}-{\overline{x}}_{\mathrm{w}2})=0$$ (9)

if the error correlation among SOT-induced magnetic reversals can be neglected.

Under these approximations, Eq. 6 can be expressed as

$$\begin{array}{c}∆X_i\approx \left\{\frac{1}{4N}{\displaystyle \sum _{j=1}^N}\left[{\left(x_{\mathrm{w}1,j}-{\overline{x}}_{\mathrm{w}1}\right)}^2+{\left(x_{\mathrm{w}2,j}-{\overline{x}}_{\mathrm{w}2}\right)}^2+{\left[t{\displaystyle \sum _{l=1}^{\mathit{ni}}}\left(v_{l,j}-{\overline{v}}_l\right)\right]}^2\right]\right.\\ {\left.+{\left[t{\displaystyle \sum _{l=1}^{n\left(i+1\right)}}\left(v_{l,j}-{\overline{v}}_l\right)\right]}^2+2\left[t{\displaystyle \sum _{l=1}^{\mathit{ni}}}\left(v_{l,j}-{\overline{v}}_l\right)\right]\left[t{\displaystyle \sum _{l^{\prime }=1}^{n\left(i+1\right)}}\left(v_{l^{\prime },j}-{\overline{v}}_l\right)\right]\right\}}^{\frac{1}{2}}\end{array}$$ (10)

If there is no error correlation among successive drives, we may assume

$${\left[{\displaystyle \sum _{l=1}^{\tilde{n}}}(v_{l,j}-{\overline{v}}_l)\right]}^2\approx {\displaystyle \sum _{l=1}^{\tilde{n}}}{(v_{l,j}-{\overline{v}}_l)}^2$$ (11)

where $\tilde{n}=\mathit{ni}$ or $\tilde{n}=n(i+1)$ , and

$$\left[{\displaystyle \sum _{l=1}^{\mathit{ni}}}(v_{l,j}-{\overline{v}}_l)\right]\left[{\displaystyle \sum _{l\prime =1}^{n(i+1)}}(v_{l\prime ,j}-{\overline{v}}_l)\right]=0$$ (12)

Furthermore, we may set

$$\begin{array}{c}\mathrm{\Delta }v\equiv v_{l,j}-{\overline{v}}_l\\ {\mathrm{\Delta }x}_{\mathrm{w}1}\equiv x_{\mathrm{w}1,j}-{\overline{x}}_{\mathrm{w}1}\\ {\mathrm{\Delta }x}_{\mathrm{w}2}\equiv x_{\mathrm{w}2,j}-{\overline{x}}_{\mathrm{w}2}\end{array}$$ (13)

if correlation of errors can be neglected. Substituting Eqs. 11 to 13 into Eq. 10, we obtain

$$∆X_i=\sqrt{\frac{{{\mathrm{\Delta }x}_{\mathrm{w}1}}^2+{{\mathrm{\Delta }x}_{\mathrm{w}2}}^2}{4}+\frac{n(2i+1)}{4}{(\mathrm{\Delta }\mathit{vt})}^2}$$ (14)

We define the variance attributed to the SOT writing as ${{\mathrm{\Delta }x}_{\mathrm{w}}}^2={{\mathrm{\Delta }x}_{\mathrm{w}1}}^2+{{\mathrm{\Delta }x}_{\mathrm{w}2}}^2$. The variance of the ith bit position $\left({\mathrm{\Delta }X}_i^2\right)$ can be expressed as

$${\mathrm{\Delta }X}_i^2=\frac{{{\mathrm{\Delta }x}_{\mathrm{w}}}^2}{4}+\frac{n(2i+1)}{4}{(\mathrm{\Delta }\mathit{vt})}^2$$ (15)

Error analyses: Maximal error correlation

We continue to use the approximation that there is no error correlation among current-induced domain wall motion and SOT-induced magnetic reversal. However, we now assume that the errors among successive current drives are maximally correlated. Under such assumption, Eq. 11 is modified as the following

$${\left[{\displaystyle \sum _{l=1}^{\tilde{n}}}(v_{l,j}-{\overline{v}}_l)\right]}^2\approx {[\tilde{n}\mathrm{\Delta }{v}_{\mathrm{m}}]}^2={\tilde{n}}^2\mathrm{\Delta }{v}_{\mathrm{m}}^2$$ (16)

where $\mathrm{\Delta }{v}_{\mathrm{m}}\equiv v_{l,j}-{\overline{v}}_l$ represents the variation in v when the shifting errors are maximally correlated. Similarly, Eq. 12 changes to

$$\begin{array}{c}\left[{\displaystyle \sum _{l=1}^{\mathit{ni}}}(v_{l,j}-{\overline{v}}_l)\right]\left[{\displaystyle \sum _{l\prime =1}^{n(i+1)}}(v_{l\prime ,j}-{\overline{v}}_l)\right]\hfill \\ \approx [\mathit{ni}\mathrm{\Delta }{v}_{\mathrm{m}}][n(i+1)\mathrm{\Delta }{v}_{\mathrm{m}}]=n^{2}i(i+1)\mathrm{\Delta }{v}_{\mathrm{m}}^2\hfill \end{array}$$ (17)

Substituting these relations into Eq. 10, we obtain

$$∆X_i=\sqrt{\frac{{{\mathrm{\Delta }x}_{\mathrm{w}1}}^2+{{\mathrm{\Delta }x}_{\mathrm{w}2}}^2}{4}+\frac{n^2{(2i+1)}^2}{4}{(\mathrm{\Delta }{v}_{\mathrm{m}} t)}^2}$$ (18)

Again, setting ${{\mathrm{\Delta }x}_{\mathrm{w}}}^2={{\mathrm{\Delta }x}_{\mathrm{w}1}}^2+{{\mathrm{\Delta }x}_{\mathrm{w}2}}^2$, the variance of the ith bit position $\left({\mathrm{\Delta }X}_i^2\right)$ can be expressed as

$${\mathrm{\Delta }X}_i^2=\frac{{{\mathrm{\Delta }x}_{\mathrm{w}}}^2}{4}+\frac{n^2{(2i+1)}^2}{4}{(\mathrm{\Delta }{v}_{\mathrm{m}} t)}^2$$ (19)

We thus find that ${\mathrm{\Delta }X}_i^2$ scales with n²(2i + 1)² if the errors among successive current drives are maximally correlated.

Supplementary Materials

The PDF file includes:

Legend for movie S1

Other Supplementary Material for this manuscript includes the following:

Movie S1