Abstract
The current exponential growth of solar electricity technologies toward consumer-oriented applications, as in building- or vehicle-integrated photovoltaics (B/VIPV), is calling for improved solar cells, not only in cost-effectiveness, but also with better adaptability and aesthetics. Here, using perovskite solar cells (PSCs) as test bed, we demonstrate an unprecedented photonic method to generate any color on a cell layout, while also increasing PV efficiency. To this end, photonic surface features were designed for PSCs, which filled the dual purpose of light-trapping (LT) and modulation of reflected light interference. A variety of geometries, from simple gratings to complex semispheroids, were optically optimized for two of the most challenging colors, magenta and green, while assuring the generation of their maximum feasible photocurrent. The best results corresponded to a current density of 22.07 mA/cm2, obtained for the magenta solar cell with top domes, exhibiting an increase of 6.68%, relative to an optimized planar reference cell. In turn, the same type of geometry was able to generate the leading green cell, with up to 21.40 mA/cm2 (a relative increase of 3.44%). Additionally, the uniformity of the optical output of the optimal solar cells was tested under a range of incident light angles, between 0◦ and 60◦, where the current density suffered relative losses only down to 6.65%.
1. Introduction
The current unsustainable energy consumption of society paved the way to new clean and unlimited energy sources. Notably, within the solar electricity sector, highly efficient colored solar cells have received considerable attention for a variety of consumer-oriented products. By combining solar panels with building infrastructures (BIPV), vehicles (VIPV), light-powered Internet-of-Things (IoT) and wearable PVs, it is possible to increase the harnessing potential of solar energy in everyday utilities. To further improve the appeal of these technologies, two main characteristics must be considered: the power output (a common merit quantity in photovoltaics) and the aesthetics, highly valued by the product/installation designers and consumers.1−5
Colored PV typically implies power losses, since the needed reflection, responsible for the solar cell chroma, cannot be used for electric current generation. Several light management techniques have been proposed to minimize current losses while maintaining a degree of structural color. The device color is then a byproduct of the structurally generated reflection peaks that result from the constructive interference of light redirected outward the cell.5−14 Thus, by modifying the respective layout, it is possible to tune the color of the cell, while avoiding the parasitic absorption associated with traditional coloring methods, such as dyes and pigments.5 To exemplify, structural color has been achieved by implementing photonic crystals, where the manipulation of the refractive indices of the materials affect the wavelength and width of the reflection peaks.11,12,15 Similarly, plasmonic nanoresonators are an alternative color generation method, as modulating the size and shape of the metallic structures can be used to tune angle-insensive colors.5,9,10,16 Structural color customization provided by the adjustment of planar antireflection coatings (ARCs) is also a widely researched topic, as their thickness and refractive index control the interference and superposition of the light that is reflected and transmitted in each layer.5,6,8,16,17
Despite the ability to generate a variety of colors, the previous methods have some drawbacks related to significant optical losses caused by a variety of phenomena, namely devaluation of the antireflection potential, parasitic absorption and high sensitivity of color and current density to the angle of light incidence. Advanced light management via front lossless nanopatterned arrays of wavelength-sized features can both generate color and enhance the optical behavior of the cell via light-trapping (LT), thus surpassing most of the above-mentioned issues.5,18 These structures promote forward scattering and longer effective optical path lengths within the absorber material, increasing the absorption in the near-infrared (NIR) region of the spectrum.5,17−21 These LT designs also contribute to broadband antireflection, by forming a continuous refractive index gradient between the air and the cell front, thus increasing the absorption mainly in the ultraviolet (UV) and visible (VIS) bands. Additionally, if appropriately tuned, surface structure arrays can enable the reflection of narrow peaks in the visible spectrum, with minimal broadband losses.5 As such, it is possible to grant structural color at specific wavelengths while boosting broadband photocurrent, thus making this a promising approach for high-performance colored solar cells.
In recent years, perovskite solar cells (PSCs) have stood out: despite stability issues, difficulty in upscaling its production and negative environmental impacts of its lead content, their low thickness and compatibility with a diverse assortment of flexible substrates make PSCs an interesting choice for the combination of colored cells with consumer products, or even construction materials.5,16,22−24 State-of-art PSCs have displayed substantial growth in performance in the past decades, particularly those made by CH3N3PbI3 (or MAPbI3) semiconductor which have reached 21% efficiencies,25−29 while the present record is at 26.54% with FA0.95Cs0.05PbI3 perovskites, showing great promise in the future PV market.30
A variety of photonic structures have been tested on PSCs, exhibiting pronounced efficiency improvements.5,17−20,31,32 These include 1D, 2D gratings17,20 and nanopillars,20 but also more complex geometries, such as checkerboard patterns,17 domes, voids,18,33 cones and pyramidal configurations.20 Regarding their material, dieletrics with high refractive index, n, and low extinction coefficient, k (oftentimes TiO2) promote intense forward scattering of low-energy photons, block harmful UV penetration toward the perovskite layer and exhibit low parasitic absorbance in the visible and near-infrared regions.18,33 However, these materials exhibit low electrical conductivity, that can deteriorate the electrical properties of the front contact, and thus the device efficiency.34 To overcome this issue, some studies select the same material to compose both the front contact and LT layers, particularly transparent conductive oxides (TCO), thereby creating photonic-structured transparent contacts.35
This work tested color output and optical absorption of LT-enhanced PSCs employing a photonic-structured front contact made of ITO (indium tin oxide), for different structural complexity levels: 1D linear grating lines, 2D crossed grating lines, checkerboards, squared and circular nanopillars and dome arrays, as illustrated in Figure 1b–f. The geometrical features of each structure were first studied to provide insight on how the shape and geometry affects the color and LT capacity. Then the different structures were optimized, considering the objective of generation of a specific color—namely magenta or green—while keeping an effective light absorption performance. The solar cells with surface domes presented the best results, for both chromaticities, recording current density values of 22.07 mA/cm2 (increase of 6.68%, relative to an optimized planar reference cell) and 21.40 mA/cm2 (relative increase of 3.44%), for magenta and green, respectively. From here, the cells’ angular performance was also evaluated, where the planar cells showed the best angular uniformity in coloration.
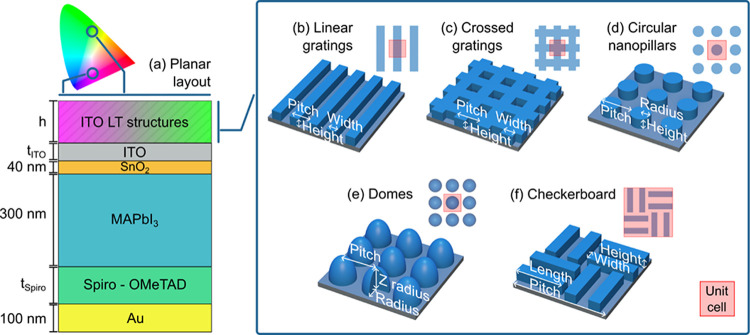
Figure 1.
(a) Layout of the planar configuration of the perovskite solar cells and placement of the LT structures, later adapted to generate magenta or green chromaticities (Section 2.3). (b)–(f) Schematics of the light-trapping structures simulated in this study with respective geometrical variables and simulation unit cells (red area): 1D linear grating lines, 2D crossed grating lines, circular nanopillars, domes and double checkerboards. As a side note, the length of the checkerboard is mentioned in most of the following results, rather than the pitch, for a clearer geometrical comparison to the pitch of the remaining structures.
While this work emphasizes the theoretical aspects of light-trapping structures for light capture and color generation, the studied configurations are feasible for future experimental applications. Among various nano/micropatterning methods, scalable soft-lithography techniques like UV-nanoimprint lithography,36 colloidal lithography (CL),21,37,38 and thermal nanoimprint39 are capable of producing the microstructures designed in this study. CL stands out due to its low cost and nanoscopic precision over large areas, with a typical resolution in the tens of nanometers, aligning well with the structures considered here.
2. Results
Figure 1a depicts the layout of the solar cell configurations of this study, composed of different planar layers, from bottom to top: a rear reflective gold electrode (100 nm thickness), a Spiro-OMeTAD hole transporting layer (varying thickness, 100 nm–200 nm), a MAPbI3 absorbing layer (300 nm thickness), a SnO2 electron transporting layer (40 nm thickness) and an ITO transparent electrode (varying thickness, 50 nm–250 nm). The ITO light-trapping features are located on top of the flat ITO layer over the cell. These were designed and optimized using the Ansys Lumerical software. A variety of geometries were applied to the photonic structures, as seen in Figure 1b–f, along with their relevant dimensional parameters: pitch/length, width/radius and height/Z radius. For the case of the particular checkerboard structure in Figure 1f, the variation of the results with the array periodicity is presented as a function of the features’ length, instead of the full pitch as performed for the other cases, in order to allow a clearer geometrical comparison betweeen all the structures.
A series of analyses was performed in this study, to understand how different photonic structures affect the optical mechanisms that generate structural color in the test devices. To this end, the chromaticity and optical performance (short-circuit current density values, calculated according to eq 5—see Methods section) were tested for a variety of geometries, symmetries and sizes (analyzed in Section 2.2), to further conclude how these aspects impact the quality of the colored solar cells.
Following the optimization of the structures in Figure 1 for an assortment of colors (results exhibited in Section 2.3), the optimal solar cells were then subjected to different light source angles (0◦–60◦), where the uniformity and stability of the merit quantities—JSC and RGB—were put to test (explored in Section 2.4).
2.1. Planar Configuration and Reference Cell
In this section we start by analyzing the flat cell configuration (Figure 2a), to understand the impact of the ITO and Spiro thicknesses on the optical properties of the device, namely color and JSC. This configuration will also be used henceforth as a reference for comparison with the structured devices.
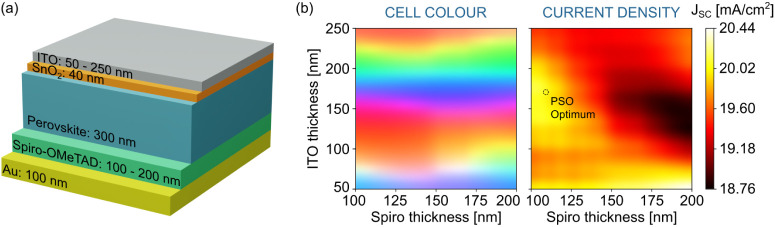
Figure 2.
(a) Illustration of the planar layers of the cell, as well as their fixed/ranged thicknesses: rear gold reflector, Spiro-OMeTAD hole transporting layer, Perovskite layer, SnO2 electron transporting layer and the top ITO electrode. The ITO and Spiro thicknesses are defined as optimization variables. (b) Chromaticity, left, and current density, right, profiles of the planar configuration of the solar cells, for a range of ITO and Spiro-OMeTAD thickness values. The current density profile highlights the optimal point, attained by Particle Swarm Optimization.
Figure 2b shows the chromaticity and JSC, changing ITO and Spiro thicknesses. It is evident that the ARC layer (ITO) height is the main factor affecting the cell chromaticity, due to the horizontal color streaks in the left contour plot. These results are justified by the prominent impact of the ARC layer thickness on the cell reflection and the constructive interference directed outward the cell. Remarkably, this effect seems less significant for lower ITO thicknesses (<125 nm). This may result from the higher transmission of light to the solar cell, thence increasing the impact of the other layers on the color. Nonetheless, the optical output of the flat cell revealed that the current density was heavily influenced by the thickness of both planar layers, as seen on the right contour plot of Figure 2. According to the patterns in the profiles, it is possible to select the ITO thickness to tune the color of the cell and to select the Spiro thickness to maximize the corresponding current density.
Subsequently, the flat configuration was optimized to determine a maximum JSC, employing the Particle Swarm Optimization (PSO) method, for the same variable ranges of the parameter sweeps of Figure 2. This algorithm determines the optimum parameter set by iteratively improving potential solutions (particles) with the intent to maximize the figure of merit within the search space defined for the variables (this process is further described in the Methods section). The PSO algorithm converged to the optimal layout marked in the JSC contour plot, delivering up to JSC = 20.69 mA/cm2, for ITO and Spiro thicknesses of 168.58 and 108.33 nm, respectively. This particular solar cell will be mentioned throughout this work as a planar reference, serving as a baseline comparison for the optical performances of the photonic-managed cells.
2.2. Photonic Geometries
This section explores the impact of the light-trapping structures, shown in Figure 1, on the optical performance of the solar cells. Figure 3 shows the cell color (top heatmaps) and photocurrent (bottom heatmaps) for the different studied structures, namely (a) linear grating lines, (b) double-checkerboards, (c) crossed gratings, (d) nanopillars and (e) prolate semispheroids (referred as domes).
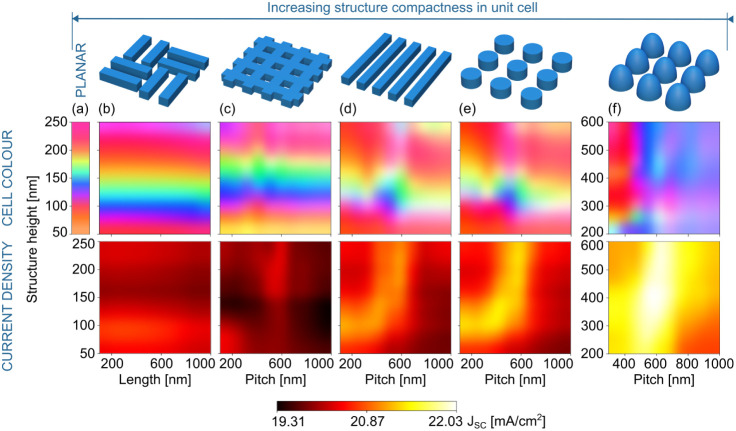
Figure 3.
Chromaticity (top plots) and photocurrent density (bottom plots) for different combinations of pitch and grating height (grating widths fixed at 0.5, checkerboard width at 0.3 and radii at 0.4) for a variety of LT structures: (b) checkerboards (c) crossed gratings, (d) linear gratings, (e) circular nanopillars, (f) domes (latter two in square symmetry layout) and (a) equivalent flat ITO layer. The volume in unit cell increases from domes to pillars, to linear gratings, to crossed gratings, to checkerboards and to flat configuration.
Initially, two nanopillar shapes were tested, circular and squared, which showed identical chromaticity and JSC, for various sizes (further analysis in S2 and Figure S5). As such, it was deemed unnecessary to study both shapes, only circular nanopillars are addressed here, as their radial symmetry provides higher accuracy in the simulation results. Additionally, two different array symmetries were applied to nanopillars and domes: square and hexagonal layout symmetries. Numerous studies have proven that LT features arranged in hexagonal arrays result in significant optical advantages, namely higher JSC values.5,18,33 However, its unit cell is rather bigger than its alternative square symmetry, leading to a notable increase in simulation time. Differences in the merit quantities were observed for different symmetries, but regarded as minor. Accordingly, this work solely addresses these structures in squared arrays, to minimize computational resources. The corresponding results can be observed in Figure S6.
The geometry of the structures exhibited strong impact on the chromaticity and current density. The screening of the relevant dimensional parameters, indicated in Figure 1b, resulted in the RGB and JSC profiles of Figures 3 and 4.
Figure 4.
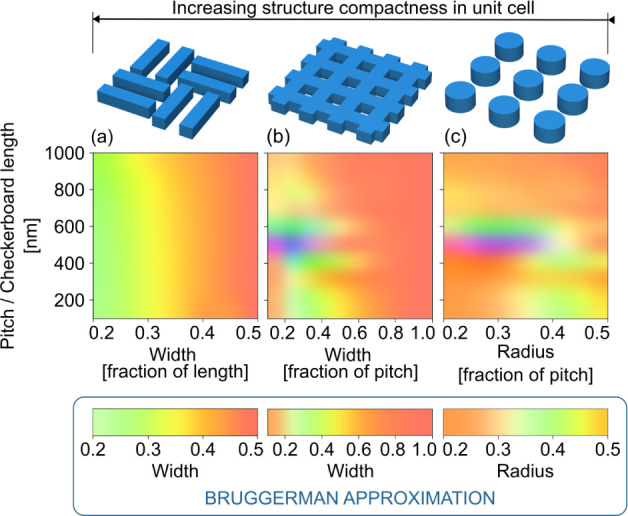
Chromaticity spectra for different combinations of pitch and width/radius (structure height fixed at 100 nm) for a variety of LT structures: (a) checkerboards, (b) crossed gratings and (c) circular nanopillars in square symmetry. The volume in unit cell increases from pillars, to crossed gratings and to checkerboards. The chromaticity of the cells in planar configuration with a top layer with the equivalent refractive index of the photonic layer (obtained by the Bruggerman approximation) is illustrated below.
The chromaticity graphs of Figure 3 reveal that the reflected coloration has a notably more significant correlation with the height of the structures than with the pitch/length, as most of the parameter sweeps display horizontal-leaning streaks of color. This height/color association is most prominent in the checkerboard features and in crossed gratings, followed by linear gratings and circular nanopillars (seen in Figure 3b–e). Moreover, when comparing these results to a planar solar cell, similar hues were obtained for height-equivalent flat ITO thicknesses (seen in Figure 3a). By analyzing these results, it is visible that, as the structures become denser in the unit cell (higher ratio of structure volume per unit cell), the chromaticity becomes less dependent on the geometry of the photonic structure itself, and more dependent on interfacial reflections (or layer thicknesses). This tendency can be explained by the dependency of the interference of the reflected light on the effective refractive index of the structured layer. Notably the dome structures (Figure 3e) do not follow this pattern. We believe this is a result of the rounded shape, that enforces a gradual geometrical index matching, thus reducing light reflection.
To evaluate the impact of the structures’ density, we simulated a planar solar cell configurations in which the front structured layer is replaced by an homogeneous flat layer having the same effective refractive index as the LT layer (approximated via the Bruggerman method).40 Here, the width/radius of the structures define the density used in the model. Figure 4 presents this comparison, tested for checkerboard, crossed grating and circular nanopillar shaped features. As the structures’ compactness increases in the unit cell, the effective index of the structured layer has an increasing impact on the color attribution throughout different shape dimensions (pitch, width and radius), as seen by the resemblance of the Bruggerman contours (considering a flat effective-index front layer) with those of the photonic-structured layers. This effect is more pronounced in checkerboards (most dense structure, presenting no chromaticity alteration in pitch), followed by crossed gratings and then nanopillars.
The photocurrent output of the photonically managed test devices was also evaluated. The most optically favorable photonic structures are domes, reaching 22.03 mA/cm2 in the profile of Figure 3f—as expected, since their gradually increasing effective refractive index is a strong contributor for light in-coupling (antireflection), while their resonant particle shape provides strong scattering cross sections. As depicted in Figure 3, the pitch/length and height of the designed structures have a strong impact on the JSC values, as well as the width/radius (results shown in Figure S7). This adds to the complexity of the search space to be defined for the Figure of Merit (FoM) function, highlighting the need for a thorough optimization process and subsequent optical analysis. However, the current density spectra of the solar cells with checkerboards appear to differ from the remaining profiles, as the structures’ length has little effect on this attribute. Such profile may result in poor search spaces, where the JSC factor is not as easily articulated by different geometry sizes as the chromaticity.
2.3. Optimization Results
The enhancement of the current density and the color modulation of the device were achieved by tuning the geometrical parameters of the solar cells. This optimization required the conceptualization of a Figure of Merit (FoM), to assess the broadband absorption quality of the solar cells and their color. Respectively, two merit quantities were defined: the current density generated in the perovskite layer and the euclidean distance between the RGB coordinates of the desired color, (R,G,B), and the color of the cell with the set of parameters of the PSO iteration, (r,g,b) (eq 1).
| 1 |
Besides the implementation of these two variables in the FoM, a “limitRGB″ factor was also considered to represent the human eye sensitivity to similar hues (eq 2). Figure 5a shows changes in hue for different color distances (0, 10, 15, 20, and 30). It is clear that, below RGB distances of 15, the actual change in perceived hue is quite small and can thus be ignored. This parameter enables the tolerance of an RGB subspace, sufficiently identical to the ideal chromaticity, to be viewed as optimal by the FoM, hence broadening the search space maxima peaks and facilitating their detection during the PSO. Accordingly, the FoM, within the “limitRGB″, is defined by solely the JSC value—meaning it is always within the wanted color—while outside, it adds a factor to account for and minimize the color distance.
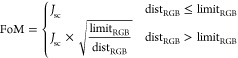 |
2 |
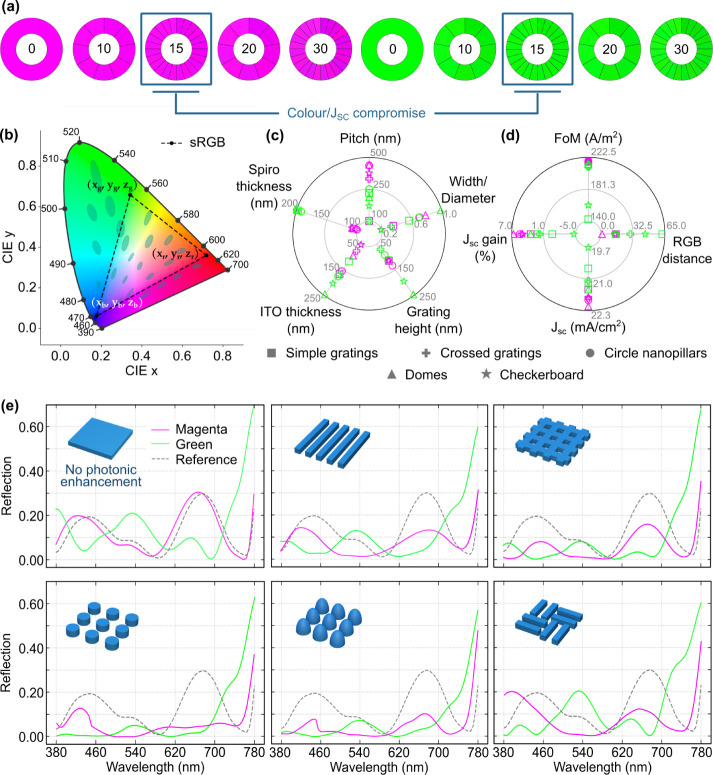
Figure 5.
(a) Chromaticity wheels at an assortment of RGB distances from magenta (255, 0, 255) and green (0, 255, 0) (defined by eq 1), between 0 and 30, indicated at the center of each wheel. (b) 1931 CIE color gamut, with respective wavelengths shown around the outline. The dashed triangle represents the standardized RGB (sRGB) area of the gamut, which was adopted in this work; its vertices (located in the green, red and blue region) are represented as (x,y,z) coordinates. The oval highlights are the MacAdam ellipses—areas where the human eye cannot perceive the different colors (for better visualization, the ellipse sizes are amplified by 10 times). (c) Optimal geometrical parameters of magenta and green solar cells with photonic-enhancing structures: simple gratings, crossed gratings, circle nanopillars, domes and checkerboards (values in Table S3). (d) Figure of merit maxima (as defined by eq 2) attained by particle swarm optimizations and corresponding cell merit quantities: RGB distance (determined by eq 1), JSC and respective gain, relative to the reference cell. The color of the markers corresponds to the cell chromaticity (Table S4). (e) Reflection spectra of the optimal magenta and green solar cells with and without photonic structures, along with the reference spectrum. The colors of the line plots correspond to the cell chromaticities.
Various expressions were tested as figure of merit, from which eq 2 was selected. This process is explained in S3.
The photonic structures were optimized for two different colors: magenta (RGB = (255, 0, 255)) and green (RGB = (0, 255, 0)). By selecting these colors, the reflection peaks of all primary colors of the standardized RGB (sRGB) color system were explored. Magenta results from the combination of red and blue colors, and thus requires the solar cell geometry to search, simultaneously, for the distinct reflection peaks of both these colors. Green assesses the adequacy of the model to consider color at the peak of the solar spectrum, thus being the most difficult case for photocurrent enhancement. By choosing this approach, this work is focused on challenging the method, while minimizing the amount of required simulations.
This section exhibits the optimal geometries of the solar cells and photonic structures, to display magenta and green hues, as well as the corresponding optimization parameters, FoM, JSC and chromaticity.
The variable ranges introduced in the PSO algorithm to optimize the planar and photonic-enhanced solar cells are detailed in S4. These intervals were selected based on preliminary studies of the FoM function in extended search spaces. The value assortments for each variable are similar for all structures to ensure the correct conditions for accurate comparisons. The ranges are extensive due to the complexity of the search space and the large amount of parameters. For this reason, some restrictions were applied to the variables. Namely, the width or radius of the photonic structures are defined in units of the pitch, to avoid extreme size aspect ratios. The possible impediment of the best convergence of the particles, combined with the stochastic nature of the algorithm, prompted the need to perform multiple optimizations for each cell layout. The optimal geometrical parameters of each process are in Section S4.
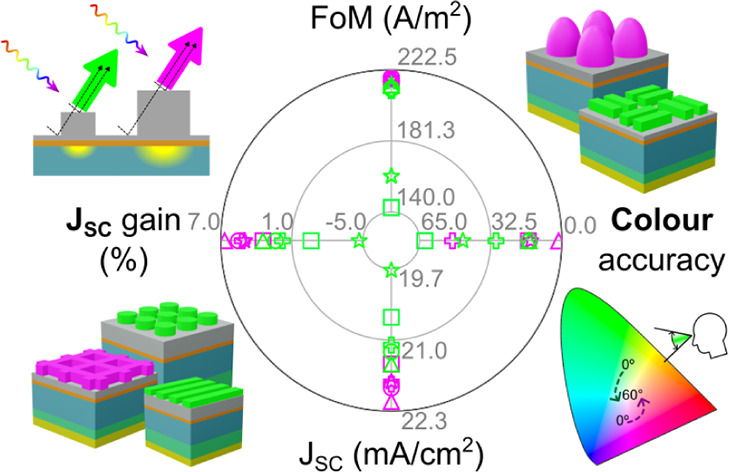
The optimal geometrical parameters of the magenta and green photonic-enhanced cells are summarized in Figure 5c, and the optimization results are shown in Figure 5d (FoM, RGB distance, JSC and respective gain, relative to the reference cell). As a note, the FoM values in this work are expressed in SI units of photocurrent density A/m2, which assists in distinguishing them from the JSC values commonly expressed in mA/cm2.
The top FoM values attained in the optimization of the magenta and green solar cells, with and without the photonic structures, can be seen in Table S4, along with the corresponding cell chromaticity, in RGB code, and JSC. Moreover, proportionally accurate schematics of the optimized solar cells are seen in Table S3, for better comparative analysis.
To further understand the process of color generation, Figure 5e contains the reflection spectra of the optimal solar cells, to assess the peaks that confer green chromaticity (in the wavelength band between 495 and 570 nm) and magenta (a peak in the blue band, 450 nm–495 nm, and another in the red band, between 620 and 750 nm). The reflection of the reference cell is also present, to ascertain the optical response inherent to the presence of the photonic structures.
The lower FoM and JSC values and the higher RGB distance correspond to the flat solar cells (results present in Table S4), indicating a clear underperformance of the planar configurations. This was expected, chiefly because the planar solar cells do not take advantage of the broad antireflection effects provided by the structured layer, resulting in more prominent reflection peaks in the visible band. The presence of the photonic structures is proven to be a vital asset to color attribution to solar cells, since the merit properties excelled for most of these configurations—higher FoM values were obtained and the JSC gain was mostly positive while guaranteeing the selected coloration. When the optimization of the colored cells with LT features results in higher JSC than the reference, 20.69 mA/cm2, it is assumed that the generation of color has not overly degraded the optical enhancement provided by the photonic structures.
No planar geometry generated the wanted color (either for green or magenta) within the limitRGB of 15. In this configuration, the magenta cell was able to reach a higher value of JSC, 20.69 mA/cm2, and a closer chromaticity to the intended hue, than the green cell. The reflection spectra for both colors, in the top-left plot of Figure 5e, shows two prominent peaks in the magenta cell, of values between 20% and 30%, in the blue and red regions, respectively. The spectrum of this cell is overall identical to the reference, previously optimized for maximum JSC, which explains the high current density value, relative to the alternative color. Regarding the green planar cell, its reflection spectrum shows a well-defined peak in the green wavelength band, of around 20%, but a significant increase in the reflection of the near-infrared (NIR) light, up to 70%. This explains why its current density value was lower, JSC = 20.04 mA/cm2, with a loss of 3.14%, relative to the reference cell. In terms of dimension, the thickness of the planar layers presented higher values for the green solar cell, according to Figure 5b.
The LT-enhanced solar cells achieved the best optical performances and color adaptation. This is clear by the increase of the FoM and gain in current density, relative to the reference cell, up to 220.66 A/m2 and 6.68%, respectively. For the initial wide-ranged PSOs, the exceptions to the optical improvement were the green solar cells with grating lines, crossed gratings and checkerboards, as these were unable to find optimal dimensions that generated a color that assured an RGB distance lower than limitRGB= 15. Thus, it was apparent that these structures are not able to produce the required hue, within the specified RGB range, which prompted an increase of the FoM parameter, limitRGB, to 30. The increase of this limit serves as a gateway for the PSO to find higher values of JSC within the widened FoM maxima peaks. Despite this effort, the optimal green cells with linear gratings and checkerboards were still not able to satisfy the color requirements, resulting in JSC losses of 0.62% and 4.68%, respectively, to the reference value.
Altogether, the results summarized in Figure 5b,c,e show that the best photonic structures to produce magenta were, by order of FoM, domes, circular nanopillars, crossed gratings, checkerboards and linear gratings. All these structures were able to generate a color within the requirement limitRGB= 15, while improving the optical performance, relative to its reference, having reached JSC gain up to 6.68%, for dome shaped LT features. The order of merit for the generation of green color is identical to magenta, except for the checkerboards, which recorded the worst optical behavior of all the solar cells. For the green chromaticity, the checkerboards and linear gratings showed optical degradation, as previously mentioned.
The radar chart in Figure 5c compiles all the optimal geometrical parameters of the photonic-enhanced magenta and green solar cells, whereas Figure 5d presents the relevant PSO results, from which the following conclusions can be drawn:
-
1
The light-trapping structures are generally larger in the magenta solar cells, seen by higher values of pitch, agglomerated between 250 and 500 nm. The linear gratings are the only exception to this remark.
-
2
Width/radius values for each structure are similar for both colors (domes and linear gratings are the exception). As expected by the variable sweeps from Figure 4, this parameter showed insignificant alteration of the cell chromaticity, thus converged with the main intent to maximize JSC, resulting in similar values, despite the optimal color.
-
3
The planar layers of the optimal green solar cells are thicker, for every geometry. This tendency supports the hypothesis whereby the thickness of the ITO and Spiro layers has a relevant weight on color selection, by controlling the constructive interference of the light directed outward the cell, at the appointed wavelengths.
-
4
Overall, despite the complexity of the generation of magenta, the green cells resulted in lower FoM and JSC, and a chromaticity within the defined range was more difficult to be found by the PSO. The decrease in current density is, most likely, due to the increase in reflection of wavelengths above 700 nm, as observed in the reflection spectra (Figure 5e) of the solar cells with photonic structures. Although the reflection peak in the green region is intense, the chromaticity is affected in the cells with linear gratings and checkerboards by peaks present in the visible band (particularly in the blue and red regions), which the geometry was not able to completely filter out, resulting in distanceRGB > limitRGB.
The sensitivity of the chromaticity and JSC with variations of the geometrical parameters is a relevant factor in this study, in view of assessing the acceptable tolerances for future industrial fabrication. For PV application, the coloring method must guarantee good optical stability in solar cells for a reasonable amplitude of geometries surrounding the optimal parameters, in order to accommodate the deviations intrinsic to the production techniques. A Monte Carlo study was conducted to test the mutability of these properties, where the optimal geometrical values were simultaneously varied, randomly, within a range of 5%, for 500 iterations. This revealed that, as predicted by the photonic parameter sweeps and Bruggerman approximation comparison (Figures 3 and 4), the divergence of the chromaticity of the cells was more significant for the parameter variances in less compact structures. Thus, domes and circular nanopillars revealed a larger deviation of the RGB distance values, relative to the original color, up to σ = 44.90, whereas crossed gratings and checkerboards presented the lowest variation (σ ≈ 15). Regarding JSC, the values attained for solar cells with linear gratings and with domes showed more stability (σ ≈ 0.07 mA/cm2), while crossed gratings and circular nanopillars originated the largest expanse in values (up to σ = 0.11 mA/cm2). The results are graphically represented in Figure S16.
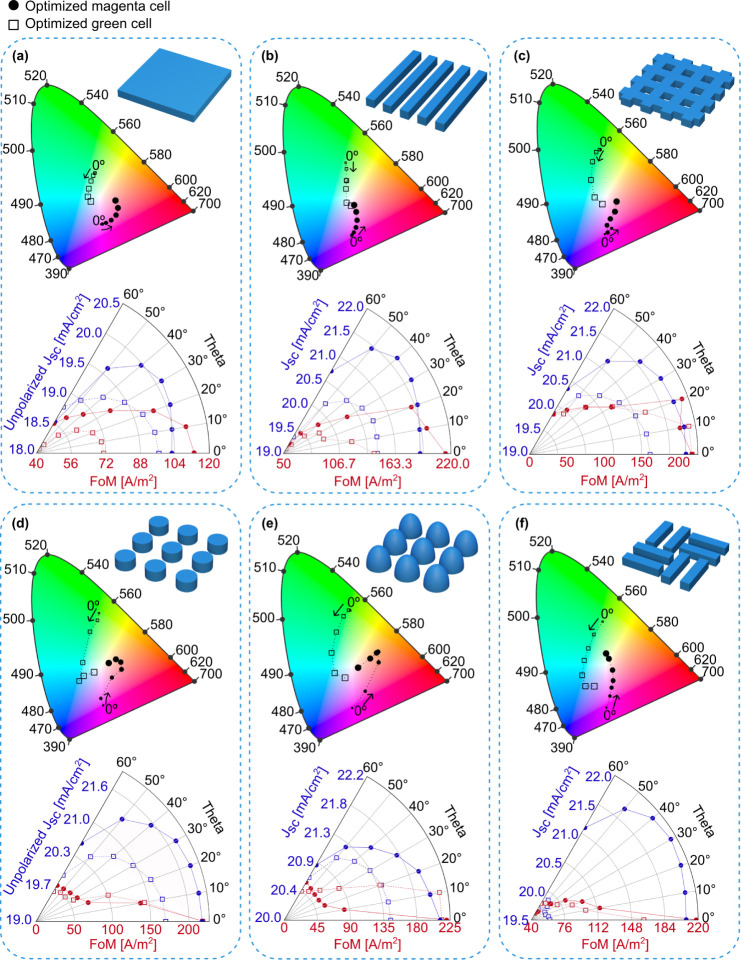
2.4. Angular Uniformity
The performance for different illumination angles is an important factor for any nontracking PV application. Figure 6 shows the effect of changing incidence angle on the merit properties, between 0◦ (normal incidence) and 60°: the variation of the chromaticity is marked in 1931 CIE gamuts, while the JSC and FoM values are seen in polar charts. In the color spectra, the inclination angle is visualized by the increasing size of the markers. At oblique incidence, the simulation results are sensitive to the polarization angle, despite the symmetry of the unit cell. Thus, the results portrayed in this section represent the average between two different light polarizations: transverse-magnetic (TM) and transverse-electric (TE).
Figure 6.
Solar cell chromaticity (shown in CIE gamut), unpolarized JSC and FoM (shown in polar plots) for the optimal magenta (circular markers) and green (squared markers) cells in (a) planar layout, (b) linear gratings, (c) crossed gratings, (d) circular nanopillars, (e) domes, and (f) checkerboards. The incident angles of illumination (θ) varied between 0° and 60°, with a step of 10°. In the CIE gamuts, the marker size increases along with the angle.
Figure 6 shows that the optimal color of the solar cells (chromaticity at 0°) degrades throughout the increase in inclination, shifting toward white, for most cases, as the growing intensity of the baseline reflection blends with the color-inducing diffracted peaks. The decay of the current density is also detectable in the polar plots, exhibiting amplitudes up to 6.65%. Both of these tendencies lead to significant reductions of the FoM, up to 79.22%.
According to the results marked in the 1931 CIE gamut of Figure 6, the color instability was more impactful on the solar cells with photonic structures, compared to their planar configuration. The optimized planar cells showed the lowest FoM divergence, recording a 40.55% drop. On the contrary, the solar cells with circular nanopillars and domes presented the largest FoM decay, up to 79.22%. For these complex structures, the magenta coloration shifted to orange (premature blue reflection peak extinction) and then to white (both peaks lost their prominence), while the green cells became blue (blueshift of the reflection peak), followed by white. This contrasts with some cases found in literature where surface structuring has led to better angular uniformity, due to the complexity of the redirecting phenomena of the incident light.5,10,41 A possible explanation to this distinct conclusion is that the color-inducing reflection peaks seen in the optimal planar cells showed intensity values between 20% and 30%, while the photonic-enhanced cells had significantly lower peaks, from 5% to 20%. Consequently, when the latter structures are subjected to the slightest change of incident light angle, a significant change of the reflection spectra is observed, leading to a large divergence in color. This issue can be mitigated by adding the luminosity of the color to the chromaticity estimation, thus increasing the intensity of the reflection associated with the optimal color.
Despite the lack of chromaticity uniformity of the front structured cells under angular variation, their photocurrent gains are still considerable even for oblique incidence. The planar cells showed some of the highest losses in JSC (over 6%), whereas the checkerboards showed the lowest variations (between 0.98% and 3.73%), as visible in the polar plots of Figure 6a,f, respectively.
3. Conclusion
This work has successfully developed a design method to confer chromaticity to standard and complex solar cell geometries, while enhancing their power density. To this end, a set of high-performing front photonic structures were evaluated and their geometries optimized for the primary colors of the standard RGB color system.
Despite the optical loss associated with the reflection peaks in the visible spectrum responsible for the color of the device, the light in-coupling and trapping provided by the surface structures was sufficient to increase the current density of the cell, as most of the optimized solar cells with photonic features resulted in JSC gain (relative to the optimized planar cell taken as reference).
When studying the underlying optical effects of the geometry of the front photonic elements, a pronounced correlation between the height of the structured layer and the color attribution is observed. This is more notorious as the compactness of the form, per unit cell, is increased. Similarly, when testing different thicknesses of the ARC layer, a variety of colors were attained, pointing to the possibility of producing a diversity of colors with identical shapes only by varying the thickness of the top layers. Moreover, regarding the optimal solar cell geometries, some layout parameters converged to similar values to produce the same color (namely the pitch and Spiro and ITO layer thicknesses). This facilitates the incorporation of these photonic elements into industrial settings: by assigning a specific color to the manufactured devices, it remains possible to maintain color consistency even in the presence of minor manufacturing variations such as pitch, width or radius, seen by the Monte Carlo assessment.
At a normal light incidence, with no regard for the luminosity of the color, the best optimization results were obtained for the magenta solar cell with dome-shaped structures, which presented (R, G, B) = (254, 0, 255) and JSC = 22.07 mA/cm2 (gain of 6.68%, relative to the reference). This dome geometry was also able to converge to the best green solar cell, with (R, G, B) = (13, 255, 7) and JSC = 21.04 mA/cm2 (3.44% gain).
When testing the optical performance of the devices under oblique light incidence, the implementation of photonic features in the solar cells resulted in larger color shifting and overall FoM decrease, which may constitute a drawback for most applications. However, the optical uniformity of these structures can be improved by implementing the level of luminosity of the color in this method, thus increasing the intensity of the reflection at the selected wavelength ranges.
In closing, this work unprecedentedly managed to develop a method that achieved the compatibility between two opposing physical effects: the enhancement of the generation of photocurrent, and the reflection of light for color application, by carefully optimizing the geometry of advanced photonic structures. This work serves as a groundbreaking proof of concept for a solar energy harvesting technology that can be seamlessly integrated into consumer products, while adding value through its aesthetic appeal.
4. Methods
The study of structural color generation in PSCs with light-trapping features was conducted using optical simulations in Ansys Lumerical’s 3D Finite-Difference Time-Domain (FDTD) numerical method.42 This method, which models the electromagnetic response of light in nonlinear materials, is commonly used to simulate optoelectronic devices such as solar cells33,43 and LEDs.44−46 The optimizations of the geometrical variables were conducted by a particle swarm optimization (PSO) algorithm, where the specific figure of merit (FoM) in eq 2 was implemented.
In order to estimate the color of the solar cells, a Python script was developed to obtain the reflection spectrum of the cell from the FDTD simulation, and convert to RGB using the 1931 International Commission on Illumination (CIE) color system.47,48 This spectrum-to-color conversion can be depicted in a series of steps: (1) the CIE color matching functions, x̅, y̅ and z̅ (three fixed primary colors, each outputs the amount of primary needed to create a desired color when all three are mixed)49 are multiplied by the reflection spectrum (R(λ)) and spectrally integrated, resulting in the tristimulus values, X,Y,Z (eq 3); (2) the tristimulus values are normalized in Z, resulting in x,y,z coordinates; (3) the vertices of the RGB region are defined as a (xrgb, yrgb, zrgb) matrix (illustrated in Figure 5b) which, when divided by the x, y, z vector, results in the (r, g, b) chromaticity (eq 4).
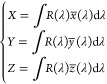 |
3 |
In the previous transition, the luminosity of the color is disregarded, as the RGB values represent only the chromaticity of the reflected spectrum from the cell. This simplification is taken into consideration in the results discussion.
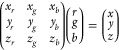 |
4 |
The simulation settings applied to the FDTD environment were selected after extensive convergence tests, for normal-incident and oblique-incident illumination sources, as elaborated in S1.1 and S1.2 of Supporting Information, respectively. Subsequently, the FDTD solver was utilized to calculate the merit quantity, JSC, according to eq 5.42
| 5 |
In eq 5, Abs is the
absorption determined via the integration of the normalized absorbed
power density across the perovskite volume, 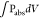 , and
, and 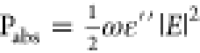 .42 The angular
frequency is
.42 The angular
frequency is 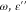 is the imaginary part of the dielectric
permittivity,
is the imaginary part of the dielectric
permittivity, 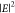 is the electric field intensity, V is the volume
of the absorber, e is the
electron charge, h is the Planck’s constant, c is the speed of light in vacuum and IAM1.5 is
the standard solar power spectrum at sea level. Considering no electric
losses in the generation of electrons in the perovskite layer (internal
quantum efficiency equal to one), it is possible to assume the simplification JPH = JSC.
is the electric field intensity, V is the volume
of the absorber, e is the
electron charge, h is the Planck’s constant, c is the speed of light in vacuum and IAM1.5 is
the standard solar power spectrum at sea level. Considering no electric
losses in the generation of electrons in the perovskite layer (internal
quantum efficiency equal to one), it is possible to assume the simplification JPH = JSC.
In summary, the values of the geometrical variables are inserted into the FDTD simulation domain, where the reflection spectrum and JSC are attained. By performing the calculations described by eqs 3 and 4, the chromaticity of the cell is estimated by translating the reflection spectrum to its relative red, green and blue intensities. After selecting a desired cell color, it is possible to compare it to the RGB of the simulated cell, by determination of their euclidean distance (eq 1), as well as the corresponding figure of merit (eq 2). Then the PSO search space is updated in each iteration, and the characteristics of the parameter sets (particle swarm) altered based on this result.50 This cycle runs for a certain number of iterations, updating the particle swarm until the optimal cell geometry is found for the maximum attainable value of FoM, which according to eq 2 maximizes JSC and advances the cell layout toward the parameters that produce the intended color.
Acknowledgments
This work is funded by FCT-MCTES (Fundação para a Ciência e Tecnologia, I.P.) via the projects LA/P/0037/2020, UIDP/50025/2020 and UIDB/50025/2020 of the Associate Laboratory Institute of Nanostructures, Nanomodelling and Nanofabrication–i3N, and by the project SpaceFlex (2022.01610.PTDC), FlexSolar (PTDC/CTM-REF/1008/2020), as well as by the project M-ECO2 (Industrial cluster for advanced biofuel production, ref. C644930471-00000041) cofinanced by PRR - Recovery and Resilience Plan of the European Union (Next Generation EU). This work also received funding from the European Community’s H2020 program under the project SYNERGY (H2020-WIDESPREAD-2020-5, CSA, proposal no. 952169). M.A. and I.M.S. also acknowledge funding by FCT, I.P through the respective grants SFRH/BD/148078/2019 and 2023.03929.BD.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c04979.
The setup of the simulation software for the optical analysis of the solar cells as well as the material data implemented in the latter (ZIP)
Additional study results, deemed complementary, are also portrayed, namely, the screening of shape and array symmetry, the defining process of the FoM, PSO and Monte Carlo simulation results (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Shukla A. K.; Sudhakar K.; Baredar P. A comprehensive review on design of building integrated photovoltaic system. Energy Build. 2016, 128, 99–110. 10.1016/j.enbuild.2016.06.077. [DOI] [Google Scholar]
- Norton B.; Eames P. C.; Mallick T. K.; Huang M. J.; McCormack S. J.; Mondol J. D.; Yohanis Y. G. Enhancing the performance of building integrated photovoltaics. Sol. Energy 2011, 85 (8), 1629–1664. 10.1016/j.solener.2009.10.004. [DOI] [Google Scholar]; Progress in Solar Energy 1
- Jelle B. P.; Breivik C. State-of-the-art building integrated photovoltaics. Energy Procedia 2012, 20, 68–77. 10.1016/j.egypro.2012.03.009. [DOI] [Google Scholar]
- Vicente A. T.; Araújo A.; Mendes M. J.; Nunes D.; Oliveira M. J.; Sanchez-Sobrado O.; Ferreira M. P.; Águas H.; Fortunato E.; Martins R. Multifunctional cellulose-paper for light harvesting and smart sensing applications. J. Mater. Chem. C 2018, 6, 3143–3181. 10.1039/C7TC05271E. [DOI] [Google Scholar]
- Schuster C. S.; Crupi I.; Halme J.; Koç M.; Mendes M. J.; Peters I. M.; Yerci S.. Empowering Photovoltaics with Smart Light Management Technologies, Lackner M.; Sajjadi B.; Chen W.-Y.; Springer: Cham, 2022; pp. 1165–1248.. 10.1007/978-3-030-72579-2_112. [DOI] [Google Scholar]
- Jiang Y.; Luo B.; Jiang F.; Jiang F.; Fuentes-Hernandez C.; Liu T.; Mao L.; Xiong S.; Li Z.; Wang T.; Kippelen B.; Zhou Y. Efficient colorful perovskite solar cells using a top polymer electrode simultaneously as spectrally selective antireflection coating. Nano Lett. 2016, 16, 7829–7835. 10.1021/acs.nanolett.6b04019. [DOI] [PubMed] [Google Scholar]
- Li J.; Wang H.; Chin X. Y.; Dewi H. A.; Vergeer K.; Goh T. W.; Lim J. W. M.; Lew J. H.; Loh K. P.; Soci C.; Sum T. C.; Bolink H. J.; Mathews N.; Mhaisalkar S.; Bruno A. Highly efficient thermally co-evaporated perovskite solar cells and mini-modules. Joule 2020, 4, 1035–1053. 10.1016/j.joule.2020.03.005. [DOI] [Google Scholar]
- Ro̷yset A.; Kolås T.; Jelle B. P. Coloured building integrated photovoltaics: Influence on energy efficiency. Energy Build 2020, 208, 109623. 10.1016/j.enbuild.2019.109623. [DOI] [Google Scholar]
- Lee K.-T.; Jang J.-Y.; Zhang J.; Yang S.; Park S.; Park H. J. Highly efficient colored perovskite solar cells integrated with ultrathin subwavelength plasmonic nanoresonators. Sci. Rep. 2017, 7, 10640. 10.1038/s41598-017-10937-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peharz G.; Berger K.; Kubicek B.; Aichinger M.; Grobbauer M.; Gratzer J.; Nemitz W.; Großschädl B.; Auer C.; Prietl C.; Waldhauser W.; Eder G. C. Application of plasmonic coloring for making building integrated PV modules comprising of green solar cells. Renewable Energy 2017, 109, 542–550. 10.1016/j.renene.2017.03.068. [DOI] [Google Scholar]
- Yoo G. Y.; Azmi R.; Kim C.; Kim W.; Min B. K.; Jang S. Y.; Do Y. R. Stable and colorful perovskite solar cells using a nonperiodic SiO2/TiO2 multi-nanolayer filter. ACS Nano 2019, 13, 10129–10139. 10.1021/acsnano.9b03098. [DOI] [PubMed] [Google Scholar]
- Lizcano J. C. O.; Villa S.; Zhou Y.; Frantzi G.; Vattis K.; Calcabrini A.; Yang G.; Zeman M.; Isabella O. Optimal design of multilayer optical color filters for building-integrated photovoltaic (BIPV) applications. Sol. RRL 2023, 7 (19), 2300256. 10.1002/solr.202300256. [DOI] [Google Scholar]
- Cho D.-H.; Hong S.-H.; Lee W.-J.; Kim J. Y.; Chung Y.-D. Colorful solar cells utilizing off-axis light diffraction via transparent nanograting structures. Nano Energy 2021, 80, 105550. 10.1016/j.nanoen.2020.105550. [DOI] [Google Scholar]
- Mahani F. F.; Mokhtari A. TiO2 circular nano-gratings as anti-reflective coatings and potential color filters for efficient organic solar cells. J. Nanoelectron. Optoelectron. 2018, 13, 1624–1629. 10.1166/jno.2018.2412. [DOI] [Google Scholar]
- MacLeod H. A.Thin-Film Optical Filters, 3 rd ed.; CRC Press: Boca Raton, 2001. 10.1201/9781420033236. [DOI] [Google Scholar]
- Koh T. M.; Wang H.; Ng Y. F.; Bruno A.; Mhaisalkar S.; Mathews N. Halide perovskite solar cells for building integrated photovoltaics: Transforming building façades into power generators. Adv. Mater. 2022, 34 (25), 2104661. 10.1002/adma.202104661. [DOI] [PubMed] [Google Scholar]
- Li K.; Martins R.; Haque S.; Martins A.; Fortunato E.; Mendes M. J.; Schuster C. S. Light trapping in solar cells: simple design rules to maximize absorption. Optica 2020, 7, 1377–1384. 10.1364/OPTICA.394885. [DOI] [Google Scholar]
- Haque S.; Mendes M. J.; Sanchez-Sobrado O.; Águas H.; Fortunato E.; Martins R. Photonic structured TiO2 for high-efficiency, flexible and stable perovskite solar cells. Nano Energy 2019, 59, 91–101. 10.1016/j.nanoen.2019.02.023. [DOI] [Google Scholar]
- Mendes M. J.; Haque S.; Sanchez-Sobrado O.; Araújo A.; Águas H.; Fortunato E.; Martins R. Optimal-enhanced solar cell ultra-thinning with broadband nanophotonic light capture. iScience 2018, 3, 238–254. 10.1016/j.isci.2018.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chong T. K.; Wilson J.; Mokkapati S.; Catchpole K. R. Optimal wavelength scale diffraction gratings for light trapping in solar cells. J. Optics 2012, 14, 024012. 10.1088/2040-8978/14/2/024012. [DOI] [Google Scholar]
- Santos I. M.; Alexandre M.; Mihailetchi V. D.; Silva J. A.; Mateus T.; Mouquinho A.; Boane J.; Vicente A. T.; Nunes D.; Menda U. D.; Aguas H.; For-tunato E.; Martins R.; Mendes M. J. Optically-boosted planar IBC solar cells with electrically-harmless photonic nanocoatings. Adv. Opt. Mater. 2023, 11, 2300276. 10.1002/adom.202300276. [DOI] [Google Scholar]
- Brenner T. M.; Egger D. A.; Kronik L.; Hodes G.; Cahen D. Hybrid organic–inorganic perovskites: low-cost semiconductors with intriguing charge-transport properties. Nat. Rev. Mater. 2016, 1, 1–16. 10.1038/natrevmats.2015.7. [DOI] [Google Scholar]
- Unger E.; Jacobsson T. J. The perovskite database project: A perspective on collective data sharing. ACS Energy Lett. 2022, 7 (3), 1240–1245. 10.1021/acsenergylett.2c00330. [DOI] [Google Scholar]
- Zhu H.; Teale S.; Lintangpradipto M. N.; Mahesh S.; Chen B.; McGehee M. D.; Sargent E. H.; Bakr O. M. Long term operating stability in perovskite photovoltaics. Nat. Rev. Mater. 2023, 8, 569–586. 10.1038/s41578-023-00582-w. [DOI] [Google Scholar]
- Green M.; Ho-Baillie A.; Snaith H. The emergence of perovskite solar cells. Nat. Photonics 2014, 8, 506–514. 10.1038/NPHOTON.2014.134. [DOI] [Google Scholar]
- Correa-Baena J.-P.; Saliba M.; Buonassisi T.; Grätzel M.; Abate A.; Tress W.; Hagfeldt A. Promises and challenges of perovskite solar cells. Science 2017, 358 (6364), 739–744. 10.1126/science.aam6323. [DOI] [PubMed] [Google Scholar]
- Kim J. Y.; Lee J.-W.; Jung H. S.; Shin H.; Park N.-G. High-efficiency perovskite solar cells. Chem. Rev. 2020, 120 (15), 7867–7918. 10.1021/acs.chemrev.0c00107. [DOI] [PubMed] [Google Scholar]
- Xie P.; Xiao H.; Qiao Y.; Qu G.; Chen J.; Liu X.; Xu Z. X. Radical reinforced defect passivation strategy for efficient and stable MAPbI3 perovskite solar cells fabricated in air using a green anti-solvent process. Chem. Eng. J. 2023, 462, 142328. 10.1016/j.cej.2023.142328. [DOI] [Google Scholar]
- Zhang P.; Xiong J.; Chen W. H.; Du P.; Song L. Air-processed MAPbI3 perovskite solar cells achieve 20.87% efficiency and excellent bending resistance enabled via a polymer dual-passivation strategy. Dalton Trans. 2023, 52, 15974–15985. 10.1039/D3DT02080K. [DOI] [PubMed] [Google Scholar]
- Liu S.; Li J.; Xiao W.; Chen R.; Sun Z.; Zhang Y.; Lei X.; Hu S.; Kober-Czerny M.; Wang J.; Ren F.; Zhou Q.; Raza H.; Gao Y.; Ji Y.; Li S.; Li H.; Qiu L.; Huang W.; Zhao Y.; Xu B.; Liu Z.; Snaith H. J.; Park N.-G.; Chen W. Buried interface molecular hybrid for inverted perovskite solar cells. Nature 2024, 632, 536. 10.1038/s41586-024-07723-3. [DOI] [PubMed] [Google Scholar]
- Peter Amalathas A.; Alkaisi M. M. Nanostructures for light trapping in thin film solar cells. Micromachines 2019, 10 (9), 619. 10.3390/mi10090619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saive R. Light trapping in thin silicon solar cells: A review on fundamentals and technologies. Prog. Photovoltaics: Res. Appl. 2021, 29 (10), 1125–1137. 10.1002/pip.3440. [DOI] [Google Scholar]
- Haque S.; Alexandre M.; Mendes M. J.; Águas H.; Fortunato E.; Martins R. Design of wave-optical structured substrates for ultra-thin perovskite solar cells. Appl. Mater. Today 2020, 20, 100720. 10.1016/j.apmt.2020.100720. [DOI] [Google Scholar]
- Sanchez-Sobrado O.; Mendes M. J.; Haque S.; Mateus T.; Aguas H.; Fortunato E.; Martins R. Lightwave trapping in thin film solar cells with improved photonic-structured front contacts. J. Mater. Chem. C 2019, 7, 6456–6464. 10.1039/C8TC06092D. [DOI] [Google Scholar]
- Sanchez-Sobrado O.; Mendes M. J.; Mateus T.; Costa J.; Nunes D.; Aguas H.; Fortunato E.; Martins R. Photonic-structured TCO front contacts yielding optical and electrically enhanced thin-film solar cells. Sol. Energy 2020, 196, 92–98. 10.1016/j.solener.2019.11.051. [DOI] [Google Scholar]
- Glinsner T.; Lindner P.; Muhlberger M.; Bergmair I.; Schoftner R.; Hingerl K.; Schmid H.; Kley E.-B. Fabrication of 3D-photonic crystals via UV nanoimprint lithography. J. Vac. Sci. Technol. 2007, 25, 2337–2340. 10.1116/1.2798733. [DOI] [Google Scholar]
- Chou S. Y.; Krauss P. R.; Renstrom P. J. Imprint lithography with 25 nm resolution. Science 1996, 272, 85–87. 10.1126/science.272.5258.85. [DOI] [Google Scholar]
- Mendes M. J.; Sanchez-Sobrado O.; Haque S.; Mateus T.; Águas H.; Fortunato E.; Martins R. Wave-optical front structures on silicon and perovskite thin-film solar cells. Solar Cells Light Manage. 2020, 315–354. 10.1016/B978-0-08-102762-2.00009-4. [DOI] [Google Scholar]
- Pourdavoud N.; Wang S.; Mayer A.; Hu T.; Chen Y.; Marianovich A.; Kowalsky W.; Heiderhoff R.; Scheer H.-C.; Riedl T. Photonic nanostructures patterned by thermal nanoimprint directly into organo metal halide perovskites. Adv. Mater. 2017, 29, 1605003. 10.1002/adma.201605003. [DOI] [PubMed] [Google Scholar]
- Bergman D. J.Effective medium approximation for nonlinear conductivity of a composite medium. Composite Media and Homogenization Theory, Springer, 1991, pp. 67–79, 10.1007/978-1-4684-6787-1_5. [DOI] [Google Scholar]
- Roosloot N.; Neder V.; Haug H.; You C. C.; Polman A.; Marstein E. S. Broadband angular color stability of dielectric thin film-coated pyramidal textured Si for photovoltaics. J. Appl. Phys. 2021, 129 (17), 173104. 10.1063/5.0048102. [DOI] [Google Scholar]
- Ansys Lumerical FDTD | Simulation for Photonic Components. https://www.ansys.com/products/photonics/fdtd. accessed 2023 November 23.
- Solar Cell Methodology. https://optics.ansys.com/hc/en-us/articles/360042165634-Solar-cell-methodology. accessed 2024 July 29.
- Ryu H.-Y.; Pyo J.; Ryu H. Y. Light extraction efficiency of gan-based micro-scale light-emitting diodes investigated using finite-difference time-domain simulation. IEEE Photonics J 2020, 12 (2), 1–10. 10.1109/JPHOT.2020.2977401. [DOI] [Google Scholar]
- Ibrahim F.; Adhika D. R.; Nurlis A. G.; Pradana A. FDTD simulation to investigate the effect of nanopattern on light extraction distribution of ZnS: Cu LED. J. Phys.: conf. Ser 2023, 2673 (1), 012010. 10.1088/1742-6596/2673/1/012010. [DOI] [Google Scholar]
- Jia J.; Ruan Y.; Gu Y.; Zhang Z.; Zhang S.; Guo R.; Cui X.; Tian P. Numerical simulation of deep ultraviolet LED, micro-LED, and nano-LED with different emission wavelengths based on FDTD. Opt. Express 2024, 32 (13), 22321. 10.1364/OE.524916. [DOI] [Google Scholar]
- Converting a Spectrum to a Colour. https://scipython.com/blog/converting-a-spectrum-to-a-colour/. accessed 2023 November 23.
- Alexandre M.EM Software Repository; GitHub. https://github.com/perspe/em_methods. accessed 2023 September 23.
- CIE JTC 2: CIE 018:2019 The Basis of Physical Photometry 3 rd ed.; International Commission on Illumination (CIE). 10.25039/TR.018.2019. [DOI] [Google Scholar]
- Mendes M. J.; Schmidt H. K.; Pasquali M. Brownian dynamics simulations of single-wall carbon nanotube separation by type using dielectrophoresis. J. Phys. Chem. B 2008, 112, 7467–7477. 10.1021/jp711450w. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.