A quasi-Monte Carlo Metropolis algorithm

Abstract

This work presents a version of the Metropolis–Hastings algorithm using quasi-Monte Carlo inputs. We prove that the method yields consistent estimates in some problems with finite state spaces and completely uniformly distributed inputs. In some numerical examples, the proposed method is much more accurate than ordinary Metropolis–Hastings sampling.

Monte Carlo simulation methods are widely used in science, engineering, finance, industry, and statistical inference. Recent decades have seen many improvements in Monte Carlo (MC) methods. Much of the progress has been in quasi-MC (QMC) sampling and in Markov chain MC (MCMC). QMC methods improve the accuracy of MC, from a root mean square error of O(n^–1/2) using n samples to O(n^–1+ε) for any ε > 0, or even O(n^–3/2+ε) in some settings, for randomized QMC (RQMC). MCMC greatly extends the range of problems that can be handled by MC. It is thus of interest to combine QMC and MCMC. These subjects both have large bodies of literature, but their published intersection is conspicuously small.

In this work, we prove that some, though not all, QMC methods can yield consistent estimators in Metropolis–Hastings MCMC. The QMC constructions that can be made to work are ones that are “completely uniformly distributed” (CUD) as described below. Using such a QMC construction is similar to using the entire period of a (small) random number generator (RNG). In numerical investigations, QMC can bring a dramatic improvement over MC in some examples and no improvement in others. In the numerical examples we tried, our hybrid of QMC and MCMC always reduced the variance, sometimes by a factor of >200.

This work is organized into the following sections. Background gives our notation and some background information on MC, QMC, and MCMC. A Hybrid of QMC and MCMC describes CUD sequences and presents our hybrid method, using CUD points for proposals and acceptance in the Metropolis–Hastings algorithm. Consistency gives sufficient conditions under which the hybrid yields consistent estimates. Gibbs Sampler describes how to fit Gibbs sampling into the framework of this work. Illustration has some numerical examples. Conclusions states our findings. We finish this section by describing related prior work.

The absence of a QMC approach for the Metropolis algorithm was noted in ref. 1 and again in the recent dissertation by Chaudary (2). Ostland and Yu (3) propose a manually adaptive QMC as an alternative to the Metropolis algorithm. Liao (4) published a proposal for using QMC points in MCMC sampling. He runs a Gibbs sampler using proposals built from a list of n QMC points assembled in a randomized order. He reports an empirical variance reduction but notes that there is no mathematical justification for his procedure. Reordering of quasirandom heat particles (5) between steps has been shown to work for simulation of kinetic equations, but the structure of that problem is different from that of Liao. Particle filters using QMC are discussed in ref. 6. Chaudary (2) uses QMC for the proposal step of a modified Metropolis algorithm that weights rejected proposals. The result was improved accuracy for some numerical examples and essentially unchanged accuracy for others but no mathematical justification.

Our inspiration for looking at these sequences arises from recent work viewing the entire period of a RNG as a QMC rule, a possibility suggested by ref. 7. That technique has been tried on finite dimensional quadrature problems using congruential generators (8) and shift register (Tausworthe) generators (9). MCMC requires simulation of a process that typically uses infinite dimensional inputs. An infinite dimensional ruin process of an insurance company is simulated in ref. 10 using the whole period of a small congruential generator. They report a variance reduction but provide no mathematical justification.

Our proposed hybrid uses QMC within one or more simulated Markov chains. It is also possible to use variance reduction methods, similar to QMC, between two (11) or more (12) chains, where different chains have antithetically coupled movements.

Background

We suppose that the reader is already familiar with simple MC, which we briefly outline here. Then we introduce QMC, RQMC, and MCMC. For a full exposition, see ref. 13 for MC, ref. 14 for QMC, ref. 15 for RQMC, and ref. 16 for MCMC.

MC. In simple MC, a quantity μ of interest is expressed as μ = E(f(X)) for a real valued function f of a random vector X with distribution p. Often p is a probability density on 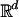and then μ is the integral 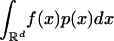. In other settings p may be a probability mass function. In simple MC, one employs independent random vectors x_i = (x_i1,..., x_id) ∼ p for i = 1,..., n and then estimates μ by 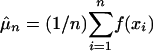. The justification for simple MC is the law of large numbers. If E(f(X)²) <∞, then the root mean square error for MC is O(n^–1/2), and asymptotic confidence intervals are available by the central limit theorem.

The p distributed random vectors x_i are usually computed by transformations of d or more independent uniformly distributed random variables (17). Typically, one uses imperfect but well-tested pseudo-random numbers to simulate the underlying uniform random numbers.

QMC. The focus in QMC sampling is integration over the unit cube. QMC is applicable when one can rearrange the problem so that x_i has the U[0, 1]^d distribution, perhaps changing the value of d in the process. Usually d is finite, though some methods of coping with infinite dimension are given in ref. 18. As with MC,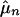 takes the form 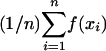, but now the x_i values are carefully chosen deterministic points in [0, 1]^d.

In QMC, the points x_i are arranged to be more uniformly distributed than random points would be. Their degree of uniformity typically is quantified as a distance between the discrete uniform distribution on x_i and the continuous uniform distribution on [0, 1]^d. The most prominent such distance is the star discrepancy, a generalization of the Kolmogorov–Smirnov distance. To define the star discrepancy, first let 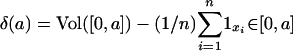be the local discrepancy function at the point a ε [0, 1]^d. Here Vol(S) is the d-dimensional volume of the (measurable) set S, and [0, a] denotes a d-dimensional box with 0 and a at opposite corners. The star discrepancy is

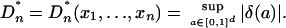When , then for Riemann integrable f, providing a deterministic version of the law of large numbers for QMC.

The significance of star discrepancy arises from the Koksma–Hlawka inequality

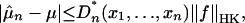[1]

where ∥ f ∥_HK is the d-dimensional total variation of f in the sense of Hardy and Krause. There are many alternative discrepancies for x_i, and corresponding norms on f, for which a bound like Eq. 1 holds (19).

Widely used QMC points satisfy 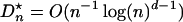as n → ∞. Thus, the error in QMC is O(n^–1+ε) for any ε > 0. This rate of convergence is superior to that for MC. The rate is slow to take hold, but empirical comparisons often find that QMC outperforms MC for reasonable n and seldom find QMC to be worse than MC.

To fix ideas, we describe some QMC sequences. Let the integer n ≥ 0 be written as 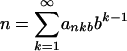for an integer base b ≥ 2 and nonnegative integers a_nkb < b. The radical inverse function 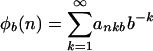“reflects” the base b expansion of n through the decimal point. The van der Corput sequence has x_i = φ₂(i) ε [0, 1]. Halton's sequence has x_i = (φ_p1(i),..., φ_pd(i)) ε [0, 1]^d, where the p_j are relatively prime. Usually p_j is the jth prime.

Lattice rules (20) are another form of QMC sequence. For a positive integer N and a vector g = (1, g₁,..., g_d–1) of integers, the lattice rule has x_i = ig/N – ⌊ig/N⌋ componentwise for i = 1,..., N, where ⌊z⌋ is the greatest integer less than or equal to z. A special case are Korobov rules where g_j = a^j–1 (modulo N) for carefully chosen integers a and N with 1 < a < N. The Korobov points are related to the points of a multiplicative congruential RNG with r_i = ar_i–1 mod N. Commonly N is a prime number and a a primitive element modulo N. In this case the RNG has period 1 if started at r₀ = 0 and period N – 1 otherwise. After a reordering, the nonzero Korobov points are the N – 1 points (r_i/N,..., r_i+d–1/N) for i = 1,..., N – 1 and any r₀ ≠ 0.

If we run through the RNG once, then we use only (N – 1)/d of the possible d-tuples from the Korobov points. To use all of the d-tuples among the Korobov points requires multiple runs through the RNG, taking care not to repeat Korobov points.

RQMC. The Koksma–Hlawka bound in Eq. 1 is poorly suited to error estimation. It contains the discrepancy D*_n, which can be hard to compute, and the variation ∥f∥_HK that is ordinarily harder to find than μ. Also, although the Inequality 1 holds as an equality for some worst case f, it can be extremely conservative for integrands arising in applications.

RQMC methods are a hybrid of QMC and MC. RQMC points are usually constructed so that, individually, x_i has the U[0, 1]^d distribution, whereas collectively the x_i have low discrepancy, with probability one. RQMC allows error estimation through confidence intervals for μ based on independent replications of the RQMC estimate. A surprising benefit is that some forms of RQMC reduce the root mean square error to O(n^–3/2+ε) on suitably smooth integrands, as shown in ref. 21.

A particularly simple form of randomization is Cranley–Patterson rotation (22). The rotated versions of a₁,..., a_n ε [0, 1]^d are x_i = a_i + U – ⌊a_i + U⌋ for a rotation vector U ∼ U[0, 1]^d common to all n points.

Standard Construction for Markov Chains. For very simple Markov chains on finite state spaces, one can sample by a standard construction based on inversion of the cumulative distribution function. Let Z be a random variable on values ω_k for 1 ≤ k ≤ K <∞. To sample Z by inversion, define P_k =Σ_1≤l≤k P(Z = ω_l), draw a sample u ∼ U[0, 1], and take Z = ω_k where k is the smallest index with u ≤ P_k.

The standard construction for sampling a Markov chain is as follows. Begin by sampling x₁ by inversion from the stationary distribution p. Then for i ≥ 1 sample x_i+1 by inversion using the conditional distribution of x_i+1 given x_i. This standard construction is used as a mathematical device in our proofs. We do not assume it can be implemented.

MCMC. MCMC is commonly used in problems where it is difficult or virtually impossible to sample x_i independently from p, by inversion or any other method. Instead, one samples x_i dependently from a Markov chain constructed to have p as a stationary distribution.

Metropolis–Hastings algorithms for MCMC work in two stages: proposal and acceptance. Given x_i, a value y_i+1 is drawn from a proposal distribution. If that proposal is accepted, then x_i+1 = y_i+1, and otherwise x_i+1 = x_i. Let p_i(x → y) denote the probability, or the probability density, of proposing y_i+1 = y when x_i = x. When y = x it is moot whether y is accepted or rejected. For y ≠ x the acceptance probability in Metropolis–Hastings is always

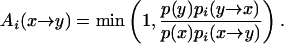[2]

The term Metropolis–Hastings is used for the generalization by ref. 23 of the Metropolis algorithm in ref. 24.

Where versions of Metropolis–Hastings differ is in the proposal distribution. In the original Metropolis algorithm, the proposed increments y_i+1 – x_i are independent and identically distributed. In the independence sampler, the proposals y_i+1 themselves are independent and identically distributed. Sometimes the standard construction can be viewed as Metropolis–Hastings with acceptance probability one. For example, it suffices to have a reversibility condition wherein p(y)p_i(y → x) = p(x)p_i(x → y) > 0.

In the Gibbs sampler, the proposal y_i+1 changes at most one of the components of x_i. In one version the changing component j(i) is chosen randomly and in another j(i) repeatedly cycles through the components of x_i in order. In both cases the changing component is sampled from its conditional stationary distribution given the values of all the nonchanging components.

A Metropolis–Hastings algorithm is “homogenous” if the proposal distribution p_i(x → y) does not depend on the step i. In that case A_i does not depend on i either. All of the proposals described above are homogenous except for the cyclic Gibbs sampler.

Once again μ = ∫ f(x)p(x) dx is estimated by a sample mean 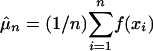, but now we rely on ergodicity to determine when 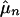tends to μ. Sometimes the first few x_i are skipped. Skipping a finite number of x_i does not affect whether 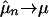, and so we ignore it in this work.

A Hybrid of QMC and MCMC

Our QMC–MCMC hybrid generates the proposals and the acceptances in MCMC using QMC points instead of MC points. There are intuitive arguments for and against this proposal.

First, MCMC sampling has a sequential nature that the usual QMC sampling methods do not respect. For example, with van der Corput points v_i ε [0, 1], it is easy to show that v_2k ε [0, 1/2) and v_2k+1 ε [1/2, 1). Clear and even humorous failures will arise from using van der Corput points in MCMC. Morokoff and Caflisch (25) describe an example where a heat particle supposed to undergo a symmetric random walk will instead move only to the left when sampled by van der Corput points.

The argument in favor of using QMC is that one might expect a good result from MCMC if one ran the chain through one complete period of the underlying RNG. Such a strategy essentially would average together many shorter portions of the generator that might have been presumed to be usable. The entire period of an RNG typically has much lower discrepancy than one would see in an independently and identically distributed sample of the same size. Some, but not all, finite QMC sequences look like RNGs with a small period. Those that do approximate CUD sequences as described below.

Definition 1 (CUD): The sequence u₁, u₂, ··· ε [0, 1] is CUD, if for every integer d ≥ 1, the points z_i = (u_i,..., u_i+d–1) ε [0, 1]^d satisfy lim_n→∞ D*_n(z₁,..., z_n) = 0.

The concept of CUD sequences originated with Korobov (26) and is used as definition R1 of randomness by Knuth (27). An up-to-date account of CUD sequences, including some new constructions, is in ref. 28. CUD sequences exist in which 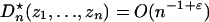holds for z_i = (u_i,..., u_i+d–1) ε [0, 1]^d and for all integers d ≥ 1. Definition 1 applies to an infinite sequence, and RNGs with finite state spaces must have finite length, or at least a finite period. Typically, the CUD property applies to a sequence of RNGs of increasing period. See, for example, theorems 7.3 and 7.4 of ref. 14, which show how certain sequences of linear congruential generators approximate CUD sequences. The role of CUD sequences in simulating processes has been noted previously for stochastic differential equations (29).

Definition 1 groups the u_i into overlapping d-tuples. The hybrid we propose in Consistency uses nonoverlapping d-tuples. Chentsov (30) notes the following.

Lemma 1. If the sequence u₁, u₂, ··· ε [0, 1] is CUD and z_i = (u_di–l+1,..., u_di–l+d) for integers d ≥ l ≥ 1, then

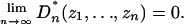Our grouping uses l = d. The more general result in Lemma 1 allows one to skip the first d – l values u_i.

Independent random points u_i ∼ U[0, 1] are CUD in the sense of strong convergence: Pr(lim_n→∞ D*_n = 0) = 1 for any d, using either blocked or overlapping vectors (see ref. 28). A definition in the sense of weak convergence suffices for our purposes.

Definition 2 (Weakly CUD): The random sequence u₁, u₂, ··· ε [0, 1] is weakly CUD if

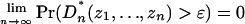holds for every integer d ≥ 1 and every ε > 0, when z_i = (u_di+1,..., u_di+d).

Consistency

Here we show that one can employ CUD sequences in some Metropolis–Hastings samplers and obtain consistency. We consider chains with finite state spaces Ω = {ω₁,..., ω_K} and give conditions under which

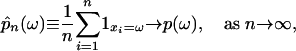[3]

for all states ω ε Ω. In the finite state space setting 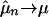follows from Eq. 3 for all bounded f. Consistency for CUD sampling of Markov chains was proved by Chentsov (30), assuming the standard construction.

Theorem 1 (30). Let x_i ε {ω₁,..., ω_K} for i ≥ 1 be sampled from the standard construction for Markov chains, using a CUD sequence u_i. Assume that all K² transition probabilities are positive. Then the limit (Eq. 3) holds.

Chentsov's proof uses a coupling idea that we will extend to some Metropolis–Hastings samplers. Where the standard construction uses one number to generate the transition, we suppose that Metropolis–Hastings uses d numbers to generate each transition where 1 ≤ d < ∞. We suppose that the proposal y_i+1 can be written as a function Ψ_i of x_i and d – 1 uniformly distributed random variables. The proposal functions we have in mind are from inversion or other transformations, many of which are described in ref. 17. Then one random variable is used to make the acceptance rejection decision. Specifically, for i = 0,..., n – 1,

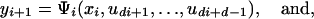[4]

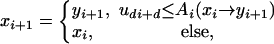[5]

for a state x_i ε Ω and points u_j ε [0, 1]. For a homogenous sampler Ψ_i and A_i do not depend on i.

The law of large numbers for MC sampling applies to Lebesgue integrable functions, whereas that for QMC requires Riemann integrable functions. In typical applications, the distinction need not be drawn. One can, however, make mischief by using a well-behaved transformation Ψ_i when all of (u_di+1,..., u_di–d–1) are irrational numbers and setting y_i to some arbitrary value otherwise. To rule out such pathologies, we suppose that the transitions are regular as described below. Recall that a Jordan measurable set is one whose indicator function is Riemann integrable.

Definition 3 (Regular proposals): The proposals are regular if for all i ≥ 0, k ε {1,..., K}, and l ε {1,..., K}, the set S_i,k→l = {(u_di+1,..., u_di+d–1) | y_i+1 = ω_l if x_i = ω_k} ⊆ [0, 1]^d–1 is Jordan measurable.

By Lebesgue's theorem (ref. 31, Chapter 8.4) a bounded function on a bounded set 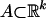is Riemann integrable if and only if that function (when extended to 0 on 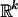– A) is continuous except on a set of measure zero. Indicator functions are of course bounded, as is the domain [0, 1]^d–1 in Definition 3. Accordingly, the proposals are regular if and only if the sets S_i,k→l have a boundary with d – 1 dimensional volume zero. We know of no commonly used proposal functions Ψ_i for which S_i,k→l ⊆ [0, 1]^d–1 has a boundary of positive d – 1-dimensional volume.

Regularity extends easily from proposal sets to transition sets, because unions, complements, and tensor products of Jordan measurable sets are again Jordan measurable. For example, the set of (u_di+1,..., u_di+d) such that x_i = ω_k transitions to x_i+1 = ω_l ≠ ω_k is simply T_i,k→l = S_i,k→l × [0, A_i(ω_k → ω_l)]. The set T_ik→k for self-transitions x_i = x_i+1 = ω_k is the complement of ∪_l≠kT_i,k→l. A multistep transition through r specific states corresponds to a subset of [0, 1]^rd equal to the Cartesian product of r transition sets. The set of vectors in [0, 1]^rd for which an r-step transition from x_i = ω_k to x_i+r–1 = ω_l takes place is a union of finitely many multistep transitions sets. When we state below that a set is Jordan measurable, it follows from the reasoning described in this paragraph.

To generalize Chentsov's Theorem, we will need a “home” state that can be visited from any other and a d-dimensional hyperrectangular region that guarantees a return to the home state.

Definition 4 (Home state): A home state ω ε {ω₁,..., ω_K} is one for which there is a box 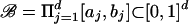of positive volume such that x_i+1 = ω whenever 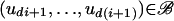, regardless of x_i.

As an example, consider proposals y_i+1 taken from a discrete approximation to the d-dimensional Gaussian distribution. Perhaps y_i+1 is (Φ^–1(u_di+1),..., Φ^–1(u_di+d–1)) rounded to a discrete set, where Φ is the standard Gaussian cumulative distribution function. Then there is a d – 1 dimensional box of positive volume near (1,..., 1) that always gives the “highest” proposal y_i+1. When the acceptance probability has a positive lower bound, then this highest proposal state is a home state.

Theorem 2. Let x₀ ε Ω = {ω₁,..., ω_K}. Suppose that for i ≥ 0 the proposal y_i+1 ε Ω is generated from (u_di+1,..., u_di+d–1) by a homogenous regular proposal and that x_i+1 is given by Eq. 5. If the sequence (u_i)_i≥1 is CUD and Ω contains a home state with box ℬ, then the Limit 3 holds.

Proof: We will couple x_i to some idealized chains of finite length. These chains exist mathematically, but we do not need to be able to sample from them. For integer m ≥ 1 let x̃_i,m = (x̃_i,m,0,..., x̃_i,m,m) ε Ω^m+1 where x̃_i,m,0 is sampled from the stationary distribution p by inversion applied to u_di, and for t = 1,..., m, the transition from x̃_i,m,t–1 to x̃_i,m,t is made by the same function of (u_di+1,..., u_d(i+1)) that the Metropolis–Hastings rule uses to find the successor of x̃_i,m,t–1.

Fix a state ω ε Ω and let ε > 0. Next,

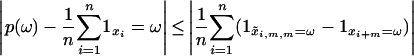[6]

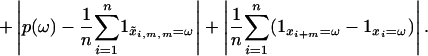The point x_i+m can only differ from the coupled point x̃_i,m,m if the box ℬ leading to the home state is avoided by m consecutive transitions. There is thus a dm-dimensional hyperrectangle 𝒯₁ of volume (1 – Vol(ℬ))^m such that x̃_i,m,m = x_i+m when (u_di+1,..., u_di+dm) ∉ 𝒯₁. We choose m large enough that (1 – Vol(ℬ))^m < ε. Because u_i is CUD, the limit as n → ∞ of the first term in the bound Eq. 6 is no larger than ε.

For the second term in Eq. 6, notice that x̃_i,m,m = ω if and only if (u_di+1,..., u_di+dm) lies in a dm-dimensional region 𝒯₂. The region 𝒯₂ has volume p(ω) because the construction of x̃_i,m,m would generate x̃_i,m,m ∼ p had (u_di+1,..., u_di+dm) been sampled U[0, 1]^dm. For regular proposals, the indicator function of 𝒯₂ is Riemann integrable. Because u_i are CUD, it follows that 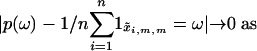n → ∞.

The third term in Eq. 6 is no larger than m/n → 0. Therefore the limit, as n → ∞, of the bound in Eq. 6 is no larger than ε. □

Chentsov's Theorem 1 requires that every transition probability is positive, whereas our Theorem 2 requires a home state. Chentsov's Theorem 2 requires neither assumption but requires sampling by the standard construction. His Theorem 2 contains his Theorem 1, but they use different techniques, and he remarks that the first one might extend more easily to continuous state spaces. Our Theorem 3 below extends his Theorem 2 from chains sampled by the standard construction to chains sampled by Metropolis–Hastings. We also cover weakly CUD points. If a regular and homogenous Metropolis–Hastings sampler is consistent for independently and identically distributed u_i, then it is also consistent for u_i that are CUD or weakly CUD:

Theorem 3. Let x₀ ε Ω = {ω₁,..., ω_K}. Suppose that for i ≥ 0 the proposal y_i+1 ε Ω is generated (u_di+1,..., u_di+d–1) by a homogenous regular proposal and that x_i+1 is given by Eq. 5. Assume that

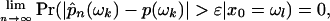[7]

holds for all ω_k, ω_l ε Ω and all ε > 0 when u_i are independent U[0, 1] random variables. If u_i are replaced by CUD u_i, then the consistency result 3 holds. If u_i are replaced by weakly CUD u_i, then Eq. 7 still holds.

Proof: First, we assume that u_i are CUD and then define some sets of consecutive u_i for which poor convergence is seen. Given x₀ the value p̂_n(ω_k) is a function of u₁,..., u_nd, though we suppress this dependence to avoid unwieldy notation. With this understanding, pick ε > 0 and let

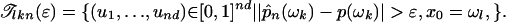From Eq. 7 there is a value m such that Vol(𝒯_lkm(ε)) < ε/K for all l, k ε {1,..., K}. Let 𝒯_km(ε) = 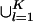𝒯_lkm(ε). Because the proposals are regular, the set 𝒯_km(ε) is Jordan measurable. Also Vol(𝒯_km(ε)) < ε.

For i = 1,..., n let Z_i ε {0, 1} with Z_i = 1 if and only if (u_d(i+m–1)) ε 𝒯_km(ε). Define 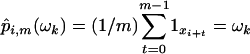. Notice that |p̂_i,m(ω_k) – p(ω_k)| ≤ε holds whenever Z_i = 0, and regardless of x_i–1.

Next we write

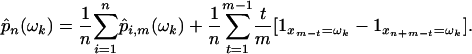[8]

We note that there is a minor error in Chentsov's version of this identity, his equation 19 (30). The second term in Eq. 8 is smaller than m/n. Then,

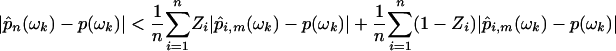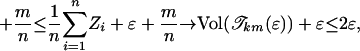as n → ∞, establishing our result for CUD u_i.

If u_i are weakly CUD then as before |p̂_n(ω_k) – p(ω_k)| < (1/n) 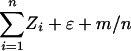. Now taking d = m in the definition of weakly CUD sequences yields for n > m/ε that

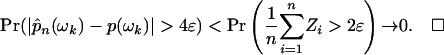Chentsov (30) proves a converse for the standard construction. For the sequence u_i to be suitable for every Markov chain under the standard construction, it must be CUD. For each non-CUD sequence (30) constructs a chain for which that sequence applied to the standard construction fails to be consistent. A converse holds for Theorem 3, too. A sequence u_i that is not CUD must fail to properly cover some rectangle R in some dimension d. We can then construct a chain on {ω₁, ω₂} that samples independently visiting state ω₂ at step i if and only if (u_(i–1)d+1,..., u_di) ε R. So the sequence fails to provide consistent estimates for this constructed chain.

Gibbs Sampler

The Gibbs sampler is slightly different from the other samplers. Minor changes are required to handle it. We outline the details in this section.

In MCMC, we use d for the number of variables u_j needed to generate a transition. Let D be the (finite) number of components of x_i. This D may differ from d. The random scan version of the Gibbs sampler takes the changing components j(i) independent and uniformly distributed on {1,..., D}. Accordingly, only one random variable is needed to choose j(i). To fit our framework the same number m of random numbers must be required to make the proposal y_i+1 regardless of j(i). When inversion is used, then m = 1. Counting the acceptance variable, d = m + 2 for random scan Gibbs. If updating the jth component takes m_j <∞ random variables, then one can take m = max_1≤j≤D m_j and simply ignore m – m_j(i) of the u_l values at step i.

Because all proposals are accepted in Gibbs sampling, the values u_di for i ≥ 1 are not even used by the method. Instead of ignoring every dth variable, it is more natural to use the whole sequence in blocks of d – 1 values, with u_(d–1)i+1,..., u_(d–1)(i+1) generating y_i+1 = x_i+1. Let û_i be a sequence made by taking consecutive blocks of d – 1 u_i values and inserting some value v_k ε [0, 1] between the kth and k + 1-st block. The value v_k provides the (ignored) variable that determines acceptance of y_k. If there exists a sequence v_k for which û_i is CUD, then Theorem 3 applies to the Gibbs sampler. In fact, independent random v_k ∼ U[0, 1] yield a weakly CUD sequence û_i, and so Eq. 7 holds for Gibbs sampling driven by û_i. But p̂_n is not random because it ignores the v_k, and so Eq. 7 implies that the consistency Eq. 3 also holds for random scan Gibbs sampling.

Deterministic scan Gibbs sampling does not have homogenous proposals. There are D different proposal distributions. Commonly the component j(i) with a proposed change in y_i+1 satisfies j(i) – 1 = i mod D. Rather than considering a general nonhomogenous sampler, one instead can split the chain x_i into D subchains of the form x_l+Di for i ≥ 1 and 1 ≤ l ≤ D. Each such chain is homogenous, and if each of them is consistent, then so is the original chain.

Illustration

Our consistency results show that as n → ∞, the QMC–MCMC estimate 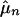will converge to μ. They do not indicate whether QMC–MCMC is better than MCMC, either asymptotically as n → ∞ or in finite sample sizes. The asymptotic superiority of QMC over MC is well established for finite dimensional problems with sample size approaching infinity. To study the effect of finite sample sizes, infinite dimensions, and the use of continuous instead of discrete state spaces, we try some small numerical examples.

Our first example has for p the N(0, 1) distribution, and we study estimates of μ = E(x), known to be zero. We consider the independence sampler with proposals y_i ∼ N(0, 2.4²), for which the acceptance rate is ∼50%. We also consider a random walk sampler, y_i ∼ N(x_i–1, 2.4²). For each proposal type, the MC version used pseudo-random numbers to propose and accept/reject (by means of Eq. 2) for 65,521 steps. The QMC version used all 65,521 points from the LCG with N = 65,521 and a = 17,364 given in ref. 8. They were arranged in order (0, 0), (u₁, u₂), (u₃, u₄),..., (u₆₅₅₁₉, u₆₅₅₂₀), (u₂, u₃), (u₄, u₅),..., (u₆₅₅₂₀, u₁). We applied Cranley–Patterson rotation to these N pairs. The first element in each pair generates the proposal, and the second generates the accept/reject decision.

Each algorithm was repeated 300 times. The mean and mean squared error taken over the 300 answers are displayed in Table 1. In each case the mean is close to the true answer, zero. The square mean is small compared with the mean squared error (MSE) so that bias is a negligible part of the MSE. QMC achieves a MSE reduction factor of 2.65 for the random walk example and 10.3 for the independence sampler.

Table 1. Comparison of QMC and MC for independence sampling and random walk sampling on a small numerical example.

	Independence		Random walk
	Mean	MSE	Mean	MSE
MC	-3.58 × 10-4	3.44 × 10-5	-7.90 × 10-4	6.67 × 10-5
QMC	-7.50 × 10-6	3.32 × 10-6	4.10 × 10-4	2.52 × 10-5

QMC reduces the MSE by 10.3 for the independence sampler and by 2.65 for the random walk.

Our second example has been used by refs. 4 and 32. It features 10 pumps, of which pump j has failed s_j times in t_j × 1,000 h. The statistical model is Poisson with Pr(n_j = m) = e^–λ_j t_j (λ_jt_j)^m/m!. The unknown failure rates λ_j ≥ 0 have a Gamma density proportional to 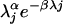where α = 1.802 is known and β ≥ 0 has prior density proportional to β^γ–1e^–δβ where γ = 0.1 and δ = 1. A table with s_j and t_j appears in ref. 32 along with the formula they used to choose α. The state vector x = (β, λ₁,..., λ₁₀) has 11 dimensions.

We used a Gibbs sampler with deterministic cycles. The starting point used the maximum likelihood estimates s_j/t_j for λ_j together with the full conditional mean of β, given the starting λ_j values. The Gibbs sampling was driven by inversion of Gamma CDFs applied to RQMC points, as described in ref. 32. The RQMC points were an 11-dimensional Cranley–Patterson rotation applied to QMC points. The QMC points using N = 1021 and a = 65 from ref. 8 start as (0,..., 0), (u₁,..., u₁₁),...,(u₁₀₁₃,..., u₁₀₂₀, u₁, u₂, u₃), the next run through the RNG starts with (u₄,..., u₁₄), and so on, until all 1,021 vectors have been used once. Each algorithm was repeated 300 times. Table 2 shows variance reductions between ≈14 and ≈210 for QMC–MCMC.

Table 2. Comparison of QMC and MC for pump example.

Pump	MC	QMC	Ratio
λ1	6.71 × 10-7	3.99 × 10-9	168.0
λ2	7.66 × 10-6	5.61 × 10-8	136.5
λ3	1.52 × 10-6	8.92 × 10-9	170.1
λ4	9.79 × 10-7	4.65 × 10-9	210.5
λ5	9.40 × 10-5	7.25 × 10-7	129.8
λ6	1.49 × 10-5	1.09 × 10-7	136.1
λ7	3.31 × 10-4	8.71 × 10-6	38.0
λ8	3.12 × 10-4	2.25 × 10-5	13.9
λ9	3.93 × 10-4	3.96 × 10-6	99.3
λ10	1.84 × 10-4	1.03 × 10-6	178.9
β	8.68 × 10-4	1.07 × 10-5	80.8

Shown are MC and QMC variances and their ratio for the parameters of the pump data model described in the text.

Conclusions

In this work, we have shown that QMC points can be used in Metropolis–Hastings sampling without inconsistency. The points must be CUD. In our numerical examples, the QMC–MCMC hybrid consistently had smaller variance than MCMC, sometimes by a small amount, sometimes by a factor of hundreds. The largest of these gains are better than those reported in related empirical work (2, 4, 6). A rough assessment of our estimated variance reductions can be obtained from the F_300,300 distribution. With 300 replicates, estimated variance reduction factors are within a multiplication factor of 1.25 of the true factors ≈95% of the time. In quadrature problems, the largest QMC gains have been found for integrals of lower effective dimensionality (33). It remains to see where MCMC problems might have similar structure. We saw larger gains in the higher-dimensional Gibbs sampling problem than in the low-dimensional problem, possibly because the lower-dimensional problem involved a discontinuity at the acceptance threshold. We conclude by noting that the extra work in implementing MCMC with QMC is very small. One replaces the RNG by another RNG that has a smaller period and then uses the entire period one or more times.