Evaluating size effects on the thermal conductivity and electron-phonon scattering rates of copper thin films for experimental validation of Matthiessen’s rule

Abstract

As metallic nanostructures shrink towards the size of the electronic mean free path, thermal conductivity decreases due to increased electronic scattering rates. Matthiessen’s rule is commonly applied to assess changes in electron scattering rates, although this rule has not been validated experimentally at typical operating temperatures for most of the electronic systems (e.g., near room temperature). In this study, we experimentally evaluate the validity of Matthiessen’s rule in determining the thermal conductivity of thin metal films by measuring the in-plane thermal conductivity and electronic scattering rates of copper (Cu) films with varying thicknesses (27 nm — 5 µm), microstructures, and grain boundary segregation. Comparing total electron scattering rates measured with infrared ellipsometry to infrared ultrafast pump-probe measurements, we find that the electron-phonon coupling factor is independent of film thickness, whereas the total electronic scattering rate increases with decreasing film thickness. Our findings provide experimental validation of Matthiessen’s rule for electron transport in thin metal films at room temperature and also introduce an approach to discern critical heat transfer processes in thin metal interconnects, which holds significance for the advancement of future CMOS technology.

The authors examine Matthiessen’s rule for determining the thermal conductivity in thin Cu film. They attribute reductions in the thermal conductivity of Cu to electron scattering at boundaries and grain boundary segregation.

Introduction

The electron-driven heat transfer mechanisms in metals are strongly impacted by the electron-phonon interaction, which at room temperature can account for the majority of the electronic scattering processes in bulk metals¹. However, as the physical length scales of these metals (e.g., film thickness and grain size) decrease below that of their intrinsic electron-phonon mean free paths, additional electron-boundary scattering processes can lead to further reductions in thermal conductivity². These series of resistance processes, involving additional electronic scattering mechanisms beyond electron-phonon scattering, are a well-established prediction of Matthiessen’s rule^1,3. The key assumption in Matthiessen’s rule is that the scattering processes are independent (i.e., the presence of one scattering mechanism does not impact the way in which the other scattering mechanism functions). Moreover, Ziman¹ points out that variations in the elastic properties, lattice constants, and electronic structure of the materials could refute this key assumption of Matthiessen’s rule. Indeed, several studies have investigated electron scattering mechanisms, delineating possible shortcomings of Matthiessen’s rule at both low and high temperatures^4–12. These studies have also revealed size-dependent deviations from Matthiessen’s rule in metals at low temperatures^4,5 and in alloys at high temperatures^10–12. At lower temperatures, the size effects in metals arise from the small-angle character of electron-phonon scattering⁴, while the presence of defects can accelerate interactions between electrons, phonons, and defects^6–9. Furthermore, Matthiessen’s rule has been insufficient in explaining changes in resistivity at elevated temperatures for noble metals-based¹² and Al-based alloys^10,11, with the failure in noble metal-based alloys attributed to alterations in the phonon spectral function. While room temperature investigations on metal/nonmetal substrates^13,14 reveal emerging interference mechanisms among electron scattering processes when the film thickness approaches the electron mean free path, this rule has not been verified experimentally at room temperature to the best of our knowledge. Given the scientific and technological importance of electrical and thermal transport of thin metal films for the future of interconnects in electronic devices^15–17, the fundamental understanding of which relies on intimate knowledge of various competing electronic scattering processes, the ability to validate Matthiessen’s rule is critical.

In this work, we measure the thermal conductivity and electron-phonon coupling factor of a series of thin Cu films with thicknesses ranging between 27 nm and 5 µm. The polycrystalline films are processed to vary their grain size and grain boundary segregation. We measure the in-plane thermal conductivity of these Cu films using a novel steady-state thermoreflectance (SSTR), demonstrating reductions in thermal conductivity due to boundary scattering for the thin, small-grained films, with additional reductions in thermal conductivity arising in annealed films with grain boundary segregation. Our measurements agree well with first-principles-based calculations of the electronic thermal conductivity of Cu. We also confirm, using an infrared variable angle spectroscopic ellipsometry (IR-VASE), that the reduction in thermal conductivity is due to an increase in electron scattering rates. Our ability to measure in-plane thermal conductivity with a pump-probe thermoreflectance technique also facilitates direct comparison of our measured thermal conductivity with values derived from electrical resistivity measurements, thus assessing the application of the Wiedemann–Franz Law with the low-temperature value of the Lorenz number (L₀) to calculate the in-plane thermal conductivity of these films. To gain more fundamental insight into the trends in thermal conductivity at different film thicknesses and annealing conditions, we employ an ultrafast (sub-picosecond) pump-probe technique with a variable probe wavelength in the infrared regime to monitor the intraband transient thermoreflectance response of the Cu films and extract the electron-phonon coupling factor (G). We show that G in the Cu films is relatively constant regardless of thickness, grain size, and grain boundary segregation changes in the Cu films, and agrees well with our first-principles calculations of the full electron-phonon coupling matrix to determine G. By comparing our measured values of thermal conductivity, total electronic scattering rates, and G, our experimental results indicate that electron-phonon scattering processes are independent of electron-boundary and electron-segregation scattering processes in their respective contributions to reducing thermal conductivity, thus providing experimental validation of Matthiessen’s rule for electronic transport in Cu.

Results

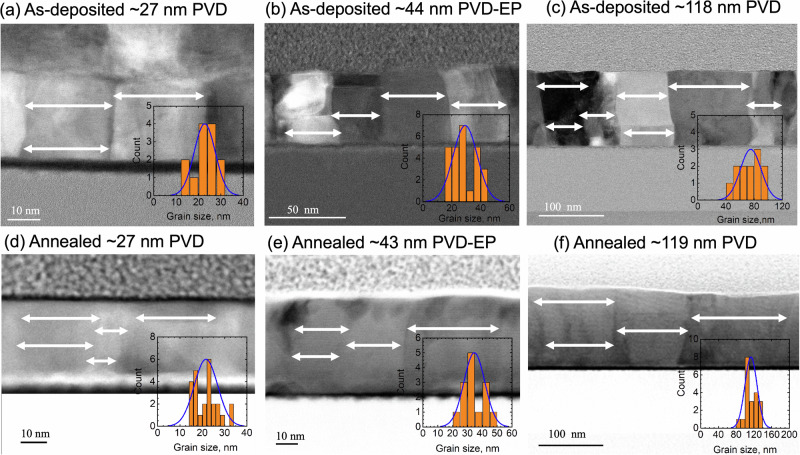
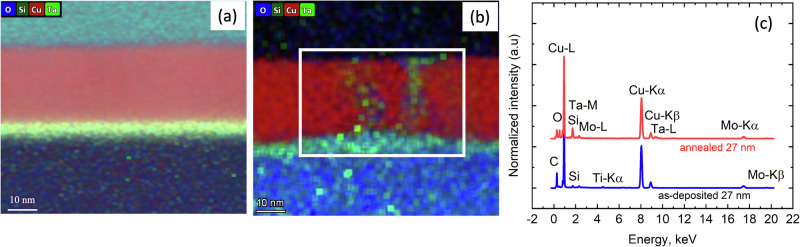
We grow a series of Cu films ranging from 27 nm to 5 µm thick on 3 nm Ta/100 nm SiO₂/Si by physical vapor deposition (PVD) and electroplating (EP) methods described in detail elsewhere^18,19. We have practical limitations when growing Cu films by PVD beyond the thicknesses of ≈100 nm. Therefore, we exclusively synthesize 27, 57, and 118 nm films using the PVD technique. To synthesize thicker films (>100 nm), we employ EP methods, supplemented by a 10 nm fixed PVD Cu seed layer (PVD-EP). The films synthesized by different methods exhibit similar morphology and surface roughness. They do not contain considerable levels of oxygen and other impurities. Hence, their in-plane thermal conductivity and electron-phonon scattering rates should not be impacted by the synthesis method. To vary the microstructure of the Cu films, we then anneal a subset of these as-deposited films at 300, 400, and 500 °C for 15 min in argon. We examine the resulting grain morphology and chemical composition of the Cu films with scanning transmission electron microscopy (STEM). We find that grain coarsening occurs in most of the characterized films after annealing (as shown in Fig. 1, Table 1, and Supporting Information). However, annealing of the 27 nm Cu PVD film does not increase its grain size, as shown in Fig. 1a, d. The grain coarsening of 27 nm Cu film during annealing is impeded by Ta migration in the grain boundary and subsequent oxidation, as shown in the corresponding energy-dispersive X-ray (EDX) analysis in Fig. 2b, c. The thermal stability of Cu/Ta/SiO₂/Si structures has been thoroughly investigated under annealing conditions^20–22. During annealing of 27 nm Cu at 500 °C, Ta undergoes diffusion along its grain boundaries (Fig. 2b) since it is not soluble in its grains^20,23. The oxygen already present along grain boundaries oxidizes Ta and leads to form TaO_x complexes, which act as the scattering centers for the electron. Segregation phenomena also occur in other materials, such as Al and Mg-based alloys^24,25, during annealing due to solubility issues. In a segregation scenario, the potential barrier of the grain boundary might modify, which can alter the grain boundary scattering and reduce the thermal conductivity of the system^26–28. The segregation can significantly impede the heat carrier mobility at the grain boundaries and increase the thermal resistance. Thus, for any given Cu film thickness, TaO_x segregation to grain boundaries will introduce an additional, and potentially limiting, electronic scattering process.

Fig. 1. The microstructure of as-deposited and annealed Cu films.

STEM image of (a–c,) as-deposited ≈27 nm PVD, ≈44 nm PVD-EP, and ≈118 PVD films, respectively. The morphology of these films after annealing at 500 °C is shown in (d–f). The micrographs show the representative area of the as-deposited and annealed films. The grain size distribution of both as-deposited and annealed films is shown in the inset. The grains of these films are columnar. There is no noticeable porosity in the films. Annealing at 500 °C leads to grain coarsening in most of the characterized films, as shown in (e, f) and Table 1.

Table 1.

Synthesis method, thickness, and grain size of the as-deposited and annealed Cu films at 500 °C

STEM thickness of as-deposited PVD films (nm)	Grain size of as-deposited PVD films (nm)	STEM thickness of annealed PVD films (nm)	Grain size of annealed PVD films (nm)	STEM thickness of as-deposited PVD-EP films (nm)	Grain size of as-deposited PVD-EP films (nm)	STEM thickness of annealed PVD-EP films (nm)	Grain size of annealed PVD-EP films (nm)
≈27.0	22.8  ± 4.6	≈27.0	21.6 ± 5.2	≈44.0	29.2 ±  8.2	≈43.0	34.6 ± 6.8
≈57.0	32.9 ± 7.2	≈57.0	49.4 ± 7.3	≈109.0	62.7 ± 15.9	≈119.0	125.8 ± 13.9
≈118.0	75.2 ± 14.1	≈119.0	113.4 ± 13.4	≈595.0	289.9 ± 37.8	≈559.0	672.1 ± 170.8
				≈1108.0	926.8 ± 173.8
				≈5550.0	978.3 ± 290.6

The thickness and grain size of the films are determined over a large area. We find that the thickness of PVD films is uniform. Thick PVD-EP films (thickness of ≈109 nm or greater) exhibit non-uniform thickness (see also in Supporting information). However, this variation does not impact the in-plane thermal conductivity trends, as both the grain size and film thickness are significantly larger than the electron mean free path. The grain size does not vary much for as-deposited PVD and PVD-EP films having comparable thicknesses.

Fig. 2. The appearance of grain boundary segregation due to annealing.

EDX mapping of a as-deposited 27 nm Cu PVD film and b 500 °C annealed 27 nm Cu PVD film. c EDX spectra of as-deposited and 500 °C annealed 27 nm PVD films. During annealing of 27 nm Cu at 500 °C, Ta undergoes diffusion along its grain boundaries (Fig. 2b) since it is not soluble in its grains^20,23. The oxygen already present along grain boundaries oxidizes Ta and leads to form TaO_x complexes, which act as the scattering centers for the electrons.

We measure the in-plane thermal conductivities of the films with the SSTR technique, the details of which are extensively discussed elsewhere^29,30. In short, SSTR is a pump-probe technique that operates in the low-frequency limit of pump modulation (e.g., 1000 Hz) where the steady-state thermal gradients are induced by the pump heating. These steady-state conditions make the SSTR measurements more sensitive to the in-plane thermal conductivity of thin films compared to other thermoreflectance techniques under similar experimental conditions (e.g., similar pump and probe spot sizes, shape, and alignment)^29–31. To facilitate constant opto-thermal transduction among all Cu film thicknesses and avoid any non-thermal optical artifacts from the substrate, we coat the Cu films with a 20 nm Al/60 nm Ti transducer. This thickness ensures optical opacity, maximum thermoreflectance sensitivity at our probe wavelengths (i.e., with the Al surface), and minimizes in-plane spreading of the pump energy. To this later point, by suppressing the in-plane thermal conduction in the transducer, with the majority of its thermal resistance being that of Ti, we ensure better sensitivity to the in-plane thermal conductivity of the Cu. The thicknesses of the films are verified by STEM analysis. All other pertinent details regarding the experiments, analysis, and uncertainties are provided in the Method section and Supporting Information.

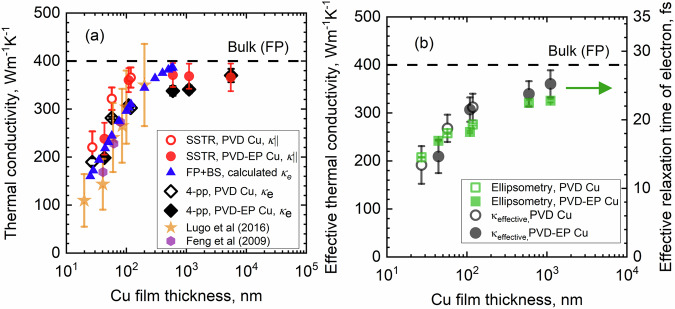
Figure 3a shows that SSTR measured in-plane thermal conductivities (k_||) (indicated by red circle symbol) of as-deposited Cu films with thicknesses of ≈109 nm or greater remain relatively constant within uncertainty. At these thicknesses, both the grain sizes and film thicknesses are larger than our calculated electronic mean free path (λ_ep ≈39 nm), which are in agreement with those reported by Gall³². Note that we determine this average mean free path for electrons with energies near and at the Fermi energy of copper through our density-functional perturbation theory (DFPT) calculations (details in Supporting Information). The thermal conductivity of thicker as-deposited Cu films (thickness >100 nm) is within the uncertainty of our calculated bulk value, and is consistent with literature³³. We observe a reduction in thermal conductivity for the films with thicknesses less than the electron mean free path, which is expected due to electron-boundary scattering. For the three thinnest Cu films (with thicknesses ≤57 nm), the thermal conductivities of the as-deposited films drop from that of bulk, implying the occurrence of additional electron scattering processes that suppress the electron mean free path. In these as-deposited cases, the average grain sizes are less than both the film thicknesses and smaller than λ_ep (Fig.1 and Table 1), and therefore we attribute the reduction in thermal conductivity to scattering at both grain and film boundaries.

Fig. 3. Thermal transport in Cu film based on its thickness and electron scattering rates.

a In-plane thermal conductivity (k_||) of the as-deposited Cu films measured with SSTR is indicated by a red circle symbol. The dashed line represents the calculated bulk thermal conductivity of Cu from our first-principles (FP) calculations. The solid triangle symbol shows the electrical thermal conductivity of Cu film for different thicknesses procured by calculating the total scattering rate of electrons using Matthiessen’s rule to include boundary scattering (BS) of electrons along with the electron-phonon scattering rate obtained from first-principles calculations (FP + BS). SSTR measured in-plane thermal conductivity of the as-deposited Cu films mostly comply with the thermal conductivity of the same films derived from the application of the Wiedemann–Franz law to electrical resistivity measurement (presented by black diamond symbol) assuming the low-temperature value for the Lorenz number. The calculated thermal conductivity using first principles is greater than the experimental value found with the 4-point probe method. This discrepancy happens because our calculations are performed with a constant electron-boundary scattering length of ≈39 nm. However, the grain size of the Cu films (Table 1 and Fig. 1) can be less than ≈39 nm. With a reduced grain size, there is more grain boundary scattering which decreases the measured electrical thermal conductivity^38–40 compared to the calculated value. However, our measured thermal conductivities are found to be close to those reported in the previous works for similar film thicknesses^34,35. b The effective thermal conductivity (black circle symbol) calculated from the cross-plane and in-plane thermal conductivities shows a thickness-dependent trend similar to the relaxation time of electrons (green square symbol) in different thicknesses of Cu films determined from IR-VASE measurements.

Indeed, we extract the effective electron scattering rates in these as-deposited Cu films by fitting a Drude oscillator model on their wavelength-dependent IR-VASE data. As shown in Fig. 3b, the relaxation time of electron (green square symbol), which is found from the extracted scattering rates, exhibits a thickness dependence trend complying with the trend of effective thermal conductivity (details in Supporting Information), indicating that the reduction in thermal conductivity is due to an increase in electron scattering rates. Our DFPT-calculated thermal conductivity (blue triangle symbol) of these thin films shows a similar trend as the measured values: it decreases when thickness is below λ_ep, as depicted in Fig. 3a. Here, we account for the boundary scattering of electrons computed using Matthiessen’s rule along with the electron-phonon scattering rates acquired from DFPT calculations to quantify total thermal conductivity. The first principle calculations slightly underpredict the measured thermal conductivities of thin films by SSTR. This discrepancy may be related to our calculated Fermi velocity (≈1.05 × 10⁶ m/s) being smaller than literature values³², mainly due to computational constraints, particularly pseudopotentials and k-point grid. Higher thermal conductivity values measured by the SSTR can also be attributed to the larger thicknesses and grain sizes of these films as compared to the electron mean free path. Therefore, the first-principles calculations, which take into account a constant electron-boundary scattering length of λ_ep, predict lower values of thermal conductivity for these films as compared to the SSTR.

Moreover, Fig. 3a depicts that our measured thermal conductivities are comparable to those reported in previous works for similar film thicknesses^34,35. To assess the adherence of these Cu films to the Wiedemann–Franz law, we also determine k_e derived from four-point probe measurements of electrical resistivity, using this Wiedemann–Franz Law with the low-temperature value for L₀ = 2.44 × 10⁻⁸ WΩK⁻². These electrical resistivity-derived values (black diamond symbol) are compared with SSTR measured k_|| in Fig. 3a. They generally agree within our experimental uncertainty, which is owing to negligible phononic contribution to the thermal conductivity of Cu (<6% for the bulk value)^36,37. The slight deviation in a few films is due to electron-grain boundary scattering (see Supporting Information). The grain size of these films is smaller than or approaches the length scale of the electron mean path. Prior works have found that grain boundary scattering reduces the electrical conductivity more than the in-plane thermal conductivity^38–40, which also leads to a higher Lorenz number than L₀. On the other hand, a previous study demonstrates that the Lorenz number of a suspended Cu film is lower than that of L₀ by ~20%⁴¹; we do not currently understand the reasoning behind this discrepancy, however, we find that the 75 nm Cu film reported by ref. ⁴¹ has ~3 times lower thermal conductivity than the films of similar thicknesses reported in our work. Therefore this, combined with different film boundary conditions potentially leading to different electron-boundary scattering interactions, could explain these different conclusions. An investigation into the electronic scattering mechanisms that lead to validation or failure of the Wiedemann–Franz law in Cu is beyond the scope of this work, since our goal is to evaluate the use of Matthiessen’s rule in describing the electronic scattering processes that contribute to thermal conductivity.

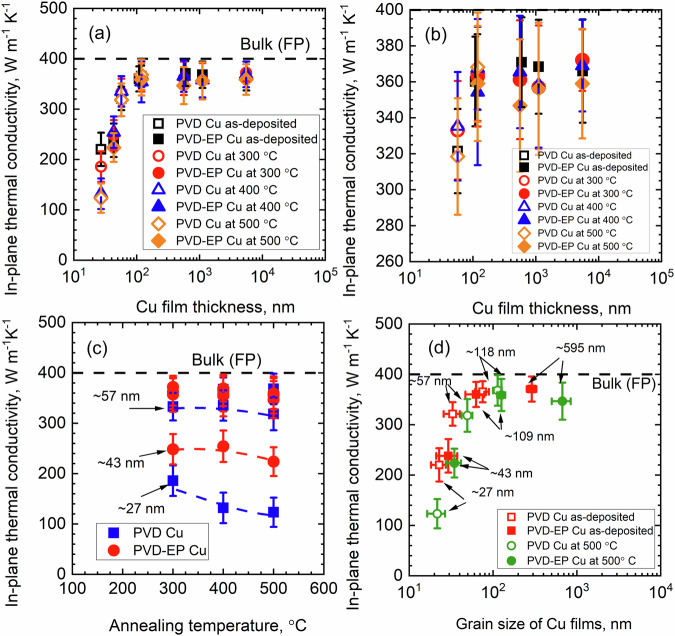
While annealing generally increases the length scale of the electron-grain boundary scattering process, it can introduce segregation at the grain boundary, as depicted in Fig. 2, the presence of segregation at the boundaries accelerates electron scattering rates. We study the effect of grain coarsening and segregation at the grain boundary on thermal conductivity. Figure 4a shows the in-plane thermal conductivity of Cu annealed at different temperatures. Annealing reduces the thermal conductivity of the PVD-grown thin films, which we attribute to the presence of TaO_x defect complexes along the grain boundaries. Note, since annealing did not change the grain size of the 27 nm films, as shown in Fig. 1d and Table 1, this reduction in k_|| cannot be ascribed to an increase in the electron-boundary scattering processes. As further support for this assertion, we observe no TaO_x formation in thicker PVD films and all other PVD-EP films, and hence their thermal conductivity remains unchanged after annealing.

Fig. 4. Annealing effect on the in-plane thermal conductivity.

SSTR measured in-plane thermal conductivity of our annealed Cu films as a function of a, b thickness, c annealing temperature, and d grain size. Figure 4b is the magnified version of Fig. 4a for the thickness of ≈57 nm or greater. The thickness of the films is indicated with arrows in Fig. 4c, d. Figure 4c features trace lines for film thicknesses of 27, 43, and 57 nm, highlighting thermal conductivity trends with annealing. The appearance of grain boundary segregation during annealing reduces the thermal conductivity of 27 nm Cu.

Collectively, our thermal conductivity measurements demonstrate reductions due to film thickness, grain size and grain boundary segregation from processing. This finding is consistent with various types of electronic scattering events reducing the electron mean free path. The trends predicted from our DFPT simulations suggest that the reductions in thermal conductivity are driven by boundary scattering, while the intrinsic electron-phonon scattering rates in Cu remain unaffected at these reduced thicknesses and grain sizes, consistent with Matthiessen’s rule. We also observe relatively sizeable reductions in the thermal conductivity due to the grain boundary segregation that arises from processing—a scattering process that is more challenging to account for in DFPT due to finite simulation size considerations. Thus, based on thermal conductivity measurements alone, the fundamental electronic heat transport mechanisms and whether intrinsic electron-phonon scattering remains unaffected with reductions in thickness, grain size and grain boundary segregation spacing—thus adhering to Matthiessen’s rule—is still speculative.

To rectify this and gain further insight into the electron scattering mechanisms in Cu films, we measure the electron-phonon coupling rates using a sub-picosecond pump (2.38 eV)-probe (0.775 eV) technique on films with thicknesses ranging from 27 to 5550 nm. The advantage of using this near-infrared probe energy in monitoring the ultrafast dynamics of the excited electrons in Cu is that this probe energy is much less than the interband transition energy of Cu (2.16 eV)^42,43. This allows us to measure a nearly free-electron-like thermoreflectivity response, with the resulting temporal dynamics being indicative of electron scattering near the Fermi surface, thus providing direct insight into the diffusive electronic transport. Additionally, probing the free-electron dynamics after the pump heating simplifies the extraction of the electron–phonon coupling factor (G) from the transient optical response of the films, as we have reported in detail previously⁴⁴.

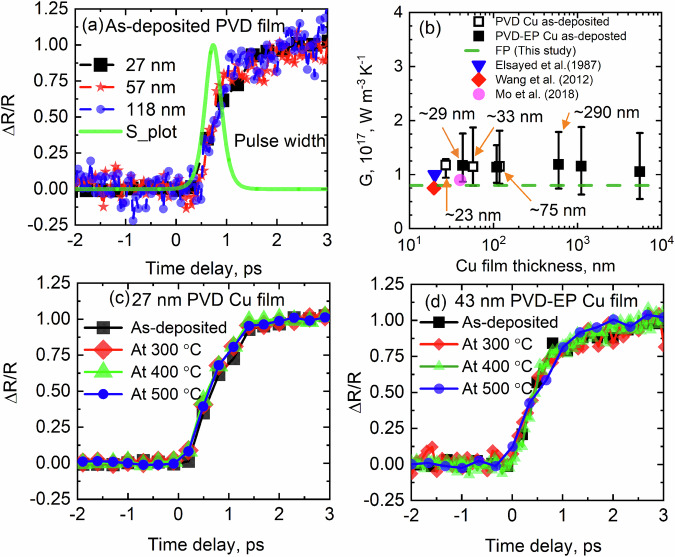
Figure 5a shows the ultrafast thermoreflectivity response of as-deposited PVD Cu films. After pump excitation, the excited electrons at high temperatures equilibrate with the lattice via electron-phonon scattering. The nearly identical signals of as-deposited 27, 57, and 118 nm Cu films indicate that electron-phonon scattering is not influenced by changes in grain size or thickness. We observe the same response in the as-deposited electroplated Cu films (see Supporting Information). We quantify G from our measurements with the two-temperature model (TTM; details in Supporting Information). Figure 5b shows that G is relatively constant with Cu film thickness and grain size. The derived G is consistent with prior measurements on Cu films for the comparable thickness^42,45,46. Note we also verify our TTM-derived G using first-principles calculations. We consider both electron and phonon density of states to calculate G as explained in the Supporting Information. The calculated G from the first-principles calculations is consistent with our TTM-derived values and prior first-principles calculations⁴⁷. TTM-derived G is insensitive to changes in the pump-probe energies. The longer pulse duration minimizes the contribution of non-thermalized electrons to the electron-phonon coupling factor, leading to a more consistent coupling factor^48,49 (see details in the Supporting Information). We expect a near-thermalized Fermi distribution during the pump-probe time regime in which we determine G. The electron-electron scattering can be considered negligible, and the near-thermalized Fermi distribution of electron cools due to electron-phonon scattering⁴⁷. This process is indicative of the scattering that influences the electron thermal conductivity of Cu.

Fig. 5. Electron-phonon interactions at non-equilibrium conditions.

a Normalized thermoreflectance as a function of pump-probe delay time for as-deposited 27, 57, and 118 nm Cu films at probing energy of 0.775 eV. b Two-temperature model derived electron–phonon coupling factor (G) of the as-deposited films, with grain sizes indicated for selected films. G across the film thicknesses remain constant within uncertainty. Our TTM-derived electron-phonon coupling factor is in agreement with our first-principles calculations (green dashed line) and reported values from the literature^42,45,46 (c, d) normalized thermoreflectance as a function of pump-probe delay time for as-deposited and annealed for 27 and 43 nm Cu films at probing energy of 0.775 eV. The films exhibit almost identical transient reflectivity rises at as-deposited and different annealing conditions.

While the electron-phonon coupling factors in our Cu films are relatively constant within uncertainty, the thermal conductivity of Cu decreases for thicknesses at 57 nm and below, which we attribute to electron-boundary scattering processes, as confirmed by our IR-VASE measurements (c.f., Fig. 3b). The constant G values of these thin films imply that electron-phonon scattering is not impacted by boundary scattering, indicating that electron-boundary scattering processes act independently from the electron-phonon scattering process, thus providing experimental validation of Matthiessen’s rule for electronic thermal transport in Cu.

In further agreement with Mattheissen’s rule, grain boundary segregation in annealed Cu films also does not influence the electron-phonon scattering rate. Figure 5c, d represent the ultrafast transient dynamics of the as-deposited and annealed 27 and 43 nm Cu films, which show nearly identical transient reflectivity rise for these films. Note that we observe the grain boundary segregation in the annealed 27 nm film, and thus we conclude that neither grain size nor the changing grain boundary segregation is influencing G even though thermal conductivity is impacted. To confirm this observation, we perform our TTM calculations to obtain G for annealed film thickness ranging from 27 to 5550 nm. We find G of these annealed films do not change due to the presence of segregation, as shown in Supplementary Fig. 31.

To sum up, Matthiessen’s rule is validated for determining the thermal conductivity in thin Cu films across different thicknesses, microstructures, and grain boundary segregation. We ascertain the reductions in the thermal conductivity of Cu stemming from electron scattering at boundaries and grain boundary segregation employing cutting-edge experiments and analyses, while the electron-phonon coupling factor remains consistent. These outcomes offer experimental evidence supporting Matthiessen’s rule in electronic transport within Cu, providing crucial insights for the development of future CMOS technology. Furthermore, our research underlines the critical role of Matthiessen’s rule in estimating thermal conductivity within integrated circuits, highlighting its pivotal role in guiding semiconductor device design, and optimizing its performance.

Methods

First-principles calculations

We study the electron-phonon interactions in Cu employing the Electron-Phonon Wannier (EPW) framework within Quantum Espresso⁵⁰. The Eliashberg spectral function α²F(ω) is determined to quantify electron-phonon coupling strengths across each phonon mode. The overall electron-phonon coupling strength, λ, is evaluated as the Brillouin zone average of mode-specific coupling strengths λ_qv for a particular mode v and wave vector q. These calculations are carried out within the dense grids of electron and phonon wave vectors through interpolation using maximally localized Wannier functions derived from Bloch energy bands⁵¹. The PS Library’s norm-conserving pseudopotentials for Cu are implemented⁵², with a plane wave cutoff set at 1632.7 eV (120 Ry). The overall coupling parameter λ at room temperature, is ≈0.13, agrees well with prior findings⁵³. Using parameter-free density-functional perturbation theory (DFPT), we compute electron-phonon scattering rates, and the average mean free path of electrons (Λ) in copper is calculated to be ≈39 nm, which is also in excellent agreement with prior theoretical calculations³². Electronic density of states (eDOS) and the Fermi surface of Cu are calculated using Quantum Espresso. Using this information, we calculate the temperature-dependent electronic heat capacity and electron-phonon coupling factor (G). The calculated G is ~8 × 10¹⁶ W m⁻³ K⁻¹, closely matching previous calculations⁴⁷. The thermal conductivity of Cu at room temperature is estimated to be ~400 W m⁻¹ K⁻¹, which complies with our experimental measurements. We introduce the effect of boundary scattering on the total electron scattering rate as⁵⁴:

$$\frac{1}{{\tau }_{\mathrm{tot}}}=\frac{v_F}{\mathrm{\Lambda }}+\frac{v_F}{d}$$ 1

where d is the thickness of the thin film, and τ_tot represents the total scattering rate, including electron-phonon and boundary scattering of electrons, v_F is the Fermi velocity (≈1.05 × 10⁶ m/s) of Cu. Here, we consider electron scattering primarily with phonons at room temperature and discard electron-electron scattering. Further details of the first-principles calculation can be found in the Supporting Information.

Scanning transmission electron microscopy (STEM)

We investigate the grain morphology and chemical composition of Cu films through scanning transmission electron microscopy (STEM). Cross-sectional samples are prepared using a Thermo Fisher Helios system and are thinned to 50 nm or less. A platinum layer is deposited on the Cu films to mitigate damage from the gallium ion beam during thinning. STEM analysis is conducted using a Thermo Fisher Scientific Themis Z-STEM, which operates at 200 kV and is equipped with a SuperX detector for compositional analysis at a beam current of 400 pA. Bright-field scanning transmission electron microscopy (STEM) and high-angle annular dark field (HAADF) imaging are performed concurrently; bright-field images are utilized for grain size measurement, while HAADF images provide atomic number contrast. The SuperXG2 EDX detector, when operates in STEM mode, can perform simultaneous imaging and elemental mapping, eliminating the requirement for mode switching. We align a sample to an edge-on orientation by observing the diffraction pattern of the Si substrate. We also carry out supplementary TEM imaging and diffraction pattern analysis using a Titan TEM operating at 300 kV. The ImageJ software is utilized to analyze grain size statistically, which enables accurate measurement and quantification of grain size distributions. This analysis is included along with STEM images of different thick Cu films.

In-plane thermal conductivity measurements

We measure the in-plane thermal conductivity using a steady-state thermoreflectance (SSTR) which works based on a linear relationship between the temperature rise and the change in reflectivity on the sample surface^29,30. In this SSTR technique, a 637 nm continuous pump beam is modulated at 1000 Hz and focused on the sample surface to generate a steady-state temperature rise during heating. The change in reflectivity due to this temperature rise is detected by a 785 nm probe laser. Both the pump and probe paths are fiberized until they reach the same 20X magnification microscopic objective⁵⁵. A lock-in amplifier detects the change in probe signal at the modulation frequency of the pump and records the magnitude of this reflected signal. The pump power is varied to alter the probe response keeping the modulation frequency fixed. The linear relationship between the applied pump power and the probe response is a related ratio of temperature to heat flux in the material through a proportionality constant, γ. This γ is determined from a reference sample, typically sapphire, with known thermal properties, using an analogous transducer as the sample of interest. The assumption here is that γ does not change between the samples. The details of this procedure are discussed in ref. ²⁹. After determining γ from the reference sample, the thermal conductivity of any other material can be calculated by the steady-state thermal model²⁹.

Electron–phonon interaction measurements

We study the electron scattering mechanisms in Cu films employing an ultrafast (sub-picosecond) pump-probe technique with wavelength tunability into the infrared to monitor the intraband transient thermoreflectance response of the Cu films. In this technique, a Nd:YVO₄ laser with a central wavelength of ~1040 nm operates at 1 MHz repetition rate. This infrared laser beam is passed through an optical parametric amplifier (OPA). Inside this OPA, a portion of this beam is focused through a second harmonic generation (SHG) crystal to produce a 520 nm (2.38 eV) pump beam. This pump beam amplifies another portion of the laser beam which passes through several delay stages and finally is focused through another SHG to generate a wavelength tunable probe beam. The probe wavelength spans from 600 nm (2.06 eV) to 2500 nm (0.5 eV). The pump pulses with a pulse duration of 379 fs are mechanically chopped at 450 Hz on the optical table. We measure the pump pulse duration by fitting the thermoreflectance signals of Pt using sech² time function discussed in the Supporting Information. In this experiment, we pump the electrons in Cu films out of equilibrium with the phonons at 2.38 eV energy. Then we probe the thermoreflectivity of the heated Cu films as a function of pump-probe delay time with a probing energy of 0.775 eV. This probing energy is far from the interband transition energy of Cu (2.16 eV)^42,43 and allows us to measure a nearly free electron-like reflectivity response. We employ the following two-temperature model (TTM) on the thermoreflectivity response to extract the electron-phonon coupling factors of the Cu films as discussed in detail in the Supporting Information:

$$C_e\left(T_e\right)\frac{\partial T_e}{\partial t}=\nabla \cdot \left({\kappa }_e\nabla T_e\right)-G\left(T_e-T_p\right)+S\left(x,t\right)$$ 2

$$C_p\left(T_p\right)\frac{\partial T_p}{\partial t}=\nabla \cdot \left({\kappa }_p\nabla T_p\right)+G\left(T_e-T_p\right)$$ 3

where $C_e$ and $C_p$ are the heat capacities of the electrons and phonons, respectively, and $T_e$ and $T_p$ are the temperatures of the electrons and phonons, respectively. S (x, t) represents the source term.

Effective electron relaxation time determination

We find the effective electron relaxation time in the Cu films from fitted oscillator models on complex frequency-dependent ellipsometric data. We obtain the ellipsometric data in the spectral range of 750–5000 cm⁻¹ (2–13.33 µm) using an infrared ellipsometer (IR-VASE Mark II, J.A. Woollam Company). We perform the measurements at two incident angles of 60° and 70°, with a resolution of 16 cm⁻¹ (2 meV). Supplementary Fig. 38 shows the measured data for as-deposited Cu films with thicknesses ranging from 27 to 1108 nm. We create an isotropic multi-layer optical model on this measured ellipsometric data to extract the complex frequency-dependent dielectric function of the Cu film. The free-electron contribution dominates the optical properties of the Cu films in the infrared regime. As such, we utilize the Drude free-electron model to determine the optical properties of these films as⁵⁶:

$${\epsilon }_{Drude}\left(\omega \right)={\epsilon }_1\left(\omega \right)+i{\epsilon }_2\left(\omega \right)=1-\frac{{\omega }_p^2}{{\omega }^2+i\mathrm{\Gamma }\omega }$$ 4

where ω_p and Γ are the plasma frequency and the scattering rate, respectively. We optimize the parameters of the Drude model by minimizing the mean square error so that the modeled and measured ellipsometric data agree. We find the effective relaxation time of electron (τ) from the fitted scattering rate in the Drude model as τ = Γ⁻¹.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

M.R.I., J.A.T., C.D.L., and P.E.H. designed the experiments. C.J., S.W.K., and C.D.L. synthesized the films. M.R.I., D.M.H., M.S.B.H., S.Z., K.A., T.W.P., A.G. and P.K. performed the experiments and analyses. P.K. and A.G. performed DFPT calculations. E.R.H. performed the STEM characterization. M.R.I., A.G., and P.E.H. wrote the manuscript.

Peer review

Peer review information

Nature Communications thanks Sooheyong Lee, Michał Piasecki and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Code availability

The code that support the findings of this study are available from the corresponding author upon reasonable request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53441-9.