Abstract
Upon binding to the 15.5K protein, two tandem-sheared G–A base pairs are formed in the internal loop of the kink-turn motif of U4 snRNA (Kt-U4). We have reported that the folding of Kt-U4 is assisted by protein binding. Unstable interactions that contribute to a large opening of the free RNA (‘k–e motion’) were identified using locally enhanced sampling molecular dynamics simulations, results that agree with experiments. A detailed analysis of the simulations reveals that the k–e motion in Kt-U4 is triggered both by loss of G–A base pairs in the internal loop and backbone flexibility in the stems. Essential dynamics show that the loss of G–A base pairs is correlated along the first mode but anti-correlated along the third mode with the k–e motion. Moreover, when enhanced sampling was confined to the internal loop, the RNA adopted an alternative conformation characterized by a sharper kink, opening of G–A base pairs and modified stacking interactions. Thus, loss of G–A base pairs is insufficient for achieving a large opening of the free RNA. These findings, supported by previously published RNA structure probing experiments, suggest that G–A base pair formation occurs upon protein binding, thereby stabilizing a selective orientation of the stems.
INTRODUCTION
The 5′ stem–loop of U4 snRNA binds the 15.5K protein during the hierarchical assembly of the spliceosomal U4/U6 snRNP (1,2). The RNA fold in the crystallographic structure of the complex belongs to the family of kink-turn (K-turn) structural motifs (3). The K-turn was also identified in different loci in the large ribosomal subunit, where it is associated with different proteins such as L30 or L7AE (4–9). It is remarkable that among all the K-turns identified to date, only one is found not to be associated with proteins. Structural data based on X-ray crystallography or NMR are not yet available for the unbound K-turns. However, several studies have shown that the isolated K-turn is a rather flexible entity (10,11). Single molecule fluorescence resonance energy transfer (FRET) studies performed by Goody et al. (10) provided evidence for large amplitude conformational transitions in the K-turn Kt7, which contains most of the motif's consensus sequence [for description of the K-turn nomenclature see (4)]. They observed that the K-turn is dimorphic, undergoing a transition between a closed (‘kinked’) and an open (‘extended’) conformation (‘k–e motion’). The reported k–e motion depended on the ionic strength. However, a significant population of the extended structure was observed even at high concentrations of divalent cations (10). However, our understanding of the atomic details of such transitions remains inadequate.
In the K-turn motif, two stems are connected via a purine-rich asymmetric internal loop. A sharp kink of the RNA backbone in the internal loop allows the stems to form a scissors-like structure. Most of the K-turns have such a kink only on one strand while Kt58 has two kinks, one in each strand. The angle between the stems varies among different K-turns and is sequence-dependent. In most cases, the two stems adopt a conformation close to canonical A-RNA, the non-canonical stem (NC-stem) being extended into the internal loop with several tandem-sheared G–A base pairs or other non-Watson–Crick interactions. The canonical stem (C-stem) lacks the non-Watson–Crick extension. The internal loop consists of a purine-rich sequence with 1 or 2 flipped-out nt and a stretch of non-Watson–Crick interactions such as tandem-sheared G–A base pairs. Several inter-stem contacts (A-minor contacts) bridge the two stems at the origin of their ramification. The scissors-like structure allows proteins such as L15E to bind the K-turns by contacting both the C- and NC-stems, thus playing an important role in folding of large RNAs such as ribosomal RNA.
In the crystallographic structure of Kt-U4, the C-stem consists of three G–C base pairs (G26–C47, C27–C46 and C28–G45), which represent merely a fraction of the long C-stem that reaches deeper into the U4 snRNA. The NC-stem is very short in comparison with the ribosomal K-turns, consisting of only two Watson–Crick base pairs (G35–C41 and G34–C42) that are extended with two tandem-sheared G–A base pairs (G32–A44 and G43–A33) into the internal loop. The uridine U31 is flipped out in a pocket of the 15.5K protein, and two unpaired adenines (A29 and A30) establish a ‘3 + 1’ stacking pattern in which A30 stacks on A44 and A33, while A29 stacks on the G45–C28 base pair of the C-stem (3). The angle between the helical axes of the two stems has a value of 79° when only the two G–C base pairs are considered as the NC-stem, and 65° when the G–A base pairs are also included (values calculated with the CURVES program). In Kt-U4, the NC-stem is attached to a flexible external loop that is thought to play a role in the subsequent binding of the 61K protein to the U4 snRNA (2,12). It has been shown that mutations of the nucleotides forming the G–A base pairs abolish binding of the 15.5K protein (1,3).
Computer simulations have been widely used to study macromolecular motions occurring in processes such as protein–RNA interactions (13–17), RNA folding (18–20), RNA–metal ion interactions (21–23) or macromolecular solvation (24–27). Nevertheless, simulating a protein-assisted RNA folding event poses several challenges: (i) there is a lack of structural data on the free RNA, owing to its flexibility; (ii) the time scale of the transitions relevant for the folding is often significantly larger than that accessible by standard molecular dynamics (MD) protocols; (iii) the evolution of the system during MD simulations is largely dependent on the initial structure; and (iv) there are a multitude of factors influencing the process occurring in the cell.
In two complementary studies, Rázga et al. (28,29) applied standard MD simulations to different ribosomal K-turns and Kt-U4. Although the reported simulations were relatively long (up to 74 ns), only partial opening of K-turns was observed while the G–A base pairs remained stable throughout the simulations. The standard MD trajectories that we obtained for the free Kt-U4 showed a similar behavior of the RNA to that observed by Rázga et al. (28,29) while chemical RNA structure probing experiments indicate that both G32 and G43 are clearly accessible to chemical modifications in the absence of the 15.5K protein (12).
The simulation of RNAs undergoing protein-assisted folding requires the use of enhanced sampling techniques in combination with standard MD if started from their bound structures (12). We have employed standard MD combined with locally enhanced sampling molecular dynamics (LES-MD) simulations starting from the 2.9 Å crystal structure of the Kt-U4 from the Kt-U4–15.5K complex (pdbid 1E7K). LES is a mean-field-based theory that can be coupled with explicit solvent treatment and Particle Mesh Ewald (PME) in constant pressure simulations using periodic boundary conditions (30–33). It functions by dividing the system into separate regions and replacing them with multiple copies. In this way, the energy potential surface is smoothened and the copies are allowed to sample more of the conformational space (34). Such an approach has been successfully employed to explore structural diversity in RNA or protein loops (31,33). It was also shown that the application of LES triggers a large conformational transition in the lateral and diagonal thymine loops of DNA G-quartets (35). However, the structures to which the simulations converged were very different from the experimental structures. Since free energy calculations confirmed that the new structures were more stable, it was proposed that the inconsistencies arose from force-field inaccuracies rather than artifacts introduced by the application of LES methodology.
We reported that the folding of Kt-U4 is assisted by the binding to the 15.5K protein. Using LES-MD simulations, we found that the unbound RNA is significantly more flexible than the bound RNA. Large amplitude motion of opening–closing in the free RNA was accompanied by the loss of secondary structures, such as the G–A base pairs or the stacking patterns. A30 was very flexible, rotating constantly about the N9–C1′ bond. The stability of the Watson–Crick G–C base pairs of the NC-stem depends both on protein binding and on the structure of the RNA loop attached to the NC-stem. The simulations were in excellent agreement with chemical RNA structure probing experiments. The opening–closing motion of the Kt-U4 observed in the simulations may be similar to the k–e transition of the K-turn Kt7 revealed by single molecule FRET experiments. However, FRET does not provide atomic details of the different states involved (10).
The aim of the current study was to provide details of the structural transitions occurring in the LES-MD simulations and to explore correlated motions in the free RNA. We present an in-depth analysis of simulations performed with different LES setups, finding that the largest k–e motion was observed when LES regions were defined both in the internal loop and in the stems (LES4 trajectory). When LES was confined to the internal loop (LES1 trajectory), the RNA adopted an alternative conformation characterized by a sharper kink in the backbone, loss of G–A base pairs and modified stacking interactions. Essential dynamics (ED) of the free RNA in the LES4 trajectory showed that the opening of G–A base pairs was correlated along the first mode but anti-correlated along the third mode with the k–e motion. The dynamics along the third mode were similar to that observed in the LES1 trajectory. Thus, loss of G–A base pairs was insufficient for large opening of the free RNA, the k–e motion of the K-turn being promoted by structural flexibility both in the internal loop and in the helical regions. Based on these findings complemented by the previously published RNA structure probing experiments, we propose that G–A base pair formation occurs upon protein binding, stabilizing a selective orientation of the stems rather than contributing to the k–e motion in the free RNA.
Despite the emphasis on the LES-MD simulations, the reader should be aware that the enhanced sampling simulations were performed in combination with standard MD simulations. While LES proved very useful for studying large conformational transitions, such as the opening of the K-turn, the standard MD simulations provided a more accurate description of fine contacts, such as the inter-stem hydrogen bonds (A-minor contacts) (12,29).
MATERIALS AND METHODS
LES-MD simulations
The free RNA and the complex were simulated by standard MD protocols with explicit solvent and neutralizing Na+ ions using the Cornell et al. (36) force field as described previously (12). The equilibrated structures from standard MD simulations were used as input for LES-MD simulations. The LES systems were set up with the ADDLES program and the simulations were performed using the SANDER module from the AMBER7 distribution (37). All LES-MD simulations were 10 ns long and were performed for both the bound and unbound RNAs on 16 CPUs on a p690 IBM cluster running on AIX 5.2 operating system. All the LES setups that produced trajectories in which the bound RNA was unstable were excluded from further processing.
Here, we present results obtained using three different LES setups. For the LES4 trajectory, four different LES regions were defined in the RNA and each region was replaced with four identical copies: (i) C27, C28, G45 and G46 (two G–C base pairs from the C-stem); (ii) A29, A30 and U31 (the unpaired nucleotides); (iii) G32, A33, G43 and A44 (the tandem-sheared G–A base pairs); and (iv) G34, G35, C41 and C42 (the two G–C base pairs of the NC-stem). For the LES1 trajectory, one region confined to the entire internal loop (A29, A30, U31, G32, A33, G43 and A44) was replaced with four identical copies. For the LES2 trajectory, two different regions were defined in the RNA and each region was replaced with four identical copies: (i) A29, A30, U31, G32, A33, G43 and A44 (the internal loop); and (ii) G34, G35, C41 and C42 (the two G–C base pairs of the NC-stem).
All LES-MD trajectories presented were performed on the naturally occurring RNA sequence that has the flexible pentaloop attached to the NC-stem (K2 RNA). Since this external loop was not revealed by the crystallographic structure, we modeled the loop as described previously (12).
The trajectories were decomposed into individual trajectories of each copy, further processed, visualized and analyzed using the VMD software (38) and the ptraj and carnal modules from the AMBER7 distribution. In the final step, snapshots were taken every 10 ps for data visualization.
Final figures were generated with COREL DRAW. The structural snapshots in Figures 1, 5 and 8 were taken with VMD, the graphs in Figures 2, 6 and 7 were created with GRACE and the scatter 3D graphs in Figures 3 and 4 were drawn in MATLAB.
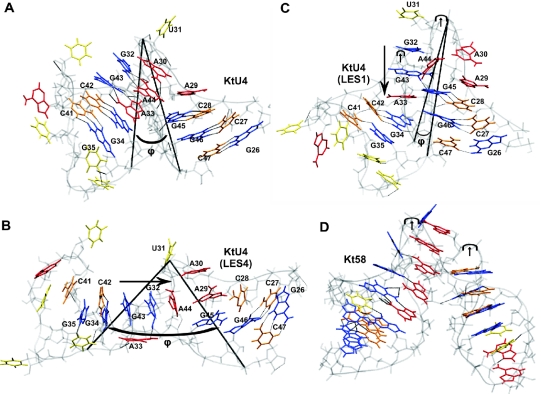
Figure 1.
Different conformations of Kt-U4; guanines are shown in blue, cytosines in orange, adenines in red and uracils in yellow; long arrows indicate newly formed stacking patters; the short arrows indicate the kink in the backbone; ϕ is the angle between the P atoms of C47, U31 and G35. (A) Kt-U4 RNA structure from the crystallographic structure of Kt-U4–15.5K complex with the UUUAU external loop modeled. (B) Open conformation observed during the LES4 trajectory. (C) Tightly kinked alternative conformation captured in the LES1 trajectory. (D) Structure of the Kt58 for comparison with the structure in Figure 1C.
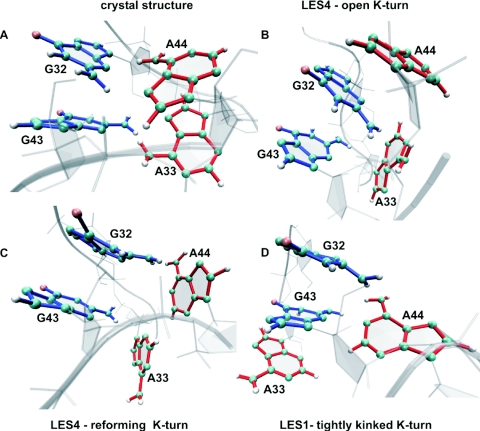
Figure 5.
Structural view of the transitions between different stacking patterns in the free RNA. (A) G32/G43 and A44/A33 stacking interactions as observed in the crystal structure of Kt-U4–15.5K complex. (B) A44/G32/G43 stacking interactions formed in the LES4 trajectory after ∼7 ns. (C) Rotation about the N9–C1′ bond in A33 and A44 as observed in the LES4 trajectory after ∼9 ns. (D) G32/G43/A33 stacking interactions formed in the LES1 trajectory. Guanines are blue, adenines red, oxygens pink, nitrogens cyan and the sugar–phosphate backbone gray.
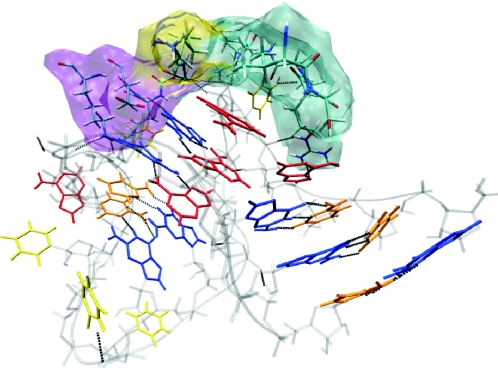
Figure 8.
Protein cavity at the protein–RNA interface; α-helical regions are shown in purple, β-sheet regions in yellow and unstructured regions in cyan. For RNA coloring see Figure 1.
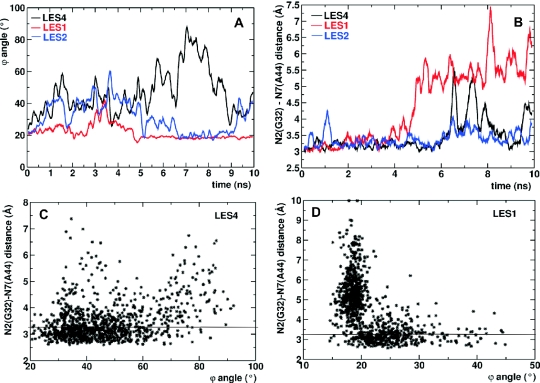
Figure 2.
Correlation between opening of G–A base pairs and the k–e motion. (A) The ϕ angle during the LES4 (black), LES1 (red) and LES2 (blue) trajectories. (B) The distance d between N2 of G32 and N7 of A44 during the LES4 (black), LES1 (red) and LES2 (blue) trajectories. (C) 2D diagram of d(ϕ) in the LES4 trajectory. (D) 2D diagram of d(ϕ) in the LES1 trajectory. In (C) and (D), the maximal donor–acceptor distance (3.2 Å) for hydrogen-bond interaction is indicated with a horizontal line.
Figure 6.
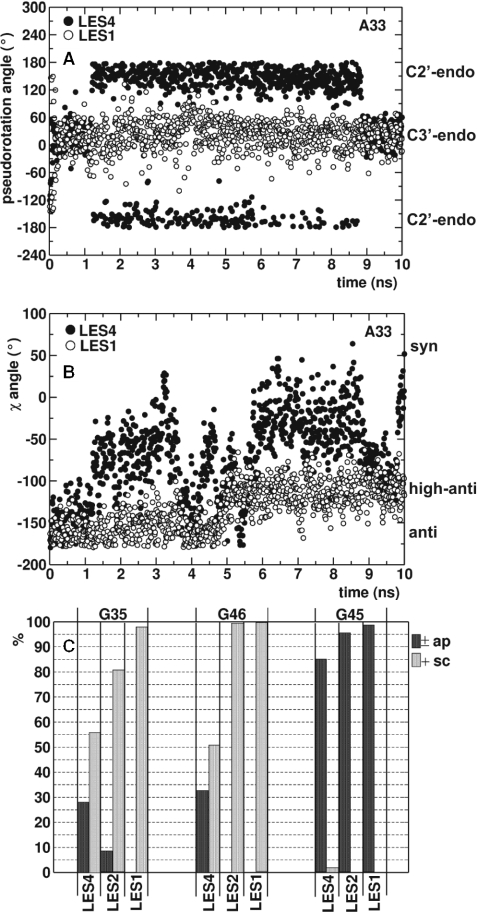
Correlation between backbone flexibility and the k–e motion. (A) The pseudorotation angle describing the sugar pucker of A33 during the LES4 (filled circles) and LES1 (empty circles) trajectories. (B) The χ angle describing the rotation about N9–C1′ bond in A33 during the LES4 (filled circles) and LES1 (empty circles) trajectories. (C) relative populations of ±ap (black) and +sc (gray) configurations (describing the rotation about the C4′–C5′ bond) in G35, G46 and G45 in the LES4, LES1 and LES2 trajectories; the percentage of trajectory frames, in which intermediate configurations were sampled is not shown.
Figure 7.
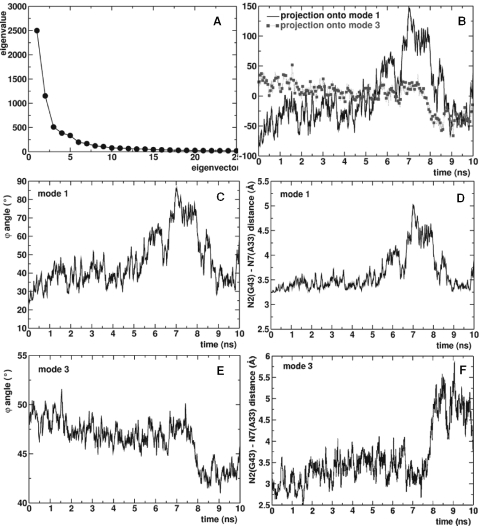
PCA of LES4 trajectory. (A) Decomposition of the trajectory along the first 25 modes. (B) Projection of the LES4 trajectory onto first (continuous line) and third (dotted line with square symbols) modes. (C) ϕ angle along the first mode. (D) Distance between N2 of G43 and N7 of A33 along the first mode. (E) ϕ angle along the third mode. (F) Distance between N2 of G43 and N7 of A33 along the third mode.
Figure 3.
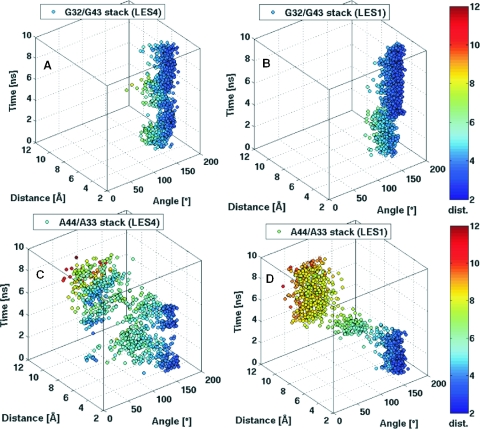
Scatter 3D plots of the stacking interactions between: (A) G32/G43 in the LES4 trajectory; (B) G32/G43 in the LES1 trajectory; (C) A44/A33 in the LES4 trajectory; (D) A44/A33 in the LES1 trajectory. Stacking interactions occur when the distance (D) is minimal and the dihedral angle (θ) between the planes of the nucleotides is either ∼0° or ∼180° between the planes of the nucleotides. Rotation of the base about the N9–C1′ bond occurs when θ approaches intermediate values. The scatter points are colored according to their y value (D) with a colormap ranging from blue to red.
Figure 4.
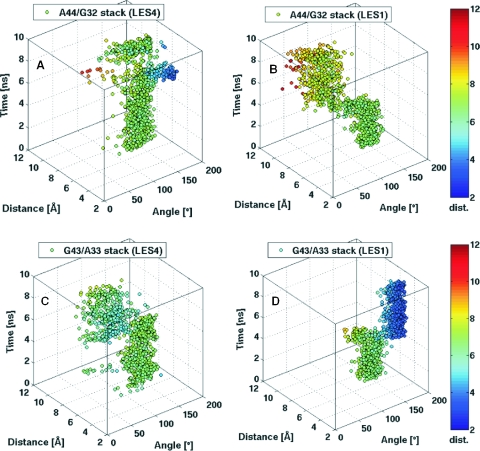
Scatter 3D plots of the stacking interactions between: (A) A44/G32 in the LES4 trajectory; (B) A44/G32 in the LES1 trajectory; (C) G43/A33 in the LES4 trajectory; (D) G43/A33 in the LES1 trajectory. For details clarifying the plots and coloring see Figure 3.
Essential dynamics
Principal component analysis (PCA) of MD trajectory data, often called essential dynamics, is frequently used to separate large-scale correlated motions from local harmonic fluctuations (39–42). ED analysis constructs a new orthogonal basis set for the atomic coordinates in a trajectory such that the greatest variance occurs along the first vector, with decreasing variances along successive vectors. The eigenvalues from the decomposition of the eigenvectors represent the relative motion that occurs along each mode. The motion of a system during MD trajectories can be described by the displacement along the first few eigenvectors (43). There are a number of limitations associated with ED (44), but the method proved useful in identifying motions correlated with the large amplitude k–e motion in the RNA that was captured in the LES-MD trajectories.
To perform ED, coordinate data from each time-step were fitted to the initial structure to remove translational and rotational motion. The fitted trajectory data were used to construct a covariance matrix. The matrix was diagonalized so as to determine the eigenvalues and eigenvectors. The trajectory can be reconstructed using the eigenvectors with significant contribution to the global motion. The matrix of the projections of each time-step onto each mode was calculated by multiplying the trajectory matrix by the matrix of column eigenvectors. We performed ED of the LES4 trajectory using the ptraj module from the AMBER8 distribution and visualized the modes with VMD using the IED program (42). We generated the covariance matrix for all the atomic coordinates in the RNA, diagonalized it, and wrote out the first 25 eigenvectors. The projections onto the first three modes were calculated and the motions along first and third modes were analyzed further.
RESULTS
The behavior of the free RNA was not influenced by the number of LES regions as long as the conformational sampling was enhanced both in the internal loop and in the two stems. Only those LES setups under which the bound RNA was stable were considered for further processing. The dependence of the results on the number of copies/region is discussed elsewhere (12). We chose to present in detail the LES4 trajectory because it was the longest (10 ns) and captured a significant reformation of the K-turn during the last 2 ns.
To study how the backbone flexibility in the stems influences the k–e motion of the K-turn, we restricted the degree of conformational freedom in the C- and NC-stems by confining LES to the internal loop (LES1) or to the internal loop and the NC-stem (LES2). Simulations of the LES1 and LES2 systems were performed and the resulting trajectories were compared with the LES4 trajectory.
MPEG movies of the three trajectories of the unbound Kt-U4 (LES1, LES2 and LES4), all 10 ns long, are available for downloading from the following webpage: www.mpibpc.gwdg.de/abteilungen/060/Cojocaru_NAR/Additional_Material.html.
Opening–closing of Kt-U4
The conformation of Kt-U4 as observed in the crystal structure with the external loop modeled is shown in Figure 1A. We use the angle ϕ formed by the P atoms of C47, U31 and G35 to characterize the degree of kinking in the RNA. The ϕ angle is sharper than the angle formed by the two helical axes (Φ) (∼25° compared with ∼68°) but displays the same profile during the simulations. ϕ is independent of structural instabilities as opposed to Φ, which cannot be defined if the NC-stem loses its helical properties. During the LES4 trajectory, the RNA undergoes a large conformational transition to an extended structure. Figure 1B shows a snapshot from the LES4 trajectory taken at maximum ϕ (Supplementary Structure S2). In the LES4 system, regions of enhanced sampling were defined both in the internal loop and in the stems (see Materials and Methods). The large opening of the K-turn is accompanied by the loss of G–A base pairs, modification of the stacking pattern in the internal loop and opening of G–C base pairs in the NC-stem. In the LES1 trajectory, enhanced sampling was confined to the internal loop and the RNA adopted an alternative conformation (Figure 1C) characterized by the loss of G–A base pairs and a distinct modification of the stacking pattern in the internal loop (Supplementary Structure S3). However, no opening of G–C base pairs in the NC-stem was observed. The new stacking patterns formed in the LES4 and LES1 trajectories are indicated by long arrows. The conformation observed in the LES1 trajectory had kinks in both strands (indicated by short arrows), the fold resembling that of K-turn Kt58 (Figure 1D). The LES2 trajectory was obtained by applying enhanced sampling to the internal loop and the G–C base pairs of the NC-stem but not to nucleotides from the C-stem. Interestingly, opening of the K-turn occurred in the LES2 trajectory, but the amplitude of the transition was far smaller than that observed in the LES4 trajectory (Supplementary Structure S4). The ϕ angle for the three trajectories is shown in Figure 2A. In the LES4 trajectory, the K-turn opening occurred rather quickly, reaching a peak after ∼1.5 ns, after which the structure closed back such that after 3.7 ns the value of ϕ was close to the value observed in the crystal structure. After 4 ns, the RNA opened gradually, reaching the highest ϕ (∼90°) after ∼7.1 ns. For ∼1 ns, the structure remained open while during the last 2 ns, the K-turn partially reformed to a ϕ value of 30° (Supplementary Structure S5). In the LES1 trajectory, partial opening occurred only after 2.6 ns and ϕ reached a maximum value of 40° after ∼3.2 ns. The partial open conformation was short-lived; after 3.5 ns, the K-turn reformed while after 5 ns, ϕ decreased to lower values than those observed in the crystal structure and remained constant for the rest of the trajectory. In the LES2 trajectory, partial opening occurred quickly and the amplitude was comparable with that in the LES4 trajectory for the first 4.5 ns. However, after ∼5 ns the RNA closed and remained closed until the last nanosecond, when partial opening was observed again.
Opening of G–A base pairs
Tandem-sheared G–A base pairs are formed by establishing N2(G)-H-N7(A) and N6(A)-H-N3(G) hydrogen bonds. For studying the opening of G–A base pairs during the three different trajectories, we calculated the donor–acceptor distance (d) between the N2 atom of guanines and N7 atom of adenines. Figure 2B represents the results obtained for the G32–A44 base pair, the G43–A33 base pair behaving in a similar manner. During the LES4 trajectory, we observed large opening of the G32–A44 base pair only after 5.6 ns. In the interval 6–9 ns, the base pair did not reform, but the relative movement of the 2 nt showed a rather random distribution that did not correlate with the time evolution of ϕ. The base pair reformed after ∼9 ns but immediately opened again. In the LES1 trajectory, the same base pair opened partially after ∼2 ns and completely after ∼4 ns. Surprisingly, during the last 6 ns of the LES1 trajectory, d was larger than in the LES4 trajectory and the G32–A44 base pair never reformed. Also unexpectedly, the movement of A44 relative to G32 was much larger in the tightly kinked LES1 conformation than in the highly open LES4 conformation. The 2D plot of d against ϕ shows that d increased with ϕ for the most part of the LES4 trajectory. However in a number of snapshots the G–A base pair was open (large d) while the K-turn was relatively closed (small ϕ) (Figure 2C). In the LES1 trajectory, there was an anti-correlation between the opening of G–A base pairs and the opening of the K-turn, very large values for d corresponding to a very tight K-turn (Figure 2D).
In the crystallographic structure of the Kt-U4–15.5K complex G32 stacks on G43 and A44 stacks on A33. The planes of the two guanines are displaced, owing to hydrogen bond contacts between the RNA and the protein. The O6 atom of G32 is hydrogen-bonded with the peptide backbone N atom of GLU41, and the O6 and N7 atoms of G43 are hydrogen-bonded with the side-chains of ASN40 and LYS44. There is no protein contact involving A44 and A33; therefore, their planes are oriented such as to allow a maximized stacking interaction. To measure the stacking between two RNA bases, we calculated the distance between their geometrical centers (D) and the angle between their planes (θ). Maximum stacking is achieved when D is minimal and θ is either close to 0° or 180°. For G32/G43 and A44/A33 stacking interactions, θ has a value close to 180° because the Watson–Crick edges of the stacked bases point in different directions. When a purine rotates about the N9–C1′ bond, θ fluctuates between ∼180° and ∼0°. We plotted in scatter 3D graphs, θ (x-axis) against D (y-axis) and time (z-axis) and colored the points according to their y (D) values with a colormap ranging from blue (bases close to each other) to red (bases far from each other). In this way, we could monitor the transitions between different stacking patters and identify rotations of bases about the N9–C1′ bond. The stacking between the two guanines was preserved and maximized during both the LES4 (Figure 3A) and LES1 trajectories (Figure 3B), while the stacking between the two adenines did not persist in either trajectory (Figure 3C and D). Either A44 or A33 rotated sharply about the N9–C1′ bond in both LES4 and LES1 trajectories. In the LES4 trajectory, A33 rotated until its plane was almost perpendicular to the plane of G43, such as to increase the gap between the two stems, contributing to the large opening of the K-turn. During the last 2 ns of the LES4 simulation, the reformation of the kinked structure was accompanied by the rotation of both A33 and A44 and a random distribution of the relative orientations of the two adenines was observed. In the LES1 trajectory, three different structure clusters could be distinguished: (i) A44 stacked on A33 in the first 4 ns of the trajectory; (ii) A44 rotated, allowing the stems to achieve close proximity; (iii) the tightly kinked conformation formed, with the plane of A44 being almost perpendicular to the plane of G32.
In summary, the transition to the open conformation (LES4) was facilitated by the rotation of A33 about its N9–C1′ bond, while the tightly kinked structure (LES1) was formed upon equivalent rotation of A44. Interestingly, rotation of A44 was also observed during the reformation of the K-turn in the LES4 trajectory.
Modified stacking patterns in the internal loop
The rotations about the N9–C1′ bond of A33 in the LES4 trajectory and of A44 in the LES1 trajectory were accompanied by the formation of new stacking patterns in the region corresponding to the internal loop. In the LES4 trajectory, the A44 stacked on G32 and further on G43 during the time of maximal K-turn opening (7–8 ns) (Figure 4A), while no such stacking interaction was formed in the LES1 trajectory (Figure 4B). The new stacking pattern formed by G43, G32 and A44 was interpolated horizontally between the two stems reflecting the maximal value of ϕ. In the LES1 trajectory, A33 formed a new stacking interaction with G43 (Figure 4D) and no stacking was formed between A44 and G32 (Figure 4C). The new stacking pattern formed by G32, G43 and A33 was extruded vertically from the stems, reflecting the minimal value of ϕ.
In both LES4 and LES1 trajectories, one of the two adenines rotated about the N9–C1′ bond while the other formed a new stacking pattern with the guanines. A structural view of the transitions between different stacking patters is shown in Figure 5.
Two significantly different conformations, one tightly kinked and one highly opened, were formed depending on the LES setup employed. However, both conformations were characterized by the loss of G–A base pairs. Because the difference between the two trajectories was the degree of backbone flexibility permitted, we analyzed the correlation between the K-turn opening and motions in the sugar–phosphate backbone.
Opening of Kt-U4 is correlated with backbone flexibility in the stems
Local motions in the sugar rings and the phosphate groups of nucleotides at the point where the two stems branch revealed that certain conformations were required for the formation of the kinked structure. Stabilizing inter-stem contacts can form only if the interacting atoms were properly oriented for hydrogen-bond formation. The following contacts were established between the C-stem and the NC-stem: (i) the 2′ OH group of A29 is hydrogen-bonded with the N1 atom of A44; (ii) the 2′ OH group of A33 is hydrogen-bonded with the 2′ OH group of G45; (iii) the N2 atom of G45 is hydrogen-bonded with the O3′ atom of A33; and (iv) the 2′ OH group of G46 is hydrogen-bonded with the phosphate group of G34. Applying LES to the stems loosens these contacts because the backbone has more conformational freedom, thus promoting the opening of the RNA.
We investigated the local conformational transitions within different nucleotides that were correlated with the K-turn opening, calculating: (i) the sugar pucker (the pseudorotation angle); (ii) the orientation between the base and the sugar (the χ angle) and (iii) the orientation about the C4′–C5′ bond (the γ angle) [for detailed description of the parameters see (45)]. A33 was very flexible in terms of the sugar pucker and the χ angle in the LES4 trajectory (Figure 6A and B). In the kinked conformation, A33 had a C3′-endo sugar pucker and an anti-base-sugar orientation. When the RNA opened, the sugar pucker changed to C2′-endo and the χ angle varied toward a syn orientation describing the rotation of A33 about the N9–C1′ bond. In the LES1 trajectory, although A33 was part of the defined LES region, its conformation was confined to a C3′-endo sugar pucker and an anti or high anti-base-sugar orientation. The high anti-configuration was adopted after 5 ns, corresponding to lower ϕ values.
The orientation about the C4′–C5′ bond allows O5′ to assume different positions relative to the furanose ring. If rotation about the C4′–C5′ bond is permitted in a single nucleotide, the entire backbone can adopt a different orientation. In the LES4 trajectory, such a rotation occurred in the G34, G35 and G46 nucleotides (Figure 6C). Both ±ap [γ ∈ (±150° ±180°)] and +sc [γ ∈ (30° 90°)] configurations were sampled by these nucleotides in the LES4 trajectory but not in the LES1 trajectory. Other nucleotides, such as G45, showed no difference in the sampled configurations between LES4 and LES1 trajectories (Figure 6C). In the LES2 trajectory, the +sc configuration was less sampled than in the LES4 trajectory by G35 and G34, while the γ dihedral of G46 was restricted to values corresponding to the +sc configuration.
Essential dynamics of the LES4 trajectory
To study the types of motions that are correlated with the k–e motion of Kt-U4 in the LES4 trajectory, we performed ED analysis. First, the motion was decomposed onto the 25 slowest modes (see Materials and Methods), the contribution of the first three modes to the total motion being 68% (Figure 7A). The projection of the trajectory onto the first three modes showed that: (i) the first mode accounts for the large opening observed between 6 and 8 ns; (ii) the second mode accounts for the partial opening observed between 1 and 2 ns; and (iii) the third mode accounts for the reformation of the K-turn observed between 8 and 10 ns (Figure 7B). For clarity, the projection onto the second mode is not shown.
The plot of ϕ along the first mode (Figure 7C) shows that the PCA captures the large opening of the RNA, separating it from partial opening that occurs due to higher frequency motions. The motions along the first mode included: (i) opening of G–A base pairs (Figure 7D); (ii) rotation of A33 about N9–C1′ bond; (iii) formation of the A44–G32–G43 stacking pattern; and (iv) rotation of A30 about the N9–C1′ bond. No correlated motion occurred in the NC-stem or in the external loop.
The plot of ϕ along the third mode (Figure 7E) shows that the motion along this eigenvector reflected the closing of the RNA observed after 8 ns. The G–A base pairs remained largely open, although the K-turn reformed (Figure 7F). This anti-correlation was similar to that observed during the LES1 trajectory. The motions along the third slowest mode included: (i) closing of the K-turn; (ii) rotation of A33 about the N9–C1′ bond; (iii) rotation of A44 about the N9–C1′ bond; and (iv) motions in the NC-stem and in the external loop. The similarity with the LES1 trajectory was striking with the exception that the G32–G43–A33 stacking pattern did not formed and the RNA did not kink as tightly.
DISCUSSION
The role of G–A base pair formation in the folding of the K-turn motif
It has been shown that mutation of any of the purines forming the G–A base pairs abolishes binding of the 15.5K protein (2,3). Therefore, the formation of G–A base pairs in the internal loop is required for the correct folding of Kt-U4 RNA. However, their precise role is not understood. Here, we provide the first insights at atomic detail into the correlation between G–A base pair formation and K-turn folding. The G–A base pairs are unstable in the absence of the 15.5K protein. Thus, a reasonable assumption would be that they are required for the formation of the kinked structure. However, the opening of G–A base pairs is not tightly correlated with the k–e motion of the K-turn. When increased sampling was applied to both the internal loop and parts of the stems, the k–e motion was accompanied by the loss of G–A base pairs (LES4). Strikingly, when LES was confined to the internal loop, the RNA adopted a relatively stable alternative conformation, in which the G–A base pairs did not form while the RNA was a more tightly kinked structure resembling that of the K-turn Kt58 (Figure 1D), having backbone kinks on both strands. We investigated whether this alternative conformation was stabilized due to LES artifacts by comparing the dynamics observed in the LES1 and LES4 trajectories. In the absence of experimental data at atomic level describing the dynamics of the free RNA, the identification of convergent motions between the LES1 and LES4 trajectories provides a reasonable argument that at least some of the dynamics observed in the LES1 trajectory occur during the k–e motion of the RNA. The behavior of the RNA in the LES4 trajectory was in agreement with the data obtained by single molecule FRET experiments (10) and by chemically probing the RNA structure in the presence and absence of the 15.5K protein (12). To characterize the concerted motions in the free K-turn, we applied ED analysis of the LES4 trajectory. The slowest mode captured the k–e motion that is correlated with the opening of G–A base pairs. Surprisingly, along the third slowest mode, the degree of kinking in the RNA increased without the formation of G–A base pairs. Furthermore, the movement of the adenines relative to the guanines was even larger than that observed along the first mode and similar to the motions observed in the LES1 trajectory. The projection of the LES4 trajectory along different modes shows that the third eigenvector reflected the reformation of the K-turn in the last 2 ns of the trajectory. Therefore, the two simulations showed convergent motions, suggesting that the RNA is capable of adopting intermediate conformations characterized by a sharp angle between the two stems without the formation of G–A base pairs. The stabilization of the alternative conformation in the LES1 trajectory enabled the search for local structural dynamics contributing to the large opening of the RNA, such dynamics being identified by analyzing the divergent motions between the LES4 and LES1 trajectories.
From these findings, we infer that the loss G–A base pair is insufficient for the k–e transition. The opening of the K-turn causes the G–A base pair to open, thus accounting for the correlation between these two motions along the slowest mode of the LES4 trajectory. The stability of the stacking interaction between G32 and G43 suggests that G32 and G43 together with the flipped out U31 and a particular orientation of A30 could be the recognition motif for the 15.5K protein. The protein has a tight cavity (Figure 8) formed by residues 37 to 41, 44 and 95 to 99, which recognizes the RNA and selects a specific orientation of the two stems. We propose that the role of the G–A base pairs is to stabilize the orientation of the two stems at a precise angle, which is selected during protein recognition.
The ribosomal K-turns vary in the angle between the stems and in the number and nature of non-canonical interactions, extending the NC-stem into the internal loop. Kt46 and Kt58 have the highest degree of kinking (∼21° and ∼41° between the helical axes of the two stems). They contain three G–A base pairs followed by a G–U base pair while K-turns with a lower degree of kinking bear two G–A base pairs, sometimes followed by a C–C base pair. This distribution suggests that there might be a connection between the orientation of the two stems and the number of G–A base pairs formed in the internal loop. The major function of the K-turns is to orient the two stems such as to permit binding of proteins that contact both stems, or to provide the frame for large RNAs such as the ribosomal RNA to compact in the structures observed in the ribosomes. Therefore, it is plausible to suggest that the RNA folding in large structures requires specific orientations of helices that are regulated by non-Watson–Crick interactions in flexible motifs, such as the K-turns. It is very challenging to experimentally verify this hypothesis because adding or subtracting G–A base pairs from the RNA abolishes binding to their cognate proteins. Computer simulations are also limited due to the flexibility of the free RNAs, which has to be accounted for to obtain an accurate representation of the simulated systems.
It was suggested by one of the reviewers of this paper that the instability of the G–A base pairs in the free Kt-U4 was incompatible with thermodynamics experiments [(46) and references therein] and may thus have been due to the limitations of LES and the force fields. However, chemical RNA structure probing experiments have shown that both G32 and G43, as well as G34 and G35, are accessible to modification by kethoxal in the absence of 15.5K protein, indicating that the G–A base pairs and the G–C base pairs in the NC-stem are not formed in the unbound RNA (12). The stability of G–A base pairs during standard MD simulations of the free Kt-U4 might be due to the limited sampling accessible by standard MD. We believe that LES has proved useful in simulating the opening of G–A base pairs in the unbound Kt-U4. Nevertheless, we do not question the stability of sheared G–A base pairs in other RNAs or even in other K-turns. Additional studies are required to assess the stability of the G–A base pairs in the related ribosomal K-turns by considering both their bound proteins and attached RNA fragments.
The role of backbone flexibility in the folding of the kink turn motif
If the loss of G–A base pairs is insufficient for the large opening of the K-turn, it is likely that other factors contribute to the k–e transition. Capturing the LES1 conformation enabled us to characterize the motions in the backbone of nucleotides situated at the branching origin of the stems that are relevant for the opening of the K-turn. The rotational freedom about backbone bonds in A33, G34, G35 and G46 drives the k–e motion of the RNA. When this flexibility is restricted, the ability of the RNA to open is diminished (as observed in the LES1 and LES2 trajectories), suggesting that the formation of the K-turn is not a selective property of the internal loop but also involves the stems. A33 plays a special role in the transitions, being the most flexible nucleotide during the K-turn opening. Its pucker and χ angle are highly correlated with the global RNA motions, suggesting that the degree of conformational freedom in A33 is of crucial importance for the K-turn dynamics. We show that the flexibility of A33 is influenced by the degree of rotational freedom about the C4′–C5′ bond in G46. The 2′ OH group of G46 must adopt a correct orientation to form a hydrogen bond with the phosphate group of G34 that bridges the gap between the two stems at their branching origin. G45 does not show the same type of flexibility as G46, although it is closer to the internal loop, suggesting that the flexibility of G46 backbone directs the movement of the C-stem relative to the rest of the RNA. In the LES2 trajectory, the amplitude of the k–e motion is significantly lower than in the LES4 trajectory because conformational sampling in the C-stem was not enhanced. The backbone of G46 does not have a sufficient degree of conformational freedom to promote large RNA opening. Nevertheless, a certain degree of opening was observed in comparison with the LES1 trajectory, suggesting that flexibility in the backbone of G34 and G35 is equally important.
Perspectives in the simulation of protein-assisted RNA folding
We have shown that simulating protein-assisted RNA folding in the absence of structural data for the free RNA requires a computational approach that uses standard MD simulations in combination with enhanced conformational sampling techniques to enable the investigation of transitions such as the k–e motion of the K-turn motif (12). Partial opening of the K-turn accompanied by loss of stabilizing inter-stem contacts has been observed in standard MD simulations of the free RNA (12,28,29). However, we observed opening of the G–A base pairs and a significantly larger opening of the K-turn only when applying LES (12). Thus, enhancing the conformational sampling is required to obtain a more accurate description of the dynamics of the free K-turn. We chose LES because it has been previously applied to locate the experimental structure of a RNA loop starting from a different conformation (30). LES can be used in combination with PME in periodic simulations with explicit solvent.
Considering the benefits of applying LES despite the drawbacks apparent in the study of DNA G-quartets (35), we propose that in the absence of atomic resolution structures of unbound RNAs, such theoretical approaches are suitable for studying the dynamics of RNAs undergoing protein-assisted folding starting from structures of protein–RNA complexes. However, they do not provide structural predictions. Thus, the structures observed during the LES-MD trajectories should only be regarded as possible, perhaps even highly plausible, transition states during dynamic motions rather than assumed as unique 3D arrangements of the free Kt-U4. In reality, the unbound RNA may undergo transitions of much greater amplitudes that cannot be simulated even with more extensive conformational sampling.
Nevertheless, using LES we obtained excellent agreement with experimental data available in characterizing the behavior of Kt-U4. However, it was necessary to simulate both the free and bound RNAs under the same conditions to ensure that we were observing protein-assisted RNA folding and not random transitions in the RNA. This resulted in a sharp increase in CPU time required to obtain a viable trajectory. The next step in developing a protocol that can be extensively applied to study the mechanism of protein-assisted RNA folding would be to test whether the behavior of the K-turn motif can be reproduced by employing other enhanced sampling techniques such as replica exchange MD simulations (47–49). Ideally, such a standardized protocol would not require the simulations of the bound RNAs and could predict induced fit or conformational capture mechanisms (50,51) only from the simulations of the free RNAs starting from their bound structures. Such a protocol would be justified in studying systems for which structural data are very difficult to obtain due to their flexibility. The K-turn motif constitutes a typical example of such a system.
Understanding the dynamics of such RNA motifs is required to elucidate the mechanisms of large RNA folding, with the ultimate goal of characterizing the folding of structures such as the ribosome, the single recognition particle, the telomerase or the dynamical events occurring during the assembly of the functional spliceosome.
SUPPLEMENTARY MATERIAL
Supplementary Material is available at NAR Online.
Supplementary Material
Acknowledgments
The authors are very grateful to Reinhard Lührmann for constant support of this project. The authors thank Stephanie Nottrott for a fruitful collaboration, Annemarie Schultz and Ping Li for discussions, and Bernd Rieger for help with data visualization. This work was part of the research performed in the International PhD Program Molecular Biology-International Max Planck Research School at the Georg August University, Göttingen, Germany. Funding to pay the Open Access publication charges for this article was provided by the Max Planck Society.
Conflict of interest statement. None declared.
REFERENCES
- 1.Nottrott S., Hartmuth K., Fabrizio P., Urlaub H., Vidovic I., Ficner R., Lührmann R. Functional interaction of a novel 15.5kD U4/U6 center dot U5 tri-snRNP protein with the 5′ stem–loop of U4 snRNA. EMBO J. 1999;18:6119–6133. doi: 10.1093/emboj/18.21.6119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nottrott S., Urlaub H., Lührmann R. Hierarchical, clustered protein interactions with U4/U6 snRNA: a biochemical role for U4/U6 proteins. EMBO J. 2002;21:5527–5538. doi: 10.1093/emboj/cdf544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Vidovic I., Nottrott S., Hartmuth K., Lührmann R., Ficner R. Crystal structure of the spliceosomal 15.5kD protein bound to a U4 snRNA fragment. Mol. Cell. 2000;6:1331–1342. doi: 10.1016/s1097-2765(00)00131-3. [DOI] [PubMed] [Google Scholar]
- 4.Klein D.J., Schmeing T.M., Moore P.B., Steitz T.A. The kink-turn: a new RNA secondary structure motif. EMBO J. 2001;20:4214–4221. doi: 10.1093/emboj/20.15.4214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Charron C., Manival X., Clery A., Charpentier B., Marmier-Gourrier N., Branlant C., Aubry A. The archaeal sRNA binding protein L7Ae has a 3D structure very similar to that of its eukaryal counterpart while having a broader RNA-binding specificity. J. Mol. Biol. 2004;342:757–773. doi: 10.1016/j.jmb.2004.07.046. [DOI] [PubMed] [Google Scholar]
- 6.Hamma T., Ferre-D'Amare A.R. Structure of protein L7Ae bound to a K-turn derived from an archaeal box H/ACA sRNA at 1.8 angstrom resolution. Structure. 2004;12:893–903. doi: 10.1016/j.str.2004.03.015. [DOI] [PubMed] [Google Scholar]
- 7.Moore T., Zhang Y.M., Fenley M.O., Li H. Molecular basis of box C/D RNA–protein interactions: cocrystal structure of archaeal L7Ae and a box C/D RNA. Structure. 2004;12:807–818. doi: 10.1016/j.str.2004.02.033. [DOI] [PubMed] [Google Scholar]
- 8.Kuhn J.F., Tran E.J., Maxwell E.S. Archaeal ribosomal protein L7 is a functional homolog of the eukaryotic 15.5kD/Snu13p snoRNP core protein. Nucleic Acids Res. 2002;30:931–941. doi: 10.1093/nar/30.4.931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen Y.W., Bycroft M., Wong K.B. Crystal structure of ribosomal protein L30e from the extreme thermophile Thermococcus celer: thermal stability and RNA binding. Biochemistry. 2003;42:2857–2865. doi: 10.1021/bi027131s. [DOI] [PubMed] [Google Scholar]
- 10.Goody T.A., Melcher S.E., Norman D.G., Lilley D.M.J. The kink-turn motif in RNA is dimorphic, and metal ion-dependent. RNA. 2004;10:254–264. doi: 10.1261/rna.5176604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Matsumura S., Ikawa Y., Inoue T. Biochemical characterization of the kink-turn RNA motif. Nucleic Acids Res. 2003;31:5544–5551. doi: 10.1093/nar/gkg760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cojocaru V., Nottrott S., Klement R., Jovin T.M. The snRNP 15.5K protein folds its cognate K-turn RNA: a combined theoretical and biochemical study. RNA. 2005;11:197–209. doi: 10.1261/rna.7149605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Reyes C.M., Kollman P.A. Investigating the binding specificity of U1A-RNA by computational mutagenesis. J. Mol. Biol. 2000;295:1–6. doi: 10.1006/jmbi.1999.3319. [DOI] [PubMed] [Google Scholar]
- 14.Reyes C.M., Nifosi R., Frankel A.D., Kollman P.A. Molecular dynamics and binding specificity analysis of the bovine immunodeficiency virus BIV Tat–TAR complex. Biophys. J. 2001;80:2833–2842. doi: 10.1016/S0006-3495(01)76250-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pitici F., Beveridge D.L., Baranger A.M. Molecular dynamics simulation studies of induced fit and conformational capture in U1A-RNA binding: do molecular substates code for specificity? Biopolymers. 2002;65:424–435. doi: 10.1002/bip.10251. [DOI] [PubMed] [Google Scholar]
- 16.Réblová K., Špačková N., Koča J., Leontis N.B., Šponer J. Long-residency hydration, cation binding, and dynamics of loop E/helix IV rRNA-L25 protein complex. Biophys. J. 2004;87:3397–3412. doi: 10.1529/biophysj.104.047126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Guo J.X., Gmeiner W.H. Molecular dynamics simulation of the human U2B′ protein complex with U2 snRNA hairpin IV in aqueous solution. Biophys. J. 2001;81:630–642. doi: 10.1016/s0006-3495(01)75728-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Guo J.X., Daizadeh I., Gmeiner W.H. Structure of the Sm binding site from human U4 snRNA derived from a 3 ns PME molecular dynamics simulation. J. Biomol. Struct. Dyn. 2000;18:335–344. doi: 10.1080/07391102.2000.10506670. [DOI] [PubMed] [Google Scholar]
- 19.Li W., Ma B.Y., Shapiro B.A. Molecular dynamics simulations of the denaturation and refolding of an RNA tetraloop. J. Biomol. Struct. Dyn. 2001;19:381–396. doi: 10.1080/07391102.2001.10506748. [DOI] [PubMed] [Google Scholar]
- 20.Réblová K., Špačková N., Štefl R., Csaszar K., Koča J., Leontis N.B., Šponer J. Non-Watson–Crick basepairing and hydration in RNA motifs: molecular dynamics of 5S rRNA loop E. Biophys. J. 2003;84:3564–3582. doi: 10.1016/S0006-3495(03)75089-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Auffinger P., Bielecki L., Westhof E. The Mg2+ binding sites of the 5S rRNA loop E motif as investigated by molecular dynamics simulations. Chem. Biol. 2003;10:551–561. doi: 10.1016/s1074-5521(03)00121-2. [DOI] [PubMed] [Google Scholar]
- 22.Auffinger P., Bielecki L., Westhof E. Anion binding to nucleic acids. Structure. 2004;12:379–388. doi: 10.1016/j.str.2004.02.015. [DOI] [PubMed] [Google Scholar]
- 23.Auffinger P., Bielecki L., Westhof E. Symmetric K+ and Mg2+ ion-binding sites in the 5S rRNA loop E inferred from molecular dynamics simulations. J. Mol. Biol. 2004;335:555–571. doi: 10.1016/j.jmb.2003.10.057. [DOI] [PubMed] [Google Scholar]
- 24.Auffinger P., Westhof E. RNA solvation: a molecular dynamics simulation perspective. Biopolymers. 2000;56:266–274. doi: 10.1002/1097-0282(2000)56:4<266::AID-BIP10027>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- 25.Auffinger P., Westhof E. Hydration of RNA base pairs. J. Biomol. Struct. Dyn. 1998;16:693–707. doi: 10.1080/07391102.1998.10508281. [DOI] [PubMed] [Google Scholar]
- 26.Auffinger P., Westhof E. RNA hydration: three nanoseconds of multiple molecular dynamics simulations of the solvated tRNA(Asp) anticodon hairpin. J. Mol. Biol. 1997;269:326–341. doi: 10.1006/jmbi.1997.1022. [DOI] [PubMed] [Google Scholar]
- 27.Auffinger P., Louise-May S., Westhof E. Molecular dynamics simulations of solvated yeast tRNA(Asp) Biophys. J. 1999;76:50–64. doi: 10.1016/S0006-3495(99)77177-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rázga F., Špačková N., Réblová K., Koča J., Leontis N.B., Šponer J. Ribosomal RNA kink-turn motif—a flexible molecular hinge. J. Biomol. Struct. Dyn. 2004;22:183–193. doi: 10.1080/07391102.2004.10506994. [DOI] [PubMed] [Google Scholar]
- 29.Rázga F., Koča J., Šponer J., Leontis N.B. Hinge-like motions in RNA kink-turns: the role of the second A-minor motif and nominally unpaired bases. Biophys. J. 2005;88:3466–3485. doi: 10.1529/biophysj.104.054916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Elber R., Karplus M. Enhanced sampling in molecular dynamics—use of the time-dependent hartree approximation for a simulation of carbon-monoxide diffusion through myoglobin. J. Am. Chem. Soc. 1990;112:9161–9175. [Google Scholar]
- 31.Simmerling C., Kollman P. Improved simulation of flexible systems through locally enhanced sampling. Abstracts of Papers of the American Chemical Society. 1996;212:153. [Google Scholar]
- 32.Simmerling C., Miller J.L., Kollman P.A. Combined locally enhanced sampling and Particle Mesh Ewald as a strategy to locate the experimental structure of a nonhelical nucleic acid. J. Am. Chem. Soc. 1998;120:7149–7155. [Google Scholar]
- 33.Simmerling C., Fox T., Kollman P.A. Use of locally enhanced sampling in free energy calculations: testing and application to the α (β anomerization of glucose. J. Am. Chem. Soc. 1998;120:5771–5782. [Google Scholar]
- 34.Stultz C.M., Karplus M. On the potential surface of the locally enhanced sampling approximation. J. Chem. Phys. 1998;109:8809–8815. [Google Scholar]
- 35.Fadrná E., Špačková N., Štefl R., Koča J., Cheatham T.E., III, Šponer J. Molecular dynamics simulations of guanine quadruplex loops: advances and force field limitations. Biophys. J. 2004;87:227–242. doi: 10.1529/biophysj.103.034751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cornell W.D., Cieplak P., Bayly C.I., Gould I.R., Merz K.M., Ferguson D.M., Spellmeyer D.C., Fox T., Caldwell J.W., Kollman P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1996;117:5179–5197. [Google Scholar]
- 37.Pearlman D.A., Case D.A., Caldwell J.W., Ross W.S., Cheatham T.E., Debolt S., Ferguson D., Seibel G., Kollman P. Amber, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun. 1995;91:1–41. [Google Scholar]
- 38.Humphrey W., Dalke A., Schulten K. VMD—Visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 39.Kitao A., Go N. Investigating protein dynamics in collective coordinate space. Curr. Opin. Struct. Biol. 1999;9:164–169. doi: 10.1016/S0959-440X(99)80023-2. [DOI] [PubMed] [Google Scholar]
- 40.Doruker P., Atilgan A.R., Bahar I. Dynamics of proteins predicted by molecular dynamics simulations and analytical approaches: application to α-amylase inhibitor. Proteins. 2000;40:512–524. [PubMed] [Google Scholar]
- 41.Alakent B., Doruker P., Camurdan M.C. Application of time series analysis on molecular dynamics simulations of proteins: a study of different conformational spaces by principal component analysis. J. Chem. Phys. 2004;121:4759–4769. doi: 10.1063/1.1778377. [DOI] [PubMed] [Google Scholar]
- 42.Ota N., Agard D.A. Enzyme specificity under dynamic control II: principal component analysis of α-lytic protease using global and local solvent boundary conditions. Protein Sci. 2001;10:1403–1414. doi: 10.1110/ps.800101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mongan J. Interactive essential dynamics. J. Comput. Aided Mol. Des. 2004;18:433–436. doi: 10.1007/s10822-004-4121-z. [DOI] [PubMed] [Google Scholar]
- 44.Balsera M.A., Wriggers W., Oono Y., Schulten K. Principal component analysis and long time protein dynamics. J. Phys. Chem. 1996;100:2567–2572. [Google Scholar]
- 45.Saenger W. Principles of Nucleic Acids Structure. New York, NY: Springer-Verlag; 1984. [Google Scholar]
- 46.Chen G., Znosko B.M., Kennedy S.D., Krugh T.R., Turner D.H. Solution structure of an RNA internal loop with three consecutive sheared GA pairs. Biochemistry. 2005;44:2845–2856. doi: 10.1021/bi048079y. [DOI] [PubMed] [Google Scholar]
- 47.Rhee Y.M., Pande V.S. Multiplexed-replica exchange molecular dynamics method for protein folding simulation. Biophys. J. 2003;84:775–786. doi: 10.1016/S0006-3495(03)74897-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sanbonmatsu K.Y., Garcia A.E. Structure of Metenkephalin in explicit aqueous solution using replica exchange molecular dynamics. Proteins. 2002;46:225–234. doi: 10.1002/prot.1167. [DOI] [PubMed] [Google Scholar]
- 49.Zhou R.H. Exploring the protein folding free energy landscape: coupling replica exchange method with P3ME/RESPA algorithm. J. Mol. Graph. Model. 2004;22:451–463. doi: 10.1016/j.jmgm.2003.12.011. [DOI] [PubMed] [Google Scholar]
- 50.Williamson J.R. Induced fit in RNA–protein recognition. Nature Struct. Biol. 2000;7:834–837. doi: 10.1038/79575. [DOI] [PubMed] [Google Scholar]
- 51.Leulliot N., Varani G. Current topics in RNA–protein recognition: control of specificity and biological function through induced fit and conformational capture. Biochemistry. 2001;40:7947–7956. doi: 10.1021/bi010680y. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.