Abstract
Red blood cell (RBC) indices serve as clinically important parameters for diagnosing various blood-related diseases. Conventional hematology analyzers provide the highly accurate detection of RBC indices but require large blood volumes (>1 mL), and the results are bulk mean values averaged over a large number of RBCs. Moreover, they do not provide quantitative information related to the morphological and chemical alteration of RBCs at the single-cell level. Recently, quantitative phase imaging (QPI) methods have been introduced as viable detection platforms for RBC indices. However, coherent QPI methods are built on complex optical setups and suffer from coherent speckle noise, which limits their detection accuracy and precision. Here, we present spectroscopic differential phase-contrast (sDPC) microscopy as a platform for measuring RBC indices. sDPC is a computational microscope that produces color-dependent phase images with higher spatial resolution and reduced speckle noise compared to coherent QPIs. Using these spectroscopic phase images and computational algorithms, RBC indices can be extracted with high accuracy. We experimentally demonstrate that sDPC enables the high-accuracy measurement of the mean corpuscular hemoglobin concentration, mean corpuscular volume, mean corpuscular hemoglobin, red cell distribution width, hematocrit, hemoglobin concentration, and RBC count with errors smaller than 7% as compared to a clinical hematology analyzer based on flow cytometry (XN-2000; Sysmex, Kobe, Japan). We further validate the clinical utility of the sDPC method by measuring and comparing the RBC indices of the control and anemic groups against those obtained using the clinical hematology analyzer.
Keywords: red blood cell indices, quantitative phase imaging, image-based cytometry, incoherent imaging, differential phase-contrast microscopy
Introduction
Red blood cells (RBCs) play a critical role as oxygen transporters, delivering oxygen from the lungs to various organs in the human body.1 Dysfunction of RBCs causes critical health problems and complications, such as kidney and spleen diseases,2 hemolytic crises,3 vascular occlusion, and thrombotic complications.4 RBC conditions are commonly evaluated using RBC indices,5 namely mean corpuscular hemoglobin concentration (MCHC), mean corpuscular volume (MCV), mean corpuscular hemoglobin (MCH), red cell distribution width (RDW), hematocrit (Hct), hemoglobin concentration (Hgb), and RBC count. RBC indices provide clinically important information related to various blood disorders accompanying anemia, including hereditary spherocytosis and sickle cell disease,6,7 as well as diseases that induce abnormal states for RBCs. For example, iron deficiency anemia features high RDW and low levels of MCHC, MCV, Hct, and Hgb;8 patients with hereditary spherocytosis typically exhibit high MCHC and RDW;9,10 and hyperglycemia increases MCHC, MCV, MCH.11
Various techniques for blood testing have been applied to evaluate such abnormal states of RBCs. For instance, a hemocytometer (e.g., Neubauer’s chamber) provides an effective platform for cell counting but does not provide important parameters for RBC assays, such as hemoglobin (Hb) content and cell volume, which are crucial for the measurement of RBC indices. Flow cytometry-based hematology analyzers are commonly employed in clinical laboratories to measure RBC indices.12 They provide the highly precise detection of RBC indices, but the results are the gross properties averaged over a large population of RBCs, and they cannot provide information about the morphology and Hb concentration of individual cells. The instruments are also complex and expensive and require specific reagents, such as a lysis agent or a cleaning agent, as well as trained operators to maintain them. Various image-based cytometers have also been applied to measure the Hb concentration of RBCs. Quantitative absorption cytometry,13 for instance, demonstrated highly precise measurement of Hb content and cell volume. Yet, its operation requires RBCs to be suspended in an index-matching absorption buffer with a precalibrated absorption coefficient. Multimodal multiphoton microscopy14 has also been suggested to measure the hemoglobin content of a single RBC. However, the method requires the synchronous operation of ultrafast lasers, making the measurement expensive and complicated.
Recently, quantitative phase imaging (QPI) methods have been introduced as viable detection platforms for RBC indices. QPIs are capable of measuring optical thickness information of transparent thin specimens15 and thus do not suffer from issues related to labeling and enable highly accurate morphological analysis of blood cells at the cellular level.16,17 However, the measured phase is proportional to the product of the refractive index and the physical thickness, and decoupling these optical properties is thus necessary for the accurate extraction of RBC indices (see the definitions of each RBC index in the Methods section).
Various strategies have been suggested to tackle this decoupling problem.18 QPI has been combined with scanning imaging modalities, such as atomic force microscopy19 or confocal microscopy,20 to perform accurate measurements of the physical thickness of RBCs and subsequent RI decoupling. This method, however, requires imaging with both QPI and scanning-based methods, which increases system complexity, cost, and the total measurement time and cannot be applied to rapidly moving RBCs. Lue et al.21 and Kemper et al.22 decoupled RI and the physical thickness of cells using approximations of cell morphology. The method may be effective for well-shaped suspended cells, but any discrepancy between the approximation and the actual cell structures can lead to measurement errors. Other methods suggested the use of immersion media23,24 to successfully decouple the RI and the thickness. Rappaz et al.24 measured phase images under different immersion media and solved for the RI and physical thickness of the cells with the RI information on the immersion media. This method, however, requires the cells to be stationary during the medium change to accurately measure the physical thickness of the cells. Jafarfard et al.23 also presented a decoupling scheme by immersing the cells in a biocompatible medium with a precalibrated spectral response and measuring the phase images. Yet, this method requires a precalibrated, dispersive immersion medium to operate.
Optical diffraction tomography (ODT) has also been applied to map out the three-dimensional RI information on RBCs.25−29 For instance, Ryu et al.26 combined a microfluidic device and ODT to achieve the actuation- and dilution-free formation of sparse RBC distribution in the measurement volume and applied the ODT method to measure the RI and 3D volume maps. These methods can reliably decouple the RI and the thickness of RBCs but require multiple measurements with various incident angles, and the cells should be stationary during the measurement. Advanced forms of ODT demonstrated a tomographic RI imaging capability from a single image acquisition. Zhou et al., for example, introduced color-multiplexed diffraction tomography capable of producing an RI tomogram in a single shot.30 This method, however, exhibits nonisotropic spatial resolution and image artifacts due to the significant amount of missing information in the object 3D spectrum that can be obtained with a single measurement. Kuś et al.31 introduced a high-throughput ODT scheme by segmenting the image sensor into multiple regions over which projections under various illumination angles can be simultaneously recorded. The method is effective in terms of improving the tomographic imaging throughput for a single cell but may compromise the spatial resolution or the field of view. Single-shot RI slice imaging has been demonstrated based on the depth-resolved transfer function. Yet, this method enables RI imaging at a given depth, and thus axial scanning is required to generate a 3D RI tomogram.32 Ge et al. reported on a high-speed ODT method based on angle multiplexing and a deep-learning-based image reconstruction network.33 However, this method involves network training with large paired data sets.
Recently, spectroscopic digital holographic microscopes (DHMs) have been introduced for blood testing.34−37 These methods quantify the Hb concentration and physical thickness of RBCs by performing spectroscopic phase imaging at multiple wavelengths. However, DHM based on a coherent light source suffers from coherent speckle and other interference noises, which may degrade detection accuracy. These noise patterns arise from the interference among the light scattered from surfaces and particles in the beam paths and form random or distinct patterns superimposed onto the RBCs in the resultant phase images. Consequently, they hinder accurate cell segmentation and volume measurement. Several DHM methods have been proposed to address such limitations. For instance, Pan et al. proposed several strategies for speckle reduction by averaging multiple images acquired by either laterally shifting the camera38,39 or by illumination with a multimode laser.40 Choi et al. also reported on a single-shot, speckle-free DHM method using dynamic speckle illumination, which exhibits a short spatial coherence length.41 Spatial light interference microscopy can also produce speckle-free phase images using the light interference with a partially coherent light source.42,43 These methods have demonstrated viability in producing high-quality phase images with reduced speckle noise but require multiple image acquisitions or complicated optical design for speckle reduction.
Differential phase-contrast (DPC) represents one of the intensity-based computational phase imaging methods capable of producing quantitative phase images using asymmetric illuminations and image deconvolution.44,45 Owing to its reference-free operation with partially coherent light sources,44,46−48 it provides speckle-free quantitative phase images with higher spatial resolution compared to coherent imaging schemes. The method can also be readily built with inexpensive components such as a programmable LED array and is thus simple and robust. Various forms of DPCs have been demonstrated over the years and have been applied to, for example, measuring sperm cell motility,49 RBC morphologies,50 and visualizing birefringence materials.51 Here, we introduce a functional derivative of DPC microscopy, termed spectroscopic differential phase-contrast (sDPC) microscopy, as a novel detection platform for image-based RBC indices. Unlike the conventional DPC method, or other color-multiplexed DPC or Fourier ptychographic microscopy (FPM)-based QPI methods that are aimed to obtain phase images for nondispersive samples at nominally selected wavelengths,52,53 sDPC employs three color-multiplexed illuminations to obtain three color-dependent phase images, thereby acquiring dispersive information on RBCs. Based on the acquired quantitative phase images, a gradient-descent-based optimization algorithm was developed to decouple the Hb concentration and the physical thickness of RBCs, which in turn enables the extraction of RBC indices with high accuracy and precision. The experimental setup and reconstruction algorithms of sDPC are presented, and the performance of our method is evaluated by comparing the measured RBC indices against those from a clinical hematology analyzer (XN-2000; Sysmex, Kobe, Japan). We also demonstrate the clinical viability of our method by measuring and comparing the sDPC-measured RBC indices of the control and anemic groups with those from the hematology analyzer.
Methods
Blood Sample Preparation
The Institutional Review Board (IRB) of Severance Hospital (Seoul, Republic of Korea) approved both the collection of residual blood samples from patients and all the experimental protocols (IRB 4–2022–11152). Prior to sDPC imaging, the whole blood sample was first diluted with 1X PBS at a ratio of 1:100. After mixing, the diluted sample was loaded into a blood imaging chamber (CELLOP-Chip, Small Machines, Korea), which features a chamber depth of 100 μm, for sDPC imaging. The chip used in this study featured a tolerance of ∼5 μm in chamber depth, which may influence cell segmentation performance. To resolve the issue, we first acquired a reference image of the chamber with no blood cells and used the information to normalize sDPC images of the same field of view (FoV) with blood cells. Further, we thresholded the image and counted the RBCs to minimize detection error due to spatial phase fluctuations.
sDPC Optical Setup
The sDPC microscope was constructed in a 4f configuration using a 20x/0.4 NA objective lens (RMS20X, Olympus, Japan) and a tube lens (TTL180-A, Thorlabs, USA) (Figure 1). For illumination, a programmable color LED matrix (32 × 32 RGB LED matrix panel with 4 mm pitch, Adafruit, USA) was employed. The LED array emits light of three colors at 630, 530, and 470 nm with a spectral bandwidth of 10 nm. Note that one may use other wavelengths that are more sensitive to Hb contents based on the dispersive curve of the RBCs. For instance, Jang et al. used lasers at 633, 532, and 450 nm to perform RBC assays in the DHM microscope.34 In our study, we used a commercially available LED array as it enables the cost-effective implementation of sDPC. We employed azimuthally cosine-modulated patterns of red, green, and blue colors to achieve an axi-symmetric frequency response for each color.54 Three colored illumination patterns rotated by 120° sequentially illuminated the blood-loaded imaging chamber, and the light transmitted through the sample was collected by the objective lens and captured by a color camera (DFK 33UX264, The Imaging Source, Germany). Image acquisition was performed at a frame rate of 4 fps and synchronized with the LED matrix using an Arduino Mega 2560. The exposure time was 0.25 s. The imaging FoV was measured to be 350 × 350 μm.
Figure 1.
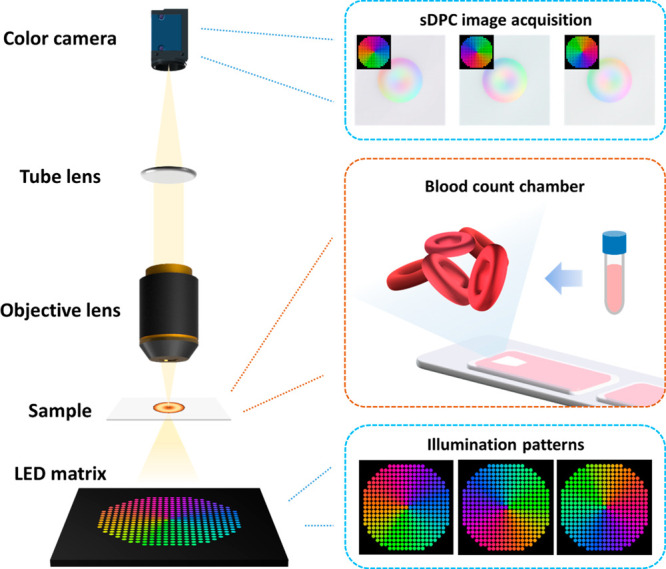
sDPC microscope schematic. A color LED matrix is located 80 mm away from the specimen plane. sDPC uses three color-multiplexed patterns to illuminate blood samples, and the light transmitted through the sample is recorded by a color image sensor. Each illumination pattern is composed of azimuthally cosine-modulated patterns of red, green, and blue that are rotated 120° relative to each other. The acquired images are then used to obtain phase images of red, green, and blue, which are subsequently utilized to decouple the refractive index and the thickness of RBCs. The illumination numerical aperture (NA) is matched to the objective lens NA.
sDPC Phase Imaging
The process of sDPC phase reconstruction is outlined in Figure 2. Upon image acquisition under three azimuthally cosine-modulated, color-multiplexed LED patterns, each color image is decomposed into images of red, green, and blue, resulting in a total of nine images (i.e., three images per color). Each image was then pixel-demosaicked (debayered) using the gradient-corrected linear interpolation method55 and corrected for color leakage,47,53,56 as described in the Supporting Information. Using the three images at each color, a color-dependent phase image can be reconstructed as described below.
Figure 2.
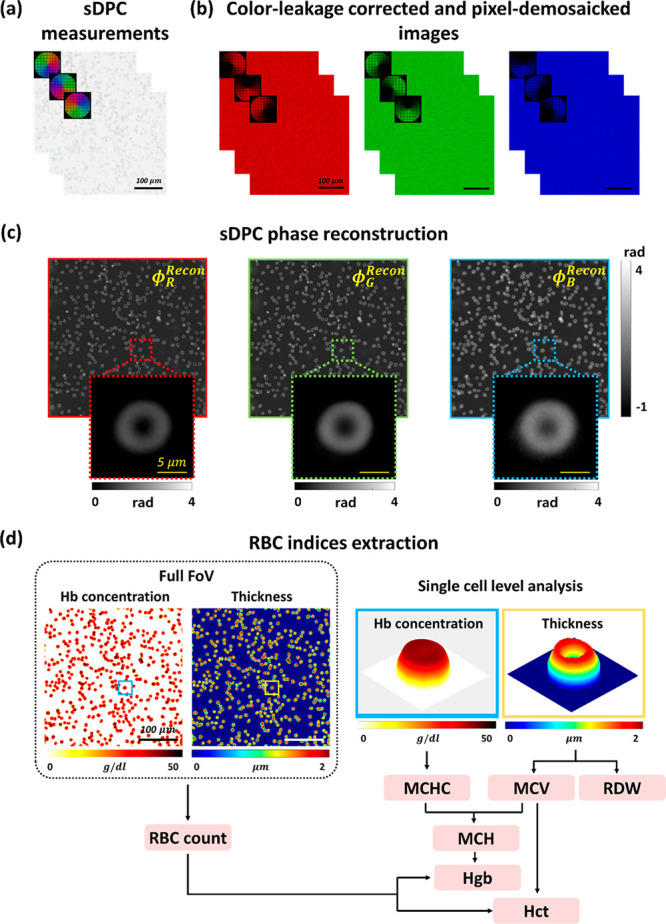
sDPC-based RBC index extraction. (a) Three intensity images are acquired using specially designed color-multiplexed LED patterns. (b) The acquired images are corrected for color leakage and decomposed into the images at red, green, and blue. (c) Quantitative phase images are then obtained through the sDPC phase reconstruction algorithm. (d) The phase images of three colors are used to obtain the Hb concentration and physical thickness of each RBC, which are in turn utilized to extract the RBC indices.
For weakly scattering objects such as thin transparent biological cells, the object transmission function can be approximated as
| 1 |
where r, μ(r), and ϕ(r) are the spatial coordinates in the object plane and the absorption and phase distribution of the sample, respectively. The measured intensity information under a partially coherent illumination can then be expressed as44
| 2 |
where u, δ, 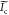 ,
, 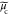 , and
, and 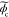 are the spatial frequency coordinates,
the Dirac delta function, the frequency spectrum of the image at color
c, and the Fourier transforms of the absorption and phase of the object
at color c (c = R, G, or B), respectively. Bc, Hμc, and Hϕc are the background, absorption, and phase transfer functions
at color c, respectively. Note that the amplitude and phase transfer
functions at each color are determined by the source (Sc(u)) and pupil (Pc(u)) functions, given as
are the spatial frequency coordinates,
the Dirac delta function, the frequency spectrum of the image at color
c, and the Fourier transforms of the absorption and phase of the object
at color c (c = R, G, or B), respectively. Bc, Hμc, and Hϕc are the background, absorption, and phase transfer functions
at color c, respectively. Note that the amplitude and phase transfer
functions at each color are determined by the source (Sc(u)) and pupil (Pc(u)) functions, given as
| 3 |
| 4 |
| 5 |
where ★ and * denote two-dimensional cross-correlation and complex conjugate operators, respectively. Using the images under the three illumination patterns at color c, we compute the corresponding DPC image as
| 6 |
where l, m, and, n (l ≠ m,n) indicate the illumination patterns at a given color. Since
the illumination patterns l, m, and n have equal area and total intensity,
one can easily see that the background signal and absorption information
are eliminated in the evaluation of the numerator terms in eq 6. Consequently, the DPC
image  can be expressed as
can be expressed as
| 7 |
where HDPCϕc,l(u) is the DPC phase transfer function, given by
| 8 |
It can be seen from eq 7 that the object phase can simply be obtained via the deconvolution of the DPC image with the DPC phase transfer function. However, a direct inversion of eq 7 may lead to incorrect phase estimations, since the DPC transfer function has zero or small values outside of the spatial frequency passband and along the axis of symmetry.44 In order to achieve noise-robust phase retrieval, we solve the minimization problem set as
| 9 |
where γtik,c is the regularization parameter for the term related to the L2 norms of each phase at each color c. The regularization parameters were determined experimentally with a precalibrated phase target (see the Results and Discussion section). The quantitative phase image at color c can then be reconstructed as
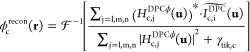 |
10 |
where 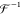 is the inverse Fourier transform operator.
is the inverse Fourier transform operator.
sDPC-Based RBC Index Extraction
The phase image of the RBCs at color c is related to the Hb concentration (C) and physical thickness (h) of the RBCs, as follows:
| 11 |
where λc, α(λc), and nx are the wavelength of light at color c, the proportionality constant of the refractive index as a function of Hb concentration, and the refractive index of cytoplasmic molecules other than Hbs,34 respectively. Using prior information for α(λc) from previous studies,57 the decoupling problem turns into solving nonlinear sets of equations with three unknowns and three equations. Yet, the problem involves solving nonlinear equations with the variables coupled to each other. Accordingly, optimization is required to solve this problem.34,35 We developed a gradient-descent-based optimization method on the data fidelity term and a proximal operation of the two-dimensional total variation to solve these nonlinear sets of equations with the approximation that RBCs exhibit a homogeneous molecular distribution. The optimization problem was set as
| 12 |
where the first term is the data fidelity term and the second and third terms are the total variation penalty terms related to the concentration of Hb and other molecules inside the RBCs, which are introduced to impose sparsity in the variation of C and nx inside the blood cells. Note that ϕc is the phase information at color c, as defined in eq 11. ∇ denotes the gradient operator. η1 and η2 are the weighting parameters of the penalty terms for the gradients of C and nx, respectively. To deal with the data fidelity term, a gradient-descent-based optimization algorithm was applied, and for the penalty terms, we employed the proximal operation of the total variation using the UNlocBox toolbox.58 To segment the RBCs in the phase images, the marker-controlled watershed segmentation (MCWS) algorithm was used. Detailed information on the MCWS algorithm is provided in the Supporting Information.
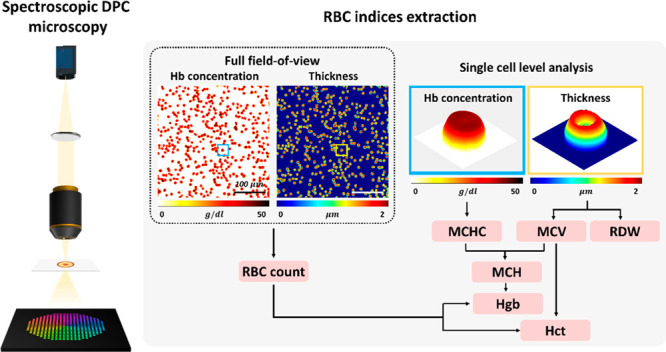
From the measured Hb concentration and physical thickness of the RBCs (Figure 2d), the RBC indices can be obtained as follows:8
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
where A, N, RBC count, and σ denote the area of each RBC, the number of RBCs in the imaging FoV, the number of RBCs in unit volume in millions/mm3, and the standard deviation of each RBC volume, respectively. We estimated the RBC count by counting the number of RBCs in a single FoV using the Hough circle detection algorithm. All of the computation algorithms applied herein were implemented using MATLAB software (MathWorks, USA). The total computation time of RBC index extraction from one image took less than 5 min using a desktop computer (AMD Ryzen 7 3700X 8-Core Processor, 3.60 GHz).
Results and Discussion
Phase Accuracy Evaluation
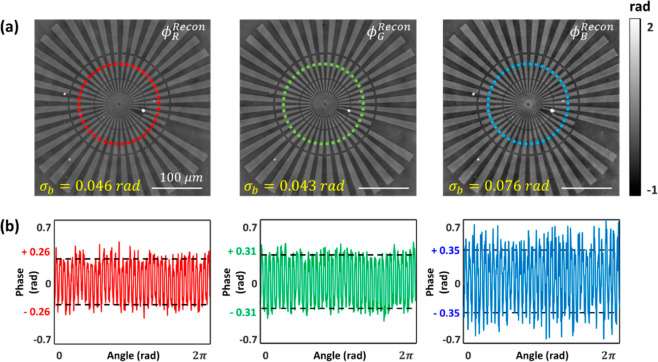
We first assessed the phase measurement accuracy of the sDPC microscope by imaging a Siemens star phase target (Benchmark Technologies, USA; Figure 3). It is clearly seen that sDPC could produce high-contrast, high-resolution phase images at red, green, and blue colors. The regularizers used for the image reconstruction were γtik,r = 7 × 10–4, γtik,g = 5 × 10–4, and γtik,b = 3.9 × 10–4 for the red, green, and blue colors, respectively. The phase measurement error was computed based on the phase profile shown in Figure 3b. We first identified the positions of the peaks and valleys of the phase profile using the MATLAB “findpeaks” function. We then evaluated the difference between the mean phase values of the peaks and valleys as
| 19 |
where ϕpeaki,c and ϕvalleyj,c are the phase values of
the ith and jth peaks and valleys
at color c and M and N are the numbers
of peaks and valleys found in the circular line in Figure 3b, respectively. The obtained 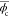 was then compared against the phase change
estimated from the refractive index and etch depth of the target provided
by the manufacturer (Benchmark Technologies, USA). The theoretical
phase changes of the spoke patterns at the red, green, and blue colors
were evaluated as 0.52, 0.62, and 0.69 rad, respectively, and the
differences between sDPC and the theoretical estimations at each color
were measured to be 0.2%, 0.7%, and 1.9%, which was obtained as
was then compared against the phase change
estimated from the refractive index and etch depth of the target provided
by the manufacturer (Benchmark Technologies, USA). The theoretical
phase changes of the spoke patterns at the red, green, and blue colors
were evaluated as 0.52, 0.62, and 0.69 rad, respectively, and the
differences between sDPC and the theoretical estimations at each color
were measured to be 0.2%, 0.7%, and 1.9%, which was obtained as 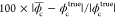 with the theoretical phase change ϕtruec. We also performed imaging of randomly distributed microbeads
with phase delays of 0.997, 1.186, and 1.337 rad in the R, G, and
B colors, respectively, which are comparable to the expected phase
delays of the RBCs. Using the same regularizers (i.e., γtik,r = 7 × 10–4, γtik,g = 5 × 10–4, and γtik,b = 3.9 × 10–4), the phase
delays of the beads relative to the background region were measured
to be 1.00, 1.19, and 1.36 rad at the R, G, and B colors, respectively.
The results agreed well with the theoretically estimated phase values,
with errors of 0.2%, 0.8%, and 1.7% (see Section 3 of the Supporting Information).
with the theoretical phase change ϕtruec. We also performed imaging of randomly distributed microbeads
with phase delays of 0.997, 1.186, and 1.337 rad in the R, G, and
B colors, respectively, which are comparable to the expected phase
delays of the RBCs. Using the same regularizers (i.e., γtik,r = 7 × 10–4, γtik,g = 5 × 10–4, and γtik,b = 3.9 × 10–4), the phase
delays of the beads relative to the background region were measured
to be 1.00, 1.19, and 1.36 rad at the R, G, and B colors, respectively.
The results agreed well with the theoretically estimated phase values,
with errors of 0.2%, 0.8%, and 1.7% (see Section 3 of the Supporting Information).
Figure 3.
sDPC phase images of a Siemens star phase target (Benchmark Technologies, USA). (a) Reconstructed quantitative phase images in each color. Each phase image is shown with the corresponding phase noise measured in the background (σb). (b) Line phase profiles along the red, green, and blue dashed circles in (a). The reconstructed phase values (red, green, and blue solid lines) agree greatly with the theoretical estimations (black dashed line).
We then quantified the spatial phase noise by evaluating the standard deviation of the phase fluctuations in the pattern-free region of 80 × 80 pixels in Figure 3a. The spatial phase noise values of the phase images at the R, G, and B colors were found to be 0.046, 0.043, and 0.076 rad, respectively. In addition, sDPC with a partially coherent light source provides higher spatial resolution than coherent imaging methods44 (see Section 4 in the Supporting Information), which helps with highly precise RBC segmentation.
sDPC-Based Measurements of RBC Indices
We then performed the sDPC measurement of the RBC indices for a blood sample acquired from a normal subject. Approximately 10 μL of the diluted blood sample was loaded into a blood imaging chamber, and sDPC imaging was performed. Note that all the regularization parameters were identical to those in the previous section. For a single sDPC imaging FoV (350 × 350 μm), 402 RBCs were identified and segmented, and the RBC indices were evaluated over the segmented cells. The RBC indices from the same sample were separately measured using a clinical hematology analyzer (XN-2000; Sysmex, Kobe, Japan). The measurement results from the sDPC and hematology analyzer are summarized in Figure 4. The mean and standard deviation values for Hb concentration, cell volume, and Hb content were 34.4 ± 2.6 g/dl, 92.9 ± 11.5 fl, and 32.1 ± 5.7 pg, respectively. The bulk mean values of the RBC indices, including MCHC, MCV, MCH, RDW, Hct, Hgb, and RBC count, were also evaluated and compared against those from the hematology analyzer (Figure 4d). One can note that the sDPC-measured RBC indices agreed well with those from the hematology analyzer even with 402 RBCs in a single FoV, with relative errors of less than 7% for all of the indices. Compared to other RBC indices, the indices that require statistical analysis for a large number of measurements, including RDW and RBC count, exhibited relatively larger errors. However, it should be noted that this performance can be improved by evaluating more RBCs from phase images over multiple FoVs. Indeed, we performed measurements of the RBC indices over five FoVs by laterally scanning the blood chamber and found that the errors reduced to 4.7% and 2.9% for the RDW and RBC counts, respectively (Table S1 in the Supporting Information).
Figure 4.
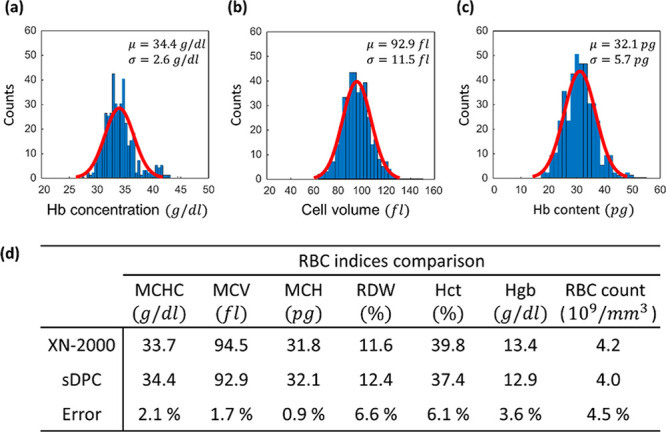
sDPC-based measurements of the RBC indices. Single-cell-level distribution histograms of the Hb concentration (a), cell volume (b), and Hb content (c). All histograms are presented with Gaussian fits (red solid line) and the mean (μ) and standard deviation (σ) values. (d) Mean values of the extracted RBC indices are compared with those from the clinical hematology analyzer.
sDPC-Based Blind Screening of Control and Anemic Groups
The sDPC platform was further applied to screen the control and anemic groups and classify the anemic group into specific categories. Blood samples were first separated into control and anemic groups, and the anemic samples were further classified into common morphologic and chemical abnormalities, which are macrocytic–normochromic anemia with mild anisocytosis (A1) and microcytic–hypochromic anemia with moderate anisocytosis (A2) according to the medical convention based on the RBC indices from the hematology analyzer. The control group (C) was characterized by the normal ranges for the RBC indices (i.e., MCHC, 32–36 g/dl; MCV, 80–100 fl; MCH, 27–31 pg; RDW, 12–15%; Hct, 41–50% and 36–48% for male and female, respectively; Hgb, 13.8–17.2 and 12.1–15.1 g/dl for male and female, respectively; and RBC count, 4.0–5.9 and 3.8–5.2 millions/mm3 for male and female, respectively), while the RBC indices of the anemic groups were outside of these reference ranges. Microcytic–hypochromic anemia is possibly related to iron deficiency, thalassemia, and chronic bleeding,59 while macrocytic anemia includes the possibilities of vitamin B12 deficiency or folate deficiency.60,61
We then blindly performed the sDPC-based blood assay to evaluate its diagnostic performance for the RBC abnormalities. The RBC indices for the same blood specimens were measured, and the results were compared against the those from the hematology analyzer (XN-2000; Sysmex, Kobe, Japan) (Figure 5a). Note that the measurements were performed on blood specimens from the same batch. As can be noted, sDPC could successfully differentiate the anemic groups from the control group based on the Hct (C, 42.1%; A1 and A2, 34.7% and 24.8%, respectively) and Hgb levels (C, 14.5 g/dl; A1 and A2, 11.6 and 7.7 g/dl, respectively) and could classify the anemic groups into macrocytic–normochromic anemia (A1) and microcytic–hypochromic anemia (A2) with the RBC indices (Figures 5b and 5c). The A1 group featured high MCV and RDW and normal-range MCHC, which are the characteristics of macrocytic–normochromic anemia with mild anisocytosis. On the other hand, the A2 group exhibited very high RDW and low levels of MCHC and MCV compared to the normal reference ranges for the RBC indices and therefore can be classified as microcytic–hypochromic anemia with moderate anisocytosis. Note that the measurements of RBC indices were performed with 560, 306, and 309 RBCs for the C, A1, and A2 groups, respectively. All of the p-values were less than 0.001, clearly indicating that the differences were not due to sampling error. The RBC indices extracted from sDPC not only matched well with the reference measurements from the hematology analyzer (XN-2000; Sysmex, Kobe, Japan) with errors less than 7% but could also provide single-cell-level quantitative measurements of the RBC indices.
Figure 5.
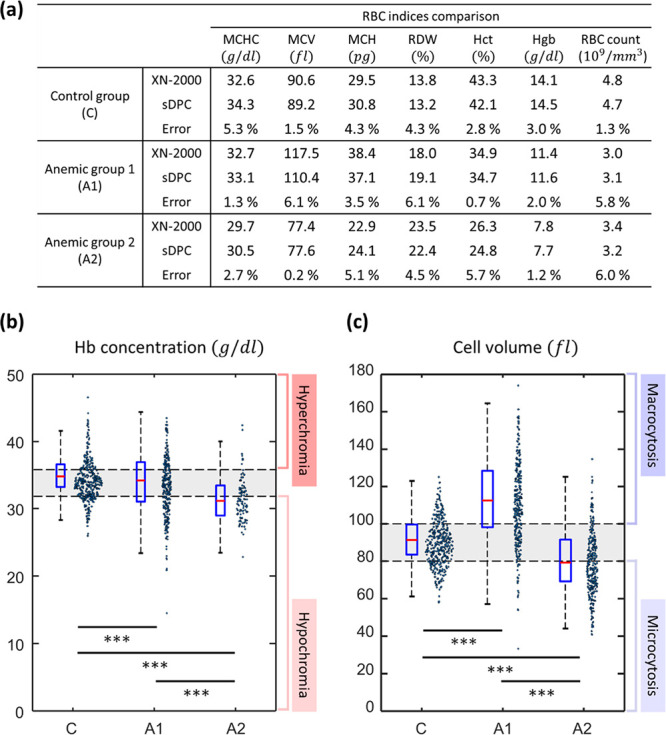
sDPC-based measurements of RBC indices for the control and anemic groups. (a) Compared bulk mean values of RBC indices from the hematology analyzer and sDPC. Hb concentration (b) and cell volume (c) are presented as the boxplots and swarm charts, along with the p-values of the student’s t test. *** indicates that the p-value of the selected two groups is less than 0.001. The gray shaded regions in (b) and (c) denote the normal reference ranges of MCHC and MCV, indicating normochromia and normocytosis, respectively. Each box plot indicates the median value (red line) and interquartile range (blue box) of a given set, and the whiskers are extended to the extreme values.
Conclusion and Future Perspectives
In summary, we demonstrated an sDPC microscope as a viable image-based detection platform for RBC indices. sDPC can be readily built in a conventional microscope using an inexpensive LED array as the light source and provides speckle-free quantitative phase images at multiple colors. We implemented spectroscopic phase reconstruction and gradient-descent-based optimization algorithms to decouple the Hb concentration and physical thickness of RBCs from the measured sDPC images, which were then used for the evaluation of RBC indices. The high-accuracy phase imaging capability of the sDPC was validated by imaging a calibrated phase target (error < 2% for all colors considered), and the detection performance of the RBC indices was demonstrated by comparing the sDPC results against those from a clinical hematology analyzer (XN-2000; Sysmex, Kobe, Japan). For ∼400 RBCs in a single FoV, the measured errors were less than 7% for seven RBC indices, including MCHC, MCV, MCH, RDW, Hct, Hgb, and RBC count. We further employed sDPC for the detection of RBC indices and the classification of the control and anemic groups.
It should be noted that spectroscopic QPIs have been demonstrated previously.34−37,62 However, to the best of our knowledge, spectroscopic QPI in the platform of DPC microscopy has not been demonstrated and applied to the quantitative detection of RBC indices. Previous spectroscopic QPIs reported thus far have mostly been demonstrated in DHM, which exhibits issues with speckle noise and sensitivity to experimental disturbances. DPC microscopes based on color-multiplexed illuminations/detections have been demonstrated; however, all the methods rely on the assumption that objects are nondispersive to obtain a phase image at a nominally selected wavelength. For instance, Fan et al. employed color-multiplexed illumination to generate phase image at a blue color (i.e., 461 nm).52 Some studies examined optimal illumination patterns to achieve isotropic DPC imaging at a single wavelength. In contrast, our method considers RBC as a dispersive object that exhibits a wavelength-dependent refractive index as a function of Hb concentration. To obtain a wavelength-dependent phase image, we utilized color-multiplexed illumination, and the obtained images at red, green, and blue were used to decouple the physical thickness and refractive index.
Several features of sDPC should be noted. First, sDPC is capable of producing quantitative phase images of unprocessed blood cells and thus eliminates the preparation procedures, markedly simplifying the detection protocols for the RBC indices. Its reference-free optical setup with partially coherent LEDs also enables speckle-free image acquisition with spatial resolution higher than that of holography-based imaging methods. This feature offered phase reconstruction with spatial phase noise ≤0.08 rad without any hardware-based noise reduction methods. This noise performance is expected to be further improved by being combined with various computational denoising methods, such as wavelet denoising63 or convolutional neural-network-based methods,64 which will help with precise cell segmentation and volume detection. Moreover, unlike a conventional hematology analyzer, sDPC allows for the observation of RBC morphology at the single-cell level. This feature enables quantitative analysis of the heterogeneity of the RBC indices at the single-cell level and can be used for various morphological and dynamic studies, including surface area, sphericity, and membrane fluctuation.25 Microscopic information on RBCs at the cellular level is of great importance in the differentiation of various RBC cell types, which is highly related to various diseases. For instances, Hb content and morphological information can be used to diagnose malaria37 and sickle cell diseases,65 and a recent report found that elevated schistocyte counts are associated with increased all-cause mortality.66
In our prototype, a single FoV of the sDPC microscope contains about ∼400 RBCs for normal subjects. This small number of RBCs compared to that measured by a hematology analyzer (∼millions of RBCs) for the RBC index extraction may largely contribute to the discrepancies between the sDPC and hematology analyzer measurements. As observed in Figure 4, the RBC indices that require statistical measurements with a large population of RBCs (e.g., RDW and RBC count) exhibited relatively larger errors against those from the hematology analyzer compared to other RBC indices. Computation with images over multiple FoVs improves the precision. Indeed, RBC indices computed with the sDPC measurements over five FoVs resulted in error reduced to 4.7% and 2.9% in terms of RDW and RBC count, respectively. As such, the integration of an automated specimen translation stage into the sDPC platform would enable the highly precise and automated detection of the RBC indices by taking images over multiple FoVs. Several computational imaging methods have demonstrated large-FoV, high-resolution imaging capabilities for thin transparent objects.67−69 However, these methods generate such high space–bandwidth product images by capturing multiple images under different imaging conditions (e.g., various illumination angles or object positions) and synthesizing the frequency information on the captured images for a single imaging area. Consequently, these methods may not be suitable for imaging suspended RBCs, which may move around during multiple image acquisitions.
Several improvements can be pursued to facilitate the adoption of sDPC in clinical laboratories. The imaging speed of the current sDPC setup is limited largely by the low light intensity on the specimen plane from the LED array. We employed a planar LED array as the light source, which was located ∼80 mm from the sample plane. Therefore, rapidly diverging light from the LEDs resulted in a very small irradiance on the imaging FoV. This problem may be resolved using a domed LED array with the integrated collimators. In doing so, quasi-collimated LED light will be incident onto the sample plane, thereby increasing the light intensity. Another strategy for improving the imaging throughput is to implement sDPC in the format of image-based flow cytometry or microfluidic devices.26 In such a scenario, the stationary sDPC performs the imaging while the blood cells continuously flow across the imaging FoV with the monolayer. However, sDPC requires three image acquisitions to obtain phase images at multiple colors, and thus the cells may be positioned at different locations in the FoV during the DPC image acquisition. These motion-related issues have recently been addressed by Kellman et al.70 The implementation of such a method or other motion-correction algorithms may allow phase imaging of the flowing RBCs and enable the high-throughput detection of the RBC indices for a large number of cells.
The integration of deep-learning-based methods can also be considered. In our analysis, we performed extraction of the Hb concentration and the physical thickness of RBCs based on the inverse problem set with phase images of multiple colors. Deep-learning-based approaches may be exploited to decouple the Hb concentration and physical thickness directly from quantitative phase images or to obtain RBC indices directly. To realize this end-to-end detection framework, however, a large number of sDPC images and the corresponding ground-truth information are required to train the network. It should also be emphasized that the sDPC microscope can be readily transformed into a portable platform integrated with smartphones. For instance, Jung et al.71 previously demonstrated a smartphone-based multicontrast microscope based on color-multiplexed LED illuminations. The state-of-the-art smartphones are equipped with high-density color image sensors and high-performance computing resources, and thus the integration of the color LED arrays into the smartphone-based microscope and the implementation of sDPC image reconstruction algorithms in the smartphone-embedded GPUs could generate a compact and cost-effective detector for RBC analysis. This small device, if realized, can potentially benefit healthcare at local hospitals in resource-limited countries.
Acknowledgments
This work is supported by the Samsung Research Funding & Incubation Center of Samsung Electronics under Project SRFC-IT2002-07, the National Research Foundation of Korea (NRF) Grant funded by the government of Korea (MSIT) (2023R1A2C3004040), the Korea Institute for Advancement of Technology (KIAT) Grant funded by the government of Korea (MOTIE) (P0019784), the Ministry of Science and ICT (Project 2023-22030004-20) (NTIS, 1711179106), the Commercialization Promotion Agency for R&D Outcomes (COMPA) funded by the Ministry of Science and ICT (MSIT) (1711198541, development of key optical technologies of inspection and measurement for the analysis of 3D complex nanostructures), and the Korea Medical Device Development Fund (KMDF_PR_20200901_0099, Project Number: 9991007255).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/cbmi.3c00090.
Additional information including the color leakage correction method, the RBC segmentation algorithm, the polystyrene microbead imaging results, the spatial resolution comparison of the coherent QPI and sDPC methods, and the improved sDPC detection performance for RBC indices via measurements over multiple FoVs (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Kasper D.; Fauci A.; Hauser S.; Longo D.; Jameson J.; Loscalzo J.. Harrison’s principles of internal medicine, 19th ed.; McGraw-Hill: New York, NY, USA, 2015. [Google Scholar]
- Tsaras G.; Owusu-Ansah A.; Boateng F. O.; Amoateng-Adjepong Y. Complications associated with sickle cell trait: a brief narrative review. American journal of medicine 2009, 122 (6), 507–512. 10.1016/j.amjmed.2008.12.020. [DOI] [PubMed] [Google Scholar]
- Perrotta S.; Gallagher P. G.; Mohandas N. Hereditary spherocytosis. Lancet 2008, 372 (9647), 1411–1426. 10.1016/S0140-6736(08)61588-3. [DOI] [PubMed] [Google Scholar]
- Charneski L.; Congdon H. B. Effects of antiplatelet and anticoagulant medications on the vasoocclusive and thrombotic complications of sickle cell disease: a review of the literature. American Journal of Health-System Pharmacy 2010, 67 (11), 895–900. 10.2146/ajhp090229. [DOI] [PubMed] [Google Scholar]
- Dixon L. R. The complete blood count: physiologic basis and clinical usage. Journal of perinatal & neonatal nursing 1997, 11 (3), 1–18. 10.1097/00005237-199712000-00003. [DOI] [PubMed] [Google Scholar]
- Park S. H.; Park C.-J.; Lee B.-R.; Cho Y.-U.; Jang S.; Kim N.; Koh K.-N.; Im H.-J.; Seo J.-J.; Park E. S.; Lee J. W.; Yoo K. H.; Jung H. L. Comparison study of the eosin-5′-maleimide binding test, flow cytometric osmotic fragility test, and cryohemolysis test in the diagnosis of hereditary spherocytosis. American journal of clinical pathology 2014, 142 (4), 474–484. 10.1309/AJCPO7V4OGXLIIPP. [DOI] [PubMed] [Google Scholar]
- Valavi E.; Ansari M. J. A.; Zandian K. How to reach rapid diagnosis in sickle cell disease?. Iranian Journal of Pediatrics 2010, 20 (1), 69–74. [PMC free article] [PubMed] [Google Scholar]
- Fischbach F. T.; Dunning M. B.. A manual of laboratory and diagnostic tests; Lippincott Williams & Wilkins, 2009. [Google Scholar]
- Emilse L. A. M.; Cecilia H.; María T. M.; Eugenia M. M.; Alicia I. B.; Lazarte S. S. Cryohemolysis, erythrocyte osmotic fragility, and supplementary hematimetric indices in the diagnosis of hereditary spherocytosis. Blood research 2018, 53 (1), 10. 10.5045/br.2018.53.1.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eberle S. E.; Sciuccati G.; Bonduel M.; Díaz L.; Staciuk R.; Torres A. F. Erythrocyte indexes in hereditary spherocytosis. Medicina 2007, 67 (6 Pt 2), 698–700. [PubMed] [Google Scholar]
- Alamri B.; Bahabri A.; Aldereihim A.; Alabduljabbar M.; Alsubaie M.; Alnaqeb D.; Almogbel E.; Metias N.; Alotaibi O.; Al-Rubeaan K. Hyperglycemia effect on red blood cells indices. Eur. Rev. Med. Pharmacol Sci. 2019, 23 (5), 2139–2150. 10.26355/eurrev_201903_17259. [DOI] [PubMed] [Google Scholar]
- DeNicola D. B. Advances in hematology analyzers. Topics in companion animal medicine 2011, 26 (2), 52–61. 10.1053/j.tcam.2011.02.001. [DOI] [PubMed] [Google Scholar]
- Schonbrun E.; Malka R.; Di Caprio G.; Schaak D.; Higgins J. M. Quantitative absorption cytometry for measuring red blood cell hemoglobin mass and volume. Cytometry Part A 2014, 85 (4), 332–338. 10.1002/cyto.a.22450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francis A. T.; Shears M. J.; Murphy S. C.; Fu D. Direct quantification of single red blood cell hemoglobin concentration with multiphoton microscopy. Anal. Chem. 2020, 92 (18), 12235–12241. 10.1021/acs.analchem.0c01609. [DOI] [PubMed] [Google Scholar]
- Park Y.; Depeursinge C.; Popescu G. Quantitative phase imaging in biomedicine. Nat. Photonics 2018, 12 (10), 578–589. 10.1038/s41566-018-0253-x. [DOI] [Google Scholar]
- Mir M.; Tangella K.; Popescu G. Blood testing at the single cell level using quantitative phase and amplitude microscopy. Biomedical optics express 2011, 2 (12), 3259–3266. 10.1364/BOE.2.003259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham H. V.; Bhaduri B.; Tangella K.; Best-Popescu C.; Popescu G. Real time blood testing using quantitative phase imaging. PloS one 2013, 8 (2), e55676 10.1371/journal.pone.0055676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dardikman G.; Shaked N. T. Review on methods of solving the refractive index–thickness coupling problem in digital holographic microscopy of biological cells. Opt. Commun. 2018, 422, 8–16. 10.1016/j.optcom.2017.11.084. [DOI] [Google Scholar]
- Zhang Q.; Zhong L.; Tang P.; Yuan Y.; Liu S.; Tian J.; Lu X. Quantitative refractive index distribution of single cell by combining phase-shifting interferometry and AFM imaging. Sci. Rep. 2017, 7 (1), 1–10. 10.1038/s41598-017-02797-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lue N.; Choi W.; Popescu G.; Yaqoob Z.; Badizadegan K.; Dasari R. R.; Feld M. S. Live cell refractometry using Hilbert phase microscopy and confocal reflectance microscopy. J. Phys. Chem. A 2009, 113 (47), 13327–13330. 10.1021/jp904746r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lue N.; Popescu G.; Ikeda T.; Dasari R. R.; Badizadegan K.; Feld M. S. Live cell refractometry using microfluidic devices. Optics letters 2006, 31 (18), 2759–2761. 10.1364/OL.31.002759. [DOI] [PubMed] [Google Scholar]
- Kemper B.; Kosmeier S.; Langehanenberg P.; von Bally G.; Bredebusch I.; Domschke W.; Schnekenburger J. Integral refractive index determination of living suspension cells by multifocus digital holographic phase contrast microscopy. Journal of biomedical optics 2007, 12 (5), 054009 10.1117/1.2798639. [DOI] [PubMed] [Google Scholar]
- Jafarfard M. R.; Moon S.; Tayebi B.; Kim D. Y. Dual-wavelength diffraction phase microscopy for simultaneous measurement of refractive index and thickness. Optics letters 2014, 39 (10), 2908–2911. 10.1364/OL.39.002908. [DOI] [PubMed] [Google Scholar]
- Rappaz B.; Marquet P.; Cuche E.; Emery Y.; Depeursinge C.; Magistretti P. J. Measurement of the integral refractive index and dynamic cell morphometry of living cells with digital holographic microscopy. Opt. Express 2005, 13 (23), 9361–9373. 10.1364/OPEX.13.009361. [DOI] [PubMed] [Google Scholar]
- Kim G.; Jo Y.; Cho H.; Min H.-s.; Park Y. Learning-based screening of hematologic disorders using quantitative phase imaging of individual red blood cells. Biosens. Bioelectron. 2019, 123, 69–76. 10.1016/j.bios.2018.09.068. [DOI] [PubMed] [Google Scholar]
- Ryu D.; Nam H.; Jeon J. S.; Park Y. Reagent-and actuator-free analysis of individual erythrocytes using three-dimensional quantitative phase imaging and capillary microfluidics. Sens. Actuators, B 2021, 348, 130689 10.1016/j.snb.2021.130689. [DOI] [Google Scholar]
- Son M.; Lee Y. S.; Lee M. J.; Park Y.; Bae H.-R.; Lee S. Y.; Shin M.-G.; Yang S. Effects of osmolality and solutes on the morphology of red blood cells according to three-dimensional refractive index tomography. PLoS One 2021, 16 (12), e0262106 10.1371/journal.pone.0262106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Firdaus M. E. R.; Muh F.; Park J.-H.; Lee S.-K.; Na S.-H.; Park W.-S.; Ha K.-S.; Han J.-H.; Han E.-T. In-depth biological analysis of alteration in Plasmodium knowlesi-infected red blood cells using a noninvasive optical imaging technique. Parasites & Vectors 2022, 15 (1), 1–8. 10.1186/s13071-022-05182-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergaglio T.; Bhattacharya S.; Thompson D.; Nirmalraj P. N. Label-free digital holotomography reveals ibuprofen-induced morphological changes to red blood cells. ACS Nanoscience Au 2023, 3, 241. 10.1021/acsnanoscienceau.3c00004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou N.; Li J.; Sun J.; Zhang R.; Bai Z.; Zhou S.; Chen Q.; Zuo C. Single-exposure 3D label-free microscopy based on color-multiplexed intensity diffraction tomography. Opt. Lett. 2022, 47 (4), 969–972. 10.1364/OL.442171. [DOI] [PubMed] [Google Scholar]
- Kuś A. Real-time, multiplexed holographic tomography. Optics and Lasers in Engineering 2022, 149, 106783 10.1016/j.optlaseng.2021.106783. [DOI] [Google Scholar]
- Lee C.; Hugonnet H.; Park J.; Lee M. J.; Park W.; Park Y. Single-shot refractive index slice imaging using spectrally multiplexed optical transfer function reshaping. Opt. Express 2023, 31 (9), 13806–13816. 10.1364/OE.485559. [DOI] [PubMed] [Google Scholar]
- Ge B.; He Y.; Deng M.; Rahman M. H.; Wang Y.; Wu Z.; Wong C. H. N.; Chan M. K.; Ho Y.-P.; Duan L. Single-frame label-free cell tomography at speed of more than 10,000 volumes per second. arXiv 2022, n/a. 10.48550/arXiv.2202.03627. [DOI] [Google Scholar]
- Jang Y.; Jang J.; Park Y. Dynamic spectroscopic phase microscopy for quantifying hemoglobin concentration and dynamic membrane fluctuation in red blood cells. Opt. Express 2012, 20 (9), 9673–9681. 10.1364/OE.20.009673. [DOI] [PubMed] [Google Scholar]
- Turko N. A.; Shaked N. T. Erythrocyte volumetric measurements in imaging flow cytometry using simultaneous three-wavelength digital holographic microscopy. Biomedical Optics Express 2020, 11 (11), 6649–6658. 10.1364/BOE.404368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park Y.; Yamauchi T.; Choi W.; Dasari R.; Feld M. S. Spectroscopic phase microscopy for quantifying hemoglobin concentrations in intact red blood cells. Optics letters 2009, 34 (23), 3668–3670. 10.1364/OL.34.003668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rinehart M. T.; Park H. S.; Walzer K. A.; Chi J.-T. A.; Wax A. Hemoglobin consumption by P. falciparum in individual erythrocytes imaged via quantitative phase spectroscopy. Sci. Rep. 2016, 6 (1), 24461 10.1038/srep24461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan F.; Xiao W.; Liu S.; Wang F.; Rong L.; Li R. Coherent noise reduction in digital holographic phase contrast microscopy by slightly shifting object. Opt. Express 2011, 19 (5), 3862–3869. 10.1364/OE.19.003862. [DOI] [PubMed] [Google Scholar]
- Pan F.; Xiao W.; Liu S.; Rong L. Coherent noise reduction in digital holographic microscopy by laterally shifting camera. Opt. Commun. 2013, 292, 68–72. 10.1016/j.optcom.2012.11.091. [DOI] [Google Scholar]
- Pan F.; Yang L.; Xiao W. Coherent noise reduction in digital holographic microscopy by averaging multiple holograms recorded with a multimode laser. Opt. Express 2017, 25 (18), 21815–21825. 10.1364/OE.25.021815. [DOI] [PubMed] [Google Scholar]
- Choi Y.; Yang T. D.; Lee K. J.; Choi W. Full-field and single-shot quantitative phase microscopy using dynamic speckle illumination. Optics letters 2011, 36 (13), 2465–2467. 10.1364/OL.36.002465. [DOI] [PubMed] [Google Scholar]
- Wang Z.; Millet L.; Mir M.; Ding H.; Unarunotai S.; Rogers J.; Gillette M. U.; Popescu G. Spatial light interference microscopy (SLIM). Opt. Express 2011, 19 (2), 1016–1026. 10.1364/OE.19.001016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X.; Kandel M. E.; Popescu G. Spatial light interference microscopy: principle and applications to biomedicine. Advances in optics and photonics 2021, 13 (2), 353–425. 10.1364/AOP.417837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian L.; Waller L. Quantitative differential phase contrast imaging in an LED array microscope. Opt. Express 2015, 23 (9), 11394–11403. 10.1364/OE.23.011394. [DOI] [PubMed] [Google Scholar]
- Mehta S. B.; Sheppard C. J. Quantitative phase-gradient imaging at high resolution with asymmetric illumination-based differential phase contrast. Optics letters 2009, 34 (13), 1924–1926. 10.1364/OL.34.001924. [DOI] [PubMed] [Google Scholar]
- Phillips Z. F.; Chen M.; Waller L. Single-shot quantitative phase microscopy with color-multiplexed differential phase contrast (cDPC). PloS one 2017, 12 (2), e0171228 10.1371/journal.pone.0171228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee W.; Jung D.; Ryu S.; Joo C. Single-exposure quantitative phase imaging in color-coded LED microscopy. Opt. Express 2017, 25 (7), 8398–8411. 10.1364/OE.25.008398. [DOI] [PubMed] [Google Scholar]
- Lee D.; Ryu S.; Kim U.; Jung D.; Joo C. Color-coded LED microscopy for multi-contrast and quantitative phase-gradient imaging. Biomedical optics express 2015, 6 (12), 4912–4922. 10.1364/BOE.6.004912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee W.; Choi J.-H.; Ryu S.; Jung D.; Song J.; Lee J.-S.; Joo C. Color-coded LED microscopy for quantitative phase imaging: Implementation and application to sperm motility analysis. Methods 2018, 136, 66–74. 10.1016/j.ymeth.2017.11.010. [DOI] [PubMed] [Google Scholar]
- He L.; Shao M.; Yang X.; Si L.; Jiang M.; Wang T.; Ke Z.; Peng T.; Fang S.; Zhang S.; Ouyang X.; Zhao G.; Zhou J. Morphology analysis of unlabeled red blood cells based on quantitative differential phase contrast microscopy. Cytometry Part A 2022, 101, 648. 10.1002/cyto.a.24546. [DOI] [PubMed] [Google Scholar]
- Hur S.; Song S.; Kim S.; Joo C. Polarization-sensitive differential phase-contrast microscopy. Opt. Lett. 2021, 46 (2), 392–395. 10.1364/OL.412703. [DOI] [PubMed] [Google Scholar]
- Fan Y.; Sun J.; Chen Q.; Pan X.; Trusiak M.; Zuo C. Single-shot isotropic quantitative phase microscopy based on color-multiplexed differential phase contrast. APL Photonics 2019, 4 (12), 121301. 10.1063/1.5124535. [DOI] [Google Scholar]
- Sun J.; Chen Q.; Zhang J.; Fan Y.; Zuo C. Single-shot quantitative phase microscopy based on color-multiplexed Fourier ptychography. Optics letters 2018, 43 (14), 3365–3368. 10.1364/OL.43.003365. [DOI] [PubMed] [Google Scholar]
- Fan Y.; Sun J.; Chen Q.; Pan X.; Tian L.; Zuo C. Optimal illumination scheme for isotropic quantitative differential phase contrast microscopy. Photonics Research 2019, 7 (8), 890–904. 10.1364/PRJ.7.000890. [DOI] [Google Scholar]
- Malvar H. S.; He L.-W.; Cutler R.. High-quality linear interpolation for demosaicing of Bayer-patterned color images. In 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Vol. 3; IEEE, 2004; pp iii–485. [Google Scholar]
- Wu Y.; Zhang Y.; Luo W.; Ozcan A. Demosaiced pixel super-resolution for multiplexed holographic color imaging. Sci. Rep. 2016, 6 (1), 28601 10.1038/srep28601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friebel M.; Meinke M. Model function to calculate the refractive index of native hemoglobin in the wavelength range of 250–1100 nm dependent on concentration. Applied optics 2006, 45 (12), 2838–2842. 10.1364/AO.45.002838. [DOI] [PubMed] [Google Scholar]
- Perraudin N.; Kalofolias V.; Shuman D.; Vandergheynst P. UNLocBoX: A MATLAB convex optimization toolbox for proximal-splitting methods. arXiv 2014, n/a. 10.48550/arXiv.1402.0779. [DOI] [Google Scholar]
- Chaudhry H. S.; Kasarla M. R.. Microcytic Hypochromic Anemia; StatPearls Publishing, 2017. [PubMed] [Google Scholar]
- Nagao T.; Hirokawa M. Diagnosis and treatment of macrocytic anemias in adults. Journal of general and family medicine 2017, 18 (5), 200–204. 10.1002/jgf2.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore C. A.; Adil A.. Macrocytic Anemia; StatPearls Publishing, 2017. [PubMed] [Google Scholar]
- Rinehart M.; Zhu Y.; Wax A. Quantitative phase spectroscopy. Biomedical optics express 2012, 3 (5), 958–965. 10.1364/BOE.3.000958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malfait M.; Roose D. Wavelet-based image denoising using a Markov random field a priori model. IEEE Transactions on image processing 1997, 6 (4), 549–565. 10.1109/83.563320. [DOI] [PubMed] [Google Scholar]
- Zhang K.; Zuo W.; Zhang L. FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Transactions on Image Processing 2018, 27 (9), 4608–4622. 10.1109/TIP.2018.2839891. [DOI] [PubMed] [Google Scholar]
- Ozpolat H. T.; Chang T.; Chen J.; Wu X.; Norby C.; Konkle B. A.; Lopez J. A. Evaluation of Cell Types and Morphologies in Sickle Cell Disease with an Imaging Flow Cytometer. Blood 2015, 126 (23), 972. 10.1182/blood.V126.23.972.972.26022238 [DOI] [Google Scholar]
- Foy B.; Stefely J.; Bendapudi P. K.; Hasserjian R. P.; Al-Samkari H.; Louissaint A.; Fitzpatrick M. J; Hutchison B.; Mow C.; Collins J.; Patel H. P.; Patel C.; Patel N.; Ho S.; Kaufman R. M; Dzik W.; Higgins J. M.; Makar R. S A Machine-Learning Derived Red Blood Cell Morphology Tool Enables Differential Diagnosis and Novel Single-Cell Analyses. Blood 2022, 140 (Suppl. 1), 10704–10705. 10.1182/blood-2022-170422. [DOI] [Google Scholar]
- Zheng G.; Horstmeyer R.; Yang C. Wide-field, high-resolution Fourier ptychographic microscopy. Nat. Photonics 2013, 7 (9), 739–745. 10.1038/nphoton.2013.187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo W.; Greenbaum A.; Zhang Y.; Ozcan A. Synthetic aperture-based on-chip microscopy. Light: Science & Applications 2015, 4 (3), e261–e261. 10.1038/lsa.2015.34. [DOI] [Google Scholar]
- Jiang S.; Guo C.; Hu P.; Hu D.; Song P.; Wang T.; Bian Z.; Zhang Z.; Zheng G. High-throughput lensless whole slide imaging via continuous height-varying modulation of a tilted sensor. Opt. Lett. 2021, 46 (20), 5212–5215. 10.1364/OL.437832. [DOI] [PubMed] [Google Scholar]
- Kellman M.; Chen M.; Phillips Z. F.; Lustig M.; Waller L. Motion-resolved quantitative phase imaging. Biomedical Optics Express 2018, 9 (11), 5456–5466. 10.1364/BOE.9.005456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung D.; Choi J.-H.; Kim S.; Ryu S.; Lee W.; Lee J.-S.; Joo C. Smartphone-based multi-contrast microscope using color-multiplexed illumination. Sci. Rep. 2017, 7 (1), 7564 10.1038/s41598-017-07703-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.