Abstract
Background
Recent developments in causal inference and machine learning (ML) allow for the estimation of individualized treatment effects (ITEs), which reveal whether treatment effectiveness varies according to patients’ observed covariates. ITEs can be used to stratify health policy decisions according to individual characteristics and potentially achieve greater population health. Little is known about the appropriateness of available ML methods for use in health technology assessment.
Methods
In this scoping review, we evaluate ML methods available for estimating ITEs, aiming to help practitioners assess their suitability in health technology assessment. We present a taxonomy of ML approaches, categorized by key challenges in health technology assessment using observational data, including handling time-varying confounding and time-to event data and quantifying uncertainty.
Results
We found a wide range of algorithms for simpler settings with baseline confounding and continuous or binary outcomes. Not many ML algorithms can handle time-varying or unobserved confounding, and at the time of writing, no ML algorithm was capable of estimating ITEs for time-to-event outcomes while accounting for time-varying confounding. Many of the ML algorithms that estimate ITEs in longitudinal settings do not formally quantify uncertainty around the point estimates.
Limitations
This scoping review may not cover all relevant ML methods and algorithms as they are continuously evolving.
Conclusions
Existing ML methods available for ITE estimation are limited in handling important challenges posed by observational data when used for cost-effectiveness analysis, such as time-to-event outcomes, time-varying and hidden confounding, or the need to estimate sampling uncertainty around the estimates.
Implications
ML methods are promising but need further development before they can be used to estimate ITEs for health technology assessments.
Highlights
Estimating individualized treatment effects (ITEs) using observational data and machine learning (ML) can support personalized treatment advice and help deliver more customized information on the effectiveness and cost-effectiveness of health technologies.
ML methods for ITE estimation are mostly designed for handling confounding at baseline but not time-varying or unobserved confounding. The few models that account for time-varying confounding are designed for continuous or binary outcomes, not time-to-event outcomes.
Not all ML methods for estimating ITEs can quantify the uncertainty of their predictions.
Future work on developing ML that addresses the concerns summarized in this review is needed before these methods can be widely used in clinical and health technology assessment–like decision making.
Keywords: machine learning, causal inference, individualized treatment effect, health technology assessment, observational data
Cost-effectiveness analysis (CEA) results are often used to inform health technology assessment adoption decisions. Several contributions have extended the standard economic evaluation framework to show that nuanced treatment and funding decisions that take into account patient characteristics may yield greater population health gains compared with one-size-fits-all policies.1–3 One important way in which patient characteristics can influence the value for money of a given treatment is through treatment effect heterogeneity—the fact that some individuals may gain more from a treatment than others. Learning heterogeneous treatment effects allows the identification of those patients who benefit the most (and the least) from certain treatments, facilitating stratified policy decisions.
Treatment effect heterogeneity has typically been investigated via subgroup analyses of randomized controlled trial (RCT) data using traditional statistical solutions such as treatment-by-covariate interactions in a regression model. However, these solutions yield only average treatment effects for prespecified subgroups and hence might miss important drivers of systematic variation.
A new area of research in statistics, economics, and computer science has focused on estimating treatment effect heterogeneity in a way that does not require prespecified subgroups yet yields estimates of heterogeneous treatment effects in transparent and reproducible ways. This literature aims to capture the potential complex relationship between observable patient characteristics and the expected treatment effect, often referred to as the conditional average treatment effect (CATE) function. Predictions from the CATE function can yield estimates of individualized treatment effects (ITEs). Although ITE and CATE are often used interchangeably (and we adopt this convention in our article), it is important to note that predictions of ITEs from estimated CATE functions are only individualized to the extent allowed by the richness of the observed covariate information and do not capture unobservable heterogeneity in the treatment effects. 4
Most of this literature incorporates machine learning (ML) in a formal causal inference framework, often referred to as causal machine learning.5,6 The formal causal inference framework ensures that the sources of bias that may affect a treatment effect estimate derived from observational data, most importantly confounding, are addressed. The strengths of ML can be exploited for ITE estimation in several ways. First, ML can be used to specify so-called nuisance models (outcome regressions and propensity score models) that can help reduce the bias due to confounding in estimates of treatment effects. 7 ML models for nuisance model estimation may be preferable to parametric models as they can data-adaptively take into account nonlinearities and interactions in the data-generating mechanism and can also select an ensemble of models to improve performance. 8 As real-world data may be high dimensional, some ML algorithms (for example, random forests and LASSO) can also allow for selection among a large number of potential confounders. 9 Methods that estimate ITEs can rely on these nuisance models (see more details in the “ML Methods to Estimate ITE” section) but can also flexibly characterize the relationship between observed covariates and the expected treatment effects, like the causal forests approach.47-51 Here, the ability of ML to perform variable selection is once again crucial as there may be only a few variables that contribute to treatment effect heterogeneity among a large number of candidates.
Applications of ML in health care have multiplied rapidly in recent years, thanks to the development of freely available estimation algorithms.9–17 Health economics and outcomes researchers have embraced this new approach with enthusiasm, and it is now recognized that ML is a valuable tool to capture the complexities (e.g., nonlinearity and heterogeneity) in the disease process and the costs and outcomes associated with given health states and treatments. 9 Several published health economics and outcomes research studies have used ML to assist with, for example, selecting study population and key covariates, and a summary of these studies can be found elsewhere. 9 However, there is little practical guidance to help health technology assessment practitioners aiming to apply ML methods specifically to estimate heterogeneous treatment effects such as ITEs. As existing ML approaches to ITE estimation have often been developed outside health care, it is not clear which (if any) of the available methods meets the needs of health technology assessment practitioners.
We use the example of migraine to illustrate the potential use of ITEs in health technology assessment. ML methods have been previously used to predict the occurrence of migraine and to identify the relevant features for prediction.18,19 However, when assessing the cost-effectiveness of a new migraine medication, researchers may need to go further than simple predictions and need to model the treatment-specific risk and duration of each episode as a function of an individual patient’s characteristics. Such treatment-specific risk parameters can be constructed from a baseline risk and an ITE and estimated via ML methods reviewed here. Heterogeneity can also affect the (potentially treatment-specific) cost and health-related quality-of-life parameters. A cost-effectiveness model, encapsulating these heterogeneous input parameters, 20 can then usefully inform stratified decisions that aim to provide the right treatment to the right patient and report the value of stratification. 21 Even when the interest is in making one-size-fits-all decisions for a predefined target population that is relevant for a given treatment, stratified model inputs can help produce more accurate cost-effectiveness analysis both for the population average and subgroup-specific results, due to the nonlinear relationship between model inputs and outputs.
This scoping review aims to identify ML methods available for estimating ITEs, for the purposes of health technology assessment decisions regarding whether payers should fund or reimburse a health technology or intervention. In the following sections, we clarify key concepts of ITE and causal inference and identify key challenges that ML methods need to overcome to be useful for estimating ITEs for use in health technology assessment, including confounding, modeling time-to-event outcomes and estimating uncertainty. We then present an intuitive overview of the currently available ML methods for ITE estimation, classifying them in terms of how they can tackle these key challenges. The article concludes by highlighting gaps and hurdles that currently hinder a more rapid adoption and successful implementation of ML for ITE estimation in health technology assessment and offers some recommendations for future research.
Health Technology Assessment Considerations for ITE Estimation
Challenges of Confounding in Observational Data
While RCTs are the gold standard for evaluating new health technologies, there are instances in which conducting an RCT is either unfeasible, not required for regulatory approval, or—due to strict inclusion criteria—not relevant for real-world clinical practice. In such cases, well-designed observational studies offer an alternative for nuanced estimation of comparative effectiveness and cost-effectiveness.22–24
To derive estimates of treatment effectiveness from observational data, the main challenge to tackle is potential bias due to confounding, as illustrated in the Directed Acyclic Graphs in Figure 1.
Figure 1.
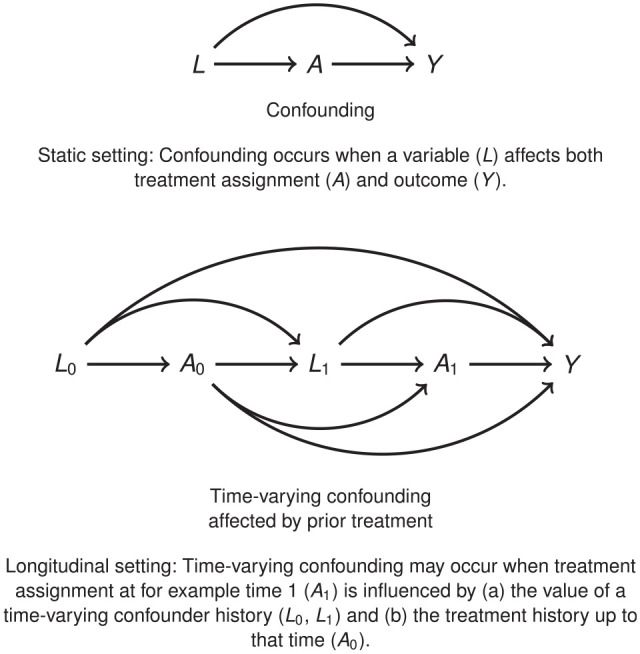
Confounding. (Top) Static setting: confounding occurs when a variable affects both treatment assignment and outcome . (Bottom) Time-varying confounding affected by prior treatment. Longitudinal setting: time-varying confounding may occur when treatment assignment at for example time 1 is influenced by (a) the value of a time-varying confounder history and (b) the treatment history up to that time . 20
There is an established set of methods designed to estimate average treatment effects from observational data,26,27 such as regression and matching for estimating one-off treatment, 28 inverse probability weighting estimation and g-estimation 25 and double-robust methods 29 for sustained treatment strategies, and instrumental variables methods for settings in which unobserved confounders cannot be excluded. 30 While these methods do not automatically apply to estimating ITEs, the main ideas (e.g., regression adjustment in an outcome model, the weighting or double-robust correction) are exploited in causal ML estimators for ITEs. In the later sections, we discuss in detail how these can handle observed (baseline and time-varying) or even unobserved confounding.
Estimating Relevant Parameters for Health Technology Assessment
CEA for health technology assessment often involves decision modeling.31,32 In this context, available data are analyzed with the aim of developing prediction models of the expected health outcomes and health care costs for a cohort of individuals, conditional on their characteristics and treatment allocation. The model will require a set of parameters to be used to make probabilistic predictions about the value of the outcomes of interest (e.g., survival time, costs, and utilities).
Some parameters capture treatment effectiveness and are expressed as treatment effects or treatment-specific mean parameters, requiring the use of causal inference methods when derived from observational data. 33 These parameters vary depending on the outcome types and causal contrasts. For instance, quality-of-life measures may involve average treatment effects, while binary outcomes such as adverse events may require risk differences, risk ratios, or odds ratios. Time-to-event outcomes involve parameters such as differences in mean counterfactual survival times or survival probabilities. Many of these parameters can be transformed into ITE estimands by conditioning on observed characteristics (see, e.g., Hu et al. 34 for survival outcomes). With time-to-event data, beyond the challenge of confounding, models for treatment effectiveness should also account for further potential biases from informative censoring and event-induced covariate shift where censoring or event hazard are related to individual characteristics and treatment assignment.35,36
Uncertainty Quantification
The uncertainty in the input parameter values of a CEA model is a key component in the resulting decision uncertainty. 37 Therefore, ML models used to inform treatment and funding decisions must produce a measure of uncertainty surrounding their estimates of treatment effects and predicted counterfactual outcomes. These measures of uncertainty can include standard errors, confidence intervals, or, in the case of Bayesian techniques, credible intervals of posterior distributions. Probabilistic sensitivity analysis can then be used to propagate the uncertainty in the CEA input parameters through the model and to assess their effects on decision uncertainty.
ITE Defined
We first illustrate the counterfactual reasoning necessary to conceptualize ITE in Table 1. The treatment received is represented by a binary variable , which takes value 1 if the subject receives treatment and 0 if not. For simplicity, we define a binary outcome variable , taking value 1 if the event of interest occurs and 0 otherwise, but the setting holds more generally. For each subject, we have access to a set of covariates .
Table 1.
Illustrating the Fundamental Problem of Causal Inference
| 1 | 1 | 1 | 0 | 1 | 1 | |
| 2 | 1 | 0 | 0 | 0 | 0 | |
| … | … | … | … | … | … | … |
| n-2 | 0 | 1 | 1 | 0 | −1 | |
| n-1 | 1 | 0 | 1 | 0 | −1 | |
| n | 0 | 0 | 0 | 0 | 0 |
A, treatment variable (0 = no treatment; 1 = treatment); Y, outcome variable (0 = no event; 1 = event); X, baseline covariates; and , (potential) outcomes that would have been observed under treatment values a = 0 and a = 1, respectively. To indicate that we can observe the outcome only under the treatment the subject actually received, the counterfactual is represented in bold font.
We assume that for each subject we observe their outcomes under each alternative exposure level, that is, their potential outcomes38,39: is the outcome that would have been observed under treatment value and is the outcome that would have been observed under treatment value .
The true treatment effect for individual is defined as . The average treatment effect (ATE) is defined as the population average of these individual differences, , while the conditional average treatment effect (CATE) is defined as the expected difference in the potential outcomes, for a specific profile of covariate values :
| (1) |
While the economics and statistics literature refers to the above quantity as CATE, 6 this article adopts the language of ITE from the causal ML community 40 to highlight the fact that the resulting estimates can potentially be very granular, individualized to the extent of the observable information.
We also note that the above is defined for the setting of one-off binary treatment with baseline confounding, in which an additive causal contrast is of interest. The methods reviewed in the next section for more complex settings may modify and extend this estimand, 34 but due to space constraints, we restricted our illustration to the simple case of the .
Due to the fundamental problem of causal inference, only one potential outcome can be observed at any given time, and therefore, cannot be derived without further assumptions: consistency, conditional exchangeability, positivity, and no interference (see Table 2).
Table 2.
Identifiability Assumptions
| Consistency | The consistency assumption implies that an individual’s potential outcome under observed exposure history is the outcome that will actually be observed for that person. With a dichotomous treatment , consistency can be expressed as . |
| Conditional exchangeability | The potential outcomes are independent of treatment assignment, conditional on a set of observed covariates . In randomized controlled trials, exchangeability holds unconditionally. |
| Positivity | Each subject should have a nonzero probability of either treatment assignment. |
| No interference | The potential outcomes for one subject do not depend on the treatment assignment of others. |
When these assumptions hold, they allow us to reexpress the in terms of observed variables only 41 :
| (2) |
With a sufficiently large data set, one could estimate this quantity by finding matched pairs for each covariate value combination of interest, and the difference in the observed outcomes for these pairs could be interpreted as a nonparametric estimate of . Such an approach has two drawbacks. First, in practice, analysts work with limited data sets providing an insufficient number of treatment-control pairs, if the covariate vector of interest is more complex than a few categorical variables. Furthermore, such analysis would be prone to overfitting; that is, ITEs estimated in one data set would not be a good characterization of treatment effects in a different sample of the same population.
To overcome these problems, a wide range of ML methods have been proposed in the literature to estimate . Some methodological approaches derive the by first generating predictions for both potential outcomes, via flexible modeling of the outcome regression, and constructing the ITE as a difference in predicted potential outcomes and . Other approaches also involve further nuisance models, such as propensity scores, and may directly target the estimation of the as opposed to generating predictions of the potential outcomes.
In this review, we focus on methods that aim to estimate ITEs, and we note whether they also generate predicted potential outcomes. Predicted potential outcomes play an important role in health technology assessment, as they capture treatment-specific mean parameters for a given covariate profile. The related literature of counterfactual predictions focuses on generating such predictions, 42 and we briefly refer to it in the “Discussion” section.
ML Methods to Estimate ITE
This section provides an intuitive summary of the currently available methods in the statistical, causal inference, and computer science literature for estimating ITEs.
We direct readers who are unacquainted with ML methods to explore informative tutorials or introductory articles that elucidate the utilization of ML methods in health care and health economics.40,43,44 It is important to note that the article does not encompass all limitations associated with ML methods. The Professional Society for Health Economics and Outcomes Research (ISPOR)’s ML Methods Emerging Good Practices Task Force has published comprehensive guidance addressing the use of ML in health economics and outcomes research and decision making. 9
To identify the relevant ML methods, we use the citation pearl searching method, 45 asking experts for key articles in this area and integrating these with two key reviews: Bica et al. 40 reviewed ML methods for ITEs for a clinical and computer science audience, while Jacob 44 considered them from an econometric perspective.
We thoroughly examined the references and citations of these review articles and used search engines (such as Google Scholar) to search for the latest advancements in relevant ML methods. We note that the literature on optimal policy learning and dynamic treatment regimes46–48 was out of scope for this review, as they are concerned with finding the individualized treatment rule with the largest expected benefits, and while they may use estimates of ITEs, generating these is not their main focus.
We then developed a taxonomy that organized the methods reviewed to address the key challenges in health technology assessment. This taxonomy was shared with a group of 20 health economists specializing in health technology assessment methods, who provided valuable feedback on its content and structure.
In our final taxonomy (see Tables 3 and 4), we focus on the following challenges for health technology assessment: 1) whether the ML methods address confounding, in particular time-varying confounding and unobserved confounding; 2) whether the ML methods can be used to estimate ITEs on time-to-event outcomes; 3) whether the ML methods produce uncertainty estimates, and for what kinds of outputs (predicted potential outcomes or estimated treatment effects or both). We also group the ML methods based on the settings they deal with (static or longitudinal). Finally, we provide information about the accessibility of ML methods.
Table 3.
Methods to Estimate Individualized Treatment Effect in Static Settings
| Method | Confounding | Outcome | Uncertainty | Software |
|---|---|---|---|---|
| ML for continuous and binary outcomes | ||||
| Bayesian additive regression trees,49–51 Bayesian causal forest 10 | O | B, C | UoT, UoP | R: BART, bart-Cause, bcf |
| Causal forest,10–14 causal multitask Gaussian processes, 52 nonstationary Gaussian processes 53 | O | B, C | UoT, UoP | R: random-Forest-SRC, grf, BayesTree, causal-Forest |
| Virtual twins random forests, virtual twins interaction models, counterfactual random forest, counterfactual synthetic, bivariate random forest54–56 | O | B, C | UoT, UoP | R: aVirtualTwins, model4you |
| Balancing neural network 57 | O | B, C | No | No |
| Treatment-agnostic representation network 58 | O | B, C | UoT | Python: cfrnet |
| Local similarity preserved individual treatment effect 59 | O | B, C | No | Python: SITE |
| Deep counterfactual networks with propensity dropout 60 | O | B, C | UoT | Python: DCN-PD |
| Multitask deep learning and K-nearest neighbors 61 | O | B, C | No | Python: CNN |
| Generative adversarial nets for inference of individualized treatment effects 62 | O | B, C | UoP | Python: GANITE |
| Person-centered treatment effects using a local instrumental variables 63 | O, U | B, C | UoT, UoP | Stata: petiv |
| ML for time-to-event outcomes | ||||
| Counterfactual survival analysis 36 | O | TTE | UoT, UoP | Python: CSA |
| Individualized treatment effect estimator for survival analysis (SurvITE) 35 | O | TTE | No | Python: SurvITE |
| Cox proportional hazards deep neural network (DeepSurv) 64 | No | TTE | UoP | Python: DeepSurv |
| Nonparametric accelerated failure time models64,65 | O | TTE | UoT, UoP | R: AFTrees |
| Nonparametric Bayesian additive regression trees within the framework of accelerated failure time model 34 | O | TTE | UoT, UoP | R: AFTBART-NP |
| Random survival forests66–68 | O | TTE | UoT | No |
| Causal survival forest 66 | O | TTE | UoT | R: grf |
| Deep multitask Gaussian processes52,53,69 | O | TTE | UoT, UoP | Python: DMGP |
B, binary outcome; C, continuous outcome, O, observed confounding; ML, machine learning; TTE, time-to-event outcome; U, unobserved confounding; UoP, produces uncertainty estimates of predicted counterfactual outcomes; UoT, produces uncertainty estimates of treatment effect estimates.
Table 4.
Methods to Estimate Individualized Treatment Effect i n Longitudinal Settings
| Method | Confounding | ||||
|---|---|---|---|---|---|
| Baseline | Time Varying | Outcome | Uncertainty | Software | |
| ML for continuous and binary outcomes | |||||
| Bayesian nonparametric method 70 | O | O | C | UoP | No |
| Bayesian treatment response curves 71 | No | No | C | UoP | No |
| Counterfactual Gaussian process 72 | O | O | C | UoP | No |
| Recurrent marginal structural networks 73 | O | O | B, C | No | Python: RMSN |
| Counterfactual recurrent network 74 | O | O | B, C | No | Python: CRN |
| Deep sequential weighting 75 | O, U | O, U | C | No | Python: DSW |
| SyncTwin 76 | O | O | C | No | Python: synth control |
| Time series deconfounder 77 | O, U | O, U | B, C | No | Python: TimeSeries -Deconfounder |
| ML for time-to-event outcomes | |||||
| Causal dynamic survival model 78 | O | No | TTE | UoT, UoP | Python: CDS |
B, binary outcome; C, continuous outcome, ML, machine learning; O, observed confounding; TTE, time-to-event outcome; U, unobserved confounding; UoP, produces uncertainty estimates of predicted counterfactual outcomes; UoT, produces uncertainty estimates of treatment effect estimates.
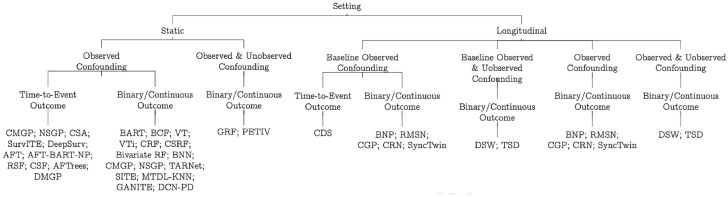
In Figure 2, we categorize all of the ML techniques reviewed in this article, using a tree-based diagram, following the taxonomy outlined above. Readers interested in reading these ML articles can go to the study by Bi et al. 79 first, as it summarizes some commonly used ML terms and their equivalent terms in epidemiology. We structure our review into three parts: methods applicable for static settings, those handling longitudinal settings, and methods that can handle time-to-event outcomes, for both static and dynamic settings.
Figure 2.
A taxonomy of statistical and machine learning individualized treatment effects estimation methods for use in health technology assessment.
AFT, non-parametric accelerated failure time models; AFT-BART-NP, nonparametric Bayesian additive regression trees within the framework of accelerated failure time model; BART, Bayesian additive regression trees; BCF, Bayesian causal forest; BNN, balancing neural network; BNP, Bayesian nonparametric method; BRF, bivariate random forest; BTRC, Bayesian treatment response curves; CDS, causal dynamic survival model; CF, causal forest; CGP, counterfactual Gaussian process; CMGP, causal multitask Gaussian processes; CRF, counterfactual random forest; CRN, counterfactual recurrent network; CSA, counterfactual survival analysis; CSF, causal survival forest; CSRF, counterfactual synthetic RF; DeepSurv, Cox proportional hazards deep neural network; DMGP, deep multitask Gaussian processes; DCN-PD, deep counterfactual networks with propensity dropout; DSW, deep sequential weighting; GANITE, generative adversarial nets for inference of individualized treatment effects; MTDL-KNN, multitask deep learning and K-nearest neighbors; NSGP, nonstationary Gaussian processes; PETIV, person-centered treatment effects using a local instrumental variables; RMSN, recurrent marginal structural networks; RSF, random survival forests; SITE, local similarity preserved individual treatment effect; SurvITE, individualized treatment effect estimator for survival analysis; TARNet, treatment-agnostic representation network; TSD, time series deconfounder; VT, virtual twins random forests; VTi, virtual twins interaction models.
Static Settings
In a static setting, the aim is to estimate the effect of one-time treatment decisions using data collected once (so-called cross-sectional data) or data where baseline confounders, a treatment variable, and the outcome are measured only once. When using observational data, confounding according to baseline characteristics may be present and needs to be dealt with.
We report the key features of the available ML methods to estimate ITE in a static setting in Table 3. These ML algorithms differ in the way they handle observed confounding. Some control directly for covariates (e.g., Bayesian additive regression trees, random forests), some flexibly control for the propensity score (e.g., Bayesian additive regression trees, 80 Bayesian causal forest, 10 ) while deep counterfactual networks with propensity dropout 60 and nonstationary Gaussian processes 53 use a doubly robust approach in which they estimate a propensity function and an outcome model using a deep multitask network or Bayesian nonparametric methods. Causal multitask Gaussian processes 52 use a Bayesian approach to learn about the unobserved counterfactual outcomes and take into account the uncertainty in counterfactual outcomes without explicitly modeling the propensity score.
The balancing neural network approach 57 and treatment-agnostic representation network 58 use representation learning, a process that encourages similarity between the treated and control populations. The approach of local similarity preserved individual treatment effect 59 not only balances the distributions of control and treated groups but also uses information on local similarity—akin to nearest neighbor methods—that provides meaningful constraints on the ITE estimation.
Many of the algorithms reported in Table 3 have been designed for binary or continuous outcomes. Those methods that have been extended for use with time-to-event data are summarized in the subsection “Time-to-Event Outcomes.” The nonstationary Gaussian processes 53 approach performs well in regimes of both small and large samples.
Methods that account for the uncertainty of treatment effect estimates include all forest-based models and deep counterfactual networks with propensity dropout. The approach of generative adversarial nets for inference of individualized treatment effects 62 only provides uncertainty for the counterfactual outcomes. Few approaches provide uncertainty estimates for both the counterfactual outcomes and treatment effect estimates, including Bayesian additive regression trees, causal multitask Gaussian processes, and nonstationary Gaussian processes. The approaches of balancing neural network, local similarity preserved individual treatment effect, and multitask deep learning and K-nearest neighbours do not provide uncertainty quantification at all.
None of the ML methods reviewed in this section deal with unobserved confounding. Hence, we consider an alternative, parametric approach to estimate ITEs when unobserved confounding cannot be ruled out, the method of person-centered treatment effects using local instrumental variables (IV). 63 The method, implemented as a Stata package, 81 can be used for continuous, binary, or count data. A simplified version for continuous outcomes has been developed by Zhou and Xie 82 for estimation in R. ML can also be applied to learn the local average treatment effect in an IV setting,83,84 as the first stage of a linear instrumental variables regression is effectively prediction. ML IV may perform better than non-ML IV because they are better at prediction. Nonetheless, if the ML method does not produce uncertainty estimates, it is of no use in health technology assessment. Besides IV, traditional methods also use panel data and fixed-effects or random-effects models to control for unobserved confounding, and we will discuss in the next section how ML methods deal with unobserved confounding in longitudinal settings.
Longitudinal Settings
In a longitudinal setting, a sequence of treatment decisions and treatment effects is studied, using data collected repeatedly, such as longitudinal electronic health records or registry data. In such settings, for example when evaluating interventions for chronic conditions, treatment exposure may change over time, with decisions to start, discontinue, or switch treatment depending on the changing prognosis of the patient. Estimating relevant measures of treatment effects necessitates controlling for time-varying confounding (see Figure 1).
Most of the existing ML methods for longitudinal data, as shown in Table 4, make the unconfoundedness assumption (“sequential randomization”) that at each time step, all the past variables affecting the patient’s treatment and outcomes are observed. The Bayesian nonparametric method 70 can predict counterfactual outcomes and estimate individualized treatment response in a continuous-time trajectory. The Bayesian treatment response curves approach 71 extends the previous method to model multivariate outcomes, albeit not being able to handle confounding. The counterfactual Gaussian process method 72 can both predict counterfactual outcomes and estimate ITEs on a continuous-time trajectory while accounting for baseline and time-varying confounding. The recurrent marginal structural networks approach 73 accounts for time-varying confounding using inverse probability of treatment weighting and predicts time-dependent counterfactual outcomes using deep learning. The counterfactual recurrent networks approach 74 accounts for time-varying confounding using representation learning that, at each time step, breaks the association between patient history and treatment assignment.
Only two ML methods75,77 account for unobserved confounders. The time series deconfounder approach takes advantage of the dependencies between the multiple treatment assignments and estimates a factor model to capture the distribution of assigned treatments, using histories of covariates and treatment assignments. 77 The sequence of latent variables is used to adjust for bias due to unobserved confounding. The deep sequential weighting approach infers the unobserved confounders using a deep recurrent weighting neural network that leverages the currently observed covariates and previous covariates and treatment assignments and computes the time-varying inverse probability of treatment for each individual to balance the confounders. The learned representations, a process in which ML algorithms are used to extract meaningful patterns from raw data to create representations of the latter that are easier to understand and process for analysis purposes, of hidden confounders and observed covariates are then combined together to predict the required potential outcomes. 75 The SyncTwin approach 76 uses a unique verification procedure to assess the presence of unobserved confounders. While it cannot control for unobserved confounding, it offers insights into the magnitude of the unobserved confounding problem by assessing the potential impact of unobserved confounders on pretreatment outcomes.
Estimating uncertainty in longitudinal settings becomes more intricate due to the need to estimate not only the individual-level random error at each time point but also the time-dependent random error specific to a particular treatment type. Of the methods reported in Table 4, only the Bayesian nonparametric method, the Bayesian treatment response curves, and the counterfactual Gaussian process approach can quantify uncertainty around the estimates.
Time-to-Event Outcomes
Time-to-event outcomes such as progression-free survival or overall survival are of key interest for health technology assessment. Our review found that ML methods for estimating ITE on time-to-event outcomes are sparse (see Tables 3 and 4, “ML for time-to-event outcomes”). Among them, counterfactual survival analysis 36 can estimate ITEs with nonparametric uncertainty quantification. The individualized treatment effect estimator for survival analysis (SurvITE) 35 estimates treatment-specific hazard and survival functions but does not calculate uncertainty and assumes random censoring. The Cox proportional hazards deep neural network (DeepSurv) 64 models interactions between a patient’s covariates and treatment using a neural network and produces confidence intervals for the predicted counterfactual outcomes. The nonparametric accelerated failure time approach 65 extends Bayesian additive regression trees to survival outcomes but does not account for informative censoring. A further development is the approach of nonparametric Bayesian additive regression trees within the framework of accelerated failure time, 34 which fits two survival outcome regression models to two sets of the observed data (one for treatment and one for control groups) and produces counterfactual survival curves conditional on individual covariate profiles. This method can also account for covariate-dependent censoring given baseline covariates. Both nonparametric accelerated failure time models and nonparametric Bayesian additive regression trees produce estimates of standard errors and uncertainty intervals for the regression coefficients.
The random survival forest methods67,68 have been used to estimate ITEs, assuming unconfoundedness conditional on the baseline covariates and random censoring. The causal survival forest 66 approach adapts the causal forest algorithm 13 and adjusts for censoring using doubly robust estimation. Modeling competing risks is another challenge in estimating ITE for time-to-event data. Deep multitask Gaussian processes52,53,69 can be used for survival analysis with competing risks and produces patient-specific and cause-specific survival curves with uncertainty estimates. Nonetheless, the above methods handle confounding only at baseline.
For use with longitudinal data and time-to-event outcomes, the causal dynamic survival model 78 is the first to estimate sequential treatment effects on time-to-event outcomes in the presence of time-varying covariates. Nonetheless, this approach does not account for time-varying confounders or unobserved confounding.
Discussion
This article provides an overview of existing ML algorithms for estimating ITEs using real-world data, for the purposes of assessing them in relation to their suitability for use in the context of health technology assessment to support more nuanced treatment and funding decisions. We find two major areas in which existing ML methods do not yet meet the needs of data analysis for health technology assessment.
First, real-world data used for health technology assessment are often longitudinal, with concerns of time-varying confounding and handling time-to-event data to derive effectiveness. The few ML methods that can estimate ITEs while accounting for time-varying confounding cannot currently handle time-to-event data. Issues of informative censoring and event-induced covariate shift make estimating ITEs technically more challenging in the context of real-world time-to-event data analysis.
Second, many of the ML algorithms this article discussed do not quantify uncertainty surrounding the ITEs or potential outcomes predictions, especially ML methods developed for longitudinal settings. The ability to produce appropriate measures of uncertainty should be a key consideration when selecting among methods. 21 Analysts are also encouraged to use more than one method to assess the robustness of the results and consult published simulation evidence to assess the strength and weaknesses of different methods.
To ensure the acceptability of causal effects estimated using real-world data and ML for regulators and decision makers, it is crucial to evaluate the assumptions underlying specific models. The unconfoundedness assumption requires informed judgments rooted in domain expertise, usually supported by covariates-rich data sets. The overlap assumption necessitates empirical validation. Although this article focuses on the challenges of real-world data, the methods reviewed can also use RCT data to estimate ITEs. 85
While data-driven approaches such as ML can help to arrive at a flexible yet parsimonious model, they are not substitutes for content knowledge and clinicians’ opinions. Researchers should not choose variables purely based on their performance in the model. 26 Clinicians’ insights are important in discerning which patient characteristics influence treatment decisions and responses, and they play a pivotal role in validating a model’s treatment effects or potential outcomes estimates.86,87
Two related strands of the methodological literature have made progress in solving some of the challenges identified. First, causal inference methods that can account for time-varying confounding and handle time-to-event outcomes such as the longitudinal targeted minimum loss-based estimation method (LTMLE) 88 can benefit from ML to improve model specification (see, e.g., Schomaker et al. 89 ). However, these methods estimate average treatment effects, not ITEs, and are thus not reviewed here. Second, the optimal treatment regimes (in static settings) and optimal dynamic treatment regimes (in longitudinal settings)90,91 methods have similar goals compared with estimating ITEs, which is tailoring the right treatment to the right individual. Some of these methods 47 use estimates of ITEs to make the treatment allocation decisions, while others, such as outcome weighted learning 92 and dynamic weighted ordinary least squares, 93 search for the optimal allocation without estimating ITEs. A key difference with the methods reviewed here is that the optimal treatment rules focus on the expected ATE of administering a given individualized treatment rule rather than predictions of the ITEs or counterfactual outcomes.
The policy implications of more granular cost-effectiveness results are that policy makers can appreciate the tradeoff resulting from a one-size-fits-all reimbursement decision versus one that allows reimbursing different interventions for different subgroups. Even when the interest is in making population average decisions, there is still a need to predict the prognosis, costs, and health-related quality of life more accurately for individuals by taking into account factors that truly affect these outcomes.2,3,94
Recommendations for Future Research
Our article highlighted the dearth of options to estimate ITEs when there is longitudinal data with time-varying confounding. The emerging literature on ML methods for counterfactual prediction, or predictions under hypothetical interventions (details can be found in the scoping review of Lin et al. 42 ) is promising in this setting and has a potential for augmenting the health technology assessment toolbox. These methods aim to estimate predicted outcomes of individuals who were to follow a particular treatment strategy, given their individual characteristics, and can produce ITEs by taking differences of counterfactual predictions under different hypothetical interventions. However, challenges such as how to validate the counterfactual prediction models or how to estimate uncertainty are currently unresolved. 95
This article did not consider the challenges of estimating popular measures of relative treatment effects for survival data, such as the hazard ratios, as Hernán 96 points out that hazard ratios are not an ideal treatment effect estimate for causal inference because of the sensitivity to the duration of follow-up and the inherent selection bias in period-specific hazard ratios. Nonetheless, hazard ratios can be produced by directly modeling counterfactual outcomes in a time-to-event process and transforming the counterfactual survival probabilities to hazard ratios.
Future work on developing ML methods that address the concerns summarized in this review is needed before they can be widely used in clinical and health technology assessment–like decision making. Cross-disciplinary collaboration between health science and computer science, and involving researchers as well as regulators, can accelerate the process.
Conclusions
More work needs to be done for ML methods to become an established health economics and outcomes research tool. Researchers should focus on developing existing and new algorithms that deal with the typical data structures analyzed in health economics and outcomes research for health technology assessment and that produce the types of output required to inform individualized decisions. Programmers should try and develop more accessible software packages and tutorials to facilitate the application of the methods. Licensing and reimbursement authorities should make their position clear with regard to the role and use of evidence derived from real-world data for their decision making.
Acknowledgments
An earlier version of this manuscript was presented at the 100th meeting of the UK Health Economists’ Study Group (held in Sheffield in July 2022) and subsequently at one of the departmental seminars in the authors’ institution.We are grateful to colleagues that participated in the discussion of the manuscript and to David Glynn for useful feedback on our latest draft. All errors and omissions are the authors’.
Footnotes
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article. The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Financial support for this study was provided entirely by The HTx project. The funding agreement ensured the authors’ independence in designing the study, interpreting the data, writing, and publishing the report. The HTx project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 825162 for 5 years from January 2019. This dissemination reflects only the authors’ view, and the Commission is not responsible for any use that may be made of the information it contains. The main aim of HTx is to create a framework for the Next Generation Health Technology Assessment (HTA) to support patient-centered, societally oriented, real-time decision making on access to and reimbursement for health technologies throughout Europe.
ORCID iDs: Yingying Zhang  https://orcid.org/0000-0002-8419-0934
https://orcid.org/0000-0002-8419-0934
Vijay S. GC.  https://orcid.org/0000-0003-0365-2605
https://orcid.org/0000-0003-0365-2605
Contributor Information
Yingying Zhang, Centre for Health Economics, University of York, UK.
Noemi Kreif, Centre for Health Economics, University of York, UK; Department of Pharmacy, University of Washington, Seattle, USA.
Vijay S. GC, School of Human and Health Sciences, University of Huddersfield, UK
Andrea Manca, Centre for Health Economics, University of York, UK.
References
- 1. Coyle D, Buxton MJ, O’Brien BJ. Stratified cost-effectiveness analysis: a framework for establishing efficient limited use criteria. Health Econ. 2003;12(5):421–7. [DOI] [PubMed] [Google Scholar]
- 2. Basu A, Meltzer D. Value of information on preference heterogeneity and individualized care. Med Decis Making. 2007;27(2):112–27. [DOI] [PubMed] [Google Scholar]
- 3. Espinoza MA, Manca A, Claxton K, Sculpher MJ. The value of heterogeneity for cost-effectiveness subgroup analysis: conceptual framework and application. Med Decis Making. 2014;34(8):951–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Lei L, Candès EJ. Conformal inference of counterfactuals and individual treatment effects. arXiv preprint arXiv:200606138, 2020. [Google Scholar]
- 5. Blakely T, Lynch J, Simons K, Bentley R, Rose S. Reflection on modern methods: when worlds collide—prediction, machine learning and causal inference. Int J Epidemiol. 2020;49(6):2058–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Athey S, Imbens GW. Machine learning methods that economists should know about. Annu Rev Econom. 2019;11:685–725. [Google Scholar]
- 7. Díaz I. Machine learning in the estimation of causal effects: targeted minimum loss-based estimation and double/debiased machine learning. Biostatistics. 2020;21(2):353–8. [DOI] [PubMed] [Google Scholar]
- 8. Van der Laan MJ, Polley EC, Hubbard AE. Super learner. Stat Appl Genet Mol Biol. 2007;6(1):1–23. [DOI] [PubMed] [Google Scholar]
- 9. Padula WV, Kreif N, Vanness DJ, et al. Machine learning methods in health economics and outcomes research—the PALISADE checklist: a good practices report of an ISPOR task force. Value Health. 2022;25(7):1063–1080. [DOI] [PubMed] [Google Scholar]
- 10. Hahn PR, Murray JS, Carvalho CM. Bayesian regression tree models for causal inference: regularization, confounding, and heterogeneous effects (with discussion). Bayesian Anal. 2020;15(3):965–1056. [Google Scholar]
- 11. Athey S, Imbens G. Recursive partitioning for heterogeneous causal effects. Proc Natl Acad Sci U S A. 2016;113(27):7353–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Wager S, Athey S. Estimation and inference of heterogeneous treatment effects using random forests. J Am Stat Assoc. 2018;113(523):1228–42. [Google Scholar]
- 13. Athey S, Tibshirani J, Wager S. Generalized random forests. Ann Stat. 2019;47(2):1148–78. [Google Scholar]
- 14. Seibold H, Zeileis A, Hothorn T. Individual treatment effect prediction for amyotrophic lateral sclerosis patients. Stat Methods Med Res. 2018;27(10):3104–125. [DOI] [PubMed] [Google Scholar]
- 15. Crown WH. Real-world evidence, causal inference, and machine learning. Value Health. 2019;22(5):587–92. [DOI] [PubMed] [Google Scholar]
- 16. Chen H, Harinen T, Lee JY, Yung M, Zhao Z. Causalml: Python package for causal machine learning. arXiv preprint arXiv:200211631. 2020. [Google Scholar]
- 17. Smith MJ, Mansournia MA, Maringe C, et al. Introduction to computational causal inference using reproducible stata, R, and Python code: a tutorial. Stat Med. 2022;41(2):407–32. [DOI] [PubMed] [Google Scholar]
- 18. Garcia-Chimeno Y, Garcia-Zapirain B, Gomez-Beldarrain M, Fernandez-Ruanova B, Garcia-Monco JC. Automatic migraine classification via feature selection committee and machine learning techniques over imaging and questionnaire data. BMC Med Inform Decis Mak. 2017;17(1):1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Stubberud A, Ingvaldsen SH, Brenner E, et al. Forecasting migraine with machine learning based on mobile phone diary and wearable data. Cephalalgia. 2023;43(5):03331024231169244. [DOI] [PubMed] [Google Scholar]
- 20. Krijkamp EM, Alarid-Escudero F, Enns EA, Jalal HJ, Hunink MGM, Pechlivanoglou P. Microsimulation modeling for health decision sciences using r: a tutorial. Med Decis Making. 2018;38(3):400–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Glynn D, Giardina J, Hatamyar J, Pandya A, Soares M, Kreif N. Integrating decision modelling and machine learning to inform treatment stratification. Health Econ. Epub ahead of print April 25, 2024. DOI: 10.1002/hec.4834 [DOI] [PubMed] [Google Scholar]
- 22. Rothwell PM. External validity of randomised controlled trials: “to whom do the results of this trial apply?” Lancet. 2005;365(9453):82–93. [DOI] [PubMed] [Google Scholar]
- 23. Bothwell LE, Greene JA, Podolsky SH, Jones DS. Assessing the gold standard—lessons from the history of RCTs. N Engl J Med. 2016;374(22):2175–81. [DOI] [PubMed] [Google Scholar]
- 24. Frieden TR. Evidence for health decision making—beyond randomized, controlled trials. N Engl J Med. 2017;377(5):465–75. [DOI] [PubMed] [Google Scholar]
- 25. Robins JM, Hernan MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11(5):550–60. [DOI] [PubMed] [Google Scholar]
- 26. National Institute for Health and Care Excellence. NICE real-world evidence framework. 2022. Available from: https://www.nice.org.uk/corporate/ecd9/chapter/overview [DOI] [PMC free article] [PubMed]
- 27. Kreif N, Grieve R, Sadique MZ. Statistical methods for cost-effectiveness analyses that use observational data: a critical appraisal tool and review of current practice. Health Econ. 2013;22(4):486–500. [DOI] [PubMed] [Google Scholar]
- 28. Kreif N, Grieve R, Radice R, Sadique Z, Ramsahai R, Sekhon JS. Methods for estimating subgroup effects in cost-effectiveness analyses that use observational data. Med Decis Making. 2012;32(6):750–63. [DOI] [PubMed] [Google Scholar]
- 29. Van Der Laan MJ, Rubin D. Targeted maximum likelihood learning. Int J Biostat. 2006;2(1):1–38. [Google Scholar]
- 30. Sargan JD. The estimation of economic relationships using instrumental variables. Econometrica. 1958;26(3):393–415. [Google Scholar]
- 31. Sculpher MJ, Claxton K, Drummond M, McCabe C. Whither trial-based economic evaluation for health care decision making? Health Econ. 2006;15(7):677–87. [DOI] [PubMed] [Google Scholar]
- 32. Buxton MJ, Drummond MF, Van Hout BA, et al. Modelling in ecomomic evaluation: an unavoidable fact of life. Health Econ. 1997;6(3):217–27. [DOI] [PubMed] [Google Scholar]
- 33. Faria R, Alava MH, Manca A, Wailoo AJ. NICE DSU technical support document 17: the use of observational data to inform estimates of 2015. Available from: http://www.nicedsu.org.uk
- 34. Hu L, Ji J, Li F. Estimating heterogeneous survival treatment effect in observational data using machine learning. Stat Med. 2021;40(21):4691–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Curth A, Lee C, van der Schaar M. Survite: Learning heterogeneous treatment effects from time-to-event data. Presented at: Thirty-Fifth Conference on Neural Information Processing Systems. 2021. [Google Scholar]
- 36. Chapfuwa P, Assaad S, Zeng S, Pencina MJ, Carin L, Henao R. Enabling counterfactual survival analysis with balanced representations. In: Proceedings of the Conference on Health, Inference, and Learning 2021. New York: Association for Computing Machinery; 2021. p 133–45. [Google Scholar]
- 37. Claxton KP, Sculpher MJ. Using value of information analysis to prioritise health research. Pharmacoeconomics. 2006;24(11):1055–68. [DOI] [PubMed] [Google Scholar]
- 38. Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70(1):41–55. [Google Scholar]
- 39. Hernán M, Robins J. Causal Inference: What If. Boca Raton (FL): Chapman & Hall/CRC; 2020. [Google Scholar]
- 40. Bica I, Alaa AM, Lambert C, Van Der Schaar M. From real-world patient data to individualized treatment effects using machine learning: current and future methods to address underlying challenges. Clin Pharmacol Ther. 2021;109(1):87–100. [DOI] [PubMed] [Google Scholar]
- 41. Hoogland J, IntHout J, Belias M, et al. A tutorial on individualized treatment effect prediction from randomized trials with a binary endpoint. Stat Med. 2021;40(26):5961–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Lin L, Sperrin M, Jenkins DA, Martin GP, Peek N. A scoping review of causal methods enabling predictions under hypothetical interventions. Diagn Progn Res. 2021;5:1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. James G, Witten D, Hastie T, Tibshirani R. An Introduction to Statistical Learning, Vol. 112. New York: Springer; 2013. [Google Scholar]
- 44. Jacob D. Cate meets ml. Digit Finance. 2021;3(2):99–148. [Google Scholar]
- 45. De Brún C, Pearce-Smith N. Searching Skills Toolkit: Finding the Evidence. Hoboken (NJ): John Wiley & Sons; 2014. [Google Scholar]
- 46. Athey S, Wager S. Policy learning with observational data. Econometrica. 2021;89(1):133–61. [Google Scholar]
- 47. Luedtke AR, van der Laan MJ. Super-learning of an optimal dynamic treatment rule. Int J Biostat. 2016;12(1):305–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Murphy SA. Optimal dynamic treatment regimes. J R Stat Soc Series B Stat Methodol. 2003;65(2):331–55. [Google Scholar]
- 49. Chipman HA, George EI, McCulloch RE. Bart: Bayesian additive regression trees. Ann Appl Stat. 2010;4(1):266–98. [Google Scholar]
- 50. Hill JL. Bayesian nonparametric modeling for causal inference. J Comput Graph Stat. 2011;20(1):217–40. [Google Scholar]
- 51. Sparapani R, Spanbauer C, McCulloch R. Nonparametric machine learning and efficient computation with bayesian additive regression trees: the bart r package. J Stat Softw. 2021;97:1–66. [Google Scholar]
- 52. Alaa AM, van der Schaar M. Bayesian inference of individualized treatment effects using multi-task gaussian processes. arXiv preprint arXiv:170402801. 2017. [Google Scholar]
- 53. Alaa A, van der Schaar M. Limits of estimating heterogeneous treatment effects: guidelines for practical algorithm design. Proc Int Conf Mach Learn. 2018;80:129–38. [Google Scholar]
- 54. Breiman L. Random forests. Mach Learn. 2001;45(1):5–32. [Google Scholar]
- 55. Lu M, Sadiq S, Feaster DJ, Ishwaran H. Estimating individual treatment effect in observational data using random forest methods. J Comput Graph Stat. 2018;27(1):209–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Seibold H, Zeileis A, Hothorn T. model4you: an R package for personalised treatment effect estimation. J Open Res Softw. 2019;7(17):1–6. [Google Scholar]
- 57. Johansson F, Shalit U, Sontag D. Learning representations for counterfactual inference. Proc Int Conf Mach Learn. 2016;48:3020–9. [Google Scholar]
- 58. Shalit U, Johansson FD, Sontag D. Estimating individual treatment effect: generalization bounds and algorithms. Proc Int Conf Mach Learn. 2017;70:3076–85. [Google Scholar]
- 59. Yao L, Li S, Li Y, Huai M, Gao J, Zhang A. Representation learning for treatment effect estimation from observational data. Adv Neural Inf Process Syst. 2018;31:2638–2648. [Google Scholar]
- 60. Alaa AM, Weisz M, Van Der Schaar M. Deep counterfactual networks with propensity-dropout. arXiv preprint arXiv:170605966. 2017. [Google Scholar]
- 61. Chen P, Dong W, Lu X, Kaymak U, He K, Huang Z. Deep representation learning for individualized treatment effect estimation using electronic health records. J Biomed Inform. 2019;100:103303. [DOI] [PubMed] [Google Scholar]
- 62. Yoon J, Jordon J, Van Der Schaar M. GANITE: Estimation of individualized treatment effects using generative adversarial nets. Presented at: International Conference on Learning Representations, Vancouver (Canada), 2018. [Google Scholar]
- 63. Basu A. Estimating person-centered treatment (pet) effects using instrumental variables: an application to evaluating prostate cancer treatments. J Appl Econ. 2014;29(4):671–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Katzman JL, Shaham U, Cloninger A, Bates J, Jiang T, Kluger Y. DeepSurv: personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med Res Methodol. 2018;18(1):1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Henderson NC, Louis TA, Rosner GL, Varadhan R. Individualized treatment effects with censored data via fully nonparametric bayesian accelerated failure time models. Biostatistics. 2020;21(1):50–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Cui Y, Kosorok MR, Sverdrup E, Wager S, Zhu R. Estimating heterogeneous treatment effects with right-censored data via causal survival forests. J R Stat Soc Series B Stat Methodol. 2023;85(2):179–211. [Google Scholar]
- 67. Tabib S, Larocque D. Non-parametric individual treatment effect estimation for survival data with random forests. Bioinformatics. 2020;36(2):629–36. [DOI] [PubMed] [Google Scholar]
- 68. Zhang W, Le TD, Liu L, Zhou ZH, Li J. Mining heterogeneous causal effects for personalized cancer treatment. Bioinformatics. 2017;33(15):2372–8. [DOI] [PubMed] [Google Scholar]
- 69. Alaa AM, van der Schaar M. Deep multi-task Gaussian processes for survival analysis with competing risks. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, CA: Curran Associates Inc.; 2017, p 2326–34. [Google Scholar]
- 70. Xu Y, Xu Y, Saria S. A Bayesian nonparametric approach for estimating individualized treatment-response curves. Mach Learn Healthc Conf. 2016;56:282–300. [Google Scholar]
- 71. Soleimani H, Subbaswamy A, Saria S. Treatment-response models for counterfactual reasoning with continuous-time, continuous-valued interventions. arXiv preprint arXiv:170402038. 2017. [Google Scholar]
- 72. Schulam P, Saria S. Reliable decision support using counterfactual models. Adv Neural Inf Process Syst. 2017;30:1697–708. [Google Scholar]
- 73. Lim B, Alaa A, van der Schaar M. Forecasting treatment responses over time using recurrent marginal structural networks. NeurIPS. 2018;18:7483–93. [Google Scholar]
- 74. Bica I, Alaa AM, Jordon J, van der Schaar M. Estimating counterfactual treatment outcomes over time through adversarially balanced representations. arXiv preprint arXiv:200204083. 2020. [Google Scholar]
- 75. Liu R, Yin C, Zhang P. Estimating individual treatment effects with time-varying confounders. In: 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy. New York: IEEE; 2020. p 382–91. [Google Scholar]
- 76. Qian Z, Zhang Y, Bica I, Wood A, van der Schaar M. SyncTwin: transparent treatment effect estimation under temporal confounding. 2020. Available from: https://openreview.net/forum?id=IVwXaHpiO0
- 77. Bica I, Alaa A, Van Der Schaar M. Time series deconfounder: estimating treatment effects over time in the presence of hidden confounders. Proc Int Conf Mach Learn. 2020;119:884–95. [Google Scholar]
- 78. Zhu J, Gallego B. CDS–causal inference with deep survival model and time-varying covariates. arXiv preprint arXiv:210110643. 2021. [Google Scholar]
- 79. Bi Q, Goodman KE, Kaminsky J, Lessler J. What is machine learning? A primer for the epidemiologist. Am J Epidemiol. 2019;188(12):2222–39. [DOI] [PubMed] [Google Scholar]
- 80. Hill J, Linero A, Murray J. Bayesian additive regression trees: a review and look forward. Annu Rev Stat Appl. 2020;7:251–78. [Google Scholar]
- 81. Basu A. Person-centered treatment (pet) effects: individualized treatment effects using instrumental variables. Stata J. 2015;15(2):397–410. [Google Scholar]
- 82. Zhou X, Xie Y. Marginal treatment effects from a propensity score perspective. J Polit Econ. 2019;127(6):3070–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Chernozhukov V, Chetverikov D, Demirer M, et al. Double/debiased machine learning for treatment and structural parameters. Econ J. 2018;21(1):C1–68. [Google Scholar]
- 84. Mullainathan S, Spiess J. Machine learning: an applied econometric approach. J Econ Perspect. 2017;31(2):87–106. [Google Scholar]
- 85. Sadique Z, Grieve R, Diaz-Ordaz K, Mouncey P, Lamontagne F, O’Neill S. A machine-learning approach for estimating subgroup-and individual-level treatment effects: an illustration using the 65 trial. Med Decis Making. 2022;42(7):923–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Beaulieu-Jones BK, Finlayson SG, Yuan W, et al. Examining the use of real-world evidence in the regulatory process. Clin Pharmacol Ther. 2020;107(4):843–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Eichler HG, Koenig F, Arlett P, et al. Are novel, nonrandomized analytic methods fit for decision making? The need for prospective, controlled, and transparent validation. Clin Pharmacol Ther. 2020;107(4):773–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Lendle SD, Schwab J, Petersen ML, van der Laan MJ. ltmle: an R package implementing targeted minimum loss-based estimation for longitudinal data. J Stat Softw. 2017;81:1–21. [Google Scholar]
- 89. Schomaker M, Luque-Fernandez MA, Leroy V, Davies MA. Using longitudinal targeted maximum likelihood estimation in complex settings with dynamic interventions. Stat Med. 2019;38(24):4888–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Robins JM. Optimal structural nested models for optimal sequential decisions. In: Lin DY, Heagerty PJ, eds. Proceedings of the Second Seattle Symposium in Biostatistics: Analysis of Correlated Data. New York: Springer. p 189–326. [Google Scholar]
- 91. Moodie EE, Platt RW, Kramer MS. Estimating response-maximized decision rules with applications to breastfeeding. J Am Stat Assoc. 2009;104(485):155–65. [Google Scholar]
- 92. Zhao Y, Zeng D, Rush AJ, Kosorok MR. Estimating individualized treatment rules using outcome weighted learning. J Am Stat Assoc. 2012;107(499):1106–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93. Wallace MP, Moodie EE. Doubly-robust dynamic treatment regimen estimation via weighted least squares. Biometrics. 2015;71(3):636–44. [DOI] [PubMed] [Google Scholar]
- 94. Basu A. Economics of individualization in comparative effectiveness research and a basis for a patient-centered health care. J Health Econ. 2011;30(3):549–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Keogh RH, van Geloven N. Prediction under hypothetical interventions: evaluation of performance using longitudinal observational data. arXiv preprint arXiv:230410005. 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Hernán MA. The hazards of hazard ratios. Epidemiology. 2010;21(1):13–5. [DOI] [PMC free article] [PubMed] [Google Scholar]