Fully Distributed Shape Sensing of a Flexible Surgical Needle Using Optical Frequency Domain Reflectometry for Prostate Interventions

Abstract

In minimally invasive procedures such as biopsies and prostate cancer brachytherapy, accurate needle placement remains challenging due to limitations in current tracking methods related to interference, reliability, resolution or image contrast. This often leads to frequent needle adjustments and reinsertions. To address these shortcomings, we introduce an optimized needle shape-sensing method using a fully distributed grating-based sensor. The proposed method uses simple trigonometric and geometric modeling of the fiber using optical frequency domain reflectometry (OFDR), without requiring prior knowledge of tissue properties or needle deflection shape and amplitude. Our optimization process includes a reproducible calibration process and a novel tip curvature compensation method. We validate our approach through experiments in artificial isotropic and inhomogeneous animal tissues, establishing ground truth using 3D stereo vision and cone beam computed tomography (CBCT) acquisitions, respectively. Our results yield an average RMSE ranging from 0.58 ± 0.21 mm to 0.66 ± 0.20 mm depending on the chosen spatial resolution, achieving the submillimeter accuracy required for interventional procedures.

I. INTRODUCTION

Prostate cancer represents 7.3% of new cancer cases and 3.8% of cancer-related deaths worldwide [1]. The management of prostate cancer involves procedures such as biopsies, cryoablation, and brachytherapy, requiring precise needle placement [2]. Tracking needles during these procedures is crucial, with methods including ultrasound, CT, fluoroscopy, and electromagnetic tracking. Ultrasound is the preferred modality due to its safety, as CT and fluoroscopy expose patients to ionizing radiation [3], and electromagnetic tracking is prone to interference [4]. However, ultrasound has limitations, including spatial resolution, 3D needle shape determination, and tissue contrast [5], leading to needle read-justments and complications during the interventions, such as tissue damage [6]. To address these challenges, optical fiber sensors have gained interest due to their flexibility, biocompatibility, safety and real-time capabilities [7]. Optical fibers are immune to electromagnetic interference, making them compatible with MRI environments [8], [9].

Measuring local longitudinal core strains in an optical fiber triplet enables the determination of fiber optic shape sensor curvature and orientation [8]. Strain sensing methods involve fiber Bragg gratings (FBGs) and Rayleigh backscatter [10], [11]. Mechanical or temperature-related stress changes an FBG grating period or the refractive index and hence the Rayleigh scatter position, thereby shifting the reflection spectrum. FBGs offer accurate strain sensing with high signal-to-noise ratios, yet limitations in sensing point density require spatial interpolation, potentially omitting strain variations [12]. Standard optical fiber has weak Rayleigh signals, but signal enhancement techniques like UV laser exposure, nanoparticle-doping, or uniform/random gratings improve light scatter strength [13], [14], [15], [16], [17]. Optical frequency domain reflectometry (OFDR), with a swept laser and Fourier transforms, enables high-speed, millimeter-resolution distributed strain sensing [11].

Numerous studies have explored optical fiber sensors for medical tool shape reconstruction. Recent notable contributions include works for needle insertions [18], [19], [20], flexible devices interacting with tissue [21], [22], [23], or for steerable needles [24], [25], [26]. These studies predominantly focus on needle insertion procedures, encompassing flexible needles and epidural needles. Additionally, some researchers have focused on catheter shape monitoring, as demonstrated by Khan et al. [27], Al-Ahmad et al. [28], Jäckle et al. [29], and our previous work [30]. The sensors are either externally (e.g., [26]) or internally (e.g., [21]) embedded into devices, utilizing varying numbers of cores and FBGs, with some using single-core fibers (e.g., [22], [23]) and others opting for multi-core fibers (e.g., [24], [27], [29]). Errors vary from submillimeter to a few millimeters, depending on the specific application and method.

The current literature on optical fiber-based shape sensing techniques presents several noteworthy limitations. Many algorithms require prior knowledge of tissue properties, specific shapes, and anticipated needle deflections, limiting clinical practicality (e.g., [18], [22], [23]). Using discrete FBGs introduces challenges in spatial interpolation, leading to curvature estimation inaccuracies. Precise FBG placement becomes crucial for optimal sensing, demanding careful placement for maximal efficiency (e.g. [20]). The high insertion loss associated with FBGs further limits their sensing range. The materials used to assemble and embed the sensor, such as epoxy glue, can hinder strain transfer to the fibers (e.g., [19], [31]). Furthermore, shape reconstruction methods relying on single-core FBGs demand meticulous positioning and alignment of the fibers, which can present practical challenges during device assembly (e.g. [21], [31]). While multi-core fibers eliminate these issues, they tend to sacrifice strain sensitivity due to core proximity (e.g. [24], [29], [27]). Finally, some studies lack comprehensive assessments across various scenarios, limiting broader applicability.

This paper introduces a 3D shape-sensing device for flexible needles, employing a distributed grating-based fiber optic sensor. We conduct automated insertions in various scenarios, including single and double-layer artificial tissues and an animal model, performing needle shape reconstruction without complex models, prior data on surrounding tissue, or needle deflection predictions. Our sensor consists of three polyimide-coated SMF28 fibers arranged equilaterally within a polyethylene-polypropylene copolymer, whose flexibility allows strain to be fully transmitted to the fibers without allowing slippage [32]. We enhance backscatter power using randomly chirped FBGs inscribed by a femtosecond laser [33], offering lower insertion loss than uniform FBGs and high SNR compared to ultra-weak uniform FBGs. We obtain ground truth measurements through stereo vision for artificial tissues and CBCT imaging for real tissue insertions. The paper’s main contributions can be summarized as follows:

• We propose a needle assembly method for accurate sensor registration, strain transfer optimization, and reduced sensor movement and torsion risks.

• We present a robust and reproducible calibration procedure that eliminates the need for precise fiber positioning and alignment, simplifying device assembly.

• We introduce a tip curvature compensation approach for distributed sensing, improving system accuracy and reliability.

• The shape-sensing model performance is evaluated in clinically relevant scenarios, ensuring practicality.

II. METHODS

A. Shape Sensing Theory

The continuous sensor’s shape reconstruction is based on OFDR for strain measurements, following the approach described by Froggatt et al. [11]. Luna Innovations’ Optical Distributed Sensor Interrogator (ODiSI-B) was used to acquire the raw time domain signals from each fiber, separately, in both reference and sampling states. Subsequent OFDR data processing in MATLAB, detailed in our prior work [30], resulted in distributed strain measurements with a maximum noise amplitude of 10 μstrain. To enhance accuracy, we employed an interpolation method from [17], using zero padding to the spatial domain data to artificially increase spectral resolution. A quadratic fit further refined the cross-correlation peak determination. Eq.(1) links local strain ($\epsilon$) and temperature ($T$) changes to spectral shifts, with their respective constants ${\kappa }_{\epsilon }$, ${\kappa }_T$, and local Bragg wavelength ${\lambda }_B$ [12]:

$$\frac{\Delta {\lambda }_B}{{\lambda }_B}={\kappa }_{\epsilon }\Delta \epsilon +{\kappa }_T\Delta T.$$ (1)

When using OFDR for distributed sensing, a compromise between spatial resolution and sensitivity must be made [34], [35]. The spatial resolution is determined by the length of a sliding window used during one step of the OFDR process. Adjusting this window length introduces a tradeoff: increasing the window size degrades spatial resolution, but improves sensitivity by processing more data points. Section II-C explores the impact of spatial resolution on shape sensing accuracy.

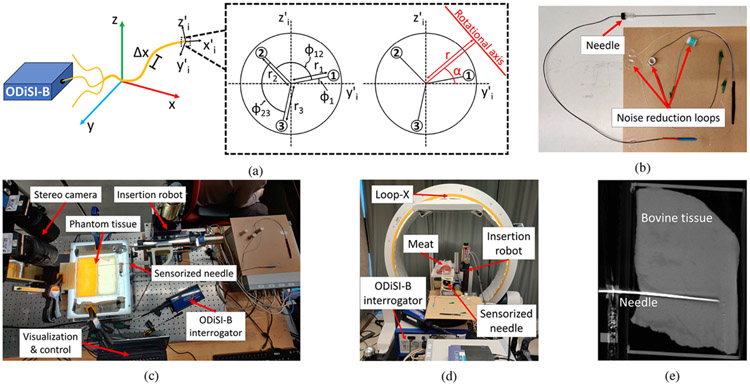
The sensor’s 3D spatial coordinates in the tracking frame are computed using a geometrical model based on parameters from the sensor’s cross-section (Fig. 1a), inspired by Froggatt et al. [36]. This model employs a spatial resolution $\Delta x$ to define sensor sections. Strain equations for the three fibers (Eq.(2)) are expressed in terms of local curvature radius ($r$) and orientation ($\alpha$), with detailed derivation shown in [36]. Solving the nonlinear system from Eq.(3) relies on the triplet’s geometrical parameters, including distances between the triplet center and each fiber core ($r_1$, $r_2$, $r_3$), the transverse angular positions of the three fibers (${\varphi }_1$, ${\varphi }_{12}$, ${\varphi }_{23}$), and their respective strain measurements (${\epsilon }_1$, ${\epsilon }_2$, ${\epsilon }_3$). Estimations of $r$ and $\alpha$ are performed for each sensor segment, as previously demonstrated in [30]. To account for OFDR sensitivity to both temperature and strain, it is assumed that the three fibers experience identical temperature fluctuations at a same sensing location, allowing common-mode elimination of temperature-induced offsets on strain measurements (${\epsilon }_0$) by solving equations calculating strain differences between the fibers:

$$\begin{gathered} {\epsilon }_1=-\frac{r_1\cos ({\varphi }_1-\alpha )}{r}+{\epsilon }_0 \\ {\epsilon }_2=-\frac{r_2\cos ({\varphi }_1+{\varphi }_{12}-\alpha )}{r}+{\epsilon }_0 \\ {\epsilon }_3=-\frac{r_3\cos ({\varphi }_1+{\varphi }_{12}+{\varphi }_{23}-\alpha )}{r}+{\epsilon }_0 \end{gathered}$$ (2)

$$\begin{gathered} {\epsilon }_{12}={\epsilon }_1-{\epsilon }_2 \\ {\epsilon }_{13}={\epsilon }_1-{\epsilon }_3 \\ {\epsilon }_{23}={\epsilon }_2-{\epsilon }_3 \end{gathered}$$ (3)

Fig. 1:

(a) The experimental setup and geometric model for shape reconstruction, inspired by [30]. It uses variables like ${\varphi }_1$ (transverse angular position of fiber 1), ${\varphi }_{12}$ (angle between fibers 1 and 2), ${\varphi }_{23}$ (angle between fibers 2 and 3), $\alpha$ (curvature orientation), $r$ (curvature radius), $r_1$, $r_2$, and $r_3$ (distances between the triplet center and each fiber core). The local frame of the sensor segment is defined by the coordinate system ($x_i\prime$, $y_i\prime$, $z_i\prime$), while ($x$, $y$, $z$) refers to the tracking frame. (b) Picture of the assembled needle. (c) Experimental setup for needle insertion in phantom tissue under stereo visualization. (d) Experimental setup for needle insertion in real tissue under CBCT visualization. (e) CBCT layer from a real tissue insertion trial.

This process also cancels axial strain, as demonstrated in our previous work [30].

B. Sensorized Needle Fabrication

In this study, we used a sensor fabricated from our previous work [30]. To fabricate this sensor, we selected 155 μm diameter polyimide-coated SMF28 equivalent fibers from Fibercore (SM1250(10.4/125)P). To enhance the backscatter signal over a 1.5 m length, we inscribed randomly chirped gratings through the polyimide coating of the three fibers using a femtosecond laser plane-by-plane direct-writing technique, as described in [33]. These gratings had a random spectral response with a central wavelength around 1540 nm, resulting in an increase in backscatter levels of approximately 40 dB above those of unexposed fibers. After laser writing, we arranged the three fibers in an equilateral configuration through an extrusion process in a copolymer of polyethylene and polypropylene from TOTAL (M6823MZ) using a Leistritz twin-screw extruder. Additional details on the extrusion process can be found in [32]. The final device had a diameter of approximately 600 μm.

We built the sensorized needle using a 50 cm segment of the sensor, with half inserted into a nitinol tube (635 μm ID). Minimizing the gap between the sensor and needle’s inner stylet restricted sensor mobility, decreasing torsion risks and improving strain transfer during needle deflection. To strengthen the assembly, we covered the remaining half and the proximal end of the nitinol tube with shrink tubing. The inner stylet-to-outer sheath connection was glued to the nitinol tube’s base. We used an 18G nitinol MRI-compatible needle (type KIM18/20, Innovative Tomography Products GmbH, Germany). Fiber pigtails were looped to slightly reduce signal amplitude, eliminating unwanted ghost reflections that could induce noise. To minimize reflections at the distal end, we applied a drop of light-curing glue (AA 3922, Loctite, Henkel) to index match the sensor at the extremity of the nitinol tube. Fig. 1b depicts the assembled needle. Accurate signal alignment from all three fibers was achieved by matching the drops in backscattered signals caused by the sensor’s cut end.

C. Sensor Calibration and Validation

We determine the geometric parameters using a calibration method inspired by Roesthuis et al. [37]. This approach maps ${\varphi }_1$, ${\varphi }_{12}$, ${\varphi }_{23}$, $r_1$, $r_2$ and $r_3$ from Eq.(2) and Fig. 1a along the sensorized needle’s length. The needle is bent to a known curvature and rotated about its axis, inducing sinusoidal strain variations in each fiber per Eq.(2), allowing to derive ${\varphi }_1$, ${\varphi }_{12}$ and ${\varphi }_{23}$ from the phases and $r_1$, $r_2$, and $r_3$ from the amplitudes of the sine curves. This process is repeated for all sensing locations. However, unlike [37], needle tip boundary conditions are addressed with direct strain measurements, enabling nonlinear strain correction through a new technique.

We used two 3D printed ABS jigs (Stratasys F170 printer) with 13 grooves with curvatures ranging from 0 to 4 m⁻¹ and composed of 16G needles to deflect the sensorized needle with constant curvature. A custom XY linear setup allows for needle movement within and between the grooves, with a rotating piece enabling needle rotation. For each curvature, we performed 18 insertions at angles from 0° to 340° (or 10° to 350°) in 20° increments. We divided the 11 nonzero curvatures into two sets, one for calibration purposes with values of 0.25, 0.5, 1, 1.6, 2, 2.5, 3.2, and 4 m⁻¹, and the other for validation purposes, consisting of curvatures of 0.8, 1.25, and 3.125 m⁻¹, to assess calibration accuracy.

We processed backscattered signals using a custom software to obtain distributed strain measurements. The sinusoidal strain variation at each sensing location of each fiber was curve-fitted, extracting phase and amplitude for calibration. Initially, constant values were approximated for all parameters except ${\varphi }_1$ since fiber arrangement was uniform using the extrusion process [30]. Here, ${\varphi }_1$ varied along the sensor’s length as fibers could rotate transversely during extrusion. We then used the estimated calibration parameters and known needle orientation to solve Eq.(3) and recover its curvature, comparing it to the expected curvature. Ratios of output to real curvature were calculated for each calibration groove over the sensor’s length and averaged over all 18 trials. This was repeated for five resolutions (1 mm to 1 cm) to assess spatial resolution’s impact on shape recovery.

Shapes from both the calibration and validation datasets were recovered at all five different spatial resolutions using the calibrated parameters. Initially, orientation and curvature were computed by solving Eq.(3) along the entire sensor length. Subsequently, the curvature amplitude at the proximal needle end determines the ratio, which is then applied to the curvature to determine the 3D coordinates. These coordinates are compared to the expected values using the RMSE metric to characterize the overall shape-reconstruction accuracy of each trial. Error statistics for each bending scenario were compiled by averaging the RMSE values of all trials and calculating standard deviation.

D. Experimental Methodology on Synthetic and Real Tissues

Following needle calibration, we performed 3D shape sensing experiments and assessed its accuracy across various tissue insertion scenarios. Error calculation involved comparing the reconstructed shape with the registered ground truth. In artificial tissue experiments, we used stereo vision (Flea2 FL2-0852C, Point Grey Research Inc., 1024 × 768 resolution) to measure the 3D ground truth needle shape. We used calibrated biplanar cameras to reconstruct the 3D stereo needle shape, relying on manual labeling of the needle as our input data.

We first created isotropic gel phantoms to mimic soft and stiff tissues using plastic materials from M-F Manufacturing Company in TX, USA. For stiff tissue, we mixed liquid plastic and plastic hardener in a 4:1 ratio, while soft tissue was formed without hardener. To create a two-layer gel tissue, we poured an initial layer into a mold with a divider for size control. After cooling, we removed the divider and poured the second layer, causing the boundary of the first layer to melt and fuse the two layers. We used a 4-degree of freedom linear stage (XYR-6060 & LM-400, Dover Motion, Boxborough, MA, USA) for needle insertion (Fig. 1c), consistent with our prior work [23]. Each artificial tissue underwent a dozen insertion trials, with a maximum depth of 120 mm. We acquired the optical reference state of the needle in a straight needle jig. Before each insertion trial, we captured a stereo image pair to establish a reference. After the needle was inserted, we captured another stereo image pair and collected optical data from each fiber. These data served both as ground truth and as information for shape-sensing purposes.

For the real tissue experiments, we acquired bovine meat which possessed a stiffness varying between soft and hard artificial tissues. We followed a similar experimental setup to the artificial tissue insertions, with the exception of using a mobile CBCT imaging robotic system (Loop-X, medPhoton, Brainlab) instead of using stereo-vision to acquire the needle’s ground truth data (Fig. 1d). We conducted a dozen insertions in the meat model, with a maximum depth of 120 mm. We collected 3D CBCT data before the first insertion and after each trial, along with optical data from each fiber for ground truth and shape-sensing information, respectively. The CBCT reconstruction process involves segmenting fiducials through image thresholding, determining their positions in CBCT space with K-means, and aligning them with their actual locations in the needle box’s frame via point cloud registration. Similarly, we segmented the needle through CBCT image thresholding and identify its centerline in CBCT space (Fig. 1e), which was then interpolated and smoothed using 3^rd order 3D B-splines. Finally, we mapped the needle shape in CBCT space into box coordinates using a point cloud registration using the fiducials.

In tissue insertion experiments, OFDR shape-sensing and error estimation followed the same approach detailed in Section II-C. The needle tip, consistently identified and matched in biplanar images during gel phantom experiments, was used as a reference point for aligning needle shapes obtained via OFDR shape-sensing, stereo reconstruction, and CBCT reconstruction. A point-cloud registration aligned the shapes after adjusting their lengths and sample counts to same values.

III. RESULTS AND DISCUSSION

A. Sensor Calibration and Tip Deflection

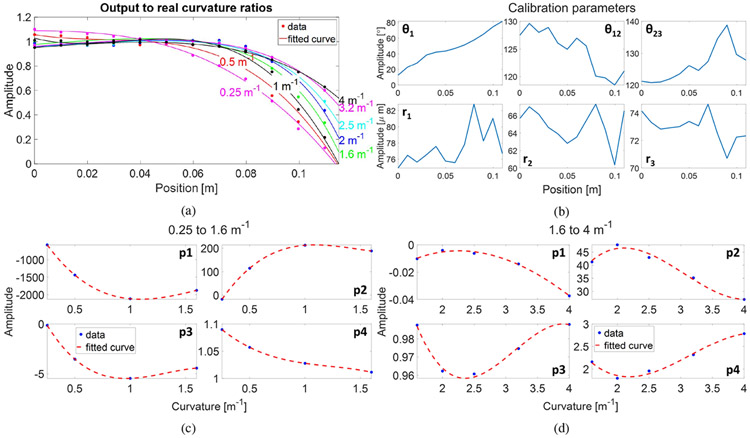
Fig. 2a illustrates the declining trend of output-to-real curvature ratios across all calibration curvatures at a spatial resolution of 10 mm, suggesting lower strain values closer to the needle tip. Per Euler-Bernoulli beam theory, a beam’s curvature (and strain) decreases and approaches zero towards the free end, as observed. Curvature-dependent trends among the ratios were quantified through curve fitting: 0.25 to 1.6 m⁻¹ used third-degree polynomials, and 1.6 to 4 m⁻¹ used exponential base 2 functions. Coefficients from these fittings were also curve-fitted as functions of curvature with third-degree polynomials (Fig. 2c and Fig. 2d). Using these quantified ratios to compensate for tip strain reduction, we refined calibration parameters along the sensor’s length. Averaging calibration dataset results (Fig. 2b) yielded optimal flexible needle shape-sensing.

Fig. 2:

(a) Ratios of the estimated curvatures to the real curvatures. (b) Calibration parameters results. Fittings of the ratios’ coefficients as functions of curvature ranging from (c) 0.25 to 1.6 m⁻¹ and (d) 1.6 to 4 m⁻¹. Results at a spatial resolution of 10 mm are shown.

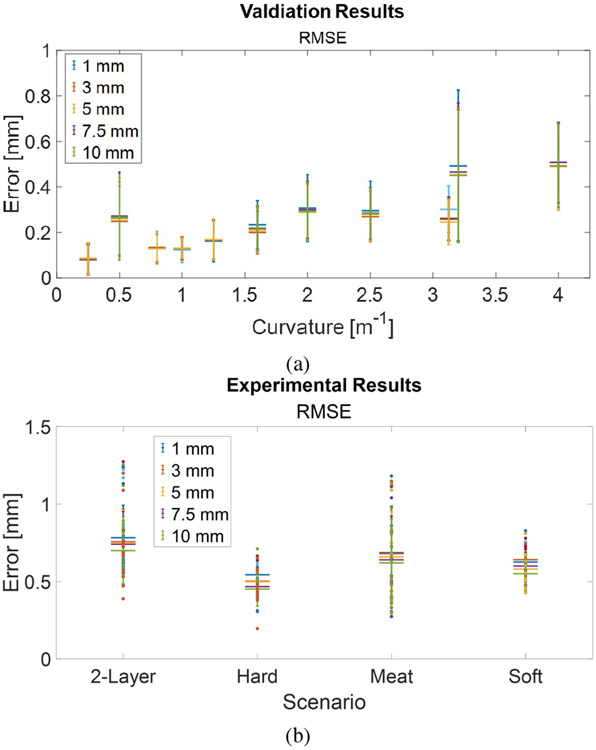
The shape errors for both calibration and validation datasets are shown in Fig. 3a. The average RMSE values obtained for the validation-only grooves, i.e., curvatures of 0.8, 1.25, and 3.125 m⁻¹, were 0.13 ± 0.06 mm, 0.17 ± 0.09 mm, and 0.26 ± 0.10 mm, respectively. Needle deflections during procedures like prostate interventions are typically minimal, which is why curvatures < 1.5 m⁻¹ hold greater significance in clinical applications. An average RMSE of 0.15 ± 0.09 mm is achieved for all curvatures < 1.5 m⁻¹. Fig. 3a shows that when superimposing results from all spatial resolutions, there is little change in shape errors for both smaller and larger curvatures. This is attributed to the reconstruction model’s characteristics and the noise in strain signals. The iterative segment-by-segment reconstruction from the sensor’s base leads to cumulative errors. Our previous simulations have demonstrated that position error increases with spatial resolution and noise amplitude [30]. Hence, while sensitivity increases with larger spatial resolution, shape error remains relatively consistent.

Fig. 3:

(a) Shape reconstruction results for both calibration and validation datasets. (b) Experimental results in artificial and real tissues.

B. Synthetic and Real Tissue Experiments

We report insertion experiment results in diverse materials, including single-layer soft, single-layer hard, and double-layer soft-hard artificial tissues, along with real animal tissue. Fig. 3b displays RMSE results across all experimental configurations. Our shape-sensing approach consistently performs well across a wide range of insertion scenarios. The RMSE results range from 0.55 ± 0.11 mm (10 mm) to 0.63 ± 0.11 mm (1 mm) for soft tissue, 0.45 ± 0.11 mm (10 mm) to 0.54 ± 0.08 mm (1 mm) for hard tissue, 0.70 ± 0.22 mm (10 mm) to 0.78 ± 0.21 mm (1 mm) for double-layer tissue, and 0.62 ± 0.28 mm (10 mm) to 0.69 ± 0.30 mm (1 mm) for animal tissue.

As expected, homogeneous tissues (soft and hard phantoms) yielded slightly better results compared to non-homogeneous tissues (double-layer and meat), with RMSE values ranging from 0.50 ± 0.12 mm (10 mm) to 0.58 ± 0.10 mm (1 mm) versus RMSE values ranging from 0.67 ± 0.24 mm (10 mm) to 0.74 ± 0.25 mm (1 mm). This difference arises from noisier stereo images in the case of the double-layer tissue and increased variability in needle deflections during insertions into non-homogeneous tissues. This confirms the observed phenomena that more complex shapes result in larger reconstruction errors [30].

Fig. 3b illustrates that the results remain consistently reliable across various spatial resolutions, with a slight improvement observed in larger spatial resolutions. However, smaller spatial resolutions may be desirable for clinical applications requiring more data points. In summary, our method achieves submillimeter accuracy, with RMSE values ranging from 0.58 ± 0.21 mm (10 mm) to 0.66 ± 0.20 mm (1 mm) across all experiments. This level of accuracy meets the typical requirements for surgical interventions.

C. Comparison with Discrete Sensorized Needles

By comparing the tissue insertion results presented here with previous synthetic experiments in [23], where in both cases we used stereo vision for ground truth comparison, important differences can be established. Our previous work employed a Lie-group theoretic approach with a four-active-area FBG-sensorized needle for shape assessment during insertion into artificial tissues similar to those in our current study. At a 125 mm insertion depth, this approach yielded RMSE values of 0.41 ± 0.14 mm in soft tissue, 0.45 ± 0.16 mm in hard tissue, and 0.26 ± 0.04 mm in double-layer soft-hard tissue. Furthermore, we can compare our results in animal tissue with our recent research [38]. In the latter, a single-core sensorized needle [23] yielded an RMSE of 0.59 ± 0.28 mm, while a multi-core fiber, which exhibited an RMSE of 0.27 ± 0.09 mm in soft phantom tissue, achieved an RMSE of 0.80 ± 0.31 mm.

Our results using the distributed sensorized needle show similarities to results with discrete sensorized needles, though a minor increase in errors is observed in artificial tissues. Importantly, our approach overcomes certain limitations. The discrete FBG-based methods proposed in [23] and [38] require knowledge of tissue properties and needle deflection patterns for accurate shape reconstruction. Experimental parameters including inflection points (C-shape and S-shape), along with number and stiffness of tissue layers, are factored in the reconstruction algorithm. Beam mechanics depend on experimental scenarios, described by different intrinsic curvature functions and coefficients, restricting clinical practicability.

D. Source of Errors on Shape Sensing Accuracy

Shape tracking errors and error distributions arise from limitations in the geometric reconstruction model, sensor torsion, noise in strain signals, artifacts in shape visualization through stereo vision and CBCT imaging, and the gap between the needle’s inner stylet and outer sheath. To counter error accumulation during segmented reconstruction, particularly over longer lengths, one strategy is to monitor the curvature difference between consecutive segments, taking corrective actions if it exceeds a predetermined threshold [39]. Device torsion significantly impacts shape tracking accuracy by altering the calibration-derived ${\varphi }_1$ values, necessitating a compensation strategy during tissue insertion. The strain induced by twisting remains relatively low due to sensor fiber proximity and pitch [40], [41]. Integrating additional fibers and inducing a controlled pitch during the polymer extrusion process can enhance torsion sensitivity [42]. A potential twist detection method involves comparing strain measurements from outer cores to inner cores, similar to Ko et al.’s approach [43]. These measures would collectively address the impact of device torsion. However this remains limited to compare to catheter guidance [30]. To minimize stochastic noise in distributed strain signals, a deeper analysis is required to identify its sources and plan potential hardware adjustments. Discrepancies between experimental and ground truth shapes are often linked to artifacts from stereo vision and CBCT imaging. For artificial tissue scenarios, improving needle segmentation by using clearer materials and optimizing the tissue fabrication process to reduce air bubbles can help mitigate these imaging issues. Implementing the aforementioned modifications to our measurement approach can significantly improve sensor position accuracy. Lastly, the gap between the needle’s inner stylet (813 μm OD) and outer sheath (838 μm ID) causes slightly varying deflection patterns between the two, introducing errors in OFDR-measured shapes compared to those from imaging modalities.

IV. CONCLUSION

In this study, we demonstrated a 3D shape reconstruction method for flexible surgical needles guided by a linear stage in both artificial and real tissues, using a fiber triplet embedded with distributed gratings and an OFDR technique. We validated our method by comparing it to ground-truth data obtained from stereo vision (gel phantom insertions) and CBCT imaging (real animal tissue insertions). Following thorough needle calibration and a novel tip curvature compensation approach, our method achieved reliable errors in shape tracking, meeting the required clinical accuracy standards. Future research will explore real-time shape sensing using an OFDR interrogator with multiple channels to assess our method’s accuracy over time and varying insertion depths. Additionally, we will investigate scenarios where the needle adopts an S-shaped configuration and develop a method to correct needle torsion.