SeqDance: A Protein Language Model for Representing Protein Dynamic Properties

Abstract

Proteins perform their functions by folding amino acid sequences into dynamic structural ensembles. Despite the important role of protein dynamics, their complexity and the absence of efficient representation methods have limited their integration into studies on protein function and mutation fitness, especially in deep learning applications. To address this, we present SeqDance, a protein language model designed to learn representation of protein dynamic properties directly from sequence alone. SeqDance is pre-trained on dynamic biophysical properties derived from over 30,400 molecular dynamics trajectories and 28,600 normal mode analyses. Our results show that SeqDance effectively captures local dynamic interactions, co-movement patterns, and global conformational features, even for proteins lacking homologs in the pre-training set. Additionally, we showed that SeqDance enhances the prediction of protein fitness landscapes, disorder-to-order transition binding regions, and phase-separating proteins. By learning dynamic properties from sequence, SeqDance complements conventional evolution- and static structure-based methods, offering new insights into protein behavior and function.

Introduction

Deep learning has achieved considerable success in predicting various protein attributes such as structure (e.g., AlphaFold^{1, 2} and RoseTTAfold³), function, stability, localization, and interactions. A central challenge in developing effective deep learning models is choosing a representation that allows models to interpret and learn from easily. The simplest form of representation, one-hot encoding of amino acids, is unbiased and rooted in the idea that a protein’s sequence determines its properties. Yet, one-hot encoding often underperforms due to its simplicity. To overcome this, researchers have introduced more informative representations incorporating amino acid physicochemical properties, structural features, evolutionary profiles, and, more recently, embeddings from deep learning models. We generally classify these representations into two categories: evolution-based and biophysics-based⁴.

Evolution-based representation (EBR) introduces extra information of protein homologs in other species that experience similar selective pressures. A major source of EBR is multiple sequence alignment (MSA), which proves particularly valuable for identifying functional sites⁵, pathogenic mutations⁶, and predicting 3D structures^{1, 2}. Recently, protein language models (pLMs) like ESM1,2^{7, 8}, ProtTrans⁹, and ProGen¹⁰ have emerged as powerful tools for generating implicit EBR. Trained in an unsupervised manner on large-scale protein sequence datasets, pLM has been shown to effectively memorize conserved patterns during the pre-training process^11–15. pLM provides a computationally efficient alternative to MSA and has been successfully applied to various biological questions, including predicting 3D structures (e.g., ESMFold⁷), predicting signal peptides¹⁶, and even generating proteins¹⁰. However, the effectiveness of EBR relies on the quality and quantity of sequenced homologs. For instance, the prediction confidence scores from protein structure predictors are directly related to the number of homologous sequences^{1, 7}. As a result, EBR is less effective for rapidly evolving viral proteins, immune proteins, and proteins from under-studied species such as extremophiles¹¹, where homologous sequences are either sparse or highly divergent. Moreover, evolutionary profiles are consequences of functional protein behaviors rather than their causes (Figure 1A). Overreliance on EBR might bias the model toward the conservation pattern. For example, EBR-based pathogenic mutation predictors perform worse when evaluated solely on conserved or unconserved regions, as they can achieve good performance by simply predicting mutations in conserved regions to be pathogenic and those in unconserved regions to be benign.

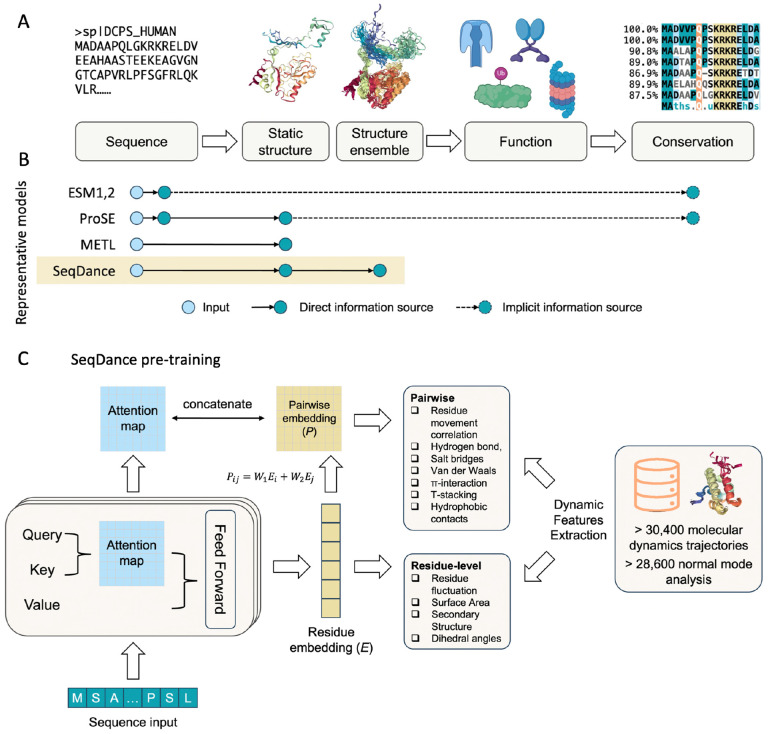
Figure 1: Information flow in protein study, representative protein language models, and SeqDance pre-training.

A. Illustration of the “sequence - structure ensemble - function - evolution” paradigm. Sequences are the basic elements of proteins that fold into structural ensembles to perform specific functions. Functionally important regions exhibit conserved patterns across species. B. Representative protein language models (pLMs) and their information sources. ESM1, ESM2 and other pLMs trained in unsupervised manners memorize co-evolution information and conserved motifs during pre-training, thus implicitly relying on evolution data. ProSE was trained to predict masked residues, pairwise contact in static structures, and structure similarity. METL was trained to predict 55 biophysical terms calculated from static structures. SeqDance was trained on protein dynamic features from molecular dynamics (MD) simulations, experimental data, as well as normal mode analysis (NMA) of static structures. C. Diagram of the SeqDance pre-training process. SeqDance is a transformer encoder that takes a protein sequence as input and predicts residue-level and pairwise dynamic features extracted from over 30,400 MD trajectories and 28,600 NMA. For a protein of length L, the residue embedding dimension is L×480. A linear layer is added to this embedding to predict residue-level features. Pairwise embeddings derived from residue embeddings are concatenated with attention maps to predict pairwise features. After pre-training, the residue embeddings can be applied to study biological questions; users can also fine-tune all parameters for downstream tasks.

Biophysics-based representation (BBR), primarily derived from protein structures, avoids the limitations of EBR and typically maintains uniform performance across the entire protein space. Predicting protein behaviors from BBR aligns with the idea that sequence determines structure, which in turn dictates function (Figure 1A). Although the experimental determination of protein structures has historically been time-consuming and resource-intensive, recent advancements such as AlphaFold^{1, 2}, RoseTTAfold³, and ESMFold⁷ have revolutionized static protein structure prediction, enabling proteome-wide analyses. BBR has been applied to a variety of biology questions. For example, predicted structures have been used to predict mutation effects and functional and binding sites¹⁷. The AAindex¹⁸ database, which compiles a number of physicochemical properties of amino acids derived from structures in the Protein Data Bank¹⁹ (PDB), is widely utilized in bioinformatics tools. Similarly, PScore²⁰ and LLPhyScore²¹ leverage physical features from PDB structures to identify phase-separating proteins²². Additionally, there have been initiatives to integrate biophysical properties into protein language models (pLMs). For example, ProSE⁴ was trained to predict masked residues, contacts within static structures, and structural similarities, while METL²³ was developed to predict 55 biophysical properties derived from Rosetta models of mutated structures.

However, current BBRs are derived exclusively from static protein structures. These structural snapshots lack crucial thermodynamic information and overlook the topological landscape of catalysis, allostery, and other long-range interactions. Moreover, static structures cannot describe the dynamic structure ensembles of intrinsically disordered regions (IDRs), which constitute more than 30% of the human proteome²⁴. Despite lacking fixed structures, IDRs use their inherent flexibility to mediate essential biological processes such as signal transduction, transcriptional regulation, and phase separation^{25, 26}.

To capture dynamic protein properties, molecular dynamics (MD) simulations are widely employed for both ordered structures and IDRs. MD simulations utilize Newton’s laws to update atomic coordinates based on interaction forces, generating ensembles of structures over a specified simulation time. However, all-atom MD simulations are computationally intensive, often requiring at least a week of GPU time to simulate a single protein at the microsecond scale. To mitigate computational demands, coarse-grained MD simulations simplify protein residues into pseudo-atoms and use specialized force fields to model interactions at the reduced scale. Another commonly used approach is normal mode analysis^{27, 28} (NMA), which describes protein vibrations (normal modes) around equilibrium conformations. Normal modes with varying frequencies represent distinct behaviors, with low-frequency modes capturing global movements. While these methods enable large-scale studies of protein dynamics, the data generated from MD and NMA are often high-dimensional and irregularly shaped. One current challenge is to represent these dynamic properties in a meaningful and efficient manner that can be integrated into deep learning models.

Here, we introduce SeqDance, a pLM designed to provide representation of protein dynamic properties. We first collected over 30,400 protein dynamics trajectories for ordered structures, membrane proteins, and IDRs, along with performing over 28,600 NMAs for proteins in the Protein Data Bank (PDB). From this dataset, we extracted rich residue-level and pairwise dynamic features and pre-trained SeqDance to predict these features from protein sequences (Figure 1B). SeqDance effectively learned both local and global dynamic properties in the pre-training process. These properties can be easily retrieved from SeqDance by inputting a protein sequence and can be applied to various biological questions. We also demonstrate that SeqDance provides informative dynamic embeddings for proteins that lack homologs in the pre-training set.

Results

Pre-training SeqDance with dynamics properties of over 59,000 proteins.

We collected high-resolution and low-resolution protein dynamics data to pre-train SeqDance (Table 1). High-resolution dynamics data includes experimental data and all-atom molecular dynamics (MD) simulation trajectories from ATLAS²⁹, GPCRmd³⁰, and PED³¹ (Table 1). ATLAS contains all-atom MD structure ensembles for over 1,500 representative non-membrane proteins, each simulated for 100 nanoseconds with three replicates. GPCRmd includes more than 500 MD simulations of G-protein-coupled receptors, with most proteins simulated for 500 nanoseconds in three replicates. PED provides ensembles of disordered proteins from both experiments and MD simulations, from which we filtered 382 ensembles. Since high-resolution dynamics data is limited, we augmented SeqDance pre-training with low-resolution dynamics data, including coarse-grained MD trajectories and normal mode analysis (NMA). We processed coarse-grained structure ensembles of 28,058 human disordered regions from IDRome²⁴ and converted them to all-atom trajectories³² (see Methods for details). We also conducted NMA^{27, 28, 33} for over 28,600 representative structures in the PDB, covering single proteins, antibodies, and protein complexes³⁴ (Table 1).

Table 1:

the protein dynamic datasets used to pre-train SeqDance

	Source	Description	Number	Method
High resolution	ATLAS	Ordered structures in PDB (no membrane proteins)	1,516	All-atom MD, 3*100 ns
	PED	Disordered regions	382	Experiment and others
	GPCRmd	Membrane proteins	509	All-atom MD, 3*500 ns
Low resolution	IDRome	Disordered regions	28,058	Coarse-grained MD, convert to all atom
	Proteinflow	Ordered structures in PDB	28,631	Normal mode analysis

We extracted residue-level and pairwise dynamic features that describe the distribution of features in structure ensembles (Figure 1B, Supplementary Table 1, A detailed explanation can be found in the Discussion). Residue-level features include root mean square fluctuation (RMSF), surface area, eight-class secondary structures, and dihedral angles (phi, psi, chi1) which describe the rotation angles around bonds in the protein backbone and side chains. Pairwise features include the correlation of Cα movements and frequencies of hydrogen bonds, salt bridges, Pi-cation, Pi-stacking, T-stacking, hydrophobic interactions, and van der Waals interactions. For NMA data, we categorized normal modes of each structure into three frequency-based clusters. For each cluster, we calculated residue fluctuation and pairwise correlation maps (see Methods for details, Supplementary Table 1).

SeqDance is a transformer encoder model with 12 layers and 20 heads per layer, with 35 million parameters in total. SeqDance takes protein sequences as input and predicts residue-level and pairwise dynamic features (Figure 1B). For residue-level feature prediction, we added a linear layer to the last layer’s residue embeddings. For pairwise feature prediction, we transformed the residue embeddings into pairwise embeddings, concatenated them with SeqDance’s attention maps, and applied a linear layer to the concatenated matrix (A detailed explanation can be found in the Discussion). We randomly sampled approximately 95% of the protein dynamics data to pre-train SeqDance. We adjusted the weights for different data sources and features in the loss function (see Methods for details).

After pre-training, we observed a strong correlation between the weights for predicting co-movement in MD and NMA (Supplementary Figure 1). Specifically, the Pearson correlation between that for MD and low-frequency normal modes was 0.75, suggesting that NMA closely mimics dynamic movements captured by MD simulations. This finding supports the use of NMA to augment SeqDance pre-training.

Next, we evaluated whether SeqDance had effectively learned protein dynamic properties. Specifically, we examined if SeqDance’s self-attention mechanisms captured dynamic interactions and residue co-movement, and whether SeqDance embeddings encoded information about protein conformational properties.

SeqDance’s attention captures local dynamic residue interactions and co-movement.

Transformer model employs the self-attention mechanism³⁵ to update the representation for each word by aggregating information from other words, with attention values representing the relationship between words (in this context, amino acid residues). Given that SeqDance’s attention maps were utilized to predict dynamic interactions and residue co-movement, we investigated whether SeqDance’s attention effectively capture these properties.

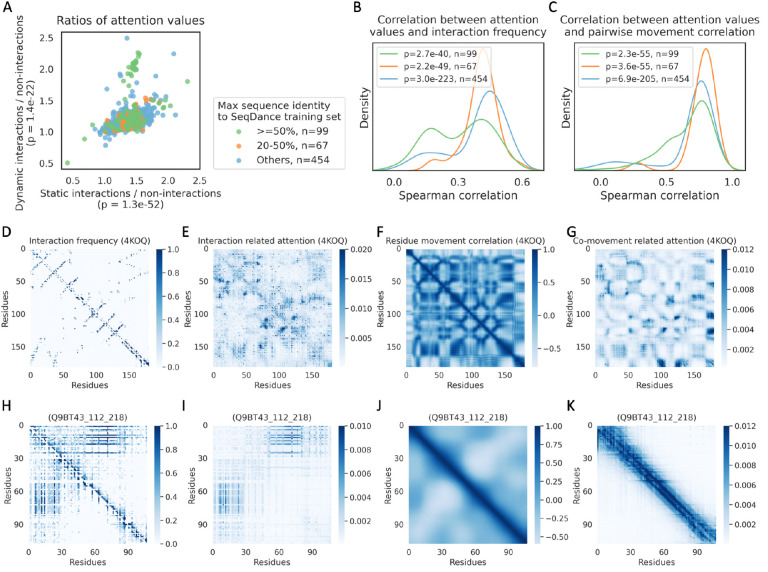
To analyze pairwise feature-related attention, we first selected the top 10 attention heads with the highest weights for predicting interactions out of 240 total attention heads (Supplementary Figure 1A). We then compared their averaged attention values with pairwise features across 620 held-out proteins from ATLAS, GPCRmd, PED, and IDRome. Interacting pairs were classified as either static interactions (observed in the first frame of the structural ensemble) or dynamic interactions (observed in subsequent frames). A subset of non-interacting control pairs was also sampled with the same distance distribution to account for the distance dependence of attention values. As shown in Figure 2A, SeqDance assigned significantly higher attention values to both static and dynamic interactions compared to non-interacting pairs (pairwise t-test P-values: 1.3e-52 for static interactions, 1.4e-22 for dynamic interactions). Moreover, we observed a significant positive correlation between attention values and interaction frequency (Figure 2B). For residue co-movement, we conducted the same analysis and found a significant positive relationship between attention values and pairwise movement correlations in held-out proteins, with a median Spearman correlation of 0.75 (Figure 2C). The same analysis on held-out NMA data also revealed significant positive correlations between attention values and co-movements from low- and medium-frequency normal modes (Supplementary Figure 2). These results underscore SeqDance’s ability to capture biologically meaningful dynamic interactions and co-movements across different datasets.

Figure 2. SeqDance’s attention mechanism captures local dynamic residue interactions and co-movement.

A. Comparison of SeqDance’s attention values assigned to static interactions (present in the first frame of the structure ensemble), dynamic interactions (formed in subsequent frames), and a subset of non-interacting control pairs that matched to the distance distribution of interacting pairs. Each dot represents one of 620 held-out proteins. The legend on the right shows the numbers of proteins in three clusters with different sequence identities to training sequences. P-values on the x and y axes were calculated using pairwise t-tests. B-C. Distributions of Spearman correlation between SeqDance’s interaction-related attentions and interaction frequency (sum of nine types of interactions) (B), and between SeqDance’s co-movement related attentions and pairwise movement correlations (C), of three clusters of held-out proteins described above. P-values were calculated using a one-sample t-test with the null hypothesis that the mean value is zero. D-K. Visualization of pairwise features and related attention maps for a structured protein (PDB ID 4KOQ) and a disordered region (Q9BT43_112_218), including the interaction frequency (sum of nine types of interactions) map (D, H), the averaged attention map of the top 10 heads with the highest weights for interaction prediction (E, I), the residue movement correlation map (F, J), and the averaged attention map of the top 10 heads with the highest weights for co-movement prediction (G, K).

To assess SeqDance’s ability to capture pairwise relationships beyond homologous sequences, we categorized 620 held-out proteins based on their similarity to training sequences: 99 proteins had at least 50% sequence identity (with at least 80% coverage) to at least one training sequence, 67 proteins had at least 20% sequence identity (with at least 60% coverage), and 454 proteins were dissimilar to any training sequence. As shown in Figure 2A–C, the observed trends persisted for dissimilar held-out proteins. Additionally, we visualized two dissimilar held-out proteins: a structured protein (PDB ID: 4KOQ) from the ATLAS dataset (Figures 2D–G), and a disordered region (Q9BT43_112_218) from the IDRome dataset (Figures 2H–K). In both cases, we observed consistent patterns between interaction-related attention and interaction maps, as well as between co-movementrelated attention and residue movement correlations. Overall, these findings indicate that SeqDance can capture biologically meaningful relationships beyond homologous sequences.

SeqDance learns global protein conformation properties in the pre-training process.

Next, we investigated whether SeqDance embeddings encode additional protein conformational properties not included in the pre-training tasks. Since these dynamic features cannot be directly extracted from the embeddings, we applied supervised learning by using the mean-pooled embeddings for linear regression on protein conformational properties.

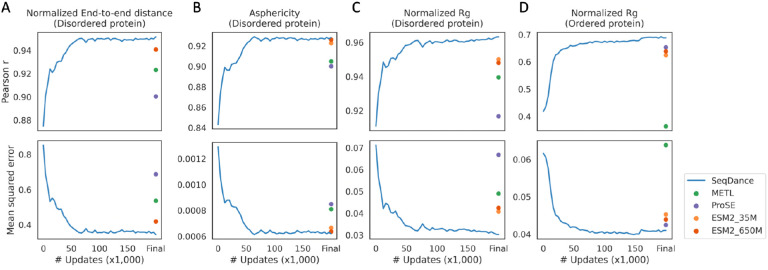
We first evaluated the models on structural ensembles of 18,415 Intrinsically disordered regions (IDRs) from coarse-grained MD simulations³⁶ (see Methods for data filtering). These simulations employed a distinct IDR dataset and force field compared to IDRome. For evaluation, we used the average values of end-to-end distance, asphericity, and radius of gyration (R_g) within the ensembles. End-to-end distance reflects flexibility and motion range, asphericity quantifies deviation from a spherical shape, and R_g measures the distribution of atoms around the protein’s center of mass, indicating its compactness. To account for protein length, we used normalized values. The training and test sets were split using a 20% sequence identity cutoff to prevent information leakage. As shown in Figure 3A–C, SeqDance outperformed METL, ProSE, and ESM2 in predicting normalized end-to-end distance, asphericity, and R_g of IDRs, with performance improving as training progressed. To further assess SeqDance’s performance on proteins without homologs in the pre-training dataset, we removed IDRs with over 20% sequence identity (with at least 60% coverage) to any SeqDance training sequence. SeqDance maintained its performance on these dissimilar IDRs (Supplementary Figure 3), demonstrating its generalization capability.

Figure 3. SeqDance embeddings encode global protein conformational properties.

Performance comparison of embeddings from SeqDance, METL, ProSE, and ESM2 in predicting the normalized end-to-end distance of disordered proteins (A, two ESM2 models overlapped), asphericity of disordered proteins (B), normalized radius of gyration (R_g) of disordered proteins (C) and ordered proteins (D). The training and test split was 6:4 with a 20% sequence identity cutoff. The results presented are the averages of ten repeats. The x-axis represents the number of pre-training steps for SeqDance, “Final” on the x-axis represents the evaluation of released weights of the other methods, and 200k steps for SeqDance.

For ordered proteins, obtaining conformational properties from structure ensembles is more challenging. Therefore, we used normalized R_g values (see Methods for details) of over 11,000 static monomer structures in the PDB from the paper³⁷. Since SeqDance was trained on NMA of nearly all representative PDB structures³⁴, we did not exclude sequences with homologs in the SeqDance pre-training dataset. Using the same evaluation method as for disordered regions, we found that SeqDance outperformed METL, ProSE, and ESM2 in predicting normalized R_g of ordered proteins, with performance improving as training progressed (Figure 3D).

Overall, these results demonstrate that SeqDance learns both local and global dynamic properties for ordered proteins and IDRs in the pre-training process. We hypothesized that the dynamic features encoded in SeqDance embeddings are informative for understanding protein behavior and function. Thus, we further applied SeqDance to specific biological questions.

SeqDance enhances understanding of protein fitness landscapes.

We first applied SeqDance to predict protein fitness landscapes³⁸, which are essential for interpreting disease mutations and guiding protein engineering. Mutation effects are determined by the residue context and the differences between wild-type and mutant amino acids³⁹. Previous methods have leveraged sequence and structural contexts to study mutation effects^{6, 39–44}, based on the hypothesis that mutations affecting linear motifs or 3D structures can alter protein behaviors. It is important to recognize that while evolution-based representations are effective at predicting mutation effects, they reflect the consequence, not the cause, of mutation effects. Previous studies have emphasized the role of protein dynamics as a causal context in understanding mutation effects^45–49. For instance, mutations in residues that co-move with the catalytic core can disrupt its dynamics, thereby affecting enzyme activity. We hypothesized that SeqDance can help predicting protein fitness by providing additional protein dynamic-based representations.

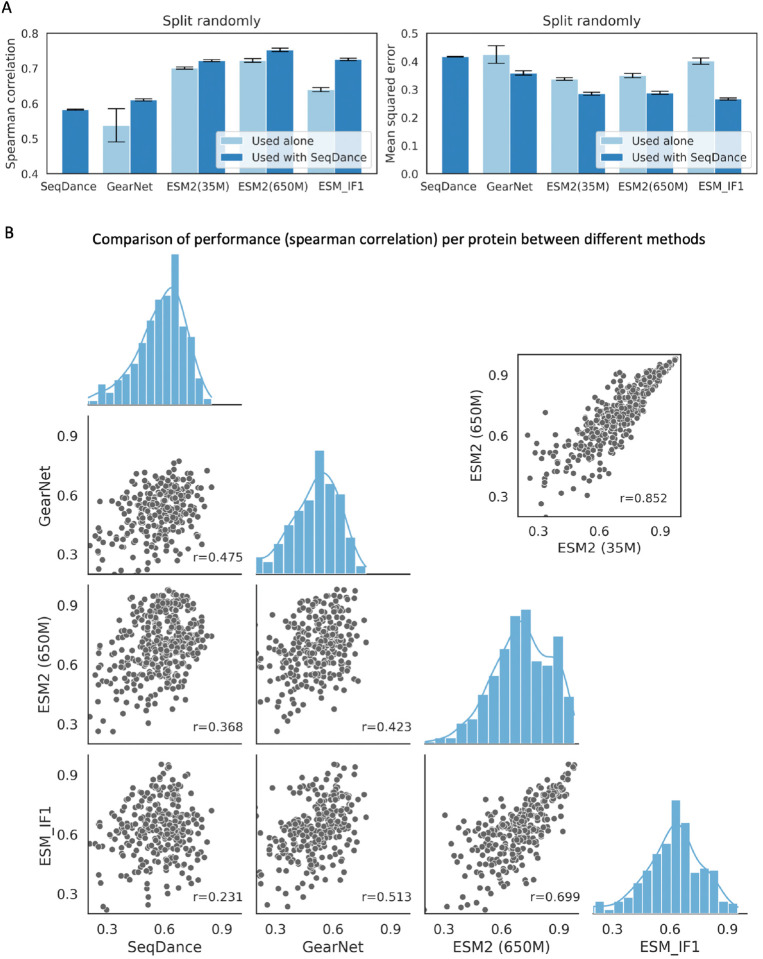
We used mutations on 20,955 residues from 412 proteins in a protein folding stability dataset³⁸ (including both designed and PDB proteins, see Methods for details). SeqDance was compared with several published methods for predicting stability-related residue context (mean ddGs of all mutations on each residue), including GearNet⁵⁰, a static structure-based pre-trained model that provides structural context; ESM2⁷ that offers implicit evolution-based representations; and ESM_IF1⁵¹, an inverse folding algorithm that provides evolution-based representations conditioned on structures. The training and test sets were divided either randomly or by protein. Our analysis revealed that, when evaluated individually, SeqDance’s dynamic-based representations consistently outperformed GearNet’s static structure-based representations, suggesting that static structures alone miss important information; ESM2 achieved the best overall performance, consistent with the fact that evolution-based representation is most effective in predicting mutation effects³⁹ (Figure 4A, Supplementary Figure 4A). Although both ESM2 (35M) and ESM2 (650M) performed better than SeqDance individually, the combination of SeqDance and ESM2 (650M) outperformed the combination of two ESM2 models (Supplementary Figure 4B, SeqDance and ESM2 (35M) have the same embedding dimensions). Moreover, integrating SeqDance embeddings significantly improved the performance of all methods. Combining the results in Figure 4A and Supplementary Figure 4A, for GearNet, Spearman correlation increased by 13%, and mean squared error (MSE) decreased by 72%; for ESM_IF1, Spearman correlation rose by 12% and MSE dropped by 29%; for ESM2 (35M), Spearman correlation improved by 1.7% and MSE decreased by 13%; and for ESM2 (650M), Spearman correlation increased by 3.2% and MSE decreased by 14% (Figure 4A). Overall, these results indicate that SeqDance provides additional information that complements exiting methods.

Figure 4. SeqDance enhances the understanding of protein fitness landscapes.

A. Comparison of SeqDance, GearNet, ESM2, and ESM_IF1 embeddings in predicting mutation effects on protein folding stability. The training and test sets were divided randomly, and four-fold cross-validation was employed to determine Spearman correlation and mean squared error. The plots show the means and standard deviations of evaluation metrics across ten independent repeats. B. Performance comparison on individual proteins. Each dot represents the mean Spearman correlation for each protein in random split across ten repeats. The Pearson correlations were used to quantify the relationship between the performances of two methods across diverse proteins. The histograms illustrate the distribution of Spearman correlations for individual proteins for different methods.

We further analyzed SeqDance’s performance on individual proteins (see Methods for details). First, we observed that SeqDance’s performance was relatively orthogonal to both ESM2 and ESM_IF1 while it had a slightly higher correlation to GearNet, reflecting some overlap in structural context information (Figure 4B). In contrast, the performances of two ESM2 models, as well as between ESM2 and ESM_IF1, were highly correlated, due to their shared reliance on evolution-based information. Second, SeqDance performed particularly well on designed proteins (Supplementary Figure 5A) and showed comparable performance on PDB proteins, regardless of whether they had homologs in the pre-training set. (Supplementary Figure 5B), highlighting its generalizability across different protein types.

Finetuning SeqDance for protein disorder region-related tasks.

Intrinsically disordered regions (IDRs) are flexible protein segments essential for signal transduction, transcription regulation, and phase separation²⁵. Since IDRs are less conserved than ordered regions, evolution-based predictors typically perform well in IDR prediction, while sequence-only predictors often underperform⁵². Given that SeqDance captures the local and global dynamics of IDRs, we evaluated its potential for IDR-related tasks.

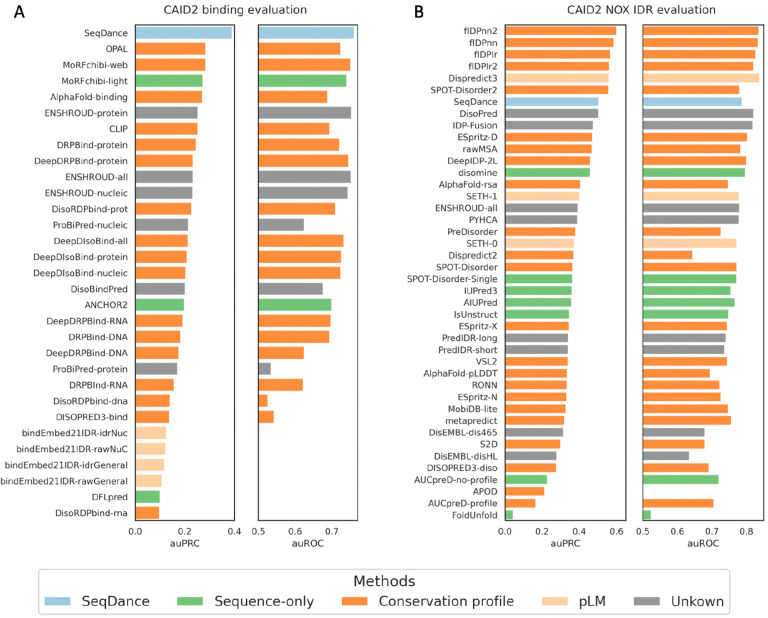
Using the Critical Assessment of Intrinsic Disorder (CAID2) benchmark⁵², which includes four tasks—the NOX IDR (missing residues in PDB), the PDB IDR (disordered residues in PDB), binding regions undergoing disorder-to-order transitions, and linker regions—we fine-tuned SeqDance on the training data of methods evaluated in CAID2 to prevent data leakage (see Methods for details). SeqDance achieved the best performance in predicting disorder-to-order transition binding regions and ranked among the top-performing sequence-only predictors for NOX IDR (Figure 5, Supplementary Figure 6). These results highlight that SeqDance learns valuable dynamic properties of IDRs, offering competitive performance as a sequence-only predictor for IDR-related tasks.

Figure 5. Fine-tuning SeqDance for predicting intrinsically disordered regions (IDRs) related tasks.

Performance comparison for predicting the binding regions (A) and NOX IDRs (missing residues in PDB structures) (B) in Critical Assessment of Intrinsic Disorder (CAID2). Performance is evaluated using the area under the Receiver Operating Characteristic curve (auROC) and the area under the Precision-Recall curve (auPRC). The auROC and auPRC for other methods were obtained from the CAID2 website. Methods evaluated in CAID2 are classified into four categories: sequence-only methods using features from single sequences; conservation profile-based methods; protein language model (pLM)-based methods; and methods with unknown inputs.

SeqDance augmented structure and sequence features in predicting phase-separating proteins.

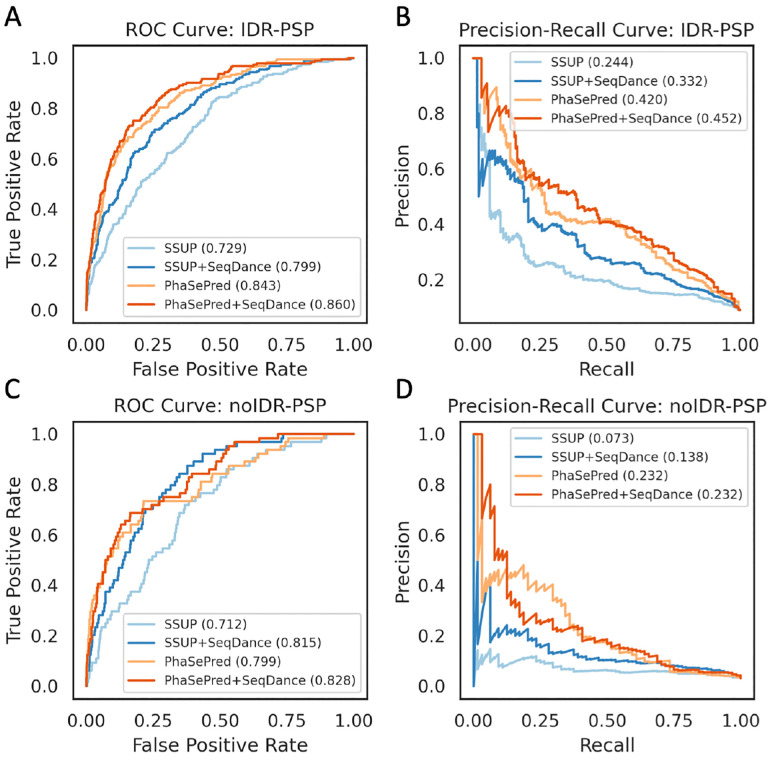
Phase separation is a crucial cellular process in which biomolecules assemble into membrane-less organelles to regulate cellular organization, metabolism, and stress responses⁵³. Phase-separating proteins (PSPs) are driven by dynamic interactions between IDRs and/or interacting surface patches on ordered regions. Previous methods, such as PhaSePred-8feat⁵⁴ (sequence-based) and SSUP⁵⁵ (static structure-based), have been used to predict PSPs. We hypothesized that the dynamic properties learned by SeqDance could improve PSP prediction.

Using the datasets of PSPs with IDR (IDR-PSPs) and without IDR (noIDR-PSPs) established by Hou et al.⁵⁵, we found that SeqDance embeddings significantly enhanced the performance of both PhaSePred and SSUP in predicting IDR-PSP and noIDR-PSP. The improvement was particularly notable for static structure-based SSUP: for IDR-PSP, SeqDance embeddings increased the area under the receiver operating characteristic curve (auROC) by 9.6% (from 0.729 to 0.799) and the area under the precision-recall curve (auPRC) by 36.1% (from 0.244 to 0.332). For noIDR-PSP, SeqDance embeddings improved SSUP’s auROC by 14.5% (from 0.712 to 0.815) and the auPRC by 89.0% (from 0.073 to 0.138).

Discussion

In this work, we started from the information flow in protein study (Figure 1A) and developed SeqDance, a novel protein language model (pLM) pre-trained on dynamic properties derived from molecular dynamics (MD) simulations and normal mode analysis (NMA). SeqDance captures both local dynamic interactions, co-movement, and global conformational features, complementing traditional evolution- and static structure-based methods. Our results demonstrate that SeqDance improves predictions in several biological questions, including protein fitness landscapes, intrinsically disordered regions (IDRs), and phase-separating proteins (PSPs).

In the pre-training process, we did not directly train SeqDance on full structure ensembles due to the immense size of the dataset (over 50 million frames) and the complexity of modeling entire ensembles. In fact, we are still unable to predict a static structure from a single sequence without relying on conservation profiles, let alone predict entire structure ensembles. To address this, we used simplified dynamic feature descriptors such as the mean, standard deviation, and interval distribution of ensemble-derived properties. Prior study has demonstrated that mean values from structure ensembles provide significantly more information than static structural values⁵⁶. This strategy enables SeqDance to learn from simplified but informative representations of protein dynamics, without the overwhelming computational demand of full ensemble modeling.

During SeqDance pre-training, we employed attention maps and pairwise embeddings to predict dynamic interactions and residue co-movements (Supplementary Figure 1). Although using attention maps increases memory usage, it does not slow down training speed. The use of attention maps in predicting these features helped constrain SeqDance to focus on interacting and co-moving residue pairs, reducing random or irrelevant attention. This approach is crucial for learning biophysically meaningful representations and improves the model’s ability to extrapolate to unseen proteins. Besides, using attention maps and pairwise embeddings as input can capture the distinct characteristics of pairwise features: the mean value of interaction feature depends on sequence length, as the maximum number of interactions a residue can form is fixed, while the mean value of correlation feature is length-independent. By combining length-dependent attention values (which sum to one after SoftMax operation in attention calculation) with length-independent pairwise embeddings, the model can effectively capture both pairwise features. In Supplementary Figure 2, we observed a negative correlation between attention values and co-movements derived from high-frequency normal modes. We attribute this to the smaller absolute values of high-frequency features, which contribute less to the training loss, thus underrepresented in the pre-training process.

SeqDance embedding effectively captures global conformational properties of both ordered and disordered proteins, which are essential for understanding protein shape and flexibility. In comparison, METL²³ underperformed in predicting the radius of gyration (R_g) for ordered proteins (Figure 3A), despite having R_g prediction as a pre-training task. This may be due to an overabundance of pre-training tasks and limited training set diversity. ProSE⁴ performed well in predicting the conformational properties of ordered regions but struggled with disordered regions, likely because its pre-training focused on contact prediction in ordered PDB structures. SeqDance, on the other hand, was pre-trained on dynamic properties of both ordered and disordered proteins, providing a comprehensive representation of protein dynamics. Evolution-based representations from ESM2⁷ also performed well, as conformational properties are conserved among homologs³⁶.

SeqDance enhances understanding of protein fitness landscapes by providing dynamic context information that complements traditional evolution-based and static structure-based representations. SeqDance embedding significantly improved GearNet’s ability to predict protein fitness, this suggests that static structures alone miss important information, consistent with the fact that static structure-based predictors often underperform in mutation-related tasks⁴⁰. Combining representations from static and dynamic structure ensembles could be especially valuable for studying novel or rapidly evolving proteins where evolutionary profiles are limited or misleading. Further studies are needed to validate these findings across diverse experimental and clinical mutation datasets.

Furthermore, SeqDance yielded promising results in tasks related to IDRs and PSPs. SeqDance excelled in predicting disorder-to-order binding regions, likely because these regions exhibit specific dynamic patterns in the MD simulation that SeqDance captures in pre-training. In PSP prediction, SeqDance improved performance by integrating dynamic features with existing structure- and sequence-based features. The greater enhancement seen with SSUP⁵⁵ compared to PhaSePred⁵⁴ may be due to PhaSePred already utilizing biophysical features, such as predicted pi-interactions and physicochemical properties, which have overlap with information encoded in SeqDance embeddings.

We envision several directions to further improve SeqDance. First, expanding protein dynamic data: while high-resolution dynamic data is scarce compared to the vast number of sequenced proteins, lower-resolution data, like coarse-grained MD simulations and NMA, have proven valuable. More dynamic data from these faster methods could be generated to further pre-train SeqDance. Second, incorporating more detailed features that can describe higher-order relationships and time dependence. Third, scaling up model size: as seen in deep learning field, larger models with more parameters could capture more complex relationships.

In conclusion, SeqDance represents a significant advancement in the field of protein representation. By learning representations of protein dynamics, we gain valuable insights into protein behaviors that were previously reliant on extensive MD simulations. This capability has the potential to reduce our dependence on computationally expensive MD simulations, offering a more efficient approach to study protein behaviors and functions.

Methods

Molecular dynamic data collection and processing

The ATLAS²⁹ database (v1) contains 1,516 molecular dynamics (MD) simulations, each conducted using the CHARMM36m force field for 100 ns with three replicates. Trajectory files comprising 10,000 frames were downloaded. The Protein Ensemble Database³¹ (PED) provides conformational ensembles for intrinsically disordered proteins, primarily derived from experiments, with some from simulations or predictions. All available ensembles were retrieved, and sequences shorter than 16 residues were excluded. GPCRmd³⁰ is a community-driven database of MD simulations of G-protein-coupled receptors (GPCRs), with most proteins simulated for 500 ns in three replicates. IDRome²⁴ contains conformational ensembles of human disordered regions generated via the coarse-grained residue-level CALVADOS model. All coarse-grained trajectories were downloaded and converted to all-atom trajectories using cg2all³². All data was obtained in January 2024. For each trajectory, the first 20% of frames were discarded (except for IDRome, where the first 10 frames were excluded as described in the original paper²⁴). All frames were aligned to the first frame based on Cα atoms using MDTraj⁵⁷, and trajectories of the same protein were merged.

Feature extraction from MD trajectories

GetContacts (https://getcontacts.github.io) was used to extract nine types of interactions from MD trajectories: backbone-to-backbone hydrogen bonds, side-chain-to-backbone hydrogen bonds, side-chain-to-side-chain hydrogen bonds, salt bridges, Pi-cation, Pi-stacking, T-stacking, hydrophobic interactions, and van der Waals interactions. Default definitions of these interactions were used as described in https://getcontacts.github.io/interactions.html. For each residue pair, nine interaction frequencies were calculated, resulting in a matrix with the size of L×L×9 for a protein of length L.

MDTraj⁵⁷ was used to extract residue-level features. Root mean square fluctuations (RMSF) were calculated using mdtraj.rmsf; Eight-class secondary structure was determined using mdtraj.compute_dssp; Surface area per residue was computed using the Shrake-Rupley algorithm (mdtraj.shrake_rupley(mode=‘residue’)), and the mean and standard deviation of surface areas were recorded; For dihedral angles, mdtraj.compute_phi, mdtraj.compute_psi, and mdtraj.compute_chi1 were employed to extract the phi, psi, and chi1 angles, respectively. Dihedral angles across all frames were partitioned into 12 bins (30° intervals), and the percentage of frames falling into each bin was calculated for each residue. Collectively, this yielded a residue-level feature matrix of size L×(1+8+2+3×12) for a protein of length L, the dimension corresponds to RMSF (1), secondary structure (8), surface area (2), and dihedral angle distributions (3×12), respectively.

For the calculation of pairwise residue movement correlations, we first computed the covariance matrix for the x, y, and z coordinates of all Cα atoms:

$$C_{3L}=\frac{1}{p-1}\sum _{i=0}^p\left(X_i-\stackrel{`}{X}\right){\left(X_i-\stackrel{`}{X}\right)}^T$$ (1)

Where p is the number of trajectory frames, X_i represents the positions (x, y, z) of all Cα atoms in frame i, and $\overline{X}$ is the mean position of the Cα atoms over all frames. The matrix C_3L has a dimension of 3L×3L where L is the number of Cα atoms (protein length).

To reduce this 3D covariance matrix to residue level, the trace over the spatial dimensions is taken:

$$C_L=T{r}_{x,y,z}\left(C_{3L}\right)$$ (2)

Here, C_L is the reduced covariance matrix, and the diagonal of C_L corresponds to the squared fluctuation of L residues. The correlation matrix R_L is then computed by normalizing the covariance matrix:

$${\sigma }_i=\sqrt{C_{L,ii}}$$ (3)

$$R_{L,ij}=\frac{C_{L,ij}}{{\sigma }_i{\sigma }_j}$$ (4)

where C_L,ij is the covariance between residues i and j, σ_i and σ_j are their respective standard deviations. This correlation matrix describes the linear relationship between the displacements of residue pairs, independent of their absolute motion magnitude.

Normal mode analysis

For normal mode analysis (NMA), PDB structures in ProteinFlow³⁴ were used. Structures containing sequence gaps or exceeding 5,000 residues were excluded. Terminal missing residues were removed. For the 20230102_stable dataset, MMseqs2⁵⁸ clustering at 90% sequence identity yielded 26,670 representative structures. For the 20231221_sabdab dataset, MMseqs2 clustering at 100% identity resulted in 2,097 structures. Structures of complexes were also used, ‘X’ was added between chains for MMseqs2 clustering.

NMA was conducted using the Gaussian Network Model (GNM)²⁷ and the Anisotropic Network Model (ANM)²⁸, both implemented in ProDy³³. These models represent macromolecules as elastic node-and-spring networks, where Cα atoms serve as nodes, and springs connect residues within a defined cutoff distance. A distance-dependent spring force constant was applied as in ProDy website (http://www.bahargroup.org/prody/tutorials/enm_analysis/gamma.html): for Cα atoms 10–15 Å apart, a unit force constant was used; for atoms 4–10 Å apart, a force constant twice as strong was used; and for atoms within 4 Å (i.e., connected residue pairs), a force constant 10 times stronger was employed. GNM, which models isotropic motion, was used to compute residue-level features, while ANM, which captures anisotropic motion, was employed to calculate pairwise features.

After building the elastic network (Kirchhoff matrix for GNM or Hessian matrix for ANM), normal modes were computed by eigenvalue decomposition. Eigenvalues (λ_m) and eigenvectors (v_m) were used to describe the collective motions of residues in mode m. The individual contribution of each mode is the proportion of the inverse eigenvalue to all modes:

$$\frac{1/{\lambda }_m}{{\sum }_{k=1}^{M}1/{\lambda }_k}$$ (5)

Where M is the number of total modes (L-1 for GNM and 3L-6 for ANM, L is protein length). Modes of GNM and ANM were first ranked by contribution, then partitioned into three ranges separately. The ranges were selected such that the first set of modes accounts for ~33% of the dynamics, the second set for ~33–66%, and the final set for ~66–100%. This ensures that the slow, intermediate, and fast modes are separated.

For each set of modes, the mean-square fluctuation (MSF) of each residue was calculated from GNM modes as:

$${\text{MSF}}_i=\sum _m\frac{v_{\mathit{\text{mi}}}^2}{{\lambda }_m}$$ (6)

Where v_mi is the eigenvector component corresponding to mode m and residue i, and λ_m is the corresponding eigenvalue. This calculation was repeated for three mode ranges.

The residue covariance matrix was calculated using ANM modes. Firstly, the covariance matrix with the size of 3L×3L was first computed as:

$$C_{3L}=V{\Lambda }^{-1}{V}^T$$ (7)

Where V is the matrix of eigenvectors and Λ⁻¹ is the inverse diagonal matrix of eigenvalues. To reduce the 3D covariance matrix to the residue-level, we used the same method as described in the calculation of pairwise residue movement correlations (equation 2–4). Readers can also read the paper⁵⁹ for the calculation of pairwise correlation in NMA.

SeqDance model architecture

SeqDance is a transformer encoder based on the ESM2⁷ architecture of 35 million parameters, using the same sequence tokenizer. All parameters were randomly initialized as described in the paper⁷. ESM2 weights were not used to avoid incorporating conservation information implicitly. The model consists of 12 layers with 20 attention heads each and employs rotational positional embeddings. The final embedding dimension is 480. A linear layer is added to predict residue-level features from the final residue embedding. For pairwise feature prediction, we compute pairwise embeddings from residue embeddings as:

$$P_{ij}=W_1{E}_i+W_2{E}_j$$ (8)

where E_i and E_j represent the final residue embeddings of residues i and j, and W₁ and W₂ are learnable transformation matrices. The pairwise embeddings P_ij, along with attention values from 240 attention heads, are passed through a linear layer to predict pairwise features.

Pre-training procedure

The model was implemented and trained using PyTorch⁶⁰ (version 2.2.0). SeqDance was pre-trained on over 95% of all data, and randomly selected 600 proteinflow³⁴ PDB structures, 500 IDRome trajectories, 75 ATLAS trajectories, 25 GPCRmd trajectories, and 20 PED ensembles were held out for evaluation. The batch size was set to 72, and parameters were updated every 10 batches: one batch from high-resolution data, four batches from IDRome, four batches from the 20230102_stable dataset, and one batch from the 20231221_sabdab dataset. Different weights were assigned to training data from different sources in the loss function, after adjustments to the batch numbers, considering the different resolutions and relative confidences: 0.5 for high-resolution data, 0.2 for IDRome, and 0.2 for NMA data. Due to limited computational resources, we did not experiment with adjusting the batch size or the weights assigned to different data sources.

The model was optimized using the AdamW optimizer, with a peak learning rate of 1×10⁻⁴, an epsilon value of 1×10⁻⁸, and betas of (0.9, 0.98). A weight decay of 0.01 was applied, and the learning rate followed a schedule with 5,000 warm-up steps, followed by a linear decay to 1×10⁻⁵. A dropout rate of 0.1 was applied, and the maximum input sequence length was set to 512. For sequences longer than this, random peptides of 512 residues were selected in each epoch. Training lasted for a total of 200,000 updates, for ten days, using six Nvidia A6000 GPUs.

Loss function

Mean squared error (MSE) was used as the loss function for SeqDance pre-training. For secondary structure and dihedral angles, where the values for each feature sum to one, the predicted values were first passed through a softmax function to ensure they sum to one before calculating the MSE. The loss for pairwise interaction frequency was calculated as:

$$L_{\mathit{\text{interaction}}}=\frac{1}{2}\left(\text{MSE}(p-f\mid f=0)+\text{MSE}\left(p-f^{1/3}\mid f>0\right)\right)$$ (9)

Where p is the prediction from SeqDance and f is the interaction frequency. As most interaction frequencies are zero, we balanced the MSEs for interacting and non-interacting pairs. Additionally, some interacting pairs exhibit interaction frequencies close to zero, which are biologically meaningful but are treated similarly to zero in the MSE. To address this, we applied the transformation f^1/3 to scale up low-frequency interactions.

SeqDance was pre-trained on multiple tasks of varying scales. To balance the losses across these tasks, we first used a baseline model that predicts the mean value for each feature of each protein to calculate the training set losses. These baseline losses were then employed to adjust the weights for each task. Since pairwise features are more abundant than residue-level features, we set the pairwise-to-residue loss ratio at 4:1. The loss weights for solvent accessible surface area (SASA), root mean square fluctuation (RMSF), secondary structure, and dihedral angles were set to be equal. Additionally, the cumulative loss for nine interaction features was balanced against the pairwise correlation loss, maintaining a 4:1 ratio. Due to limited computational resources, we did not experiment further with adjusting these ratios.

Evaluation of attention map

For the evaluation of attention maps, we selected the top 10 attention heads based on their weights from the pairwise feature prediction layer (Supplementary Figure 1A). To compute the sequence identity of the held-out sequences compared to the training set, we used MMseqs2 for iterative best-hit identification. The following command was applied: mmseqs search qDB tDB rDB tmp --start-sens 1 --sens-steps 3 -s 7 -a 1. The coverage of the training sequences was calculated based on the held-out proteins.

Evaluation of Conformational Properties for IDRs and Ordered Structures

We analyzed normalized conformational properties from MD trajectories of over 40,000 IDR sequences³⁶. IDRs with a normalized R_g value below 1 were excluded, as they were considered too compact to be truly disordered. Additionally, only IDRs ranging from 32 to 320 residues in length were included, resulting in 18,415 IDRs for downstream analysis. MMseqs2 search was used to identify homologous sequences in SeqDance’s training set as in the evaluation of attention map. IDRs with over 20% sequence identity (at least 60% coverage) to any SeqDance training sequence were removed to further assess SeqDance’s performance on dissimilar sequences.

R_g values for PDB structures were downloaded from the paper³⁷, and normalized as described in the paper³⁷:

$$\mathit{\text{normalized}}{R}_g=\frac{R_g}{L^{0.4}}$$ (10)

Where L is the sequence length.

For both IDRs and ordered structures, MMseqs2 easy-cluster was used to cluster sequences for supervised learning with parameters: --min-seq-id 0.2 -c 0.6 --cov-mode 0. Sequences from 60% of randomly selected clusters were used as the training set, and the remaining sequences formed the test set. To ensure a fair comparison, we used the first 200 principal components of the embedding from each method. Linear regression (sklearn.linear_model.LinearRegression with default parameters) was applied to predict conformational properties. This process was repeated five times, and the mean values of the evaluation metrics were reported to assess the model’s performance.

Evaluation of protein folding stability dataset

For the evaluation of the protein folding stability dataset³⁸, single-point replacement mutations from the dataset “Tsuboyama2023_Dataset2_Dataset3_20230416.csv” were utilized. Residues with at least 10 mutations that have “ddG_ML” values were used, resulting in a final dataset of 20,955 residues from 412 proteins. The mean value across all mutations was calculated for each residue for evaluation. AlphaFold-predicted structures were downloaded and used as input for both ESM_IF1⁵¹ and GearNet (pre-trained weight in mc_gearnet_edge.pth was used)⁵⁰ models.

A multi-layer perceptron (MLP) with two layers was employed to predict the average mutation effect, utilizing the MLPRegressor from scikit-learn with parameters set to hidden_layer_sizes=(10,) and max_iter=1000. Four-fold cross-validation was conducted to evaluate model performance, with the validation repeated ten times. The predicted values from all ten repeats in random split were saved to calculate the performance for each protein. It should be noted that the performance of individual proteins was not solely based on training and testing within that protein, the training process also included other proteins.

Evaluation of intrinsically disordered regions and phase separation proteins

For the tasks involving intrinsically disordered regions (IDRs), the datasets provided by CAID2⁵² were used for evaluation. For the PDB, NOX, and linker prediction tasks, SeqDance was fine-tuned and validated on DisProt (version: DisProt_2023_12)⁶¹. We removed DisProt entries where the protein appeared in the CAID2 test set or could not be matched to the UniProt sequence. For the binder task, SeqDance was fine-tuned and validated on the training sequences from two methods (MoRFchibi⁶² and DeepDISOBind⁶³) that were also evaluated in CAID2. For fine-tuning, we applied a balanced cross-entropy loss function. The peak learning rate was set to 1×10⁻⁴, with a warm-up phase of 1,000 steps and a dropout rate of 0.3. Model weights were saved every 100 steps, and the best model based on validation set performance was used for evaluation.

For the tasks of predicting phase-separating proteins (PSPs), the dataset from the paper⁵⁵ was used, and separate models were trained and tested for noIDR-PSP and IDR-PSP categories. Two-fold random negative protein samples were used. The XGBoost Python package (https://xgboost.readthedocs.io/) was used for training the models. The following parameters were applied: the objective function was set to binary logistic classification (objective: binary:logistic), the maximum tree depth was set to 3 (max_depth: 3), the learning rate was 0.3 (eta: 0.3), and the evaluation metric was the area under the curve (AUC) (eval_metric: auc). The models were trained for 100 boosting rounds (num_round: 100).

Figure 6. SeqDance augmented structure and sequence-based features in predicting phase-separating proteins.

A-D. Performances for predicting intrinsically disordered phase-separating proteins (IDR-PSPs) and non-intrinsically disordered phase-separating proteins (noIDR-PSPs) using PhaSePred or SSUP as input, either alone or combined with SeqDance embeddings. The results presented are the averages of ten independent repeats.

Data and code availability

All the training data and evaluation data are publicly available. Codes used in model training and analysis can be found at GitHub: https://github.com/ShenLab/SeqDance, we also provide the pre-trained weight at https://zenodo.org/records/13909695.