Extreme dynamics in a biomolecular condensate

Abstract

Proteins and nucleic acids can phase-separate in the cell to form concentrated biomolecular condensates(Gibson et al. 2019; Gibbs and Kriwacki 2018; Shin and Brangwynne 2017; Banani et al. 2017). Their functions span many length scales: Condensates modulate interactions and chemical reactions at the molecular scale(Nakashima, Vibhute, and Spruijt 2019), organize biochemical processes at the mesoscale(Snead and Gladfelter 2019), and compartmentalize cells(Banani et al. 2017). Understanding the underlying mechanisms will require detailed knowledge of the rich dynamics across these scales(Lyon, Peeples, and Rosen 2021). The mesoscopic dynamics of biomolecular condensates have been extensively characterized(Alshareedah, Kaur, and Banerjee 2021), but the behavior at the molecular scale has remained more elusive. Here, as an example of biomolecular phase separation, we study coacervates of two highly and oppositely charged disordered human proteins(Borgia et al. 2018). Their dense phase is 1000 times more concentrated than the dilute phase, and the resulting percolated interaction network(Farag et al. 2022) leads to a bulk viscosity 300 times greater than that of water. However, single-molecule spectroscopy optimized for measurements within individual droplets reveals that at the molecular scale, the disordered proteins remain exceedingly dynamic, with their chain configurations interconverting on sub-microsecond timescales. Massive all-atom molecular-dynamics simulations reproduce the experimental observations and explain this apparent discrepancy: The underlying interactions between individual charged side chains are remarkably short-lived and exchange on a pico- to nanosecond timescale. Our results suggest that, despite the high macroscopic viscosity of phase-separated systems, local biomolecular rearrangements required for efficient reactions at the molecular scale can remain rapid.

Biological macromolecules in the cell can form assemblies where high local concentrations of proteins and nucleic acids accumulate in biomolecular condensates(Shin and Brangwynne 2017; Banani et al. 2017). Condensates play a key role in cellular processes operating at different scales, such as ribosome assembly, RNA splicing, stress response, mitosis, and chromatin organization(Gibson et al. 2019; Gibbs and Kriwacki 2018), and they are involved in a range of diseases(Shin and Brangwynne 2017; Vendruscolo and Fuxreiter 2022). An essential driving force for the underlying phase separation is the multivalency of binding domains or motifs in the participating proteins. Such interactions are particularly prevalent for intrinsically disordered proteins (IDPs), which either lack a well-defined three-dimensional structure or contain large disordered regions that can mediate interactions with multiple binding partners(Toretsky and Wright 2014; Brangwynne, Tompa, and Pappu 2015; Ruff, Pappu, and Holehouse 2019; Dignon, Best, and Mittal 2020). However, the dynamic disorder in these viscoelastic assemblies have rendered it challenging to perform molecular-scale investigations of their dynamical properties. NMR spectroscopy has provided evidence that IDPs can retain their disorder and backbone dynamics on the pico- to nanosecond timescale in condensates(Murthy and Fawzi 2020; Ahmed and Forman-Kay 2022), but most experimental information related to condensate dynamics has been limited to translational diffusion and mesoscopic physical properties, such as viscosity and surface tension(Alberti, Gladfelter, and Mittag 2019; Wei et al. 2017; Jawerth et al. 2020; Alshareedah, Kaur, and Banerjee 2021).

To extend our understanding beyond the mesoscopic level, we probe the dynamics within a biomolecular condensate at the molecular scale using a combination of single-molecule spectroscopy and large-scale all-atom explicit-solvent molecular dynamics (MD) simulations. Single-molecule Förster resonance energy transfer (FRET) and nanosecond fluorescence correlation spectroscopy provide a unique opportunity to obtain experimental information on intramolecular distance distributions on nanometer length scales and associated dynamics down to nanosecond timescales(Nasir et al. 2019; Mazal and Haran 2019; Lerner et al. 2021; Schuler et al. 2016). MD simulations validated with such experimental data can provide atomistic insight into the molecular conformations, dynamics, and interactions underlying the properties of biomolecular condensates(Dignon, Best, and Mittal 2020; Ruff, Pappu, and Holehouse 2019).

Here we investigate coacervates of two highly and oppositely charged intrinsically disordered human proteins, histone H1 (net charge +53) and its nuclear chaperone, prothymosin α (ProTα, net charge −44). In dilute solution, these two IDPs form dimers with picomolar affinity, although they fully retain their structural disorder, long-range flexibility, and highly dynamic character when bound to each other(Borgia et al. 2018; Schuler et al. 2020) (Fig. 1a). Both proteins modulate chromatin condensation; they are involved in transcriptional regulation(Heidarsson et al. 2022; Gibson et al. 2019; Gibbs and Kriwacki 2018); and condensates of H1 are present in the nucleus(Shakya et al. 2020). At high protein concentrations, solutions of ProTα and H1 can exhibit phase separation into a dilute phase and a protein-rich and viscous dense phase. We find that the individual IDPs retain rapid chain dynamics on the hundreds-of-nanoseconds timescale, remarkably close to their behavior in the dilute phase, despite the high bulk viscosity of the dense phase. These rapid dynamics enable a direct comparison with large-scale MD simulations of ProTα-H1 condensates, which reveal the origin of the similarity: The electrostatic interactions between the IDPs are highly transient both in the dilute and the dense phase and on average involve a similar number of contacts. The resulting dynamic network reconciles slow translational diffusion with rapid conformational dynamics and intermolecular interactions, a behavior that may enable the occurrence of fast local processes and exchange of binding partners even in dense biomolecular condensates.

Fig. 1. Mesoscopic and microscopic properties of ProTα-H1 droplets.

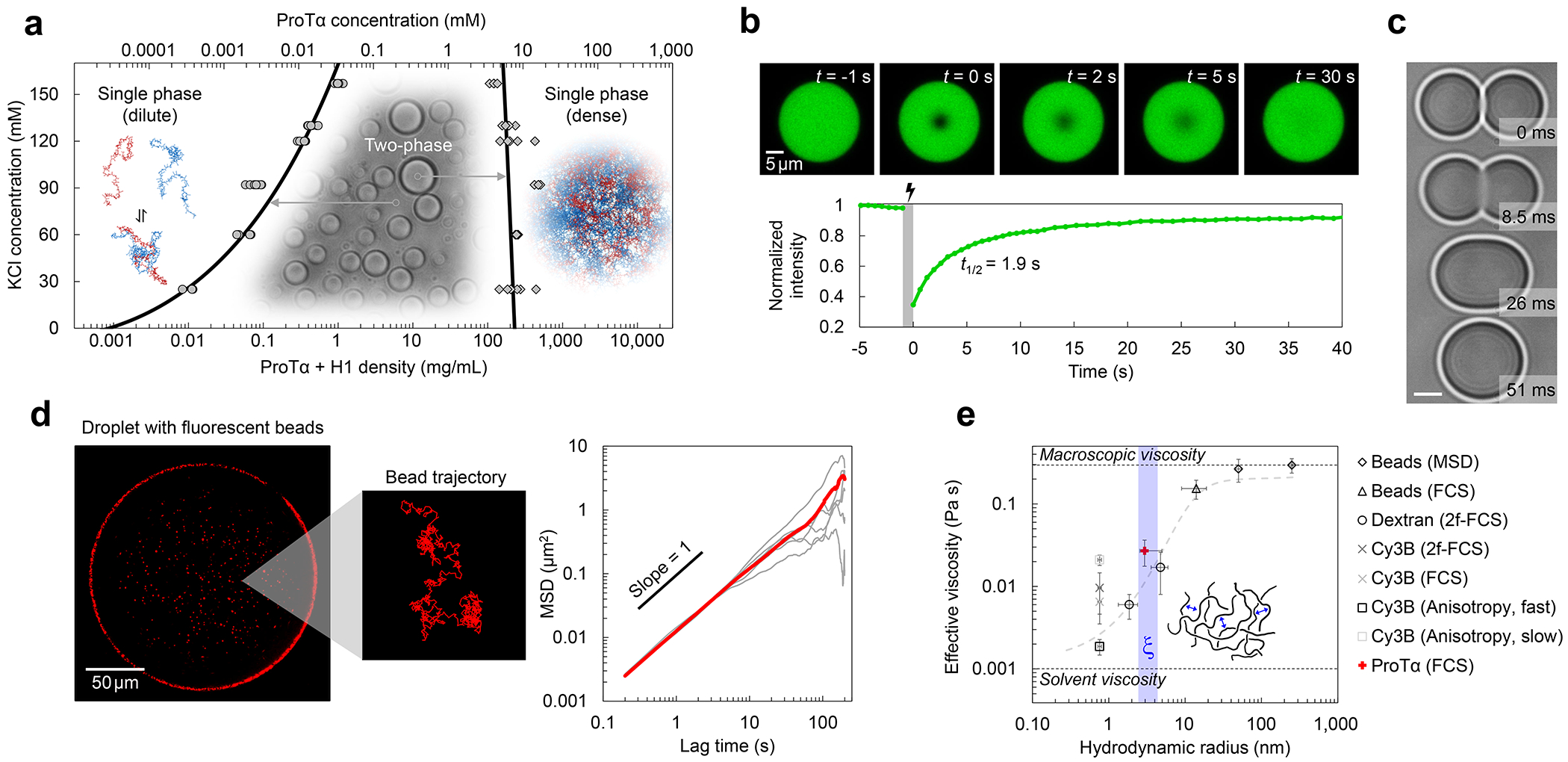
a, Phase diagram from coexistence measurements of dense and dilute phase as a function of salt concentration (each condition n ≥ 3). The total protein density (bottom axis) is based on the measured ProTα concentrations (top axis) and the charge-balanced 1.2:1 ratio at which ProTα and H1 were mixed (Extended Data Fig. 1a). Phenomenological fit with a binodal curve based on Voorn-Overbeek theory(Lin et al. 2019) (solid line). Structural representations of ProTα and H1 are depicted in red and blue, respectively. b, Fluorescence recovery after photobleaching the center of a droplet doped with labeled ProTα. c, Time series of two droplets fusing (scale bar 2 μm; Extended Data Fig. 1c). d, (left) Fluorescence image and representative trajectory of a bead (500 nm diameter) diffusing in a droplet. (right) Mean squared displacement (MSD) from five representative trajectories (gray) and their average (red). e, Probe-size-dependent effective viscosity from measurements of rotational (Extended Data Fig. 3i,j) and/or translational diffusion of Cy3B, dextran, ProTα, and polystyrene beads within droplets using particle tracking (MSD, see d), time-resolved fluorescence anisotropy (Extended Data Fig. 3i,j), single-focus fluorescence correlation spectroscopy (FCS), or two-focus FCS (2f-FCS). The shaded band indicates the range estimated for the correlation length, ξ, in the dense phase. The dashed line shows the dependence expected from the theory of depletion interactions(Tuinier, Dhont, and Fan 2006). Data presented as mean values (n = 20 different beads for tracking, n = 3 different droplets for FCS). Averages and error bars for hydrodynamic radii from the providers or the literature (see Methods); effective viscosity: standard error of the fit for anisotropy; standard deviations for nanorheology and FCS. See Methods for details, the range shown for ξ, and hydrodynamic radius of ProTα. All measurements except a were performed in TEK buffer at 120 mM KCl (ionic strength 128 mM).

ProTα and H1 form viscous droplets

The strong electrostatic interactions between ProTα and H1(Borgia et al. 2018; Sottini et al. 2020) can lead to complex coacervation, as observed for other highly charged biological and synthetic polyelectrolytes(Brangwynne, Tompa, and Pappu 2015; Srivastava and Tirrell 2016; Rumyantsev, Jackson, and de Pablo 2021; Schuler et al. 2020). At sufficiently high protein concentrations, and favored by low salt concentration, mixtures of the two proteins separate into two phases (Fig. 1a, Extended Data Fig. 1a): a dilute phase, where heterodimers between ProTα and H1 dominate(Borgia et al. 2018; Sottini et al. 2020) (Extended Data Fig. 2), and droplets of a dense phase consisting of a total protein mass fraction of ^~20%, similar to other biomolecular condensates(Fisher and Elbaum-Garfinkle 2020; Martin et al. 2020). Since phase separation is most pronounced when ProTα and H1 are present at a ratio of 1.2:1 (Extended Data Fig. 1a), where their charges balance, we investigated their phase behavior in mixtures with this stoichiometry. A strong influence of the salt concentration is evident from the phase diagram (Fig. 1a): The protein concentration in the dense phase depends only weakly on KCl concentration, but the protein concentration in the dilute phase increases from nanomolar at low salt to tens of micromolar at the highest KCl concentrations where we observed phase separation. However, the dependence of the dilute-phase protein concentration on ionic strength is much less steep than that of the ProTα-H1 affinity in the heterodimer(Borgia et al. 2018; Sottini et al. 2020), indicating that less ions are released(Record, Anderson, and Lohman 1978) and thus only few additional inter-chain charge interactions formed upon transfer of a dimer to the dense phase (Extended Data Fig. 1b). We use buffer conditions with 120 mM KCl (total ionic strength 128 mM) for all further experiments (see Methods). To probe the translational diffusion of protein molecules inside the droplets, we employed fluorescence recovery after photobleaching (FRAP) on a sample doped with nanomolar concentrations of fluorescently labeled ProTα. Bleaching with a confocal laser spot in the dense phase results in recovery within a few seconds (Fig. 1b), reflecting the rapid motion of ProTα within the condensate. Furthermore, the proportionality between the millisecond fusion times of the droplets (Fig. 1c) and their radii indicates that the dense phase can be approximated as a viscous fluid(Alshareedah, Kaur, and Banerjee 2021) (Extended Data Fig. 1c).

To further characterize the viscosity of the dense phase, we employed nanorheology and monitored particle diffusion inside the droplets. From the mean squared displacement of fluorescent beads (Fig. 1d), we obtained a viscosity of 0.30 ± 0.06 Pa s according to the Stokes-Einstein relation (see Methods). The inferred bulk viscosity of the ProTα-H1 coacervates is thus ~300 times higher than that of water, and within the range of dense-phase viscosities of other biomolecular condensates(Jawerth et al. 2020; Wei et al. 2017; Wang et al. 2021; Fisher and Elbaum-Garfinkle 2020). For complex fluids like coacervates, the viscosity inferred in this way is expected to depend on the size of the diffusing probe relative to the correlation length(Tuinier, Dhont, and Fan 2006; Wei et al. 2017), ξ (~2.4–4.3 nm, see Methods), which is related to the effective mesh size of the underlying polymer network(Wei et al. 2017; Rubinstein and Colby 2003) and results from a confluence of excluded-volume, hydrodynamic, and electrostatic interactions(Muthukumar 2023; Muthukumar 1997). We thus employed probe particles with hydrodynamic radii between ~1 and 250 nm, ranging from the fluorophore Cy3B and labeled dextran of different molecular masses to fluorescent beads of different radii. We assessed rotational diffusion with time-resolved fluorescence anisotropy (Extended Data Fig. 3j), and translational diffusion with fluorescence correlation spectroscopy (FCS) or bead tracking. Across this size range, we indeed observed a pronounced change in effective viscosity from ~0.002 Pa s to ~0.30 Pa s, with a transition near ξ (Fig. 1e). Diffusion of molecules smaller than ξ is hardly affected by the dense solution of interacting IDP chains, whereas the motion of particles larger than ξ is strongly hindered and dominated by the bulk viscosity of the droplet. The self-diffusion of ProTα in the droplets is slower than the diffusion of similar-sized dextran, as expected from its attractive interactions with H1 in the network. In summary, ProTα and H1 exhibit liquid-liquid phase separation with a dense-phase viscosity more than two orders of magnitude greater than that of the dilute phase. How is this large viscosity reflected in the structure and dynamics of the IDPs making up the coacervate?

Rapid dynamics in the dense phase

To investigate the behavior of individual protein molecules within the droplets, we doped the solution of unlabeled ProTα and H1 with picomolar concentrations of ProTα labeled with Cy3B as a FRET donor and CF660R as an acceptor at positions 56 and 110 (ProTαC). Confocal single-molecule FRET experiments allowed us to probe the conformations and dynamics of ProTα both in the dilute and in the dense phase (Fig. 2a–e). The mean transfer efficiency, $\langle E\rangle$, reports on intramolecular distances and distance distributions(Schuler et al. 2016). Owing to efficient mutual screening of the two highly charged IDPs, ProTα is more compact when bound to H1 in the heterodimer $({\langle E\rangle }_{PH}=0.55\pm 0.03)$ than in isolation $({\langle E\rangle }_P=0.55\pm 0.03)$ (Sottini et al. 2020; Borgia et al. 2018) (Fig. 2f). The dimer is the dominant population in the dilute phase (Extended Data Fig. 2), as expected from the corresponding protein concentrations(Sottini et al. 2020) (Fig. 1a). In the dense phase, we obtained values of $\langle E\rangle$ intermediate between these two values (Fig. 2f), indicating that ProTα is more expanded than in the dimer with H1, but more compact than in isolation.

Fig. 2. Single-molecule spectroscopy in the dilute and dense phases.

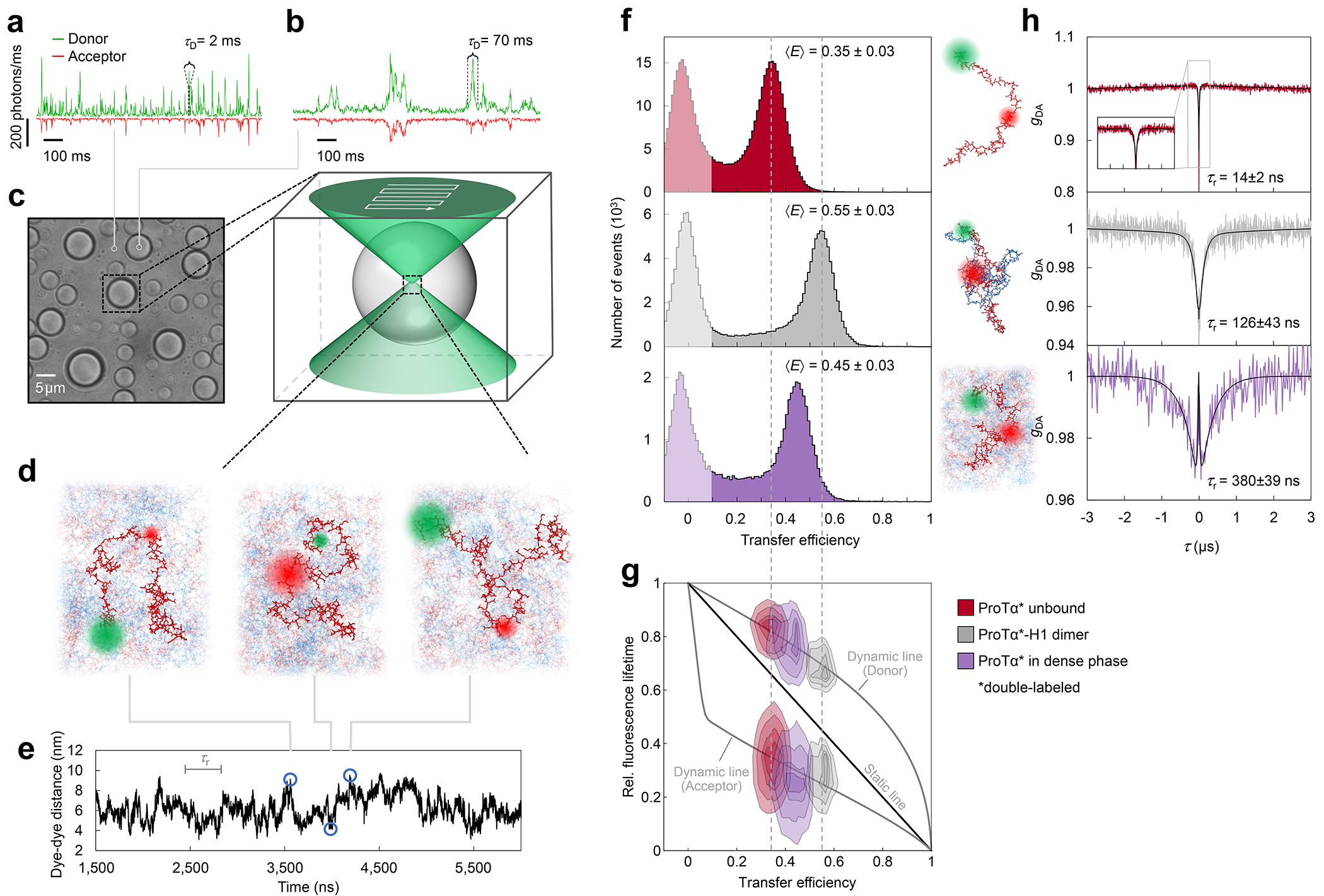
a, Photon time traces in the dilute phase (100 μW laser power) and b, in the ProTα-H1 droplets (30 μW laser power in scanning mode, see c) doped with picomolar concentrations of double-labeled ProTα. c, Single-molecule measurements were performed by positioning the confocal volume in the dilute phase or inside droplets that are stationary at the bottom of the sample chamber. d, Configurations of double-labeled ProTα (red) in the dense phase rapidly sampling different dye-dye distances, with FRET efficiency-dependent fluorescence illustrated in red and green along with a molecular trajectory from MD simulations (e). The scale bar indicates the magnitude of the reconfiguration time, τ_r, in the dense phase. f, Single-molecule transfer efficiency histograms of ProTαC (ProTα labeled at positions 56 and 110) as a monomer in solution (top), in the heterodimer with H1 (middle), and within droplets (bottom, continuous-wave excitation with scanning, see c). Uncertainties represent the accuracy due to instrument calibration (see Methods). g, 2D histograms of relative donor and acceptor fluorescence lifetimes versus transfer efficiency(Schuler et al. 2016) for all detected bursts (pulsed excitation). The straight line shows the dependence for fluorophores at a fixed distance; curved lines show the dependences for broad distance distributions (self-avoiding walk polymer(Zheng et al. 2018), see Methods; upper line: donor lifetime; lower line: acceptor lifetime). h, Nanosecond fluorescence correlation spectroscopy probing chain dynamics in double-labeled ProTαC free (top), in the ProTα-H1 dimer (middle), and in the dense phase (bottom); data are donor–acceptor fluorescence cross-correlations with fits (black lines, see Extended Data Fig. 5) normalized to 1 at their respective values at 3 μs to facilitate direct comparison. Resulting reconfiguration times, τ_r, are averages of three independent measurements (fits and uncertainties discussed in Methods). All measurements were performed in TEK buffer at 120 mM KCl (ionic strength 128 mM).

The analysis of fluorescence lifetimes from time-correlated single-photon counting demonstrates the presence of broad distance distributions in all three cases (Fig. 2g), as expected if the proteins remain disordered(Schuler et al. 2016), as shown for other systems by NMR(Ahmed and Forman-Kay 2022; Aznauryan et al. 2016; Murthy and Fawzi 2020). Similar results were obtained for ProTα labeled at positions 2 and 56 (ProTαN, Extended Data Fig. 4). Based on the single-molecule measurements, we infer average end-to-end distances(Zheng et al. 2018) of 10.9 ± 0.5 nm, 9.2 ± 0.5 nm, and 9.4 ± 0.3 nm for ProTα alone, in the heterodimer, and in the droplet, respectively (see Methods for details). Especially the expansion of the C-terminal segment of ProTα relative to the dimer is suggestive of ProTα interacting with multiple H1 molecules simultaneously in the dense phase. The dimensions of ProTα in the droplet are in the same range as the correlation length in the dense phase (Fig. 1e), indicating that the proteins within the droplets form a semidilute solution in which the chains can overlap but are not entangled(Rubinstein and Colby 2003; Brady et al. 2017).

ProTα samples broad intramolecular distance distributions (Fig. 2g), but on which timescale do its conformations interconvert? We can probe these long-range chain reconfiguration times, τ_r, in single-molecule FRET experiments combined with nanosecond FCS (nsFCS, Fig. 2h): Fluctuations in inter-dye distance cause fluctuations in the intensity of donor and acceptor emission, which can be quantified by correlating the fluorescence signal(Schuler et al. 2016). Based on this approach, we measured τ_r = 14 ± 2 ns for unbound ProTα(Soranno et al. 2012) and τ_r = 126 ± 43 ns in the ProTα-H1 dimer, as previously observed(Borgia et al. 2018). To enable such measurements in the dense phase, we used longer-wavelength dyes compared to previously published work(Borgia et al. 2018; Sottini et al. 2020) to reduce background caused by autofluorescence, and we combined nsFCS with sample scanning (Fig. 2c) to compensate for bleaching losses owing to the slow translational diffusion of the molecules in the droplets (Extended Data Fig. 5). The resulting correlation functions yielded τ_r = 380 ± 39 ns, only a factor of ~3 slower than the corresponding dynamics in the dimer, although the bulk viscosity in the droplets is ~300 times greater than in the dilute phase (Fig. 1e). Even if we consider the length-scale dependence of effective viscosity (Fig. 1e), a large discrepancy remains between the relative slowdown of translation diffusion and chain dynamics. In summary, single-molecule FRET thus reveals a more expanded average conformation of disordered ProTα in the dense phase compared to the dimer and remarkably rapid intrachain dynamics. To elucidate the molecular origin of this behavior, we turned to MD simulations.

Interaction dynamics from simulations

Since we aim to compare absolute timescales with experiment, we require all-atom molecular dynamics simulations with explicit solvent. In view of the experimentally determined reconfiguration timescale of ~380 ns for protein chains in the dense phase, a direct comparison is within reach. We thus performed large-scale simulations of a dense phase consisting of 96 ProTα and 80 H1 molecules (ensuring charge neutrality) in a slab configuration(Zheng et al. 2020) with 128 mM KCl, corresponding to ~4 million atoms in the simulation box (Fig. 3a). We employed the Amber ff99SBws force field(Best, Zheng, and Mittal 2014) with the TIP4P/2005s water model(Abascal and Vega 2005), a combination that has previously performed well in IDP and condensate simulations(Zheng et al. 2020; Shea, Best, and Mittal 2021). Based on a total simulation time of ~6 μs (Supplementary Video 1, Supplementary Video 2), and aided by the large number of protein copies in the system, we obtained enough sampling for a meaningful comparison with experimentally accessible quantities. For comparison, we also simulated unbound ProTα and the ProTα-H1 dimer free in solution.

Fig. 3. Large-scale molecular dynamics simulations of ProTα-H1 phase separation.

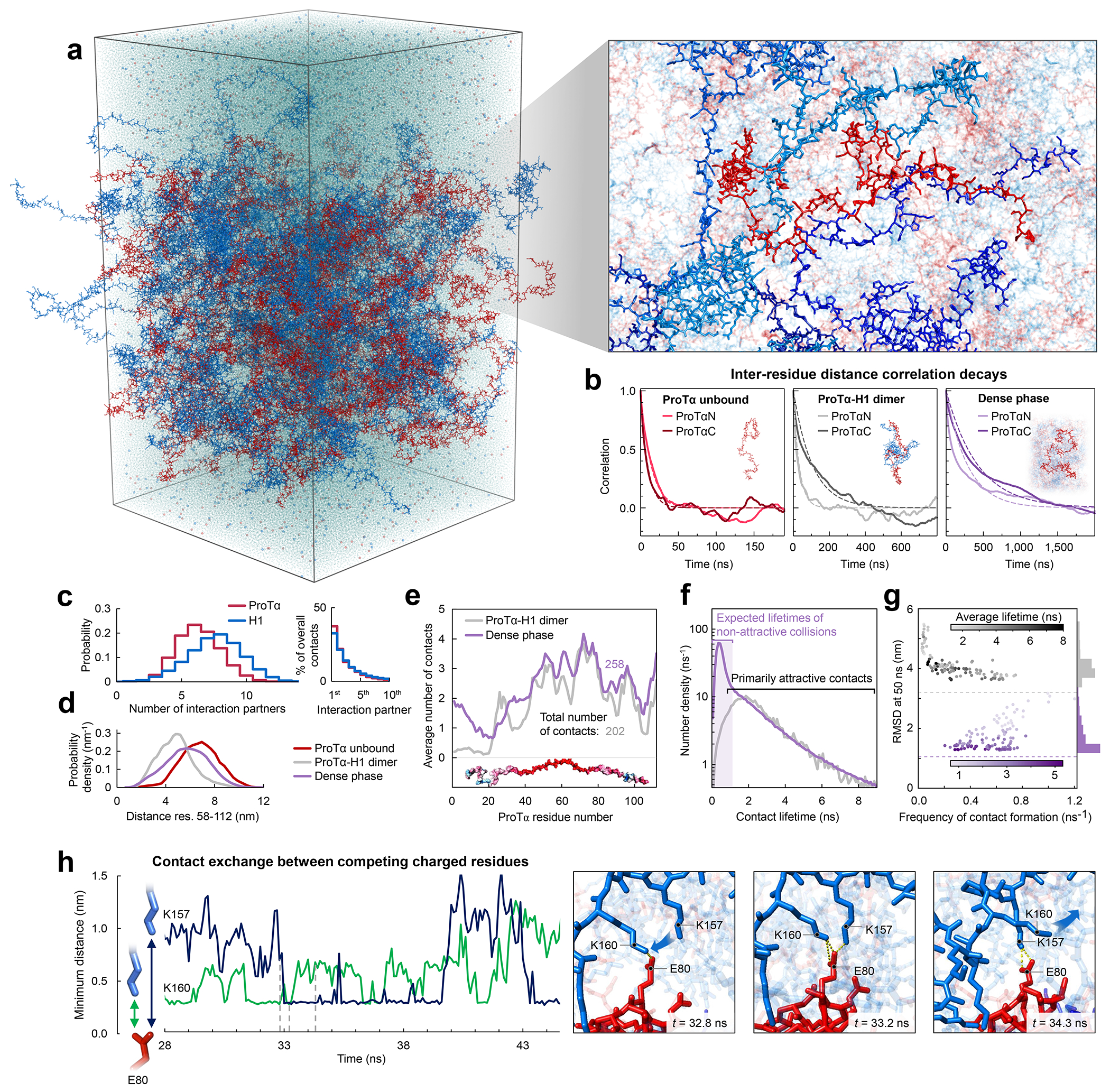
a, All-atom explicit solvent simulation of 96 ProTα (red) and 80 H1 molecules (blue) in slab geometry(Zheng et al. 2020), including water (light blue spheres), K⁺ ions (blue spheres), and Cl⁻ ions (red spheres). The zoom-in highlights a ProTα molecule (red) and four H1 interaction partners (shades of blue, see Supplementary Videos 1–3). b, Time correlation functions of the distance between residues 5 and 58 (ProTαN) and residues 58 and 112 (ProTαC) from simulations of ProTα unbound (left), in the heterodimer (middle), and in the dense phase (right), with single-exponential fits (dashed lines). c, Histograms of the number of H1 molecules simultaneously interacting with a single ProTα (red) and vice versa (blue). Right: Contributions of each interaction partner to the total number of residue-residue contacts. d, Distance distributions between ProTα residues 58 and 112 in the different conditions (see legend). e, Average number of contacts each residue of ProTα makes in the dimer (gray) and dense phase (purple), with the average total number of contacts indicated. Only ~11% of all ProTα contacts in the dense phase are with other ProTα chains. f, Distribution of the lifetimes of contacts made by ProTα in the heterodimer (gray) and the dense phase (purple). Areas under the curves correspond to the total number of new contacts formed per chain in one nanosecond. Shaded band: contact lifetimes expected for non-attractive collisions (see Extended Data Fig. 9a,b). g, Root-mean-square displacement (RMSD) of the 112 individual ProTα residues within 50 ns vs their average frequency of contact formation (color scales: average contact lifetimes; horizontal dashed lines: average RMSD at 50 ns for the center of mass of ProTα in the dimer (gray) and dense phase (purple), a lower bound for the RMSD of the individual residues; numbers of residues with similar RMSD histogrammed on the right). h, Example of rapid exchange between salt bridges in the dense phase, illustrated by two time trajectories of the minimum distance between the residue pairs involved (left) and corresponding snapshots from the simulation (right) (see Supplementary Video 3).

Both the total protein concentration and the translational diffusion coefficient of ProTα in the simulated dense phase are comparable to the experimental values (see Table 1) at the same salt concentration, suggesting that the overall balance of interactions in the simulations is consistent with experiment. Similarly, the average transfer efficiencies of ProTα from the simulations are close to the experimental values (Fig. 2f), both for free ProTα, in the dimer, and in the dense phase (Table 1). Furthermore, as expected from the fluorescence lifetime analysis (Fig. 2g), the intramolecular distance distributions are broad (Fig. 3d). Most remarkably, even the chain dynamics, based on intrachain distance correlation functions (Fig. 3b), are in the same range as the experimental result. Although the distribution of reconfiguration times, τ_r, is wide owing to the remaining limitations(Nuesch et al. 2022) of conformational sampling during the simulation time, the mean value of ~400 ns for ProTαC compares well with experiment and is only a factor of ~4 slower than in the dimer (Fig. 3b, Table 1). Based on this validation by experiment, we examine the simulations for the origin of such rapid chain dynamics despite the large viscosity in the dense phase.

Table 1.

Comparison between observables from experiments (EXP) and simulations (MD) (⟨E⟩: average transfer efficiency; τ_r: reconfiguration time). ProTαN and ProTαC refer to the measurements with FRET dyes on the N-terminal and the C-terminal segments of full-length ProTα, respectively (see Extended Data Table 1). All data are presented as mean values. Experimental protein densities and uncertainties from average, minimum, and maximum values obtained; uncertainties of experimental transfer efficiencies indicate accuracies from instrument calibration; uncertainties of experimental reconfiguration times, diffusion coefficients, and simulated observables are described in Methods.

Sample	Protein density (mg/mL)	ProTα Diffusion coefficient (10−12 m2/s)	ProTαN		ProTαC
			⟨E⟩	τ r	⟨E⟩	τ r
ProTα [EXP]	—	85 ± 9	0.41 ± 0.03	21 ± 2 ns	0.35 ± 0.03	14 ± 2 ns
ProTα [MD]	—	91 ± 7	0.49 ± 0.02	14 ± 4 ns	0.30 ± 0.02	10 ± 3 ns
ProTα-1H dimer [EXP]	—	74 ± 8	0.46 ± 0.03	64 ± 10 ns	0.55 ± 0.03	0.13 ± 0.05 μs
ProTα-1H dimer [MD]	—	71 ± 3	0.48 ± 0.08	32 ± 9 ns	0.65 ± 0.07	0.11 ± 0.03 μs
Dense phase [EXP]	${\text{220}}_{\text{−70}}^{\text{+210}}$	2.7 ± 0.7	0.49 ± 0.03	0.30 ± 0.03 μs	0.45 ± 0.03	0.38 ± 0.04 μs
Dense phase [MD]	290 ± 10	1.8 ± 0.1*	0.51 ± 0.11	0.29 ± 0.07 μs	0.46 ± 0.18	0.4 ± 0.1 μs

^*Finite-size effects from hydrodynamic interactions with periodic images generally reduce the diffusion coefficients in MD simulations(Yeh and Hummer 2004). An approximate analytical correction was applied for ProTα and the ProTα-H1 dimer (see Methods).

As expected from the optimal charge compensation between ProTα and H1 and the large protein concentration in the dense phase, with a mass fraction of ~20% (Extended Data Fig. 6), ProTα and H1 engage in a network of interactions with oppositely charged chains. Each ProTα molecule interacts on average with ~6 H1 molecules simultaneously (Fig. 3c) and is slightly more expanded than in the dimer (Fig. 3d), in line with the measured transfer efficiencies (Fig. 2f). Similarly, each H1 molecule interacts with ~8 ProTα molecules. These intermolecular networking effects are expected to cause the high viscosity observed in the droplets(Rubinstein and Colby 2003) (Fig. 1e), but how can the intramolecular chain dynamics remain so rapid? An important cue comes from the inter-residue contact profiles, which reveal comparable interaction patterns in the heterodimer and in the dense phase (Fig. 3e, Extended Data Fig. 7d), suggesting a remarkable similarity between the local environments experienced by the protein molecules. Indeed, the total number of contacts that a ProTα chain makes in the dense phase is only ~28% greater than in the dimer, mainly due to contributions from the chain termini, which are sparse in charged residues (Fig. 3e). The small number of additional charge interactions formed in the dense phase is consistent with the much weaker salt concentration dependence of the dilute-phase protein concentration (Fig. 1a, Extended Data Fig. 1b) compared to the heterodimer affinity(Borgia et al. 2018; Sottini et al. 2020).

Another important insight comes from the lifetimes of these inter-chain contacts: In contrast to the persistent interactions expected for more specific binding sites, the duration of individual contacts between residues in ProTα and H1 is at most a few nanoseconds (Fig. 3f, Extended Data Figs. 7e, 8), with a median value of 0.9 ns, orders of magnitude shorter than the chain reconfiguration time. Individual contacts thus never become rate-limiting for the motion of the polypeptide chain. The distributions of the longest contact lifetimes, above ~2 ns, are very similar in the heterodimer and the dense phase, but a discrepancy is apparent for very short-lived contacts, which are much more prevalent in the dense phase (Fig. 3f). Many of these events can be attributed to the N-terminus of ProTα, whose fleeting encounters with other proteins in the crowded environment occur on a timescale expected for non-attractive random collisions (Extended Data Fig. 9a,b). Notably, this N-terminal region of ProTα makes hardly any contacts with H1 in the dimer because of its low net charge(Borgia et al. 2018) (Fig. 3e). The lack of specific residue-residue interactions combined with the high concentrations of competing interaction partners in the dense phase can thus lead to rapid exchange between individual contacts (Fig. 3h, Extended Data Fig. 9c). It is worth emphasizing that the total concentration of charged side chains in the dense phase is in the range of 1 M.

Despite the similarity in the local environments and the kinetics of contact formation for the heterodimer and the dense phase, there are also notable differences. In contrast to the simple Brownian translational diffusion of the dimer in the dilute phase, protein molecules in the dense phase exhibit subdiffusion on timescales below the reconfiguration time (Extended Data Fig. 10a), indicating locally correlated dynamics among polymers in the semidilute regime(Guenza 2002). At the level of individual amino acid residues, we observe a broad distribution of mobilities, but on average, residues in the dimer are more mobile than those in the dense phase (Fig. 3g, Extended Data Fig. 7f). Among the residues in the dimer, those that make more contacts tend to be the less mobile, as expected. In the dense phase, however, we observe the opposite behavior, where higher mobility is correlated with a higher frequency of contact formation (Fig. 3g). These contacts are primarily due to the short-lived fleeting collisions of the N-terminal residues, suggesting that they are a byproduct of the high protein density but hardly impede chain motion. In contrast, residues that experience more long-lived contacts exhibit lower mobility and pronounced subdiffusion (Extended Data Fig. 10f). Overall, subdiffusion is much more prominent in the dense phase than in the dimer (Extended Data Fig. 10), reflecting different dynamic regimes of contact formation and chain interactions in the two phases.

Discussion

The combination of our single-molecule experiments with large-scale simulations enables an unprecedented view of the conformational distributions and rapid dynamics of IDPs in a biomolecular condensate. Altogether, the results provide a comprehensive picture of ProTα-H1 coacervates and their complex dynamics across a wide range of length- and timescales (Fig. 4). Proteins take seconds to diffuse across the micron-sized droplets, and milliseconds to diffuse through the confocal detection volume, but at the molecular level, they can exchange their partners and interconvert between different chain conformations in less than 1 μs. The contact dynamics at the Ångström scale are even faster, with individual residues competing for contacts in nanoseconds or less. Correspondingly, at length scales much greater than the mesh size, the condensate appears as a continuous viscous fluid, ~300 times more viscous than water (Fig. 1e). At short length scales, the effective viscosity within the polymer network is lower, which facilitates rapid intra- and intermolecular dynamics. MD simulations validated by their agreement with the experimental data provide an unprecedented atomistic view of the condensate; they point to two main conclusions: As opposed to the dilute phase, which is dominated by one-to-one interactions between ProTα and H1 in the dimer, the dense phase is formed by a network of multivalent interactions between the oppositely charged proteins (Fig. 3c), which causes the large macroscopic viscosity(Rubinstein and Colby 2003). Since each protein contacts on average about 6 to 8 other chains (Fig. 3c, Extended Data Fig. 7c), a system-spanning or percolated network is formed(Farag et al. 2022). At the molecular scale, however, the picture is remarkably dynamic: The dense phase is a semidilute solution in which the proteins remain highly solvated; they rearrange rapidly; and their contacts with other chains exchange quickly and are exceedingly short-lived compared to the global chain reconfiguration dynamics. The resulting average local environment that a protein experiences — within a Bjerrum length of about 1 nm — is strikingly similar in the dense and the dilute phases, and the average number of contacts that a residue makes is dominated by its charge (Fig. 3e).

Fig. 4. The complex hierarchy of length- and timescales in phase-separated droplets.

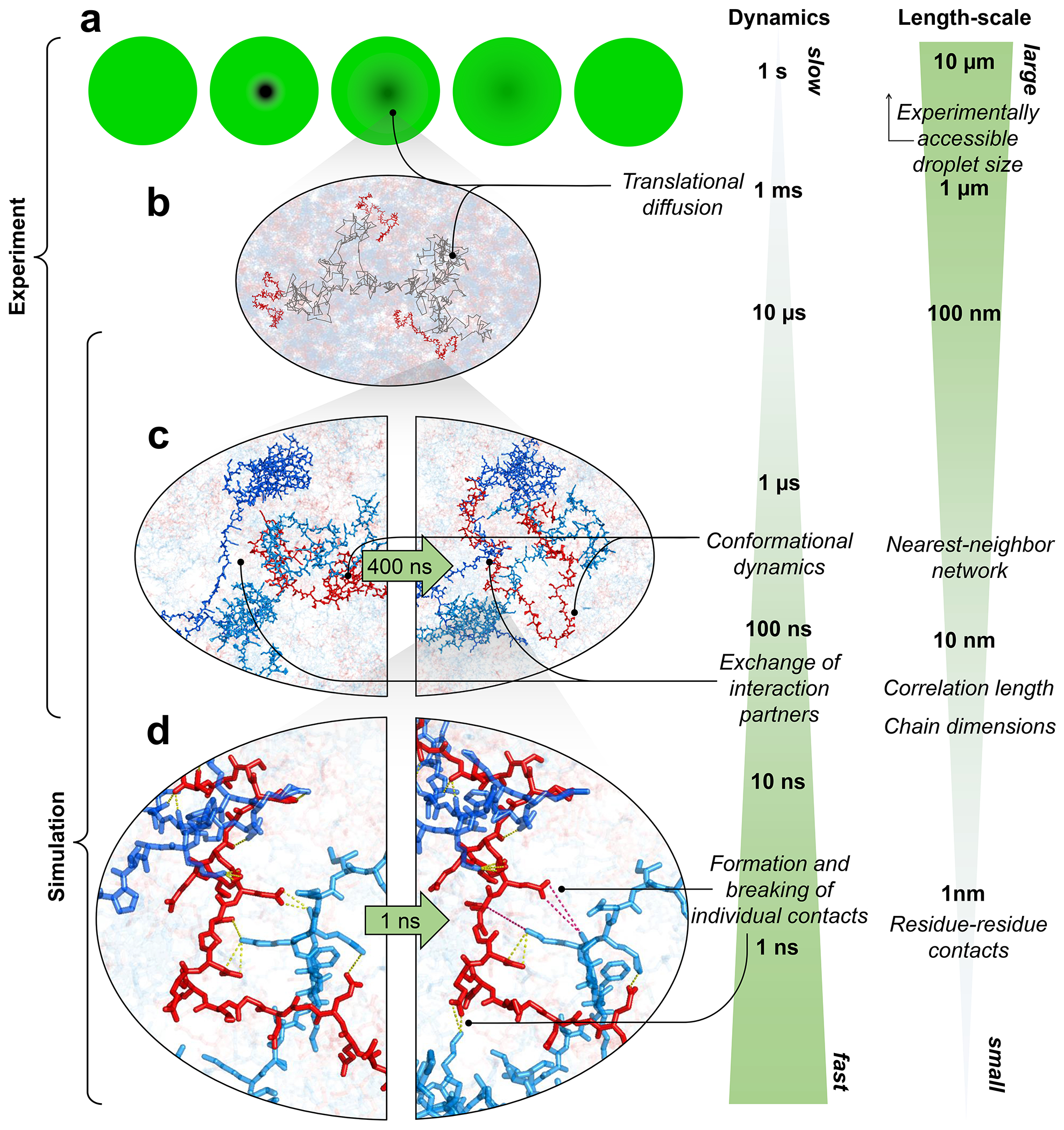
a, Cartoon of a FRAP experiment reflecting (b) translational diffusion of protein molecules inside droplets. c, Chain reconfiguration is linked to the rapid exchange between interaction partners on the submicrosecond timescale. d, Intricate networks of competing contacts among residues exchange in nanoseconds (intact salt bridges with inter-charge distance <0.5 nm shown as yellow dotted lines, broken salt bridges as magenta dotted lines). Images in half oval frames are snapshots of the same view at different times.

The behavior we observe is an example of the subtle balance of intermolecular interactions in biomolecular phase separation: On the one hand, the interactions must be strong enough for the formation of stable condensates; on the other hand, they need to be sufficiently weak to enable translational diffusion and liquid-like dynamics within the dense phase and molecular exchange across the phase boundary — processes that are essential for function, such as biochemical reactions occurring in condensates(Shin and Brangwynne 2017; Banani et al. 2017; Reinkemeier and Lemke 2021). Our results on the two nuclear IDPs ProTα and H1 indicate that charge-driven condensates — of which there are many in the nucleus(Gibson et al. 2019; Gibbs and Kriwacki 2018) — can comprise surprisingly rapid dynamics on molecular length scales by facilitated breaking and forming of contacts. This highly dynamic regime may facilitate the fast exchange between binding partners within condensates even if they have high affinities(Heidarsson et al. 2022; Sottini et al. 2020), and may enable efficient biochemical reactions. Similarly, the kinetics of molecular self-assembly processes that require large rearrangements of the chain, including the formation of amyloid-like structures within condensates(Wen et al. 2021; Vendruscolo and Fuxreiter 2022), may not be strongly hindered by the dense yet liquid-like environment.

The combination of single-molecule spectroscopy in individual droplets with all-atom molecular simulations is a promising strategy for probing the molecular dimensions and dynamics in condensates. The resulting information on long-range intramolecular distances and dynamics from FRET is complementary to the information on local backbone and side chain structure, contacts, and dynamics from NMR spectroscopy(Brady et al. 2017; Murthy and Fawzi 2020; Ahmed and Forman-Kay 2022). The agreement of our experimental results with the simulations indicates that current atomistic force fields are of suitable quality not only for describing isolated IDPs(Shea, Best, and Mittal 2021) but even for their complex multimolecular interactions in condensates(Zheng et al. 2020). The chemical detail and timescales of dynamics available from such experimentally validated simulations ideally complement the computationally less demanding coarse-grained simulations(Bottaro and Lindorff-Larsen 2018; Borgia et al. 2018), which have proven powerful for describing thermodynamic and structural aspects of biomolecular condensates(Ruff, Pappu, and Holehouse 2019; Shea, Best, and Mittal 2021). Single-molecule spectroscopy inside live cells(Koenig et al. 2015) may enable intracellular measurements, e.g. in charge-driven biomolecular condensates in the nucleus(Gibson et al. 2019; Gibbs and Kriwacki 2018). We also note that in spite of a century of research on the complexation of synthetic polyelectrolytes(Srivastava and Tirrell 2016; Rumyantsev, Jackson, and de Pablo 2021) and a growing understanding of the remarkable parallels with disordered biomolecules(Perry 2019; Brangwynne, Tompa, and Pappu 2015; Muthukumar 2023; Schuler et al. 2020), the underlying molecular structures, distributions, and dynamics have been challenging to elucidate. Our approach is likely to be transferrable to synthetic polymers, thus offering a strategy for deciphering the molecular basis of such dense polymeric environments, be it in biology, chemistry, or physics.

Methods

Protein preparation and labeling

Recombinant wild-type human histone H1.0 was used (H1; New England Biolabs M2501S). ProTαC and unlabeled ProTα were prepared as previously described(Sottini et al. 2020); ProTαN cloned into a pBAD-Int-CBD-12His vector was prepared according to a previously described protocol(Chowdhury et al. 2019). Cysteine residues introduced at positions 2 and 56, and 56 and 110, respectively, were used for labeling the protein with fluorescent dyes (see SI Table 1 for all protein sequences). Before labeling the double-Cys variants of ProTα, the proteins in phosphate-buffered saline (PBS), pH 7, 4 M guanidinium hydrochloride (GdmHCl), and 0.2 mM EDTA were reduced with 10 mM Tris(2-carboxyethyl)phosphine hydrochloride (TCEP) for one hour. Subsequently, the buffer was exchanged to PBS pH 7, 4 M GdmHCl, 0.2 TCEP, and 0.2 mM EDTA without TCEP via repeated (5x) buffer exchange using 3-kDa molecular weight cutoff centrifugal concentrators (Sigma-Aldrich). The protein variants were labeled with Cy3B maleimide (Cytiva) and CF660R maleimide (Sigma-Aldrich) using a protein-to-dye ratio of 1:6:6, and incubated for one hour at room temperature and then overnight at 277 K. The excess dye was quenched with 10 mM dithiothreitol for ten minutes and then removed using centrifugal concentrators. The labeled protein was purified by reversed-phase HPLC on a Reprosil Gold C18 column (Dr. Maisch, Germany) without separating labeling permutants. The correct masses of all labeled proteins were confirmed by electrospray ionization mass spectrometry.

Turbidity measurements

Turbidity measurements for assessing the extent of phase separation were performed using a NanoDrop 2000 UV-Vis spectrophotometer (Thermo Scientific). ProTα was added to a fixed volume of an H1 solution to achieve a final concentration of 10 μM H1 and investigate a wide range of ProTα:H1 ratios. The experiments were performed in TEK buffer (10 mM Tris-HCl, 0.1 mM EDTA, pH 7.4, ionic strength adjusted with specified concentrations of KCl). The samples were mixed by rapid pipetting for ~10 s, and relative turbidity was assessed by the attenuation of light at 350 nm. Four measurements were made for every sample, and the attenuance values averaged. Prior to mixing, the stocks of both proteins were diluted in identical buffers.

Single-molecule fluorescence spectroscopy

For confocal single-molecule measurements, concentration determination, and fluorescence correlation spectroscopy (all performed at 295 K), we used a MicroTime 200 (PicoQuant) equipped with an objective (UPlanApo 60×/1.20-W; Olympus) mounted on a piezo stage (P-733.2 and PIFOC; Physik Instrumente GmbH), a 532-nm continuous-wave laser (LaserBoxx LBX-532-50-COL-PP; Oxxius), a 635-nm diode laser (LDH-D-C-635M; PicoQuant), and a supercontinuum fiber laser (EXW-12 SuperK Extreme, NKT Photonics). Florescence photons were separated from scattered laser light with a triple-band mirror (zt405/530/630rpc; Chroma), then separated first into two channels with a polarizing or a 50/50 beam splitter and finally into four detection channels with a dichroic mirror to separate donor and acceptor emission (T635LPXR; Chroma). Donor emission was additionally filtered with an ET585/65m band-pass filter (Chroma) and acceptor emission with an LP647RU long-pass filter (Chroma), followed by detection with SPCM-AQRH-14-TR single-photon avalanche diodes (PerkinElmer). SymPhoTime 64 version 2.4 (PicoQuant) was used for data collection.

For single-molecule measurements, ProTα labeled with Cy3B and CF660R was excited either by the 532-nm continuous-wave laser or by pulsed interleaved excitation(Müller et al. 2005) at 20 MHz using the 635-nm diode laser and the SuperK supercontinuum fiber laser operated with a z532/3 band pass filter (Chroma). Measurements were performed in TEK buffer including 120 mM KCl, resulting in an ionic strength of 128 mM. To avoid the pronounced adhesion of H1 to glass surfaces, plastic sample chambers (μ-Slide, ibidi) were used in all measurements. For single-molecule measurements in the dilute phase, the average power at the back aperture of the objective was 100 μW for 532-nm continuous-wave excitation, and 50 μW for donor and 50 μW for acceptor excitation for pulsed interleaved excitation; the confocal volume was positioned 30 μm inside the sample chamber. Transfer efficiency histograms in the dilute phase were acquired on samples with concentrations of labeled protein between 50 and 100 pM. For single-molecule measurements in the dense phase, the average power at the back aperture of the objective was between 10 and 30 μW for continuous-wave excitation, and 5-15 μW for donor and 5-15 μW for acceptor excitation for pulsed interleaved excitation, depending on the background level; the confocal volume was placed at the center of the spherical droplets, whose radius was between 4 and 15 μm. The samples were prepared by mixing unlabeled proteins (12 μM ProTα and 10 μM H1, charge balanced) doped with 5 to 10 pM of double-labeled ProTα. Bursts of photons emitted by labeled molecules diffusing through the confocal volume positioned in the droplets were identified from background-subtracted fluorescence trajectories binned at 3.5 ms with a threshold of 111 photons per bin. Bursts in dilute conditions were identified as sequences of at least 111 consecutive photons with interphoton times below 40 μs.

Ratiometric transfer efficiencies were obtained from $E=N_A/(N_A+N_D)$, where $N_A$ and $N_D$ are the numbers of donor and acceptor photons, respectively, in each photon burst, corrected for background, channel crosstalk, acceptor direct excitation, differences in quantum yields of the dyes, and detection efficiencies(Schuler 2007; Hellenkamp et al. 2018). From the transfer efficiency histograms, we obtained mean transfer efficiencies, $〈E〉$, from fits with Gaussian peak functions. To infer end-to-end distance distributions, P(r), from $〈E〉$, we use the relation(Schuler et al. 2016)

$$⟨E⟩=⟨\epsilon ⟩\equiv {\int }_0^{\infty }\epsilon (r)P(r)dr,$$ Eq. 1

where

$$\epsilon (r)=R_0^6/(R_0^6+r^6).$$ Eq. 2

The Förster radius, R₀,(Van Der Meer 1994) of 6.0 nm for Cy3B/CF660R in water(Klose et al. 2021) was corrected for the refractive index, n, in the droplets according to the published dependence of n on the protein concentration(Zhao, Brown, and Schuck 2011), which is linear up to a mass fraction of at least 50 %(Barer and Tkaczyk 1954) and only marginally dependent on the type of protein(Zhao, Brown, and Schuck 2011). At 220 mg/mL, n is 3% greater than in water, resulting in R₀ = 5.9 nm inside the droplets. Based on measurements on different instruments and over extended periods of time, we estimate a systematic uncertainty of transfer efficiencies due to instrument calibration and uncertainty in R₀ of ~0.03, similar to the value reported in a recent multi-laboratory benchmark study(Hellenkamp et al. 2018). The precision of repeated measurements performed with the same instrument is much higher, typically with a statistical uncertainty below 0.01(Klose et al. 2021). For P(r), we applied an empirical modification of the self-avoiding-walk polymer model, the SAW-ν model(Zheng et al. 2018). We obtained the length scaling exponent, ν, for the 2-56 and the 56-110 segments of ProTα, taking into account a total dye linker length for both fluorophores of nine amino acids(Aznauryan et al. 2016). In all cases, the value of ν was between 0.58 and 0.64. To estimate the end-to-end distance of the complete ProTα chain, we used the total number of amino acids, N_tot = 110, and the average value of ν obtained for the two segments. Note that fluorophore labeling has previously been shown to have only a small influence on the affinity between ProTα and H1(Borgia et al. 2018; Sottini et al. 2020). Since the fraction of labeled protein in the dense phase is <10⁻⁶, a detectable effect of labeling on the dense-phase behavior is unlikely. Data analysis was performed using the Mathematica version 12.3 (Wolfram Research) package Fretica (https://github.com/SchulerLab).

Protein concentration measurements in the dilute and dense phases

We employed both fluorescence correlation spectroscopy (FCS) and quantitative fluorescence intensity measurements on a MicroTime 200 (PicoQuant) to determine the concentrations of double-labeled ProTα (Cy3B and CF660R at residues 56 and 110) in the dense and dilute phases(Martin et al. 2020). A mixture of unlabeled proteins (12 μM ProTα and 10 μM H1, charge-balanced), doped with a small concentration (~10 pM to 10 nM)(Martin et al. 2020) of labeled ProTα in TEK buffer including the specified concentrations of KCl was allowed to phase-separate at 295 K. For measurements in the dilute phase, the phase-separated mixture was centrifuged at 295 K for 30 mins at 25,000 g, such that the dense phase coalesced into a one large droplet. The supernatant was carefully aspirated and transferred into sample chambers (μ-Slide, ibidi) for microscopy. For measurements in the dense phase, the phase-separated mixture was directly transferred to the sample chambers, and droplets were allowed to settle on the bottom surface of the sample chamber by gravity; the boundaries of individual droplets were identified via 3D confocal imaging, and FCS and intensity measurements were performed by focusing inside the droplets.

CF660R was excited with 635-nm continuous-wave laser light at 5 μW (measured at the back aperture of the objective), and the fluorescence photons were separated with a polarizing beam splitter and recorded on two detectors. Measured correlation functions were fitted with a model for translational diffusion through a 3D Gaussian-shaped confocal volume:

$$G(\tau )=1+G_0{\left[\left(1+\frac{\tau }{{\tau }_D}\right)\sqrt{1+s^2\frac{\tau }{{\tau }_D}}\right]}^{-1},$$ Eq. 3

where τ is the lag time, $G_0$ is the amplitude, τ_D is the translational diffusion time, and s is the ratio of the lateral and axial radii of the confocal volume. N is proportional to the concentration of labeled molecules, which can thus be estimated from FCS based on a calibration curve(Martin et al. 2020). The calibration curve was obtained by measuring samples of known concentrations of labeled ProTα (0.3, 1, 3 10, 30, and 100 nM) in TEK buffer including 120 mM KCl. The laser power used for the measurements was 5 μW (measured at the back aperture of the objective).

The average number of labeled proteins in the confocal volume, N, was obtained from $N={\left(1-\frac{b}{F}\right)}^2/G_0$, as previously described(Martin et al. 2020), where b is the background count rate estimated from samples without labeled protein, F the average count rate of the measurement with labeled ProTα, and N is used for concentration estimation. Similar to N obtained from FCS, the background-subtracted fluorescence intensity given by the mean photon count rates is proportional to protein concentration, and can thus also be used for concentration estimation based on the calibration curve. The total ProTα concentrations in the dense and the dilute phases were obtained by dividing the concentrations of labeled ProTα, measured using FCS or intensity detection, by the known doping ratio. The doping ratio was chosen so that the fluorescence signal from labeled ProTα in the samples was within the linear detection range, which required higher doping ratios for dilute-phase compared to dense-phase measurements. For every condition measured, at least two estimates of concentrations were obtained, one from FCS and one from intensity measurements. In most cases, however, measurements were replicated several times, also with different doping ratios.

As indicated by turbidity measurements, the maximum formation of dense phase occurs at a molar ProTα:H1 ratio of 1.2:1 (Extended Data Fig. 1a), corresponding to charge balance, so all experiments were performed by mixing the two proteins at this ratio, and H1 concentrations were inferred from the ProTα concentrations based on this ratio in both the dilute and the dense phases. We note that cellular concentrations of tens of micromolar have been reported for ProTα(Haritos, Tsolas, and Horecker 1984); the nuclear H1 concentration is commonly assumed to be in the range of the number of nucleosomes per nuclear volume(Alberts 2022) (~0.4 mM), but it is likely that only a fraction of H1 is not bound to chromatin. Since reproducible droplet formation becomes difficult and exceedingly sample-consuming at higher salt concentrations closer to the critical point, we chose to work at an ionic strength of 128 mM (TEK buffer including 120 mM KCl) as a compromise between experimental feasibility and physiologically relevant salt concentrations for all measurements, unless stated explicitly.

Fluorescence recovery after photobleaching (FRAP)

FRAP experiments were performed on a Leica SP8 confocal microscope with an HC PL APO CS2 63×/1.4 NA oil immersion objective. An area of ~1.5 μm² in droplets doped with ~10 nM labeled ProTαC was bleached with a laser beam (530 nm wavelength) for 1 second, and fluorescence recovery was recorded by rapid confocal scanning. Images were processed with the Fiji open-source software(Schindelin et al. 2012), and recovery curves were analyzed in Mathematica (Wolfram Research) by fitting them with a single-exponential decay function. No aging or changes in the fluidity of the droplets were observed over the course of our observations (up to about four days).

Droplet fusion measurements

A condensate-forming sample (3 μl) was placed on a polymer coverslip (ibidi GmbH, Germany) at the center of an enclosure formed by double-sided tape. Another polymer coverslip was placed on top of the sample, sandwiching and sealing it. The condensate sample was left to equilibrate for 30 min. The sample was then placed on a dual-trap optical tweezers instrument (C-Trap, LUMICKS, Amsterdam) equipped with a 60× water immersion objective and a bright-field camera. Fusion experiments were performed by trapping two droplets of similar size, each in a different trap, lifting the droplets ~20 μm above the surface and moving one droplet towards the other at a constant speed of 2 μm/min — slow compared to the fusion time. Fusion events were recorded with the camera at a variable frame rate depending on the field of view (>100 Hz). The relaxation time of fusion was obtained from a single-exponential fit of A = (L_max- L_min)/(L_max + L_min), where L_max and L_min are the lengths of the major and minor axes, respectively, of the resulting ellipsoidal droplet (after the two fusing droplets are no longer distinguishable) relaxing to a spherical shape(Alshareedah, Kaur, and Banerjee 2021; Leal 2007). Image processing and fitting were performed in Mathematica (Wolfram Research).

Nanorheology

We mixed 12 μM unlabeled ProTα and 10 μM unlabeled H1 with a small aliquot of fluorescent beads (100 nm and 500 nm diameter, Fluoro-Max, Thermo Fisher Scientific), centrifuged the sample to obtain a single droplet (diameter ≳100 μm), and transferred to a sample chamber. The motion of the beads inside the droplet was tracked at 295 K with an Olympus IXplore SpinSR10 microscope using a 100×/1.46 NA Plan-Apochromat oil immersion objective for 300 s with 50 ms exposure time and 200-ms time intervals. Trajectories were obtained with the ImageJ version 1.53t plugin TrackMate(Tinevez et al. 2017) and analyzed using MATLAB 2016b (MathWorks). Mean square displacements (MSD) as a function of time were calculated in 2 dimensions and averaged over $n$ trajectories ($n=22$ for 100-nm beads, $n=20$ for 500-nm beads). The diffusion coefficient, $D$, was calculated from

$$\langle MSD(t)\rangle =4Dt,$$ Eq. 4

where $t$ is the time. The adherence to Brownian diffusion and the consistency between different beads probed (Fig. 1d) indicates homogeneity of the viscous properties across droplets, in agreement with the uniform fluorescence intensity observed in microscopy images. The effective viscosity, ${\eta }_{eff}$, was estimated from the Stokes–Einstein equation assuming freely diffusing Brownian particles of hydrodynamic radius $R$ of the beads or probe molecules used (see below):

$${\eta }_{eff}=\frac{k_{B}T}{6\pi DR}.$$ Eq. 5

In complex liquids, however, such as the coacervate of ProTα and H1, the effective viscosity observed experimentally depends on the size of the probe used and needs to be treated by more general relations(Cai, Panyukov, and Rubinstein 2011; Squires and Mason 2010; Wei et al. 2017; Muthukumar 2023; Kalwarczyk et al. 2015). If the probe particle is very large relative to the correlation length, the friction it experiences can be interpreted in terms of the macroscopic (or bulk) viscosity of the medium, whereas for a probe particle much smaller than the correlation length, friction is dominated by the solvent viscosity. One physical rationalization for the transition between these limiting regimes is in terms of depletion interactions(Lekkerkerker and Tuinier 2011): Owing to a loss of configurational entropy of the IDP chains near the surface of the probe particle, the polypeptide segment density decreases in the vicinity of the particle, resulting in the formation of a depletion layer. Within the depletion layer, the viscosity is thus expected to decrease from the bulk viscosity at large distances from the surface, to the solvent viscosity at the particle surface. As a particle diffuses, the effective viscosity it experiences is therefore between the limiting cases of the solvent and the bulk of the coacervate. Fig. 1e shows the calculated dependence for translational diffusion based on the theory of Tuinier et al.(Tuinier, Dhont, and Fan 2006; König et al. 2021), with a value of 3.8 nm for R_g of ProTα, 3.4 nm for the correlation length, 0.001 Pa s for the solvent viscosity, and 0.3 Pa s for the macroscopic viscosity.

Two-focus fluorescence correlation spectroscopy

Two-focus fluorescence correlation spectroscopy measurements(Dertinger et al. 2007) were performed at 295 K on a MicroTime 200. A Normaski prism and pulsed interleaved excitation with two orthogonally polarized supercontinuum fiber lasers (EXW-12 SuperK Extreme, NKT Photonics, equipped with a z520/5 band pass filter (Chroma), and Solea, PicoQuant, operating at 520 ± 3 nm) were used to form two laser foci. Both lasers were operated at a power of 5 μW (measured at the back aperture of the objective) and a repetition rate of 20 MHz, with the SuperK electronics triggering the Solea with a phase difference of half a period. The distance between the two foci was calibrated as previously described(Hofmann et al. 2012) with reference samples of Cy3b(Gilboa et al. 2019) and 10 kDa dextran(Armstrong et al. 2004). The diffusion coefficient was determined by fitting the correlation functions as previously described(Dertinger et al. 2007) using Fretica (https://schuler.bioc.uzh.ch/programs). Note that two-focus FCS minimizes the effects of refractive index differences between dilute and dense phase on the observed translational diffusion coefficients(Dertinger et al. 2007), and the measurements of Cy3B thus cross-validate the single-focus FCS measurements (Fig. 1e).

Hydrodynamic radii, effective viscosity, and correlation length

Hydrodynamic radii (R_h) of the beads were used as specified by the supplier. For 10 kDa and 40 kDa dextran, we used the R_h values reported previously(Armstrong et al. 2004) (1.86 nm and 4.78 nm, respectively); we report the uncertainty based on the size-dependent polydispersity of our samples as specified by the manufacturer. R_h of Cy3B was measured with two different techniques previously(Gilboa et al. 2019); we used the average value and provide the deviation from the mean as an uncertainty (0.76 ± 0.04 nm, Fig. 1e). R_h of Cy3B used for the analysis of the time-resolved anisotropy measurements (Extended Data Fig. 3i) based on reference anisotropy measurements in water was also found to be within this range (0.80 nm). R_h for a polymer diffusing in a semidilute solution is less well defined, so for ProTα, we used a value for R_h inferred from experiments of ProTα in dilute solution: Based on the root-mean-square end-to-end distance (r_rms) of ProTα measured in the dense phase (9.4 nm), we estimated the radius of gyration from R_g = r_rms/6^1/2 ≈ 3.8 nm. We observe the ratio R_g/R_h for ProTα to be ~1.3 in buffer, independent of salt concentration, so we used this ratio to obtain the corresponding value of R_h in the dense phase (3.0 nm). As conservative estimates of uncertainty, we used as lower and upper bounds for this conversion the theoretical limits of R_g/R_h for polymers (0.77 and 1.5)(Hofmann et al. 2012; Rubinstein and Colby 2003). Effective viscosities were obtained from D and R_h using equation 5. Error bars of the effective viscosity represent the standard deviations from at least three measurements. The correlation length in the dense phase was estimated from ξ ≈ R_g (c/c*)^−3/4, where c is the total protein concentration, and c* is the overlap concentration (c* = 1/V, where $V\approx 4/3\pi R_g^3$ is the volume pervaded by an IDP chain), which separates the dilute from the semidilute regime and is a rough measure of the onset of the interpenetration of chains(Rubinstein and Colby 2003; Muthukumar 2023). The range 2.4 nm ≤ ξ ≤ 4.3 nm indicated as a shaded band in Fig. 1e was obtained by using R_g and R_h for estimating lower and upper bounds for c*, respectively (Table 1, Fig. 1e). The measured viscosity of the dilute phase in TEK buffer including 120 mM KCl was equal to that of buffer solution within experimental uncertainty, as expected based on the low protein concentrations in the dilute phase(Pamies et al. 2008).

Nanosecond fluorescence correlation spectroscopy (nsFCS)

Samples for nsFCS were prepared as described in the section Single-molecule measurements. To avoid signal loss from photobleaching in measurements inside droplets owing to the slow translational diffusion in the dense phase, the confocal volume (continuous-wave excitation at 532 nm) was continuously moved during data collection at a speed of 3 μm/s in a serpentine pattern (Fig. 2c) in a horizontal plane inside the droplet. Only photons from bursts of the FRET-active population ($E>〈E〉-0.15$) were used for correlation analysis. Autocorrelation curves of acceptor and donor channels, and cross-correlation curves between acceptor and donor channels were computed from the measurements and analyzed as previously described(Soranno et al. 2012; Nuesch et al. 2022).

Full FCS curves with logarithmically spaced lag times ranging from nanoseconds to milliseconds are shown in Extended Data Fig. 5. The equation used for fitting the correlations between detection channels $i,j=A,D$ is

$$G_{ij}(\tau )=a_{ij}\frac{(1-c_{ab}^{ij}{e}^{-|\tau |/{\tau }_{ab}^{ij}})(1+c_{cd}^{ij}{e}^{-|\tau |/{\tau }_{cd}})(1+c_{rot}^{ij}{e}^{-|\tau |/{\tau }_{rot}})(1+c_T^{ij}{e}^{-|\tau |/{\tau }_T^{ij}})}{\left(1+\frac{|\tau |}{{\tau }_D}\right){\left(1+\frac{|\tau |}{s^2{\tau }_D}\right)}^{1/2}}.$$ Eq. 6

The four terms in the numerator with amplitudes c_ab, c_cd, c_rot, c_T, and timescales τ_ab, τ_cd, τ_rot, τ_T describe photon antibunching, conformational dynamics, dye rotation, and triplet blinking, respectively. τ_D and s are defined as in Eq. 1. Conformational dynamics result in a characteristic pattern with a positive amplitude in the autocorrelations ($c_{cd}^{DD}>0$ and $c_{cd}^{AA}>0$) and a negative amplitude in the cross-correlation ($c_{cd}^{AD}<0$), but with a common correlation time, ${\tau }_{cd}$. All three correlation curves ($G_{DD}\left(\tau \right)$, $G_{AA}\left(\tau \right)$, $G_{AD}\left(\tau \right)$) were fitted globally with τ_cd and τ_rot as shared fit parameters. τ_cd was converted to the reconfiguration time of the chain, τ_r, as previously described(Gopich et al. 2009), by assuming that chain dynamics can be modeled as a diffusive process in the potential of mean force derived from the sampled inter-dye distance distribution, P(r)(Gopich et al. 2009; Nettels et al. 2007). The reported uncertainty of the reconfiguration time is either the standard deviation of three measurements or a systematic error of the fit, whichever was greater. The systematic error was estimated by fitting different intervals of the FCS data, especially by varying the lower bound of the fitted interval: We report as uncertainties the range of reconfiguration times obtained by fitting from 0.8 ns and from 1.3 ns, a dominant source of variability in the results. We note that the conversion from τ_cd to τ_r does not entail a large change in timescale, and τ_cd and τ_r differ by less than 20% in all cases investigated here, depending on the average distance relative to the Förster radius(Gopich et al. 2009). We assign the correlated component at ~30 ns to dye rotation because of the asymmetry between the photon correlations for positive and negative lag times when a polarizing beam splitter is used to separate the two major channels of detection(Loman et al. 2010) (Extended Data Fig. 3a,b), and because time-resolved anisotropy decays show a slow component on a similar timescale (see Extended Data Fig. 3g,h).

Fluorescence lifetime analysis

To obtain more information about the interdye distance distribution, $P(r)$, we determined in addition to $E$ also the donor and acceptor fluorescence lifetimes,${\tau }_D$ and ${\tau }_A$, for each burst. We first calculate the mean detection times, ${\tau }_D^{\prime }$ and ${\tau }_A^{\prime }$, of all photons of a burst detected in the donor and acceptor channels, respectively. These times are measured relative to the preceding synchronization pulses of the laser triggering electronics. Photons of orthogonal polarization with respect to the excitation polarization are weighted by $2G$ to correct for fluorescence anisotropy effects; $G$ corrects for the polarization-dependence of the detection efficiencies. For obtaining the mean fluorescence lifetimes, we further correct for the effect of background photons and for a time shift due to the instrument response function (IRF) with the formula: ${\tau }_{c=D,A}=\frac{{\tau }_c^{\prime }-\alpha \cdot {〈t〉}_{bg,c}}{1-\alpha }-{〈t〉}_{IRF}$, with $\mathrm{\alpha }=n_{bg,c}\mathrm{\Delta }/N_c$. Here, ${〈t〉}_{bg,c}$ is the mean arrival time of the background photons, ${〈t〉}_{IRF}$ is the mean time of the IRF, $n_{bg,c}$ is the background photon detection rate, $\mathrm{\Delta }$ the burst duration, and $N_c$ the (uncorrected) number of photons in the donor ($c=D$) or acceptor ($c=A)$ channels. The 2D-histograms of relative lifetimes, ${\tau }_D/{\tau }_D^0$ and $\left({\tau }_A-{\tau }_A^0\right)/{\tau }_D$, versus transfer efficiency are shown in Fig. 2g, where ${\tau }_D^0$ and ${\tau }_A^0$ are the mean fluorescence lifetimes of donor and acceptor, respectively, in the absence of FRET. The theoretical dynamic FRET lines(Barth et al. 2022) in Fig. 2g were calculated assuming for P(r) the distance distribution expected from the SAW-ν model(Zheng et al. 2018). For the case that P(r) is sampled rapidly compared to the interphoton time (~10 μs) but slowly compared to the lifetime of the excited state of the donor, it has been shown(Gopich and Szabo 2012) that $\frac{{\tau }_D}{{\tau }_D^0}=1-〈\epsilon 〉+{\sigma }_c^2/(1-〈\epsilon 〉)$ and $\frac{{\tau }_A-{\tau }_A^0}{{\tau }_D}=1-〈\epsilon 〉-{\sigma }_c^2/〈\epsilon 〉$, where the variance ${\sigma }_c^2=\underset{0}{\overset{\infty }{\int }}{\left(〈⟨\epsilon ⟩〉-\epsilon \left(r\right)\right)}^{2}P(r)dr$. The dynamic FRET lines in Fig. 2g were obtained by varying the average end-to-end distance in the SAW-ν model by changing ν. The static FRET lines correspond to single fixed distances.

Fluorescence anisotropy

We measured time-resolved fluorescence anisotropy decays with pulsed excitation of Cy3B (Extended Data Fig. 3i,j) or with pulsed interleaved excitation(Müller et al. 2005) of donor (Cy3B) and acceptor (CF660R) for double-labeled ProTα (Extended Data Fig. 3c–h). We obtained time-correlated single-photon counting histograms from photons polarized parallel and perpendicular with respect to the polarization of the excitation lasers. We corrected and combined them as previously described(Koshioka, Sasaki, and Masuhara 1995) to obtain the anisotropy decays for the acceptor (after direct acceptor excitation, Extended Data Fig. 3d,f,h) and donor (after donor excitation, using donor-only bursts, Extended Data Fig. 3c,e,g) with the time origin as a free fit parameter with lower constraint the actual time of the laser pulse at the source. The steady-state anisotropies of labeled ProTα unbound, in the dimer, and in the dense phase were 0.05, 0.07, and 0.18 for the donor, and 0.05, 0.05, and 0.18 for the acceptor, respectively, indicating that rotational averaging of the fluorophores is sufficiently rapid for approximating the rotational factor κ² by 2/3.(Hellenkamp et al. 2018)

Molecular dynamics (MD) simulations

All-atom simulations of unbound ProTα, the ProTα-H1 dimer, and the phase-separated system were performed with the Amber99SBws force field(Best, Zheng, and Mittal 2014; Lindorff-Larsen et al. 2010) with the TIP4P/2005s water model(Abascal and Vega 2005; Luo and Roux 2010). The temperature was kept constant at 295.15 K using stochastic velocity rescaling(Bussi, Donadio, and Parrinello 2007) (τ = 1 ps), and the pressure was kept at 1 bar with a Parrinello-Rahman barostat(Parinello and Rahman 1981). Long-range electrostatic interactions were modeled using the particle-mesh Ewald method(Darden, York, and Pedersen 1993) with a grid spacing of 0.12 nm. Dispersion interactions and short-range repulsion were described by a Lennard-Jones potential with a cutoff at 0.9 nm. Bonds involving hydrogen atoms were constrained to their equilibrium lengths using the LINCS algorithm(Hess et al. 1997). Equations of motion were integrated with the leap-frog algorithm with a time step of 2 fs, with initial velocities taken from a Maxwell-Boltzmann distribution at 295.15 K. All simulations were performed using GROMACS(Abraham et al. 2015), versions 2020.3 or 2021.5. We used the unlabeled variant of ProTα (Extended Data Table 1) in all simulations, since the droplets under experimental conditions had 1000-fold higher concentration of unlabeled than labeled ProTα.

For the single ProTα chain, an initial extended structure was placed in a 20-nm truncated octahedral box. Subsequently, a short steepest-descent minimization was performed, and the simulation box was filled with TIP4P/2005s water(Best, Zheng, and Mittal 2014) and again energy-minimized. In the next step, 518 potassium and 475 chloride ions were added to the simulation box by replacing water molecules to match the ionic strength of the buffer used in the experiments (128 mM) and to ensure charge neutrality. Finally, a short energy minimization was performed for the whole system (809,843 atoms in total), before running molecular dynamics for a total simulation length of 3.19 μs. The first 100 ns were treated as system equilibration and omitted from the analysis.

We performed 6 simulations of the ProTα-H1 dimer. The first four systems were set up by placing extended ProTα and H1 chains close to each other (but not in contact, to minimize the initial structure bias) inside a 21-nm truncated octahedral box. Subsequently, the system was energy-minimized, and the simulation box was filled with TIP4P/2005s water(Best, Zheng, and Mittal 2014) and again energy-minimized. In the next step, 550 potassium and 560 chloride ions were added to the simulation box by replacing water molecules to match the ionic strength of the buffer used in the experiment (128 mM) and to ensure charge neutrality. After the insertion of ions, the system (938,892 atoms in total) was again energy-minimized before initiating MD simulations. The simulation length of each of four runs was ~3 μs. The first 300 ns of each run were treated as system equilibration and omitted from the analysis. Runs 5 and 6 (~2.2 μs each) were started from configurations at 1 μs of runs 1 and 2, respectively. The first 100 ns of runs 5 and 6 were omitted from the analysis to minimize the initial structure bias. In total, 15.15 μs of ProTα-H1 dimer simulations were used for the analysis.

The initial structure for all-atom simulations of the phase-separated system in slab configuration(Zheng et al. 2020) was obtained with coarse-grained (CG) simulations. We utilized the one-bead-per-residue model that was previously developed to study the 1:1 ProTα-H1 dimer(Borgia et al. 2018). Briefly, the potential energy had the following form:

$$\begin{gathered} V=\frac{1}{2}\sum _{i<N}{k}_b{\left(d_{ij}-d_{ij}^0\right)}^2+\frac{1}{2}\sum _{i<N-1}{k}_{\theta }{\left({\theta }_{ijk}-{\theta }_{ijk}^0\right)}^2 \\ +\sum _{i<N-2}\sum _{n=1}^4{k}_{i,n}(1+\cos (n{\varphi }_{ijkl}-{\delta }_{i,n}))+\sum _{a<b}\frac{q_a{q}_b}{4\pi {ϵ}_d{ϵ}_0{d}_{ab}}\exp \left[-\frac{d_{ab}}{{\lambda }_D}\right]+ \\ \sum _{(a,b)\notin \text{nat}}4{\epsilon }_{pp}\left({\left(\frac{{\sigma }_{ab}}{d_{ab}}\right)}^{12}-{\left(\frac{{\sigma }_{ab}}{d_{ab}}\right)}^6\right)+\sum _{(a,b)\in \text{nat}}4{\epsilon }_{ab}\left(13{\left(\frac{{\sigma }_{ab}}{d_{ab}}\right)}^{12}-18{\left(\frac{{\sigma }_{ab}}{d_{ab}}\right)}^{10}+4{\left(\frac{{\sigma }_{ab}}{d_{ab}}\right)}^6\right), \end{gathered}$$ Eq. 7

where $i,j,k,l$ denote consecutive residues. The first term represents the harmonic bond energy with force constant $k_b=3.16\times {10}^5\text{kJ}.{\text{mol}}^{-1}{\text{nm}}^{-2}$, and the second term represents the angle energy with force constant $k_{\theta }=6.33\times {10}^2\text{kJ}{\text{mol}}^{-1}{\text{rad}}^{-2}$; reference values for $d_{ij}^0$ and ${\theta }_{ijk}^0$ were taken from an extended backbone structure. The third term represents a sequence-based statistical torsion potential taken from the Go model of Karanicolas and Brooks(Karanicolas and Brooks 2002), which was applied to all residues. The fourth term represents a screened coulomb potential, with Debye screening length ${\lambda }_D$ applied to all residues with non-zero charges $q_i$; ${ϵ}_0$ is the permittivity of free space; the dielectric constant, ${ϵ}_d$, was set to 80. The fifth term represents a generic short-range attractive potential applied to all residue pairs not identified as native in the H1 globular domain. This interaction is characterized by a contact distance ${\sigma }_{ab}=({\sigma }_a+{\sigma }_b)/2$, where ${\sigma }_{a,b}$ are the residue diameters (all ~0.6 nm) determined from residue volumes(Creighton 1993), and a contact energy ${\epsilon }_{pp}$, which is the same for all such non-native residue pairs and was set to $0.16k_{B}T$, or $~0.40\text{kJ}/{\text{mol}}^{-1}$. The final term represents an attractive potential applied only to the residues identified as native in the H1 globular domain. The values of the parameters ${\sigma }_{ij}$ and ${\epsilon }_{ij}$ for native pairs are given by the Karanicolas and Brooks Go model(Karanicolas and Brooks 2002). The Debye length, ${\lambda }_D$, is given by

$${\lambda }_D={\left(\frac{{ϵ}_d{ϵ}_0{k}_{B}T}{2e^{2}I}\right)}^{1/2},$$ Eq. 8

where k_B is the Boltzmann constant, T the temperature, e the elementary charge, and I the ionic strength.

Initially, 12 ProTα and 10 H1 molecules were randomly placed in a 25-nm cubic box, and the energy of the system was minimized with the steepest-descent algorithm. Although the CG model itself is capable of capturing the structure of the small globular domain (GD) of H1, we performed a 1-ns NVT run at 300 K with PLUMED(Tribello et al. 2014) restraints, using the list of native contacts based on the experimental structure(Martinsen et al. 2022) (PDB 6HQ1), to ensure that the structure of the GDs was sufficiently close to the experimental one (needed for all-atom reconstruction, below). In the next step, the box edge was decreased to 13.35 nm in a 30-ps NPT run to obtain an average protein density close to that of the dense phase in experiment. The system configuration was further randomized via a 280-ns (using a 10-fs time step) NVT run at 500 K and an implicit ionic strength of 300 mM to ensure relatively uniform protein density in the box. Each chain from the final CG structure was independently reconstructed in all-atom form using a lookup table from fragments drawn from the PDB, as implemented in Pulchra(Rotkiewicz and Skolnick 2008). Side-chain clashes in the all-atom representation were eliminated via a short Monte Carlo simulation with CAMPARI(Vitalis and Pappu 2009) in which only the side chains were allowed to move. The relaxed configuration obtained with CAMPARI was multiplied 8 times, which, by tiling the box in X, Y, and Z directions, resulted in a 26.7-nm cubic box that contained 96 ProTα and 80 H1 molecules. Subsequently, the box edge was extended to 44 nm in the Z direction, and the resulting system was energy-minimized with the steepest-descent algorithm. To eliminate any non-proline cis-bonds that might have emerged during all-atom reconstruction, we ran a short simulation in vacuum with periodic boundaries, using a version of the force field that strongly favors trans peptide bonds(Zheng et al. 2020) and applying weak position restraints to the protein backbone atoms and dihedral angles (5 kJ/mol/rad).

Subsequently, the simulation box was filled with TIP4P/2005s water(Best, Zheng, and Mittal 2014) and energy-minimized. In the next step, 2418 potassium and 2530 chloride ions were added to the simulation box (4’000’932 atoms in total) to match the ionic strength of the buffer used in the experiments (128 mM) and to ensure charge neutrality. In the next step, the system was again energy-minimized, and a 20-ns MD run was performed with strong position restraints on protein backbone atoms (10⁵ kJ mol⁻¹ nm⁻²) to stabilize the trans isomer for any peptide bonds that had isomerized in the previous step. Subsequently, a 1.7-ns simulation with PLUMED restraints on the native contacts of the GDs was performed to ensure that the structure of the reconstructed GDs was not perturbed during the equilibration procedure. The final structure of the run with native-contact restraints was used for the production run (with no restraints used), using GROMACS(Abraham et al. 2015), versions 2020.3 and 2021.5. The free production run was 6.02 μs long, with a timestep of 2 fs, employing 36 nodes (each consisting of an Intel Xeon E5-2690 v3 processor with 12 cores and an NVIDIA Tesla P100 GPU at the Swiss National Supercomputing Centre) with a performance of ~35 ns/day, corresponding to ~6 months of supercomputer time. The first 1.5 μs were treated as system equilibration (Extended Data Fig. 7a) and not used for the analysis.

Analysis of MD simulations

Mean transfer efficiencies, ⟨E⟩, were obtained for each ProTα chain by calculating the instantaneous transfer efficiencies with the Förster equation (Eq. 2) every 10 ps for both the ProTα-H1 dimer and the free ProTα simulations, and every 50 ps for all ProTα molecules in the dense-phase simulation. Subsequently, the instantaneous transfer efficiencies for each ProTα chain were averaged over the simulation length. ⟨E⟩ for the dimer was determined by averaging the transfer efficiencies calculated from six simulation runs, and ⟨E⟩ for the dense phase was determined by averaging over the 96 transfer efficiencies calculated for the individual ProTα chains. R₀ = 6.0 nm(Klose et al. 2021) was used for simulations of unbound ProTα and the ProTα-H1 dimer, R₀ = 5.9 nm for the dense-phase simulations (see Single-molecule spectroscopy). Since we simulated ProTα without explicit representation of the fluorophores, the interdye distance, r, was estimated from the simulations via $r=d{\left((N+9)/N\right)}^{\nu }$, where d denotes the distance between the Cα atoms of the labeled residues (residues 5-58 in ProTαN and residues 58-112 in ProTαC); N denotes the sequence separation of the labeling sites; and the scaling exponent ν was set to 0.6 (within the experimentally determined range, see Single-molecule spectroscopy) — we thus approximate the length of dyes and linkers by adding a total of nine additional effective residues(Holmstrom et al. 2018). We note that the choice of ν has only a small effect on the result, with a variation in ν by ±0.1 corresponding to a change in the inferred transfer efficiencies of approximately ±0.01. The uncertainty in the transfer efficiency of unbound ProTα was estimated from block analysis: the trajectory was divided into 3 intervals of equal length, for which transfer efficiencies were calculated separately; the uncertainty reported is the standard deviation of these efficiencies. For the ProTα-H1 dimer, the transfer efficiency of ProTα was calculated as the average of the transfer efficiencies from six independent runs, and the uncertainty was estimated as the standard deviation. The transfer efficiency of ProTα in the dense-phase simulation was calculated by averaging the transfer efficiencies of 96 chains, and the uncertainty was estimated as the standard deviation of the average transfer efficiencies for the individual chains.

Chain reconfiguration times were estimated by integrating the residue-residue distance autocorrelations, C(t) (normalized to C(0) = 1), up to the time where C(t) = 0.03 and assuming the remaining decay to be single-exponential(Best et al. 2007). For the simulation of unbound ProTα, the uncertainties of the reconfiguration times were estimated by block analysis. For the ProTα-H1 dimer, autocorrelation functions from six independent simulations were determined, the reconfiguration times of ProTα chain were determined by analyzing the corresponding correlation functions as described above, and uncertainties were estimated by bootstrapping: the data were randomly resampled 100 times with replacement, and the uncertainty was taken as the standard deviation of the correlation times obtained. In the dense-phase simulation, some chains sampled a relatively narrow range of distance values. To address this simulation imperfection, we omitted from the analysis those chains whose variance of transfer efficiency was below 0.05 (for ProTαN, 3 out of 96 chains were omitted; for ProTαC, 23 chains were omitted). The global mean and variance of the remaining chains were used to compute the correlation function, rather than the mean and variance for each run separately. Uncertainties were estimated by bootstrapping from the set of reconfiguration times of the individual chains, using 200 samples with replacements per observable, similar to the procedure for the dimer.

The average number of H1 molecules that simultaneously interact with a single ProTα chain, as well as the average number of ProTα chains that simultaneously interact with a single H1 molecule (Fig. 3c) in the dense-phase simulation were determined by calculating the minimum distance between each ProTα and each H1 for each simulation snapshot. The two molecules were considered to be in contact if the minimum distance between any two of their Cα atoms was within 1 nm. Distances between Cα atoms were used instead of the commonly used distances between all atoms of the residues to facilitate the large calculations. The 1-nm cutoff between the Cα atoms of two residues yields similar results as the commonly used 0.6-nm cutoff for interactions between any pair atoms from the two residues(Abraham et al. 2015). The same contact definition was employed when calculating residue-residue contacts (Fig. 3e): Two residues were considered to be in contact if the distance between their Cα atoms was within 1 nm, but the conclusions are robust to the choice of cutoff (Extended Data Fig. 7d).

Lifetimes of residue-residue contacts were calculated by a transition-based or core-state approach(Best, Hummer, and Eaton 2013). In short, rather than using a single distance cutoff to separate bound versus unbound states – which tends to underestimate contact lifetimes – separate cutoffs were used to determine the formation and breaking of contacts. For each pair of residues, a contact was based on the shortest distance between any pair of heavy atoms, one from each residue. Starting from an unformed contact, contact formation was defined to occur when this distance dropped below 0.38 nm; an existing contact was considered to remain formed until the distance increased to more than 0.8 nm(Best, Hummer, and Eaton 2013) (Extended Data Fig. 9a). Given the large number of possible contacts in the dense-phase simulation (342,997,336), the simulation was broken down into nine 500-ns blocks and each analyzed separately with parallelized code. Average lifetimes of each residue-residue contact were calculated by dividing the total bound time by the total number of contact breaking events for that contact. Intra-chain contacts were not included in the analysis. Average lifetimes of each pair of ProTα-H1 residues (averaged over the different combinations of ProTα and H1 chains that the two residues could be part of) were calculated by dividing the total contact time (summed over all combinations of ProTα and H1 chains) of a specific residue pair by the total number of the contact breaking events for the same residues (summed over the same combinations of chains). Similarly, to calculate average lifetimes of residue-residue contacts according to the residue type (Extended Data Fig. 8e,f), we first identified all contacts involving a particular pair of residue types, in which one residue was from the ProTα chain and the second was from either H1 or ProTα. Subsequently, the average lifetime of that residue-residue combination was calculated by dividing the total bound time by the total number of contact breaking events for the contacts involving those residue types. Excess populations of specific residue-residue type pairs (Extended Data Fig. 8g,h) were determined by dividing the average number of observed contacts for a pair of residue types by the value that would be expected if residues paired randomly in a mean field approximation. The average number of contacts for a pair of residue types was calculated as a sum of all times that residues of those types were in contact, divided by the simulation length. The expected average number of contacts between two residue types (type 1 and 2) were calculated as N f(1) f(2), where N is the average total number of contacts, and f(1) and f(2) are the fraction of residues of type 1 and 2, respectively.

The mean square displacement (MSD) of individual residues and of the center of mass (COM) of ProTα molecules were calculated using the Gromacs function gmx msd. For the ProTα-H1 dimer simulations, MSD curves of each ProTα residue (for residues 1 to 112) were averaged over six simulation runs. MSD curves of each ProTα residue for each of the 96 chains were calculated in four 1-μs blocks, using residue coordinates every 100 ps. Subsequently, MSD curves of each specific residue were averaged over all chains and blocks. The translational diffusion coefficient, D, of the COM of unbound ProTα was calculated by fitting the MSD with MSD(t) = 6Dt up to 700 ns, and the uncertainty was estimated from block analysis: The MSD was calculated from each third of the trajectory (each part being ~1 μs long); diffusion coefficients of each segment were determined by fitting them up to 250 ns, and the uncertainty given is the standard error of the mean. Diffusion coefficients of the COM of ProTα in the ProTα-H1 dimer were calculated by fitting the averaged MSD curves up to 1 μs, and the uncertainty was estimated as the standard error of the mean of the fits of six individual chains up to 500 ns. The diffusion coefficient of the COM of ProTα in the dense-phase simulation was calculated by fitting the MSD curve averaged over all 96 molecules up to 1 μs, and the uncertainty was estimated as the standard error of the mean of the fits of 96 individual chains. Translational diffusion coefficients of free ProTα and ProTα in the heterodimer were corrected for finite-size effects resulting from hydrodynamic interactions with periodic images by increasing the determined diffusion coefficient by the additive correction term k_BTξ/6πηL,(Yeh and Hummer 2004) where η denotes water viscosity and L the box edge length. The constant ξ was set to 3.639 for the truncated octahedral simulation box(Hasimoto 1959), yielding corrections by additive terms of 32·10⁻¹² m²/s and 31·10⁻¹² m²/s for free ProTα and the dimer, respectively. The correction for the dense-phase simulations is complicated by the inhomogeneous distribution of molecules and was thus not applied. We estimate the correction to be much smaller in that case, and it is also expected to increase the diffusion coefficient toward the experimental value. Diffusion exponents, α, for the diffusion of individual residues (Extended Data Fig. 10f) were estimated by fitting their MSD with MSD(t) = 6Dt^α up to 2 ns, a range where the MSD curves are linear in double-logarithmic plots (Extended Data Fig. 10a–e). Densities of protein, water, and ions from dense-phase simulations were calculated perpendicular to the longest slab axis (Z axis in Extended Data Fig. 6), using the calculated density profiles between 15 nm and 30 nm (Extended Data Fig. 6).

Extended Data

Extended Data Fig. 1. Dependence of phase separation on solution conditions and droplet fusion dynamics.

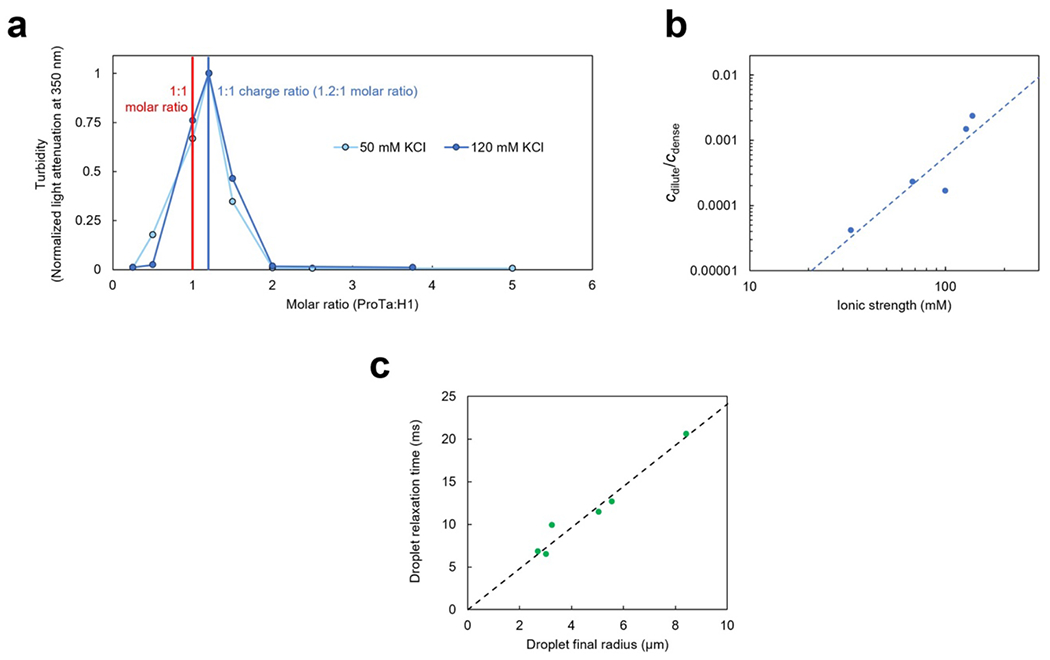
a. Phase separation is most pronounced in a charged-balanced mixture of H1 and ProTα. The extent of droplet formation was assessed using turbidity at 350 nm in TEK buffer with 50 mM KCl and at 120 mM KCl at a constant concentration of H1 (10 μM and 20 μM, at 50 mM and 120 mM KCl, respectively) and varying amounts of ProTα. At both salt concentrations, maximum phase separation was observed at a stoichiometric ratio of 1.2:1 for ProTα:H1, where the charges of the two proteins balance. b. Lohman-Record plot(Record, Anderson, and Lohman 1978) of the ionic strength dependence of the dilute (c_dilute) over dense-phase protein concentration (c_dense). If we treat the ratio c_dilute/c_dense as an effective equilibrium constant for the partitioning of H1 and ProTα between the dilute and dense phases, its logarithm approximates the free energy difference between the heterodimer in the dilute phase (Extended Data Fig. 2) and in the dense phase. The slope of a graph of these values versus the logarithm of the ionic strength (or salt concentration) can then be interpreted in terms of the number of ions released(Record, Anderson, and Lohman 1978) upon the transfer of a ProTα-H1 dimer into the dense phase (since Log(c_dilute/c_dense) diverges close to the critical point, we only included data points up to 120 mM KCl). The resulting value of 2.5±0.7 ions (uncertainty from error of the fit) is small compared to the ^~18 ions released upon ProTα-H1 dimerization(Borgia et al. 2018; Sottini et al. 2020), in accord with the small number of additional charge-charge interactions of ProTα in the dense phase compared to the heterodimer obtained from the simulations (Fig. 3e). Note that c_dilute = 35±5 μM at an ionic strength of 165 mM, which explains why no phase separation was observed in the NMR experiments of ProTα and H1 reported previously(Borgia et al. 2018). Even at the highest protein concentrations used there, the signal is expected to be dominated by the dilute phase, and in case droplets did form, their volume fraction was presumably too small to be apparent by eye. We chose to work at an ionic strength of 128 mM in the present work as a compromise between physiologically relevant salt concentrations and experimental feasibility, especially regarding sample consumption. c. The droplet relaxation time upon droplet fusion (measured in dual-trap optical tweezers(Alshareedah, Kaur, and Banerjee 2021), see Fig. 1c) is proportional to the radius of the final droplet, which indicates that the viscoelasticity of the dense phase on the millisecond timescale is dominated by the viscous (rather than the elastic) component(Alshareedah, Kaur, and Banerjee 2021). In this case, the slope of the fit (dashed line) is(Leal 2007; Jeon et al. 2018) $(2\lambda +3)(19\lambda +16)/[40\left(\lambda +1\right)]·{\eta }_s/\sigma$, where $\lambda ={\eta }_m/{\eta }_s$ is the ratio of macroscopic (or bulk) viscosity in the droplet over the solvent viscosity (η_s = 0.001 Pa s), and σ is the interfacial tension. With the resulting value of 2.4·10³ s/m for the slope and η_m = 0.3 Pa s, we estimate σ ≈ 1.2·10⁻⁴ N/m.

Extended Data Fig. 2. The ProTα-H1 dimer is the dominant population in the dilute phase.

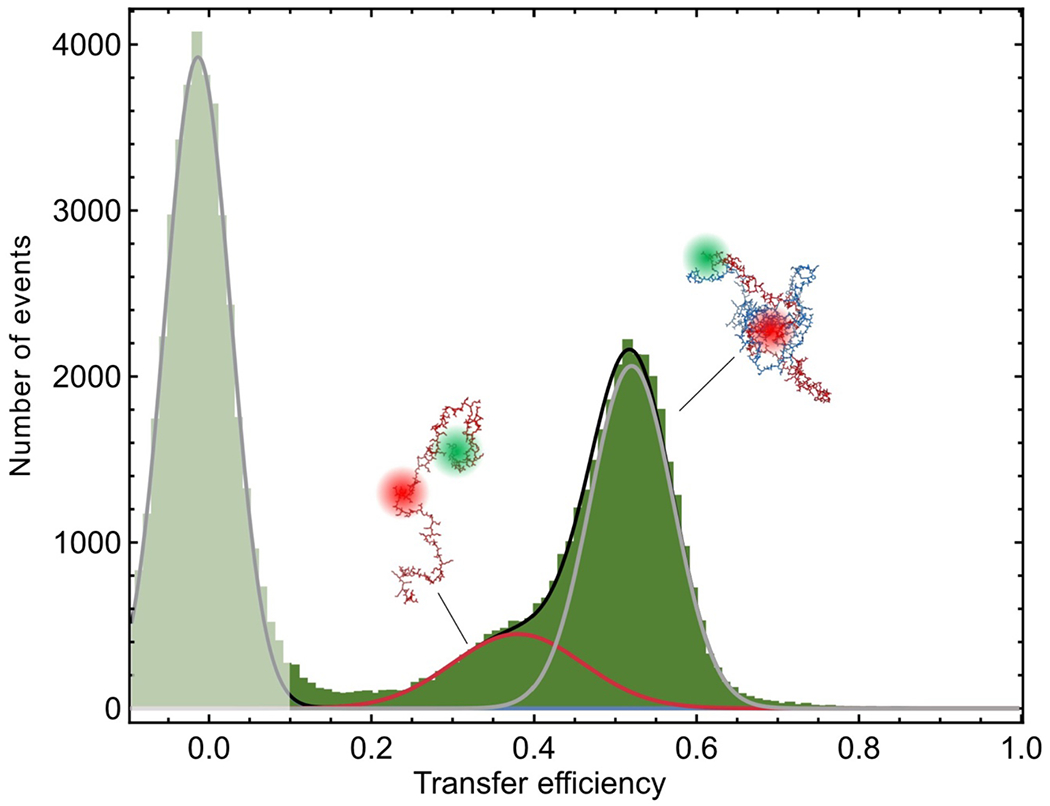
Single-molecule transfer efficiency histogram of ProTαC (labeled at position 56 and 110) in the dilute phase at 128 mM ionic strength (TEK buffer including 120 mM KCl). The phase-separated mixture was centrifuged, so that the dense phase coalesced into a single large droplet and no small droplets remained in the dilute phase. The dilute phase was aspirated and transferred into a sample chamber for single-molecule measurements. In the fit (lines), the centers of the Gaussian peak functions were constrained to the transfer efficiencies measured for unbound ProTα and the ProTα-H1 dimer (Fig. 2f) to within experimental uncertainty. The shaded peak near a transfer efficiency of zero originates from molecules lacking an active acceptor dye.

Extended Data Fig. 3. Polarization-resolved fluorescence probing rotational effects.

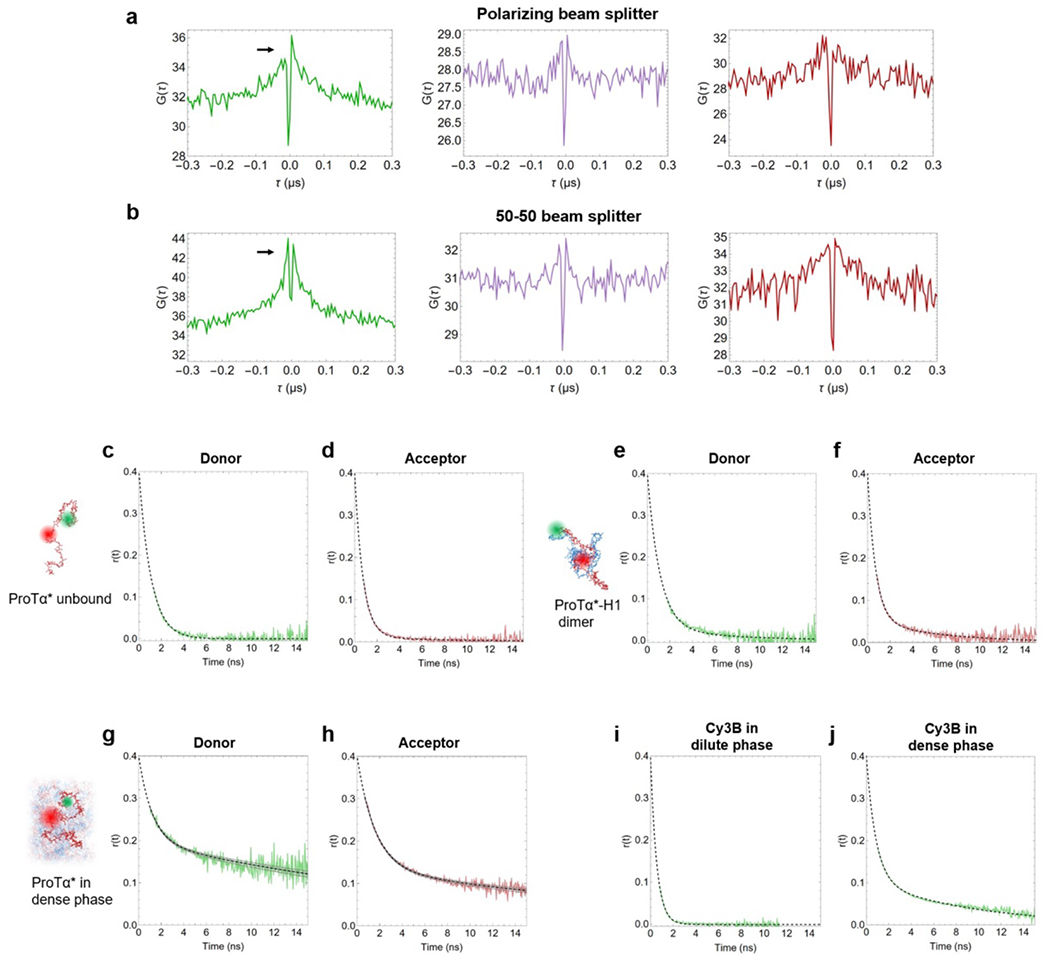
a. Donor and acceptor emission autocorrelations (green and red, respectively; parallel vs perpendicular channels) and donor-acceptor crosscorrelation (purple; sum of correlations of respective parallel and perpendicular channels) of the FRET-active subpopulation of labeled ProTαC in the dense phase when a polarizing beam splitter is used show an asymmetry of the branches for positive and negative lag-times, τ, in the positively correlated component (correlation time of 30 ns). In contrast, this component is more symmetric when a 50-50 beam splitter is used (b), indicating that the component is caused by residual polarization anisotropy. (c-h) Time-resolved anisotropy decays, r(t), measured for double-labeled ProTαC unbound (c, d), in the dimer (e,f), and in the dense phase (g,h) with pulsed interleaved excitation using (c, e, g) photons from donor-only bursts (transfer efficiency < 0.1, excitation at 532 nm) or (d, g, h) acceptor photons from bursts with transfer efficiency > 0.2 (excitation at 635 nm). Data were fitted with the function $r\left(t\right)=r_0(\left(1-A_{rot}\right)e^{-t/{\tau }_{fast}}+A_{slow})e^{-t/{\tau }_{slow}}$ (dashed black lines)(Lipari and Szabo 1980) with $r_0=0.4$. No significant amplitude $A_{slow}$ for a slow component is present for free ProTαC (c, d), and only a small amplitude in the dimer (e, f). In the dense phase (g, h), a distinct slow decay component is observed in the anisotropy decay, which is well described with the decay time τ_slow = 30 ns from the correlated component of the nsFCS (a, b). This agreement further supports the role of residual rotation as the source of the latter. (i, j) Time-resolved anisotropy decays for free Cy3B in the dilute (i) and dense phase (j). The dilute-phase decay was fit with a single exponential, $r\left(t\right)=r_0{e}^{-t/\tau }$, and the resulting value of $\tau =0.53ns$ was used to obtain the hydrodynamic radius of Cy3B based on the Stokes-Einstein-Debye relation, $\tau =({\eta }_{eff}\frac{4}{3}\pi R_{probe}^3)/k_{b}T$. With the viscosity of water ($0.0010Pas$), we obtain 0.80 nm for the radius of Cy3B, within the range of the previously reported values (0.76 nm ± 0.04)(Gilboa et al. 2019). (j) The anisotropy decay in the dense phase was fit with a sum of two exponentials, $r\left(t\right)=r_0(\left(1-A_{slow}\right)e^{-t/{\tau }_{fast}}+A_{slow}{e}^{-t/{\tau }_{slow}})$. The effective viscosities obtained from the fast and slow components, ${\tau }_{fast}$ and ${\tau }_{slow}$, are reported in Fig. 1e, and we assign the fast component to the rotational diffusion of the dye virtually unaffected by attractive protein interactions. Note that despite the slow rotational component of Cy3B, almost no partitioning of the dye into the droplets was observed (partition constant <1.05 from confocal fluorescence microscopy images).

Extended Data Fig. 4. ProTα labeled at positions 2 and 56 (ProTαN) shows behavior similar to ProTα labeled at positions 56 and 110 (ProTαC, Fig. 2).

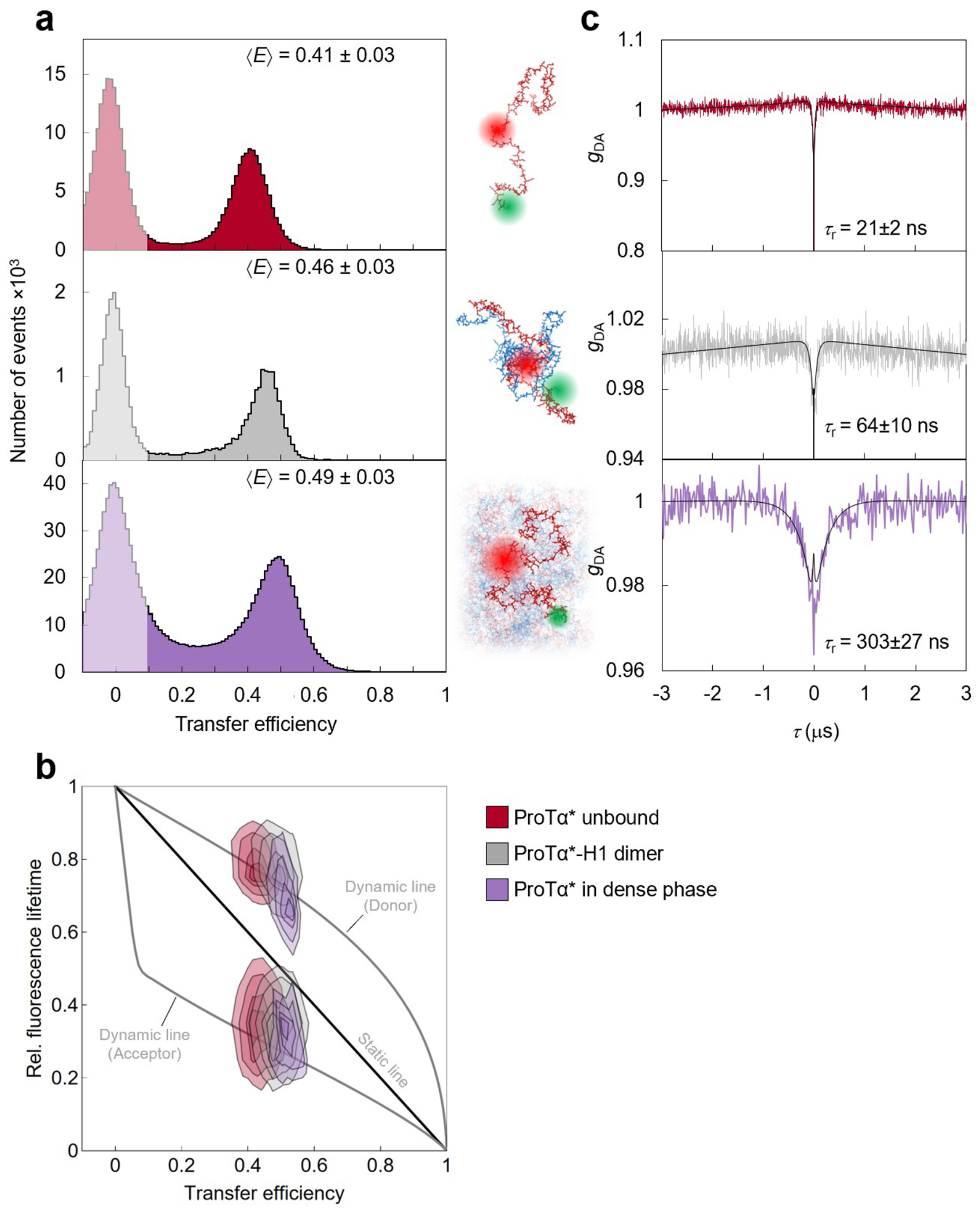
a. Single-molecule transfer efficiency histograms of ProTαN at 128 mM ionic strength (TEK buffer including 120 mM KCl) as a monomer free in solution (top), in the 1:1 complex with H1 (middle), and within droplets (bottom) measured with continuous-wave excitation. Note the greater compaction in the dense phase compared to the ProTα-H1 dimer than for ProTαC. b. 2D histograms of relative donor and acceptor fluorescence lifetimes versus FRET efficiency for all detected bursts measured with pulsed excitation of ProTαN. The straight line shows the dependence expected for fluorophores separated by a static distance; curved lines show the dependences for fluorophores that rapidly sample a distribution of distances (self-avoiding walk (SAWν)(Zheng et al. 2018), see Methods; upper line: donor lifetime; lower line: acceptor lifetime). c. nsFCS probing chain dynamics based on intramolecular FRET in double-labeled ProTαN; data show donor–acceptor fluorescence cross-correlations with fits (black lines). Reconfiguration times, τ_r, are averages of n = 3 independent measurements (uncertainties discussed in Methods).

Extended Data Fig. 5. Full FCS curves with logarithmic binning.

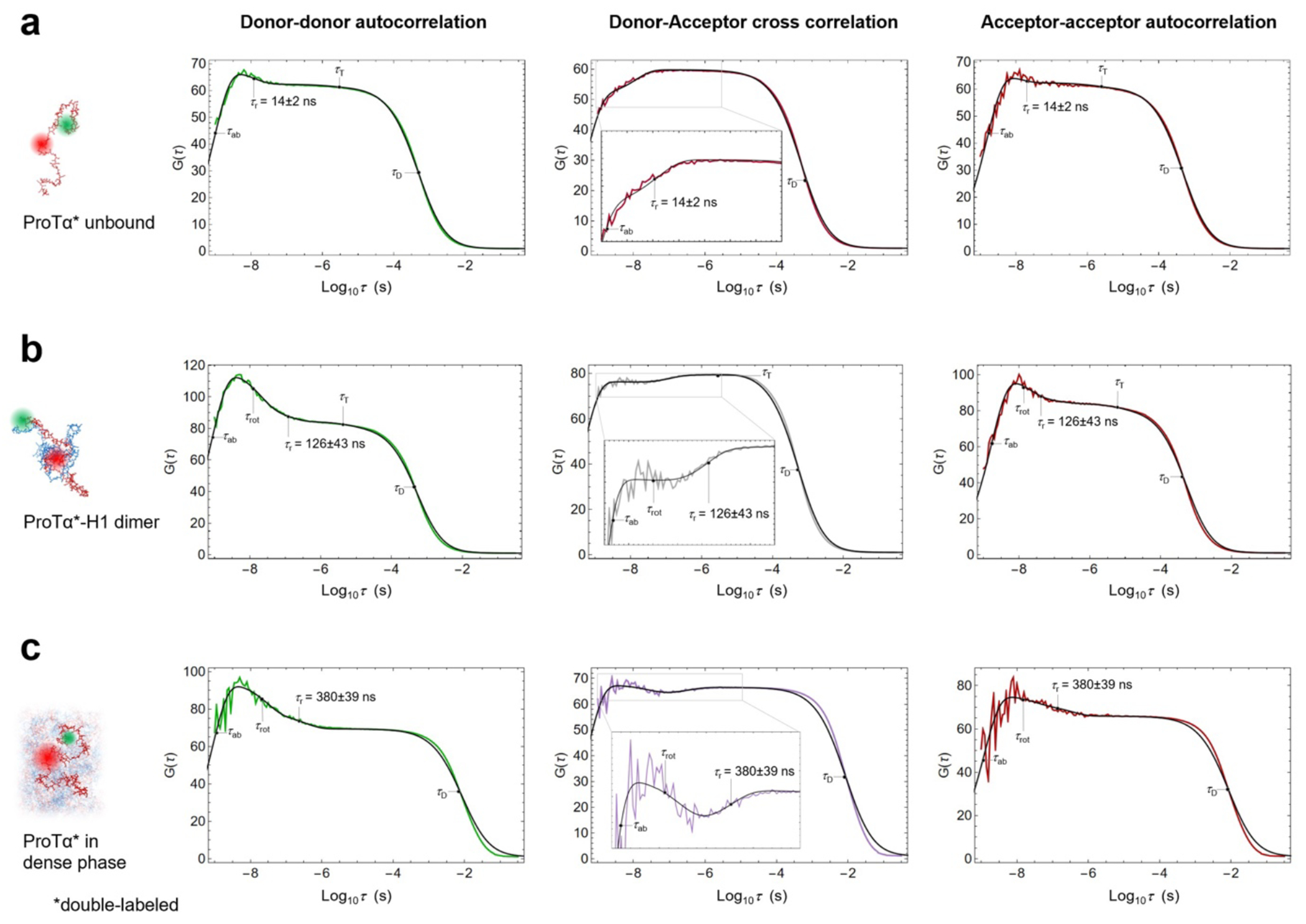
Donor and acceptor autocorrelations (green, red) and donor-acceptor crosscorrelations (purple; same color scheme as in Fig. 2h, which shows the same data and fits but on a linear scale and normalized to an amplitude of 1 at ±3 μs) of ProTαC (labeled at position 56 and 110) in 128 mM ionic strength (TEK buffer with 120 mM KCl) as an unbound monomer in solution (a), in the 1:1 complex with H1 (b), and within ProTα-H1 droplets (c). For each sample, the three correlations are fitted globally (black solid lines, see Methods) with shared correlation times for translational diffusion (τ_D), triplet blinking (τ_T), dye rotation (τ_rot), and conformational dynamics (τ_cd); photon antibunching (τ_ab) is fitted individually. τ_cd was then converted to the reconfiguration time of the chain, τ_r, as previously described(Gopich et al. 2009) (we note that the conversion from τ_cd to τ_r does not entail a large change in timescale, and τ_cd and τ_r differ by less than 20% in all cases investigated here). τ_D, τ_T, τ_rot, τ_r, and τ_ab are shown in the panels if the corresponding term was included in the fit function (Eq. 6), and they point to their respective timescales. The value of τ_r reported here is the mean of three measurements, as in Fig. 2h, and corresponds to the distance correlation time between the dyes at position 56 and 110.(Gopich et al. 2009) τ_T in the donor-acceptor cross correlation in (B) shows a small negative amplitude, possibly indicating a slight contribution of slower distance dynamics on the microsecond timescale. Note that the deviation between fit and measurement in (c) for the translational diffusion component is caused by sample scanning, which was required to improve statistics inside the droplets.

Extended Data Fig. 6.

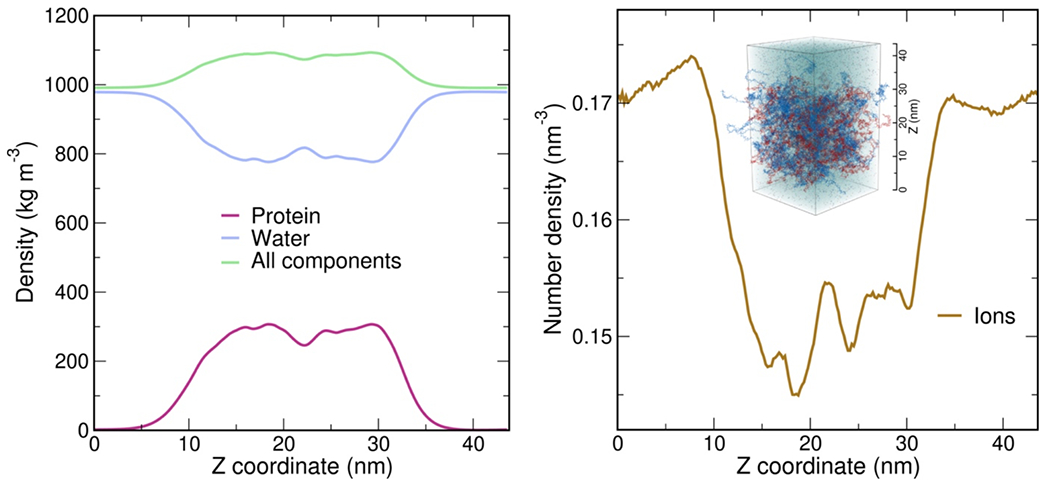
Density profiles of protein, water, all components (protein, water, and ions; left), and ions (right) along the Z axis (see inset on the right) of the simulation box. The water density in the dense phase (central part of the slab, 15 nm < Z < 30 nm) is ^~80.7% of the water density in the bulk regions (Z < 2.5 nm and Z > 40.0 nm). The number density of ions in the dense phase (15 nm < Z < 30 nm) is ~88.4% of the value close to the box edges (Z < 1.5 nm and Z > 41.0 nm). With respect to only the water density in the respective phases, the ion concentration is ~10% higher in the dense phase than in the dilute phase.

Extended Data Fig. 7. Equilibration of dense phase simulation, stability of H1 globular domain in simulations, and robustness to cutoff variation.

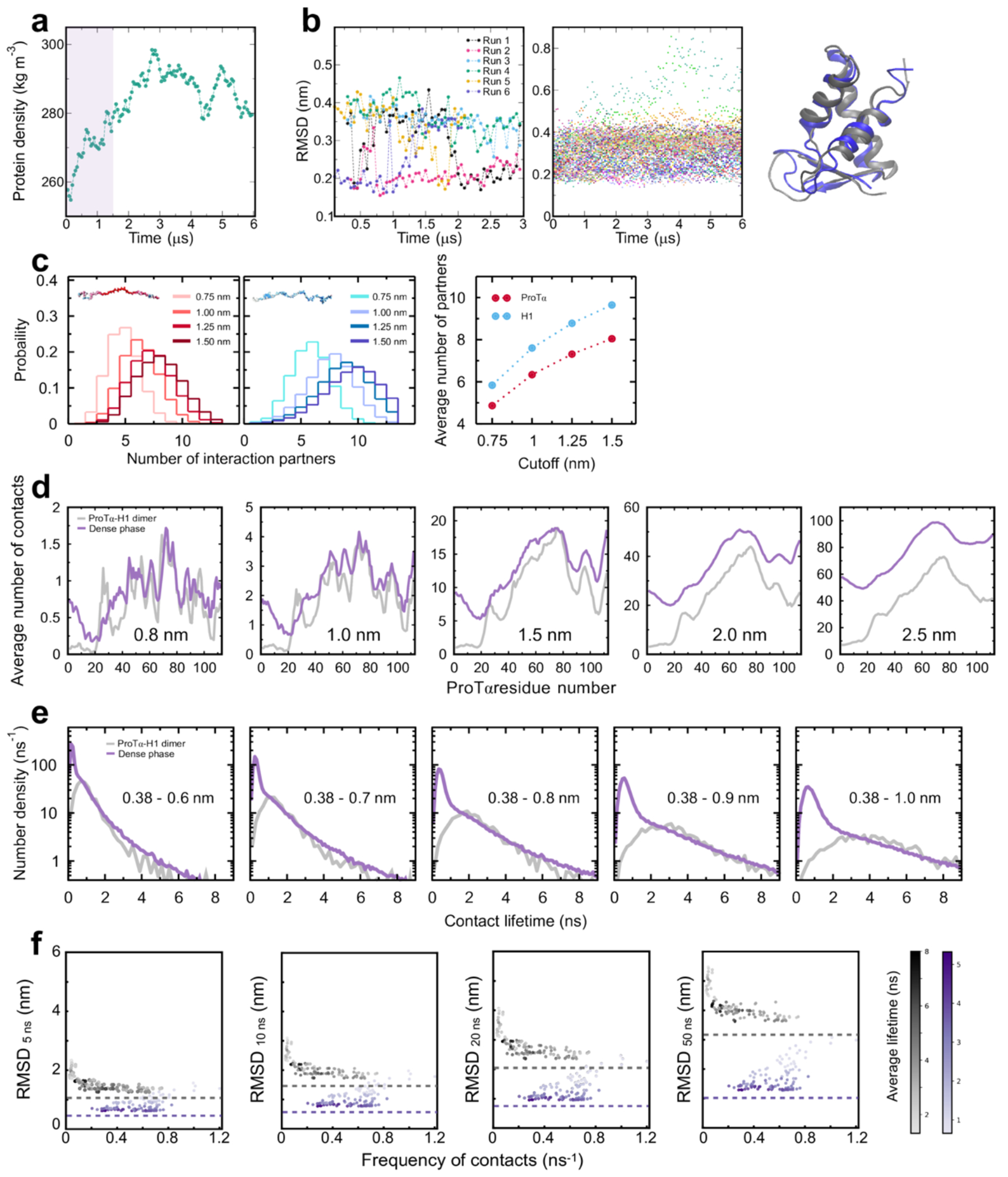
a. Protein density in the central part of the slab simulation as a function of time, calculated in 50-ns blocks. The first 1.5 μs of the simulation (shaded band) were treated as equilibration and omitted from further analysis. b. Stability of the H1 globular domains (GDs), quantified as the backbone RMSD between simulated and experimental structure (PDB 6HQ1)(Martinsen et al. 2022), over the course of dimer (left) and dense-phase simulations (middle). The fraction of partially unfolded domains (< 10% with RMSD > 0.4 nm) is in line with the experimental stability previously determined in dilute solution(Martinsen et al. 2022). Note that the backbone RMSD of 0.2-0.4 nm for the folded domain can be attributed to the flexibility of the loops in the structure, illustrated by superposition of two structures with RMSD = 0.4 nm (right). c. Histograms of the number of H1 chains simultaneously interacting with a single ProTα chain (left) and vice versa (middle) using different distance cutoffs (see legend; 1.0 nm(Abraham et al. 2015) was used in Fig. 3c). Note that the number of ProTα chains interacting with a single H1 chain is always ~1.2 times the number of H1 chains interacting with a single ProTα chain, as expected from charge balance (Extended Data Fig. 1a). d. Average number of contacts that each residue of ProTα makes in the heterodimer with H1 (gray) and in the dense phase (purple) with different distance cutoffs (1.0 nm — approximately the Bjerrum length — was used in the Fig. 3e). As expected, the increase of the number of contacts with the cutoff is more pronounced in the dense phase than in the dimer, reflecting the higher protein density in the condensate. Owing to the computational costs of the distance calculations for each residue (10,752 distances in total), only 500 ns of the dense-phase trajectory (2.0 to 2.5 μs) were used for cutoff variation (in contrast to Fig. 3e, where the complete trajectory was used). e. Distribution of the lifetimes of contacts formed by ProTα residues in the dimer (gray) and in the dense phase (purple) using different upper bounds for the contact definition (see Methods; 0.8 nm(Best, Hummer, and Eaton 2013) was used in Fig. 3f). Owing to the computational costs of the lifetime calculations, only 500 ns of the dense-phase trajectory (1.5 to 2.0 μs) and only one dimer simulation was used for cutoff variation (in contrast to Fig. 3f, where the complete trajectory was used). While the increased cutoff leads to a slight increase in the absolute value of the lifetimes, the reported trends are consistent: the distributions of longer-lived contacts are very similar for the dimer and dense-phase simulations, and the number of short-lived contacts is larger in the dense phase. f. Root-mean-square displacement (RMSD) of the 112 individual ProTα residues with different contact lifetimes (see legend) vs their average frequency of contact formation.

Extended Data Fig. 8. Contact lifetime heatmaps.

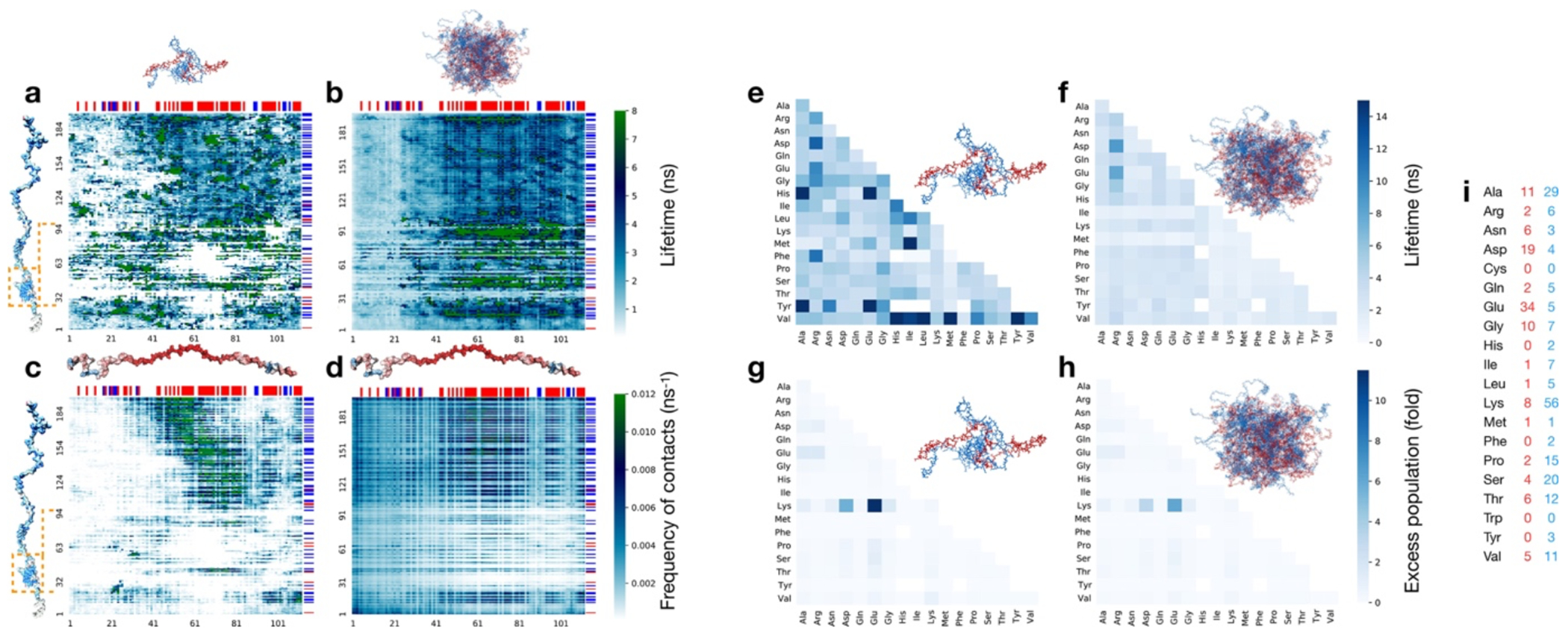
Average lifetime of residue-residue contacts from 6 simulations of the ProTα-H1 dimer (a) and the dense-phase simulation (b). Numbers along the bottom and left denote the residue numbers of ProTα and H1, respectively. Orange rectangles denote the globular domain (GD) of H1 (residues 22 to 96). Frequency of contacts (i.e. the number of newly formed contacts by one ProTα per nanosecond) calculated from dimer and dense phase simulations are shown in (c), and (d), respectively. Blue and red bars at the top and on the right side of the plots denote positively and negatively charged residues of ProTα and H1, respectively. In general, the N-terminal part of ProTα makes fewer contacts than the rest of the chain both in the dimer and dense phase simulations (see also Fig 3e), and the lifetime of those contacts is on average shorter, especially in the dense-phase simulation. As is obvious from (d), contacts between oppositely charged residues are most frequent. White regions in a and c correspond to reside-residue combinations that were never formed during the simulations. White regions are particularly frequent in the GD, since it remains folded during the dimer simulations (Extended Data Fig. 7b). Some of the GD residues make relatively long-lived contacts, but those contacts are infrequent. In contrast to the dimer simulations, some residues of the GD do form contacts with ProTα residues in the dense phase simulation, since a small fraction of partially unfolded GDs are populated (Extended Data Fig. 7b), as expected from the low equilibrium stability of the GD(Martinsen et al. 2022; Borgia et al. 2018). e-h. Residue type-specific contact lifetime heatmaps. Average lifetimes of residue-residue contacts in the ProTα-H1 dimer (e) and the dense-phase simulations (f) classified by residue types. Excess population of contacts for specific residue pairs in the ProTα-H1 dimer (g) and in the dense-phase simulation (h) (see Methods for details). i. Numbers of contacts for specific residue types in ProTα (red) and H1 (blue). Residue pairs that are never observed (white squares) and extremely long-lived pairs (dark blue) in (e) correspond to residue types that are infrequent in the ProTα and H1 sequence (compare with i). In the dense phase, Arg forms contacts that are on average longer-lived than any other residue (F), in line with the phase separation-promoting role of Arg(Boeynaems et al. 2017; Qamar et al. 2018; Paloni, Bussi, and Barducci 2021; Vernon et al. 2018; Wang et al. 2018). The excess populations (see Methods) of contacts for specific residue pairs suggest that the interactions between charged residues are the most favorable interactions both in the dimer and in the dense-phase simulations. Note that the oppositely charged residues Glu (most abundant residue in ProTα) and Lys (most abundant residue in H1) form the largest number of contacts (g,h) but have lifetimes comparable to other residue pairs (e,f).

Extended Data Fig. 9. Lifetime of non-attractive collisional contacts and competitive substitution between residues.

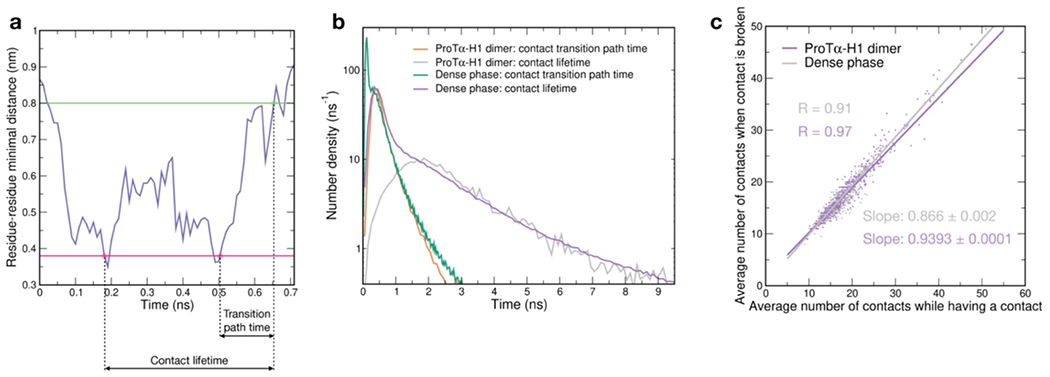
a. We used the transition path times of residue-residue contact breaking as an estimate for the lifetime of non-attractive collisional contacts between two residues. The duration of a contact between two residues was estimated from the time when the distance between any two heavy atoms of the two residues falls below 0.38 nm to the first time when no distance between any two heavy atoms of those residues is below 0.80 nm (see Methods). The transition path time for the breaking of a given contact was estimated as the time from the last time when the distance between any two heavy atoms of the two residues is below 0.38 nm to the first time it reaches 0.8 nm (A). The timescale expected for non-attractive collisions in the dense-phase simulation (shaded area in Fig. 3f) was estimated as the time that includes 95% of all transition path times in the dense-phase simulation. b. Comparison between the contact lifetimes and the transition path times in ProTα-H1 dimer and the dense phase (see legend). The areas under the curves correspond to the total numbers of contact events per chain per nanosecond. c. A fingerprint of rapid exchange or competitive substitution between charged side chains in the dense phase. Average number of contacts at the time when the contact between two residues is broken plotted as a function of the average number of contacts that those two residues make with other residues during the time being in contact. Given the large number of contact events in the dense phase simulation, only every 20’000^th data point is plotted. The definition of a contact is identical to the one described in Methods, but the average number of contacts per residue is larger than the one shown in Fig. 3e since in this case the bonds between neighboring residues were also recorded as contacts. The significantly lower value of the slope of a linear fit in the dimer simulation suggests that multiple contacts tend to be broken simultaneously in this case owing to the concerted motions of parts of the protein chains. In contrast, owing to the high local density of potential interaction partners in the dense phase and the competition for contacts, less contacts are broken simultaneously, as the interaction partners are often rapidly substituted (Fig. 3h), resulting in the greater slope in the dense phase simulation.

Extended Data Fig. 10. Mean square displacement (MSD) curves from molecular dynamics simualtions simulations reveal subdiffusion.

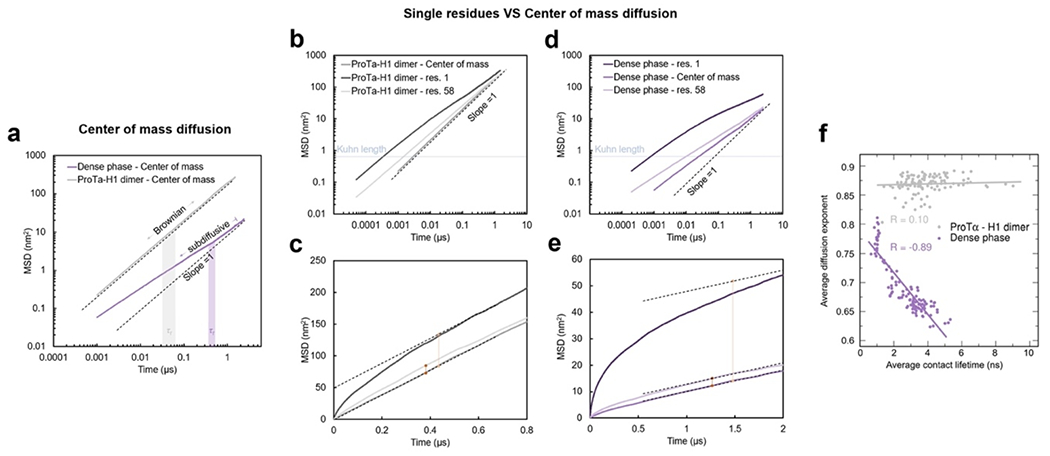
a. ProTα center-of-mass diffusion of ProTα in the dense phase (purple, average of 96 chains) compared to ProTα in the ProTα-H1 dimer (gray, average of 6 chains). In the dimer, at all timescales investigated, the diffusion of ProTα is Brownian, whereas in the dense phase, we observe subdiffusive behavior at timescales equal to or shorter than the chain reconfiguration time (shaded bands indicate full-length chain reconfiguration time ± uncertainty), as expected in the presence of cooperative dynamics of the network(Guenza 2002) (MSDs are only shown for the time range where the standard deviation σ_MSD < 0.5·MSD). b,c. Comparison between the diffusion of residue 1 of ProTα, of the central residue 58, and of the ProTα center of mass in the dimer (b) and the dense phase (c). The residues of an ideal chain are expected to show subdiffusive behavior in a time window between t_Kuhn, the time a residue needs to diffuse over the Kuhn length of the chain, and the time the entire chain takes to diffuse a distance corresponding to its own size(Sokolov 2012), which, for a Rouse chain(Doi and Edwards 1988), approximately corresponds to the chain reconfiguration time, τ_r. Below t_Kuhn, the individual residues are expected to diffuse independently of the chain. Building on the ideal chain model, in (f) we report the diffusion exponent for times below 2 ns (approximately t_Kuhn), where the single-residue behavior is largely unaffected by the slowdown due to chain reconfiguration. d,e. Same data as in (b,c), but in linear scale to highlight the transition at timescales >τ_r, where the diffusion of the entire chain dominates the diffusion of the individual residues. The yellow and orange vertical lines indicate the MSD traveled by the residue in excess of the MSD of the center of mass of the chain. Dashed lines indicate the slope expected for Brownian dynamics. f. Diffusion of individual ProTα residues (1-112) is examined in terms of their mean squared displacement, MSD(t) = 6Dt^α, for timescales shorter than t_Kuhn (see b,c), where D is the diffusion coefficient, t is the lag time, and α = 1 for Brownian diffusion. Diffusion of the residues in the ProTα-H1 dimer is close to Brownian and does not correlate with the average contact lifetime of the corresponding residues, whereas in the dense phase, the diffusion of the residues is more subdiffusive (α < 1) and shows a negative correlation with their average contact lifetime. The residues in the dense phase with low average contact lifetime show less subdiffusive behavior but form a larger number of contacts per unit time (compare with Fig. 3g).

Extended Data Table 1. Amino acid sequences of the proteins used.

Cys residues introduced for labeling are indicated in bold. Unlabeled ProTα is a variant of human ProTα isoform 2, while ProTα 2C/56C and 56C/110C are variants of isoform 1(Borgia et al. 2018; Sottini et al. 2020). The isoforms differ by a single Glu at position 39.

ProTα (unlabelled)	GPMSDAAVDTSSEITTKDLKEKKEVVEEAENGRDAPANGNANEENGEQEADNEVDEEEEEGGEEEEEEEEGDGEEEDGDEDEEAESATGKRAAEDDEDDDVDTKKQKTDEDD
ProTαN (2C/56C labelled)	GCDAAVDTSSEITTKDLKEKKEVVEEAENGRDAPANGNAENEENGEQEADNEVDEECEEGGEEEEEEEEGDGEEEDGDEDEEAESATGKRAAEDDEDDDVDTKKQKTDEDDGA
ProTαC (56C/110C labelled)	GPSDAAVDTSSEITTKDLKEKKEVVEEAENGRDAPANGNAENEENGEQEADNEVDEECEEGGEEEEEEEEGDGEEEDGDEDEEAESATGKRAAEDDEDDDVDTKKQKTDEDC
H1 (unlabelled)	TENSTSAPAAKPKRAKASKKSTDHPKYSDMIVAAIQAEKNRAGSSRQSIQKYIKSHYKVGENADSQIKLSIKRLVTTGVLKQTKGVGASGSFRLAKSDEPKKSVAFKKTKKEIKKVATPKKASKPKKAASKAPTKKPKATPVKKAKKKLAATPKKAKKPKTVKAKPVKASKPKKAKPVKPKAKSSAKRAGKKK

Data availability

The simulation trajectories of the condensates have been deposited at Zenodo (https://doi.org/10.5281/zenodo.7963359). Source data are provided with this paper for the experimental measurements and simulation results.