Abstract
Kinematic analysis is a central component of movement biomechanics, describing the relative motion of joint segments during different activities, in different subject cohorts, and at different timepoints. Establishing whether two sets of kinematic signals represent fundamentally similar or different underlying motion patterns is especially challenging, given 1) the lack of consensus around reference frame and joint axis definition, and 2) the substantial effect that minimal variations in frame position and orientation are known to have on signal magnitude and characteristics. As such, enormous variability in the reporting of tibiofemoral kinematics has resulted in joint movement patterns that remain controversially discussed. Previously, we demonstrated the ability of the REference FRame Alignment MEthod (REFRAME) to reorientate and reposition differently aligned local segment frames to achieve convergence in signals representing the same underlying motion, thereby offering a novel approach to consistently report joint motion. In this study, for the first time, we apply REFRAME to assess the rotational and translational in vivo tibiofemoral motion of ten healthy subjects during stair descent based on kinematic signals collected using a moving videofluoroscope. Kinematics were analysed before and after different REFRAME implementations, revealing generally neutral ab/adduction behaviour, accompanied by varying degrees of a sinusoidal int/external tibial rotation pattern over the activity cycle. Our data demonstrate that different selected implementations of REFRAME are able to highlight different characteristics of the motion patterns: Minimisation of the translational root-mean-square revealed proximodistal translation patterns with overall neutral progression, while anteroposterior translation showed seemingly different levels of correlation with flexion/extension in different subjects. On the other hand, REFRAME minimisation of translational variances exposed differences in the relative mean displacement between the femoral and tibial origins between subjects, highlighting differences in mean centre of rotation positions. This early application of REFRAME for providing an understanding of tibiofemoral kinematics demonstrates the potential of this novel approach to bring clarity to an otherwise complex representation of highly variable time-series signals, while highlighting the philosophical challenges of clinically interpretating kinematic signals in the first place.
Keywords: Gait analysis, Knee, Tibiofemoral, Kinematics, Joint coordinate system, Reference frame, Motion capture, Stair descent
Subject terms: Orthopaedics, Biomedical engineering, Musculoskeletal system
Introduction
In clinical movement biomechanics, motion analysis can be divided into two main components, joint kinematics and kinetics, where the former investigates the relative movement of joint segments. At the most basic level, joint kinematics fundamentally describe the rotational and/or translational displacements of a rigid body relative to another, where both rigid segments are connected by an articulating joint. Characterisation of these displacements can be achieved by defining a coordinate frame fixed to each segment, and tracking the movement of one frame with respect to the other. The position and orientation of each frame relative to the segment it represents can be defined based on e.g. anatomical landmarks1,2 or functional calibration movements3,4. The exact pose (i.e. orientation and position) of a segment’s local coordinate frame will depend on the specific frame definition approach; in other words, for a single joint segment, two different approaches will, in almost all cases, lead to two different reference frames5. As a result, the set of joint axes identified using one landmark-based approach will not necessarily match the set of axes identified by a different landmark-based approach, let alone axes identified using a functional method.
In the specific case of the knee joint, early studies inferred that different axes could be used interchangeably. For instance, Churchill and co-workers stated that the transepicondylar axis “closely approximates” the optimal flexion axis, where the latter “can be considered the true flexion axis of the knee”2. Such statements have been misinterpreted to mean that the transepicondylar axis and a functional flexion axis could be suitable substitutions for one another, which inherently assumes that minor differences between joint axes lead to proportionally small differences between the kinematic signals stemming from those reference frames. This notion has, in turn, contributed to the false impression that, when comparing two or more sets of kinematic signals, clearly visible differences in their shape and magnitude could immediately be interpreted as evidence of fundamentally different underlying joint motion patterns. Despite the subsequent publication of studies that have explicitly challenged these early simplified models5–7, as well as official attempts to establish uniformity across studies to allow comparisons between datasets8, a clear understanding that different kinematic signals do not necessarily imply different underlying joint motion patterns is not ubiquitous among the biomechanics community.
In recent years, our investigations have conclusively shown that even minor (e.g. < 3°) differences in frame orientation can lead to substantial variation in the shape and magnitude of kinematic signals due to cross-talk between reference frames9,10; an effect that is further exacerbated by differences in frame origin position, which can be present even when relying on a single common joint axis approach11,12. As a result, an easily reconcilable representation and understanding of movement patterns remains lacking5, hence limiting our ability to compare kinematic datasets across studies and between labs, and even hindering a consistent clinical interpretation of joint motion patterns. To address this issue, we previously presented the REference FRame Alignment MEthod (REFRAME)13, which expands on the Frame Orientation Optimisation Method (FOOM)9 by enhancing flexibility and incorporating joint translations (see Supplementary Material for details on how FOOM relates to REFRAME), to allow consistent local reference frame alignment even among datasets derived using different joint axis approaches.
Importantly, considerable work has already been undertaken to investigate knee movement patterns during different functional activities14–17. Our recent analysis found that healthy knees exhibited a range of motion (ROM) of approximately 13° in int/external tibial rotation and 6° in ab/adduction during stair descent14. Results also indicated that although there was large variation in the degree of int/external tibial rotation present at heel strike, subjects consistently demonstrated a tendency to rotate their tibia internally during the stance phase to reach peak internal rotation shortly before toe-off, ending with an externally rotating tibia in preparation for the next heel strike.
Given that the aforementioned studies were also potentially susceptible to the cross-talk effects described above, it is important to assess whether past work needs to be revisited, and explore whether a revised analysis that incorporates tools such as REFRAME produces a different interpretation of the underlying joint movement patterns. Since REFRAME offers the ability to retrospectively analyse datasets and account for inherent cross-talk artefact, we therefore aimed to understand whether new insights into the interpretation of functional joint kinematics can be gained through application of these techniques. In this study, we thus expand on the aforementioned investigations by including a larger cohort of ten healthy subjects in order to explore how subject differences manifest before and after REFRAME implementation.
Methods
One clear requirement prior to comparing kinematic signals before and after REFRAME implementation was to further validate REFRAME’s ability to produce convergence in kinematic signals that were derived using different joint axis approaches, yet correspond to a single common underlying movement pattern. Here, we relied on in vivo kinematic data previously collected as part of a separate study14. In that study, moving videofluoroscopy18 was used to capture the tibiofemoral kinematics of ten healthy subjects with neutral knee alignments as they performed a minimum of five valid cycles of stair descent. Similar to our previous investigation5,13 three different approaches were used to establish a primary flexion axis: a cylindrical axis approach (CA), a functional flexion axis approach (FFA), and a transepicondylar axis approach (TEA) (for further details on axis definitions see1–3,5,19–21). By designating corresponding ab/adduction and int/external rotation axes, as well as a femoral reference frame origin, three local femoral frames were defined based on the three specified flexion axis variations. Conversely, a single common local reference frame was defined for the tibial segment. Six degrees-of-freedom (DOFs) tibiofemoral kinematics (i.e. joint rotations and translations) were calculated according to each of these three variations of the femoral segment frame. Joint rotations were given by the relative orientations of the tibial relative to the femoral segment frame, following an intrinsic XYZ (extension-adduction-internal tibial rotation for a right knee) rotation sequence as previously described13,22. (Extension, adduction, and tibial internal rotation are positive rotations as per the right-hand rule). Joint translations were dictated by the position of the femoral frame origin relative to the tibial frame origin, in the tibial coordinate system.
After raw CA, FFA and TEA kinematic signals had been derived, reference frame orientations were optimised based on an adaptation of our previously presented FOOM approach9 (a precursor and specific sub-implementation of the larger REFRAME framework) that we recommended for flexion dominant gait activities. (Note: the term raw is used to refer to reference frames and/or kinematic signals that have not yet undergone optimisation with REFRAME.) This configuration of REFRAME consisted of minimising the root-mean-square (RMS) of ab/adduction and int/external rotation, both with a weighting of 1. Transformations of the raw tibial frame consisting of rotations around the mediolateral axis were restricted to zero. Additionally, transformations of the raw femoral frame consisting of rotations around the mediolateral axis were minimally penalised (criteria weighting: 0.0001). This REFRAME configuration prevented considerable changes in the orientations of the local frames’ anteroposterior and longitudinal axes in the sagittal plane. The effect of the additional constraints ensured the REFRAMEd kinematics could still be reconciled with our general existing clinical understanding of joint angles (Supplementary Figure S1). Based on the resulting optimally oriented local reference frames, the REFRAMEd rotational tibiofemoral kinematics were calculated for each individual subject and trial.
After optimisation of the coordinate system orientations, two different REFRAME variations were investigated for the optimisation of frame origin positions (i.e. joint translations). The first consisted of a minimisation of the RMS of mediolateral (ML), anteroposterior (AP), and proximodistal (PD) translations, while the second minimised the variance of the same three joint translations. In both cases, all three minimisations were weighted equally with a weighting of 1. Once again, REFRAMEd translational kinematic signals were calculated according to each of the two presented REFRAME implementations. All REFRAME implementations were executed in MATLAB (vR2022a; The Mathworks Inc., Natick, Massachusetts, USA).
For each subject and trial, kinematic signals were plotted to assess differences between axis approaches, as well as whether signal convergence can be achieved for all individual trials through application of REFRAME. Mean intra-subject kinematic signals (and the corresponding standard deviations) were additionally plotted to examine tibiofemoral movement profiles with and without REFRAME. Finally, box plots were made to illustrate the different subject mean ROMs (calculated from each subject’s mean curve) in each DOF.
Ethics declarations
Collection of the original fluoroscopy data that was analysed here occurred within the scope of a separate cited study, which was performed in accordance with relevant guidelines and states that all subjects “provided written, informed consent to participate in this study, which was approved by the local ethics committee (KEK-ZH-Nr. 2016-00410)”5.
Results
Differences between the three raw sets of kinematic signals were strongly apparent according to the joint axis approach used (CA, FFA, TEA). For several subjects, raw CA-based signals visually displayed a higher level of agreement with raw FFA-based signals than with TEA (see e.g. Subject 2, Supplementary Figs. S15–24). Furthermore, raw TEA-based signals presented clear indications of being affected by cross-talk artefact, as evidenced by visible amplifications of AP translation signals with flexion angle (see e.g. Subject 1, Supplementary Figs. S5–14). Despite the stronger similarity observed between raw CA- and FFA-based signals in most participants and most DOFs, two subjects (3 and 8) displayed high agreement in the raw translation signals derived from CA and TEA approaches (Supplementary Figs. S26, 28, 30, 32, 34 and S76, 78, 80, 82, 84).
Much like in our previous investigation13, essentially no visible differences were discernible between the three sets of tibiofemoral kinematics after REFRAME implementation in all six DOFs (Supplementary Figs. S5–104), consistent with the notion that all three datasets corresponded to a single common underlying motion pattern.
Joint rotations – raw signals
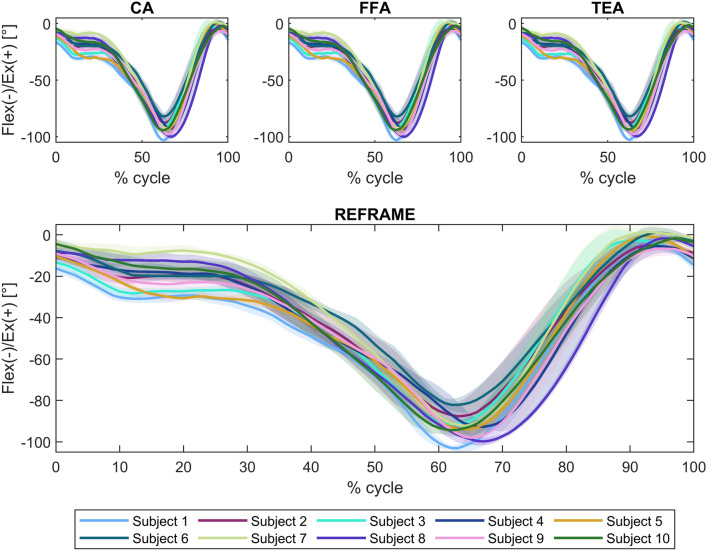
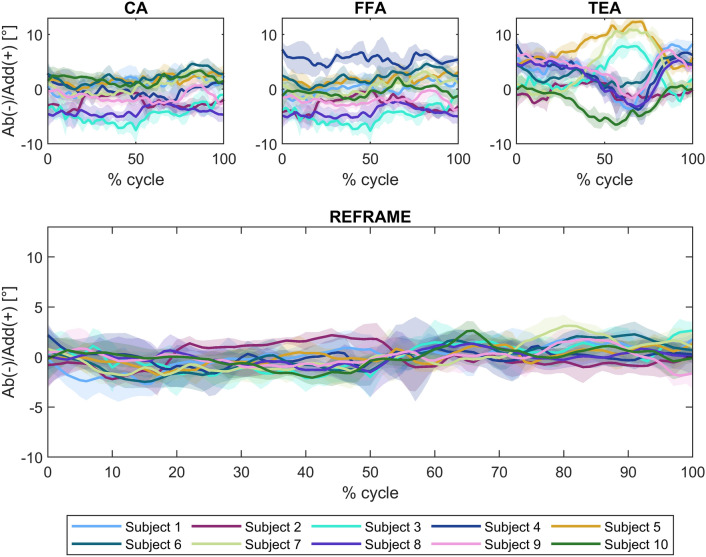
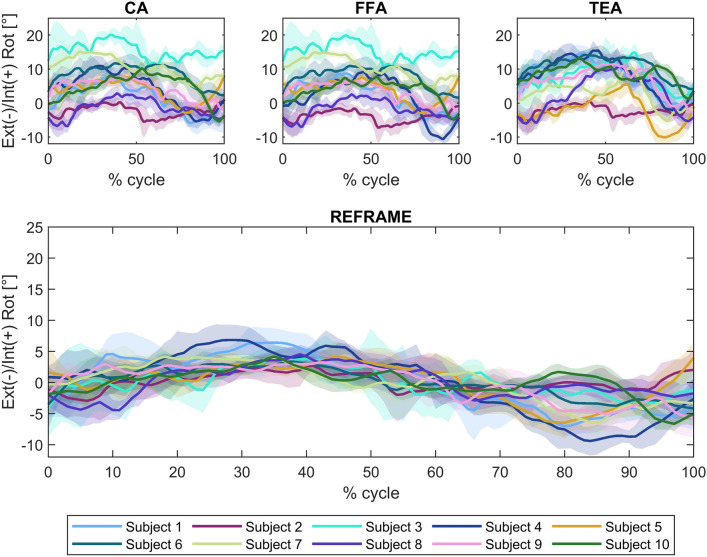
In the sagittal plane, no notable differences were visible between the three sets of raw flexion/extension signals (Fig. 1). Average ROM was consistent across joint axis approaches, falling between 90.7° ± 5.4° and 90.9° ± 5.3° (Fig. 2). In the frontal plane, the lowest inter-subject variability was seen in the raw CA-based ab/adduction signals, followed by FFA- and finally TEA-based signals (Fig. 3). While average ab/adduction ROMs were 4.3° ± 1.1° and 4.3° ± 1.0° for CA and FFA, respectively, TEA-based signals reached an average ROM of 8.9° ± 2.7° (Fig. 4). In the transverse plane, raw CA- and FFA-based int/external rotation signals were generally similar for most subjects, with both signal sets displaying higher inter-subject variation than TEA (Fig. 5). On average, TEA-based signals exhibited higher ROM (13.9° ± 3.7°) than CA- (11.1° ± 3.2°) and FFA-based (11.1° ± 3.6°) int/external rotation signals (Fig. 6).
Fig. 1.
Rotational kinematics: Flexion(flex)/extension(ex) (in degrees) of the tibial relative to the femoral segment frame over a stair descent cycle. Solid lines represent the mean across all trials for each subject, while the corresponding shaded areas depict the associated standard deviations for each individual. Values are illustrated for each of the three joint axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis) before REFRAME (top), and after REFRAME (bottom). Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore coincide graphically. Additional note to readers from a clinical background: knee extension is illustrated here as positive because following the right-hand rule it corresponds with a positive rotation around the laterally pointing mediolateral axis for a right knee.
Fig. 2.
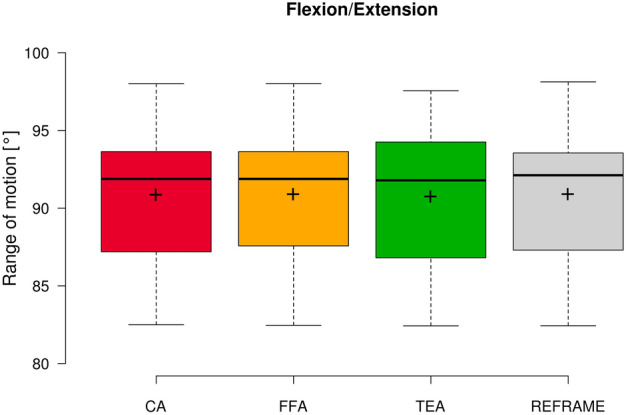
Box plot of flexion/extension range of motion (all subjects and repetitions) according to each of the three different axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis), as well as after REFRAME implementation. Centre lines illustrate the medians, while box limits depict the 25th and 75th percentiles. Whiskers extend to data points that are less than 1.5 times the interquartile range away from the 1st and 3rd quartiles. Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore all display the same range of motion values.
Fig. 3.
Rotational kinematics: Abduction(ab)/adduction(add) (in degrees) of the tibial relative to the femoral segment frame over a stair descent cycle. Solid lines represent the mean across all trials for each subject, while the corresponding shaded areas depict the associated standard deviations for each individual. Values are illustrated for each of the three joint axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis) before REFRAME (top), and after REFRAME (bottom). Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore coincide graphically.
Fig. 4.
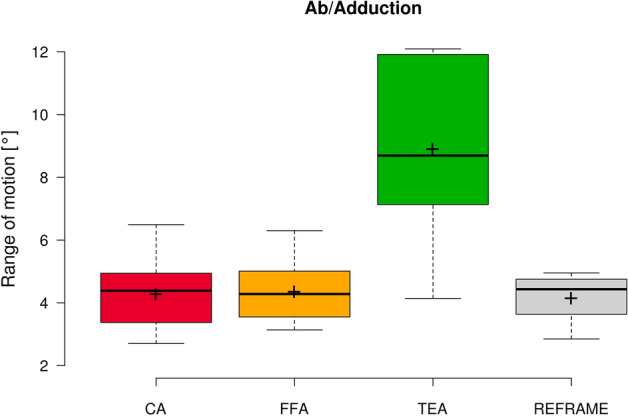
Box plot of ab/adduction range of motion (all subjects and repetitions) according to each of the three different axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis), as well as after REFRAME implementation. Centre lines illustrate the medians, while box limits depict the 25th and 75th percentiles. Whiskers extend to data points that are less than 1.5 times the interquartile range away from the 1st and 3rd quartiles. Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore all display the same range of motion values.
Fig. 5.
Rotational kinematics: External(ext)/internal(int) rotation (in degrees) of the tibial relative to the femoral segment frame over a stair descent cycle. Solid lines represent the mean across all trials for each subject, while the corresponding shaded areas depict the associated standard deviations for each individual. Values are illustrated for each of the three joint axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis) before REFRAME (top), and after REFRAME (bottom). Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore coincide graphically.
Fig. 6.

Box plot of int/external rotation range of motion (all subjects and repetitions) according to each of the three different axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis), as well as after REFRAME implementation. Centre lines illustrate the medians, while box limits depict the 25th and 75th percentiles. Whiskers extend to data points that are less than 1.5 times the interquartile range away from the 1st and 3rd quartiles. Outliers are indicated by circles. Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore all display the same range of motion values.
Joint translations – raw signals
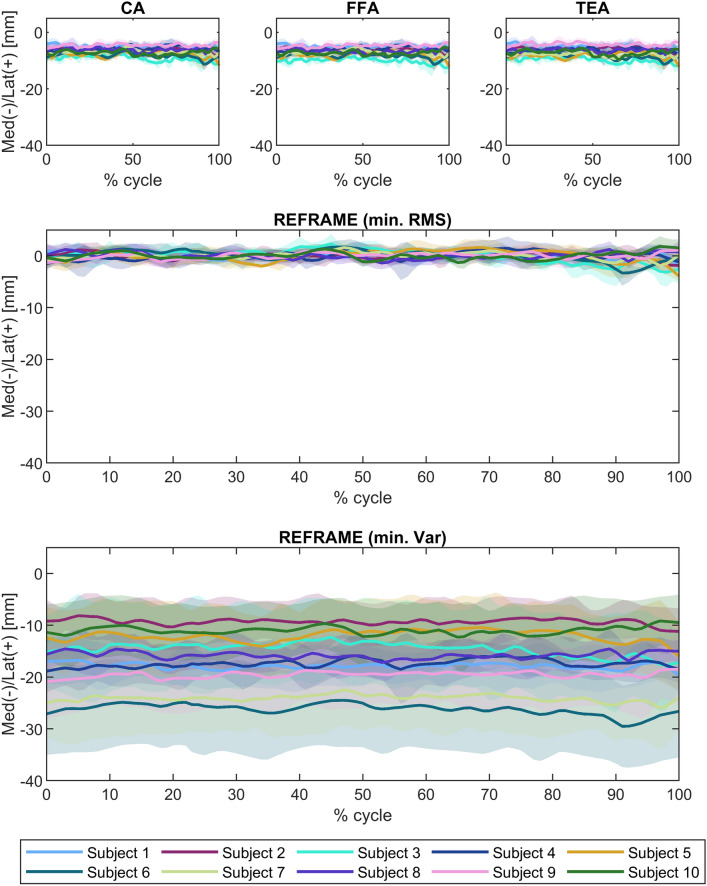
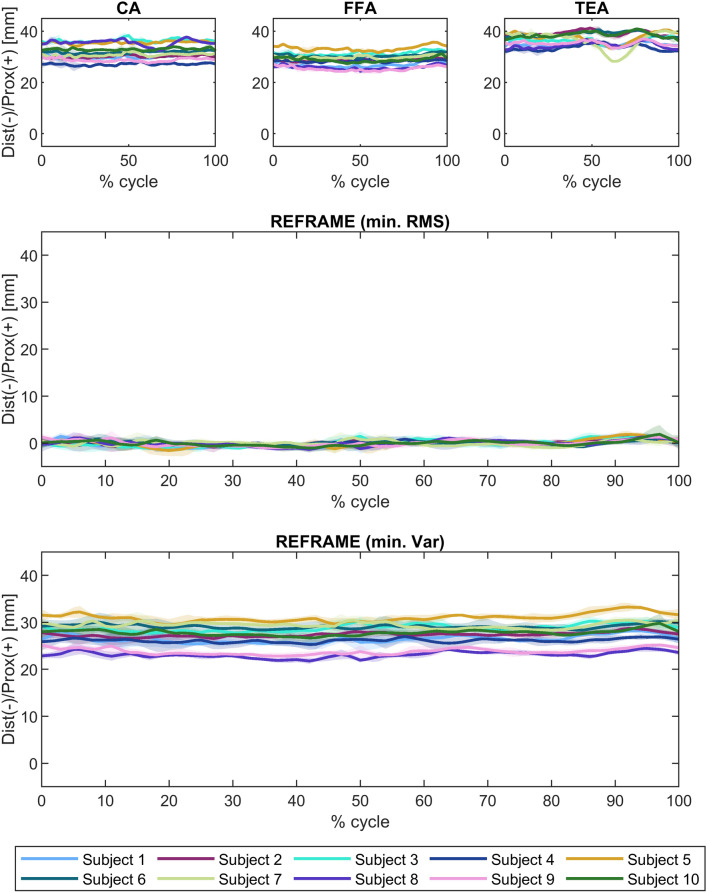
Raw ML translation signals were comparable among the three joint axes approaches (Fig. 7), as were average raw ROMs along the ML axis (3.5 mm ± 0.9 mm, 3.6 mm ± 1.0 mm, and 3.7 mm ± 1.0 mm for CA-, FFA-, and TEA-based signals, respectively; Fig. 8). The average position of the raw femoral frame origin relative to the tibial origin was fairly constant (roughly 7 mm medially) in the ML direction. Among the three sets of raw AP translations, TEA-based signals seemed to be the most affected by cross-talk, as indicated by the visible association between AP translation and flexion/extension; FFA-based signals, on the other hand, appeared to be the least affected (Fig. 9). FFA-based translation signals along the AP axis also displayed the lowest levels of inter-subject variability out of the three axis approaches investigated. Mean AP translation ROMs varied between the axis approaches, ranging from 6.7 mm ± 1.6 mm for FFA-based signals, to 11.3 mm ± 4.8 mm for CA-based signals, and 17.5 mm ± 3.3 mm for TEA-based signals (Fig. 10). Lastly, of the three PD translation signals, TEA-based signals once more appeared to be the most susceptible to cross-talk artefact (especially Subject 7), while CA- and FFA-based signals displayed similar levels of inter-subject variability (Fig. 11). Regarding PD translation signals, before REFRAME implementation, the average PD position of the femoral frame origin relative to the tibial origin varied little throughout the gait cycle for most subjects. Femoral origins were mostly positioned between approximately 25 and 40 mm proximal to the tibial origin. Average translational ROM along the PD axis was highest for TEA-based signals (5.0 mm ± 2.7 mm), followed by FFA- (2.9 mm ± 0.7 mm) and CA-based signals (2.5 mm ± 1.0 mm) (Fig. 12).
Fig. 7.
Translational kinematics: Medio(med)-lateral(lat) translation (in mm) of the femoral relative to the tibial segment frame over a stair descent cycle. Solid lines represent the mean across all trials for each subject, while the corresponding shaded areas depict the associated standard deviations for each individual. Values are illustrated for each of the three joint axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis) before REFRAME (top), after minimisation of root-mean-square using REFRAME (middle), and after minimisation of variance using REFRAME (bottom). Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore coincide graphically.
Fig. 8.
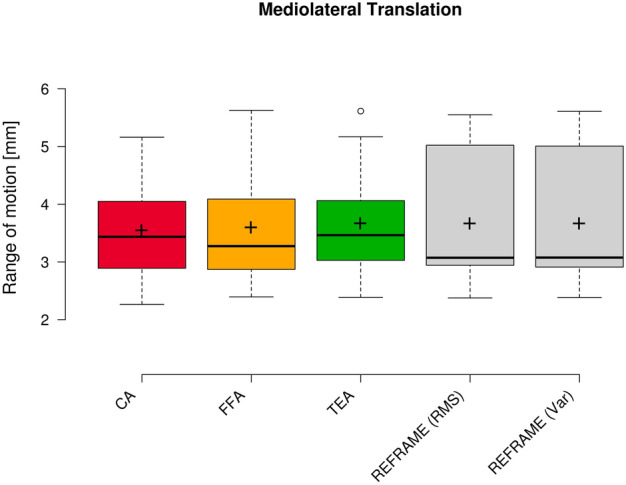
Box plot of mediolateral translation range of motion (all subjects and repetitions) according to each of the three different axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis), as well as after REFRAME implementation. Centre lines illustrate the medians, while box limits depict the 25th and 75th percentiles. Whiskers extend to data points that are less than 1.5 times the interquartile range away from the 1st and 3rd quartiles. Outliers are indicated by circles. Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore all display the same range of motion values.
Fig. 9.
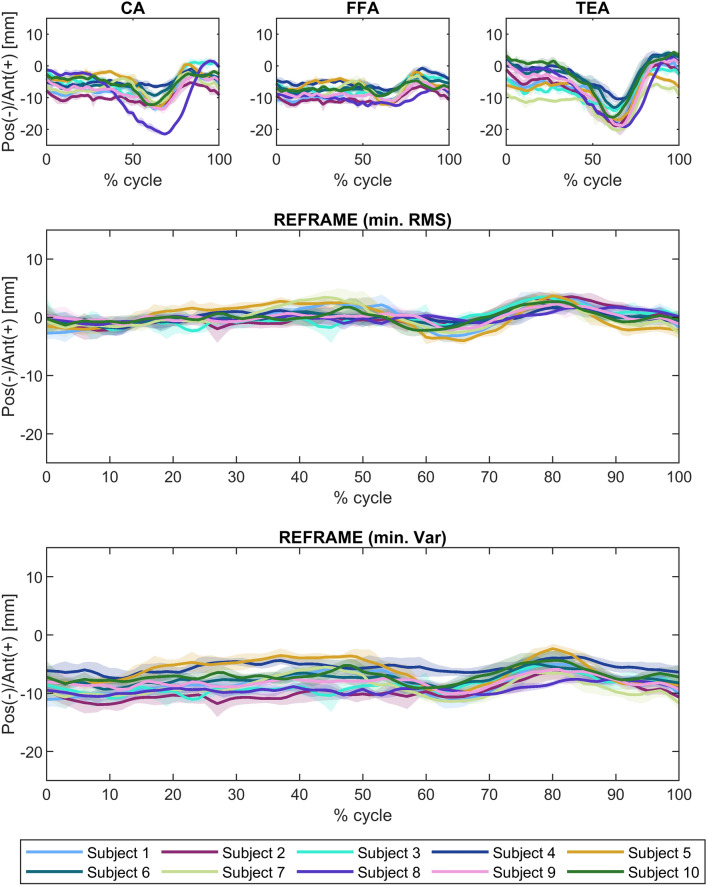
Translational kinematics: Antero(ant)-posterior(pos) translation (in mm) of the femoral relative to the tibial segment frame over a stair descent cycle. Solid lines represent the mean across all trials for each subject, while the corresponding shaded areas depict the associated standard deviations for each individual. Values are illustrated for each of the three joint axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis) before REFRAME (top), after minimisation of root-mean-square using REFRAME (middle), and after minimisation of variance using REFRAME (bottom). Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore coincide graphically.
Fig. 10.
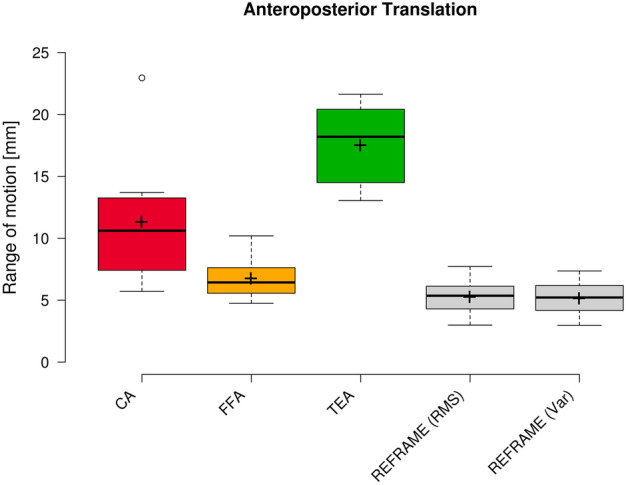
Box plot of anteroposterior range of motion (all subjects and repetitions) according to each of the three different axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis), as well as after REFRAME implementation. Centre lines illustrate the medians, while box limits depict the 25th and 75th percentiles. Whiskers extend to data points that are less than 1.5 times the interquartile range away from the 1st and 3rd quartiles. Outliers are indicated by circles. Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore all display the same range of motion values.
Fig. 11.
Translational kinematics: Proximo(prox)-distal(dist) translation (in mm) of the femoral relative to the tibial segment frame over a stair descent cycle. Solid lines represent the mean across all trials for each subject, while the corresponding shaded areas depict the associated standard deviations for each individual. Values are illustrated for each of the three joint axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis) before REFRAME (top), after minimisation of root-mean-square using REFRAME (middle), and after minimisation of variance using REFRAME (bottom). Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore coincide graphically.
Fig. 12.
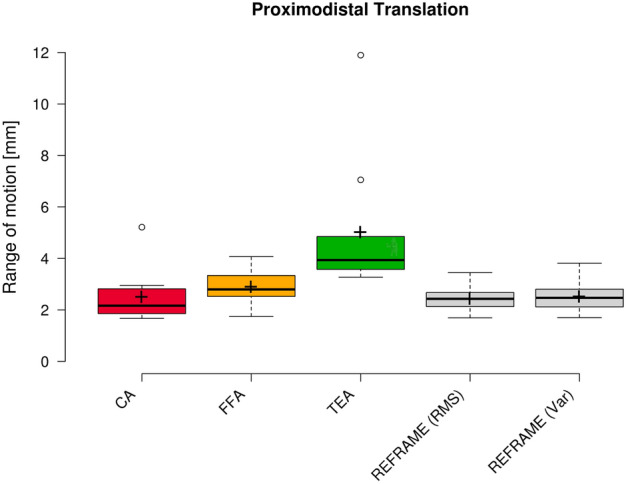
Box plot of proximodistal range of motion (all subjects and repetitions) according to each of the three different axis approaches (CA: cylindrical axis; FFA: functional flexion axis; TEA: transepicondylar axis), as well as after REFRAME implementation. Centre lines illustrate the medians, while box limits depict the 25th and 75th percentiles. Whiskers extend to data points that are less than 1.5 times the interquartile range away from the 1st and 3rd quartiles. Outliers are indicated by circles. Note: kinematic patterns for all three axes converge to a single solution upon application of REFRAME, and therefore all display the same range of motion values.
Joint rotations – after REFRAME
In the sagittal plane, implementation of REFRAME did not lead to distinguishable changes in the flexion/extension signal (Fig. 1). Similarly, flexion/extension ROM was not substantially affected by the optimisation of local frame orientations, averaging 90.9° ± 5.4° after REFRAME (Fig. 2). For rotations in the frontal plane, implementation of REFRAME led to comparatively less variable ab/adduction signals (Fig. 3), and a reduced average ROM of 4.1° ± 0.8° (Fig. 4). In the transverse plane, REFRAME also decreased inter-subject variability of int/external tibial rotation signals, resulting in a perceivable sinusoidal pattern over the activity cycle (Fig. 5), and a decrease in ROM from peak values as high as 19.8° (Subject 4, FFA) to an average of 10.1° ± 3.0° (Fig. 6).
For the femoral reference frame, the differences in orientation between raw and REFRAMEd coordinate systems were virtually negligible around the ML axis. Orientation differences averaged 2.8° ± 2.7° and 2.6° ± 2.5° across all joint axis approaches, subjects, and trials around the AP and PD axes, respectively (Table 1). For the tibial frame, no changes were applied to the local segment frame around the ML axis (in line with our chosen optimisation constraints), while average rotational changes around the AP and PD axes were 2.3° ± 1.5° and 5.2° ± 4.2°, respectively.
Table 1.
Maxima and mean values ± standard deviation of absolute values of rotations (in degrees) and translations (in mm) applied to raw local reference frames as part of REFRAME implementation; Rotations are expressed as an XYZ intrinsic Cardan angle sequence; Transformations are expressed in the corresponding raw reference coordinate systems (x-axis = mediolateral; y-axis = anteroposterior; z-axis = proximodistal).
| Absolute values | |||
|---|---|---|---|
| Maximum | Mean ± SD | ||
| Femur | |||
| Rot [°] | x | 0.0 | 0.0 ± 0.0 |
| y | 11.6 | 2.8 ± 2.7 | |
| z | 10.1 | 2.6 ± 2.5 | |
| Trans [mm] (min. RMS) | x | 25.9 | 10.2 ± 6.6 |
| y | 10.9 | 3.8 ± 3.6 | |
| z | 10.9 | 3.7 ± 2.9 | |
| Trans [mm] (min. Var) | x | 26.8 | 10.5 ± 7.0 |
| y | 10.8 | 4.0 ± 3.6 | |
| z | 10.8 | 3.7 ± 2.9 | |
| Tibia | |||
| Rot [°] | x | 0.0 | 0.0 ± 0.0 |
| y | 7.2 | 2.3 ± 1.5 | |
| z | 15.0 | 5.2 ± 4.2 | |
| Trans [mm] (min. RMS) | x | 33.8 | 16.7 ± 6.9 |
| y | 10.9 | 6.2 ± 2.2 | |
| z | 30.9 | 27.8 ± 2.1 | |
| Trans [mm] (min. Var) | x | 0.0 | 0.0 ± 0.0 |
| y | 0.0 | 0.0 ± 0.0 | |
| z | 0.0 | 0.0 ± 0.0 | |
Joint translations – after REFRAME (minimising RMS)
REFRAME optimisation based on the minimisation of translation RMSs led to an offset in the ML translation signals, such that the mean ML position of the femoral origin relative to the tibial origin was approximately 0 mm (Fig. 7). These effects were in line with our previous investigation of the impact of choosing RMS as the optimisation parameter13. Translational ROM along this axis was not substantially affected by the implementation of REFRAME, averaging 3.7 mm ± 1.2 mm (Fig. 8), although it did increase for one of the ten subjects, leading to a larger interquartile range. For AP translation, REFRAME implementation visibly reduced inter-subject variability, and similarly to ML, consistently shifted the mean AP values towards 0 mm (Fig. 9). After REFRAME, subtle differences in the levels of variation in AP signal magnitude with flexion/extension were discernible among different subjects. AP ROM also noticeably declined, reaching an average of 5.2 mm ± 1.4 mm (Fig. 10). In terms of PD translation, REFRAMEd signals exhibited fairly constant behaviour throughout the entire activity cycle, once again settling at approximately 0 mm (Fig. 11), as upheld by the minimisation of RMS. After minimisation of translational RMSs through REFRAME, average ROM along the PD axis was 2.4 mm ± 0.5 mm (Fig. 12).
This REFRAME implementation resulted in modifications to the femoral origin position of up to 25.9 mm along the ML axis, and 10.9 mm along both the AP and PD raw femoral axes. The tibial origin, on the other hand, was translated a maximum of 33.8 mm along the ML axis, 10.9 mm along the AP axis and 30.9 mm along the PD axis.
Joint translations – after REFRAME (minimising variance)
As previously described, a second REFRAME adaptation was implemented to optimise the position of local reference frame origins based on the minimisation of variance (instead of RMS) for all three translations. After this alternative implementation of REFRAME, the general patterns of all three translational signals were consistent with the results obtained after minimising RMS. This second version of REFRAME led to greater inter-subject variability in mean translation values, especially along the ML and AP axes (Figs. 7 and 9). Despite this increased variation, ML translation signals for all subjects became negative, indicating a medially located joint centre of rotation relative to the tibial origin. On the other hand, mean tibiofemoral PD translation values for all subjects fell between 20 and 35 mm for the relative position of the femoral relative to the tibial origin, coherent with a femoral origin that was located proximally to the tibial origin (Fig. 11). Average ROMs were comparable to those resulting from REFRAME optimisation based on RMS, averaging 3.7 mm ± 1.2 mm, 5.1 mm ± 1.4 mm, and 2.5 mm ± 0.6 mm for ML, AP and PD translations, respectively (Figs. 8, 10, and 12).
The implementation of REFRAME based on translational variance minimisation led to changes in the position of the femoral origin within the bone segment as high as 26.8 mm, 10.8 mm and 10.8 mm around the ML, AP and PD axes, respectively. Changes in the position of the tibial origin as a result of REFRAME implementation were negligible in all directions. In fact, the largest translation applied to the raw tibial origin along any given axis by the optimisation was 3.9 × 10–5 mm, i.e. virtually 0 mm.
Discussion
Despite multiple studies showing that kinematic signals are sensitive to the orientation of the knee flexion axis5,23–25, the influence of local 3D reference frame orientation and position is frequently underestimated (or in some cases, haphazardly ignored), especially in investigations involving the comparison and interpretation of kinematic signals. Difficulties in achieving a repeatable and reproducible representation of human joint motion has therefore limited our ability to attain a robust understanding of knee kinematics, even among asymptomatic populations, let alone detect differences in pathological joints. In this study, the fluoroscopy-based tibiofemoral kinematics of ten healthy subjects were analysed before and after the implementation of REFRAME, thereby substantiating results obtained in a previous investigation13 in nine additional subjects. Moreover, these latest findings served as a starting point for the analysis of inter-subject differences in kinematic signals in which cross-talk artefacts due to frame alignment inconsistencies have been addressed repeatably.
Analysis of the raw kinematic signals obtained from calculating tibiofemoral rotations and translations based on three different joint axis methodologies, strongly indicated that the CA and FFA approaches produced generally closer approximations of each other than the TEA approach. We therefore challenge Churchill and colleagues’ early proposal that a TEA based on the palpation of bony landmarks acts as an accurate approximation of the knee joint’s functional flexion axis2. Instead, in the absence of post-processing methods such as REFRAME, our results partially support the findings of our recent work5 favouring the use of an FFA or CA approach to avoid the high susceptibility to cross-talk artefact demonstrated by TEA-based kinematics. Under the assumption that joint segments are rigid bodies (for measurements affected by soft-tissue artefact, pre-processing raw data with dedicated algorithms to reduce motion artefact and approximate rigid marker configurations would be required), REFRAME then additionally allows users to optimise frame pose in all six DOFs, rather than performing no frame optimisation (e.g. TEA, CA) or only optimising the orientation of the ML axis (e.g. FFA). Notably, joint axes defined using REFRAME are effectively functional in nature (and as such both subject- and activity-dependent), as they leverage information contained within the kinematic signals to arrive at the optimised reference frames (thus inherently less susceptible to intra- and inter-observer errors). In this study, the availability of fluoroscopic data to assess the pose of local segment frames relative to each subject’s bone geometry after REFRAME optimisation could potentially be crucial to explore whether kinematic signals represent similar motion in different subjects (Supplementary Fig. S2). It is important to note, however, that the pose of the true instantaneous axis of rotation (i.e. axis with zero translational velocity) is not constant relative to the moving segment’s bone geometry. As a result, any anatomically fixed axis will deviate from the instantaneous axis of rotation as soon as complex motion like e.g. rolling without slipping occurs, leading to cross-talk between flexion and translation (Supplementary Fig. S3). Consequently, any segment-fixed axis may be able to correctly characterise relative segment motion at particular timepoints (whenever the axis coincides with the instantaneous axis of rotation) but will likely introduce translational cross-talk over the rest of the movement cycle. While an exploration of the philosophical discussion that arises regarding the advantages and pitfalls of anatomically fixed axes versus functional joint axes is beyond the scope of this study, researchers should stay aware of the implications that choosing one type of axes over the other has on the interpretability of their reported results.
Comparison of raw kinematic signals in all six DOFs was followed by optimisation of frame orientations and positions using REFRAME. In line with the previously presented two-stage implementation of REFRAME13, only frame orientations were optimised in the first stage, followed by the optimisation of frame origin positions in the second stage. In this study, we chose to minimise ab/adduction and int/external rotation RMS, while restricting changes in the orientation of the tibial local reference frame around the ML (x-) axis, and minimally penalising analogous changes to the femoral reference frame. This REFRAME configuration was selected to minimise cross-talk artefact and maximise rotations in the sagittal plane, which we previously recommended for aligning the axes in clearly flexion-dominant activities13. Here, the most notable changes that resulted from REFRAME axis realignment were present in out-of-sagittal-plane rotations. After REFRAME, the resultant ab/adduction patterns over stair descent became both more constant and neutral, while subjects exhibited subtly varying degrees of a sinusoidal pattern in their int/external rotation. These observations are consistent with previous interpretations that suggest knee motion is dominated by rotation in the sagittal and transverse planes2. Even though the resulting kinematic signals appear smaller in magnitude, it is important to note here that REFRAME minimisation does not reduce the actual motion that occurs in the joint. Given as the transformations applied to the local segment reference frames are constant over the entire cycle, REFRAME can help illustrate the same articulating movement patterns while excluding artefact amplifications linked to cross-talk13. Notably, the magnitude of rotations around the AP (y-) and PD (z-) axes performed by REFRAME to reconcile the orientation of local reference frames averaged only 2.8° ± 2.7° and 2.6° ± 2.5°, respectively, for the femur. For the tibia, they averaged 2.3° ± 1.5° around the AP axis, and 5.2° ± 4.2° around the PD axis. These magnitudes were well within the range of uncertainty typically associated with joint axis methods11,26, especially considering that while absolute changes to the tibial frame orientation did exceed 5° around the PD axis, relative changes between femur and tibia did not. Researchers are encouraged to review cases where relative changes in frame orientation drastically exceed 5° to evaluate the possible clinical implications of such transformations. Importantly, the standardisation of kinematic signals towards a single repeatable representation (c.f. Subject 8 in Fig. 9) brings us closer to achieving a common and consistent interpretation of joint motion patterns between subjects, studies and even laboratories. By excluding any signal differences that could be explained by distinctions in analysis methodology (specifically, by harmonising reference frame orientations and positions), optimised signals offer stronger evidence of potential differences in joint motion.
The first REFRAME configuration we explored for the optimisation of local frame origin locations relied on a minimisation of the RMS of joint translations along all three coordinate frame axes, targeting a zero-mean signal with minimal variation over the activity cycle. While this choice of objective criteria held the potential to highlight inter-subject differences by minimising signal variability, it targeted mean value of 0 mm along all three axes, corresponding with the underlying assumption that the femoral and tibial origins would ideally coincide or be only minimally offset.
A second implementation of REFRAME was also investigated, which minimised translational variance instead of RMS. The minimisation of variance for all three joint translations effectively minimised signal amplitude over the activity cycle (consistent with the notion that changes in joint translation are generally small in magnitude), while allowing for any mean translation value. This philosophy better aligns with a more clinically intuitive model of the knee that does not assume the femoral and tibial origins should be coincident during standing. Instead, this second implementation facilitates a knee model in which the femoral and tibial origins are likely offset by roughly fixed distances of easily 10 mm or more (Supplementary Fig. S4).
For joint translations, these two different implementations of REFRAME each appear to highlight different relevant aspects of joint motion during stair descent. The first REFRAME minimisation of translation RMS aimed for coincident origins along all axes, thereby “flattening” the kinematic signals towards a common mean close to 0. This implementation emphasised differences in the progression of the kinematic signal over the activity cycle, especially in AP translation. While PD translation appears to have been rather constant, ML translation signals showed slightly more local fluctuations around a constant mean. These fluctuations, however, are likely the result of out-of-plane errors in the 2D/3D registration of uniplanar fluoroscopy data. Moreover, for one of the ten subjects, the set of optimal orientations and positions found after REFRAME were associated with an increase in average ML ROM. This effect could be explained by the choice to weigh the minimisation of all parameters equally, such that the subtle increase in ML ROM was offset by the comparably larger decrease in e.g. AP ROM, rendering that solution for the objective function to nevertheless be optimal. Given the limitations of single-plane fluoroscopy, the ML translation results presented in this study should be interpreted with caution, especially considering that the ML registration of images had to be manually adjusted for several trials14,27. Future research leveraging state-of-the-art dual-plane moving fluoroscopy could lead to confirmation of this interpretation, as well as support insights into the advantages provided by other REFRAME implementations. On the other hand, AP translation patterns displayed subtle peaks at approximately 50% and 80% of the gait cycle, with a slight global minimum between 60 and 70%. While this general overall pattern was fairly repeatable across all subjects, signal amplitude varied between subjects, likely a manifestation of variation in the degree to which different individuals’ AP translation relates to knee flexion.
The second implementation of REFRAME minimising translation variance effectively “flattened” the curve (similar to RMS) but towards a mean value (not necessarily 0) for each individual. Although differences in pattern progression over the activity cycle are less evident than when minimising RMS, this implementation minimising variance reveals potentially interesting differences in the mean values after optimisation. The translational offset between the femoral and tibial origins axially is consistently between 20 and 35 mm over the entire gait cycle which, when combined with the almost negligible ab/adduction ROM, suggests that little (if any) condylar lift-off occurs in healthy knees. This REFRAME interpretation is more compatible with current clinical understanding of joint motion (e.g. that effectively no condylar lift-off takes place in healthy knees during gait) than the far more extreme interpretation of movement patterns suggested by the raw joint axes (e.g. that the joint gap is compressed by over 10 mm in Subject 7, according to TEA, Fig. 11).
The location of the REFRAME origins can also provide critical insights into other aspects of joint functionality, especially considering the optimised origin after translation variance minimisation is conceptually comparable to an average pivot point. Taking into account that the initial mediolateral position of the tibial origin was at the midpoint between lateral and medial epicondyles, and that this origin barely moved with REFRAME optimisation, our results suggest a joint centre of rotation that is located medially, in line with Freeman and Pinskerova’s proposed general description of knee motion28,29. Here, one valuable aspect of REFRAME is that such functional characteristics of joint motion can be directly extracted without further analysis (although additionally exploring the motion of specific bony landmarks can certainly still be valuable in several cases). Notably, even though the variance-based implementation of REFRAME predictably led to larger differences in the mean relative displacement of femoral and tibial origins, results show that both REFRAME implementations led to almost identical average translational ROM along all three axes. These results exemplify how different REFRAME implementations could emphasise different motion characteristics, highlighting intra- and inter-subject patterns that become noticeable only after REFRAME has successfully excluded signal variations associated with reference frame pose. Nevertheless, the practical implications of different REFRAME formulations are highly nuanced, and further investigations are necessary before a full understanding of the potential of this approach for interpreting joint kinematics can be gained.
In this study, our results clearly demonstrate that the numerical magnitude of kinematic signals can vary greatly depending on the exact orientation and position of joint axes. For example, for a unique physical motion pattern, an AP displacement measurement of -10 mm, could easily become 0 mm or + 5 mm after slight local frame reorientation and/or repositioning9,13. As a result, evidence suggests that any attempt to clinically interpret joint kinematics based on the plots of joint angles and/or translations should generally avoid extracting inferences from their absolute values. Instead, the focus should be on assessing relative differences, either for a single knee joint (e.g. at different instances in time), or between knees (e.g. left knee vs. right knee of the same subject, or different subjects). On the one hand, there may be a potential advantage to switching our focus from the interpretation of kinematic pattern shape and instead concentrating on the extraction of discrete, yet informative, kinematic features (e.g. position of the femoral origin after minimisation of translational variances to examine the centre of rotation in the transverse plane). On the other, however, as long as traditional plots of kinematic time series continue to be used for interpretation, our findings clearly substantiate that the removal of kinematic signal differences caused by inconsistent representations of joint segments is critical to allow the detection of actual differences in joint motion (while showcasing REFRAME’s ability to tackle a key component of this challenge). In this manner, this study compellingly illustrates the pivotal role that methods like REFRAME (which can successfully account for differences in frame orientation and position) stand to play in our clinical understanding of joint movement patterns.
Supplementary Information
Acknowledgements
The authors wish to thank Michael Utz for his valuable insights and ongoing support.
Author contributions
Conceptualisation: A.O.V., W.T., B.P., P.S., A.S.; Methodology: A.O.V., A.S.; Software: A.O.V., A.S.; Formal analysis: A.O.V., B.P., P.S., A.S.; Investigation: A.O.V., A.S.; Resources: W.T., B.P., P.S., A.M., T.G.; Data curation: A.O.V., B.P., P.S., A.S.; Writing—original draft: A.O.V., W.T., A.S.; Writing—review and editing: A.O.V., W.T., B.P., P.S., A.M., T.G., A.S.; Supervision: W.T., A.M., T.G., A.S.; Project administration: W.T., T.G., A.S.; Funding acquisition: W.T., A.M., T.G. All authors have read and agreed to the published version of the manuscript.
Data availability
The implemented method (REFRAME) can be openly accessed by downloading the standalone application and accompanying user documentation available in https://bbraun.info/reframe and https://movement.ethz.ch/data-repository/reframe.html. Additional MATLAB files to enable advanced custom features are also available under license from the corresponding author upon reasonable request. The original subject data used during the current study to validate the proposed method is part of a dataset generated within the scope of a separate, previously published study5. For further information regarding the data availability of this referenced kinematic dataset, please refer to the original article available here: https://doi.org/10.1016/j.jbiomech.2022.111306; and/or contact the respective corresponding author of that study.
Declarations
Competing interests
A.O.V., A.M., T.G. and A.S. are employees of B. Braun Aesculap AG, Tuttlingen, Germany. W.T. has received compensation as a member of a scientific advisory board of the company. A.O.V., A.S., and A.M. are all listed as co-inventors on a pending patent application submitted by Aesculap AG under number DE102022125697A1, which claims a system for standardising axis orientation and position in kinematic data relating to a patient’s body joint. A version of the REFRAME code is nevertheless openly available upon request for non-commercial purposes.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-76275-3.
References
- 1.Berger, R. A., Rubash, H. E., Seel, M. J., Thompson, W. H. & Crossett, L. S. Determining the rotational alignment of the femoral component in total knee arthroplasty using the epicondylar axis. Clin. Orthop. Relat. Res.286, 40–47 (1993). [PubMed] [Google Scholar]
- 2.Churchill, D. L., Incavo, S. J., Johnson, C. C. & Beynnon, B. D. The transepicondylar axis approximates the optimal flexion axis of the knee. Clin. Orthop. Relat. Res.356, 111–118 (1998). [DOI] [PubMed] [Google Scholar]
- 3.Ehrig, R. M., Taylor, W. R., Duda, G. N. & Heller, M. O. A survey of formal methods for determining functional joint axes. J. Biomech.40(10), 2150–2157 (2007). [DOI] [PubMed] [Google Scholar]
- 4.Ehrig, R. M., Taylor, W. R., Duda, G. N. & Heller, M. O. A survey of formal methods for determining the centre of rotation of ball joints. J. Biomech.39(15), 2798–2809 (2006). [DOI] [PubMed] [Google Scholar]
- 5.Postolka, B. et al. Interpretation of natural tibio-femoral kinematics critically depends upon the kinematic analysis approach: A survey and comparison of methodologies. J. Biomech.144, 111306 (2022). [DOI] [PubMed] [Google Scholar]
- 6.Victor, J. Rotational alignment of the distal femur: A literature review. Orthopaed. Traumatol. Surg. Res.95(5), 365–372 (2009). [DOI] [PubMed] [Google Scholar]
- 7.Feng, Y. et al. In-vivo analysis of flexion axes of the knee: Femoral condylar motion during dynamic knee flexion. Clin. Biomech. (Bristol, Avon)32, 102–107 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wu, G. & Cavanagh, P. R. ISB recommendations for standardization in the reporting of kinematic data. J. Biomech.28(10), 1257–1261 (1995). [DOI] [PubMed] [Google Scholar]
- 9.Ortigas-Vásquez, A. et al. A frame orientation optimisation method for consistent interpretation of kinematic signals. Sci. Rep.13(1), 9632 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ortigas-Vásquez, A. et al. A framework for analytical validation of inertial-sensor-based knee kinematics using a six-degrees-of-freedom joint simulator. Sensors (Basel)23(1), 348 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jenny, J. Y. & Boeri, C. Low reproducibility of the intra–operative measurement of the transepicondylar axis during total knee replacement. Acta Orthopaedica Scandinavica75(1), 74–77 (2004). [DOI] [PubMed] [Google Scholar]
- 12.Jerosch, J., Peuker, E., Philipps, B. & Filler, T. Interindividual reproducibility in perioperative rotational alignment of femoral components in knee prosthetic surgery using the transepicondylar axis. Knee Surg. Sports Traumatol. Arthrosc.10(3), 194–197 (2002). [DOI] [PubMed] [Google Scholar]
- 13.Ortigas-Vásquez, A., et al., A reproducible and robust representation of tibiofemoral kinematics of the healthy knee joint during stair descent using REFRAME – Part I: REFRAME foundations and validation. Preprint available at Research Square, (2024).
- 14.Postolka, B. et al. Tibio-femoral kinematics of the healthy knee joint throughout complete cycles of gait activities. J. Biomech.110, 109915 (2020). [DOI] [PubMed] [Google Scholar]
- 15.Hamai, S. et al. In vivo healthy knee kinematics during dynamic full flexion. Biomed. Res. Int.2013, 717546 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hoshino, Y., Wang, J. H., Lorenz, S., Fu, F. H. & Tashman, S. The effect of distal femur bony morphology on in vivo knee translational and rotational kinematics. Knee Surg. Sports Traumatol. Arthrosc.20(7), 1331–1338 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Thomeer, L. et al. Six-degree-of-freedom tibiofemoral and patellofemoral joint motion during activities of daily living. Ann. Biomed. Eng.49(4), 1183–1198 (2021). [DOI] [PubMed] [Google Scholar]
- 18.List, R. et al. A moving fluoroscope to capture tibiofemoral kinematics during complete cycles of free level and downhill walking as well as stair descent. PLoS One12(10), e0185952 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kurosawa, H., Walker, P. S., Abe, S., Garg, A. & Hunter, T. Geometry and motion of the knee for implant and orthotic design. J. Biomech.18(7), 487–499 (1985). [DOI] [PubMed] [Google Scholar]
- 20.Asano, T., Akagi, M., Tanaka, K., Tamura, J. & Nakamura, T. In vivo three-dimensional knee kinematics using a biplanar image-matching technique. Clin. Orthop. Relat. Res.388, 157–166 (2001). [DOI] [PubMed] [Google Scholar]
- 21.Eckhoff, D. G., Dwyer, T. F., Bach, J. M., Spitzer, V. M. & Reinig, K. D. Three-dimensional morphology of the distal part of the femur viewed in virtual reality. J. Bone Jt. Surg. Am.83, 43–50 (2001). [DOI] [PubMed] [Google Scholar]
- 22.Grood, E. S. & Suntay, W. J. A joint coordinate system for the clinical description of three-dimensional motions: Application to the knee. J. Biomech. Eng.105(2), 136–144 (1983). [DOI] [PubMed] [Google Scholar]
- 23.Most, E., Axe, J., Rubash, H. & Li, G. Sensitivity of the knee joint kinematics calculation to selection of flexion axes. J. Biomech.37(11), 1743–1748 (2004). [DOI] [PubMed] [Google Scholar]
- 24.Walker, P. S., Heller, Y., Yildirim, G. & Immerman, I. Reference axes for comparing the motion of knee replacements with the anatomic knee. Knee18(5), 312–316 (2011). [DOI] [PubMed] [Google Scholar]
- 25.Piazza, S. J. & Cavanagh, P. R. Measurement of the screw-home motion of the knee is sensitive to errors in axis alignment. J. Biomech.33(8), 1029–1034 (2000). [DOI] [PubMed] [Google Scholar]
- 26.Yin, L. et al. Identifying the functional flexion-extension axis of the knee: An in-vivo kinematics study. PLOS ONE10(6), e0128877 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Postolka, B. et al. Evaluation of an intensity-based algorithm for 2D/3D registration of natural knee videofluoroscopy data. Med. Eng. Phys.77, 107–113 (2020). [DOI] [PubMed] [Google Scholar]
- 28.Freeman, M. A. R. & Pinskerova, V. The movement of the normal tibio-femoral joint. J. Biomech.38(2), 197–208 (2005). [DOI] [PubMed] [Google Scholar]
- 29.Iwaki, H., Pinskerova, V. & Freeman, M. A. Tibiofemoral movement 1: The shapes and relative movements of the femur and tibia in the unloaded cadaver knee. J. Bone Jt. Surg. Br.82(8), 1189–1195 (2000). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The implemented method (REFRAME) can be openly accessed by downloading the standalone application and accompanying user documentation available in https://bbraun.info/reframe and https://movement.ethz.ch/data-repository/reframe.html. Additional MATLAB files to enable advanced custom features are also available under license from the corresponding author upon reasonable request. The original subject data used during the current study to validate the proposed method is part of a dataset generated within the scope of a separate, previously published study5. For further information regarding the data availability of this referenced kinematic dataset, please refer to the original article available here: https://doi.org/10.1016/j.jbiomech.2022.111306; and/or contact the respective corresponding author of that study.