Multicenter Normative Data for Mesopic Microperimetry

Abstract

Purpose

The purpose of this study was to provide a large, multi-center normative dataset for the Macular Integrity Assessment (MAIA) microperimeter and compare the goodness-of-fit and prediction interval calibration-error for a panel of hill-of-vision models.

Methods

Microperimetry examinations of healthy eyes from five independent study groups and one previously available dataset were included (1137 tests from 531 eyes of 432 participants [223 women and 209 men]). Linear mixed models (LMMs) were fitted to the data to obtain interpretable hill-of-vision models. A panel of regression models to predict normative data was compared using cross-validation with site-wise splits. The mean absolute error (MAE) and miscalibration area (area between the calibration curve and the ideal diagonal) were evaluated as the performance measures.

Results

Based on the parameters “participant age,” “eccentricity from the fovea,” “overlap with the central fixation target,” and “eccentricity along the four principal meridians,” a Bayesian mixed model had the lowest MAE (2.13 decibel [dB]; 95% confidence interval [CI] = 1.9–2.36 dB) and miscalibration area (0.13; 95% CI = 0.07–0.19). However, a parsimonious linear model provided a comparable MAE (2.17 dB; 95% CI = 1.93–2.4 dB) and a similar miscalibration area (0.14; 95% CI = 0.08–0.2).

Conclusions

Normal variations in visual sensitivity on mesopic microperimetry can be effectively explained by a linear model that includes age and eccentricity. The dataset and a code vignette are provided for estimating normative values across a large range of retinal locations, applicable to customized testing patterns.

Best-corrected visual acuity (BCVA) is the most commonly used method to assess visual function in clinical trials.¹ It is suitable for tracking the progression of diseases that imminently threaten foveal vision. However, in retinal conditions where there is either extensive foveomacular atrophy or foveal-sparing atrophy, BCVA may remain stable at a low or high level, respectively, for a prolonged duration.² In such conditions, including geographic atrophy (GA) secondary to age-related macular degeneration (AMD) or inherited retinal diseases, central visual field measurement may be more suitable for assessing disease progression.³

Microperimetry, also known as fundus-controlled perimetry, is a technique that allows for retinotopic mapping of light sensitivity, even in patients with unstable fixation.³ This technique has been used as a clinical trial outcome measure, particularly in the form of mesopic white-on-white microperimetry.^4,5 Although microperimetry testing is often performed with standardized stimulus patterns, customized and spatially specific testing tailored to the disease – such as those sampling regions at high risk of disease progression – could allow functional changes to be more effectively characterized and monitored over time. This has been performed, for instance, using patient-tailored stimulus patterns that predominantly sample the perilesional regions in eyes with GA,⁶ or high-density targeted testing of early atrophic lesions in AMD.^7–9 Furthermore, analyses of the results from microperimetry testing with standardized stimulus patterns could also be limited post hoc to at-risk locations, such as those in the junctional zone external to atrophic regions in eyes with GA^10,11 and Stargardt disease,^12,13 or those internal to the boundary of atrophic region in retinitis pigmentosa.¹⁴

To accurately interpret microperimetry (or any type of perimetry) data, it is critical to determine the sensitivity loss from the expected age- and location-specific normal sensitivity.¹⁵ In addition, there are specific regions of the visual field where the interindividual variation in visual sensitivity may be lower or higher.¹⁶ Thus, the determination of pathological visual sensitivity loss relies on the knowledge of the age- and location-dependent normative sensitivity and interindividual variability; both of which are challenging to measure, especially with customized or patient-tailored microperimetry testing due to the individualized nature of the test locations.^6,7

To date, most work seeking to establish such normative data for microperimetry is based on separate analyses of predefined test locations from standardized stimulus patterns.^17–19 One previous publication by Denniss and Astle²⁰ proposed using spatial interpolation to obtain normative data from specific retinal locations and contributed their data as a first public dataset.²¹ However, their data covered only a limited age range (with all but one participant being between 19 and 31 years old) and it was only obtained from one site and device. A systematic comparison of statistical modeling approaches for normative sensitivity and variability was also not explored in their study.

We hypothesized that a flexible model (such as a thin plate regression spline-based regression model) could most accurately recapitulate the normal hill-of-vision shape.²² Thus, this study aims to (1) provide a comprehensive, multicenter, normative dataset for mesopic microperimetry with a widely used device, (2) systematically compare regression models regarding goodness-of-fit, marginal coverage, and conditional coverage, and (3) assess the benefit of limited site-specific normative data.

Methods

This study includes data from healthy individuals examined across five centers (participants described in Table 1, microperimetry grids described in Supplementary Table S1, Fig. 1). The data collection adhered to the Declaration of Helsinki, and the study protocols were reviewed by the respective ethics committees. All participants were informed of the nature of the study and provided written informed consent.

Table 1.

Included Data

	Participants	Age, Median [Min, Max]	Female	Male	Grid	Eyes	No. of Examinations, Median [Min, Max]
Astle16	60	23.0 [19.0, 50.0]	38 (63.3%)	22 (36.7%)		60	1
Bonn1	54	41.2 [19.1, 82.0]	37 (68.5%)	17 (31.5%)		103	1.00 [1.00, 2.00]
Bonn2	102	59.4 [18.0, 84.5]	38 (37.3%)	64 (62.7%)		102	2.00 [1.00, 2.00]
CERA	28	69.0 [53.0, 79.0]	16 (57.1%)	12 (42.9%)		33	3.00 [1.00, 3.00]
LEI	103	52.0 [16.0, 75.0]	49 (47.6%)	54 (52.4%)
	32	62.0 [21.0, 75.0]	16 (50.0%)	16 (50.0%)	LEI 10	32	1.00 [1.00, 1.00]
	58	53.5 [21.0, 75.0]	26 (44.8%)	32 (55.2%)	LEI 2	65	1.00 [1.00, 3.00]
	63	55.0 [16.0, 75.0]	24 (38.1%)	39 (61.9%)	LEI 4	74	1.00 [1.00, 2.00]
	20	45.0 [20.0, 74.0]	14 (70.0%)	6 (30.0%)	LEI 6	34	1.00 [1.00, 1.00]
Oxford	85	29.0 [18.0, 85.0]	45 (52.9%)	40 (47.1%)
	47	29.0 [18.0, 76.0]	27 (57.4%)	20 (42.6%)	Oxford 1	48	7.00 [1.00, 13.0]
	40	37.0 [19.0, 85.0]	19 (47.5%)	21 (52.5%)	Oxford 4	80	1.50 [1.00, 3.00]
Overall	432	45.0 [16.0, 85.0]	223 (51.6%)	209 (48.4%)		N = 531	1137

Some participants at LEI and Oxford were tested with multiple grids. Thus, the total number of participants is smaller than the number of participants per grid.

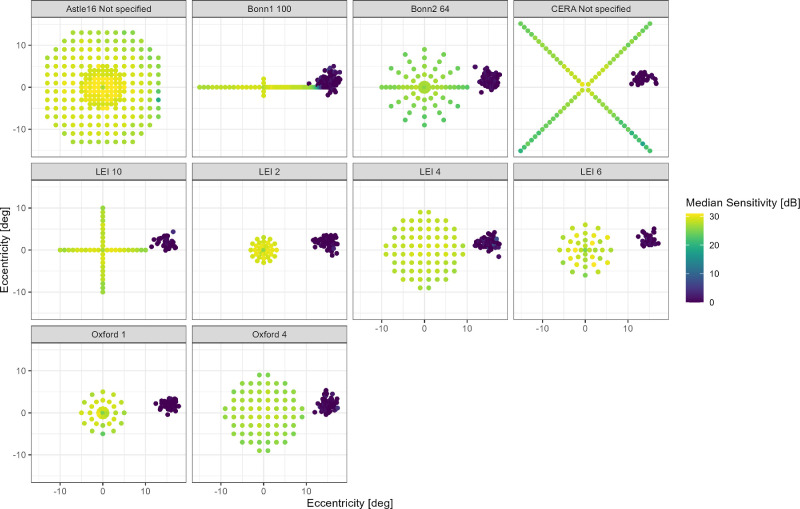
Figure 1.

Included perimetry data. The dot plots show the perimetry data included in this study. The color denotes the sensitivity. The “0 dB” dots on the temporal margin of the image denote the position of the optic nerve head.

Supplementary Table S2 shows an overview of the eligibility criteria of the studies. Microperimetry testing was performed in all studies using the Macular Integrity Assessment (MAIA) device. The MAIA device's background luminance is mesopic (1.27 cd/m²), with a maximum stimulus luminance of 318 cd/m², and a dynamic range of 36 decibels (dB). The device was previously shown to show no ceiling effects in healthy volunteers.²³ All studies used the pre-set 4-2 staircase strategy (stimulus size = Goldmann III, stimulus duration 200 ms). The standard red circle with a diameter of 1 degree was used in all studies as the fixation target.

Data Extraction and Availability

Sensitivity data was extracted from the *.tgz export of the MAIA device using a custom R script. All data are available at https://doi.org/10.5281/zenodo.13625812.²⁴ An R vignette to obtain personalized normative data by using limited site-specific data in combination with the now-published data, which is also available in the same repository.

Data Analysis

The analysis was structured in three parts: (1) fitting of parsimonious (interpretable) hill-of-vision models, (2) systematically comparing regression algorithms for normative data modeling regarding their goodness-of-fit in held-out data from other clinical sites, and (3) evaluating how adding site-specific data improves goodness-of-fit.

Parsimonious Hill-of-Vision Models

To obtain a interpretable hill-of-vision model, we fitted a linear mixed model (LMM) using the R package lmer. In the most basic model (null model), the retinal sensitivity (dependent variable) was described as a “cone” (linear effect of eccentricity), that could be shifted and up- and downward (linear effect of age). In addition, we added a binary term indicating overlap with the fixation target based on previous literature (i.e. “foveal” for eccentricities <1 degree).²⁵ In the Wilkinson-Rogers syntax, the null model was:

$$\begin{array}{ccc}& & \mathrm{Sensitivity}\sim \mathrm{Eccentricity}+\mathrm{Age}\hfill \\ & & +\mathrm{Foveal}+\left(1\right|\mathrm{Site}/\mathrm{Participant}/\mathrm{Eye}/\mathrm{ExamID})\hfill \end{array}$$

We also explored more complex models (Supplementary Results 1) selected by stepwise forward selection based on the Bayesian information criterion (BIC), based on previous hill-of-vision modeling.²⁶ We considered the following additional explanatory variables: eccentricity² (quadratic term to describe steepening/flattening of the peripheral hill-of-vision), age² (quadratic term to describe steepening/flattening of the effect of age), X coordinate + Y coordinate (plane to tilt the hill-of-vision), superior-eccentricity + inferior-ecc. + temporal-ecc. + nasal-ecc. (pyramidal deformation of the hill-of-vision), eccentricity × age (interaction to describe variation in the aging effect in dependence of eccentricity), sex, and baseline examination (binary indicator to differentiate baseline examinations from follow-up examinations).

Comparison of Regression Models and Prediction Interval Calibration

The regression algorithms for normative data estimation were initially compared using six-fold cross-validation (site-wise splits). Data from Bonn were split into two sites because it was acquired on different MAIA devices by different principal investigators (PIs; MAIA1 [author P.L.M.] and MAIA2 [author M.P.]). Thus, the resulting goodness-of-fit and coverage estimates are representative of the performance in the setting of a new (“unknown”) clinical site.

Candidate Models

To model the average differential light sensitivity and quantiles, we considered both complex and parsimonious (i.e. interpretable) models.

• •
  Linear regression: For the linear regression models, we used the prediction intervals to obtain the quantiles. The sequence of models was based on the results from the step-wise forward selection in the section above (see also Table 2).

  • ○
    LM0: Sensitivity ∼ Ecc. + Age + Foveal
  • ○
    LM1: Sensitivity ∼ Ecc. + Age + Foveal + Superior-Ecc. + Inferior-Ecc. + Temporal-Ecc. + Nasal-Ecc.
  • ○
    LM2: Sensitivity ∼ Ecc. + Age + Foveal + Superior-Ecc. + Inferior-Ecc. + Temporal-Ecc. + Nasal-Ecc. + Eccentricity²
  • ○
    LM3: Sensitivity ∼ Ecc. + Age + Foveal + Superior-Ecc. + Inferior-Ecc. + Temporal-Ecc. + Nasal-Ecc. + Eccentricity² + Age²
• •Quantile regression: For quantile regression, we fitted the formula from LM1 (to allow for variation of the centile surface across the visual field) using the R package quantreg.²⁷
• •Bayesian nonparametric quantile regression: The model included an isotropic smooth (thin plate regression spline) for the x and y coordinate, a spline for the age, and a tensor product smooth for age and the x coordinate, as well as for age and the y coordinate. We used the R package qgam to obtain the quantiles of interest (0.1, …, 0.9).²⁸ Given that it is based on a thin plate regression spline, it can be considered an extension of prior work estimating hill-of-vision volume at the level of individuals.²²
• •Bayesian mixed model: We fitted Bayesian mixed models with the above formula from LM1 and with the clinical site and participant as random effects using the R package brms.²⁹ The predict intervals function included the group-level uncertainty for new data based on the variation among the existing levels of clinical sites and participants.

Table 2.

Linear Mixed-Model Analysis

	Linear Mixed Model 0
	Estimates	CI	P Value
Predictors
(Intercept)	31.27	30.35 to 32.18	<0.001
Eccentricity, degrees	−0.3	−0.30 to −0.29	<0.001
Age, decades	−0.44	−0.53 to −0.36	<0.001
Fovea, <1 degree	−3.16	−3.27 to −3.05	<0.001
Random effects
σ2	4.05
τ00 ExamID:(EID:(ParticipantID:Site))	0.56
τ00 EID:(ParticipantID:Site)	0.39
τ00 ParticipantID:Site	1.28
τ00 Site	1.03
ICC	0.45
NExamID	1137
NEID	531
NParticipantID	432
NSite	6
Observations	82095
Marginal R2/Conditional R2	0.206/0.560

Boldface entries indicate P values < 0.05.

Performance Metrics

To compare the models, we considered four factors. These concepts are visually explained in Figure 2.

• •Goodness-of-fit: The mean absolute error (MAE in dB) between measured sensitivity and predicted sensitivity, with lower values indicating better performance.³⁰
• •Coverage (marginal coverage): The prediction intervals should cover the prespecified fraction of measurements across locations. The coverage can be visualized by plotting the observed against the predicted proportion of measurements for each centile surface (called a calibration curve; see Fig. 2). The closeness of this curve to the ideal diagonal can be quantified based on the mean absolute calibration error.^31,32
• •Adaptivity (conditional coverage): Prediction intervals should be smaller in easier-to-predict regions in the feature space (e.g. young individuals) and larger prediction in challenging-to-predict regions in the feature space (e.g. older individuals). As a metric of adaptivity, we assessed the mean absolute calibration error stratified by age and eccentricity bins.^31,32
• •Parsimony: Models with few interpretable coefficients (i.e. parsimonious models) are preferred if they provide similar performance to more complex models.

Figure 2.

Concepts. The figure explains key consideration for the assessments of normative data, illustrated with simulated data. The left column shows the prediction (orange line) and the 80% prediction interval (red lines). The middle column shows the calibration plots across all data. The right column shows the calibration plots stratified by eccentricity. The miscalibration area (i.e. area between the calibration lines and the ideal diagonals) is reflective of the model calibration. The first model (row 1) is unsuitable to describe the data due to a poor goodness-of-fit. The second model (row 2) fits the data well and shows good overall calibration, but the prediction interval is constant resulting in poor conditional calibration (i.e. poor adaptivity). The third model (row 3) shows excellent goodness-of-fit, overall calibration, and conditional calibration.

As a goodness-of-fit measure, we estimated the MAE using linear mixed models (fitted with lme4) by estimating the absolute error (between predicted and measured sensitivity) for each test point with the regression model as the explanatory variable. Examinations nested in eye, nested in participant, and nested in site were considered as a random effects term. As a measure of calibration, we computed the miscalibration area (i.e. the absolute area between the calibration line and the ideal diagonal; see for example Fig. 2).

Effect of Site-Specific Data

The same analysis was repeated with participant-wise splits (5-fold cross-validation). This scenario estimates the performance of the normative data in the setting of available site-specific data.

Further, we implemented a simulation analysis to understand how much site-specific data are required to optimize the goodness-of-fit of normative data. For each clinical site, we fitted a normative data model with the data from all but one site, adding in a step-wise manner 2, 4, 8, and 16 local participants. The performance of the resulting normative data model was then assessed on the remaining participants of this site. We repeated this procedure 25 times. In this simulation, we used LM0 with the site added as an additional explanatory variable. The parsimonious LM0 was selected for this simulation analysis considering the computational burden.

Results

Included Data

This study included perimetry data from a total of 1137 tests from 531 eyes of 432 healthy participants, who had a median age of 45 years (minimum = 16 years and maximum = 85 years). Table 1 lists the details about the age, sex, and perimetry grids separately for each clinical center. Figure 1 and Supplementary Table S1 provide a detailed description of the perimetry grids.

Modeling Mean Visual Sensitivity

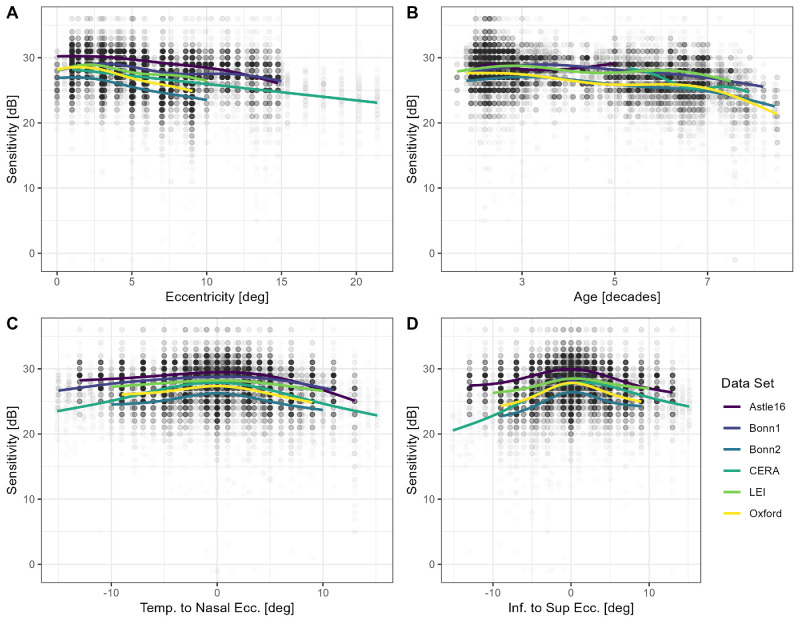
Qualitative inspection of the data (see Fig. 3) revealed that eccentricity and age were associated with visual sensitivity. Sensitivity was slightly lower in proximity to the fixation target (at eccentricities <1 degree), peaked at 2 degrees, and then decreased with increasing eccentricity.

Figure 3.

Visual sensitivity. The panels show retinal sensitivity in dependence of eccentricity (A), age (B), position along the horizontal (C), and vertical (D) meridian. The colored lines are regression splines. Besides the dip in sensitivity in proximity to the fovea (fixation target), mesopic sensitivity decreases linearly with eccentricity as a first order approximation in the central visual field.

The null model (LM0, linear mixed model to predict sensitivity with eccentricity, age, and foveal location as predictors) had a substantial explanatory power (conditional R² of 56.0%) with a marginal R² relating to the fixed effect alone of 20.6% (see Table 2). The model’s intercept was 31.27 dB (95% confidence interval [CI] = 30.35 to 32.18), the effect of eccentricity was −0.30 dB/degrees (95% CI = −0.30 to −0.29), and the effect of age was −0.44 dB/decade (95% CI = −0.53 to −0.36). The foveal test point in proximity to the fixation target (i.e. eccentricity <1 degree) was predicted to have a lower sensitivity (−3.16 dB, 95% CI = −3.27 to −3.05).

The random effects estimates (random intercept variance [τ00]) revealed considerable between-site/device variability (standard deviation [SD] = √(1.03 dB²) = 1.01 dB) and between-participant variability (SD = √(1.28 dB²) = 1.13 dB). The between-eye variability was small (SD = √(0.39 dB²) = 0.62 dB), and there was within eyes evidence of examination-to-examination variation (SD = √(0.56 dB²) = 0.75 dB).

Using stepwise forward selection allowed to fit LMMs with a slightly better goodness-of-fit, but the improvements in marginal R² were small (Supplementary Table S3).

Comparison of Normative Data Models

Overall, most regression models performed similar data from “new” clinical sites (i.e. cross-validation with the clinical site as the grouping variable). The MAE between predicted and observed sensitivity ranged from (mixed model estimate, 95% CI) 2.13 dB (95% CI = 1.9 to 2.36) for the Bayesian mixed model to 2.23 dB (95% CI = 2 to 2.47) for the Bayesian nonparametric additive model (Fig. 4A, Table 3). Post hoc pair-wise comparison of the MAE revealed that the Bayesian mixed model performed indeed statistically significantly better compared to the other models, although the actual magnitude of the difference was small (Supplementary Table S4).

Figure 4.

Cross-validated model performance with site-wise splits. Panel (A) shows the mean absolute error (MAE) between predicted and observed sensitivity (each dot represents the MAE for one participant, and the red bar represents the median). Panel (B) shows the miscalibration area overall and stratified by eccentricity (ecc.), age, and clinical site. The overall miscalibration area is remarkably similar across models. The Bayesian mixed model had the smallest miscalibration area. The linear models 2 and 3 and the Bayesian nonparametric additive model were better calibrated for eccentric test points (i.e. eccentricity >10.7 degrees). BRMS, Bayesian mixed model; LM, linear model; qgam, Bayesian nonparametric additive model; quantReg, Quantile Regression.

Table 3.

Model Performance With Cross-Validation by Clinical Site

	Mean Absolute Error [dB]		Miscalibration Area
	Est.	95% CI	Est.	95% CI
Bayesian mixed model	2.13	[1.9 to 2.36]	0.13	[0.07 to 0.19]
Linear model 0	2.17	[1.93 to 2.4]	0.14	[0.08 to 0.2]
Linear model 2	2.19	[1.96 to 2.42]	0.14	[0.08 to 0.2]
Linear model 1	2.2	[1.97 to 2.43]	0.15	[0.09 to 0.21]
Linear model 3	2.2	[1.97 to 2.43]	0.14	[0.08 to 0.2]
Quantile Regression	2.2	[1.96 to 2.43]	0.15	[0.09 to 0.21]
Bayesian nonparametric additive model	2.23	[2 to 2.47]	0.15	[0.09 to 0.21]

In terms of overall calibration (marginal coverage), the Bayesian mixed model also showed the best performance, with a miscalibration area of 0.13 (95% CI = 0.07 to 0.19; see Table 3). However, the calibration curves stratified by eccentricity (conditional coverage) indicated that the linear models, including the eccentricity² term as an explanatory variable (linear models 2 and 3), as well as the Bayesian nonparametric additive model, performed better in test points with >16 degrees eccentricity (Supplementary Fig. S2).

Normative Data Models with Site-Specific Data

With cross-validation using participant-wise splits (and adding the clinical site as a predictor variable), the Bayesian nonparametric additive model performed best in terms of MAE (1.81 [95% CI = 1.68 to 1.95]) and miscalibration area (0.04 [95% CI = 0.02 to 0.06]; Supplementary Table S5, Supplementary Fig. S3). Post hoc comparison of the models revealed comparable performance (i.e. no statistically significant differences; Supplementary Table S6). Again, all regression models were comparable for the central test points, but the conditional coverage for test points with an eccentricity >10.7 degrees was markedly better for the Bayesian nonparametric additive model (Supplementary Fig. S4). Figure 5 shows the predicted visual field surfaces by the Bayesian nonparametric additive model as a function of age.

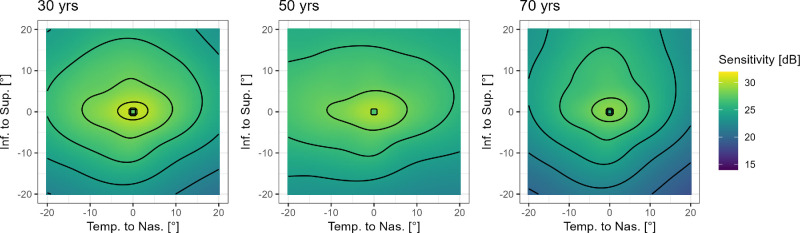
Figure 5.

Visualization of the effect of aging. The panels show the predicted 50th percentile surfaces for the ages of 30, 50, and 70 years. The black lines denote 2 dB contour lines. Notably, the effect of aging between 30 and 50 years is mild. Most aging is observable later, with a notable steepening of the decline in retinal sensitivity along the inferior meridian in the mid-periphery.

Effect of Follow-Up and Sex

Microperimetry tests are usually performed without prior information available at each specific location to seed the thresholding procedure during the first test (a “baseline” test), except for initial estimates obtained at four primary seeding locations.⁷ However, subsequent tests can use estimates from the previous test to seed its testing (usually called a “follow-up” test). There was no significant difference in the final goodness-of-fit or calibration of the Bayesian nonparametric additive model based on whether a test was a follow-up or baseline test or based on the sex of the participant, and these variables were thus not included in the above model fitting procedures (Supplementary Table S7).

Impact of Adding Site-Specific Data

Because adding site-specific data drastically improves model calibration, we assessed how much site-specific data are needed for this gain. Thus, we evaluated the impact of adding limited site-specific data (e.g. 2, 4, 8, or 16 randomly selected participants) to the model fitting process. Adding site-specific data improved the model fit and calibration markedly (see Supplementary Figs. S5, S6). Data from just eight site-specific participants were sufficient for achieving a quasi-optimal fit and calibration (miscalibration area of 0.056 (95% CI = 0.046 to 0.066) with N = 8 vs. 0.051 (95% CI = 0.041 to 0.061) with N = 16; Supplementary Table S8).

Discussion

This study presents an extensive dataset for mesopic microperimetry collected from multiple centers. It compares quantile regression techniques based on their goodness-of-fit, marginal coverage, and conditional coverage, while also examining the usefulness of site-specific normative data. These data are crucial for analyzing microperimetry data, both for everyday clinical use and for research used, particularly in the setting of patient-tailored (individualized) perimetry and multicenter clinical trials.

Importantly, our models recapitulate free-viewing perimetry data on the mesopic hill-of-vision. Aulhorn and coworkers demonstrated that the shape of the mesopic hill-of-vision mirrors mostly the photopic hill-of-vision, but with a slightly flatter slope of the sensitivity decrease with increasing eccentricity.³³ This shape was later recapitulated for photopic and mesopic perimetry studies using the Octopus perimeter and the Humphrey perimeter.^26,34,35 Our parsimonious linear mixed model analysis for data from the MAIA perimetry was compatible with these prior data, with the exception of the relatively low foveal sensitivity. This peculiarity for the MAIA device was reported previously and is linked to its fixation target close to the fovea.²⁵ Our models are also in line with the previous quadratic trend surface-based model for the MAIA from Denniss and Astle with a relatively flat hill-of-vision in the temporal macula.

Regarding the underlying biology, spectral perimetry studies imply that Goldmann III stimuli in mesopic conditions are mediated by a combination of S-cones and M+L-cones centrally (<13 degrees), whereas for more peripheral sensitivity it is determined by rods and M+L-cones.³⁴ Thus, our central data are compatible with the human photoreceptor topography considering the oval-shaped topography of the cone density in the central 10 degrees.³⁶ Previous studies reported that Ricco’s area (area of complete spatial summation) is close to the size of a Goldmann III stimulus in mesopic conditions and does not vary (significantly) in the central 10 degrees,^37,38 which could explain the relative flat hill-of-vision (compared to previous photopic perimetry studies). With 7 decades of aging, light sensitivity will decrease by 3 dB based on our data. Free-viewing perimetry studies using stimuli designed to be minimally affected by increased media absorption imply that age-related sensitivity loss is largely driven by neural loss.³⁹ Based on histopathologic studies, the combined cone and rod density in the central 4 mm decreases by 30.7%.⁴⁰ In addition, age-related loss of ganglion cell density is associated with an overall loss in contrast sensitivity.⁴¹

Apart from the central tendency of normal visual sensitivity, detailed knowledge about its expected healthy interindividual and measurement variability is critical for detecting early dysfunction. First, we used a linear mixed model to identify sources of variability. The largest source of variability was the retest variability, consisting of the point-wise residual variance and global fluctuations. The derived 95% repeatability coefficients for the point-wise sensitivity and the mean sensitivity (approximately ±6 dB and ±2 dB, respectively) align with previous retest reliability studies in healthy subjects and patients with retinal diseases.^42–44 Moreover, these global fluctuations (i.e. vigilance and positioning in front of the device) are comparable to free-viewing perimetry estimates in the absence of severe visual field defects.^45,46 In addition, there was considerable between-participant variability but only very little between-eye variability. There was also site-associated variability (discussed in the next paragraph).

The regression algorithms for centile estimation performed all very similarly in terms of goodness-of-fit and marginal coverage (overall calibration). However, the Bayesian mixed model outperformed the other models in terms of conditional coverage (calibration in age- or eccentricity-strata) with site-wise cross-validation. The higher prediction error of the linear models is likely an indicator of overfitting, whereas the Bayesian mixed model is regularized through the priors and the partial-pooling.

Nevertheless, all regression models used in our study were not very effective in generalizing across different sites. Our study design does not provide information on whether the differences observed between sites are due to device calibration, test conditions, stimulus patterns used, or biological differences. However, a random intercept model considering site-specific data achieved perfect calibration across sites (see Supplementary Fig. S6). Thus, device calibration-related differences are a plausible explanation. Based on the International Organization for Standardization (ISO) standard for perimetry devices, the calibration tolerance for the increment luminance over the background (ΔL/LB) is +25% to −20%.⁴⁷ This corresponds to dB scale shifts of ±1 dB. All except one site random effects estimates for the site fell into this range (Bonn 2).

Clinically, relying solely on the manufacturer’s normative data could result in diagnostic errors, particularly in older individuals and test points near the peripheral macula.^17,18 The manufacturer defines sensitivity measurements below 25 dB as abnormal, based on data from 270 subjects with a mean age of 43 years ± 15.⁴⁸ The Gaussian distribution shown on the pre-set printout indicates that measurements below 25 dB are outside of 3 SDs (i.e. 0.135% quantile), which is also reflected by the device’s pre-set color palette for displaying test results. However, our analysis and previous studies have revealed that aging and eccentricity have a significant impact on mesopic retinal sensitivity.^17,18 Based on our findings, we predict, for example, that around half of the sensitivity measurements at 10 degrees eccentricity will fall below 25 dB in healthy individuals at the age of 75 years, which is compatible with prior publications (see for example fig. 1 in Ref. 20).

For research, sensitivity loss should ideally be computed with site/device-specific normative data. Using the here published data and code vignette in R, site/device-specific normative data can be obtained efficiently with 8 to 16 normative subjects.

Limitations

A key limitation of this study is that the data collected were retrospective in nature and performed using different stimulus patterns. In addition, the testing protocol (e.g. pupil dilation or prior light exposure⁴⁹) could differ among sites, as well as the definition of healthy individuals. Pupillary dilation has been empirically shown to have no effect (given the small required pupil diameter of 2.5 mm).⁵⁰ This study was not designed to distinguish between age-associated sensitivity loss due to media opacities versus outer and inner retinal aging. Given that surgery-requiring cataracts were reported only to have a 1 to 2 dB effect on visual sensitivity,⁵¹ and that clinically clear media were inclusion criteria for all studies, the here observed age effect indicates visual sensitivity loss beyond mere media opacification.

Based on our data, no sex differences were evident. But large epidemiologic data imply small differences that would necessitate a markedly larger sample size to detect.⁵² The test duration (number of test points) might influence the response variability (i.e. resulting in a wider or narrower spread of the centile surfaces). Device and test pattern-specific normal data may be preferable to detect very subtle defects.

Moreover, the presented models here apply to the normal hill-of-vision in the central 10 degrees (radius) only. More flexible regression models are necessary for individual patient data to estimate their hill-of-vision with scotomatous lesions.^22,53–57

Summary

In conclusion, our study provides a comprehensive analysis of normal retinal sensitivity measured with the MAIA device across different age ranges. Determinants of mesopic light sensitivity were the eccentricity and age. Considerable between-site variability was evident, which could be due to device calibration, participant population, or protocol differences.