Abstract
The MRI-derived brain network serves as a pivotal instrument in elucidating both the structural and functional aspects of the brain, encompassing the ramifications of diseases and developmental processes. However, prevailing methodologies, often focusing on synchronous BOLD signals from functional MRI (fMRI), may not capture directional influences among brain regions and rarely tackle temporal functional dynamics. In this study, we first construct the brain-effective network via the dynamic causal model. Subsequently, we introduce an interpretable graph learning framework termed Spatio-Temporal Embedding ODE (STE-ODE). This framework incorporates specifically designed directed node embedding layers, aiming at capturing the dynamic inter-play between structural and effective networks via an ordinary differential equation (ODE) model, which characterizes spatial-temporal brain dynamics. Our framework is validated on several clinical phenotype prediction tasks using two independent publicly available datasets (HCP and OASIS). The experimental results clearly demonstrate the advantages of our model compared to several state-of-the-art methods.
Keywords: Effective networks, Spatio-temporal, Ordinary differential equation, Brain dynamics, dMRI, fMRI
1. Introduction
Neuroimaging techniques, such as Magnetic Resonance Imaging (MRI), have significantly advanced our understanding of the brain by providing a non-invasive way to explore its anatomical structures and functions. Recent advances in network science have allowed for the analysis of MRI-derived brain networks, revealing new biomarkers for diseases such as Alzheimer’s and enabling the study of complex neural interactions across different brain regions [3].
Different MRI techniques reveal diverse aspects of brain organization and dynamics. For example, diffusion MRI (dMRI) maps white matter connections by tracking water molecule diffusion, showing how brain regions are structurally linked. Functional MRI (fMRI), on the other hand, utilizes blood-oxygen level-dependent (BOLD) signals to monitor brain activity, offering insights into functional brain dynamics. Recent research utilizing fMRI BOLD signals to delineate functional brain networks has made significant strides in identifying patterns of connectivity through temporal correlations (e.g., Pearson correlation) across different brain regions. These studies highlight the utility of fMRI in mapping the intricate web of neural interactions, presenting the brain’s complex connectivity patterns [20]. However, traditional methods primarily focus on synchronous BOLD signals, which may overlook the nuanced directional influences (e.g., causality) between brain regions over time. To capture the directional influences among brain regions, we employ Dynamic Causal Modeling (DCM) [5,10] with time-lagged BOLD signals to construct temporal effective connectivity networks. The temporal effective networks represent the dynamic causal relationships where the activity of one brain region influences another over time.
In recent years, Graph Neural Networks (GNNs) [13] have become increasingly prominent in brain network studies, showing significant advancements in mining brain structural and functional networks [24]. Despite this progress, a scarcity of graph learning methods is designed for dynamic effective network learning [4]. The dynamic effective brain networks are a series of time-evolving directed graphs, which may present two challenges when we build up GNNs on these networks. First, existing GNNs focused on embedding nodes in undirected graphs, which may not effectively handle directed graph embeddings. Effective brain networks feature pairs of brain regions connected by directed edges with different weights, where the edge direction and weight represent the causal sequence and its magnitude, respectively. To address this, we propose a directed graph encoder specifically designed for capturing these causal sequences in brain node embedding. Furthermore, the dynamic effective brain network consists of temporal sequences of brain graphs, with changing connectivity over time. Thus, current GNNs need to be adapted to capture both spatial and temporal dynamics of the brain. Recent efforts in dynamic graph learning include approaches such as recurrent graph neural network [6], graph temporal attention network [15], and graph transformer [29]. In this study, we tackle the brain spatial-temporal dynamics with an ordinary differential equation (ODE) model. Particularly, we introduce a graph learning framework, Spatio-Temporal Embedding ODE (STE-ODE), designed to simultaneously solve an Ordinary Differential Equation (ODE) and embed brain networks, capturing both their structural and functional properties. The framework’s unique approach ensures that the training process yields brain network embeddings that are, in essence, solutions to the ODE, thereby intertwining the learning model with the ODE resolution. These embedded graph representations are then leveraged for different clinical predictions, such as brain disease classifications. Beyond prediction tasks, our study aims to identify most significant connectomes related to various clinical phenotypes and neurodegenerative diseases, tracking their changes over time for different tasks. To this end, we develop an interpretable toolkit within our directed node embedding layer. This toolkit focuses on pinpointing the top edges with significant temporal changes, marking them as potential biomarkers for distinct phenotypes. This method directly connects dynamic brain network changes to specific biological traits, enhancing our comprehension of the mechanisms tied to different phenotypes. Our contributions can be summarized as follows. (1) We design a directed graph embedding layer tailored for encoding effective network under the constrains of its structural counterpart. (2) We present a learning framework with the directed graph embedding layer, referred to as STE-ODE, which captures temporal effective network representations by solving an ordinary differential equation that models the brain spatial-temporal dynamics. (3) We develop a toolkit to enhance the interpretability of our framework, which enables the identification of the most significant connectome changes, marking them as potential biomarkers for different clinical phenotypes.
2. Methodology
We first introduce our method for constructing directed effective networks through the dynamic causal model (DCM). Additionally, we propose our interpretable directed graph node embedding layer, which is tailored to encode both directed effective networks and their structural counterparts. Subsequently, we detail our comprehensive spatio-temporal framework with the directed graph embedding layer for downstream tasks. This framework involves solving an ordinary differential equation that captures the spatial-temporal dynamics of the brain.
2.1. Preliminaries
A brain network is a weighted graph with nodes, where is the set of graph nodes representing brain regions, and is the edge set. is the node feature matrix where is the row of representing the node feature () of . is the adjacency matrix where represents the weights of the edge between and . A brain structural network, denoted as , is an undirected graph, where . In stead, a brain effective network, denoted as , is a directed graph, where . The sign of indicates the causal sequence between and , where signifies the causal effect on induced by , vice versa. Additionally, we denote the blood-oxygen-level-dependent (BOLD) signal (with signal points) obtained from fMRI as .
2.2. Construction of Brain Effective Network
We employ fMRI BOLD signals to construct brain effective networks using the dynamic causal modeling (DCM) approach [17,21]. Each brain region serves as a graph node embedded within the brain effective network, while the temporal dynamic effective connectivity comprises the edge set. Given the fMRI BOLD signals, the dynamic adjacency matrix can be modeled as follows:
| (1) |
represents the term governing the influence of external neuronal inputs on the dynamics of . In this work, as we concentrate on resting-state fMRI studies. The parameter serves as a constant regulating the neuronal lag among brain nodes. Consequently, we can derive the expression of as follows:
| (2) |
We construct the effective connectivity by deriving the discrete expression of the Eq. (2):
| (3) |
We define the connectivity between brain node and at timepoint as follows, with :
| (4) |
where is the BOLD signal of . The process of constructing brain effective networks is illustrated in Fig. 1(a).
Fig. 1.
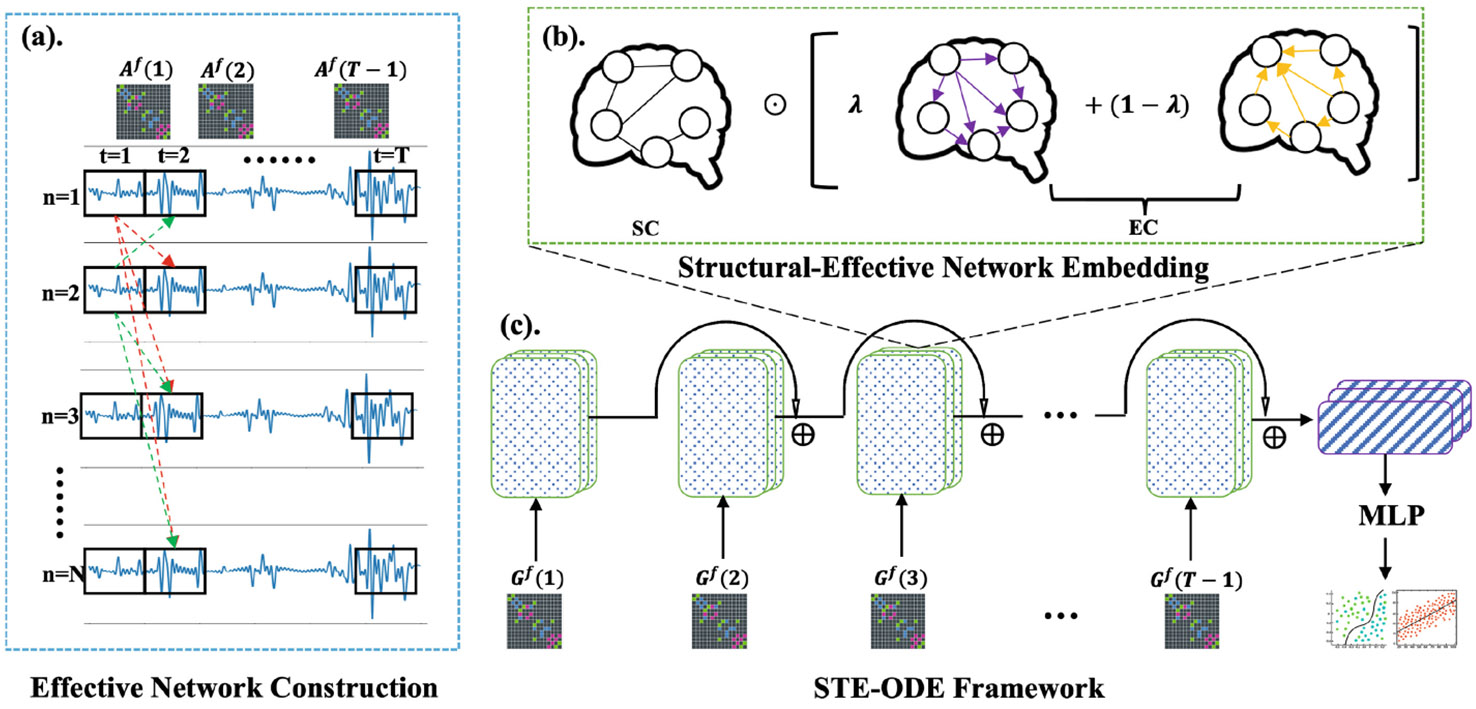
(a) describes the construction of brain effective networks from the BOLD signals. (b) is the directed graph embedding layer for structural and effective networks. (c) presents the STE-ODE framework for different clinical prediction tasks.
2.3. Interpretable Structural-Effective Network Embedding
Given a directed effective network , we first perform asymmetric Laplacian normalization on its adjacency matrix. The normalized adjacency matrix can be represented as:
| (5) |
where and are in-degree and out-degree of the adjacency matrix, respectively. Then, our node embedding layer for the structural-effective network can be formulated as a function :
| (6) |
where represents the Laplacian-normalized adjacency matrix of the brain structural network [13]. The brain structural network serves as spatial information to constrain the temporal function dynamics, under the assumption that two brain regions are functionally interconnected as long as they are structurally connected [22]. is a nonlinear activation function, such as . is a parameter that balances the information flow into and out of each brain node. represents trainable parameters for brain node embedding. are trainable parameters used for model interpretability, enabling edge weights to adapt themselves for different prediction targets. During the model validation stage, we utilize self-adapted edge weights to track the most important connectomes for various prediction tasks. The brain node embedding layer is depicted in Fig. 1(b).
2.4. Spatio-Temporal Embedding with ODE
Given a series of temporal effective networks (i.e., , ), their dynamic embeddings can be modeled using the following ordinary differential equation:
| (7) |
where is the parameter sets (i.e., ) of the embedding function. We can approximate the Eq. 7 into the discrete expression with our proposed node embedding layer (see Eq. 6) as:
| (8) |
We unfold the temporal brain network embedding into an residual graph learning framework. In this framework, each embedding layer processes the dynamic effective network at , while the previous dynamic network embedding (i.e., ) is treated as a residual term.
2.5. STE-ODE Framework for Brain Network Predictions
The proposed STE-ODE framework, incorporating the spatio-temporal embedding model, is depicted in Fig. 1(c). Assuming we have obtained the last node embedding (i.e., ), we employ an average global pooling layer () to extract the entire graph representation. Subsequently, a fully connected neural network (such as a Multilayer Perceptron or MLP) is employed to generate the final classification or regression output (i.e., ). For the classification task, we utilize the negative log likelihood loss function, where . For the regression task, we use the loss function, where .
3. Experiments
3.1. Dataset Description and Preprocessing
Two publicly available datasets were used to evaluate our framework. The first includes data from 1206 young healthy subjects (mean age 28.19 ± 7.15, 657 women) from the Human Connectome Project [25] (HCP). The second includes 1326 subjects (mean age = 70.42 ± 8.95, 738 women) from the Open Access Series of Imaging Studies (OASIS) dataset [14]. Details of each dataset can be found on their official websites. The preprocessing of functional BOLD signals and the reconstruction of structural networks were conducted using CONN [26] and FSL Probtrackx [12], respectively. For the HCP data, both structural and effective networks have a dimension of 82 × 82 based on 82 ROIs defined using FreeSurfer (V6.0) [9]. For the OASIS data, both networks have a dimension of 132 × 132 based on the Harvard-Oxford Atlas and AAL Atlas. This intentional variation in network resolutions for the HCP and OASIS datasets served to examine whether the dimension of the network or the choice of atlas influences the efficacy of our newly developed framework.
3.2. Implementation Details and Experimental Setup
Implementation Details.
We divided the BOLD signal into time segments and calculated the mean value of the points within each segment to construct 4 effective networks. The edge weights of both the effective networks and structural networks were normalized to the intervals [−1, 1] and [0, 1], respectively. Node features were initialized by sampling from a standard Gaussian distribution with feature dimensions set to 16. Each dataset was randomly partitioned into 5 disjoint sets for 5-fold cross-validation in subsequent experiments. The Adam optimizer was utilized to train the model with a batch size of 128. The initial learning rate was set to 0.001 and decayed by . We also regularized the training with an weight decay of . We terminated training if the validation loss fails to improve for 100 epochs, following the epoch termination condition outlined in [19], with a maximum of 500 epochs. All experiments were conducted on 1× NVIDIA A100 GPU.
Experimental Setup.
We compared our approach against 6 baseline methods, including 3 static models (SVM [23], GCN [13] with global pooling, and DiffPool [28]), and 3 dynamic brain network embedding methods (LSTM [8], ST-GCN [11], and FE-STGNN [4]). The parameter is set to 0.5 for all experiments. We conducted a search for optimal parameter within the range of [0.1, 0.3, 0.5, 0.7, 0.9] (refer to Supplementary for details). The resulting values were for HCP and for OASIS.
3.3. Brain Network Predictions
Classification Tasks.
allele is a strong risk factor for the Alzheimers’ Disease (AD) [18]. Table 1 presents classification results for gender on HCP, as well as for AD and on OASIS. It shows that our model achieves the highest accuracy across all tasks compared to other methods. Meanwhile, the comparison between results obtained with and without structural connectivity (SC) demonstrates the importance of anatomical (or spatial) constraints on effective network representation learning. Furthermore, the dynamic methods consistently outperform the static methods, indicating their efficacy in brain network analysis by capturing brain dynamics.
Table 1.
Classification accuracy and F1-scores, along with their standard deviations under 5-fold cross-validation. The best results are highlighted in bold.
| Method | HCP | OASIS | ||||
|---|---|---|---|---|---|---|
| Gender | Disease | |||||
| Acc. | F1 | Acc. | F1 | Acc. | F1 | |
| SVM | 59.25 ± 1.39 | 60.85 ± 2.29 ± | 57.72 ± 0.98 | 56.58 ± 1.93 | 58.09 ± 2.37 | 59.83 ± 0.99 |
| GCN | 68.83 ± 1.48 | 67.48 ± 2.32 | 64.64 ± 1.05 | 66.58 ± 2.12 | 65.56 ± 1.51 | 64.28 ± 1.11 |
| DiffPool | 73.25 ± 0.71 | 70.43 ± 1.87 | 71.67 ± 0.83 | 69.58 ± 1.75 | 69.04 ± 2.52 | 70.42 ± 0.87 |
| LSTM | 70.95 ± 1.09 | 72.37 ± 2.16 | 68.22 ± 2.04 | 68.90 ± 0.74 | 69.33 ± 1.88 | 67.31 ± 2.65 |
| ST-GCN | 78.44 ± 0.86 | 76.15 ± 1.17 | 76.26 ± 0.98 | 77.02 ± 1.47 | 77.20 ± 1.79 | 78.14 ± 1.35 |
| FE-STGNN | 81.04 ± 0.39 | 81.75 ± 1.26 | 79.92 ± 0.73 | 79.39 ± 1.15 | 78.98 ± 0.92 | 80.06 ± 0.85 |
| Ours w/o SC | 80.66 ± 2.02 | 80.77 ± 0.63 | 80.59 ± 1.71 | 81.05 ± 1.20 | 78.42 ± 1.07 | 78.59 ± 1.63 |
| Ours | 82.12 ± 1.17 | 83.97 ± 0.96 | 80.01 ± 1.26 | 81.31 ± 1.37 | 81.35 ± 0.86 | 80.92 ± 1.03 |
Regression Tasks.
The Mini-Mental State Exam (MMSE [2]) serves as a quantitative assessment tool for cognitive status in adults. The Diagnostic and Statistical Manual of Mental Disorders (DSM [1]) offers a comprehensive measure system for mental disorders utilized by mental health professionals worldwide. Within the DSM system, DSM-Depr and DSM-Antis gauge two mental disorders linked to depression and rebellious personality, respectively. Table 2 summarizes the regression results for DSM and MMSE on the HCP and OASIS datasets, showing that our model outperforms all baseline methods with lowest mean absolute values.
Table 2.
Regression mean absolute values with their std under 5-fold cross-validation. The best results are highlighted in bold.
| Method | HCP | OASIS | ||
|---|---|---|---|---|
| MMSE | DSM-Depr | DSM-Antis | MMSE | |
| SVM | 4.06 ± 0.33 | 4.66 ± 0.79 | 3.43 ± 0.59 | 3.91 ± 0.24 |
| GCN | 3.16 ± 0.43 | 3.62 ± 0.98 | 3.41 ± 0.37 | 3.70 ± 1.06 |
| DiffPool | 2.82 ± 0.93 | 3.23 ± 0.54 | 2.09 ± 0.56 | 2.48 ± 0.90 |
| LSTM | 2.74 ± 0.91 | 2.37 ± 0.61 | 1.91 ± 0.47 | 1.88 ± 0.51 |
| ST-GCN | 1.97 ± 0.84 | 1.35 ± 0.17 | 1.24 ± 0.33 | 1.19 ± 0.23 |
| FE-STGNN | 0.73 ± 0.29 | 1.19 ± 0.14 | 1.08 ± 0.06 | 0.96 ± 0.15 |
| Ours w/o SC | 0.93 ± 0.44 | 1.24 ± 0.32 | 1.19 ± 0.24 | 1.08 ± 0.33 |
| Ours | 0.62 ± 0.23 | 1.08 ± 0.45 | 0.92 ± 0.79 | 0.76 ± 0.17 |
3.4. Biological Insights and Model Interpretability
We provided two distinct biological insights from our interpretable framework. Firstly, we utilized the designed parameter () to identify the most crucial effective connectomes for various prediction tasks. Specifically, we pinpointed the top 400 and 256 connectomes (highlighted in bold red curve in Fig. 2(a)) with the highest weights for disease classification on OASIS and DSM-Depr regression tasks, respectively. Our disease classification results indicate that the highlighted connectomes are predominantly linked to the most relevant brain nodes of Alzheimer’s Disease (AD), such as the right/left insula cortex, anterior/posterior cingulate gyrus, and anterior/posterior divisions of the parahippocampal gyrus. Additionally, connectomes associated with AD-relevant subnetworks, such as the Default Mode Network (DMN) [7,27], are highlighted. Similarly, connectomes connected to the most relevant brain nodes (e.g., left/right amygdala, hippocampus and orbitofrontal) of depression are identified from DSM-Depr regression. The Salience Network (SN) subnetwork, crucial for emotional regulation [16], is also highlighted. Furthermore, we present the brain temporal dynamics of the identified connectomes in Fig. 2(b), visualizing the related derived from the disease classification task at each of the four time-points to illustrate how the effective connectomes change during an fMRI scan period. To quantify this change, we show the average of these weighted connectomes in Fig. 2(c). It demonstrates that the causal influence strength of the normal control(NC) group and the AD group decays simultaneously over time. However, the degree of decline in the AD group is more pronounced than in the NC group.
Fig. 2.
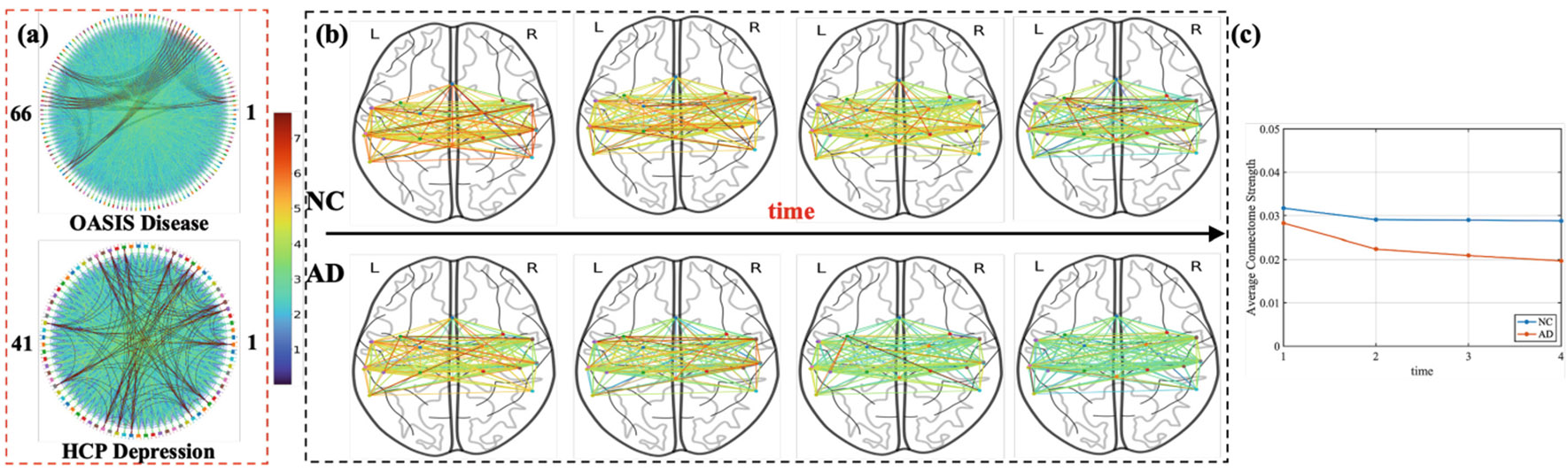
(a) illustrates the importance of various effective connectomes (i.e., ) for disease classification and DSM-Depr regression, with the most crucial connectomes highlighted in bold red. (b) visualizes the brain dynamics of the identified effective connectomes during an fMRI scan period, where colors tending towards red indicate large values. (c) quantifies the change in the average strength of identified connectomes during an fMRI scan period.
4. Conclusion
We propose an interpretable spatio-temporal framework with directed graph embedding layers for learning brain effective network representations, leveraging ordinary differential equations to model brain dynamics. Our framework contributes to important clinical prediction tasks, pinpointing important connectomes linked to different clinical phenotypes and illustrating dynamic causal influence strengths across fMRI scan periods. Future work will investigate dynamic causal influences at the level of brain ROIs.
Supplementary Material
Acknowledgments.
This study was partially supported by the Presidential Research Fellowship (PRF) in the Department of Computer Science at the University of Texas Rio Grande Valley (UTRGV), and the UTRGV seed grant, as well as by the NSF (2112631, 2045848, 2319449, 2319450, 2319451, 2215789, 2319451), and the NIH (R01AG071243, R01MH125928, U01AG068057, R21EY034179).
Footnotes
Disclosure of Interests. The authors have no competing interests to declare that are relevant to the content of this article.
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1007/978-3-031-72069-7_22.
References
- 1.American Psychiatric Association, D., Association, A.P., et al. : Diagnostic and statistical manual of mental disorders: DSM-5, vol. 5. American psychiatric association; Washington, DC: (2013) [Google Scholar]
- 2.Arevalo-Rodriguez I, Smailagic N, i Figuls MR, Ciapponi A, Sanchez-Perez E, Giannakou A, Pedraza OL, Cosp XB, Cullum S: Mini-mental state examination (mmse) for the detection of alzheimer’s disease and other dementias in people with mild cognitive impairment (mci). Cochrane Database of Systematic Reviews (3) (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bullmore E, Sporns O: Complex brain networks: graph theoretical analysis of structural and functional systems. Nature reviews neuroscience 10(3), 186–198 (2009) [DOI] [PubMed] [Google Scholar]
- 4.Chen D, Zhang L: Fe-stgnn: Spatio-temporal graph neural network with functional and effective connectivity fusion for mci diagnosis. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. pp. 67–76. Springer (2023) [Google Scholar]
- 5.Chuang KC, Ramakrishnapillai S, Madden K, St Amant J, McKlveen K, Gwizdala K, Dhullipudi R, Bazzano L, Carmichael O: Brain effective connectivity and functional connectivity as markers of lifespan vascular exposures in middle-aged adults: The bogalusa heart study. Frontiers in Aging Neuroscience 15, 1110434 (2023) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Demirbilek O, Rekik I: Recurrent multigraph integrator network for predicting the evolution of population-driven brain connectivity templates. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. pp. 584–594. Springer; (2021) [Google Scholar]
- 7.Dennis EL, Thompson PM: Functional brain connectivity using fmri in aging and alzheimer’s disease. Neuropsychology review 24, 49–62 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dvornek NC, Ventola P, Pelphrey KA, Duncan JS: Identifying autism from resting-state fmri using long short-term memory networks. In: Machine Learning in Medical Imaging: 8th International Workshop, MLMI 2017, Held in Conjunction with MICCAI 2017, Quebec City, QC, Canada, September 10, 2017, Proceedings 8. pp. 362–370. Springer; (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fischl B: Freesurfer. Neuroimage 62(2), 774–781 (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Friston KJ, Harrison L, Penny W: Dynamic causal modelling. Neuroimage 19(4), 1273–1302 (2003) [DOI] [PubMed] [Google Scholar]
- 11.Gadgil S, Zhao Q, Pfefferbaum A, Sullivan EV, Adeli E, Pohl KM: Spatio-temporal graph convolution for resting-state fmri analysis. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. pp. 528–538. Springer; (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM: Fsl. Neuroimage 62(2), 782–790 (2012) [DOI] [PubMed] [Google Scholar]
- 13.Kipf TN, Welling M: Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907 (2016) [Google Scholar]
- 14.LaMontagne PJ, Benzinger TL, Morris JC, Keefe S, Hornbeck R, Xiong C, Grant E, Hassenstab J, Moulder K, Vlassenko AG, et al. : Oasis-3: longitudinal neuroimaging, clinical, and cognitive dataset for normal aging and alzheimer disease. MedRxiv (2019) [Google Scholar]
- 15.Li J, Pan W, Huang H, Pan J, Wang F: Stgate: Spatial-temporal graph attention network with a transformer encoder for eeg-based emotion recognition. Frontiers in Human Neuroscience 17, 1169949 (2023) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pinto AM, Geenen R, Wager TD, Lumley MA, Häuser W, Kosek E, Ablin JN, Amris K, Branco J, Buskila D, et al. : Emotion regulation and the salience network: a hypothetical integrative model of fibromyalgia. Nature Reviews Rheumatology 19(1), 44–60 (2023) [DOI] [PubMed] [Google Scholar]
- 17.Sanchez-Romero R, Ramsey JD, Zhang K, Glymour MR, Huang B, Glymour C: Estimating feedforward and feedback effective connections from fmri time series: Assessments of statistical methods. Network Neuroscience 3(2), 274–306 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Serrano-Pozo A, Das S, Hyman BT: Apoe and alzheimer’s disease: advances in genetics, pathophysiology, and therapeutic approaches. The Lancet Neurology 20(1), 68–80 (2021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shchur O, Mumme M, Bojchevski A, Günnemann S: Pitfalls of graph neural network evaluation. arXiv preprint arXiv:1811.05868 (2018) [Google Scholar]
- 20.Shinn M, Hu A, Turner L, Noble S, Preller KH, Ji JL, Moujaes F, Achard S, Scheinost D, Constable RT, et al. : Functional brain networks reflect spatial and temporal autocorrelation. Nature Neuroscience pp. 1–12 (2023) [DOI] [PubMed] [Google Scholar]
- 21.Smith SM, Miller KL, Salimi-Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD, Woolrich MW: Network modelling methods for fmri. Neuroimage 54(2), 875–891 (2011) [DOI] [PubMed] [Google Scholar]
- 22.Stam C, Van Straaten E, Van Dellen E, Tewarie P, Gong G, Hillebrand A, Meier J, Van Mieghem P: The relation between structural and functional connectivity patterns in complex brain networks. International Journal of Psychophysiology 103, 149–160 (2016) [DOI] [PubMed] [Google Scholar]
- 23.Suykens JA, Lukas L, Van Dooren P, De Moor B, Vandewalle J, et al. : Least squares support vector machine classifiers: a large scale algorithm. In: European Conference on Circuit Theory and Design, ECCTD. vol. 99, pp. 839–842. Citeseer; (1999) [Google Scholar]
- 24.Tang H, Guo L, Fu X, Wang Y, Mackin S, Ajilore O, Leow AD, Thompson PM, Huang H, Zhan L: Signed graph representation learning for functional-to-structural brain network mapping. Medical image analysis 83, 102674 (2023) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium WMH, et al. : The wu-minn human connectome project: an overview. Neuroimage 80, 62–79 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Whitfield-Gabrieli S, Nieto-Castanon A: Conn: a functional connectivity toolbox for correlated and anticorrelated brain networks. Brain connectivity 2(3), 125–141 (2012) [DOI] [PubMed] [Google Scholar]
- 27.Yildirim E., SONCU BÜYÜKİŞCAN, E.: Default mode network connectivity in alzheimer’s disease. Turkish Journal of Psychiatry 30(4) (2019) [PubMed] [Google Scholar]
- 28.Ying Z, You J, Morris C, Ren X, Hamilton W, Leskovec J: Hierarchical graph representation learning with differentiable pooling. Advances in neural information processing systems 31 (2018) [Google Scholar]
- 29.Zhao C, Zhan L, Thompson PM, Huang H: Revealing continuous brain dynamical organization with multimodal graph transformer. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. pp. 346–355. Springer; (2022) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


