Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Oct 11;15(42):10473–10478. doi: 10.1021/acs.jpclett.4c02332

Prediction of Threonine-Tyrosine Kinase Receptor–Ligand Unbinding Kinetics with Multiscale Milestoning and Metadynamics

Lane W Votapka 1, Anupam Anand Ojha 1,2, Naoya Asada 3, Rommie E Amaro 4,*
PMCID: PMC11514002  PMID: 39392497

Abstract

graphic file with name jz4c02332_0004.jpg

Accurately describing protein–ligand binding and unbinding kinetics remains challenging. Computational calculations are difficult and costly, while experimental measurements often lack molecular detail and can be unobtainable. Here, we extend our multiscale milestoning method, Simulation-Enabled Estimation of Kinetics Rates (SEEKR), with metadynamics molecular dynamics simulations to yield accurate small molecule drug residence times. Using the pharmaceutically relevant threonine-tyrosine kinase (TTK) and eight long-residence-time (tens of seconds to hours) inhibitors, we demonstrate accurate prediction of absolute and rank-ordered ligand residence times and free energies of binding.

Biological systems involve a vast array of complex intermolecular interactions. The binding and unbinding of a ligand–receptor pair can be described by 1) thermodynamics, which considers equilibrium quantities like the free energy of binding (ΔGbind) and the equilibrium constant (KD), and 2) kinetics, which considers time-dependent quantities like the rate constant of binding (kon), the rate constant of unbinding (koff), and the residence time (1/koff).1 Knowledge of these quantities is desirable for predicting a drug’s efficacy2−5 and optimizing specificity in drug discovery.6−8 While experimental measurements of binding/unbinding kinetics and thermodynamics are possible, accurate and efficient computational predictions remain attractive. Simulation-Enabled Estimation of Kinetics Rates (SEEKR) is a multiscale, simulation-based, enhanced sampling method used to characterize the kinetics and thermodynamics of a variety of binding/unbinding systems.9−15

Metadynamics (metaD) is an enhanced sampling method that estimates the free energy landscapes of complicated systems.16−20 It accelerates the exploration of the free energy landscape by introducing a collective variable (CV)-based history-dependent bias potential that evolves over time, searching for new metastable states during MD simulations.17,21 Previously, SEEKR used steered molecular dynamics (SMD) for generating starting structures. In this work, we use the GPU-accelerated well-tempered metaD implementation within SEEKR. Threonine-tyrosine kinase (TTK), also known as monopolar spindle 1 (MPS1), is frequently overexpressed in highly proliferative cancers, making it a promising drug target for human breast cancer.22 A recent study revealed that residence time, rather than potency (IC50), has a stronger correlation with antiproliferative activity.23 Improving the kinetic properties of TTK inhibitors is essential, but the binding and unbinding mechanism is still unclear.

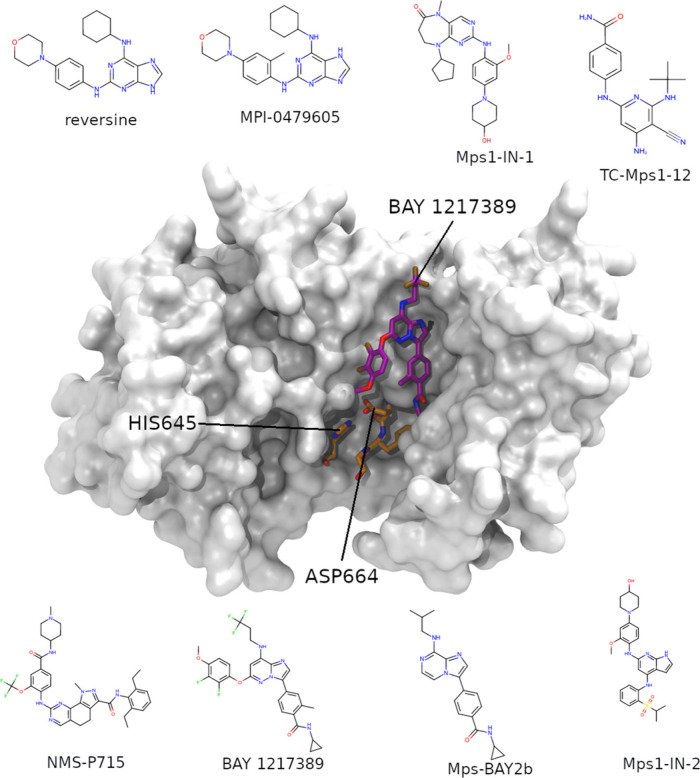
We ran SEEKR on eight TTK systems with experimental residence times available (Figure 1). Details of the computational methods, benchmarks, and simulation costs are in the Supporting Information (SI). SEEKR requires generating starting structures for simulations within the milestoning framework. Previously, this was done with SMD, which uses a harmonic restraint moving at a constant velocity along the CV to sample starting structures. In this study, we explore the use of metaD, which gradually fills the energy landscape with Gaussian boosts, allowing the ligand to gradually sample steep energy landscape portions. This comparison of initial sampling approaches within SEEKR - using SMD versus metaD - can be found in Figure 2 (Exact numerical values can be found in Tables S1 and S2).

Figure 1.

Figure 1

Open in a new tab

TTK structure, prominent features, and ligands. In the center, the TTK protein is shown as a translucent white surface, taken from the X-ray crystal structure 5NAD23.

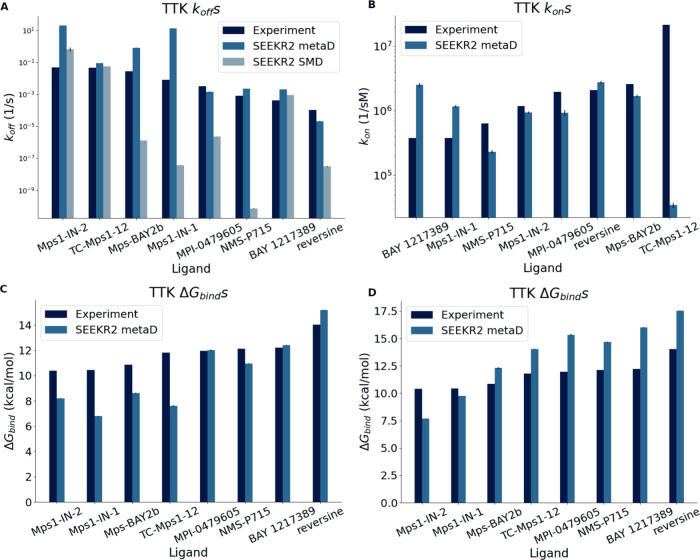
Figure 2.

Figure 2

Open in a new tab

TTK koff rate constants (A), kon rate constants (B), and ΔGbind using: kBT·ln(koff/kon) (C) and the difference in free energies of the MMVT anchors between bound and ‘escaped’ states (D) for known inhibitors.

Results for koff show that SEEKR2 with metaD produced the best results (Figure 2A; medium blue). In contrast, SMD (Figure 2A; light blue) produces suboptimal results. Predictions within a single order of magnitude of the experiment were found for all TTK system kon estimates except TC-Mps1–12 (Figure 2B). We examined the reasons for the large deviation and believe it is due to the reparametrized partial charges of the ligand in the bound state using QMrebind, which caused the charges to become highly polarized. The kon calculation depends on an accurate description of the unbound state, where molecular charges are likely to be less polarized. By applying the bound state QMrebind charges to the unbound state of compound TC-Mps1–12, as done in this study, a large desolvation penalty is incurred, significantly slowing the binding rate. Preliminary studies (data not shown) support this hypothesis, though further careful analysis is needed to fully validate it. The free energies of binding were computed by using the equation ΔGbind = kBT·ln(koff/kon) (Figure 2C). Clearly, the biggest deviation in TC-Mps1–12 was caused by the highly incorrect kon obtained for that system. In addition, the free energies of binding were computed by the difference in free energies of the MMVT anchors between the bound state and the predefined ‘escaped’ state at the mouth of the binding site (Figure 2D). Definitions of the binding sites are provided in the SI. While a large systematic bias is caused by the missing solvation energy of a true separation between ligand and receptor, the trend is very good - generating an almost perfect ranking.

SEEKR obtains a Kendall’s tau of 0.64 and a mean absolute log10 error of 1.2 for ranking of absolute unbinding kinetics using metaD, and a Kendall’s tau of 0.50 with a mean absolute log10 error of 3.1 for the same with SMD and QMrebind. Values for kon and ΔGbind were also computed for the TTK systems and are reported in Figures 2B, 2C, and 2D. The Kendall’s tau for this series of kon values was found to be −0.18, and the mean absolute log10 of the error was computed to be 0.66; for this series of ΔGbind values (computed from kBT·ln(koff/kon)), the Kendall’s tau was 0.71, with a mean absolute error of 1.9 kcal/mol. When the ΔGbind values were computed from the relative free energies of Markovian milestoning with Voronoi tesselations (MMVT) anchors, it gives Kendall’s tau of 0.93 and a mean absolute error of 2.5 kcal/mol. (Exact numerical values for koff values can be found in Table S1, kon and ΔGbind values can be found in Table S2).

In addition to the method of kinetics prediction, the choice and preparation of system structure files for the receptor and ligand are very important,24−27 including the selection of high-quality experimentally determined structures, ensuring physical realism (matching experimental conditions like temperature, pressure, ion concentrations, and pH), carefully considering protonation states of ligands and receptor residues, and performing adequate minimization and equilibration to ensure that the system is modeled near a thermodynamic equilibrium state. The choice of force field parameters for SEEKR calculations is also critical. We use the QMrebind method13 to redefine the partial charges of the ligand in the bound state, which works well for the TTK system, particularly affecting the partial charges on a tert-butyl side group (Figure S1) - although, as we mentioned before, this likely negatively impacted the kon estimate for TC-Mps1–12. Other force field parameters, such as ligand torsions, may also benefit from refinement - a topic we do not address here. All the partial charges, both before and after using QMrebind to reparametrize them, can be found in Table S3.

Challenges arise when modeling halogens28 due to the 'sigma hole', producing a positive partial charge opposite the covalent bond with chlorine, bromine, or iodine atoms. In particular, inaccuracies have been observed when the halogen interacts with Lewis bases. However, fluorine’s small sigma hole can be adequately described with a point charge,29 as shown by the successful application of SEEKR to the TTK 'BAY 1217389' and 'NMS-P715' systems, which contain many fluorines.

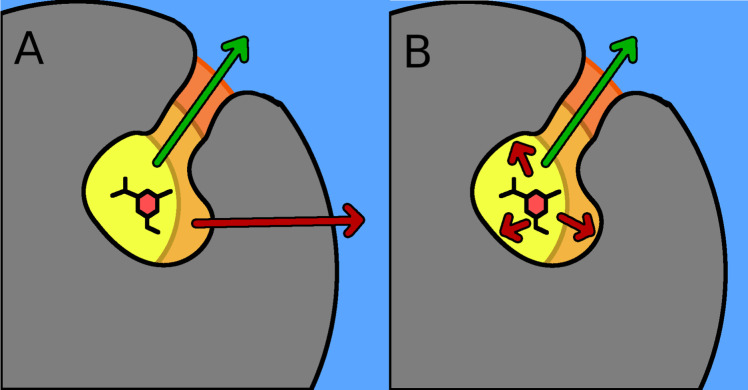
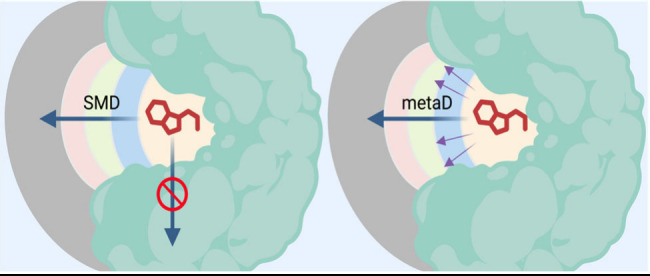
After system preparation, choosing the CV, and providing force field parameters, the SEEKR MMVT algorithm populates each Voronoi cell with starting structures to run simulations and gather milestoning times and statistics. The HIDR tool within SeekrTools (https://github.com/seekrcentral/seekrtools.git) facilitates this by exploring the entire reaction coordinate span and saving potential starting structures. We found that metaD provides superior starting structures compared to other methods. Previously, SMD was commonly used for generating starting structures for SEEKR. However, more complex ligands with large, flexible structures lead to artificial tearing and unfolding of the protein. SMD sometimes pushed the ligand along the wrong unbinding pathway or through the binding site’s interior surface, resulting in inaccurate SEEKR kinetics predictions (Figure 3A).

Figure 3.

Figure 3

Open in a new tab

Cartoon schematic comparing exploration of correct and incorrect unbinding pathways using SMD (panel A) and metaD (panel B). In both panels, the green arrow represents the correct unbinding path, while the incorrect unbinding paths are red arrow(s).

While adverse effects of SMD can sometimes be mitigated by carefully reselecting the atoms defining the binding site, alternative sampling algorithms like metaD allow the ligand to backtrack and explore multiple exit pathways (Figure 3B). MetaD works well for this purpose, unlike SMD, which constrains the ligand to a particular CV value and can push it through the binding site’s interior surface if stuck. As shown in Figure 3A, SMD might explore the correct unbinding path, but if the ligand gets pushed along the incorrect unbinding path, up against an interior surface of the binding site, the inability of SMD to 'back up' causes the ligand to get pushed through the interior surface. In contrast, in Figure 3B, metaD can also sample the correct unbinding path, but if the incorrect unbinding path is explored, the surface of the binding site will stop the ligand, and the metaD sampling algorithm will allow the ligand to backtrack.

However, using metaD to generate starting structures has its challenges. If the Gaussian height is too large, it can disrupt the molecular system, affecting the accuracy of the SEEKR calculation (data not shown). Conversely, generating starting structures can be time-consuming and resource-intensive if the Gaussian heights are too small. The choice of CV is also nontrivial and can complicate practical use, especially for less-studied receptors.30−32

Convergence is important for SEEKR calculations to determine if additional sampling is necessary or if an incorrect physical description impacts accuracy. Convergence plots in Figure S2 show that metaD starting structures converge better than SMD, likely because metaD sample structures with lower energy closer to the true unbinding pathway.

In this work, we expand SEEKR’s capabilities and demonstrate its success in estimating binding and unbinding kinetics for the TTK system and eight small molecules with residence times from seconds to hours. The combined use of metaD for initial structure generation and quantum-mechanically reparametrized ligands significantly improves SEEKR calculations. We believe this protocol, which integrates SEEKR and metaD to predict binding and unbinding kinetics and thermodynamics, will be broadly useful for various ligand–receptor systems, provided each system is described with sufficient physical accuracy. However, challenges remain for systems with heavy halogens due to sigma holes, systems where protonation states or partial charges change significantly along the unbinding pathway, or systems lacking suitable molecular mechanics force fields. Additionally, increasingly large or complex ligands may pose significant challenges. Efforts to address these and other unforeseen issues are ongoing and will be resolved in future research iterations. SEEKR2 open-source software is available at GitHub: https://github.com/seekrcentral/seekr2.git, and SeekrTools, which runs metaD and SMD, at https://github.com/seekrcentral/seekrtools.git. Files to prepare systems and inputs for SEEKR calculations can be found at https://github.com/seekrcentral/seekr2_systems/tree/master/systems/TTK. Data for the systems in this study can be obtained from 10.6075/J0571C7G.

Acknowledgments

The authors thank Steffen Wolf, University of Freiburg, for his insightful and valuable discussions. The authors express their gratitude to Shiksha Dutta and Mac Kevin E. Braza for their assistance with the figures. Thanks to Jeff Wagner for helpful discussions about force field parametrization as well as assistance with testing, continuous integration, and GitHub. A. A. O. acknowledges the support of the Merkin Fellowship from the University of California San Diego. All simulations were performed using the Popeye computing cluster at the San Diego Supercomputing Center (SDSC) and the Delta supercomputing system at the National Center for Supercomputing Applications (NCSA), University of Illinois Urbana–Champaign. The authors acknowledge support from NSF Advanced Cyberinfrastructure Coordination Ecosystem: Services and Support (ACCESS) CHE060063. The authors thank the Laboratory for Medicinal Chemistry Research, Shionogi and CO. Ltd, Osaka, Japan, for their collaborative efforts and contributions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.4c02332.

  • Computational Methods Benchmarking and Simulation Costs; Table S1 - Unbinding kinetics for TTK systems; Table S2 - Binding kinetics and free energies for TTK systems; Figure S1: Reparametrization of charges using QMrebind on compound TC-Mps1-12; Table S3 - TTK system ligand charge reparametrization from AM1BCC charges to QMrebind charges; Figure S2 - Convergence of koff for TTK Systems; Table S4 - TTK system binding site definitions; Table S5 - TTK system anchor radii (PDF)

  • Transparent Peer Review report available (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz4c02332_si_001.pdf (654.5KB, pdf)
jz4c02332_si_002.pdf (151.1KB, pdf)

References

  1. Bernetti M.; Masetti M.; Rocchia W.; Cavalli A. Kinetics of Drug Binding and Residence Time. Annu. Rev. Phys. Chem. 2019, 70 (1), 143–171. 10.1146/annurev-physchem-042018-052340. [DOI] [PubMed] [Google Scholar]
  2. Copeland R. A.; Pompliano D. L.; Meek T. D. Drug–Target Residence Time and Its Implications for Lead Optimization. Nat. Rev. Drug Discov. 2006, 5 (9), 730–739. 10.1038/nrd2082. [DOI] [PubMed] [Google Scholar]
  3. Copeland R. A. The Drug-Target Residence Time Model: A 10-Year Retrospective. Nat. Rev. Drug Discov. 2016, 15 (2), 87–95. 10.1038/nrd.2015.18. [DOI] [PubMed] [Google Scholar]
  4. Huggins D. J.; Sherman W.; Tidor B. Rational Approaches to Improving Selectivity in Drug Design. J. Med. Chem. 2012, 55 (4), 1424–1444. 10.1021/jm2010332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Fang Y. Ligand-Receptor Interaction Platforms and Their Applications for Drug Discovery. Expert Opin. Drug Discov. 2012, 7 (10), 969–988. 10.1517/17460441.2012.715631. [DOI] [PubMed] [Google Scholar]
  6. Tang Z.; Roberts C. C.; Chang C. A. Understanding Ligand-Receptor Non-Covalent Binding Kinetics Using Molecular Modeling. Front. Biosci. Landmark Ed. 2017, 22, 960–981. 10.2741/4527. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Liu W.; Jiang J.; Lin Y.; You Q.; Wang L. Insight into Thermodynamic and Kinetic Profiles in Small-Molecule Optimization. J. Med. Chem. 2022, 65 (16), 10809–10847. 10.1021/acs.jmedchem.2c00682. [DOI] [PubMed] [Google Scholar]
  8. Tonge P. J. Drug–Target Kinetics in Drug Discovery. ACS Chem. Neurosci. 2018, 9 (1), 29–39. 10.1021/acschemneuro.7b00185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Votapka L. W.; Amaro R. E. Multiscale Estimation of Binding Kinetics Using Brownian Dynamics, Molecular Dynamics and Milestoning. PLOS Comput. Biol. 2015, 11 (10), e1004381. 10.1371/journal.pcbi.1004381. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Votapka L. W.; Jagger B. R.; Heyneman A. L.; Amaro R. E. SEEKR: Simulation Enabled Estimation of Kinetic Rates, A Computational Tool to Estimate Molecular Kinetics and Its Application to Trypsin–Benzamidine Binding. J. Phys. Chem. B 2017, 121 (15), 3597–3606. 10.1021/acs.jpcb.6b09388. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Jagger B. R.; Lee C. T.; Amaro R. E. Quantitative Ranking of Ligand Binding Kinetics with a Multiscale Milestoning Simulation Approach. J. Phys. Chem. Lett. 2018, 9 (17), 4941–4948. 10.1021/acs.jpclett.8b02047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Jagger B. R.; Ojha A. A.; Amaro R. E.. Predicting Ligand Binding Kinetics Using a Markovian Milestoning with Voronoi Tessellations Multiscale Approach J. Chem. Theory Comput. 2020, 16 ( (8), ), 5348. 10.1021/acs.jctc.0c00495 [DOI] [PubMed] [Google Scholar]
  13. Ojha A. A.; Votapka L. W.; Amaro R. E. QMrebind: Incorporating Quantum Mechanical Force Field Reparameterization at the Ligand Binding Site for Improved Drug-Target Kinetics through Milestoning Simulations. Chem. Sci. 2023, 14 (45), 13159–13175. 10.1039/D3SC04195F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ojha A. A.; Srivastava A.; Votapka L. W.; Amaro R. E. Selectivity and Ranking of Tight-Binding JAK-STAT Inhibitors Using Markovian Milestoning with Voronoi Tessellations. J. Chem. Inf. Model. 2023, 63 (8), 2469–2482. 10.1021/acs.jcim.2c01589. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Votapka L. W.; Stokely A. M.; Ojha A. A.; Amaro R. E. SEEKR2: Versatile Multiscale Milestoning Utilizing the OpenMM Molecular Dynamics Engine. J. Chem. Inf. Model. 2022, 62 (13), 3253–3262. 10.1021/acs.jcim.2c00501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Barducci A.; Bonomi M.; Parrinello M. Metadynamics. WIREs Comput. Mol. Sci. 2011, 1 (5), 826–843. 10.1002/wcms.31. [DOI] [Google Scholar]
  17. Bussi G.; Laio A. Using Metadynamics to Explore Complex Free-Energy Landscapes. Nat. Rev. Phys. 2020, 2 (4), 200–212. 10.1038/s42254-020-0153-0. [DOI] [Google Scholar]
  18. Tiwary P.; Parrinello M. From Metadynamics to Dynamics. Phys. Rev. Lett. 2013, 111 (23), 230602. 10.1103/PhysRevLett.111.230602. [DOI] [PubMed] [Google Scholar]
  19. Laio A.; Gervasio F. L. Metadynamics: A Method to Simulate Rare Events and Reconstruct the Free Energy in Biophysics. Chemistry and Material Science. Rep. Prog. Phys. 2008, 71 (12), 126601. 10.1088/0034-4885/71/12/126601. [DOI] [Google Scholar]
  20. Ensing B.; De Vivo M.; Liu Z.; Moore P.; Klein M. L. Metadynamics as a Tool for Exploring Free Energy Landscapes of Chemical Reactions. Acc. Chem. Res. 2006, 39 (2), 73–81. 10.1021/ar040198i. [DOI] [PubMed] [Google Scholar]
  21. Laio A.; Parrinello M. Escaping Free-Energy Minima. Proc. Natl. Acad. Sci. U. S. A. 2002, 99 (20), 12562–12566. 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Schmidt M.; Budirahardja Y.; Klompmaker R.; Medema R. H. Ablation of the Spindle Assembly Checkpoint by a Compound Targeting Mps1. EMBO Rep 2005, 6 (9), 866–872. 10.1038/sj.embor.7400483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Uitdehaag J. C. M.; de Man J.; Willemsen-Seegers N.; Prinsen M. B. W.; Libouban M. A. A.; Sterrenburg J. G.; de Wit J. J. P.; de Vetter J. R. F.; de Roos J. A. D. M.; Buijsman R. C.; Zaman G. J. R. Target Residence Time-Guided Optimization on TTK Kinase Results in Inhibitors with Potent Anti-Proliferative Activity. J. Mol. Biol. 2017, 429 (14), 2211–2230. 10.1016/j.jmb.2017.05.014. [DOI] [PubMed] [Google Scholar]
  24. Gathiaka S.; Liu S.; Chiu M.; Yang H.; Stuckey J. A.; Kang Y. N.; Delproposto J.; Kubish G.; Dunbar J. B.; Carlson H. A.; Burley S. K.; Walters W. P.; Amaro R. E.; Feher V. A.; Gilson M. K. D3R Grand Challenge 2015: Evaluation of Protein–Ligand Pose and Affinity Predictions. J. Comput. Aided Mol. Des. 2016, 30 (9), 651–668. 10.1007/s10822-016-9946-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Gaieb Z.; Liu S.; Gathiaka S.; Chiu M.; Yang H.; Shao C.; Feher V. A.; Walters W. P.; Kuhn B.; Rudolph M. G.; Burley S. K.; Gilson M. K.; Amaro R. E. D3R Grand Challenge 2: Blind Prediction of Protein–Ligand Poses, Affinity Rankings, and Relative Binding Free Energies. J. Comput. Aided Mol. Des. 2018, 32 (1), 1–20. 10.1007/s10822-017-0088-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Gaieb Z.; Parks C. D.; Chiu M.; Yang H.; Shao C.; Walters W. P.; Lambert M. H.; Nevins N.; Bembenek S. D.; Ameriks M. K.; Mirzadegan T.; Burley S. K.; Amaro R. E.; Gilson M. K. D3R Grand Challenge 3: Blind Prediction of Protein–Ligand Poses and Affinity Rankings. J. Comput. Aided Mol. Des. 2019, 33 (1), 1–18. 10.1007/s10822-018-0180-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Parks C. D.; Gaieb Z.; Chiu M.; Yang H.; Shao C.; Walters W. P.; Jansen J. M.; McGaughey G.; Lewis R. A.; Bembenek S. D.; Ameriks M. K.; Mirzadegan T.; Burley S. K.; Amaro R. E.; Gilson M. K. D3R Grand Challenge 4: Blind Prediction of Protein–Ligand Poses, Affinity Rankings, and Relative Binding Free Energies. J. Comput. Aided Mol. Des. 2020, 34 (2), 99–119. 10.1007/s10822-020-00289-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Ibrahim M. A. A. Molecular Mechanical Study of Halogen Bonding in Drug Discovery. J. Comput. Chem. 2011, 32 (12), 2564–2574. 10.1002/jcc.21836. [DOI] [PubMed] [Google Scholar]
  29. Wehrhan L.; Keller B. G. Fluorinated Protein–Ligand Complexes: A Computational Perspective. J. Phys. Chem. B 2024, 128 (25), 5925–5934. 10.1021/acs.jpcb.4c01493. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Hayward S.; Go N. Collective Variable Description of Native Protein Dynamics. Annu. Rev. Phys. Chem. 1995, 46, 223–250. 10.1146/annurev.pc.46.100195.001255. [DOI] [PubMed] [Google Scholar]
  31. Berendsen H. J.; Hayward S. Collective Protein Dynamics in Relation to Function. Curr. Opin. Struct. Biol. 2000, 10 (2), 165–169. 10.1016/S0959-440X(00)00061-0. [DOI] [PubMed] [Google Scholar]
  32. Bhakat S. Collective Variable Discovery in the Age of Machine Learning: Reality, Hype and Everything in Between. RSC Adv. 2022, 12 (38), 25010–25024. 10.1039/D2RA03660F. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz4c02332_si_001.pdf (654.5KB, pdf)
jz4c02332_si_002.pdf (151.1KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES