Abstract
BACKGROUND
The quality of a radiotherapy plan often depends on the knowledge and expertise of the plan designers.
AIM
To predict the uninvolved liver dose in stereotactic body radiotherapy (SBRT) for liver cancer using a neural network-based method.
METHODS
A total of 114 SBRT plans for liver cancer were used to test the neural network method. Sub-organs of the uninvolved liver were automatically generated. Correlations between the volume of each sub-organ, uninvolved liver dose, and neural network prediction model were established using MATLAB. Of the cases, 70% were selected as the training set, 15% as the validation set, and 15% as the test set. The regression R-value and mean square error (MSE) were used to evaluate the model.
RESULTS
The volume of the uninvolved liver was related to the volume of the corresponding sub-organs. For all sets of R-values of the prediction model, except for Dn0 which was 0.7513, all R-values of Dn10-Dn100 and Dnmean were > 0.8. The MSE of the prediction model was also low.
CONCLUSION
We developed a neural network-based method to predict the uninvolved liver dose in SBRT for liver cancer. It is simple and easy to use and warrants further promotion and application.
Keywords: Dose prediction, Sub-organ, Machine learning, Stereotactic body radiotherapy, Liver cancer
Core Tip: In this study, a neural network prediction model for the uninvolved liver dose was established using the MATLAB neural network application. The regression R-value and mean square error (MSE) were used to evaluate the model. All R-values for Dn10-Dn100 and Dnmean were > 0.8, except for Dn0, which was 0.7513, respectively. The MSE of the prediction model was also very low.
INTRODUCTION
Radiation therapy (RT) is an important cancer treatment method required by approximately 70% of patients with cancer[1]. A radiotherapy plan is designed based on a reverse plan design method, namely, the doctor gives the prescription dose and dose limit data for the relevant organ(s) at risk (OAR)[2]. Then, this information is used to optimize and set constraints for the target area and relevant normal tissues. Next, the optimization algorithm is used in the RT planning system to obtain a therapy plan that meets the clinical requirements. Plan optimization is one of the most important steps in designing a radiotherapy plan, and selecting the optimization goals and constraints is the most critical step, as it directly affects the quality performance of the final plan[3]. However, the goals and constraints are unknown when the clinical radiotherapy plan is designed[4-6]. Planners usually refer to the goals provided by doctors based on general population data, the Radiation Therapy Oncology Group guidelines, or clinical statistical specifications. These reference goals have universal applicability, but for some patients, the optimal conditions are not the same owing to the uniqueness of their anatomical structures. Therefore, meeting only universal target requirements is insufficient. The primary clinical solution to this issue is to continuously modify the statistical protocol-based goals or constraints by relying on manual experience, optimizing the results, and then re-evaluating until a new optimal result is determined. However, this manual trial and error method causes the quality of the plan to be completely dependent on the experience of the plan designer, resulting in large discrepancies in radiotherapy plan quality among institutions and planners[7-9]. To address this challenge, planners frequently modify statistical protocol-based goals or constraints through manual attempt, optimization of results, and reassessment until an optimal outcome is achieved. However, this approach renders the quality of the plan solely dependent on the planner's experience, leading to significant variations in radiotherapy plan quality across institutions and planners.
Recently, OAR dose prediction has gained widespread application in RT[10-13], owing to its numerous advantages. One of its primary benefits is the ability to forecast the quality of RT plans by evaluating and identifying suboptimal plans. This predictive capability enables the identification of potential issues or inefficiencies in an RT plan before it is executed, allowing adjustments and optimizations to be made. Consequently, this leads to an improvement in the overall plan quality, ensuring that the treatment is as effective and safe as possible.
Furthermore, OAR dose forecasting plays a crucial role in enhancing quality consistency across RT planning. By minimizing variations among planners with diverse levels of experience[14-16], this technique ensures that RT plans are standardized and aligned with best practices. This reduction in variability is particularly important in complex cases where the margin of error is minimal and consistent high-quality planning is essential for achieving optimal patient outcomes. Ultimately, the application of OAR dose prediction in RT not only improves plan quality but also contributes to more reliable and effective treatments for patients.
Stereotactic body radiotherapy (SBRT) has emerged as a new radiotherapy technology that delivers high doses of radiation to the target area in fewer fractions[17,18]. SBRT accurately transfers a large dose of multiple beams to the target tumor within one to five fractions owing to technical progress, respiratory movement management, and daily image guidance[19-21]. A short treatment period benefits patients by reducing interference with other treatment measures. Our practice recommends SBRT for patients with unresectable primary and metastatic liver cancer; however, the SBRT treatment strategy is highly individualized.
To meet the individualized needs of patients, reduce variations in treatment dosage, and enhance patient treatment safety, we established a novel predictive model for the uninvolved liver during liver cancer SBRT based on a neural network. This model was derived from our self-developed dose-prediction method, which is protected by Chinese patent ZL201610529290.8. This method aims to minimize the impact of subjective factors on plan quality and provide personalized SBRT plans for patients.
MATERIALS AND METHODS
Patient data
A total of 114 patients with liver cancer who underwent liver biopsy between January 2017 and December 2023 were selected for retrospective analysis. When splitting the relatively small dataset into training, validation, and testing sets, we utilized stratified random sampling to maintain consistency in basic patient characteristics across the sets, thereby enhancing the reliability of results. Specifically, 70% of the 114 SBRT plans were randomly assigned to the training set, 15% to the validation set, and the remaining 15% to the test set using the MATLAB neural net-fitting application. Furthermore, to address concerns regarding reliability with a small dataset, we ensured that the process was repeated multiple times, and the average results were considered, strengthening the stability of our findings. The inclusion criteria were designed to ensure a homogeneous cohort comprising individuals who: (1) Underwent preoperative imaging with dual-phase contrast-enhanced computed tomography (CT); (2) Had no prior history of RT or chemotherapy; (3) A definitive diagnosis of malignant liver tumor via postoperative pathological analysis accompanied by comprehensive clinical documentation; and (4) Were 18-80 years of age, with no contraindications for RT, and with a projected lifespan exceeding three months. The exclusion criteria rigorously screened cases that might compromise the validity of the study, including: (1) CT scans exhibiting severe motion artifacts or overt noise, precluding accurate image analysis; (2) Tumors measuring less than 1.0 cm in diameter, which may not fully reflect the population of interest; (3) Coexisting malignancies or additional tumor conditions; and (4) Pregnant or lactating females, as well as those who declined to employ adequate contraceptive measures, thereby presenting ethical concerns or potential confounding factors.
Prescription dose and limiting requirements
The gross tumor volume (GTV) was determined based on the tumor displayed on enhanced CT and magnetic resonance imaging. The internal target volume (ITV) was defined as the sum of multiphase GTVs. The planning target volume (PTV) included the ITV, with a margin of 3-5 mm. The design plan specified the prescribed dose in the isodose line containing > 95% of the PTV, and the PTV prescription dose was 25-50 Gy, divided into five fractions. The mean dose to the unaffected liver was 15 Gy[22,23].
SBRT plans
All SBRT plans were generated using a 7- or 9-coplanar field intensity-modulated RT technique with 6-MV photon beams. All planning was performed using the Eclipse treatment planning system (TPS) (Varian Medical Systems, Palo Alto, CA, United States). The planning parameters were to avoid the uninvolved liver as much as possible and conform the dose to the target volumes within the OAR constraints. Individualize the number and location of radiation fields to minimize the liver exposure volume and dose.
Deriving the sub-organs from the uninvolved liver
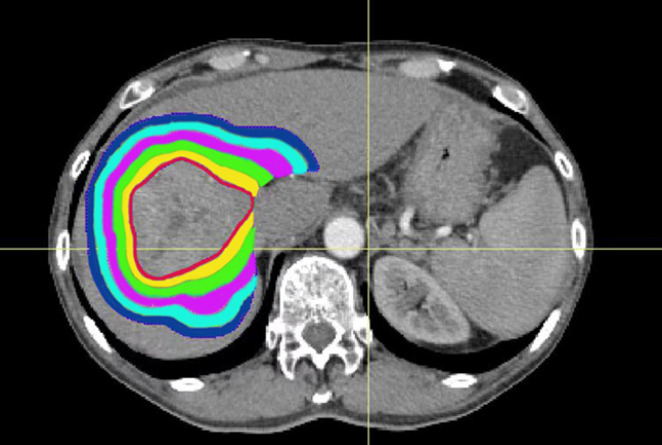
The PTV was expanded externally to a plurality of rings (ring1-ringn) with a width of 0.5 cm. Ring1-ringn and different uninvolved liver intersection regions (ring1-ringn∩uninvolved liver) were used as independent sub-organs; ringn∩uninvolved liver was defined as a sub-organ (e.g., ring1∩uninvolved liver was defined as sub-organ1). The total number of sub-organs was maintained at 20. The intersecting regions for sub-organ1-sub-organ of the uninvolved liver are shown in Figure 1. The sub-organ volume was normalized to improve data analysis. The normalized sub-organ volume (Vnsub-organ) was calculated as the sub-organ volume divided by the total uninvolved liver volume.
Figure 1.
Sub-organ of the uninvolved liver. The red line indicates planning target volume, the yellow shadow indicates the sub-organ1, the green shadow indicates the sub-organ2, the pink shadow indicates the sub-organ3, the sky blue shadow indicates the sub-organ4, the blue shadow indicates the sub-organ5.
The red line indicates PTV, the yellow shadow indicates the sub-organ1, the green shadow indicates the sub-organ2, the pink shadow indicates the sub-organ3, the sky blue shadow indicates the sub-organ4, the blue shadow indicates the sub-organ5.
Preprocessing
To eliminate the effects of different prescription doses, the uninvolved liver dose was normalized using the following equation: Dnx = Dx (Dx: Dose of x% of the uninvolved liver volume)/prescription dose of the PTV (Dprescription). The neural network prediction model was established based on the correlations between Vnsub-organ, Dn0-Dn100, and the normalized mean dose (Dnmean) of the uninvolved liver, with Vnsub-OAR as the independent variable and Dn0-Dn100 and Dnmean as the dependent variables. The correlation between DNX and VN was also analyzed.
Neural network model
Neural networks, inspired by biological systems, are computational models comprising interconnected processing units (neurons) with weighted connections. They learn complex input-output relationships by adjusting the weights. In this study, we employed a multilayer feedforward neural network to capture the nonlinear relationships between input features (e.g., volumes of unaffected liver sub-organs) and outputs (e.g., dose to the uninvolved liver). The advantages of neural networks include their nonlinear modeling capability, adaptability for solving complex prediction problems, and universal approximation capability. However, they also have disadvantages, such as computational complexity, risk of overfitting, and lack of interpretability. In this study, we leveraged nonlinear modeling and the adaptability of neural networks to predict the dose to the uninvolved liver in SBRT planning, overcoming the limitations of traditional linear models. In our study, we set up a three-layer neural network in which the number of neurons in the first two hidden layers was 10, and the number of neurons in the last output layer was 1. We used the Rectified Linear Unit activation function to mitigate the vanishing gradient problem and accelerate training. The cross-entropy loss function was used to evaluate the prediction accuracy, and the Levenberg-Marquardt algorithm was employed for training to optimize the network parameters. Given the constraints of the small dataset, the hyperparameter tuning process was conducted rigorously and accurately. The dataset was divided into training, validation, and test sets. The validation set was used to monitor the performance of the model during training to stop promptly to prevent data overfitting. The prediction model was established using the MATLAB neural net-fitting application, with the best results selected from 100 training iterations. A five-fold cross-validation method was used to ensure good generalization and model stability. The MATLAB application was used for the automatic generation and reading of sub-organ volumes and doses.
Prediction accuracy evaluation
The regression R-value measures the correlation between the outputs and targets. An R-value of 1 indicates a perfect relationship, whereas 0 indicates a random relationship. The mean square error (MSE) is the average squared difference between the outputs and targets, where lower values are better and 0 means no error. The R-values and MSE were evaluated using a neural network prediction model.
Statistical analysis
Pearson’s correlation test was performed to analyze the correlation between Dnx and Vnsub-organ using SPSS software version 19.0.
RESULTS
The Vnsub-organ was correlated with the Dn0-Dn100 and Dnmean of the uninvolved liver (P < 0.05), and prediction models for Dn0-Dn100 and Dnmean were established based on this correlation. Table 1 shows the correlation coefficients between Dn0-Dn100 and Dnmean for the uninvolved liver and Vnsub-organs.
Table 1.
Correlation coefficients between Dn0-Dn100 and Dnmean of the uninvolved liver and the Vnsub-organ
|
Dose
|
Vnsub-organ1
|
Vnsub-organ2
|
Vnsub-organ3
|
Vnsub-organ4
|
Vnsub-organ5
|
P value
|
| Dn0 | 0.529b | 0.414b | 0.332b | 0.276b | 0.238a | P < 0.01 |
| Dn10 | 0.689b | 0.694b | 0.674b | 0.662b | 0.654b | P < 0.01 |
| Dn20 | 0.653b | 0.704b | 0.702b | 0.706b | 0.710b | P < 0.01 |
| Dn30 | 0.587b | 0.667b | 0.686b | 0.706b | 0.721b | P < 0.01 |
| Dn40 | 0.542b | 0.630b | 0.664b | 0.693b | 0.718b | P < 0.01 |
| Dn50 | 0.533b | 0.608b | 0.641b | 0.670b | 0.695b | P < 0.01 |
| Dn60 | 0.563b | 0.628b | 0.654b | 0.676b | 0.697b | P < 0.01 |
| Dn70 | 0.605b | 0.642b | 0.653b | 0.664b | 0.676b | P < 0.01 |
| Dn80 | 0.653b | 0.670b | 0.669b | 0.668b | 0.672b | P < 0.01 |
| Dn90 | 0.664b | 0.669b | 0.663b | 0.652b | 0.649b | P < 0.01 |
| Dn100 | 0.539b | 0.466b | 0.417b | 0.378b | 0.354b | P < 0.01 |
| Dnmean | 0.675b | 0.725b | 0.732b | 0.742b | 0.752b | P < 0.01 |
P < 0.05. This suggests that the observed correlation is statistically significant at the 5% level, meaning there is less than a 5% chance of observing such results if the null hypothesis were true.
P < 0.01, indicating a higher level of statistical significance. This implies that the observed correlation is statistically significant at the 1% level, with less than a 1% chance of occurring under the null hypothesis.
Pearson’s correlation test was used to analyze the correlation. The P value provides a quantitative measure of the statistical significance of the observed results.
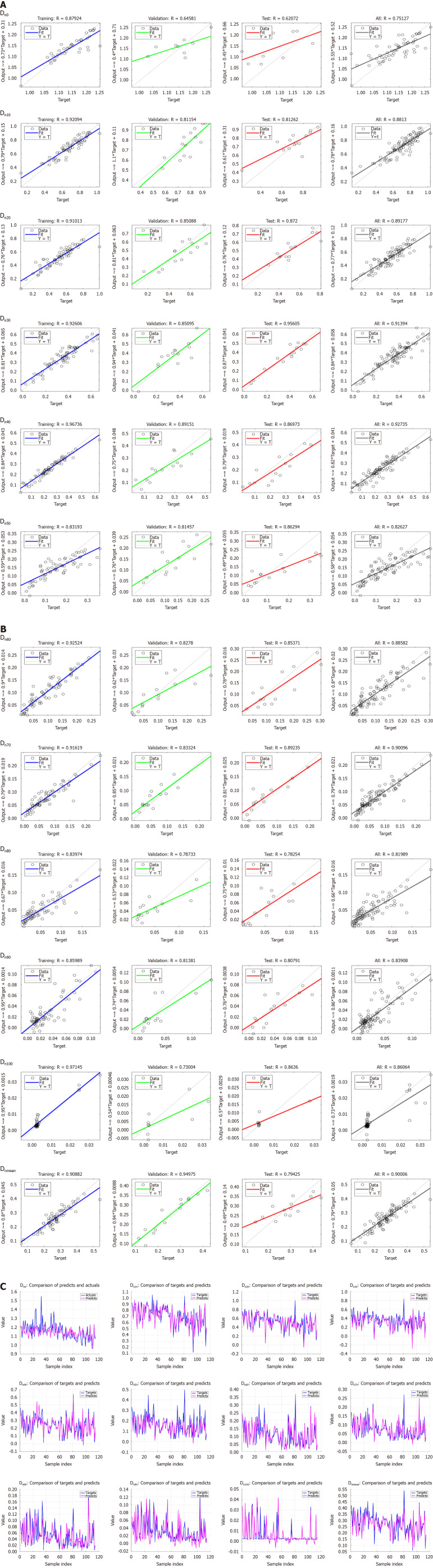
Figure 2A illustrates the regression diagram of the neural network prediction model for Dn0-Dn50. The figure demonstrates a strong positive correlation between the predicted and actual doses, with R-values indicating a good fit for the prediction model across different dose levels.
Figure 2.
The neural network prediction model. A: Regression diagram of Dn0-Dn50 for the neural network prediction model; B: Regression diagram of Dn60-Dn100 and Dnmean for the neural network prediction model; C: The predicted value by the neural network model and the actual planned value. Pink is the predicted value of the neural network model; blue is the target planned value. Dnx = Dx (Dx: Dose of x% uninvolved liver volume)/prescription dose of planning target volume (Dprescription).
Figure 2B shows the regression diagrams for Dn60-Dn100 and Dnmean. Similarly, there was a close agreement between the predicted and actual doses, with all R-values > 0.8, indicating the reliability of the prediction model in estimating the mean dose and different dose levels.
The R-values of the neural network prediction models are listed in Table 2. For all R-values of the prediction model, the highest R-value was 0.9274 for Dn40, and the lowest R-value was 0.7513 for Dn0. The R-values of Dn10-Dn100 and Dnmean were > 0.8.
Table 2.
R-value of the neural network prediction model
|
Dose
|
Training
|
Verification
|
Test |
All
|
| Dn0 | 0.8792 | 0.6458 | 0.6207 | 0.7513 |
| Dn10 | 0.9209 | 0.8115 | 0.8126 | 0.8813 |
| Dn20 | 0.9101 | 0.8509 | 0.8720 | 0.8918 |
| Dn30 | 0.9261 | 0.8510 | 0.9561 | 0.9139 |
| Dn40 | 0.9674 | 0.8915 | 0.8697 | 0.9274 |
| Dn50 | 0.8319 | 0.8146 | 0.8629 | 0.8263 |
| Dn60 | 0.9252 | 0.8278 | 0.8537 | 0.8858 |
| Dn70 | 0.9162 | 0.8332 | 0.8924 | 0.9010 |
| Dn80 | 0.8397 | 0.7873 | 0.7825 | 0.8199 |
| Dn90 | 0.8599 | 0.8138 | 0.8079 | 0.8391 |
| Dn100 | 0.9715 | 0.7300 | 0.8336 | 0.8606 |
| Dnmean | 0.9088 | 0.9498 | 0.7943 | 0.9006 |
The MSE values for the neural network prediction model are listed in Table 3. The MSE of the prediction model was also low (0.0004-0.0080).
Table 3.
Mean square error of the neural network prediction model
|
Dose
|
MSE
|
| Dn0 | 0.0071 |
| Dn10 | 0.0066 |
| Dn20 | 0.0080 |
| Dn30 | 0.0075 |
| Dn40 | 0.0035 |
| Dn50 | 0.0046 |
| Dn60 | 0.0022 |
| Dn70 | 0.0012 |
| Dn80 | 0.0006 |
| Dn90 | 0.0004 |
| Dn100 | 0.0006 |
| Dnmean | 0.0019 |
MSE: Mean square error.
Figure 2C shows the predicted and actual plots of uninvolved liver doses. The pink line represents the doses predicted by the neural network model and the blue line indicates the planned target doses. The close alignment between the two lines validated the accuracy of the prediction model across different dose levels, further emphasizing its potential for clinical applications.
DISCUSSION
The primary goal of RT is to protect the OAR as much as possible while ensuring that the target area reaches the prescribed dose[24,25]. In clinical applications, RT requires professionals to design treatment plans before implementation[26]. Completing the plan requires the planner to pass the TPS according to the target area, OAR designated by the doctor, and the prescription dose as well as multiple adjustments to optimize the target and constraint conditions for the optimal plan. After the design is completed, the doctor checks the dose distribution, considers whether the plan requires improvement, and ensures that maximum treatment gain ratios are achieved[27]. However, the quality of an RT plan often depends on the knowledge and expertise of the plan designers, making it difficult to guarantee high quality. Clinical plans are subject to uniform norms and standards, making it difficult to design plans that meet individual patient needs and clinical norms[13]. Using our prediction model, the patient’s dose can be predicted before designing the plan. The model assists the planner by performing quality assessments during the design phase and determining whether the plan meets dosimetry verification and quality control requirements. Consequently, predicting the OAR dose before designing a plan can automatically adjust plans to meet individual patient needs and provide a basis for RT automation[28,29]. The value of predicting the OAR dose before planning lies in the ability to evaluate plan quality[30,31].
Numerous studies have explored the use of machine-learning techniques in RT planning, particularly for dose prediction. However, few studies have specifically focused on predicting the dose to the uninvolved liver during SBRT for liver cancer. Our study establishing a prediction model based on neural network methodology, which has been granted a Chinese invention patent.
This study is the first to find a correlation between the Vnsub-organ, Dn0-Dn100, and Dnmean of the uninvolved liver and establish a prediction model based on the neural network method. This method has been granted a Chinese invention patent. For the prediction model, except for Dn0, the R-values for Dn10-Dn100 and Dnmean were > 0.8. The MSE value of the prediction model was also low, which shows that the method used in our study can still provide a reference for high- and low-dose areas that are difficult to predict. Therefore, this study model was accurate and reliable for predicting the uninvolved liver dose, demonstrating its potential for quality assurance in RT plans.
Compared with other studies in the field[32-34], our prediction model offers several advantages. First, it serves as a valuable quality assurance tool for RT plans, enabling precise control of individualized OAR doses. Specifically, a threshold value can be established for both the individual OAR-predicted and TPS values, determining the maximum acceptable difference between the predicted and planned doses. This approach minimizes the influence of subjective factors and ensures that the RT plan meets the required quality standards. Second, our method of establishing a predictive model is both simple and reliable. It utilizes the open-source MATLAB software and employs a dataset partitioned into five folds to prevent overfitting. This ensures a reliable estimate of the final model’s forecast accuracy when trained with a complete dataset. Furthermore, the self-written MATLAB application program can automatically generate sub-organs for each OAR and extract relevant data, such as Vnsub-organ, Dn0-Dn100, and Dnmean, significantly enhancing efficiency and reducing time costs compared with manual TPS use. The entire process is automated, eliminating the need for manual intervention and further improving efficiency. Manual TPS use can be time-consuming and labor-intensive, especially when dealing with large datasets, which may hinder the widespread adoption of this research method. Therefore, our predictive modeling approach offers a simple, reliable, and cost-effective solution without the need to purchase additional TPS software modules.
Our study also had some limitations. First, all included patients were recruited from a single institution. To validate the generalizability of the model, further research incorporating multiple centers and a larger dataset of SBRT plans for liver cancer is necessary. If a sufficiently extensive dataset is obtained, a refined neural network model that can predict the OAR dose in liver cancer SBRT plans with enhanced accuracy can be developed. Second, the method used to establish predictive models in this study cannot currently be extended to other tumors, so the participation of additional tumor centers is required. Although data augmentation techniques were not directly utilized in this study to artificially increase the dataset size, we recognized their potential value in machine-learning applications. Therefore, we plan to explore the use of data augmentation in future studies to enhance the predictive accuracy and generalizability of our models for RT planning.
In summary, our neural-network-based prediction model has great potential for improving the quality and personalization of RT programs for patients with liver cancer. By predicting the dose to the liver before planning, we can ensure that patients receive the highest possible therapeutic benefit while minimizing the risk of complications. Although our study has certain limitations, it provides valuable references for research in this important field and highlights the potential of machine learning in RT planning.
CONCLUSION
We developed a method based on machine learning for predicting the OAR dose in an SBRT plan for liver cancer. This method is simple, easy to use, and demonstrates promising results, warranting further investigation and potential clinical application.
Footnotes
Institutional review board statement: This retrospective study was approved by the institutional review board of Jiangxi Cancer Hospital, No. 2024ky057.
Informed consent statement: Consent for publication is not applicable in this study, because there is not any individual person’s data.
Conflict-of-interest statement: Dr. Pang has a patent ZL201610529290.8 licensed.
Provenance and peer review: Unsolicited article; Externally peer reviewed.
Peer-review model: Single blind
Specialty type: Oncology
Country of origin: China
Peer-review report’s classification
Scientific Quality: Grade B, Grade B
Novelty: Grade B, Grade C
Creativity or Innovation: Grade B, Grade B
Scientific Significance: Grade B, Grade B
P-Reviewer: Wang XZ S-Editor: Li L L-Editor: A P-Editor: Zhao S
Contributor Information
Huai-Wen Zhang, Department of Radiotherapy, Jiangxi Cancer Hospital, Nanchang 330029, Jiangxi Province, China.
You-Hua Wang, Department of Oncology, Gulin People’s Hospital, Luzhou 646500, Sichuan Province, China.
Bo Hu, Key Laboratory of Nondestructive Testing (Ministry of Education), Nanchang Hang Kong University, Nanchang 330063, Jiangxi Province, China.
Hao-Wen Pang, Department of Oncology, The Affiliated Hospital of Southwest Medical University, Luzhou 646000, Sichuan Province, China. haowenpang@foxmail.com.
Data sharing statement
All data generated and analyzed during this study are included in this published article.
References
- 1.Chandra RA, Keane FK, Voncken FEM, Thomas CR Jr. Contemporary radiotherapy: present and future. Lancet. 2021;398:171–184. doi: 10.1016/S0140-6736(21)00233-6. [DOI] [PubMed] [Google Scholar]
- 2.Wright JL, Yom SS, Awan MJ, Dawes S, Fischer-Valuck B, Kudner R, Mailhot Vega R, Rodrigues G. Standardizing Normal Tissue Contouring for Radiation Therapy Treatment Planning: An ASTRO Consensus Paper. Pract Radiat Oncol. 2019;9:65–72. doi: 10.1016/j.prro.2018.12.003. [DOI] [PubMed] [Google Scholar]
- 3.Chen M, Gu X, Lu W. Global optimization for spot-based treatment planning. Med Phys. 2022;49:7648–7660. doi: 10.1002/mp.15890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Craft D. Multi-criteria optimization methods in radiation therapy planning: a review of technologies and directions. 2013 Preprint. Available from: arXiv: 1305.1546.
- 5.Schlaefer A, Viulet T, Muacevic A, Fürweger C. Multicriteria optimization of the spatial dose distribution. Med Phys. 2013;40:121720. doi: 10.1118/1.4828840. [DOI] [PubMed] [Google Scholar]
- 6.Wheeler PA, West NS, Powis R, Maggs R, Chu M, Pearson RA, Willis N, Kurec B, Reed KL, Lewis DG, Staffurth J, Spezi E, Millin AE. Multi-institutional evaluation of a Pareto navigation guided automated radiotherapy planning solution for prostate cancer. Radiat Oncol. 2024;19:45. doi: 10.1186/s13014-024-02404-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chung HT, Lee B, Park E, Lu JJ, Xia P. Can all centers plan intensity-modulated radiotherapy (IMRT) effectively? An external audit of dosimetric comparisons between three-dimensional conformal radiotherapy and IMRT for adjuvant chemoradiation for gastric cancer. Int J Radiat Oncol Biol Phys. 2008;71:1167–1174. doi: 10.1016/j.ijrobp.2007.11.040. [DOI] [PubMed] [Google Scholar]
- 8.Nelms BE, Robinson G, Markham J, Velasco K, Boyd S, Narayan S, Wheeler J, Sobczak ML. Variation in external beam treatment plan quality: An inter-institutional study of planners and planning systems. Pract Radiat Oncol. 2012;2:296–305. doi: 10.1016/j.prro.2011.11.012. [DOI] [PubMed] [Google Scholar]
- 9.Scaggion A, Fusella M, Roggio A, Bacco S, Pivato N, Rossato MA, Peña LMA, Paiusco M. Reducing inter- and intra-planner variability in radiotherapy plan output with a commercial knowledge-based planning solution. Phys Med. 2018;53:86–93. doi: 10.1016/j.ejmp.2018.08.016. [DOI] [PubMed] [Google Scholar]
- 10.Wu B, Pang D, Simari P, Taylor R, Sanguineti G, McNutt T. Using overlap volume histogram and IMRT plan data to guide and automate VMAT planning: a head-and-neck case study. Med Phys. 2013;40:021714. doi: 10.1118/1.4788671. [DOI] [PubMed] [Google Scholar]
- 11.Burton A, Norvill C, Ebert MA. Predictive performance of an OVH-based treatment planning quality assurance model for prostate VMAT: Assessing dependence on training cohort size and composition. Med Dosim. 2019;44:315–323. doi: 10.1016/j.meddos.2018.11.003. [DOI] [PubMed] [Google Scholar]
- 12.Cros S, Bouttier H, Nguyen-Tan PF, Vorontsov E, Kadoury S. Combining dense elements with attention mechanisms for 3D radiotherapy dose prediction on head and neck cancers. J Appl Clin Med Phys. 2022;23:e13655. doi: 10.1002/acm2.13655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yu W, Xiao C, Xu J, Jin J, Jin X, Shen L. Direct Dose Prediction With Deep Learning for Postoperative Cervical Cancer Underwent Volumetric Modulated Arc Therapy. Technol Cancer Res Treat. 2023;22:15330338231167039. doi: 10.1177/15330338231167039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Saito Y, Suzuki R, Miyamoto N, Sutherland KL, Kanehira T, Tamura M, Mori T, Nishioka K, Hashimoto T, Aoyama H. A new predictive parameter for dose-volume metrics in intensity-modulated radiation therapy planning for prostate cancer: Initial phantom study. J Appl Clin Med Phys. 2024;25:e14250. doi: 10.1002/acm2.14250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ge Y, Wu QJ. Knowledge-based planning for intensity-modulated radiation therapy: A review of data-driven approaches. Med Phys. 2019;46:2760–2775. doi: 10.1002/mp.13526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bera S, Choudhury D, Roy S, Mukhopadhyay P, Sarkar S. Development of Prediction Model for Mean Parotid Dose of HNC Undergoing Radiotherapy - A Single Institutional Study. J Med Phys. 2023;48:274–280. doi: 10.4103/jmp.jmp_52_23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sterzing F, Brunner TB, Ernst I, Baus WW, Greve B, Herfarth K, Guckenberger M. Stereotactic body radiotherapy for liver tumors: principles and practical guidelines of the DEGRO Working Group on Stereotactic Radiotherapy. Strahlenther Onkol. 2014;190:872–881. doi: 10.1007/s00066-014-0714-1. [DOI] [PubMed] [Google Scholar]
- 18.Hall JT, Moon AM, Young M, Tan X, Darawsheh R, Danquah F, Tepper JE, Yanagihara TK. Biochemical Safety of SBRT to Multiple Intrahepatic Lesions for Hepatocellular Carcinoma. J Hepatocell Carcinoma. 2024;11:443–454. doi: 10.2147/JHC.S447025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jaksic N, Modesto A, Meillan N, Bordron A, Michalet M, Riou O, Lisbona A, Huguet F. Stereotactic body radiation therapy for liver metastases in oligometastatic disease. Cancer Radiother. 2024;28:75–82. doi: 10.1016/j.canrad.2023.04.008. [DOI] [PubMed] [Google Scholar]
- 20.Burkoň P, Slavik M, Kazda T, Pospíšil P, Prochazka T, Vrzal M, Šlampa P. Stereotactic Body Radiotherapy - Current Indications. Klin Onkol. 2019;32:10–24. doi: 10.14735/amko201910. [DOI] [PubMed] [Google Scholar]
- 21.Xu D, Descovich M, Liu H, Lao Y, Gottschalk AR, Sheng K. Deep match: A zero-shot framework for improved fiducial-free respiratory motion tracking. Radiother Oncol. 2024;194:110179. doi: 10.1016/j.radonc.2024.110179. [DOI] [PubMed] [Google Scholar]
- 22.Dawson LA, Winter KA, Katz AW, Schell MC, Brierley J, Chen Y, Kopek N, Crane CH, Willett CG. NRG Oncology/RTOG 0438: A Phase 1 Trial of Highly Conformal Radiation Therapy for Liver Metastases. Pract Radiat Oncol. 2019;9:e386–e393. doi: 10.1016/j.prro.2019.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.George K, Chopra S, Rajamanickam K, Joshi K, Swamidas J, Shetty N, Engineer R. Evaluation of liver segmental dose threshold for hepatocyte regeneration following liver stereotactic body radiation therapy. Indian J Med Res. 2024;159:232–240. doi: 10.4103/ijmr.ijmr_1171_21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wong FC, Ng AW, Lee VH, Lui CM, Yuen KK, Sze WK, Leung TW, Tung SY. Whole-field simultaneous integrated-boost intensity-modulated radiotherapy for patients with nasopharyngeal carcinoma. Int J Radiat Oncol Biol Phys. 2010;76:138–145. doi: 10.1016/j.ijrobp.2009.01.084. [DOI] [PubMed] [Google Scholar]
- 25.Antolak J. The Physics of Radiation Therapy. Med Phys. 2015;42:5001–5002. [Google Scholar]
- 26.O'Sullivan-Steben K, Galarneau L, Judd S, Laizner AM, Williams T, Kildea J. Design and implementation of a prototype radiotherapy menu in a patient portal. J Appl Clin Med Phys. 2024;25:e14201. doi: 10.1002/acm2.14201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dean M, Jimenez R, Mellon E, Fields E, Yechieli R, Mak R. CB-CHOP: A simple acronym for evaluating a radiation treatment plan. Appl Radiat Oncol. 2017 [Google Scholar]
- 28.Moore KL, Brame RS, Low DA, Mutic S. Experience-based quality control of clinical intensity-modulated radiotherapy planning. Int J Radiat Oncol Biol Phys. 2011;81:545–551. doi: 10.1016/j.ijrobp.2010.11.030. [DOI] [PubMed] [Google Scholar]
- 29.Fiandra C, Rossi L, Alparone A, Zara S, Vecchi C, Sardo A, Bartoncini S, Loi G, Pisani C, Gino E, Ruo Redda MG, Marco Deotto G, Tini P, Comi S, Zerini D, Ametrano G, Borzillo V, Strigari L, Strolin S, Savini A, Romeo A, Reccanello S, Rumeileh IA, Ciscognetti N, Guerrisi F, Balestra G, Ricardi U, Heijmen B. Automatic genetic planning for volumetric modulated arc therapy: A large multi-centre validation for prostate cancer. Radiother Oncol. 2020;148:126–132. doi: 10.1016/j.radonc.2020.04.020. [DOI] [PubMed] [Google Scholar]
- 30.Cao W, Gronberg M, Olanrewaju A, Whitaker T, Hoffman K, Cardenas C, Garden A, Skinner H, Beadle B, Court L. Knowledge-based planning for the radiation therapy treatment plan quality assurance for patients with head and neck cancer. J Appl Clin Med Phys. 2022;23:e13614. doi: 10.1002/acm2.13614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vaniqui A, Canters R, Vaassen F, Hazelaar C, Lubken I, Kremer K, Wolfs C, van Elmpt W. Treatment plan quality assessment for radiotherapy of rectal cancer patients using prediction of organ-at-risk dose metrics. Phys Imaging Radiat Oncol. 2020;16:74–80. doi: 10.1016/j.phro.2020.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Maniscalco A, Mathew E, Parsons D, Visak J, Arbab M, Alluri P, Li X, Wandrey N, Lin MH, Rahimi A, Jiang S, Nguyen D. Multimodal radiotherapy dose prediction using a multi-task deep learning model. Med Phys. 2024;51:3932–3949. doi: 10.1002/mp.17115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wu Z, Liu M, Pang Y, Deng L, Yang Y, Wu Y. A Comparative Study of Deep Learning Dose Prediction Models for Cervical Cancer Volumetric Modulated Arc Therapy. Technol Cancer Res Treat. 2024:23:15330338241242654. doi: 10.1177/15330338241242654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gronberg MP, Jhingran A, Netherton TJ, Gay SS, Cardenas CE, Chung C, Fuentes D, Fuller CD, Howell RM, Khan M, Lim TY, Marquez B, Olanrewaju AM, Peterson CB, Vazquez I, Whitaker TJ, Wooten Z, Yang M, Court LE. Deep learning-based dose prediction to improve the plan quality of volumetric modulated arc therapy for gynecologic cancers. Med Phys. 2023:50:6639–6648. doi: 10.1002/mp.16735. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated and analyzed during this study are included in this published article.