Gating residues govern ligand unbinding kinetics from the buried cavity in HIF‐2α PAS‐B

Abstract

While transcription factors have been generally perceived as “undruggable,” an exception is the HIF‐2 hypoxia‐inducible transcription factor, which contains an internal cavity that is sufficiently large to accommodate a range of small‐molecules, including the therapeutically used inhibitor belzutifan. Given the relatively long ligand residence times of these small molecules and the lack of any experimentally observed pathway connecting the cavity to solvent, there has been great interest in understanding how these drug ligands exit the buried receptor cavity. Here, we focus on the relevant PAS‐B domain of hypoxia‐inducible factor 2α (HIF‐2α) and examine how one such small molecule (THS‐017) exits from the buried cavity within this domain on the seconds‐timescale using atomistic simulations and ZZ‐exchange NMR. To enable the simulations, we applied the weighted ensemble path sampling strategy, which generates continuous pathways for a rare‐event process [e.g., ligand (un)binding] with rigorous kinetics in orders of magnitude less computing time compared to conventional simulations. Results reveal the formation of an encounter complex intermediate and two distinct classes of pathways for ligand exit. Based on these pathways, we identified two pairs of conformational gating residues in the receptor: one for the major class (N288 and S304) and another for the minor class (L272 and M309). ZZ‐exchange NMR validated the kinetic importance of N288 for ligand unbinding. Our results provide an ideal simulation dataset for rational manipulation of ligand unbinding kinetics.

1. INTRODUCTION

Buried cavities in proteins present special opportunities for the design of highly specific drug inhibitors. One such protein is the hypoxia‐inducible factor (HIF) family member, HIF‐2α, which mediates our body's adaptive response to decreased tissue oxygen levels (hypoxia). To activate this response, HIF‐2α must form a heterodimer with the aryl hydrocarbon receptor translocator (ARNT; also known as HIF‐1β) via multiple protein/protein interaction domains in the two proteins. One of these domains, the second Per‐ARNT‐Sim domain of HIF‐2α (HIF‐2α PAS‐B) contains a 290 ų internal cavity that is sufficiently large to accommodate drug ligands (Key et al. 2009). Among these ligands are ones that allosterically lower the affinity of the heterodimer and are specific for the HIF‐2α PAS‐B domain over other PAS‐B domains (Rogers et al. 2013; Scheuermann et al. ^{2009, 2013, 2015}; Wallace et al. ²⁰¹⁶). Given that the misregulation of HIF pathways is found in several cancers (Bos et al. 2003; Zagzag et al. ²⁰⁰⁰), targeted disruption of the HIF‐2α/ARNT interaction by ligand binding to the buried HIF‐2α cavity has become a clinically useful therapeutic strategy for certain cancers (Chen et al. 2016; Jonasch et al. ²⁰²¹).

As demonstrated for many drug targets (Bernetti et al. 2019), the efficacies of various drug inhibitors of the HIF‐2α PAS‐B domain correlate with the residence time, or the inverse of the off‐rate (Key et al. 2009). Of great interest is therefore the mechanism by which drug inhibitors dissociate from the buried cavity of the HIF‐2α PAS‐B domain. While experimental techniques can measure k _off values for the ligand unbinding process, they can only provide atomic details of the stable ligand‐free and ligand‐bound states at either end of this process. On the other hand, conventional molecular dynamics (MD) simulations can, in principle, provide atomistic structures of all states along the unbinding process—including transient states. However, due to the inaccessible timescales (seconds), such simulations have been limited to only the stable states (unbound and bound states) (Diao et al. 2022; Masetti et al. ²⁰¹⁴) and rapid exiting of water molecules from the receptor cavity (Key et al. 2009).

Various enhanced sampling strategies have therefore been developed with the aim of either efficiently ranking compound libraries based on relative residence times [τRAMD (Nunes‐Alves et al. ²⁰²¹), scaled‐MD (Mollica et al. 2015), targeted MD (Wolf et al. 2019)] or estimating absolute values of the k _off [metadynamics (Tiwary et al. 2015), Gaussian accelerated MD (Wang and Miao 2023), path sampling (Dixon et al. 2021; Nunes‐Alves et al. ²⁰¹⁸; Ray et al. ²⁰²⁰)]. Among these strategies, steered MD (Chong and Anderson 2020) or metadynamics (Callea et al. 2021) have been applied to study ligand unbinding from the HIF‐2α PAS‐B domain, either applying biasing forces or altering the free energy landscape, respectively. Thus, these strategies strongly depend on previous knowledge of the unbinding process. Furthermore, pathways generated using biasing forces miss key aspects of the relevant rugged energy landscape (Panteva et al. 2011). Alternatively, path sampling strategies (Chong et al. 2017) such as the weighted ensemble (WE) strategy (Huber and Kim 1996; Zuckerman and Chong ²⁰¹⁷) can provide an ensemble of unbiased pathways and direct estimates of the k _off in a blind manner.

Here, we apply a combination of atomistic simulations and NMR experiments to study the mechanism by which a small‐molecule ligand (THS‐017) exits from the buried cavity of the HIF‐2α PAS‐B domain (Figure 1) (Key et al. 2009). The simulations of this seconds‐timescale process were enabled by the application of the WE strategy. To measure the kinetics of ligand unbinding, ZZ‐exchange NMR experiments were performed, taking advantage of the ability of this method to directly measure equilibrium k _ex rates that can be deconvoluted into their component k _on and k _off contributions (Palmer 3rd and Koss ²⁰¹⁹). Together, our simulations and experiments provide unprecedented insights on the mechanism by which a drug ligand exits the buried cavity.

FIGURE 1.

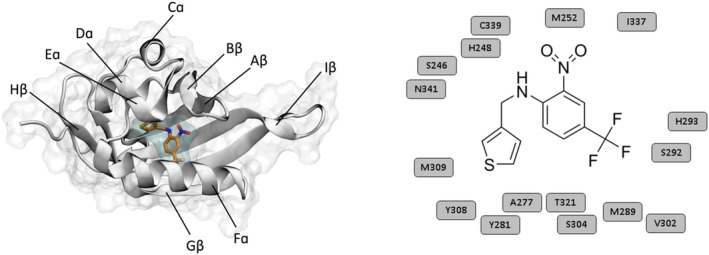
The THS‐017 small‐molecule ligand binds to a buried cavity (cyan) of the HIF‐2α PAS‐B domain (gray). Crystal structure of the ligand‐bound HIF‐2α PAS‐B receptor (PDB 3H7W) (Key et al. 2009), revealing the internal cavity (cyan) on the left and the structure of the THS‐017 ligand and surrounding residues of the receptor cavity on the right.

2. RESULTS

2.1. Simulations reveal an encounter complex intermediate

Our application of the WE path sampling strategy enabled the generation of >4000 atomistic pathways among three independent, simulations of the HIF‐2α/ligand unbinding process. Figure 2a shows the aggregate simulation data from these pathways as a function of the three‐dimensional WE progress coordinate consisting of (i) the cavity solvent accessible surface area (SASA) of the receptor, (ii) ligand unbinding RMSD, and (iii) the ligand–receptor distance. These results reveal a metastable, encounter complex intermediate in which the ligand has exited the cavity, but forms contacts with the receptor outside of the cavity and subsequently dissociates to the unbound ligand and receptor. Assuming a reversible unbinding process, this intermediate might be formed in the first step of the binding process, enabling the ligand to “crawl” into the receptor cavity once the cavity opens.

FIGURE 2.

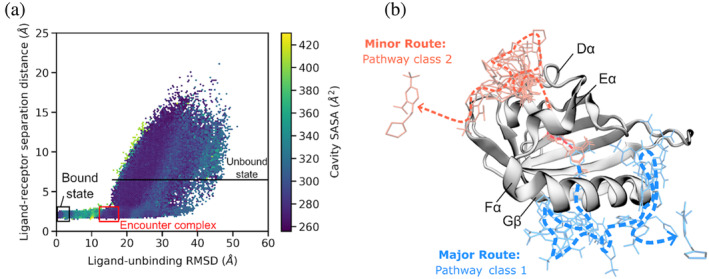
Unbinding of the THS‐017 ligand from HIF‐2α PAS involves an encounter complex intermediate and two distinct classes of pathways. (a) Hexagonal binned plot of conformations along all successful ligand unbinding pathways generated by three independent WE simulations as a function of the ligand–receptor separation distance and ligand unbinding RMSD (see section 4). Hexagonal bins are colored according to the solvent accessible surface area (SASA) of the receptor cavity. The bound and unbound states are delineated in black and a metastable, encounter complex intermediate is delineated in red. (b) Two pathway classes revealed by clustering of successful unbinding pathways. The most probable pathway for each class is illustrated using ligand conformations sampled every 5 ns. In pathway class 1, the ligand exits between the Fα helix and Gβ strand of the receptor. In pathway class 2, the ligand exits between the Eα and Dα helices of the receptor.

Our simulations estimate a ligand off‐rate (k _off) ranging from 1.3 × 10⁴ s⁻¹ to 8.7 × 10⁴ s⁻¹ (Figure S2). While this estimated k _off is three orders of magnitude higher than the experimental value (1.4 ± 0.3 s⁻¹) (Key et al. 2009), our simulations have extensively sampled the ligand unbinding pathways, providing a reliable probe of the force field's ability to yield accurate kinetics for a long‐timescale process. Using the current force field (Amber ff19SB) (Tian et al. 2020), the internal cavity of HIF‐2α PAS is likely opening too quickly. Given that the ligand unbinding process is on the seconds timescale (mean first‐passage time of 0.71 s) (Key et al. 2009), conventional MD simulations would require decades to generate a single unbinding event using 16 NVIDIA A100 GPUs in parallel. Using the same number of GPUs, our WE simulations generated the first unbinding event within a day.

2.2. Identification of two ligand exit points

A hallmark of the WE strategy is not only to provide rigorous kinetics, but also an unbiased path ensemble for mechanistic analysis. Upon clustering of all simulated unbinding pathways, our results revealed two distinct pathway classes that correspond to different ligand exit points from the buried cavity of the receptor and the probabilities of each pathway class (Figure 2b). Pathway class 1 is the more probable, major route (63%) that involves the ligand exiting between the Fα helix and Gβ strand. Pathway class 2 is a relatively minor route (37%) that involves the ligand exiting between the Eα and Dα helices of the receptor. As indicated by the event durations, or barrier‐crossing times (Figure S6), the most probable pathways of class 1 are more direct (shorter) than those of class 2.

2.3. Mechanism of ligand unbinding at the atomic level

Consistent with previous simulations of water exiting from the receptor cavity (Key et al. 2009), our simulations reveal that ligand unbinding involves not only large‐scale motions of the receptor backbone to open the cavity (e.g., movement of the Fα helix in pathway class 1), but also transitions to alternate rotamers of certain sidechains as conformational gates for the unbinding process. To identify conformational gates for the ligand unbinding process, we searched for residues that (i) are kinetically important for the ligand unbinding process and (ii) exhibit motions that are correlated with the exiting of the ligand from the internal cavity, as detected using the Leiden network clustering method (Traag et al. 2019) (see section 4.1). A residue was considered kinetically important if it either loses native contacts or gains non‐native contacts in the transition state ensemble (TSE) (“native” refers to contacts in a reference bound‐state structure) for forming the encounter complex intermediate. To predict mutations that might impact the k _off by either stabilizing or destabilizing the bound state, we focused on sidechains of residues that lost native contacts in the majority (>80%) of conformations in the TSE.

To identify receptor residues whose dynamics are correlated with ligand unbinding, we focused on the “characteristic” (most probable) pathway in each of the two pathway classes. Upon examining probability maps of native residue‐level contacts in the TSE, four contacts were lost in >80% of the TSE for both pathway classes 1 and 2 (Figure 3a). Two of these contacts involved backbone–backbone interactions (S249‐Q335 and D285‐Q306) and the other two involved interactions that contained at least one sidechain (L272‐M309 and N288‐S304). The latter two interactions involve (i) the sidechains of L272 in the Dα helix and M309 in the Gβ strand, and (ii) the sidechain of N288 in the Fα helix and backbone of S304 in the Gβ strand. Our results from the Leiden network clustering analysis identified the L272 and M309 residues as conformational gates for pathway class 2, and the N288 and S304 residues as conformational gates for pathway class 1 (Figure 3b). As shown in Figure 3c, the distance between each of these pairs of residues increases by >8 Å in the TSE of the corresponding characteristic pathway and then returns to values in range of its initial bound state (see also Movies S1 and S2, Supporting Information).

FIGURE 3.

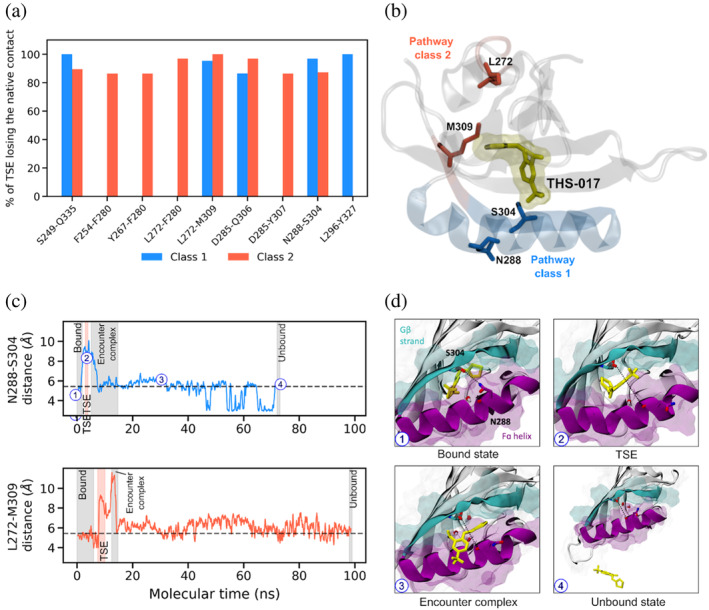
Conformational gating residues in pathway class 1 identified by simulation. (a) Native residue contacts in the receptor residues that are lost in the majority (>80%) of the TSE for forming the encounter complex intermediate in the THS‐017 ligand unbinding process. Data shown is based on characteristic pathways for classes 1 and 2. (b) Locations of gating residues relative to the receptor cavity containing the THS‐017 ligand (yellow): N288 and S304 for pathway class 1, and L272 and M309 for pathway class 2. (c) Time evolution of the N288‐S304 distance (between heavy atoms) in the receptor during the characteristic ligand unbinding pathway for class 1 (top) and of the L272‐M309 distance in the receptor during the characteristic pathway for class 2 (bottom). (d) Snapshots of the characteristic pathway for class 1, highlighting a substantial increase in the N288‐S304 distance (dashed line) upon transitioning from the closed internal cavity of the bound state (1) to a partial opening of the cavity (2) that permits the ligand (yellow) to exit. Upon rearranging from the encounter complex intermediate (3) to the unbound state (4), the N288‐S304 distance returns to that of the apo receptor.

A closer inspection of the characteristic pathway for the major pathway class (class 1) reveals the following mechanistic details for the ligand binding process. Once the N288 and S304 conformational gates open the cavity in the TSE, the ligand exits the cavity. Shortly afterwards, N288 and S304 reclose the cavity, returning to their positions in the bound state and the ligand contacts a part of the receptor outside of the cavity, forming the encounter complex intermediate. Ligand exit from the internal cavity may also be facilitated by water molecules entering the cavity. While the cavity is completely dehydrated in the crystal structure of the ligand–receptor complex, in our generation of bound‐state conformations using conventional MD simulations, a single water molecule entered the cavity in the bound state and remained in the TSE. This water molecule overlaps with the position of one of the eight crystallographic water molecules within the cavity of the HIF‐2α PAS structure in the apo form (Scheuermann et al. 2009). Upon forming the encounter complex intermediate, an additional water molecule entered the cavity and remained after closure of the cavity, occupying the position of another crystallographic water molecule in the apo HIF‐2α PAS structure.

Based on a representative conformation of the TSE for pathway class 1, we predicted two mutations involving N288 that would impact the k _off via the absence or presence of contacts with S304 (Figure 4). First, we predicted that mutation of N288 to a glutamine (N288Q) would enable the formation of a hydrogen bond with the S304 residue and therefore reduce the k _off via stabilization of the bound state. Second, we predicted that mutation of N288 to an alanine (N288A) would eliminate short‐range contacts of the sidechain with nearby residues thereby increasing the k _off via destabilization of the bound state.

FIGURE 4.

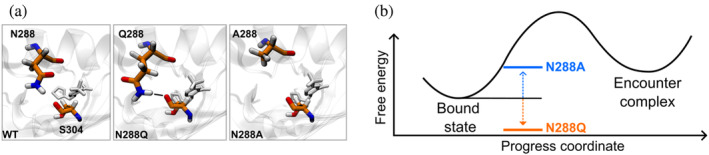
Mutations of N288 predicted to impact k _off rates of ligand unbinding. (a) In silico mutations of N288 to glutamine or alanine in representative bound‐state conformations, indicating the possibility of Q288 forming a hydrogen bond with the backbone carbonyl of S304; in contrast, no hydrogen bond would be expected for N288 or A288 with S304. (b) Predicted impact of N288Q and N288A mutations on the k _off for the THS‐017 ligand. The N288Q mutation was expected to stabilize the bound state, increasing the barrier of transition from the bound state to the encounter complex and yielding a slower k _off. On the other hand, the N288A mutation was expected to destabilize the bound state, decreasing the barrier of transition from the bound state to the encounter complex and yielding a faster k _off.

2.4. Experimental validation of the importance of N288 in ligand entry and exit

To validate the importance of the N288 residue for the ligand unbinding process, we made point mutations to generate the N288A and N288Q variants of the HIF‐2α PAS‐B domain and assayed the impact of these changes on both thermodynamic and kinetic parameters (Table S3 and Figure 5). To determine the thermodynamic parameters of complex formation between the HIF‐2α PAS‐B mutants and the THS‐017 and the related THS‐020 small compounds (Key et al. 2009), we used isothermal titration calorimetry (ITC) by titrating concentrated protein into solutions of dilute ligands (“reverse mode”) and measuring the evolved heat (Figure S7). These data were analyzed with a single set binding model to determine affinities and various energies of the interaction.

FIGURE 5.

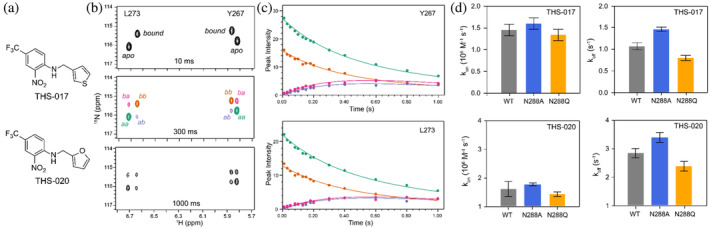
NMR ZZ‐exchange data from HIF‐2α PAS‐B and small‐molecule ligands. (a) Structures of the THS‐017 and THS‐020 small‐molecule ligands. (b) ZZ‐exchange NMR spectra of mixing delays of 10, 300, and 1000 ms showing the generation of crosspeaks of L273 and Y267 residues while increasing the mixing delays from 10 to 1000 ms. The autopeaks are indicated as “aa” and “bb,” crosspeaks are indicated as “ba” and “ab” to indicate their states as either apo [a] or bound [b] in the ¹⁵N and proton chemical shift evolution periods, respectively. (c) Peak intensities of Y267 and L273 residues were fitted as a function of exchange mixing time showing the time‐dependent decays of peaks. Peak colors correspond to the peaks in the 300 ms spectrum of (b). (d) Bar plots showing association (k _on) and dissociation rate (k _off) constants of HIF‐2α PAS‐B variants with the THS‐017 and THS‐020 ligands.

Upon complex formation, we found K _d values ranging from 0.5 to 1.6 μM (Table S2) indicating moderately strong affinities between the HIF‐2α PAS‐B mutants and these small compounds (Figure S7). The affinities for both compounds to wild‐type HIF‐2α PAS‐B were very similar to those previously measured (THS‐017: 0.60 ± 0.06 μM here vs. 0.59 ± 0.05 μM in Key et al. ²⁰⁰⁹; THS‐020: 1.35 ± 0.11 μM vs. 1.5 ± 0.7 μM in Key et al. ²⁰⁰⁹), giving us confidence in the measured parameters. For both compounds, we observed slightly higher affinities for the N288A mutant compared to wild‐type; correspondingly, affinities were slightly weaker for the N288Q mutant. In all cases, ligand binding was enthalpically driven with minor entropic contributions (Table S3 and Figure S7). Consistent with the similar dissociation constants measured for THS‐017 and THS‐020 to all three HIF‐2α PAS‐B variants, ¹⁵N/¹H HSQC spectra of all three proteins are strikingly similar (Figure S8), suggesting no substantial structural changes among them.

To test the role of N288 in the ligand entry/exit pathways out of the HIF‐2α PAS‐B pocket predicted by the MD models (Figures 3b and 4), we measured the ligand association and dissociation rate constants of THS‐017 and THS‐020 against the HIF‐2α PAS‐B variants using NMR ZZ‐exchange spectroscopy (Figure 5). This method has been used to measure such exchange rates (k _ex) in a range of macromolecular systems undergoing slow (millisecond‐to‐second timescale) dynamic equilibria (Farrow et al. 1994; Iwahara and Clore ²⁰⁰⁶; Rubinstenn et al. ¹⁹⁹⁸), including for these two THS compounds against wild‐type HIF‐2α PAS‐B (Key et al. 2009). Such experiments are conducted by preparing samples with roughly equal populations of apo‐ and compound‐bound protein and recording 2D ¹⁵N/¹H correlation spectra with a modified pulse sequence where the two chemical shift evolution periods are separated by a delay of up to 1 s (compared to approximately 10 ms separation in conventional ¹⁵N/¹H sensitivity‐enhanced HSQC; Kay et al. ¹⁹⁹²). During this extended delay, chemical exchange allows the observation of crosspeaks coupling signals from apo‐protein molecules which bind a ligand during that period (or alternatively, by a ligand‐bound protein releasing compound). By fitting the time‐dependent decays of such peaks (and corresponding “autopeaks” representing proteins which neither dissociate or bind a ligand during the delay) from the ZZ‐exchange data, one can obtain NMR‐derived k _ex values representing the sum of the on‐ and off‐rates. Using these with the K _d values independently determined from ITC data, we calculated second‐order association rate constants (k _on) and first‐order ligand dissociation rate constants (k _off) (Table S4).

From these analyses, we measured increased on‐ and off‐rates for both compounds to the N288A mutant receptor, consistent with a lower energetic barrier for small molecules transiting between solvent and the HIF‐2α PAS‐B internal cavity. Such a result is consistent with decreasing the sidechain bulk of N288 from the side of pathway class 1 in Figures 3b and 4. Additional support for this role was seen by the reduced rate of entry and exit for both THS compounds with the N288Q mutation, which we anticipated from enlarging the N288 sidechain along this entry and exit pathway. Notably, the wild‐type rates are very similar to those previously reported in Key et al. (2009), providing an independent measure of the precision and accuracy of our measurements. We also underscore that all these association rates are quite rapid (k _on > 10⁶ M⁻¹ s⁻¹) for all compounds and proteins despite the completely internal nature of the cavity, supporting the relatively rapid nature of protein conformational changes needed to access it.

3. DISCUSSION

Several simulation studies have explored potential pathways by which a ligand might enter or exit the cavity of the HIF‐2α PAS‐B receptor. In the first such study in 2009, Key et al. (2009) carried out conventional MD simulations of the ligand‐free (apo) receptor and found that water molecules in the cavity can exchange with bulk solvent via two primary routes and a third minor route. The primary routes are (i) between the Fα helix and Gβ strand, and (ii) between the short Eα helix, Fα helix, and AB loop. The minor route is between the Eα and Dα helices. More recently, two studies have simulated pathways involving either binding or unbinding of a drug ligand by applying an external bias to “steer” the ligand along the primary water‐exit routes identified by Key et al. (2009). Chong and Anderson (2020) applied steered MD to simulate ligand binding and Callea et al. (2021) applied steered MD and metadynamics to simulate ligand unbinding. A parallel study by Diao et al. (2022) on the related HIF‐3α system has used conventional MD approaches to suggest ligand entry and exit pathways via dynamics identified in simulations of the apo‐ and ligand‐bound protein.

Compared to these previous studies, our simulated unbinding pathways of the THS‐017 small‐molecule ligand differ in two respects. First, our ligand unbinding pathways involved only one of the two primary routes, that is, between the Fα helix and Gβ strand. Second, our simulations captured pathways along the minor route between the Eα and Dα helices but found this route to be more probable than previously suggested [37% vs. only 3% in Key et al. (2009)]. These differences are not surprising given that the previously identified ligand exit routes from the internal cavity of the receptor were based on exit routes for a single water molecule, which is much smaller than an organic small‐molecule ligand. Notably, pathway class 2 is suggested in MD simulations on HIF‐3α PAS‐B, and aspects of ligand binding into a site immediately adjacent to the flexible regions are suggested by structures of photoactive yellow protein covalently bound to hydroxycinnamic acid (PYP) (Kort et al. 1996) and small carboxylic acids to the CitA PAS domain (Kramer et al. 2007). Finally, despite the absence of the ARNT binding partner for HIF‐2α in our simulations, none of the pathways involved ligand exiting at the HIF‐2α/ARNT heterodimer interfaces identified in crystal structures of the isolated PAS‐B domains (Scheuermann et al. 2009) or larger multidomain constructs (Wu et al. 2015).

It is worth noting that neither of the two previous studies involving steered MD simulations identified any of the conformational gating residues revealed in our study (N288 and S304 in pathway 1; L272 and M309 in pathway 2). These gating residues were likely missed due to the use of a biasing force in the simulations. Importantly, several experimental findings validate the gating role of these residues. First, the kinetic importance of N288 has been validated by NMR experiments on N288A and N288Q mutants of HIF‐2α PAS‐B in our study. Additionally, the importance of S304 is consistent with a negative control in which the mutation of the cavity‐facing S304 to a methionine was found to obliterate drug binding HIF‐2 (Rogers et al. 2013).

A wide range of artificial small molecules bind to the HIF‐2α PAS‐B cavity, including academic and industrially‐derived compounds that led to the clinically used belzutifan (Rogers et al. 2013; Scheuermann et al. ^{2013, 2015}; Wallace et al. ²⁰¹⁶). The affinities and potencies of many of those compounds are in the nanomolar regime, making them substantially tighter than the THS‐017 and THS‐020 compounds we chose for simulation and experiment here. Our choice is deliberate, as the THS compounds bind to the same internal cavity as the higher affinity compounds and have higher off‐rates, which are essential to “tuning” the residence times to the ms–sec timescales amenable for both WE simulation and ZZ exchange NMR analysis.

We note that these higher‐affinity compounds are typically larger than THS‐017, potentially impacting the relative use of the two different exit routes described in our work, as may the presence of other protein domains in the HIF‐2α protein or the larger HIF‐2α/ARNT heterodimer. This said, we are encouraged by results of conventional MD simulations of apo‐ and drug‐loaded HIF‐3α/ARNT heterodimers that suggest that a ligand entrance/exit pathway analogous to our pathway class 2 is used by that system, which the authors support with studies of a single point mutation (Diao et al. 2022). From our perspective, both pathways classes 1 and 2 identified here are inherently accessible to the isolated HIF‐2α PAS‐B domain—and likely other PAS domains—and appear to be solvent‐accessible in structures of HIF‐3α/ARNT, suggesting that further comprehensive experimental and simulation studies are needed to fully address the relative uses of these pathways across diverse PAS‐containing transcription factors.

In closing, we have characterized the seconds‐timescale process by which a small‐molecule ligand (THS‐017) exits from a completely buried cavity in the HIF‐2α PAS domain at the atomic level using a combination of WE‐enabled MD simulations and NMR experiments. The resulting pathways offer unprecedented views of ligand dissociation from the HIF‐2α PAS domain. First, our pathways revealed a two‐step unbinding mechanism in which the first step is the formation of a metastable encounter complex intermediate. Second, based on the transition‐state ensemble for this initial step, we identified two pairs of conformational gating residues (N288/S304 in the major pathway class and L272/M309 in the minor pathway class). Both of the above findings were overlooked by previous simulation studies using steered MD and/or metadynamics (Callea et al. 2021; Chong and Anderson ²⁰²⁰), underscoring the value of generating pathways in an agnostic manner using methods such as WE, that is, without applying any biasing forces or altering the energy landscape. Importantly, the gating roles of N288/S304 and L272/M309 are consistent with NMR experiments, including the present ZZ‐exchange NMR results that validate the kinetic importance of the N288 residue.

Our WE simulation workflow is a general strategy that can be adapted for any ligand exiting process from the buried cavity of a protein, including other PAS domains such as those of the transcription factor subunit, aryl hydrocarbon receptor nuclear translocator (ARNT) (Xu et al. 2024) and the related light‐oxygen‐voltage (LOV) photoreceptors (Harper et al. 2003; Losi et al. ²⁰¹⁸). As a direct characterization of mechanism, the resulting pathways can facilitate the rational enhancement of kinetics for protein engineering or drug discovery. Given the importance of controlling the activity of these “protein switches” by differential occupancy of internal binding sites by small molecule cofactors, such insights—along with their implications for ligand selectivity and residence—can provide crucial routes to the natural and artificial control of many protein systems.

4. MATERIALS AND METHODS

4.1. Computational methods

4.1.1. Preparation of the simulation system

Heavy‐atom coordinates for the receptor (HIF‐2α PAS domain) in complex with the ligand (THS‐017) were extracted from chain A of the crystal structure (PDB code: 3H7W) (Key et al. 2009). The three unresolved residues 234, 235, and 350 at the N‐ and C‐termini of the receptor were built using the builder module of the PyMol molecular visualization program (Schrodinger 2015). Hydrogens were added using the Reduce tool (Word et al. 1999), as implemented in MolProbity (Williams et al. 2018) according to neutral pH. The AMBER ff19SB force field (Tian et al. 2020) was used to model the protein receptor and GAFF2 parameters (Wang et al. 2004) were derived for the THS‐017 ligand (Table S1) with partial charges fit to electrostatic potentials using the restricted electrostatic potential (RESP) method (Bayly et al. 1993); electrostatic potentials were calculated at the HF/6‐31G* level of theory using the Gaussian 16 A03 software package (Frisch et al. 2016). The ligand–receptor complex was solvated in a truncated octahedral box of OPC water molecules (Izadi et al. 2014) with a 18‐Å clearance between the complex and the edge of the box. To ensure a net neutral charge for the simulation system, 7 Na⁺ and 3 Cl⁻ counterions were added using Li‐Merz parameters for the OPC water model (Sengupta et al. 2021). Additional ions were included to yield the same salt concentration (17 mM NaCl) as NMR experiments described below. The simulation system was then energy‐minimized and equilibrated in multiple stages. In the first stage, 20 ps of dynamics were performed in a constant volume and a target temperature of 25°C while applying harmonic positional restraints of 1.0 kcal mol⁻¹ Å⁻² to all heavy atoms of the receptor that are resolved in the crystal structure. In the second stage, the systems were equilibrated for 1 ns at a target temperature of 25°C and target pressure of 1 bar while maintaining positional restraints on the protein heavy atoms. In the final stage, 1 ns of unrestrained dynamics were performed at a constant temperature of 25°C and constant pressure of 1 bar. Constant temperature was maintained using a weak Langevin thermostat with a frictional coefficient of 1 ps⁻¹ and constant pressure was maintained using a Monte Carlo barostat (Allen and Tildesley 2017) with pressure changes attempted every 0.2 ps. To enable a time step of 2 fs, bonds to hydrogens were restrained to their equilibrium values using the SHAKE algorithm (Ryckaert et al. 1977). Short‐range, non‐bonded interactions were truncated at 10 Å and long‐range electrostatic interactions were treated using the particle mesh Ewald method (Essmann et al. 1995).

4.1.2. Generation of initial bound‐state conformations

To generate representative conformations of the bound state for our ligand unbinding simulations, five 1‐μs conventional MD simulations were initiated from the energy‐minimized and equilibrated ligand‐bound structure of the HIF‐2α PAS receptor (as described above) using the GPU‐accelerated AMBER22 dynamics engine (Case et al. 2020). A set of 25 bound‐state conformations was then selected every ns from the latter 5 ns of each simulation. Consistent with the NMR experiments below, these simulations were run at a constant temperature of 25°C and constant pressure of 1 bar. Further simulation details are the same as described above for the final stage of equilibration.

4.1.3. Weighted ensemble simulations of ligand unbinding

Simulations of the ligand unbinding process were enabled using the weighted ensemble (WE) path sampling strategy (Huber and Kim 1996; Zuckerman and Chong ²⁰¹⁷). The WE strategy is a parallel algorithm for enhancing the efficiency of sampling rare events [e.g., protein–protein binding (Saglam and Chong 2019), large‐scale transitions in proteins (Sztain et al. 2021)]. This strategy typically involves defining a progress coordinate toward a target state, dividing this coordinate into bins, running multiple trajectories in parallel, and subjecting these trajectories to an iterative resampling procedure at fixed short time intervals 𝜏 to maintain a target number of trajectories per bin. The resampling procedure involves replicating trajectories that visit less‐visited bins and splitting the parent trajectory weight evenly among the resulting child trajectories; to save computing time, trajectories that remain in already‐visited bins are occasionally terminated and the weight of the terminated trajectory is merged with that of a trajectory that will be continued. This resampling procedure ensures that all trajectory weights (probabilities) sum to one at any point during the simulation such that no statistical bias is introduced, enabling direct calculations of rates.

All WE simulations were run using the open‐source WESTPA 2.0 software package (Russo et al. 2022). To generate pathways and rates for the unbinding of the THS‐017 ligand from the HIF‐2α PAS receptor, we carried out three independent weighted ensemble (WE) simulations of the ligand unbinding process. Each WE simulation was carried out for a molecular time N𝜏 of 100 ns where N is the number of WE iterations and 𝜏 is the resampling time interval of 100 ps, yielding a total simulation time of 35.1–41.5 μs within 14–16 days using 16 NVIDIA A100 GPUs in parallel.

An overview of our WE simulation workflow is as follows:

1. Randomly selected five conformations from the pre‐equilibrated ensemble of 25 initial bound‐state conformations (described above).

2. Initiated a WE simulation from the five, equally weighted conformations using a multistage adaptive binning scheme. To maintain a non‐equilibrium steady state, trajectories that reached a ligand–receptor separation distance of 10 Å were “recycled” by initiating a new trajectory with the same statistical weight from a conformation that was randomly selected from the pre‐equilibrated ensemble of bound‐state conformations.

3. Once the calculated off‐rate (k _off) remained at a steady value for at least 100 WE iterations, the WESS reweighting procedure (Bhatt et al. 2010) was applied to accelerate convergence of the simulation to a non‐equilibrium steady state.

4. Extended each WE simulation for 100 WE iterations with updated trajectory weights to further verify simulation convergence.

5. Repeated steps #3 and #4 until the k _off value remained at a steady value, that is, the instantaneous mean of the k _off at the final iteration of the simulation was within the 95% confidence interval [as determined using Monte Carlo blocked bootstrapping (Efron and Tibshirani 1986; Huber and Kim ¹⁹⁹⁶)] of the mean values at prior iterations.

Further details of the multistage adaptive binning scheme (Torrillo et al. 2021; Zhang et al. ²⁰²²), WESS reweighting procedure (Bhatt et al. 2010), and calculation of the k _off are provided below.

For each WE simulation, we used a three‐dimensional progress coordinate consisting of (i) a cavity solvent accessible surface area (SASA) to monitor the extent to which the receptor cavity (residues within 7 Å of the ligand) opens to the surrounding solvent, (ii) a “ligand unbinding” RMSD, defined as the heavy‐atom RMSD of the ligand after aligning on the receptor in the crystal structure of the ligand–receptor complex, to monitor relative orientations of the ligand and receptor, and (iii) the ligand–receptor separation distance to monitor the extent of ligand dissociation. A resampling time interval 𝜏 of 100 ps was used along with a multistage adaptive binning scheme (Torrillo et al. 2021; Zhang et al. ²⁰²²) (see below) and a target number of 8 trajectories/bin.

Dynamics were propagated in the NPT ensemble at 25°C and 1 bar, as described above for conventional MD simulations of the bound state. As required for WE simulations (Bogetti et al. ^2023b), a stochastic thermostat (i.e., a weak Langevin thermostat) was used to maintain constant temperature.

4.1.4. Multistage adaptive binning scheme

As shown previously (Zhang et al. 2022), application of the minimum adaptive binning (MAB) scheme in multiple stages distributes trajectory weights more evenly along the progress coordinate to make more effective use of the WESS reweighting procedure for a non‐equilibrium steady state (Bhatt et al. 2010). Here we applied a three‐stage MAB scheme. The MAB scheme adaptively positions a specified number of bins (Figure S1) along a progress coordinate after each WE iteration based on the positions of the leading, trailing, and “bottleneck” trajectories along the progress coordinate (Torrillo et al. 2021). The WE resampling procedure is then applied with the goal of populating each bin with the target number of trajectories (here, 8 trajectories/bin).

4.1.5. Weighted ensemble steady‐state reweighting procedure

To accelerate the convergence of each WE simulation to a non‐equilibrium steady state, we periodically applied a weighted ensemble steady‐state (WESS) reweighting procedure (Bhatt et al. 2010), as implemented in WESTPA. WESS reweighting was applied whenever the calculated k _off value had leveled off for at least 100 WE iterations (see Figure S2). This reweighting procedure updates trajectory weights for a steady state by solving the following set of steady‐state equations:

$${\sum }_j{p_i}^{\mathrm{SS}}{k}_{\mathit{ij}}={\sum }_j{p_j}^{\mathrm{SS}}{k}_{\mathit{ij}},$$

where ${p_i}^{\mathrm{SS}}$ is the steady‐state population in bin $i$, and $k_{\mathit{ij}}$ is the rate of transition between bins $i$ and $j$. Only bins along the third dimension of the progress coordinate (ligand–receptor separation distance) were used for the reweighting procedure; the positions of these bins were defined as indicated by the following array: [0, 0.5, 0.75, 1, 1.25, 1.5, 1.75, 2, 2.25, 2.5, 2.75, 3, 3.5, 4, 4.5, 5, 6, 7, 8, 9, 10, 20, “inf”].

4.1.6. Calculation of the dissociation rate constant

We calculated the dissociation rate constant k _off directly from our WE simulations using the Hill Relation for a first‐passage process (Aristoff et al. 2023; Hill ²⁰⁰⁵),

$$k_{\mathrm{off}}=\frac{1}{\text{MFPT}\left(A\to B\right)}=\text{Flux}\left(A\to B|\mathrm{SS}\right),$$

where the inverse of the mean first‐passage time from state $A$ to state $B$ $\text{MFPT}\left(A\to B\right)$ is given exactly by the conditional probability flux $\text{Flux}\left(A\to B|\mathrm{SS}\right)$, for the non‐equilibrium steady state consisting of trajectories from an initial state $A$ (i.e., bound state) to a target state $B$ (i.e., unbound state). This probability flux was calculated as the running average probability per unit time (every 𝜏 of 100 ps) of trajectories that have exited state $A$ and entered state $B$, given that the trajectories were more recently in state $A$.

4.1.7. State definitions

For rate‐constant estimation and all other simulation analysis, states were defined based on the two‐dimensional probability distribution as a function of the ligand–receptor separation distance and the ligand unbinding RMSD (Figure 1a). The initial bound state was defined as any conformation with a ligand–receptor separation distance <2.5 Å and a ligand unbinding RMSD <3 Å. The target unbound state was defined as having a ligand–receptor separation distance >6 Å. As mentioned above in the WE simulation workflow, trajectories were recycled at a ligand–receptor separation distance of 10 Å to permit the calculation of k _off values for unbound states with shorter separation distances. An encounter complex, metastable intermediate in which the ligand has exited from the cavity and is bound to a different part of the receptor was defined as any conformation with a ligand unbinding RMSD between 12 and 17 Å, and a ligand–receptor distance <2.5 Å.

4.1.8. Clustering of pathways into distinct classes

To characterize pathway diversity, we clustered all ligand unbinding pathways from our three independent WE simulations into distinct classes using the Linguistics Pathway Analysis of Trajectories with Hierarchical clustering (LPATH) method (Bogetti et al. ^2023a). The LPATH method involves a three‐step procedure: (1) discretize configurational space into states visited by successful pathways, (2) extract a text‐string representation of each pathway using conformations sampled at a specified time interval, (3) apply the Gestalt pattern matching algorithm (Ratcliff and Metzener 1988) to yield a similarity score for each pair of pathways $A$ and $B$ (${\text{similarity}}_{\mathit{AB}}$) and then cluster the pathways into distinct classes based on a distance metric ($d=1-{\text{similarity}}_{\mathit{AB}}$). In the last step, clustering is performed using a hierarchical agglomerative approach with Ward linkage criteria (Ward 1963).

In our study, we discretized the configurational space based on ligand exit points (step 1), that is, selecting six residues beyond the receptor cavity that are positioned on different secondary structure elements (K253, A277, F280, S292, G305, and L310) and assigning conformations to states 1–6 that correspond to the residue that is closest to the ligand (Figure S3a). Text‐string representations of each pathway were then extracted as sequences of possible states 1–6 for conformations sampled every WE iteration (100 ps) (step 2). Only the barrier‐crossing portions of each pathway were considered, leaving out conformations of the stable states (bound and unbound states). Based on the resulting dendrogram of pathway clusters (step 3), we identified two distinct pathway classes (Figure S3b).

4.1.9. Identification of correlated residue motions

To identify residue motions of the protein receptor that are correlated with the ligand unbinding process, we applied the Leiden network clustering (a.k.a. community detection) algorithm (Traag et al. 2019) to the most probable pathway for each of the two pathway classes. In our application of this method, we considered pairs of residues to be in contact if they were separated by at least two residues in the amino‐acid sequence and the distance between their closest heavy atoms was <4.5 Å for more than 10% of the simulation time. Conformations were sampled every 10 ps along each pathway for the network clustering analysis. We then calculated a linear correlation matrix using the Pearson correlation coefficient $\rho \left(X/Y\right)$ for a pair of residue contacts $X$ and $Y$,

$$\rho \left(X/Y\right)=\frac{\left(X-⟨X⟩\right)\left(Y-⟨Y⟩\right)}{{\sigma }_X{\sigma }_Y},$$

where <…> is the time average over the ligand unbinding pathway and σ is the standard deviation. The value of $\rho \left(X/Y\right)$ ranges from −1 (negative correlation) to 1 (positive correlation), with 0 indicating no correlation between the pair of residue contacts. To identify clusters of residues that correlate to various extents with ligand exiting from the receptor cavity (Figure S4), we rearranged the correlation matrix into an approximate block‐diagonal form and applied the Leiden network clustering algorithm, as implemented in the Python package MoSAIC (Diez et al. 2022). Following others (Post et al. 2022), we used a resolution parameter γ of 0.5.

4.1.10. Identification of kinetically important residues

To identify kinetically important residues in the ligand unbinding process, we examined probability maps of pairwise residue contacts in the TSE (see below). To generate these maps, we first calculated a heavy‐atom distance matrix for each protein conformation in the TSE using the cpptraj program of the AMBER 22 software package (Case et al. 2020). Next, we assigned each matrix the statistical weight of the corresponding conformation from the WE simulation. In the resulting maps, we divided the residue contacts into two sets: (i) non‐native contacts gained relative to the bound‐state reference structure (equilibrated crystal structure), and (ii) native contacts lost relative to the bound‐state reference structure. To predict mutations that could impact the ligand unbinding kinetics, we focused on the latter set of residue contacts.

The TSE consisted of 20 conformations with equal probabilities of committing to the encounter complex intermediate and initial bound state, that is, pseudo‐committor values ranging from 0.4 to 0.6 to include an approximate uncertainty of 0.2 (Figure S5). We use the “pseudo‐committor” term given that our simulations were run under non‐equilibrium steady state conditions, generating trajectories in primarily a unidirectional steady state (unbinding direction). In our pseudo‐committor analysis, we calculated the probability of each conformation committing to the intermediate state before reaching the initial bound state. Pseudo‐committor values were calculated from a history‐augmented Markov state model (haMSM) using the msm_we package (Russo et al. 2022) by numerically solving for the stationary distribution with an initial dual‐absorbing boundary condition (i.e., probabilities of the bound state and encounter complex intermediate were each set to one and the probabilities of all other microbins were set to zero). The initial distribution was then propagated (multiplied) with the transition matrix until a convergence of <10⁻⁵ was reached.

4.2. Experimental methods

4.2.1. Protein expression and purification of HIF‐2α PAS‐B mutants

Human HIF‐2ɑ PAS‐B constructs (residues 240–350 of wild‐type and N288Q, N288A mutants) were generated in the pHis6x‐Gβ1 expression plasmid, as described earlier (Harper et al. 2003; Scheuermann et al. ²⁰⁰⁹). His₆‐tagged HIF‐2α PAS‐B proteins were overexpressed in E. coli BL21(DE3) cells, grown in M9 minimal media supplemented with 1 g/L U‐¹⁵N‐NH₄Cl at 37°C until OD₆₀₀ ~ 0.7–0.9, followed by 16–18 h additional growth at 18°C in the presence of 0.5 mM isopropyl β‐D‐thiogalactoside (IPTG). Cells were harvested, lysed by sonication in a lysis buffer (50 mM Tris–HCl, pH 7.4 at 25°C, 150 mM NaCl, 10 mM imidazole, 1 mM DTT, 1 mM PMSF) and centrifuged at 34,500g for 45 min to precipitate the cell debris. Proteins were purified by Ni²⁺ affinity chromatography, and subsequently diluted 1:10 with a cleavage buffer (50 mM Tris–HCl, pH 7.5 at 25°C, 0.1 mM EDTA). After cleavage of the N‐terminal affinity tag by His₆‐tobacco etch virus (TEV) protease (Blommel and Fox 2007), a second round of Ni²⁺ affinity column purification was performed to remove the cleaved tags and TEV protease. HIF‐2ɑ PAS‐B proteins were further purified using a Superdex 75 size‐exclusion column in the final buffer (50 mM Tris–HCl, pH 7.4 at 25°C, 17 mM NaCl, 1 mM DTT). Proteins were concentrated to 350–400 μM using a stirred ultrafiltration unit with a 10 kDa filter, as determined by ultraviolet absorption using the predicted molar absorptivity (ε₂₈₀ = 17,670 M⁻¹ cm⁻¹).

4.2.2. Compound sources

THS‐017 (2‐nitro‐N‐[(thiophen‐3‐yl)methyl]‐4‐(trifluoromethyl)aniline) and THS‐020 (N‐[(furan‐2‐yl)methyl]‐2‐nitro‐4‐(trifluoromethyl)aniline) were purchased from ChemSpace and BLDpharm, respectively.

4.2.3. Isothermal titration calorimetry

All isothermal titration calorimetry (ITC) measurements were carried out at 25°C with a Nano ITC calorimeter (TA Instruments). Titrations were performed in “reverse mode” (250–300 μM protein in syringe, 20 μM ligand in cell), with 25 injections of 1.8 μL of protein solutions (50 mM Tris, pH 7.4, 17 mM NaCl, 1 mM DTT, 0.2% DMSO), using 350 rpm stirring and 250 s delay between succeeding injections. Compound solutions were diluted from 10 mM stock solution to 20 μM in a buffer containing 50 mM Tris, pH 7.4, 17 mM NaCl, 1 mM DTT, with the final DMSO concentration of 0.2%. Evolved heats were experimentally determined from control titrations of HIF‐2ɑ PAS‐B into compound‐free buffer and were subsequently subtracted from the corresponding ligand titrations. The resulting data were analyzed using the NanoAnalyze software package (version 3.12.5) and fitted to the single site binding model to obtain the stoichiometry (n), the dissociation constant (K _d ) and the enthalpy of binding (ΔH).

4.2.4. ZZ‐exchange NMR spectroscopy

NMR experiments were performed at 25°C using an 800 MHz Bruker Avance III cryoprobe‐equipped spectrometer. To determine the association and dissociation rate constants for ligand binding, we employed a ZZ‐exchange‐modified ¹⁵N/¹H heteronuclear single quantum correlation (HSQC) experiments with a Z‐axis pulsed‐field gradient, which gives rise to the time‐dependent exchange peaks via heteronuclear longitudinal magnetization transfer between the bound and unbound states (Farrow et al. 1994). Samples for NMR spectroscopy were prepared as follows: 120 μM of compound (THS‐017 or THS‐020) was added (from a 100 mM stock solution in DMSO‐d ₆) to 240 μM HIF‐2α PAS‐B mutants in 50 mM Tris, pH 7.4, 17 mM NaCl, 1 mM DTT, 7% (v/v) D₂O in a 5 mm NMR sample tube. The total DMSO concentration in the prepared sample was 0.12%. Ligand association (k _on) and dissociation rate (k _off) constants were calculated from a simultaneous fit of the crosspeak and autopeak intensities measured from a series of spectra with mixing delays of 10, 30, 50, 80, 100, 130, 150, 180, 200, 300, 400, 600, 800, and 1000 ms (collected in random order to minimize errors which might correlate with delay length) to the McConnell equations (Farrow et al. 1994). All NMR data processing, analysis, and curve fitting were performed using NMRFx Analyst version 11.4.4 (Norris et al, 2016) modified to incorporate ZZ‐exchange analyses.

Practically, fits to peak intensities followed the approach outlined by Farrow et al. (1994), with the intensities of the auto peaks for the two states (apo and ligand‐bound) denoted by “a” and “b” given by

$$I_{\mathit{aa}}\left(T\right)=I_a\left(0\right)\left[–\left({\lambda }_2–a_{11}\right){{e^{-\lambda }}_1}^T+\left({\lambda }_1–a_{11}\right){{e^{-\lambda }}_2}^T\right]/\left({\lambda }_1–{\lambda }_2\right),$$

$$I_{\mathit{bb}}\left(T\right)=I_b\left(0\right)\left[–\left({\lambda }_2–a_{22}\right){{e^{-\lambda }}_1}^T+\left({\lambda }_1–a_{22}\right){{e^{-\lambda }}_2}^T\right]/\left({\lambda }_1–{\lambda }_2\right),$$

while the intensities of the exchange peaks corresponding to the transfer of magnetization from “a” to “b” (I _ab (T)) and from “b” to “a” (I _ba (T)) are given by

$$I_{\mathit{ab}}\left(T\right)=I_a\left(0\right)\left(a_{21}{{e^{-\lambda }}_1}^T–a_{21}{{e^{-\lambda }}_2}^T\right)/\left({\lambda }_1–{\lambda }_2\right),$$

$$I_{\mathit{ba}}\left(T\right)=I_b\left(0\right)\left(a_{12}{{e^{-\lambda }}_1}^T–a_{12}{{e^{-\lambda }}_2}^T\right)/\left({\lambda }_1–{\lambda }_2\right),$$

respectively. λ _1,2 is defined according to the relation λ _1,2 = ½ [(a ₁₁ + a ₂₂) ± {(a ₁₁ – a ₂₂)² + 4k _ab k _ba }^1/2], where a ₁₁ = R _a  + k _ab , a ₁₂ = −k _ba , a ₂₁ = −k _ab , a ₂₂ = R _b  + k _ba , R _a and R _b are the longitudinal relaxation rates of magnetization in sites a and b, respectively. I _a (0) and I _b (0) denote the amount of longitudinal nitrogen magnetization associated with states a and b at the start of the mixing period T. k _ab and k _ba are the exchange rates for magnetization converting from site a to b and b to a, respectively.

AUTHOR CONTRIBUTIONS

Marion L. Silvestrini: Investigation; writing – original draft; writing – review and editing; methodology; formal analysis; data curation. Riccardo Solazzo: Investigation; writing – original draft; writing – review and editing; methodology; formal analysis; data curation. Soumendu Boral: Methodology; validation; writing – review and editing; writing – original draft; investigation. Melanie J. Cocco: Methodology; validation; formal analysis; writing – review and editing; investigation. Joseph D. Closson: Methodology; formal analysis; validation; investigation. Matteo Masetti: Conceptualization; writing – review and editing; resources; supervision. Kevin H. Gardner: Conceptualization; funding acquisition; writing – original draft; writing – review and editing; formal analysis; project administration; supervision; resources. Lillian T. Chong: Conceptualization; writing – original draft; writing – review and editing; project administration; supervision; resources; formal analysis; funding acquisition.

CONFLICT OF INTEREST STATEMENT

L.T.C. serves on the scientific advisory board of OpenEye Scientific Software and is an Open Science Fellow with Psivant Sciences.

Supporting information

Data S1. Supporting Information.

Movie S1. Movies of the most probable ligand unbinding pathways for (S1) pathway class 1 with conformational gating residues, N288 in the Fα helix (magenta) and S304 in the Gβ strand (cyan), and (S2) pathway class 2 with conformational gating residues, L272 in the Dα helix (magenta) and M309 in the Gβ strand (cyan). The THS‐017 ligand and gating residues are highlighted using van der Waals representations.

Movie S2. Movies of the most probable ligand unbinding pathways for (S1) pathway class 1 with conformational gating residues, N288 in the Fα helix (magenta) and S304 in the Gβ strand (cyan), and (S2) pathway class 2 with conformational gating residues, L272 in the Dα helix (magenta) and M309 in the Gβ strand (cyan). The THS‐017 ligand and gating residues are highlighted using van der Waals representations.

Silvestrini ML, Solazzo R, Boral S, Cocco MJ, Closson JD, Masetti M, et al. Gating residues govern ligand unbinding kinetics from the buried cavity in HIF‐2α PAS‐B. Protein Science. 2024;33(11):e5198. 10.1002/pro.5198

DATA AVAILABILITY STATEMENT

All input files and scripts needed for running and analyzing the ligand unbinding simulations using WESTPA are provided in a GitHub repository: https://github.com/westpa/HIF2alpha_unbinding. Trajectory data (including explicit water molecules) for the most probable pathway of each pathway class are openly available in Zenodo at https://doi.org/10.5281/zenodo.13737481. Due to the large file size, the full simulation dataset for all three WE simulations of this study is available from the corresponding author upon reasonable request.