Comparative analysis of more than 3000 sequences reveals the existence of two pseudoknots in area V4 of eukaryotic small subunit ribosomal RNA

Abstract

The secondary structure of V4, the largest variable area of eukaryotic small subunit ribosomal RNA, was re-examined by comparative analysis of 3253 nucleotide sequences distributed over the animal, plant and fungal kingdoms and a diverse set of protist taxa. An extensive search for compensating base pair substitutions and for base covariation revealed that in most eukaryotes the secondary structure of the area consists of 11 helices and includes two pseudoknots. In one of the pseudoknots, exchange of base pairs between the two stems seems to occur, and covariation analysis points to the presence of a base triple. The area also contains three potential insertion points where additional hairpins or branched structures are present in a number of taxa scattered throughout the eukaryotic domain.

INTRODUCTION

Secondary structure models for small subunit (SSU) and large subunit (LSU) rRNA were postulated nearly as soon as the first primary structures became available for these molecules. Although experimental approaches were used initially to gain information on the secondary structure, the models presently available are based essentially on comparative sequence analysis, which derives the folding from the observation of compensating substitutions that allow different sequences to adopt similar base pairing patterns. Secondary structure models were drawn up in this way and gradually improved as more sequences became available for SSU rRNA (1,2) as well as LSU rRNA (3,4). A number of tertiary interactions in both molecules have been discovered by similar methods (5).

Detailed knowledge of rRNA higher order structure is important for several reasons. First, it contributes to the ultimate goal of a complete molecular description of the ribosome and of the way it functions. Attempts (6) to reconstruct the complete spatial structure of the ribosome combine RNA secondary structure models with results from cross-linking experiments, spatial maps of ribosomal proteins and electron-microscopic observation of ribosomal subunits. Low resolution X-ray crystallographic structures of ribosomal subunits (7,8) and complete ribosomes (9) are just beginning to confirm the existence of the most easily recognizable RNA helices predicted by the secondary structure models. Secondly, the availability of thousands of SSU rRNA and LSU rRNA sequences (10,11) has allowed a breakthrough in our insight into evolutionary relationships between bacterial divisions (12) and between the major eukaryotic kingdoms and protist taxa (13). In order to use rRNA sequences for the reconstruction of phylogenetic trees, dependable alignments are required, and to draft these a thorough knowledge of the secondary structure is often necessary.

The alternation in SSU and LSU rRNAs of conserved, slowly evolving and variable, fast evolving areas has long been recognized (e.g. 14). Recently this observation has been put on a more quantitative basis by the measurement of the relative substitution rate of individual sites in both molecules (13,15,16). Woese (12) cited this as a useful property of rRNAs as molecular chronometers because it should allow the investigation of phylogenetic problems at different depths of the evolutionary scale. However, this prediction has not materialized because the fast-evolving areas are also harder to align and their secondary structure is harder to discover. As a result, the most variable areas are often eliminated before tree construction because their alignment is not considered reliable.

Whereas the secondary structure of prokaryotic 16S rRNA can be considered as completely established, the structure of certain variable areas in the eukaryotic 18S rRNA leaves room for different interpretations. This is especially the case for area V4 (see Fig. 1 for the numbering system) which forms a complex structure in most eukaryotes whereas the corresponding area in prokaryotes is considerably shorter and forms a single hairpin. A secondary structure model containing a pseudoknot has been proposed for this area (17) and has been further refined since (2). Some of the helix structures of the model are present in a limited number of taxa. Recent comparisons of sequences of area V4 in certain arthropod taxa (18–20) have confirmed the existence of most of the helices and provided some detail as to the presence of exceptional helices in this area. The availability of more than 3000 carefully aligned eukaryotic SSU rRNA sequences in our database (10) prompted us to re-examine systematically the secondary structure of area V4 in the majority of eukaryotes and to survey the exceptional cases of taxa, scattered throughout the eukaryotic evolutionary tree, where some helices are absent or additional ones are present.

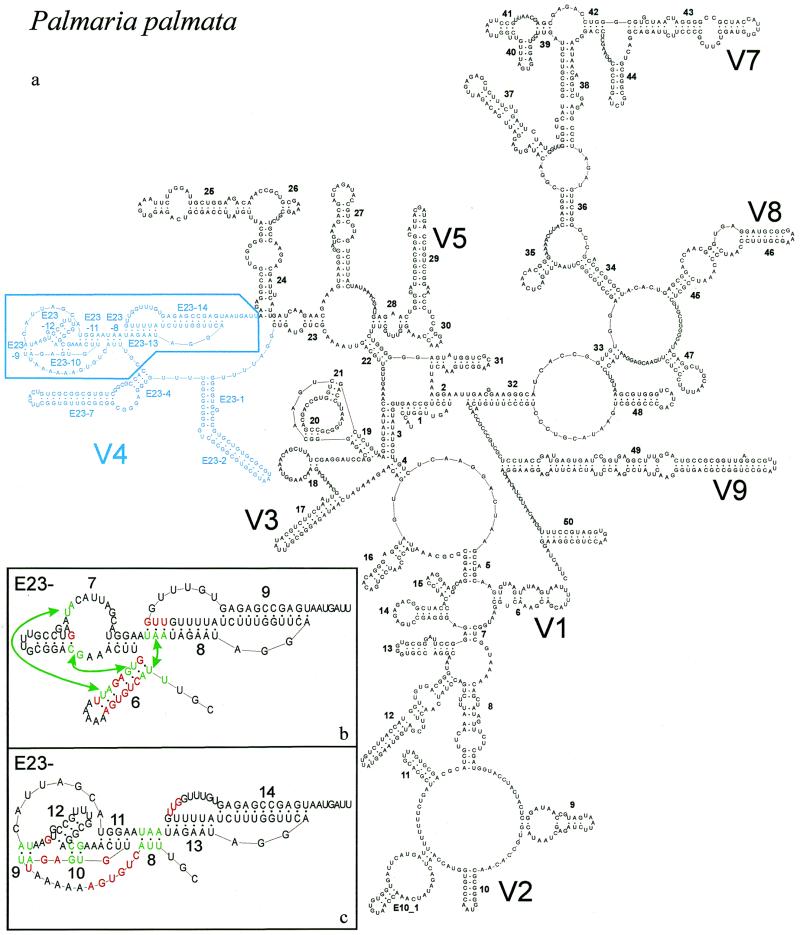
Figure 1.

New secondary structure model illustrated with P.palmata SSU rRNA. (a) Complete model with indication of variable areas V1–V9. V6 is variable only in prokaryotic SSU rRNA where helix 37 is branched. Area V4 is in blue; base pair compensation and base covariation was examined systematically for the boxed part, details of which are shown in the inserts (b) and (c). (b) Old model and helix numbering for part of area V4. Abolished base pairs are in red and new ones, connected by arrows, are in green. (c) New model and helix numbering for part of area V4. Color conventions as in (b). The numbering system was changed to fit the new helix succession and to allow numbering of extra helices present in certain taxa (see Table 3). The correspondence between old and new helix number is as follows: helix E23-6 of the old model is dismantled; E23-7 (old) is transformed into helices E23-11 and 12 (new); E23-8 (old) is partly conserved as E23-13 (new); E23-9 (old) becomes E23-14 (new). Helices E23-8,9 and 10 of the new model do not exist in the old model.

MATERIALS AND METHODS

Nucleotide sequences, alignment, drawing of secondary structure models

The European small ribosomal subunit RNA database (10) contains ∼13 000 SSU rRNA sequences from bacterial, plastidial, mitochondrial, archaeal and eukaryotic genomes. The sequences are regularly collected from nucleotide sequence libraries and stored in the form of an alignment based on the secondary structure model adopted for the molecule, as explained by Van de Peer et al. (10). The secondary structure was re-examined for the eukaryote-specific variable area V4, which is situated between helices 23 and 24, and contains a set of helices numbered E23-n as indicated in Figure 1a. A partial alignment was used for this purpose, limited to area V4 and consisting of 3253 eukaryotic sequences, distributed over the animal, fungal and plant kingdoms and a number of protist taxa as listed in Table 1. After examination of base covariation and base complementarity compensation (see below), slight adjustments to the alignment were carried out, where necessary, using the alignment editor DCSE (21). Secondary structure models were drawn using the program RnaViz (22). The program mfold (23) was used to look for possible local foldings of inserts with unknown secondary structure.

Table 1. Distribution of compared SSU rRNA sequences over the eukaryotic taxa^a.

Taxon	No. of sequences
Fungi	898
Viridiplantae	775
Metazoa	773
Alveolata	253
Rhodophyta	171
Stramenopiles	114
Microsporidia	59
Euglenozoa
Kinetoplastida	55
Euglenida	4
Acanthamoebidae	58
Cryptophyta	24
Parabasalidea	20
Haptophyceae	15
Chlorarachniophyceae	10
Heterolobosea	6
Entamoebidae	4
Hartmannellidae	4
Choanoflagellida	2
Euglyphina	2
Glaucocystophyceae	2
Dictyosteliida	1
Plasmodiophorida	1
Leptomyxida	1
Myxogastria	1
Total	3253

^aThe taxa correspond with those listed in the taxonomy browser of the National Institute for Biotechnology Information (http://www.ncbi.nlm.nih.gov/Taxonomy/taxonomyhome.html/) and they are listed in order of descending number of examined SSU rRNA sequences. In the case of Euglenozoa, the component taxa Kinetoplastida and Euglenida are mentioned separately because area V4 of their SSU rRNA has a different number of helices.

Estimating the strength of base pair compensation

A compensating substitution in a sequence alignment is defined as the substitution of both bases of a complementary pair, present at two positions in a sequence, by other complementary bases at the same positions in another sequence. Complementary base pairs are defined as A·U, U·A, G·C, C·G, G·U and U·G. As an example, a substitution of A·U by G·C is a compensating substitution. A substitution of A·U by G·U is not compensating because only one base changes. Base pair compensation can serve as evidence for the existence of base pairing between two alignment positions, but the evidence can be weak or strong depending on the fraction of base pairs that are complementary and their distribution over the six cases.

Consider the bases occupying two columns i and j in an alignment matrix of n rows (nucleotide sequences) and m columns (nucleotide sites). Comparison of rows k and l at sites i and j can show base pair compensation or not. If each row is compared with each other row we define the compensation index C for sites i and j as

where p_c is the number of pairs of rows showing a compensating base pair substitution and p_t is the total number of pairs of rows. The square root is taken because the number of pairs of rows is essentially quadratic in the number of rows itself. Note that C always lies between 0 and 1.

A straightforward computation of C requires consideration of all p_t = n(n – 1)/2 pairs of rows, which in our case, with n = 3253, means p_t = 5 289 378 pairs of sequences. C has to be computed for all m(m – 1)/2 pairs of positions, which in our case, with m = 118 for the examined part of area V4, amounts to 6903 pairs. As a result, verification of the existence of base pair compensation becomes very time-consuming.

The following algorithm allows a faster computation of C. For a fixed pair of positions (i,j), each row contains a pair of bases, rows that have a gap in either or both positions being ignored. By passing through the rows once we can record the number of times that each of the 16 possible pairs AA, AC, etc. occurs. The complexity of this computation is O(n), which means that the computation time increases linearly with n, whereas the straightforward algorithm is O(n²) because it has to verify each pair of rows. We denote the fraction of rows for which AU occurs as f_AU, and similarly f_UA, f_GC, f_CG, f_GU and f_UG. It turns out that we do not need to record the fractions of the 10 non-complementary pairs such as AA, AC, etc. For two rows k and l, with 1< k < l < n, we say that they constitute a compensating substitution when their combination is labeled as 1 in matrix 1.

There are 22 ones out of the 36 entries in this matrix. If we add the 10 non-complementary pairs AA, AC, etc. to this matrix then all the additional entries are zeros. Since the number p_c of compensating row pairs remains the same for any permutation of the rows, it follows that

p_c = n²(f_AU f_UA + f_AU f_GC + f_AU f_CG + f_AU f_UG + f_UA f_GC + f_UA f_CG +

f_UA f_GU + f_GC f_CG + f_GC f_UG + f_CG f_GU + f_GU f_UG)

where the sum contains 22/2 = 11 terms because matrix 1 is symmetrical. Since the total number of pairs of rows is p_t = n(n – 1)/2 we can compute C by the formula

2

Once the six fractions f_AU, f_UA, f_GC, f_CG, f_GU and f_UG are known, expression 2 is only a simple computation, so the computation time of the entire algorithm for C remains linear in n.

Estimating the strength of base covariation

Covariation (24) is the phenomenon that a base change in one column of the alignment matrix is matched by a base change in another column, but the two bases do not have to be complementary. Base covariation can point to a secondary or tertiary interaction if the corresponding bases are complementary; it usually points to a tertiary interaction if they are not.

Cramer’s ϕ is an index that allows determination of the strength of a relationship between two variables (25). In order to measure the strength of covariation between two sites, Cramer’s ϕ was calculated on the 4 × 4 table listing the numbers of each of the 16 base pairs occurring in the two alignment columns considered. If there are n sequences, ϕ is given by the expression:

where

with n_o the observed number of each of the 16 base pairs, and n_e the expected number assuming that both positions are independent. χ² is calculated on the 16 elements of the table and k is the number of columns or rows in the table, whichever is the smallest. Usually k = 4 in the case of the base pair table, unless a column or a row is empty, in which case k can be smaller, e.g. k = 3 if the four base pairs UU, UC, UA and UG are absent. Cramer’s ϕ assumes a value between 0 (no measurable covariation) and 1 (strongest possible covariation).

The strength of covariation was also measured using the mutual information (24) M, which can assume values between 0 and ln(4) = 1.386.

RESULTS

Presence of two pseudoknots in area V4

Figure 1a shows the complete secondary structure model for the SSU rRNA of the red alga Palmaria palmata (nucleotide sequence accession no. X53500), which is representative of the vast majority of eukaryotic SSU rRNAs. Among 3253 examined sequences 2832 fit this model, whereas in those remaining some of the helices are missing or additional ones are present, as described in the next paragraph. Detailed changes made to the folding in area V4 with respect to the previously assumed structure (26) are shown in Figure 1b and c. The helix numbering system is different in the old and in the new model, on the one hand because of the change in structure, on the other hand in order to allow consistent numbering of newly discovered extra helices present only in the SSU rRNAs of a minority of taxa. The changes in the majority model can be summarized as follows, using the old numbering system (Fig. 1b): (i) hairpin E23-6, poorly supported by compensating substitutions, is abolished; (ii) the sequence UUA at its 5′-end is paired with the sequence UAA in the 5′-strand of helix E23-8, which is therefore shortened by three base pairs; (iii) four bases from the 3′-strand of helix E23-6 are paired with bases in or near the large internal loop in helix E23-7.

As a result, the new model, shown in Figure 1c with the new numbering system, contains two pseudoknots, rather than the single one present in the old model. The 5′-stem of the new pseudoknot is formed by helices E23-9 and E23-10, which are separated by hairpin E23-12. Its 3′-stem is formed by helix E23-11. The second pseudoknot, consisting of contiguous helices E23-13 and 14, remains as in the old model except that E23-13 is shortened by three base pairs at its 5′-end. The new helix E23-8 connects the two pseudoknots. Different drawing schemes were tried to represent the new structure in two dimensions, the one finally chosen proving the least confusing. The helix numbering system is in accordance with the principles followed in the SSU rRNA database (10 and references cited therein).

The new structure was discovered by systematically computing Cramer’s ϕ for all pairs of alignment positions situated between helices E23-4 and 24 (Fig. 1c) and occupied by a nucleotide in at least 90% of the 3253 eukaryotic SSU rRNA sequences. This amounts to 118 sites, hence the computations were made on 6903 pairs of sites. The values of ϕ were found to be considerably higher for the seven base pairs forming the new helices E23-8, E23-9 and E23-10 (Fig. 1c) than for the 12 rejected pairs of the abolished helix E23-6 and the shortened helices E23-7 and E23-8 (Fig. 1b). A high ϕ points to covariation of two sites, which may be due to a tertiary or a secondary interaction. However, the fact that the sites could form neighboring base pairs rather than isolated ones suggested that they belong to secondary structure elements. This was confirmed by computation of the compensation index C for each base pair. Figure 2 gives a graphic representation of the geometric average of ϕ and C calculated for the 6903 pairs of nucleotide sites. Most of the helices can be seen as diagonals of darker dots in a half matrix of dots with an intensity commensurate with .

Figure 2.

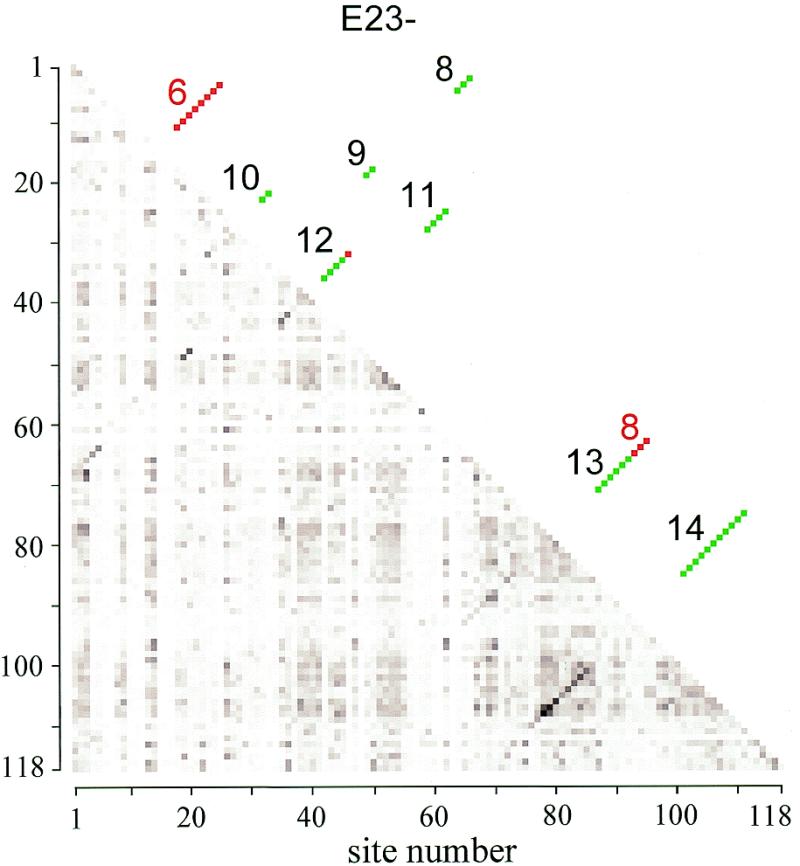
Matrix of base pair compensation and covariation strength. The lower half matrix consists of dots with a darkness proportional to the value of √ϕC measured for each pair that can be formed by the 118 sites lying between helix E23-4 and helix 24 and occcupied by nucleotides in at least 90% of the 3253 sequences examined. There are 256 shades of gray ranging from white (value 0) to black (the highest value measured, 0.8016). Most helices showing base pair compensation are visible as diagonals of darker dots. The upper half matrix, symmetrical with the lower half, shows the position of the helices E23-8 to 14 of the new secondary structure model (Fig. 1c) as green dots. The red dots are abolished base pairs with old helix numbers (Fig. 1b).

In Table 2 the scores C and ϕ are listed for the 32 base pairs of the pseudoknot area comprising helices E23-8 to E23-14. The mutual information M (24) is added for comparison. All the base pairs show compensation to various extents, except for the fourth pair of pseudoknot helix E23-11, where the only complementary pairs found are A·U and G·U. There are other strongly conserved base pairs, such as base pair 1 of helix E23-8, which is U·A in 97.5% of the sequences, yet each of the other five base pairs is present in a small number of sequences. This results in a higher compensation score than that of base pair 1 of helix E23-13, which is less conserved (67% U·G) but only four of the six complementary base pairs are found and the two base pairs present in the largest proportion, U·G and C·G, are not compensating. The highest compensation scores are found for the base pairs of helix E23-14, with base pair 3 attaining score 0.78 due to the presence of G·C, U·A and C·G in nearly equal amounts. Five of the base pairs in Table 2 contain a non-complementary pair in >10% of the sequence set. In each case, among the 10 possible non-complementary pairs one is present in large excess, and this is A·C in three cases and C·U in the two other cases. This could point to some structural peculiarity at these sites that allows the presence of these particular base pairs. Of the four R·Y pairs, A·C is the only non-complementary one but it can form a pair bound by two H-bridges with the same geometry as Watson–Crick pairs if either A or C is in the imino tautomeric form. It is noteworthy that each of the base pairs with a high occurrence of A·C occupies the end of a helix.

Table 2. Composition and degree of compensation for the base pairs of the pseudoknot structure in area V4.

Helixa	Base pairb	No. of sequences comparedc	Base pair composition, %d								Base pair score
			Complementarye							Non-Complementaryf	Compensation C	Cramer’s ϕ	Mutual Inform M
			G·C	G·U	A·U	U·A	U·G	C·G	Total
E23-8	1	3164	0.57	0.03	0.22	97.50	0.98	0.32	99.62		0.1498	0.7366	0.0586
	2	3185	0.38	0	0.16	96.55	0.66	1.63	99.37		0.2052	0.7622	0.0952
	3	3171	0	0.06	99.34	0.03	0	0	99.43		0.0250	0.1662	0.0016
E23-9	1	3184	0.25	0.88	1.16	90.89	1.22	3.86	98.27		0.3381	0.7067	0.2050
	2	3185	3.67	0.09	94.44	0.88	0	0.13	99.22		0.2986	0.9384	0.1896
E23-10	1	3182	98.59	0	0.69	0.44	0	0.06	99.78		0.1537	0.8444	0.0695
	2	3181	0.06	0	0.03	1.92	95.76	1.89	99.65		0.0510	0.3505	0.0059
E23-11	1	3185	0	0.63	0	56.92	4.65	12.24	74.44	23.27% C·A	0.3856	0.5285	0.1105
	2	3187	0	0	0	0.09	95.64	4.20	99.94		0.0089	0.0053	0.0001
	3	3186	0	0	0.03	0.60	7.38	91.09	99.09		0.1072	0.2486	0.0133
	4	3184	0	0.06	94.94	0	0	0	95.01		0	0.4034	0.0283
E23-12	1	3176	0.50	2.33	65.96	0	0	0	68.80	28.56% A·C	0.0815	0.0355	0.0023
	2	3156	46.29	29.72	21.99	0.48	0.03	0.03	98.54		0.4628	0.4352	0.1764
	3	3163	93.23	2.34	1.71	1.77	0	0.13	99.18		0.2623	0.6827	0.1440
	4	3148	0	0.03	0	0.10	2.06	97.17	99.36		0.0498	0.2229	0.0076
E23-13	1	3110	0	0	0.03	3.22	66.62	29.39	99.26		0.1398	0.1672	0.0109
	2	3052	5.96	27.33	60.35	0	0	0.10	93.74		0.2717	0.1471	0.0190
	3	3085	2.37	48.04	21.65	2.72	5.45	2.59	82.82	10.11% (C·U)	0.4084	0.4207	0.2464
	4	3117	6.35	11.39	67.28	0.19	0	0.06	85.27	10.52% C·U	0.2998	0.3158	0.1098
	5	3107	0.26	3.19	94.08	0.06	0	0.03	97.62		0.0820	0.1167	0.0063
	6	3017	1.69	0.03	0.56	79.18	5.27	2.06	88.80	6.63% C·A	0.2689	0.3954	0.0798
E23-14	1	3023	0.96	1.09	94.34	0.50	0	0.03	96.92		0.1683	0.4376	0.0518
	2	3058	0.29	0.13	0.36	2.55	14.19	79.73	97.25		0.2363	0.4203	0.0637
	3	3109	26.44	0.29	1.16	35.25	3.80	30.46	97.39		0.7802	0.8235	0.9138
	4	3083	22.51	1.23	3.89	31.07	15.02	20.37	94.10		0.7153	0.7287	0.6893
	5	3093	4.72	1.68	3.39	13.39	21.31	52.25	96.73		0.5599	0.6818	0.3950
	6	2800	77.50	13.18	1.21	0.86	1.71	0.50	94.96		0.2746	0.4138	0.1238
	7	3102	58.35	24.95	5.32	5.03	1.13	1.39	96.16		0.4441	0.5707	0.2646
	8	2913	2.88	0.41	1.82	69.58	14.49	5.25	94.44		0.4069	0.5873	0.2078
	9	3104	1.51	0.74	1.51	33.99	22.26	34.44	94.46		0.5505	0.5671	0.3069
	10	3084	0.49	0.23	1.04	7.00	2.98	83.63	95.36		0.3874	0.5970	0.2067
	11	2946	0.24	0.14	1.15	42.46	42.43	4.68	91.11		0.2593	0.2683	0.0477

^aSee Figure 1c for helix numbering. Helix E23-12 has four base pairs in most species but up to six in some.

^bBase pairs are numbered from the 5′-end of the 5′-strand of each helix onwards.

^cThis number is different for each base pair and smaller than the total number of compared sequences (3253) because of gaps in the sequence alignment. See text for full details.

^dThe first nucleotide is that in the 5′-strand.

^eThe total fraction of complementary base pairs is expressed as % of the number of sequences compared for each base pair (column 3). Since this is of the order of 3000, if a given base pair composition is found in only one sequence, it amounts to 0.03% of the total, which is therefore the lowest non-zero value found in the table.

^fIn cases where <90% of the base pairs are complementary, i.e. (G·C), (A·U) or (G·U), the non-standard base pair present in the largest proportion in mentioned in this column. In the case of base pair 3 of helix E23-13, C·U and U·C are present in nearly equal proportions.

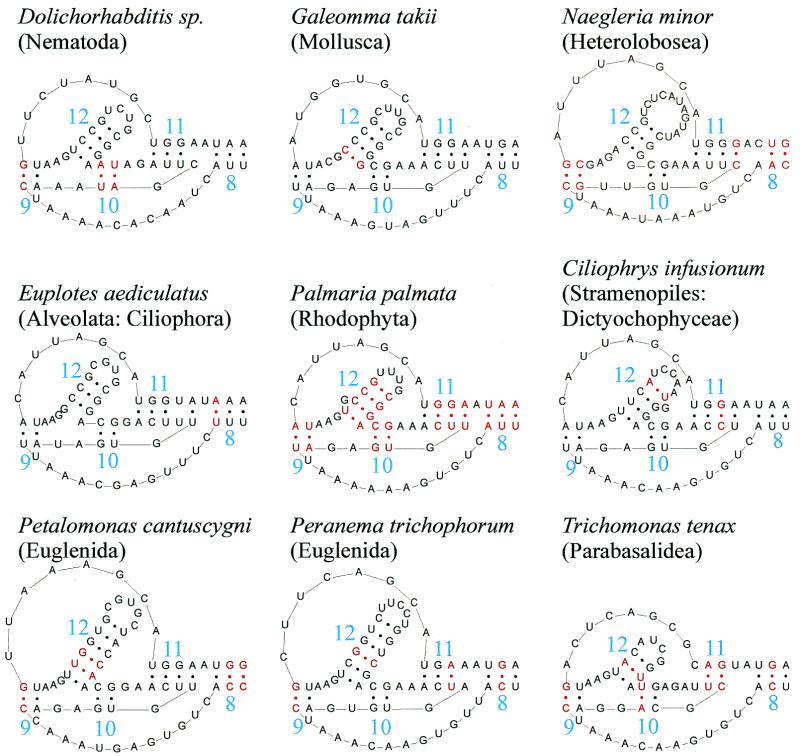
The existence of base pair compensation in helices E23-8 to E23-12, the area containing the newly discovered pseudoknot, is illustrated in Figure 3 with a set of nine structures. In most sequences this area contains 15 base pairs. Fourteen of these are proven by compensating substitution in the examined sequence set.

Figure 3.

Base pair compensation in helices E23-8 to E23-12. Helices E23-8 to E23-12 comprise 15 base pairs in most species. Fourteen of these, in red in the P.palmata structure in the centre, show compensation in other species, as can be seen in the eight structures surrounding it. The first base pair of helix E23-11 (U·A, at right in the figure), though subject to compensation, is non-complementary in ∼1/4 of the sequences. In Trichonomas tenax this base pair cannot be formed if it is assumed that the pseudoknot loop between helices E23-10 and 11 must contain at least one nucleotide (G in this case). Compensation of the second base pair of helix E23-11 occurs between the structures of Ciliophrys infusionum (C·G) and Peranema trichophorum (U·A). The last base pair (A·U) is not compensated in presently known species but becomes G·U in two species. See also Table 2.

The net difference between the old secondary structure model (Fig. 1b) and the new one (Fig. 1c) amounts to the dissolution of 12 base pairs and the creation of seven new ones. The average compensation score of the abolished base pairs is C = 0.0329, the average score of the new base pairs, C = 0.1745. For each of the base pairs of helices E23-8 to E23-14, Table 2 mentions the number of sequences where it was observed, which is always smaller than 3253, the total number of sequences compared. There are several reasons for this. First, the 59 Microsporidia sequences form exceptional structures described below and miss all the helices mentioned in Table 2, which leaves 3194 sequences to be compared. Secondly, some helices, especially E23-12 to E23-14, show length heterogeneity. Table 2 lists the base pairs occurring in the majority of sequences but a pair can be missing due to a symmetrical deletion in both strands, or a bulge can result from a deletion in one strand. Thirdly, some of the compared sequences contain a few ambiguity codes such as R, Y, S, W and N. If one of the bases of a pair is incompletely identified the pair is not counted in Table 2. Taking as an example helix E23-9, which consists of only two base pairs, examination of the alignment shows that both pairs are present in 3190 out of 3194 sequences if ambiguous nucleotide symbols are included. Allowing for the possibility of a few sequencing errors, it seems highly probable that helix E23-9 exists in all structures except those of the Microsporidia. Similar observations for the other helices listed in Table 2 leads us to the conclusion that they exist in all the examined eukaryotic SSU rRNA sequences, with certain exceptions for the taxa with a reduced structure described below.

Deviant structures of area V4 in certain taxa

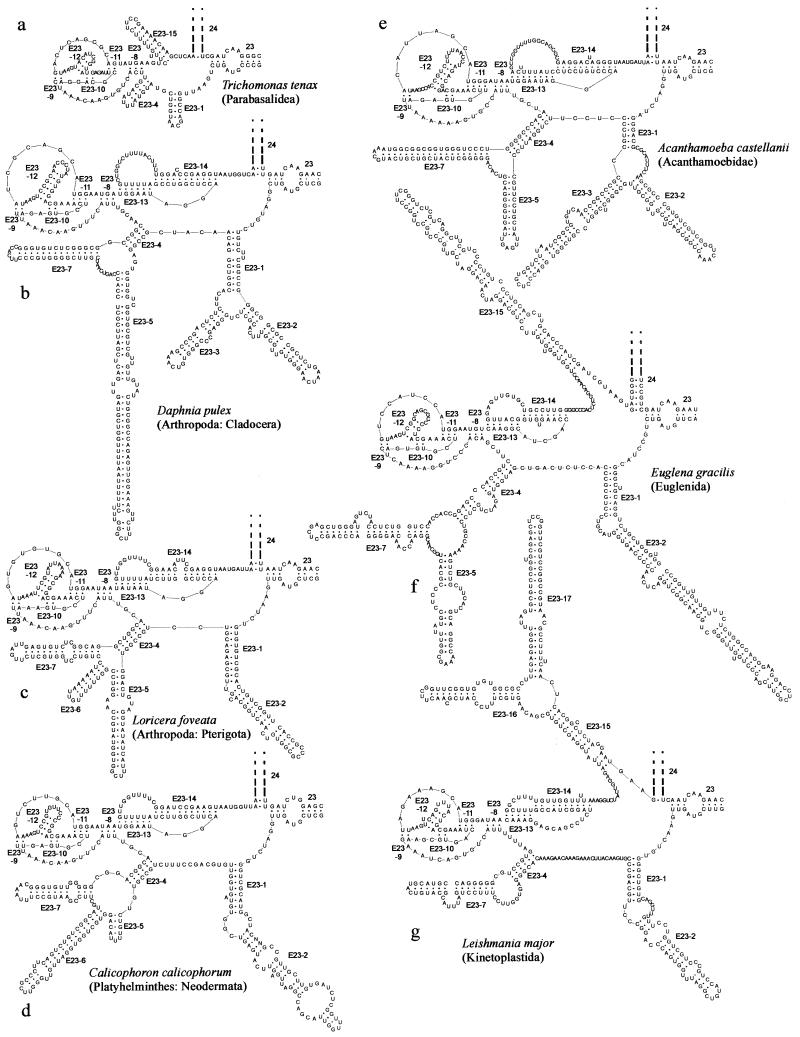
Of the 3253 sequences examined, 2832 follow the secondary structure model for area V4 shown for P.palmata in Figure 1a. However, the variability of area V4 is not limited to a high substitution rate but also involves a higher rate of deletion and insertion, which in extreme cases results in the deletion or insertion of entire helices. A survey of sequences with an exceptional number of helices was made (2) in 1992 when only 197 eukaryotic SSU rRNA sequences were known, but other cases of deviant secondary structures in area V4 have been discovered in the meantime (e.g. 19,27). We therefore made a systematic survey of exceptional structures in area V4, present in 421 of the 3253 sequences.

Figure 4 shows the three sites in the secondary structure model where additional helices are inserted. Two of them are at the potential branching points between helices E23-1 and 2 and between E23-4 and 7. The third site is at the 3′-end of the area, between pseudoknot helix E23-14 and helix 24. Examples of exceptional structures are given in Figure 5. Table 3 summarizes which helices are present in which taxa. Helix E23-1 is listed as a long range interaction because it contains a potential branching point to helices E23-2 and 3. However, since helix E23-3 is only exceptionally present, helices E23-1 and 2 look like a long hairpin in most species. The same applies to helices E23-4 and 7.

Figure 4.

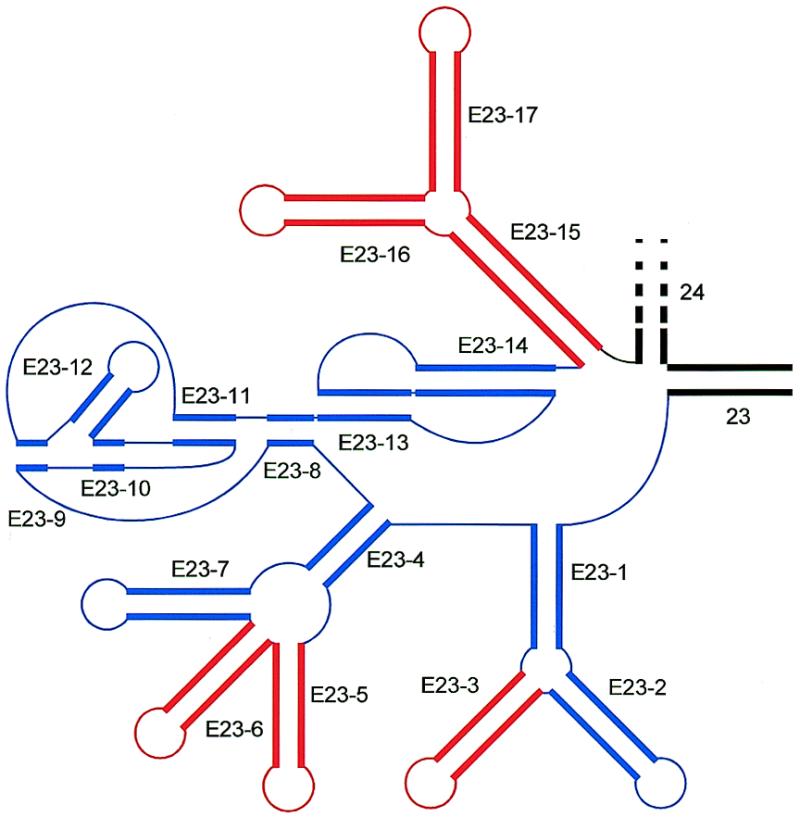
Position of exceptional helices in area V4. Double stranded areas are drawn as thick parallel lines, single stranded areas as thin lines. Universal helices 23 and 24 are drawn in black, eukaryote-specific helices are in color, blue for those present in the majority of species, red for those present only in specific taxa (cf. Table 3).

Figure 5.

Examples of exceptional structures in area V4 in specific taxa. (a) Parabasalidea; (b) Cladocera; (c) Pterigota; (d) Neodermata; (e) Acanthamoebidae; (f) Euglenida; (g) Kinetoplastida. Cf. Table 3.

Table 3. Helix presence in area V4 of eukaryotic SSU rRNA secondary structure^a.

Taxonb	Helix number n in E23-nc
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
	L	H	H	L	H	H	H	L	Ψ1	Ψ1	Ψ2	H	Ψ1	Ψ2	L	H	H
Microsporidiad	o
Parabasalideae	o			o				·	·	·	·	·			·
Euglenidaf	·	·		·	·		·	·	·	·	·	·	·	·	·
Kinetoplastida	·	·		·			·	·	·	·	·	·	·	·	·	·	·
Heterolobosea	·	·		·	·		·	·	·	·	·	·	·	·
Acanthamoebidae	·	·	·	·	·		·	·	·	·	·	·	·	·
Myxogastriag	·	·		·	·		·	·	·	·	·	·	·	·
Babesiidae (Alveolata, Apicomplexa)	·	·		o			o	·	·	·	·	·	·	·
Neodermatah (Platyhelminthes)	·	·		·	·	·	·	·	·	·	·	·	·	·
Cladocera, Cyclestherida (Arthropoda, Crustacea)	·	·	·	·	·		·	·	·	·	·	·	·	·
Pterygotah
(Arthropoda, Insecta)	·	·		·	·	o	·	·	·	·	·	·	·	·	o
Most eukaryotes	·	·		·			·	·	·	·	·	·	·	·

^aA helix is indicated by ‘·’ if present in all known SSU rRNAs of a taxon, by ‘o’ if present only in a fraction of them.

^bTaxa correspond to those listed in Table 1 except for Babesiidae and the metazoan taxa, in which case the rough taxonomic situation is indicated. See the taxonomy browser (http://www.ncbi.nlm.nih.gov/Taxonomy/taxonomyhome.html/) for details.

^cHelix numbers are accompanied by the following symbols: L, long range interaction; H, hairpin; Ψ₁, 5′-stem of a pseudoknot, Ψ₂, 3′-stem of a pseudoknot. Helices E23-1 and 2 together are seen as a hairpin in most species because branching hairpin E23-3 is usually absent. The same applies to helices E23-4 and 7. For certain helices, their presence does not necessarily prove that they are homologous with similarly numbered helices in other taxa (see text and other footnotes).

^dThe entire area V4 is lacking in the genus Vairimorpha and most species of the genus Nosema. In other Microsporidia it consists of a single hairpin arbitrarily placed in column 1 but which may not be homologous with E23-1 in other species.

^eIn Parabasalidea pseudoknot E23-13-14 is absent and replaced by a hairpin structure which was assigned no. E23-15, but homology with similarly numbered helices in other taxa in doubtful.

^fThe structure of helix E23-15 in Euglenida is tentative (see text).

^gThis taxon is represented by a single species, Physarum polycephalum, hence the presence of the extra hairpin E23-5 is not proven by compensating substitutions.

^hThe Neodermata (subphylum of the Platyhelminthes), as well as certain representatives of Pterigota (winged insects; Arthropoda) contain two hairpins labeled E23-5 and E23-6. In neither case is it known which of these, if any, is homologous to helix E23-5 in other taxa and which one is supernumerary.

In short, exceptional structures were derived as follows. In case a sequence contains a large deletion or insertion with respect to the majority of sequences, the first step consists of localizing its position as precisely as possible on the basis of similarity of the flanking sequences to segments of the alignment. This is usually straightforward in the case of a deletion, but it can be difficult in the case of an insertion in an already variable area, such as that enclosed by helix E23-1. In this case, the entire area containing helix E23-1 plus the insert was examined with the secondary structure prediction program mfold which for certain taxa yielded an enlarged single hairpin and for others a branched structure. The existence of the stem helix E23-1 and the hairpins E23-2 and eventually E23-3 could then usually be confirmed by the observation of compensating substitutions among the sequences of each taxon. Structures at other potential insertion points were derived similarly.

There are three protist taxa, the Microsporidia, the Parabasalidea and the Babesiidae, that miss some of the 11 helices forming the consensus model for area V4 as indicated on the bottom row of Table 3. In most Microsporidia the entire area V4 is absent, the others contain a sequence that can be folded into a single hairpin, as in the bacteria. This hairpin is labeled rather arbitrarily helix E23-1 in Table 3, because it is the only helix present in the area and it follows universal helix 23 in the sequence. However, there is no evidence whatsoever that this hairpin is homologous with E23-1, or any other helix E23-n, in other eukaryotes. In the Parabasalidea (Fig. 5a) helix E23-1 is present in 12 out of 20 sequences of the examined set. Homology with E23-1 of other eukaryotes is probable because many other helices of the area are present in the same succession. Helix E23-4 is present in 18 out of 20 species, but its extension E23-7 found in other eukaryotes is absent. The second pseudoknot, E23-13 and 14, also seems to be absent and replaced by a single hairpin, which was labeled E23-15 because it occupies a position similar to that of helix E23-15 in other taxa treated below, but there is no evidence for homology with these helices. In the Babesiidae, among 17 examined sequences, helix E23-4 is absent in 11, helix E23-7 in 14 of them. There is one more protist taxon, the Diplomonadida, with a reduced area V4, but the small number of available sequences and high variability made alignment too uncertain to derive a structure, hence it was not included in the examined set.

Eight taxa contain all 11 helices of the consensus model (bottom row of Table 3) plus some additional ones. At branching point E23-1/2, an extra helix E23-3 is found in the protist taxon Acanthamoebidae (Fig. 5e) and in the crustacean taxa Cladocera and Cyclestherida (Fig. 5b). At branching point E23-4/7, a single helix E23-5 is inserted in a range of taxa (see Table 3), examples being given in Figure 5b, e and f. At the same branching point, two helices, E23-5 and 6, are inserted in certain representatives of the Pterigota (winged insects; Fig. 5c) and in the Platyhelminth subphylum Neodermata (Fig. 5d). There is no apparent homology between the helices inserted at this branching point in different taxa. Where a single helix was found, it was given the number E23-5, if two were found, the second one was labeled E23-6. Between helix E23-14 and universal helix 24, inserts are found in the Euglenida and in the Kinetoplastida, which together belong to the protist taxon Euglenozoa. Since only four euglenid sequences were available there were not enough compensating substitutions to derive a dependable structure for the insert. The single hairpin E23-15 shown in Figure 5f was derived by mfold and should be regarded as tentative. In the case of Kinetoplastida a branched structure E23-15-16-17 (Fig. 5g) is inserted. Except for helix E23-5 in Myxogastria and E23-15 in Euglenida, all extra helices are supported by compensating substitutions, though usually not in each base pair.

The presence of extra helices in certain species at the potential branching point E23-4/7 and between helix E23-14 and universal helix 24 has been known for several years (2,28). The structure of the insert at branching point E23-4/7 in insects was examined more thoroughly recently (20). The branching of hairpin E23-3 from junction E23-1/2 was observed in branchiopod crustaceans (Cladocera and Cyclestherida, Table 3) by Crease and Taylor (19). However, the latter authors assumed the presence of an extra helix, which they named E23-c, between E23-1-2-3 and E23-4. Our comparative study shows that this helix is in fact helix E23-5 and that the structure should be modified as illustrated with the Daphnia pulex model in Figure 5b.

DISCUSSION

Implications for phylogenetic studies

Alignments of eukaryotic SSU rRNA sequences have been used extensively for the reconstruction of phylogenetic trees, from studies encompassing nearly the entire Eukarya domain (e.g. 13) to others focusing on specific low level taxa (e.g. 18). rRNA molecular evolutionists are well aware that their alignments should take into account secondary structure patterns, while improvements in the alignment can in turn lead to discovery of new details of the secondary structure, the entire process being enhanced by the availability of an ever-increasing set of sequences. Although the accuracy of phylogenetic trees increases with the length of the sequence alignment used, entire sequence chunks are often omitted because the secondary structure of certain variable areas is too poorly known to allow a justifiable alignment. This is a waste of data that can be avoided by a better knowledge of the detailed secondary structure of variable areas. The largest such area in eukaryotic SSU rRNA, V4, has already been the focus of several studies (2,17–20), but the present work achieves a new degree of detail in its description, made possible by comparison of an extensive sequence set covering the most diverse eukaryotic taxa. It also gives an inventory of the insertion sites, and which structures are inserted in which taxa (Table 3). This should constitute an aid in phylogenetic studies in the sense that it allows it to be decided which parts of the sequence can be used, depending on the problem studied. The secondary structure of helices E23-8 to 14 is sufficiently conserved to be aligned among all eukaryotes except for three primitive potist taxa, the Microsporidia, Parabasalidea and Diplomonadida, where the structure is either absent or strongly reduced in size. Helices E23-8 to 14 can therefore be used in nearly all studies on eukaryotic evolution, general as well as specific. On the other hand, helices E23-1 to 7 and E23-15 to 17 are so variable that meaningful alignments should be limited to sets of closely related species having sufficiently similar structures. Even within such taxa a search for homologous nucleotides can be futile in strongly expanded segments of helices such as E23-2 or E23-5.

Table 3 shows that some helices such as E23-5 are found in taxa as distant as euglenids and certain insects, while being absent in the majority of other eukaryotic species. It thus seems that the SSU rRNA molecule comprises a basic structure which at certain points leaves room for insertion of sequences. These seem to happen independently at certain points in evolution, leading to structures that, though present at similar sites of the molecule, are not homologous. In other words, they constitute a homoplasy between the taxa where they occur.

Structure of the pseudoknots and evidence for a tertiary interaction

Our study shows that area V4 contains two pseudoknots in succession. The first one is formed by helices E23-9 to 12, the second one by helices E23-13 and 14. The latter pseudoknot is of the simplest known type consisting of two stem–loop structures with each loop intertwined with the stem of the other. The newly discovered pseudoknot, though containing fewer base pairs, has a more complicated structure. Its 5′-stem, consisting of helices E23-9 and 10, is interrupted in its 3′-strand by the short hairpin E23-12. Consultation of the pseudoknot database (29) showed that this arrangement is most similar to pseudoknots PKB134, PKB135, PKB168 and PKB168 found in plant viruses.

The pseudoknot consisting of helices E23-13 and 14 has a peculiar property, already described when it was first reported (17), and illustrated in Figure 6. Helix E23-13 can acquire base pairs at the expense of helix E23-14 and vice versa, in other words the boundary between the two stems of the pseudoknot seems to be able to shift in both directions. The presumption of a mobile boundary is strengthened by the fact that the shift is possible in the large variety of species now examined, in spite of the variability of the local nucleotide sequence. Although no specific function has yet been ascribed to this area of SSU rRNA it seems possible that mobility of this part of the molecule would be associated with the ribosome switching between allosteric states associated with its protein synthesizing function.

Figure 6.

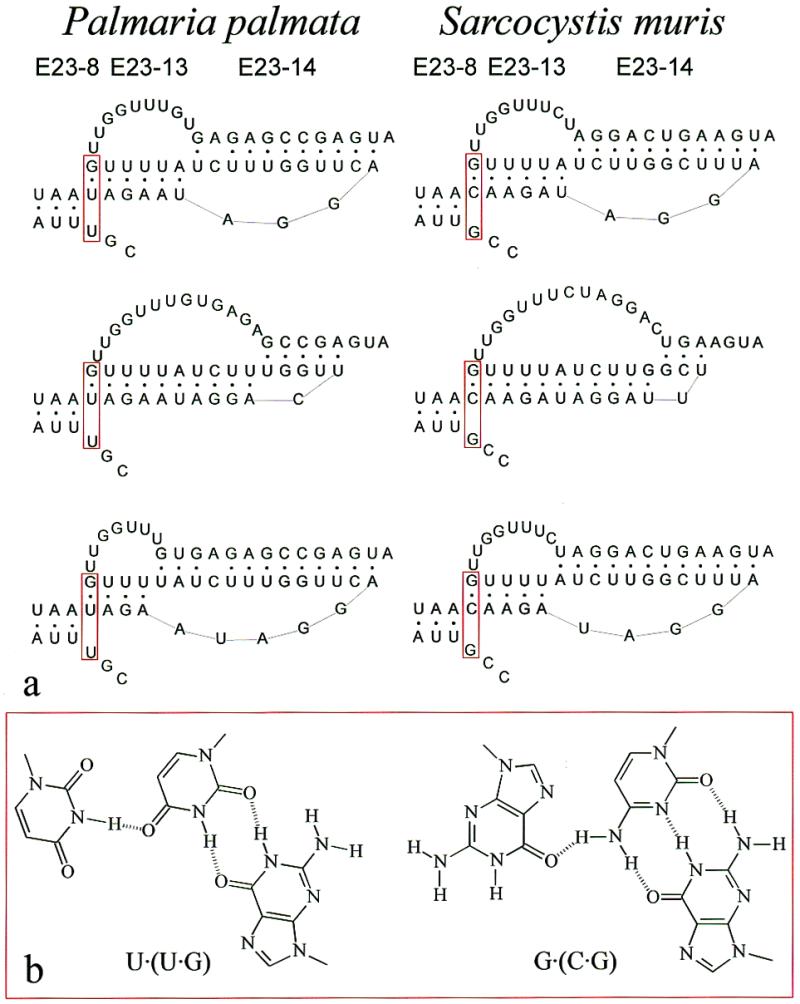
Possible dynamic structure and base triple in pseudoknot E23-13-14. (a) The structure of helix E23-8 and of the pseudoknot E23-13-14 is shown for two species, the red alga P.palmata and the apicomplexan Sarcocystis muris. The uppermost structure corresponds to the model of Figure 1a and c. In the middle structures the boundary between the pseudoknot helices is shifted to the right, in the lower structure to the left, by disrupting base pairs of one helix in favour of the other. Postulated base triples U·(U·G) in P.palmata and G·(C·G) in S.muris are boxed in red. (b) Structural formulas of the most isomorphic forms of the base triples U·(U·G) on the left and G·(C·G) on the right.

There is a strong covariation between the base preceding the 5′-strand of helix E23-8 (U in P.palmata) and the base pair at the 5′-end of helix E23-13 (U·G in P.palmata). The base pair is U·G in 66.5% of the sequences and C·G in 29.3%. The combination U (U·G) is found in 64% of the sequences, the combination G (C·G) in 27.4% of them. We therefore postulate that these three sites form a base triple. A search for isoform triples with these compositions by the program ISOPAIR (30) yielded the structures shown in Figure 6b. The existence of two base triples in more conserved areas of eukaryotic SSU rRNA has been deduced by Gutell and coworkers (http://www.rna.icmb.utexas.edu/) but to our knowledge this is the first indication of the presence of such a structure in a variable area.

Matrix.

	row l
		AU	UA	GC	CG	GU	UG
	AU	0	1	1	1	0	1
	UA	1	0	1	1	1	0
row k	GC	1	1	0	1	0	1
	CG	1	1	1	0	1	0
	GU	0	1	0	1	0	1
	UG	1	0	1	0	1	0