Abstract
Transition characteristics and thermodynamic properties of the single-stranded self-transition and the double-stranded association were investigated and analyzed for 9-, 15- and 21-bp non-self-complementary DNA sequences. The multiple transition processes for the single-stranded self-transition and the double-stranded association were further put forth. The experimental results confirmed that the double-stranded association transition was generally imperfect and the thermodynamic properties of the single-stranded self-transition would exert an influence on a duplex formation. Combining ultraviolet melting experiments in various molar ratios, the extent of duplex association was estimated for three double-stranded DNAs. In our experimental range, the extent of duplex association decreases with increasing the number of base pairs in DNA sequences, which suggest that the short oligonucleotides may proceed in a two-state transition while the long oligonucleotides may not. When the extent of duplex association was considered, the true transition enthalpies of a duplex formation derived from UV and differential scanning calorimetry measurements were in good agreement.
INTRODUCTION
The thermodynamic analysis on the stability of oligonucleotide duplex formation is an ancient and interesting subject, and a large number of papers have been published on this aspect (1–10). When the thermodynamic enthalpies derived from optical and calorimetric methods were compared directly for long oligomeric sequences, however, a discrepancy between the two quantities was often found (11–16). The exact interpretation of these deviations varied from study to study, but they almost considered that a real duplex formation proceeded in a partial two-state transition (10,11,14,16,17). Surprisingly, quantitative evaluation for the imperfect duplex association, except for a few studies (10,11,14,17), has been lacking.
Do the thermodynamic properties of single strands exert an influence on the thermodynamic stability and the transition behavior of a duplex formation? How does one quantify the extent of duplex association? How much deviation will be introduced by using the two-state model to estimate the thermodynamic parameters of a duplex formation? Quantitative answers to these questions will be useful for designing appropriate experiments to identify the genetic markers for diseases (18), calculating the minimum dosage of the genetic drugs, selecting optimal conditions for hybridization experiments (19), determining the minimum length of a probe required for hybridization and DNA microarray (18,20), identifying single nucleotide polymorphisms (SNPs) on a genome-wide scale (21), and so on.
In this paper, we first analyzed the thermodynamic property and transition characteristics of the single-stranded self-transition and the double-stranded association based on ultraviolet (UV), differential scanning calorimetry (DSC) and circular dichroism (CD) data, and then proposed a segregated transition model (STM). Combining UV melting experiments in various molar ratios, the extent of duplex association was calculated for three duplex-stranded DNAs (dsDNAs). Finally, the true transition enthalpies were further obtained by considering the imperfect DNA duplex formation.
MATERIALS AND METHODS
DNA synthesis and purification
DNA oligomers were synthesized on solid support using the standard phosphoramidite chemistry and purified by reversed-phase high-performance liquid chromatography (HPLC) with Wakosil-II 5C18RS cartridges after de-blocking operations (5,9). Oligonucleotides were aliquoted for UV melting and DSC transition experiments. These oligonucleotides were further purified and desalted with Sep-Pak C-18 cartridges. All experiments were carried out in a buffer solution containing 1 M NaCl/10 mM Na2HPO4 /1 mM Na2EDTA (pH 7.0). Single strand concentrations of DNA samples were determined by measuring the absorbance at 260 nm at high temperature as described previously (22). The total species concentration was calculated by extinction coefficients and molar fractions of single strands in a stock solution.
DNA sequence selection
Genetic variations in human CC chemokine receptor 5 (CCR5), the major human immunodeficiency virus type 1 (HIV-1) co-receptor, were shown to influence HIV-1 transmission and disease progression (23–25). Up to now, at least 12 SNPs within the 5′ upstream regulatory region of CCR5 and HIV-1 receptor gene have been found (25). McDermott and co-workers (24) synthesized allele-specific oligonucleotides in vitro, and revealed that the T-bearing oligonucleotide at site 208 displayed 5–12-fold greater binding to a specific nuclear binding protein than the G-bearing oligonucleotide. In this study, we synthesized six DNA oligomers as follows: S1, d(GCTTGTTGC); S2, d(GCAACAAGC); S3, d(GCAGGTTGTTTCCGC); S4, d(GCGGAAACAACCTGC); S5, d(GCAACAGGTTGTTTCCGTTGC); S6, d(GCAACGGAAACAACCTGTTGC). S1, S3 and S5 (underlined) represent allele-specific oligonucleotides of CCR5 sites 208 in the context of their adjacent nucleotides. To reduce end-fraying of the duplex strands, both ends were capped with two GC base pairs (11,14). S2, S4 and S6 are complementary single strands of S1, S3 and S5, respectively.
Experimental procedures
UV melting experiments were carried out on Hitachi U-3210 spectrophotometers equipped with a Hitachi SPR-10 thermoprogrammer and temperature probes (5,9). All samples were annealed and degassed by heating the cuvette to 95°C for 20 min, and heating rates were fixed at 0.5°C/min or 1°C/min. DSC scans were performed on a MicroCal VP–DSC Microcalorimeter. Buffer and samples were vacuum-degassed prior to scanning. For each sample, six to eight scans were collected from 15 to 95°C at a rate of 1°C/min. Sample scans were averaged and buffer baseline was subtracted to obtain excess heat capacity (ΔCP) versus temperature curves. Transition temperature was determined by the peak maximum of the normalized ΔCP versus temperature curves, and the calorimetric enthalpy and entropy were obtained directly by integrating the area of the corresponding curves (11,13,14,16). CD spectra were recorded on a Jasco J-600 spectropolarimeter equipped with a PTC-348 temperature controller (5,9). The spectra were accumulated over the wavelength range of 200–350 nm and temperature range of 0–90°C in a 0.1 cm path-length cell at a scanning rate of 10 nm/min. The resulting CD spectra were an average of six scans.
RESULTS AND DISCUSSION
Self-transition of the single-stranded DNAs
UV, CD and DSC measurements were performed for six non-self-complementary ssDNAs (see Supplementary Material available at NAR Online). The experimental data show that the absorbances of S1 and S2 display approximate linear increase with temperature in a broad range. Despite a relatively wide melting range, S3 and S4 exhibit clear melting points. In contrast, the melting curves of S5 and S6 show typical sigmoidal shapes and significant transition features and their melting temperatures are obviously concentration dependent. These observations are further confirmed by DSC data and are excellently consistent with previous studies (26). Moreover, CD spectra depend on temperature, while they do not change with strand concentrations, suggesting that the conformational changes of single strands are intrinsically temperature-dependent and the single-stranded self-transition may occur primarily in a monomolecular pattern (11).
To reasonably interpret these thermodynamic characteristics and transition behaviors, we consider that multiple transitions may coexist in the course of the single-stranded self-transition (14,26,27). These potential transitions include: (i) the intrastrand folding (hairpin structure); (ii) the intrastrand self-helix formation (the single-stranded helix structure); (iii) the interstrand weak cooperativity (the interstrand aggregation). Process (i) contains the formation of base pairs and therefore belongs to chemical transition that is accompanied by a large energy change and has a clear melting point. Processes (ii) and (iii) only involve the ordered single-stranded arrangement and the interstrand loose aggregation, the main features of which are a small energy change and the appearance of a broad melting range. As to which process actually takes place and what accounts for a dominant process of the single-stranded self-transition will depend on the composition, context and number of bases in a DNA sequence. However, due to a greater chance of base pairing with accidental sequence complementary, longer ssDNAs may have larger thermodynamic driving force and transition energy than shorter ssDNAs.
Association transition of the duplex-stranded DNAs
In contrast to the single-stranded self-transition, the duplex association displays the significant feature of chemical transition in which the melting temperature clearly depends on the strand concentrations and melting curves exhibit dramatic changes around the melting temperature. These observations are in excellent agreement with the general features of a duplex formation (2,11,17,26).
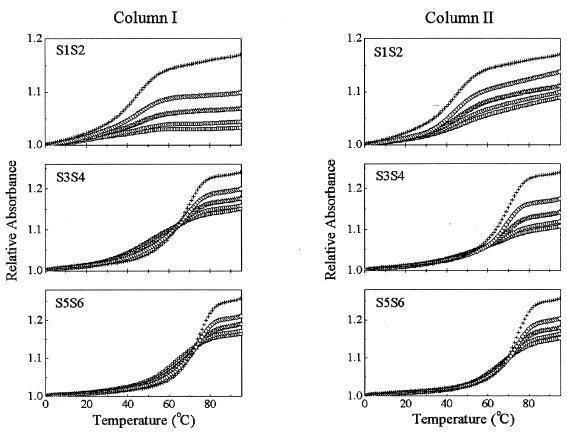
Considering that the temperature-induced duplex association is a second-order reaction in terms of strand concentration (28), changes in molar fraction of two complementary single strands may affect the thermodynamic property and transition characteristics of a duplex formation. In order to obtain further insights into the transition nature of a duplex formation, UV melting experiments were conducted in various molar ratios as shown in Figure 1, where the relative absorbance versus temperature were plotted for three dsDNAs in two adding modes and various molar ratios. These experimental results demonstrate that the presence or absence of complementary strands in the host strand solutions exhibits obvious difference in the transition behavior. The single-stranded self-transition, as described above, displays a broad melting range. However, when a very small amount of the complementary strands was added to the stock solution containing the host strands, for example, given a molar ratio of host to guest strands of 20, the melting curves were greatly altered, exhibiting a typical transition feature of the duplex formation. This direct comparison suggests that, despite a large difference in the concentration between two complementary single strands, the thermodynamic driving force and contributions come mainly from the interstrand association (i.e. docking) (14,26). Alternatively, when the single-stranded self-transition and the double-stranded association transition take place simultaneously in a mixing solution, the duplex association is a dominant thermodynamic deriving force.
Figure 1.
UV relative absorbance versus temperature curves for three dsDNAs in two adding modes and various molar ratios. Column I indicates that S2, S4 and S6 are guest strands and added into host strands S1, S3 and S5, respectively. Column II shows an inverse-adding mode to Column I. Plots for various molar ratios of 20:1 (squares), 10:1 (circles), 5:1 (triangles), 2.5:1 (diamonds) and 1:1 (crosses).
A segregated transition model (STM) of DNA duplex formation
Considering the general thermodynamic characteristics and transition behavior of DNA duplex formation, it is assumed that a duplex formation may proceed in the following transitions (14,26,27): (i) the duplex association of two complementary strands in the equimolar proportion; (ii) the self-transition of single strands; (iii) the interstrand weak interaction or cooperativity. For an extreme case in which all of the above processes occur in an independent fashion and the thermodynamic contributions of interstrand weak interaction to the over-all transition are very small and can be ignored (see the text below), we further obtain a STM:
The single-stranded self-transition and the double-stranded association are independent transition processes.
The thermodynamic property and transition characteristics of each transition in a mixing solution are identical to those in the isolated system.
The interstrand weak interaction or cooperativity can be neglected.
The above assumption can be characterized by a pattern whereby the entire transition in a mixing solution can be divided into several different units, in each of which the corresponding strands behave in the same way as they would in an individual entity. Therefore, DNA duplex formation will include the following potential processes:
Key transition SA + SB ⇔ D 1
Side transition nASA ⇔ SAn complex 2a
nBSB ⇔ SBn complex 2b
where the single strand complex includes all types of the strand states and structures for the single-stranded self-transition; however, their thermodynamic contributions will come primarily from the formation of the intrastrand hairpin.
The extent of duplex association
Due to a remarkable difference in the thermodynamic driving force between the single-stranded self-transition and the double-stranded association transition, it can be assumed that in a mixing solution where the molar amount of a given single strand, SB, is in excess over that of the corresponding complementary strand, SA, the limiting SA associates completely with an equimolar SB, whereas the excessive SB behaves in a self-transition fashion, as described by the following equilibrium:
SA + mSB ⇔ D + (m – 1)SB 3
If we merely consider the two end-states of a transition, the coil state and the structured state, the absorbances of a stock solution at high and low temperature, AHT and ALT, can be assumed to be the sloped upper and lower baselines of absorbance versus temperature curves (29,30), and extinction coefficients of duplex and two single strands, ɛD, ɛA and ɛB, are also linearly dependent on temperature (2,6,26,29,31). Following the development made by Turner and co-workers (2,32), the absorbance versus temperature curves may be corrected by upper and lower baselines, therefore, the upper and lower baseline-corrected absorbances, 
and 
, at high and low temperatures depend only on the initial and the final states and are independent of temperature and transition path. Alternatively, 
and 
can be regarded as the temperature-independent absorbance values in the coil state and the structured state, and may be determined simply by the corresponding absorbances separating the melting curve from upper and lower baselines. Then, hyperchromicity factor, h, defined by equation 4:
4
is, in principle, a state function and independent of temperature as well. According to STM and Beer–Lambert law, the resulting absorbances, as described above in equation 3, in the coil state and the structured state can be related to the concentrations of each absorbing species:
5
6
where 
, 
and 
are the extinction coefficients corrected by a linear temperature-dependence of single strands, SA and SB, and duplex D, and can be approximately calculated by the method described by Fasman (33). It is worth noting that the baseline-corrected extinction coefficient of each strand should also be temperature-independent. m is the molar ratio of two complementary single strands. l is the pathlength of the incident light through cell, [SA]0 is the concentration of SA in the coil state, and hB is hyperchromicity factor of SB.
Dividing equation 6 by equation 5 and simplifying yields:
7
where
8
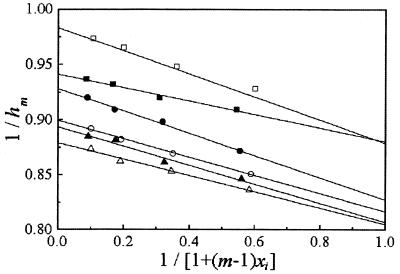
and hm is the hyperchromicity factor of a stock solution in various molar ratios, m, and hD is the hyperchromicity factor of a duplex that is assumed to occur in a strictly two-state transition. Figure 2 shows plots of h–1m versus [1 + (m – 1)xi]–1, which display linear relationships as expected. Consequently, hA, hB and hD are obtained by the slope and intercept of a linear fitting of equation 7, and these results are summarized in Table 1. The data in Table 1 reveal that hD derived from two adding modes are nearly identical, which provides convincing evidence that the interstrand weak interaction or cooperativity can be neglected. Furthermore, the regression lines for two adding modes, except S1S2, do not intersect at the point of equimolar mixing (i.e. [1 + (m – 1)xi]–1 = 1) as shown in Figure 2, suggesting that various molar ratios do not affect the S1S2 transition behavior. However, this case is not applicable to S3S4 and S5S6. In other words, for longer DNA sequences, the duplex association in non-equimolar mixing solution proceeds in a different transition behavior from that in equimolar mixing solution, i.e. the duplex association in equimolar mixing solution may occur in a partial two-state transition.
Figure 2.
Plots of 1/hm versus 1/[1 + (m – 1)xi] (i = A or B) for three duplex association transitions. The experiments were performed in two adding modes: S1 plus various S2 (closed squares), S2 plus various S1 (open squares), S3 plus various S4 (closed circles), S4 plus various S3 (open circles), S5 plus various S6 (closed triangles), S6 plus various S5 (open triangles). It is worth noting that linear fitting does not include the experimental data of the equimolar mixing of two single strands.
Table 1. Hyperchromicity factors for six ssDNAs and the resulting dsDNAs derived from linear fitting of 1/hm versus 1/[1 + (m – 1)xi] in two adding modes.
| Strand | Adding mode | hia | hDb | Average hDc | Yd (%) |
|---|---|---|---|---|---|
| S1S2 | S2 plus various S1 | hS1 = 1.017 | 1.123 | 1.130 | 0.991 |
| S1 plus various S2 | hS2 = 1.062 | 1.136 | |||
| S3S4 | S4 plus various S3 | hS3 = 1.112 | 1.224 | 1.216 | 0.945 |
| S3 plus various S4 | hS4 = 1.077 | 1.208 | |||
| S5S6 | S6 plus various S5 | hS5 = 1.137 | 1.242 | 1.241 | 0.919 |
| S5 plus various S6 | hS6 = 1.119 | 1.239 |
ahi indicates the hyperchromicity factor of ssDNAs and was calculated by the intercept of a linear fitting of 1/hm versus 1/[1 + (m – 1)xi] (i = A or B).
bhD indicates hyperchromicity factor of the resulting dsDNAs and was determined by the slope of a linear fitting in two adding modes.
cAverage hD indicates the average hyperchromicity factor of the two adding modes and relative deviations of S1S2, S3S4 and S5S6 are 1.15, 1.32 and 0.242%, respectively.
dY is the extent of duplex association and can be calculated by equation 10.
To quantify this imperfect duplex association, we define Y as the extent of duplex association, a ratio of the concentration of the single strand associating into the duplex to its initial concentration. For a real transition process of DNA duplex formation in equimolar mixing, the resulting absorbances in the structured state can be attributed to the fractional contributions from the duplex association and the two single-stranded self-transitions according to STM, as described above in equations 1 and 2. One obtains:
9
In this case, the observed hyperchromicity factor of a duplex formation, hobs, can be derived by dividing equation 5 into equation 9. Thus, the extent of duplex association is further obtained as follows:
10
The calculated Y values for three dsDNAs are also listed in Table 1. The data show that S1S2 nearly exhibits a strictly two-state transition while SS4 and S5S6 do not. To interpret that Y decreases with an increase in the number of base pairs of DNA sequences in our experimental range, we consider that the thermodynamic properties of single strands will exert an influence on the transition behavior of a duplex association. In essence, DNA duplex formation proceeds in an imperfect two-state mode. For short DNA sequences, the thermodynamic and transition contributions of the single-stranded self-transition to the over-all transition are very small and can often be ignored due to the small thermodynamic driving force. However, for longer DNA sequences, the thermodynamic driving force of the single-stranded self-transition will increase with the increasing number of base pairs with a greater chance of sequence complementarity, which weakens the ability of duplex association and results in a partial population of non-heteroduplex strands.
Transition enthalpy of DNA duplex formation
Since the duplex association has essentially been characterized in an imperfect two-state fashion, the real transition enthalpy can be determined by coupling multi-state equilibria of the duplex association and the single-stranded self-transition, as described by Longfellow et al. (26) and Allawi and SantaLucia (27). According to stoichiometric equations of a duplex association reaction (i.e. equations 1 and 2), each strand concentration at any temperature can be written as:
11
12
13
and the equilibrium constant of a duplex formation is given by:
14
where α is the molar fraction of the duplex in the double helix state for the double-stranded association. α1 and α2 are the molar fractions of the stacked single strands in the corresponding structured states for the single-stranded self-transitions of SA and SB, respectively. CT is the initial total species concentration. ΔHvH and ΔSvH are the van’t Hoff enthalpy and entropy of a duplex formation. When the thermodynamic contribution of the single-stranded self-transition to the entire transition comes mainly from the formation of an intrastrand hairpin (26,27), nA and nB should be equal to 1. Substituting equations 11–13 into equation 14, simplifying and rearranging the terms yields a developed van’t Hoff equation as follows:
15
where Tm is the melting temperature and can be determined by the maximum of the derivative of absorbance versus temperature curves (14). The advantage of equation 15 is to consider a partial two-state transition for a duplex formation and to introduce the extent of duplex association into the van’t Hoff equation. The van’t Hoff enthalpies and entropies for three dsDNAs are summarized in Table 2 (see Supplementary Material).
Table 2. van’t Hoff thermodynamic parameters for three dsDNAs derived from UV measurementa.
| DNA | Tmb (°C) | Non-two-state transition | Average curve fitting | ||||
|---|---|---|---|---|---|---|---|
| Sequence | –ΔH (kcal/mol) | –ΔS (eu) | –ΔG37c (kcal/mol) | –ΔH (kcal/mol) | –ΔS (eu) | –ΔG37c (kcal/mol) | |
| S1S2 | 45.2 | 64.4 ± 1.6 | 175.3 ± 5.1 | 10.0 ± 0.06 | 62.2 ± 2.1 | 169.6 ± 6.7 | 9.6 ± 0.17 |
| S3S4 | 65.8 | 105.9 ± 2.9 | 285.7 ± 8.8 | 17.3 ± 0.17 | 108.4 ± 1.6 | 292.7 ± 5.1 | 17.6 ± 0.02 |
| S5S6 | 75.8 | 144.8 ± 3.0 | 388.5 ± 9.7 | 24.3 ± 0.03 | 147.9 ± 2.5 | 396.1 ± 7.5 | 25.0 ± 0.12 |
aAll experiments were carried out in a buffer solution containing 1 M NaCl/10 mM Na2HPO4 /1 mM Na2EDTA (pH 7.0).
bMelting temperature were determined at 5 µM total species concentration.
cFree energy of a duplex formation at 37°C.
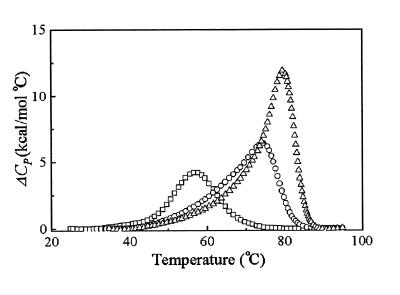
The calorimetric measurement is usually considered to be model-independence (8,10,11,13,14,16,17), and comparison of the thermodynamic parameters derived from optical and calorimetric measurements is typically used to assess the population of the intermediate states and the validity of an all-or-none assumption (10,11,17). In order to confirm the above consideration, DSC measurements were carried out for three dsDNAs in which the concentrations of S1S2, S3S4 and S5S6 were 185, 110 and 110 µM, respectively, as shown in Figure 3. In general, the calorimetric enthalpy should be regarded as a complex enthalpy and can be attributed to the sum of fractional contributions from all transitions (12). Therefore:
Figure 3.
Calorimetric excess heat capacity, ΔCp, versus temperature profiles for the three dsDNAs. Plots for duplex strand transition of S1S2 (squares), S3S4 (circles) and S5S6 (triangles). The thermodynamic parameters derived from these curves are summarized in Table 3.
ΔHT = Y ΔHDSC 16
where ΔHT is the true transition enthalpy used only for a duplex formation in a real transition process and ΔHDSC is the calorimetric enthalpy derived directly from DSC transition profiles, respectively. The transition enthalpies of three dsDNAs with a quantitative consideration of the imperfect duplex association are listed in Table 3. Comparative thermodynamic data in Table 3 show that the enthalpies of a duplex formation derived from UV and DSC are in good agreement when the extent of duplex association is considered.
Table 3. Comparative thermodynamic enthalpies of calorimetric and optical measurements for three dsDNAsa.
| DNA sequence | –ΔHDSC (kcal/mol) | –ΔHTa (kcal/mol) | –ΔHvH (kcal/mol) |
|---|---|---|---|
| S1S2 | 65.1 ± 0.8 | 64.5 ± 0.8 | 64.4 ± 1.6 |
| S3S4 | 111.1 ± 1.3 | 105.0 ± 1.2 | 105.9 ± 2.9 |
| S5S6 | 157.2 ± 4.0 | 144.5 ± 3.7 | 144.8 ± 3.0 |
aAll experiments were carried out in a buffer solution containing 1 M NaCl/10 mM Na2HPO4 /1 mM Na2EDTA (pH 7.0).
bΔHT was calculated by equation 16.
In summary, thermodynamic properties of the single-stranded self-transition may contribute significantly to the transition behavior of a duplex formation, and the thermodynamic parameters derived directly from UV and DSC are essentially different due to an imperfect all-or-none transition. The van’t Hoff analysis is to determine the true enthalpy change of a duplex formation, whereas the calorimetric analysis is to obtain the complex enthalpy change involving all transitions in a stock solution. For short oligonucleotides, a duplex formation often displays a two-state transition due to a small thermodynamic driving force and contribution of the single-stranded self-transition to the entire transition. However, for longer oligonucleotides, the thermodynamic properties of the single-stranded self-transition will affect the transition nature of a duplex formation, resulting in a population of the intermediate states. As a consequence, the duplex association is characterized in a partial two-state transition (10,11,14,17). When the extent of duplex association is considered, the transition enthalpies of a duplex formation derived from the two methods are nearly identical for long oligonucleotides. Moreover, the extent of duplex association in this paper has a remarkable similarity to the cooperative unit illustrated in previous studies (4,11,17). Finally, although our experiments and DNA sequences are limited and the general conclusions still need further experimental verification, this work provides new insights into the thermodynamic characteristics and transition nature of DNA duplex formation and presents a reasonable interpretation of the discrepancy between thermodynamic enthalpies derived from UV and DSC methods.
SUPPLEMENTARY MATERIAL
See Supplementary Material available at NAR Online.
Acknowledgments
ACKNOWLEDGEMENTS
We thank Prof. Fu-Ming Chen, Tennessee State University, for a critical reading of the manuscript and helpful comments. This work was supported in part by Grants-in-Aids from the Ministry of Education, Science, Sports and Culture, Japan, and a Grant from the ‘Research for the Future’ Program of the Japan Society for the Promotion of Science to N.S.
REFERENCES
- 1.Borer P.N., Dengler,B., Tinoco,I.,Jr and Uhlenbeck,O.C. (1973) Stability of ribonucleic acid double-stranded helices. J. Mol. Biol., 80, 759–771. [DOI] [PubMed] [Google Scholar]
- 2.Petersheim M. and Turner,D.H. (1983) Base-stacking and base-pairing contributions to helix stability: thermodynamics of double-helix formation with CCGG, CCGGp, CCGGAp, ACCGGp, CCGGUp and ACCGGUp. Biochemistry, 22, 256–263. [DOI] [PubMed] [Google Scholar]
- 3.Freier S.M., Kierzek,R., Jaeger,J.A., Sugimoto,N., Caruthers,M.H., Neilson,T. and Turner,D.H. (1986) Improved free energy parameters for predictions of RNA duplex stability. Proc. Natl Acad. Sci. USA, 83, 9373–9377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Marky L.A. and Breslauer,K.J. (1987) Calculating thermodynamic data for transitions of any molecularity from equilibrium melting curves. Bioploymers, 26, 1601–1620. [DOI] [PubMed] [Google Scholar]
- 5.Sugimoto N., Nakano,S., Katoh,M., Matsumura,A., Nakamuta,H., Ohmichi,T., Yoneyama,M. and Sasaki,M. (1995) Thermodynamic parameters to predict stability of RNA/DNA hybrid duplexes. Biochemistry, 34, 11211–11216. [DOI] [PubMed] [Google Scholar]
- 6.Xia T., SantaLucia,J.,Jr, Burkard,M.E., Kierzek,R., Schroeder,S.J., Jiao,X., Cox,C. and Turner,D.H. (1998) Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson-Crick base pairs. Biochemistry, 37, 14719–14735. [DOI] [PubMed] [Google Scholar]
- 7.Bommarito S., Peyret,N.P. and SantaLucia,J.,Jr (2000) Thermodynamic parameters for DNA sequences with dangling ends. Nucleic Acids Res., 28, 1929–1934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pilch D.S., Dunham,S.U., Jamieson,E.R., Lippard,S.J. and Breslauer,K.J. (2000) DNA sequence context modulates the impact of a cisplatin 1,2-d(GpG) intrastrand cross-link on the conformational and thermodynamic properties of duplex DNA. J. Mol. Biol., 296, 803–812. [DOI] [PubMed] [Google Scholar]
- 9.Sugimoto N., Nakano,M. and Nakano,S. (2000) Thermodynamics-structure relationship of single mismatches in RNA/DNA duplexes. Biochemistry, 39, 11270–11281. [DOI] [PubMed] [Google Scholar]
- 10.Jelesarov I., Crane-Robinson,C. and Privalov,P.L. (1999) The energetics of HMG box interactions with DNA: thermodynamic description of the target DNA duplexes. J. Mol. Biol., 294, 981–995. [DOI] [PubMed] [Google Scholar]
- 11.Vesnaver G. and Breslauer,K.J. (1991) The contribution of DNA single-stranded order to the thermodynamics of duplex formation. Proc. Natl Acad. Sci. USA, 88, 3569–3573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Naghibi H., Tamura,A. and Sturtevant,J. (1995) Significant discrepancies between van’t Hoff and calorimetric enthalpies. Proc. Natl Acad. Sci. USA, 92, 5597–5599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Riccelli P.V., Vallone,P.M., Kashin,I., Faldasz,B.D., Lane,M.J. and Benight,A.S. (1999) Thermodynamic, spectroscopic and equilibrium binding studies of DNA sequence context effects in six 22-base pair deoxyoligonucleotides. Biochemistry, 38, 11197–11208. [DOI] [PubMed] [Google Scholar]
- 14.Holbrook J.A., Capp,M.W., Saecker,R.M. and Record,M.T.,Jr (1999) Enthalpy and heat capacity changes for formation of an oligomeric DNA duplex: interpretation in terms of coupled processes of formation and association of single-stranded helices. Biochemistry, 38, 8409–8422. [DOI] [PubMed] [Google Scholar]
- 15.Rouzina I. and Bloomfield,V.A. (1999) Heat capacity effects on the melting of DNA. 1. General aspects. Biophys. J., 77, 3242–3251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vallone P.M. and Benight,A.S. (2000) Thermodynamic, spectroscopic and equilibrium binding studies of DNA sequence context effects in four 40 base pair deoxyoligonucleotides. Biochemistry, 39, 7835–7846. [DOI] [PubMed] [Google Scholar]
- 17.Vesnaver G., Chang C.N., Eisenberg,M., Grollman,A.P. and Breslauer,K.J. (1989) Influence of abasic and anucleosidic sites on the stability, conformation and melting behavior of a DNA duplex: correlations of thermodynamic and structural data. Proc. Natl Acad. Sci. USA, 86, 3614–3618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chee M., Yang,R., Hubbel,E., Berno,A., Huang,X.H.C., Stern,D., Winkler,J., Lockhart,D.J., Morris,M.S. and Fodor,S.P.A. (1996) Accessing genetic information with high-density DNA arrays. Science, 274, 610–614. [DOI] [PubMed] [Google Scholar]
- 19.Fodor S.P.A., Rava,R.P., Huang,X.C., Pease,A.C., Holmes,C.P. and Adams,C.L. (1993) Multiplexed biochemical assays with biological chips. Nature, 364, 555–556. [DOI] [PubMed] [Google Scholar]
- 20.Williams J.C., Case-Green,S.C., Mir,K.U. and Southern,E.M. (1994) Studies of oligonucleotide interactions by hybridisation to arrays: the influence of dangling ends on duplex yield. Nucleic Acids Res., 22, 1365–1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jobs M., Gyllensten,U., Brookes,A.J. and Howell,W.M. (1999) Dynamic allele-specific hybridization. Nat. Biotechnol., 17, 87–88. [DOI] [PubMed] [Google Scholar]
- 22.Sugimoto N., Kierzek,R., Freier,S.M. and Turner,D.H. (1986) Energetics of internal G-U mismatches in ribooligonucleotide helixes. Biochemistry, 25, 5755–5759. [DOI] [PubMed] [Google Scholar]
- 23.Wu L.J., Paxton,W.A., Kassam,N., Ruffing,N., Rottman,J.B., Sullivan,N., Choe,H., Sodroski,J., Newman,W., Koup,R.A. and Mackay,C.R. (1997) CCR5 levels and expression pattern correlate with infectability by macrophage-tropic HIV-1, in vitro. J. Exp. Med., 185, 1681–1691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.McDermott D.H., Zimmerman,P.A., Guignard,F., Kleeberger,C.A., Leitman,S.F. and Murphy,P.M. (1998) CCR5 promoter polymorphism and HIV-1 disease progression. Lancet, 352, 866–870. [DOI] [PubMed] [Google Scholar]
- 25.Martin M.P., Dean,M., Smith,M.W., Winkler,C., Gerrard,B., Michael,N.L., Lee,B., Doms,R.W., Margolick,J., Buchbinder,S., Goedert,J.J., O’Brien,T.R., Hilgartner,M.W., Vlahov,D., O’Brien,S.J. and Carrington,M. (1998) Genetic acceleration of AIDS progression by a promoter variant of CCR5. Science, 282, 1907–1911. [DOI] [PubMed] [Google Scholar]
- 26.Longfellow C.E., Kierzek,R. and Turner,D.H. (1990) Thermodynamic and spectroscopic study of bulge loops in oligoribonucleotides. Biochemistry, 29, 278–285. [DOI] [PubMed] [Google Scholar]
- 27.Allawi H.T. and SantaLucia,J.,Jr (1997) Thermodynamics and NMR of internal G·T mismatches in DNA. Biochemistry, 36, 10581–10594. [DOI] [PubMed] [Google Scholar]
- 28.Wetmur J.G. and Davidson,N. (1968) Kinetics of renaturation of DNA. J. Mol. Biol., 31, 349–370. [DOI] [PubMed] [Google Scholar]
- 29.Evertsz E.M., Rippe,K. and Jovin,T.M. (1994) Parallel-stranded duplex DNA containing blocks of trans purine-purine and purine-pyrimidine base pairs. Nucleic Acids Res., 22, 3293–3303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Smirnov I. and Shafer,R.H. (2000) Effect of loop sequence and size on DNA aptamer stability. Biochemistry, 39, 1462–1468. [DOI] [PubMed] [Google Scholar]
- 31.Turner D.H. (2000) Conformational changes. In Bloomfield,V.A., Crothers,D.M. and Tinoco,I.,Jr (eds), Nucleic Acids: Structures, Properties and Functions. University Science Books, Sausalito, CA, pp. 259–334.
- 32.Albergo D.D., Marky,L.A., Breslauer,K.J. and Turner,D.H. (1981) Thermodynamics of (dG-dC)3 double-helix formation in water and deuterium. Biochemistry, 20, 1409–1413. [DOI] [PubMed] [Google Scholar]
- 33.Fasman G.D. (ed.) (1975) Handbook of Biochemistry and Molecular Biology: Nucleic Acids, 3rd Edn. CRC Press, Cleveland, OH, Vol. 1, pp. 597.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.