Continuous-Flow Capillary Assay for Measuring Bacterial Chemotaxis

Abstract

Bacterial chemotaxis may have a significant impact on the structure and function of bacterial communities. Quantification of chemotactic motion is necessary to identify chemoeffectors and to determine the bacterial transport parameters used in predictive models of chemotaxis. When the chemotactic bacteria consume the chemoeffector, the chemoeffector gradient to which the bacteria respond may be significantly perturbed by the consumption. Therefore, consumption of the chemoeffector can confound chemotaxis measurements if it is not accounted for. Current methods of quantifying chemotaxis use bacterial concentrations that are too high to preclude chemoeffector consumption or involve ill-defined conditions that make quantifying chemotaxis difficult. We developed a method of quantifying bacterial chemotaxis at low cell concentrations (∼10⁵ CFU/ml), so metabolism of the chemoeffector is minimized. The method facilitates quantification of bacterial-transport parameters by providing well-defined boundary conditions and can be used with volatile and semivolatile chemoeffectors.

Chemotaxis, the self-directed movement of an organism or cell toward or away from a chemical (chemoeffector) along a concentration gradient, is a well-known bacterial behavior (1, 5, 6, 12). The interest in bacterial chemotaxis is broad. Knowledge is sought of how the bacteria sense chemicals (4, 21-23), how chemotaxis affects pathogenesis and symbiosis (10, 29, 57), the role of chemotaxis in the formation and structure of bacterial communities (70), the influence of chemotaxis on oceanic nutrient cycling (8, 9, 17, 75), and the effect of chemotaxis on pollutant biodegradation (43, 52, 54-56).

The chemoeffectors to which bacteria are attracted (chemoattractants) are often nutrients that the bacteria consume. Many methods for quantifying chemotactic transport use bacterial concentrations that are high enough that significant consumption of the chemoattractant occurs, affecting the chemoattractant gradient that forms. For example, Marx and Aitken (49) reported diminished chemotaxis at bacterial concentrations of ≥10⁶ CFU per ml, which was believed to be a result of significant consumption of the chemoattractant (naphthalene). Therefore, complexity is introduced when interpreting measurements of bacterial migration by chemotaxis because consumption of the chemoeffector must be accounted for. Furthermore, bacterial accumulation by chemotaxis and consumption of a chemoattractant may create a secondary gradient that the bacteria also sense. For example, aerobic biodegradation of a chemoattractant by bacteria that are also aerotactic (responsive to oxygen) could create an oxygen gradient that influences bacterial migration, confounding measurements of movement toward the primary chemoattractant. Methods that are used to quantify chemotaxis, therefore, should minimize metabolism of a biodegradable chemoeffector so that the observed bacterial motion would be in response only to diffusion of the primary chemoeffector.

Methods in which metabolism can be minimized are the traditional capillary assay (2, 3) and modifications thereof (7, 38, 51, 53). Metabolism is minimized because a low cell concentration can be used, mainly due to the sensitive nature of enumerating cell accumulations in the capillaries. However, the experimental conditions in capillary assays make determining bacterial motility parameters difficult.

Here, we describe a modified capillary assay for quantifying bacterial chemotaxis that is amenable to relatively simple mathematical modeling. The method is inexpensive and can be used with volatile or semivolatile chemicals. The bacterial-transport parameters determined with this method can be used in population-scale models to examine the effect of chemotaxis on consumption of nutrients or biodegradation of contaminants.

MATERIALS AND METHODS

Media and chemicals.

Bacterial growth media are described elsewhere (49). Motility buffer (pH 6.8) consisted of 25 mM KH₂PO₄, 25 mM Na₂HPO₄, and 1% Hutner's mineral base (34). Naphthalene (Sigma-Aldrich, St. Louis, MO) and sodium salicylate (Mallinckrodt, Hazelwood, MO) purities were greater than 99%.

Culture conditions.

Suspensions of wild-type, nonmotile, and nonchemotactic (51) Pseudomonas putida G7 were prepared as described previously (45). Briefly, batches of bacterial cultures were grown by lightly scraping a frozen stock (−70°C) with a sterile wooden applicator stick and transferring the scraping to tryptone broth. After 24 h of growth at 25°C and 250 rpm in an incubator shaker, the cells were centrifuged for 1 min and resuspended in mineral salts medium. Aliquots of the resuspended cells were added to 20 ml mineral salts medium containing 5 mM sodium salicylate (an inducer of naphthalene biodegradation and chemotaxis). The bacteria were grown to mid-exponential phase (optical density, 0.2 to 0.4 cm⁻¹ at a wavelength of 590 nm; approximately 10⁸ CFU/ml) at 25°C and 250 rpm in an incubator shaker. The cell suspensions were then centrifuged at 2,800 × g for 3 min and resuspended in motility buffer. Dilutions to the desired cell concentration were done in motility buffer.

Continuous-flow capillary apparatus.

The continuous-flow capillary assay is a modification of the traditional capillary assay (2, 3). Instead of a capillary placed into a stagnant pool of bacteria, a bacterial suspension flows past the open end of a capillary that is perpendicular to the flow path. The flowing suspension creates a constant concentration of chemical attractant and bacterial cells at the mouth of the capillary. The constant-concentration conditions at the mouth of the capillary simplify treatment of the data because only the capillary domain needs to be considered for mathematical modeling. In the absence of a chemoattractant, bacteria swim into the capillaries randomly. If the capillaries are filled with a chemoattractant, the bacteria will swim into the capillary, sense the chemoattractant gradient that forms in the capillary and swim chemotactically inside the capillary. Movement of bacteria into the capillaries is measured by enumerating the cells that accumulate in the capillaries. For random motility of cells or diffusion of a chemoattractant in the absence of bacterial consumption, there are closed-form analytical solutions to the transport equations.

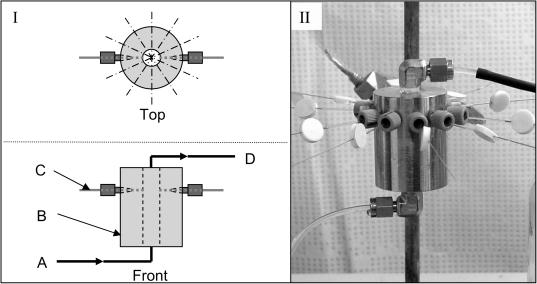
The apparatus for the continuous-flow capillary assay consisted of a cylindrical stainless steel (type 318) block with a flow channel drilled through the center (axially) and 12 holes drilled around the circumference (Fig. 1). The bacterial suspension was passed through the cylinder by a syringe pump, and capillaries were inserted through the holes along the circumference. The mouths of the capillaries protruded into the flow channel 1 mm. The capillaries contained a 40-mm liquid plug of motility buffer or naphthalene-saturated motility buffer for random motility and naphthalene chemotaxis experiments, respectively. At a designated time, the capillaries were removed to quantify the number of bacteria that accumulated by random motility or chemotaxis.

FIG. 1.

Diagram (I) and photograph (II) of the continuous-flow capillary assay apparatus. Bacterial suspension is pumped into the flow channel (A) through the stainless-steel block (B), past the capillaries (C), and through an exit port (D). The stainless-steel block is a cylinder with a diameter of 38 mm and a height of 50 mm. The cylindrical flow channel through the center is 6 mm in diameter, and the capillary ports are located 38 mm from the bottom of the stainless-steel block.

Preparation of capillary assemblies.

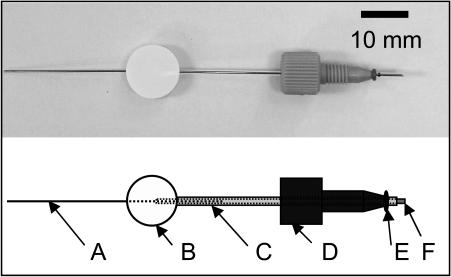
Modified 5-μl PCR pipettes (Drummond Scientific, Broomall, PA) were used as capillaries. The PCR pipettes consisted of a glass capillary with 1-μl graduations and a stainless-steel plunger. The plunger provided an easy way to fill the capillaries reproducibly with buffer or chemoattractant solution and to expel the contents of the capillaries. The outside end of the capillary pierced a Teflon-faced silicone septum (12-mm diameter by 3-mm thickness) to provide a seal, and the plunger penetrated the septum through its diameter (Fig. 2). If the capillaries were not sealed, buffer would travel by capillary action into the space between the plunger and capillary wall and leak out of the capillary. As a result, liquid from the flow channel would be drawn into the capillary, leading to an artificially high bacterial accumulation. To protect the tip of the capillary while inserting the capillary assemblies into the flow channel, a snug-fitting sheath made of a 40-mm length of a 100-μl glass capillary (Drummond Scientific) was placed over the PCR pipette. The sheath was extended over the tip of the PCR pipette while the capillary assemblies were inserted, and once all the assemblies were inserted, the pipette tips were pushed past the tip of the sheath (the position of the plunger in the capillary was not altered). Each capillary and sheath was inserted into a high-performance liquid chromatography (HPLC) fitting (no. 10-32 one-piece finger-tight fitting; Upchurch Scientific, Oak Harbor, WA) to hold the capillary in place while it was inserted into the flow channel. Viton o-rings (size AS568A-001; McMaster-Carr, Atlanta, GA) placed on the sheath were used to create a seal between the HPLC fitting and the outside of the sheath.

FIG. 2.

Photograph and schematic of capillary assembly showing the stainless-steel plunger (A), septum (B), sheath (C), HPLC fitting that holds the capillary and screws into the steel block (D), viton o-ring (E), and open mouth of the capillary that is inserted into the flowing bacterial suspension (F). The outside and inside diameters of the capillary are 1.0 and 0.5 mm, respectively. In the photograph, the sheath is omitted for clarity and the plunger is shown pushed all the way to the mouth of the capillary.

Protocol.

Experiments were conducted in an incubator at 25°C. Prior to use, the assay apparatus was washed, rinsed with reagent water, and autoclaved. Before the capillaries were inserted, the capillary ports were plugged with no. 10-32 HPLC column plugs (Upchurch Scientific), and air was purged from the system by passing 100 ml of bacterial suspension through the flow channel with a syringe connected to the assay apparatus with Teflon tubing. The syringe was then refilled and reconnected to the assay apparatus, and an additional 20 ml of bacterial suspension was passed through the flow channel. After the flow was stopped, the exit tube from the assay apparatus was clamped, and the capillary assemblies were inserted. The exit tube was unclamped, and the syringe pump was then started to pump the bacterial suspension through the assay apparatus at 0.5 ml/min.

At designated time points, replicate capillaries were removed and replaced with plugs. The capillary was removed from the sheath, and the liquid plug was drawn into the capillary by withdrawing the plunger 10 mm. Drawing the liquid plug into the capillaries protected the contents of the capillary while rinsing its exterior. The contents of each capillary were then expelled into a known volume of motility buffer. The interior of the capillary was rinsed by drawing and expelling the buffer at least 10 times with the mouth of the capillary submerged in the buffer. Bacteria were enumerated by plate counting on R2A agar (BD, Franklin Lakes, NJ). Dilutions were planned so there were 50 to 120 colonies on a plate, because plate-counting variability was smallest (coefficient of variation, less than 15%) when colony numbers were within this range. The statistical validity of the data in a given experiment was improved by using at a minimum duplicate plates for counting bacterial accumulations in a given capillary and by analyzing at least three capillaries per time point in a time course assay or at least five capillaries in a single-time-point assay.

The continuous-flow capillary assay was also configured with bacteria initially in the capillaries. Bacterial transport was quantified in this configuration by measuring the number of bacteria in the buffer exiting the flow channel.

Salicylate transport.

The assay was tested by using it to measure diffusive transport of salicylate. The experimental protocol followed that of the experiments with bacteria, except that a 25 mM solution of sodium salicylate in deionized water was used instead of a bacterial suspension. The salicylate solution was initially either in the capillaries or in the flowing water, so diffusion both into and out of the capillaries was measured. Salicylate concentrations were determined spectrophotometrically at a wavelength of 209 nm.

The data from the salicylate diffusion experiments were fitted to a one-dimensional, semi-infinite-domain diffusion model (27). A constant-concentration boundary condition was used at the end of the domain corresponding to the open mouth of a capillary. When the salicylate was initially in the capillaries, the concentration at the mouth was zero, and when the salicylate was in the flowing water, the concentration at the mouth was the concentration in the flowing water. The length of the liquid domain (40 mm) was enough that the semi-infinite-domain assumption was valid over the course of a 2-hour experiment. The equation is a solution to Fick's second law of diffusion:

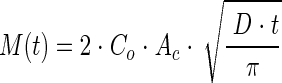(1)

M(t) is the mass of salicylate that diffused at time t, C_o is the initial salicylate concentration in the capillaries or the flowing water, A_c is the cross-sectional area of the capillary, and D is the diffusion coefficient of salicylate. Nonlinear regression (ProStat; Poly Software International, Salt Lake City, UT) was used to calculate the diffusion coefficient from the assay data, and it is reported as the estimate ± 95% confidence interval. The Wilke-Chang equation (59) was used to estimate the diffusion coefficient of salicylate for comparison to the measured value.

Random-motility and chemotactic-sensitivity coefficients.

Bacterial transport in chemical gradients can be modeled with an advection-dispersion-type equation (42). In one dimension:

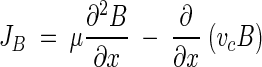(2)

where J_B is the flux of bacteria, μ is the random-motility coefficient, B is the bacterial concentration, and v_c is the chemotactic velocity (generally a function of the attractant concentration and its gradient and bacterial swimming properties). In the absence of a gradient, v_c is zero, allowing the use of equation 1 for modeling bacterial transport in the capillaries by random motility.

An expression for the chemotactic velocity that incorporates the attractant gradient and the dynamics of the chemotactic sensory pathway is:

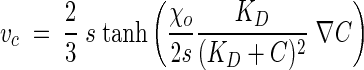(3)

where s is the swimming speed, χ_o is the chemotactic sensitivity coefficient, K_D is a receptor binding constant, and C is the chemoeffector concentration (25). This expression has been used successfully to simulate chemotactic migration of bacteria (46, 50).

The chemotactic sensitivity coefficient was quantified using a finite-difference numerical model (50) with constant-concentration conditions at the mouth of the capillary. For experiments where chemoattractant consumption could be ignored, the chemoattractant concentration and gradient were determined analytically using the following equations (27):

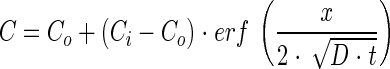(4)

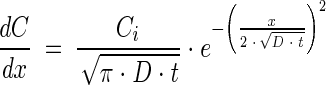(5)

where C_o is the constant concentration at the mouth of the capillary, C_i is the initial uniform chemoattractant concentration in the capillary, and x is distance in the capillary (zero at the mouth of the capillary). Preliminary simulation results using a model that accounted for chemoattractant consumption indicated that it was not necessary to account for consumption of the chemoattractant over the range of conditions we evaluated experimentally. Parameter estimates were obtained using the NLINFIT and NLPARCI functions in MATLAB (Mathworks, Inc., Natick, MA) and are reported as the estimate ± 95% confidence interval.

RESULTS

The continuous-flow capillary assay apparatus was designed to provide constant-concentration conditions at the mouth of a capillary, both to improve experimental reproducibility and to simplify quantitative analysis of the data relative to other capillary assays. Since the fluid velocity in the flow channel was in the laminar range (Reynolds number = 2) and there is a no-slip boundary condition at the open mouth of the capillaries, we expected that fluid flow would not disturb the contents of the capillaries. To verify that transport in the capillaries was by diffusion only, mass transport of a chemical (salicylate) in the capillaries was measured and compared to a model that simulates diffusive mass transport within the capillaries.

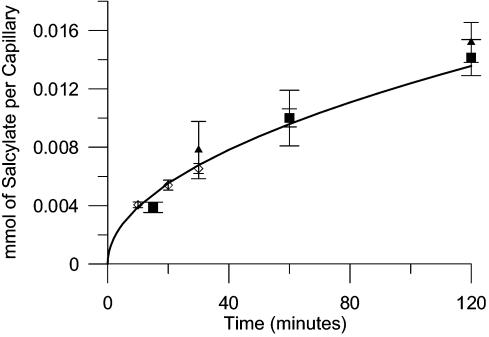
Salicylate was chosen as the test chemical because it is water soluble, nonvolatile, and easy to measure and has a diffusion coefficient similar to that of naphthalene, the chemoattractant of interest in our chemotaxis experiments. The mass of salicylate that entered the capillaries from the flowing water or exited the capillaries into the flowing water was measured in three separate experiments (Fig. 3). The best-fit value for the diffusion coefficient (9.3 × 10⁻⁶ ± 1.1 × 10⁻⁶ cm²/s) compares favorably with the diffusion coefficient estimated from the Wilke-Chang equation (8.8 × 10⁻⁶ cm²/s). In a separate experiment, 97% of the salicylate mass was recovered in the effluent and in the capillaries following a 60-minute run in which the capillaries were initially filled with salicylate. Therefore, we concluded that salicylate transport in the capillaries was by diffusion only.

FIG. 3.

Mass of salicylate that diffused into or out of capillaries versus time. The data comprise measurements of the mass of salicylate exiting the capillaries (▪) and entering the water flowing through the assay apparatus flow channel (⋄), or entering the capillaries (▴) from the flowing water. The solid line is equation 1 plotted using the theoretical value for the diffusion coefficient, 8.8 × 10⁻⁶ cm²/s. The error bars are 1 standard deviation of three independent measurements. The initial salicylate concentration was 25 mM.

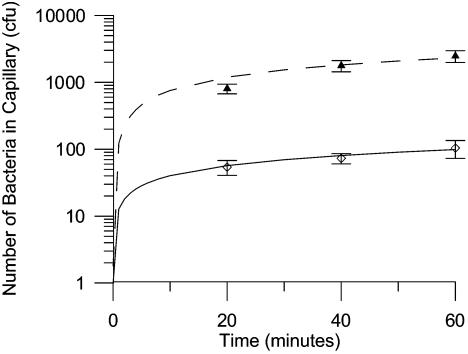
The continuous-flow capillary assay was used to measure movement of P. putida G7 by random motility and chemotaxis. P. putida G7 is a motile gram-negative bacterium that degrades naphthalene and is also chemotactic toward naphthalene (36, 37). Experiments were conducted in which the capillaries were filled with either motility buffer or naphthalene-saturated motility buffer (Fig. 4). The best-fit values for the random-motility coefficient and chemotactic-sensitivity coefficient from these experiments were 3.0 × 10⁻⁶ ± 1.2 × 10⁻⁶ cm²/s and 6.7 × 10⁻⁵ ± 0.7 × 10⁻⁵ cm²/s, respectively. The random-motility coefficient is about 10 times higher than the value for P. putida G7 measured previously (49) in the conventional (static) capillary assay (3.2 × 10⁻⁷ cm²/s) but is more consistent with a theoretical prediction of what the random-motility coefficient should be (47) based on the swimming speed of P. putida G7 (48 μm/s [49]). We believe the difference between the two random-motility coefficients is related more to the motility buffer used than to the differences between the assay methods. The previous measurement (49) was done with the bacteria suspended in a phosphate buffer (25 mM KH₂PO₄, 25 mM K₂HPO₄, 10 mM EDTA), but we found that in that buffer the fraction of motile bacteria was only 30 to 40%, and after 2 hours of incubation, there was a 50% decrease in the number of viable bacteria. The motility buffer we used in the continuous-flow assays, which was based on phosphate buffer but contained other minerals, did not cause a decrease in viable cells, and the fraction of motile cells remained nearly 100% during the assay period.

FIG. 4.

Accumulation of Pseudomonas putida G7 cells in capillaries by chemotaxis to naphthalene (▴) or random motility (⋄). The initial bacterial concentration was 4 × 10⁵ CFU/ml. The solid line is a solution to the bacterial-transport equation using the fitted random-motility coefficient, 3.0 × 10⁻⁶ cm²/s, and the dashed line is a solution to the equation using the fitted random-motility coefficient and the fitted chemotactic-sensitivity coefficient, 6.7 × 10⁻⁵ cm²/s. The error bars are 1 standard deviation of measurements from three capillaries. Naphthalene-saturated motility buffer was used in the capillaries for the chemotaxis experiment.

The chemotactic-sensitivity coefficient measured for P. putida G7 with the continuous-flow assay is close to a previously published value (7.2 × 10⁻⁵ cm²/s [49]) but more than three times higher than another published value (1.8 × 10⁻⁵ cm²/s [58]). In the latter case, long experimental times (>24 h) were used, and the experiments were done in phosphate buffer, which may have negatively affected the viability and motility of the bacteria as discussed above.

The reproducibility of the number of bacteria that accumulated in the capillaries at a given time point was generally good, with coefficients of variation (CV) ranging from 10 to 30%. Variation in the accumulations associated with random motility alone (buffer-filled capillaries) tended to be higher (CV, 15 to 30%) than those associated with chemotaxis (naphthalene-saturated buffer-filled capillaries; CV, 10 to 20%). Variability in plate counting could account for some of the variation, since it was possible for duplicate plates associated with a given capillary to differ by as much as 20%.

We tested the response of nonchemotactic bacteria to a naphthalene gradient using a strain of P. putida G7 [strain G7.C1(pHG100)] that is specifically nonchemotactic to naphthalene (36). The accumulation of cells was the same whether or not a naphthalene gradient was present, indicating that the response we measured with the wild-type strain was caused by chemotaxis to naphthalene.

A lower limit of the random-motility coefficient that could be measured by the assay was obtained by quantifying the diffusive transport of nonmotile P. putida G7 cells. The value obtained for the apparent random-motility coefficient, 4.8 × 10⁻⁸ ± 12.0 × 10⁻⁸ cm²/s, is over an order of magnitude greater than that predicted for a nonmotile bacterium, 2 × 10⁻⁹ cm²/s (13), but nearly 2 orders of magnitude lower than the random-motility coefficient we measured for P. putida G7. The unexpectedly high coefficient could occur if a small volume of the bacterial suspension is carried over on the outside of the capillary and the cells associated with that volume are counted as cells that accumulated in the capillary. The volume of carryover for an apparent random-motility coefficient of 4.8 × 10⁻⁸ cm²/s obtained after a 60-minute run is only 0.03 μl.

The fluid velocity in the flow channel may affect bacterial accumulations in the capillaries, since the shear forces caused by flowing water can align the cells parallel to the flow path (11), even at low Reynolds numbers. However, any effect of alignment is expected to be small, because the fluid velocity at the capillary mouths will be zero due to the no-slip boundary condition there. The effect of fluid flow on bacterial alignment was tested in an experiment in which cell accumulations by random motility were measured when the bacterial suspension was either flowing or static. There was not a statistically significant difference (Student's t test, P = 0.66) between bacterial accumulations in the capillaries under flow and no-flow conditions, consistent with the expectation that a constant concentration of bacteria should exist at the mouth of the capillary even under static conditions (65). Therefore, if alignment of bacteria did occur in our system, it did not affect bacteria near the capillary mouths.

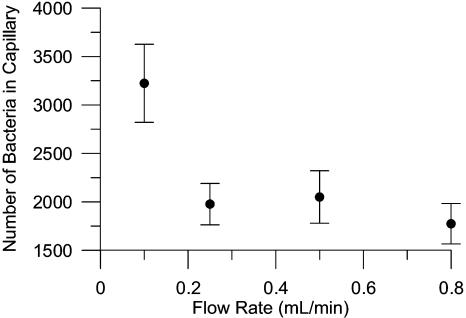
At low fluid velocities, it is possible that bacteria can accumulate at the capillary mouths by migrating upstream in the flowing bacterial suspension in response to the chemoattractant gradient that forms downstream of the capillaries. If bacteria accumulate at the mouths of the capillaries, the con-stant-concentration assumption at the capillary mouths is invalidated. Although the average fluid velocity in the flow channel (0.3 mm/s at 0.5 ml/min) is almost an order of magnitude greater than the swimming speed of PpG7 (0.048 mm/s [49]), the fluid velocities will vary across the diameter of the flow channel and are expected to be lower near the capillary mouths (no-slip boundary condition at the capillary mouths and flow channel walls). The effect of fluid velocity on bacterial accumulations resulting from chemotaxis was evaluated by measuring accumulations in the capillaries over a range of flow rates (0.1 to 0.8 ml/min) (Fig. 5). There was no difference in bacterial accumulations above a flow rate of 0.25 ml/min, indicating that the flow rate used in the other experiments (0.5 ml/min) was adequate to ensure that the flow rate did not influence the results.

FIG. 5.

Effect of flow rate on bacterial accumulation in capillaries initially filled with naphthalene-saturated motility buffer. Bacterial accumulations were measured at 35 min, and the initial bacterial concentration was 10⁶ CFU/ml. The error bars are the standard deviation from five replicate measurements.

The continuous-flow capillary assay can be configured with bacteria initially in the capillaries. However, this configuration greatly reduces the sensitivity of the assay. The sensitivity was examined experimentally, and it was found that the number of bacteria that exited the capillaries by chemotaxis to naphthalene was only twice as much as without chemotaxis after 60 min. This observation was supported by simulation modeling of the expected response for this configuration.

DISCUSSION

Assays that examine the chemotactic motion of bacteria are necessary to understand the response of bacteria to chemical stimuli. The bacterial responses to stimuli can be determined, and parameters for bacterial motion can be quantified. The parameters can in turn be used in simulation models that examine the roles of chemotaxis in various biological and environmental phenomena.

Assays that examine the motion of individual bacteria are useful for elucidating the sensing mechanism of a bacterium (16, 24, 26, 35, 41, 62, 64, 66) and the swimming strategy bacteria use in a gradient (8, 14, 39, 44, 67-69, 71). Assays that measure the motion of a population of bacteria (population-scale assays), on the other hand, are useful for determining bulk bacterial-transport parameters that can be used in population-scale chemotaxis models. Population-scale models have been used to determine the effect of chemotaxis on the biodegradation of chemoattractants (19, 50, 58).

Quantitative population-scale assays for chemotaxis can be divided into two groups, methods that measure bacterial accumulations and those that measure bacterial density profiles. Methods that measure bacterial accumulations involve sampling one or more fixed points in an experimental system. Examples are the capillary assay (2, 3), the fused capillary array assay (15), and a highly sensitive microfluidic assay (48). Methods that determine the bacterial density profile track the motion of a band of bacteria through time. Examples are the stopped-flow diffusion chamber (32, 60), the diffusion gradient chamber (30), the defined-gradient system of Dahlquist et al. (28), the densitometry assay (52), the time lapse capillary assay (20), and other light-scattering methods (18, 40, 63, 74). However, since the methods that track the motion of a band of bacteria use light scattering to measure bacterial density profiles, the bacterial concentrations are typically too high (on the order of 10⁷ cells/ml and greater) to ignore metabolism of the chemoeffector. Automated cell-counting methods like that used in the microfluidic assay (48) can facilitate data analysis, but the bacterial concentration necessary to image a sufficient number of cells is also high.

Other population-scale assays exist, including the swarm plate assay (1) and the agarose-in-plug method (73). However, these assays are primarily qualitative. They are generally used to determine whether chemotaxis occurs at all or to compare chemotactic responses.

The continuous-flow capillary assay is based on the traditional quantitative capillary assay developed by Adler (2, 3) and modifications thereof (7, 38, 51, 53). In the traditional assay, a capillary filled with chemoattractant dissolved in buffer is placed into a pool of bacteria. As chemoattractant diffuses from the capillary, bacteria sense the chemoattractant gradient and swim toward and into the capillary. The capillary is removed at a specific time, and the number of bacteria in the capillary is determined, typically by plate counting. Mathematical analysis of chemical and bacterial transport has enabled the use of capillary assay data for quantifying bacterial-transport parameters (31, 33, 46, 49-51, 58, 61, 65).

An advantage of the traditional and modified capillary assays over other assays is that they can be used with a low bacterial concentration (∼10⁵ cells/ml) because enumeration of bacterial accumulation by plate counting is very sensitive. Low bacterial concentrations are advantageous because metabolism of a chemoeffector or an electron acceptor is low enough that chemoeffector gradients are not affected by metabolism (50). Measurement of a chemotactic response by plate counting also provides an economic advantage to capillary assays. The disadvantages of plate counting, however, are that it is labor-intensive and the results from an experiment are obtained only after colony growth has occurred on the plates. Automated systems, such as that developed by Bainer et al. (7), eliminate the need for plate counting and substantially reduce the labor required for a chemotaxis assay.

For quantifying bacterial-transport parameters, a shortcoming of the traditional capillary assay and most of its variants arises from the necessity of modeling the pool of bacteria into which the capillary is inserted. Poorly defined conditions in the pool can occur as a result of poorly defined convective flow that disturbs chemical and bacterial gradients (72) and/or by sedimentation of bacteria (14, 58). Simplifications of the bacterial and chemoattractant concentrations at the capillary mouth (31) can be made so that only the capillary needs to be modeled, but the simplifications can have a significant impact on estimates of motility parameters, such as chemotactic sensitivity (46, 49). The continuous-flow capillary assay eliminates consideration of the pool of bacteria because constant-concentration conditions at the mouth of the capillary are created by the flowing bacterial suspension.

The chemoeffector gradient is steeper in the continuous-flow assay than in the traditional capillary assay, which potentially increases the sensitivity of the continuous-flow assay. In both assays, there is an initial step change in the chemoattractant concentration at the interface between two fluid domains. In the traditional assay, the chemoattractant diffuses into the domain that is initially chemoattractant free and accumulates there, spreading the gradient across the two domains. In the continuous-flow assay, the diffusing chemoattractant does not accumulate in the domain outside the capillary. We did not evaluate the apparatus, however, to test the lowest attractant concentration at which chemotaxis could be detected. In work to be submitted subsequently (A. M. J. Law and M. D. Aitken, unpublished data), we will illustrate the use of the continuous-flow assay to examine the effects of low μM concentrations of dissolved oxygen on taxis of P. putida G7.

Our experimental results demonstrate that the continuous-flow apparatus accurately measures diffusive transport. The measured diffusion coefficient for salicylate was, within experimental error, equivalent to the theoretical value. The assay is also sensitive, permitting the measurement of very low values of random-motility coefficients, and the method is economical. Its reproducibility is good and is limited largely by the reproducibility of plate counting.