Ultralow-pressure-driven polarization switching in ferroelectric membranes

Abstract

Van der Waals integration of freestanding perovskite-oxide membranes with two-dimensional semiconductors has emerged as a promising strategy for developing high-performance electronics, such as field-effect transistors. In these innovative field-effect transistors, the oxide membranes have primarily functioned as dielectric layers, yet their great potential for structural tunability remains largely untapped. Free of epitaxial constraints by the substrate, these freestanding membranes exhibit remarkable structural tunability, providing a unique material system to achieve huge strain gradients and pronounced flexoelectric effects. Here, by harnessing the excellent structural tunability of PbTiO₃ membranes and modulating the underlying substrate’s elasticity, we demonstrate the tip-pressure-induced polarization switching with an ultralow pressure (down to 0.06 GPa). Moreover, as an application demonstration, we develop a prototype non-volatile ferroelectric field-effect transistor integrated on silicon that can be operated mechanically and electrically. Our findings underscore the great potential of oxide membranes for utilization in advanced non-volatile electronics and highly sensitive pressure sensors.

The authors realize low-pressure-driven polarization switching in PbTiO₃ membranes by leveraging their structural tunability and substrate elasticity, enabling ferroelectric field-effect transistors on silicon, operatable mechanically and electrically.

Introduction

Recently, the rich properties and diverse applications of freestanding oxide membranes have attracted great attention^1–3. By breaking the chemical bond between films and substrates, oxide membranes exhibit great structural tunablility, achieving huge strain and strain gradient far exceeding the range which can be reached in bulk materials and epitaxial films^3–7. Additionally, the freestanding membranes can also be freely transferred onto any desired substrates to construct novel interfaces and devices. For example, high-density polar nanodomains⁸, tunable ferroelectric domain walls⁹, ferroelectric tunnel junctions^10,11, were demonstrated by integrating ferroelectric membranes with silicon wafers. Excitingly, van der Waals integration of perovskite-oxide membranes and two-dimensional semiconductors has become a promising strategy to construct high-performance field-effect transistors (FETs)^12–14, showing a high on/off current ratio, a near-ideal subthreshold swing value, and more. In these FETs, freestanding oxide membranes have primarily used as dielectric layers due to their excellent dielectric or ferroelectric properties^12,13, yet their remarkable structural tunability remains largely untapped. The great structural tunability in membranes should enable effective mechanical switching of the polarization and ferroelectric domains via flexoelectric effect, providing promising routes to design novel mechanically-operated electronic devices.

Flexoelectricity is an electromechanical coupling between polarization and strain gradient, which enables the mechanical control of ferroelectric polarization. The flexoelectric effect finds wide applications in flexoelectronics^15–17, sensing and actuating^18,19, data storage^20,21, and energy harvesting²². Although flexoelectric effect is a weak effect of little practical significance in bulk materials, its role can be more pronounced in thin films^23–25, especially in freestanding oxide membranes and in van der Waals layered materials^26–28 due to their remarkable structural tunability, superior elasticity and flexibility^2,3,5. By bending the membranes, giant strain gradients and flexoelectric response has been reported in BiFeO₃^6,29 and ferroelectric 2D material CuInP₂S₆^26–28,30. However, whether such pronounced flexoelectric effects can be utilized in realizing low-pressure-mechanical polarization switching and applied in designing non-volatile FeFETs remains to be explored.

In this work, benefiting from the excellent structural tunability of freestanding PbTiO₃ membranes and the adjustment of underlying substrate’s elasticity, we achieved ultralow pressure (down to 0.06 GPa) for mechanical polarization switching. Moreover, as an application demonstration, we developed a prototype non-volatile ferroelectric field-effect transistor (FeFET) on silicon that can be operated mechanically and electrically for the first time. By constructing freestanding PbTiO₃/MoS₂ heterostructures, tip-pressure-induced flexoelectric effect can switch the polarization state in PbTiO₃ layer and thus further influence the transport behavior in the MoS₂ channel.

Results

Design for low-pressure-driven polarization switching

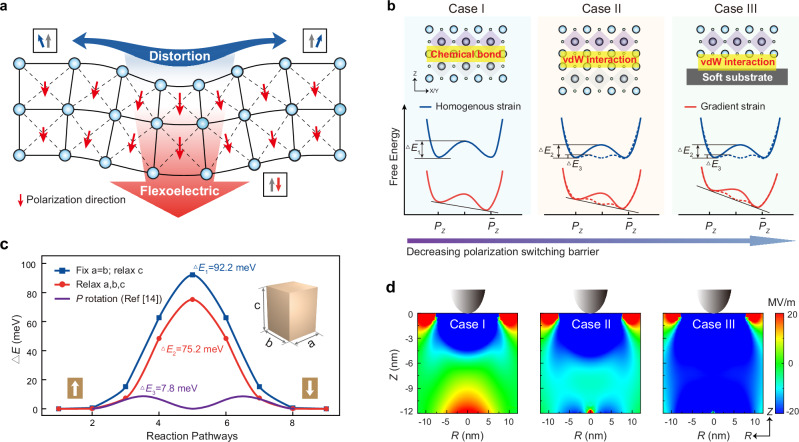
To achieve low-pressure-driven polarization switching, we propose to tune the energy barrier height and potential profile by utilizing the excellent structural tunability in freestanding membranes and optimizing the elasticity of the underlying substrate. Our experimental design is illustrated in Fig. 1b. In case I, PTO membranes are epitaxially grown on STO substrates, where the double well (blue line) in the energy profile becomes asymmetric (red line) when incorporating flexoelectricity into Landau free energy²⁸. Thus, the upward polarization state is destabilized and can be switched to the downward polarization state when the flexoelectric field is strong enough by applying large tip pressure to bend the film and substrate. In case II, freestanding membranes are released from the original substrate and transferred onto a rigid oxide substrate. In this case, the in-plane lattice parameters (a and b) are free to relax since there is no chemical bonding between the membrane and substrate. As shown in the theoretical calculations (Fig. 1c), allowing relaxation of a and b lattice constants can apparently lower the polarization switching energy barrier even fixing the switching path to be 180° polarization switching. Effective Hamiltonian calculations also show that this energy barrier can be further lowered by allowing the polarization in freestanding membranes to tilt and flip to the in-plane direction as an intermediate step³¹, which means the 180° switching consists of two 90° rotations. In fact, similar two-step polarization switching has been commonly observed in many ferroelectrics, including BiFeO₃²⁰, Pb(Zr_0.2Ti_0.8)O₃³², Pb(Zr_0.1Ti_0.9)O₃³³, etc. In case III, we further manipulate the substrate elasticity, by transferring PTO membranes on a softer substrate. Thus, the tip-pressure will cause more obvious deformation in membranes, which leads to a larger strain gradient and a more pronounced flexoelectric effect. Although the energy barrier height is the same as it is in case II under homogenous strain (blue solid and dotted lines), a larger strain gradient would cause a more inequivalent energy double-well (red solid and dotted lines), which maximizes the mechanical switching efficiency. Finite-element simulation (Fig. 1d) shows that vertical flexoelectric field is widely distributed in nearly the entire region beneath the tip in case III, also indicating a more pronounced flexoelectric effect when transferring membranes on soft substrate. During the FEM calculation, for the epitaxial PTO film (case I), the displacement continuity boundary was adopted due to the strong covalent bonding in PTO/LNO interfacial layer. the Young’s modulus and the Poisson’s ratio of LNO were set as E_LNO = 299 GPa³⁴ and ν_LNO = 0.27³⁴, respectively. For freestanding PTO membrane (cases II and III), the contact boundary and Coulomb friction model were adopted to simulate the possible sliding at interface. The underlying substrates in cases II and III are LNO and Au, respectively. The Young’s modulus and the Poisson’s ratio of Au were set as E_Au = 78 GPa³⁵ and ν_Au = 0.42³⁵. Details of theoretical calculations can be found in Methods.

Fig. 1. Design schematics for low-pressure-driven polarization switching in PTO membranes.

a Schematic diagram of tip-induced flexoelectricity in freestanding membranes. b Experimental design of achieving low-pressure mechanical writing. The double-well potential of Landau free energy with homogeneous strain (blue solid and dotted lines) and with strain gradient (red solid and dotted lines) of cases I–III. The solid lines refer to straight 180° switching; the dotted lines refer to 180° switching consisted of two 90° rotations. PTO membranes epitaxially grown on STO substrates (case I) and freestanding PTO membranes transferred onto oxide substrates (case II) and softer underlying substrates (case III). c Energy barrier height for direct 180° polarization switching based on DFT calculations (blue and red lines); Switching barrier consisted of two 90° rotation has been obtained from an effective Hamiltonian model³¹ (purple line). d Finite-element method (FEM)-calculated vertical flexoelectric field distributions in PTO membranes subjected with the same tip force (2 μN).

Experimental demonstration of ultralow-pressure-induced polarization switching

By using reactive molecular beam epitaxy, high-quality PTO films were epitaxially grown on (001) SrTiO₃ (STO) substrates with 8 nm thick LaNiO₃ (LNO) as a bottom electrode denoted as Epi(27 nm)/LNO(8 nm)/STO. PTO membranes (12, 18, 27 nm) were grown on (001) SrTiO₃ (STO) substrates with a Sr₃Al₂O₆ (SAO) sacrificial layer. Subsequently, freestanding PTO membranes were prepared by dissolving SAO and then transferred onto LNO/STO substrates (denoted as FS | | LNO/STO), platinum-coated silicon substrate (denoted as FS | |Pt/Si) and gold-coated silicon substrate (denoted as FS | |Au/Si). Schematic images of these samples are shown in Fig. 2a. The spring constant and inverse optical lever sensitivity of AFM tip were calibrated using the force curve and thermal noise method for obtaining the accurate tip force^28,36–40. More details about the membrane growth, transfer, and characterizations can be found in the Methods and Fig. S2.

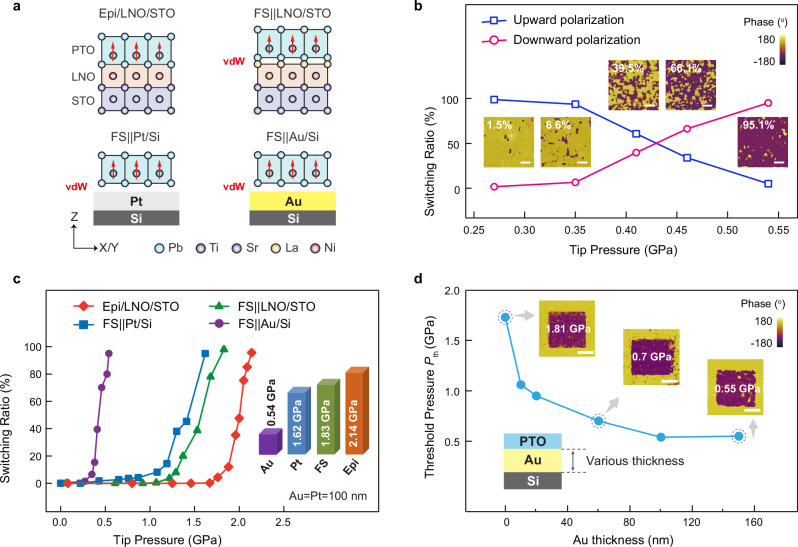
Fig. 2. Mechanical pressure switching in 27 nm PTO membranes.

a Schematic images of samples: PTO film epitaxially grown on LNO/STO substrate (Epi/LNO/STO), freestanding PTO membrane transferred on LNO/STO substrate (FS||LNO/STO), platinum-coated silicon substrate (FS||Pt/Si) and gold-coated silicon substrate (FS||Au/Si). b The mechanical switching of ferroelectric polarization. The vertical PFM phase images with the increase of tip pressure in FS||Au/Si sample. Scale bar, 400 nm. c Ratio of switching area as a function of tip pressure. The inset shows threshold tip pressure P_th for different samples, which is defined as the load required to switch 90% of polarization volume. The thickness of coating layer (Pt or Au) is 100 nm. d P_th as a function of gold thickness (d_Au) in FS||Au/Si samples, d_Au = 0, 10, 20, 60, 100, 150 nm. The inset shows vertical PFM phase images: the purple region is loaded by the AFM tip with various pressures. Scale bar, 1 μm.

Piezoresponse force microscopy (PFM) measurements demonstrate that both the epitaxial and freestanding PTO membranes exhibit upward spontaneous polarization. The vertical-PFM (VPFM) phase images of Epi/LNO/STO and FS | |Au/Si are shown in Figs. S3d, h, and the polarization state of the region polarized with −10 V sample bias is similar to that of the as-grown region, implying that the latter has an upward self-polarization⁴¹. During mechanical writing process, the downward polarization grows gradually at the expense of the upward one with the increasing flexoelectric field with larger mechanical load pressure (Figs. 2b and S4). Here, the scanning mode is used in our experiments to induce polarization switching by AFM tip. The percentage of the switching area as a function of the tip pressure is shown in Fig. 2c. The threshold tip pressure P_th becomes lower in FS||LNO/STO sample (1.83 GPa) than that in Epi/LNO/STO sample (2.14 GPa), which demonstrates that the “freestanding” state indeed lowers the switching barrier since it enables greater freedom in lattice deformation. As illustrated in Fig. 1, in freestanding membranes, the relaxation of in-plane lattice parameters (a and b) can lower the switching barrier and this energy barrier can be further decreased when polarization is tilted and flipped to in-plane direction as an intermediate step. The two-step switching is confirmed by LPFM amplitude measurements as shown in Fig. S1. The LPFM amplitude of the data taken under the intermediate pressure shows the maximum value, indicating the polarization is lying along the in-plane directions. In contrast, the initial (P_up) and final (P_down) states exhibit much weaker LPFM amplitudes, which is consistent with the two-step model.

Next, we investigate the effect of substrate elasticity on tip-induced polarization switching. For freestanding membranes transferred to different target substrates, P_th is significantly different with the lowest value (0.54 GPa) found in FS||Au/Si sample. Substrate elasticity is a contributing factor to this phenomenon, as the Young’s modulus of LNO, platinum, and gold are 299³⁴, 168⁴², and 78 GPa³⁵, respectively. This demonstrates that mechanical polarization switching is more efficient when transferring membranes onto a substrate with the lowest Young’s modulus, which means that modulating the underlying substrate’s elasticity can enhance the flexoelectric field significantly. To exclude the potential contribution of metal work function^43–45, we performed contrast experiments by inserting monolayer MoS₂ into the oxide/metal interfaces. As shown in Fig. S5, P_th in FS | |Au(Pt)/Si and FS | |MoS₂/Au(Pt)/Si are the same, thus the existence of MoS₂ barely influences mechanical polarization switching behavior. In addition, the gold thickness dependence of the threshold tip pressure in FS | |Au/Si samples is obviously shown in Fig. 2d. P_th decreases with increasing gold thickness and finally reaches its minimum for d_Au = 100 nm. This is because the overall substrate elasticity decreases with the increasing thickness of gold coating layer (the Young’s modulus of silicon is 160 GPa⁴⁶, which is larger than gold) and the Young’s modulus for Au film decreased with increasing film thickness⁴⁷. This phenomenon further proves that mechanical writing pressure is affected by the substrate elastic properties other than metal work function. Besides, we also investigated the effect of probe size on mechanical writing behavior (Fig. S6). Fig. S6a, b show that the P_th is 2.96 GPa when AFM tip radius is 10 nm, which is much higher than that written by an AFM tip with 25 nm radius (0.54 GPa). This is mainly due to the highly localized flexoelectric field when the tip radius is 10 nm, which may fail to switch the polarization completely along the thickness direction of the film, as constrained by the long-range Coulomb interactions between electric dipoles⁴⁸. Our FEM simulations (Figs. S6c, d) also prove that vertical flexoelectric field is confined within a small spatial region along the thickness direction (R_tip = 10 nm), however, it is widely distributed into nearly the entire region when the tip radius is 25 nm.

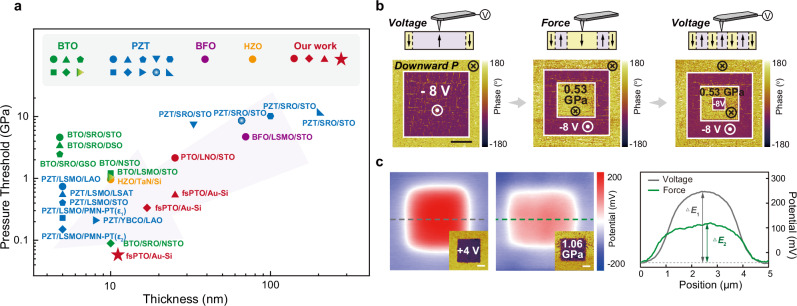
We compare the P_th in our samples with other ferroelectric perovskite oxide membranes from previous works (Figs. 3a and S7), showing that the required tip pressure is getting lower as the membrane thickness decreases. Notably, an ultralow switching pressure down to 0.06 GPa is achieved in 12 nm freestanding PTO membranes transferred on gold (100 nm)-coated silicon, which is the lowest value ever reported^{36,38,49–54}, even lower than those with thinner thickness. From the view of device applications, high-quality ultrathin membranes are technically demanding in fabrication and integration³², thus it will be more attractive to achieve mechanical domain switching in relatively thicker membranes. However, for epitaxial films constrained by hard substrates, it is challenging to mechanically switch the polarization in thicker films due to the contribution of tip-induced flexoelectricity decreases substantially when the film thickness is above ~25 nm^32,33,38,55. Here, we successfully achieve low switching pressure (0.54 GPa) in 27 nm freestanding PTO membranes transferred on gold (100 nm)-coated silicon (FS(27 nm)||Au(100 nm)/Si), showing three times smaller than that in epitaxial membrane with the same thickness.

Fig. 3. Ultralow switching pressure and surface potential of polarization poled by electricity and loading force.

a Summary of threshold pressure and thickness for mechanically induced polarization switching in several ferroelectric membranes reported to date^{36,38,49–54}. b Vertical PFM phase images of FS(27 nm)||Au/Si after electrical writing (left), mechanical erasing (middle) and electrical writing again (right). Scale bar, 2 μm. c SKPFM images of FS(27 nm)||Au/Si after electrical (top left) and mechanical (top right) switching. The inset shows corresponding PFM phase images. Section profiles of the SKPFM images along the gray line (voltage) and green line (force), respectively. Scale bar, 1 μm.

Reversible polarization switching can be achieved by mechanical writing and electrical erasing in FS(27 nm)||Au(100 nm)/Si, as shown in Fig. 3b. The initial downward polarization state (the yellow region) can be switched to the upward state (the violet region) by applying the negative voltage of −8 V (Fig. 3b, left). Next, this upward polarization poled by electric field can be mechanically written to the downward state (the yellow region) (Fig. 3b, middle). Then, to test the repeatability, a negative voltage (−8 V) reverses the polarization to upward again (the violet region)(Fig. 3b right). Moreover, the mechanical polarization switching region is stable and it barely evolves over time (Fig. S8). Scanning kelvin probe force microscopy (SKPFM) is performed to investigate the surface potential of polarization poled by electricity and loading force (Fig. 3c). Section profiles of the SKPFM images demonstrate that the surface potential of electrically poled region (ΔE₁) is higher than that by tip pressure (ΔE₂), indicating charge injection is inevitable during the electrical switching process^36,53.

Flexoelectricity-tuned ferroelectric field-effect transistors

Next, we explore transferrable PTO membranes as a mechanically-tuned ferroelectric gate dielectric for two-dimensional (2D) field-effect transistors, as a preliminary attempt. In ferroelectric field-effect transistors (FeFETs), the ferroelectric polarization state can be tuned by tip pressure via flexoelectricity and detected by the conductance of the channel material. Meanwhile, 2D materials such as MoS₂ have been widely used as channel materials due to their atomic thickness, absence of dangling bonds, and potentially high mobility^56,57. Thus, integrating PTO with MoS₂ offers a promising route for realizing low-power, high-speed operation and reconfigurable functionalities devices.

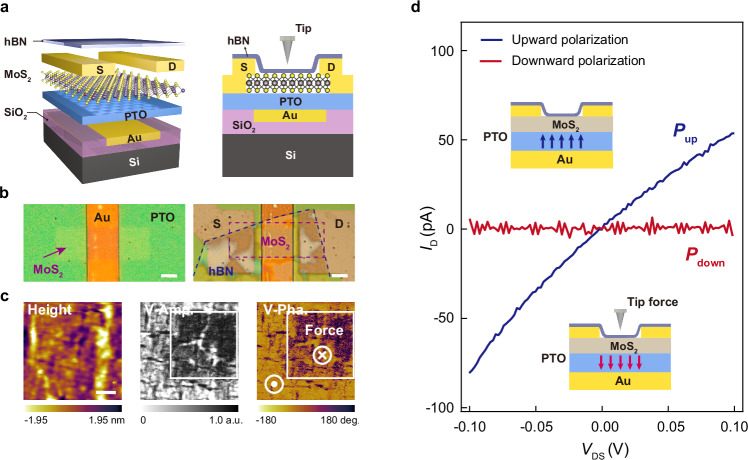
To fabricate MoS₂ transistors with PTO bottom-gate dielectrics, we sequentially transferred PTO, MoS₂, and hBN on Au/SiO₂/Si substrates (Figs. 4a, b and S9). PTO membrane with a thickness of 27 nm was transferred onto an Au/SiO₂/Si substrate. A monolayer MoS₂ thin film grown by chemical vapor deposition (CVD) was then transferred on the top of the freestanding PTO membrane. The shape of the MoS₂ channel was then defined by electron beam lithography (EBL) and subsequent reactive ion etching (RIE). Next, source and drain electrodes (Ti/Au) were deposited at the end of MoS₂ channels. Finally, devices were encapsulated by hBN to avoid sample degradation and more importantly, it can protect MoS₂ from damage during mechanically writing. In our experiments, we can effectively avoid electron doping during the fabricating process of MoS₂ transistors. The method of releasing monolayer MoS₂ from a sapphire is shown in Fig. S10.

Fig. 4. Flexoelectricity-tuned MoS₂ transistors with PTO bottom-gate dielectrics.

a Schematic of a bottom-gate MoS₂ FET. The charge state of MoS₂ channel is controlled by mechanical switching polarization of underlying PTO membranes across top encapsulating hBN and MoS₂ layer. b Optical images of the device. The boundaries of MoS₂ and hBN are outlined by dashed lines. Scale bar, 5 μm. c Topography, vertical-PFM amplitude and phase images after mechanical polarization switching in hBN/MoS₂/PTO. Scale bar, 600 nm. d Output characteristics of the device obtained when the PTO membrane at P_up or P_down states, respectively (V_GS = 0 V).

Schematic of a bottom-gate MoS₂ FET and optical images of the device can be seen in Fig. 4a, b, respectively. PFM results (Fig. 4c) indicate that the PTO polarization state can be mechanically switched by AFM tip even across hBN and MoS₂ layers. Vertical PFM signal of PTO region covered by MoS₂ is obviously weaker than that without MoS₂ capping layer (Fig. S11), due to the screening effect of semiconductor MoS₂⁵⁸. In addition, a relatively thick hBN layer (13 nm) on the top of MoS₂ also weakens the flexoelectric effect. These might be the reasons for incomplete polarization reversal. In flexoelectricity-tuned MoS₂ transistors, the n-type MoS₂ channel’s charge state is controlled by an underlying PTO membrane. Tip-induced flexoelectricity can switch the polarization state of the underlying PTO membrane and then a scanning of the drain current (I_D) can read the state of the polarization since different states are associated with distinct transport behaviors. Specifically, the initial polarization state of PTO region under the channel area is uniformly points upward, which accumulates electrons into MoS₂ and the I_D is in a high current state (‘on’ state). Mechanically switching the polarization of PTO to P_down state depletes electrons from MoS₂, leading to a low current state of I_D (‘off’ state). Fig. 4d shows the room temperature drain current (I_D) vs voltage (V_DS) relations of the device, which are obtained when the PTO membrane at initial P_up state and after mechanical writing to P_down states at zero back-gate voltage (V_GS = 0 V), respectively. At V_DS = 0.1 V, I_D is suppressed, changing from 53 pA in the P_up state to 3.5 pA in the P_down state, indicating that mechanically-tuned on/off state is achieved effectively in our prototype FeFET device.

Discussion

While ultralow pressure mechanical polarization switching has been realized and flexoelectricity-tuned FeFET has been demonstrated, there are still some challenges to be solved in the near future. At present, for the prototype flexoelectricity-tuned FeFETs, a relatively high mechanical pressure (1.8 GPa) is needed. This is because an encapsulating hBN with a thickness of up to 13 nm is required to protect the underlying MoS₂ due to the poor mechanical durability of the monolayer MoS₂⁵⁹. Replacing MoS₂ with other suitable 2D channel materials that have better mechanical properties should lower the required pressure and will be explored in the future. Moreover, reversible polarization switching still relies on a combination of a mechanical and an electrical switching process so far. Reversible mechanical switching⁶⁰ has been demonstrated in epitaxial membranes by manipulating the competition between the flexoelectric field and effective dipolar field delicately⁶¹. Following the same mechanism, using a bilayer membrane as the ferroelectric layer, reversible mechanical polarization switching should be applied in membrane-based FeFETs.

In summary, we report an ultralow-pressure-driven polarization switching in freestanding PTO membranes. Without epitaxial constraints, the greater freedom in lattice deformation lowers the energy barrier for polarization switching. Besides, tip-pressure can be further reduced by tuning the substrate elasticity. Finally, a prototype non-volatile flexoelectricity-tuned FeFET has been fabricated by integrating PTO with MoS₂ and the ‘on’ and ‘off’ states can be controlled by mechanical switching polarization of the freestanding PTO membrane. Mechanical switching with ultralow pressure can effectively avoid sample damage, and benefit low-energy-consumption and high-sensitivity devices. Our work demonstrates great potential in combining ferroelectric memebranes with 2D materials for novel electronic applications, and paves the way for stress-modulated devices with low energy-consumption or high sensitivity.

Methods

Density functional theory (DFT) calculations

The nudged elastic band (NEB) method^62,63 is used to estimate the ferroelectric switching energy barrier, which is implemented in the Vienna ab initio simulation package code^64,65. The projected augmented wave method^66,67 and the Perdew-Burke-Ernzerhof revised for solids exchange correlation⁶⁸ are used in the calculations. The plane-wave cutoff energy is 520 eV and the k-mesh is 9 × 9 × 8. The geometry structure is relaxed until the force on each atom is less than 0.01 eV Å⁻¹, and the energy convergence criterion is 10⁻⁷ eV. As for PTO epitaxially grown on STO substrate, PTO in-plane lattice parameters are fixed (a = b = 3.877 Å) and out-of-plane lattice parameter (c) is free to relax. In freestanding membranes, the lattice constants of a, b, and c are all allowed to relax.

The flexoelectric calculations

The strain and strain gradient distributions in PTO films were calculated using finite element method (FEM). The model of an AFM tip in contact with a 12 nm-thick PTO film on 100 nm-thick substrates was built for FEM calculations. The radius of AFM tip was set as 25 nm. A vertical force of 2 μN was applied on the top surface of tip. Different mechanical boundary conditions at interface were adopted in the epitaxial and freestanding films. For the epitaxial films, the displacement continuity boundary was adopted due to the strong covalent bonding in PTO/LNO interfacial layer. For the freestanding films on different metal-coated substrates, the contact boundary and Coulomb friction model were adopted to simulate the possible sliding at interface. The Young’s modulus and Poisson’s ratio of PTO, LNO, Au were set as E_PTO = 142 GPa⁶⁹, E_LNO = 299 GPa³⁴, E_Au = 78 GPa³⁵, ν_PTO = 0.29⁶⁹, ν_LNO = 0.27³⁴, ν_Au = 0.42³⁵, respectively. The vertical flexoelectric field can be calculated as

$$E_{flexo}=f_{3333}{\epsilon }_{zz,z}+f_{3113}\left({\epsilon }_{rr,z}+{\epsilon }_{\theta \theta ,z}\right)+f_{3131}{\epsilon }_{rz,r},$$ 1

where the transverse, longitudinal and shear flexoelectric coupling coefficients were set as f₃₁₁₃ = 5 V, f₃₃₃₃ = 2 V, f₃₁₃₁ = 2 V, respectively⁷⁰. The flexoelectric field was then incorporated into the Landau free energy to obtain the double-potential well curves.

Deposition of epitaxial thin films

The water-soluble SAO layer was grown first on (001) STO single-crystalline substrate followed by the growth of a thin film PTO by reactive MBE system. The SAO films were grown with an oxidant (10% O₃ and 90% O₂) background partial pressure of oxygen p_O2 of 1 × 10⁻⁶ Torr and at a substrate temperature T_substrate = 950°C. The SAO and PTO films were grown layer by layer, for each of which the thickness was monitored by reflection high-energy electron diffraction (RHEED) oscillations. The PTO films were grown with an oxidant (distilled O₃) background pressure of 2×10⁻⁵ Torr and at T_substrate = 625 °C. Due to the volatility of lead, PTO films were grown in adsorption-controlled mode with a fixed Pb:Ti flux ratio of 13:1 and the thickness was controlled by deposition time of titanium. The perovskite LaNiO₃ (LNO) film were grown first on (001) STO single-crystalline substrate followed by the growth of PTO film. The LNO films were grown on the TiO₂-terminated SrTiO₃ (001) substrates by reactive MBE using a DCA R450 MBE system, with the substrate temperature of 600 °C and an oxidant background pressure of 1×10⁻⁵ Torr using the distilled ozone.

Release and transfer PTO films

Freestanding PTO films were directly transferred to desired substrate without any mechanical support from polydimethylsiloxane (PDMS) or other tapes during the whole process, which avoids chemical residue on the film surface.

Structural characterization

The crystal structure was examined by a high-resolution single-crystal X-ray diffractometer using a Bruker D8 Discover instrument. The incident X-ray was from Cu-Kα emission and had a wavelength of 1.5418 Å.

Piezoresponse force microscopy measurements

The local ferroelectric properties were measured on freestanding films on a conducting Si wafer using an Asylum Research MFP-3D Origin+ SPM scanning probe microscope. Olympus AC240TM Pt/Ti-coated tip (2 N m⁻¹ in force constant) were used in the PFM measurements. Hysteresis loops were collected in the dual AC resonance tracking (DART) mode. PFM images were taken in the DART mode with driving voltage (1 V a.c.) applied at the tip. During the domain writing, the voltage was also applied at the tip. The corresponding pressure can be estimated with a tip radius of 25 nm (Olympus AC240TM) under the assumption that the tip-sample contact is represented by a disc with radius equivalent to the tip radius^36,51,60,71.

CVD growth and transfer of monolayer MoS₂

We grew single-crystal monolayer n-type MoS₂ on c/a sapphire (0001) substrates, with α_a ranging from 0.2° to 1.0° under 1000 °C annealing for 4 h. To transfer the CVD MoS₂ film off the sapphire, PMMA was spin coated at a speed of 600 r.p.m. for 10 s and 1000 r.p.m. for 45 s and then cured at 100 °C for 2 min, followed by lamination of PDMS. Next, the sample was immersed in deionized water and the whole stack was spontaneously delaminated from the sapphire and transferred onto a target substrate. Finally, the PDMS/PMMA can be removed by soaking in acetone.

Device fabrication

On a silicon substrate with 300 nm SiO₂, a back-gate was defined by electron-beam lithography (EBL), and 3 nm Ti/60 nm Au was deposited by an electron-beam evaporator. Freestanding PTO film with 27 nm is then transferred on it. Next, assisted by PDMS/PMMA, the MoS₂ film was transferred to the freestanding PTO film. Then, the unnecessary MoS₂ is etched by using SF₆ and O₂ plasma in a reactive ion etcher. The last step of EBL defined the S/D pattern, and 10 nm Ti/35 nm Pd/10 nm Ti were deposited by the electron-beam evaporator. Finally, an hBN flake with 13 nm picked up and put down onto the top of the device.

Electrical measurements

Electrical characterization of the FETs was performed using a Keithley 4200 semiconductor parameter analyzer and a Keithley 2450 source meter in a closed-cycle probe station with base pressure ~ 10⁻⁶ Torr.

Author contributions

Y.F.N. conceived the idea and directed the project. X.R.Y. and L.H. synthesized the samples and characterized the crystalline structure with the help of Y.Y.L. under the supervision of Y.F.N. and Z.B.G.; X.R.Y. and L.H. performed the PFM measurements and data analysis under the supervision of Y.F.N. and D.W.; S.Q.X. performed finite-element simulation with the help of Y.Z.L. under the supervision of J.W.H.; Y.C.L. performed DFT calculations under the supervision of J.Z.; X.R.Y. and L.H. fabricate devices with the help of B.H., S.J.Y., H.K.N., Y.G. T.T.L., C.Y.G. and W.S.L. under the supervision of Y.F.N., X.R.W., and Y.S.; H.K.N. and Y.G. performed the electrical measurements of FeFETs under the supervision of X.R.W. and Y.S.; X.R.Y. and L.H. wrote the manuscript. All authors discussed the data and contributed to the manuscript.

Peer review

Peer review information

Nature Communications thanks Chang Liu and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data supporting the findings of this study have been included in the main text and Supplementary Information. All other information can be obtained from the corresponding author upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53436-6.