Study of direct and indirect risk assessment of landslide impacts on ultrahigh-voltage electricity transmission lines

Abstract

Ultrahigh-voltage electricity systems are a vital part of energy networks, often across wide regions passing through mountainous terrains. The instability of slopes forming tower foundations along transmission lines poses a large risk to the entire energy network. Moreover, the tower foundations along extra-high-voltage electricity transmission lines are a very special type of element that are also highly vulnerable to landslides. In this study, an integrative risk assessment framework, including a hazard assessment, vulnerability analysis for the specified element at risk, and consequence estimation, is proposed to quantify the direct and indirect risks of landslides to power transmission lines. The Yanzi landslide, where a tower of the major ultrahigh-voltage transmission line from Sichuan (western China) to Shanghai (eastern China) has just been constructed, is taken as a case study. The correlation between landslide displacement and tower structure tilting is studied. In terms of the precipitation return period, factors of safety, failure probability, and deformation are simulated. A physical vulnerability curve is fitted by assuming a Weibull relationship between the horizontal deformation (hazard intensity) of the landslide and the tower inclination ratio. The total risk is calculated as the sum of the direct and indirect losses, among which the potential indirect risk due to tower damage is much greater than the direct risk. This work demonstrates the importance of landslide treatment strategies along electricity transmission lines by considering the potential indirect risks. The risk assessment model of landslides affecting ultrahigh-voltage electricity transmission lines proposed in this study could be useful for other types of indirect landslide risk evaluations.

Introduction

Ultrahigh-voltage transmission lines are essential in large-area power supplies for transporting and distributing electricity over long distances with minimal power loss¹. Currently, ultrahigh-voltage networks are being built across China for energy transmission and distribution. Since customers are spatially scattered, especially in mountainous areas, the transmission towers utilized for power system connections are highly vulnerable to landslides. The deformation or catastrophic failure of hillslopes may cause settlement, displacement, tilting, or even collapse of transmission towers^2–4, resulting in disruption of the power network. For example, a rainfall-induced landslide occurred in Chongqing, China, on July 21, 2007, damaging a steel-structure electrical tower, which triggered a considerable indirect risk. The destruction of the tower foundation resulted in power cuts affecting more than four hundred thousand people because 60% of the power lines connected to that point. The acceleration of climate change and increased occurrence of rainfall extremes may cause more landslide hazards and impact the operation of transmission lines^5,6. It is therefore essential to establish a risk assessment process for landslides along power transmission lines while considering their direct and indirect impacts on energy networks.

In the 1970s, the term “risk” was initially introduced in the context of landslide disasters^7,8. Since then, experts and scholars have continuously refined this concept, proposing detailed expressions of landslide risk based on their respective understanding. Varnes (1984) defined risk as the expected number of lives lost, persons injured, damage to property, and disruption of economic activity due to a particular phenomenon causing damage for a given area and reference period⁹. Fell (1994) clarified the conceptual importance of risk and hazard in landslide risk assessments, examined methods for quantifying risk, and supported the use of qualitative approaches in certain contexts¹⁰. It is emphasized that acceptable risks should be considered alongside other socially acceptable risks. The purpose of landslide hazard analysis is to predict the locations where landslides are likely to occur, the timing of such occurrences, and the potential magnitudes of the events^11–16. Most spatial analysis models for hazards lack reliable validation of the probability of future landslide occurrences, making it challenging to conduct probability-based risk analyses ^17,18. Dai et al. (2002) provided a comprehensive framework for landslide risk assessments and management; reviewed the current state of research on landslide occurrence probability, sliding processes, and vulnerability assessment; offered effective strategies to reduce the economic and social impacts of landslides; and addressed the challenges and issues in landslide risk assessment and management ¹⁹. The Joint Technical Committee on Information Technology (JTC-1) of the International Organization for Standardization (ISO) has appointed a scientific committee tasked with developing internationally accepted guidelines specifically for the susceptibility, hazard, and risk zoning of landslides and land use ¹². This guidance advocates the use of quantitative risk management principles, which are crucial for comparing landslide risks in different regions and establishing acceptable standards for loss of life. Building upon these guidelines, Van Westen et al. (2008) conducted a detailed analysis and supplementation of the spatial data types required for each step, providing a comprehensive overview of research progress in collecting spatial information on environmental factors, including digital elevation models, geology and soil, topography, land use, and risk elements ²⁰. Corominas et al. (2008, 2014) further analysed the time and magnitude probability aspects of landslide risk analyses, achieving a more comprehensive quantification of risk ^21,22. The existing studies on landslide risk analyses include comprehensive risk assessments for specific geographic regions ^23–26, assessments focused on individual buildings or infrastructure ^27–30 and integrated assessments that account for the cascading effects of secondary hazards triggered by landslides ^31–33. These studies provide diverse perspectives and methodologies, contributing to a more thorough understanding and management of landslide risk across various spatial scales and dimensions.

Researchers suggest that any landslide risk analysis should consider both direct and indirect risks^34,35. Secondary risks are those risks that arise as a direct result of implementing a risk response³⁶. Based on theoretical research and long-term practical experience in the Three Gorges Reservoir area, Yin et al. (2016) proposed incorporating secondary risk or indirect risk into classic risk calculation formulas, illustrated examples highlighting the risk characteristics of different types of landslides, and emphasized key aspects of risk control³⁷. Li et al. (2020), using a risk calculation formula that considered secondary disasters, quantitatively calculated the risk of tsunamis after the Liangshuijing landslide for the case of rapid landslide movement into the water, highlighting the importance of secondary risk analyses³⁸. The indirect risk caused by landslides also plays a critical role in assessments of energy transmission systems. In recent years, risk assessments of geohazards have been integrated into the disaster management of power grid systems³⁹. The influence of ground motion on power grid performance caused by earthquake damage has been studied^40,41. The risk of transmission lines in power grid systems has been evaluated using various methods, including the contribution weight model, analytic hierarchy process (AHP), backpropagation neural network (BPNN), and support vector machines (SVMs) model^42–44.

The tower foundations along ultrahigh-voltage electricity transmission lines represent a very special type of element at risk, and they are highly vulnerable to landslides. Owing to the height and structure of transmission towers, even small horizontal displacements can result in significant tilting⁴⁵. The high centre of gravity makes transmission towers extremely sensitive to base movements^7,46, with small horizontal shifts at the foundation level causing amplified displacement effects at the top, leading to noticeable tilting⁴⁷. The Power Transmission Project from the West to the East two decades ago in China built hundreds of thousands of high-grade transmission towers in mountainous regions. The complex geological conditions and steep topography have caused frequent landslides in the western region, which may pose significant threats to tower safety. The author’s team directed a collaborative research project with other institutes to study landslide risk assessments and early warnings along ultrahigh-voltage electricity transmission lines two thousand kilometres in length from Chengdu to Shanghai across 8 provinces. The authors studied the risk assessment framework by considering the direct and indirect risks from the damage to transmission towers caused by landslides and subsequent calculations to assess the total economic losses associated with engineering operations.

Methodologies

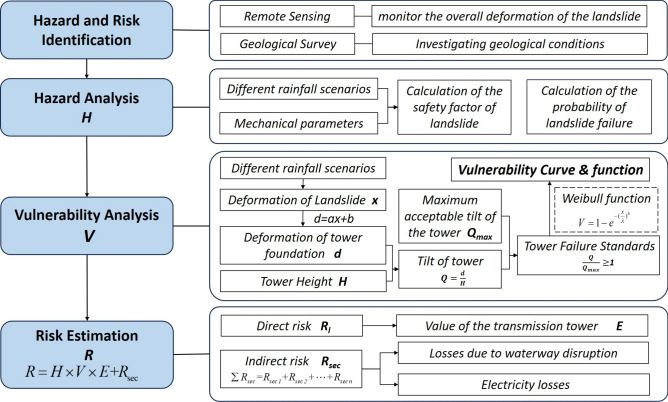
This section proposes a flowchart for assessing the landslide hazards and the risks from damage to transmission towers (Fig. 1), which is based on the methods of Thomas Glade et al. (2005)⁴⁸ and Fell (2008)¹². This flowchart focuses on the specific element at risk of transmission lines to assess the indirect risk following Yin et al. (2016)³⁷. The substages of the risk analysis process are described in detail.

Fig. 1.

Flowchart for risk assessments of landslide impacts on power transmission lines based on Glade et al. (2005)⁴⁸, Fell et al. (2008)¹² and Yin et al. (2016)³⁷.

To enhance the comprehension of the sample notation presented in the text, Table 1 provides a detailed overview of the nomenclature employed.

Table 1.

Sample nomenclature.

Nomenclature	Description
H	Hazard
Pf	Probability of a landslide occurring within the recurrence period of certain causal factors
V	Vulnerability
I	Landslide intensity
r	The resistance of the element at risk
x	The horizontal deformation of the landslide
λ	Constants in Weibull function
k	Constants in Weibull function
d	The horizontal deformation of the transmission tower foundation
α	The coefficient for horizontal surface deformation of structures
b	A negligible correction factor
Q	The tower inclination
h	The transmission tower height
R	Landslide risk
E	The value of the elements at risk
Rsec	The indirect losses resulting from the landslide consequences

Hazard analysis

The landslide hazard refers to the probability of landslide occurrence in a specific area⁴⁹. The aim of landslide hazard analysis is to assess and quantify the potential threats posed by landslides to human life, property, and infrastructure. Probabilistic analyses are widely used for calculating single landslide hazards, and some quantified methods, such as Monte Carlo simulations, statistical moment approximations, and stochastic finite element methods, are widely used^50,51. Monte Carlo simulations, in particular, are widely favoured because of their flexibility and adaptability; their key advantage lies in the ability to perform partial sampling and reduce the number of iterations needed, thereby significantly lowering computational time, a benefit that is especially important for landslide analyses that require extensive calculations⁵². Therefore, in this study, the failure probability of landslide occurrence (P_f) is evaluated through the limit equilibrium method within the Monte Carlo framework in Geo-Studio software. The limit equilibrium method determines the stability of a landslide by analysing the equilibrium state of each part of the landslide mass, whereas the Monte Carlo simulation performs extensive random sampling of this analysis to estimate the overall probability of landslide occurrence^53,54.

$$p_f=p(F_s\le 1)=\frac{M}{N}$$ 1

where P_f is the failure probability, M is the number of samples below 1, and N is the total number of samples.

Vulnerability assessment

The vulnerability of the element at risk refers to the degree of damage from the hazard, which is usually expressed by a value of 0–1. 0 means no damage to the element at risk^12,55,56. A value equal to 1 indicates damage to the entire element^57–59, such as a collapsed building or deaths. A quantitative vulnerability function relies on the hazard intensity and resistance of the element at risk^30,60,61.

$$\text{V = f}(\text{I},\text{r})$$ 2

where V indicates the vulnerability, I indicates the landslide intensity, and r indicates the resistance of the element at risk.

Three common methods are used to assess the vulnerability: the vulnerability matrix, vulnerability curve, and vulnerability index⁶². The vulnerability curve graphically illustrates the vulnerability levels of structures under different conditions; it is useful for understanding how the vulnerabilities change with varying inputs. This approach is particularly applicable to important structures such as transmission towers, which are sensitive to small deformations. The Weibull distribution is a continuous probability distribution that is widely used in reliability engineering^63,64. It is widely utilized in life testing data analyses for various products due to its ability to efficiently infer distribution parameters from probability values^65,66. Ye et al. (2021)⁶⁷ and Papathoma-Kohle et al. (2015)⁶⁸ indicated that this type of distribution curve is a suitable method for analysing the failure of a power grid system. The relationship between vulnerability and landslide intensity affecting transmission towers in this study is modelled via the Weibull (1951)⁶⁹ function, which is an S-shaped curve. The modified Weibull function to calculate the physical vulnerability is defined as follows:

$$\text{V =}\left\{\begin{array}{c}{\text{1 - e}}^{-{(\frac{\text{x}}{\lambda })}^{\text{k}}},\text{x}\ge 0\\ 0,\text{x < 0}\\ \end{array}\right)$$ 3

where x is the landslide deformation and where λ and k are constants, which need to be derived by fitting the observed crack width data x to the calculated vulnerability values v according to Eq. 3.

Intensity

The landslide hazard intensity is used to describe the potential extent of damage that a landslide can cause to the surrounding environment and infrastructure⁵¹. The degree of damage to transmission towers is directly correlated with the degree of deformation induced by landslides (Fig. 2). While moving landslide bodies directly affect transmission towers, the structures may tilt or even collapse⁷⁰, resulting indirectly in interruptions to power transmission lines⁷¹. There are compressional and tensile deformations during landslide displacements^72,73. Tensile deformations normally occur in the crowns and upper parts of landslide bodies, whereas compressional deformations occur at the feet of landslide bodies. In this study, the transmission tower is located in the crown and upper part of the landslide; this means that the vulnerability of the tower structure is predominantly influenced by tensile forces. A relationship between landslide-induced horizontal deformation and the structural response of transmission towers is constructed.

Fig. 2.

Landslide damage to transmission towers. a, b, c: In Shaanxi Province; d: In Sichuan Province; e: In Chongqing; f: In Anhui Province; g, h: In Qinghai Province; and i: In Hunan Province

(Source: Authors).

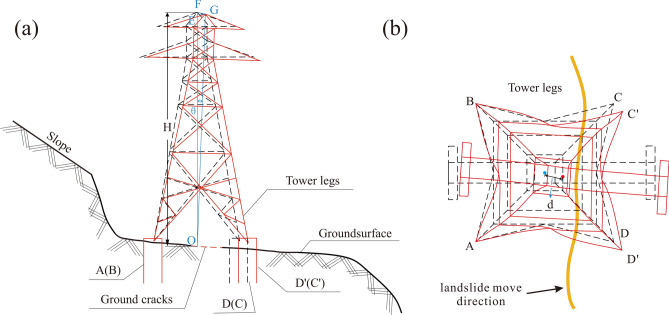
Small ground tensile deformation causes cracks in the tower foundations. When a landslide moves, the foundation of the transmission tower deforms parallel to the sliding mass⁷⁴. However, the deformation observed in the foundation of the transmission tower is not entirely equal to the deformation of the landslide mass. Assuming the deformation correlation coefficient between the deformation of the foundation of the transmission tower and the deformation of the landslide⁷⁵, as shown in Fig. 3, the top of the transmission tower is projected at the centre point of the ground foundation. Once a landslide occurs, the upper structure of the transmission tower will tilt with the deformation of the foundation.

$$d=\alpha x+b$$ 4

Fig. 3.

Diagram of ground-level deformation of the tower foundation.

Here, d indicates the horizontal deformation of the transmission tower foundation, and x indicates the horizontal deformation of the landslide, which is the correlation coefficient of the horizontal deformation. In this work, the coefficients for the horizontal surface deformations of structures are calculated with a specific numerical value of $\alpha$ = 0.8927 (Fig. 3b). b is a negligible correction factor.

Damage degree

The degree of damage is regarded as an output of physical vulnerability^76,77. In all the regulations for managing power transmission lines in China, there are no explicit criteria for assessing the degrees of tower deformation induced by landslides. Notably, the "Guide for running state assessment strategy of overhead transmission Line" (DL/T1249-2013) defines tower inclination as the tilt degree, which is calculated as the tilt distance from the tower top to the longitudinal axis of the transmission tower divided by the total height of the tower, multiplied by 100% (Fig. 3a). The tower inclination ratio within a specified threshold delineates the extent of damage. The standard outlines criteria for high-risk tower inclinations (Table 2). For the tower under scrutiny in this study, a 50-m high-angle steel tower, the maximum acceptable inclination is defined as 0.5%.

Table 2.

Maximum allowable values for pole/tower inclination, top displacement, and horizontal deviation.

Category	Reinforced Concrete pole	Steel Tube Pole	Angle Tower	Steel Tube Tower
Direct Pole Inclination Including Pole Displacement	1.5%	0.5%	0.5%(H ≥ 50 m) 1.0%(H < 50 m)	0.5%
Maximum Displacement of Direct Angle Pole	/	0.7%	/	/
Maximum Displacement of Angle and Terminal Towers 66 kV and Below	/	/	1.5%	/
Maximum Displacement of Angle and Terminal Towers 110 kV to 220 kV and Below	/	2.0%	/	/
Horizontal Deviation of Tower	1.0%	/	1.0%	0.5%

Current research lacks a quantitative methodology to calculate the long-term impact of slow landslides on the inclinations of transmission towers, resulting in damage. Traditional measurement techniques such as the plumb-bob method⁷⁸ and theodolite method⁷⁹ are suitable for assessing tower inclinations under wind-induced vibrations or extreme weather conditions. In response to the distinctive movements that are observed in slow-moving landslides, this study introduces an approach to calculate the inclinations of transmission towers in terms of landslide displacements. The objective is to assess the deformation status of towers located within landslide-prone areas.

Landslides cause deformations of the foundations of transmission towers. The four legs of the piles of the transmission tower base deform synchronously. Since the transmission tower is a rigid structure, the upper part of the transmission tower tilts forwards or backwards from the deformation of the base, as shown in Fig. 3a.

Therefore, when the ground deformation is used to characterize the tilt distance at the top of the tower, the tilt can be approximately characterized via Eq. (5).

$$Q=\frac{d}{h}\times 100\%$$ 5

where Q indicates the tower inclination; d indicates the offset distance of the foundation centre of the transmission tower which is the same as Eq. (4); and h indicates the height of the transmission tower.

Risk assessment method

In 1984, Varnes proposed the basic definition of landslide risk. Landslide risk equals the product of the hazard, the vulnerability, and the element at risk.

$$R=H\times V\times E$$ 6

in which R refers to risk, H refers to the occurrence probability of a landslide, V refers to the vulnerability of the elements at risk, and E indicates the value of the elements at risk.

For the ultrahigh-voltage electricity transmission line, if the tower is damaged, the direct impact on the tower itself is only one small portion of the element to be considered. Many elements at risk are indirectly involved in the disruption of the energy network. Therefore, Yin’s (34) analysis method, which considers indirect risk, is more suitable for transmission towers.

$$R=R_l+R_{sec}=H\times V\times E+R_{sec}$$ 7

The first part on the right side of the equation is the basic formula for landslide risk that was proposed by Varnes, which mainly considers the direct losses caused by damage to transmission towers from landslides. R_sec represents the indirect losses resulting from landslide consequences, such as road closures, the shutdown of the energy supply, and the disruption of industrial manufacturing systems. The indirect losses discussed in this study refer to a series of economic losses that result from the failure of the transmission tower due to a landslide.

Direct risk

Direct risk refers to the immediate and tangible threats or dangers posed by a specific hazard⁸⁰. For transmission towers, the direct risk R_l of transmission towers caused by landslides may be calculated via Formula (6).

Indirect risk

Indirect risk assessments consider the effects of hazards and elements beyond the immediate impact zone of the landslide body⁸¹. For small landslide deformations that do not cause instability of the foundation of the transmission tower, structural repairs and landslide stabilization measures are common risk treatments. However, if the landslide continues to deform, emergent measures such as relocation and reconstruction of the tower foundation are essential. In the case of a sudden landslide, the collapse of the tower may cause the energy supply system to be disrupted, resulting in large indirect losses.

$$\sum R_{sec}=R_{sec1}+R_{sec2}+···+R_{sec\text{n}}$$ 8

where R_sec represents the total value of indirect economic risk, R_sec n represents indirect economic losses from different scenarios, economic losses from power outages, losses from transportation line disruption, and costs of reconstructing transmission towers.

The electricity transmission system is essentially a network that connects nodes through power lines, and damage to one tower will cause a shutdown of the electricity supply within a large region. In general, one week is needed to rebuild a new tower on an 800-kV ultrahigh-voltage line; this probably affects many consumers within the supply area. An electricity line outage may cause a rapid drop in transmission system frequency, which can overload multiple transmission devices connected to it. The scenarios are very complex; this means that the indirect risk of landslides along ultrahigh-voltage electricity transmission systems is much greater than the direct risk.

Case study: Yanzi landslide

Geological background

General description

The Yanzi landslide is located on the northern bank of the Yangtze River, Badong County, Hubei Province, China (Fig. 4a, 4b). The area is located within the epicentre of intense rainfall that occurs during the rainy season from June to August. The annual average precipitation is approximately 1200 mm, and the annual maximum rainfall is 1522.4 mm. The highest hourly precipitation was recorded as 75.2 mm, and the highest daily precipitation reached 193.3 mm. There was an incorrect site investigation for the studied tower, and it was sited within the old landslide body. The tower is part of a very important 500-kV ultrahigh-voltage energy transmission line that runs from western to eastern China. The old landslide was reactivated in 2002 by heavy rainfall. Ground cracks formed across the middle between the four legs of the tower, which caused a large risk to the energy transmission network. (Fig. 4c).

Fig. 4.

Location of the Yanzi landslide (The figure was created by Chenchen Huang using ArcGIS 10.2, (http://www.esri.com/) and CorelDRAW 2018 (https://www.corel.com/cn/)).

The elevation of the toe of the landslide is 295 m a.s.l., and the head of the landslide is approximately 400 m a.s.l. The slope angle varies from 25° to 40°; its length is approximately 400 m, and its width is 150 m. The average thickness of the sliding mass is 10 m, and the volume is 0.6 million cubic m (Fig. 5).

Fig. 5.

Topographic map of the Yanzi landslide. (The figure was created by Chenchen Huang using CAD 2020 (https://www.autodesk.com.cn/) and CorelDRAW 2018 (https://www.corel.com/cn/)).

The upper layer of the landslide body is a weathered deposit (Q^{el+ dl}) that formed from the Triassic claystone and sandstone of the Badong Formation (T₂b²). The thickness varies from 0.5 to 3.0 m. The main composition is silty clay mixed with debris. The debris size the varies between 10 and 30 cm. The ratio of clay to debris is 6:4. The bedrock dips towards the river, and the dip angle is approximately 29°. The geological structure is very susceptible to landslides (Fig. 6). The old landslide is a consequent landslide, which means that it slid along the bedding.

Fig. 6.

Geological cross Sect. (1–1') of the Yanzi landslide

(Source: Authors).

Landslide activity

The Yanzi landslide was reactivated by heavy rainfall in 2002. Creep deformation caused tension cracks on the upper part of the slope. In 2016, the slope-cutting construction for the G209 National Road on the lower slope intensified the displacement of the landslide (see Fig. 6), which directly impacted the foundation of the 500-kV cross-river tower (Fig. 4c, Fig. 7) located on the higher part of the landslide body. The cracks across the foundation of the four legs of the tower significantly threaten the safety of the structure. The cracks extend approximately 35 m, and the maximum opening width is 82 mm (Fig. 7).

Fig. 7.

Cracks on the tower foundation.

The local power grid company quickly initiated an emergency monitoring program. From February 5 to February 16, the cracks increased in width by 18 mm, which means that the daily increment was 1.5 mm. Later, the landslide continuously moved. The movement rate accelerated during March (Fig. 8).

Fig. 8.

Variations in the opening of the crack from 01/02/2016 to 17/03/2016.

Model and parameters

Based on the cross Sect. 1–1', a two-dimensional model consisting of 2967 elements and 3061 nodes is established using Geo-Studio to calculate the collapse probabilities and deformations of the Yanzi landslide under various rainfall conditions. Table 3 lists the physical and mechanical parameters relevant to the landslide, which are derived from extensive soil sampling and laboratory testing.

Table 3.

Physical and mechanical parameters of landslides (γ is the specific weight, c is cohesion, φ is the angle of internal friction, v is Poisson’s ratio, E is the elastic modulus, and K is the hydraulic conductivity).

	γ(kN/m3)	c(kpa)	φ(°)	v	E(kpa)	K (m/d)
Slide body	24	14.5	19.5	0.38	23,000	0.5
Bedrock	30	28	30	0.2	130,000	1e-10

Rainfall data analysis

Extreme rainfall may trigger landslides in large areas. Landslide occurrences are intimately linked to sustained, accumulating precipitation over multiple days^82,83. To comprehensively evaluate the influence of both daily rainfall and the cumulative precipitation on landslide occurrences, an analysis is conducted on rainfall-induced landslides in Badong County from 2008 to 2017. Six days of cumulative rainfall preceding the landslides are most likely correlated with landslide events (Table 4); this means that 1-day and 6-day rainfall events are mostly linked to the landslides. One day represents instant triggering, and the other 6 days represent the cumulative precipitation for the 6 days preceding landslides.

Table 4.

Correlation analysis between cumulative precipitation and landslide events.

Days of precedent accumulative rainfall triggering the landslide	1	2	3	4	5	6	7	8	9	10
Coefficient of correlation	0.593	0.204	0.143	0.161	0.25	0.684	0.565	0.013	0.01	0.144

Based on historical rainfall data of the study area from 1970 to 2019, the Gumbel function is used to predict the return periods of 6-day extreme cumulative rainfall amounts over 5, 10, 20, 50 and 100 years (Table 5).

Table 5.

Cumulative rainfall for various return periods.

Number	Scenarios	Accumulative rainfall/mm	Mean daily intensity/mm D-1
a	The 5-year return period of continuous rainfall on 6 days	179	29.8
b	The 10-year return period of continuous rainfall on 6 days	209	34.9
c	The 20-year return period of continuous rainfall on 6 days	248	41.3
d	The 50-year return period of continuous rainfall on 6 days	277	46.1
e	The 100-year return period of continuous rainfall on 6 days	305	50.8

Results

Probability of landslide failure

Based on the rainfall and seepage simulations for the Yanzi landslide, the safety factors and probabilities of failure are calculated via the Morgenstern-Price method and the Monte Carlo method, as shown in Table 6. There are two sliding surfaces in Fig. 6: shallow sliding and global sliding (or deep sliding). The current activation of the landslide was caused by shallow landslides.

Table 6.

Landslide safety factors and failure probabilities.

Scenarios	Most critical shallow sliding		global sliding
	Fs	Pf	Fs	Pf
a	1.023	35.85%	1.235	9.65%
b	1.016	37.5%	1.226	10.1%
c	1.006	39.5%	1.215	10.8%
d	0.999	40.95%	1.206	11.35%
e	0.993	42.05%	1.198	12.35%

According to the "Technical Code for Building Slope Engineering" (GB 50,330–2013) in China, a landslide is defined as marginally stable if Fs ranges from 1.0 to 1.05, and treatment measures are needed to increase the stability of the landslide and mitigate risks. If Fs is less than 1.0, stabilization is imperative. Based on the computation of landslide stabilities under different rainfall scenarios, the safety factors of the global sliding surface are greater than the margin of Fs. The P_f of 12.35% in extreme scenarios i.e., with a one-hundred-year rainfall return period, is not high. All safety factors for shallow sliding in different scenarios are smaller than 1.05. For a five-year rainfall return period (scenario a), Fs is 1.023, and the probability of failure is 35.85%. Therefore, the shallow sliding of the Yanzi landslide causes long-term risk to the tower foundation.

Scenario-based vulnerability analysis

Landslide displacement and vulnerability values of transmission towers

For the Geo-Studio software, transient seepage is simulated for five rainfall return periods. The results of rainfall seepage are imported into the SIGMA module to simulate landslide displacements. The horizontal displacements at the centre of the transmission tower foundation are obtained. The statistical results of the landslide displacement simulations are shown in Table 6. The horizontal displacements of the ground surface at the centre of the tower foundation increase as the rainfall intensity increases.

Equation (4) is used to calculate the horizontal displacement at the centre of the tower foundation according to the simulated horizontal ground displacement. Using Eqs. (3) and (5) and the simulated deformation values at the centre of the foundation, the tilt of the tower and the corresponding vulnerability values can be calculated. The calculation results are listed in Table 7.

Table 7.

Landslide deformations, tilt and vulnerability of transmission towers.

Scenarios	Landslide deformation (m)	Deformation of transmission tower foundation (m)	Inclination of tower	Vulnerability values
a	0.037	0.033	0.067%	0.134
b	0.111	0.099	0.198%	0.396
c	0.157	0.140	0.280%	0.561
d	0.202	0.180	0.361%	0.721
e	0.279	0.249	0.498%	0.996

The results indicate that the vulnerability of the transmission tower is minimal (0.134) for small precipitation scenarios (five-year return period rainfall), with a tilt of 0.067%. However, during extreme rainfall events, the landslide deformation increases and causes damage to the transmission tower. At a return period of 50 years (scenario d), the value of the vulnerability of 0.721 is very large. For the scenario of a one-hundred-year rainfall event (scenario e), the tilt of the transmission tower is 0.498%, which is close to the maximum tilt value of 0.5% for steel towers 50 m in height according to the transmission line operation regulations (DL/T741-2019). A vulnerability value of 0.996 is extremely large, indicating very high risk in scenario e.

Vulnerability curve

The vulnerability curves of the transmission towers are formulated based on the vulnerability data in Table 6 (Fig. 9). This fitting process involves minimizing the differences between the observed data and the theoretical Weibull distribution curve, ensuring the best representation of the relationship between landslide surface deformation and the capacity of transmission towers to resist deformation. The fitting is performed via the least squares method, resulting in a vulnerability curve with a value of 0.04381 for λ and a value of 1.73111 for k. The vulnerability curve presents the relationship between landslide surface deformation and the capacity of towers to resist deformation. As the surface landslide deformation reaches 0.4 m, the vulnerability of the transmission towers is almost 1.0. According to the monitoring data from 2016, the foundation crack across base of the transmission tower widens from 0.07 m to 0.105 m, resulting in an increase in the vulnerability value from 0.26 to 0.38; this degrades the stability and structural integrity of the towers, which increases the possibility of damaging the structures.

Fig. 9.

Vulnerability curve verification.

In terms of the vulnerability curve, it is easier to quantitatively estimate the physical vulnerability of transmission towers in areas that are susceptible to slow-moving landslides.

Risk Estimation

Direct Economic Risk

The tower structure within the Yanzi landslide spans the ground crack, which is caused by a shallow sliding surface, and it is highly unstable. The landslide movement has already damaged the tower structure. The potential fast movement along the shallow sliding surface of the landslide may result in the collapse of the tower. Therefore, based on the failure probability of the most critical sliding surface, the vulnerability curve, and the economic cost of the tower (1.1 million euros), the direct risks in various scenarios were calculated, as shown in Table 8. When the vulnerability exceeds 0.5, the transmission tower is considered to be in a dangerous state, where simple repairs may not ensure its stability. Vulnerability levels above 0.5 generally indicate a significantly increased risk of structural failure^84,85, requiring attention and possible intervention. Reconstruction of the tower is necessary at this point, with the direct risk being the initial construction cost of the tower.

Table 8.

Direct risk calculation results.

Scenarios	H	V	E(million)	Rl(million)
a	35.85%	0.134	€1.1	€0.053
b	37.5%	0.396	€1.1	€0.163
c	39.5%	0.561	€1.1	€1.1
d	40.95%	0.721	€1.1	€1.1
e	42.05%	0.996	€1.1	€1.1

Indirect Economic Risk

The shallow landslide exhibits continuous in motion, and the failure possibility in extreme rainfall scenarios is very high. Therefore, risk treatment measures are urgently needed. There are two options: relocation of the tower or stabilization of the landslide. In these emergency circumstances, the best strategy is to relocate the transmission tower to a point outside of the landslide body because stabilization takes a very long time. However, in addition to the direct costs associated with this relocation and the rebuilding of the tower, the risk mitigation process may result in indirect economic losses and various associated costs during reconstruction, consisting of two main components: losses due to disruption of navigation channels and electricity losses.

The ultrahigh-voltage electricity transmission tower serves as the terminal structure for the Badong cross-river transmission line. A potential sudden collapse of this tower will indirectly influence navigation on the Yangtze River due to the drop-down of 14 cables, which could suspend ship navigation. The waterway must be temporarily closed for the cable removal process. Authorities estimate 24-h timeframes from hazard identification to complete resolution. According to data provided by the grid company, the daily economic loss resulting from the closure of the Yangtze River is approximately €5 million.

China’s power grid system is equipped with protective devices that are capable of swiftly redirecting power in the event of damage to transmission towers caused by natural hazards, helping to prevent widespread power shortages. However, the damage caused by the Yanzi landslide necessitated the suspension of the affected transmission lines for repairs. Specifically, the 500-kV transmission line connecting Wanzhou station to the Three Gorges Dam station required a temporary shutdown. Following the landslide in February–March 2016, this line experienced a 100-day outage, with power restored by the end of June 2016. This line has a daily transmission capacity of 5 million kilowatt-hours of electricity, with an average price of €0.07 per kilowatt-hour in Hubei and Chongqing Provinces. Timely interventions prevented a loss of €0.035 billion for power companies in these two provinces during the outage. However, brief power outages still caused economic losses of 0.1 million euros to the areas surrounding the transmission towers, affecting both economic production and residents’ daily lives.

Risk estimation

The transmission tower damage caused by landslides in the 5 scenarios is shown in Table 9.

Table 9.

Economic losses incurred by the power grid as a result of the Yanzi landslide.

Scenarios	Rl(million)	Rsec(million)	R(million)	Indirect impact
a	€0.053	€0.002	€0.055	strengthening the tower
b	€0.163	€0.05	€0.168	1. Losses due to disruption of navigation channels 2. Electricity losses
c	€1.1	€5.1	€6.2
d	€1.1	€5.1	€6.2
e	€1.1	€5.1	€6.2

The aforementioned findings unequivocally demonstrate that when a landslide is prone to further deformation, the affected transmission towers give rise to a cascade of indirect economic losses that significantly surpass the direct economic losses. Consequently, gaining insights into the vulnerability of transmission towers and implementing timely and judicious measures can efficiently mitigate avoidable economic losses.

Practical mitigation measures

Given the emergence of potential landslides, it is essential to take urgent protective measures to avoid sudden power disruptions caused by the collapse of the tower. To ensure the stable operation of the power transmission system, the reconstruction of a new tower is a better choice to replace the tower located within the landslide body.

In 2016, the Yanzi landslide was reactivated by excavation on a lower slope, which caused unacceptable deformation across the four legs of Transmission Tower #200 towards the Yangtze River. Tower #200 is at imminent risk of toppling, which threatens the line’s operational stability. In anticipation of the upcoming summer peak electricity demand, the power company has formulated an emergency rescue plan. The decision was to rebuild a new tower 62 m behind the original tower #200, which is beyond the Yanzi landslide body; this means that the risk was entirely reduced. The reconstruction cost was €1.875 million. Moreover, the position of the next tower (#201) must be changed due to line management. The additional cost was €1.5 million. The relocation of two towers further involves the dismantling of 14 cables over the Yangtze River. To ensure the safety of the waterway, the Yangtze River channel was closed for 34 h and 30 min. A total of 108 households involving 352 residents in the vicinity of the towers were evacuated. This expense was estimated to be approximately €5.1 million.

The emergency treatment measures in 2016 successfully ensured a stable electricity supply during the peak demand period. Furthermore, Tower 199#, which is located on the opposite bank of the Yangtze River, was dismantled and moved approximately 60 m northwest. All these factors increased the additional cost of €6 million.

Discussion

This study presents a scenario-driven risk assessment approach that considers the direct and indirect risks posed by landslides to ultrahigh-voltage electricity transmission lines. The physical vulnerability curve for transmission towers located on active landslides is formulated to quickly determine the potential vulnerability of these structures. The direct risk from the tower reconstruction can be evaluated easily. The indirect economic loss estimation is complicated and depends on the elements at risk that are related to landslides or treatment measures. In this study, the elements at risk included towers linked to each other, navigation interruptions, residential evacuations, and electricity consumption. Some indirect risks can be calculated. Some indirect risks are difficult to estimate.

Landslide risk management is designed to formulate scientific response strategies based on the outcomes of risk assessments. This comprehensive approach encompasses acceptable levels of risk, risk avoidance, strategies for risk reduction, postdisaster consequence control, and risk transfer. In the case of unacceptable risk assessment results, the implementation of a suitable risk control plan becomes imperative to effectively mitigate the identified risks. Given the critical nature of transmission towers within point-to-point line projects, sudden failure of a single tower due to a landslide may cause cascading effects along the entire line, and the indirect risk is not acceptable. Therefore, the choice of proper risk control measures is important to minimize the risks that are triggered by potential landslides. This study delineates a nuanced risk management approach in terms of direct and indirect risk assessments. There is a nationwide ultrahigh-voltage electricity transmission system in China. The transmission lines from west to east at 500 kV pass through high mountainous areas and large rivers. Landslides threaten the stability of towers, which may cause large risks to the entire network. Therefore, in the event of a landslide, preventing the collapse of transmission towers is the priority of risk mitigation because of the potential threat to the power supply and power outages in large areas. These abrupt power interruptions not only engender economic losses but also may precipitate social ramifications. For example, sudden power outages can influence public services, including medical facilities, schools, and transportation systems, thereby inconveniencing the daily lives of residents.

This study focuses primarily on risk calculation methods for transmission towers. As a result, a relatively simple monitoring method was used, where a simple tool (such as a ruler) is employed to measure the width of cracks at the base of the transmission tower, allowing for a quick assessment of changes in tower stability. InSAR (interferometric synthetic aperture radar) is a powerful tool for detecting ground displacements over large areas with high precision, which can significantly enhance the rapid assessment of landslide risk. In future work, InSAR technology could be used to monitor tower deformation to further improve the accuracy and timeliness of monitoring.

The landslide scale is usually characterised by parameters such as landslide area or volume, which provide important insights into the potential intensity of a landslide event and changes in the susceptibility of risk elements. We also recognise the potential value of integrating landslide size estimations in future risk assessments, where the inclusion of the landslide size in the assessment can provide a deeper understanding of the impacts of different displacement scenarios on infrastructure; this would help optimise risk management strategies, especially in areas with high landslide risk and limited resources.

In this study, only the rainfall return period is used in the simulations of landslide deformation. In practical applications, rainfall thresholds are typically used in landslide risk assessments to determine the critical rainfall amounts that may trigger landslides. Future research could establish specific rainfall thresholds for the study area to more accurately predict the likelihood of landslide occurrence under various rainfall conditions. By incorporating real-time monitoring data, early warnings for potential landslide events could be provided, enabling more refined risk assessments and determining when preventive or mitigation measures are necessary.

By integrating these insights into the risk assessment framework, this study provides a foundation for developing more robust and adaptive strategies to manage landslide risk in vulnerable regions, ensuring the continuity and reliability of power transmission in diverse and challenging environments.

Conclusion

This study presents methods to assess the indirect risk of landslides along ultrahigh-voltage electricity transmission lines precisely. Indirect losses from social disruptions are still a major issue to be quantitatively evaluated. Nevertheless, this study demonstrates the importance of indirect losses as a case study of the Yanzi landslide to manage emergence risk. The main findings of the study are as follows:

1. The vulnerability curve provides a quantitative representation of the vulnerability of the tower structure. The tower vulnerability is determined by considering the amount of ground deformation and tower height, which helps in quickly assessing damage to transmission towers caused by landslides.

2. The risk chain includes direct losses of transmission towers and indirect losses from relevant elements at risk. A comprehensive risk analysis of the impact of landslides on the transmission tower system reveals that the series of indirect risks arising from tower damage significantly outweigh the risks associated with rebuilding the tower. This framework provides a broader reference for landslide risk assessments within power grid systems.

Author contributions

Chenchen Huang: methodology, investigation, formal analysis, visualization, software, data curation, writing original draft preparation. Kunlong Yin: conceptualization, supervision, writing reviewing and editing, funding acquisition, resources. Xin Liang and Lei Gui: conceptualization, supervision, writing reviewing and editing, writing original draft preparation. Binbin Zhao and Yi Liu: conceptualization, supervision, data curation, resources.

Funding

National Key Research and Development Program of China, No. 2018YFC0809400, National Natural Science Foundation of China, No. 41702304.

Data availability

The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-76726-x.