Abstract
In the era of digital transformation, securing data on metaverse platforms poses significant challenges. This paper proposes Multiparty Space Sharing and Authentication (MSSA), a novel approach for secure user login and location access control within specialized metaverse platforms. MSSA leverages Quantum Multiparty Secret Computation (QMSC) integrated with a quantum blockchain network. This integration facilitates user verification within the presence of potentially untrusted metaverse authority. The underlying quantum blockchain employs a Delegated Proof-of-Stake (DPoS) consensus mechanism with a Borda voting scheme for authority node selection. By harnessing the principles of quantum cryptography, MSSA offers enhanced security against both classical and anticipated future quantum attacks. This research demonstrates the feasibility and potential of quantum blockchain for securing metaverse platforms, paving the way for secure and decentralized digital ecosystems.
Subject terms: Computational science, Computer science, Information technology
Introduction
The metaverse represents a complex simulation of real-world activities within a three-dimensional (3D) environment. It is not a singular technology; instead, it comprises a sophisticated amalgamation of interdependent technologies. These include artificial intelligence (AI) for natural language processing, 3D imaging and video processing for creating immersive visuals, avatar generation for user representation, blockchain for enhanced security and traceability, and sensor data integration to produce lifelike virtual environments1. Building on the foundation of the metaverse as a complex interplay of technologies, it is evident that metaverse platforms can vary significantly according to their application and the services they provide2. These variations can create dedicated metaverses designed for education, industry, social interaction, and other specific purposes. Regardless of the type, secure authentication and access control remain paramount across all metaverse platforms. This aspect becomes critically important in the context of special-purpose metaverses, such as those utilized by government organizations3,4, or military applications5. In these environments, the leakage of information or the potential for eavesdropping can result in significantly big consequences than in general-purpose metaverses. Therefore, in these cases, the implementation of additional precautions is indispensable.
Ryu et al6. propose a mutual authentication framework for two metaverse users utilizing blockchain technology. In this framework, a Certificate Authority (CA) stores and verifies user information, which can be used to authenticate users across multiple metaverse platforms. When a user attempts to communicate with another user, they send a request through a blockchain transaction. The receiving user then verifies the requesting user’s information stored in the blockchain by the CA. Yang et al7. introduce a two-factor authentication method, combining biometric data and a chameleon signature, to verify users through the blockchain and establish one-to-one communication among metaverse users. Furthermore, Thakur et al8. propose a three-factor authentication model to facilitate user-to-server and user-to-user interactions in the metaverse. In addition to the studies mentioned above, a significant amount of ongoing research is focused on improving the security of authentication mechanisms within the virtual metaverse9–12. These authentication processes aim to verify user identities within both virtual and real-world contexts, thereby establishing secure mutual connections between meta-humans. It is important to note that a single metaverse platform can encompass multiple spaces, not all of which may be accessible to every user. Consequently, authentication within specific spaces of the metaverse also becomes crucial. For example, consider spaces designated for a university campus, a government organization, or an international organization within the metaverse. Certain areas within these spaces may not be open to all users, necessitating the implementation of space-specific authentication measures. Seo et al13. proposes a user-centric, space-based authentication method for the metaverse, wherein smart contracts authenticate users through the use of cosine similarity matrices. However, a fully trusted authority is considered here, which is not practical.
Quantum computing is advancing rapidly, transitioning from the noisy intermediate-scale quantum (NISQ) era to the fault-tolerant quantum computer (FTQC) era14. This foreseen rapid progress in both quantum hardware and software creates significant challenges to the current security system, particularly for encryption, financial, and computer security systems, which rely on complex mathematical problems. For instance, present-day blockchain technology frequently employs encryption algorithms such as the Digital Signature Algorithm (DSA), Rivest-Shamir-Adleman (RSA), and Elliptic Curve Diffie-Hellman (ECHD), all of which are vulnerable to powerful quantum computing by using Shor’s algorithm. Furthermore, Grover’s algorithm introduces security concerns for hash functions by facilitating rapid hash creation and the detection of hash collisions. Therefore, it is imperative to explore and adopt postquantum solutions, specifically quantum-enabled blockchain and encryption systems1.
A blockchain system allows users to build public consensus without the need for third parties like organizations or governments. The first commercial application of blockchain was the decentralized cryptocurrency called Bitcoin15. However, blockchain technology later gained popularity in various fields, including securing Internet of Things (IoT) devices, UAV authentication, carbon credit trading, the metaverse, and more. Traditional blockchain systems use hash or hash collision functions, which are not secure against powerful quantum computers. Therefore, ensuring security and privacy in the quantum era has led to the development of post-quantum blockchain, a combination of quantum computing and blockchain technology. To secure quantum blockchain transactions, a quantum-enabled digital signature is crucial. A digital signature is akin to a handwritten signature in the real world, verifying that a message is authentic. In blockchain applications, the signature is used to verify transactions. Gottesman et al16., proposed the first quantum digital signature, which fundamentally reforms the classical digital signature in quantum form. Similar to a classical digital signature, the authors use a quantum one-way function to generate a secure public key. However, in this scheme, the same key is shared among all recipients, which raises the possibility of insider attacks. Yin et al17. utilized Quantum Key Distribution (QKD) to acquire a quantum digital signature that covers 100 km in practical deployment. Several features need to be addressed when designing a quantum digital signature, such as the distance covered in QKD-based key transfer, hiding source attacks, designated verification, repudiation prevention, and others. A significant amount of research is ongoing in the field of quantum digital signatures18–20.
Research on blockchain is still in its early stages, resulting in a lack of sufficient research, implementation, and infrastructure. As a result, blockchain is still far from practical application. The idea of quantum Bitcoin was first proposed by J. Jogenfors21in 2016, as a quantum version of traditional Bitcoin that uses public and private keys and mining in a quantum manner. Ikeda et al22. proposed a quantum-based cryptocurrency scheme called qBitcoin, which diverges from the traditional blockchain by eliminating mining and hashing concepts and instead employing EPR pairs and the QKD protocol. EPR pairs are used for teleportation to connect blocks, or in other words, the remitter and receiver, while QKD securely transfers the private key between them. Here, teleportation prevents double spending, and quantum digital signatures verify transactions. This process is faster and more secure compared to traditional Bitcoin23. Later Rajan et al24. introduced a quantum blockchain idea utilizing the GHZ state for entanglement and QKD. Subsequent research25,26improved the blockchain model by adding consensus algorithms and voting mechanisms to select the responsible parties for block verification. In the metaverse, the adoption of blockchain technology is necessary for maintaining security and provenance. To effectively implement blockchain in the metaverse, it is necessary to employ a consensus algorithm to ensure the reliability and uniformity of its distributed ledger. Up to the present, several consensus algorithms have been proposed in the academic literature. Notably, proof of work (PoW)27, proof of stake (PoS)28, delegated proof of stake (DPoS)29, delegated proof of stake with node’s behavior and Borda count (DPoSB)30,31, and byzantine fault tolerance (BFT)32 are among the well-recognized and widely accepted consensus algorithms. Unlike PoW and PoS, DPoS is much faster and better suited for large-scale applications like the metaverse.
The light of the approaching era of quantum computing and the ongoing development of the metaverse, it is prudent to consider quantum solutions for the metaverse to facilitate the seamless integration of quantum technology. Therefore, this paper proposes a novel quantum blockchain-based secure authentication framework for a specialized metaverse, wherein the metaverse space is divided into multiple subspaces. Each subspace is assigned multiple authorities to verify and grant user access. Recognizing that some authorities may be untrustworthy, we incorporate quantum secret multiparty computation to handle this situation. A quantum version of DPoS proposed by Li et al26. is utilized with Borda voting count mechanism, where classical information is stored in entangled quantum states in the form of a chain. QDPoS possesses identical features to those of DPoS, which consumes fewer resources compared to the previously mentioned consensus algorithm. Furthermore, our proposed system aims to achieve centralized control in a decentralized context; therefore, DPoS is considered the preferred consensus mechanism for the blockchain utilized in the proposed metaverse framework. The spaces in the metaverse are identified and accessible with a secret key.
One of the renowned encryption challenges is the millionaires’ problem, proposed by Andrew Yao in 198233. The problem involves verifying information without revealing it. To address the challenge, several encryption techniques are available, including homomorphic encryption34, zero-knowledge proofs35, and secure multiparty computation36. Considering our system requirements, quantum-secure multiparty computation37 is considered at the authority level, considering potentially dishonest or partially dishonest authorities.
There’s a lack of research and commercial development focused on integrating quantum computing with the metaverse. This limits the creation of devices, like head-mounted displays and AR/VR systems, that could offer advanced features made possible by quantum technology. Furthermore, the advancement of auxiliary technologies for transmitting or receiving quantum bits (qubits) through quantum channels remains insufficiently explored. Implementing quantum environments for the masses remains a challenge due to limitations such as decoherence and complexity38. Consequently, this paper deliberately targets specialized metaverses relevant to government, international organizations, and the military. These domains prioritize security, making them more suitable for integrating quantum technologies at the current development stage of quantum technology, compared to general-purpose metaverses. Our prior work employed quantum superdense coding to ensure secure authentication within a military metaverse context, although blockchain technology was not considered in that scope39.
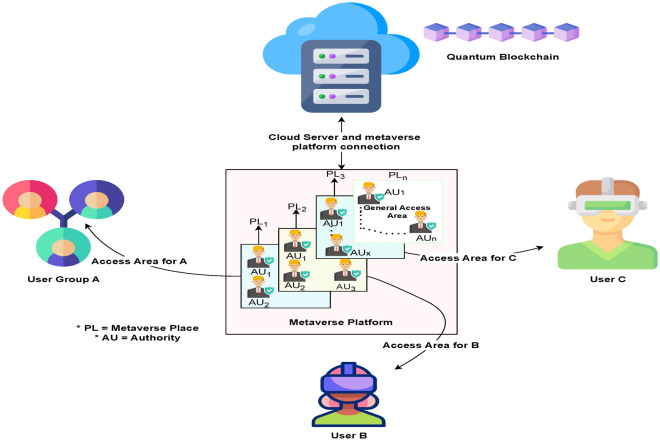
Figure1 shows the overall system model. In real-world scenarios, access within an organization is not uniformly granted to all individuals. Certain areas are designated as general access zones, open to all authorized personnel, while other areas are restricted and accessible only to individuals with specific permissions. This tiered access structure ensures that sensitive locations are protected from unauthorized entry, thereby ensure safety of the organizational assets and information. This principle applies to the metaverse as well, where not all spaces should be accessible to all users. While user authentication is essential, access control based on user privilege is equally important. Addressing this critical need, this article proposes a novel framework for multiparty space sharing and authentication (MSSA) for the specialized metaverse platform. This framework leverages quantum blockchain technology to authenticate users and permit them to access various spaces within the metaverse. The key contributions and innovations are summarized below.
This paper introduces a QDPoS consensus algorithm-based quantum blockchain-enabled metaverse space authentication mechanism called MSSA.
The proposed MSSA framework considers multiple spaces inside a metaverse, where the user needs access from the authority assigned for the specific space.
Considering real-world scenarios the authority can not be fully trusted, therefore multiparty quantum secret computation is considered for user verification.
Fig. 1.
Overall system architecture for secure multiparty space sharing and authentication (MSSA).
Proposed MSSA framework
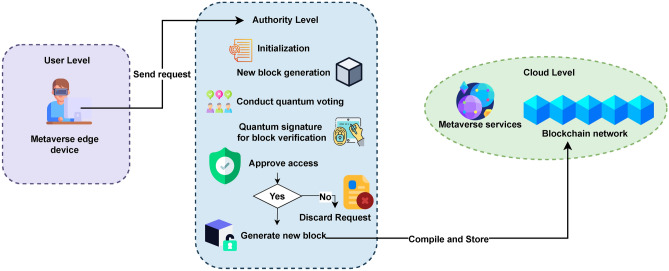
The overall architecture of the MSSA is depicted in figure2, illustrating a comprehensive authentication framework designed to enhance security in multiparty space sharing. The proposed MSSA is a tripartite structure system segmented into three distinct levels, each serving a critical function within the architecture. First, the user level serves as the interface for individuals interacting with the system, it is a user-centric low level within the architecture. Second, the authority level encompasses mechanisms for regulatory oversight and enforcement, ensuring adherence to established security standards. Lastly, the cloud level integrates quantum cloud computing, offering scalable and robust data storage and processing capabilities.
Fig. 2.
Diagram of the tripartite architecture for MSSA.
User level
Within the MSSA framework, the interaction commences at the user level, where participants of the metaverse environment initiate their engagement by transmitting a set of crucial access credentials directed toward the authority level, aiming for a rigorous identity verification process. This initial step ensures that users are authenticated, thereby maintaining the integrity and security of the metaverse environment. Upon successful verification, a unique avatar is generated for the user, symbolizing their digital persona within the virtual world. Subsequently, the authentication mechanism, leveraging the quantum-safe protocol alongside the user’s credentials, facilitates access to various designated virtual spaces.
Authority level
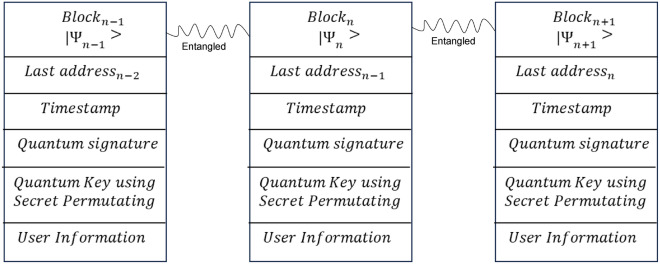
At the authority level, the primary responsibility is user verification, and maintaining blockchain infrastructure. This level undertakes the processing of new user’s personal information, a critical step aimed at verifying the authenticity of new participants within the system. Upon successful verification, the authority level proceeds to create and integrate a new block into the blockchain. This involves a thorough process wherein the newly formed block undergoes verification, is digitally signed to ensure its integrity and authenticity, and is subsequently transmitted securely to the cloud level for permanent storage within the blockchain framework. Over time, this iterative process results in the formation of a comprehensive and interconnected chain of blocks, symbolically representing the digital ledger’s continuous growth and expansion. Figure 3 illustrates the structural configuration of the quantum blockchain, highlighting its layered complexity and the dynamic interplay between various components of the system. Given the fundamental characteristic of quantum blocks as manifestations of quantum states, the application of traditional hash values is rendered ineffective. In contrast, the adoption of quantum entanglement as a mechanism for chain formation addresses the vulnerability of hash functions to sophisticated cryptographic attacks facilitated by quantum computing capabilities. This method capitalizes on the principles of quantum mechanics to significantly bolster the cryptographic robustness of blockchain infrastructures, effectively countering the advanced threat landscape introduced by the advent of quantum computing technologies. User authentication and block generation at the authority level follow a well-defined sequence of steps, which can be outlined as follows:
Fig. 3.
Diagram of the quantum blockchain architecture.
Initialization
The system utilizes a distributed quantum blockchain, where each block at the authority level is interconnected. Registered users possess the ability to measure quantum states and exchange information of both quantum and classical nature. To initiate access to the metaverse, the user undergoes an identity verification process with the authority level. Upon successful verification, the authority grants access to the user in the metaverse with a specific location.
Voting for authority node
The proposed MSSA integrates a QDPoS protocol, augmented by the Borda count voting mechanism, to facilitate the selection of representative authority nodes. Typically, the DPoS framework employs a voting mechanism to designate representative nodes tasked with the verification of blocks. Through the implementation of a voting mechanism, the computational resources traditionally allocated for mining activities can be substantially conserved. Within the MSSA framework, the election of selecting authority level is done through the voting process, where all the nodes within the selected area are involved. This methodology ensures a democratic and decentralized approach to maintaining the integrity and security of the blockchain. Within the voting process, m authority nodes are selected from the total user M active in the metaverse. Subsequently, 2m candidate nodes, given that , are elected through a democratic voting procedure.
However, not all authority nodes within the system are fully trustworthy. The presence of potentially malicious nodes could adversely affect block generation. Let us consider four types of malicious behavior, each denoted by f. Each f is associated with a weight , and represents the maximum acceptable level of this behavior. The types of f are as follows:
: This denotes the failure in block detection, where and .
: This represents the failure in node-to-node communication, where and is set to Max2.
: This denotes node failure characterized by a lack of response. In this case, and .
: This indicates the presence of other malicious behaviors. Assume and .
The inclusion of Borda voting within the QDPoS scheme aims to fairly select the authority nodes, ensure accountability for the behavior of the authority nodes, and implement punishment in cases of misconduct. MSSA framework offers a systematic approach to assessing malicious behavior within a network. A crucial element within the MSSA framework is the calculation of the malicious behavior weight ratio () for each node (i). This ratio quantifies the likelihood that a node engages in malicious behavior.
| 1 |
where represents the frequency of the specific behavior performed by the ith node. The following vote is legitimate to define the ith node:
| 2 |
where denotes the number of votes cast by the jth node in favor of the ith node during the t th round of block generation.
Following this, the nodes should be ranked based on their calculated effective voting power. Subsequently, the node possessing the highest effective voting power is designated as the authority node. This selection is predicated on the assumption that this node exhibits a lower propensity for malicious activity and concurrently enjoys a greater level of trust from the network participants, as evidenced by their accumulated voting power. The preference matrix P is expressed as:
| 3 |
here is total number of candidate participate in the voting, and
Subsequently, the MSSA framework calculates the preference value of the k th node for the i th candidate node, given =, from which the Borda score matrix is derived:
| 4 |
The Borda score of each candidate node is calculated as: . Candidate nodes are ranked according to their Borda scores. The top m nodes with the highest ranking become the authority nodes. The voting process and the candidate selection steps are shown in Algorithm 1.
Algorithm 1.
Quantum Voting for MSSA Framework
New block generation
After successful voting, a group of authority nodes is selected for validating and generating blocks. When a user wants to register on the metaverse platform, a new block is generated using some access information. The new block will not be stored on the blockchain immediately until the verification is complete. The user Alice combines , ,..., and makes access credential , where INFO could be mail, passport number, or any other personal identity verification information. The user combine this information () and sends the request to the authority level.
Block verification by authority node
To enhance fairness and accountability, the proposed blockchain model requires the signature of more than one authority node for the signing and validation of the block. For simplicity, consider two authority nodes AU1, and AU2 for a certain place PL1. Suppose that Alice wanted to join the metaverse in a specific place PL1. The steps are described as follows:
Block creation:
Step 1: Alice ask permission to authority to join to the metaverse place PL1. Upon request, AU1 and AU2 create randon secret key and same length as , respectively and send them via quantum channel to Alice. Importantly, if the random secret key and access credential are odd, then Alice replaces the last bit with two bits as
| 5 |
Step 2: After receiving keys from the authority nodes, Alice calculates the keys
| 6 |
where .
Step 3: Next, Alice split into two parts: and , where and . Alice divided its into parts as and and calculate:
| 7 |
| 8 |
The encrypted part and can be represented as:
| 9 |
| 10 |
where and are the first and second part
Where and represent the initial and subsequent segments of encrypted using and , respectively. Through the application of the exclusive-OR (XOR) operation, an additional encoded segment is generated, denoted as = , wherein signifies the XOR operation.
Alice generates new encoded parts 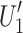 and
and 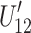 by checking the bit value of
by checking the bit value of 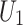 and
and 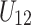 . If
. If 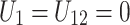 then
then 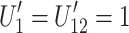 ; if
; if 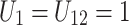 then
then 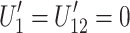 . Conversely, if none of the conditions are met,
. Conversely, if none of the conditions are met, 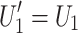 and
and 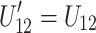 . Therefore,
. Therefore,
| 11 |
| 12 |
and
| 13 |
Alice uses the XOR function to encrypt with ’, resulting in transformed encrypted data as:
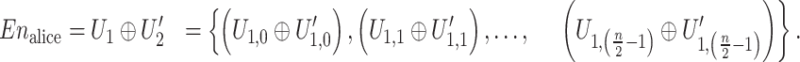 |
14 |
Ultimately, Alice determines the comprehensive credentials required for access as
| 15 |
Upon the authority’s signature, the encrypted value is recorded in the blockchain. Subsequently, the blockchain enables authorities or other members of the metaverse to authenticate the user without disclosing the actual data. It is pertinent to note that our proposed model exhibits subtle distinctions from the traditional blockchain network, wherein the principal objective is to achieve decentralization and equitable treatment within a centrally governed framework.
Block sign and verification:
Step 4: Alice sends an encrypted message and to the authority level. One of the nodes within the authority possesses a copy of the same secret keys that were shared with Alice. Assume that the authority node, is tasked with the verification and signing of blocks among other authorities for location PL1. Similarly, prepares 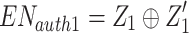 and using the same method employed by Alice, as mentioned above.
and using the same method employed by Alice, as mentioned above.
Step 5: In the preparation of her quantum states, Alice generates a sequence consisting of single-photon states, hereafter denoted as . These states correspond to and are structured in accordance with the standard Z-basis, which comprises the states , or alternatively, the X-basis, represented by . When considering the Y base, the coefficients incorporate the imaginary unit i, reflecting the complex nature of the quantum states involved.
Step 6: To evaluate the presence of any potential eavesdropping, Alice incorporates a sequence of decoy photons, symbolized as . These photons are randomly prepared in one of the quantum states from the set . This sequence serves as a test to detect any disturbance indicative of interception. Alice then intersperses these random decoy photons at intervals within the original sequence, , thus creating an augmented photon sequence. Once this integration is complete, Alice transmits the new sequence of to the authority level.
Step 7: Alice communicates the randomized positions and the corresponding measurement bases of the photon sequence to the authority node to facilitate the execution of single-photon measurements. subsequently analyses to ascertain the error rate present within the sequence. Should this rate exceed a predetermined threshold, the authority node is then obliged to reject and discard the entire block in question. In contrast, if the error rate falls below this threshold, proceeds to eliminate the decoy photons from the modified photon sequence and subsequently isolates the original photon sequence . Subsequently, is placed to reconstruct the energy levels , where is representative of .
Step 8: The key send by the authority node is served as public key for that authority node. And the XOR value of the all the keys sent from authority nodes is served as private key for that user. In this process Alice is signer and and authority node is the varifiyer. engages in a verification procedure whereby it computes the sum S by ; from its secret key which is used for ’s key. and that of Alice’s initial segment. If the result , this condition suggests a potential equivalence of Z and . The final verification comes after the total message comparison results.
Step 9: The second part of the block information is verified by , where is derived using the same process as by the authority node, using the same length information. If then and are equal and the blocks are verified. When all the authority node verify the information, then the information block is considered as verified. Finally, this verified block is stored in the blockchain at the cloud level. For subsequent verification, any authority-level member can retrieve the relevant information from the blockchain, along with the user’s access credentials. The authority can then validate the user’s authenticity partially by comparing this data with the key issued during the registration process.
Cloud level
Services and applications associated with the metaverse are hosted at the cloud level, ensuring scalability and accessibility. Furthermore, data blocks relevant to these services are secured within a blockchain infrastructure to enhance security and integrity. Upon the successful recording of such blocks, users are provided with access credentials and a public key by the overseeing authority. These credentials serve as essential tools for users to access, navigate, and communicate within the metaverse platform, ensuring a secure and authenticated user experience.
Formation of quantum blockchain
We employed quantum coin flipping game theory with N-party senario to constract blockchain network40. According to coin flipping game theory two parties can verify correctness of each other using network. Figure 4 shows a blockchain network where each block in the network can verify information in the network is not tampered. Upon successful verification of Alice’s user information block , the authority level transmits it to the cloud level. Within the cloud level, a predetermined bijective function B operates on , transforming it into a corresponding phase angle as . Following this, the state undergoes the rotation operation , resulting in the generation of:
| 16 |
where is a function dependent on . The quantum block encapsulates a function, , which stores the classical user information CR. The connection procedure of two block using coin flipping game is given below: Suppose two block A and B share measurement value on entangled state using:
| 17 |
where and are information carried by block A and B recpectively. carried the measurement value of B and carries the measurement value of A; and . In this way block Acan confirm the validity of B by looking its own qubit. Therefore, the probability of A is observed as:
| 18 |
Same way B observed as:
| 19 |
In equation (18) there is no way to trace the change of the block in the blockchain network. Another module called Witness is added to prevent block manupulation or trace. Witness module can be written as:
| 20 |
This Witness block can be used by both parties to prevent block manupulation. Therefore to confirm the correct:
| 21 |
For N blocks the the Witness can be check as:
| 22 |
Fig. 4.
Quantum blockchain circuit diagram using n-party coin flipping technique with n blocks.
Security analysis
Formal security analysis
To analyze MSSA protocol security two conditions must be met as (1) the eavesdropper Eve should not gain any information about the message and comprehensive credentials ; (2) the value of must remain enshrouded, so that Eve remains uncertain about it even if they know and the key provided by authority node. Before we prove that the MSSA protocol meets these requirements, let’s define the key concepts: the entropies and , which measures the uncertainty of these variables. Since the protocol deals with the random key strings, and each part of combined with the key is treated as random variable with uniform distribution over , giving . Calculating is more complex, as it depends on the probability distribution of the variabled, which are also uniformly random. Therefore, for any means the entire string K has an entropy .
Proof of requirement (1)
This requirement is mathematically expressed as bits, indicating that Eve gain no information about from knowing . To learn any , Eve need to know the corresponding pair of encoding symbols and . However, given the encoding, even with all , Eve cannot deduce the values of . The mutual information gained is:
| 23 |
To fully understand , Eve would also need to know , , which depends on XOR operations as follows:
| 24 |
From , it follows that . The information about that Eve can access is:
| 25 |
Thus, the information about gained by Eve is:
| 26 |
This shows that the protocol meets requirement (1).
Proof of requirement(2)
If Eve gains any information about , the scheme’s security is compromised. However, knowing does not reveal , as:
| 27 |
Even with all , Eve can not determine XOR values like because:
| 28 |
This relationship ensures the protocol meets requirement (2).
Entangle-measure attack
In an entangle-measure attack, an attacker measures quantum particles that have been entangled with those utilized in a quantum communication channel. Through this process, the attacker seeks to extract information about the ongoing communication without directly disturbing the quantum particles exchanged between the legitimate communicating parties, therefore it is difficult to detect.particles exchanged between the legitimate communicating parties. Therefore, suppose the attaker Eve tries to endure entangle-measure attack to get the information. As we can see in figure3, wants to teleport state to . informs about the user qubit transformation and keeps particle , sends particle to . To get information about the target qubit, Eve entangle the transmitted particle with the auxiliary particle through unitary operation. The unitary operation performed by the Eve is , , where , and is orthogonal tp , is orthogonal to . In a scenario where attacker Eve is present
| 29 |
| 30 |
It is important to mention that, if , Eve can not be detected. This may be recognized as , whare . The particle attacked by Eve becomes entangled with the auxiliary particles that it introduced, forming a direct product relationship between them. This means that even if Eve attracted the information being transmitted within the blockchain network, the entanglement with these auxiliary particles prevents any extraction of valid or meaningful data through entangle-measure attacks. The information remains entangled with the auxiliary states, rendering it ineffective for gaining any actionable insights about the original data.
Intercept-resend attack
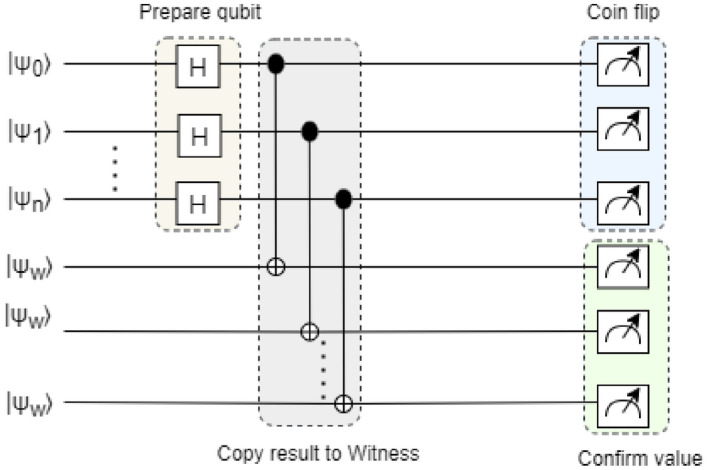
The attacker Eve may intercept particles between user and authorities to collect information unauthorized way and resend the fake sequence randomly to the authority node, same as block verification process discussed in step 6. In this case there is possibility to access information by measuring the intercept particles. However, this kind of attack by Eve will be detected as the decoy particles are randomly selected from and inserted into a sequence to create an augmented photon sequence. The probability of detection of Eve’s intercept-resend attack can be given as41- , where P(M) refers to the possibility of Eve selecting the correct basis for measurement so that she can hide her activity; P(E|M) denotes the avoiding of detection probability after selecting the right basis for measurement; P(D) is the probability of selecting wrong basis for measurement; P(E|D) refers to the avoiding of detection of wrong measurement; and is the number of decoy photons. If the positions and measurement bases of the decoy particles are unknown, the attack will inevitably introduce errors. When becomes sufficiently large, this type of attack will almost certainly be detected, as the probability of detection approaches 1. According to block verification step 7, the block will be discarded if the error exceeds the predetermined threshold.
Replay attack
In this attack scenario, the attacker intercepts a block of information and transmits a modified version to another node with the intent of disrupting the metaverse environment. Due to the indistinguishability of linear and diagonal polarization bases, the attacker faces a 50% error rate for each manipulated qubit.
In the context of single-particle decoy qubit transmission, the attacker’s success probability in extracting information is estimated to be . This can be mathematically expressed as42:
| 31 |
where represents the probability of successful information detection by the attacker in a single round, and N denotes the total number of information transfer rounds as shown in Figure 5. This equation highlights how the attacker’s success probability increases with the number of transmission rounds.
Fig. 5.
Probability of attack being detected under replay attack.
Outside attack
Suppose a scenario where metaverse user Alice and Bob wishes to communicate in metaverse place . Alice and Bob send quantum states, labeled and to a authority , utilizing decoy photon for security. After transmission, Alice and Bob announce the measurement bases and positions of the decoy photons, and reveals the measurement results. Then they verify the security of the communication by checking the decoy photon meaasurements and consistent. An outside attacker Eve has lack of knowledge about the measurement bases and positions. Therefore successful attack is challanging for Eve. Attack like entangle-resend and intercept-resend can be detected with a non-zero probability. For instance, if Eve measures the decoy photons with the correct basis, she might pass the eavesdropping check. However, using the incorrect basis gives a 50% chance of detection per photon, with the overall detection probability increasing as the number of decoy photons increases. As more decoy photons are used the detection probability approaches certainty. Furthermore, the protocol is secure against Trojan-horse attacks since photons are transmitted only once from the participants to . These security measures insures MAAS protocol is rubust against outsider attacks.
Authority attack
Traditional centralized authority structures introduce potential security vulnerabilities due to the possibility of dishonest or malicious actors. Our proposed system mitigates this risk by distributing encryption across multiple authorities in Eqs. (5) . Consequently, no single authority possesses the ability to decrypt the entirety of the information. Instead, each authority is only capable of decrypting the portion of the message encrypted with its respective key Eqs. (7) .
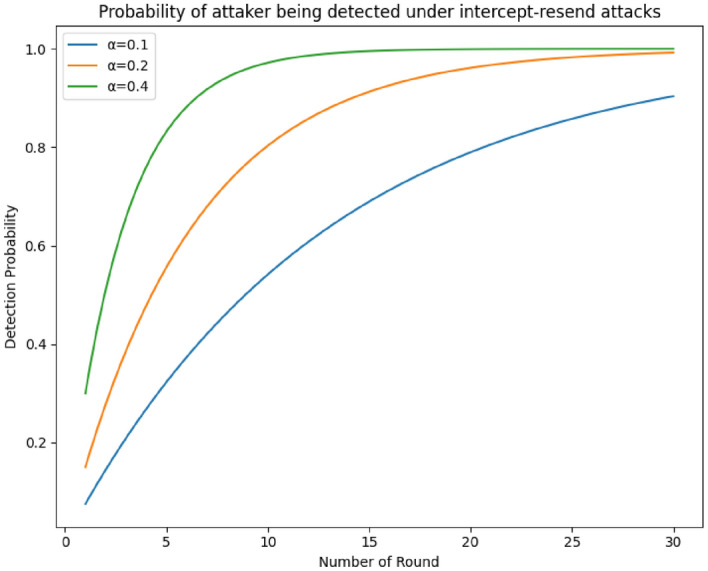
Result analysis
For proof of concept, we constructed a three-block quantum blockchain within the IBM quantum simulator Qiskit. To create three blocks, one needs to apply six qubits as shown in Figure 6. First three qubit is the information bit, and other three qubit is used for witness to prevent any alteration of the blockchain network. The blocks and are represented as and other three qubits are use to keep track of qubit respectively. In this blockchain, we assume a consensus mechanism is adopted where a function, , converts the classical bit information into block i. Here, i denotes the chronological order of the block, and maps to , and apply coin flipping technique to measure correctness of a block in the network. Individual peers select the weights by . We consider the phases of blocks as .
Fig. 6.
Diagram of the quantum blockchain architecture of three blocks and three witness blocks for MSSA.
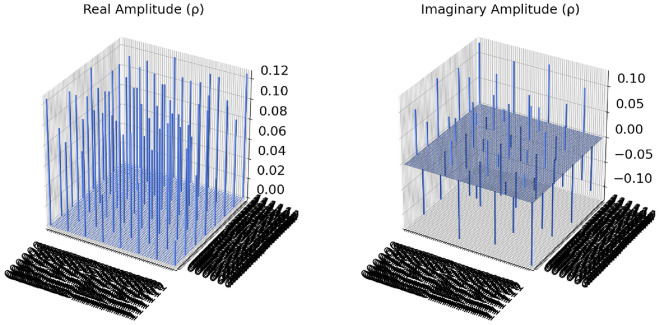
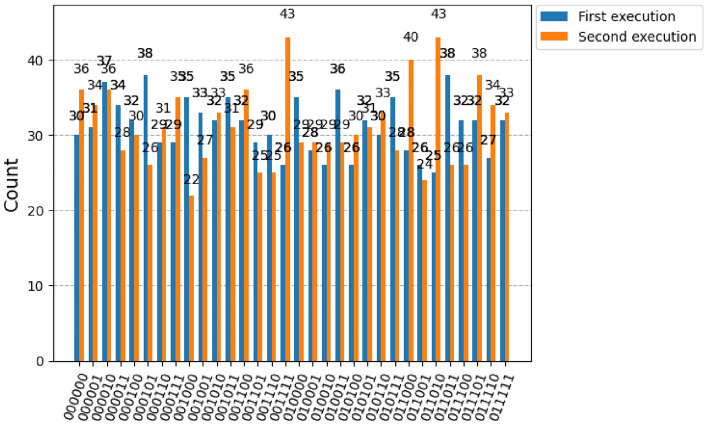
Figure 7 shows the density matrix of the 3-blocks quantum blockchain simulated in qiskit statevector simulator. The density matrix shows the coherence of the combination of positive and negative values, the imaginary part indicates the presence of quantum mechanics within the circuit. Our 3-blocks blockchain system takes six qubits, therefore two density matrices are created, one part for real amplitude and another part for imaginary amplitude. The diagonal elements of the matrix correspond to the probabilities of the system being found in one of the 36 possible computational basis states. The off-diagonal elements of the density matrix encode the quantum coherence between these basis states, reflecting the entanglement within the blockchain structure. Figure 8 shows the qubit measurement value using qiskit qsam simulator results after 1000 shots. The coincidences of the phrase of the entangaled particle is measured using rotation angle of the first block state is shown in Figure 9 projected onto a specific basis of the idler photons. As it can see that the first three qubit information is repeat in later three witness qubit respectively. Therefore is any block try to modify its information, others block easily indentify it by looking at witness block.Table 1 shows the comparative study of the existing authentication method for the metaverse and the novelty of our proposed method.
Fig. 7.
Density matrix of the 3-block blockchain circuit running on statevector-simulator.
Fig. 8.
Measured six-photon interference visibility of the polarisation-entangled states 3-block blockchain circuit.
Fig. 9.
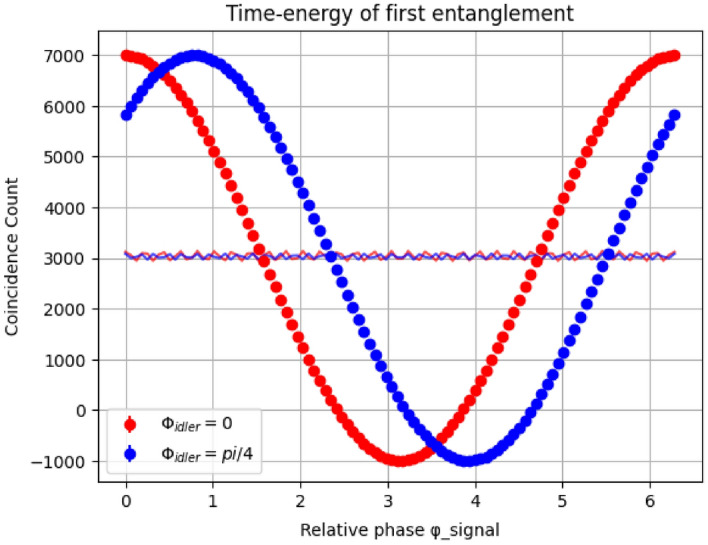
Two photon interference of the first entangled state.
Table 1.
Comparative analysis of existing approaches and the proposed approach in metaverse environments.
| Ref. | QAR | Hash function | MSM | Authority | Limitation |
|---|---|---|---|---|---|
| 6 | ✗ | ✓ | ✗ | Fully Trusted | A single verification authority across multiple independent platforms create a potential bottleneck, hindering scalability and efficiency |
| 7 | ✗ | ✓ | ✗ | Fully Trusted | Person-to-person authentication systems that utilize a trusted intermediary for user information storage present privacy risks |
| 8 | ✗ | ✓ | ✗ | Partially Trusted | Redundant authority used as certificate authority and platform server authority |
| 13 | ✗ | ✓ | ✓ | Fully Trusted | Not quantum-safe, and network communication costs is high |
| Proposed | ✓ | ✗ | ✓ | Untrusted, Multiple | Significant research gap exists in the current studies to protect from quantum attack. Therefore we propose a nobel MSSA framwork for metaverse authentication. |
*QAR: Quantum Attack Resistance. *MSM: Multiple Space in a Metaverse.
✓: Considered, ✗: Not Considered.
Conclusion
To ensure robust space authentication within the metaverse, this paper introduces a quantum blockchain-based secure authentication mechanism MSSA. Reflecting on real-world scenarios, multiple authorities are considered, acknowledging the potential existence of untrustworthy entities among them. To mitigate this risk, quantum secret multiparty computation is employed to first verify a user’s block and subsequently confirm the registered user. The authority node selection is facilitated through the Borda count mechanism. Consequently, the integration of quantum mechanisms within the MSSA framework assures enhanced security on the metaverse platform, thereby establishing a highly secure environment.
Acknowledgements
This work was partly supported by the Innovative Human Resource Development for Local Intellectualization program through the Institute of IITP grant funded by the Korea government (MSIT) (IITP-2024-RS-2020-II201612, 33%), the Priority Research Centers Program through the NRF funded by the MEST (2018R1A6A1A03024003, 33%), and the IITP-ICAN grant funded by the Korean government (Ministry of Science and ICT) (IITP-2024-2022-00156394*, 34%).
Author contributions
E. A. T. conducted the research strategies, methodologies, and writing. All authors reviewed the manuscript. D.-S. K. manages funding.
Data and code availability
No datasets were generated or analysed during the current.
Footnotes
The original online version of this Article was revised: The original version of this Article contained an error in the Acknowledgements section. It now reads: “This work was partly supported by the Innovative Human Resource Development for Local Intellectualization program through the Institute of IITP grant funded by the Korea government (MSIT) (IITP-2024-RS-2020-II201612, 33%), the Priority Research Centers Program through the NRF funded by the MEST (2018R1A6A1A03024003, 33%), and the IITP-ICAN grant funded by the Korean government (Ministry of Science and ICT) (IITP-2024-2022-00156394*, 34%).”
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
11/20/2024
A Correction to this paper has been published: 10.1038/s41598-024-80207-6
References
- 1.Tuli, E. A., Lee, J.-M. & Kim, D.-S. Integration of quantum technologies into metaverse: Applications, potentials, and challenges. IEEE Access 12, 29995–30019. 10.1109/ACCESS.2024.3366527 (2024). [Google Scholar]
- 2.Huynh-The, T. et al. Artificial intelligence for the metaverse: A survey. Engineering Applications of Artificial Intelligence 117, 105581. 10.1016/j.engappai.2022.105581 (2023). [Google Scholar]
- 3.Yfantis, V. & Ntalianis, K. Exploring the potential adoption of metaverse in government. In Jacob, I. J., Kolandapalayam Shanmugam, S. & Izonin, I. (eds.) Data Intelligence and Cognitive Informatics, 815–824 (Springer Nature Singapore, Singapore, 2023).
- 4.Metaverse seoul, the new continent of seoul (2022). [Accessed: Mar. 27, 2024].
- 5.Solly, R. & McArdle, J. Unlocking the military potential of the metaverse (2022).
- 6.Ryu, J., Son, S., Lee, J., Park, Y. & Park, Y. Design of secure mutual authentication scheme for metaverse environments using blockchain. IEEE Access 10, 98944–98958. 10.1109/ACCESS.2022.3206457 (2022). [Google Scholar]
- 7.Yang, K., Zhang, Z., Youliang, T. & Ma, J. A secure authentication framework to guarantee the traceability of avatars in metaverse. IEEE Transactions on Information Forensics and Security 18, 3817–3832. 10.1109/TIFS.2023.3288689 (2023). [Google Scholar]
- 8.Thakur, G. et al. A robust privacy-preserving ecc-based three-factor authentication scheme for metaverse environment. Computer Communications 211, 271–285. 10.1016/j.comcom.2023.09.020 (2023). [Google Scholar]
- 9.Kim, M. et al. Secure and privacy-preserving authentication scheme using decentralized identifier in metaverse environment. Electronics 12, 10.3390/electronics12194073 (2023).
- 10.Tuan, D. T., Duy, P. T., Hau, L. C. & Pham, V.-H. A blockchain-based authentication and access control for smart devices in sdn-enabled networks for metaverse. In 2022 9th NAFOSTED Conference on Information and Computer Science (NICS), 123–128, 10.1109/NICS56915.2022.10013416 (2022).
- 11.Yao, Y. et al. Dids-assisted secure cross-metaverse authentication scheme for mec-enabled metaverse. In ICC 2023 - IEEE International Conference on Communications, 6318–6323, 10.1109/ICC45041.2023.10279761 (2023).
- 12.Ruan, C. et al. A revocable and fair outsourcing attribute-based access control scheme in metaverse. IEEE Transactions on Consumer Electronics 1–1, 10.1109/TCE.2024.3377107 (2024).
- 13.Seo, J., Ko, H. & Park, S. Space authentication in the metaverse: A blockchain-based user-centric approach. IEEE Access 12, 18703–18713. 10.1109/ACCESS.2024.3357938 (2024). [Google Scholar]
- 14.Preskill, J. Quantum computing in the nisq era and beyond. Quantum 2, 79 (2018). [Google Scholar]
- 15.Ikeda, K. Chapter seven - security and privacy of blockchain and quantum computation. In Raj, P. & Deka, G. C. (eds.) Blockchain Technology: Platforms, Tools and Use Cases, vol. 111 of Advances in Computers, 199–228, 10.1016/bs.adcom.2018.03.003 (Elsevier, 2018).
- 16.Gottesman, D. & Chuang, I. Quantum digital signatures. arXiv preprint quant-ph/0105032 (2001). Available at: arXiv:quant-ph/0105032, Accessed: August 27, 2024.
- 17.Yin, H.-L., Fu, Y. & Chen, Z.-B. Practical quantum digital signature. Phys. Rev. A 93, 032316. 10.1103/PhysRevA.93.032316 (2016). [Google Scholar]
- 18.Prajapat, S. et al. Designing high-performance identity-based quantum signature protocol with strong security. IEEE Access 12, 14647–14658. 10.1109/ACCESS.2024.3355196 (2024). [Google Scholar]
- 19.Qin, J.-Q., Jiang, C., Yu, Y.-L. & Wang, X.-B. Quantum digital signatures with random pairing. Phys. Rev. Appl. 17, 044047. 10.1103/PhysRevApplied.17.044047 (2022). [Google Scholar]
- 20.Wang, M.-Q., Wang, X. & Zhan, T. An efficient quantum digital signature for classical messages. Quantum Information Processing 17, 275. 10.1007/s11128-018-2047-y (2018). [Google Scholar]
- 21.Jogenfors, J. Quantum bitcoin: An anonymous and distributed currency secured by the no-cloning theorem of quantum mechanics, 10.48550/arXiv.1604.01383 (2016). 17 pages, no figures, extended abstract; 2019 IEEE International Conference on Blockchain and Cryptocurrency (ICBC); 10.1109/BLOC.2019.8751473,1604.01383.
- 22.Ikeda, K. qbitcoin: A peer-to-peer quantum cash system. In Intelligent Computing: Proceedings of the 2018 Computing Conference, Volume 1, 763–771 (Springer, 2019).
- 23.Anderson, M. qbitcoin: A way of making bitcoin quantum-computer proof? IEEE Spectrum (2017). Accessed: 2024-07-24.
- 24.Rajan, D. & Visser, M. Quantum blockchain using entanglement in time. Quantum Reports 1, 3–11. 10.3390/quantum1010002 (2019). [Google Scholar]
- 25.Gao, Y. L., Chen, X. B., Xu, G. & et al. A novel quantum blockchain scheme base on quantum entanglement and dpos. Quantum Information Processing 19, 10.1007/s11128-020-02915-y (2020).
- 26.Li, Q., Wu, J., Quan, J., Shi, J. & Zhang, S. Efficient quantum blockchain with a consensus mechanism qdpos. IEEE Transactions on Information Forensics and Security 17, 3264–3276 (2022). [Google Scholar]
- 27.Nakamoto, S. Bitcoin: A peer-to-peer electronic cash system (Decentralized Bus. Rev, White Paper (Oct, 2008). [Google Scholar]
- 28.King, S. & Nadal, S. Ppcoin: Peer-to-peer crypto-currency with proof-of-stake. self-published paper, August 19 (2012).
- 29.Larimer, D. Delegated proof-of-stake (dpos). Bitshare whitepaper 81, 85 (2014). [Google Scholar]
- 30.Wang, W., Yu, Y. & Du, L. Quantum blockchain based on asymmetric quantum encryption and a stake vote consensus algorithm. Scientific Reports 12, 1–12 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tan, C. & Xiong, L. Dposb: Delegated proof of stake with node’s behavior and borda count. In 2020 IEEE 5th information technology and mechatronics engineering conference (ITOEC), 1429–1434 (IEEE, 2020).
- 32.Tseng, L. Recent results on fault-tolerant consensus in message-passing networks. In Structural Information and Communication Complexity: 23rd International Colloquium, SIROCCO 2016, Helsinki, Finland, July 19-21, 2016, Revised Selected Papers 23, 92–108 (Springer, 2016).
- 33.Yao, A. C. Protocols for secure computations. In 23rd annual symposium on foundations of computer science sfcs 1982, 160–164 (IEEE, 1982).
- 34.Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the forty-first annual ACM symposium on Theory of computing, 169–178 (2009).
- 35.Goldreich, O. A uniform-complexity treatment of encryption and zero-knowledge. Journal of Cryptology 6, 21–53 (1993). [Google Scholar]
- 36.Damgård, I., Pastro, V., Smart, N. & Zakarias, S. Multiparty computation from somewhat homomorphic encryption. In Annual Cryptology Conference, 643–662 (Springer, 2012).
- 37.Abulkasim, H., Farouk, A., Hamad, S., Mashatan, A. & Ghose, S. Secure dynamic multiparty quantum private comparison. Scientific reports 9, 17818 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Paing, S. N. et al. Counterfactual quantum byzantine consensus for human-centric metaverse. IEEE Journal on Selected Areas in Communications 42, 905–918. 10.1109/JSAC.2023.3345420 (2024). [Google Scholar]
- 39.Tuli, E. A., Golam, M., Lee, J.-M. & Kim, D.-S. Quantum superdense coding-based secure authentication for military metaverse. In Korea Communications Society Conference Proceedings, 835–836 (Korea Communications Society, 2024).
- 40.Ikeda, K. & Lowe, A. Quantum protocol for decision making and verifying truthfulness among n-quantum parties: Solution and extension of the quantum coin flipping game. IET Quantum Communication 4, 218–227 (2023). [Google Scholar]
- 41.Huang, X., Zhang, W. F. & Zhang, S. B. Efficient multiparty quantum private comparison protocol based on single photons and rotation encryption. Quantum Information Processing 22, 10.1007/s11128-023-04027-9 (2023).
- 42.Qu, Z., Meng, Y., Liu, B., Muhammad, G. & Tiwari, P. Qb-imd: A secure medical data processing system with privacy protection based on quantum blockchain for iomt. IEEE Internet of Things Journal 11, 40–49. 10.1109/JIOT.2023.3285388 (2024). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No datasets were generated or analysed during the current.