High-throughput phenotyping in maize and soybean genotypes using vegetation indices and computational intelligence

Abstract

Building models that allow phenotypic evaluation of complex agronomic traits in crops of global economic interest, such as grain yield (GY) in soybean and maize, is essential for improving the efficiency of breeding programs. In this sense, understanding the relationships between agronomic variables and those obtained by high-throughput phenotyping (HTP) is crucial to this goal. Our hypothesis is that vegetation indices (VIs) obtained from HTP can be used to indirectly measure agronomic variables in annual crops. The objectives were to study the association between agronomic variables in maize and soybean genotypes with VIs obtained from remote sensing and to identify computational intelligence for predicting GY of these crops from VIs as input in the models. Comparative trials were carried out with 30 maize genotypes in the 2020/2021, 2021/2022 and 2022/2023 crop seasons, and with 32 soybean genotypes in the 2021/2022 and 2022/2023 seasons. In all trials, an overflight was performed at R1 stage using the UAV Sensefly eBee equipped with a multispectral sensor for acquiring canopy reflectance in the green (550 nm), red (660 nm), near-infrared (735 nm) and infrared (790 nm) wavelengths, which were used to calculate the VIs assessed. Agronomic traits evaluated in maize crop were: leaf nitrogen content, plant height, first ear insertion height, and GY, while agronomic traits evaluated in soybean were: days to maturity, plant height, first pod insertion height, and GY. The association between the variables were expressed by a correlation network, and to identify which indices are best associated with each of the traits evaluated, a path analysis was performed. Lastly, VIs with a cause-and-effect association on each variable in maize and soybean trials were adopted as independent explanatory variables in multiple regression model (MLR) and artificial neural network (ANN), in which the 10 best topologies able to simultaneously predict all the agronomic variables evaluated in each crop were selected. Our findings reveal that VIs can be used to predict agronomic variables in maize and soybean. Soil-adjusted Vegetation Index (SAVI) and Green Normalized Dif-ference Vegetation Index (GNDVI) have a positive and high direct effect on all agronomic variables evaluated in maize, while Normalized Difference Vegetation Index (NDVI) and Normalized Difference Red Edge Index (NDRE) have a positive cause-and-effect association with all soybean variables. ANN outperformed MLR, providing higher accuracy when predicting agronomic variables using the VIs select by path analysis as input. Future studies should evaluate other plant traits, such as physiological or nutritional ones, as well as different spectral variables from those evaluated here, with a view to contributing to an in-depth understanding about cause-and-effect relationships between plant traits and spectral variables. Such studies could contribute to more specific HTP at the level of traits of interest in each crop, helping to develop genetic materials that meet the future demands of population growth and climate change.

Introduction

Population growth and the increasing demand for food require greater accuracy, efficiency in management, grain yield, competitiveness in the market and protection of the environment, so that policies can be put in place to guarantee food safety [1]. To do this, it is necessary to adopt more precise technologies for appropriate management and plant phenotyping. By linking genotype to phenotype, stress-tolerant and high-yielding plants can be quickly and effectively identified [2].

Indeed, developing genetically superior cultivars depends on the efficiency of phenotypic evaluation in the field. Traditional phenotyping methods are based on manual measurements and visual observations of traits, which makes the process time-consuming, labor-intensive, and less precise [3, 4].

Advanced plant phenotype evaluation techniques, such as high-throughput phenotyping (HTP), allows for evaluation more complex traits, such as growth, stress, resistance, pest and disease incidence, physiology, nutrition, and yield [3, 4]. HTP can be understood as a set of technologies, such as the use of remote sensing imaging, unmanned aerial vehicles (UAVs) or screening platforms to measure plant traits in a faster, more accurate, non-destructive and large-scale way. Digital phenotyping technologies, such as using canopy reflectance spectrometers in the visible/near-infrared (VIS/NIR) region, combined with robust evaluation approaches enables accurate and faster identification of superior genotypes in breeding programs [5].

Currently, there are several HTP tools available, but most involve the use of expensive equipment and skilled labor [6, 7]. Thus, there is a need to develop modern phenotyping methods for non-destructive measurement of several traits under different field conditions for selecting genetic materials, which is essential in breeding programs [8]. IVs are mathematical models with spectral bands that allow association with plant biomass. The most widely used IV is the normalized difference vegetation index (NDVI), because there is a high relationship between spectral behavior and morphological, physiological and biochemical processes of plants [4, 9]. However, the use of other IVs is as efficient or more efficient in this relationship with plant biomass.

A potential way to achieve this is to use vegetation indices obtained from remote sensing [10]. When compared to traditional phenotyping methods, HTP enables a larger number of plants to be screened over time, as well as providing highly accurate information on the plant's phenotype, which until now has been measured in the field with a high degree of bias, such as grain yield [10]. In conventional phenotyping, a single measurement of final yield for replicated plots in multiple seasons. However, grain yield is one of the traits with the lowest heritability in breeding, making traditional plant selection for yield more imprecise [11–13].

Nowadays, HTP approaches have been developed to cover complex plant traits such as growth, architecture, biotic and abiotic stresses, and grain yield [14]. Physical and chemical characteristics of the plants, such as canopy architecture, water status, and nitrogen concentration, for example, are captured by reflectance in VIS/NIR spectra, which can contribute to the identification of physiologically superior plants, such as water- and nitrogen-use efficient plants [11–13]. However, these approaches are still limited in terms of the range of species, covering small rosette plants such as Arabidopsis [11–13] and major cereal crops [15, 16]. Therefore, it is necessary to build models and generic solutions that allow the phenotypic evaluation of complex traits in crops of global economic interest such as soybeans and maize, evaluating highly complex traits such as grain yield in these species.

Although there are some publications that used vegetation indices (VIs) for HTP, to the best of our knowledge, little research evaluates these variables in a breeding program over different crop seasons in maize and soybean. Our hypothesis is that the best VIs to indirectly measure agronomic variables are different in both crops. The objectives were to study the association between agronomic variables in maize and soybean genotypes with VIs obtained from remote sensing and to identify computational intelligence for predicting GY of these crops from VIs as input in the models.

Material and methods

Field experiments

Comparative trials were carried out 30 maize genotypes in the 2020/2021, 2021/2022 and 2022/2023 crop seasons. In the 2021/2022 and 2022/2023 crop season, comparative trials were carried out with 32 soybean genotypes. The field trials were carried out in the municipality of Chapadão do Sul, Mato Grosso do Sul, Brazil, at the experimental area of the Federal University of Mato Grosso do Sul (UFMS/CPCS, Fig. 1). Region climate is Aw (Tropical Savannah) according to the Köppen-Geiger classification.

Fig. 1.

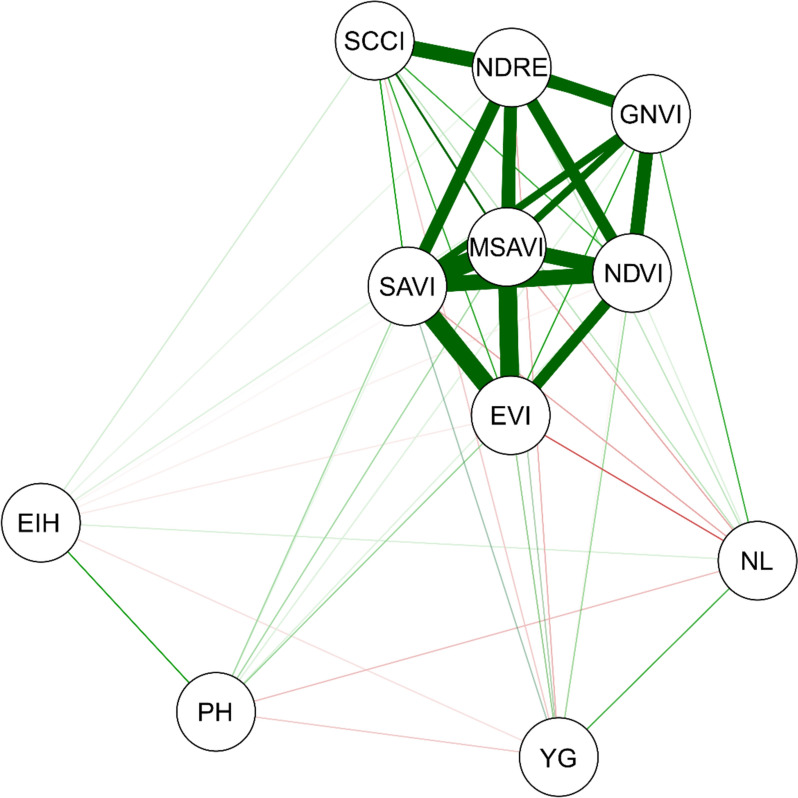
Pearson’s correlation network for the variables leaf nitrogen (NL), ear insertion height (EIH), plant height (PH), grain yield (YG) and vegetation indices (NDVI, SAVI, GNDVI, NDRE, SCCCI, EVI and MSAVI) evaluated in 30 maize genotypes during three crop seasons

A randomized block design with four replications was used in all trials. The plots consisted of seven 5 m-long rows spaced 0.45 m apart. A stand of 15 plants m⁻¹ was used for soybean, while three plants per meter was adopted for maize trials. The evaluations took place in the three central rows, disregarding 0.5 m from each end of the lines.

To set up each trial, the soil was desiccated with the herbicide Glyphosate at a dose of 6 L ha⁻¹. Subsequently, conventional soil preparation was carried out. Fungicide (pyraclotrobin + methyl thiophanate) and insecticide (fipronil) at 200 mL of the commercial product for every 100 kg of seeds were used in seed treatment. The soybean seeds were inoculated with Bradyrhizobium spp bacteria using a rate of 200 mL of concentrated inoculant for every 100 kg of seeds. The furrows were opened mechanically and 200 kg ha⁻¹ of the 04-20-20 formulation was applied, followed by manual sowing.

Weeds were controlled with the herbicide Gliphosate at a dose of 4 L ha⁻¹ and pests with tamethoxam + lambda-cyhalothrin at a dose of 200 mL ha⁻¹. No irrigation was performed in the experiments. To control diseases, two preventive applications were carried out in each crop using mancozeb at a dose of 1.5 kg ha⁻¹, the first when more than 50% of the genotypes were in full flowering and the second 30 days later. On these same dates, pest control applications were carried out using tiametoxam at a dose of 1.0 L ha⁻¹. Applications were carried out between 8:30 and 9:30 and between 15:30 and 17:00 to avoid product drift and hotter times of the day.

Obtaining vegetation indices

Vegetation indices (VIs) were obtained in all trials from UAV imagery using a Sensefly eBee RTK (Real Time Kinematics) fixed-wing remotely piloted aircraft with autonomous take-off, flight plan and landing control. The eBee was equipped with the Sensefly Sequoia multispectral sensor, which is a multispectral camera used in agricultural activities that uses the sunlight sensor and the additional 16 Mpx RGB camera for recognition. The multispectral sensor used was acquired with a horizontal field of view (HFOV) of 61.9°, vertical field of view (VFOV) of 48.5° and diagonal field of view (DFOV) of 73.7° as explained by [4], which acquires reflectance in the green (550 nm), red (660 nm), Rededge (735 nm) and near-infrared (790 nm) wavelengths, and has a brightness sensor that enables the calibration of the acquired values.

The information acquired at these wavelengths made it possible to calculate the VIs (Table 1), which were used in the computer algorithms. In each trial, an overflight was carried out at R1 stage, which corresponded to 60 days after emergence (DAE), period when most genotypes are in full bloom. Radiometric correction of the images was performed using Pix4Dmapper software, in conjunction with the camera’s reflectance calibration plate, which is specific to each device. This reflectance calibration plate contains detailed information on the reflectance rates for each wavelength captured by the multispectral sensor. The field calibration procedure was performed immediately before the flight, with the capture of the reference photo for calibration being managed by the e-Motion software. Since the flight had a maximum duration of 15 min, no new calibration was necessary after the flight was completed. The processing of the vegetation index models was performed based on the reflectance factor data obtained during the field images. The maps were manipulated and the Vegetation Indices extracted from the respective plots using the ArcGis software version 10.5.

Table 1.

Equations and references for vegetation indices (VIs) used for high-throughput phenotyping

VIs	Vegetation Index	Equation	References
NDVI	Normalized difference vegetation index	$NDVI=\frac{Nir-Red}{Nir+Red}$	[15]
SAVI	Soil-adjusted vegetation index	$SAVI=(1+\text{0,5})\frac{nir-red}{nir+red+\text{0,5}}$	[16]
GNVDI	Green normalized difference vegetation index	$GNDVI=\frac{Nir-Green}{Nir+Green}$	[17]
NDRE	Normalized difference red edge index	$NDRE=\frac{nir-rededge}{nir+rededge}$	[18]
SCCCI	Simplified canopy chlorophyll content index	$SCCCI=\frac{\mathit{NDRE}}{\mathit{NDVI}}$	[19]
EVI	Enhanced vegetation index	EVI = $\frac{nir-red}{(nir+6red-\text{7,5}green)+1}$	[20]
MSAVI	Modified soil adjusted vegetation index	$MSAVI=\frac{2Nir+1-\sqrt{{\left(2,N,i,r,+,1\right)}^2}-(8Nir-Red)}{2}$	[21]

RNIR near infrared reflectance, RGREEN green reflectance, RRED red reflectance, REDGE Red-edge reflectance, L soil effect correction factor

Agronomic traits evaluated in maize

Agronomic traits evaluated in maize crop were: leaf nitrogen content at full bloom (LNC), plant height (PH), first ear insertion height (EIH), and grain yield (GY). For the evaluations, ten plants were randomly harvested from each plot and the variables LNC, PH and EIH were measured in cm using a millimeter tape at 60 DAE. To determine GY, the central rows of each plot were harvested and the grains were weighed, corrected to 13% moisture and the values extrapolated to kg ha⁻¹. For leaf nitrogen analysis, diagnostic leaves were removed from the corn plant, which were washed with water, neutral detergent solution (0.1%), acid solution (HCl 0.3%) and deionized water, and then placed in paper bags and dried in a hot air oven at 65 ± 5 ºC until they reach a constant temperature. pasta. After drying the material, the samples were ground in a Wiley mill. Leaf nitrogen analyzes were carried out following the Bataglia methodology [17].

Agronomic traits evaluated in soybean

In the soybean experiments, the agronomic traits at maturity were: days to maturity (DM), plant height (PH), first pod insertion height (PIH) and grain yield (GY). DM consisted of the number of days from emergence to maturity in at least 95% of the plants in each plot. For the other assessments, ten plants were randomly harvested from each plot and the variables PH and PIH were measured in cm using a millimeter tape at 60 DAE. GY was estimated by harvesting the center rows of each plot, in which the grains were weighed, corrected to 13% moisture and the values extrapolated to kg ha⁻¹.

Statistical analyses

Initially, a joint analysis of variance was carried out for each variable evaluated in the maize and soybean experiments, according to the statistical model shown in Eq. 1.

$$Y_{\mathit{ijk}}=\mu +B_k+G_i+S_j+G{S}_{\mathit{ij}}+e_{\mathit{ijk}}$$ 1

wherein: Y_ijk is the observation in the k-th block evaluated in the i-th genotype and j-th crop year, µ is the overall mean, B_k is the block effect considered as fixed, G_i is the genotype effect considered as fixed, S_j is the crop effect considered as random, GS_ij is the random effect of the interaction between genotype i and crop j, and e_ijk is the random error associated with the observation Y_ijk.

Pearson correlations (r) between the traits evaluated in each experiment were obtained according to Eq. 2:

$$r_{\mathit{XY}}=\frac{CO{V}_{\left(\mathit{xy}\right)}}{\sqrt{{\widehat{\sigma }}_x^2}\times {\widehat{\sigma }}_y^2}$$ 2

where: COV_(XY) is the covariance between traits X and Y, ${\widehat{\sigma }}_x^2$ is the phenotypic variance of trait X and ${\widehat{\sigma }}_y^2$ is the phenotypic variance of trait Y. Correlation coefficients between the traits were expressed by a correlation network, in which the proximity between the nodes (traits) is proportional to the absolute value of the correlation between these nodes. Thickness of the edges was controlled by a cut-off value equal to 0.60, which means that just |$r_{\mathit{XY}}$|≥ 0.60 had their edges highlighted. Lastly, green color represents positive correlations, while red color highlights negative correlations.

In order to identify which indices are best associated with each of the traits evaluated in maize and soybean, path analysis was used, according to the model shown in Eq. 3. For this purpose, the multicollinearity of the X'X correlation matrix was initially diagnosed following the classification by Montgomery et al. (2001). In all cases, moderate multicollinearity was detected (condition number > 100). Therefore, the path analyses were carried out by adding a constant k = 0.05 to the diagonal of the X'X matrix to provide weak multicollinearity.

$$Y={\widehat{\beta }}_{1}NDVI+{\widehat{\beta }}_{2}SAVI+\dots +{\widehat{\beta }}_{7}MSAVI+p_{\epsilon }$$ 3

where: Y are the traits evaluated in maize and soybean experiments; β₁, β₂, …β₇ are the direct effects obtained for the VIs described in Table 1; p_ε is the residual effect of the analysis. VIs with a cause-and-effect relationship to each trait, i.e., high direct effects and in the same direction as their correlation with these traits, will be selected.

VIs with a cause-and-effect relationship with each trait evaluated in maize and soybean trials were used as independent explanatory variables in multiple linear regression model (MLR) and multilayer perceptron neural network (ANN). For this purpose, original datasets from each crop (three maize trials and two soybean trials) were divided into two subsets: training (80% of the data) and validation (20% of the data).

Multiple regression model tested for each trait with the selected VI is contained in Eq. 4. This model will be used as a control to verify the gain from using computational intelligence techniques.

$$Y={\widehat{\beta }}_{1}NDVI+{\widehat{\beta }}_{2}SAVI+\dots +{\widehat{\beta }}_{7}MSAVIY={\widehat{\beta }}_{1}I{V}_1+{\widehat{\beta }}_{2}I{V}_2+\dots +{\widehat{\beta }}_{i}I{V}_j+{\epsilon }_{\mathit{ij}}$$ 4

where Y is the traits evaluated in the maize and soybean experiments; β₁, β₂, …β_i are the regression coefficients obtained for the j-th VIs selected by the path analysis.

The input layer was comprised of the VIs selected by the path analysis; the output layer was comprised of the agronomic variable to be predicted. For the intermediate layers, a logistic activation function (fx) was applied to each neuron (Eq. 3), which uses as argument the scalar product of the input vector (x) and the weight vector (w) associated with that node.

$$f\left(x\right)=\frac{1}{1+e^{-x}}$$ 5

where: x is a binary value representing neuron activation (1) versus non-activation (0).

The training adopted was a feedforward type using the supervised approach. Thus, 3600 ANN topologies were tested, consisting of the following combination: two hidden layers (20 × 20 possibilities), three hidden layers (20 × 20x20 possibilities), and four hidden layers (20 × 20x20 × 20 possibilities). Only the 10 best topologies able to simultaneously predict all the agronomic variables evaluated in each crop were saved.

The following statistics were used to select the 10 best ANNs saved at both steps (training and validation): Pearson correlation ($r_{\mathit{XY}}$—Eq. 6) and root mean squared error (RMSE—Eq. 6).

$$r_{\mathit{XY}}=\frac{CO{V}_{\left(\mathit{xy}\right)}}{\sqrt{{\widehat{\sigma }}_x^2\times {\widehat{\sigma }}_y^2}}$$ 6

wherein: ${\mathit{COV}}_{(xy)}$ is the covariance between the observed (X) and estimated (Y) values; ${\widehat{\sigma }}_x^2$ is the variance of the observed values; ${\widehat{\sigma }}_y^2$ is the variance of the estimated values.

$$RMSE\left(\%\right)=\frac{100}{\underset{\_}{Y}}\sqrt{\frac{{\sum }_{i=1}^n{\left(Y_i-{\widehat{Y}}_i\right)}^2}{n}}$$ 7

wherein: ${\widehat{Y}}_i$ is the mean of the observed values; $n$ is the total number of observations.

Results

Maize trials

The block effect was non-significant (p < 0.05) for all the variables evaluated, while the genotype effect was significant only for the SCCCI (Simplified Canopy Chlorophyll Content Index) index (Table 2). However, there was significance for crop season and the genotype by crop season interaction (GxS) for all variables. The coefficient of variation was higher than 10% only for the ear insertion height (EIH) and grain yield (GY).

Table 2.

P-value of the joint analysis of variance for the variables leaf nitrogen (LNC), ear insertion height (EIH), plant height (PH), grain yield (GY) and vegetation indices (NDVI, SAVI, GNDVI, NDRE, SCCCI, EVI and MSAVI) evaluated in 30 maize genotypes during three crop seasons

Variable	Block	Genotype (G)	Crop season (CS)	GxCS	Mean	CV (%)
LNC	0.27	0.12	0.00	0.00	31.86	3.28
EIH	0.14	0.34	0.00	0.00	0.93	13.35
PH	0.26	1.00	0.00	0.00	1.87	6.89
GY	0.05	0.99	0.00	0.02	7540.56	19.21
NDVI	0.21	1.00	0.00	0.00	0.79	3.93
SAVI	0.28	1.00	0.00	0.00	0.58	5.07
GNVDI	0.29	0.42	0.00	0.00	0.71	2.34
NDRE	0.22	0.07	0.00	0.00	0.24	5.61
SCCCI	0.29	0.00	0.00	0.00	0.29	3.61
EVI	0.26	1.00	0.00	0.00	0.28	6.00
MSAVI	0.27	1.00	0.00	0.00	0.61	5.84

Pearson correlation network reveals a positive and high magnitude relationship between the VIs evaluated (Fig. 1). However, the association between these indices and the agronomic variables evaluated in maize was low. SAVI (Soil-Adjusted Vegetation Index) and EVI (Enhanced Vegetation Index) were closest to the EIH and plant height (PH) variables, while SAVI and NDVI (Normalized Difference Vegetation Index) were closest to GY and leaf nitrogen content (LNC).

Figure 1 Correlation network for leaf nitrogen (LNC), ear insertion height (EIH), plant height (PH), grain yield (GY) and vegetation indices (NDVI, GNDVI, NDRE, SAVI, MSAVI, EVI and SCCCI) assessed in 30 maize genotypes during three crop seasons

However, Pearson correlation coefficient does not show a cause-and-effect relationship between the variables, especially when some of them are highly correlated such as the VIs evaluated. For this reason, a path analysis was carried out to split the Pearson correlation values into direct and indirect effects on the main variable of interest.

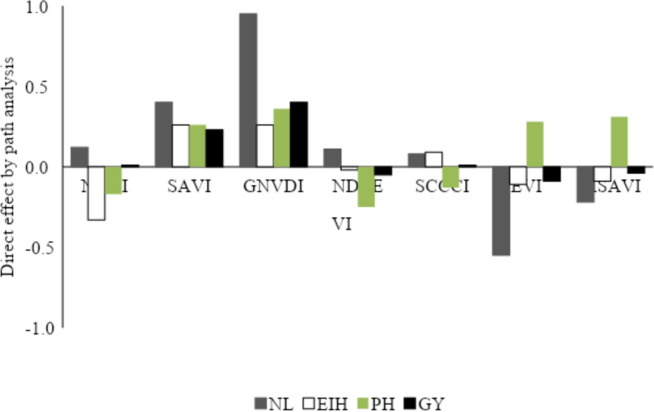
Figure 2 shows the direct effects of each VI evaluated on the agronomic variables of corn. The NDVI, NDRE (Normalized Difference Red Edge Index) and SCCCI have a direct effect of low magnitude on LNC. Similarly, EVI and MSAVI (Modified Soil Adjusted Vegetation Index) have a moderate direct effect on PH. SAVI and GNDVI have a positive direct effect of high magnitude on all the agronomic variables evaluated in maize. Therefore, these VIs were used in the computational intelligence analyses carried out.

Fig. 2.

Direct effect obtained by path analysis of vegetation indices (NDVI, SAVI, GNDVI, NDRE, SCCCI, EVI and MSAVI) on the variables leaf nitrogen (NL), ear insertion height (EIH), total height (PH), grain yield (GY) evaluated in 30 maize genotypes during three crop seasons

The accuracy values of the ten best topologies out of the 3600 tested for predicting maize agronomic variables are shown in Tables 3 and 4. All the topologies presented obtained higher correlation coefficient (r) values between the observed and estimated values compared to MLR for all agronomic variables in the training and validation steps. The best topology for NL reached values of 0.9 in validation, 0.48 for EIH, 0.8 for PH and 0.7 for YG.

Table 3.

Pearson's correlation between the values observed and predicted by the 10 best artificial neural networks selected and multiple linear regression (MLR) for predicting the variables leaf nitrogen (LNC), ear insertion height (EIH), total height (PH), grain yield (GY) in maize using the SAVI and GNDVI vegetation indices as input

Topology*	LNC		EIH		PH		GY
	T	V	T	V	T	V	T	V
2–8	0.77	0.79	0.40	0.40	0.69	0.70	0.29	0.30
4–10	0.80	0.82	0.41	0.40	0.68	0.70	0.33	0.35
5–10	0.81	0.82	0.44	0.45	0.71	0.72	0.45	0.46
6–6	0.83	0.83	0.42	0.43	0.70	0.70	0.41	0.42
8–8	0.84	0.85	0.44	0.45	0.73	0.73	0.44	0.47
2–4-8	0.85	0.85	0.44	0.46	0.75	0.78	0.61	0.62
2–6-8	0.87	0.87	0.45	0.45	0.75	0.76	0.63	0.63
2–10-10	0.87	0.87	0.45	0.46	0.76	0.76	0.67	0.70
4–4-8	0.88	0.88	0.46	0.47	0.75	0.77	0.66	0.67
4–8-2	0.89	0.90	0.47	0.48	0.77	0.80	0.68	0.69
MLR	0.64	0.65	0.39	0.39	0.51	0.52	0.28	0.30

^*the values between the lines refer to the number of neurons in each layer; T: training (80% of the data); V: validation (20% of the data)

Table 4.

Root mean squared error (%) between observed and predicted values from the 10 best artificial neural networks selected and multiple linear regression (MLR) for the for predicting the variables leaf nitrogen (LNC), ear insertion height (EIH), total height (PH), grain yield (GY) in maize using the SAVI and GNDVI vegetation indices as input

Topology*	LNC		EIH		PH		GY
	T	V	T	V	T	V	T	V
2–8	18.92	18.36	42.10	41.03	27.19	26.56	43.46	42.17
4–10	18.15	18.13	40.15	39.99	26.99	26.19	43.18	42.99
5–10	17.95	17.76	39.95	39.57	25.68	25.60	42.98	42.98
6–6	17.45	17.43	39.10	38.17	24.36	23.44	42.67	42.15
8–8	17.03	16.96	38.52	37.10	23.79	22.11	42.01	41.15
2–4-8	16.15	14.15	37.35	36.50	22.31	20.19	41.40	40.45
2–6-8	15.89	15.02	36.55	36.17	21.27	21.03	40.15	38.99
2–10-10	15.00	14.93	35.17	34.94	20.45	20.02	39.19	38.93
4–4-8	14.97	14.12	34.46	33.33	19.50	18.91	38.98	38.10
4–8-2	14.28	13.11	33.21	31.99	18.19	17.50	37.45	36.12
MLR	25.24	23.29	56.01	52.15	39.15	36.18	70.89	70.01

^*the values between the lines refer to the number of neurons in each layer; T: training (80% of the data); V: validation (20% of the data)

Following this pattern, the RMSE values between the values observed and estimated by the 10 best networks were lower than those obtained by the MLR in the training and validation steps for all agronomic variables, in which the MLR value achieved for NL was 23.29 in the validation and the topology with the lowest RMSE reached 13.11, for EIH the error was 52.15 in the evaluation and the topology with the highest error was 47.10, falling below the MLR with emphasis on the YG variable that reached RMSE of 70.01 for MLR and the topologies with the highest error approached 43, much lower than what was presented by the traditional technique. Overall, the two-layer topologies had lower r values and higher RMSE values than the three-layer topologies.

Soybean trials

Block effects were non-significant for all the variables evaluated in soybean crop (Table 5). Genotype effects were only significant for DM, PIH, and NDRE. These same variables showed a non-significant GxCS interaction, while this effect was significant for the other variables. Crop season effect was non-significant only for DM, plant height (PH) and NDVI. CV values were below 20% for all the soybean variables evaluated.

Table 5.

P-value of the joint analysis of variance for the variables days to maturity (DM), first pod insertion height (PIH), plant height (PH), grain yield (GY) and vegetation indices (NDVI, SAVI, GNDVI, NDRE, SCCCI, EVI and MSAVI) evaluated on 32 soybean genotypes during two crop seasons

Variable	Block	Genotype (G)	Crop season (CS)	GxCS	Mean	CV (%)
DM	0.45	0.00	0.99	0.87	106.49	3.12
PIH	0.32	0.04	0.00	1.00	8.15	19.16
PH	0.25	1.00	1.00	0.00	77.13	12.51
GY	0.06	0.28	0.02	0.04	3573.08	19.39
NDVI	0.34	0.42	1.00	0.01	0.66	9.96
SAVI	0.33	0.35	0.00	0.00	0.33	12.76
GNVDI	0.39	1.00	0.00	0.00	0.64	4.71
NDRE	0.41	0.01	0.00	0.00	0.17	8.57
SCCCI	0.38	0.46	0.00	0.03	0.26	10.79
EVI	0.41	0.20	0.00	0.00	0.14	16.06
MSAVI	0.36	0.32	0.00	0.00	0.30	15.42

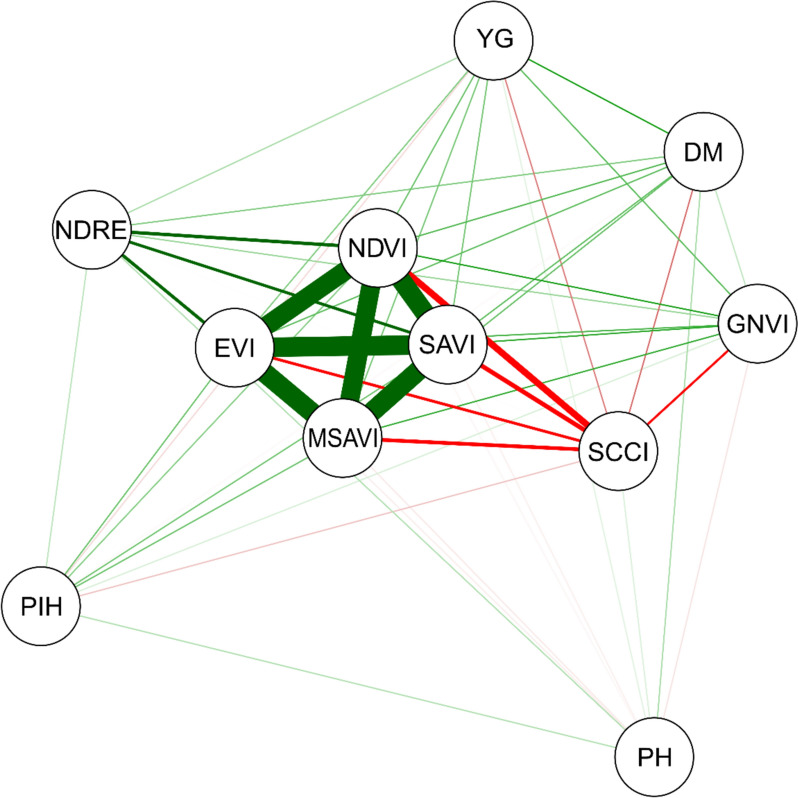
Figure 3 shows the correlation network obtained for the variables evaluated. NDVI and SAVI showed the strongest correlations with GY and DM. Conversely, MSAVI and SCCCI were correlated with the PIH and PH variables. However, it is important to note that the magnitude of these correlations is considered low as it is less than 0.30 in all cases.

Fig. 3.

Pearson's correlation network between the variables days to maturity (DM), first pod insertion height (PIH), plant height (PH), grain yield (YG) and vegetation indices (NDVI, SAVI, GNDVI, NDRE, SCCCI, EVI and MSAVI) evaluated in 32 soybean genotypes during two crop seasons

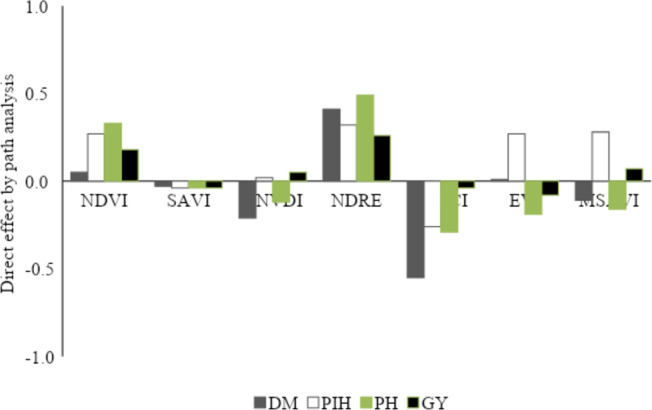
Direct effects of the VIs on each agronomic variable in the soybean are shown in Fig. 4. NDVI and NDRE indices had high-magnitude positive effects on all the variables. Therefore, these indices were used in the computational intelligence analyses to predict the agronomic variables in soybean.

Fig. 4.

Direct effect obtained by path analysis of vegetation indices (NDVI, SAVI, GNDVI, NDRE, SCCCI, EVI and MSAVI) on the variables days to maturity (DM), first pod insertion height (PIH), plant height (PH), grain yield (YG) evaluated in 32 soybean genotypes during two crop seasons

Tables 6 and 7 show the accuracy metrics of the 10 best topologies out of the 3,600 tested for predicting soybean agronomic variables. All the selected topologies obtained r values higher than and RMSE values lower than the MLR model for all the agronomic variables in the training and validation steps. As in the maize experiments, the two-layer topologies showed lower r values and higher RMSE values than the three-layer topologies. It is important to note that layers with more than 10 neurons were not found in any of the topologies selected in both cases. DM, PH and GY reached values ​​close to or greater than 0.5, indicating high accuracy especially for these variables that are difficult to predict due to the strong influence of the environment.

Table 6.

Pearson's correlation between the values observed and predicted by the 10 best artificial neural networks selected and multiple linear regression (MLR) for predicting the variables days to maturity (DM), first pod insertion height (PIH), plant height (PH), and grain yield (GY) in soybean using the NDVI and NDRE vegetation indices as input

Topology*	DM		PIH		PH		GY
	T	V	T	V	T	V	T	V
2–6	0.49	0.49	0.36	0.36	0.60	0.60	0.40	0.40
3–10	0.49	0.50	0.36	0.37	0.60	0.61	0.40	0.41
5–10	0.48	0.49	0.38	0.38	0.61	0.63	0.40	0.41
6–6	0.51	0.53	0.38	0.39	0.61	0.62	0.41	0.41
8–8	0.50	0.54	0.39	0.39	0.63	0.64	0.41	0.41
2–4-6	0.54	0.54	0.39	0.39	0.64	0.65	0.44	0.44
4–6-8	0.55	0.56	0.40	0.40	0.65	0.65	0.44	0.45
2–10-10	0.56	0.56	0.40	0.40	0.67	0.67	0.47	0.48
4–4-8	0.57	0.57	0.40	0.41	0.68	0.69	0.49	0.50
4–8-2	0.58	0.60	0.41	0.41	0.69	0.70	0.51	0.52
MLR	0.43	0.44	0.35	0.36	0.57	0.59	0.30	0.31

^*the values between the lines refer to the number of neurons in each layer; T: training (80% of the data); V: validation (20% of the data)

Table 7.

Root mean squared error (%) between the values observed and predicted by the 10 best artificial neural networks selected and multiple linear regression (MLR) for predicting the variables days to maturity (DM), first pod insertion height (PIH), plant height (PH), and grain yield (GY) in soybean using the NDVI and NDRE vegetation indices as input

Topology*	DM		PIH		PH		GY
	T	V	T	V	T	V	T	V
2–6	30.29	30.01	37.98	37.87	19.98	19.31	46.89	46.71
3–10	29.96	29.17	37.91	37.90	19.39	18.99	45.91	45.34
5–10	29.85	29.11	37.44	37.31	19.26	19.01	45.19	44.98
6–6	28.78	28.16	37.29	37.01	18.56	18.02	44.76	44.16
8–8	27.54	26.76	36.94	36.77	17.69	17.56	43.89	43.16
2–4-6	25.13	24.49	36.59	36.11	16.77	16.02	42.94	41.98
4–6-8	23.97	23.17	35.88	35.09	16.01	15.87	41.88	40.79
2–10-10	22.10	21.87	35.35	34.12	15.17	14.49	40.87	39.87
4–4-8	21.57	21.04	35.16	34.67	14.15	14.00	39.46	39.15
4–8-2	20.89	20.02	33.19	31.11	14.04	13.51	39.01	37.98
MLR	34.31	32.99	39.17	38.27	26.13	25.85	50.73	49.81

^*the values between the lines refer to the number of neurons in each layer; T: training (80% of the data); V: validation (20% of the data)

Discussion

The presence of genotype x crop season interaction for all the agronomic variables evaluated in the maize and soybean trials shows that climatic conditions from one crop season to the next affect the behavior of genotypes, especially changes in temperature and rainfall. By evaluating the phenotype using VIs, it is possible to quickly and accurately understand the relationship between genetic components and phenotypic expression [18]. Using VIs as an approach for evaluating and selecting genotypes in maize and soybean breeding programs is still recent in Brazil.

Overall, the vegetation indices showed low correlations with the agronomic variables of maize and soybean. There are several studies in the literature reporting low or moderate magnitude associations between vegetation indices and agronomic variables evaluated in maize [19] and soybean [20]. However, for vegetation indices to be used as criteria for selecting the best genotypes in these programs, it is necessary to evaluate them in different seasons, as was carried out in this research, as pointed out by [21].

Although important, investigating only the Pearson correlation coefficient between agronomic variables and vegetation indices is not enough. In order to establish a cause-and-effect relationship, it is necessary to use the path analysis proposed by [22]. This analysis splits the correlation values into direct effects, removing the influence of secondary variables by obtaining indirect effects. Its use is important due to the high correlation observed between the vegetation indices in the maize and soybean trials.

Path analysis made it possible to select specific VIs for each crop. For maize, the VIs with the greatest direct effect were SAVI and GNDVI. Both VIs have the capacity to speed up evaluations in crop genetic improvement programs, which is essential for sustaining high food production in order to meet population growth while maintaining a commitment to the environment [23]. Maize plants showing higher SAVI are often observed from 60 DAS onwards, a period of maximum leaf area exhibited by the hybrids [24–27]. According to [28] GNDVI is the most relevant index for estimating maize yields and biomass.

For soybean, the VIs with the greatest direct effect on agronomic variables were NDVI and NDRE. Santana et al. [29] reported a high association between NDRE and DM, while NDVI had a higher relationship with GY, a variable governed by many genes that are greatly influenced by environmental conditions. Santana et al. [29] also reported that NDRE has a cause-and-effect relationship with the plant cycle in soybean. High-throughput phenotyping is a crucial technological advance in the crop genetic improvement and is essential for selecting new genotypes with high grain yield and greater tolerance to multiple stresses, especially abiotic stresses caused by climate changes [23].

Using machine learning algorithms can assist in data processing, making the process more accurate and efficient. During the learning process, ANNs acquire the ability to respond correctly to tasks proposed to them by adjusting parameters, which can be supervised or unsupervised [30]. Computational intelligence techniques such as ANNs can provide an accurate estimation of the plant phenotype, performing non-linear tasks efficiently and with the flexibility to integrate data from multiple sources. [31, 32]. Elmetwalli et al. [33] state that the use of ANNs is a relatively simple, accurate, reliable and highly efficient way of processing data from large-scale and non-destructive approaches, such as HTP using VIs.

The experiments carried out demonstrate that HTP actions need to be directed to the crop that the breeder is working on. Our findings demonstrate that it is not recommended to use the same vegetation indices for HTP in corn and soybeans. The results reported here are encouraging for soybean and corn breeding programs, which annually evaluate hundreds or even thousands of genotypes in the traditional way. Now these programs can use specific VIs for each crop and precisely obtain the agronomic variables, which represents greater savings in financial resources.

Future studies should evaluate other plant traits, such as physiological or nutritional ones, as well as different spectral variables from those evaluated here, with a view to contributing to an in-depth understanding about cause-and-effect relationships between plant traits and spectral variables. Such studies could contribute to more specific HTP at the level of traits of interest in each crop, helping to develop genetic materials that meet the future demands of population growth and climate change. The flight date and the performance of multiple flights are crucial to optimize the performance of phenotyping based on spectral data. The flight in this study was performed 60 days after emergence, when the crop is at the peak of the photosynthetic period. However, flights on different dates allow capturing temporal variability, improving model calibration, identifying phenological patterns, improving results in more accurate and robust predictions, and are indicated for future work.

Conclusions

Path analysis enabled specific VIs to be selected for each crop to predict agronomic variables. Our findings reveal that SAVI and GNDVI indices have a positive and high magnitude direct effect on all agronomic variables evaluated in maize, while NDVI and NDRE have a positive cause-and-effect relationship with all soybean agronomic variables. The selected ANNs outperformed MLR, providing higher correlation and lower RMSE values when predicting agronomic variables using the VIs select by path analysis as input. In light of these findings, HTP using VIs with a higher cause-and-effect relationship on agronomic traits associated with computational intelligence models shows to be a promising tool for faster, accurate and large-scale evaluation of complex traits aiming to select genotypes for traits of interest in breeding programs.

Author contributions

P.E.T., L.P.R.T. and D.C.S. wrote the main manuscript text. F.H.R.B. and C.A.S.J. assisted in collecting spectral data. L.L.B. helped with computational intelligence analyses. All authors reviewed the manuscript.

Funding

No funding were avaliable.

Availability of data and materials

No datasets were generated or analysed during the current study.

Declarations

Ethics approval and consent to participate

Not applicable.

Competing interests

The authors declare no competing interests.