Weighing risks and benefits in the presence of competing risks

Abstract

Purpose of Review:

When competing events occur, there are two main options for handling them analytically that invoke different assumptions: 1) censor person-time after a competing event (which is akin to assuming they could be prevented) to calculate a conditional risk; or 2) do not censor them (allow them to occur) to calculate an unconditional risk. The choice of estimand has implications when weighing the relative frequency of a beneficial outcome and an adverse outcome in a risk-benefit analysis.

Recent findings:

We review the assumptions and interpretations underlying the two main approaches to analyzing competing risks. Using a popular metric in risk-benefit analyses, the Benefit-Risk Ratio, and a toy dataset, we demonstrated that conclusions about whether a treatment was more beneficial or more harmful can depend on whether one uses conditional or unconditional risks.

Summary:

We argue that unconditional risks are more relevant to decision-making about exposures with competing outcomes than conditional risks.

Analytic options when there are competing events

A competing event is an event that precludes the event of interest from occurring. When competing events occur in a time-to-event (i.e. survival analysis) setting, there are two main options for handling them analytically: 1) censor person-time after a competing event (which is akin to assuming they could be prevented); or 2) do not censor person-time after a competing event. In a closed cohort, one could estimate risk of the event of interest with option 2 by dividing the number of people who experience the event of interest by the number at risk at the start of follow-up; people who experience a competing event are included in the denominator of the estimator. In contrast, with option 1, person-time after a competing event is excluded from the denominator of the estimator.

When participants with a competing event are censored, such as when data are analyzed with a Cox proportional hazards model, the corresponding risk curves (often calculated as the complement of a Kaplan-Meier survival curve) are sometimes called conditional risk functions or cause-specific risk functions (we will use the term “conditional risk” throughout)(1,2). They are “conditional” because they are the risk curves that condition on removal of the competing events through some hypothetical intervention that does not alter the hazard of the event of interest. The conditional risk corresponds to the proportion of people who would have had the event of interest in a closed population/closed cohort if we had prevented all competing risks from occurring. Young et al. call contrasts of conditional risks “controlled direct effects,” in that they are the effect of the exposure that we would see if we set the value of the mediator (here, the competing event) to zero (i.e., if we prevented the competing event from occurring)(3). The hazards modeled in the Cox model are the instantaneous rate of the event of interest among people who have survived from both the event of interest and the competing event. These are often referred to as “cause-specific hazards” and the hazard ratio (HR) a “cause-specific HR.”

The other option for handling competing events is to estimate unconditional risks (often referred to as cumulative incidence functions or subdistribution risks; we will use the term “unconditional risk” throughout)(4, pp.69–70). The unconditional risk corresponds to the proportion of people who experience the event of interest in a closed population/closed cohort. If there are competing events, the sum of the unconditional risks for each event type will equal the risk of the composite event (experiencing either the primary or competing event). The Aalen-Johansen estimator is commonly used to estimate the unconditional risks(5–7). The conditional risk will always be greater than the unconditional risk in the presence of competing events because, when people who have a competing event are censored, the Kaplan-Meier estimator imputes for them an event time for the event of interest(8). Young et al. refer to contrasts of unconditional risks as “total effects,” in that they incorporate the direct effect of exposure on the outcome of interest and the indirect effect of exposure that goes through the competing event(3). The Fine and Gray subdistribution PH model produces subdistribution hazard ratios that correspond to inference from the unconditional risk functions(9). The two analytic choices laid out here, as well as terms commonly used for each risk function, are outlined in Table 1.

Table 1.

Summary of terminology and approaches

Approach	Censor person-time after a competing event	Do not censor person-time after a competing event
Terms for risk	Conditional risk Cause-specific risk Pure risk	Unconditional risk Subdistribution risk Cumulative incidence function Absolute risk
Estimators for risk	Complement of the Kaplan-Meier or the Nelson-Aalen estimator of survival	Aalen-Johansen estimator
Interpretation	Risk that would be observed if competing events could be prevented without altering the cause-specific hazard of the event of interest; controlled direct effects (where value of the mediator – the competing event – is set to zero)	Proportion of the cohort who would experience the event of interest in a closed cohort where competing events were allowed to occur; total effects (including any effects on risk of the event of interest that go through the competing event)
Proportional hazards/model	Cox proportional hazards model; cause-specific hazards	Fine & Gray subdistribution hazards model; subdistribution hazards

Interpreting estimands when there are competing events

There is a common perception, perpetuated by several seminal papers on analyzing data in the presence of competing events, that cause-specific HRs and conditional risks are somehow more inherently etiologic than subdistribution HRs and unconditional risks (10–12), whereas the primary utility of the unconditional risks is for planning or resource allocation(10–12). For example, Lau et al. say the “[cause-specific HR] may be better suited for studying etiology of diseases, whereas the [subdistribution HR] has use in predicting an individual’s risk or allocating resources(12, p.245).” Andersen et al. say “cause-specific hazards may be more relevant when the disease aetiology is of interest, since [they quantify] the event rate among the ones at risk of developing the event of interest. [Unconditional risks] are easier to interpret and are more relevant for the purpose of prediction(10, p.869).” Finally, Koller et al. say “we believe that etiology/efficacy hypotheses in the presence of competing risks are most naturally formulated in terms of cause-specific hazards. This allows for a ‘direct’ formulation of the effect of exposure on the instantaneous forces that drive the patients remaining at risk at each time point t, that is, those without any prior event(11, p.1092).”

The difference between “etiology” and causation (clearly assumed in these publications) and the definition of an “etiologic effect” are not provided by any of the authors making these assertions. Furthermore, these assertions are not rationalized, other than to point out that, 1) in the absence of any differences in the cause-specific hazards of the outcome of interest associated with some exposure, we might see differences in the unconditional risks that result from shifts in the number of people who remain at risk to develop the event of interest (if the exposure causes or prevents the competing event); and 2) the cause-specific hazards represent forces acting on people still at risk whereas the subdistribution hazard includes people in the denominator who are no longer at risk (i.e., those who already had a competing event). The second argument seems to be that, because the cause-specific hazards measure the development of disease (or the event of interest) only among people still at risk to experience disease, they must quantify the entire etiologic process, ignoring the fact that part of the etiologic effect might be in shaping who remains at risk(3,13). However, one can simulate data in which some individual characteristic (e.g., frailty) is associated with the cause-specific hazard of the event of interest and the competing event, while exposure only alters the cause-specific hazard of one event, but if the exposure interacts with the characteristic (e.g., frailty), the exposure will end up being associated with a non-null cause-specific HR for the other event. Thus, even simulating data where there is no “etiologic” effect of exposure on some outcome cannot guarantee that the cause-specific HR will reflect the “etiologic” effect. Beyond the choice of how to handle competing events, there are cogent arguments that HRs – cause-specific or subdistribution – do not have a causal interpretation(3,13,14) because the denominator of the hazards changes over time and hazards are therefore subject to selection bias. However, as regards Koller et al.’s statements about cause-specific hazards providing a “‘direct’ formulation of the effect of exposure on the [outcome]”(11), we suggest reading Young et al.(3) for a clear definition of the causal effect estimated by a contrast of conditional risks as the (controlled) direct effect of exposure on the event of interest not mediated by the competing event. This interpretation is only valid under certain untestable and often unmet assumptions. In contrast to assertions by previous scholars that unconditional risks do not have a causal interpretation(10–12), Young et al. clarify that contrasts of unconditional risks can equal the total effect of exposure on the event of interest, again under certain assumptions.

While our focus has been on the causal interpretation of contrasts of risks or hazards calculated under different assumptions, all the cautions about the assumptions required to interpret conditional risks or rates apply to descriptive estimands as well(15). If one is interested in describing the incidence of some event as it occurs in the real world, it is usually antithetical to that goal to report the conditional risk without specifying the real-world intervention that would completely and instantaneously prevent all the competing events from occurring(15–17). For example, the oft-cited 1-in-8 (12.6%) lifetime risk of developing breast cancer is a conditional risk(18). The lifetime risk of developing breast cancer that does not assume other causes of death could be prevented (the unconditional risk) is only 8.4%(19). While it is a type III error to interpret parameter estimates from a descriptive query as causal effects,(20) we might be interested in contrasts of risks or rates to quantify a disparity. In that case, inappropriate adjustment (e.g., for competing risks) would lead us to inaccurate conclusions about the magnitude of the disparity(21). There may be some scenarios in which estimating a conditional risk is warranted – for example, estimating the risk of spontaneous abortion while censoring induced abortions that are not undertaken for an indication that would have led to a spontaneous abortion. For a more complete discussion of analytic choices for descriptive estimands when there are competing events see (15,22).

Herein, we discuss the implications of the choice of estimand (conditional risks or unconditional risks) when weighing risks and benefits in pharmacoepidemiologic research.

Risk-benefit analyses

Risk-benefit analyses are fundamentally questions about weighing the probability of experiencing a beneficial outcome (e.g., cancer remission, survival from cardiovascular disease death) against the probability of experiencing a harmful outcome (e.g., gastrointestinal distress, kidney damage, or death) arising from some clinical treatment. Harmful outcomes (colloquially, “risks”) exist along a spectrum from self-limiting adverse events (such as nausea upon administration) that should be monitored or managed while a patient remains on the treatment under consideration, to serious adverse events (including death) that preclude treatment continuation.

When interventions – in this example, drugs – affect multiple outcomes, all outcomes should be considered when evaluating the causal effects of the interventions(23,24). Serious adverse events that preclude patients from experiencing the beneficial effects of a drug should be considered competing events for the beneficial outcome of interest. However, even the “mildest” adverse events might alter the hazard of the beneficial outcome of interest – e.g., if patients treated with immune checkpoint inhibitors experience an immune-related adverse event that is a marker that the drugs are working (albeit non-specifically)(25). Some adverse events that do not completely preclude the beneficial outcome of interest are so unpleasant that patients may implicitly (and epidemiologists could explicitly) discount additional survival time conferred by the drug in the presence of these adverse events. Indeed, a Benefit-Less-Risk analysis explicitly calculates the net benefit associated with a drug as the probability of a beneficial outcome (the event of interest) minus the probability of an adverse outcome (the competing event), where the probability of the adverse outcome is weighted by a measure of its “seriousness”. The worst adverse event receives a weight of 1, equal to the weight implicitly given to the beneficial outcome, while a less serious adverse event receives a weight <1, and an adverse event without any safety concerns might receive a weight of 0 – that is, the decision about whether or not to take a drug would only depend on the probability of receiving a benefit(26,27).

Similarly, beneficial outcomes may or may not be competing events for adverse outcomes. For example, achieving cancer remission might mean that a cancer therapy can be discontinued and people would no longer be at risk of, and thus would be precluded from, experiencing toxicity from ongoing therapy (i.e., remission is a competing event for toxicity). In contrast, people with HIV who achieve viral suppression on antiretroviral therapy do not discontinue their antiretroviral medications and thus viral suppression is not a competing event for adverse events.

When harmful outcomes (adverse events) preclude the occurrence of the beneficial outcome, and vice versa, we should account for both outcomes as competing events. Similar principles apply if the beneficial and harmful outcomes constitute semi-competing events (i.e., one event is a competing event for the other but not vice versa) as in the HIV treatment example above(28,29). We illustrate the potential impact of competing events by focusing on one risk-benefit metric, the Benefit-Risk Ratio.

The Benefit-Risk Ratio can be calculated as the Number Needed to Harm (NNH) divided by the Number Needed to Treat (NNT), where NNH is the inverse of the risk difference (RD) for the effect of the drug on the adverse event, and NNT is the inverse of the RD for the effect of the drug on the beneficial outcome. A Benefit-Risk Ratio >1 implies the treatment does more good than harm, whereas a Benefit-Risk Ratio <1 implies the treatment does more harm than good(27). In general, it is not specified whether the “risks” used in these calculations should be conditional or unconditional risks, but the default is typically conditional risks(27). However, when the beneficial and harmful outcomes are competing events for one another, and the incidence of the competing event is non-trivial, the conditional risk function will overstate the benefit of a drug because it imputes beneficial events for people who are censored with the competing event(8,30). It will also overstate the risks of the drug because it imputes adverse events for people who are censored due to having the outcome of interest. The differences between the unconditional and conditional risks will only perfectly balance each other out in the rarest of circumstances. Thus, using conditional risk functions might lead to inappropriate conclusions about the risk-benefit balance.

A toy example

Imagine an oversimplified example where we randomize 200 people with Stage IIB non small-cell lung cancer, pre-existing autoimmune disease, and COPD to adjuvant immune checkpoint inhibitor (ICI) therapy (i.e., subsequent to surgery/radiation) or to placebo on top of standard platinum doublet chemotherapy. We simulated data such that the drug shortens the time to both cancer remission and severe (i.e., dose limiting) or fatal drug toxicity. ICI therapy can confer tumor shrinkage and remission, and potentially dose-limiting or fatal autoimmune toxicity (particularly in this subgroup of patients with pre-existing autoimmune disease and COPD)(31,32), through the same underlying mechanism of action(25). We simulated times for each event type, took the minimum of the simulated times and the end of administrative follow-up, and assigned an event type indicator equal to the event that occurred first. The simulated data and code to analyze it are included in the Appendix and results are summarized in Table 2. (We ignore random error in our toy example.)

Table 2.

Toy data demonstrating two alternate calculations of the Benefit-Risk Ratio

Data	Standard of Care	Drug
Number at start of follow-up	100	100
Remission (Benefit)	13	54
Severe or fatal toxicity (Harm)	1	39
Censored	86	7
Conditional Risk
Cause-specific HR, Remission (Benefit)		10.61
Cause-specific HR, Severe/fatal toxicity (Harm)		112.47
Risk Remission (Benefit)	0.13	0.75
Risk Severe or fatal toxicity (Harm)	0.01	0.72
RD Remission (Benefit) → NNT	0.	0.75–0.13 = 0.62 → 1.61
RD Severe or fatal toxicity (Harm) → NNH	0.	0.72–0.01 = 0.71 → 1.41
Benefit-Risk Ratio (NNH/NNT)		1.41/1.61 = 0.87
Unconditional Risk
Subdistribution HR, Remission (Benefit)		5.87
Subdistribution HR, Severe/fatal toxicity (Harm)		49.07
Risk Remission (Benefit)	0.13	0.54
Risk Severe or fatal toxicity (Harm)	0.01	0.39
RD Remission (Benefit) → NNT	0.	0.54–0.13 = 0.41 → 2.45
RD Severe or fatal toxicity (Harm) → NNH	0.	0.39–0.01 = 0.38 → 2.64
Benefit-Risk Ratio (NNH/NNT)		2.64/2.45 = 1.08
Semi-competing Risk: Benefit precludes harm, harm does NOT preclude benefit
Remission (Benefit)	15	85
Side-effect (Harm)	1	39
Risk Remission (Benefit; no competing risks)	0.13	0.75
Unconditional Risk Side-effect (Harm)	0.01	0.39
RD Remission (Benefit) → NNT	0.	0.75–0.13 = 0.62 → 1.61
RD Side-effect (Harm) → NNH	0.	0.39–0.01 = 0.38 → 2.64
Benefit-Risk Ratio (NNH/NNT)		2.64/1.61 = 1.64
Semi-competing Risk: Harm precludes benefit, benefit does NOT preclude harm
Remission (Benefit)	13	54
Side-effect (Harm)	2	75
Unconditional Risk Remission (Benefit)	0.13	0.54
Risk Death/Toxicity (Harm; no competing risks)	0.01	0.72
RD Remission (Benefit) → NNT	0.	0.54–0.13 = 0.41 → 2.45
RD Death/Toxicity (Harm) → NNH	0.	0.72–0.01 = 0.71 → 1.41
Benefit-Risk Ratio (NNH/NNT)		1.41/2.45 = 0.58

At the end of one year of follow-up, in the placebo arm, 13 people experienced complete cancer remission and 1 had to stop treatment due to severe or fatal toxicity. In the ICI arm, 54 people experienced complete cancer remission, but 39 people died or had to stop treatment due to severe toxicity. Thus, out of 100 people, this drug benefits 41 more people than the standard of care alone, but 38 more people experience severe or fatal drug toxicity. Do the benefits of this drug outweigh the harms?

Our conclusions about benefits and harms depend on the causal estimands used to summarize the drug’s effects. Using the conditional risks, we would report that the drug increased the probability of cancer remission by 0.62(Figure 1A) and increased the probability of fatal drug toxicity by 0.71(Figure 1C). The Benefit-Risk Ratio using the conditional risks is therefore 0.88, which implies the drug does more harm than good.

Figure 1.

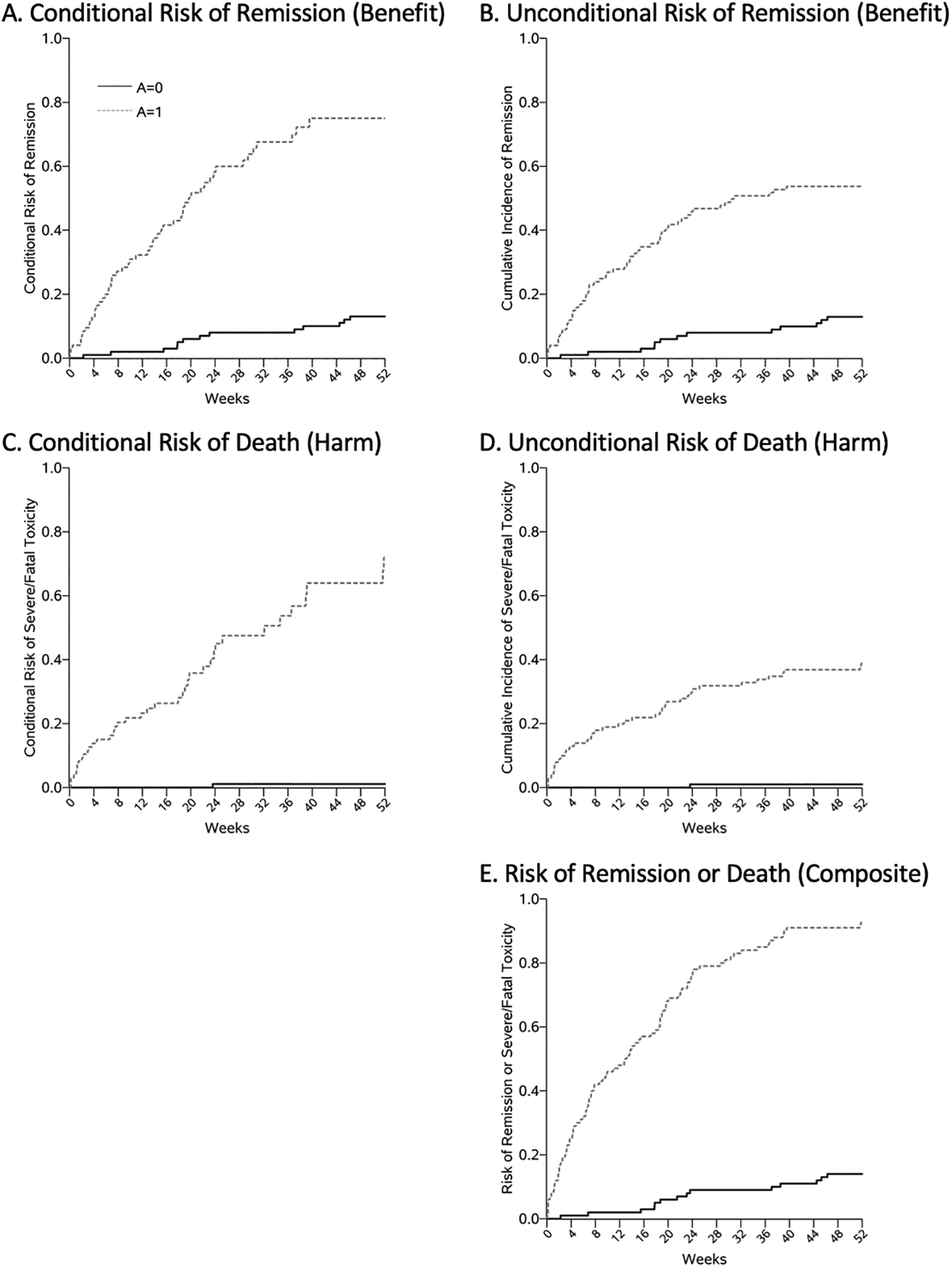
In contrast, if we use the unconditional risks to calculate the Benefit-Risk Ratio, we would estimate the RD for cancer remission to be 0.41 (Figure 1B) and the RD for fatal drug toxicity to be 0.38 (Figure 1D). Then the Benefit-Risk Ratio using the unconditional risks is 1.08, which implies the drug does more good than harm.

So we did our analysis two different ways and came up with conflicting answers. Which is correct? They are both correct under different assumptions. The estimand we prefer should depend on some sort of utility function for the beneficial and the harmful outcome(33,34) (in our example let us imagine the utility functions are approximately equal) and on the assumptions we are willing to accept as plausible.

If we assume that the adverse events could be managed and their incidence reduced or eliminated through some actual intervention, the conditional risk would reflect the true benefit of the drug (absent any additional benefits or harms induced by the intervention to prevent the competing event). But the conditional risk typically reflects a hypothetical scenario rather than the reality that patients are facing. Therefore, in most cases, inference based on unconditional risks is most relevant for patients. Unconditional risks do not require imagining a hypothetical intervention that does not exist, or attributing an untested assumption (no effect on the cause-specific hazards of the event of interest) to an actual intervention that does exist. When an actual intervention to prevent competing events does exist, we could directly model the joint effect of the drug and the intervention.

Cause-specific hazard ratios or conditional risks censor person-time after a competing event and censoring is assumed to be independent of the risk of the outcome (perhaps conditional on some variables including exposure). The cause-specific hazards of beneficial and harmful events may be independent of one another. For example, methadone can prevent opioid overdoses but typically, Opioid Treatment Programs require people come daily to the center to get their methadone. People might be precluded from experiencing the beneficial effects of methadone if they are at higher risk of dying in a traffic accident. In this case, conditional risks might be of interest because one could imagine an intervention on the competing event that is independent of the estimated effects of the treatment on the event of interest (“what would be the effect of methadone on opioid overdoses if we could eliminate traffic-related deaths through multi-dose dispensing?”) However, even if the biological pathways by which a treatment influences the harmful and beneficial outcomes are somehow completely orthogonal to one another, if there are any underlying patient factors (e.g., frailty) that were related to both the treatment effect on one outcome and the hazard of the other outcome, the cause-specific hazards will not be disentangleable and the assumptions underlying the conditional risks will be untenable. For example, in our example of ICIs, patients who are susceptible to the beneficial effects of the drug (whose immune system is effectively up-regulated by the ICIs) are the same people who are at higher risk of an immune-related adverse event (because their immune system was too up-regulated). There is no meaningful interpretation (given the current state of the science) of the direct effect of ICIs on cancer remission not through these adverse, competing events.

Some thoughts on semi-competing events

When the harmful outcome does not preclude the beneficial outcome from occurring, one might estimate the risk of the beneficial outcome without censoring person-time after a harmful outcome and use that in a risk-benefit ratio combined with the unconditional risk of the harmful outcome (appropriately treating the beneficial outcome as a competing event).

Using the same toy example data from above, we assume that the harmful outcome is not death but perhaps a temporary or medically manageable side effect of the drug. We calculated time to remission (without censoring person-time after an adverse event) using the complement of the Kaplan-Meier estimator and we calculated the unconditional risk of the side effect (where cancer remission is a competing event for experiencing a side effect). Then the Benefit-Risk Ratio was 1.64, demonstrating that the benefits outweigh the harms more definitively than when the adverse event was a competing risk for the benefit (when it precluded remission from occurring, resulting in fewer people able to experience remission). Briefly, if we assumed the harmful outcome was a competing risk for the beneficial outcome (e.g., severe or fatal toxicity) but the beneficial outcome did not preclude a harmful outcome (e.g., if people with cancer remission needed to continue the drug and could go on to die of drug toxicity), the Benefit-Risk Ratio was 0.58, indicating that harms outweighed the benefits (Table 2). The simulated data and code to analyze it are included in the Appendix and results are summarized in Table 2.

In this example, we used standard Benefit-Risk Ratios that discretize time and summarize the total number of events at one year of follow-up. Standard Benefit-Risk Ratios ignore the timing of the events and weight events with a utility of 0 or 1. A more nuanced treatment of risks and benefits of a treatment might incorporate metrics such as restricted mean survival time (35–37) or utility functions that weigh “how bad” the adverse event is against “how good” the beneficial outcomes is(33,34).

A few real-world complications

In our first toy example, for simplicity, we imagined both a harmful outcome (severe or fatal drug toxicity) and a beneficial outcome (cancer remission). In practice, the benefit might be the postponement of an outcome (e.g., delaying death due to cancer). Table 3 shows another toy example in which the drug delays death due to cancer but increases the risk of severe or fatal toxicity. The simulation code is in the Appendix. In this toy example, we again see that using conditional risks results in a Benefit-Risk Ratio of 0.88 (the harms appear to outweigh the benefits) but using unconditional risks results in a Benefit-Risk Ratio of 1.56 (the benefits appear to outweigh the harms).

Table 3.

Toy data demonstrating two alternate calculations of the Benefit-Risk Ratio – drug delays death due to cancer but increases risk of severe or fatal toxicity

Data	Standard of Care	Drug
Number at start of follow-up	100	100
Death due to cancer (“Inverse Benefit”)	81	53
Severe or fatal toxicity (Harm)	12	30
Censored	7	17
Conditional Risk
Cause-specific HR, Remission (Benefit)		0.44
Cause-specific HR, Death (Harm)		1.83
Risk Remission (Benefit)	0.91	0.68
Risk Death (Harm)	0.20	0.46
RD Remission (Benefit) → NNT	0.	0.68–0.91 = −0.23 → 4.36
RD Death (Harm) → NNH	0.	0.46–0.20 = 0.26 → 3.85
Benefit-Risk Ratio (NNH/NNT)		3.85/4.36 = 0.88
Unconditional Risk
Subdistribution HR, Remission (Benefit)		0.44
Subdistribution HR, Death (Harm)		2.69
Risk Remission (Benefit)	0.81	0.53
Risk Death (Harm)	0.12	0.30
RD Remission (Benefit) → NNT	0.	0.53–0.81 = −0.28 → 3.59
RD Death (Harm) → NNH	0.	0.30–0.12 = 0.18 → 5.58
Benefit-Risk Ratio (NNH/NNT)		5.58/3.59 = 1.56

Extending the example of ICI therapy for treating cancer, national vital statistics have shown 5-year survival for Stage II non small-cell lung cancer to be around 57%(38)while ICI therapy could increase 5-year survival to 76%(39). Fatal toxicity associated with ICI occurs in about 1% of people who are treated(40) and dose-limiting toxicity occurs in about 5–7% of people(41–43), although both of these proportions vary across subgroups. In people with pre-existing autoimmune disease and COPD, 15–20% might experience fatal or dose-limiting toxicity(31,32). People with pre-existing autoimmune disease and COPD who are treated with ICIs would be expected to have fewer cancer deaths than people treated with chemotherapy alone but also more deaths and study washout due to intolerable or fatal toxicity; in this subgroup the proportion experiencing a benefit is similar to the proportion experiencing harm. Our toy example has tried to simulate a similar scenario in which a treatment truly has big benefits and big risks. In most examples and in other subpopulations, the balance of risks to benefits are likely to be more clearly in one direction or the other (i.e., Benefit-Risk Ratios based on conditional risks and unconditional risks will both be on the same side of 1), but the magnitude of the Benefit-Risk Ratio may be misleading if it is based on an improper choice of risk estimand(44). A proper analysis of the risks and benefits of a treatment will depend on whether each outcome precludes the other from occurring and the frequency of the two events.

The Benefit-Risk Ratio answers a question about a contrast of contrasts: a treatment has a benefit (in the form of a RD) and a harm (also in the form of a RD) and the Benefit-Risk Ratio contrasts those two RDs. In our toy example (Table 2), whether we used the conditional or unconditional risk, the drug increased the risk of benefit and the risk of harm – the Benefit-Risk Ratio only changed directions based on the relative magnitude of the two RDs. However, there are also scenarios in which the analytic choice for handling the competing risks can actually change the direction of the RD and the qualitative conclusions about the effects of the exposure(45). In the toy data in Table 4, a drug speeds up time to cancer remission substantially, and only minimally changes time to development of severe or fatal toxicity. The conditional risk difference for severe or fatal toxicity is 0.003 – effectively showing no effect of the drug on the harmful outcome. However, the unconditional risk difference for severe or fatal toxicity is −0.25, reflecting the true reduction in severe or fatal toxicity experienced by the treated individuals who are removed from being at risk for severe or fatal toxicity because they are quicker to experience cancer remission.

Table 4.

Toy data demonstrating two alternate calculations of risk with different qualitative conclusions

Data	Standard of Care	Drug
Number at start of follow-up	1000	1000
Remission (Benefit)	84	604
Severe or fatal toxicity (Harm)	580	332
Conditional Risk
Cause-specific HR, Remission (Benefit)		13.35
Cause-specific HR, Severe/fatal toxicity (Harm)		1.07
Risk Remission (Benefit)	0.13	0.83
Risk Severe or fatal toxicity (Harm)	0.62	0.62
RD Remission (Benefit)	0.	0.83–0.13 = 0.71
RD Severe or fatal toxicity (Harm)	0.	0.62–0.62 = 0.003
Unconditional Risk
Subdistribution HR, Remission (Benefit)		10.71
Subdistribution HR, Severe/fatal toxicity (Harm)		0.52
Risk Remission (Benefit)	0.08	0.60
Risk Severe or fatal toxicity (Harm)	0.58	0.33
RD Remission (Benefit)	0.	0.60–0.08 = 0.52
RD Severe or fatal toxicity (Harm)	0.	0.33–0.58 = −0.25

Conclusion

Ultimately, we cannot state whether conditional risks are more or less “causal” than unconditional risks, or by extension, whether cause-specific HRs are more or less “causal” than subdistribution HRs without clear consensus on what is meant by “causal”. There are causal interpretations of both unconditional and conditional risks(3). However, the conditional risks (and cause-specific HRs) rely on often-untenable assumptions about hypothetical interventions on the competing events that do not reflect the real-world outcomes experienced by patients. Using a risk-benefit lens, we have demonstrated that unconditional risks are more relevant to decision-making about interventions or treatments and should be used more often in epidemiologic research.

Availability of data and materials

All code (including toy data) used in this paper is available in the Appendix.