Active Learning in Brain Tumor Segmentation with Uncertainty Sampling and Annotation Redundancy Restriction

Abstract

Deep learning models have demonstrated great potential in medical imaging but are limited by the expensive, large volume of annotations required. To address this, we compared different active learning strategies by training models on subsets of the most informative images using real-world clinical datasets for brain tumor segmentation and proposing a framework that minimizes the data needed while maintaining performance. Then, 638 multi-institutional brain tumor magnetic resonance imaging scans were used to train three-dimensional U-net models and compare active learning strategies. Uncertainty estimation techniques including Bayesian estimation with dropout, bootstrapping, and margins sampling were compared to random query. Strategies to avoid annotating similar images were also considered. We determined the minimum data necessary to achieve performance equivalent to the model trained on the full dataset (α = 0.05). Bayesian approximation with dropout at training and testing showed results equivalent to that of the full data model (target) with around 30% of the training data needed by random query to achieve target performance (p = 0.018). Annotation redundancy restriction techniques can reduce the training data needed by random query to achieve target performance by 20%. We investigated various active learning strategies to minimize the annotation burden for three-dimensional brain tumor segmentation. Dropout uncertainty estimation achieved target performance with the least annotated data.

Supplementary Information

The online version contains supplementary material available at 10.1007/s10278-024-01037-6.

Introduction

Deep learning (DL) in medical imaging has made substantial progress, achieving near or superior performance to that of human experts [1]. These models, however, are limited by requiring substantial training data and annotations, which are expensive and time-consuming to produce [2].

Active learning (AL) is a strategy that only annotates the most informative subset of data to reduce the amount of training data needed without compromising performance [2]. Models are built iteratively until acceptable performance is achieved. By reducing the training data required, a wider gamut of clinical problems, including more niche tasks, can be addressed with DL. Model building would no longer require as much manpower and funding as traditionally required to annotate large datasets. In addition, DL models may be now accessible to institutions in earlier stages of incorporating artificial intelligence where resources to annotate local datasets are limited. The need for reducing the annotation burden not only exists to first develop the models but also to update them. For magnetic resonance imaging (MRI) images for example, acquisition parameters are being constantly adjusted to enhance image resolution and reduce acquisition times, while more images are being produced with higher strength magnets [3, 4]. Unless training data is augmented with these newer images, existing models are quickly outdated. Furthermore, there is increased data that earlier models trained on smaller cohorts may have biases against marginalized communities, necessitating new annotations and retraining with a more inclusive dataset [5]. With how much DL models depend on annotation reduction in order to stay relevant, we were motivated to pursue this study and investigate the efficacy of various AL strategies.

AL strategies generally have two approaches: (a) calculating uncertainty and annotating the most uncertain images or (b) grouping images based on similarity and selecting a subset from each similarity group to identify a representative cohort [2]. To identify uncertain images, Wang et al. used a preliminary model to predict on unannotated data and assigned images with the smallest probability of the most probable class as most uncertain [6]. An ensemble approach instead estimates uncertainty by quantifying the disagreement among models [7]. Bayesian neural networks generate a probability distribution from one model, and wider distributions suggest higher uncertainty [8, 9]. To reduce annotation redundancy, Yang et al. compared the output from convolutional neural networks, which are ultimately high-level feature vectors, to assess the similarity of images and identify a representative cohort to annotate [7]. Similarly, traditional computer vision techniques have also been used for feature extraction [10]. Kim et al. combined both uncertainty and representativeness techniques for their AL approach when selecting data to annotate for skin lesion classification and segmentation [11].

Many AL strategies, including the ones above, have focused on 2D imaging, classification tasks, or non-medical imaging [2, 6, 7, 9, 10]. However, application of validated techniques onto 3D medical imaging, such as MRI or CT, is not straightforward. Some medical imaging tasks have an additional complexity in that they focus on a small region of interest (ROI). Prognosis of brain cancer for example focuses on contrast-enhancing tumor, which is much smaller than the whole brain [12]. This characteristic is exacerbated in 3D imaging as uncertainty calculations can be immensely sensitive to background noise. Sharma et al. demonstrated remarkable success here by combining least confidence uncertainty estimation and representativeness to create a high-performing model using less than 15% of the 2018 Brain Tumor Segmentation (BraTS) dataset [13].

In this paper, we take multiple uncertainty and representative techniques used in general DL model building and evaluate their impact on reducing the annotation burden on medical images. First, we discuss how each of the AL methods iteratively identify images to annotate. Then, we apply our methods on a popularly studied task of brain tumor segmentation on a real-world, multi-institutional brain MRI dataset and go into detail the experiment parameters, the degree each AL technique reduces data requirements, and the statistical tests we use to compare techniques. Peng et al. evaluated DL model performance using the full brain MRI dataset, finding the model’s predictions were in strong agreement with human segmentations, and here we explore how AL can reduce the data necessary to achieve similar performance [14]. The contributions of this study are briefly summarized below:

• Quantifying how effective AL techniques that use uncertainty and redundancy reduction strategies can be in reducing annotations

• Showing the impact of combining various AL techniques to determine synergy

• Demonstrating that AL strategies can be computationally efficient and robust to background noise

Materials and Methods

Neural Network Architecture

Our models incorporated the 5-layered 3D U-net neural network architecture and hyperparameters from Peng et al. [14, 15]. Models used both contrast-enhanced T1-weighted and T2-weighted sequences to segment the contrast-enhancing region. Two patches of size 128 × 128 × 128 from each image were used for training. Data augmentation included scaling, rotation, and flipping transformations. Models optimized a joint Dice and cross entropy loss function on the validation set until there was no improvement for 50 epochs or had trained for 500 epochs. During validation and testing, we inputted the full image. For training and predicting, models used a 16 GB NVIDIA V100 Tensor Core graphical processing unit (GPU). Table 1 displays the full implementation details of the network architecture, and Supplementary Fig. 1 shows a diagram of the 3D U-net architecture [16].

Table 1.

Implementation architecture of the neural networks used

Implementation	Details
Input/tensor size	128 × 128 × 128 × 2
Kernel size	3 × 3 × 3
Batch size	1
Stride	1
Patch overlap	75%
Learning rate	0.001
Learning rate scheduler	Cosine anneal with warm restarts
Weight decay	0.00002
Optimizer	Stochastic gradient descent
Levels	5
Input image orientation	Right, anterior, inferior
Input image resolution	1 mm × 1 mm × 1 mm
Image resampling	Bspline interpolation
Ground truth resampling	Nearest neighbors
Activation function	Rectified linear unit (ReLU)
Pooling operation	Maxpool
Normalization method	Group normalization
Upsampling used in decoder	Trilinear interpolation
Voxel-wise probability cutoff for foreground class	0.5

Active Learning Algorithm

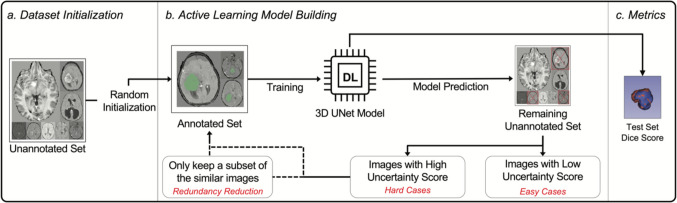
Our proposed methods to improve AL for 3D image segmentation consisted of two major components: (1) uncertainty sampling and (2) annotation redundancy restriction (Fig. 1). After randomly selecting a subset of the data for training an initial model, uncertainty sampling and annotation redundancy restriction techniques then iteratively selected additional images to be incorporated for model retraining.

Fig. 1.

Workflow of the full active learning framework

Uncertainty Sampling

Uncertainty sampling uses a preliminary model trained on a subset of data to predict segmentations on unannotated data. We calculated uncertainty using the predicted segmentations and annotated k images with the highest uncertainty. Uncertainty scores estimate the model’s confidence on data that was not included in training. We explored three different uncertainty estimating techniques as outlined below.

The first technique involved bootstrapping. At each AL iteration, we generated n bootstrapped datasets by sampling with replacement and used each to train a separate model. Higher variance in predictions across models suggested ensemble disagreement and higher uncertainty [7]. The uncertainty score was the mean of the variance map of all the probability maps returned from each bootstrapped model.

Next, we discuss margins sampling. Each voxel-probability within a probability map $p_i$ for image $i$ ranged from values from [0,1]. Voxel probabilities closer to 0.5 are associated with higher uncertainty [17]. Eq. 1 demonstrates how the uncertainty score $u_i$ was calculated.

$$u_i=-(\text{mean}(|p_i-0.5|))$$ 1

The final uncertainty estimation technique involved Bayesian approximation using dropout. Bayesian models return a probability distribution rather than a single probability. Wider distributions suggest higher uncertainty. These models can be approximated by generating $n$ predictions from a model that includes a dropout layer [8]. To create a Bayesian approximation model, we added a dropout layer to the last decoding convolutional layer in the model and compared performance when dropout was enabled during both training and testing versus only at testing. We used a variance map from the n predictions to measure the distribution spread. To localize uncertainty estimation to ROIs and to filter out noise, we used the mean of only the top 0.1% of values within the variance map to calculate uncertainty.

Annotation Redundancy Restriction

While uncertainty sampling identifies images unfamiliar to the current model, annotation redundancy restriction prevents annotation of images similar to one another. The first annotation redundancy restriction method selected the most representative uncertain images. Consider a subset of $k$ uncertain, unannotated images. If there are $j$ images, where $j<k$, similar to one another, then annotating only some of $j$ images may be sufficient. To evaluate image similarity, we compared the high-level features between two images. U-net has both an encoder and decoder arm [15]. The encoder arm uses multiple convolutional layers in series to generate an array of high-level features. We modified Yang et al.’s approach of using cosine similarity to compare arrays of high-level features for 3D images [7]. The encoder arm returns a 4D array of size (x, y, z, 512), where x, y, and z are variable to the size of the input image. We flattened this 4D array to a 1D array of size 512 by taking the mean across other axes. We then measured the similarity between two images by calculating the similarity score $ss\left(I_i,,,I_j\right)$, as shown in Eq. 2 where $h_i$ is flattened high-level features of image $i$, and $h_j$ is that of image $j$.

$$ss(I_i,I_j)=\text{cosine}\_\text{similarity}\left(h_i,,,h_j\right)=\frac{h_i{\bullet h}_j}{\Vert h_i\Vert \Vert h_j\Vert }$$ 2

Next, we used the maximum set cover approach to approximate a subset $S_m$ that most represents the entire set of uncertain, unannotated images $S_k$ (Supplementary Algorithm 1) [7].

The second redundancy restriction method selected uncertain images most non-similar to the already annotated data. Consider a subset of $k$ uncertain, unannotated images where there are $j$ images, where $j<k$, similar to the images already annotated. Then, annotating images from $S_j$ may not be informative to the model. In order to get a subset $S_m\subset S_k$ that is most non-similar to the set of already annotated images $S_a$ and images already selected to be annotated, we iteratively built $S_m$ by comparing each image in $S_k$ to the images in $S_a$ and those already in $S_m$ and added the one least similar to these images to $S_m$ from $S_k$ (Supplementary Algorithm 2).

Dataset Details

We retrospectively collected the imaging prior to treatment from pediatric patients with intracranial brain tumors who were admitted to the Children’s Hospital of Philadelphia (CHOP) from January 2005 to December 2019 and 4 large academic hospitals in Hunan Province, China, from January 2011 to December 2018. We manually reviewed the data for deidentification. Exclusion criteria included patients above 18 years old or patients with missing pathological reports or image sequences. The institutional review boards of all involved institutions approved this study and waived the requirement for informed consent.

A neuro-oncologist (JP) with 7 years of post-graduate experience manually segmented the contrast-enhancing tumor using the Level Tracing and Threshold tools in 3D Slicer (v.4.10) in all patients, and a radiologist (HXB) with 4 years of post-graduate experience reviewed the segmentations. JP and HXB resolved any disagreements in consensus. We specifically segmented the contrast-enhancing region as it is the primary area of interest for determining prognosis [12]. Supplementary Figs. 2 and 3 show the MR acquisition parameters. We partitioned 20% of the data at the patient level as the testing set. At each AL iteration, we used 20% of the annotated training data as the validation set. Images were preprocessed before training and predicting. Preprocessing included resampling to isotropic 1 mm [3] resolution, co-registration, skull stripping, N4 bias correction, and finally normalization. For experimentation purposes, we proactively annotated all images for the contrast-enhancing lesion. However, we assigned the images unannotated and annotated states based on the AL algorithm and only used images with annotated states for training.

Experiments

For clarification on how our results were generated and interpreted, we defined the true positive (TP), true negative (TN), false positive (FP), and false negative (FN) cases at the voxel level and the individual patient level. At the voxel level, a TP was where a model assigned a voxel that was labeled as tumor by a human annotator as the ROI. A TN was where a model agreed with a human annotator that a voxel was background. A FP was where a model assigned a voxel that a human annotator considered background as ROI, and a FN was where a model assigned a voxel that a human annotator considered tumor as background. At the individual level, the TP was the averaged performance of voxel level TPs in the entire image. TN, FP, and FN were defined similarly.

Experiment 1 compared different uncertainty sampling techniques. We initialized a random training set of 40 images and trained a preliminary model. We then iteratively annotated 50 of the most uncertain, unannotated images (~ 10% of entire dataset) returned by the uncertainty sampling technique and retrained the model. We evaluated model performance at each AL iteration with Dice scores. To determine if the results would depend on the initial random set of 40 images, we also trained models on 15 different randomly initialized datasets and compared their performances.

Experiment 2 compared different annotation redundancy restriction techniques after uncertainty sampling. We initialized a random training set of 40 images and trained a preliminary model. For each subsequent iteration, of the 100 most uncertain images, we annotated 50 of the most representative images and retrained the model incorporating these 50 images.

Because we were interested in when the performance of the model was similar to that of the full data model, we used a statistical test for equivalence for Experiments 1 and 2. The equivalence test consisted of two one-sided Student’s $t$ tests (TOST) where the null hypotheses were that there is a difference relative to the full data model that is: (1) less than a lower equivalence bound and (2) greater than a upper equivalence bound [18]. Rejecting both null hypotheses (α = 0.05) suggested the model performance could be considered equivalent. We first calculated the upper and lower equivalence bounds (${\mathit{UE}}_{\mathit{FD}},{\mathit{LE}}_{\mathit{FD}}$) at which the full data model was considered equivalent to itself with a p value of 0.05 using this test. We then determined the upper and lower equivalence bounds used for statistical analysis by doubling the range between ${\text{UE}}_{\text{FD}}$ and ${\text{LE}}_{\text{FD}}$ (upper equivalence = ${2\text{UE}}_{\text{FD}}$; lower equivalence = ${2\text{LE}}_{\text{FD}}$).

Results

Contrast-enhanced T1-weighted and T2-weighted sequences with contrast-enhancing tumor segmentation were available for 683 two-dimensional brain MRIs from 683 patients (598 CHOP, 85 Hunan). We excluded 39 patients due to skull stripping failure and 6 patients due to co-registration failure. Table 2 shows the characteristics for the remaining 638 patients. Each model took approximately 1–5 h to train depending on the AL iteration or training data size. The mean number of epochs at which the model’s validation loss saturated during model development was 90 epochs for all models in Table 3. There was no correlation between the number of epochs at which improvements in the model’s validation loss saturated and AL iteration number with no significant difference between the average number of epochs at iteration 1 (n = 90) versus at iteration 7 (n = 340) (p = 0.287). Supplementary Fig. 4 shows graphs of the training and validation dice scores and loss during model development. The AL framework and pre-trained models are publicly accessible at https://github.com/naddan27/ActiveLearning.

Table 2.

Study population characteristics

Characteristics	Number (percent)
Median age at diagnosis in years: mean (range)	9.4 (0.1–17.9)
Sex
Male	355 (55.6%)
Female	283 (44.4%)
Anaplastic astrocytoma	53 (8.4%)
Fibrillary astrocytoma	35 (5.5%)
Glioblastoma	22 (3.4%)
Infiltrating astrocytoma	20 (3.1%)
Pilocytic astrocytoma	119 (18.7%)
Pilomyxoid astrocytoma	13 (2.1%)
Medulloblastoma	72 (11.3%)
Craniopharyngioma	32 (5%)
Dysembryoplastic neuroepithelial tumor (DNET)	25 (3.9%)
Ependymoma	54 (8.5%)
Gangliocytoma/ganglioglioma	58 (9.1%)
Meningioma	22 (3.4%)
Neurocytoma	4 (0.6%)
Pleomorphic xanthoastrocytoma (PXA)	3 (0.4%)
Schwannoma	4 (0.6%)
Subependymal giant cell tumor	10 (1.6%)
Embryonal tumor group
Atypical teratoid rhabdoid tumor	18 (2.8%)
Pineoblastoma	4 (0.6%)
Primitive neuroectodermal tumor	17 (2.7%)
Germ cell tumor group
Germinoma	15 (2.4%)
Germ cell tumor	4 (0.6%)
Choroid plexus papilloma	26 (4.1%)
Other	8 (1.2%)

Table 3.

Mean dice of uncertainty and redundancy reduction methods. First iteration considered to have equivalent performance to full data model is bolded. Standard deviation in parentheses

Percentage of training data	7.8% n = 40	17.5% n = 90	27.3% n = 140	37.0% n = 190	46.8% n = 240	56.5% n = 290	66.3% n = 340	100% n = 513
Random query	0.552 (0.341)	0.568 (0.332)	0.615 (0.337)	0.644 (0.329)	0.652 (0.328)	0.715 (0.308)	0.675 (0.309)	|
Uncertainty only								|
Dropout train test	0.547 (0.330)	0.683 (0.322)	0.670 (0.318)	0.691 (0.335)	0.607 (0.346)	0.774 (0.253)	0.756 (0.267)	|
Bootstrapping	0.585 (0.332)	0.644 (0.320)	0.729 (0.281)	0.696 (0.297)	0.697 (0.303)	0.731 (0.281)	0.762 (0.266)	0.724 (0.295)
With dropout train test								|
Redundancy representative	0.547 (0.330)	0.561 (0.333)	0.613 (0.341)	0.663 (0.317)	0.638 (0.316)	0.612 (0.335)	0.707 (0.301)	|
Redundancy non-similar	0.547 (0.330)	0.621 (0.338)	0.590 (0.345)	0.650 (0.330)	0.697 (0.303)	0.651 (0.329)	0.730 (0.285)	|

p values of bolded dice scores: random query (p = 0.001), dropout train test (p = 0.018), bootstrapping (p = 0.001), representative (p = 0.003), non-similar (p = 0.006). Note that these reported p values represent the larger of the two obtained from the two one-sided Student’s $t$ tests when testing for equivalence

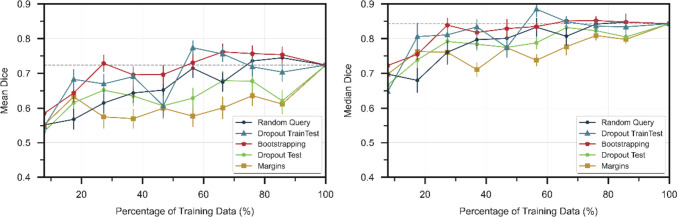
Figure 2 compares the mean and median Dice scores of the uncertainty estimation techniques at different percentages of the training data from Experiment 1. Both bootstrapping and Bayesian approximation using dropout at training and testing (dropout train test) outperformed random query. In contrast, margins and Bayesian approximation using dropout only at testing (dropout test) performed worse than random query. Random query was able to train a model that achieved mean Dice performance equivalent to that of the model trained with the full data at 56.5% of the data. This suggests that a model can be fully trained with about half of the data, and therefore, we will report when a model trained with an AL strategy was able to achieve full data performance relative to when the random query model was able to. The model trained with the bootstrapping strategy was able to achieve full data performance at 48.3% of the data needed by random query (p = 0.001), whereas the model trained with dropout train test needed 31.0% of the data needed by random query (p = 0.018). The performance of the initial model was consistent with any random dataset initialization. The mean of the mean dice scores across 15 first iteration models trained with randomly initialized datasets was 0.549 with the standard deviation of the distribution of the means 0.008.

Fig. 2.

Dice scores of uncertainty techniques at different percentages of training data. Horizontal dashed line is performance with full training data. Error bars represent the standard error

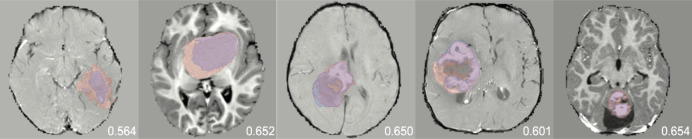
In Experiment 2, we used dropout train test to identify the uncertain, unannotated images before annotation redundancy restriction due to its performance in Experiment 1 and smaller computational burden than bootstrapping. Table 3 shows the effect of adding an annotation redundancy restriction technique after uncertainty sampling versus just uncertainty sampling alone. While the non-similar restriction technique achieved equivalent performance to that of the full model before random query, both redundancy restriction techniques were not able to outperform AL strategies that solely used uncertainty sampling. Figure 3 shows examples of predicted segmentations by models that were built using uncertainty and annotation redundancy restriction strategies.

Fig. 3.

Examples of predicted (blue) vs. expert (red) segmentations at 17.5% of training data with random query, dropout train test, bootstrapping, redundancy representative, and redundancy non-similar in order. The contrast-enhanced T1-weighted sequence is shown. Dice scores are shown for each respective image

Discussion

We compared multiple uncertainty and representative techniques and evaluated their individual and synergistic performance in reducing the annotations burden on multi-institutional clinical data. We showed that an AL framework using Bayesian approximation with dropout at training and testing only needs approximately 30% of the data that a random query strategy would need to achieve full data performance.

We used a U-net architecture within our AL framework given its ubiquity in medical imaging models and its successful performance in brain tumor segmentation within the literature. In a review of state-of-the-art deep learning methods for brain tumor segmentation, Magadza et al. compared the performances of U-net, cascaded, and ensemble architectures using multiple BraTS datasets, finding that the U-net architecture was able to produce exceptional results and to achieve Dice scores of above 0.9 for whole tumor segmentation [19]. In their review of brain tumor image analysis, Sailunaz et al. similarly supported that U-net models were successful in brain tumor segmentation, also reaching Dice scores above 0.9 when applied to BraTS datasets [20]. They described other successful methods as well, including a deep learning-based feature selection method known as saliency-based deep learning for tumor detection, achieving Dice scores of over 0.8 using BraTS datasets, in addition to a long short-term memory model evaluated on BraTS and a dataset for stroke lesions, reaching Dice scores above 0.9 [20]. Lastly, in their review of brain tumor segmentation describing pretrained architecture, cascaded methods, and ensemble networks, Ahamed et al. highlighted ensemble methods that included U-net models reaching Dice scores above 0.9 for whole tumor segmentation using BraTS datasets [21].

Our study demonstrates the utility of AL in annotation burden restriction in 3D imaging. Whereas Sharma et al. similarly used an AL framework for reducing the amount of labeled data necessary for training a brain tumor segmentation model using the 2018 BraTS dataset, our study demonstrates the success of AL in brain tumor segmentation using real-world clinical data [13]. Other works have pursued AL in 3D medical imaging, including by incorporating techniques such as reinforcement learning rather than traditional uncertainty and representative strategies [22, 23]. Wang et al. demonstrated a reduction in the amount of labeled data needed for classifying lung disease from chest CT and for classifying the degree of diabetic retinopathy from fundus images by employing a reinforcement learning approach for the AL framework [22]. Li et al. used an AL method based on uncertainty to reduce the annotation effort necessary for gland segmentation in colon histology images in addition to brain MRI segmentation [23].

For 3D brain tumor segmentation, we compared four different uncertainty estimation techniques to random query: bootstrapping, margins, dropout train test, and dropout test. While bootstrapping did reduce training data by 50%, its computational demand can be prohibitive. We were therefore interested in using dropout as an alternative. The primary concern was that a single dropout layer would not be able to generate distinct enough predictions to generate a reliable uncertainty score compared to having multiple models trained on different datasets or model architectures [2, 9]. Furthermore, the prediction variability, which is generally concentrated at the ROI, would be diluted by the substantial number of background voxels in 3D imaging. To address this concern, we presented a dropout strategy that focuses on regions of high disagreement within the image to estimate uncertainty. With this strategy, we show that dropout is generalizable to AL in 3D segmentation tasks and in fact superior to bootstrapping. We also attempted removing dropout training stabilization by implementing dropout only at testing to force more diverse predictions. However, model prediction instability had a stronger negative effect than the possible positive effects of having diverse predictions for uncertainty estimation as demonstrated by its low performance. Results also show that uncertainty estimation may require calibration given the substantial amount of noise contributed by the background voxels in 3D imaging. This may explain margins sampling performing worse than random query in our paper despite other studies showing better performance on 2D images [2].

We were also interested in reducing annotation redundancy. While these techniques were able to reduce the training data needed by approximately 20%, they were not able to outperform AL strategies that only incorporated uncertainty. Adding a redundancy restriction strategy can bias training away from uncertain images. Future projects may prioritize more uncertain images within the representative cohort. Uncertain images can be clustered based on similarity, where each cluster is assigned an overall uncertainty. While only a subset of images from each cluster are selected for annotation, training can be biased toward the uncertain images by artificially increasing images from uncertain clusters with data transformations or generative adversarial networks [24–28].

The major strength of our study is its demonstration of the specific reduction in annotation burden of each AL technique when applied by itself or when combined with multiple techniques. Recent studies have used combined uncertainty and representative approaches [11, 13], but as demonstrated in our uncertainty experiments, AL frameworks are sensitive to calibration when applied to clinical imaging. By doing a detailed analysis of each technique on annotation reduction, our study can guide future studies that combine AL techniques. Furthermore, given the calibration sensitivity and need to optimize hyperparameters at each iteration, our study suggests that AL frameworks may benefit from an adaptative strategy as AL iterations are added. Wang et al. incorporated reinforcement learning with Markov models to create an adaptive AL framework for example [22], and our study can be used to understand the adaptive strategies returned by reinforcement learning strategies in future studies.

Our study does have limitations. First, we purposefully used the hyperparameters optimized for the full data model on all AL models to address hyperparameter confounding bias, and therefore, results at each iteration may be lower than if they were trained with hyperparameters optimized for each iteration. We assumed performance would be similarly affected for each iteration. Additionally, we randomly split the annotated data into the training and validation set at each AL iteration rather than having a consistent validation set at each iteration. We designed experiments as such with the thought that already deployed AL models should continuously look for more informative samples to add to the training data as time passes and more imaging is available. However, this may bias and overfit models to the training data, hindering model performance at larger AL iterations. Furthermore, our sole metric was Dice score, which is the most common metric for segmentation models for medical images. However, Dice has limitations in that it does not consider the distance of nonoverlapping regions between the prediction and ground truth and is more sensitive to smaller ROI [29]. Our study shows how AL can be a catalyst in enabling DL to be more accessible within radiology, but further metrics should also be included to truly understand the clinical significance behind performance improvements of each iteration. Lastly, we apply AL strategies on a single task of brain tumor segmentation. Further studies with different datasets and tasks are needed before AL strategies are regularly incorporated into models for medical imaging.

Conclusions

In conclusion, we demonstrate that AL can be successfully applied onto medical imaging to reduce the annotation burden through our experiments on brain tumor segmentation. Reducing the annotation burden is increasingly becoming a necessity to keep DL models relevant in medical imaging. With imaging constantly becoming refined with new acquisition parameters and improving scanning technology, existing models quickly become outdated. Furthermore, as imaging volume increases and a wider range of demographics has access to imaging, newer models that accommodate all patient backgrounds must be trained to keep biases within DL models in check. Unless the annotation burden is addressed, constantly retraining models is impossible, and therefore, our study was necessary to demonstrate AL as a solution to preserving the sustainability of medical DL models. Furthermore, the contributions of our study are quantifying the efficacy of multiple AL techniques and showing the impact of combining various uncertainty estimation and annotation redundancy restriction methods, finding that a dropout uncertainty estimation framework is optimal.

Supplementary Information

Below is the link to the electronic supplementary material.

Funding

This project was supported by Alpert Medical School Summer Assistantship award to DDK. This work was supported by National Science Foundation of Hunan Province, China (2022JJ30762), International Science and Technology Innovation Joint Base of Machine Vision and Medical Image Processing in Hunan Providence, China (2021CB1013), and the 111 project (B18059) to CZ. This work was supported by Hunan Province Key Areas Research and Development Program, China (2022SK2054) to BZ. This work was supported by Huxiang High-level Talent Gathering Project-Innovation Talent, China (2021RC5003) to WL. This work was supported by the Natural Science Foundation of China (81971696 to LY), Natural Science Foundation of Hunan Province (2022JJ30861 to LY), and Sheng Hua Yu Ying Project of Central South University to LY.

Declarations

Conflict of Interest

RSC reports personal fees from Roivant Sciences and personal fees from Sumitovant Biopharma, outside the submitted work. CB is a consultant for Depuy-Synthes, Bionaut Labs, Galectin Therapeutics, Haystack Oncology, and Privo Technologies. CB is a co-founder of Belay Diagnostics and OrisDx.