An explainable autoencoder with multi-paradigm fMRI fusion for identifying differences in dynamic functional connectivity during brain development

Abstract

Multi-paradigm deep learning models show great potential for dynamic functional connectivity (dFC) analysis by integrating complementary information. However, many of them cannot use information from different paradigms effectively and have poor explainability, that is, the ability to identify significant features that contribute to decision making. In this paper, we propose a multi-paradigm fusion-based explainable deep sparse autoencoder (MF-EDSAE) to address these issues. Considering explainability, the MF-EDSAE is constructed based on a deep sparse autoencoder (DSAE). For integrating information effectively, the MF-EDASE contains the nonlinear fusion layer and multi-paradigm hypergraph regularization. We apply the model to the Philadelphia Neurodevelopmental Cohort and demonstrate it achieves better performance in detecting dynamic FC (dFC) that differ significantly during brain development than the single-paradigm DSAE. The experimental results show that children have more dispersive dFC patterns than adults. The function of the brain transits from undifferentiated systems to specialized networks during brain development. Meanwhile, adults have stronger connectivities between task-related functional networks for a given task than children. As the brain develops, the patterns of the global dFC change more quickly when stimulated by a task.

1. Introduction

The human brain is a complex and efficient system composed of many interconnected regions, and its organization has been studied through functional connectivity (FC) networks (Li, 2022; Li et al., 2021; Xiao et al., 2020). Functional magnetic resonance imaging (fMRI) techniques are widely used for the analysis of functional connectivity networks in the brain due to their non-invasiveness, high spatial resolution (Allen et al., 2014; Tokuda, Yamashita, & Yoshimoto, 2021). By studying FC networks with fMRI data, we can discover functional networks inherent in the brain and understand how neural developmental patterns change throughout the life span (Zhang et al., 2021). Recently, dynamic functional connectivity (dFC) networks have received increasing attention because they can further discover the spontaneous activity, macro-scale spatio-temporal organization of the brain, and topological characteristics, while capturing the functional diversity and switching properties of the brain networks (Allen et al., 2014; Zhu et al., 2021).

Deep learning models have been widely applied in FC analysis due to their ability to extract highly abstract features (Jang, Plis, Calhoun, & Lee, 2017; Lu, Liu, Wei, Chen, & Geng, 2021; Qiao, Yang, Calhoun, Xu, & Wang, 2021). In recent years, multi-paradigm deep learning methods have gained extensive attention because they can comprehensively utilize data from different paradigms to discover biomarkers that cannot be found based on a single paradigm alone (Baltrušaitis, Ahuja, & Morency, 2018). For example, Qu et al. (2021) proposed a multi-paradigm graph neural network to fuse information from different paradigms of fMRI data to predict an individual’s wide range of achievement test scores. Huang, Zhou, Wang, and Zhang (2020) proposed an attentional diffusion bilinear neural network to integrate brain functional connectivity features from fMRIs to predict epilepsy. Hu et al. (2021) proposed a convolutional collaborative model to integrate multi-paradigm fMRI data for classifying low/high cognitive groups. However, there remain many issues with the use of such multi-paradigm deep learning models. Firstly, despite their good performances in classification (Nandakumar et al., 2021), they lack good explainability, i.e., the ability to identify the features that contribute to decision making (Talukder, Barham, Li, & Hu, 2021). An explainable model is especially crucial in neuroimaging, where we are often interested in identifying biomarkers underlying brain development or disorders. In addition, many fusion models combine latent vectors learned from different paradigms respectively (Huang et al., 2020; Qu et al., 2021), without effective use of complementary information from multi-paradigm data (Ning, Xiao, Feng, Chen, & Zhang, 2021).

To address these issues, we propose a multi-paradigm fusion-based explainable deep sparse autoencoder (MF-EDSAE). For the explainability, we construct MF-EDSAE based on a deep sparse autoencoder (DSAE). DSAE not only has powerful data representation but also good explainability by only keeping essential features (Qiao, Hu, Xiao, Calhoun, & Wang, 2021). In particular, the use of sparsity constraints ensures generalizability and promotes the learning capacity of the model. Moreover, a feature selection layer with k-means and relief strategies is added to the reconstruction layer for better explainability. The proposed MF-EDSAE exploits multi-paradigm information through the following two strategies. Firstly, the combining layer of different paradigms is replaced by the nonlinear fusion layer. Secondly, a hypergraph regularization is enforced to preserve the high-order relationships both within each paradigm and between paradigms. Through the above methods, the MF-EDSAE integrates complementary information from multiple paradigm data effectively and identify biomarkers that are common or specific to each paradigm.

The proposed MF-EDSAE is finally applied to characterize intrinsic functional changes during brain development based on three different fMRI data including resting-state fMRI, fMRI of working memory, and emotion identification tasks (called rest fMRI, nback fMRI, and emoid fMRI) from the Philadelphia Neurodevelopmental Cohort (PNC) and demonstrated it achieves better performance in detecting dFC that differs significantly during brain development than the single-paradigm deep sparse autoencoder. As a result, we can gain an insight into the dFC networks and understand the functional mechanism of the brain. Our results show that, in commonality, children have more dispersive dFC patterns while the dFC patterns in adults are more focused, and the function of the brain transits from undifferentiated systems to specialized networks during brain development. In specificity, adults can update their patterns of global dFC more quickly stimulated by a task than children. Adults in a given task have stronger connectivities between task-related functional networks relative to children, for example, adults have stronger dFC between subcortical network and visual network in emoid fMRI, between subcortical network and salience network in nback fMRI.

2. Methodology

In this section, we will introduce the proposed MF-EDSAE. It contains a deep sparse autoencoder to reconstruct the data, a nonlinear fusion layer to fuse information from different paradigms, a hypergraph regularization term to incorporate the high-order relationships in each paradigm, a multi-paradigm hypergraph regularization to consider the high-order relationships within and across different paradigms, and a feature selection layer to remove the redundant features for better explainability. Firstly, we will present the hypergraph regularization with its extension to multi-paradigms. Then, we discuss the training process of MF-EDSAE including both the single-paradigm training and multi-paradigm cases. Finally, we describe the details of the feature selection layer. The architecture of MF-EDSAE with its learning process is shown in Fig. 1.

Fig. 1.

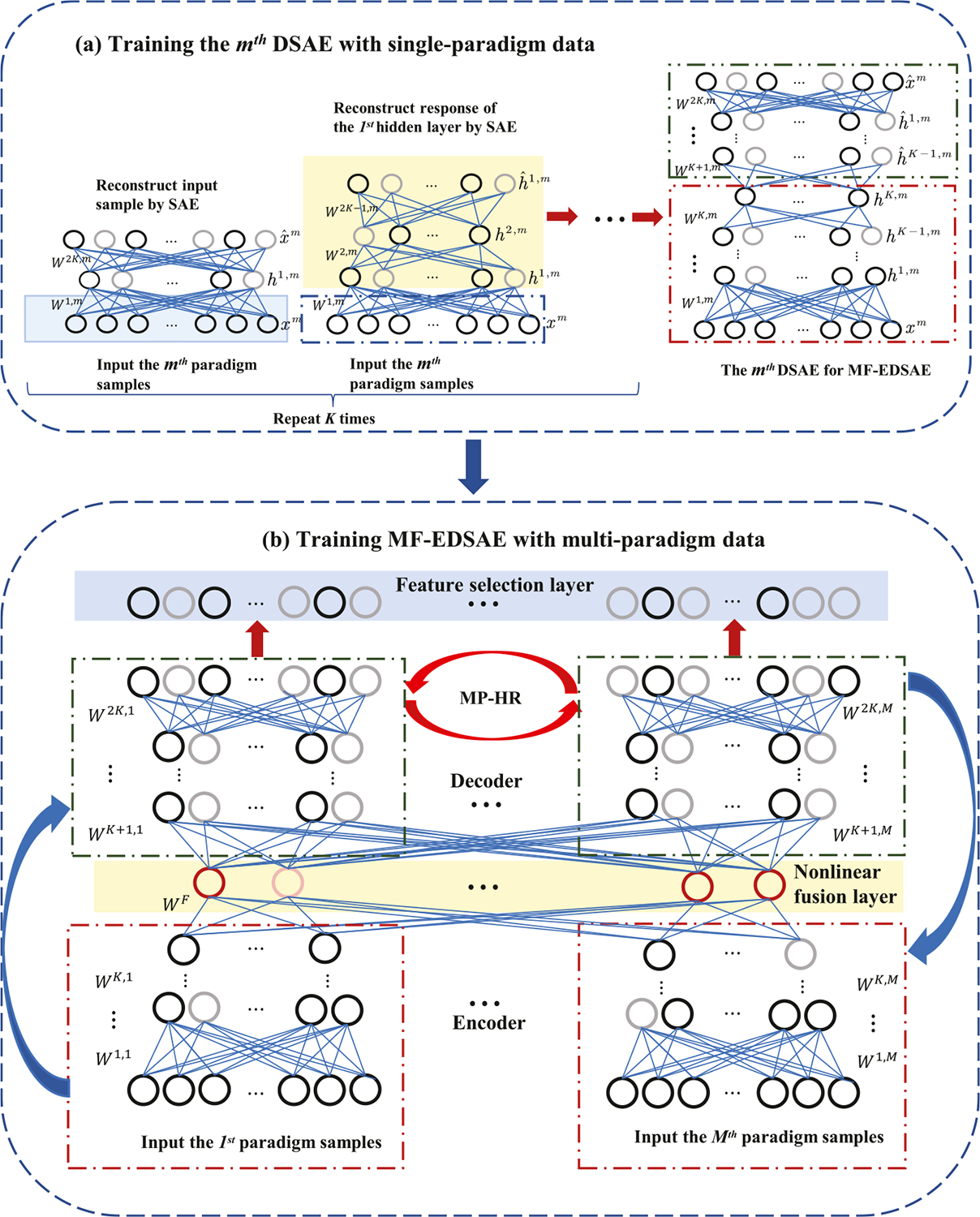
The entire training process of MF-EDSAE: (a) shows the stack-wise sparse training process of single-paradigm data to initialize subnetwork weights of MF-EDSAE. The hypergraph regularization (HR) is also introduced to consider high-order relationships of samples. (b) shows the architecture of MF-EDSAE with encoders, fusion layer, decoders, and feature selection layer. The fine-tuning process of MF-EDSAE adapts to the back-propagation algorithm with sparse learning, HR, and multi-paradigm hypergraph regularization (MP-HR), which can improve the model learning ability by maintaining the sparsity of the hidden layers and considering high-order relationships within and between paradigms.

2.1. Hypergraph regularization

Hypergraph, as a generalization of a graph, has been widely used in machine learning to analyze high-dimensional data (Ma & Fu, 2012; Weighill & Jacobson, 2015). The hypergraph can consider higher-order relationships among samples to better characterize the structural information of the data. Unlike an edge of a graph linking two subjects, the edge of a hypergraph, called hyperedge, connects multiple nodes to represent high-order relationships among samples. A hypergraph $G$ is defined as $G=(V,E,W)$ comprising a node set $V=\left\{v_j\mid j=\mathrm{1,2},\dots ,N\right\}$ with each $v_j={\left[v_{j1},\dots ,v_{jd}\right]}^T$ being a $d$-dim node vector, a hyperedge set $E=\left\{e_i\mid i=\mathrm{1,2},\dots ,S\right\}$ and a weight matrix $W$. A hyperedge $e_i$ is a subset of the node set $V$ with size $\left|e_i\right|$ and has a non-negative weight $W_{e_i}$. The structure of a hypergraph is described by $H\in {\mathbb{R}}^{N\times S}$, which is defined as

$$H_{ji}=H\left(v_j,e_i\right)=\{\begin{array}{ll}1\hfill & v_j\in e_i\hfill \\ 0\hfill & \mathit{\text{other}}\mathit{\text{wise}}\hfill \end{array}$$

The degree matrices of nodes and hyperedges are defined as diagonal matrices $D_v$ and $D_e$ with their diagonal elements as follows:

$$D_{v_j}=\sum _{e_i\in E}{W}_{e_i}H\left(v_j,e_i\right)j=1,2,\dots ,N$$

$$D_{e_i}=\sum _{v_j\in V}H\left(v_j,e_i\right)i=1,2,\dots ,S$$

The geometrical relationship can be approximately represented by the nearest neighbor graph of data points (Wang, Yu, & Tao, 2013). Therefore, we use the $k$-nearest neighbor (KNN) method to construct the hyperedge (Zien, Schlag, & Chan, 1999). Specifically, we select a node as the central node, calculate the distance between the central node and the rest nodes, and connect the central node and the $k$ nearest nodes into a hyperedge. The weight of $e_i$ is calculated by

$$W_{e_i}=\sum _{v_j\in e_i}\text{exp}\left(-\frac{\Vert v_i-v_j{\Vert }_2^2}{{\sigma }_i}\right)i=1,2,\dots ,S$$

where ${\sigma }_i={\sum }_{v_j\in e_i}{‖v_i-v_j‖}_2^2/k$, with $k$ being the number of nearest neighbors.

Based on the definition of hypergraph, the hypergraph regularization is thus defined as

$$\begin{gathered} \frac{1}{2}\sum _{v_q,v_p\in e_i}\sum _{e_i\in E}\frac{W_{e_i}}{D_{e_i}}\Vert v_q-v_p{\Vert }_2^2 \\ =\frac{1}{2}\sum _{v_q,v_p\in e_i}\sum _{e_i\in E}{\varphi }_i\Vert v_q-v_p{\Vert }_2^2 \\ =\mathit{\text{Tr}}\left(V^T{L}_{\mathit{\text{hyper}}}V\right) \end{gathered}$$ (1)

where ${\varphi }_i\triangleq \frac{W_{e_i}}{D_{e_i}}$ is the weight, $L_{\mathit{\text{hyper}}}\triangleq D_v-S$ is the hypergraph Laplace matrix with $S\triangleq HW{D}_e^{-1}{H}^T$ being the similarity matrix, and $W$ is a diagonal matrix with $W_{e_i}$ being the diagonal element. $V=\left[v_1,\dots ,v_N\right]$ represents the node matrix. Compared with graph based regularization, hypergraph based regularization can better capture the relationship among multiple samples (Nguyen & Mamitsuka, 2020).

2.2. Multi-paradigm hypergraph regularization

We apply the hypergraph regularization to multi-paradigm manifold learning. Compared to the work in Xiao, Stephen, Wilson, Calhoun, and Wang (2019), multi-paradigm hypergraph regularization used here can effectively capture and utilize the high-order relationships within and between paradigms. The multi-paradigm hypergraph regularization is defined as

$$\begin{gathered} \frac{{\beta }_1}{2}\sum _{p=1}^M\sum _{i,j}^N{S}_{ij}^p{\Vert v_i^p-v_j^p\Vert }_2^2+\frac{{\beta }_2}{2}\sum _{p=1}^M\sum _{p\ne q}^M\sum _{i,j}^M{S}_{ij}^{p,q}{\Vert v_i^p-v_j^q\Vert }_2^2 \\ =Tr\left({\tilde{V}}^T{L}_{\mathit{\text{mhyper}}}\tilde{V}\right) \end{gathered}$$ (2)

where the first term is to incorporate manifold structure information within each paradigm, and the second term considers the mutual relationship between paradigms. $N$ is the number of samples, and $M$ is the number of paradigms. ${\beta }_1$ and ${\beta }_2$ are the tuning parameters for intra-paradigm and inter-paradigms, respectively. $\tilde{V}=\left[V^1;\cdots ;V^M\right]$ with $V^p=\left[v_1^p,\dots ,v_N^p\right]$ $(p=1,\dots ,M)$ being the node matrix of the $p$th paradigm. $L_{\mathit{\text{mhyper}}}\triangleq D-S$ is the multi-paradigm hypergraph Laplacian matrix, where $D$ is a diagonal matrix, with $D_{ii}={\sum }_j{S}_{ij}$, and $S$ is the similarity matrix. Specifically,

$$S=\left[\begin{array}{cccc}{\beta }_1{S}^{1,1}& {\beta }_2{S}^{1,2}& \cdots & {\beta }_2{S}^{1,n}\\ {\beta }_2{S}^{2,1}& {\beta }_1{S}^{2,2}& \cdots & {\beta }_2{S}^{2,n}\\ ⋮& ⋮& & ⋮\\ {\beta }_2{S}^{n,1}& {\beta }_2{S}^{n,2}& \cdots & {\beta }_1{S}^{n,n}\end{array}\right]$$

where $S^{p,q}\triangleq S^p{S}^q,S^p$ is the similarity matrix of the $p$th paradigm. The element $S_{ij}^{p,q}$ of $S^{p,q}$ is calculated by $S_{ij}^{p,q}={\sum }_{k=1}^N{S}_{ik}^p{S}_{kj}^q$.

2.3. Model training

2.3.1. Training with single-paradigm data

In the training stage, data from each paradigm are used to train a deep sparse autoencoder (DSAE) in a stack-wise way. Specifically, using single-paradigm data we first train a sparse autoencoder (SAE) with Kullback–Leibler (KL) divergence and hypergraph regularization. Next, only the weights between the input layer and the hidden layer, and the responses of the hidden neurons are kept, which are then used as the input to train a sparse autoencoder. In this way, the pre-training of DSAE is formed by repeating the above process with $K$ SAEs. Based on this, DSAE with $2K+1$ layers is set up to be a pre-trained component in the multi-paradigm network.

For the $m$th paradigm, let $W^{k,m}=\left(W^{k,m},b^{k,m}\right)\triangleq \left\{{\tilde{w}}_{ji}^{k,m}\right\}\in {\mathbb{R}}^{n_{k+1}^m\times \left(n_k^m+1\right)}$, where $W^{k,m}\triangleq \left\{w_{ji}^{k,m}\right\}\in {\mathbb{R}}^{n_{k+1}^m\times n_k^m}$ is the connection weight matrix between the $k$ layer and the $(k+1)\text{th}$ layer and $b^{k,m}\triangleq \left\{b_j^{k,m}\right\}\in {\mathbb{R}}^{n_{k+1}^m}$ is the bias of the $(k+1)\text{th}$ layer. In order to maintain the sparsity of the hidden layer and the high-order relationships between samples, which can improve the learning ability of the autoencoder, the loss function of SAE is defined with KL divergence and hypergraph regularization

$$L\left(\tilde{W}\right)=\frac{1}{2}\sum _{p=1}^N\sum _{j=1}^{n_3}{\left(x_{pj}^m-{\hat{x}}_{pj}^m\right)}^2+{\lambda }_1\sum _{j=1}^{n_2}KL\left(\rho \Vert {\hat{\rho }}_j^{2,m}\right)+{\lambda }_2\sum _{k=2}^3\mathit{\text{Tr}}\left({\left(A^{k,m}\right)}^T{L}_{\mathit{\text{hyper}}}{A}^{k,m}\right)+\frac{{\lambda }_3}{2}\sum _{k=1}^2\sum _{i=1}^{n_k}\sum _{j=1}^{n_{k+1}}{\left({\tilde{w}}_{ji}^{k,m}\right)}^2$$ (3)

where $N$ is the number of samples, $m$ is the $m$th paradigm, $n_k(k=\mathrm{1,2},3)$ is the number of neurons in the $k$-layer, $x_{pj}^m$ is the value of the $j$th feature of the $p$th sample, and ${\hat{x}}_{pj}^m$ is the reconstructed value of $x_{pj}^m$. $KL\left(\rho \Vert {\hat{\rho }}_j^{2,m}\right)$ is the KL divergence between two Bernoulli random variables; one has mean value $\rho$, and the other has mean value ${\hat{\rho }}_j^{2,m}$. It is defined as

$$KL\left(\rho \Vert {\hat{\rho }}_j^{2,m}\right)=\rho \text{log}\frac{\rho }{{\hat{\rho }}_j^{2,m}}+\left(1-\rho \right)\text{log}\frac{1-\rho }{1-{\hat{\rho }}_j^{2,m}}$$

where $\rho$ is a sparsity parameter and ${\hat{\rho }}_j^{2,m}=\frac{1}{N}{\sum }_{p=1}^N{a}_{pj}^{2,m}\cdot a_{pj}^{k,m}(k=2,3)$ is the activation value of the $j$th neuron in the $k$th layer for the $p$th sample. $\mathit{\text{Tr}}\left({\left(A^{k,m}\right)}^T{L}_{\mathit{\text{hyper}}}{A}^{k,m}\right)$ is the hypergraph regularization defined by Eq. (1), where $A^{k,m}=\left[a_1^{k,m},\dots ,a_N^{k,m}\right]$ and $a_p^{k,m}={\left[a_{p1}^{k,m},\dots ,a_{p,n_k}^{k,m}\right]}^T$ represent the activation matrix in the $k$th layer and the activation vector of the $p$th sample in the $k$th layer, respectively.

The goal of training with single-paradigm data is to minimize the loss function (3). For the $p$th sample, the residual terms of the $j$th neuron in the output layer and the hidden layer, i.e., ${\delta }_{pj}^{3,m}$ and ${\delta }_{pj}^{2,m}$, are calculated by

$$\begin{gathered} {\delta }_{pj}^{3,m}=\left\{\left({\hat{x}}_{pj}^m-x_{pj}^m\right)+{\lambda }_2\sum _{e_i^m\in E^m}\sum _{a_q^m\in e_i^m}{\varphi }_i\left(a_{pj}^{3,m}-a_{qj}^{3,m}\right)\right\}{f}^{\prime }\left(z_{pj}^{3,m}\right) \\ {\delta }_{pj}^{2,m}=\{\sum _{i=1}^{n_3}{\delta }_{pi}^{3,m}{\tilde{w}}_{ij}^{2,m}+{\lambda }_1\left(\frac{1-\rho }{1-{\hat{\rho }}_j^{2,m}}-\frac{\rho }{{\hat{\rho }}_j^{2,m}}\right)+{\lambda }_2\sum _{e_i^m\in E^m}\sum _{a_q^m\in e_i^m}{\varphi }_i\left(a_{pj}^{2,m}-a_{qj}^{2,m}\right)\}{f}^{\prime }\left(z_{pj}^{2,m}\right) \end{gathered}$$

where $z_{pj}^{k,m}$ is the activation value of the $j$th neuron in the $k$th layer ($k=2,3$) for the $p$th sample, $f(\cdot )$ is a nonlinear differentiable function and $f^{\prime }(\cdot )$ is its derivative function. Thus, the gradient is

$$\nabla {\tilde{w}}_{ji}^{k,m}=\{\begin{array}{ll}{\delta }_{pj}^{k+1,m}{a}_{pi}^{2,m}\hfill & k=2\hfill \\ {\delta }_{pj}^{k+1,m}{x}_{pi}^m\hfill & k=1\hfill \end{array}$$

its matrix form is

$$\nabla {\tilde{W}}_p^{k,m}=\{\begin{array}{ll}{\delta }_p^{k+1,m}{\left(a_p^{k,m}\right)}^T\hfill & k=2\hfill \\ {\delta }_p^{k+1,m}{\left(x_p^m\right)}^T\hfill & k=1\hfill \end{array}$$

where $a_p^{k,m}={\left[a_{p1}^{k,m},\dots ,a_{p,n_k}^{k,m}\right]}^T,{\delta }_p^{k,m}={\left[{\delta }_{p1}^{k,m},\dots ,{\delta }_{p,n_k}^{k,m}\right]}^T$.

Thus, we can get the parameter update formula

$${\tilde{W}}^{k,m}={\tilde{W}}^{k,m}-\frac{\eta }{N}\sum _{p=1}^N\left[\nabla {\tilde{W}}_p^{k,m}+{\lambda }_3{\tilde{W}}^{k,m}\right]$$

where $\eta$ is the learning rate.

After the training of SAE is over, the decoder will be ignored while the encoder and the responses of the hidden neurons are kept, and the responses are used as the input to train a new SAE. Repeating the above process with $K$ autoencoders, a DSAE with $2K+1$ layers is obtained.

2.3.2. Feature fusion

For an MF-EDSAE consisting of $M$ deep autoencoders, where $M$ is the number of paradigms and each autoencoder has an input layer, an output layer and $2K-1$ hidden layers, we add a nonlinear fusion layer between the $(K+1)\text{th}$ layer and the $(K+2)\text{th}$ layer. The activation value of nonlinear layer for the $p$th sample is

$$a_p^F=f\left(\sum _{m=1}^M{W}^{F,m}{a}_p^{K+1,m}\right)$$

where $a_p^{K+1,m}$ represents the activation value in the $(K+1)\text{th}$ layer. $W^{F,m}\triangleq \left\{w_{ji}^{F,m}\right\}\in {\mathbb{R}}^{n^F\times n_{K+1}^m}$ is the weight for fusion and $n^F$ is the dimension of the fusion layer. $f(\cdot )$ is a nonlinear differentiable function. After adding the nonlinear fusion layer, MF-EDSAE has $2K+2$ layers, where the $k$th layer $(k=1,\dots ,K+1)$ is the encoding layer, the $k$th layer ($k=K+2,\dots ,2K+1$) is the decoding layer, and $k=F$ is used to denote the fusion layer between the $(K+1)\text{th}$ and the $(K+2)\text{th}$ layers. The parameter update formula for the fusion layer will be given in the next subsection.

By adding a nonlinear fusion layer, the semantic and complementary information learned from each paradigm can be well combined.

2.3.3. Training with multi-paradigm data

In the training stage with multi-paradigm data, we add KL divergence to the reconstruction layer and the hidden layers to obtain sparse reconstruction. Meanwhile, the hypergraph regularization and the multi-paradigm hypergraph regularization are added to the encoding layers and the decoding layers respectively to incorporate high-order relationships within and between paradigms. To further avoid overfitting, we use the log-sum regularization, which is an effective approximation to the $L_0$ regularization (Rao & Kreutz Delgado, 1999). The loss function of the multi-paradigm training is thus defined as

$$L\left(x,\tilde{W}\right)=\sum _{m=1}^M\{\frac{1}{2}\sum _{p=1}^N\sum _{j=1}^{n_{2K+1}}{\left(x_{pj}^m-{\hat{x}}_{pj}^m\right)}^2+{\lambda }_1\sum _{k=2}^{2K+1}\sum _{j=1}^{n_k}KL\left(\rho \Vert {\hat{\rho }}_j^{k,m}\right)+{\lambda }_2\sum _{k=2}^{K+1}Tr\left({\left(A^{k,m}\right)}^T{L}_{\mathit{\text{hyper}}}^m{A}^{k,m}\right)\}+\sum _{k=K+2}^{2K+1}Tr\left({\left(A^k\right)}^T{L}_{\mathit{\text{mhyper}}}{A}^k\right)+{\lambda }_3\sum _{m=1}^M\sum _{k=1}^{2K}\sum _{i=1}^{n_k}\sum _{j=1}^{n_{k+1}}\text{log}\left(1+\frac{\left|w_{ji}^{k,m}\right|}{ϵ}\right)$$

where $n_k^m$ is the number of neurons in the $k$th layer of the $m$th paradigm. For the $p$th sample in the $m$th paradigm, $x_{pj}^m$ is the value of the $j$th feature, ${\hat{x}}_{pj}^m$ is the reconstruction of $x_{pj}^m$, and $a_{pj}^{k,m}$ represents the activation value of the $j$th neuron in the $k$th layer. Specifically, $a_{pj}^{1,m}$ and $a_{pj}^{2K+1,m}$ denote $x_{pj}^m$ and ${\hat{x}}_{pj}^m$.

$$\{\begin{array}{l}{a}_{pj}^{k+1,m}=f\left(\sum _{i=1}^{n_k^m}{w}_{ji}^{k,m}{a}_{pi}^{k,m}+b_j^{k,m}\right)k=1,\dots ,K,K+2,\dots ,2K\hfill \\ a_{pj}^{k+1,m}=f\left(\sum _{i=1}^{n^F}{w}_{ji}^{k,m}f\left(\sum _{m=1}^M\sum _{t=1}^{n_k^m}{w}_{it}^{F,m}{a}_{pt}^{k,m}\right)+b_j^{k,m}\right)k=K+1\hfill \end{array}$$ (4)

where $n^F$ is the number of neurons in the fusion layer. $f(\cdot )$ is a nonlinear differentiable function.

In the loss function $L(x,\tilde{W})$, the last term is only related to the weight $\tilde{W}$, while the first four terms are related to the weight $\tilde{W}$ and the response values. So the first four terms are denoted as $L_1(x,\tilde{W})$ and the last term is $L_2\left(\tilde{W}\right)$.

In $L_1(x,\tilde{W})$, the first term is the reconstruction error of the autoencoder. The second term $\text{KL}\left(\rho \Vert {\hat{\rho }}_j^{k,m}\right)$ is the KL divergence between two Bernoulli random variables; one has mean value $\rho$, and the other has mean value ${\hat{\rho }}_j^{k,m}$. It is defined as

$$KL\left(\rho \Vert {\hat{\rho }}_j^{k,m}\right)=\rho \text{log}\frac{\rho }{{\hat{\rho }}_j^{k,m}}+\left(1-\rho \right)\text{log}\frac{1-\rho }{1-{\hat{\rho }}_j^{k,m}}$$

where $\rho$ is a sparsity parameter and ${\hat{\rho }}_j^{k,m}=\frac{1}{N}{\sum }_{p=1}^N{a}_{pj}^{k,m}$. The third term $Tr\left({\left(A^{k,m}\right)}^T{L}_{\mathit{\text{hyper}}}^m{A}^{k,m}\right)$ is the hypergraph based regularization and calculated by Eq. (1), where for the $p$th sample in the $m$th paradigm, $A^{k,m}=\left[a_1^{k,m},\dots ,a_p^{k,m}\right]$ with $a_i^{k,m}={\left[a_{i1}^{k,m},\dots ,a_{i,n_k^m}^{k,m}\right]}^T$ representing the activation matrix and the activation vector in the $k$th layer respectively. The fourth term $Tr\left({\left(A^k\right)}^T{L}_{\mathit{\text{mhyper}}}{A}^k\right)$ is the multi-paradigm hypergraph regularization and calculated by Eq. (2), where $A^k=\left[A^{k,1};\cdots ;A^{k,M}\right]$. In $L_2\left(\tilde{W}\right),\text{log}\left(1+\frac{\left|w_{ji}^{k,m}\right|}{ϵ}\right)$ is the log-sum regularization and $ϵ$ is the disturbance term to ensure the validity of the log-sum regularization when $w_{ji}^{k,m}\to 0.{\beta }_1,{\beta }_2,{\lambda }_1,{\lambda }_2,{\lambda }_3$ are penalty parameters.

In the following we derive the gradient update formula during model training. We provide the gradient calculation of $L_1(x,\tilde{W})$ on ${\tilde{w}}_{ji}^{k,m}$. For convenience, let $a_{pi}^F=f\left({\sum }_{m=1}^M{\sum }_{t=1}^{n_{K+1}^m}{w}_{it}^{F,m}{a}_{pt}^{K+1,m}\right)$. For the $p$th sample in the $m$th paradigm, $z_{pj}^{k,m}$ is the net activation of the $j$th neuron in the $k$th layer. The detailed derivation process can be found in our supplement. First, we give the gradient formula of the connection weight matrix in the decoding layers ${\tilde{W}}^{K+1,m},\dots ,{\tilde{W}}^{2K,m}\left(m=1,\dots ,M\right).$ Let

$${\delta }_{pj}^{k,m}=\{\begin{array}{l}\left\{\left(x_{pj}^m-{\hat{x}}_{pj}^m\right)+{\lambda }_1\left(\frac{1-\rho }{1-{\hat{\rho }}_j^{k,m}}-\frac{\rho }{{\hat{\rho }}_j^{k,m}}\right)+{\beta }_1\sum _{q=1}^N{S}_{pq}^m\left({\hat{x}}_{pj}^m-{\hat{x}}_{qj}^m\right)+{\beta }_2\sum _{t\ne m}^M\sum _{q=1}^N\left(S_{pq}^{m,t}+S_{pq}^{t,m}\right)\left({\hat{x}}_{pj}^m-{\hat{x}}_{qj}^t\right)\right\}{f}^{\prime }\left(z_{pj}^{k,m}\right)k=2K+1\hfill \\ \left\{\sum _{i=1}^{n_{k+1}^m}{\delta }_{pi}^{k+1,m}{\tilde{w}}_{ij}^{k,m}+{\lambda }_1\left(\frac{1-\rho }{1-{\hat{\rho }}_j^{k,m}}-\frac{\rho }{{\hat{\rho }}_j^{k,m}}\right)+{\beta }_1\sum _{q=1}^N{S}_{pq}^m\left(a_{pj}^{k,m}-a_{qj}^{k,m}\right)+{\beta }_2\sum _{t\ne m}^M\sum _{q=1}^N\left(S_{pq}^{m,t}+S_{pq}^{t,m}\right)\left(a_{pj}^{k,m}-a_{qj}^{k,t}\right)\right\}{f}^{\prime }\left(z_{pj}^{k,m}\right)k=K+2,\dots ,2K\hfill \end{array}$$

Thus, the gradient is

$$\nabla {\tilde{w}}_{ji}^{k,m}=\{\begin{array}{ll}{\delta }_{pj}^{k+1,m}{a}_{pi}^{k,m}\hfill & k=K+2,\dots ,2K\hfill \\ {\delta }_{pj}^{k+1,m}{a}_{pi}^F\hfill & k=K+1\hfill \end{array}$$

and its matrix formula is

$$\nabla {\tilde{W}}_p^{k,m}=\{\begin{array}{ll}{\delta }_p^{k+1,m}{\left(a_p^{k,m}\right)}^T\hfill & k=K+2,\dots ,2K\hfill \\ {\delta }_p^{k+1,m}{\left(a_p^F\right)}^T\hfill & k=K+1\hfill \end{array}$$ (5)

where $a_p^{k,m}={\left[a_{p1}^{k,m},\dots ,a_{p,n_k^m}^{k,m}\right]}^T,a_p^F={\left[a_{p1}^F,\dots ,a_{p,n^F}^F\right]}^T$, ${\delta }_p^{k,m}={\left[{\delta }_{p1}^{k,m},\dots ,{\delta }_{p,n_k^m}^{k,m}\right]}^T$.

Furthermore, we present the gradient formula of the fusion layer. Since

$$\begin{gathered} \frac{\partial L_1}{\partial w_{ji}^{F,m}}=\left[\sum _{n=1}^M\sum _{t=1}^{n_{K+2}}{\delta }_{pt}^{K+2,n}{w}_{tj}^{K+1,n}\right]f^{\prime }\left(z_{pj}^F\right)a_{pi}^{K+1,m} \\ ={\delta }_{pj}^F{a}_{pk}^{K+1,m} \end{gathered}$$

then

$$\nabla W_p^{F,m}={\delta }_p^F{\left(a_p^{K+1,m}\right)}^T$$

Lastly, we give the gradient formula of the connection weight matrix in the encoding layers ${\tilde{W}}^{1,m},\dots ,{\tilde{W}}^{K,m}(m=1,\dots ,M)$. Here $E^m$ and $e_i^m$ denote the set of hyperedges and the ith hyperedge to the $m$th paradigm, respectively.

$${\delta }_{pj}^{k,m}=\{\begin{array}{l}\left\{\sum _{i=1}^{n_F}{\delta }_{pi}^F{w}_{ij}^{F,m}+{\lambda }_1\left(\frac{1-\rho }{1-{\widehat{\rho }}_j^{k,m}}-\frac{\rho }{{\widehat{\rho }}_j^{k,m}}\right)+{\lambda }_2\sum _{e_i^m\in E^m}\sum _{a_q^m\in e_i^m}{\varphi }_i^m\left(a_{pj}^{k,m}-a_{qj}^{k,m}\right)\right\}{f}^{\prime }\left(z_{pj}^{k,m}\right)k=K+1\hfill \\ \left\{\sum _{i=1}^{n_{k+1}}{\delta }_{pi}^{k+1,m}{\tilde{w}}_{ij}^{k,m}+{\lambda }_1\left(\frac{1-\rho }{1-{\widehat{\rho }}_j^{k,m}}-\frac{\rho }{{\widehat{\rho }}_j^{k,m}}\right)+{\lambda }_2\sum _{e_i^m\in E^m}\sum _{a_q^m\in e_i^m}{\varphi }_i^m\left(a_{pj}^{k,m}-a_{qj}^{k,m}\right)\right\}{f}^{\prime }\left(z_{pj}^{k,m}\right)k=2,\dots ,K\hfill \end{array}$$

Thus, the gradient is

$$\nabla {\tilde{w}}_{ji}^{k,m}=\{\begin{array}{ll}{\delta }_{pj}^{k+1,m}{a}_{pi}^{k,m}\hfill & k=2,\dots ,K\hfill \\ {\delta }_{pi}^{k+1,m}{x}_{pi}^m\hfill & k=1\hfill \end{array}$$

its matrix formula is

$$\nabla {\tilde{W}}_p^{k,m}=\{\begin{array}{ll}{\delta }_p^{k+1,m}{\left(a_p^{k,m}\right)}^T\hfill & k=2,\dots ,K\hfill \\ {\delta }_p^{k+1,m}{\left(x_p^m\right)}^T\hfill & k=1\hfill \end{array}$$ (6)

The gradient of $L_2$ is calculated by

$$\{\begin{array}{l}\frac{\partial L_2\left(\tilde{W}\right)}{\partial w_{ji}^{k,m}}=\frac{\mathit{\text{sign}}\left(w_{ji}^{k,m}\right)}{ϵ+w_{ji}^{k,m}}\hfill \\ \frac{\partial L_2\left(\tilde{W}\right)}{\partial b_j^{k,m}}=0\hfill \end{array}$$

Based on the above derivations, we can give the parameter update formula used in MF-EDSAE. For the fusion layer, the parameters update formula is

$$W^{F,m}=W^{F,m}-\frac{{\eta }_1}{N}\sum _{p=1}^N\nabla W_p^{F,m}$$

For the decoding layers and encoding layers, the parameters update formula is

$${\tilde{W}}^{k,m}={\tilde{W}}^{k,m}-\frac{{\eta }_1}{N}\sum _{p=1}^N\left(\nabla {\tilde{W}}_p^{k,m}+{\lambda }_3\frac{\partial L_2\left(\tilde{W}\right)}{\partial {\tilde{W}}^{k,m}}\right)$$

where ${\eta }_1$ is the learning rate, $\frac{\partial L_2\left(\tilde{W}\right)}{\partial {\tilde{W}}^{k,m}}=\left\{\frac{\partial L_2\left(\tilde{W}\right)}{\partial {\tilde{w}}_{ji}^{k,m}}\right\},{\tilde{W}}_p^{k,m}$ is calculated by Eq. (5) for decoding layers and is calculated by (6) for encoding layers.

2.4. Feature selection layer

Through the above training process, we can obtain the sparse reconstruction of the original data to identify the features, i.e., dFC with significant differences in brain development. In order to further improve the explainability of the model, a feature selection layer is added.

In the feature selection layer of MF-EEDSAE, k-means (Aloise, Deshpande, Hansen, & Popat, 2009) with $k=2$ is firstly used to cluster the features of the reconstructed data into two clusters. Cluster with mean value near to zero is considered as inactive and thus removed, while the other cluster is consider as active features and kept. Then, relief (Brankovic & Piroddi, 2019) is used to select the most discriminative features. By adding the feature selection layer, the redundant features are removed and only the most discriminative features are retained, resulting in better explainability of the model.

3. Analysis of multi-paradigm dynamic functional connectivity data

3.1. Data collection and preprocessing

The Philadelphia Neurodevelopmental Cohort (PNC) is a large scale collaborative project between the Brain Behavior Laboratory at the University of Pennsylvania and the Children’s Hospital of Philadelphia, which contains nearly 900 adolescents with ages from 8 to 21 underwent multi-paradigm neuroimaging including resting-state fMRI, fMRI of working memory and emotion identification tasks (called rest fMRI, nback fMRI, and emoid fMRI) (Satterthwaite et al., 2014). We selected the children under 144 months and the adults over 216 months to study the difference of brain function network between the two groups based on the rest fMRI, nback fMRI, and emoid fMRI, which continues the way of dividing the age range of PNC data in our previous works (Qiao, Hu, et al., 2021; Qiao, Yang, et al., 2021). The details of the subjects are listed in Table 1. The statistical parametric mapping 12 (SPM12) was used to implement the standard brain imaging preprocessing (Xiao et al., 2019), which includes motion correction, spatial normalization to the standard Montreal Neurological Institute space (spatial resolution of 3 × 3 × 3 mm), and spatial smoothing with a 3 mm full width half maximum Gaussian kernel. Then a regression procedure was implemented to remove the influence of motion. Finally, according to the definition of brain region by Power et al. (2011), the brain is divided into 264 regions of interest (ROI) with a sphere radius parameter of 5 mm to reduce the dimensionality of the data. The time sequences from different voxels in the same ROI are averaged, thus the data is finally reduced to a $264\times T$ matrix for every subject, in which $T$ denotes the number of time points with a repetition time value being 3 s and the value of $T$ is different for different paradigms. The value of $T$ for emoid fMRI is 210, for nback fMRI is 231 and for rest fMRI is 124. We use the sliding-window technique to estimate the dynamic functional connectivity (dFC). In the sliding-window technique, a window with length $r$ moves along with the time series with step size $s$, and the dFC between two ROIs are calculated for each window by calculating the Pearson correlation coefficient. For a time series including $T$ time points, there are totally $K=(T-r)/s+1$ sliding windows. By grid search, $r$ and $s$ are chosen to be 14 and 1 for emoid fMRI, 17 and 1 for nback fMRI, 33 and 1 for rest fMRI. As a result, each subject get a dFC matrix $D\in {ℝ}^{K\times C_{264}^2}$ in different paradigms, where $C_{264}^2=34716$ and $K=197$ for emoid fMRI, $K=215$ for nback fMRI, $K=92$ for rest fMRI. To reduce the computational complexity, we implement the random sampling way in Qiao, Yang, et al. (2021). However, compared with the rest fMRI, the task fMRI not only has more time points but also has more complex temporal information. Considering both the temporal information in multi-paradigm and the computational complexity, we finally select 20 rows from each subject in different paradigms, based on the experimental results that the time series in each paradigm with random 20 sliding windows can still keep a good discriminative ability. In other words, 20 samples are obtained from a subject. For all subjects, we get 2460 samples for children and 2920 samples for young adults, thus there totally are 5380 samples. 80% samples are randomly selected from the two groups respectively as the training data to select the significant differences of dFC between the two groups, and the rest 20% samples are used as test data to test the validity of the selected dFC.

Table 1.

Demographic characteristics of the subjects.

	Children	Young Adults
Number	123	146
Gender (male/female)	53/70	57/89
Age (Mean ± SD, months)	123.98 ± 11.12	231.23 ± 12.03
Ethnicity
ASIAN	2(1.6%)	0(0%)
AFRICAN	46(37.4%)	55(37.7%)
AMERICAN	0(0%)	0(0%)
OTHER/MIXED	13(10.6%)	13(8.9%)
CAUCASIAN/WHITE	61(49.6%)	78(53.4%)
HAWAIIAN/PACIFIC	1(0. 8%)	0(0%)

3.2. Data reconstruction and dFC selection

In this section, we implement MF-EDSAE to search for the dFC that show significant differences during brain development. The architecture of MF-EDSAE contains 6 hidden layers with 12 000, 6000, 3000, 3000, 6000, 12 000 units respectively. Both the input layer and the output layer of MF-EDSAE have 34716 units. To determine hyperparameters, the training data is further divided, where 70% of the training data is used to train the model, and 30% of the training data is used to evaluate the hyperparameters. Additionally, the grid search method is used to select hyperparameters, because it can simply make a complete search over a given hyperparameters space and easily be parallelized to find more stable optimal hyperparameters (Fayed & Atiya, 2019; Saud, Jamil, Upadhyay, & Irshad, 2020). Specifically, each of the hyperparameters is selected by the grid search method, when other hyperparameters are fixed. By repeating the above process, all hyperparameters are thus selected. After grid search, the sparsity parameter, penalty coefficients of KL, and $L_2$ regularization are all set to 0.01, the global learning rate, gradient decay factor, and squared gradient decay factor for Adam update are 1 × 10⁻³, 0.95, and 0.95 respectively in the training stage with single-paradigm data. In the multi-paradigm training stage, the parameters of KL, log sum regularization, hypergraph regularization are selected to be 1 × 10⁻³, 5 × 10⁻⁷ and 5 × 10⁻⁶. The sparsity parameter, the penalty coefficients of multi-paradigm hypergraph regularization for inter-paradigm and intra-paradigm are chosen to be 1 × 10⁻³, 5 × 10⁻⁶, 5 × 10⁻⁷. The global learning rate, gradient decay factor and squared gradient decay factor for Adam update are 1 × 10⁻⁴, 0.95 and 0.95, respectively. In MF-EDSAE, the sigmoid function is selected as the activation function $f$ and the Adam updating with mini-batch strategy is used to update the model parameters. In order to verify that the proposed model can more effectively identify the dFCs with significant differences during brain development than other reconstruction methods, the support vector machines (SVMs) are used to distinguish between children and adults based on the data reconstructed by different methods. Specifically, reconstruction methods include the single paradigm DSAE, the proposed MF-EDSAE with and without a feature selection (FS) layer, where MF-EDSAE with FS refers to adding a feature selection layer after the output layer, and MF-EDSAE without FS refers to not adding a feature selection layer. The classification accuracy of SVM on the test data is used to evaluate the discriminative ability of the reconstructed data with each reconstruction method. For the fairness of comparison, we use the same network architecture and parameters for all networks. For the testing data, the classification accuracy of traditional DSAE on emoid fMRI, nback fMRI, and rest fMRI are 88.10 ± 2.37%, 88.57 ± 4.09% and 94.33 ± 1.32% respectively, the classification accuracy of MF-EDSAE without FS on emoid fMRI, nback fMRI and rest fMRI are 94.14 ± 2.47%, 96.28 ± 0.96% and 99.26 ± 0.26% respectively, and the classification accuracy of MF-EDSAE with FS on emoid fMRI, nback fMRI and rest fMRI are 94.33 ± 1.98%, 96.38 ± 0.93% and 99.91 ± 0.16% respectively.

The above results show that the classification accuracy of MF-EDSAE (both with and without FS) are significantly improved compared to DSAE. It shows that MF-EDSAE can accurately pick out the dFC with significant differences between children and adults, by using multi-paradigm information and high-order relationships in the data. The classification accuracy of MF-DSAE with FS is improved on emoid fMRI and nback fMRI compared to MF-DSAE without FS. It indicates that the feature selection layer can further remove redundant features, resulting in better classification. Among the total 34716 dFC, the number of activating dFC in emoid fMRI, nback fMRI, rest fMRI are 10 130, 12 801, 11 998 respectively after sparse reconstruction. After the feature selection layer, we finally retain 2400 dFC in emoid fMRI, 7400 dFC in nback fMRI, and 2600 dFC in rest fMRI. These dFC with the most significant difference during brain development are used for subsequent analysis.

3.3. The group differences in the FNs

In order to better understand the relationship between ROIs, the 264 ROIs are divided into 13 functional regions called functional networks (FN) according to Power et al. (2011). They are sensory/somatomotor network (SSN), cingulo-opercular task control network (COTCN), auditory network (AN), default mode network (DMN), memory retrieval network (MRN), visual network (VN), frontoparietal task control network (FPTCN), salience network (SN), subcortical network (SCN), ventral attention network (VAN), dorsal attention network (DAN), cerebellar network (CN) and uncertain network (UN). The first 12 FNs are mainly related to brain functions such as movement, memory, language, vision, and cognition. The UN contains 29 ROIs that are not strongly associated with other FNs. For the dFC selected from emoid fMRI, nback fMRI, and rest fMRI, the hypothesis testing methods in Qiao, Hu, et al. (2021) are used to test whether the changes found in dFC are significant. After the hypothesis testing, 134, 318, 345 significantly enhanced dFC with age and 2260, 7083, 2255 significantly weakened dFC with age are found in emoid fMRI, nback fMRI, and rest fMRI, respectively. The details of the hypothesis test methods can be found in Appendix B.

Fig. 2 shows the distribution of the selected dFC among ROIs and FNs. It indicates that the distribution of the selected dFC is still roughly the same in all three paradigms and the number of enhanced dFC is far less than the weakened ones during brain development. Fig. 2(a) illustrates the distribution of dFC in different ROIs under the three paradigms, and the purple lines represent the enhanced dFC, the yellow lines represent the weakened ones during development. Fig. 2(b) shows that compared with children, adults have enhanced dFC between SSN and DMN, SSN and AN, SSN and FPTCN, SN and UN in all three fMRIs, and there are also many enhanced dFC within SN. Unlike emoid fMRI, adults have obviously enhanced dFC between SCN and SN, DMN and VN in nback fMRI and rest fMRI. Moreover, in the emoid fMRI, there is enhanced dFC between SCN and VN during development. Fig. 2(c) shows the weakened dFC are mainly distributed between DMN, SSN, VN, FPTCN, SN, and there are also many weakened dFC within DMN in all three fMRI data during brain development. In emoid fMRI and nback fMRI, adults have weakened dFC between VN and FPTCN, SN and VN during brain development, which is not observed in rest fMRI.

Fig. 2.

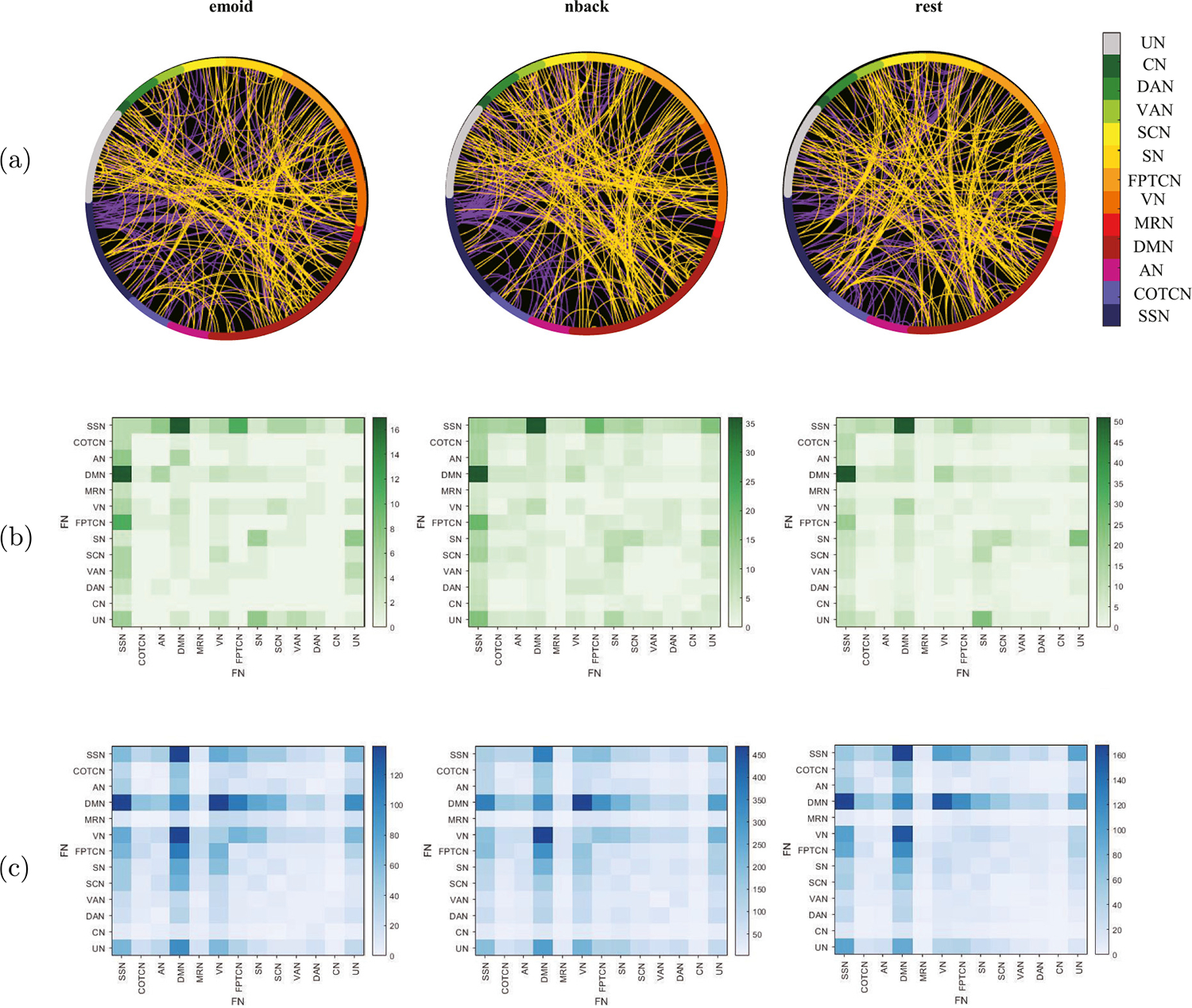
Functional networks: (a) Different distributions of the selected dFC in different paradigms, where the purple lines represent the enhanced dFC during brain development and the yellow lines represent the weakened dFC. (b) The figure shows the enhanced dFC within and among FNs during brain development in different paradigms. (c) The figure shows the weakened dFC within and among FNs during brain development in different paradigms.

3.4. Analysis of dynamic functional connectivity states

To study the time-vary patterns of dFC differing between children and adults, k-means is used to identify the brain states. The elbow criterion defined in Eq. (7) is used to calculate the optimal number of states, where $K$ is the number of clusters, $C_i$ is the $i$th cluster, and $c_i$ is the cluster center of $C_i$.

$$SSE=\sum _{i=1}^K\sum _{x\in C_i}{\left|x-c_i\right|}^2$$ (7)

According to the elbow criterion, the optimal number of states for emoid fMRI, nback fMRI and rest fMRI are 4, 4, 3 respectively. For the emoid fMRI, the proportions in the four dFC states for the children are 17.16%, 23.82%, 27.76%, 31.26% and the proportions in four dFC states for the adults are 15.00%, 10.99%, 43.02%, 30.99%. For the nback fMRI, the proportions in the four dFC states for the children are 18.25%, 24.76%, 29.35%, 27.64% and the proportions in four dFC states for the adults are 15.68%, 33.73%, 43.43%, 7.16%. For the rest fMRI, the proportions in the three dFC states for children are 28.58%, 35.04%, 36.38% and the proportions in the three dFC states for adults are 21.30%, 40.72%, 37.98%.

Fig. 3 shows the changes in each state during brain development for different paradigms. Fig. 3(a) shows that in emoid fMRI, there are more weakened dFC than enhanced ones in all four states. The distributions of weakened dFC in different states are roughly the same, but the distributions of enhanced dFC are different. For example, compared with children, adults have weakened dFC within DMN and between DMN and other FNs such as SSN, SN, SCN, etc., and between VN and FPTCN, VN and SN in all four states. Fig. 3(a) also shows there exists enhanced dFC between SSN and other FNs such as DMN, VN, FPTCN, UN in all four states. The enhanced dFC within VN and between AN and DMN, AN and UN and DMN, VN and FPTCN are observed in state 1. Meanwhile, there exists enhanced dFC between DMN and other FNs such as VN, SN, SCN, between VN and FPTCN, SCN, VAN in state 3 and state 4, and the enhanced dFC between MRN and VN, FPTCN, SN, SCN are found.

Fig. 3.

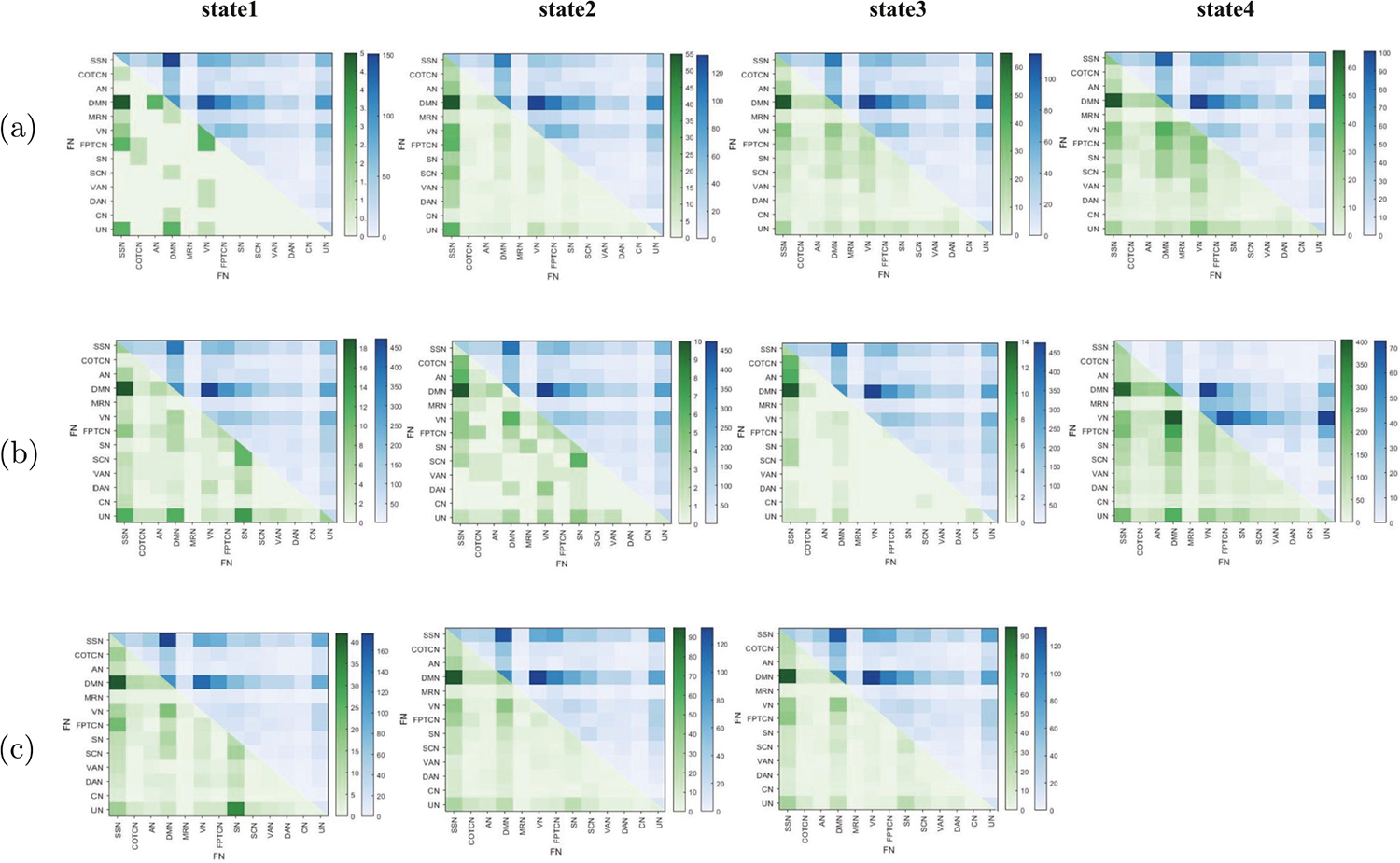
Extraction of dFC: (a), (b), (c) respectively, show the changes of dFC between and within FNs in different states of emoid fMRI, nback fMRI and rest fMRI during brain development. For each subfigure, the part of upper triangle represents the weakened dFC, the part of lower triangle represents the enhanced dFC.

Fig. 3(b) shows that, in nback fMRI, except for state 4, the weakened dFC is far more than the enhanced dFC, and the weakened dFC distributions in state 1, state 2, state 3 are very similar, and they are the same as the distributions of enhanced dFC in state 4. In Fig. 3(b), we find that the weakened dFC exists within DMN and between DMN and such as SSN, FPTCN, SN, SCN, etc., between VN and FPTCN, SN, which is consistent with the weakened dFC distributions in emoid fMRI. However, the weakened dFC of state 4 is mainly concentrated within VN and between VN and DMN, MRN, FPTCN, SN, SCN, VAN and UN. And there is enhanced dFC between DMN and SSN. For state 1, the enhanced dFC between UN and SN, DMN, SSN, between SN and SCN and within SN are observed. For state 2, the enhanced dFC between SSN and COTCN, AN, between DMN and VN, between SN and SCN are observed. For state 4, we can also find the enhanced dFC between SSN and VN, between DMN and VN, FPTCN, SN, and SCN, between VN and VAN, SN, and FPTCN.

Fig. 3(c) shows in rest fMRI, there are more weakened dFC than enhanced dFC in all three states, and the distributions of weakened dFC under different states are roughly the same, and the same is true for enhanced dFC. In Fig. 3(c), we observe that the weakened dFC are mainly concentrated within DMN and between DMN and other FNs such as SSN, FPTCN, SN, SCN, etc., and between VN and FPTCN, SN, and the enhanced dFC are mainly concentrated in between SSN and DMN, AN, VN, FPTCN, between DMN and VN in three states. Otherwise, the enhanced dFC between SN and UN is also observed in state 1.

To further investigate the time occupied divergence of each state, we estimate both the dwell time (DT) and the fraction of time (FT) for children and adults from the state transition vector (Cai et al., 2017). For the 123 children and 146 adults, the values of DT and FT are calculated. At the same time, the mean dwell time (MDT) and the mean fraction time (MFT) of each state are also calculated. The results of DT, FT, MDT, and MFT for children and adults are shown in Fig. 4, and the curve in this figure is the mean curve obtained by connecting mean values in different states. Compared with children, adults spend more time in state 3 and state 4, based on emoid fMRI. In nback fMRI, adults mainly stay in state 2 and state 3 longer than children, and children stay in state 1 for much longer than adults. In rest fMRI, the difference in stay time between children and adults in different states is not as obvious as in the task fMRI (nback, emoid). Compared with children, adults stay longer in state 2 and state 3 than children, and children spend more time in state 1, in rest fMRI.

Fig. 4.

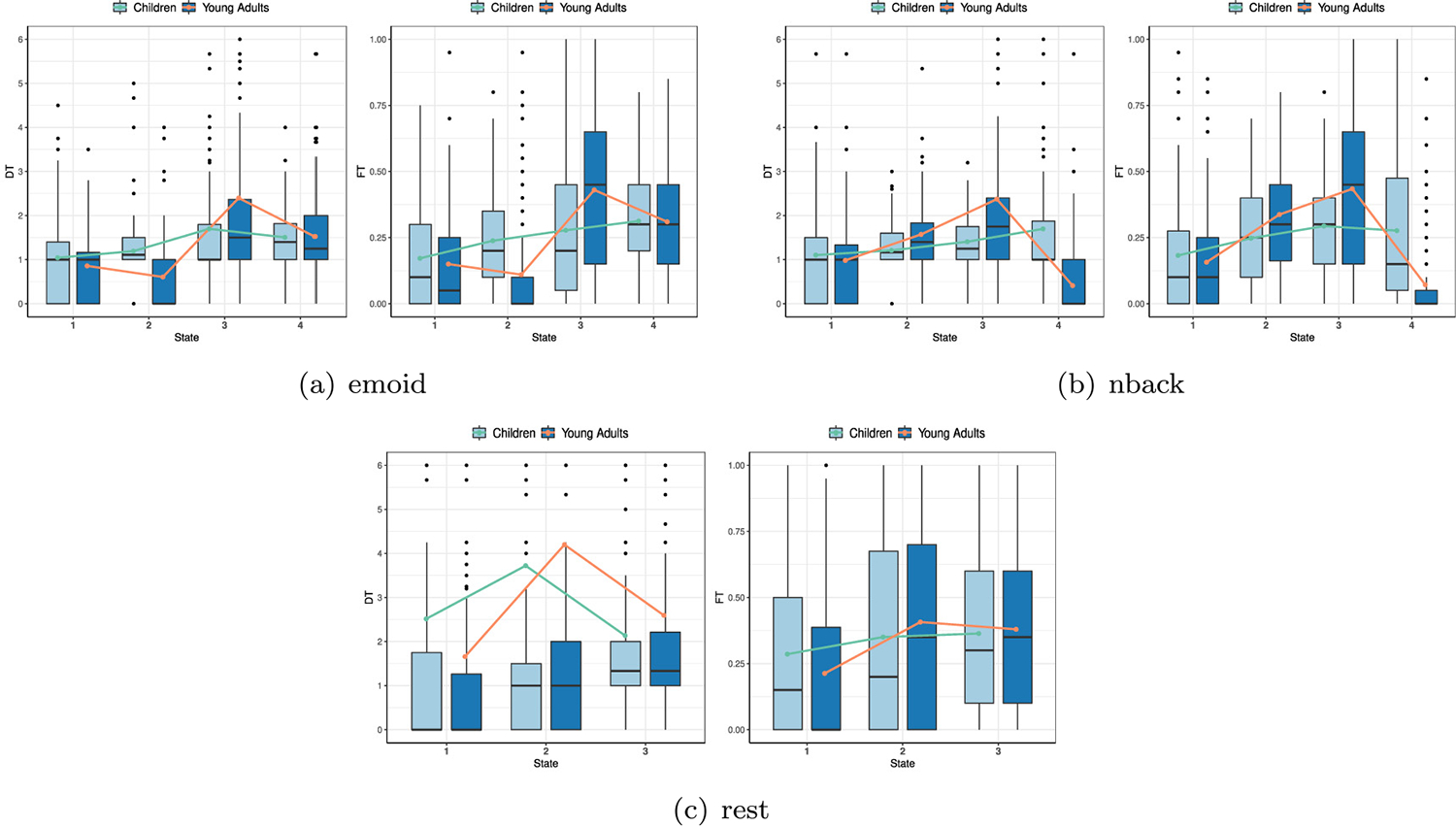
Distribution of DT and FT in different states in three paradigms.

4. Discussion

In this study, we propose an MF-EDSAE model and apply it to investigate the differences in dFC between children and adults in emoid fMRI, nback fMRI, and rest fMRI. The dFC with significant differences between children and adults are mainly distributed within or between DMN, VN, FPTCN, SN, SSN, AN, and SCN, which are closely related to information processing, attention, alertness, cognition, and working memory. DMN is a brain system, including the posterior cingulate gyrus, medial frontal lobe, hippocampus, and lateral temporal lobe, and is mainly related to mental activities such as memory (Raichle et al., 2001). VN includes the middle occipital gyrus and inferior gyrus, tongue gyrus, cuneiform lobe, and other brain regions, which are mainly responsible for visual information processing. FPTCN contains brain regions such as the upper parietal lobe and frontal lobe, which are related to attention processing (Sheffield et al., 2015). SN includes the paracentral lobules, superior marginal gyrus, insula, cingulate gyrus, and other brain regions. It is responsible for judging the salience of the stimulus through the physical characteristics and the relevant information of the task and regulating the attention (Seeley, 2019). SSN mainly includes the precuneus, central anterior and posterior gyrus, cingulate gyrus, and superior frontal gyrus, which are related to cognitive activities (Londei et al., 2010). AN contains the superior temporal gyrus and insula, central anterior gyrus, and posterior gyrus, which are innervated by autonomic nerves and are responsible for activities related to sound information, including collection, conduction, and processing (Smith et al., 2009). SCN includes the thalamus, extranuclear and lentiform. It plays an important role in memory, attention, perception, and consciousness (Kang, Pae, & Park, 2017).

Our results show that, as brain develops, the weakened dFC is far more than the enhanced dFC, and they are mainly concentrated within the DMN and between DMN and other FNs, in all three paradigms. This is consistent with the conclusions of previous studies (Anderson, Ferguson, Lopez Larson, & Yurgelun Todd, 2011; Cai et al., 2017). This finding shows that adults have better intra-network connectivity, while children have stronger inter-network connectivity (Zhang et al., 2019). In addition, it can explain that the FNs of children are not effective enough (Jolles, van Buchem, Crone, & Rombouts, 2011). In particular, we find there are weakened dFC between DMN and SSN, SN, VN, AN, showing the FNs of children are not effective in processing information (Cai et al., 2018). The weakened dFC between DMN and FPTCN is observed which is considered to be related to higher reading abilities during development in Jolles et al. (2020). In a prior study, the enhanced connectivity between DMN and SN is associated with the more defensive brain organization of the allostatic-interoceptive brain system (Kozlowska et al., 2018). The dFC between DMN and SN in children is stronger than in adults in the three paradigms, indicating children show more defensive brain organization than adults. It has been observed that the weakening of the dFC intensity between DMN and AN is due to the existence of some causal interacting circuits between DMN and AN, and through the asynchronous interregional interactions, the decline of auditory cortex response will lead to the declining ability of AN to inhibit DMN (Xu et al., 2017). In addition, the enhanced dFC between SCN and SN, between SCN and VN are observed in emoid fMRI and nback fMRI respectively, indicating that adults are more capable of dealing with specific tasks than children.

By comparing the distribution of weakened dFC in different paradigms, we can find that the connectivities between VN and FPTCN, SN of adults in the task fMRI (emoid, nback) are weaker than in children, which cannot be found in the rest fMRI. Previous research has shown that weakened dFC between the FPTCN and VN support cognitive flexibility (Qiao et al., 2020). In addition, compared with weakened dFC, the distributions of enhanced dFC under different paradigms are more distinct. The enhanced dFC between SSN and other FNs are observed in three different paradigms, which can be explained by the significantly enhanced interaction of SSN with other FNs to receive information after mid-adolescence (Zhang et al., 2020). In addition, we found that compared with weakened dFC, enhanced dFC can better reflect the differences of dFC networks in different paradigms.

Through the analysis of time-varying patterns between children and adults, we find that the differences in dFC patterns under three paradigms are easier to identify based on brain states. In the rest fMRI, the distributions of enhanced dFC and weakened dFC are almost the same in different states. However, in the task fMRI (emoid, nback), the distribution of enhanced dFC changes significantly with time. In the nback fMRI, the distribution of weakened dFC in state 4 is different from that in other states. Compared with task fMRI, the FNs of rest fMRI are more stable. Compared with children, the FNs in the brain of adults update more quickly when stimulated by a task, so that functionally specialized networks can interact and gain multi-function ability (Jiang et al., 2020). Based on the time-varying pattern of FCs, we can find information that cannot be found only based on differences between groups. It also shows that the analysis of multi-paradigm fMRIs provides a more complete understanding of brain FNs.

To summarize, our results indicate that, in all the three paradigms, most dFC become gradually weakened during brain development. It is consistent with the observation that the dFC patterns of children are more dispersive but are more focused in adults (Kelly et al., 2009). It shows that the function of the brain transits from undifferentiated systems to specialized networks during brain development (Jolles et al., 2011). The patterns of dFC can change more quickly when stimulated by a task with the development of the brain. In addition, adults have stronger connectivities between task-related functional networks for a given task compared to children.

5. Conclusion

In this paper, MF-DSAE, a multi-paradigm fusion-based explainable deep sparse autoencoder, is proposed to identify the dFC with significant differences during brain development. Through nonlinear fusion layer and multi-hypergraph regularization, the MF-DSAE integrates complementary information from different paradigms of fMRI data to identify dFC that is common or specific to each paradigm. We apply the model to PNC data and show that MF-EDSAE has improved performance in detecting dFC with significant differences than single-paradigm DSAE. Moreover, the experiment results also show the following findings. In commonality, the dFC patterns of children are more dispersive than those in adults, and the brain function transits from undifferentiated systems to specialized networks during development. In specificity, the patterns of the global dFC can change more quickly when stimulated by a task as one grows, and adults have stronger connectivities between task-related functional networks for a given task compared to children.

Appendix A. Gradient derivation in multi-paradigm training

For the loss function

$$L_1\left(x,\tilde{W}\right)=\sum _{i=1}^4{L}_{1i}$$

where

$$L_{11}=\frac{1}{2}\sum _{m=1}^M\sum _{p=1}^N\sum _{j=1}^{n_{2K+1}}{\left(x_{pj}^m-{\hat{x}}_{pj}^m\right)}^2$$

$$L_{12}=\sum _{m=1}^M\sum _{k=2}^{2K+1}\sum _{j=1}^{n_k}KL\left(\rho \Vert {\hat{\rho }}_j^{k,m}\right)$$

$$L_{13}=\sum _{m=1}^M\sum _{k=2}^{K+1}Tr\left({\left(A^{k,m}\right)}^T{L}_{\mathit{\text{hyper}}}^m{A}^{k,m}\right)$$

$$L_{14}=\sum _{k=K+2}^{2K+1}Tr\left({\left(A^k\right)}^T{L}_{\mathit{\text{mhyper}}}{A}^k\right)$$

For the partial derivatives of $L_{11},L_{12}$ with respect to $w_{ji}^{k,m}$, we have a detailed derivation in our previous work (Qiao, Hu, et al., 2021). For convenience, let $z_{pj}^{k+1,m}={\sum }_{i=1}^{n_k^m}{w}_{ji}^{k,m}{a}_{pi}^{k,m}+b_j^{k,m}$. Here we mainly give the calculation of the partial derivative of $L_{13},L_{14}$ with respect to $w_{ji}^{k,m}$.

For convenience, the superscript $m$ will be omitted in calculation of the partial derivative of $L_{13}$ with respect to $w_{ji}^{k,m}$. The partial derivate of $L_{13}$ with respect to $w_{ji}^{K,m}$ is

$$\begin{gathered} \frac{\partial L_{13}}{\partial w_{ji}^K}=\frac{\partial L_{13}}{\partial a_{pj}^{K+1}}\frac{\partial a_{pj}^{K+1}}{\partial z_{pj}^{K+1}}\frac{\partial z_{pj}^{K+1}}{\partial w_{ji}^K} \\ =\frac{\partial }{\partial a_{pj}^{K+1}}\left(\sum _{e_i\in E}\sum _{a_p,a_q}\frac{1}{2}{\varphi }_i{\Vert a_p^{K+1}-a_q^{K+1}\Vert }^2\right)f^{\prime }\left(z_{pj}^{K+1}\right)a_{pi}^K \\ =\left(\sum _{e_i\in E}\sum _{a_p,a_q}{\varphi }_i\left(a_{pj}^{K+1}-a_{qj}^{K+1}\right)\right)f^{\prime }\left(z_{pj}^{K+1}\right)a_{pi}^K \\ ={\delta }_{pj\_L_{13}}^{K+1}{a}_{pi}^K \end{gathered}$$

The partial derivate of $L_{13}$ with respect to $w_{ji}^{K-1,m}$ is

$$\begin{gathered} \frac{\partial L_{13}}{\partial w_{ji}^{K-1}}=\sum _{k=1}^{n_{K+1}}\frac{\partial Tr\left({\left(A^{K+1}\right)}^T{L}_{\mathit{\text{hyper}}}{A}^{K+1}\right)}{\partial a_{pk}^{K+1}}\frac{\partial a_{pk}^{K+1}}{\partial z_{pk}^{K+1}}\frac{\partial z_{pk}^{K+1}}{\partial a_{pj}^K}\frac{\partial a_{pj}^K}{\partial z_{pj}^K}\frac{\partial z_{pj}^K}{\partial w_{ji}^{K-1}}+\frac{\partial Tr\left({\left(A^K\right)}^T{L}_{\mathit{\text{hyper}}}{A}^K\right)}{\partial a_{pj}^K}\frac{\partial a_{pj}^K}{\partial z_{pj}^K}\frac{\partial z_{pj}^K}{\partial w_{ji}^{K-1}} \\ =\sum _{k=1}^{n_{K+1}}\left(\sum _{e_i\in E}\sum _{a_q\in e_i}{\varphi }_i\left(a_{pk}^{K+1}-a_{qk}^{K+1}\right)f^{\prime }\left(z_{pk}^{K+1}\right)w_{kj}^K\right)f^{\prime }\left(z_{pj}^K\right)a_{pi}^{K-1}+\sum _{e_i\in E}\sum _{a_q\in e_i}{\varphi }_i\left(a_{pk}^K-a_{qk}^K\right)f^{\prime }\left(z_{pj}^K\right)a_{pi}^{K-1} \\ =(\sum _{k=1}^{n_{K+1}}\left(\sum _{e_i\in E}\sum _{a_q\in e_i}{\varphi }_i\left(a_{pk}^{K+1}-a_{qk}^{K+1}\right)f^{\prime }\left(z_{pk}^{K+1}\right)w_{kj}^K\right)+\sum _{e_i\in E}\sum _{a_q\in e_i}{\varphi }_i\left(a_{pk}^K-a_{qk}^K\right))f^{\prime }\left(z_{pj}^K\right)a_{pi}^{K-1} \\ =\left(\sum _{k=1}^{n_{K+1}}{\delta }_{pj\_L_{13}}^{K+1}{w}_{pj}^K+\sum _{e_i\in E}\sum _{a_q\in e_i}{\varphi }_i\left(a_{pk}^K-a_{qk}^K\right)\right)f^{\prime }\left(z_{pj}^K\right)a_{pi}^{K-1} \\ ={\delta }_{pj\_L_{13}}^K{a}_{pi}^{K-1} \end{gathered}$$

The partial derivate of $L_{13}$ with respect to $w_{ji}^{K-2,m}$ is

$$\begin{gathered} \frac{\partial L_{13}}{\partial w_{ji}^{K-2}}=\sum _{t=1}^{n_K}\left(\sum _{k=1}^{n_{K+1}}\frac{\partial \mathit{\text{Tr}}\left({\left(A^{K+1}\right)}^T{L}_{\mathit{\text{hyper}}}{A}^{K+1}\right)}{\partial a_{pk}^{K+1}}\frac{\partial a_{pk}^{K+1}}{\partial z_{pk}^{K+1}}\frac{\partial z_{pk}^{K+1}}{\partial a_{pt}^K}\frac{\partial a_{pt}^K}{\partial z_{pt}^K}\frac{\partial z_{pt}^K}{\partial a_{pj}^{K-1}}\right)\times \frac{\partial a_{pj}^{K-1}}{\partial z_{pj}^{K-1}}\frac{\partial z_{pj}^{K-1}}{\partial w_{ji}^{K-2}}+\sum _{t=1}^{n_K}\frac{\partial \mathit{\text{Tr}}\left({\left(A^K\right)}^T{L}_{\text{hyper}}{A}^K\right)}{\partial a_{pt}^K}\frac{\partial a_{pt}^K}{\partial z_{pt}^K}\frac{\partial z_{pt}^K}{\partial a_{pj}^{K-1}}\frac{\partial a_{pj}^{K-1}}{\partial z_{pj}^{K-1}}\frac{\partial z_{pj}^{K-1}}{\partial w_{ji}^{K-2}}+\frac{\partial \mathit{\text{Tr}}\left({\left(A^{K-1}\right)}^T{L}_{\text{hyper}}{A}^{K-1}\right)}{\partial a_{pj}^{K-1}}\frac{\partial a_{pj}^{K-1}}{\partial z_{pj}^{K-1}}\frac{\partial z_{pj}^{K-1}}{\partial w_{ji}^{K-2}} \\ =\sum _{t=1}^{n_K}{\delta }_{pj\_L_{13}}^K{w}_{tj}^{K-1}{f}^{\prime }\left(z_{pj}^K\right)a_{pi}^{K-2}+\sum _{e_i}\sum _{a_q\in e_i}{\varphi }_i\left(a_{pj}^{K-1}-a_{qj}^{K-1}\right)f^{\prime }\left(z_{pj}^K\right)a_{pi}^{K-2} \\ =\left(\sum _{t=1}^{n_K}{\delta }_{pj\_L_{13}}^K{w}_{tj}^{K-1}+\sum _{e_i}\sum _{a_q\in e_i}{\varphi }_i\left(a_{pj}^{K-1}-a_{qj}^{K-1}\right)\right)f^{\prime }\left(z_{pj}^K\right)a_{pi}^{K-2} \\ ={\delta }_{pj\_L_{13}}^{K-1}{a}_{pi}^{K-2} \end{gathered}$$

Therefore, for each $w_{ji}^{k,m}$, we obtain the general gradient formula of $J_{13}$ is

$$\frac{\partial L_{13}}{\partial w_{ji}^k}={\delta }_{pj\_L_{13}}^{k+1}{a}_{pi}^k\left(k=1,2,\dots ,K\right)$$

The derivation method of $L_{14}$ is consistent with the above. So, we mainly give the partial derivatives of $L_{14}$ with respect to $w_{ji}^{2K,m}$. The rest of the partial derivatives can be calculated similarly.

$$\begin{gathered} \frac{\partial L_{14}}{\partial w_{ji}^{2K+1,m}}=\frac{\partial }{\partial a_{pj}^{2K+1,m}}(\frac{{\beta }_1}{2}\sum _{m=1}^M\sum _{p,q}^N{S}_{pq}^m{\Vert a_p^{2K+1,m}-a_q^{2K+1,m}\Vert }^2+\frac{{\beta }_2}{2}\sum _{t\ne m}^M\sum _{p,q}^M{S}_{pq}^{m,t}{\Vert a_p^{2K+1,m}-a_q^{2K+1,m}\Vert }^2)\frac{\partial a_{pj}^{2K+1,m}}{\partial z_{pj}^{2K+1,m}}\frac{\partial z_{pj}^{2K+1,m}}{\partial w_{ji}^{2K,m}} \\ =({\beta }_1\sum _{q=1}^N{S}_{pq}^m\left(a_{pj}^{2K+1,m}-a_{qj}^{2K+1,m}\right)+{\beta }_2\sum _{t\ne m}^M\sum _{q=1}^N\left(S_{pq}^{m,t}+S_{pq}^{t,m}\right)\left(a_{pj}^{2K+1,m}-a_{qj}^{2K+1,m}\right))f^{\prime }\left(z_{pj}^{2K+1,m}\right)a_{pi}^{2K,m} \\ ={\delta }_{pj\_L_{14}}^{2K+1,m}{a}_{pi}^{2K,m} \end{gathered}$$

Similar to $L_{13}$, we can obtain

$$\frac{\partial L_{14}}{\partial w_{ji}^{k,m}}={\delta }_{pj\_L_{14}}^{k+1,m}{a}_{pi}^{k,m}\left(k=K+1,\dots ,2K\right)$$

The residual terms of $L_{11},L_{12}$ for $w_{ji}^{k,m}$ are denoted as ${\delta }_{pj\_L_{11}}^{k+1,m},{\delta }_{pj\_L_{12}}^{k+1,m}$. The partial derivative formulas of $L_1$ for the encoder and decoder are

$$\frac{\partial L_1}{\partial w_{ji}^{k,m}}=\left({\delta }_{pj{\_L}_{11}}^{k+1,m}+{\delta }_{pj{\_L}_{12}}^{k+1,m}+{\delta }_{pj{\_L}_{13}}^{k+1,m}\right)a_{pi}^{k,m}k=1,\dots ,K$$

$$\frac{\partial L_1}{\partial w_{ji}^{k,m}}=\left({\delta }_{pj\_L_{11}}^{k+1,m}+{\delta }_{pj\_L_{12}}^{k+1,m}+{\delta }_{pj\_L_{14}}^{k+1,m}\right)a_{pi}^{k,m}k=K+1,\dots ,2K$$

For the fusion layer, according to the forward propagation formula, the partial derivative formula of $L_1$ with respect to $w_{ji}^{F,m}$ is

$$\frac{\partial L_1}{\partial w_{ji}^{F,m}}=\left(\sum _{n=1}^M\sum _{t=1}^{n_{L+2}}{\delta }_{pt}^{K+2,n}{w}_{tj}^{K+1,n}\right)f^{\prime }\left(z_{pj}^F\right)a_{pi}^{L+1,m}$$

Appendix B. The hypothesis testing of significant changes

For each pair of ROIs, the significant change of dFC is tested based on hypothesis test methods. Specifically, the $F$-test is first used to test whether there is a significant difference in variance between children and adults. Then, different $t$-tests were used to test whether there is a significant difference in mean value between the children and adults based on the results of the $F$-test.

If there was significant difference in variance between the two groups, the following $t$-test was used

$$t=\frac{{\bar{X}}_1-{\bar{X}}_2}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}$$

where ${\bar{X}}_1$ and ${\bar{X}}_2$ denote the sample mean value of adults and children, $S_1^2$ and $S_2^2$ denote the sample variance of adults and children, and $n_1$ and $n_2$ denote the sample size of adults and children respectively.

If there is no significant difference in variance between the two groups, the $t$-test of the following formula was used

$$t=\frac{{\bar{X}}_1-{\bar{X}}_2}{S_t\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$$

where $S_t^2=\frac{\left(n_1-1\right)S_1^2+\left(n_2-1\right)S_2^2}{n_1+n_2-2}$.

The significance level is set to 0.01. When the $p$-value < 0.01, we can determine that there exists a significant difference in dFC between the two groups. In other words, we can determine that the changes found in dFC are significant when the $p$-value < 0.01. Moreover, if $M={\bar{X}}_1-{\bar{X}}_2>0$, then there exists increased dFC. Similarly, the decreased dFC can be defined when $M<0$.

Data availability

The data can be downloaded from www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?studyid=phs000607.v1.p1.