Local conformational variations observed in B-DNA crystals do not improve base stacking: computational analysis of base stacking in a d(CATGGGCCCATG)₂ B↔A intermediate crystal structure

Abstract

The crystal structure of d(CATGGGCCCATG)₂ shows unique stacking patterns of a stable B↔A-DNA intermediate. We evaluated intrinsic base stacking energies in this crystal structure using an ab initio quantum mechanical method. We found that all crystal base pair steps have stacking energies close to their values in the standard and crystal B-DNA geometries. Thus, naturally occurring stacking geometries were essentially isoenergetic while individual base pair steps differed substantially in the balance of intra-strand and inter-strand stacking terms. Also, relative dispersion, electrostatic and polarization contributions to the stability of different base pair steps were very sensitive to base composition and sequence context. A large stacking flexibility is most apparent for the CpA step, while the GpG step is characterized by weak intra-strand stacking. Hydration effects were estimated using the Langevin dipoles solvation model. These calculations showed that an aqueous environment efficiently compensates for electrostatic stacking contributions. Finally, we have carried out explicit solvent molecular dynamics simulation of the d(CATGGGCCCATG)₂ duplex in water. Here the DNA conformation did not retain the initial crystal geometry, but moved from the B↔A intermediate towards the B-DNA structure. The base stacking energy improved in the course of this simulation. Our findings indicate that intrinsic base stacking interactions are not sufficient to stabilize the local conformational variations in crystals.

INTRODUCTION

Because the local structure of the DNA duplex is believed to significantly affect protein–DNA interactions, local conformational variability in DNA has attracted considerable attention. A recent crystallographic study reported an unusual structure for the dodecamer d(CATGGGCCCATG) solved at a resolution of 1.3 Å, which formed an intermediate in the A↔B-DNA duplex helix transition (1). This A/B-DNA intermediate of d(CATGGGCCCATG)₂ is important because many DNA-binding proteins force their cognate sequences to adopt an A/B-DNA intermediate or A-DNA-like structure (2,3). The key element of this unusual structure is the G-tract G₃C₃ sequence in the center of the structure. The d(CATGGGCCCATG)₂ dodecamer sequence resembles the decamer d(CATGGCCATG)₂, for which structural information from both X-ray crystallographic and NMR results are available (4,5). However, the d(CATGGCCATG)₂ decamer adopts a B-DNA conformation.

In order to understand the local conformational variability of B-DNA and the role of stacking, it is tempting to complement the experimental approaches by computational and database studies (6–16). Among the major limitations of the earlier computational attempts were the inaccuracy and physical incompleteness of the empirical potential functions (16–19) and difficulties in sampling the conformational space of the base pair steps. A change in a single conformational parameter is frequently accompanied by an adjustment of other parameters, particularly the vertical separation between the consecutive base pairs (15,16). When using crystal coordinates for calculations one should be concerned about data and refinement inaccuracies (16,20), which can cause a deterioration of the calculated stacking energies that is substantially larger than the actual stacking energy variations (16). It is thus encouraging to see recent improvements in the quality of crystal structures (21–23). Interestingly, in the highest resolution DNA crystal structures most of the sugar–phosphate backbones show multiple alternative conformations while this has not been observed for the base pairs (22,23). This suggests that the backbone has a relatively minor influence on stacking geometry.

Recent advances in quantum chemistry and molecular simulation techniques allow a substantial improvement in the quality of computational studies of nucleic acids (24–35). In the present paper we have utilized three modern computational techniques in a concerted manner to analyze base stacking in the dodecamer d(CATGGGCCCATG)₂. First, we have calculated the intrinsic base stacking energies using an accurate quantum chemical approach. Then we estimated the hydration contributions to the stacking free energies, assuming that the two stacked base pairs are immersed in water. The water environment has been modeled using a Langevin dipoles (LD) solvation model (36–38). The LD model is based on a simplified microscopic representation of the solvent that uses a linear response approximation (39). This model was chosen because all-atom representations of the solvent are currently not practical for evaluation of hydration free energies of large solutes (40,41). It should be noted that solvent effects exerted on stacked base pairs immersed in water are not necessarily identical to solvent effects exerted on stacked base pairs inside the DNA double helix. However, we do not have reliable method to calculate the hydration free energies in the DNA environment and thus our in-water LD calculations represent a reasonable compromise concerning evaluation of solvent effects on base stacking. Finally, we carried out an unrestrained molecular dynamics (MD) simulation of d(CATGGGCCCATG)₂ in water. This technique accounts for hydration effects inside DNA.

MATERIALS AND METHODS

Intrinsic base stacking energies

Method and basis set

The stacking energies were calculated using the second order Møller–Plesset (MP2) perturbational method. We have utilized a 6-31G basis set of atomic orbitals, augmented by a set of diffuse d-polarization functions with an exponent of 0.25. This basis set is designated 6-31G*(0.25) (18,19,25,42). The use of modified exponents of polarization functions is essential to include the dispersion attraction. The base stacking energies calculated by the MP2/6-31G*(0.25) method are expected to be highly accurate. This conclusion is based on extensive reference ab initio calculations carried out on smaller molecular clusters at very high levels of theory (25).

Definition of stacking energy

The stacking energy between two stacked DNA base pairs AB and CD, ΔE(AB,CD), is defined as the energy difference between the whole stacked complex and the two base pairs separated into infinity:

ΔE(AB,CD) = E(ABCD) – E(AB) – E(CD) 1

where ΔE and E stand for the interaction energy and total electronic energy, respectively. The interaction energy can be further divided into two intra-strand and two inter-strand base–base terms and the four-body term ΔE⁴

ΔE(AB,CD) = ΔE(A,C) + ΔE(A,D) + ΔE(B,C) + ΔE(B,D) + ΔE⁴ 2

Many-body (polarization) effects are neglected when pair-additive force fields are used however, they are important in nucleic acids (19,43).

The interaction energy ΔE consists of two components: the Hartree–Fock (HF) interaction energy and the correlation interaction energy. The HF component contains the electrostatic, induction and short-range repulsion contributions. The correlation part of the interaction energy includes all the dispersion attraction and brings corrections to the remaining terms, mainly to the electrostatic term (25).

Estimation of the electrostatic interaction energy

The ab initio approach does not allow unambiguous decompositions of the interaction energies into individual terms such as ‘net’ dispersion contribution, etc. (19). Nevertheless, we can estimate the electrostatic interaction energy term E^el using the Coulombic expression

E^el (kcal/mol) = ∑q_iq_i/r_ij 3

where q stands for atom-centered point charges and r represents the inter-atomic distances. The charges were derived by fitting to the molecular electrostatic potential (MEP) around the monomers at the MP2/6-31G*(0.25) level (19).

Ab initio calculations were performed using the Gaussian 94 program suite (44) and all interaction energies were corrected for the basis set superposition error. The reader can find more details about the methodology in a recent review (25). Evaluation of one base pair step requires ∼250–300 c.p.u. hours on an Origin2000 computer using a single R10000 processor (the MP2 procedure is not well parallelized) and 1 Gb RAM.

Geometries of stacked base pair steps

For standard base pair step geometries we assigned all parameters (including propeller twist) a value of 0, with the exception of rise (3.38 Å) and helical twist (36°). The C6–C8 axis centers were stacked directly above one another. These standard geometries (19) can be easily reproduced and used to test other computational techniques and it is one of the reasons why we prefer them over low resolution fiber diffraction data. For the base pair geometries we used gradiently optimized structures of base pairs obtained at the HF/6-31G** level (45).

The crystal geometries are based on the crystal structure of d(CATGGGCCCATG)₂ (1). We could not use the crystal coordinates directly since the unrelaxed intra-molecular nucleobase geometries could distort wave functions and affect the interaction energies (19). Thus, we have overlayed the crystal geometries of bases by nucleobase geometries taken from HF/6-31G** optimized base pairs (45). The sugar–phosphate units were replaced by hydrogen atoms.

Potential of mean force from quantum mechanical/Langevin dipole calculations

The mean force potential (Δg_PMF) associated with changes in the geometry of the stacked base pairs in aqueous solution was evaluated as the sum of the intrinsic stacking energies ΔE and the hydration free energies ΔG_hydr,

Δg_PMF (AB,CD) = ΔE(AB,CD) + ΔΔG_hydr(AB,CD) 4

ΔΔG_hydr(AB,CD) = ΔG_hydr(ABCD) – ΔG_hydr(AB) – ΔG_hydr(CD) 5

The calculated Δg_PMF and ΔG_hydr terms correspond to the standard conditions (1 M concentration of the solute, temperature 298 K and pressure 1 atm).

The hydration free energies were calculated using the Langevin dipole solvation model (36–38,46). Solute charge distribution and its polarization by the solvent were calculated by the polarized continuum model (PCM) (44). The atomic charges were determined by fitting to the electrostatic potential of the solute calculated at the PCM B3-LYP/6-31G*//HF/6-31G* level. Here B3-LYP stands for hybrid density function calculation utilizing the standard Becke’s three-parameter exchange and Lee–Yang–Parr correlation functions. This function provides atomic charges for nucleobases of a quality comparable with the MP2 method (47,48). The dependence of the calculated ΔΔG_hydr on position and rotation of the solute on a cubic grid was limited to 0.2 kcal/mol by averaging over 30 randomly selected grids. Total ΔG_hydr was calculated as the sum of the electrostatic, van der Waals and entropic contributions. Standard atomic van der Waals radii were used (38).

Classical molecular dynamics simulation

The simulation was carried out using the AMBER5 (49) program with a recent version of the Cornell et al. force field (26,27; PARM98). The solute was surrounded by a periodic box of TIP3P water molecules, extended to a distance of 10 Å from any solute atom. The starting structure was taken from the crystal structure of d(CATGGGCCCATG)₂. The molecules were neutralized by Na⁺ cations initially placed in the most negative locations using Coulombic potential terms with the LEAP module. The simulations were performed by the particle mesh Ewald method (50,51) and the simulation protocol has been described in detail elsewhere (33).

RESULTS

Intrinsic base stacking energies

Table 1 summarizes the intrinsic base stacking energies along the d(CATGGGCCCATG)₂ crystal structure and compares them with the data for standard base pair step geometries and high resolution B-DNA decamers. Table 2 presents a decomposition of the base-pair-step stacking energies into the individual terms for selected base pair steps. The first two columns give the intra-strand stacking contributions, columns three and four the two inter-strand contributions and column five the four-body (polarization, non-additivity) term. Finally, Table 3 presents the electrostatic interaction energy in selected base pair steps. The last column shows the base-pair-step stacking energy after subtracting the electrostatic and polarization terms from the total stacking energies. We call this term the ‘overlap’ stacking energy and it approximately corresponds to the van der Waals term in empirical potentials.

Table 1. Base pair step stacking energies ΔE(AB,CD) (kcal/mol) evaluated at the MP2/6-31G*(0.25) level along the d(CATGGGCCCATG)₂ crystal structure, standard base pair step geometries and some other high resolution crystal geometries.

Base pair step	Present crystal	Standard geometry	Another B-DNA crystal
C1G24/A2T23	–11.9 (+8.0)	–12.1 (+4.2)	–11.7 (+1.1)a,b
A2T23/T3A22	–12.6 (+8.0)	–10.7 (+11.6)
T3A22/G4C21	–11.6 (+9.9)	–12.1 (+4.2)
G4C21/G5C20	–7.8 (+13.4)	–9.5 (+12.2)	–8.9 (+12.9)c
G5C20/G6C19	–8.4 (+13.8)	–9.5 (+12.2)
G6C19/C7G18	–14.0 (+5.2)	–13.2 (+8.5)	–11.5 (+8.5)d
C7G18/C8G17	–8.4 (+11.6)	–9.5 (+12.2)
C8G17/C9G16	–7.6 (+12.2)	–9.5 (+12.2)
C9G16/A10T15	–11.5 (+10.1)	–12.1 (+4.2)
A10T15/T11A14	–12.7 (+9.5)	–10.7 (+11.6)
T11A14/G12C13	–9.0 (+7.8)	–12.1 (+4.2)
Total 11 steps	–115.5	–121.0
Total GG steps	–32.2	–38.0

The values in parentheses show the HF component of the interaction energies.

^aC2A3 step of the d(CCAAGATTGG)₂ decamer 1.5 Å crystal structure (52).

^bHigh twist, high slide, low roll geometry.

^cG4G5 step of the d(CCAGGCCTGG)₂ decamer 1.6 Å resolution crystal structure (53).

^dG5C6 step of the d(CCAGGCCTGG)₂ (53).

Table 2. Decomposition of selected base pair step stacking energies into the individual terms.

AB/CD	ΔE(A,C)	ΔE(B,D)	ΔE(A,D)	ΔE(B,C)	ΔE4	ΔE(AB,CD)
A2T23/T3A22	–6.4	–6.5	+0.1	–0.4	+0.6	–12.6
T3A22/G4C21	–2.7	–4.4	–0.5	–5.0	+1.1	–11.6
G4C21/G5C20	–2.6	–1.7	–3.4	–2.5	+2.5	–7.8
G5C20/G6C19	–2.1	–1.7	–3.2	–3.8	+2.4	–8.4
G6C19/C7G18	–9.6	–9.8	+2.1	+2.8	+0.6	–14.0
T11A14/G12C13	–2.3	–4.3	–0.5	–3.1	+1.2	–9.0
TA/GCa	–5.4	–2.1	–1.7	–2.6	+0.1	–11.7
GC/GCb	–3.5	–1.1	–4.1	–2.8	+2.0	–9.5
GC/CGb	–9.0	–9.0	+1.4	+2.5	+0.9	–13.2
TA/GCb	–4.7	–3.8	–0.9	–3.5	+0.8	–12.1
AT/TAb	–5.1	–5.1	–0.8	+0.4	+0.0	–10.7

^aHigh twist, high slide, low roll geometry (52).

^bStandard geometry.

Table 3. Decomposition of the electrostatic Coulombic stacking energy (kcal/mol) terms into the individual base–base contributions (note that the many-body contribution to the Coulombic term is 0).

AB/CD	Eel(A,C)	Eel(B,D)	Eel(A,D)	Eel(B,C)	Eel			Overlap stacking
					Intra-strand	Inter-strand	Total
A2T23/T3A22	–0.7	–0.8	+0.5	+1.5	–1.5	+2.0	+0.5	–13.7
T3A22/G4C21	+0.7	+0.1	–0.4	+0.9	+0.8	+0.5	+1.3	–14.0
G5C20/G6C19	+4.6	+2.0	–2.8	–0.3	+6.6	–3.1	+3.5	–14.3
G6C19/C7G18	–4.0	–3.1	+4.7	+3.6	–7.1	+8.3	+1.2	–15.8
TA/GCa	–1.7	+2.0	+0.3	–1.5	+0.3	–1.2	+0.9	–12.7
GC/GCb	+4.3	+3.5	–3.1	–1.3	+7.8	–4.4	+3.4	–14.9
GC/CGb	–2.9	–2.9	+4.1	+3.2	–5.8	+7.3	+1.4	–15.5
TA/GCb	+1.0	0.0	–0.4	–0.4	+1.0	–0.8	+0.2	–13.0
AT/TAb	+0.6	+0.6	+1.0	+0.8	+1.2	+1.8	+3.0	–13.7

The last column gives overlap stacking energy (see text for definition).

^aHigh twist, high slide, low roll geometry.

^bStandard geometry.

The base stacking energy in individual steps of the d(CATGGGCCCATG)₂ crystal structure vary within the range –7.8 to –14.0 kcal/mol. G–G steps show the weakest stacking, being energetically well separated from the other steps. Both guanine and cytosine have very polar electronic distributions and thus their almost parallel arrangement in intra-strand stacks leads to very unfavorable electrostatics. This is partly compensated for by inter-strand electrostatic stacking. G–G stacking is further destabilized by the many-body term. The most stable G6–C7 step shows an opposite distribution of the intra-strand and inter-strand contributions.

The energy differences between the standard and crystal geometries are subtle. The local conformational variations degrade the total stacking energy along the helix axis of the d(CATGGGCCCATG)₂ crystal by ∼5 kcal/mol. As an illustration, approximately the same interaction energy is associated with formation of a water dimer in the gas phase. More than half of the stacking energy loss can be attributed to the very last step in the crystal, i.e. T11–G12. We explain this by subtle deformation of that step due to packing of the terminal base pair against the side of the minor groove of a symmetry-related duplex (1).

A notable base pair step is CpA(TpG). We have calculated its base stacking energy assuming three very different geometries, the standard one, that observed in the present dodecamer (we consider the CpA steps in the dodecamer as a single geometry sub-state) and the high twist, high slide, low roll geometry in high resolution d(CCAXXXXTGG)₂ decamers (52–55; Fig. 1). These three structures are isoenergetic, with a different balance of intra- and inter-strand stacking.

Figure 1.

Three CpA step geometries studied in the present paper. Standard geometry (top); present crystal (middle); high slide, high twist, low role geometry (bottom). Note the van der Waals contact between the guanine amino group and the adenine six membered ring stabilizing the ‘high slide’ geometry (55).

The last column in Table 3 shows that the ‘overlap’ stacking energy (see above) varies by as little as 3 kcal/mol and is weakest for CpA steps. Its variability is on a scale of 1 kcal/mol when comparing the same steps in different geometries.

Hydrated base stacking energies

To deepen our understanding of the interplay between nucleobase stacking and conformational polymorphism of DNA in aqueous solution, it is essential to go beyond the intrinsic (in vacuo) stacking energies. Such an extension can be made in several ways. Among them, models that retain the approximation of the relative free energy of the DNA+water system as the sum of free energies of the individual base pair steps are particularly attractive. This is because the nearest neighbor model of DNA stability turned out to be remarkably successful for prediction of melting temperatures and binding free energies of short DNA oligomers (56,57). Here, augmenting the intrinsic stacking energies by the relative hydration free energies, which include the effects of both the water–DNA and water–water interactions, is intuitively the best choice for a more general yet simple descriptor of DNA stability.

Naturally, our model, in which the free energy profile for stacking of two base pairs in the DNA+water environment is replaced by the corresponding free energies for stacking in water (equations 1, 4 and 5), is only an approximate description of the DNA conformational energetics. Yet, the inaccuracies due to this choice of model system are expected to be smaller than those due to the approximations used in the evaluation of free energies. The stacking additivity, which is inherent in our model, is supported by the remarkable success of the nearest-neighbor model of DNA stability (56,57). In addition to the facile interpretation in terms of pairwise additivity, our model has the important advantage of being computationally feasible.

The standard hydration free energies (ΔΔG_hydr) of nucleic acid bases calculated with the LD solvation model (46) are –10.3, –12.3, –19.7 and –20.9 kcal/mol for adenine, thymine, cytosine and guanine, respectively. These energies agree well with the observed partition coefficients of N1- and N9-substituted nucleobases between water and cyclohexane (58). In addition, they are consistent with the results calculated using explicit representations of water (59) that typically require 10³–10⁴ longer c.p.u. times and are significantly less stable than the LD results. The LD model enables us to calculate the solvation free energy differences between different stacking geometries of each DNA step with ∼30% accuracy. After including the gas phase and solvation entropy contributions, the ab initio/LD method predicted equilibrium constants for stacking of nucleic acid bases in water in good agreement with available experimental data (60).

The predicted hydration free energy differences and the mean force potentials for hydrated base stacking are presented in Table 4. The predicted magnitudes of Δg_PMF (in absolute values) are rather large because they refer to infinitely separated base pairs without including the translational, rotational and vibrational entropies of the solute. These entropic contributions are assumed to be identical for the standard and X-ray geometries. Thus, the ΔΔg_PMF values correctly characterize the relative stability (free energy) of the standard and X-ray structures due to hydrated stacking. Note that the Δg_PMF results are not directly comparable with the empirical stabilities of DNA steps derived from DNA melting temperatures using the nearest neighbor approach (56,57). This is because the latter quantities implicitly include the contributions of both the hydrogen bonding and stacking interactions and are averaged over different sequence contexts and local geometries in solution.

Table 4. Hydration contibutions^a and the total free energy changes (potentials of mean force) for the formation of base pair steps in the crystal (X-ray) and standard^b geometries.

Base pairs involved	Step	ΔΔGhydr	ΔgPMF			ΔΔgPMFc
		X-ray	Standard	X-ray	Standard	(kcal/mol)
C1G24/A2T23	CA	4.3	7.4	–7.6	–4.9	–2.7
A2T23/T3A22	AT	2.1	–0.4	–10.5	–11.0	0.5
T3A22/G4C21	CA	3.9	7.4	–7.7	–4.9	–2.8
G4C21/G5C20	GG	–2.2	–0.4	–10.0	–9.9	–0.1
G5C20/G6C19	GG	–1.7	–0.4	–10.1	–9.9	–0.2
G6C19/C7G18	GC	6.1	4.6	–7.9	–8.6	0.7
C7G18/C8G17	GG	–0.7	–0.4	–9.1	–9.9	0.8
C8G17/C9G16	GG	–1.9	–0.4	–9.5	–9.9	0.4
C9G16/A10T15	CA	4.1	7.4	–7.4	–4.9	–2.5
A10T15/T11A14	AT	1.9	–0.4	–10.8	–11.0	0.2
T11A13/G12C13	CA	4.2	7.4	–4.8	–4.9	0.1
GG steps		–6.5	–1.6	–38.7	–39.6	0.9
Total 11 steps		20.1	31.8	–95.4	–89.8	–5.6

^aHydration free energies, ΔΔG_hydr (kcal/mol), correspond to the free energy for the transfer of 1 M solute from the gas phase to 1 M aqueous solution extrapolated to infinite dilution, under standard conditions. Δg_PMF (kcal/mol) values were obtained by combining the gas phase interaction energies ΔE (Table 1) with the ΔΔG_hydr terms according to equations 4 and 5.

^bIdeal B-DNA geometry (see Materials and Methods, Intrinsic base stacking energies).

^cΔΔg_PMF = Δg_PMF(X-ray) – Δg_PMF(standard).

Aqueous solvation greatly affects the relative stability of the stacked structures by compensating for the unfavorable electrostatic interactions between nucleobases (39,60,61). Thus, stacking in the GpC step, which is the most stable in the gas phase due to very favorable intra-strand electrostatics, would be among the least stable in water. On the other hand, the GpG step would become rather stable. It should be noted, however, that even if solvent screening effects make the GpG and GpC steps, for example, similar in total association energy in water, their stacking properties remain distinct. The steps show a different balance of various contributions (dispersion, electrostatic, solvation and inter-strand versus intra-strand). Overall, inclusion of solvation effects stabilizes the local conformational variations occurring in the crystal structure, though the greater stability of the crystal geometry obtained from the hydrated stacking free energies is mainly due to the CpA(TpG) steps.

Molecular dynamics simulation

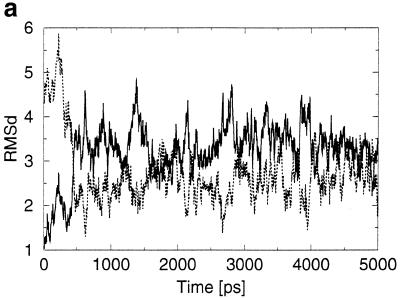
The simulation initially assumed the crystal geometry of d(CATGGGCCCATG)₂ and was extended to 5 ns. The B↔A intermediate structure was not stable and the dodecamer swiftly adopted a B-like geometry (Fig. 2). All sugars re-puckered to C2′-endo, in contrast to the crystal data, showing C3′-endo puckering. The re-puckering started at ∼0.1 ns with all cytosines within the G-tract. Then it propagated within the strand above the cytosines of the G-tract (i.e. in the 3′ direction) within the period 0.2–0.25 ns. The remaining bases re-puckered in the period 0.35–0.4 ns. Base stacking in the MD structure still showed some A-like features, although less expressed than in the crystal, as observed in simulations of poly(G) tracts (30). This indicates that the G-tract has some propensity to be shifted to the A-form (30).

Figure 2.

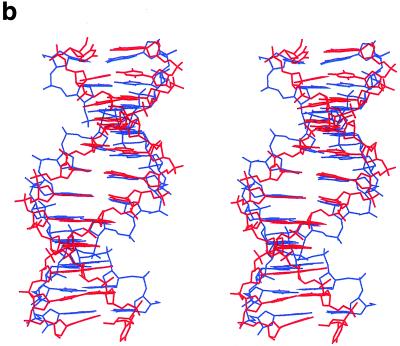
(a) RMSD (in Å) development of the MD structure with respect to the X-ray geometry (thick line) and standard B-DNA geometry (thin line). (b) Stereo overlay of the averaged simulated (red) and crystal (blue) structures.

The root mean square deviation (RMSD) (without considering the deformed terminal base pairs) of the averaged MD structure is 2.6 Å with respect to the initial X-ray structure and 2.3 Å with respect to the Arnott B-DNA fiber diffraction model. The RMSD between the two strands (ignoring again both terminal base pairs) is 0.8 Å in the MD structure, showing that on this time scale the structural motions are not completely converged. In the ideal case the RMSD would be 0 Å while the crystal structure shows an RMSD between strands of 0.5 Å.

Table 5 compares selected geometrical parameters of the averaged MD structure with the crystal. Three observations are immediately apparent. First, the terminal steps of the MD structure are largely deformed. Second, the MD structure does not reproduce the fine local variations seen in the crystal. The helical twist distribution in the G-tract region is opposite in the two structures. Third, the two sequence symmetry-related halves of the MD structure, which ideally should be identical, have quite different conformational parameters. The propeller twist adopts a smaller absolute value compared to the crystal structure over steps 1–8, but substantially increases for the remaining three steps. Also, helical twist asymmetry along the MD structure is considerable. The simulation was obviously not long enough to sufficiently sample the conformational space of the very flexible B-form duplex. As also shown by Feig and Pettitt (34), we conclude that quantitative studies of B-DNA local conformational variations will require simulations considerably longer than are currently affordable. Nevertheless, for the purposes of our study the simulation is sufficient, clearly showing that the local variations observed in the crystal are not retained in a solution simulation.

Table 5. Selected geometrical parameters (°, Å) of the averaged simulated structure, evaluated by Freehelix code.

Pair/step	Propeller	Buckle	Helical twist	Roll	Cup	Slide
1	–0.5 (–5.6)	–28.9 (2.6)	–	–	–	–
2/1-2	–2.3 (–6.6)	14.7 (–0.1)	33.6 (33.3)	–12.6 ( 6.4)	43.5 (–2.7)	–0.0 (–1.5)
3/2-3	–2.0 (–8.7)	–2.2 (1.3)	26.3 (34.0)	0.6 (–1.3)	–16.9 ( 1.5)	–0.6 (–2.0)
4/3-4	–2.9 (–8.4)	–8.12 (–0.5)	34.6 (27.7)	5.1 ( 4.4)	–6.0 (–1.8)	–0.1 (–1.9)
5/4-5	–7.6 (–11.3)	–3.8 (6.8)	31.1 (33.2)	4.3 ( 2.5)	4.3 ( 7.3)	–0.8 (–1.4)
6/5-6	–9.0 (–7.4)	6.6 (7.6)	32.0 (33.2)	4.7 ( 4.8)	10.4 ( 0.9)	–1.2 (–1.6)
7/6-7	–3.6 (–7.2)	7.5 (–6.9)	37.5 (28.7)	–0.3 ( 4.7)	0.9 (–14.5)	–0.4 (–0.6)
8/7-8	–3.4 (–12.5)	3.4 (–9.3)	25.8 (33.5)	3.3 ( 3.1)	–4.1 (–2.4)	–0.5 (–1.2)
9/8-9	–4.8 (–8.9)	1.5 (–4.2)	36.3 (32.4)	1.4 ( 2.0)	–1.9 ( 5.0)	0.1 (–1.5)
10/9-10	–12.5 (–7.9)	6.3 (0.9)	33.9 (31.3)	8.0 ( 5.8)	4.9 ( 5.1)	–0.0 (–1.7)
11/10-11	–16.6 (–2.0)	3.4 (–2.0)	32.8 (32.7)	–4.2 (–3.4)	–3.0 (–2.9)	–0.6 (–2.0)
12/11-12	–26.0 (7.1 )	34.6 (–23.6)	35.5 (23.0)	14.3 (10.4)	31.25 (–21.6)	0.9 (–1.6)

The values in parentheses show the respective crystal values.

Table 6 summarizes the base stacking energies calculated by the AMBER force field along the X-ray and averaged MD structures. The force field provides correct description of base stacking in the crystal geometries compared with the ab initio data (compare with Table 1). The force field slightly overestimates the stacking stabilization. This difference, however, falls within the accuracy limits of the ab initio procedure and could be eliminated by a simple scaling of the Lennard–Jones term. The energy gap between G–G stacking and the other steps is somewhat underestimated (by ∼2 kcal/mol), due to neglect of explicit polarization effects. During the simulation the base stacking energy is improved over the starting geometry. This concerns both van der Waals and electrostatic terms.

Table 6. Base stacking energies (kcal/mol) evaluated by the Cornell et al. force field (26,27) for the initial crystal structure and the averaged MD structure.

	Total stacking, MD structure	Total stacking, X-ray structure	van der Waals, MD	van der Waals, X-ray	Coulombic, MD	Coulombic, X-ray
C1G24/A2T23	–13.73	–13.94	–12.33	–15.34	–0.89	1.40
A2T23/T3A22	–15.64	–15.14	–17.82	–16.29	2.19	1.16
T3A22/G4C21	–16.94	–12.74	–16.13	–14.91	–0.81	2.17
G4C21/G5C20	–11.88	–11.62	–17.15	–16.45	5.27	4.83
G5C20/G6C19	–11.61	–10.85	–16.96	–16.46	5.35	5.62
G6C19/C7G18	–15.32	–15.04	–17.06	–16.73	1.74	1.68
C7G18/C8G17	–10.68	–11.75	–17.27	–16.74	6.59	4.98
C8G17/C9G16	–13.31	–11.50	–16.68	–16.42	3.37	4.92
C9G16/A10T15	–16.52	–13.75	–16.32	–15.46	–0.20	1.71
A10T15/T11A14	–14.80	–14.88	–17.64	–16.32	2.89	1.45
T11A14/G12C13	–17.69	–10.60	–15.52	–13.06	–2.16	2.45
Total	–158.12	–141.8	–180.88	–174.18	23.34	32.43
Total, steps 2–10	–126.7	–117.27	–153.03	–145.78	26.39	28.55
GGGCCC segment	–62.8	–60.76	–85.12	–82.80	22.32	22.03

DISCUSSION AND CONCLUSIONS

In this work we have correlated observed local variations in the geometry of the DNA duplex d(CATGGGCCCATG)₂ with the strength of base stacking interactions. Ab initio calculations showed no improvement in the total intrinsic stacking energy for the crystal structure compared to the ideal (standard) B-DNA geometry. The same conclusion also holds for high resolution B-DNA decamers. The calculations did not reveal any significant variability in base stacking energy associated with the crystal geometry and, especially, variability in the overlap-dependent stacking energy term was very small. This finding questions the merit of a visual inspection of stacking overlap as a measure of stacking stability. Further, such visual evaluations ignore the electrostatic terms dominating the variability of intrinsic stacking energies.

The picture derived from the ab initio calculations is consistent with the outcome of MD simulation. During the MD trajectory in a water environment all local variations seen in the crystal were lost. Nevertheless, the force field description of base stacking interactions is reasonably accurate and stacking improves during the simulation. Thus, the simulation would indicate the presence of conformational sub-states with marked improvements in stacking, if such sub-states exist. On the other hand, in the absence of crystal packing we do not necessarily expect to see the same local variations. Simulations by Darden and co-workers suggest that when crystal symmetry is imposed the simulation can retain local variations (although their simulations may still be too short) (35). There has been debate about the importance of crystal packing forces in affecting local conformational variations (35,62). In this case and that of many A-DNA crystal structures (63–65), crystal packing forces apparently do play a significant role in determining local structure. Interestingly, one of the terminal CpA steps in the present crystal is deformed by crystal packing. The corresponding stacking energy loss (2.5 kcal/mol) is larger than the range of variability in stacking energy in all other CpA(TpG) step geometries studied.

The results show that local variations and the A↔B intermediate crystal geometry of d(CATGGGCCCATG)₂ are not caused by optimization of intrinsic base stacking. Each base pair step may adopt a wide range of geometries with basically isoenergetic stacking interactions while these low energy regions are considerably different for different steps. Our results support the view that crystal structures provide different snapshots of the low energy range of conformations of duplexes.

The d(CATGGGCCCATG)₂ duplex contains abundant GpG(CpC) and CpA(TpG) steps. The GpG step is characterized by significant intra-strand electrostatic repulsion between consecutive and almost parallel polar nucleobases in either strand accompanied by polarization repulsion, while the minor groove amino groups preclude substantial propeller twisting. The crystal geometries of the GpG steps in the dodecamer do not show intrinsic stacking energy improvements compared to the standard one. Nevertheless, it is likely that the salient stacking properties of GpG steps contribute to the anomalous behavior of the G-tracts. The stacking properties of G-tracts contrast with so-called A-tract structures, which are known to be stiff and favor the B-form (66–68). G-tracts serve only rarely as protein-binding sequences (69), while A-tracts and G-tracts have very different elastic properties (66). G-tracts are characterized by fast base pair opening rates (67), which may be facilitated by the repulsive intra-strand molecular dipole–molecular dipole terms, because this repulsion would be reduced by counter-rotation of consecutive bases within a strand during opening.

The calculations illustrate why the sequence CpA(TpG) is the most flexible base pair step, adopting an exceptionally wide range of isoenergetic geometries with a large variability in the mutually compensating individual base–base contributions. The ‘high twist, high slide, low roll’ geometry of the CpA step known from B-DNA decamers is not associated with a stacking energy loss, contrary to suggestions based on simple geometrical evaluations (10). Pyrimidine–purine steps may also be a facilitator of the A- to B-DNA transition. Not only do they appear to play that role in this case, they are also apparently responsible for the A-DNA-like conformation of the common promoter sequence TATA when bound to transcription complex proteins (70,71). The unique intrinsic flexibility of the CpA step also makes it very sensitive to environmental effects. In fact, our ab initio/LD calculations show that hydration favors the CpA crystal geometries over the standard ones.

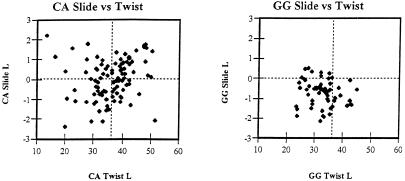
Sequence-dependent flexibility and local conformational variability of DNA duplexes undoubtedly contribute to biological functions of nucleic acids. Interestingly, characterization of the stacking properties of the GpG and CpA steps based on evaluation of DNA crystals and computations agrees well with their behavior in crystals of protein–DNA complexes. Compared with DNA crystal structures, X-ray studies of protein–DNA complexes reveal the biologically relevant deformability of DNA and are less influenced by crystal packing forces. As demonstrated by Dickerson for 63 protein–DNA complexes (69), the CpA step has a broad distribution of slide, twist and roll values (see also Fig. 3). This suggests that the potential well of base–base interactions is shallow, in line with the present calculations and the flexibility of CpA steps seen in uncomplexed DNA duplexes. In contrast, the distribution of slide, twist and roll values in GpG steps in protein–DNA complexes is more tightly clustered and shifted to an A-like helical structure (69), as seen in the DNA crystal of d(CATGGGCCCATG)₂ analyzed here.

Figure 3.

The broad distribution of slide and twist values in the CpA steps contrasts with a tight and A-like distribution of these parameters in GpG steps. The same set of protein–DNA complexes as used by Dickerson (69) is utilized; present calculations are made relative to a locally defined axis (for definition see 72).