ZeroCAL: Eliminating Carbon Dioxide Emissions from Limestone’s Decomposition to Decarbonize Cement Production

Abstract

Limestone (calcite, CaCO₃) is an abundant and cost-effective source of calcium oxide (CaO) for cement and lime production. However, the thermochemical decomposition of limestone (∼800 °C, 1 bar) to produce lime (CaO) results in substantial carbon dioxide (CO_2(g)) emissions and energy use, i.e., ∼1 tonne [t] of CO₂ and ∼1.4 MWh per t of CaO produced. Here, we describe a new pathway to use CaCO₃ as a Ca source to make hydrated lime (portlandite, Ca(OH)₂) at ambient conditions (p, T)—while nearly eliminating process CO_2(g) emissions (as low as 1.5 mol. % of the CO₂ in the precursor CaCO₃, equivalent to 9 kg of CO_2(g) per t of Ca(OH)₂)—within an aqueous flow-electrolysis/pH-swing process that coproduces hydrogen (H_2(g)) and oxygen (O_2(g)). Because Ca(OH)₂ is a zero-carbon precursor for cement and lime production, this approach represents a significant advancement in the production of zero-carbon cement. The Zero CArbon Lime (ZeroCAL) process includes dissolution, separation/recovery, and electrolysis stages according to the following steps: (Step 1) chelator (e.g., ethylenediaminetetraacetic acid, EDTA)-promoted dissolution of CaCO₃ and complexation of Ca²⁺ under basic (>pH 9) conditions, (Step 2a) Ca enrichment and separation using nanofiltration (NF), which allows separation of the Ca-EDTA complex from the accompanying bicarbonate (HCO₃^–) species, (Step 2b) acidity-promoted decomplexation of Ca from EDTA, which allows near-complete chelator recovery and the formation of a Ca-enriched stream, and (Step 3) rapid precipitation of Ca(OH)₂ from the Ca-enriched stream using electrolytically produced alkalinity. These reactions can be conducted in a seawater matrix yielding coproducts including hydrochloric acid (HCl) and sodium bicarbonate (NaHCO₃), resulting from electrolysis and limestone dissolution, respectively. Careful analysis of the reaction stoichiometries and energy balances indicates that approximately 1.35 t of CaCO₃, 1.09 t of water, 0.79 t of sodium chloride (NaCl), and ∼2 MWh of electrical energy are required to produce 1 t of Ca(OH)₂, with significant opportunity for process intensification. This approach has major implications for decarbonizing cement production within a paradigm that emphasizes the use of existing cement plants and electrification of industrial operations, while also creating approaches for alkalinity production that enable cost-effective and scalable CO₂ mineralization via Ca(OH)₂ carbonation.

Short abstract

Zero CArbon Lime (ZeroCAL) is an electrolysis-driven pH-swing process that unlocks a pathway to decarbonize cement clinker production.

1. Introduction and Background

Concrete is the second most used material globally after water.¹ However, the production of cement (Portland Cement, PC), the binding agent in concrete, results in ∼1 tonne [t] of CO₂ emitted per t of PC produced. The direct CO₂emissions derive ∼60% from the thermochemical decomposition of CaCO₃ to produce CaO (“process emissions”, eq 1) and ∼40% from the combustion of fossil fuels to heat the kiln to ∼1500 °C (“combustion emissions”) to ensure the clinkering reactions^2,3 typically requiring >1 MWh of thermal energy per t of CaO produced.⁴⁻⁷ Additionally, typical cement plant operations require ∼10% of electrical energy input⁸⁻¹¹ that contribute ∼10% of indirect CO₂ emissions.¹² As a consequence, the annual global production of ∼4.5 billion t of PC—from an installed capital asset base of >$400 billion including cement plants, adjacent limestone quarries, transport infrastructure, etc.—results in 8–10% of anthropogenic CO₂ emissions.^13,14 Unfortunately, decarbonizing the heat source alone, e.g., through renewable heat, is insufficient to decarbonize PC production and currently supply constrained by the availability of renewable energy.¹⁵ Rather, decarbonizing the existing thermochemical paradigm of PC production requires the replacement, displacement, or the transformation of limestone as the CaO source.

1

Because PC accounts for ∼90% of the global warming potential (GWP) of concrete, substantial efforts have been directed toward replacing PC with supplementary cementitious materials such as fly ash, slag, calcined clays, etc. in the binder fraction of concrete.¹² However, this practice of “dilution”, which does reduce the PC content of the concrete binder, does not alter the embodied carbon intensity—direct CO₂ emissions—of PC/clinker production at the site and scale of a cement plant. Thus, it is not a means for decarbonizing PC production. While carbon capture and (geological) storage (CCS) is being extensively suggested as a pathway for PC decarbonization, the costs of (i) deploying carbon capture systems at typical “million tonne per annum” (MTPA) scale cement plants, CapEx ∼ $1 billion, (ii) pipeline transport of compressed CO₂, and (iii) injection and monitoring of injected CO₂ in sequestration sites implies that CCS will cost well over $120/t_CO2 and, thus nearly double the price of PC.¹⁵ Finally, after a century of industrial operations, state-of-the-art PC plants fitted with the Best Available Technologies (BATs), such as heat recovery systems and kiln insulation, are operating close to the limits of practical efficiencies.⁸⁻¹¹ Thus, only marginal improvements in these systems can be realized. This indicates that actual decarbonization of PC production requires the displacement of thermochemical routes that decompose limestone into CaO as implied by the today’s manufacturing paradigm.

Given the well-established complexities of decarbonizing PC production, two approaches have gained prominence. First, electrochemical “electron-to-molecule” approaches focus on producing an alternate cement chemistry that offers performance but not compositional equivalence to PC.^16,17 Second, alternative feedstock and manufacturing processes that produce a traditional PC.^18,19 What ties both of these, and related approaches, is that they make use of non-carbonate Ca-containing feedstocks (e.g., steel slags, fly ashes, basalts, etc.) to avoid CO₂ emissions.^16,18,19 While promising, these approaches face major challenges. For example, feedstocks such as slags and fly ashes are supply constrained in comparison to the scale of PC production,^20,21 while basalts, although not supply constrained, are far more difficult to extract alkaline metals from as compared with carbonate rocks such as limestone.²² On the other hand, many newer approaches imply a higher risk of stranding existing cement plants because of a need for different raw materials and/or different process trains,²³ thus requiring the buildout of new green-field facilities,¹⁵ a financially challenging proposition when seen from the perspective of the existing industry. This raises the question if/how the unit economics of decarbonized cement could achieve net present value (NPV) parity as compared to PC manufactured today?

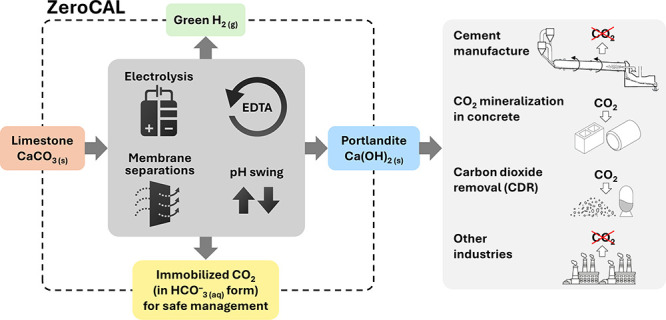
To address these challenges, this paper suggests a transformative near process-CO₂-emissions-free pathway that makes use of limestone within an aqueous electrochemical paradigm to produce portlandite (Ca(OH)₂)—a “drop in” zero-carbon feedstock for PC production. Here, the portlandite is introduced at an intermediate stage between limestone quarrying and the clinkering steps. Not only does this approach obviate the need for CCS for cement/lime decarbonization but, importantly, via the production of green hydrogen (and oxygen) it also provides (partial) clean energy for high-grade cement kiln heating or cogeneration. Taken together, the proposed ZeroCAL (Zero Carbon Lime) approach allows us to define cost-effective, accessible, and scalable electrified solutions for cement decarbonization at the site and scale of existing cement plants without resorting to CCS as the only pathway for cement (clinker) decarbonization.

2. New Concept: The ZeroCAL Process

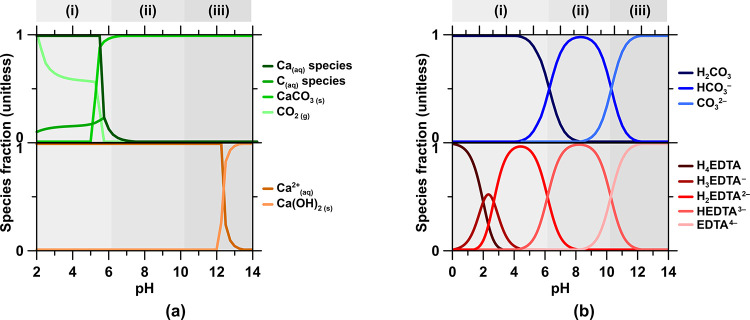
Calcium carbonate polymorphs such as calcite, aragonite, and vaterite, as well as rocks composed thereof, e.g., limestone, present an abundant source of CaO. However, under thermal activation, limestone decomposes to release its mineralized CO₂. While under circumneutral-to-alkaline aqueous conditions (pH > 6; Figure 1a), limestone can be dissolved with virtually zero CO_2(g) emission, its dissolution rate in this regime is very slow: ∼5 × 10^–6 mol/m²/s.²⁴ Furthermore, the low solubility of limestone under these conditions, 25.5 mmol/L at pH 6 to 0.1 mmol/L at pH 10,²⁴ implies an enormous water demand for Ca mobilization by ordinary dissolution. While the dissolution rates and the Ca capacity of the solution greatly increase with decreasing pH, the speciation change of dissolved inorganic carbon (DIC)—as disclosed by the Bjerrum diagram (Figure 1b)—from dominantly bicarbonate (HCO₃^–) and/or carbonate (CO₃^2–) anions at pH > 6^25,26 to carbonic acid (H₂CO₃) and CO_2(g) implies the undesirable and substantial emission of CO₂ with decreasing pH.^27,28

Figure 1.

Speciation, in aqueous solution at 25 °C and 1 bar, of (a) CaCO₃ and Ca(OH)₂ and (b) Dissolved Inorganic Carbon (DIC) and EDTA. For reference, the limiting solubilities of CaCO₃, CO₂, and EDTA in water at pH 7 are ∼4.0, ∼0.1, and ∼420 mmol/L, respectively.

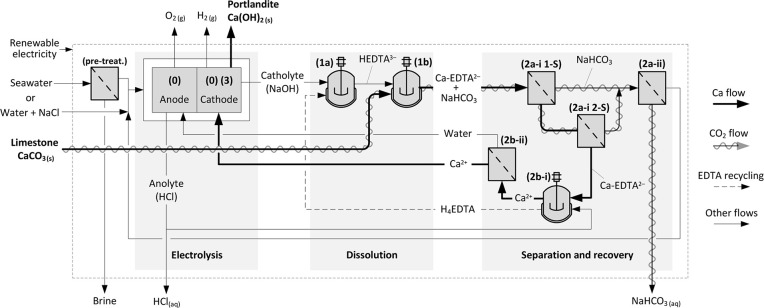
Thus, a potential approach for effective aqueous Ca mobilization from CaCO₃ and the subsequent use of this Ca for PC production implies enhancing the apparent solubility of limestone at alkaline pH. This can be achieved by making one or more dissolved solute species (e.g., of CaCO₃: Ca²⁺, CO₃^2–, and/or HCO₃^–) inconsequential in terms of affecting the undersaturation, thereby enhancing the dissolution rate and solubility, without inducing the reprecipitation of CaCO₃. The ZeroCAL approach relies on the use of chelating agents such as ethylenediaminetetraacetic acid (EDTA)²⁹⁻³¹ that enhance the dissolution rate of CaCO₃ and the Ca bearing capacity of solutions via an apparent solubility increase mechanism.³²⁻³⁴ Based on this reasoning, the process encompasses the following steps (Steps 0–3, Figure 2).

Figure 2.

Representative process flow diagram (PFD) of the ZeroCAL process showing the different unit operations and materials flows.

(Step 0) This involves the electrochemical production of acid (HCl), base (NaOH), oxygen (O_2(g)), and hydrogen (H_2(g)), by the electrolysis of a salt-in-water (NaCl; ∼ 0.5 mol/L; e.g., seawater) electrolyte using proprietary oxygen-selective anodes (OSAs) with >98 mol. % selectivity for oxygen evolution.^35,36 The electrolysis step ensures that there is no extrinsic need for stoichiometric additives to induce a pH-swing. It should be noted that, while here NaCl is implicated as a low-cost, abundant, high-conductivity electrolyte, e.g., by using softened seawater³⁷ as a reaction medium and electrolyte, it is only a viable option if Cl_2(g) evolution during electrolysis can be suppressed. On the other hand, if the electrolyte were maintained in a closed-loop by recirculating flow, it would be possible to use stable non-oxidizing salt-in-water electrolytes such as NaClO₄ and typical platinum-based anodes or other suitable catalysts, without the need for OSAs. The general electrolytic reaction may be written as follows (refer to Section A1.1 in the Appendix for details):

Step 0

Note that, during the subsequent Steps 1–3, 5 mol of NaOH and 4 mol of HCl are required per mol of Ca(OH)₂ produced, meaning that a multiplier of 5/4 needs to be applied to Step 0 to describe the overall reaction. Here, all of the acid and base needed is produced electrolytically, and in situ, ensuring that no external additives are needed for the ZeroCAL process.

(Step 1) For valence compensation, EDTA dissolution requires 1 mol of NaOH per H⁺ released from the initially dissolved H₄EDTA species, i.e., 3 mol of NaOH to form HEDTA^3– at pH 9 (Figure 1b). EDTA then promotes the dissolution of CaCO₃, and the complexation of Ca cations under basic conditions:

Step 1a

Step 1b

(Step 2a) Ca enrichment and separation using nanofiltration (NF) allows separation of the Ca-EDTA complex from the accompanying bicarbonate (HCO₃^–) anions:

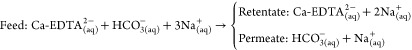Step 2a-i

Step 2a-ii

(Step 2b) The acid produced allows the decomplexation of Ca from EDTA which allows near-complete chelator recovery, and the formation of a Ca-enriched feed solution:

Step 2b-i

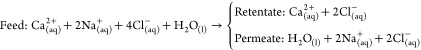Step 2b-ii

(Step 3) This involves the rapid precipitation of Ca(OH)₂ within the catholyte of a flow electrolyzer:

Step 3

(Overall reaction) Calcium carbonate, water, and the electrolyte as acid–base conjugates are transformed with the aid of the (recycled) chelating agent into aqueous sodium bicarbonate/carbonate—as determined by the dissolution pH, here simplified to NaHCO₃—for recovery/utilization or for durable storage, and coproducts including hydrogen and oxygen (gases), hydrochloric acid (liquid), and calcium hydroxide (solid). The overall reaction can be decomposed into two reactions: (i) the dissolution–precipitation reaction and (ii) the water-splitting reaction as follows:

Overall reaction:

Dissolution–precipitation reaction:

Water-splitting reaction:

Herein, deprotonated EDTA (HEDTA^3–; Figure 1 and Step 1a) is used to enhance the dissolution rate and apparent solubility of CaCO₃ at pH > 7. While this example emphasizes EDTA, it is only one of many possible chelating agents that could be used. The hexadentate structure of EDTA consists of four carboxylate and two amine groups with the general formula [CH₂N(CH₂CO₂H)₂]₂. In general, the metal-chelation capacity and stability increase with pH.^29,31 CaCO₃ dissolution is enhanced by EDTA at ambient temperature and pressure, thereby promoting the Ca-complexation reaction in Step 1b and Figure 1. In the presence of Ca species in aqueous solution, the binding affinity of EDTA ensures that the deprotonated chelator rearranges around the Ca²⁺ cation extracted from the CaCO₃ lattice through a surface chelation reaction.^32,33 Thus, Ca species are adsorbed onto the binding sites of EDTA resulting in the formation of a monocalcium-EDTA (Ca-EDTA^2–) complex at the calcite/liquid interface, while the liberated H⁺ protonates the CO₃^2– species that is released alongside the Ca²⁺ cation into its bicarbonate form (HCO₃^–).^32,33,38 This reaction sequence is well-known and in an alkaline environment prevents degassing of CO₂. Experimental evidence and optimal conditions for such are reported in Section 4.1.

Pressure-driven membrane technology has become increasingly prevalent, notably NF due to its unique properties: tailored selectivity, lower pressure, higher flow rates, and lower investment and operating costs vis-à-vis well-established (seawater) reverse osmosis (RO).³⁹ Although new applications require demonstration of technical outcomes and commercial viability at industrial scale, successful and cost-effective commercial applications of NF processes have been reported across various fields.⁴⁰⁻⁴⁷ NF membranes allow for the steric (size exclusion) and charge rejection of large molecules (>100 Da)⁴⁸ such as metal-chelator complexes.^49,50 The NF-based separation of such complexes from monovalent species has been reported.⁵¹ Modern membranes allow tailored applications via: (i) hydrophilic surface functional groups that enhance water permeability while preventing scaling,⁵² (ii) a large-pore matrix for high water flux and monovalent ion permeability,⁵³ while electrostatic interactions retain the charged complexes, and (iii) control of the state of membrane surface charge⁵⁴ resulting in high monovalent and low multivalent permeance due to Donnan and dielectric solvation-energy barrier mechanisms.^55,56 Here, combining chelator-aided dissolution with NF enables the production of a Ca-rich stream that can be used to electrochemically produce portlandite using a CaCO₃ feedstock. The complexation of calcium (Ca = 40.08 Da) by EDTA yields a relatively large molecular complex (Ca-EDTA complex mass = 332.30 Da), which is ∼8 times larger than Ca cations, with a negative divalent charge. Thus, dialytic (i.e., pressure-driven) NF membranes can be used to selectively retain and concentrate Ca species and separate CO₂ species via size exclusion, electrostatic, and/or surface interactions.^57,58 In particular, for the Ca-EDTA/Na-HCO₃ separation (Step 2a-i), it is desirable to achieve high rejection of the Ca-EDTA complex and high monovalent (HCO₃^–) ion permeation. For the NaHCO₃/water separation (Step 2a-ii) and Ca enrichment (Step 2a-iii), high monovalent rejection and high divalent ion rejection, respectively, are desired. In all cases, a high membrane flux, ∼10 L/(m²·h·bar), is desired for high-liquid throughput and low energy processing, ∼1 kWh/m³.

Following Ca-EDTA recovery, electrolytically produced HCl (Step 0) is used for dechelation, i.e., to promote tetraprotonation of EDTA resulting in the formation/precipitation of its insoluble H₄EDTA variant. This results in the release and accumulation of Ca cations in an acidic solution with Cl^– as the balancing anion. The EDTA precipitates can be separated from the decomplexed and now solvated/mobile Ca²⁺ cations (Step 2b-i), which can be further enriched using NF (Step 2b-ii).⁵⁹⁻⁶¹ The 20 mol. % stoichiometric excess of electrolytically produced HCl (see the Step 0 and Step 2b-i equations) can be neutralized by the controlled dissolution of abundant Ca- and/or Mg-bearing rocks.^35,36 Hereafter, the Ca-enriched solution is electrolytically alkalinized (Step 0) to pH > 12 to rapidly precipitate Ca(OH)₂ at ambient conditions (Figure 1a, Step 3). With progressive alkalinization, precipitation continues so long as the ion activity product (IAP) of Ca(OH)₂ exceeds its solubility product (K_sp); i.e., the logarithm of the saturation index (SI) exceeds zero: SI = log[IAP/K_sp], where for Ca(OH)₂, IAP = {Ca²⁺}{OH^–}², where {} indicate ion activities and K_sp = 5.2 × 10^–6 at p = 1 bar and T = 25 °C.⁶² The supply of alkalinity is ensured via electrolytic hydrogen evolution reaction (HER)^35,63 at the cathode, and so long as the hydroxyl ion (OH^–) generation rate and the rate of Ca supply maintain supersaturated conditions, Ca(OH)₂ precipitation occurs continuously. In the following sections, special focus is paid to describe the nonelectrolysis Steps 1–3, as these represent the unique process innovations that underlie the ZeroCAL process.

3. Materials and Methods

Unless specified, all experimental data imply at least triplicate measurements, and hence the mean and standard deviations were derived for all data points. All stoichiometries and mass, charge (Table A1 in the Appendix), and energy balances were validated experimentally. All product streams from each discrete step of the process were used in subsequent steps to establish process integration.

3.1. Materials

Solids

Two calcium precursors were used: an analytical reagent (AR)-grade calcite sample (>99 mass %) and a high-purity limestone rock. The AR calcite was used as received. The limestone rock was ground to a fine powder in a planetary ball mill and sieved to between 30 and 90 μm to retrieve a particle size distribution (PSD) similar to that of the AR calcite. Both samples were fully characterized, as described below. The results are summarized in Table 1.

Table 1. Characterization of the AR Calcite and Limestone Samples^a.

Particle Size Distribution
	d10 (μm)	d50 (μm)	d90 (μm)	SSA (cm2/g)
AR calcite	22.9	39.5	67.9	0.028
limestone	5.9	21.4	72.4	0.023

Oxide Content (mass %)
	XRF						TGA
	CaO	MgO	SiO2	Al2O3	Fe2O3	others	CO2
AR calcite	>55.8					<0.1	44.1
limestone	57.7	0.6	1.4	0.4	0.2	<0.1	39.7

Mineral Content (mass %)
	calcite (CaCO3)	dolomite [CaMg(CO3)2]	quartz (SiO2)
AR calcite	100.0
limestone	96.7	1.8	1.5

^aThe PSD from light scattering analysis, the bulk oxide composition from XRF analysis and TGA, and the mineral composition from XRD analysis are provided.

Solutions

Solid H₄EDTA powder (>99 mass%) and solid NaOH powder (>99 mass%) were used as received to prepare EDTA-containing solutions. Unless specified, all solutions were prepared with 18 MΩ·cm Milli-Q water (MQW). In some instances, NaCl-containing MQW or simulated seawater (“Instant Ocean Seawater: IOSw”) were used instead of pure MQW.

Membranes

Eight commercial NF membranes were selected for screening for separation Steps 2-i, 2-ii, and 2-iii based on common performance parameters, i.e., the normalized permeate flux and observed rejections (Table 2).

Table 2. Attributes of the NF Membranes Including the Nominal Pore Size, Pure Water Normalized Flux, and Divalent and Monovalent Salt Rejections.

membrane type	membrane pore size (102 Da)	water permeability (L/m2·h·bar)	salt rejection (%)	producer/material	reference
NF90	2	8.9	99, MgSO4; 93, NaCl	FilmTec/polyamide	Dupont,64 Ramdani65
TS40	2	4.5	90, MgSO4; 50, NaCl	Trisep/polypiperazine	Trisep66
NF270	3	11.0	97, MgSO4; 50, NaCl	FilmTec/polypiperazine	Dupont,67 Ramdani65
NFW	4	10.6	97, MgSO4; 20, NaCl	Synder/polyamide	Synder68
XN45	5	7.8	95, MgSO4; 20, NaCl	Trisep/polypiperazine	Trisep69
TS80	1.5	8.6	99, MgSO4; 80, NaCl	Trisep/polyamide	Trisep70
SB90	1.5	3.7	97, MgSO4; 85, NaCl	Trisep/cellulose acetate	Trisep71
NP030	5	>1.0	N.D., MgSO4; 86, NaCl	Microdyn Nadir/poly(ether sulfone)	Nadir72

3.2. Solid-Phase Analysis

Particle Size Distribution

The PSD of the solids was measured by light scattering from dilute suspensions of the powders in water using a Beckman Coulter LS13-320 light scattering analyzer. The uncertainty in the light scattering analysis was estimated to be ∼10% based on three measurements and assuming the density of both samples to be that of pure calcite, i.e., 2.711 g/cm³. In addition, the PSD was used to estimate the specific surface area (SSA, in cm²/g) of the samples.

X-ray Fluorescence

X-ray fluorescence (XRF) was conducted using a Hitachi X-Supreme8000 series XRF analyzer under helium (He) flow. The sample holders were double cleaned with isopropyl alcohol (IPA) prior to use. The solid (powder) sample was packed into the sample holder until “infinite” thickness condition (i.e., >2 mm) was achieved. The He flow was maintained below 10 psi and maximum tube current maintained at <30 kW during the analysis.

Thermogravimetric Analysis

Thermogravimetric analysis (TGA) was performed using a PerkinElmer STA 8000 analyzer under a flow of ultrapure nitrogen in aluminum oxide crucibles. A heating ramp of 10 °C/min was used between 35 and 950 °C, after 5 min of equilibration at 35 °C.

X-ray Diffraction

X-ray diffraction (XRD) analysis was performed using a PANalytical X’PertPro diffractometer (θ–θ configuration, Cu Kα radiation, and α = 1.54 Å) on powdered samples. The scans were acquired between 5° and 70° with a step size of 0.02° using a X’Celerator 2 detector. Rietveld refinement of the samples was performed using Profex and BGMN packages.⁷³⁻⁷⁵

Fourier Transform Infrared Spectroscopy

Solid-state attenuated-total-reflection Fourier transform infrared spectroscopy (ATR-FTIR) was performed using a PerkinElmer Spectrum Two FT-IR spectrometer. The powdered samples were pressed using around 90 N of force onto a diamond/ZnSe composite crystal to ensure good contact and generate total internal reflection. The spectra reported herein were obtained by averaging 4 scans over the wavenumber range of 4000–400 cm^–1 at a resolution of 1 cm^–1.

3.3. Solution-Phase Analysis

Inductively Coupled Plasma Optical Emission Spectrometry

Inductively coupled plasma optical emission spectrometry (ICP-OES) was performed using a PerkinElmer Avio 200 analyzer for multi-elemental analysis to quantify Ca and Na concentrations in solution (i.e., in a 5 vol % trace-metal-grade HNO₃ matrix). All intensity measurements, measured in radial view, were converted to concentration units using a calibration curve with a blank and 7 calibration points between 0.1 and 25 ppm, prepared using standard solutions (1000 ppm Inorganic Ventures). Our testing showed that the presence of trace amounts of EDTA in the samples prepared for ICP measurement does not affect the intensity reading. Note that, for the limestone sample, Mg, Fe, and Al, as elements that can all complex with EDTA, were analyzed in a following a similar method as that used for Ca analysis. In general, for both feedstocks, Mg was found to be present in trace amounts (i.e., <1 mmol/L that corresponds to <1 mol. % of the amount of Ca in solution) while Al and Fe were below the detection limit.

Titration

Volumetric titrations were performed using an OrionStar T910 instrument and using HCl as the titrant to determine the concentration of dissolved EDTA, Ca-EDTA complex, and DIC species as analytes diluted in MQW. The HCl titrant was prepared from 37 mass % concentrated HCl (ACS grade), and the acid content of the titrant was determined prior to usage by titrating a carbonate standard solution (1000 ppm Inorganic Ventures). The titration procedure consists of continuous acid addition under agitation (600 rpm) until 20 mL of acid has been dispensed, or until a pH below 3 is reached, at a pace regulated by the apparatus based on the instantaneous temperature-corrected pH measurement. The start and end points are determined from the minimum of the derivative of the pH evolution as a function of the volume of acid dispensed.

UV–Visible Spectrophotometry

Chloride concentrations in solution was determined using the iron(III) thiocyanate method with an UV–visible spectrophotometer (Hach DR1900) and DPD testing kits (TNTplus-879). After zeroing using a blank reference, sample vials were measured in the ranges of 1–70 and 70–1000 mg/L.

3.4. Gas Analysis

Gas Chromatography

Gas chromatography (GC) was used to quantify CO_2(g) evolution using an Inficon Micro GC Fusion instrument. The GC was calibrated using standard CO₂ calibration gases of 0, 0.1, 5, and 20 mol. % CO₂ with N₂ for balance. The apparatus allows for a carrier gas with a known and fixed flow rate that first passes through a hermetically closed reactor vessel where the reaction of interest occurs before/while being fed into the Inficon Micro GC instrument for analysis. The concentration of CO₂ in mol. % is recorded at intervals of 30 s for the entire reaction time and is then used to quantify the total amount of CO₂ emitted during the reaction by integration from the known flow rate of the carrier gas.

3.5. Thermodynamic Modeling

Thermodynamic modeling of solid- and solution-phase equilibria was carried out using GEM-Selektor v.3.6 (GEMS)^76,77 which incorporates the slop98.dat and Cemdata18 thermodynamic databases.^62,78−80 Property inputs from these databases are used to assess solid phase solubilities and aqueous speciation. To represent the non-ideality of the solutions, the activity coefficients were calculated using the Truesdell–Jones extension to the Debye–Hückel equation that is applicable for I_m ≈ 2 mol/L:⁸¹

2

where γ_i is the activity coefficient and z_i is the charge of the ith aqueous species, A_γ and B_γ are the temperature- and pressure-dependent coefficients, X_jw is the molar quantity of water, X_w is the total molar amount of the aqueous phase, and I is the molal ionic strength. A common ion size parameter (ȧ = 3.72 Å) and a short-range interaction parameter (b_γ = 0.64 kg/mol) were used, considering NaCl as the background electrolyte.^81,82

3.6. ZeroCAL Process

Ca Extraction and Complexation

The solubility and dissolution rates of the AR calcite and limestone rock were investigated in EDTA-containing solutions of varying pH 6–10 and EDTA concentration 2–200 mmol/L. First, H₄EDTA was fully dissolved in MQW in borosilicate beakers at room temperature under continuous agitation by the progressive addition of solid NaOH until the target pH was attained. Following the dissolution of EDTA, calcite or limestone was added so that the total calcium content in the system is slightly in excess vis-à-vis the EDTA amount, i.e., such that CaCO₃ (in mol) = 1.1 × EDTA (in mol). Considering solid-to-liquid ratios (s:l) on a g/g basis, where solid designates the calcium source and liquid designates the EDTA-containing solution, this corresponds to ratios of 1:4542, 1:454, and 1:45 for solutions containing 2, 20, and 200 mmol/L EDTA, respectively. The system was agitated at room temperature until it stabilized, that is, no further change in Ca concentration is observed. The time required to reach equilibrium, i.e., at least 95 mol. % Ca extraction, is dependent on pH and EDTA concentration as detailed in Table A2 (in the Appendix) but less than ∼1.5 h in all cases. The solution and the headspace gas phase were both sampled and analyzed using ICP-OES, titration, and gas-phase (GC) analysis.

The evolution of the calcium concentration ([Ca], in mol/L) over time resulting from the dissolution of the calcium precursors can be modeled using a first-order equation of the form

3

where k₀ (in mol/L/s) and k₁ (in s^–1) are the apparent rate constants that are dependent on the pH and EDTA concentration and t is the time (s). The dissolution rate (r, in mol/m²/s) is calculated using the following equation:⁸³

4

where m_Ca is the amount of calcium (in mol) dissolved during the time Δt (s), m_CaCo3 is the initial mass of calcite introduced in the reactor (in g), and SSA_t is the specific surface area of the sample at a time t (in m²/g) calculated as follows:⁸⁴

5

where SSA is the initial specific surface area calculated from the PSD of the sample and FSD is the fraction of solid dissolved (unitless) at any time t calculated as follows:

6

where [Ca]_t is the calcium concentration at a time t, n_Ca is the amount of calcium initially available in the solid sample (in mol), and V is the volume of solution in the reactor (in L).

Ca/CO₂ Separation and Na-HCO₃/Water Separation via Nanofiltration

A Sterlitech CF042 PTFE cross-flow cell⁸⁵ was used at a constant applied pressure of 80 psi (5.5 bar) provided by a diaphragm pump. The setup used a jacketed reactor connected to a chiller system for temperature control of the feed solution at 20 °C. The membranes were equilibrated by immersion for at least 24 h in the testing solution and stabilized/compacted under pressure for at least 1 h to achieve pseudo-steady state rejections and flux. The NF tests were carried out under batch-recirculation conditions, i.e., by circulating the retentate back to the feed tank under atmospheric pressure, at constant temperature and applied pressure⁸⁶ at selected water recoveries. The membranes were screened based on the reported normalized permeate flux and observed rejections (Table 2), and the experimental rejections and specific energy intensity as a function of water recovery for the solution system of interest herein (refer to Section A4 in the Appendix for the relevant equations). In the screening process for Ca-EDTA/Na-HCO₃ separations at 10–20 mmol/L in MQW, with and without high NaCl salinity background matrix, five membranes—N90, TS40, NF270, XN45, and NFW—were tested at a water recovery of 0% to limit concentration polarization effects recirculating both retentate and permeate streams, as well as at an increased water recovery of up to 50%, without recirculation of the permeate thereafter. This allowed examination of the separation and permeability properties to select a membrane for the high water recovery target of 85% (i.e., which yields the largest separation), typical of NF processes (80–90%).^58,86,87 The Na-HCO₃/water separation for process-water recycling was performed at 75% water recovery upon screening of four membranes (NF90, TS80, SB90, and NP030).

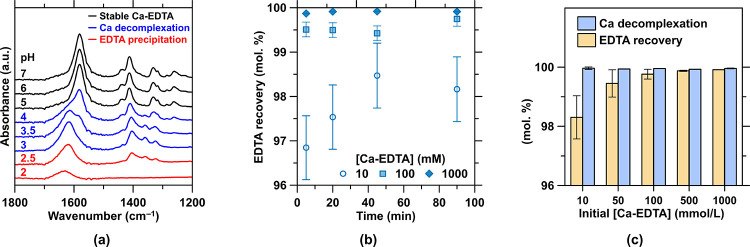
Ca Decomplexation and EDTA Recovery

Acidification using electrolytically produced HCl is used to decomplex Ca from the EDTA, while ensuring its reprotonation into the highly insoluble H₄EDTA form. Thus, HCl was used to titrate the Ca-EDTA solutions in MQW with EDTA contents ranging from 10 to 1000 mmol/L until HCl (in mol) = 4 × EDTA (in mol) has been introduced (i.e., when the EDTA is tetra-protonated). The precipitate was recovered by vacuum filtration using a Büchner apparatus and filter paper (Whatman, grade 1, >11 μm) and dried in a vacuum desiccator at room temperature prior to XRD and FT-IR analysis. The filtered solution was also analyzed so that the residual contents of aqueous EDTA, and Ca and Cl could be quantified by titration, ICP-OES analysis, and UV–visible analysis, respectively.

Ca(OH)₂ Precipitation

Ca(OH)₂ precipitation was assessed using thermodynamic modeling and validated experimentally (Figure A8a in the Appendix) by titrating model “CaCl₂/(1 – x)NaHCO₃” solutions where 0.90 < x < 1.0 on a mole basis in MQW with 1 mol/L NaOH solutions. This range was selected to assess the precipitate purity in the range of Ca-EDTA/Na-HCO₃ separation achievable via NF in single and double stages (Step 2a-i). The recovered solids were dried under vacuum in glass desiccators to prevent carbonation prior to characterization.

The ZeroCAL process implies the use of recently developed flow electrolyzers to produce acidity (HCl) and basicity (NaOH). These bifurcated anode–cathode flow “seawater” electrolyzers were developed to enable atmospheric carbon dioxide removal and hydrogen production via the Equatic process (“Project SeaChange”).^35,36 These electrolyzers—which are fitted with OSA catalysts—have been upsized and field-demonstrated from the bench (0.001 kW) to pilot (10 kW) scale over the past several years. Based on operational data using a seawater feed, these electrolyzers currently achieve a Faradaic efficiency [the Faradaic efficiency (FE, unitless) is defined in terms of the known quantity of reagent stoichiometrically converted into desired product(s), as measured by the current passed. The overall system’s energy efficiency is defined as the product of the voltage efficiency and Faradaic efficiency] of >80% with respect to the production of OH^– species at a cell voltage of ∼−3 V, and hence Ca(OH)₂, and a cell voltage that shows a change (ΔV) of <0.2 V over 7 days of continuous operations. Herein, the electrolyzer performance was based on the solubility of Ca(OH)₂ considering a seawater electrolyte of ∼0.5 mol/L of NaCl and σ ≈ 50 mS/cm within the ZeroCAL process. First, the amount of OH^– produced in the cathode half-cell was calculated as

7

where [OH^–] is the concentration of OH^– ions in the catholyte (mol/L), α is the current efficiency ratio or so-called “Faradaic efficiency”, I is the imposed current (A, for constant current operations), F is Faraday’s constant (96485 s·A/mol), and S is the electrolyte flow rate (L/s) through the electrolyzer. The [OH^–] concentration is sufficiently high such that, in general, pH > 12.5 is produced in the electrolyzer. Such high pHs are required to induce Ca(OH)₂ precipitation. For a Ca-enriched solution that transits the flow electrolyzer, the amount of Ca converted into Ca(OH)₂ can be estimated based on the difference in the inlet and outlet Ca concentrations, or the change in pH from the inlet to the outlet considering the valence (charge) mismatch between divalent calcium, and univalent hydroxyl species:

8

9

where Δ[Ca²⁺] and Δ[OH^–] indicate the quantity of the Ca(OH)₂ precipitate (mol). By integrating eqs 7–9 and considering the K_sp of portlandite, it is found that Δ[Ca²⁺ ] is a function of the inlet Ca concentration ([Ca²⁺]_initial), the Faradaic efficiency, the dosage of OH^– ions, and the solution (electrolyte) flow rate that establishes the residence time of Ca species within the electrolyzer (Section A1.2 in the Appendix for details):

10

The electric energy intensity (EEI, MWh/t_Ca(OH)2) is determined from the ratio between the power input into the electrolyzer (i.e., the product of current input, and measured cell voltage) and the rate of Ca(OH)₂ precipitation as described below:

11

where M_Ca(OH)2) is the molar mass of portlandite and U (in V) is the measured voltage, wherein the thermodynamic minimum voltage, U₀ = −2.06 V, is defined by the OER and HER half-cell reactions (eqs A1 and A2 in the Appendix).^35,36

4. Results and Discussion

4.1. Ca Extraction (Dissolution) and Chelator Complexation

In aqueous solution, EDTA binds cations with an increasing preference for valence and field strength—Z/i_r, m^–1, i.e., the ratio of the valence (Z) to the ionic radius (i_r). On account of its ability to bind divalent cations, EDTA substantially enhances the solubility of calcite (CaCO₃: Figure 3a) by up to ∼3 orders of magnitude compared to MQW. This occurs as EDTA chelates calcium species on a stoichiometric basis over a broad pH range: on average, 0.96 ± 0.04 mol of Ca are bound per mol of EDTA at equilibrium. This ensures that EDTA is fully chelated, consistent with literature reports.³³ The reaction of EDTA with calcite evolves some CO₂ under specific conditions, 6 < pH < 9, although no CO₂ evolution is observed when dissolving calcite in MQW (Figure 3b). This is because while the majority of the aqueous EDTA species are being held in the form of HEDTA^3– anions above pH 6—as disclosed by the Bjerrum diagram (Figure 1b)—minor amounts of H₂EDTA^2– exist in solution so the dissolution reaction may be written as follows:

12

where 0 < x < 1 is dictated by the pK_a of the following reaction:

13

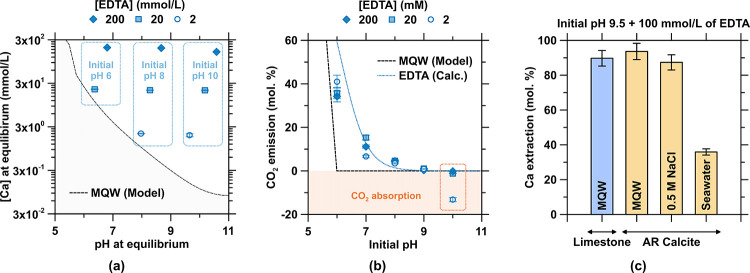
Figure 3.

Dissolution of calcite at room temperature in the presence of EDTA. (a) Increased solubility of calcite (i.e., Ca concentration) as a function of the pH across a range of EDTA concentrations. The black dashed line shows the thermodynamically modeled solubility of calcite in a system devoid of EDTA. (b) Degassing of CO₂ expressed as a molar percentage of total amount of aqueous and mineralized carbonates in the system as a function of the EDTA concentration and the initial pH of the solution. The dashed black line shows the thermodynamically modeled CO₂ emission from calcite in a system devoid of EDTA, and the blue dotted line shows the CO₂ emission of calcite in a system containing EDTA calculated using eqs 12–14. (c) Ca concentration at equilibrium at pH 9.5 and in the presence of 100 mmol/L EDTA in MQW, a 0.5 mol/L NaCl solution, and simulated seawater (“Instant Ocean Seawater: IOSw”) for reagent calcite (AR calcite) or limestone rock.

H₂CO₃ eventually evolves as CO_2(aq) and ultimately CO_2(g):

14

This reaction sequence is supported by the agreement between thermodynamic modeling (eqs 12–14) and experimental results (Figure 3b). Effectively, no CO₂ evolution is observed when calcite is dissolved in the presence of EDTA at an initial pH > 9, and net CO₂ absorption from ambient air is observed at yet higher pHs (Figure 3b). With increasing pH, the speciation of EDTA and DIC shifts toward their fully deprotonated forms (Figure 1b), and the dissolution reaction may be written as follows:

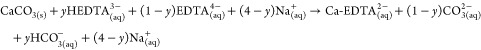15

where 0 < y < 1 is dictated by the pK_a of the following reaction:

16

At an initial pH of 9.5 and using 100 mmol/L EDTA—conditions at which no CO₂ evolution is expected—Ca extraction from limestone rock by EDTA is similar to that of AR-grade calcite (Figure 3c), despite small quantities of other solutes present in the rock. Since an electrochemical process requires a conductive electrolyte, dissolution was evaluated in a 0.5 mol/L NaCl solution and in synthetic Instant Ocean seawater to examine how salinity and ionic strength affects Ca-extraction behavior. It is noted that a “high” ionic strength alone does not affect the amount of extracted calcium in solution at equilibrium (Figure 3c). Rather, seawater is observed to strongly decrease the capacity of EDTA to extract calcium due to the native presence of ∼55 mmol/L Mg and ∼10 mmol/L Ca. These divalent “matrix cations”, particularly Mg, consume the chelation capacity of EDTA, and therefore compromise Ca chelation by EDTA, reducing its ability to uptake Ca species dissolved from calcite. This indicates that the use of natural brines and saline waters within the ZeroCAL process would require water softening, e.g., preprocessing by NF, to remove parasitic and competitive divalent cations such as Mg that may complex with EDTA.^37,39,88

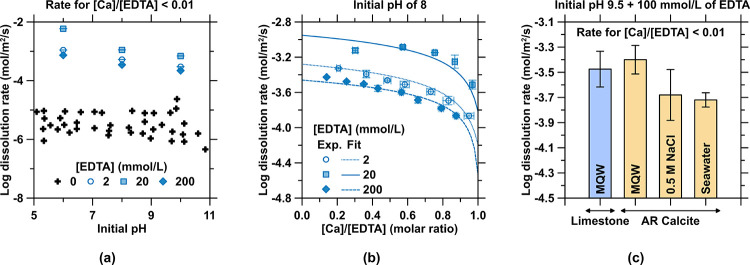
Considering the effects of EDTA on calcite dissolution, it is noted that EDTA enhances the dissolution rate of calcite enormously, as compared to MQW, across a range of pHs (Figure 4a).^24,33 In the presence of EDTA, increasing calcite dissolution rates are observed with decreasing pH (Figure 4a), at an EDTA dosage of ∼20 mmol/L EDTA (Figure 4a,b), and at low [Ca]/[EDTA] ratios (Figure 4b, where 0 < [Ca]/[EDTA] < 1, molar ratio). The highest dissolution rates at [EDTA] ∼ 20 mmol/L arise from the competing effects of EDTA’s chelation properties (favorable) (Figure 4a) and increasing ionic strength (unfavorable) (Figure A3a in the Appendix) on the dissolution rate. The dissolution rates at saturation (i.e., where [Ca]/[EDTA] = 1) imply that longer times would be required to reach saturation for 200 mmol/L EDTA solutions as compared to 2 or 20 mmol/L EDTA solutions, although the former solution contains 100 or 10 times as much extracted Ca as the latter solutions. Under similar pHs and EDTA concentrations, the AR calcite and the limestone rock feature similar dissolution rates (Figure 4c). The 0.5 mol/L NaCl solution and seawater perform similarly to each other and induce a decrease in the dissolution rate, whereby a linear decrease in the dissolution rate is observed with an increasing ionic strength (Figure A3a in the Appendix).

Figure 4.

(a) “Initial” dissolution rate of calcite at high undersaturation (i.e., far from dissolution equilibrium) as a function of the initial pH of the solution across a range of EDTA concentrations. The data for dissolution occurring in MQW (“0 mmol/L EDTA”) are taken from the literature.^24,89,90 (b) Measured and fitted (eq 3) relationship between the dissolution rate and the [Ca]/[EDTA] (molar) ratio. (c) Dissolution rates of reagent-grade calcite and limestone rock at pH 9.5 and in the presence of 100 mmol/L EDTA in MQW, 0.5 mol/L NaCl, and simulated seawater (IOSw).

4.2. Aqueous-Phase Separation of Ca-EDTA Complex and HCO₃^– Anions by NF

The mildly alkaline leachate, 9.5 < pH < 10.2, from the dissolution step that contains the Ca-EDTA complex and dissolved HCO₃^– anions and other species needs to be processed to separate the Ca-rich and bicarbonate components, i.e., to allow for downstream Ca(OH)₂ precipitation. This allows aqueous-phase stabilization of CO₂ in the form of HCO₃^– at the prevailing pH in solution, avoiding the degassing/emission of CO₂. Dialytic NF using a negatively charged membrane enables separation of the Ca-EDTA complex and HCO₃^– anions via a combination of size and charge exclusion by retaining Ca-EDTA species in the “retentate” stream, while permeating Na⁺ + HCO₃^– species in the “permeate” stream.⁵¹ A suitable NF membrane ensures a high “Ca/CO₂ separation”, i.e., high Ca-EDTA rejection and low monovalent rejection, as well as high flux, thereby reducing the required membrane area and operational energy at increasing water recovery. An initial screening of selected membranes at 0% water recovery (Figure 5a)—where concentration polarization effects are minimized—and a comparison of their performance relative to the XN45 membrane at increasing water recovery up to 50% (Figure 5b) reveals that, while Ca-EDTA rejection is 100% in all cases, the XN45 membrane is the most permeable to monovalent species ensuring the largest Ca/CO₂ separation at a relatively high flux. Unsurprisingly, as the water recovery increases to 85%, the permeate flux drops as the concentration polarization magnifies (i.e., the ionic strength increases and the ratio of the applied pressure to osmotic pressure decreases in the feed stream; Figure A4a in the Appendix). The XN45 membrane remains effective enough for practical processing, e.g., featuring a flux of 1–7 L/(m²·h·bar). Importantly, the Ca-EDTA is fully rejected by the XN45 membrane, while Na⁺ + HCO₃^– permeance increases with water recovery (Figure A4b in the Appendix). An apparent negative rejection is observed at >75% water recovery (Figure A4c in the Appendix) due to the Donnan equilibrium that emerges at high concentration polarization at the surface of charged membranes.⁹¹⁻⁹³ As a result, at 85% water recovery, the concentration factor for Ca-EDTA is around 7 × compared to the feed stream, and the bulk Ca/CO₂ separation, i.e. HCO₃^– permeation, is 85–90% at pH 8–10, for both limestone rock and AR-grade calcite streams—with and without a high salinity matrix (e.g., seawater; Figure 5c).

Figure 5.

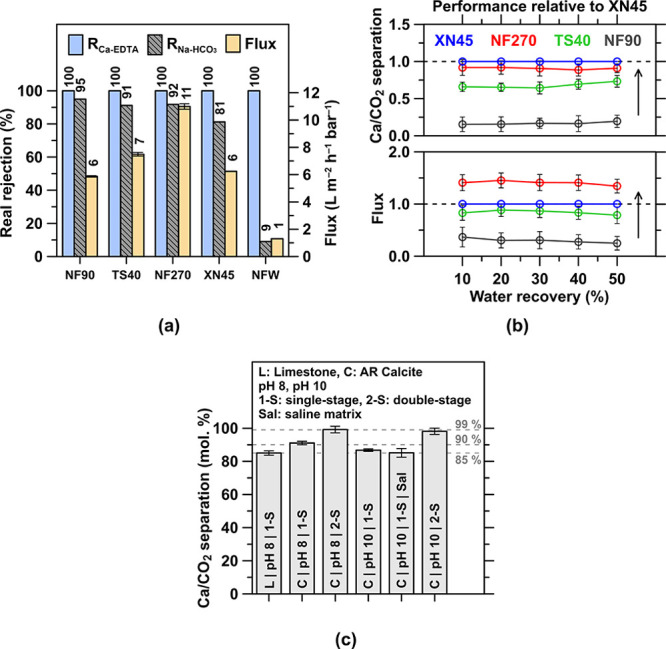
(a) Experimental performance of the selected NF membranes for Ca/CO₂ [Ca-EDTA and Na⁺ + HCO₃^–] separation at 0% water recovery. Here, R_Ca-EDTA and R_Na-HCO3 indicate the rejection of the Ca-EDTA^2– and Na⁺-HCO₃^– species, respectively. An optimal membrane maximizes R_Ca-EDTA, minimizes R_Na-HCO, and ensures a suitable flux at increasing water recovery. (b) Upon initial screening, Ca/CO₂ separation and flux of the remaining membrane candidates relative to the XN45 membrane up to 50% water recovery are shown, highlighting the Ca/CO₂ separation properties of XN45. (c) XN45 membrane’s separation of Ca/CO₂ at 85% water recovery for limestone rock and AR-grade calcite precursors at pH 8 and 10, for single- and double-stage separation, using water and a high salinity simulated seawater matrix.

Figure A4.

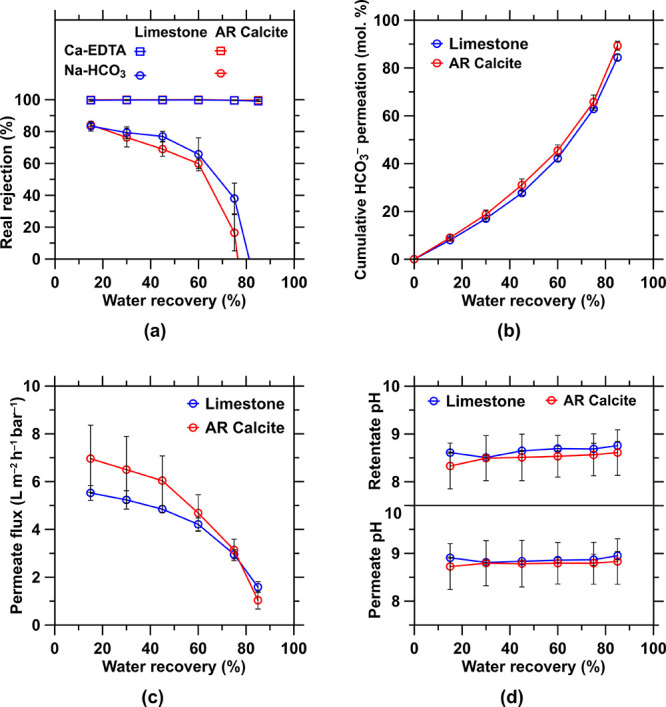
Performance of the XN45 membrane on single-stage NF with a pH 8 Ca-EDTA/Na-HCO₃ solution system as a function of water recovery comparing AR-grade calcite and natural limestone feedstocks: (a) Ca-EDTA and Na-HCO₃ real rejections; (b) profile of the cumulative HCO₃ permeation; (c) normalized permeate flux; (d) pH in the streams.

Improved separation is attainable: (i) for a single-stage system at slightly greater water recoveries due to the very steep increase in concentration factors and monovalent permeance at very high water recoveries (Figure A4a,b in the Appendix), albeit at the expense of an increasing energy demand, or (ii) by using a two-stage system that makes use of a rediluted Ca-EDTA-rich stream which enhances cumulative HCO₃^– permeance to a level of ∼99% (Figure 5c). In spite of the high water recovery, salt crystallization was not observed on the NF membranes given that the diffusing species (NaCl, NaHCO₃, and NaOH) are highly soluble and the solution did not reach saturation. It is unsurprising that this approach is very effective at Ca-EDTA separations, given that prevailing EDTA concentrations are well below the chelant solubility: ∼0.4 g_EDTA/g_water at 10 < pH < 11.⁹⁴ While the molecular size of Ca-EDTA (∼3 × 10² Da) is on the order of the membrane pore size (∼5 × 10² Da),⁶⁹ it is electrostatically repelled on account of its divalent negative net charge (Ca-EDTA^2–_(aq)) by the membrane’s surface whose functional groups are negatively charged in that pH range.⁹⁵ It should be noted that the observed difference in separation performance of the limestone rock and calcite feedstock is largely attributable to the aqueous phase contaminants introduced by the former, and from pH 8−10 due to carbonate speciation. Finally, it should be noted that the pH of the postseparation retentate and permeate remain similar, 9 < pH < 10, ensuring that dissolved carbonate species remain stable in their ionic HCO₃^– form (Figure A4d in the Appendix). This is valid for both MQW (i.e., a solution containing stoichiometric amount of Ca-EDTA^2–, HCO₃^–, and Na⁺) and in saline environments (i.e., a solution containing additional NaCl): the solution is charge- and mass-balanced regardless of the ionic strength prior to NF separation, resulting in little to no change in pH during NF.

4.3. Water Recycling and Reuse: Implementing a Once-through or Recycle-Loop Process?

Two pathways are proposed to manage the NaHCO₃ enriched permeate stream. In the first configuration where no process water reuse, recovery, or recycling is required—e.g., when utilizing seawater—the stream can be discharged into the ocean; an effectively limitless storage reservoir for bicarbonate species.⁹⁶ Thermodynamic modeling—that is validated experimentally (Figure A5 in the Appendix)—indicates that as long as this discharge stream is sufficiently diluted, e.g., by the use of well-established diffuser solutions to a level greater than 30 times,^97,98 no CO₂ will degas (Figure A5a in the Appendix) nor will any secondary aragonite precipitation occur (Figure A5b,c in the Appendix). While the ZeroCAL process effluents and discharge strategy are being designed and engineered to mitigate any changes to the receiving aqueous environment, more work is needed to understand how, at very large (“gigatonne”) scale and over long periods, ocean carbon storage may evolve.⁹⁹ This is mainly to understand/mitigate any potential detrimental ecosystem effects that could manifest, if unaddressed, in hyperlocal environments.¹⁰⁰ In the second configuration where internal process water recycling is desired, implementing another NF step on the permeate output with an energy intensity of ∼3 kWh/m³, depending on the water recovery, allows for the recirculation of 42–85% of the process water, resulting in a less water-intensive process while concentrating the carbonate stream. Here, NF is imposed on this saline stream, beyond the seawater matrix background, because it allows for higher water recovery with larger flux (3–5-fold)¹⁰¹ at a lower energy cost than RO, which rejects all ions.^102,103 For example, such recycling of process water allows for the concentration of Na-HCO₃ (rejection >95% using NF90 membrane; Figure A6a in the Appendix), while the alkalinity of the retentate stream, 8.8 < pH < 9.1, ensures that no CO₂ evolution (Figure A6b in the Appendix) will occur (Step 2a-ii in Figure 2 for this process water recycling implementation). While other solutions such as RO systems and evaporation ponds could be beneficial, they imply increases in energy intensity, or land-use (surface) area, perhaps with the benefit of allowing the recovery of even high solubility salts (e.g., NaHCO₃ and NaCl) from the process.¹⁰⁴

4.4. Ca Decomplexation from EDTA and Enabling EDTA Recovery and Reuse

The acidification of the Ca-EDTA-complex-containing retentate stream from pH 8–10 down to pH < 2 utilizes 4 moles of HCl per molar unit of the Ca-EDTA complex (Step 2b), i.e., thereby utilizing 80 mol. % of the HCl produced alongside a stoichiometric quantity of NaOH. This acidification ensures the decomplexation of Ca from the EDTA while resulting in the precipitation of H₄EDTA. Under acidic conditions, where typical Ca-bearing phases are unstable, Ca persists at high concentrations as a cationic species (Ca²⁺) in aqueous solution. The liberation of Ca from the Ca-EDTA complex occurs in the pH range of 3–4, as attested by the main peak shift and secondary peaks attenuation in the FT-IR spectra, while the precipitation of H₄EDTA occurs at pH < 2.5 where the peaks of its aqueous forms diminish (Figure 6a). In addition, settling tests have shown that the reprecipitated EDTA settles quickly, with bulk settling occurring in a static system in a few minutes, indicating that recovery of the reprecipitated EDTA solids can be achieved using conventional clarifiers. The Ca decomplexation and EDTA precipitation process occurs rapidly, i.e., within 5 min (Figure 6b). While Ca is stoichiometrically liberated, ∼100 mol. %, recovery of EDTA progressively increases up to 99.9 mol. % with its increasing initial concentration (Figure 6c), i.e., as the intrinsic solubility limit of EDTA at pH 2 (∼0.1 mmol/L) is achieved. Careful characterization of the H₄EDTA precipitate using FT-IR and XRD indicates that this product is analogous to the pristine AR-grade compound (Figure A7a in the Appendix), while Ca and Na salts intrinsic to the system constitute an additional <1 mol. % of the product. Importantly, the use of the reprecipitated material results in a CaCO₃ dissolution behavior similar to its reagent-grade form (Figure A3b in the Appendix) over at least 5 cycles of Ca recovery and release, although the long-term cyclic performance remains to be established. It should be noted that while the recovery of EDTA is carried out using the acidity produced electrolytically, this acidification dilutes the Ca content of the solution as a function of the anolyte’s acidity (pH ≤ 1) and the EDTA concentration after NF. Therefore, a terminal NF step (Step 2a-iii in Figure 2) is used to ensure a Ca-enriched solution for electrolytic precipitation. Neutralization of the ∼20 mol. % surplus HCl can be achieved via the dissolution of abundant and high H⁺ neutralization capacity Ca/Mg-silicates, e.g., olivine (Mg²⁺,Fe²⁺)₂SiO₄.³⁵

Figure 6.

(a) FT-IR spectra of the Ca-EDTA complex for pHs ranging from 2 to 7 representing the regions of stability (complexation) and instability (decomplexation). (b) EDTA recovery efficiency as a function of the initial Ca-EDTA concentrations and time of acid exposure. (c) Ca decomplexation and EDTA recovery efficiencies for different Ca-EDTA concentrations after 90 min. In general, for EDTA concentrations >100 mmol/L, near stoichiometric recovery of the EDTA is observed within 5 min.

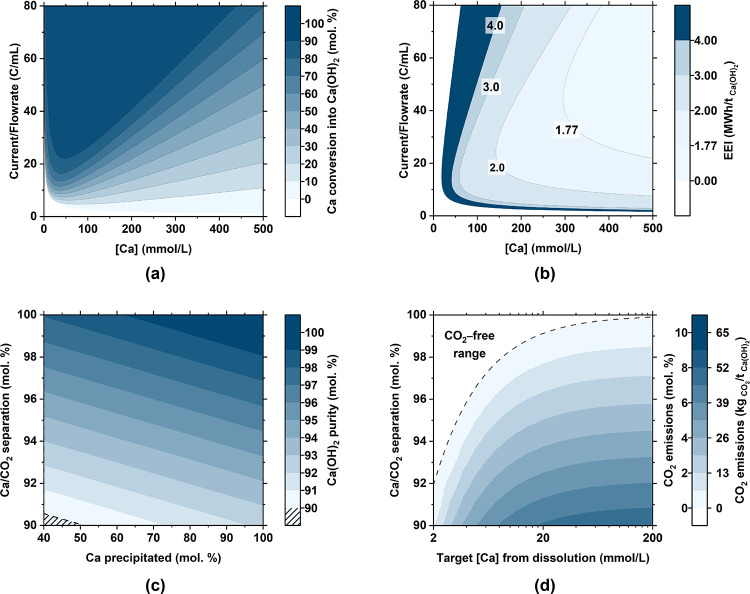
4.5. Electrolytic Precipitation of Portlandite (Ca(OH)₂) in Flow Electrolyzers

The electrolytic precipitation of portlandite is readily induced by the alkalinization of the Ca-enriched solution that is produced in Steps 2b/2a-iii using flow electrolyzers that have already been operated at the 10 kW pilot scale. In general, the performance of this electrolyzer configuration is described by the “current-to-flow rate” ratio [I/S; eqs 7–11], which describes the amount of current input that is needed to induce stoichiometric precipitation, i.e., 100 mol. % conversion of aqueous Ca into Ca(OH)₂. The resulting energy intensity (Figure 7) drives reactions in the cathode half-cell where split water molecules produce OH^– ions and thus a pH increase that promotes Ca(OH)₂ formation.

Figure 7.

Electrolyzer performance for a Faradaic efficiency of 90% and a cell voltage of −2.06 V showing (a) Ca conversion (into Ca(OH)₂) and (b) the electric energy intensity (EEI) of Ca(OH)₂ precipitation. Both parts a and b refer to Ca(OH)₂ precipitation (Step 3) only and are shown as a function of the inlet Ca concentration and the current/flow rate ratio. (c) Purity of portlandite produced as a function of the Ca/CO₂ separation in solution after Step 2a-i. (d) Extent of CO₂ degassing (as a percent of the amount of CO₂ introduced into the system via the dissolution of limestone) that could occur as a function of the initial EDTA concentration and extent of Ca/CO₂ separation after Step 2a-i.

The calculated efficiency of Ca conversion into Ca(OH)₂ at varied inlet Ca concentrations and current/flow rate ratio and the corresponding EEI for precipitation only—i.e., Step 3 only, not including Steps 0–2—are shown in Figure 7a,b (eq 10 and Section A1.2 in the Appendix). In general, it is noted that, for inlet Ca concentrations ranging between 100 mmol/L < [Ca]_inlet < 500 mmol/L and 20 C/mL < [I/S] < 40 C/mL, there exists an operational optimum wherein Ca(OH)₂ can be produced at an electrolyzer energy intensity of <2 MWh/t_Ca(OH)2 (Figure 7a,b). This gross energy intensity for electrolytic portlandite precipitation implies a net energy intensity of <1 MWh/t_Ca(OH)2 considering the energy embodied in the coproduced hydrogen (∼39.4 MWh/t_H2)¹⁰⁵ and an energy conversion efficiency on the order of 80–90% via a combined heat and power fuel cell.¹⁰⁶

An important aspect to consider in this system is the tendency to produce CaCO₃, i.e., if any dissolved CO₂ in the form of HCO₃^–/CO₃^2– were to persist in the system, given the tendency of CaCO₃ to form at lower pHs than Ca(OH)₂ and, in turn, consume Ca in the system. This emphasizes the need to effectively remove dissolved carbonate via NF, failing which (i) CaCO₃ impurities could be increasingly intermixed into the Ca(OH)₂ formed and/or (ii) CO₂ could degas during the acidic decomplexation and recovery of EDTA. Based on the thermodynamic modeling and experimental data (Figure A8a in the Appendix), it is clarified that achieving a Ca/CO₂ separation of >90 mol. % allows for high-grade Ca(OH)₂ production (Figure 7c) and minimizes the risk of CO₂ evolution during EDTA recovery (Figure 7d). Of course, minimizing CO₂ evolution implies minimizing the amount of carbonate in solution (Figure A7b in the Appendix). This suggests the use of a two-stage NF sequence and, likely, the provision of a seawater feed. It is additionally noted that the use of seawater, or natural limestone, is likely to introduce other impurities including silica, alumina, magnesia, ferrous-species, etc. Broadly speaking, most of these impurities exist at concentrations substantially lower than carbonate, and thus are disregarded at a first approximation. These contaminants may be removed using a pH swing in a judiciously selected pH range of ∼11.0–11.5 (Figure A8b in the Appendix) that allows one to precipitate and separate a range of hydroxide species (e.g., Fe(OH)₂, Fe(OH)₃, Al(OH)₃, and Mg(OH)₂) as well as amorphous silica (SiO₂) and a silicate hydrate phase that contains a small amount of magnesium and calcium (C-M-S-H)—at pHs inferior to Ca(OH)₂—to thus produce high-purity portlandite.

5. Process Outlook and General Implications

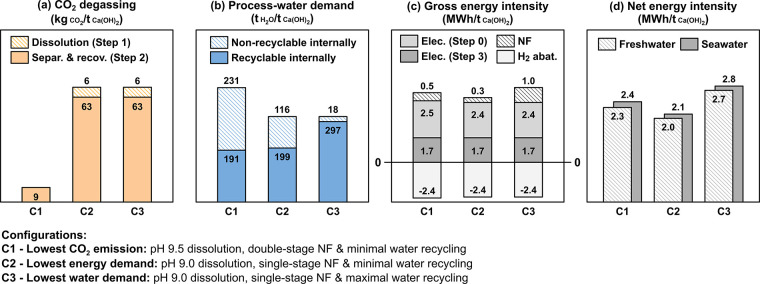
In general, considerations of Ca extraction (from limestone), its aqueous separation from “CO₂” while preventing CO₂ degassing, and the electrolytic precipitation of Ca(OH)₂, all appear reasonable (Figure 8 and Table A3 in the Appendix). Analysis of the consumable reaction stoichiometries (Section 2) shows that the production of 1 t of Ca(OH)₂ requires 1.35 t of CaCO₃, 1.09 t of water, and 0.79 t of NaCl. It should be noted that ∼75 mol. % of the NaCl used as electrolyte is recycled during the process (Section 2: Steps 2a and 2b). In addition, ∼100 mol. % of the EDTA used is recovered and reused allowing use of a pH-swing cycle that minimizes additive demand. Aside from the (sea)water consumed, i.e. ∼1 t_H2O/t_Ca(OH)2, the process water demand depends on (i) the initial EDTA concentration and (ii) the amount of water that is recycled internally (Step 2a-ii) [N.B.: without the use of a chelator, the water demand would increase ∼100 times]. The process coproduces 68 kg of H₂, 0.54 t of O₂, 0.49 t of HCl, and 1.13 t of NaHCO₃ per t of Ca(OH)₂. The H₂ coproduct from the Step 0 and Step 3 electrolysis can be co-combusted with oxygen to heat the cement kiln or produce electricity,^105,106 abating/offsetting ∼2.4 MWh/t_Ca(OH)2 of the energy demand. This reduces the gross energy intensity, across all steps (Steps 0–3), resulting in a net energy intensity ranging between 2.0–2.8 MWh/t_Ca(OH)2 for different process configurations (Figure 8b,c). The HCl coproduct 0.1–0.3 mol/L is used internally for EDTA recovery and pH conditioning within the process (80 mol. %), whereas the surplus (20 mol. %) can be either concentrated and sold or neutralized using geological rock feedstocks prior to discharge.³⁵ Two management options for the carbonate stream (0.1 mol/L of NaHCO₃) are proposed: (i) discharge into the ocean or riverine discharge to ensure carbon storage under conditions of infinite dilution (La Plante et al.)^35,36 reserved ecosystemic considerations to be established at scale or (ii) concentration up to ∼0.7 mol/L NaHCO₃ to enable the recovery of “dilute soda” for utilization.¹⁰⁷ Of note, the NF separations implied by this process on account of strong Ca binding (by the chelator) are not susceptible to mineral scaling. However, if it does occur, a simple pH-swing for cleaning (e.g., using the surplus acid) has been shown to restore membrane performance, a standard operating process in desalination plants.¹⁰⁷

Figure 8.

(a) CO₂ evolved (process emissions) across different configurations. (b) Process water demand, (c) gross energy intensity, and (d) net energy intensity of the ZeroCAL process considering Steps 0–3 across three different configurations (C1, C2, and C3) that encompass single- or double-stage NF (i.e., to minimize CO₂ evolution), with or without process water recycling (i.e., to reduce the water demand and/or the non-electrolysis process energy) for an initial Ca-EDTA concentration of 100 mmol/L. Herein, in part c, electrolytic Ca(OH)₂ precipitation (Step 3) is estimated to have a gross energy intensity of ∼1.7 MWh/t_Ca(OH)2, while the remainder of the energy is attributed to “upstream” operations (Steps 0–2).

Further analysis of CO₂ evolution during the process indicates a vanishingly small CO₂-intensity—i.e., process emissions as low as 1.5 mol. % of the total mineralized CO₂ contained in the limestone, equivalent to ∼9 kg_CO2/t_Ca(OH)2, see Configuration C1—as long as dissolution is carried out at slightly alkaline pH (9.5) and two-stage NF is used to ensure superior Ca/CO₂ separation (Figure 8a). This configuration, however, implies a substantial process water and energy demand (Figure 8). Configuration C2 offers significant reductions of the energy demand by only using a single-stage NF system and minimal process water recycling (Figure 8d). Reducing the amount of process water recycling lowers the energy demand, a configuration of interest if seawater or saline groundwater is used as the electrolyte in near-coastal regions. In water-stressed areas, Configuration C3 offers the lowest process water demand by maximizing the amount of internal recycling (NF step 2a-ii) while increasing the energy demand and the amount of CO₂ evolved in the process.

Taken together, the ZeroCAL process ultimately offers >98% process-CO₂ emissions reductions while requiring ∼2 times the total energy demand of conventional lime manufacturing, or limestone decarbonization, i.e. typically within 1.0–1.4 MWh per t of PC (clinker),⁸⁻¹¹ quicklime (CaO), or portlandite (Ca(OH)₂) production.⁴⁻⁷ This energy demand, however, is determined based on the simple linear additivity of process unit operations. Although much work remains to integrate this multistep process, across unit operations effectively, preliminary process intensification (PI) studies indicate that the energy demand of the ZeroCAL process can be reduced by ∼30% across all noted configurations, resulting in near-parity with existing thermochemical methods for limestone’s decarbonation during PC production. As one example, at atmospheric pressure, Ca(OH)₂ decomposes into CaO at a temperature that is ∼250 °C lower than limestone. This allows for decarbonation processing to be completed in the preheater/precalciner such that the feed entering the kiln is ready for clinkering.

While there is a substantial demand for a finite albeit fast-growing supply of renewable energy, electrification allows a means for decarbonizing cement production while using Ca(OH)₂ as a zero-carbon emissions feedstock for existing cement plants, using adjacent limestone quarries, to produce PC—all without resorting to geological sequestration and its associated requirements of infrastructure, e.g., reservoirs, pipelines, compression stations, etc. That said, the ZeroCAL process does require substantial process water, which for near-coastal plants can be sourced from the ocean. Conveniently, multiple high-capacity cement plants are spatially distributed near coastlines and inland saline water sources, for instance, in the United States and Europe.^15,23 But, even plants distant from the coast often have access to substantial supplies of water, e.g., in the form of millions of cubic meters of “mine water” that rises from the water table over the course of quarrying operations and that is typically discharged as a waste. Such mine water is typically not saline, and would require NaCl dosing to be utilized within the paradigm of the ZeroCAL process to ensure valence compensation of discharged bicarbonate: 1 Na⁺ cation per discharged HCO₃^– anion. Of course, in such circumstances, it would be important to consider and design the process discharge in such a way that it does not affect the salinity of prevalent groundwater in the discharge vicinity, or to reuse the discharged water during subsequent production cycles.

Heat and power account for ∼30% of the cost of PC production,¹⁰⁸ and ∼90% and 10% of the energy requirements,^10,13 respectively. Their cost basis, however, is subject to change as renewable generation expands making renewable electricity cheap,¹⁰⁹ and fossil fuels eventually become supply constrained and expensive.^15,110,111 Additionally, PC decarbonization can benefit from grants, tax credit, and Buy Clean opportunities,¹⁵ which will make adoption more attractive. This is important since industrial decarbonization in the manner of the ZeroCAL process paves the way for^112−114 (i) a CO₂-free supply chain for traditional PC and lime production and (ii) opportunities to produce cementation agents based on CO₂ mineralization with an energy intensity comparable to PC manufacturing but with a >90% reduction in CO₂ intensity.^13,115−117 Importantly, the ZeroCAL approach also opens up new pathways for (i) brucite (Mg(OH)₂) production from abundant basaltic and magnesite rocks at an even lower energy intensity than Ca(OH)₂ production due to the more favorable thermodynamics of precipitation¹¹⁸ and (ii) carbon dioxide removal (CDR) using electrolytically produced, ultra-low carbon intensity portlandite and brucite precursors.¹¹⁷ Significantly, this latter concept also enables steel decarbonization by providing Mg(OH)₂ or Ca(OH)₂ as a slag-forming CO₂-free feedstock (in lieu of limestone) for blast furnace operations, while hydrogen can be used not only to power a blast furnace, but also as a reducing agent in the direct reduction of iron (DRI) process. More broadly, but at smaller scales, a zero-carbon lime is desirable for use in the energy industry,^119−122 soil and water,¹²² food,¹²³ pharmaceutical,^124,125 and cosmetic¹²⁶ sectors. Further advancement of the ZeroCAL process encompasses activities including (i) electrolysis efficiency enhancement via cell design and electrode development and (ii) the use of better/alternative chelators with a smaller gap between the pK_a of the pristine and complexed species to reduce the intensity of the pH-swing (i.e., to reduce acid–base demands), while facilitating Ca/CO₂ separation and chelator recycling. Why does all this matter? Because based on current estimates, when powered by renewable energy, the ZeroCAL process can achieve >99% process CO₂ emissions reductions for a net energy intensity of <2 MWh/t_Ca(OH)2, thus unlocking a near-NPV parity pathway for decarbonizing PC, concrete, and steel production globally.^127−129

6. Summary and Conclusions

The ZeroCAL process demonstrated herein establishes a near process-emissions-free pathway for decarbonizing portlandite and PC production, using limestone as a feedstock. In situ electrolytic acid/base generation enables a self-contained pH-swing process wherein EDTA-promotes CaCO₃ dissolution, while preventing CO₂ exsolution. Subsequent NF steps allow (i) effective Ca/CO₂ separation, (ii) process water recycling, and (iii) scalable discharge of CO₂ in the form of aqueous HCO₃^– at sufficient alkalinity such that CO₂ can be stored durably and permanently in the near-surface environment. The effective (∼100%) and cyclic use (complexation) and recovery (decomplexation) of EDTA and Ca/EDTA separation are demonstrated ensuring that, under relevant configurations, (sea)water, electricity, and limestone (and NaCl) form the only inputs of the process. Electrolysis of a Ca-enriched feedstream reveals that, at an optimal current/flow rate ratio, the net energy intensity of process for high-purity Ca(OH)₂ production at the current point in time, ∼2 MWh per t of Ca(OH)₂, is approaching similarity to conventional cement (PC) production. Importantly, electrification and hydrogen-based kiln heating of cement production create a new pathway for cement decarbonization that does not rely on geological sequestration—potentially simplifying PC decarbonization while mitigating the trajectory of ongoing and accelerating climate change.

Appendix

The Appendix includes additional data and details relevant to electrolysis, process stoichiometry, EDTA and CaCO₃ dissolution, membrane screening and performance, process water recycling and ocean carbon storage, EDTA recovery, Ca(OH)₂ electrolytic precipitation, and configuration-specific process conditions and carbon, water, and energy intensities.

A1. Electrolyzer Definition

A1.1. Step 0: Acid and Base Generation via Water Splitting

Figure A1.

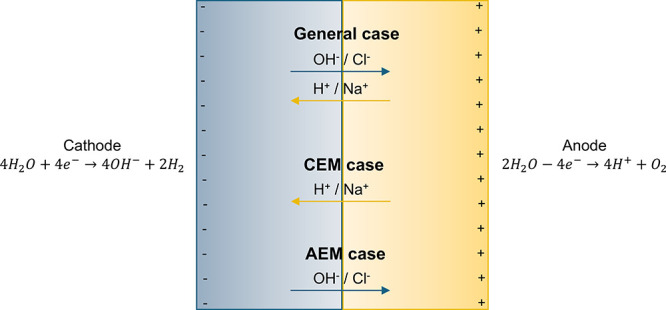
Schematic representation of the reactions and species migrations occurring in the electrolyzer. Species migrations are specified for the different types of membranes/separators that may be used to separate the anolyte and the catholyte, e.g., porous membrane (non-ion specific), cation exchange membrane (CEM), and anion exchange membrane (AEM).

Electrolytic water splitting in the flow electrolyzer considered herein follows the half-cell anodic (eq 1) and cathodic (eq 2) reactions:

A1

A2

The conductivity of the solution is a function of the presence of NaCl (∼0.5 mol/L; similar to seawater), which theoretically allows Na⁺ and/or Cl^– to act as charge compensators of the half-cell reactions by migration through the membrane separating the catholyte and the anolyte. Practically, the electroneutrality of both the catholyte and the anolyte is ensured by migration and diffusion of electroactive ions. Hence, solution-phase electroneutrality is assured by Na⁺ and H⁺ transfer from the anolyte to the catholyte and by Cl^– and OH^– from the catholyte to the anolyte.

The most general case considers the use of a porous membrane (i.e., a non-ion-selective membrane) to separate the anolyte and the catholyte. In this case, x is the number of moles of H⁺ crossing the membrane from the anolyte to the catholyte and y is the number of moles of OH^– crossing the membrane from the catholyte to the anolyte. The reactions happening in the anolyte and the catholyte, considering the species migrations (i.e., the charge carriers) can be described as follows:

Case 1: General cases (non-ion-selective membrane)

In most commercial cases, electrolyzers use ion-selective membranes (i.e., cation exchange membranes or anion exchange membranes). In those cases, the reactions are simplified, as only one type of ion can pass though the membrane:

Case 2: Cation exchange membrane (CEM, y = 0)

Case 3: Anion exchange membrane (AEM, x = 0)

Whether using one type of membrane or another depends on their efficiency for the process, as well as the electrical energy intensity reductions they allow. In the context of this study, electrolysis is considered for the general case (Case 1) which has been demonstrated at the pilot-scale. The overall reaction in the electrolyzer can be written as follows considering the two half reactions described above:

Case 1: General cases (non-ion-selective membrane)

The overall reaction depends on the ratio between H⁺/Na⁺ and OH^–/Cl^– migration through the membrane. A simplification can be made based on the following two hypotheses:

(1) The Peclet number in both cells favors migration by advection rather than diffusion.

(2) The Reynolds number is low enough so the solution inside one chamber cannot be homogenized by turbulence.

If those two conditions are met, which could be possible if the spacing between the electrodes is high enough and the flow rate low enough, then the H⁺ and OH^– produced at the electrodes should not be able to diffuse fast enough toward the membrane to be the charge carriers for the electroneutrality. In this case, only Na⁺ and Cl^– migration should be able to satisfy the solution electroneutrality. At greater pH gradients, the water-splitting ions can conduct more current via migration, and macroscopic charge neutrality can still be satisfied by counter-diffusion of the electrolyte ions through the diffusion layers. In both cases, the overall reaction may be simplified down to

A3

A1.2. Step 3: Ca(OH)₂ Precipitation

The addition rate of OH^– (in mol/L) in the flow electrolyzer catholyte can be calculated as described by eq 7. When portlandite precipitation attains equilibrium, the activities of the hydroxide and calcium ions in the effluent should ensure oversaturated conditions, i.e., the OH^– and the Ca²⁺ activity can be calculated by considering the K_sp of portlandite, such that

A4

where the {} indicate ion activities and K_sp = 5.2 × 10^–6 at p = 1 bar and T = 25 °C and

A5

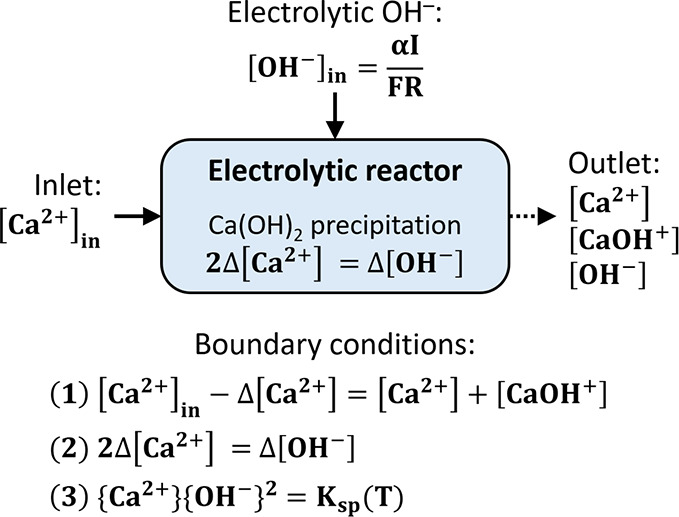
where k_CaOH⁺ is the equilibrium constant of the aqueous species CaOH⁺. From the boundary conditions shown in Figure A2:

A6

where [] indicates ion concentrations and γ indicates ion activity coefficients that can be calculated considering eq 2, such that

A7

and

A8

where α is the current efficiency ratio (0.9, unitless), I is the current (A, for constant current operations), F is Faraday’s constant (96485 s·A/mol), and S is the solution flow rate (L/s) through the electrolyzer. Substituting eqs A7 and A8 into eq A4:

A9

and by solving eq A9, eqs 10 and 11 are obtained.

Figure A2.

Schematic representation of the chemical boundary conditions considered in the flow electrolyzer.

A2. Process Stoichiometry

Table A1. Experimental Verification of Stoichiometries and Mass and Charge Balances.

process step	stoichiometric ratio (mol/mol)	mass balance (mol.)	charge balance
0 (anode)	H+/e– = 0.9a
0 (cathode)	e–/OH– = 0.9a
1a	NaOH/H4EDTA = 3.03model/2.78exp. ± 0.04 (pH 8.5)
	NaOH/H4EDTA = 3.08model/2.89exp. ± 0.03 (pH 9.0)
	NaOH/H4EDTA = 3.21model/3.07exp. ± 0.04 (pH 9.5)
1b	CaCO3/HEDTA3– = 1.0 ± 0.0
2a-i		1.1 ± 0.1	1.0 ± 0.1b
2a-ii		1.0 ± 0.1	1.1 ± 0.1b
2b-i	HCl/Ca-EDTA = 4.0 with final pH 1.82model/1.87exp. ± 0.09
3	NaOH/Ca(OH)2 = 2.0model/2.2exp. ± 0.3

^aFaradaic efficiency ratio (FE_R, unitless) assessed for pilot-scale 10 kW electrolyzers, while laboratory-scale reactors show 99.9% Faradaic efficiency.

^bRatio of positive and negative charges at each stream.

A3. EDTA and CaCO₃ Dissolution

Table A2. Time Required (in min) to Reach >95% Ca Extraction during the EDTA-Aided Calcite Dissolution for a System Where CaCO₃ (in mol) = 1.1 × EDTA (in mol).

	EDTA concentration (mmol/L)
pH	2	20	200
6	16 min	3 min	23 min
8	29 min	15 min	63 min
10	51 min	25 min	94 min

Figure A3.

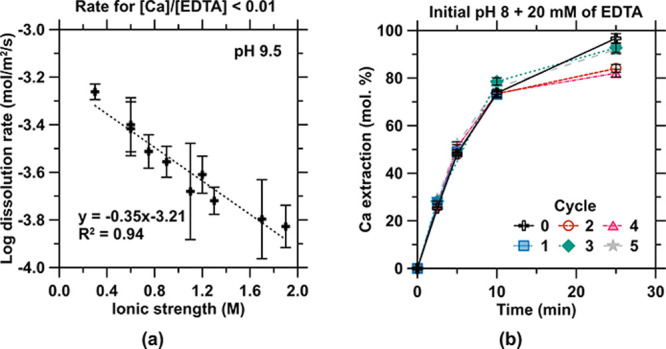
(a) Dissolution rate of calcite as a function of the solution’s ionic strength for a starting pH of 9.5. (b) Performance of the recovered EDTA in chelating Ca extracted from calcite (CaCO₃) compared to “pristine” AR-grade EDTA over 5 cycles of use and recovery.

A4. Membrane Screening and Performance

The NF membranes’ performance were assessed on the basis of: water recovery, normalized permeate flux, observed rejection, solute separation, solute mass transfer coefficient,⁵⁷ concentration polarization modulus,⁵⁷ Donnan partition coefficient in the case of monovalent permeation (NaHCO₃) in the presence of highly impermeable charged organic molecules (Ca-EDTA^2–),^91,92 real rejection, and pressure balance at increasing water recovery using the following equations:

A10

A11

A12

A13

A14

A15

A16

A17

A18

where V is the volume (m³) at water recovery j (%) or initial condition 0, A_m is the membrane active area (m²), Δt is the elapsed time (s), ΔP is the applied hydraulic pressure (Pa), x_i is species x_i, m_xi is the mass of species x_i, Sh is the Sherwood number (dimensionless), D_xi is the diffusion coefficient of species x_i (m²/s), d_h is the hydraulic diameter (m), v_Permeate is the permeate flow velocity (m/s), v_i is the number of charged groups of species i (unitless), [x_i] is the concentration of species x_i (M), ΔP_j is the applied hydraulic pressure, Δπ is the transmembrane osmotic pressure (Pa), ΔP_x is the cross-flow frictional pressure loss (Pa), J_w is the water flux (m³/s·m²), and A is the intrinsic water permeability (m³/s·m²·Pa).

A5. Process-Water Recycling and Ocean Carbon Storage

Figure A5.

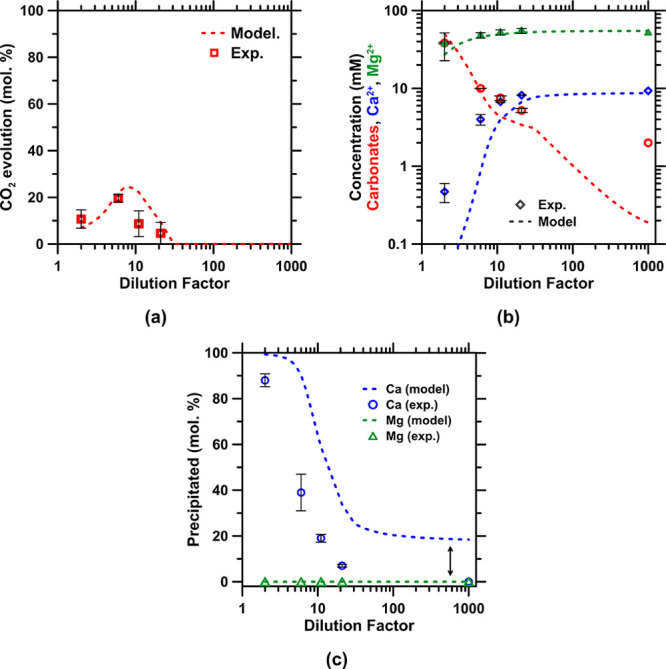
Effect of discharging a pH 9 stream containing 100 mmol/L aqueous Na-HCO₃ into seawater as a function of the considered dilution factor (the lines are thermodynamically modeled, and the points were acquired experimentally): (a) the carbonate evolution (as CO₂), (b) the concentration of Mg, Ca, and the carbonate species, and (c) the amount of Ca and Mg precipitated, highlighting the formation of calcium carbonate and the absence of hydrated magnesium carbonate formation in low dilution condition. The arrow indicates that the model fails to accurately represent the natural supersaturated state of seawater.

Figure A6.

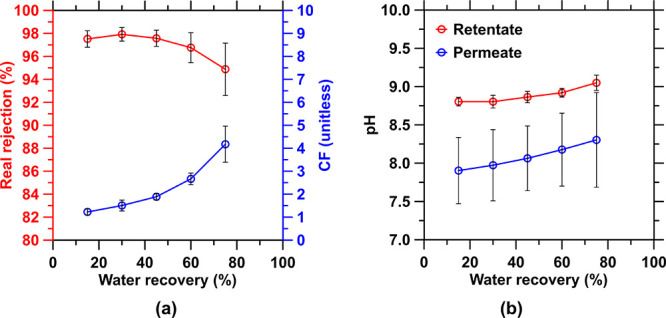
Performance of the NF90 NF membrane in Step 2a-ii on a Na-HCO₃-containing solution from the previous separation Step 2a-i: (a) instantaneous Na-HCO₃ real rejection and concentration factor (CF) in the retentate stream; (b) pH in the streams.

A6. EDTA Recovery

Figure A7.

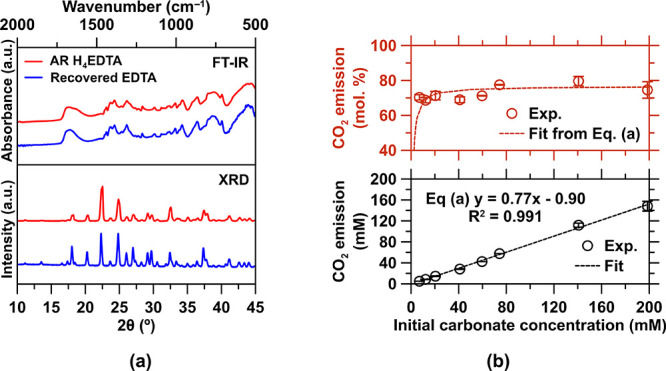
(a) XRD and FT-IR normalized patterns of the recovered EDTA precipitate and AR-grade H₄EDTA. (b) Conservative estimate of the dissolved carbonate degassed from solution (as CO₂) as a function of the initial carbonate concentration during the pH-swing from pH 8–10 to pH 2. No EDTA is present in the system, which removes the (low) dilution effect induced by EDTA titration.

A7. Ca(OH)₂ Electrolytic Precipitation

Figure A8.

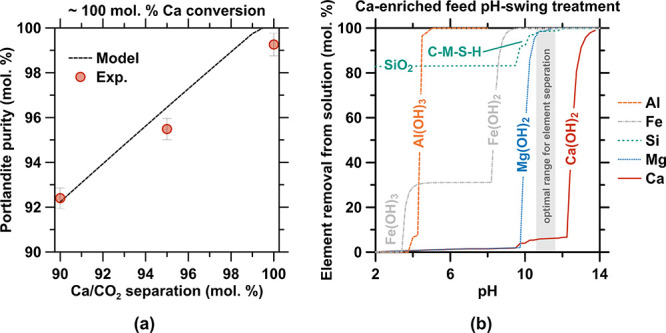
(a) Comparison between the experimental and modeled portlandite purity at ∼100% Ca conversion for different Ca/CO₂ separation values. (b) Contaminants (Al, Fe, Si, and Mg) removed from the Ca-enriched feed by precipitation of hydroxides and hydrated solids. SiO₂ is amorphous silica, and C-M-S-H is a calcium and magnesium containing silicate hydrate phase.

A8. Configuration-Specific Process Conditions and Carbon, Water, and Energy Intensities

Table A3. Summary of the Selected Main Process Conditions and the Achieved Efficiencies at Ambient (p, T) Conditions.

step	item	achieved efficiency (%)	general conditions	configuration	configuration-specific conditions	CO2degassing (mol. %)	process-water demand (t/tCa(OH)2)	energy intensity (MWh/tCa(OH)2)
0	electrochemical acid and base production	90a	optimal current-to-flow rate ratio for low energy intensity	C1		0	315	4.18
				C2, C3		0	315	4.07
1	Ca extraction	100	initial [EDTA] = 100 mmol/L, [Ca]/[EDTA] ≥ 1	C1	initial pH = 9.5	0	(135)b	(2.51)b
				C2, C3	initial pH = 9.0	∼1.0	(135)b	(2.44)b
2a	Ca/CO2 separation	98–99	XN45 membrane, 8 < pH < 10, 85% water recovery	C1	double-stage separation, minimal water recycling	0	115	0.45
		85–90		C2	single-stage separation, minimal water recycling	0	0	0.28
				C3	single-stage separation, maximal water recycling	0	0	0.96
2b	EDTA recovery	>99.9	tetra-protonation of EDTA, anolyte pH < 1	C1		<1.5	(180)b	c
				C2, C3		∼11.6	(180)b	c
3	Ca(OH)2 precipitation	55–90	[Ca] > 350 mmol/L	C1, C2, C3		0	0	(1.67)b
additional energy intensity from seawater softening				C1				0.13
				C2, C3				0.10

^aAt scale (10 kW pilot plant), while laboratory-scale reactors show 99.9% Faraday efficiency.

^bWater or energy intensity already encompassed by Step 0.

^cEnergy intensity already accounted for in Step 1, as acid and base are coproduced stoichiometrically.

Biographies

Adriano Souza Leão is a Ph.D. researcher at UCLA working on cement decarbonization technologies. He received a B.Sc. in Civil Engineering from the State University of Feira de Santana, during which he was awarded a scholarship to attend Colorado State University and the University of California, Davis, as a visiting international student. He then worked as a building design engineer. He received a M.Sc. in Industrial Technology Management from the SENAI CIMATEC University Center where he worked as a researcher in environmental modeling focusing on the life cycle assessment of industrial processes.

Marie Collin is a Staff Scientist at the Technische Universität München. She received her Ph.D. in Material Science from the Université de Montpellier. She worked at UCLA as a Postdoctoral Fellow and a Staff Scientist focusing on cement decarbonization and element recovery technologies.

Swarali Ghodkhande is a Ph.D. researcher at UCLA where she works on cement decarbonization and element recovery technologies. She received a Dual Degree (B.Tech + M.Tech) from Indian Institute of Technology, Bombay.

Arnaud Bouissonnié is a Staff R&D Engineer at UCLA’s Institute for Carbon Management. He received his Ph.D. in geochemistry at the University of Strasbourg (France). His work focuses on topics related to electrochemical control of thhe mineral dissolution and precipitation process with a focus on the carbonate–silicate system.

Xin Chen is a Staff R&D Engineer at UCLA’s Institute for Carbon Management. His works on electrochemical reactions are of relevance to the production, alteration, and corrosion of structural materials with applications in nuclear power generation, clean energy, and environmental technologies. He received his Ph.D. in Materials Engineering from the University of Illinois at Chicago.

Benjamin Malin worked as an Undergraduate Researcher at UCLA’s Institute for Carbon Management. He is currently a B.S. student in Environmental Science at Washington University in St. Louis.

Yiming Liu earned his M.S. and Ph.D. in Civil and Environmental Engineering at UCLA and a B.S. in Environmental Engineering from Tsinghua University. He is currently a Rice Academy Postdoctoral Fellow at Rice University. His interests encompass interfacial and membrane processes for water treatment, resource recovery, and desalination.

Geanna Hovey is a Senior Process Development Engineer at UCLA’s Institute for Carbon Management. She earned a BASc and MASc from the University of Waterloo and the University of Toronto, both in Environmental Engineering, and is a registered engineer in British Columbia. She has 10+ years of experience in process engineering, technology development, process scale-up, plant construction, and plant operations.

Jagannathan Govindhakannan is a Senior R&D Engineer at UCLA’s Institute for Carbon Management. He received his Ph.D. in Chemical Engineering from Texas Tech University. Prior to UCLA, he was a Lead R&D Engineer at Honeywell UOP for 9 years. Govind’s expertise is in the domains of technology scale-up, plant design, and chemical reaction engineering.

Erika La Plante is an Assistant Professor of Materials Science and Engineering at the University of California, Davis. She has a B.S. in Geology and a Ph.D. in Geochemistry (University of Illinois at Chicago) and previously held positions at UCLA and the University of Texas at Arlington. Erika applies her expertise in mineral dissolution and precipitation to discover new cements, extract critical metals, and sequester carbon dioxide.

David Jassby is a Professor of Civil and Environmental Engineering and Associate Director for Knowledge Discovery at the Institute for Carbon Management at UCLA. His research focuses on membrane separations, water treatment, electrochemistry, and resource recovery technologies.

Torben Gädt is a Professor of Chemistry at the Technical University of Munich where he holds the Chair in Construction Chemicals. His research focuses on cement, admixtures for concrete, and the chemistry of structural, inorganic materials.

Lorenzo Corsini is a scientist–entrepreneur with experience in building and scaling teams, technologies, and companies. He currently serves as the Principal Advisor of Equatic Inc. Previously, he cofounded and built PhagoMed, a biotech startup developing precision antibacterial drugs, which was sold to BioNTech in 2021. Prior to PhagoMed, he spent 9 years at the Boston Consulting Group. He has degrees in biochemistry and business administration and a Ph.D. in molecular biology.

Dante Simonetti is an Associate Professor of Chemical Engineering and Associate Director for Technology Translation at the Institute for Carbon Management at UCLA. He earned his B.S. and Ph.D. in Chemical Engineering from the University of Notre Dame and the University of Wisconsin—Madison, respectively. Prior to UCLA, he worked as an R&D Project Leader at Honeywell UOP. His research interests include reaction chemistry and engineering with a specific focus on reducing the carbon footprint of industrial processes and energy generation.

Fabian Rosner is an Assistant Professor of Civil and Environmental Engineering at UCLA. His research focuses on renewable energy and chemical technologies that offer environmentally benign solutions to meet the growing demands for energy and consumer goods. Prior to UCLA, Fabian was a Postdoctoral Fellow at Lawrence Berkeley National Laboratory. He earned an M.S. and Ph.D. in Mechanical and Aerospace Engineering, specializing in thermal sciences, from the University of California, Irvine. He also earned a B.S. and M.S. in Chemical Engineering from the Technical University of Munich in Germany.

Gaurav N. Sant is a Professor and the Pritzker Endowed Chair in Sustainability at UCLA. He holds faculty appointments in the Departments of Civil and Environmental Engineering, Materials Science and Engineering, and California Nanosystems Institute. He is the Director of UCLA’s Institute for Carbon Management, a cross-campus technology translation institute. His earned his B.S. (2006), M.S. (2007), and Ph.D. (2009), all in Civil Engineering, from Purdue University.

Author Contributions

^# A.L. and M.C. contributed equally as first coauthors.

The authors declare no competing financial interest.