Abstract
Background
High-dimensional omics data integration has emerged as a prominent avenue within the healthcare industry, presenting substantial potential to improve predictive models. However, the data integration process faces several challenges, including data heterogeneity, priority sequence in which data blocks are prioritized for rendering predictive information contained in multiple blocks, assessing the flow of information from one omics level to the other and multicollinearity.
Methods
We propose the Priority-Elastic net algorithm, a hierarchical regression method extending Priority-Lasso for the binary logistic regression model by incorporating a priority order for blocks of variables while fitting Elastic-net models sequentially for each block. The fitted values from each step are then used as an offset in the subsequent step. Additionally, we considered the adaptive elastic-net penalty within our priority framework to compare the results.
Results
The Priority-Elastic net and Priority-Adaptive Elastic net algorithms were evaluated on a brain tumor dataset available from The Cancer Genome Atlas (TCGA), accounting for transcriptomics, proteomics, and clinical information measured over two glioma types: Lower-grade glioma (LGG) and glioblastoma (GBM).
Conclusion
Our findings suggest that the Priority-Elastic net is a highly advantageous choice for a wide range of applications. It offers moderate computational complexity, flexibility in integrating prior knowledge while introducing a hierarchical modeling perspective, and, importantly, improved stability and accuracy in predictions, making it superior to the other methods discussed. This evolution marks a significant step forward in predictive modeling, offering a sophisticated tool for navigating the complexities of multi-omics datasets in pursuit of precision medicine’s ultimate goal: personalized treatment optimization based on a comprehensive array of patient-specific data. This framework can be generalized to time-to-event, Cox proportional hazards regression and multicategorical outcomes. A practical implementation of this method is available upon request in R script, complete with an example to facilitate its application.
Supplementary Information
The online version contains supplementary material available at 10.1186/s13040-024-00401-0.
Keywords: Adaptive-Elastic net, Elastic-net, High-dimensional data, Logistic regression, Multi-omics data, Priority-Lasso
Background
As technology progresses, there is a corresponding surge of high-dimensional omics data, such as genomics, transcriptomics, proteomics and metabolomics, which have widely been used to address disease diagnosis, prognosis, or possible therapies. Considering that each type of omics data contributes distinct layers of biological information, data integration serves as an efficient tool in multi-omics studies, not only providing a comprehensive understanding of the multifaceted complexity inherent in biological phenomena but also substantially improving our capabilities in elucidating disease mechanisms and identifying disease biomarkers [1, 2].
The size of these datasets, however, poses significant challenges in the realm of high-dimensional data analysis. Traditional statistical theory usually assumes that the sample size far exceeds the number of explanatory variables, allowing for the use of large-sample asymptotic theory to develop methods and assess their statistical accuracy and interpretability. However, this assumption does not hold for high-dimensional omics data, presenting a significant challenge in such contexts [3].
In this sense, omics data analysis involves transforming high-dimensional data into more informative, lower dimensions while identifying key features contributing to disease development and progression. To address this, dimensionality reduction and feature selection techniques, alongside pattern recognition methods, are employed. There are several approaches in the literature that deal with high-dimensional problems. Methods like the least absolute shrinkage and selection operator (lasso) [4] and its further versions (e.g., fused lasso [5], adaptive lasso [6], and group lasso [7]), as well as the elastic net [8], are examples of regularization methods suitable for feature selection. The lasso technique, introduced for estimating linear models, applies a penalty to the cost function. Unlike methods that concentrate on subsets, this method defines a continuous shrinking operation capable of producing coefficients exactly equal to zero [4], resulting in a sparse solution, effectively diminishing the number of variables involved. Despite its success in many applications, the lasso strategy struggles with variable selection when features are highly correlated, as it tends to select only one from a group, which is a limitation in applications like microarray data analysis where genes often interact in networks. To address this, Zou and Hastie [8] proposed the use of a penalty which is a weighted sum of the -norm and the square of the -norm of the coefficient vector . The first term enforces the sparsity of the solution, whereas the second term encourages a more balanced selection of correlated variables.
To further enhance elastic net effectiveness, more advanced methods introduced adaptive weights to improve the penalty function’s flexibility and accuracy. Zou and Zhang [9] considered the model selection and estimation in high dimensional data called the adaptive elastic net. This method combined the strengths of the quadratic regularization and the adaptive weights lasso shrinkage.
High-dimensional omics data presents both significant challenges and valuable opportunities for extracting meaningful biological insights. Nevertheless, high-dimensional omics data analyses traditionally model the relationships within a single type of omics data. Integrating multiple types of omics data, i.e. multi-omics data, provides a more comprehensive view of biological systems [10].
Using multi-omics data in prediction models is promising due to the unique and valuable information each omics type offers in predicting phenotypic outcomes. However, effectively integrating various omics data types presents several challenges. First, there is an overlap in the predictive information each data type provides. Second, the levels of predictive information differ between the “blocks” of variables (which may simply correspond to the type of data, e.g., the block of clinical variables or the block of gene expression variables) and depend on the particular outcome considered [11]. Third, the interactions between variables across different data types must be considered [12]. In recent years, different methods have been proposed to address this topic. Simon et al. [13] presented the sparse group lasso, a prediction method for grouped covariate data that automatically removes non-informative covariate groups and performs lasso-type variable selection for the remaining covariate groups. One limitation of using sparse lasso in multi-omics data applications is that it does not adequately account for the varying levels of predictive information across different data blocks. In contrast, the IPF-LASSO [14], a lasso-type regression method for multi-omics data, addresses this by assigning individual penalty parameters to various types of omics data, which allows for the incorporation of prior biological knowledge or practical concerns. One common issue for all variations of lasso, including IPF-LASSO, is instability. Even small modifications to the dataset may lead to big changes in the selected model. Vazquez et al. [15] modeled the relationship between phenotypic outcomes and multi-omics covariate data using a fully Bayesian generalized additive model. However, its high computational complexity can be a limitation for handling large-scale multi-omics datasets. Mankoo et al. [16] considered a two-step approach: in the first step, redundancies between the different blocks are removed by filtering out highly correlated pairs of variables from different blocks and in the second step, they applied standard regularized Cox regression [17] using the remaining variables. While the method is effective for integrating multiple data types and predicting clinical outcomes, it faces challenges with scalability and modeling complex interactions. Seoane et al. [18] used multiple kernel learning methods, considering composite kernels as linear combinations of base kernels derived from each block, where pathway information is incorporated in selecting relevant variables. However, it is computationally intensive due to multiple kernel learning and iterative optimizations. Similarly, Fuchs et al. [19] combined classifiers, each learned using one of the blocks. In the context of a comparison study, Boulesteix et al. [14] again consider an approach based on combining prediction rules, each learned using a single block: first, the lasso is fitted to each block and, second, the resulting linear predictors are used as covariates in a low-dimensional regression model. In addition to the approach mentioned above, Fuchs et al. [19] also consider performing variable selection separately for each block and then learning a single classifier using all blocks.
When considering prediction accuracy, it is important to acknowledge that medical experts often possess prior knowledge about the relevance of various variable sets. For instance, they might anticipate that specific clinical variables will have strong predictive power, whereas many gene expression variables might be less significant. Incorporating this expert knowledge can greatly enhance the construction of prediction models by ensuring that the most informative variables are given appropriate emphasis. Simon et al. [20] present the Priority-Lasso, a lasso-type predictive method for multi-omics data that differs from the approaches described above, distinct in its focus not primarily on prediction accuracy but applicability from a practical point of view. This method requires users to specify a priority order for the data blocks, often based on the cost of generating each data type. Blocks of lower priority are likely to be automatically excluded by this method, which should frequently yield prediction rules that are not only straightforward to implement in practical scenarios but also maintain a high level of prediction accuracy. The TANDEM approach [21], another related method, assigns a lower priority to gene expression data compared to other types of omics data. This strategy prevents the prediction rule from being overly influenced or dominated by gene expression data. The predictive capabilities of Priority-Lasso require further enhancement in light of the identified limitations associated with the standard Lasso method.
Building on the diverse methodologies applied to multi-omics data for enhancing phenotypic prediction, another pivotal aspect emerges: the critical evaluation of these models’ effectiveness. The challenge of accurately assessing model performance becomes particularly pronounced with imbalanced datasets. This imbalance presents a significant difficulty for most classifier learning algorithms, which typically assume a relatively balanced distribution of classes.
The complexity of this issue is primarily due to the inherent limitations of the most commonly used evaluation metrics, which may not always provide entirely reliable assessments in these scenarios. Since their introduction [22], sensitivity and specificity have become key metrics in evaluating diagnostic tests. However, they have limitations, particularly when the importance of sensitivity versus specificity is unequal. This issue is crucial in medical practices where different scenarios demand varying emphasis on either sensitivity or specificity [23]. Van den Bruel et al. [24] suggested that diagnostic test evaluations should thoroughly cover technical accuracy, diagnostic accuracy, patient outcomes, and cost-effectiveness. Sensitivity and specificity, therefore, need to be weighted according to their relevance in specific contexts. Pepe [25] and Perkins and Schisterman [26] developed methods to account for this issue, although accurate data on prevalence and misclassification costs can be challenging to obtain.
In addressing these challenges, it becomes imperative to adopt evaluation metrics that can accurately reflect the model’s performance in the context of imbalanced data. Traditional metrics often fail to provide a comprehensive view of how well a model handles minority class predictions, which is crucial in many clinical settings. To further refine the model assessment, measures specifically designed for imbalanced data sets were employed, including G-means [27], F-Measure, and Balanced Accuracy [28]. These metrics, tailored for imbalanced datasets, offer a nuanced view of a model’s effectiveness.
Additionally, using the glmnet package[29], which offers robust implementation of the lasso and elastic net regularization paths, the mean cross-validated errors (cvm) for each evaluated value of can be obtained based on various type measures such as AUC (Area Under the Curve) and classification error.
To overcome some of the gaps in the literature presented before, a new method is proposed: the Priority-Elastic net, which aims to integrate multi-omics and clinical data from patients belonging to different disease types. By improving upon the method of Simon et al.[20] with an elastic net penalty, this new approach contributes to more stable and accurate predictions in these complex datasets. Its moderate computational complexity, flexibility in incorporating prior knowledge, enhanced stability and accuracy in predictions make it a superior choice for many applications compared to the other methods discussed. Additionally, we have also implemented the Priority-Adaptive elastic net, which analyzes predictive performance by incorporating adaptive weights into the hierarchical structure.
Also, developing a customised optimization framework within the model is presented, enabling users to adjust the balance between sensitivity and specificity according to their specific requirements. Moreover, to present a medical application of this approach, the Priority-Elastic net is integrated with a regularized logistic regression model to improve predictions of binary outcomes in this study. The omics dataset comprising transcriptomics and proteomics data from gliomas, obtained from The Cancer Genome Atlas (TCGA) (http://cancergenome.nih.gov/), was used to illustrate the performance of the method proposed. Emphasis was placed on employing various measures and graphical performance assessments to effectively evaluate the model across different aspects of its predictive capabilities.
Methods
Regularized logistic regression
Logistic regression is a popular method for classifying problems in various fields of science, particularly in medicine. It models the relationship between one or more independent variables and a binary outcome variable.
Let represent the observed value of the independent variable j measured from subject i, , where n is the number of individuals and p the number of independent variables. The vector of the independent variables for subject i is defined by the p-dimensional vector . The observed response variable represents the value of the dichotomous outcome variable (absence vs presence of the outcome) for subject i. The observed value of the outcome variable, , corresponds to a realization of the random variable .
The logistic regression model is given by
| 1 |
where denotes the probability that subject i belongs to class 1 (that is, the outcome is present), given the vector and class 0 otherwise, and are the regression coefficients associated to the p independent variables. Equation (1) is equivalent to fitting a linear regression model in which the dependent variable is replaced by the logarithm of the odds through the logit transformation given by
| 2 |
assuming the logit transformation of the outcome variable has a linear relationship with the predictor variables.
The parameters of the logistic regression model are estimated by maximizing the respective log-likelihood function, defined as
| 3 |
A common challenge encountered in logistic regression, especially when dealing with omics data, is that data has more variables p than the sample size n , a scenario known as high dimensionality. The key goal in high-dimensional data analysis is to select a set of explanatory variables that not only simplifies the interpretation of the model but also enhances classification accuracy. However, it is not always true that this process will enhance the accuracy. While reducing the number of variables can mitigate overfitting by eliminating noise and irrelevant features, it can also lead to underfitting if important variables are excluded [8]. To achieve this objective, a regularisation technique is often employed [30]. Regularization techniques add a penalty term to the loss function, which helps get more accurate predictions by preventing overfitting. Recently, there has been an increasing focus on using regularization techniques in logistic regression models, and several regularization terms have been discussed in the literature [4, 30–32]. These approaches aim to identify the most relevant explanatory variables in classification problems, proposing various penalized logistic regression methods. However, different forms of penalty terms vary according to the application’s specific needs.
Regularized logistic regression incorporates a non-negative regularization component into the negative log-likelihood function defined above (expression (3)), such that the size of coefficients in high-dimension can be controlled. Hence, the definition of regularized logistic regression is formulated as follows:
| 4 |
where denotes the regularization (or penalization) term here constructed from a -norm, , of the vector . This term is weighted by the tuning parameter , a non-negative value that determines the balance between fitting the model to the data and the impact of regularization. Essentially, it regulates the degree of shrinkage applied to the estimates of the parameters.
In this context, the vector of parameters is estimated by minimizing the penalized negative log-likelihood function,
| 5 |
When is set to 0, the model yields the Maximum Likelihood Estimation (MLE) solution. On the other hand, as increases, the regularization term becomes more dominant in determining the coefficients’ estimates.
The least absolute shrinkage and selection operator (lasso) relies on the -norm penalization term [4], leading to the following estimate for the vector ,
| 6 |
Although the lasso has succeeded in many situations, it has some limitations. One such drawback is that it needs to be more robust to high correlation among explanatory variables and randomly chooses one of these variables and ignores the rest. Another drawback of the lasso is that in high dimensional data, when , it chooses at most n explanatory variables. In contrast, the final model may have more explanatory variables than the number of observations, n. These limitations make the lasso an inappropriate variable selection method in some situations.
Elastic net is a regularization method for variable selection, which was introduced by Zou and Hastie [8] to deal with the drawbacks of lasso. The elastic net penalty combines two different regularizers: the Ridge penalty (-norm regularization), which shrinks the coefficients and helps to reduce the model complexity, and the lasso (-norm regularization), which can lead the coefficients to zero, therefore performing feature selection. In this situation, the vector of the unknown parameters is estimated as follows,
| 7 |
with controlling the balance between the lasso and Ridge penalties and controlling the strength of the penalty.
Another direction of improvement is to correct bias in estimation by adding weight for each , which corresponds to different amounts of shrinkage, to the regression coefficients. The adaptive elastic net was introduced by Zou and Zhang [9] and Ghosh [33], combining the norm regularization with adaptive weights to enhance estimation accuracy.
In this context, we start by computing the elastic net estimates as defined in (7), and then adaptive weights are constructed by
| 8 |
where is a positive constant. Using for calculating adaptive weights in the Adaptive-Elastic net is a common and effective choice because it provides a balance between penalizing weak predictors and retaining strong ones. We know the elastic net naturally adopts a sparse representation. One can use to avoid division by zero [9].
The regularized logistic regression using the adaptive elastic net (AElastic) of is defined by introducing adaptive weights to the penalty term, where each coefficient is scaled by a weight , allowing the regularization strength to vary depending on the importance of each feature. More precisely,
| 9 |
The topic of incorporating high-dimensional omics data into predictive models has gained significant attention over the past few decades. However, a common limitation of most of these methods is their inability to accommodate different types of variables within the same dataset. Often, these variables are organized in distinct blocks, such as clinical and several layers of omics information data. While some existing methods leverage these block structures, they tend to be computationally demanding.
As discussed in the “Background” section, integrating different omics data has gained great importance in recent years, with regularization-based methodologies standing as promising in the field. The details of our proposed approach are presented next.
Priority-Elastic net
In recent years, there has been considerable focus on including high-dimensional omics data in predictive models, extending beyond using a single data type to encompass various types of data, such as clinical data, gene expression data, methylation data, among others [12].
Within this context, the Priority-Lasso method has emerged as a practical analysis strategy to build regression models based on lasso [4], utilizing a hierarchical approach to process multi-omics data [20]. This method is specifically designed to handle distinct types of variables as those present in high-throughput molecular data, setting it apart from standard lasso techniques that do not account for the group structure in datasets. However, a significant challenge with Priority-Lasso is its inability to effectively manage correlated variables. In contrast, the elastic net encourages a grouping effect, where strongly correlated predictors are kept in the model [8]. Integrating principles from the elastic net could potentially enhance Priority-Lasso’s performance by allowing it to manage correlated variables more effectively.
To overcome this issue, we propose an extension to this method, the Priority-Elastic net applied to the binary Logistic regression case. While Priority-Lasso incorporates hierarchical and structural information among the predictors, the Priority-Elastic net further enhances this framework by integrating the elastic net penalty. This integration enables more effective management of correlated predictors by incorporating the dual regularization strengths of elastic net [8]. By doing so, the Priority-Elastic net ensures a more robust and interpretable variable selection. This approach enhances the overall stability and accuracy of the model, making it more effective for complex datasets with high-dimensional and correlated predictors.
Let be the observed measurement for independent variable j from individual i, where , with n being the total number of individuals and p the number of independent variables. The vector represents the set of independent variables for individual i. The binary response variable , taking values in , denotes the dichotomous outcome for individual i; represents the probability that individual i falls into class 1 given their independent variables vector .
The model categorizes the predictors into B blocks, with the observations of the variables from block b for subject i being represented as , for and for . Just as is defined, is the regression coefficient of the jth variable from block b, with j extending from 1 to . Correspondingly, denotes the respective estimated value.
Consider as a reordering of the sequence , signifying the priority order of blocks, where represents the index of the block with highest significance and denotes the one of least priority. Subsequently, a hierarchical method is employed to construct the predictive model, adhering to this established order of block importance.
First, a Logistic regression model with elastic net regularization is fitted to block , the block with the highest priority. The objective is to estimate the coefficients . This is achieved by minimizing
| 10 |
Building upon the expression in Eq. (10), to establish the framework for the Priority-Adaptive elastic net we proceed by calculating the adaptive weights for the variables based on the assigned priority of the block (in this case, the first priority, ). Initially, we compute the adaptive weights, denoted as introduced earlier in (8), for each variable based on the specified priority of the block. Once these weights are determined, we integrate them directly into the penalty term of the elastic net regularization according to Eq. (9).
The linear predictor fitted in this step is given as:
| 11 |
Next, the elastic-net is applied to the block with the second highest priority, using the fitted linear predictor from the first step as an offset. The goal is to determine the values of which are the coefficients corresponding to the predictors within the second priority block, . These coefficients are identified by minimizing a specified criterion, detailed as follows:
| 12 |
In the process of estimating coefficients with the adaptive elastic net penalty as part of the priority algorithm, it is essential to adjust this equation to incorporate the adaptive weights associated with the second priority block into the penalty term, following the structure of Eq. (9).
The linear predictor for the second step, , is calculated by combining the offset from the first step, , with the sum of the products of the estimated coefficients for the second priority block, , and their corresponding predictors. This is formally represented as:
| 13 |
Then similarly, the model is fitted to the block with the third highest priority, using the linear score from the second step as offset. All remaining blocks are treated in the same manner.
| 14 |
where and .
When the fitting is done until the block , we obtain the set of the coefficient estimates for and the final fitted linear predictor becomes
| 15 |
The final Priority-Elastic net Logistic regression model, after processing all B blocks, is given by the logistic function applied to the sum of linear predictors from each block. For subject i, the probability of the outcome being 1 is modeled as:
| 16 |
Given the linear predictor , its over-fitting might lead to an underestimation of the influence of the second block of data, . This occurs when is utilized as an offset in further modeling stages, potentially masking the variability in that could be explained by .
To mitigate this issue, the proposed solution involves cross-validation. The dataset S is divided into K approximately equal parts, . For each partition k, the Elastic Net coefficients are estimated using all data except (denoted as ). For each element i in , a cross-validated offset is computed:
| 17 |
Consequently, we recommend the computation of cross-validated estimates, , for the offsets analogously to the first step. This approach is similarly applied to the subsequent groups, continuing in this manner up until the final fit.
The final model of Priority-Elastic net Logistic regression is a culmination of the sequential fitting process across all prioritized blocks. Each block’s contribution is adjusted using cross-validated offsets to mitigate over-fitting. The Priority-Elastic net algorithm was developed by modifying and enhancing functions from the prioritylasso package in R software to create a more specific approach for implementing the Priority-Elastic net methodology.
This function has the option cvoffset, where we select whether to use the cross-validated offsets or the standard offsets estimated without cross-validation. Furthermore, the Priority-Elastic net function includes a default argument for implementing the adaptive-elastic net within the priority framework, facilitating a more flexible approach to model fitting. The detailed algorithm is described in Algorithm 1.
Algorithm 1 Priority-Elastic Net with Cross-Validated Offsets for Logistic Regression
Performance metrics
The methods cited above estimate the probability of an individual belonging to class 1 (when the outcome is present). To construct a binary diagnostic test tool, one must establish a threshold that classifies the individual into class 1 if its estimated probability is above the threshold and into class 0 otherwise. The optimal threshold would ideally maximize the correct classification of the individuals, that is, sensitivity (true positives rate) and specificity (true negatives rate). Unfortunately, sensitivity and specificity are inversely related because when one measure increases, the other decreases [34]. Additionally, in most situations, diagnostic tests lead to misleading classifications associated with false positives and false negatives. To gain an overall understanding of the model’s performance, researchers typically plot the ROC curve, which maps sensitivity against 1-specificity for all possible values of the threshold. The corresponding Area Under the Curve (AUC) is a widely used summary measure in the literature for this purpose [35].
Depending on the problem under consideration, the error of wrongly classifying a patient as belonging to class 1 (positive for the disease under consideration) might be more or less serious than wrongly classifying a patient as class 0 (negative for the disease under consideration). In this context, several approaches to determining the best cut-off point have appeared in the literature. In this study, we employ Youden’s J method to identify the optimal threshold [36].
Youden’s J method defines the optimal threshold as the point that maximizes the Youden function, which is calculated as the difference between the true positive rate and false positive rate across all possible cut-off points, The Youden function, J(c), is thus defined as:
| 18 |
where , represent the sensitivity and specificity of the test at the cut-off point , respectively. It can be proved that . The optimal cut-off point, denoted as , is the value c that maximizes the expression (18) over all possible cut-off points.
Based on the optimal threshold obtained from the Youden function, a set of measures is derived to evaluate the predictive model’s performance in distinguishing between classes. The most common measures are sensitivity, specificity, false positive rate, and false negative rate. In this study, we will also compute a few combined performance measures appropriate to imbalanced datasets, namely F-Score, G-mean, and balanced accuracy.
- F-Score: it represents the harmonic mean between sensitivity and precision,
where (or positive predicted value) represents the probability of the diagnostic test identifying diseased individuals among those whose test results predicted positive outcomes at the optimal threshold, . - The Geometric Mean (G–Mean) measures the balance between classification performances on both the majority and the minority classes. It takes the square root of the product of sensitivity and specificity [27],
- The Balanced Accuracy (BAcc) corresponds to the average between the sensitivity and the specificity, which is more appropriate for imbalanced datasets than the usual accuracy measure [28]. It is defined in the following way,
In addition to these performance metrics, it is also important to evaluate the statistical significance of a classifier’s accuracy. A statistical measure often used for this purpose is the Null/No Information Rate (NIR) [37]. The NIR assesses whether the accuracy of a classification system is significantly better than a baseline, such as a random classifier, or it always predicts the most frequent class. This method helps determine whether a classifier’s performance is genuinely effective or due to chance. The NIR test uses a one-sided binomial test to calculate the p-value, indicating the probability that the observed accuracy is significantly higher than the baseline. This statistical test is implemented in the caret package in R, which includes functions to compare the observed accuracy to the NIR and determine the significance of the classifier’s performance [38].
Results and discussion
To illustrate the challenges associated with handling high-dimensional multi-omics data, an oncological dataset available at The Cancer Genome Atlas (TCGA) (http://cancergenome.nih.gov/) was used. The TCGA collects information on high-quality tumor samples from clinical studies and makes the annotated datasets available to the scientific community. Glioma, the most common brain tumor in adults, was the oncological disease chosen for illustrating the performance of the proposed method, Priority-Elastic net. The glioma data were collected by the TCGA-LGG and TCGA-GBM projects, which we combined into a unique PanGlioma dataset.
The LGG and GBM datasets were downloaded by (http://firebrowse.org/, a platform that provides access to terabytes of data and nearly a thousand reports. Clinical data from LGG and GBM, including the assigned diagnosis of each tumoural sample (one per patient), was acquired through the getFirehoseData function from RTCGAToolbox package [39]. We have downloaded the latest Firehose data release available, as it coincides with the latest clinical data available at the GDC Data Portal [39].
This approach allowed us to conduct a comprehensive analysis, leveraging the combined data to better understand glioma biology and improve the robustness of our findings.
In order to integrate multi-omics data, RNA sequencing (RNA-Seq) gene expression and protein expression quantification data were considered. Clinical information was also added to the analysis. For this purpose, five features were considered: age, gender, race, ethnicity, and radiation therapy. Radiation therapy, one of the major modalities of cancer therapy, plays an important role in integrated multimodality treatment for both low-grade gliomas [40, 41] and GBM [42]. Sex, race, and ethnicity are contributing factors to the incidence of glioma [43], as survival rates following a diagnosis of brain tumors have been shown to vary based on these factors.
The glioma RNA-Seq gene expression profiles were extracted from the TCGA-GBM [44, 45] and TCGA-LGG [46] projects, which classify glioma patients based on the 2007 WHO classification into two categories: GBM and LGG. The LGG includes samples of astrocytoma, oligodendroglioma, and oligoastrocytoma. To ensure that both datasets reflected current understanding, we updated it to align with the 2021 WHO classification and assigned every sample with the corresponding glioma type based on its molecular characteristics [47]. In particular, according to the latest guidelines [48], samples with IDH-wildtype status coupled with specific molecular or histological features were classified as glioblastoma, while IDH-mutant cases were assigned to astrocytoma or oligodendroglioma based on the absence or presence of 1p/19q codeletion. This resulted in some changes in diagnostic labels compared to the one provided by the TCGA clinical dataset (where glioma classification is solely based on histology).
In the preprocessing of RNA-Seq (transcriptomics) data, a base-2 logarithm transformation was applied to the expression values across all samples. This transformation stabilizes the variance across the range of expression levels, thereby enhancing the data’s comparability and interpretability.
The downloaded proteomics dataset passed through a normalization process subtracting the mean value over variables and samples, as described a:(https://bioinformatics.mdanderson.org/public-software/tcpa/). These transformations reduce the variability in the proteomics dataset and introduce negative values. To avoid different normalization affecting the results, we reproduced the same normalization steps for transcriptomics data, obtaining comparable values between the two omics datasets.
The proteomics and transcriptomics datasets were integrated by concatenating their features, resulting in a combined Transcriptomic-Proteomic dataset. The combined Transcriptomic-Proteomic dataset contains 465 samples, each characterized by 174 proteomic features and 145 transcriptomic features. The primary goal of combining these datasets was to create a unified omics dataset, which allowed us to match and find intersections with the clinical data, facilitating a more robust and holistic analysis. This dataset is further stratified into three subgroups corresponding to distinct glioma subtypes, yielding 206 astrocytoma, 116 (GBM), and 143 oligodendroglioma samples across both proteomic and transcriptomic data.
Subsequently, we matched the 465 samples from the combined Transcriptomic-Proteomic dataset with a set of 1110 clinical samples, ensuring alignment based on the exact patient ID across both datasets. This step was crucial for integrating comprehensive clinical information with molecular data, enabling a more detailed and patient-specific analysis.
In analyzing the dataset, we encountered missing values across the clinical dataset, indicative of instances where data were not available, recorded, or relevant. For the clinical dataset, several features presented missing values. After accounting for these missing values, the dataset was consolidated to 406 samples, reducing 59 samples from the initial tally of 465.
For this study, gliomas were divided into two groups. The first group, referred to as class 1, consists of 99 samples of GBM. The second group, designated as class 0, includes 307 samples of LGG, specifically astrocytoma or oligodendroglioma. This classification allows for a detailed exploration of the distinct biological and clinical characteristics inherent to each group, facilitating targeted analyses and potentially revealing differential patterns in prognosis, treatment response, and molecular profiles.
To comprehensively analyze these datasets, various scenarios were considered, prioritizing different data blocks. The details of these scenarios are elaborated in the next subsection.
Finally, the Priority-Elastic net method was used for dimensionality reduction across the comprehensive multi-omics dataset previously described. This innovative approach integrates hierarchical regression techniques with the robustness of elastic net regularization, sequentially addressing variable blocks in a prioritized manner.
The choice of the parameters used for the proposed method was performed as follows. A cross-validation procedure was used to optimize , considering a training set composed of 75% of samples and 10 folds. For the parameter, values between 0.1 and 1 were considered.
We defined six predictive models across three diverse scenarios by the Priority-Elastic net approach, and we compared the results with those obtained by the Priority - Adaptive elastic net and Priority-Lasso techniques. The comparison focused on two critical aspects: the selection of variables integrated into each model, discussed in “Priority-Elastic net models” section, and their predictive accuracy, evaluated in the “Prediction accuracy” section, which was assessed by splitting the data into training and test sets.
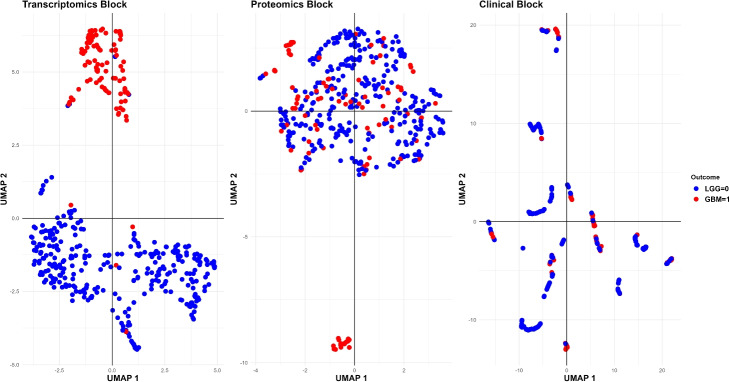
In the “UMAP-based validation” section, the multi-omics glioma data was visually inspected in a 2-dimensional space generated by the Uniform Manifold Approximation and Projection for Dimension Reduction (UMAP) method as a matter of validation of the Priority-Elastic net omics contributions. It is important to note that the construction of these models proceeded without imposing constraints on the number of variables incorporated, ensuring a comprehensive analysis.
The Priority-Elastic net algorithm was developed in software R [49], as well all the analysis, using packages UMAP[50], ggplot2[51], glmnet [29] and prioritylasso [20].
Priority-Elastic net models
The Priority-Elastic net technique was employed on the glioma dataset, which, as detailed before, consists of 406 samples across three distinct scenarios that vary based on the organization of data blocks. We also considered the algorithm with Adaptive-Elastic net penalty, and the results are presented for all scenarios in the supplementary information (Fig. 4). It is important to note that the model configuration remained the same for the Adaptive-Elastic net penalty in our Priority framework.
In each scenario, the minimum strategy coupled with 10-fold cross-validation was used to select the penalty parameter at every stage.
Each data type was attributed a different block number. Below is the description and assigned priorities for each of the three different blocks:
Block 1: 5 clinical variables measured at different scales;
Block 2: 174 continuous proteomics variables, including concentrations and phosphorylation states of various proteins
Block 3: 145 continuous RNA-seq variables represent the expression levels of the genes coding for the proteins present in the proteomics dataset, indicating the activity of these genes in each sample.
Note that the block of the clinical variables (Block 1) was not penalized when placed in priority 1, ensuring that the clinical predictors were considered without any regularization constraints. Nonetheless, we also explored and presented outcomes derived from applying penalization to this block, followed by a discussion comparing these results (Scenario B).
Next, three different scenarios, based on different block priority orders, were considered. Each scenario considers one block as the first and analyzes the model’s response to different prioritizations of the other two blocks. Consequently, every scenario is further divided into two cases of study, which explore alternative hierarchies of feature blocks. This approach allows us to evaluate the robustness of model outcomes against different prioritization schemes.
Scenario A
In the first scenario, our analysis encompasses two models differentiated by their prioritization of variable blocks, where block 2 (proteomic dataset) is prioritized first. The two different models are designed to test the impact of varying block prioritizations on model performance, which are described next:
Model 213, assigns precedence to block 2, followed by block 1, and ultimately block 3, reflecting a hierarchical approach to feature consideration based on predetermined criteria.
Model 231, conversely, prioritizes block 2 initially, then block 3, and finally block 1.
Scenario B
In the second scenario, the clinical variables (block 1) were the block with the highest priority. For this case, two approaches are considered. First, block 1 is not penalized (np), but the offsets were cross-validated, and second, block 1 is penalized (p).
Building upon the established framework, we introduce two distinct models, Model and Model , each characterized by a unique hierarchy in variable prioritization reflective of their strategic approach to predictive analysis:
Model assigns the highest priority to block 1, then to block 2, and ultimately to block 3;
Model places block 1 at the forefront, proceeds with block 3, and then concludes with block 2.
Scenario C
The third scenario evaluates the prioritization of block 3 within two distinct frameworks:
Model 321 prioritizes block 3, then moves on to block 2, and finally focuses on block 1.
Model 312 gives priority to block 3, followed by block 1, and lastly targets block 2.
Assessing optimal parameters
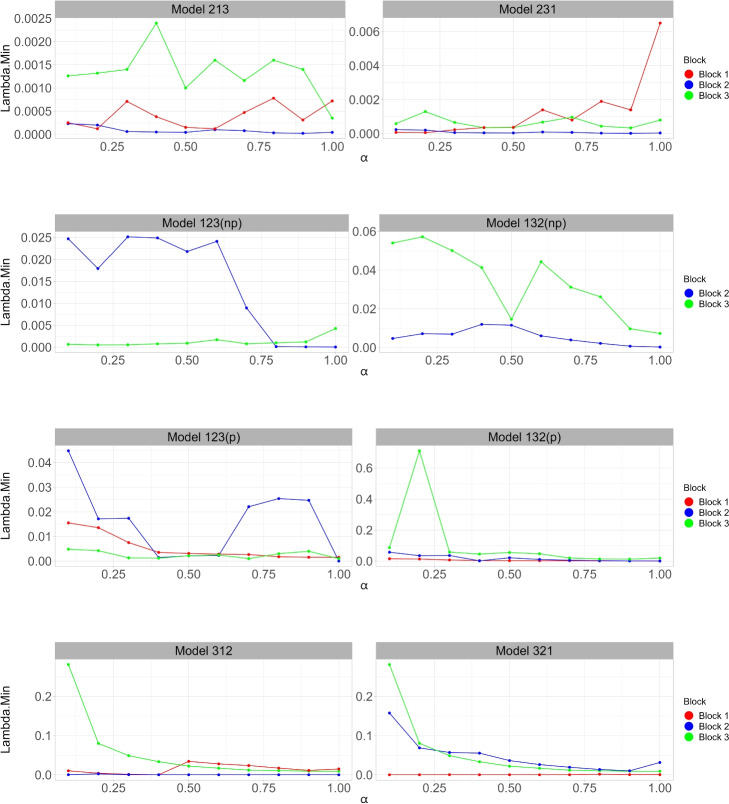
Figure 1 shows the relationship between the optimal tuning parameter (y-axis) and the elastic net mixing parameter (x-axis) across different blocks in several models (scenarios A, B, and C per lines). Ten-fold cross-validation was used to calculate the best lambda, which leads to the minimum mean cross-validated error for each unique model. The models differ in prioritizing different blocks, with three lines corresponding to separate blocks.
Fig. 1.
Comparison of the optimal tuning parameter values across varying parameters for scenarios A, B, and C. The x-axis represents the weight, which determines how much weight is given to the Lasso or Ridge regression. The y-axis denotes the corresponding , which is the lambda with the minimum cross-validated errors. Different colored lines represent different blocks (Block 1, Block 2, and Block 3), showing how varies across these blocks for each scenario
Furthermore, we permit including a maximum number of variables equivalent to the total count of variables across blocks 1-3. This approach aligns with our methodology of not imposing a limitation on the variable count for blocks 1-3 within the model framework.
In the presence of highly correlated variables, Priority-Lasso ( i.e., the model with ) tends to select one variable from a group of correlated variables and ignore the others. Priority-Elastic net, on the other hand, can select groups of correlated variables, which is often more desirable in capturing the underlying structure of the data. This capability of the Priority-Elastic net to accommodate correlated variables leads us to further consider the subtleties of how changes in and influence our model selection and the importance of individual predictors.
Notably, for most models, there was a tendency for to decrease as increases, suggesting that as the model shifts from ridge-like (lower ) to lasso-like penalties (higher ), the regularization strength required to minimize the mean cross-validated error. This effect was more pronounced in certain blocks, highlighting the varying importance of predictors depending on the degree of regularization. Additionally, some models, such as 123(p) and 132(p), show a sharp drop in around , indicating a transition point where the balance between ridge and lasso penalties significantly influences predictor selection and model performance.
Importantly, the optimal combination of and for each model plays a crucial role in balancing predictive accuracy against model simplicity. The observed trends and variations in with different values aid in selecting the most appropriate model configuration for our data. This selection process is essential, especially when dealing with complex data structures where the right balance can significantly enhance model performance and interpretability.
Prediction accuracy
To gain an overall understanding of the model’s performance, several performance metrics were presented. The metrics considered included the balance accuracy [28], F-Score and G-mean [27]. In addition to these metrics, the statistical significance of a classifier’s accuracy was evaluated using the Null/No Information Rate (NIR) [37] to assess performance against a baseline. Furthermore, the number of misclassifications (Misc.), defined as the sum of false positives (FP) and false negatives (FN), was also considered. These metrics were assessed on both the training and testing datasets to ensure a thorough evaluation of the model’s effectiveness.
Tables 1, 3, 5 and 7 present the performance metrics for train and test sets, including 95% confidence intervals, as varies. Tables 2, 4, 6 and 8 show the number of misclassifications (Misc., FP + FN) and the p-values for the corresponding values.
Table 1.
Comparison of performance metrics for Model 213 and Model 231 across different values (with 95% CI)
| Balanced Accuracy (0.95% CI) | F-Score (0.95% CI) | G-Mean (0.95% CI) | ||||
|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |
| Model 213 | ||||||
| 0.1 | 0.9624 | 0.9680 | 0.8787 | 0.9318 | 0.9617 | 0.9675 |
| (0.9447, 0.9793) | (0.9397, 0.9897) | (0.8182, 0.9343) | (0.8718, 0.9767) | (0.9430, 0.9791) | (0.9378, 0.9896) | |
| 0.2 | 0.9554 | 0.9628 | 0.8592 | 0.9213 | 0.9543 | 0.9620 |
| (0.9369, 0.9737) | (0.9329, 0.9874) | (0.7933, 0.9147) | (0.8571, 0.9714) | (0.9348, 0.9733) | (0.9306, 0.9877) | |
| 0.3 | 0.9507 | 0.9574 | 0.8467 | 0.9111 | 0.9494 | 0.9565 |
| (0.9302, 0.9710) | (0.9286, 0.9840) | (0.7794, 0.9091) | (0.8421, 0.9663) | (0.9276, 0.9706) | (0.9258, 0.9839) | |
| 0.4 | 0.9389 | 0.9415 | 0.8169 | 0.8817 | 0.9369 | 0.9397 |
| (0.9167, 0.9606) | (0.9076, 0.9725) | (0.7442, 0.8827) | (0.8052, 0.9438) | (0.9129, 0.9598) | (0.9029, 0.9721) | |
| 0.5 | 0.9319 | 0.9362 | 0.80 | 0.8723 | 0.9294 | 0.9339 |
| (0.9091, 0.9548) | (0.8990, 0.9674) | (0.7206, 0.8671) | (0.7913, 0.9357) | (0.9045, 0.9537) | (0.8933, 0.9668) | |
| 0.6 | 0.9249 | 0.9362 | 0.7838 | 0.8723 | 0.9218 | 0.9339 |
| (0.8991, 0.9502) | (0.90003, 0.9691) | (0.7015, 0.8590) | (0.7954, 0.9369) | (0.8934, 0.9489) | (0.8944, 0.9686) | |
| 0.7 | 0.9225 | 0.9362 | 0.7785 | 0.8723 | 0.9192 | 0.9339 |
| (0.8976, 0.9460) | (0.9011, 0.9659) | (0.701, 0.850) | (0.7945, 0.9350) | (0.8918,0.9445) | (0.8957,0.9653) | |
| 0.8 | 0.9272 | 0.9362 | 0.7891 | 0.8723 | 0.9244 | 0.9339 |
| (0.9028, 0.9509) | (0.901, 0.9675) | (0.7119, 0.8591) | (0.7954, 0.9362) | (0.8976, 0.9497) | (0.8944, 0.9669) | |
| 0.9 | 0.9295 | 0.9255 | 0.7945 | 0.8542 | 0.9269 | 0.9225 |
| (0.9053, 0.9526) | (0.8883, 0.9592) | (0.7176, 0.8615) | (0.7708, 0.9231) | (0.9004, 0.9514) | (0.88126, 0.9583) | |
| 1.0 | 0.9084 | 0.8989 | 0.7484 | 0.8118 | 0.9038 | 0.8932 |
| (0.8833, 0.9330) | (0.8544, 0.9368) | (0.6715, 0.8216) | (0.7174, 0.8868) | (0.8756, 0.9306) | (0.8419, 0.9347) | |
| Model 231 | ||||||
| 0.1 | 0.9990 | 0.9893 | 1 | 0.9761 | 1 | 0.9893 |
| (0.9854, 0.9987) | (0.9725, 1) | - | (0.9321, 1) | - | (0.9721, 1) | |
| 0.2 | 0.9859 | 0.9734 | 0.9508 | 0.9425 | 0.9858 | 0.9730 |
| (0.9734, 0.9954) | (0.9495, 0.9946) | (0.9075, 0.9846) | (0.880, 0.9870) | (0.9731, 0.9954) | (0.9482, 0.9945) | |
| 0.3 | 0.9929 | 0.9787 | 0.9747 | 0.9534 | 0.9929 | 0.9784 |
| (0.9837, 1) | (0.9495, 0.9946) | (0.9423, 1) | (0.88, 0.9870) | (0.9836, 1) | (0.9482, 0.9945) | |
| 0.4 | 0.9953 | 0.9787 | 0.9830 | 0.9534 | 0.9952 | 0.9784 |
| (0.9880, 1) | (0.9550, 0.9949) | (0.9541, 1) | (0.90002, 0.9892) | (0.9879, 1) | (0.9539, 0.9949) | |
| 0.5 | 0.9554 | 0.9149 | 0.8593 | 0.8367 | 0.9543 | 0.9109 |
| (0.9333, 0.9727) | (0.8750, 0.9511) | (0.7914, 0.9155) | (0.750, 0.9105) | (0.9309, 0.9723) | (0.8660, 0.9498) | |
| 0.6 | 0.9296 | 0.8670 | 0.7945 | 0.7664 | 0.9269 | 0.8568 |
| (0.9059, 0.9521) | (0.8214, 0.9082) | (0.7219, 0.8593) | (0.6667, 0.8485) | (0.9011, 0.9509) | (0.8018, 0.9035) | |
| 0.7 | 0.9460 | 0.9042 | 0.8345 | 0.820 | 0.9445 | 0.8992 |
| (0.9242, 0.9660) | (0.8623, 0.9427) | (0.7647, 0.8970) | (0.7250, 0.8972) | (0.9211, 0.9654) | (0.8517, 0.9409) | |
| 0.8 | 0.9413 | 0.8936 | 0.8227 | 0.8039 | 0.9395 | 0.8873 |
| (0.9189, 0.9614) | (0.8506, 0.9329) | (0.75385, 0.8855) | (0.7071, 0.8823) | (0.9154, 0.9606) | (0.8373, 0.9306) | |
| 0.9 | 0.9437 | 0.8989 | 0.8286 | 0.8119 | 0.9419 | 0.8932 |
| (0.9218, 0.9641) | (0.8548, 0.9381) | (0.7593, 0.8905) | (0.7158, 0.8889) | (0.9185, 0.9634) | (0.84244, 0.9360) | |
| 1.0 | 0.8474 | 0.7765 | 0.6408 | 0.6612 | 0.8335 | 0.7437 |
| (0.8153, 0.8786) | (0.7254, 0.8265) | (0.5526, 0.7192) | (0.5487, 0.7591) | (0.7941, 0.8701) | (0.6712, 0.8081) | |
Table 3.
Comparison of performance metrics for Model and Model across different values (with 95% CI)
| Balanced Accuracy(0.95% CI) | F-Score (0.95% CI) | G-Mean (0.95% CI) | ||||
|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |
| Model | ||||||
| 0.1 | 0.9671 | 0.9468 | 0.8923 | 0.8913 | 0.9665 | 0.9453 |
| (0.9495, 0.9821) | (0.9138, 0.9752) | (0.8293, 0.9412) | (0.8182, 0.9499) | (0.94818, 0.9819) | (0.9097, 0.9749) | |
| 0.2 | 0.9624 | 0.9361 | 0.8787 | 0.8723 | 0.9617 | 0.9339 |
| (0.9437, 0.9784) | (0.9019, 0.9659) | (0.8112, 0.9315) | (0.7913, 0.9346) | (0.9420, 0.9781) | (0.8966, 0.9653) | |
| 0.3 | 0.9624 | 0.9361 | 0.8787 | 0.8723 | 0.9617 | 0.9339 |
| (0.9437, 0.9784) | (0.9019, 0.9659) | (0.8112, 0.9314) | (0.7912, 0.9346) | (0.9420, 0.9781) | (0.8966, 0.9653) | |
| 0.4 | 0.9647 | 0.9361 | 0.8854 | 0.8723 | 0.9641 | 0.9339 |
| (0.9468, 0.9807) | (0.9019, 0.9659) | (0.8205, 0.9355) | (0.7912, 0.9346) | (0.9453, 0.9809) | (0.8966, 0.9652) | |
| 0.5 | 0.9624 | 0.9414 | 0.8787 | 0.8817 | 0.9617 | 0.9396 |
| (0.9434, 0.9788) | (0.9063, 0.9709) | (0.8121, 0.9316) | (0.8043, 0.940) | (0.9417, 0.9785) | (0.9014, 0.9705) | |
| 0.6 | 0.9671 | 0.9361 | 0.8923 | 0.8723 | 0.9665 | 0.9339 |
| (0.9495, 0.9821) | (0.9022, 0.9663) | (0.8293, 0.9412) | (0.79014, 0.9346) | (0.9482, 0.9819) | (0.8968, 0.9657) | |
| 0.7 | 0.9553 | 0.9148 | 0.8592 | 0.8367 | 0.9543 | 0.9109 |
| (0.9355, 0.9739) | (0.8750, 0.9505) | (0.79105, 0.9167) | (0.7475, 0.9074) | (0.9333, 0.9736) | (0.8660, 0.9492) | |
| 0.8 | 0.9483 | 0.9361 | 0.8405 | 0.8723 | 0.9469 | 0.9339 |
| (0.9269, 0.9676) | (0.9019, 0.9670) | (0.76803, 0.9007) | (0.7876, 0.9362) | (0.9239, 0.9671) | (0.8966, 0.9665) | |
| 0.9 | 0.9530 | 0.9255 | 0.8529 | 0.8541 | 0.9518 | 0.9225 |
| (0.9312, 0.9715) | (0.8876, 0.9619) | (0.7852, 0.9091) | (0.76604, 0.9231) | (0.9286, 0.9711) | (0.8805, 0.9612) | |
| 1.0 | 0.9553 | 0.9095 | 0.8592 | 0.8282 | 0.9543 | 0.9050 |
| (0.9346, 0.9743) | (0.8706, 0.9474) | (0.7934, 0.9186) | (0.7397, 0.9038) | (0.9323, 0.9739) | (0.8609, 0.9459) | |
| Model | ||||||
| 0.1 | 0.9788 | 0.9627 | 0.9280 | 0.9213 | 0.9786 | 0.9620 |
| (0.9653, 0.9910) | (0.9350, 0.9845) | (0.8776, 0.9701) | (0.8540, 0.9696) | (0.9646, 0.9909) | (0.9327, 0.9844) | |
| 0.2 | 0.9741 | 0.9574 | 0.9133 | 0.9111 | 0.9738 | 0.9565 |
| (0.9595, 0.9881) | (0.9293, 0.9831) | (0.8595, 0.9579) | (0.8445, 0.9629) | (0.9587, 0.9880) | (0.9266, 0.9829) | |
| 0.3 | 0.9741 | 0.9574 | 0.9133 | 0.9111 | 0.9738 | 0.9565 |
| (0.9595, 0.9881) | (0.9293, 0.9831) | (0.8595, 0.9579) | (0.8444, 0.9629) | (0.9587, 0.9880) | (0.9266, 0.9829) | |
| 0.4 | 0.9718 | 0.9468 | 0.9062 | 0.8913 | 0.9714 | 0.9453 |
| (0.9569, 0.9860) | (0.9130, 0.9759) | (0.8485, 0.9552) | (0.8155, 0.9514) | (0.95597, 0.9859) | (0.9088, 0.9756) | |
| 0.5 | 0.9694 | 0.9308 | 0.8992 | 0.8631 | 0.9690 | 0.9282 |
| (0.9536, 0.9839) | (0.8953, 0.9638) | (0.8400, 0.9480) | (0.7826, 0.9302) | (0.9525, 0.9838) | (0.8892, 0.9632) | |
| 0.6 | 0.9718 | 0.9414 | 0.9062 | 0.8817 | 0.9714 | 0.9396 |
| (0.9569, 0.9860) | (0.9072, 0.9725) | (0.8485, 0.9552) | (0.8059, 0.9438) | (0.9559, 0.9859) | (0.9025, 0.9721) | |
| 0.7 | 0.9694 | 0.9308 | 0.8992 | 0.8631 | 0.9690 | 0.9282 |
| (0.9537, 0.9837) | (0.8954, 0.9619) | (0.8429, 0.9479) | (0.7767, 0.9263) | (0.9526, 0.9836) | (0.8892, 0.9612) | |
| 0.8 | 0.9647 | 0.9308 | 0.8854 | 0.8631 | 0.9641 | 0.9282 |
| (0.9474, 0.9805) | (0.8954, 0.9619) | (0.8303, 0.9375) | (0.7767, 0.9263) | (0.9459, 0.9803) | (0.8892, 0.9612) | |
| 0.9 | 0.9600 | 0.9148 | 0.8721 | 0.8367 | 0.9592 | 0.9102 |
| (0.9413, 0.9769) | (0.8750, 0.9484) | (0.8088, 0.9259) | (0.7501, 0.9074) | (0.9395, 0.9766) | (0.8660, 0.9471) | |
| 1.0 | 0.9530 | 0.9042 | 0.8529 | 0.8200 | 0.9518 | 0.8991 |
| (0.9330,0.9716) | (0.8628,0.9413) | (0.7857,0.9129) | (0.7327,0.8952) | (0.9306, 0.9711) | (0.8518, 0.9393) | |
Table 5.
Performance of Models and Models for penalized Block 1 in first priority (with 95% CI)
| Balanced Accuracy (0.95% CI) | F-Score (0.95% CI) | G-Mean (0.95% CI) | ||||
|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |
| Model | ||||||
| 0.1 | 0.9906 | 0.9893 | 0.9666 | 0.9761 | 0.9905 | 0.9893 |
| (0.9805, 0.9977) | (0.9719, 0.9999) | (0.9298, 0.9935) | (0.9348, 0.9999) | (0.9803, 0.9978) | (0.9715, 1) | |
| 0.2 | 0.9906 | 0.9840 | 0.9666 | 0.9647 | 0.9905 | 0.9839 |
| (0.9802, 0.9978) | (0.9632, 0.9999) | (0.9286, 0.9928) | (0.9176, 0.9999) | (0.9799, 0.9978) | (0.9625, 0.9999) | |
| 0.3 | 0.9835 | 0.9680 | 0.9430 | 0.9318 | 0.9834 | 0.9675 |
| (0.9693, 0.9952) | (0.9402, 0.9895) | (0.8929, 0.9833) | (0.8649, 0.9772) | (0.9688, 0.9952) | (0.9383, 0.9894) | |
| 0.4 | 0.9694 | 0.9627 | 0.8992 | 0.9213 | 0.9690 | 0.9620 |
| (0.9528, 0.9835) | (0.9339, 0.9845) | (0.8394, 0.9481) | (0.8533, 0.9677) | (0.9516, 0.9834) | (0.9316, 0.9844) | |
| 0.5 | 0.9695 | 0.9574 | 0.8992 | 0.9111 | 0.9690 | 0.9565 |
| (0.9521, 0.9836) | (0.9269, 0.9835) | (0.8391, 0.9481) | (0.8388, 0.9639) | (0.9509, 0.9835) | (0.9241, 0.9833) | |
| 0.6 | 0.9647 | 0.9574 | 0.8854 | 0.9111 | 0.9641 | 0.9565 |
| (0.9457, 0.9809) | (0.9269, 0.9835) | (0.8246, 0.9388) | (0.8388, 0.9638) | (0.9442, 0.9808) | (0.9241, 0.9834) | |
| 0.7 | 0.9577 | 0.9627 | 0.8656 | 0.9213 | 0.9568 | 0.9620 |
| (0.9381, 0.9749) | (0.9339, 0.9845) | (0.7942, 0.9206) | (0.8533, 0.9677) | (0.9361, 0.9747) | (0.9316, 0.9844) | |
| 0.8 | 0.9600 | 0.9574 | 0.8721 | 0.9111 | 0.9592 | 0.9565 |
| (0.9416, 0.9765) | (0.9261, 0.9831) | (0.8052, 0.9241) | (0.8421, 0.9629) | (0.9398, 0.9762) | (0.9232, 0.9829) | |
| 0.9 | 0.9600 | 0.9627 | 0.8721 | 0.9213 | 0.9592 | 0.9620 |
| (0.9416, 0.9765) | (0.9330, 0.9843) | (0.8052, 0.9241) | (0.8536, 0.9684) | (0.9398, 0.9762) | (0.9306, 0.9842) | |
| 1.0 | 0.9530 | 0.9255 | 0.8529 | 0.8541 | 0.9518 | 0.9225 |
| (0.9319, 0.9722) | (0.8895, 0.9607) | (0.7869, 0.9117) | (0.7672, 0.9263) | (0.9294, 0.9718) | (0.8827, 0.9599) | |
| Model | ||||||
| 0.1 | 0.9929 | 0.9946 | 0.9747 | 0.9879 | 0.9929 | 0.9946 |
| (0.9844, 1) | (0.9823, 0.9999) | (0.9420, 1) | (0.9552, 0.9999) | (0.9843, 1) | (0.9822, 0.9999) | |
| 0.2 | 0.9906 | 0.9840 | 0.9666 | 0.9647 | 0.9905 | 0.9839 |
| (0.9808, 0.9977) | (0.9823, 0.9999) | (0.9298, 0.9925) | (0.955, 0.9999) | (0.9806, 0.9977) | (0.9822, 0.9999) | |
| 0.3 | 0.9953 | 0.9947 | 0.9830 | 0.9879 | 0.9952 | 0.9946 |
| (0.9879, 1) | (0.9823, 1) | (0.9555, 1) | (0.9552, 1) | (0.9879, 1) | (0.9822, 1) | |
| 0.4 | 0.9765 | 0.9680 | 0.9206 | 0.9318 | 0.9762 | 0.9675 |
| (0.9609, 0.9905) | (0.9397, 0.9893) | (0.8640, 0.9645) | (0.8675, 0.9772) | (0.9602, 0.9905) | (0.9378, 0.9893) | |
| 0.5 | 0.9812 | 0.9840 | 0.9354 | 0.9647 | 0.9810 | 0.9839 |
| (0.9665, 0.9929) | (0.9631, 0.9999) | (0.8874, 0.9756) | (0.9143, 0.9999) | (0.9659, 0.9929) | (0.9625, 0.9999) | |
| 0.6 | 0.9788 | 0.9680 | 0.9280 | 0.9318 | 0.9786 | 0.9675 |
| (0.9633, 0.9911) | (0.9421, 0.9892) | (0.8750, 0.9722) | (0.8713, 0.9778) | (0.9626, 0.9910) | (0.9403, 0.9892) | |
| 0.7 | 0.9788 | 0.9680 | 0.9280 | 0.9318 | 0.9786 | 0.9675 |
| (0.9633, 0.9911) | (0.9421, 0.9892) | (0.8750, 0.9722) | (0.8713, 0.9778) | (0.9626, 0.9910) | (0.94034, 0.9892) | |
| 0.8 | 0.9718 | 0.9627 | 0.9062 | 0.9213 | 0.9714 | 0.9620 |
| (0.9557, 0.9863) | (0.9330, 0.9844) | (0.8489, 0.9529) | (0.8537, 0.9684) | (0.9546, 0.9862) | (0.9306, 0.9842) | |
| 0.9 | 0.9671 | 0.9627 | 0.8923 | 0.9213 | 0.9665 | 0.9620 |
| (0.9493, 0.9819) | (0.9339, 0.9845) | (0.8303, 0.9440) | (0.8533, 0.9677) | (0.9479, 0.9817) | (0.9316, 0.9844) | |
| 1.0 | 0.9647 | 0.9521 | 0.8854 | 0.9010 | 0.9641 | 0.9509 |
| (0.9468, 0.9812) | (0.9195, 0.9780) | (0.8214, 0.9379) | (0.8247, 0.9565) | (0.9453, 0.9810) | (0.9160, 0.9778) | |
Table 7.
Comparison of performance metrics for Model 312 and Model 321 across different values (with 95% CI)
| Balanced Accuracy(0.95% CI) | F-Score (0.95% CI) | G-Mean (0.95% CI) | ||||
|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |
| Model 312 | ||||||
| 0.1 | 0.9530 | 0.8554 | 0.8529 | 0.7708 | 0.9518 | 0.8541 |
| (0.9325, 0.9742) | (0.7877, 0.9107) | (0.7839, 0.9155) | (0.6744, 0.8571) | (0.9301, 0.9739) | (0.7858, 0.9099) | |
| 0.2 | 0.9812 | 0.9170 | 0.9354 | 0.8571 | 0.9810 | 0.9164 |
| (0.96591, 0.9929) | (0.8607, 0.9609) | (0.8807, 0.9760) | (0.7693, 0.9269) | (0.9653, 0.9929) | (0.8596, 0.9606) | |
| 0.3 | 0.9460 | 0.8814 | 0.8345 | 0.7920 | 0.9444 | 0.8763 |
| (0.9241, 0.9676) | (0.8345, 0.9268) | (0.7610, 0.8957) | (0.7059, 0.8762) | (0.9210, 0.9670) | (0.8262, 0.9245) | |
| 0.4 | 0.9107 | 0.8229 | 0.7532 | 0.7142 | 0.9064 | 0.8086 |
| (0.8833, 0.9384) | (0.7671, 0.8762) | (0.6719, 0.8252) | (0.6139, 0.8028) | (0.8756, 0.9363) | (0.7457, 0.8689) | |
| 0.5 | 0.9624 | 0.8995 | 0.8787 | 0.8351 | 0.9617 | 0.8991 |
| (0.9426, 0.9795) | (0.8418, 0.9456) | (0.8107, 0.9333) | (0.7468, 0.9126) | (0.9408, 0.9793) | (0.8417, 0.9452) | |
| 0.6 | 0.9624 | 0.9011 | 0.8787 | 0.8297 | 0.9617 | 0.8997 |
| (0.9427, 0.9789) | (0.8512, 0.9456) | (0.8121, 0.9324) | (0.7369, 0.9032) | (0.9409, 0.9787) | (0.8485, 0.9449) | |
| 0.7 | 0.9600 | 0.8958 | 0.8721 | 0.8210 | 0.9592 | 0.8941 |
| (0.9408, 0.9773) | (0.8456, 0.9406) | (0.8058, 0.9275) | (0.7294, 0.8979) | (0.9389, 0.9771) | (0.8429, 0.9395) | |
| 0.8 | 0.9553 | 0.8798 | 0.8592 | 0.7959 | 0.9543 | 0.8769 |
| (0.9343, 0.9742) | (0.8289, 0.9278) | (0.7869, 0.9173) | (0.7013, 0.8750) | (0.9319, 0.9738) | (0.8248, 0.9266) | |
| 0.9 | 0.9507 | 0.8745 | 0.8467 | 0.7878 | 0.9494 | 0.8711 |
| (0.9286, 0.9704) | (0.8214, 0.923) | (0.7769, 0.9078) | (0.6897, 0.8713) | (0.9253, 0.9699) | (0.8149, 0.9216) | |
| 1.0 | 0.9389 | 0.8676 | 0.8169 | 0.7835 | 0.9369 | 0.8656 |
| (0.9143, 0.9608) | (0.8064, 0.9224) | (0.7417, 0.8815) | (0.6863, 0.8713) | (0.9103, 0.9601) | (0.8036, 0.9218) | |
| Model 321 | ||||||
| 0.1 | 0.6830 | 0.6436 | 0.4621 | 0.5503 | 0.6051 | 0.5359 |
| (0.6519, 0.7181) | (0.5989, 0.6907) | (0.3805, 0.5328) | (0.4461, 0.6455) | (0.5511, 0.6605) | (0.4449, 0.6176) | |
| 0.2 | 0.7769 | 0.7446 | 0.5497 | 0.6307 | 0.7443 | 0.6995 |
| (0.7439, 0.8106) | (0.6944, 0.7957) | (0.4639, 0.6244) | (0.5211, 0.7244) | (0.6984, 0.7881) | (0.6236, 0.7690) | |
| 0.3 | 0.7699 | 0.7393 | 0.5420 | 0.6259 | 0.7346 | 0.6918 |
| (0.7374, 0.8046) | (0.6893, 0.7908) | (0.4563, 0.6194) | (0.5167, 0.7218) | (0.6890, 0.7805) | (0.6153, 0.7626) | |
| 0.4 | 0.7488 | 0.7340 | 0.5201 | 0.6212 | 0.7054 | 0.6841 |
| (0.7160, 0.7837) | (0.6833, 0.7864) | (0.4332, 0.5946) | (0.5133, 0.7153) | (0.6573, 0.7532) | (0.6055, 0.7569) | |
| 0.5 | 0.7183 | 0.7021 | 0.4915 | 0.5942 | 0.6607 | 0.6358 |
| (0.6860, 0.7500) | (0.6531, 0.7530) | (0.4069, 0.5679) | (0.4882, 0.6918) | (0.6100, 0.7071) | (0.5533, 0.7114) | |
| 0.6 | 0.7042 | 0.6595 | 0.4793 | 0.5616 | 0.6391 | 0.5649 |
| (0.6729, 0.7382) | (0.6136, 0.7062) | (0.3945, 0.5533) | (0.4592, 0.6578) | (0.5882, 0.6902) | (0.4768, 0.6421) | |
| 0.7 | 0.7136 | 0.6968 | 0.4873 | 0.5899 | 0.6536 | 0.6273 |
| (0.6804, 0.7477) | (0.6474, 0.7472) | (0.4034, 0.5626) | (0.4828, 0.6874) | (0.6006, 0.7038) | (0.5429, 0.7032) | |
| 0.8 | 0.7089 | 0.6702 | 0.4833 | 0.5694 | 0.6464 | 0.5834 |
| (0.6766, 0.7421) | (0.6236, 0.7198) | (0.3983, 0.5577) | (0.4627, 0.6665) | (0.5943, 0.6958) | (0.4972, 0.6629) | |
| 0.9 | 0.6807 | 0.6648 | 0.4603 | 0.5655 | 0.6012 | 0.5742 |
| (0.6476, 0.7133) | (0.6179, 0.7134) | (0.3793, 0.5319) | (0.4616, 0.6582) | (0.5434, 0.6531) | (0.4858, 0.6534) | |
| 1.0 | 0.6502 | 0.6276 | 0.4377 | 0.5394 | 0.5481 | 0.5052 |
| (0.6182, 0.6847) | (0.5843, 0.674) | (0.3599, 0.5072) | (0.4306, 0.6296) | (0.4863, 0.6077) | (0.4106, 0.5901) | |
Table 2.
Misc.(Number of Misclassifications=FP+FN) and p-value, across the different values of
| Model 213 | Model 231 | |||||||
|---|---|---|---|---|---|---|---|---|
| Misc. | p-value | Misc. | p-value | |||||
| Train | Test | Train | Test | Train | Test | Train | Test | |
| 0.1 | 16 | 6 | 1.37e-12 | 3.45e-14 | 0 | 2 | 2.2e-16 | 2e-16 |
| 0.2 | 19 | 7 | 8.313e-11 | 2.835e-13 | 6 | 5 | 2e-16 | 3.58e-15 |
| 0.3 | 21 | 8 | 9.68e-10 | 2.02e-12 | 3 | 4 | 2e-16 | 3.077e-16 |
| 0.4 | 26 | 11 | 1.93e-07 | 3.627e-10 | 2 | 4 | 2e-16 | 3.077e-16 |
| 0.5 | 29 | 12 | 2.811e-06 | 1.675e-09 | 19 | 16 | 8.313e-11 | 3.371e-07 |
| 0.6 | 32 | 12 | 2.916e-05 | 1.675e-09 | 30 | 25 | 6.352e-06 | 0.001267 |
| 0.7 | 33 | 12 | 5.935e-05 | 1.675e-09 | 23 | 18 | 9.244e-09 | 3.129e-06 |
| 0.8 | 31 | 12 | 1.385e-05 | 1.675e-09 | 25 | 20 | 7.341e-08 | 2.274e-05 |
| 0.9 | 30 | 14 | 6.352e-06 | 2.768e-08 | 24 | 19 | 2.663e-08 | 8.686e-06 |
| 1.0 | 39 | 19 | 0.0021 | 8.68e-06 | 65 | 42 | 0.866 | 0.614 |
Table 4.
Misc.(Number of Misclassifications=FP+FN) and p-value across the different values of
| Model | Model | |||||||
|---|---|---|---|---|---|---|---|---|
| Misc. | p-value | Misc. | p-value | |||||
| Train | Test | Train | Test | Train | Test | Train | Test | |
| 0.1 | 14 | 10 | 6.521e-14 | 7.147e-11 | 9 | 7 | 2.2e-16 | 2.835e-13 |
| 0.2 | 16 | 12 | 1.376e-12 | 1.675e-09 | 11 | 8 | 3.852e-16 | 2.02e-12 |
| 0.3 | 16 | 12 | 1.376e-12 | 1.675e-09 | 11 | 8 | 3.852e-16 | 2.02e-12 |
| 0.4 | 15 | 12 | 3.099e-13 | 1.675e-09 | 12 | 10 | 2.312e-15 | 7.147e-11 |
| 0.5 | 16 | 11 | 1.376e-12 | 3.627e-10 | 13 | 13 | 1.276e-14 | 7.092e-09 |
| 0.6 | 14 | 12 | 6.521e-14 | 1.675e-09 | 12 | 11 | 2.312e-15 | 3.627e-10 |
| 0.7 | 19 | 16 | 8.313e-11 | 3.371e-07 | 13 | 13 | 1.276e-14 | 7.092e-09 |
| 0.8 | 22 | 12 | 3.065e-09 | 1.675e-09 | 15 | 13 | 3.099e-13 | 7.092e-09 |
| 0.9 | 20 | 14 | 2.913e-10 | 2.768e-08 | 17 | 16 | 5.73e-12 | 3.371e-07 |
| 1.0 | 19 | 17 | 8.313e-11 | 1.061e-06 | 20 | 18 | 2.913e-10 | 3.129e-06 |
Table 6.
Misc.(Number of Misclassifications=FP+FN) and p-value across the different values of
| Model | Model | |||||||
|---|---|---|---|---|---|---|---|---|
| Misc. | p-value | Misc. | p-value | |||||
| Train | Test | Train | Test | Train | Test | Train | Test | |
| 0.1 | 4 | 2 | 2e-16 | 2e-16 | 3 | 1 | 2e-16 | 2e-16 |
| 0.2 | 4 | 3 | 2e-16 | 2e-16 | 4 | 3 | 2e-16 | 2e-16 |
| 0.3 | 7 | 6 | 2e-16 | 3.455e-14 | 2 | 3 | 2e-16 | 2e-16 |
| 0.4 | 13 | 7 | 1.27e-14 | 2.83e-13 | 10 | 6 | 2.2e-16 | 3.455e-14 |
| 0.5 | 13 | 8 | 1.27e-14 | 2.02e-12 | 8 | 3 | 2e-16 | 2e-16 |
| 0.6 | 15 | 8 | 3.09e-13 | 2.02e-12 | 9 | 6 | 2.2e-16 | 3.455e-14 |
| 0.7 | 18 | 7 | 2.246e-11 | 2.835e-13 | 9 | 6 | 2.2e-16 | 3.455e-14 |
| 0.8 | 17 | 8 | 5.73e-12 | 2.02e-12 | 12 | 7 | 2.312e-15 | 2.835e-13 |
| 0.9 | 17 | 7 | 5.73e-12 | 2.835e-13 | 14 | 7 | 6.521e-14 | 2.83e-13 |
| 1.0 | 20 | 14 | 2.913e-10 | 2.768e-08 | 15 | 9 | 3.099e-13 | 1.271e-11 |
Table 8.
Misc.(Number of Misclassifications=FP+FN) and p-value across the different values of
| Model 312 | Model 321 | |||||||
|---|---|---|---|---|---|---|---|---|
| Misc. | p-value | Misc. | p-value | |||||
| Train | Test | Train | Test | Train | Test | Train | Test | |
| 0.1 | 20 | 22 | 2.91e-10 | 0.000132 | 135 | 67 | 1 | 0.9082 |
| 0.2 | 8 | 13 | 2e-16 | 7.09e-09 | 95 | 48 | 1 | 0.9182 |
| 0.3 | 23 | 21 | 9.24e-09 | 5.63e-05 | 98 | 49 | 1 | 0.9423 |
| 0.4 | 38 | 32 | 0.001289 | 0.05341 | 107 | 50 | 1 | 0.9604 |
| 0.5 | 16 | 15 | 1.376e-12 | 1.002e-07 | 120 | 56 | 1 | 0.9977 |
| 0.6 | 16 | 16 | 1.376e-12 | 3.371e-07 | 126 | 64 | 1 | 0.9979 |
| 0.7 | 17 | 17 | 5.73e-12 | 1.061e-06 | 122 | 57 | 1 | 0.9987 |
| 0.8 | 19 | 20 | 8.313e-11 | 2.274e-05 | 124 | 62 | 1 | 0.9999 |
| 0.9 | 21 | 21 | 9.687e-10 | 5.632e-05 | 136 | 63 | 1 | 0.9999 |
| 1.0 | 26 | 21 | 1.939e-07 | 5.632e-05 | 149 | 70 | 1 | 0.9999 |
For Model 213 (Table 1), the performance metrics exhibited excellent consistency and high values at lower values (0.1 to 0.4), demonstrating the model’s strong capability in both training and test sets. Despite this, the test set metrics remained high, though slightly decreased, which indicated that the model retained good generalization as increased beyond 0.5. Notably, at (which corresponds to Priority-Lasso), there was a sharp decline across all metrics, highlighting a threshold where model performance dropped significantly.
In comparison, Model 231 showed high performance at low values, particularly at , where Balanced Accuracy, F-Score, and G-Mean were near-optimal in both training and testing datasets. also performed strongly, showing the second highest values for these metrics. However, at , there was a notable dip in all metrics, indicating a sensitivity to this specific parameter value. Post , the performance metrics showed variability but generally recovered at higher values, although not as consistently as Model 213. This suggested that while Model 231 could achieve high performance, it was more sensitive to changes in and required precise tuning to maintain optimal performance across different conditions.
Examining Model 213 in Table 2, the misclassification (FP + FN) values revealed a distinct pattern. the number of misclassifications started relatively low but increased significantly as increases, especially for the training set. The p-values for Model 213 were extremely low across all values, highlighting strong statistical significance in predictions compared to a null hypothesis.
In contrast, Model 231 presented more variability in misclassification errors. At , the model achieved zero misclassification in the train set and minimal errors in the test set, indicating very high performance. However, as increased to 0.5, the misclassification values rose, particularly in the training set, suggesting the model’s sensitivity to the parameter. Despite the variability, the p-values remained very low, reinforcing the statistical significance of the results. However, at , there was a notable increase in misclassification errors and p-values, indicating reduced statistical significance and potential overfitting or underfitting issues at this parameter setting.
For Model Table 3 related to “Scenario B”, the performance metrics demonstrated that the model generally performed best at lower values, particularly around and . The metrics declined as increased, suggesting that lower values of were optimal for this model. Misclassification numbers were lowest at with 14 Misclassifications in training and 10 in testing, and they rose with increasing values. The p-values indicated statistical significance for both training and test sets, reinforcing the reliability of these results.
Model performed better than Model in terms of Balanced Accuracy, F-Score, and G-Mean across all values. The highest values were observed at , where the Balanced Accuracy on the test set reached 0.9627. Misclassifications for Model were also lower compared to Model , with only 9 Misclassifications in training and 7 in testing at Table 4. This model maintained strong performance even as increased, although there was a gradual decline, indicating that lower values were also preferable for Model . The p-values for this model were consistently below , indicating robust statistical significance.
The provided tables (Tables 5 and 6) present the performance metrics for penalized models and , focusing on Balanced Accuracy, F-Score, G-Mean, misclassification (Misc.), and p-values across various values.
Model illustrated strong performance at lower values, particularly at and , with Balanced Accuracy reaching 0.9906 on the training set and 0.9840 on the test set at . The F-Score and G-Mean also followed a similar trend, achieving their highest values at the lower values. However, as increased, a noticeable decline in performance was observed, with the lowest metrics recorded at . Misclassifications were minimal at and , with 4 in training and 3 in testing. These numbers increased with higher values, peaking at 20 for training and 14 for testing at . The p-values remained extremely significant (below ) across all values, indicating that the results were statistically robust and reliable.
Model outperformed Model , especially at lower values. At , Model achieved a Balanced Accuracy of 0.9953 on the training set and 0.9947 on the test set, with corresponding high F-Score and G-Mean values. Similar to Model , the performance metrics for Model declined as increased, but the decline was less steep compared to Model , showing better robustness.
Model presented fewer misclassifications at and , with only 4 and 2 in the training set, respectively, and 3 in testing. As increased, these numbers gradually rose, reaching 15 for training and 9 for testing at . The p-values were consistently significant across all values.
Model 312 Table 7 demonstrated relatively average performance across different values. The highest Balanced Accuracy on the training set was 0.9812 at , with the test set achieving 0.9170 at the same value. Similarly, the F-Score and G-Mean were highest at lower values, with showing an F-Score of 0.9354 on the training set and 0.8571 on the test set.
The number of misclassifications for Model 312, as shown in Table 8, was lowest at , with 8 errors in the training set and 13 in the testing set. The p-values indicated high statistical significance, particularly at lower values, with values well below 0.05 across most values. This suggested that the model’s performance was statistically robust.
Model 321 Table 8 generally performed less than all the remaining models. The highest Balanced Accuracy on the training set was 0.7769 at , with the test set achieving 0.7446 at the same value. The F-Score and G-Mean followed a similar pattern, with the highest metrics observed at . However, the overall performance of Model 321 was significantly lower than that of Model 312 across all values, with noticeable declines at higher values.
Model 321, presented in Table 8, showed significantly higher numbers of misclassifications across all values, with the lowest figures being 95 in the training set and 48 in the testing set at . The p-values for Model 321 were consistently high (close to 1), indicating a lack of statistical significance in the observed results. These high p-values suggest that the corresponding model is unreliable, making Model 321 the least effective among the models evaluated.
To demonstrate the performance comparison between the Priority-Adaptive elastic net and the Priority-Elastic net models, we provided a scatter plot (Fig. 4) showcasing key metrics. This plot allows for a clear understanding of how the Priority-Adaptive elastic net performs relative to the Priority-Elastic net across different scenarios. The metrics analyzed include Balanced Accuracy, F-Score, and G-Mean, each assessed for both training and testing phases, and plotted against different alpha values.
Overall, the Priority-Elastic net model stands out with its robust and consistent performance, positioning it as a more dependable option across the assessed metrics and alpha ranges.
Evaluating selected features
The number of selected features, which corresponds to the indexes j such that , for each model and corresponding block is comprehensively documented in Tables 9, 10, 11, and 12. The column labeled “Common Variables” indicates the number of variables that both models commonly select. The percentage is calculated as the ratio of common variables to the total number of variables selected for each value of .
Table 9.
Variables selected by Priority-Elastic net for scenario A, across the different values of
| Model 213 | Model 231 | Common Variables (%) | |||||
|---|---|---|---|---|---|---|---|
| Block 2 | Block 1 | Block 3 | Block 2 | Block 3 | Block 1 | ||
| 0.1 | 168 | 5 | 110 | 168 | 99 | 5 | 252 (45.41%) |
| 0.2 | 157 | 5 | 87 | 157 | 72 | 5 | 215 (44.51%) |
| 0.3 | 152 | 5 | 71 | 152 | 52 | 5 | 200 (45.77%) |
| 0.4 | 143 | 5 | 57 | 143 | 47 | 5 | 184 (46.00%) |
| 0.5 | 135 | 5 | 57 | 135 | 33 | 4 | 164 (44.44%) |
| 0.6 | 118 | 5 | 49 | 118 | 26 | 5 | 145 (45.17%) |
| 0.7 | 112 | 5 | 45 | 112 | 16 | 5 | 132 (44.75%) |
| 0.8 | 104 | 5 | 37 | 104 | 16 | 4 | 121 (44.81%) |
| 0.9 | 91 | 5 | 30 | 91 | 13 | 3 | 104 (44.64%) |
| 1.0 | 66 | 5 | 19 | 66 | 8 | 3 | 74 (44.31%) |
Table 10.
Variables selected by Priority-Elastic net for scenario B (block 1 not penalized), across the different values of
| Model | Model | Common Variables (%) | |||||
|---|---|---|---|---|---|---|---|
| Block 1 | Block 2 | Block 3 | Block 1 | Block 3 | Block 2 | ||
| 0.1 | 5 | 99 | 93 | 5 | 73 | 21 | 89 (30.07%) |
| 0.2 | 5 | 78 | 68 | 5 | 51 | 6 | 52 (24.41%) |
| 0.3 | 5 | 36 | 51 | 5 | 43 | 2 | 40 (28.17%) |
| 0.4 | 5 | 29 | 40 | 5 | 33 | 2 | 31 (27.19%) |
| 0.5 | 5 | 25 | 35 | 5 | 26 | 7 | 32 (31.07%) |
| 0.6 | 5 | 19 | 24 | 5 | 26 | 0 | 24 (30.38%) |
| 0.7 | 5 | 33 | 22 | 5 | 24 | 0 | 21 (23.60%) |
| 0.8 | 5 | 91 | 19 | 5 | 23 | 0 | 20 (13.99%) |
| 0.9 | 5 | 82 | 18 | 5 | 23 | 4 | 23 (16.79%) |
| 1.0 | 5 | 67 | 13 | 5 | 21 | 6 | 21 (17.95%) |
Table 11.
Variables selected by Priority-Elastic net for scenario B (block 1 penalized), across the different values of
| Model | Model | Common Variables (%) | |||||
|---|---|---|---|---|---|---|---|
| Block 1 | Block 2 | Block 3 | Block 1 | Block 3 | Block 2 | ||
| 0.1 | 4 | 86 | 80 | 4 | 60 | 16 | 72 (28.80%) |
| 0.2 | 3 | 81 | 54 | 3 | 47 | 4 | 42 (21.88%) |
| 0.3 | 3 | 53 | 46 | 3 | 32 | 2 | 29 (20.86%) |
| 0.4 | 3 | 45 | 32 | 3 | 38 | 1 | 28 (22.95%) |
| 0.5 | 3 | 87 | 26 | 3 | 23 | 0 | 21 (14.79%) |
| 0.6 | 3 | 75 | 24 | 3 | 26 | 0 | 21 (16.03%) |
| 0.7 | 3 | 17 | 22 | 3 | 24 | 2 | 21 (29.58%) |
| 0.8 | 3 | 12 | 19 | 3 | 22 | 2 | 19 (31.15%) |
| 0.9 | 3 | 11 | 18 | 3 | 21 | 1 | 18 (31.58%) |
| 1.0 | 3 | 65 | 18 | 3 | 19 | 0 | 16 (14.81%) |
Table 12.
Variables selected by Priority-Elastic net for scenario C, across the different values of
| Model 312 | Model 321 | Common Variables (%) | |||||
|---|---|---|---|---|---|---|---|
| Block 3 | Block 1 | Block 2 | Block 3 | Block 2 | Block 1 | ||
| 0.1 | 41 | 4 | 164 | 41 | 4 | 5 | 149 (57.53%) |
| 0.2 | 33 | 4 | 137 | 33 | 5 | 5 | 42 (19.35%) |
| 0.3 | 31 | 4 | 149 | 31 | 2 | 5 | 39 (17.57%) |
| 0.4 | 25 | 4 | 139 | 25 | 1 | 5 | 30 (15.08%) |
| 0.5 | 22 | 1 | 134 | 22 | 2 | 5 | 25 (13.44%) |
| 0.6 | 21 | 1 | 125 | 21 | 2 | 5 | 24 (13.71%) |
| 0.7 | 21 | 1 | 119 | 21 | 3 | 5 | 25 (14.71%) |
| 0.8 | 20 | 1 | 98 | 20 | 4 | 5 | 24 (16.22%) |
| 0.9 | 19 | 1 | 82 | 19 | 5 | 5 | 24 (18.32%) |
| 1.0 | 17 | 1 | 61 | 17 | 0 | 4 | 18 (18.00%) |
A key observation, as shown in Table 9, was the variation in the number of selected variables in block 3 (RNA) between the two models. This difference was attributed to the distinct information provided by block 2 (proteomics) and block 1 (clinical), which affected the selection process in the following block.
In Model 213, more RNA variables were consistently selected than in Model 231. This is because the proteomics data alone do not capture all necessary information, necessitating the addition of RNA data to enhance predictive power. This underscores the importance of integrating multi-omics data to improve model accuracy.
In contrast, Model 231 selected fewer RNA variables. This suggested that combining RNA and proteomics data already captured a substantial portion of the predictive power. Here, the clinical variables, considered last, added the final pieces of complementary information. The comprehensive insights provided by the RNA block reduced the need for further variables from the clinical data in higher values.
Further analysis of Table 9 revealed considerable overlap in relevant variables between the two model configurations at each level. The highest percentage of common variables occurred at , with 46.00% of the variables being shared between the two models, demonstrating optimal feature selection consistency. Conversely, the lowest percentage of common variables was observed at , with a 44.31% overlap.
Table 10 outlines the results from two predictive models for block 1 not penalized, Model and Model , detailing the inclusion of variables () from blocks 1, 2, and 3 for different values ranging from 0.1 to 1. Additionally, the number and percentage of common variables shared between the two models at each value is presented.
Both models consistently included five variables from block 1 across all values since no penalization was considered.
According to the principles of Priority-Elastic net, the hierarchical regression method implied that in Model , block 3 had a higher priority than block 2, leading to fewer selected features in block 2 compared to Model , where block 2 had a higher priority. This suggested that in Model , much of the information was captured by block 3, reducing the need for additional features from block 2. Conversely, in Model , where block 2 had a higher priority and block 1 provided limited additional information, more variables were selected from block 2 to capture the remaining variation.
The percentage of common variables between the two models varied with , peaking at 31.07% at and dropping to 13.99% at . This indicated that feature selection consistency between the models was not uniform across different values.
Table 11 presents the results in the same order of priorities but now considering penalization in block 1.
Overall, the number of selected features from block 1 remained consistent at 3 or 4 across all values in both models, indicating a stable but limited role of block 1 features due to the penalization. From Table 11, as increases, the number of common variables decreases, indicating that the two models converge on a smaller set of shared variables under stronger sparsity constraints.
In Model , block 3 had a higher priority than block 2, making its influence on the selected variables in block 2 more apparent. In contrast, Model , where block 2 had a higher priority, resulted in more variables being selected from block 3, which had a lower priority.
The results indicated that at , the percentage of common variables was the highest (31.58%), even though the total number of selected variables was lower across the values. This suggests that at , the models converged more on the same set of key variables, highlighting a stronger agreement in feature selection despite a more stringent overall selection process.
Findings in Table 12 present the results of two predictive models, Model 312 and Model 321, analyzed across different values of the parameter .
Both models included a consistent number of variables from block 3 across all values, suggesting a stable significance of block 3 variables in predicting the outcome.
For Model 312, despite RNA data’s primary role, block 2 still selected a substantial number of variables, highlighting that proteomics data offered complementary information not fully captured by RNA data. In contrast, block 1 consistently selected a minimal number of variables, indicating that the strong predictive power of RNA data diminished the additional contribution of clinical variables.
In the case of Model 321, the number of variables selected from block 2 was generally lower than in Model 312, suggesting some redundancy when proteomics data was considered after RNA data, reducing the need for additional proteomics variables.
The significant differences in variable inclusion between Model 312 and Model 321 at various values highlight how the order of blocks (3-1-2 vs. 3-2-1) might influence model selection. This could imply that the structural importance of each block may impact the final predictive model, depending on the penalization parameter. To provide a comprehensive overview of the features selected for the optimal model, the complete list is presented in Supplementary Information Table (13).
Analyzing block contribution and accuracy
The heatmaps in (Fig. 2) illustrate the varying contributions of different blocks to model accuracy and how these contributions are influenced by the prioritization and values.
Fig. 2.
Comparison of cvm values across varying parameters for scenarios A, B, and C. The x-axis represents the parameter, which balances Lasso and Ridge regression. The y-axis denotes the cross-validated error (cvm) for each block, representing the average AUC (Area Under the Curve) across the folds of the cross-validation. AUC is used as the type.measure in the priorityelasticnet function for binary outcomes
Overall, in the heatmaps indicated across all scenarios, the models exhibit the highest performance in block 3, with a noticeable decrease in performance when considering block 2 and block 1. This observation clarifies the underlying causes of the reduced performance when initiating block 3 and the significant differences in the number of variables selected between Models 312 and 321.
In Scenario A, Models 213 and 231 exhibited high performance in block 3 with consistently high AUC values across all levels, suggesting strong predictive capabilities for this block. However, both models showed a noticeable decline in AUC in block 2, indicating sensitivity to this parameter. Block 1 displayed the poorest performance, with AUC values decreasing significantly with higher levels in Model 231 and increasing in Model213, highlighting challenges in model accuracy for this block.
In Scenario B, Models 123p and 132p, as well as Models 123np and 132np, demonstrated similar patterns. Block 3 maintained high AUC values for all models, particularly for Models 123p and 123np, suggesting these models’ robustness. In Model 123, when considering block2, the AUC values highly improve for all levels, as they go from low values to AUC 0.913, and block3 further improves the outcomes. On the other hand, when changing the order of blocks 2 and 3, so for Model 132, block 3 is again giving excellent performances. However, if block 2 is considered after block 3, the AUC decreases slightly.
In Scenario C, comprising Models 312 and 321, the observed trends differed from previous scenarios. Even though block 3 exhibited high AUC values across all levels, the deficient performance of block 1 had a detrimental effect on the overall efficacy of Model 321. Evaluation of the data blocks suggests that block 3 holds the greatest informational value, whereas block 1 is likely the least contributive to predictive accuracy.
UMAP-based validation
A visual inspection of multi-omics glioma data was conducted using UMAP to project the data into a 2-dimensional space, aiming to identify inherent groupings and relationships. In this representation (Fig. 3), the data points correspond to samples’ projections based on the different data blocks: transcriptomics, proteomics and clinical. Each point is colored based on the associated glioma type: LGG (blue) and GBM (red). Each plot offers insights into how these glioma types can be separated or grouped based on the specific characteristics captured by each modality.
Fig. 3.
UMAP representation of the dataset (LGG: patients with astrocytoma or oligodendroglioma; GBM: patients with glioblastoma)
This analysis provided an indication of how well LGG and GBM are separated based on different data blocks, particularly supporting the results from the transcriptomics block. It serves as a confirmation of the information provided by the transcriptomics block and complements the findings presented in (Fig. 2).
The transcriptomics block plot allows a good distinction between LGG and GBM patients, which are projected in well-separated regions of the space. This result indicated that RNA-Seq data was highly effective in distinguishing between these two types of gliomas. The distinct gene expression profiles associated with each tumor type likely drove this strong differentiation, highlighting the potential of RNA-Seq data in the accurate classification and diagnosis of glioma subtypes.
Proteomic analysis revealed some grouping structure, with a few GBM samples projected in distinct areas, suggesting they might contain information beneficial for the classifier. This observation indicated that, although proteomics features provided some insights into the molecular characteristics of the tumors, they were not as substantial in distinguishing LGG from GBM as RNA-Seq data. Consequently, while proteomic data contributed to understanding tumor biology, they might have required integration with other data modalities for more accurate classification and differentiation of glioma subtypes.
Moving to the clinical block plot, we observed a somewhat different pattern. The clinical data did not provide as clear a separation between LGG and GBM as the omics data. The overlap between some LGG and GBM points suggested that clinical characteristics were not as definitive as molecular data in differentiating between these glioma types.
To conclude, the illustrated plots align with our findings regarding the importance of RNA data, which achieved the highest AUC and performance accuracy when included in the predictive model. The superior performance of the RNA data highlights its effectiveness in distinguishing between LGG and GBM, further affirming its potential for accurate glioma subtyping and diagnosis.
Conclusion
In this paper, we addressed a crucial question in biomedical research: how to integrate multiple (potentially correlated) data modalities of varying sizes and relevance to the outcome to generate a sparse prediction model.
We applied our methodology to glioma, the most common brain tumor with a poor prognosis, adding significant relevance to the biomedical research community. As glioma has recently been reclassified to incorporate molecular information into its diagnostic guidelines, the priority omics-driven insights and features revealed by our study show great potential as biomarkers. These findings are expected to attract interest for further research and therapeutic development within the biomedical and biopharmaceutical fields. It offers moderate computational complexity, flexibility in integrating prior knowledge while introducing a hierarchical modeling perspective, and, importantly, improved stability and accuracy in predictions, resulting in more reliable outcomes and consistent feature selection across different datasets, making it superior to other methods. Furthermore, Priority-elastic net’s ability to smooth the influence of correlated features can make this process more biologically meaningful, ensuring that relevant biomarkers are properly accounted for, even when they share the same information with other features.
We demonstrated the comparison between the Priority-Adaptive elastic net and the Priority-Elastic net, further illustrating the effectiveness of our proposed method. While adaptive elastic net method is typically favored for their flexibility and capacity to adjust penalties, in this instance, this appears to introduce complexities that do not translate into better model outcomes.
Furthermore, our analysis of glioma cancer utilizing transcriptomics, proteomics, and clinical data underscores the critical role of transcriptomic information in accurately classifying LGG and GBM. This emphasizes the necessity of incorporating transcriptomic data for the effective categorization of these tumor types. Our findings indicate that prioritizing data blocks from the least informative to the most informative (Model 123) yields superior performance, enabling incremental improvement in model predictions at each step. This approach aligns with the principle of prioritizing data blocks that are easily accessible, cost-effective, or routinely collected in clinical practice. This insight reflects the evolving understanding of the contributions of various omics layers to predictive modeling in oncology.
Supplementary Information
Supplementary Information S1: The scatter plots in Figure 4 presents a detailed comparison of the performance metrics for Priority-Adaptive elastic net and Priority-Elastic net models across various α values. The goal is to evaluate how each model performs under different setups, including both penalized and non-penalized structures for block of clinical data. Contrary to expectations, The Priority-Elastic net models demonstrate superior performance across most configurations.
The Priority-Elastic net models consistently presents stronger performance across a range of settings for most α values. One key advantage of the non-adaptive models is their simplicity. By applying a uniform penalty across all variables, the non-adaptive elastic net tends to be more stable.
The results suggest that the Priority-Elastic net model may offer better generalization and performance stability compared to its adaptive counterpart across these specific datasets and evaluation metrics.
Supplementary Information S2: Table 13 provides the complete list of the features selected for the optimal model.
Acknowledgements
The authors acknowledge the Portuguese Foundation for Science & Technology (FCT).
Abbreviations
- TCGA
The cancer genome Atlas
- GBM
Glioblastoma
- LGG
Lower-grade glioma
- LASSO
Least absolute shrinkage and selection operator
- MLE
Maximum likelihood estimation
- RNA-seq
RNA-sequencing
- WHO
World health organization
- CNS
Central nervous system
- TPM
Transcripts per million
- ROC
Receiver operating characteristic
- AUC
Area under the ROC curve
- NIR
Null/No information rate
- UMAP
Uniform manifold approximation and projection
Authors’ contributions
LM, HM and EC designed the study, LM implemented and performed the analysis, LM, RC, MBL, HM and EC analysed the results and wrote the manuscript. All authors read and approved the final manuscript.
Funding
The work was supported by national funds through Fundação para a Ciência e a Tecnologia (FCT) with references CEECINST/00042/2021, UIDB/00006/2020 (CEAUL, DOI: 10.54499/UIDB/00006/2020), UIDB/00297/2020 (DOI: 10.54499/UIDB/00297/2020) and UIDP/00297/2020 (DOI:10.54499/UIDP/00297/2020)(NOVA Math), UIDB/00667/2020 (DOI: 10.54499/UIDB/00667/2020) and UIDP /00667/2020 (DOI:10.54499/UIDP/00667/2020) (UNIDEMI), and the research project PTDC/CCI-BIO/4180/2020 “MONET-Multi-omic networks in gliomas” (DOI: 10.54499/PTDC/CCI-BIO/4180/2020).
Data availability
No datasets were generated or analysed during the current study.
Code availability
The code that supports the findings of this study are available from the corresponding author upon formal request.
Declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Subramanian I, Verma S, Kumar S, Jere A, Anamika K. Multi-omics data integration, interpretation, and its application. Bioinforma Biol Insights. 2020;14. 10.1177/1177932219899051. [DOI] [PMC free article] [PubMed]
- 2.Kreitmaier P, Katsoula G, Zeggini E. Insights from multi-omics integration in complex disease primary tissues. Trends Genet. 2023;39(1):46–58. 10.1016/j.tig.2022.08.005. [DOI] [PubMed] [Google Scholar]
- 3.Marx V. The big challenges of big data. Nature. 2013;498(7453):255–60. [DOI] [PubMed] [Google Scholar]
- 4.Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc Ser B Stat Methodol. 1996;58(1):267–88. [Google Scholar]
- 5.Tibshirani R, Saunders M, Rosset S, Zhu J, Knight K. Sparsity and smoothness via the fused lasso. J R Stat Soc Ser B Stat Methodol. 2005;67(1):91–108. [Google Scholar]
- 6.Zou H. The adaptive lasso and its oracle properties. J Am Stat Assoc. 2006;101(476):1418–29. [Google Scholar]
- 7.Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. J R Stat Soc Ser B Stat Methodol. 2006;68(1):49–67. [Google Scholar]
- 8.Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Ser B Stat Methodol. 2005;67(2):301–20. [Google Scholar]
- 9.Zou H, Zhang HH. On the adaptive elastic-net with a diverging number of parameters. Ann Stat. 2009;37(4):1733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Misra BB, Langefeld C, Olivier M, Cox LA. Integrated omics: tools, advances and future approaches. J Mol Endocrinol. 2019;62(1):R21–45. [DOI] [PubMed] [Google Scholar]
- 11.Zhao Q, Shi X, Xie Y, Huang J, Shia B, Ma S. Combining multidimensional genomic measurements for predicting cancer prognosis: observations from TCGA. Brief Bioinform. 2015;16(2):291–303. 10.1093/bib/bbu003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Huang S, Chaudhary K, Garmire LX. More is better: recent progress in multi-omics data integration methods. Front Genet. 2017;8:84. 10.3389/fgene.2017.00084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Simon N, Friedman J, Hastie T, Tibshirani R. A sparse-group lasso. J Comput Graph Stat. 2013;22(2):231–45. [Google Scholar]
- 14.Boulesteix AL, De Bin R, Jiang X, Fuchs M. IPF-LASSO: integrative L1-penalized regression with penalty factors for prediction based on multi-omics data. Comput Math Methods Med. 2017;2017(1):7691937. 10.1155/2017/7691937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vazquez AI, Veturi Y, Behring M, Shrestha S, Kirst M, Resende MF Jr, et al. Increased proportion of variance explained and prediction accuracy of survival of breast cancer patients with use of whole-genome multiomic profiles. Genetics. 2016;203(3):1425–38. 10.1534/genetics.115.185181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.PK M, R S, N S, DA L, C S. Time to recurrence and survival in serous ovarian tumors predicted from integrated genomic profiles. PLoS ONE. 2011;6(11):e24709. [DOI] [PMC free article] [PubMed]
- 17.Park MY, Hastie T. L1-regularization path algorithm for generalized linear models. J R Stat Soc Ser B Stat Methodol. 2007;69(4):659–77. [Google Scholar]
- 18.Seoane JA, Day IN, Gaunt TR, Campbell C. A pathway-based data integration framework for prediction of disease progression. Bioinformatics. 2014;30(6):838–45. 10.1093/bioinformatics/btt610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fuchs M, Beissbarth T, Wingender E, Jung K. Connecting high-dimensional mRNA and miRNA expression data for binary medical classification problems. Comput Methods Prog Biomed. 2013;111(3):592–601. [DOI] [PubMed] [Google Scholar]
- 20.Klau S, Jurinovic V, Hornung R, Herold T, Boulesteix AL. Priority-Lasso: a simple hierarchical approach to the prediction of clinical outcome using multi-omics data. BMC Bioinformatics. 2018;19:1–14. 10.1186/s12859-018-2344-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Aben N, Vis DJ, Michaut M, Wessels LF. TANDEM: a two-stage approach to maximize interpretability of drug response models based on multiple molecular data types. Bioinformatics. 2016;32(17):i413–20. 10.1093/bioinformatics/btw449. [DOI] [PubMed] [Google Scholar]
- 22.Yerushalmy, J. Statistical Problems in Assessing Methods of Medical Diagnosis, with Special Reference to X-Ray Techniques. Public Health Rep (1896-1970). 1947;62(40):1432–49. 10.2307/4586294. [PubMed]
- 23.Somes G. Beyond Normality: The Predictive Value and Efficiency of Medical Diagnoses R. S. Galen and S. R. Gambino. New York, Wiley, 1975, 237 pp, $14.95. J Nucl Med. 1976;17:855.
- 24.Van den Bruel A, Cleemput I, Aertgeerts B, Ramaekers D, Buntinx F. The evaluation of diagnostic tests: evidence on technical and diagnostic accuracy, impact on patient outcome and cost-effectiveness is needed. J Clin Epidemiol. 2007;60(11):1116–22. 10.1016/j.jclinepi.2007.03.015. [DOI] [PubMed] [Google Scholar]
- 25.Pepe MS. The statistical evaluation of medical tests for classification and prediction. Oxford University Press; 2003. 10.1093/oso/9780198509844.001.0001.
- 26.Perkins NJ, Schisterman EF. The inconsistency of “optimal’’ cutpoints obtained using two criteria based on the receiver operating characteristic curve. Am J Epidemiol. 2006;163(7):670–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Guo H, Liu H, Wu C, Zhi W, Xiao Y, She W. Logistic discrimination based on G-mean and F-measure for imbalanced problem. J Intell Fuzzy Syst. 2016;31(3):1155–66. [Google Scholar]
- 28.Brodersen KH, Ong CS, Stephan KE, Buhmann JM. The Balanced Accuracy and Its Posterior Distribution. 2010 20th International Conference on Pattern Recognition. Istanbul; 2010. p. 3121–34. 10.1109/ICPR.2010.764.
- 29.Friedman J, Hastie T, Tibshirani R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J Stat Softw. 2010;33(1):1–22. [PMC free article] [PubMed] [Google Scholar]
- 30.Hastie T, Tibshirani R, Wainwright M. Statistical learning with sparsity. Monogr Stat Appl Probab. 2015;143(143):8. [Google Scholar]
- 31.Liu Z, Gartenhaus RB, Tan M, Jiang F, Jiao X. Gene and pathway identification with L_p penalized Bayesian logistic regression. BMC Bioinformatics. 2008;9:1–19. 10.1186/1471-2105-9-412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lopes MB, Casimiro S, Vinga S. Twiner: correlation-based regularization for identifying common cancer gene signatures. BMC Bioinformatics. 2019;20:1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ghosh S. On the grouped selection and model complexity of the adaptive elastic net. Stat Comput. 2011;21:451–62. [Google Scholar]
- 34.Monaghan TF, Rahman SN, Agudelo CW, Wein AJ, Lazar JM, et al. Foundational Statistical Principles in Medical Research: Sensitivity, Specificity, Positive Predictive Value, and Negative Predictive Value. Medicina. 2021;57(5):503. 10.3390/medicina57050503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sokolova M, Japkowicz N, Szpakowicz S. Beyond Accuracy, F-Score and ROC: A Family of Discriminant Measures for Performance Evaluation. In: Sattar A, Kang BH, editors. AI 2006: Advances in Artificial Intelligence. AI 2006. Lecture Notes in Computer Science(), vol 4304. Berlin, Heidelberg: Springer; 2006. 10.1007/11941439_114.
- 36.Youden WJ. Index for rating diagnostic tests. Cancer. 1950;3(1):32–5. [DOI] [PubMed] [Google Scholar]
- 37.Bicego M, Mensi A. Null/No Information Rate (NIR): a statistical test to assess if a classification accuracy is significant for a given problem. arXiv preprint arXiv:230606140. 2023. 10.48550/arXiv.2306.06140.
- 38.Kuhn M. Building predictive models in R using the caret package. J Stat Softw. 2008;28:1–26.27774042 [Google Scholar]
- 39.Samur MK. RTCGAToolbox: a new tool for exporting TCGA Firehose data. PLoS ONE. 2014;9(9): e106397. 10.1371/journal.pone.0106397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.E G, SHELINE, PHD, MD. Radiation Therapy of Brain Tumors. Cancer. 1977;s2(39):873–881. [DOI] [PubMed]
- 41.Lu J, Cowperthwaite MC, Burnett MG, Shpak M. Molecular predictors of long-term survival in glioblastoma multiforme patients. PLoS ONE. 2016;11(4): e0154313. 10.1371/journal.pone.0154313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Omuro A, DeAngelis LM. Glioblastoma and other malignant gliomas: a clinical review. JAMA. 2013;310(17):1842–50. 10.1001/jama.2013.280319. [DOI] [PubMed] [Google Scholar]
- 43.Ostrom QT, Cote DJ, Ascha M, Kruchko C, Barnholtz-Sloan JS. Adult glioma incidence and survival by race or ethnicity in the United States from 2000 to 2014. JAMA Oncol. 2018;4(9):1254–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.TCGA. Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature. 2008;455(7216):1061–1068. [DOI] [PMC free article] [PubMed]
- 45.Network CGAR. Comprehensive, integrative genomic analysis of diffuse lower-grade gliomas. N Engl J Med. 2015;372(26):2481–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Louis DN, Ohgaki H, Wiestler OD, Cavenee WK, Burger PC, Jouvet A, et al. The 2007 WHO classification of tumours of the central nervous system. Acta Neuropathol. 2007;114:97–109. 10.1007/s00401-007-0243-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mendonça ML, Coletti R, Gonçalves CS, Martins EP, Costa BM, Vinga S, et al. Updating TCGA glioma classification through integration of molecular profiling data following the 2016 and 2021 WHO guidelines. bioRxiv. 2023;2023–02. https://www.biorxiv.org/content/early/2023/12/08/2023.02.19.529134.
- 48.DN L, A P, P W, DJ B, IA C, D FB, et al. The 2021 WHO Classifcation of Tumors of the Central Nervous System: a summary. Neuro-Oncol. 2021;23(8):1231—1251. 10.1093/neuonc/noab106. [DOI] [PMC free article] [PubMed]
- 49.R Core Team R, et al. R: A language and environment for statistical computing. Vienna: R foundation for statistical computing; 2013. http://www.R-project.org/.
- 50.McInnes L, Healy J, Melville J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. 2020. https://arxiv.org/abs/1802.03426.
- 51.Wilkinson L. ggplot2: Elegant Graphics for Data Analysis by WICKHAM, H. Biometrics. 2011;67(2):678–9. 10.1111/j.1541-0420.2011.01616.x. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information S1: The scatter plots in Figure 4 presents a detailed comparison of the performance metrics for Priority-Adaptive elastic net and Priority-Elastic net models across various α values. The goal is to evaluate how each model performs under different setups, including both penalized and non-penalized structures for block of clinical data. Contrary to expectations, The Priority-Elastic net models demonstrate superior performance across most configurations.
The Priority-Elastic net models consistently presents stronger performance across a range of settings for most α values. One key advantage of the non-adaptive models is their simplicity. By applying a uniform penalty across all variables, the non-adaptive elastic net tends to be more stable.
The results suggest that the Priority-Elastic net model may offer better generalization and performance stability compared to its adaptive counterpart across these specific datasets and evaluation metrics.
Supplementary Information S2: Table 13 provides the complete list of the features selected for the optimal model.
Data Availability Statement
No datasets were generated or analysed during the current study.
The code that supports the findings of this study are available from the corresponding author upon formal request.