Abstract
Objective.
Brain recordings exhibit dynamics at multiple spatiotemporal scales, which are measured with spike trains and larger-scale field potential signals. To study neural processes, it is important to identify and model causal interactions not only at a single scale of activity, but also across multiple scales, i.e. between spike trains and field potential signals. Standard causality measures are not directly applicable here because spike trains are binary-valued but field potentials are continuous-valued. It is thus important to develop computational tools to recover multiscale neural causality during behavior, assess their performance on neural datasets, and study whether modeling multiscale causalities can improve the prediction of neural signals beyond what is possible with single-scale causality.
Approach.
We design a multiscale model-based Granger-like causality method based on directed information and evaluate its success both in realistic biophysical spike-field simulations and in motor cortical datasets from two non-human primates (NHP) performing a motor behavior. To compute multiscale causality, we learn point-process generalized linear models that predict the spike events at a given time based on the history of both spike trains and field potential signals. We also learn linear Gaussian models that predict the field potential signals at a given time based on their own history as well as either the history of binary spike events or that of latent firing rates.
Main results.
We find that our method reveals the true multiscale causality network structure in biophysical simulations despite the presence of model mismatch. Further, models with the identified multiscale causalities in the NHP neural datasets lead to better prediction of both spike trains and field potential signals compared to just modeling single-scale causalities. Finally, we find that latent firing rates are better predictors of field potential signals compared with the binary spike events in the NHP datasets.
Significance.
This multiscale causality method can reveal the directed functional interactions across spatiotemporal scales of brain activity to inform basic science investigations and neurotechnologies.
Keywords: Causality, Multiscale, Spike trains, Field potentials, LFP, Neural encoding models
1. INTRODUCTION
Identifying the functional causality structure in brain networks is important for our understanding of neural mechanisms underlying brain functions and for designing neurotechnologies to decode and modulate brain states [1–11]. Further, many behaviors involve multiple spatiotemporal scales of neural activity, spanning not only neural spiking activity but also larger-scale neural population activity measured through local field potentials (LFP) [12–28]. Thus, identifying the causality structure can be important not only at a single scale of activity but also across different activity scales [2,12,29,30]. As many modern neurophysiological datasets provide measurements of the brain at multiple scales through simultaneous recordings of spike trains and field potentials [31,32], statistical tools that can assess multiscale causality are important to develop and validate. Further, it is important to study whether modeling the causality structure across different scales can lead to more accurate models of neural activity beyond what is possible through identifying a single-scale causality structure. Finally, neurophysiology experiments can record from only a subset of neurons in the brain and as such, functional causality is generally evaluated by Granger-like causality methods in which causality is statistically measured within the recorded data only. Regardless of the method used, a fundamental limitation of such Granger-like causality evaluation is that identified causal connections are not conditioned on the unrecorded activity (see also Discussion). To improve accuracy of Granger-like causality assessment, it is beneficial to consider as much data as possible within a given experimental recording. As spiking and field potential activity provide measurements of the brain at multiple scales [31, 32], considering both of these multiscale signals simultaneously could lead to more accurate causality analyses.
Identifying multiscale causality introduces additional challenges because of the signal differences in the spike train and field potential modalities. Spike trains consist of fast action potential events that take a binary 0–1 value while field potentials are continuous-valued signals [8,33–36]. Some prior multiscale studies focus on undirectional connectivity using correlation-based measures such as spike-field coherence [18,37–40] or on developing encoding models that fit correlation terms between signals [8,41,42]. But these studies do not focus on assessing causality and directional interactions between spike trains and field potentials. There are also studies on spike-field coherence that measures consistent neural spiking at a specific phase of LFP [43] and on model-free measures such as spike-triggered average of the LFP (stLFP) that assess interactions from spike trains to field potentials, but these measures are not always causal [30]. To assess causality, traditionally, Granger causality [44] is used for continuous signals like LFP and electroencephalography (EEG)/magnetoencephalography (MEG) [45–47]. Also, although Granger causality is not directly applicable for discrete signals that are not Gaussian processes [33], it has been used for filtered continuous signals generated from spike trains [47–49]. But assessing multiscale causality between spike trains and field potentials requires methods that can work on a mixture of both discrete and continuous signal modalities.
For binary spike trains alone, other methods for computing causality have also been developed beyond Granger causality [47,50–58]. Some methods use a generalized linear model (GLM) framework to model the spike trains as point processes [53, 54, 56, 57, 59]. Doing so, causality for spike trains can be computed using an information-theoretic measure termed directed information [53–56, 60], which is a generalization of Granger causality. But these methods are applicable within only spike trains rather than across spike trains and field potentials.
In general, methods for computing causality for spike trains or field potentials are either model-based or model-free. Model-based methods can explicitly incorporate the influence of various factors such as behavior on neural activity but depend on the accuracy of the constructed models. Despite this challenge, these methods have been shown to be useful tools for analyzing causality statistically and can reveal neurophyisological insights as shown in prior work [47, 56]. However, to ensure the accuracy of the estimated causality, these methods need to be carefully validated by assessing the accuracy of the underlying models in predicting the neural signals.
To measure causality in spike-field networks, one prior approach applied Granger causality by operating on the power spectrum of the spike trains computed using multitaper techniques in sliding bins [61]. This method is non-parametric and model-free. Thus, new methods are needed to produce an encoding model of spike-field network interactions as encoding models are often desired. Further, computing the spectrum required stationarity and did not consider the behavior. As a dynamic behavior such as movement makes the spectrum change over time, new methods are needed when a dynamic behavior is being performed to take it into account. Another prior approach computes a joint probability density across all signals [62]. But because computing this density is complex, this approach has focused on smaller networks, for example consisting of 3 signals or nodes [62]. As modern datasets contain recordings from tens or hundreds of electrodes, there is a need to develop and validate methods that can assess multiscale causality across larger networks. Further, as the predictor for field potentials, this prior approach directly used the binary spike trains [62]. However, compared with the measured binary spike trains, the firing rates of neurons may be a better predictor of field potentials [30,63]; but these firing rates are not measurable and are instead latent. Thus, firing rates are challenging to incorporate in a model of field potentials.
To address the above challenges in computing multiscale causality between binary and continuous spike-field signals, we recently developed a model-based Granger-like theoretical framework and tested it within numerical Monte Carlo simulations [64]. In this model-based Granger-like framework, a spike train is modeled as a point process GLM in which the instantaneous firing rate of each neuron is modeled as a function of the history of both the spike trains and the field potentials across the network. Further, in addition to their own history, field potentials can be modeled either as a function of the history of the measurable binary spike trains or the history of the latent firing rates. This framework resolves the above challenges through three main ideas. First, to enable assessing causality across networks consisting of several nodes/signals, it assumes that conditioned on the history of all signals—i.e. all spike trains and field potential time-series—, spike trains and field potentials at a given time are conditionally independent and thus their models can be separately estimated. Second, to enable using the latent firing rates of neurons as predictors of field potentials, the framework consists of a sequential maximum-likelihood estimation approach. It first fits the GLM model of the spike trains to estimate the latent firing rates and then uses these estimated latent firing rates to fit the model of field potentials. Third, time-varying dynamic behavior is modeled as covariates in both spike and field models. Thus, a stable measure of causality during behavior can be estimated. Together, these ideas resolve the challenge of estimating a large number of parameters, allow for firing rates to be predictors of field potentials, consider behavior, and generate a network encoding model. The two expanded parametric models can then be used to compute a multiscale causality measure in terms of directed information.
While this multiscale causality framework was shown effective within Monte Carlo simulations [64], its statistical tests to assess causality to field potential signals required repetitively splitting the data, which resulted in reduced data efficiency and redundant computation. To make the method suitable for real neural datasets, especially when assessing causality for a large number of signals in modern datasets that contain recordings from tens of electrodes, it is important to improve the data efficiency of the method because real datasets are length-limited and contain a large number of electrodes. Moreover, the framework was only tested in Monte Carlo simulations, and so it remained unclear whether multiscale causality can be recovered in more realistic biophysical simulations—where there exits a model mismatch between the fitted model and the ground truth network—or in real neural datasets. Further, it is not known whether multiscale spike-field network causalities exist in real neural data, and whether modeling these multiscale causalities would improve the prediction of neural signals beyond what is possible with single-scale causality. Finally, it is not known whether field potentials are better predicted from the history of the binary spike trains or that of the latent firing rates.
Here, we address the above problems by developing a new data-efficient statistical test procedure within our multiscale network causality method based on the Wald test [65], and by then demonstrating the multiscale network causality method on both biophysical simulations and experimental data collected from two non-human primates (NHP) during an arm reaching behavior. We refer to the network model with the identified causal connections as the multiscale spike-field causality graph. First, we show that our new test procedure is more data-efficient and can thus perform better with the same amount of training data. Second, we show that the method can identify multiscale causality in more realistic biophysical simulations of spike-field network activity in which the ground-truth network structure is known. Then, we apply the method to NHP spike-field data during motor behavior and show that given its data-efficiency, the method can perform causality tests within high-dimensional recordings from over 100 electrodes. Also, our results on NHP data suggest the existence of multiscale spike-field network causality. Further, we find that the multiscale causality method leads to models that improve the prediction of both spike trains and field potentials in NHP data. Finally, in the NHP datasets, we find that latent firing rates are better predictors of field potentials and explore the properties of different directed connections, such as their density as a function of distance or their density within vs. across brain regions.
2. METHODS
In this section, we first describe the spike-field causality graph identification problem. Then we describe the multiscale encoding model and the causality graph identification procedure. Finally we describe the experimental data during a motor task and the model evaluation measures.
2.1. Multiscale spike-field causality graph
We define a multiscale network as a collection of spike trains and field potentials, which we refer to as multiscale signals. The multiscale signals consist of the binary spike trains from neurons and continuous-valued field potential time-series. We denote the sets of spike trains and field potentials by and , respectively. To allow for the possibility that the timescale of spike trains is faster than field potentials, our model can use a smaller sample time for spike trains than that of field potentials if needed. In the model, spike trains are observed at time and field potentials are observed at time , where is the ratio between the sampling frequencies of field potentials and spike trains as a positive integer. Then the value of the -th spike train at time can be denoted by , and the value of the -th field potential at time can be denoted by (where the -th signal could be the one recorded from the -th recording channel for example).
We compute the causality between spike trains and field potentials by developing a multiscale model and using it to compute a directed information measure [60, 64], as we now describe. Assume that we have a recording length of , i.e. . We denote the likelihood function of the field potential , causally conditioned on all signals in the network up to time , by . Here indicates the union of sets and and indicates the relative complement of set in set , i.e. the elements in set that do not belong to . Similarly, we denote the likelihood function of a spike train , causally conditioned on all signals in the network up to time , by . Thus the conditional likelihood function of the samples of and can be denoted by and , respectively. We have
| (1) |
| (2) |
We now define the causality measure. Consider a signal and a signal , which can each be either spike train or field potential. Directed information [53–56,60,64] as a measure of causality from to is defined as the log-likelihood ratio
| (3) |
Given this definition, there is no causality from to if and only if
| (4) |
Intuitively, having no causality means that knowing the signal is not helpful in predicting the signal if one already knows all signals other than and .
We can also define a directed information rate as
| (5) |
Note that the history of all signals in the network are considered in Equation (4) to provide a measure of conditional causality. However, we can also condition on only the history of a subset of the network. In a special case, we can condition on no other network nodes to study unconditional causality. In this case, we can say that there is no unconditional causality from to if and only if
| (6) |
There are four possible kinds of causality in a multiscale network: spike-spike, spike-field, field-spike, and field-field. We can represent these causalities using an unweighted directed graph named causality graph. In this graph, each vertex represents a spike train or a field potential and each directed edge represents causality between two vertices.
2.2. Causality graph identification
Having defined the causality measure in the multiscale spike-field network, we need to estimate the likelihood models in Equation (1) and Equation (2) to compute it and develop a statistical test to assess the significance of causality. This estimation is based on our proposed multiscale parametric models defined above as we expand on below. We also devise the statistical tests for causality assessments below.
2.2.1. Spike train model and causality to spike trains.
A binary spike train can be modeled as a point-process GLM that depends on various covariates [33, 64], including the history of all observed spike trains, field potentials and the current behavioral states. Here we denote the behavioral states at time by . For each spike train at time , the model is fully specified by the instantaneous firing rate function .
Given any subset of spike trains and any subset of field potentials we write the logarithm of the firing rate of the spike train within the GLM framework as
| (7) |
where is a non-negative integer representing the length of history. Here with subscripts and superscripts are parameters to be estimated. All are vectors except . denotes the vector and denotes the vector . We note that all samples of spike trains from time to time are included as covariates in the GLM model above as can be seen in the first summation on the right side of Equation (7).
We denote the set of all unknown parameters (all ) in Equation (7) by . Elements in need to be estimated using maximum likelihood estimation (MLE) by maximizing the point process likelihood function of written as
| (8) |
where is the time-step used to bin the spikes [33,64]. Note that the likelihood of spike trains is evaluated at times because the field potential signal is only available at these times. However, the firing rates at time are evaluated using all samples of spike trains at every time-step from time to time as seen from Equation (7).
The MLE is given by
| (9) |
To find the set of signals that cause , we need to select the smallest sets and such that . This would mean that conditioning on signals other than the ones in and does not improve the likelihood function and thus all and only signals in cause . To select the hyperparameters , , and (i.e. history length), we devise a model selection procedure based on comparing with different hyperparameters [64]. We use the Akaike information criterion (AIC) for this selection [66] and thus for a given and we pick as follows:
| (10) |
where is the number of parameters with and with being the operator counting the number of elements in a given set. To determine whether a signal causes , by Wilk’s theorem [67], under the hypothesis that does not cause , we have
| (11) |
where denotes a chi-squared distribution with degree of freedom , if is a spike train and if is a field potential. If the p-value in this test is smaller than a desired threshold, we say significantly causes . This enables us to remove any signal in a given set that does not significantly cause the modeled spike train. We will further explain the model selection procedure in Section 2.2.3. For tests on spike train models, the threshold of p-value is set to 0.05 and we also control false discovery rate (FDR) using Benjamini-Hochberg procedure [68].
2.2.2. Field potential model and causality to field potentials.
We model a field potential using a linear Gaussian model. We assume a field potential is Gaussian distributed with time-variant mean at time and fixed variance . The mean of the field potential depends on various covariates, including the history of observed field potentials, the history of spike firing rates (which need to be estimated) and the current behavioral states. Instead of the history of spike firing rates, it is easy to use the history of the observed binary spike trains as predictors as well because these spike trains are directly observed. We can thus study whether the binary events or the firing rates are better predictors of the field potentials. Given any subset of spike trains and any subset of field potentials , we can write the mean of the field potential as
| (12) |
where is the history length for spike-field and field-field causality, which is a non-negative integer. Here with subscripts and superscripts are parameters to be estimated. Thus, the Gaussian likelihood function of the field potential is given by
| (13) |
We denote the set of all remaining unknown parameters by including all in Equation (12) and in Equation (13). Elements in still need to be estimated using MLE by maximizing the Gaussian likelihood function as
| (14) |
We now have to perform model selection and statistical tests of causality for the field potential models. In our previous work, this was done through a data-expensive and redundant empirical data-splitting process [64]. Here, we improve on the data efficiency of this method by devising an alternative analytical approach as described in the next paragraphs. The new method is better suited for neural data analyses as real datasets are length-limited and can contain recordings from many electrodes, thus introducing a large number of parameters and signals.
The new analytical method is devised as follows. Once are estimated, the covariance matrix of these estimates – i.e., covariance of – denoted by plays an important role in model selection procedure and statistical tests for causality as we will show below. Finding this covariance matrix is not straightforward. This is because we use the history of spike firing rates as predictors of field potentials and thus the spike train models have to be estimated before the field potential models can be estimated, resulting in a 2-step MLE problem for the field potential models. This means that in the second step of MLE, there are nuisance parameters in the spike models that are estimated from the first step. The latent spike firing rates computed using these nuisance parameters are different from the true values, and thus is also related to the variances of .
We thus need to estimate , which is the covariance of the parameters of the field potential model in the presence of nuisance parameters. To do so, we leverage a method developed for this covariance estimation in the presence of nuisance parameters [65]. Let’s use to denote the first order derivatives of a function w.r.t. and to denote the second order derivative of a function w.r.t. and . We define as the second order derivative of w.r.t. . Let be the second order derivative of w.r.t. then , and with . Also let , and where (see Equations (1), (2)). It can be shown that [65]
| (15) |
All variables in Equation (15) are evaluated at the estimated value of the parameters, i.e., at and . The first term in above is the same as the typical covariance in a 1-step MLE. The second term in is contributed by the uncertainty of the nuisance parameters due to the 2-step nature of the MLE here that affects the field potential model. Now that we have an estimate of , we can formulate the model selection procedure and statistical tests for assessing causality to field potential signals.
A model selection procedure is required when , , or are undetermined. For given and , we select the history length using an information criterion. For the multiscale model, there is uncertainty in contributed by , i.e., the second term in in Equation (15) and so AIC is not directly applicable. However, we can apply AIC to a model with only field potential signals. Thus, taking the history of spike-field connections to be no longer than the history of field-field connections in this case, we select the length of history in the multiscale model as:
| (16) |
where is the number of parameters with .
The estimated is then applied to statistical tests for assessing causality. We use the Wald test [65] to test whether a sub-vector of is 0 in Equation (12), and thus to determine whether a signal causes . The Wald statistic follows a distribution under the null hypothesis and is given by
| (17) |
where is any sub-vector of , is a sub-matrix of with selected rows and columns corresponding to and the degree of freedom is the length of . To assess causality from a signal to a field potential , we consider the that only contains parameters related to ; we then say does not cause when the p-value corresponding to the above test is larger than a threshold. We use a threshold of 0.05 for statistical tests and do separate FDR controls on spike-field and field-field connections in the following sections.
2.2.3. Model selection and causality assessment.
To find the set of signals that cause a spike train or a field potential, we use the above statistical tests described in Section 2.2.1 and 2.2.2. We now describe how we assess causality to a spike train and to a field potential signal, respectively.
For a spike train and another specific signal, we first model using its own history and the history of that other signal to decide if that specific signal unconditionally causes . We then construct the set to consist of all signals that significantly unconditionally cause . This allows us to narrow down the number of signals for which we need to compute the conditional causality to . We then proceed to testing the conditional causality within this set using Equation (11). In particular, we determine if each signal in significantly conditionally causes the modeled signal (i.e. when knowing the history of all other signals in set , does knowing still help the prediction of ). At a given significance level, we eliminate every insignificant from the set after all tests are done. This procedure provides the set of signals that significantly cause a spike train.
For a field potential signal , we first take to be i.e. all of the signals being recorded except itself. However, because these sets are high-dimensional, to reduce the computation complexity of model selection and make the method applicable to large channel counts, we devise a preprocessing procedure to reduce the number of signals that need to be considered in model-selection, i.e. the number of signals in . First, we fit a single-scale model with only field-field connections and remove the insignificant connections after FDR control from . The lengths of history are also selected using Equation (16). We then compute a residual for each field signal at each time point by subtracting the single-scale one-step-ahead prediction of the signal from its observed value (predicting the signal at the current time based on all past values of field potentials, see Section 2.4). This residual indicates the residual part of the field potential signal that is not predicted by the other field potential signals. Second, we consider each pairwise spike-field connection by fitting a pairwise field model for each residual series. Spike-field connections with p-values larger than threshold 0.05 are removed from . Together, these preprocessing steps provide us with a subset of signals before we do model selection for the multiscale model, thus reducing the complexity and allowing for causality assessment in large channel-sets.
Having obtained the , we fit the multiscale model and look at the p-values computed by Equation (17) for the causality of spike trains to the field potential signal and remove the spike train whose p-value is the largest and also larger than a relatively large threshold of 0.95 from the set and then fit the model again. This threshold means that the removed spike train has less than 5% chance of having a causal connection to the field potential and thus helps avoid false negatives. We repeat this removal and refitting procedure until all p-values corresponding to spike trains are smaller than the threshold. Then the remaining signals in are the candidates that may cause . Now, the p-values computed by Equation (17) are used to find all significant causalities to field potential signals (see also Section 2.2.2).
Based on prior evidence about the length of history for spike and field potential dynamics and for computational tractability, we consider a history length of up to 100ms for a spike train [33] and up to 300ms for a field potential [30] in our model selection procedure. History lengths around these values are generally considered long enough for spike train and field potential dynamics [30,33]. This means that we allow to be up to 10 and to be up to 30 as the NHP data is sampled at 100 Hz, i.e. at a time-step of .
2.3. Motor task and neural data recording
We use multiscale recordings from motor cortical areas of two Rhesus macaques performing a motor task [69]. The NHPs reached to objects located at different 3D locations for a liquid reward and then returned to the resting position before initiating another reach as described in [69]. For the first NHP J, 7 sessions of recordings were obtained from the dorsal premotor cortex (PMd), ventral premotor cortex (PMv), primary motor cortex (M1), and prefrontal cortex (PFC) contralateral to the arm using an array of 137 electrodes (Gray Matter Research, USA) where neighboring electrodes were spaced 1.5 mm apart in X and Y directions and the depth in Z direction was adjusted by the experimenter. For the second NHP C, 4 sessions of recordings were obtained from left PMd, right PMd, left PMv and right PMv using 128 electrodes in total from 4 arrays (Gray Matter Research, USA). Arm movements were tracked by reflective body markers attached to the subject’s skin. Marker locations were captured by near infrared cameras with sampling frequency of 100 frames per second (Motion Analysis Corp., USA). Behavioral covariates were taken as the 7 joint angle time-series corresponding to the shoulder, elbow and wrist movements (shoulder elevation, elevation angle, shoulder rotation, elbow flexion, pro supination, wrist flexion, and wrist deviation) [8]. Neural data was originally recorded with a sampling rate of 30 kHz. All surgical and experimental procedures were performed in compliance with the National Institute of Health Guide for Care and Use of Laboratory Animals and were approved by the New York University Institutional Animal Care and Use Committee.
As described in [69], local field potentials (LFPs) were extracted by applying a low-pass filter with 400 Hz cut-off frequency on the raw signals. Spike trains were obtained by band-pass filtering the raw signal from 0.3 to 6.6 kHz and then identifying the threshold crossings below the mean filtered signal. The threshold was set to 3.5 standard deviations [69]. We fit models both for all available channels in each monkey and for selected higher-quality channels. In the latter case, we eliminated low-quality noisy spike trains by keeping the 10 spike trains that can be best predicted using only behavioral states as predictors in GLM models for each session [8]. We then also used the field potentials recorded from these channels in our network causality analyses. Here we use the same sampling rate for spikes and LFPs of 100 Hz (i.e. ).
2.4. Prediction power
In the biophysical simulations, we can know the ground truth causality graph and compare that to the estimated causality graph. However, this is not the case for real neural data. As such, we evaluate the estimated causality graph in real data by asking how well the multiscale model with that causality graph can predict the spike trains and field potentials. In other words, we take the fitted multiscale model corresponding to an identified causality graph. We then use this fitted model to predict the signals one-step-ahead into the future. This means that we assess how well a signal can be predicted by the history of those signals that are identified as causing it within a fitted multiscale model. This way we can compare different causality graphs by comparing the prediction of their corresponding multiscale models. We refer to this one-step-ahead prediction capability as prediction power (PP) and define it for spike trains and field potentials as follows.
For each spike train, the one-step-ahead prediction of the continuous valued firing rates in Equation (7) can be computed from a model based on any given causality graph. Then given any threshold, we can predict the binary spike to be 1 if the one-step-ahead predicted firing rate exceeds the threshold and to be 0 otherwise. We can then construct a receiver operating characteristic (ROC) curve by sweeping the threshold and compute the area under the curve (AUC) of the ROC. We define the predictive power (PP) as PP=2×AUC-1 [8,13,42]. The range of PP is [0,1] in the training set but PP could be smaller than 0 in the test set. A perfect predictor achieves a PP score of 1 and a random predictor achieves a PP score of 0.
For each field potential, we find the one-step-ahead prediction of the field potential by computing from the multiscale model in Equation (12) based on the history of the signals that are identified as causing it in the identified causality graph. We define the normalized root mean-squared error (NRMSE) (the root mean-squared error normalized by the standard deviation of [70]) as
where is the mean of and the prediction is given in Equation (12). Given the NRMSE, for LFPs, we define PP=1-NRMSE. Thus the range of PP is also [0,1] in the training set but PP could be smaller than 0 in the test set. A perfect predictor achieves a PP score of 1 and a chance-level predictor achieves a PP of 0.
Our statistical tests are on functions of PP, for example on the PP increase ratio defined in Figure 3 that shows the ratio of improvement in PP between different cases (e.g., multiscale vs. single-scale). Further, we use cross-validation to evaluate PPs and assess statistical significance in tests on functions of PP.
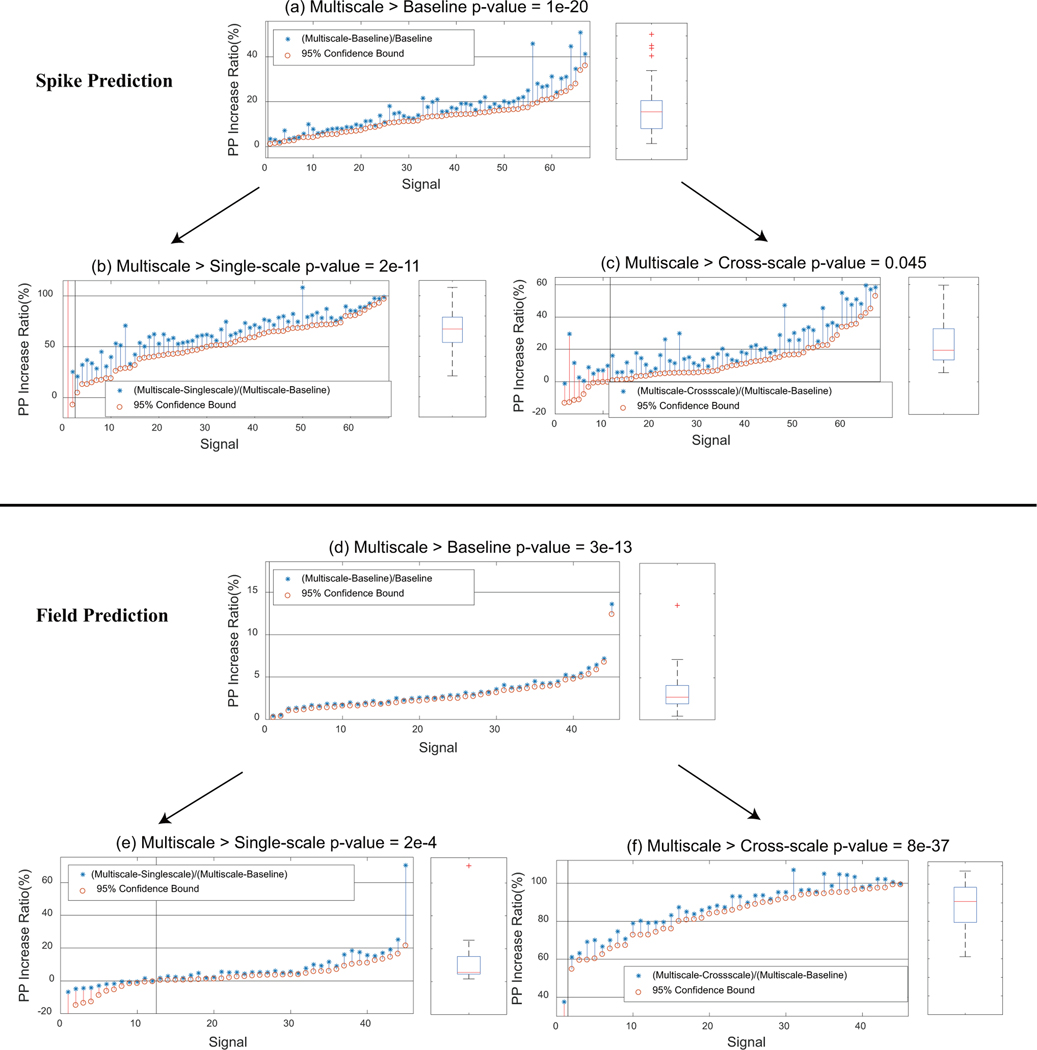
Figure 3.
(a–f) Multiscale causalities are successfully detected, thus improving the prediction of spike trains and field potentials. Signals—whether spike train signals in (a–c) or field potential signals in (d–f)—are sorted by the 95% confidence bound of PP increase ratios (these ratios are defined in the legends). PP increase ratios are significantly above 0 for signals to the right of the black vertical lines (p-value<0.05, one-sided t-test). Box plots to the right of each panel show the statistics of significant PP increase ratios, where the central mark is the median, the edges of the box are the 25th and 75th percentiles and the whiskers extend to the most extreme data points that are not outliers. Outliers are shown by red crosses and are points whose distance to the box is larger than 1.5 times of the box height. P-values are shown for comparing the average to 0 by one-sided t-tests. (a–c) Multiscale causalities improve the prediction of spike trains. (a) PP increase ratio from baseline to multiscale. Signals from all 11 sessions with multiscale connections are shown. (b) PP increase ratio from single-scale to multiscale. (c) PP increase ratio from cross-scale to multiscale. (d–f) Multiscale causalities improve the prediction of field potentials. (d) PP increase ratio from baseline to multiscale. Signals from all 11 sessions with multiscale connections are shown. (e) PP increase ratio from single-scale to multiscale. (f) PP increase ratio from cross-scale to multiscale.
Note we report p-values using the scientific notation used in MATLAB in which denotes .
3. RESULTS
In this section, we first show, using Monte-Carlo simulations, that the new statistical test on causality to field potentials in our multiscale causality method introduced in Section 2.2.2 works successfully and is data-efficient. We then use biophysical simulations with a known ground-truth causality graph to show that our method can identify the ground truth multiscale causality graph in realistic simulations of multiscale spike-field signals. Finally we use our method to examine multiscale causality in NHP spike-field neural data during a motor behavior.
3.1. Simulation showing data-efficiency of the newcausality method
To show data-efficiency of the statistical test for assessing causality to field potentials, we compare the new test to our original test in [64] using the same simulated data from [64]. In [64], 100 randomly generated 10-node networks with 16 connections were used to evaluate the performance of our original multiscale causality method. Note in our prior work, we only performed Monte Carlo simulations to validate the approach [64]. We apply our new statistical test to the 100 random networks and evaluate the AUC from data lasting for different lengths of 3-min to 24-min.
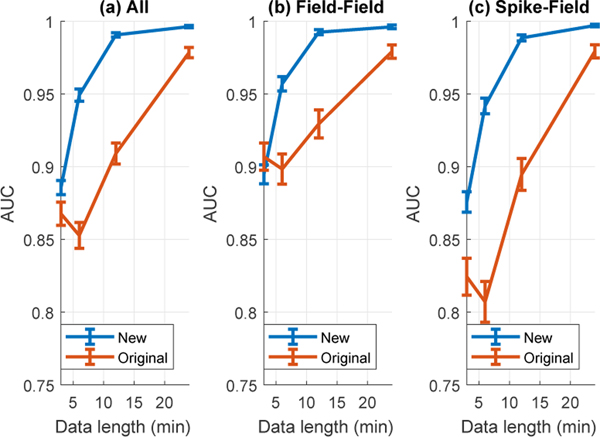
Figure 1 shows the comparison of AUCs of the two tests. We can observe that for any given length of data shown in Figure 1a, the new method has larger AUC than the original method used in [64]. At 3 min, the overall AUC using the new method is significantly larger than the original AUC by 2.1% (p-value=1.6e-2, one-sided paired t-test). At 12 min, the overall AUC using the new method is again significantly larger than the original AUC by 9.0% (p-value=8e-20, one-sided paired t-test). Furthermore, the new AUC achieved using 6-min data is larger than the original AUC using even 12-min data (p-value=0.008, one-sided paired t-test). These results show that the new method performs as well or better than the original method using much less training data and thus is more data-efficient than the original method.
Figure 1.
Comparison of new and original test procedures on causality to field potentials shows that the new method is more data-efficient. (a) AUC of field-field and spike-field connections with errorbar showing mean ± sem. (b) AUC of field-field connections with errorbar showing mean ± sem. (c) AUC of spike-field connections with errorbar showing mean ±sem. The new method can perform as well or better than the original method using much less training data.
3.2. Biophysical simulation
We use the Virtual Electrode Recording Tool for EXtracellular potentials (VERTEX) [71] to generate data from biophysical simulations. Given the position of electrodes, properties of neurons and tissues, VERTEX can calculate extracellular LFPs using a forward modeling approach [72].
3.2.1. Simulation settings.
The purpose of this simulation is to show that our method can identify the ground truth causality graph in a realistically simulated multiscale spike-field network. We simulate 10 sessions of spike-field data, with each session lasting 200 s. The placement of neurons are randomized for each session. For generality, each random simulated network includes all 4 types of causality: spike-field, field-field, spike-spike, field-spike. The overall simulated network structures are the same in each session but neurons are randomly placed in 4 different 3-D regions (A-D squares in the x-y plane in Figure 2a). The size of each region is 1 mm × 1 mm × 0.2 mm. The minimum distance between two connected regions is 6 mm. Neurons in a region are randomly placed in each session while electrodes recording LFPs are placed as shown in x-y plane with height .
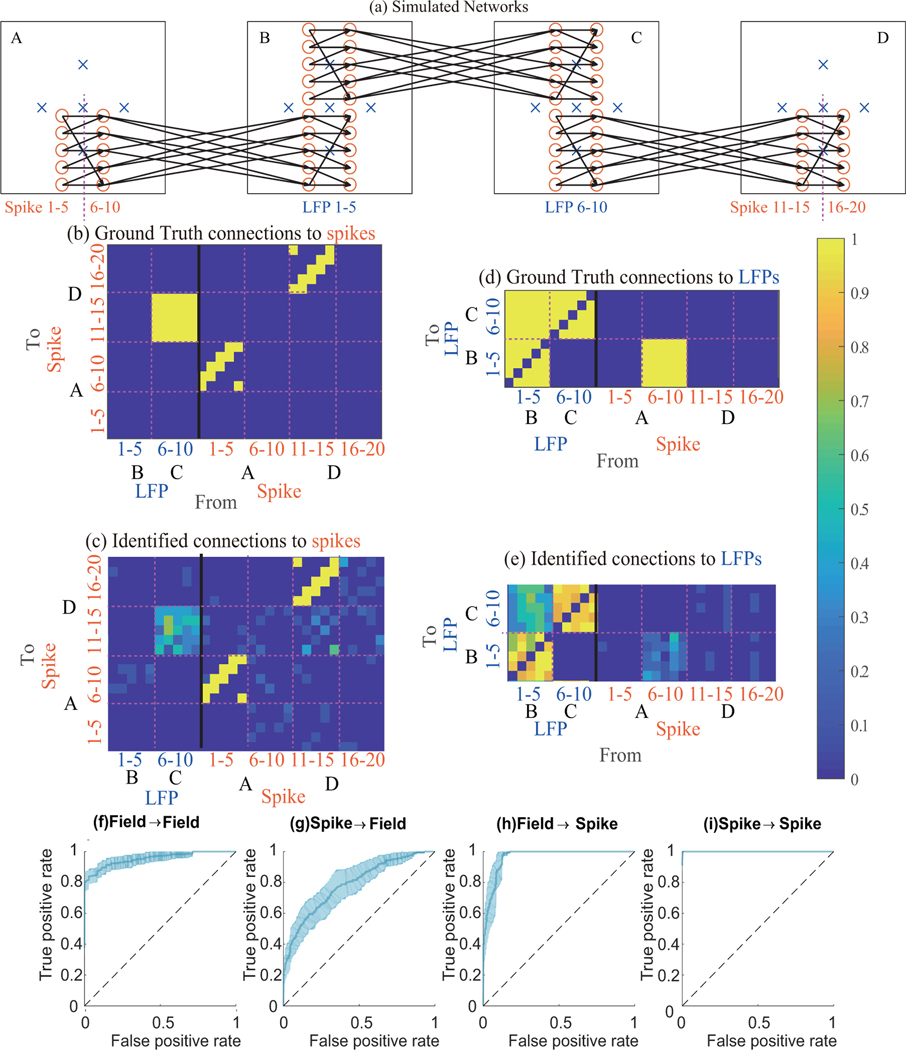
Figure 2.
Multiscale causality identification method can find the directed connections within spike-field networks in biophysical simulations. (a) Simulated network structure consists of 6120 neurons as detailed in Section 3.2.1. The figure shows 60 neurons (orange circles) and 20 electrodes (blue crosses) in 4 different 3-D regions (A–D squares in x-y plane). The size of each region is 1 mm × 1 mm × 0.2 mm. The minimum distance between two connected regions is 6 mm. Neurons in a region are randomly placed in each session while electrodes recording LFPs are placed as shown in x-y plane with height . A spike train is observed from each neuron. Connections between spike trains are shown in black arrows and are all from left to right. To have a clear ground truth between regions, 20 spike trains from regions A, D and 10 LFPs from regions B, C are modeled. (b–e) Ground truth and identified network between signals. The ground truth (b, d) and identified network (c, e) averaged across 10 sessions are shown. For (c, e), the colors indicate the ratio of sessions for which a positive connection was identified and the scale is shown by the color bar. (f–i) Receiver operating characteristic (ROC) curves of connectivity with shaded 95% confidence interval computed using the ground truth and identified networks. Our method can successfully identify (f) field-field (g) spike-field (h) field-spike and (i) spike-spike connections in the multiscale spike-field networks.
Each simulated network contains 6120 neurons. We chose our simulated network and its parameters such that we can have realistic firing rates with a reasonable number of simulated neurons and a known ground truth causality to which we can compare. Among all neurons, a network of 60 neurons (orange circles) and 20 electrodes (blue crosses) are shown in Figure 2a. The weight of the synapses is 1100 pA for every connection between these neurons. Each of the 60 displayed neurons has an input from another neuron not shown in the figure through a synapse with a weight of 4000 pA. This input neuron fires with Poisson statistics at a rate of 10 Hz if connected to a displayed neuron without other inputs or 5 Hz otherwise. Each of the 30 displayed neurons with no displayed input from the same region also has an output to another 200 neurons within the same region through synapses with a weight of 2200 pA. All neurons are excitatory pyramidal neurons. Synapses are single exponential current-based and the axon arbor is uniformly distributed within the region. Other synapse properties are specified in Table 1. The structural and passive properties are the same as the layer 2/3 pyramidal neuron model described in [71]. The 60 neurons shown in Figure 2a and the 6000 neurons driven by them follow the same adaptive exponential (AdEx) model [73] with parameters specified in Table 1. These neurons also have random current input following Ornstein Uhlenbeck process with parameters also specified in Table 1.
Table 1.
Parameters of neurons, synapses and input currents in the biophysical simulation. AHP here refers to after-hyperpolarization.
| Name | Value |
|---|---|
|
| |
| spike generation threshold | −50 mV |
| spike steepness parameter | 1 mV |
| scale factor of AHP current | 2.6 nS |
| AHP current time constant | 25 ms |
| AHP current instantaneous change | 600 pA |
| reset membrane potential | −60 mV |
| cutoff membrane potential | −45 mV |
| synapse exponential decay time constant | 2 ms |
| axon conduction speed | 0.3 m/s |
| synapse release delay | 0.5 ms |
| input current mean | 100 pA |
| input current std | 30 pA |
| input current time constant | 2 ms |
The raw output from VERTEX includes spike timings and LFPs. The original sampling rate of LFPs is 1 kHz. Under the above simulation settings, neurons rarely spike more than once every 5 ms as expected. The maximum considered here is also 30 for field potentials and 10 for spikes. For spikes, we generate spike trains from spike timings. To obtain the spike trains, we generate time-series of 0’s and 1’s by binning the spikes in 5ms time bins. If there is a spike in a time bin, we set the value of the spike train at that time to 1 and if there is no spike in a time bin, we set the value of the spike train at that time to 0. For LFPs, we down-sample the LFP signals at 100Hz sample rate and standardize them to have zero mean and unit variance. Example simulated spike and LFP signals are shown in the Appendix.
3.2.2. Multiscale causal connections can be identified in biophysical simulations.
To have a clear ground truth between regions that we can then use for assessment, we select 20 spike trains from regions A and D and 10 LFPs from regions B and C as shown in Figure 2a. All our subsequent analyses will focus on these signals. The ground truth causality graph for these signals is shown in Figure 2b, d, with former showing the causality to the spike trains in area A and D and the latter showing the causality to LFPs in regions B and C. For spike-spike connections, the ground truth is the same as synapse connections and causal connections are shown with yellow. For the other 3 types of connections, each LFP in a region is caused by every direct synaptic input to that region and also causes every signal in that region and every signal in the next region with direct synaptic connections. Thus for these 3 types of connections, the true causal connections are shown between regions (rather than being at the level of synapse connections) in yellow.
We apply the multiscale causality algorithm to each session of the simulated data. A causality from one signal to another is defined as positive if the first signal causes the second. A positive causality in an identified network is true positive if the ground truth is positive. It is false positive if the ground truth is negative. Then we can also compute the true positive rate and false positive rate by dividing the number of true positives and false positives by the number of positives and negatives in ground truth, respectively.
The ratio of sessions for which a positive causality was identified from each signal to another signal is shown by the color in Figure 2c, e. Comparing with the ground-truth causal connections in Figure 2b, d, this figure suggests that the method is successful in identifying causal connections.
To quantify this performance, we plot the receiver operating characteristic (ROC) curves for different kinds of connections by sweeping the threshold of p-values from 0 to 1 (p-values used for causality detection). The average ROC curves across 10 sessions with shaded 95% confidence are shown in Figure 2f–i. We find the area under the ROC curve (AUC) in each case. The chance-level AUC is 0.5, which we compare to. As we can observe from Figure 2i, true spike-spike causalities are accurately detected and the associated AUC is 0.999 ± 0.001 (mean ± std), which is significantly larger than chance level of 0.5 (p-value=9e-26, one-sample one-sided t-test). In addition, for field-field, spike-field and field-spike causality, the AUCs are shown in Figure 2f–h and are 0.95 ± 0.04, 0.79 ± 0.10 and 0.91 ± 0.14, respectively. All these AUCs are also significantly larger than the chance level of 0.5 (p-values=2e-11, 5e-6 and 3e-6, respectively; one-sample one-sided t-test).
3.3. Multiscale causal connections improve prediction of spike trains and field potentials in NHP datasets
Having established that the multiscale causality graph can be significantly identified in biophysical simulations, we next examined whether multiscale causal connections were also identified in real NHP motor datasets and if so whether their identification improved the prediction of spike-field activity. To investigate these questions, we define four types of PP to be compared: baseline, single-scale, cross-scale, and multiscale. Multiscale PP is the PP of full models that contain all kinds of connections including multiscale causal connections between spike-field and field-spike, as well as self-history for each signal. Baseline PP is the PP of a model acquired by removing causal connections from the full models and considers only self-history in prediction of a given signal. Single-scale PP is the PP of models acquired by removing spike-field and field-spike connections from the full models. Cross-scale PP is the PP of models acquired by removing spike-spike and field-field connections except self-history from the full models. All PP’s are computed in cross-validation as described in Methods. As a first validation and for easier visualization, in Sections 3.3.1 and 3.3.2, we focus on the causality analyses with the higher-quality 10-channel sets. In later sections, we repeat these analyses when using all channels and further provide all the other results by including all of the channels in the analyses. All conclusions are similar in the 10-channel sets and the all-channel set analyses.
3.3.1. Spike train prediction.
Here we examine spike trains and find that the identified multiscale causalities improve the prediction of spike trains in cross-validation. To show a meaningful comparison, we compute these improvements for spike trains with at least one single-scale (spike-spike) and one cross-scale (field-spike) connection in all 5 cross-validation folds. In this section we focus on a high-quality 10-channel set for each session for easier visualization and validation, and then we confirm that our conclusions for all-channel analyses are similar in Section 3.3.3.
Figure 3a shows that multiscale PP is significantly larger than baseline PP for all signals with multiscale connections (p-value<0.05 by one-sided t-test). We then asked whether the PP improvement over baseline was due to single-scale or cross-scale causal connections being identified. To answer this question, we found the normalized improvement of multiscale PP vs. both single-scale PP (p-value = 2e-11, one-sided t-test) and cross-scale PP (p-value = 0.045, one-sided t-test) as in Figures 3b and 3c, respectively. We can see when considering both connection types instead of just spike-spike or field-spike connections, most of the PPs (97.0% and 83.6% of PPs) for a spike train are significantly improved (p-value<0.05 by one-sided t-test). Figure 3b shows the normalized PP improvement contributed by field-spike connections was on average 66.0% for the significant signals, while Figure 3c shows the normalized PP improvement contributed by spike-spike connections was on average 24.7% for the significant signals. This result suggests that both spike-spike and field-spike causal connections are successfully identified, leading to improved prediction of spikes. Further, this result suggests that multiscale connections (from field potentials to spikes) exist and their identification helps the prediction of spike trains.
Interestingly, overall on average across signals, cross-scale connections were more important compared to single-scale connections in improving PP of spike trains (p-value=8e-20 by one-sided Wilcoxon rank sum test). This result suggests that the unique contribution from field potentials to spike train prediction is more than that from the spike trains.
3.3.2. Field potential prediction.
We next consider field potentials and find that the identified multiscale connections also improve the prediction of field potentials. Here we focus on the high-quality 10-channel sets for easier visualization and validation and then confirm that our conclusions for all-channel analyses are similar in Section 3.3.3. Similar to Figure 3a–c, Figure 3d–f show the PP improvements for field potentials that had at least one field-field connection and one spike-field connection identified in all 5 folds. Multiscale PP significantly improved compared with baseline PP for all signals with multiscale connections (p-value<0.05 by one-sided t-test). We then asked whether the improvement over baseline was due to single-scale or cross-scale causal connections being identified. To answer this question, we found the normalized improvement of multiscale PP vs. both single-scale PP (p-value = 2e-4, one-sided t-test) and cross-scale PP (p-value = 8e-37, one-sided t-test) as in Figure 3e and 3f, respectively. We can see that when considering both spike-field and field-field connections instead of just one kind of connection, 73.3% and 97.8% of the PPs were significantly improved, respectively (p-value<0.05 by one-sided t-test). Figure 3f shows that the normalized PP improvement contributed by single-scale (field-field) connections was on average 88.4%, while Figure 3e shows that the normalized PP improvement contributed by cross-scale (spike-field) connections was on average 10.3%. This result suggests that both spike-field and field-field causal connections are successfully identified, leading to improved prediction of field potentials. Further, this result suggests that multiscale connections (from spike to fields) exist and that is why their identification helps the prediction of field potentials.
Comparing the single-scale and cross-scale contribution to PP’s reveals that for field potential prediction, single-scale causal connections are more important than cross-scale ones. On average, the normalized PP improvement contributed by single-scale (field-field) connections (88.4%) shown by Figure 3f is much larger than that by cross-scale (spike-field) connections (10.3%) shown by Figure 3e (p-value 3e-16 by one-sided Wilcoxon rank sum test). This result shows that the unique contribution to field potential prediction from field potentials is much larger than that from spike trains.
3.3.3. Prediction considering all signals.
We now consider all channels and study how much multiscale connections improve the prediction of signals by considering all observed signals. The models are fitted using the first 80% of samples and the PPs are computed using the last 20% of samples as test set. Similar to 10-channel sets, we find that the identified multiscale causal connections improve the prediction of both spikes and field potentials. For signals with multiscale connections, the mean of PP increase ratios of spikes from baseline to multiscale model was 58% (p-value 0.004; one-sided t-test). The mean of PP increase ratios of fields from baseline to multiscale model was 6.4% (p-value 2e-47; one-sided t-test). Compared with the 10-channel sets, the improvement from baseline to multiscale is larger for all-channel sets because there are more connections being modeled in this latter case. Also, the associated averaged PP increase ratios across sessions from baseline, single-scale or cross-scale to multiscale models are summarized in Table 2. Similar to 10-channel set results, more PP improvement is contributed by field-spike or field-field connections than spike-spike or spike-field connections. All analyses that follow are done by considering all channels together.
Table 2.
Mean and sem of averaged PP increase ratio across sessions from baseline to multiscale, and from single-scale or cross-scale to multiscale models of all signals with multiscale connections. P-values are computed by one-sided paired t-tests.
| PP increase ratio | monkey | mean | sem | p-value | |
|---|---|---|---|---|---|
|
| |||||
| Spike | From Baseline to Multiscale: | J | 71.5% | 37.3% | 0.03 |
| (multiscale PP - baseline PP)/baseline PP | C | 38.7% | 3.4% | 2e-19 | |
| From Single-scale to Multiscale: | J | 76.3% | 5.0% | 4e-31 | |
| (multiscale PP - single-scale PP)/(multiscale PP - baseline PP) | C | 58.3% | 3.7% | 4e-28 | |
| From Cross-scale to Multiscale: | J | 13.9% | 6.0% | 0.01 | |
| (multiscale PP - cross-scale PP)/(multiscale PP - baseline PP) | C | 26.2% | 3.7% | 1e-10 | |
|
| |||||
| Field | From Baseline to Multiscale: | J | 7.8% | 1.0% | 4e-8 |
| (multiscale PP - baseline PP)/baseline PP | C | 6.2% | 0.31% | 2e-41 | |
| From Single-scale to Multiscale: | J | 2.7% | 0.9% | 3e-3 | |
| (multiscale PP - single-scale PP)/(multiscale PP - baseline PP) | C | 0.51% | 0.16% | 8e-4 | |
| From Cross-scale to Multiscale: | J | 91.6% | 1.0% | 7e-28 | |
| (multiscale PP - cross-scale PP)/(multiscale PP - baseline PP) | C | 97.6% | 0.41% | 5e-168 | |
3.4. Latent firing rates predict field potentials betterthan binary spike trains
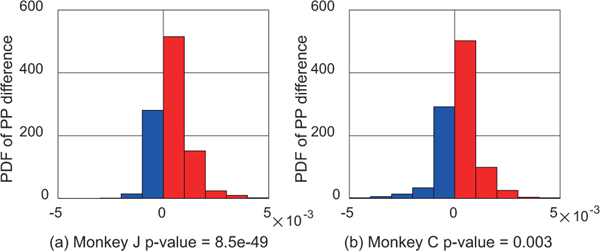
In addition to handling the case of large networks, one advantage of our multiscale causality identification framework is that it allows our multiscale models to use either the latent spike firing rates or the observed spike events as field potential predictors. This can then allow us to test the hypothesis that latent firing rates may be better predictors of field potentials as could be implied from biophysical models [63]. We thus used our framework to test this hypothesis within the NHP datasets. As a comparison, we trained an alternative multiscale model with the same length of history. Figure 4 shows the multiscale PP difference between two models. We find that using the latent firing rates predicts the field potentials better than using the observed binary spike trains (p-value= 8.5e-49 for monkey J and 0.003 for monkey C, one-sided paired t-test). This result indicates that the latent firing rates contain more information than binary spike trains about field potentials. This result is consistent with the prediction in biophysical studies suggesting firing rate can be an LFP proxy [63].
Figure 4.
Our method using latent firing rates predicts field potentials better than using binary spike trains. Panels (a) and (b) show the probability density function (PDF) of PP difference using firing rates vs. using spike trains for monkeys J and C, respectively. PP differences greater than 0 are shown in red and the rest are shown in blue. In most cases, PP differences are positive indicating that latent firing rates are better predictors of field potentials overall. The PPs are computed for all field potentials. The p-values are computed with one-sided paired t-test and indicate that PPs are larger when using latent firing rates compared to using binary spike trains as predictors.
3.5. Properties of causal connections
3.5.1. Density of Connections and correlations to distance.
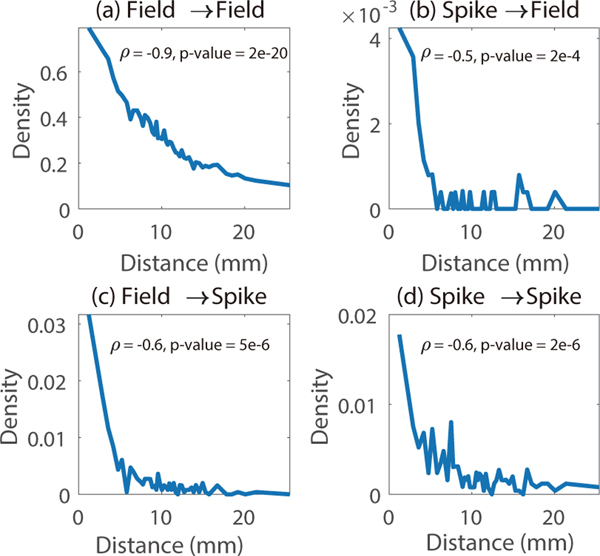
We next examined the density of connections and whether there was a relationship between the physical distance from a given signal and the density of connections from that signal. To do so, we evenly cut the sorted distances into 50 groups. Density in each group is defined by the ratio between the number of identified connections and all possible connections in that group. The distance representing each group is defined as the average of lower and upper bound of the distances in the group. Figure 5 shows the results of the correlation analyses between the distance of causal connections and their density for (a) field-field, (b) spike-field, (c) field-spike, and (d) spike-spike connections.
Figure 5.
Causal connection density from a signal is negatively correlated to physical distance from that signal. Pearson’s correlation between the physical distance (mm) from a signal and the corresponding density of connections from that signal is shown for (a) field-field (b) spike-field (c) field-spike and (d) spike-spike connections in monkey J’s dataset where we have 3-D coordinates of electrodes. There is a significant negative correlation between distance and density of connections for all connection types.
We find that there was a significant negative correlation between distance and density for all types of connections (p-value=2e-20, 2e-4, 5e-6 and 2e-6, respectively, Pearson’s correlation test). This result suggests that the density of the directed functional connectivity represented by directed information is negatively correlated with physical distance for connections from field potentials and also from spike trains.
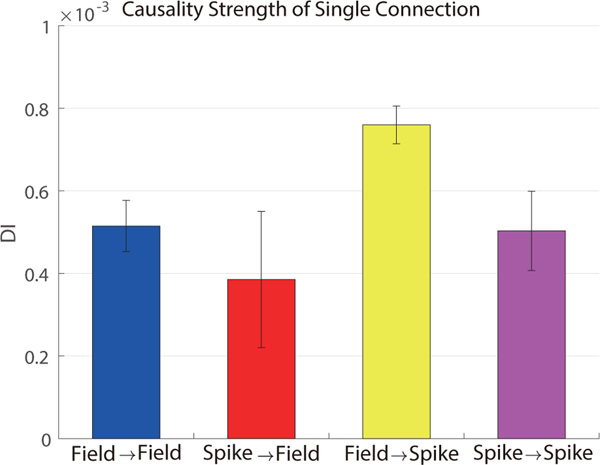
3.5.2. Strength of causality
We then examined the strength of causality between two signals. From section 3.5.1, the density of field-field connections is much larger than that of other kinds of connections. This may be due to field potentials being aggregate network-level signals that contain information from groups of neurons nearby. Here we examined the average strength of individual connections measured by directed information across 11 sessions shown in figure 6. The strength of field-spike connections was significantly larger than the strength of spike-spike connections (p-value = 0.008, paired one-sided t-test) but the strength of field-field connections was not significantly different from the strength of spike-field connections (p-value=0.46, two sided t-test). This latter result suggests that field-field causality improves the prediction power of field potentials more than spike-field causality (see section 3.3.2) mainly because of the larger density of field-field connections as the individual field-field and spike-field connection strengths are comparable.
Figure 6.
Average individual-connection strength of four types of causal connections measured by directed information (DI) with errorbar (mean ± sem) across sessions.
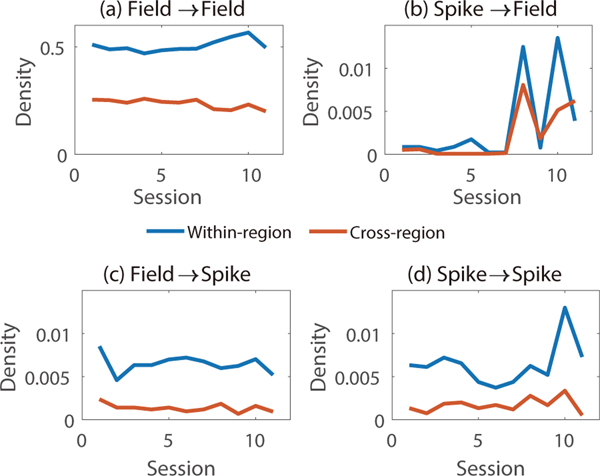
3.5.3. Causal connections within vs. across regions.
We also compared the density of causal connections across regions with that within regions. The electrode arrays were placed in different cortical regions via an MRI guided stereotax [69]. The regions for the two NHPs are specified in Section 2.3. Figure 7 shows the density of within-region and cross-region connections in each session. We can observe that the method identifies that there are more within-region connections than cross-region connections for each kind of connection (p-values: 9e-10, 0.1, 2e-9 and 1e-5, respectively; one-sided paired t-test).
Figure 7.
Within-region and cross-region density of four kinds of connections in each session.
4. DISCUSSION
Here we explore the causality structure in multiscale spike-field networks and demonstrate a multiscale spike-field causality graph identification method based on directed information in realistic biophysical simulations and in motor cortical spike-LFP data during motor behavior from two NHPs. We show that the method is data-efficient and can successfully identify the multiscale causal connections in biophysical simulations. Further, our method reveals that multiscale spike-field network causality exists in NHP spike-field motor cortical data during arm movements and can be identified; indeed, models that included the identified multiscale causal connections better predicted both spike trains and field potentials compared to models that just included either single-scale or cross-scale connections. Finally, compared to using the binary spike trains as predictors, our method better predicted the LFPs by uniquely allowing for latent firing rates to be used as LFP predictors. These results show how causality can be computed in multiscale binary-continuous data reflected in spike-field measurements and how multiscale causality identification improves the modeling of spike-field network activity.
Prior directed information measures of causality have been developed for a single scale of activity, e.g. spikes [53–56, 60]. Our method extends and demonstrates the directed information measure for estimation of multiscale causality in mixed binary-continuous spike-field signals. The multiscale directed information measure is a causal directional measure, and thus is distinct from prior non-causal measures to assess spike-field connectivity including spike-field coherence [18,37–40] or measures in encoding models that use the LFP features at a given time to predict the spikes at the same time [8,42] or to study correlations [41].
Our method is a model-based Granger-like causality method. There are some general limitations for these methods [56,74]. First, these methods depend on building statistical models of the phenomena, and thus depend on the accuracy of these models. Indeed, that is why as our main measure of how accurately causality is estimated in NHP data, we consider the model with the identified causality network, and find this model’s predictions for the measured spiking and LFP signals. As these signals are observations from the latent causality network, their better prediction can imply a better causality identification by our method. By comparing these predictions for models with the identified single-scale causality vs. models with the identified multiscale causality, we find that multiscale causality identification improves the prediction of both spike trains and LFP signals. Second, a fundamental challenge for assessing causality is that factors that are not measured in a given experiment cannot be considered or conditioned on in any causality method. Thus, the causality graph identified from the neural signals measured in an experiment provides a measure of network interactions within the measured network only and without conditioning on the unmeasured elements. Despite this challenge, model-based Granger-like causality is still a useful tool for analyzing functional connectivity statistically and could reveal insights about the neurophysiology as shown in prior work [47, 56], for example for activity during sleep or during visuomotor integration. Our work on modeling multiscale causality fills an important gap for such analyses because it allows us to model all observed signals in a given experiment for better causality assessment by including both field potentials and spike trains rather than just one or the other. As such the method enables including more factors/neural elements when assessing causality.
The method demonstrated here has several unique features. First, it allows multiscale causality to be assessed for large networks, which is needed for modern electrophysiology datasets that record from tens of electrodes. We demonstrated this capability by showing that the method can compute multiscale connections across a large number of spike and LFP signals in NHP data and in biophysical simulations. Second, our method allows the use of latent firing rates as field potential predictors. The use of latent firing rates was motivated by biophysical suggestions that firing rates may be better LFP predictors compared to binary spike events [63]. Our results confirmed this biophysical conclusion. We found that in our NHP data, the estimated history of firing rates predicted the LFPs better than the history of binary spike trains. Also, our new multiscale causality test procedure based on the Wald test was more accurate for a given training data length, and thus was data-efficient. This is key for assessing causality in high-dimensional data recorded across large-scale brain networks. Finally, our method generates an encoding model of spike-field network activity during behavior that is more predictive of neural data compared with models that only use single-scale causality.
It is also important to note that by explicitly modeling a dynamic behavior as a covariate in the spike model in Equation (7) and field model in Equation (12), the method can take into account non-stationarities that are due to a changing behavioral signal that modulates the neural signals. Having modeled the changing behavior, the method then assumes that spike and field potential models are stationary within the typical time-lengths of a dataset. If the data time-length is much longer, it may be that the models change for example due to plasticity. Future work can thus explore refitting the models intermittently or adaptively for more accurate causality assessment.
We found that the density of causal connections is negatively correlated with physical distance for connections in the NHP motor cortical data. This is consistent with a prior study [8] which has shown that the strength of non-causal correlations from LFP to spike trains drops over distance. It is also consistent with prior studies showing spike-LFP coherence drops over distance [29,75].
One future direction would be to explore whether the model selection procedure in this work may be further improved using regularization methods. Regularization methods like ridge or LASSO [76, 77] can help reduce over-fitting and can potentially be integrated into our method. However, because of the two-step model fitting procedure in our method and the fact that the distribution of regularized parameters within a regularization method are hard to find, it would be hard to statistically test the significance of causal connections with such a regularization procedure [78]. Nevertheless, a future direction could be to solve this challenge and assess whether regularization can further improve our method of multiscale causality identification.
The multiscale spike-field causality graph identification method demonstrated here can also be applied to other brain regions and behaviors to discover the multiscale causal interactions in spike-field networks that drive these behaviors. One can also use this method to explore the dependence of multiscale causality in a given brain region on behavioral and task context, or to study how the causal network topology may change as a result of adaptation, learning or plasticity [79–83]. This method can also inform the design of future closed-loop neural control systems such as brain stimulation systems [1, 3, 4, 84–98]. For example, a major question in developing deep brain stimulation (DBS) therapies for mental disorders such as treatment-resistant depression is which site within the brain should be stimulated [1,4,92]. This method can provide one approach to identify candidate sites by finding the brain site that has the strongest causal connection to the cortico-limbic regions involved in mental disorders. This method can thus help develop future closed-loop DBS systems for mental disorders that aim to causally modulate symptom-related neural activity using the decoded symptom as feedback [1,3,4,87,92–94,96]. More generally, this method can facilitate the investigation of causal directed interactions in large-scale brain networks, whose findings can guide the development of more effective neurotechnologies.
Acknowledgments
The authors acknowledge support of Office of Naval Research (ONR) Young Investigator Program (YIP) under contract N00014-19-1-2128.
Appendix
Here we show an example of simulated data from networks shown in Figure 2a. As mentioned in Section 3.2, we use VERTEX [71] to generate the simulated data. The raw output from VERTEX includes spike timings and LFPs. The sampling rate is 1 kHz. Then, we generate the binary spike trains using 5-ms time bins. If there is a spike in a time bin, the corresponding value of the spike train is 1. If there is no spike in a time bin, the corresponding spike train value is 0. LFPs are downsampled to 100 Hz and standardized to zero mean and unit variance. Figure 8 shows 20 example spike trains and 10 example LFPs during a 10-second period.
Figure 8.
We show 20 example spike trains and 10 example LFPs observed from a network shown in Figure 2a during a 10-second period. Sampling rates are 100 Hz for LFPs and 200 Hz for spikes (i.e., 5-ms spike bins). The regions to which the LFP and spike train signals belong are indicated by A-D. These regions as well as the LFP and spike train numberings are the same as in Figure 2a.
References
- [1].Shanechi Maryam M. Brain-machine interfaces from motor to mood. Nature Neurosceince, 22:1554–1564, 2019. [DOI] [PubMed] [Google Scholar]
- [2].Liu Tony, Ungar Lyle, and Kording Konrad. Quantifying causality in data science with quasi-experiments. Nature Computational Science, 1(1):24–32, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Yang Yuxiao, Qiao Shaoyu, Sani Omid G, Sedillo J Isaac, Ferrentino Breonna, Pesaran Bijan, and Shanechi Maryam M. Modelling and prediction of the dynamic responses of large-scale brain networks during direct electrical stimulation. Nature Biomedical Engineering, pages 1–22, 2021. [DOI] [PubMed] [Google Scholar]
- [4].Hoang Kimberly B., Cassar Isaac R., Grill Warren M., and Turner Dennis A.. Biomarkers and stimulation algorithms for adaptive brain stimulation. Frontiers in Neuroscience, 11:564, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Friston Karl J. Functional and effective connectivity: a review. Brain connectivity, 1(1):13–36, 2011. [DOI] [PubMed] [Google Scholar]
- [6].Schneidman Elad, Berry Michael J, Segev Ronen, and Bialek William. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature, 440(7087):1007–1012, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Pillow Jonathan W, Shlens Jonathon, Paninski Liam, Sher Alexander, Litke Alan M, Chichilnisky EJ, and Simoncelli Eero P. Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature, 454(7207):995–999, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Bighamian Ramin, Wong Yan Tat, Pesaran Bijan, and Shanechi Maryam M. Sparse model-based estimation of functional dependence in high-dimensional field and spike multiscale networks. Journal of neural engineering, 2019. [DOI] [PubMed] [Google Scholar]
- [9].Shanechi Maryam M. Brain–machine interface control algorithms. IEEE Trans. Neural Syst. Rehabil. Eng, 25(10):1725–1734, 2017. [DOI] [PubMed] [Google Scholar]
- [10].Tu Tao, Schneck Noam, Muraskin Jordan, and Sajda Paul. Network configurations in the human brain reflect choice bias during rapid face processing. Journal of Neuroscience, 37(50):12226–12237, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Jamali Mohsen, Grannan Benjamin L, Fedorenko Evelina, Saxe Rebecca, Báez-Mendoza Raymundo, and Williams Ziv M. Single-neuronal predictions of others’ beliefs in humans. Nature, 591(7851):610–614, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Abbaspourazad Hamidreza, Choudhury Mahdi, Wong Yan T, Pesaran Bijan, and Shanechi Maryam M. Multiscale low-dimensional motor cortical state dynamics predict naturalistic reach-and-grasp behavior. Nature communications, 12(1):1–19, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Truccolo Wilson, Hochberg Leigh R, and Donoghue John P. Collective dynamics in human and monkey sensorimotor cortex: predicting single neuron spikes. Nature neuroscience, 13(1):105, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Susilaradeya Damar, Xu Wei, Hall Thomas M, Galán Ferran, Alter Kai, and Jackson Andrew. Extrinsic and intrinsic dynamics in movement intermittency. Elife, 8:e40145, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Hall Thomas M, de Carvalho Felipe, and Jackson Andrew. A common structure underlies low-frequency cortical dynamics in movement, sleep, and sedation. Neuron, 83(5):1185–1199, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Bansal Arjun K, Truccolo Wilson, Vargas-Irwin Carlos E, and Donoghue John P. Decoding 3d reach and grasp from hybrid signals in motor and premotor cortices: spikes, multiunit activity, and local field potentials. Journal of neurophysiology, 107(5):1337–1355, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Schoffelen Jan-Mathijs, Oostenveld Robert, and Fries Pascal. Neuronal coherence as a mechanism of effective corticospinal interaction. Science, 308(5718):111–113, 2005. [DOI] [PubMed] [Google Scholar]
- [18].Pesaran Bijan, Pezaris John S, Sahani Maneesh, Mitra Partha P, and Andersen Richard A. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nature neuroscience, 5(8):805, 2002. [DOI] [PubMed] [Google Scholar]
- [19].Nguyen David P, Wilson Matthew A, Brown Emery N, and Barbieri Riccardo. Measuring instantaneous frequency of local field potential oscillations using the kalman smoother. Journal of neuroscience methods, 184(2):365–374, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Perel Sagi, Sadtler Patrick T, Oby Emily R, Ryu Stephen I, Tyler-Kabara Elizabeth C, Batista Aaron P, and Chase Steven M. Single-unit activity, threshold crossings, and local field potentials in motor cortex differentially encode reach kinematics. Journal of neurophysiology, 114(3):1500–1512, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Stavisky Sergey D, Kao Jonathan C, Nuyujukian Paul, Ryu Stephen I, and Shenoy Krishna V. A high performing brain–machine interface driven by low-frequency local field potentials alone and together with spikes. Journal of neural engineering, 12(3):036009, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Hsieh Han-Lin, Wong Yan T, Pesaran Bijan, and Shanechi Maryam M. Multiscale modeling and decoding algorithms for spike-field activity. Journal of Neural Engineering, 16(1):016018, Dec 2018. [DOI] [PubMed] [Google Scholar]
- [23].Flint Robert D, Lindberg Eric W, Jordan Luke R, Miller Lee E, and Slutzky Marc W. Accurate decoding of reaching movements from field potentials in the absence of spikes. Journal of neural engineering, 9(4):046006, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Mehring Carsten, Rickert Jörn, Vaadia Eilon, de Oliveira Simone Cardoso, Aertsen Ad, and Rotter Stefan. Inference of hand movements from local field potentials in monkey motor cortex. Nature neuroscience, 6(12):1253–1254, 2003. [DOI] [PubMed] [Google Scholar]
- [25].Berens Philipp, Keliris Georgios A, Ecker Alexander S, Logothetis Nikos K, and Tolias Andreas S. Comparing the feature selectivity of the gamma-band of the local field potential and the underlying spiking activity in primate visual cortex. Frontiers in systems neuroscience, 2:2, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Belitski Andrei, Panzeri Stefano, Magri Cesare, Logothetis Nikos K, and Kayser Christoph. Sensory information in local field potentials and spikes from visual and auditory cortices: time scales and frequency bands. Journal of computational neuroscience, 29(3):533–545, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Sani Omid G, Abbaspourazad Hamidreza, Wong Yan T, Pesaran Bijan, and Shanechi Maryam M. Modeling behaviorally relevant neural dynamics enabled by preferential subspace identification. Nature Neuroscience, 24:140–149, 2021. [DOI] [PubMed] [Google Scholar]
- [28].Sani Omid G., Pesaran Bijan, and Shanechi Maryam M.. Where is all the nonlinearity: flexible nonlinear modeling of behaviorally relevant neural dynamics using recurrent neural networks. bioRxiv, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Ray Supratim. Challenges in the quantification and interpretation of spike-LFP relationships. Curr Opin Neurobiol, 31:111–118, 2015. [DOI] [PubMed] [Google Scholar]
- [30].Einevoll Gaute T., Kayser Christoph, Logothetis Nikos K., and Panzeri Stefano. Modelling and analysis of local field potentials for studying the function of cortical circuits. Nature Reviews Neuroscience, 14(11):770, 2013. [DOI] [PubMed] [Google Scholar]
- [31].Viventi Jonathan, Kim Dae-Hyeong, Vigeland Leif, Frechette Eric S, Blanco Justin A, Kim Yun-Soung, Avrin Andrew E, Tiruvadi Vineet R, Hwang Suk-Won, Vanleer Ann C, et al. Flexible, foldable, actively multiplexed, high-density electrode array for mapping brain activity in vivo. Nature neuroscience, 14(12):1599, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Chiang Chia-Han, Won Sang Min, Orsborn Amy L, Yu Ki Jun, Trumpis Michael, Bent Brinnae, Wang Charles, Xue Yeguang, Min Seunghwan, Woods Virginia, et al. Development of a neural interface for high-definition, long-term recording in rodents and nonhuman primates. Science translational medicine, 12(538), 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Truccolo W, Eden UT, Fellows MR, Donoghue JP, and Brown EN. A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects. J. Neurophysiol, 93:1074–1089, 2005. [DOI] [PubMed] [Google Scholar]
- [34].Pesaran Bijan, Vinck Martin, Einevoll Gaute T, Sirota Anton, Fries Pascal, Siegel Markus, Truccolo Wilson, Schroeder Charles E, and Srinivasan Ramesh. Investigating large-scale brain dynamics using field potential recordings: analysis and interpretation. Nature neuroscience, 21(7):903–919, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Hsieh Han-Lin and Shanechi Maryam M.. Optimizing the learning rate for adaptive estimation of neural encoding models. PLOS Computational Biology, 14(5):1–34, 05 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Abbaspourazad H, Hsieh H, and Shanechi MM. A Multiscale Dynamical Modeling and Identification Framework for Spike-Field Activity. IEEE Transactions on Neural Systems and Rehabilitation Engineering, pages 1–1, 2019. [DOI] [PubMed] [Google Scholar]
- [37].Womelsdorf Thilo, Schoffelen Jan-Mathijs, Oostenveld Robert, Singer Wolf, Desimone Robert, Engel Andreas K, and Fries Pascal. Modulation of neuronal interactions through neuronal synchronization. science, 316(5831):1609–1612, 2007. [DOI] [PubMed] [Google Scholar]
- [38].Gregoriou Georgia G, Gotts Stephen J, Zhou Huihui, and Desimone Robert. High-frequency, long-range coupling between prefrontal and visual cortex during attention. science, 324(5931):1207–1210, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Benchenane Karim, Peyrache Adrien, Khamassi Mehdi, Patrick L Tierney Yves Gioanni, Battaglia Francesco P, and Wiener Sidney I. Coherent theta oscillations and reorganization of spike timing in the hippocampal-prefrontal network upon learning. Neuron, 66(6):921–936, 2010. [DOI] [PubMed] [Google Scholar]
- [40].van Wingerden Marijn, Vinck Martin, Lankelma Jan V, and Pennartz Cyriel MA. Learning-associated gamma-band phase-locking of action–outcome selective neurons in orbitofrontal cortex. Journal of Neuroscience, 30(30):10025–10038, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Manning Jeremy R, Jacobs Joshua, Fried Itzhak, and Kahana Michael J. Broadband shifts in local field potential power spectra are correlated with single-neuron spiking in humans. Journal of Neuroscience, 29(43):13613–13620, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Rule Michael Everett, Vargas-Irwin Carlos, Donoghue John P, and Truccolo Wilson. Contribution of lfp dynamics to single-neuron spiking variability in motor cortex during movement execution. Frontiers in systems neuroscience, 9:89, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Jarvis MR and Mitra PP. Sampling properties of the spectrum and coherency of sequences of action potentials. Neural Computation, 13(4):717–749, 2001. [DOI] [PubMed] [Google Scholar]
- [44].Granger Clive WJ. Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society, pages 424–438, 1969. [Google Scholar]
- [45].Brovelli Andrea, Ding Mingzhou, Ledberg Anders, Chen Yonghong, Nakamura Richard, and Bressler Steven L. Beta oscillations in a large-scale sensorimotor cortical network: directional influences revealed by granger causality. Proceedings of the National Academy of Sciences of the United States of America, 101(26):9849–9854, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Philiastides Marios G and Sajda Paul. Causal influences in the human brain during face discrimination: a shortwindow directed transfer function approach. IEEE Transactions on Biomedical Engineering, 53(12):2602–2605, 2006. [DOI] [PubMed] [Google Scholar]
- [47].Kamiński Maciej, Ding Mingzhou, Truccolo Wilson A, and Bressler Steven L. Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biological cybernetics, 85(2):145–157, 2001. [DOI] [PubMed] [Google Scholar]
- [48].Krumin Michael and Shoham Shy. Multivariate autoregressive modeling and granger causality analysis of multiple spike trains. Computational intelligence and neuroscience, 2010:10, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Nedungadi Aatira G, Rangarajan Govindan, Jain Neeraj, and Ding Mingzhou. Analyzing multiple spike trains with nonparametric granger causality. Journal of computational neuroscience, 27(1):55–64, 2009. [DOI] [PubMed] [Google Scholar]
- [50].Sameshima Koichi and Baccalá Luiz Antonio. Using partial directed coherence to describe neuronal ensemble interactions. Journal of neuroscience methods, 94(1):93–103, 1999. [DOI] [PubMed] [Google Scholar]
- [51].Zhu Liqiang, Lai Ying-Cheng, Hoppensteadt Frank C, and He Jiping. Probing changes in neural interaction during adaptation. Neural Computation, 15(10):2359–2377, 2003. [DOI] [PubMed] [Google Scholar]
- [52].Pereda Ernesto, Quiroga Rodrigo Quian, and Bhattacharya Joydeep. Nonlinear multivariate analysis of neurophysiological signals. Progress in neurobiology, 77(1–2):1–37, 2005. [DOI] [PubMed] [Google Scholar]
- [53].Quinn Christopher, Coleman Todd, Kiyavash Negar, and Hatsopoulos Nicholas. Estimating the directed information to infer causal relationships in ensemble neural spike train recordings. Journal of computational neuroscience, 30(1):17–44, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].So Kelvin, Koralek Aaron C., Ganguly Karunesh, Gastpar Michael C., and Carmena Jose M.. Assessing functional connectivity of neural ensembles using directed information. Journal of Neural Engineering, 9(2):13, 2012. [DOI] [PubMed] [Google Scholar]
- [55].Cai Zhiting, Neveu Curtis L, Baxter Douglas A, Byrne John H, and Aazhang Behnaam. Inferring neuronal network functional connectivity with directed information. J Neurophysiol, 118(2):1055–1069, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Kim Sanggyun, Putrino David, Ghosh Soumya, and Brown Emery N.. A granger causality measure for point process models of ensemble neural spiking activity. PLoS Computational Biology, 7(3):e1001110, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Sheikhattar Alireza, Miran Sina, Liu Ji, Fritz Jonathan B, Shamma Shihab A, Kanold Patrick O, and Babadi Behtash. Extracting neuronal functional network dynamics via adaptive granger causality analysis. Proceedings of the National Academy of Sciences, 115(17):E3869–E3878, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Liew Yi Juin, Pala Aurelie, Whitmire Clarissa J, Stoy William A, Forest Craig R, and Stanley Garrett B. Inferring monosynaptic connectivity across brain structures invivo. bioRxiv, 2020. [Google Scholar]
- [59].Citi Luca, Ba Demba, Brown Emery N, and Barbieri Riccardo. Likelihood methods for point processes with refractoriness. Neural computation, 26(2):237–263, 2014. [DOI] [PubMed] [Google Scholar]
- [60].Quinn Christopher J., Kiyavash Negar, and Coleman Todd P.. Directed information graphs. IEEE Trans Info Theory, 61(12):6887–6909, 2015. [Google Scholar]
- [61].Gong Xiajing, Li Wu, and Liang Hualou. Spike-field granger causality for hybrid neural data analysis. Journal of neurophysiology, 122(2):809–822, 2019. [DOI] [PubMed] [Google Scholar]
- [62].Hu Meng, Li Mingyao, Li Wu, and Liang Hualou. Joint analysis of spikes and local field potentials using copula. NeuroImage, 133:457–467, 2016. [DOI] [PubMed] [Google Scholar]
- [63].Mazzoni Alberto, Lindén Henrik, Cuntz Hermann, Lansner Anders, Panzeri Stefano, and Einevoll Gaute T.. Computing the local field potential (LFP) from integrate-and-fire network models. PLoS Comput Biol, 11(12):e1004584, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Wang Chuanmeizhi and Shanechi Maryam M. Estimating multiscale direct causality graphs in neural spike-field networks. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 27(5):857–866, 2019. [DOI] [PubMed] [Google Scholar]
- [65].Newey Whitney K and McFadden Daniel. Large sample estimation and hypothesis testing. Handbook of econometrics, 4:2111–2245, 1994. [Google Scholar]
- [66].Akaike Hirotugu. A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6):716–723, 1974. [Google Scholar]
- [67].Wilks Samuel S.. Weighting systems for linear functions of correlated variables when there is no dependent variable. Psychometrika, 3(1):23–40, 1938. [Google Scholar]
- [68].Benjamini Yoav and Hochberg Yosef. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the royal statistical society. Series B (Methodological), pages 289–300, 1995. [Google Scholar]
- [69].Wong Yan T, Putrino David, Weiss Adam, and Pesaran Bijan. Utilizing movement synergies to improve decoding performance for a brain machine interface. In 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), pages 289–292. IEEE, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Armstrong J Scott and Collopy Fred. Error measures for generalizing about forecasting methods: Empirical comparisons. International journal of forecasting, 8(1):69–80, 1992. [Google Scholar]
- [71].Tomsett Richard J, Ainsworth Matt, Thiele Alexander, Sanayei Mehdi, Chen Xing, Gieselmann Marc A, Whittington Miles A, Cunningham Mark O, and Kaiser Marcus. Virtual electrode recording tool for extracellular potentials (vertex): comparing multielectrode recordings from simulated and biological mammalian cortical tissue. Brain Structure and Function, 220(4):2333–2353, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Pettersen HL, Dale Anders M, and Einevoll Gaute T. Extracellular spikes and current-source density. handbook of neural activity measurements,. romain brette and a. destexhe, 2012. [Google Scholar]
- [73].Brette Romain and Gerstner Wulfram. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. Journal of neurophysiology, 94(5):3637–3642, 2005. [DOI] [PubMed] [Google Scholar]
- [74].Maziarz Mariusz. A review of the granger-causality fallacy. The journal of philosophical economics: Reflections on economic and social issues, 8(2):86–105, 2015. [Google Scholar]
- [75].Ray Supratim and Maunsell John HR. Network rhythms influence the relationship between spike-triggered local field potential and functional connectivity. Journal of Neuroscience, 31(35):12674–12682, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Hoerl Arthur E and Kennard Robert W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics, 12(1):55–67, 1970. [Google Scholar]
- [77].Zou Hui. The adaptive lasso and its oracle properties. Journal of the American statistical association, 101(476):1418–1429, 2006. [Google Scholar]
- [78].Buja Andeas and Brown Larry. Discussion:” a significance test for the lasso”. The Annals of Statistics, 42(2):509–517, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Green Andrea M. and Kalaska John F.. Learning to move machines with the mind. Trends in Neurosciences, 34(2):61 – 75, 2011. [DOI] [PubMed] [Google Scholar]
- [80].Sadtler Patrick T, Quick Kristin M, Golub Matthew D, Chase Steven M, Ryu Stephen I, Tyler-Kabara Elizabeth C, Byron M Yu, and Batista Aaron P. Neural constraints on learning. Nature, 512(7515):423–426, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Orsborn Amy L and Pesaran Bijan. Parsing learning in networks using brain–machine interfaces. Current Opinion in Neurobiology, 46:76–83, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Yang Yuxiao, Ahmadipour Parima, and Shanechi Maryam M. Adaptive latent state modeling of brain network dynamics with real-time learning rate optimization. Journal of Neural Engineering, 2020. [DOI] [PubMed] [Google Scholar]
- [83].Ahmadipour Parima, Yang Yuxiao, Chang Edward F, and Shanechi Maryam M. Adaptive tracking of human ecog network dynamics. Journal of Neural Engineering, 2020. [DOI] [PubMed] [Google Scholar]
- [84].Millard Daniel C, Wang Qi, Gollnick Clare A, and Stanley Garrett B. System identification of the nonlinear dynamics in the thalamocortical circuit in response to patterned thalamic microstimulation in vivo. Journal of neural engineering, 10(6):066011, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Newman Jonathan P, Fong Ming-fai, Millard Daniel C, Whitmire Clarissa J, Stanley Garrett B, and Potter Steve M. Optogenetic feedback control of neural activity. Elife, 4:e07192, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86].Shanechi Maryam M, Hu Rollin C, Powers Marissa, Wornell Gregory W, Brown Emery N, and Williams Ziv M. Neural population partitioning and a concurrent brain-machine interface for sequential motor function. Nature neuroscience, 15(12):1715, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [87].Moxon Karen A and Foffani Guglielmo. Brain-machine interfaces beyond neuroprosthetics. Neuron, 86(1):55–67, 2015. [DOI] [PubMed] [Google Scholar]
- [88].Ehrens Daniel, Sritharan Duluxan, and Sarma Sridevi V. Closed-loop control of a fragile network: application to seizure-like dynamics of an epilepsy model. Front. Neurosci, 9:58, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89].Yang Yuxiao and Shanechi Maryam M. An adaptive and generalizable closed-loop system for control of medically induced coma and other states of anesthesia. J. Neural Eng, 13(6):066019, 2016. [DOI] [PubMed] [Google Scholar]
- [90].Sadras Nitin, Pesaran Bijan, and Shanechi Maryam M. A point-process matched filter for event detection and decoding from population spike trains. J. Neural Eng, 16(6):066016, 2019. [DOI] [PubMed] [Google Scholar]
- [91].Graat Ilse, Figee Martijn, and Denys Damiaan. The application of deep brain stimulation in the treatment of psychiatric disorders. Int. Rev. Psychiatry, 29(2):178–190, 2017. [DOI] [PubMed] [Google Scholar]
- [92].Widge Alik S, Ellard Kristen K, Paulk Angelique C, Basu Ishita, Yousefi Ali, Zorowitz Samuel, Gilmour Anna, Afzal Afsana, Deckersbach Thilo, Cash Sydney S, et al. Treating refractory mental illness with closed-loop brain stimulation: progress towards a patient-specific transdiagnostic approach. Experimental neurology, 287:461–472, 2017. [DOI] [PubMed] [Google Scholar]
- [93].Yang Yuxiao, Connolly Allison T, and Shanechi Maryam M. A control-theoretic system identification framework and a real-time closed-loop clinical simulation testbed for electrical brain stimulation. J. Neural Eng, 15(6):066007, 2018. [DOI] [PubMed] [Google Scholar]
- [94].Sani Omid G, Yang Yuxiao, Lee Morgan B, Dawes Heather E, Chang Edward F, and Shanechi Maryam M. Mood variations decoded from multi-site intracranial human brain activity. Nature Biotechnology, 36:954–961, September 2018. [DOI] [PubMed] [Google Scholar]
- [95].Yang Yuxiao, Lee Justin, Guidera Jennifer, Vlasov Ksenia, Pei JunZhu, Emery N Brown Ken Solt, and Shanechi Maryam M. Developing a personalized closed-loop controller of medically-induced coma in a rodent model. J. Neural Eng, 16(3):036022, 2019. [DOI] [PubMed] [Google Scholar]
- [96].Yang Yuxiao, Sani Omid G, Chang Edward F, and Shanechi Maryam M. Dynamic network modeling and dimensionality reduction for human ECoG activity. J. Neural Eng, 16(5):056014, 2019. [DOI] [PubMed] [Google Scholar]
- [97].Wichmann Thomas and Mahlon R DeLong. Deep brain stimulation for movement disorders of basal ganglia origin: restoring function or functionality? Neurotherapeutics, 13(2):264–283, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [98].Citi Luca, Poli Riccardo, Cinel Caterina, and Sepulveda Francisco. P300-based bci mouse with genetically-optimized analogue control. IEEE transactions on neural systems and rehabilitation engineering, 16(1):51–61, 2008. [DOI] [PubMed] [Google Scholar]