Estimating cure proportion in cancer clinical trials using flexible parametric cure models

Abstract

Background

In the context of survival analysis in recent cancer clinical trials, there has been an increasing interest in the proportion of patients who are not susceptible to the event, known as the cure proportion. To estimate it, cure models implicitly specify the time point when patients are considered cured, although the impact of the cure point position on cure proportion estimates is unclear.

Methods

Sensitivity of cure proportion estimates to the knot number and placement in flexible parametric cure models was examined using data from a clinical trial of CheckMate 141, an immuno-oncology compound. The performance of the model and procedures to determine the cure point position were evaluated using a simulation study.

Results

Analysis of the CheckMate 141 data showed the impact of the last knot position on the cure proportion estimate and model fit. Simulations revealed that the flexible parametric cure model with the last knot at the last observed event time overestimated the cure proportion. This bias was reduced when the last knot was placed later.

Conclusions

For cure proportion estimation in clinical trials with survival outcomes, the flexible parametric cure model can be an attractive alternative to the Kaplan–Meier method.

Background

Survival data are typically summarised using the Kaplan–Meier (KM) curve and hazard ratio, but little attention has been paid to the fact that these methods assume that all patients are susceptible to the event of interest. In recent clinical trials of newly developed immuno-oncology (IO) compounds, for example, this assumption has not been met even in advanced cancer and after a sufficiently long follow-up period, because IO compounds significantly improved survival. In other words, some patients are considered cured, and their proportion in the study population is referred to as the cure proportion or cure rate in the context of survival analysis [1–3]. There are generally two types of survival models to estimate the cure proportion in survival data: non-parametric and parametric [4–8]. The KM method is the most common non-parametric model and is often applied to estimate the 5-year survival proportion in the population-based studies of cancer [1, 4]. However, the cure proportion estimation has limitations because the KM estimate considerably varies and is subject to bias, particularly when the follow-up period is insufficient.

An alternative approach is to use parametric models, e.g., the mixture cure model originally introduced by Boag [4] or the non-mixture cure model described by Klebanov et al. [7] A major problem with parametric models is the misspecification of the functional form of survival of individuals who are susceptible to an event of interest. To overcome these misspecifications, a flexible parametric model (FPM) was proposed [9], which has been extended to estimate the cure proportion [1]. This extended model is called the flexible parametric cure model (FPCM). A natural cubic spline is flexible enough to avoid the misspecification [1]. The knots of the splines are decided by researchers before model fitting, and with the FPCM, the last knot implies the cure point, because beyond it, the hazard is zero.

IO therapy has a delayed clinical effect when the immune response is activated, resulting in a clear change in the hazard trend [2]. This effect complicates the time-to-event distribution [10, 11]. Liao and Liu [11] proposed two- and three-component mixtures of the Weibull and piecewise exponential distributions as flexible parametric survival models. The models fit the data well in terms of predicting the survival curve; however, mixture Weibull distributions give biased cure proportion estimates, whereas piecewise exponential distributions have unnatural step hazard functions and require many parameters to fit sufficiently well. Previously, we showed that models with piecewise Weibull distributions are useful under certain conditions, and their hazard functions are continuous but not differentiable (unpublished work, YS, Doi M., ST, TS). In contrast, FPCM has a continuous and differentiable hazard function and is expected to be sufficiently flexible with fewer parameters. Here, we propose to use FPCM as an alternative approach for estimating the cure proportion of a survival dataset from a clinical trial of IO therapy.

FPCM has been applied to registries or population-based studies to estimate the cure proportion in relative survival settings [3, 12–15]. For the evaluation of cure proportion, survival data from a clinical trial are less informative than population-based data because the follow-up period is often limited, and the sample size is relatively small [14, 16]. The last observed event time of survival data with a shorter follow-up period or smaller sample size is likely to be earlier than the true cure point. Therefore, when survival data from a clinical trial are modelled using FPCM, the last observed event time may be too early to put the last knot. Furthermore, when the hazard function is considered continuous, the presence of the last knot at the last observed event time means that the hazard is zero when the last event occurs [17]. It is more natural to place the last knot after the last observed event. In their analysis, Andersson et al. compared their fit with those of other models and emphasized the importance of not placing the last knot too early [1]. However, it is not known how late the last knot should be placed or whether and how the misspecification of the last knot position causes a bias in the cure proportion estimate.

In this study, we clarify the problems of the FPCM in estimating the cure proportion of a survival dataset from a clinical trial and propose a remedy for it. Specifically, we sought to develop a practical procedure to determine the position of the last knot of the FPCM and to evaluate its performance through simulations and analysis of reconstructed data from a clinical trial of IO therapy. We first applied FPCM to the CheckMate 141 data [18] and designed simulation scenarios based on that analysis.

Methods

Analysis of CheckMate 141 data

The CheckMate 141 trial [19] was a randomized, open-label, phase III trial. The primary objective of that trial was to assess whether nivolumab, a novel IO therapy, improves overall survival compared to the effect of standard therapy in patients with recurrent squamous cell carcinoma of the head and neck. A total of 361 patients were assigned in a 2:1 ratio to receive nivolumab or standard single-agent systemic therapy. Individual-level data from the CheckMate 141 trial were reconstructed by Arfè et al. [18].

In this study, our focus was on estimating a cure proportion in one arm of CheckMate 141. We assumed that some patients were cured after treatment with nivolumab, and the cure proportions of the reconstructed CheckMate 141 data were estimated using FPCM. The FPCM is a parametric model that specifies baseline log cumulative hazard using a natural cubic spline with user-specified knots. The detailed FPCM description is provided in Supplementary Information. In this paper, the knots of FPCM signifies internal and boundary knots together. The FPCM with κ knots has κ − 2 internal knots and 2 boundary knots. The number of parameters of the FPCM with κ knots equals κ − 1. The likelihood function (Supplementary Eq. (A4) in Supplementary Information) was maximised numerically using the NLMIXED procedure (The SAS system, version 9.4.; SAS Institute Inc., Cary, NC, USA), and the maximum likelihood estimate (MLE) of the cure proportion was computed from the MLE of ${\gamma }_0$ (Supplementary Eq. (A5) in Supplementary Information). Iterative calculations started from the default initial values, which were all one, and the MLE of each parameter was obtained using the dual quasi-Newton method. The convergence criterion was the default setting of the SAS NLMIXED procedure.

We compared cure proportion estimates obtained using FPCMs with different knot numbers and placements mentioned in Andersson et al. [1] with those calculated from the KM method and Weibull non-mixture cure model (WNCM). To evaluate the impact of knot number, FPCMs with 4–9 knots were used, and the knots were distributed evenly according to centiles of observed event times with an additional knot at the 95th centile. To evaluate the impact of knot placement, FPCMs with 6 knots were used, and the knot configurations were as follows: an FPCM with knots at centiles 0, 20, 40, 60, 80, 100; an FPCM with knots at centiles 0, 35, 65, 80, 95, 100; an FPCM with knots at centiles 0, 35, 65, 75, 85, 95; an FPCM with knots at centiles 0, 100 and follow-up months 3, 6, 8, 10; and an FPCM with knots at centiles 0, 25, 50, 75, 95 and the last knot 18 months from randomization, which is after the last observed follow-up time. The cure proportion estimate from the KM method was defined as the KM estimate of survival beyond the last observed event time, and the survival function of WNCM is defined as Supplementary Eq. (A3) in Supplementary Information. The number of parameters of WNCM equals three. In this study, the knot of an FPCM at percentile 100 was placed after 0.1 months of the last observed event time because when the last knot is placed at the exact time of the last observed event or earlier, FPCM fails to converge. Andersson et al. stated that FPCM can be applied to non-relative survival data when the cause of death is known and reliable [1]. The CheckMate 141 data were obtained from a well-controlled clinical trial that met this requirement. Therefore, we used FPCM to describe the absolute survival of patients in the CheckMate 141 data.

The model fit toward the end of the follow-up period may affect the cure proportion estimate. To examine the fit to the CheckMate 141 data, we compared the survival estimate predicted by FPCM in CheckMate 141 data with that calculated from the WNCM and KM curves. The FPCM was with knots at percentiles 0, 25, 50, 75, and 95, and 0.1 months after the last observed event time.

As the position of the last knot of FPCM affects the model fit, we also evaluated its impact. FPCMs with six knots were fitted to the CheckMate 141 data. The first five knots were located at percentiles 0, 25, 50, 75, and 95, and for the last knot, we considered 11 different last knot positions, which were 0.1, 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50 months from the last observed event time. An FPCM with the last knot position at x months from the last observed event time is referred to as “FPCM with a delay of x,” and the FPCM with a delay of 0.1 is considered as “the original FPCM.”

Simulation study

Data generating mechanisms

In the analysis of the Finnish Cancer Registry Data, putting the last knot before the last observed event time resulted in overestimation; thus, the last knot was recommended to be placed at the last observed event time or later [1]. The original FPCM seemed sufficient to yield estimates consistent with those calculated using the non-parametric model. Although CheckMate 141 data analysis showed that the cure proportion estimates from the original FPCM were much larger than those obtained by the KM method, the position of the last knot had a large impact on the model fit and cure proportion estimate. Based on this analysis, a simulation study was designed to compare cure proportion estimates obtained from FPCM with different positions of the last knot and to determine an adequate position for the last knot. We simulated an exploratory analysis of clinical trial data with a limited follow-up period, sample size, and only administrative censoring at the end of the follow-up period. This simulation study focused on estimating the cure proportion of a single group.

First, the survival times were generated from the mixture cure model as follows:

$$S\left(t\right)=p_C+\left(1-p_C\right)S_u\left(t\right),$$

where $t$ is the time expressed in months, $p_C$ denotes the cure proportion, which is the proportion of individuals who are not susceptible to the event of interest or are cured, and $1-p_C$ denotes the proportion of individuals who are susceptible or uncured. The survival function of cured individuals was set to one for all finite values of $t$. $S_u\left(t\right)$ was used to describe the survival times of uncured individuals. We considered two scenarios for $S_u\left(t\right)$: an exponential distribution with a parameter of $\mathrm{\lambda }=0.18$ and a beta distribution with parameters $\mathrm{\alpha }=1$ and $\mathrm{\beta }=2.5$. The values generated from the beta distribution were multiplied by 18; thus, the event times of uncured patients were limited to less than 18 months. These parameters were selected based on the results of the CheckMate 141 trial (Supplementary Fig. S1). $S_u\left(t\right)$ of the simulation scenario was a beta distribution that reaches zero at 18 months, which is called the finite cure point scenario, and $S_u\left(t\right)$ of the simulation scenario was an exponential distribution reaches zero at infinity, which is called the asymptotic cure point scenario. We considered simulation scenarios with the parameters listed in Table 1, and 1000 Monte Carlo replications for each scenario. In finite cure point scenarios, the sums of the enrolment and follow-up periods, and thus, the longest trial periods, were 16, 18, and 20 months, corresponding to follow-up periods of 4, 6, and 8 months, respectively. These parameters represented situations in which the longest trial period was shorter than the cure point, the same as the cure point, or longer than the cure point. When the FPCM was fitted to the data generated from the asymptotic cure point scenarios, the cure point was the most misspecified.

Table 1.

Parameter settings of scenarios based on CheckMate 141 in the simulation study.

	Asymptotic cure point scenario	Finite cure point scenario
Survival function of uncured	Exponential distribution	Beta distribution
Survival probability reaches at	Infinity	18
Enrolment period	12
Follow-up period	6	4, 6, 8
Sample size	150, 600, 2000
Cure proportion	0.2, 0.4, 0.6, 0.8

Estimand

In our study, the estimand is the cure proportion. Its estimate was defined as follows; for FPCM, it was the estimated survival probability at the time point of the last knot; for the KM method, the KM estimate of survival probability at the last observed event time; for the WNCM, the estimated survival probability after an infinite period time.

Analysis methods

The FPCMs, WNCM, and KM method were applied to the generated data. The parametric cure proportion estimates were obtained as MLEs of $p_C$ from FPCM and WNCM. The estimates of the KM method comprised KM estimates of survival beyond the last observed event time. To estimate the cure proportion, FPCMs with six knots, which has four internal knots and two boundary knots, were fitted to the generated datasets. The first five knots were located at percentiles 0, 25, 50, 75 and 95, and for the last knot, we considered the original FPCM along with FPCMs with 10 different delays, 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50 months. To correctly identify the cure point, the 6-knot FPCM with the last knot at 18 months after registration was fitted as “the true FPCM” to the data from finite cure point scenarios and WNCM was fitted to the data from asymptotic cure point scenarios.

Performance measures

We evaluated the convergence frequency, mean, bias, median, and standard error of the estimated cure proportions from each model as performance measures, and Akaike’s information criterion (AIC) from FPCM and WNCM as the model fit measure.

Results

Sensitivity of CheckMate 141 data analysis outcome to knot number and placement

The trends in the cure proportion estimates from the FPCM of different knot numbers and placements were similar to the results of the Finnish Cancer Registry analysis in Andersson et al. [1] Table 2 shows the estimated cure proportions and AICs corresponding to method we used. For the different number of knots, ranging from 4 to 9, FPCM with 4 knots gave the largest cure proportion estimate. In terms of knot placement, FPCM with knots at percentiles 0, 20, 40, 60, and 80, and 0.1 months after the last observed event time gave the largest cure proportion estimate. However, the analysis of CheckMate 141 data showed that FPCM did not always provide a cure proportion estimate close to that obtained by the KM method, which was inconsistent with the results of the Finnish Cancer Registry analysis [1]. Figure 1 shows the predicted survival estimate in the CheckMate 141 trial according to an FPCM with knots at percentiles 0, 25, 50, 75, and 95, and 0.1 months after the last observed event time compared with estimates obtained from the WNCM and KM curves. Early in the follow-up, when most of the events occurred, the three predicted survival curves were close. At the end of the follow-up, the curves began to separate, resulting in different cure proportion estimates for nivolumab-treated patients: 0.360 (FPCM), 0.242 (WNCM) and 0.295 (KM).

Table 2.

Impact of knot number and placement on cure proportion estimate from FPCM in nivolumab of CheckMate141 study.

Placement of knots	Number of knots	Nivolumab
		Cure proportion	95% lower	95% upper	AIC
KM		0.295	0.209	0.387
WNCM		0.242	0.123	0.474	883.8
(0, 50, 95, 100+)	4	0.395	0.328	0.462	937.6
(0, 33, 67, 95, 100+)	5	0.374	0.305	0.443	925.0
(0, 25, 50, 75, 95, 100+)	6	0.360	0.289	0.431	917.7
(0, 20, 40, 60, 80, 95, 100+)	7	0.350	0.278	0.423	915.1
(0, 17, 33, 50, 67, 83, 95, 100+)	8	0.345	0.272	0.419	913.7
(0, 14, 29, 43, 57, 71, 86, 95, 100+)	9	0.338	0.265	0.413	907.5
(0, 20, 40, 60, 80, 100+)	6	0.395	0.327	0.461	946.9
(0, 35, 65, 80, 95, 100+)	6	0.349	0.277	0.422	912.4
(0, 35, 65, 75, 85, 95)	6	NC	NC	NC	NC
(0, 100+) and month 3, 6, 8, 10	6	0.333	0.259	0.409	906.5
(0, 25, 50, 75, 95) and month 18	6	0.338	0.265	0.412	885.7

Estimated cure proportions, 95% confidence intervals and AICs from the FPCM for nivolumab, along with those from the WNCM and the KM method.

The numbers in the parentheses denote the percentiles of the log of the observed event times at which knots are placed.

The knot position 0.1 months later than the last observed event time was denoted as percentile “100+”.

The 95% confidence interval of the KM method is pointwise confidence interval using the log-log transformation.

95% upper upper limit of 95% confidence interval, 95% lower lower limit of 95% confidence interval, AIC Akaike’s information criterion, KM the KM method, WNCM Weibull non-mixture cure model, NC not converged.

Fig. 1. Predicted survival estimates from the CheckMate 141 (nivolumab) trial according to the flexible parametric cure model (FPCM), Weibull non-mixture cure model (WNCM) and Kaplan–Meier (KM) curves.

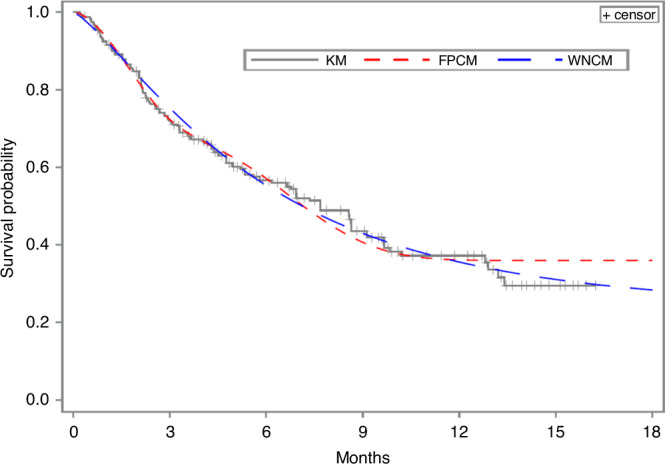
The FPCM is with knots at percentiles 0, 25, 50, 75, and 95, and 0.1 months after the time point of the last event.

The last knot position remarkably affected the cure proportion estimate and model fit of the FPCM. Figure 2 shows cure proportion estimates, 95% confidence intervals, and AICs obtained using FPCMs with different delays. When the last knot was placed later, the cure proportion estimate and AIC decreased, and the width of the 95% confidence interval increased. The decrease in AIC was initially rapid, followed by a slight change (Supplementary Table S1).

Fig. 2. Performance of cure proportion estimation from flexible parametric cure model (FPCM) with different delays.

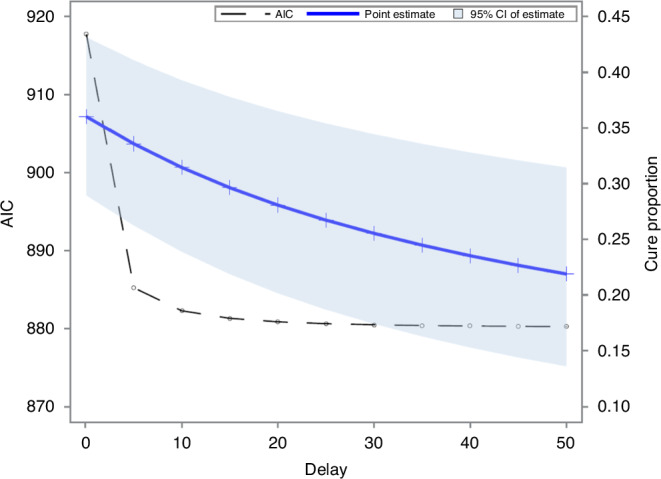
Cure proportion estimates, 95% confidence intervals and Akaike’s information criterion values (AICs) obtained from FPCM with different delays applied to the CheckMate 141 (nivolumab) trial data.

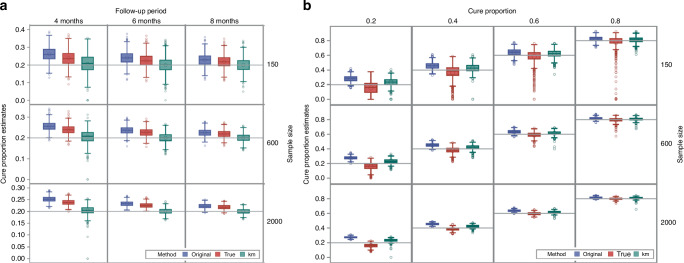
Performance of the original FPCM in the simulation study

Figure 3 shows boxplots of cure proportion estimates from the original FPCM compared to those obtained by the KM method and the model for correct cure point determination. Figure 3a presents boxplots of the estimates of data from the finite cure point scenarios with a true cure proportion of 0.2, in which the model for correct cure point determination (indicated as “true” in Fig. 3) was the true FPCM. The results were similar to those obtained using other finite cure point scenarios, with true cure proportions of 0.4, 0.6, and 0.8 (Supplementary Fig. S2). Figure 3b presents boxplots of the data estimates from asymptotic cure point scenarios, in which WNCM was the model for correct cure point determination. The mean, bias, median and standard error of the cure proportion estimates obtained using the original FPCM, true FPCM, KM method and WNCM are shown in Supplementary Tables S2–S5. The numerical calculations of FPCM and WNCM converged for all 1000 replications in all scenarios.

Fig. 3. Boxplots of cure proportion estimates obtained from the original FPCM (original), the KM method (KM) and the model of the correctly identified cure point (true).

a Finite cure point scenarios with cure proportion = 0.2. The true cure point model (true) was an FPCM with the last knot positioned at 18 months. b Asymptotic cure point scenarios. WNCM was the true cure point model (true).

The mean cure proportion estimates from the original FPCM were greater than the true values for all scenarios. When the follow-up period was longer, the bias decreased, whereas a larger sample size slightly reduced the bias. The standard error of the mean cure proportion estimates from FPCMs was smaller compared with those associated with the KM method and WNCM in all scenarios.

The mean cure proportion estimates from the true FPCM were also greater than the true values for all scenarios, but the biases were smaller than those of the original FPCMs. When the follow-up period was longer, the bias decreased, whereas a larger sample size slightly reduced the bias.

The mean cure proportion estimates from the KM method were slightly greater than the true values for all scenarios. In all finite cure point scenarios, the KM method yielded the smallest bias, which was smaller than that of the true FPCM. In the asymptotic cure point scenarios, the KM method gave the smallest bias when the sample size was 150 or the true cure proportion was 0.2, smaller than those associated with the WNCM, in which the cure point was specified correctly as infinite.

The means of the cure proportion estimates from the WNCM were smaller than the true values in all scenarios. The standard error of the mean cure proportion estimates from the WNCM was the largest compared to those associated with the KM method and FPCM in asymptotic cure point scenarios.

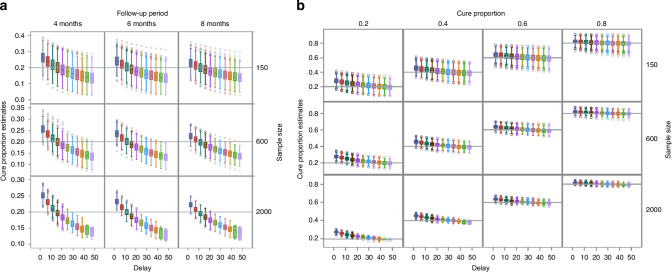
Performance of FPCMs with different delays in the simulation study

The numerical calculations converged in all 1000 replications of all FPCMs with delays of 5, 10, and 15. However, when the last knot was placed 20 months or later than the last observed event time, the convergence frequency was low. The later was the last knot position, the lower was the convergence frequency. With a larger sample size, the convergence frequency decreased (Supplementary Table S6).

Figure 4 shows boxplots of the cure proportion estimates from FPCMs with different delays. Figure 4a presents boxplots of the cure proportion estimates from the finite cure point scenarios with a true cure proportion of 0.2. The results were similar for other finite cure point scenarios, with true cure proportions of 0.4, 0.6, and 0.8 (Supplementary Fig. S3). Figure 4b presents boxplots of the estimates from the asymptotic cure point scenario. The mean cure proportion estimates from FPCMs with different delays decreased monotonously when the last knot position was delayed from the last observed event time. Delaying the position of the last knot initially reduced the bias, but eventually yielded a negative bias. The cure proportion estimate for each dataset also decreased monotonically when the last knot position was delayed.

Fig. 4. Boxplots of cure proportion estimates obtained from FPCMs with different delays.

a Finite cure point scenarios with cure proportion = 0.2. b Asymptotic cure point scenarios.

The 95% confidence interval of each cure proportion estimate from FPCMs widened in most datasets as the position of the last knot was delayed (Supplementary Fig. S4). The variance estimates of parameter ${\gamma }_0$, which is the complementary log-log of the cure proportion as shown in Supplementary Eq. (A5) of Supplementary Information, increased in almost all datasets.

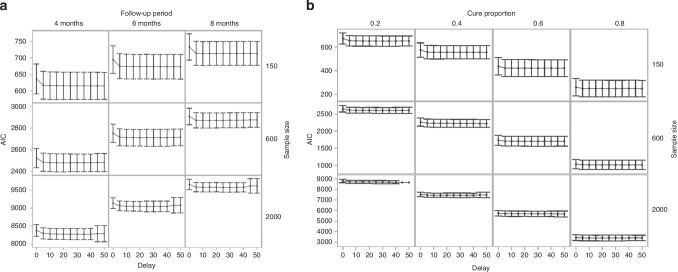
Changes in the AIC of FPCMs with different delays are shown in Fig. 5. Figure 5a presents changes in the AIC of FPCMs in finite cure point scenarios with a true cure proportion of 0.2. The results were similar for other finite cure point scenarios, with true cure proportions of 0.4, 0.6, and 0.8 (Supplementary Fig. S5). Figure 5b shows changes in the AIC of FPCMs in asymptotic cure point scenarios. Delaying the last knot position of FPCM tended to decrease the mean AIC, and a rapid decrease was observed initially, followed by a slight change.

Fig. 5. Changes in the mean and 1.96× standard deviation of AICs of FPCMs with different delays.

a Finite cure point scenarios with cure proportion = 0.2. b Asymptotic cure point scenarios.

Discussion

Our results show that FPCMs can be an attractive alternative to the KM method for cure proportion estimation, if used carefully, in clinical trials with survival outcomes. The original FPCMs yielded cure proportion estimates with reasonably small bias and smaller standard errors than those obtained using the KM method and WNCM, but use of the original FPCMs should be limited to situations in which the trial period was as long as or longer than the true cure point. When the longest trial period was shorter than the true cure point, which is often the case in clinical trials, the original FPCMs greatly overestimated the cure proportion. A larger sample size only slightly reduced this bias. To estimate the cure proportion in clinical trials where the trial period is not clearly known to be sufficient, we recommend using FPCMs with carefully chosen last knot placement, which improves the cure proportion estimation. Through simulations, we clarified the magnitude and direction of bias in cure proportion estimates from the FPCM in scenarios based on a recent clinical trial in oncology. The last knot position of the FPCM should be chosen where there is no meaningful decrease in the value of AIC or other information criteria and uncertainty does not increase too much.

FPCM allows obtaining the cure proportion estimate corresponding to the cure point, which is determined by researchers as the last knot position. Delaying the last knot position always resulted in a smaller cure proportion, as shown in the simulation. Placing the last knot later than the last observed event time reduced positive bias from the original FPCM, particularly when the follow-up period was not sufficiently long. Our results also showed that the later the last knot was placed, the wider was the confidence interval, the lower was the probability of convergence, and the smaller was the AIC. The decrease in the AIC was initially rapid, followed by a slight change. Thus, when the last knot was placed too late, while the improvement of AIC was little or none, the cure proportion estimate became negatively biased, and the confidence interval widened or the FPCM failed to converge. To estimate the cure proportion from survival data with insufficient follow-up, we recommend comparing different estimates and AICs corresponding to different last knot positions and then choosing a position with which the model fit is considered sufficient.

Our re-analysis of the CheckMate 141 data revealed that the most reliable estimate of cure proportion was 0.296, which corresponded to the FPCM with a delay of 15. This is where there is no meaningful decrease in the value of AIC. The FPCM with a delay of 15 improved the model fit sufficiently, yielded a less biased cure proportion estimate than the original FPCM, and resulted in a confidence interval that was not too wide. However, if some researchers accept the overestimation of the cure proportion or wider confidence intervals, the cure proportion estimates that correspond to FPCM with a delay of 10 or 20 may be appropriate. The results from FPCMs with different last knot positions should be presented to demonstrate the adequacy of the choice.

The biases of the original FPCM were indeed larger than those associated with the KM method; however, our simulation results showed that the bias from the FPCM could be reduced by delaying the last knot position and evaluating the improvement in model fit. Additionally, the standard errors of the mean cure proportion estimates from FPCM were smaller than those associated with the KM method and WNCM across all simulation scenarios, suggesting that FPCM provided more stable estimates. Furthermore, FPCM offers greater flexibility in incorporating covariates under the proportional hazard assumption than does the KM method. The estimates obtained from the FPCM (Supplementary Eq. (A6) in Supplementary Information) may be advantageous for comparisons of cure proportion between groups. Moreover, FPCM outperforms WNCM in terms of convergence and model fitting, as discussed by Andersson et al. [1]. Therefore, FPCM presents itself as a viable approach for estimating cure proportion in survival datasets derived from clinical trials involving IO therapy. One reviewer suggested that, in case of cures, it can be difficult to provide a concise summary of the treatment benefit or even to determine whether or not there is a benefit if the two effects go in opposite directions because the treatment effect is split into two components, the difference in cure proportion and the hazard ratio in the non-cured.

However, some properties of cure proportion estimates from FPCM remain unclear. First, in our simulation, a larger sample size slightly reduced the bias, and true FPCM yielded biased estimates. There is little discussion on the asymptotic properties of the cure proportion values estimated from the FPCM, and the reasons for these counterintuitive results of our simulation are unclear. Second, the cure proportion estimates of all datasets in our simulation scenarios decreased when the last knot was placed later. Lin and Huang mathematically proved that when non-parametric maximum likelihood estimation is used, the Yakovlev model with a shorter cure point yields a larger cure proportion estimate [20]. In contrast, the relationship between the last knot position and cure proportion estimated from FPCM is not mathematically proven. Finally, our analysis was based on the assumption of the presence of cured patients. A drawback is that the FPCM provides a non-zero estimate of the cure proportion, even when this assumption is not reasonable. Andersson et al. [1] stated that because FPCM is nested within the FPM, the assumption can be checked by comparing AIC, the Bayesian information criterion, or likelihood of FPCM with those of FPM. The likelihood ratio test results of the Finnish Cancer Registry analysis suggested that a cure was not reached, even though survival seemed to reach a plateau from the life table estimates. They concluded that the goodness-of-fit test should be interpreted cautiously, and the assumption of cure is better assessed graphically [1]. In the CheckMate 141 data, the last knot position had a large impact on the likelihood of FPCM but not on that of FPM (Supplementary Table S7). Our proposal also provides effective procedures to compare FPCM and FPM fits corresponding to the variety of last knot positions.

Author contributions

YS conceived the idea, performed all analyses and wrote the first draft of the manuscript. ST and TS provided essential feedback and suggestions for methodology and data analysis. All authors have read and approved the final version of the manuscript.

Funding

This work was supported by the Japan Agency for Medical Research and Development (AMED) under grant number JP21lk0201702.

Data availability

The CheckMate 141 data analysed in this study are included in the Supplementary Information file of ref. 18. The simulation datasets generated and analysed during this study are available from the corresponding author on reasonable request.

Code availability

SAS (version 9.4) code for analyses of CheckMate 141 data and simulation is available on request from the corresponding author.

Competing interests

The authors declare no competing interests.

Ethics approval and consent to participate

Historical, publicly available, de-identified data were used for analyses, therefore, no ethical approval was required.

Supplementary information

The online version contains supplementary material available at 10.1038/s44276-024-00092-4.