Multi-site Normative Modeling of Diffusion Tensor Imaging Metrics Using Hierarchical Bayesian Regression

Abstract

Multi-site imaging studies can increase statistical power and improve the reproducibility and generalizability of findings, yet data often need to be harmonized. One alternative to data harmonization in the normative modeling setting is Hierarchical Bayesian Regression (HBR), which overcomes some of the weaknesses of data harmonization. Here, we test the utility of three model types, i.e., linear, polynomial and b-spline - within the normative modeling HBR framework - for multi-site normative modeling of diffusion tensor imaging (DTI) metrics of the brain’s white matter microstructure, across the lifespan. These models of age dependencies were fitted to cross-sectional data from over 1,300 healthy subjects (age range: 2–80 years), scanned at eight sites in diverse geographic locations. We found that the polynomial and b-spline fits were better suited for modeling relationships of DTI metrics to age, compared to the linear fit. To illustrate the method, we also apply it to detect microstructural brain differences in carriers of rare genetic copy number variants, noting how model complexity can impact findings.

1. Introduction

Clinical neuroimaging studies often need to pool data from multiple sources and scanners, especially if the conditions studied are rare. Consequently, worldwide efforts have been initiated in the past decade to combine existing legacy data from multiple sites to increase statistical power and test how well findings generalize across diverse populations. One such effort is the ENIGMA Consortium [1]. In parallel, large-scale scanning initiatives such as UKBB [2] and HCP [3] have been launched to prospectively scan thousands of subjects at multiple sites. Multi-site analyses have introduced new challenges to the field, particularly cross-site harmonization of the MRI scans, and normative modeling of measures derived from them. These approaches are used to model site effects, including differences in scanning protocols and sample characteristics across sites.

Commonly used harmonization algorithms, such as ComBat [4], cannot fully remove site-associated variance if age and site are confounded, making it difficult to correctly model the age effect when computing a harmonized set of MRI metrics. Here we test a recently proposed method for multi-site normative modeling of derived MRI measures to create a normative model (NM) [5]. Normative modeling is a technique that estimates the normative range and statistical distribution for a metric, (e.g., brain MRI-derived measure) as a function of specific covariates, e.g., age, sex, IQ, etc. Specifically, an NM based on hierarchical Bayesian regression (HBR) can be used to model site-dependent variability in the imaging data [6]. As a Bayesian method, it infers a posterior distribution rather than a single maximum likelihood estimate for the MRI metric, conditioned on the values of the known covariates. As noted by Kia et al. [6], HBR can model the different levels of variation in the data. Structural dependencies among variables are modeled by coupling them via a shared prior distribution. The frequent statistical dependence in multi-site neuroimaging projects that occurs between age and site, caused by different inclusion criteria across cohorts, may be better tackled with HBR.

Here we apply NM with HBR to metrics derived from diffusion tensor imaging (DTI). DTI is sensitive to alterations in brain microstructure and it has proven to be valuable in the diagnosis and characterization of many brain diseases [7, 8]. Nevertheless, the derived measures are highly sensitive to differences in acquisition parameters, such as voxel size and the number of gradient directions. This causes non-trivial differences in the raw scans as well as in their derived metrics [9]. Hence, the harmonization of DTI metrics is essential when performing multi-site studies of psychiatric and neurological diseases.

We set out to establish the normative range for DTI metrics in the brain’s white matter (WM) across the lifespan, based on data from 1,377 controls across six datasets, each with a different age range. Although only limited data exists on DTI norms from limited age ranges [10], lifespan normative charts have recently been computed for morphometric measures from T1-weighted MRI using ComBat-GAM [11] and NM [12]. We tackle the problem of fitting the age trajectory for DTI metrics by using HBR with three different fitting strategies, i.e., linear, polynomial and b-spline. We aimed to determine which of these models better fits age effects across the lifespan by using standardized evaluation metrics. Finally, we compare the three model types in an anomaly detection experiment on a multi-site sample with a large age range (2–80 years) of individuals with 16p11.2 deletion syndrome (16pDel) - a rare neurogenetic syndrome caused by the deletion of 29 genes on chromosome 16 [13]. These deletions increase the risk for a myriad of neuropsychiatric disorders, including neurodevelopmental delay, autism spectrum disorder and attention deficit hyperactivity disorder [14]. As such, there is keen interest in establishing the profile of brain abnormalities in 16pDel, which in turn requires an accurate reference model for WM microstructure across the lifespan. Additionally, because it is a rare condition (1:3000 live births) [20], multisite data must inevitably be combined to achieve adequate statistical power. Rare genetic variants are an illustrative and extreme case of the ubiquitous problem where clinical sites can only scan a few dozen patients each, making multi-site data pooling crucial and beneficial.

2. Methods

2.1. Diffusion MRI Processing

Image acquisition parameters are shown in Table 1. We combined 16pDel data from six sites (8 scanners in total), resulting in the largest neuroimaging sample assessing people with these CNVs to date (see Table 2). All six sites used Pulsed Gradient Spin Echo protocols. All images were identically preprocessed with DIPY [15] and FSL [16]. DTI-based fractional anisotropy (FA), mean diffusivity (MD), radial diffusivity (RD), and axial diffusivity (AD) were computed with DIPY on the 1000 s/mm² shell. All subjects’ FA maps were nonlinearly registered to the ENIGMA-FA template with ANTs [17]; these deformations were applied to the other DTI maps. Mean DTI measures were extracted from 21 bilateral regions of interest (ROIs) from the Johns Hopkins University WM atlas (JHU-WM) [18] using the ENIGMA-DTI protocol [19].

Table 1.

Acquisition protocols.

Study cohort	Scanner	Field strength	Resolution voxel size (mm)	b-values (s/mm2)	Gradient directions	TR/TE (ms)	No. of scanners
LREN	Siemens Prisma	3T	96 × 106 2 × 2 × 2	1000	30	71/4100	1
UMon	Siemens Prisma	3T	150 × 154 1.7 × 1.7 × 1.7	1000	30	71/4100	1
CHUV	Siemens Prisma	3T	150 × 154 1.7 × 1.7 × 1.7	1000	30	71/4100	1
SVIP	Siemens Trio Tim	3T	128 × 128 2 × 2 × 2	1000	30	80/10000	2
UKBB	Siemens Skyra	3T	104 × 104 2.01 × 2.01 × 1	1000	53	92/3600	2
HCP	Siemens Prisma	3T	168 × 144 1.25 × 1.25 × 1.25	1000	111	89.5/5520	1

LREN: Laboratoire de Recherche en Neuroimagerie; UMon: Université de Montréal; CHUV: Centre Hospitalier Universitaire Vaudois; SVIP: Simons Variation in Individuals Project; UKBB: United Kingdom BioBank; HCP: Human Connectome Project - Young Adult.

Table 2.

Demographics of the cohorts.

Study cohort	Diagnostic group	No. of subjects	Age (years)	Sex
LREN	16p11.2 Del	11	22.87, SD 13.64	M: 7/F: 4
	Healthy controls	29	40.68, SD 11.85	M: 16/F: 13
UMon	16p11.2 Del	2	42.09, SD 19.06	M: 2/F: 0
	Healthy controls	43	35.73, SD 15.07	M: 19/F: 24
CHUV	16p11.2 Del	12	6.17, SD 1.70	M: 9/F: 3
	Healthy controls	33	6.23, SD 1.83	M: 12/F: 21
SVIP	16p11.2 Del	41	14.03, SD 10.03	M: 25/F: 16
	Healthy controls	106	25.92, SD 14.76	M: 58/F: 48
UKBB	16p11.2 Del	4	65.65, SD 3.25	M: 3/F: 1
	Healthy controls	767	62.76, SD 7.32	M: 360/F: 407
HCP	Healthy controls	399	29.07, SD 3.77	M: 182/F: 217
TOTAL	16p11.2 Del	70	17.82, SD 16.65	M: 46/F: 24
	Healthy controls	1377	47.50, SD 19.25	M: 647 /F: 730

LREN, UMon, CHUV, SVIP, UKBB and HCP are independent studies.

JHU-WM ROIs.

PCR = Posterior corona radiata, CGH = Cingulum of the hippocampus, CGC = Cingulum of the cingulate gyrus, UNC = Uncinate fasciculus, RLIC = Retrolenticular part of internal capsule, SCR = Superior corona radiata, ACR = Anterior corona radiata, EC = external capsule, PLIC = Posterior limb of internal capsule, GCC = Genu, SS = Sagittal stratum, ALIC = Anterior limb of internal capsule, FXST = Fornix crus/Stria terminalis, BCC = Body of corpus callosum, TAP = Tapetum of the corpus callosum, CST = Corticospinal tract, SLF = Superior longitudinal fasciculus, SFO = Superior fronto-occipital fasciculus, SCC = Splenium, FX = Fornix, PTR = Posterior thalamic radiation.

2.2. Multi-site Normative Modeling

Let ${X\in R}^{n\times p}$ be a matrix of $p$ clinical covariates and $n$ the number of subjects. Here, we denote the dependent variable as $y\in R$. Typically, NM assumes a Gaussian distribution over y, i.e., $y~N\left(\mu ,{\sigma }^2\right)$, and it aims to find a parametric or non-parametric form for $\mu$ and $\sigma$ given $\mathbf{X}$. Then, $\mu$ and $\sigma$ are respectively parameterized on $f_{\mu }\left(\mathbf{X},{\theta }_{\mu }\right)$ and $f_{\sigma }^{+}\left(\mathbf{X},{\theta }_{\sigma }\right)$, where ${\theta }_{\mu }$ and ${\theta }_{\sigma }$ are the parameters of $f_{\mu }$ and $f_{\sigma }^{+}.f_{\sigma }^{+}$ is a non-negative function that estimates the standard deviation of the noise. Consequently, in a multi-site scenario, a separate set of model parameters could be estimated for each site, or batch, $i$ as follows:

$$y_i=f_{{\mu }_i}\left(\mathbf{X},{\theta }_{{\mu }_i}\right)+{ϵ}_{i}i\in \{1,\dots ,m\}$$ (1)

However, an assumption in HBR is that ${\theta }_{{\mu }_i}$ (and ${\theta }_{{\sigma }_i}$) across different batches come from the same joint prior distribution that functions as a regularizer and prevents overfitting of small batches. HBR is described as a partial pooling strategy in the multi-site scenario, compared to a complete pooling approach such as ComBat [4]. Similar to the no-pooling scenario, the parameters for $f_{\mu }$ and $f_{{\sigma }_i}^{+}$ are estimated separately for each batch. Then, in the NM framework, the deviations from the norm can be quantified as Z-scores for each subject in the ith batch:

$$z_i=\frac{y_i-f_{{\mu }_i}\left({\mathbf{X}}_i,{\theta }_{{\mu }_i}\right)}{f_{{\sigma }_i}^{+}\left({\mathbf{X}}_i,{\theta }_{{\sigma }_i}\right)}$$ (2)

These z-scores are then adjusted for additive and multiplicative batch effects using the estimated $f_{{\mu }_i}$ and $f_{{\sigma }_i}^{+}$ for each batch. The harmonization of Z-scores happens at this stage. The predictions of HBR for $f_{\mu }$ are not harmonized but the Z-scores are. Consequently, the model does not yield a set of “corrected” data, i.e., with the batch variability removed, as in ComBat. It instead preserves the sources of biological variability that correlate with the batch effects. This approach may be better able to model the heterogeneity of disease that is not captured by individual case-control studies [6]. We used the PCN-toolkit package to fit all HBR models¹.

Data from 80% of the 1,377 control participants were used as the training sample to estimate the norms. The remaining control subjects were used as a test set. Train-test splitting was stratified for the sites. Z-scores were calculated, measuring their deviations from the reference distribution. Z-scores for the 16pDel sample were also computed separately from the same estimated norm to detect abnormalities in the WM DTI metrics. We calculated probabilities of abnormality (p-values) from the Z-scores for the controls and the 16pDel subjects:

$$P_{abn}(z)=\frac{2}{\sqrt{2\pi }}{\int }_{-\mathrm{\infty }}^{\left|z\right|}{e}^{\frac{-t^2}{2}}dt-1$$ (3)

ROI-wise areas under the ROC curves (AUCs) were calculated to determine the classification accuracy of the computed deviations, using a binary threshold on the Z-scores. To achieve stability, we repeated the same procedure 10 times. Subsequently, we performed permutation tests with 1,000 random samples to derive permutation p-values for each DTI metric per ROI, and applied a false discovery rate (FDR) correction on each DTI metric separately across ROIs to identify those that showed significant group differences. To improve robustness, the ROIs that showed significance in 9 out of the 10 experimental iterations were retained for comparison [12].

Model Type Comparison.

We used three evaluation metrics to compare the three model fits across DTI metrics: 1) the Pearson’s correlation coefficient (Rho) between observed and estimated DTI metrics; 2) the standardized mean squared error (SMSE); and 3) the mean standardized log-loss (MSLL) [21]. The higher the Rho, and the lower the SMSE, the better the predicted mean. The MSLL (more negative scores being better) also assesses the quality of the estimated variance. After estimating the three models 10 times, we compared these model types by using the percentile bootstrap of the $M$-estimators [22], determining significant differences in three cases: linear vs polynomial (LP), linear vs. b-spline (LS) and polynomial vs. b-spline (PS).

3. Results

In all experiments, the linear fits had lower Rho, higher SMSE and higher MSLL than the polynomial and the b-spline fits. Figure 1 summarizes the results of the model comparisons: LP, LS, PS for all 10 experimental iterations. We found no significant differences between the three model types in any of the iterations for FA. There were no significant differences between the polynomial and b-spline models for any of the DTI metrics. Nor were there any significant differences between the linear and the polynomial models (LP) for AD, but there were differences between the linear and the b-spline models (LS) for MSLL, Rho and SMSE. MD and RD showed the most significant differences between the linear and the polynomial (LP), and the linear and b-spline models (LS) in most of the experiments and for the evaluation metrics. Nevertheless, the LS comparison yielded more significant differences across tests than LP for both MD and RD.

Fig. 1.

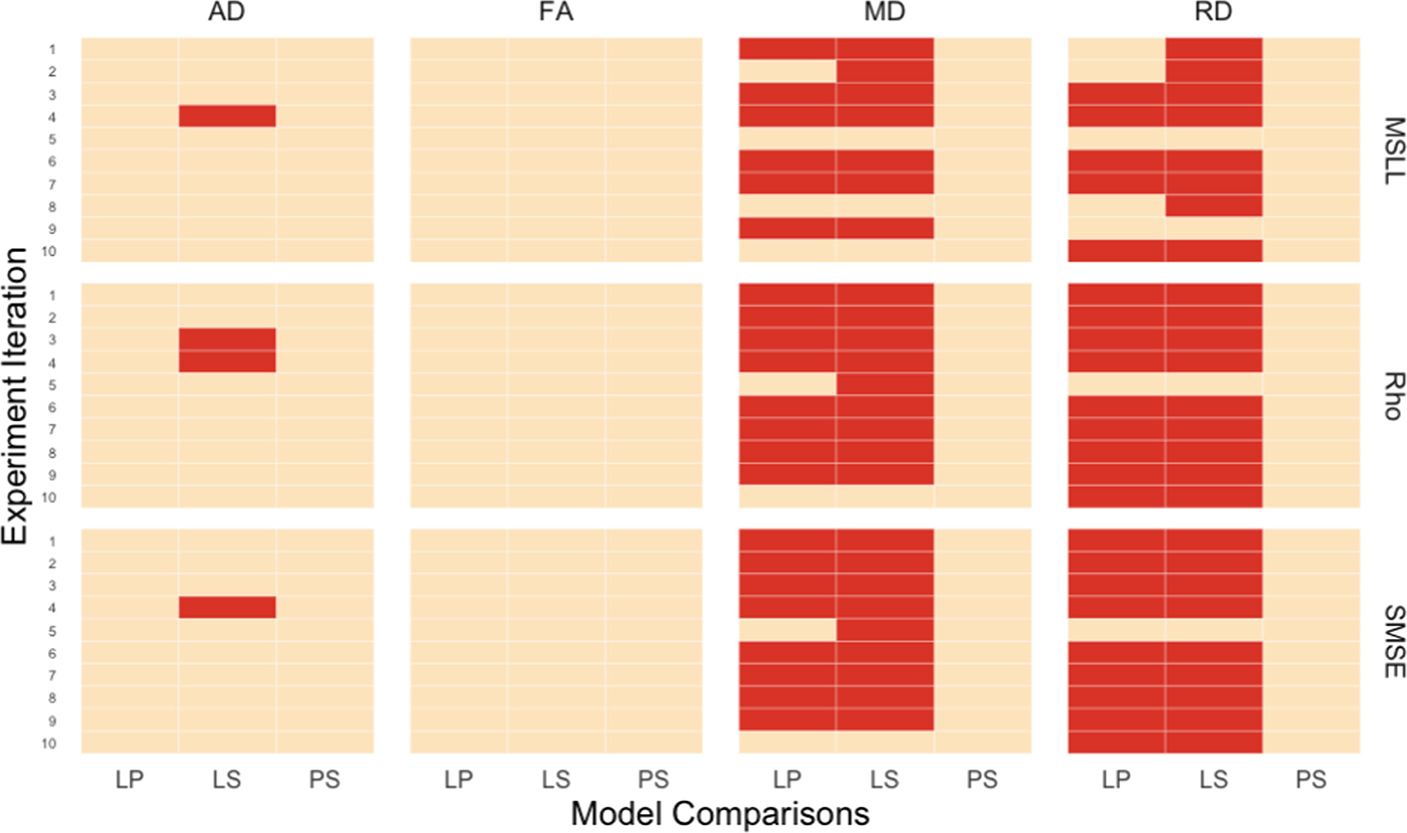
Model comparisons for the DTI metrics (AD, FA, MD, RD) on three evaluation metrics: Rho, SMSE, MSLL. Red cells indicate significant differences between the model types. Orange cells indicate non-significant differences. LP: linear vs. polynomial; LS: linear vs. b-spline; PS: polynomial vs. b-spline.

For the anomaly detection experiment, the polynomial and b-spline models showed significant ROIs for FA, RD and AD; only three ROIs for RD: CGC, SFO and TAP, and seven ROIs for AD: CGC, CGH, GCC, PCR, PLIC, SCR, SFO. Coincidences were found for FA between the three models in the CGH, CGC, PLIC, TAP. Interestingly, the linear model produced the greatest number of significant ROIs for MD and AD (Fig. 2), despite having significantly worse evaluation metrics than the polynomial (MD and RD) and the b-spline fits (MD, RD, AD). The most dramatic case was observed for MD, where neither the b-spline and polynomial fits yielded significant differences in any of the ROIs between healthy controls and 16pDel, but the linear model detected significant differences in six ROIs (i.e., ALIC, CGC, CGH, EC, GCC, PLIC). To explain these results, we performed an additional analysis of the Z-scores for those six significant MD ROIs in the linear model. We made bee-swarm plots (Fig. 3) for the Z-scores of these 6 ROIs for the linear and b-spline fits, for the controls and the 16pDel separately, and calculated the mean and mode for the Z-scores. For the 16pDel group, the Z-scores for linear fit had higher mean and mode (mean = 0.82, mode = 1.05), than those of the b-spline fit (mean = 0.37, mode = 0.27). For the controls, the mean and mode of the Z-scores for linear and b-spline fits were closer to each other. For the linear model, the tails of the distributions are longer than for the b-spline model which yields scores that appear closer to Gaussian, probably due to the better fits. For additional data, please see the Supplements.

Fig. 2.

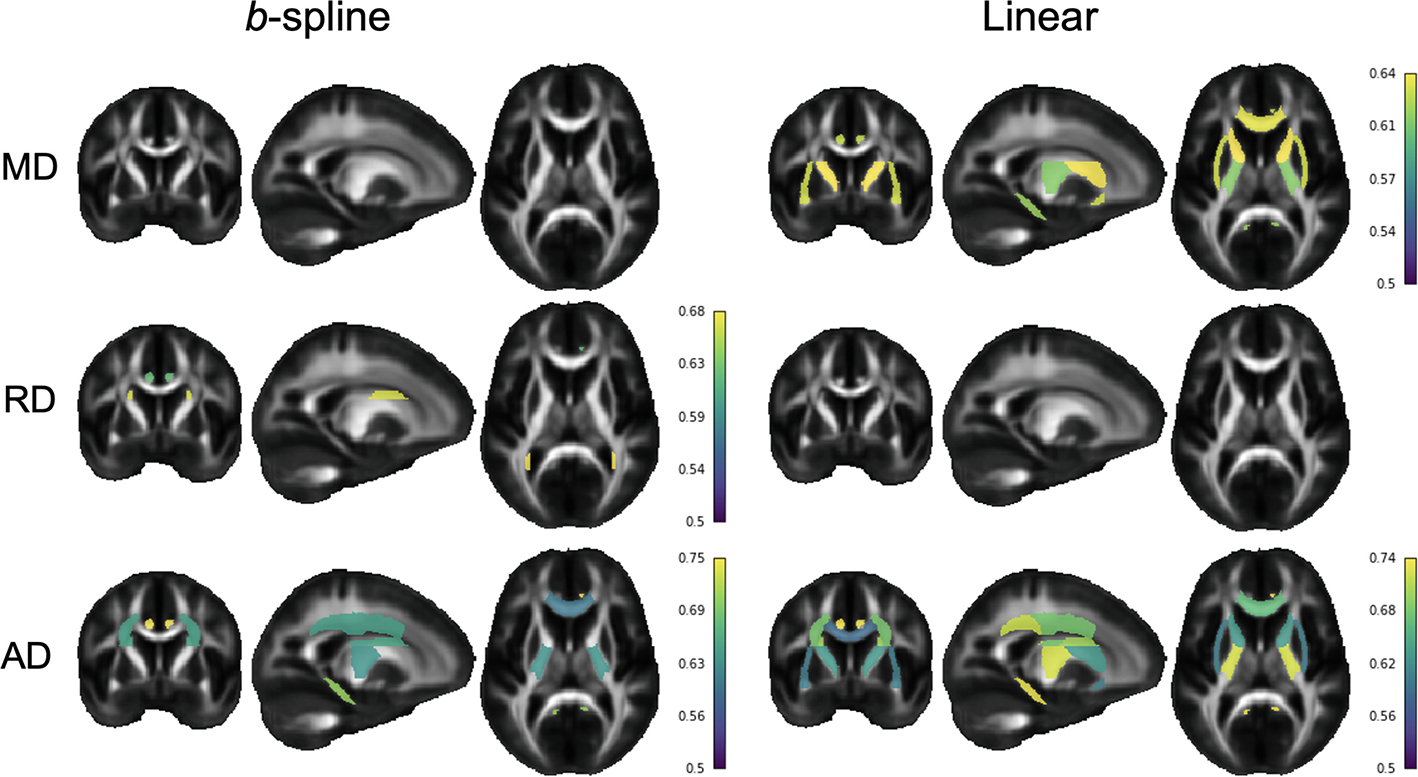
Comparison of the significant ROIs between the linear and the b-spline model. Colored ROIs passed FDR in at least 9 out of 10 experimental iterations. Color bars show the mean AUC for the ROIs across iterations. MD = mean diffusivity, AD = axial diffusivity, RD = radial diffusivity.

Fig. 3.

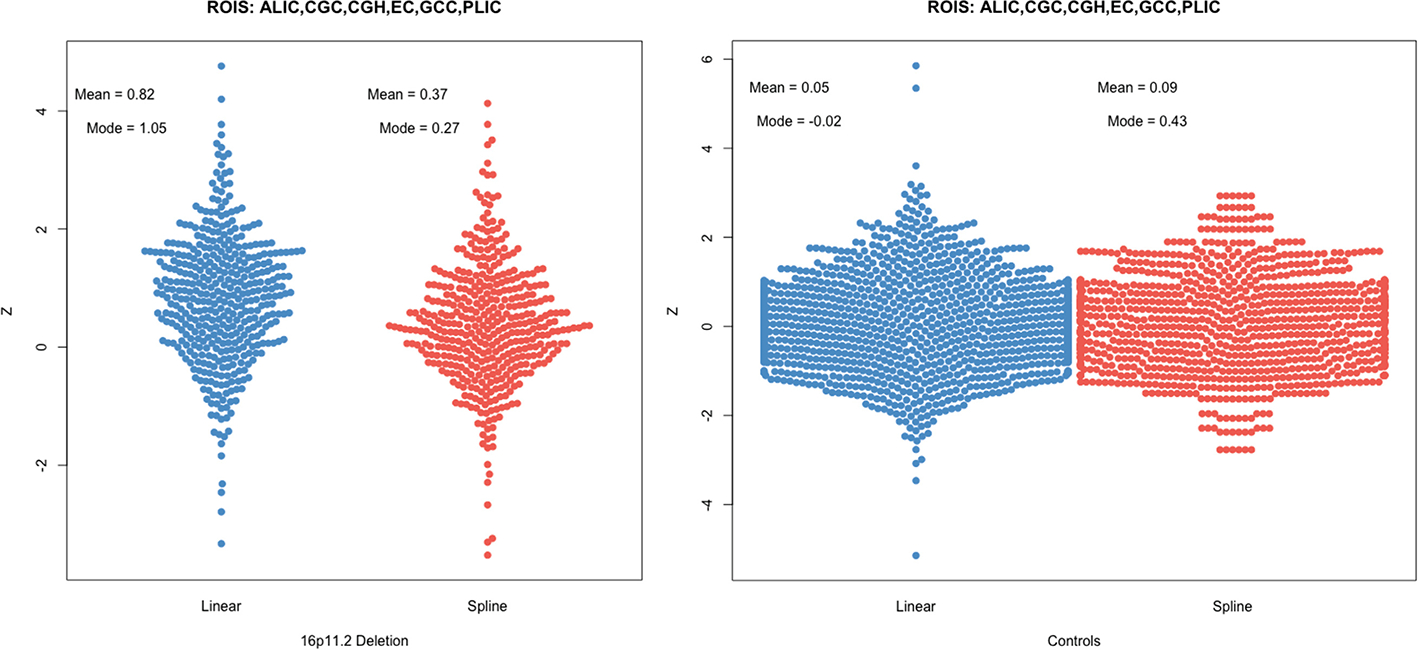
Comparison of the Z-score distribution between linear and b-spline models for the ROIs that were significant for MD for the linear model but not for the b-spline model. Notably, for the 16pDel group, the mode of the Z-scores for the linear model (mode = 1.05) is substantially higher than for the b-spline model (mode = 0.27), consistent with the notion that it is a poor fit for the data (high bias, as well as high variance).

4. Discussion

Here we used HBR normative modeling to infer the distributional properties of the brain’s WM microstructure based on large datasets from healthy subjects, spanning a wide age range. We were able to map the normal range of variation for four DTI metrics and to detect the deviations from this range in 16pDel. Based on the results of the b-spline fits, the abnormal deviations in FA and AD may be associated with abnormal axonal density, dispersion and/or dispersion secondary to altered cell migration failures or aberrant pruning, arising from the deletion of genes crucial for these processes.

This is the first study adapting nonlinear HBR theory to study rare neurogenetic conditions, and the first to analyze multi-site brain DTI. It is crucially important to test new open-source medical imaging algorithms on new data modalities (e.g., DTI), and in novel contexts (rare genetic variants), to offer a roadmap to generate rigorous, reproducible findings. Our work aims to ameliorate the reproducibility crisis in the field, as rare variant effects detected in small samples would be unlikely to be robust or reproducible. By adapting the mathematics of normative models beyond structural MRI to DTI, we thoroughly compare alternative models and parameterization choices when merging diverse international data into a single coherent model. Our results reveal how model selection and diverse reference data affect the conclusions regarding abnormalities, in a field (i.e., rare variant genetics) where secure knowledge is lacking.

We were also able to determine which type of model better fits the lifespan trajectory of the DTI metrics in the WM. All our experiments indicated that the polynomial and b-spline models offered better fits to the data than the linear fits, with significant differences (in fit, across models) for MD, RD, AD but not for FA. The b-spline model was slightly better, on average across all 10 experiments, than the polynomial model. In general, a more highly parameterized model will give a better fit to the test data so long as it is not overfitting the training data, which is less likely in the $n>>p$ regime (where our number of samples exceeds the model complexity). Additionally, several prior publications show the non-linear effect of age on DTI metrics [10, 23]. Even so, this is the first report, to our knowledge, to model age effects on WM DTI metrics using HBR. Although the linear model performed significantly more poorly than the other models, it nonetheless yielded a higher number of significant ROIs for anomaly detection for 16pDel subjects versus healthy controls. A possible explanation for this may be that the b-spline models are more complex; thus, given the same amount of data, they may be less stable than linear models. Such a hypothesis will be testable with more data. Hence, in the b-spline model, fewer ROIs survived the stringent stability test (showing a significant group difference in at least 9 out of 10 random draws from the data). These findings may serve as a warning to be cautious with any linear fitting strategy for DTI metrics, especially when the age range is large. In summary, we show the feasibility of fitting hierarchical Bayesian models to multi-cohort diffusion data, noting that the model complexity may influence the achievable fit to the data and the brain regions where anomalies can be confidently detected. Further work with an expanded dataset will be valuable to confirm these observations.