Large-scale Normative Modeling of Brain Microstructure

Abstract

Normative models of brain metrics based on large populations are extremely valuable for detecting brain abnormalities in patients with dementia, psychiatric, or developmental conditions. Here we present the first large-scale normative model of the brain’s white matter (WM) microstructure derived from 18 international diffusion MRI (dMRI) datasets covering almost the entire lifespan (totaling N=51,830 individuals; age: 3–80 years). We extracted regional diffusion tensor imaging (DTI) metrics using a standardized analysis and quality control protocol, and used Hierarchical Bayesian Regression (HBR) to model the statistical distribution of derived WM metrics as a function of age and sex, while modeling the site effect. HBR overcomes known weaknesses of some data harmonization methods that simply scale and shift residual distributions at each site. To illustrate the method, we applied it to detect and visualize profiles of WM microstructural deviations in cohorts of patients with Alzheimer’s disease, mild cognitive impairment, Parkinson’s disease and in carriers of 22q11.2 copy number variants, a rare neurogenetic condition that confers increased risk for psychosis. The resulting large-scale model offers a common reference to identify disease effects in individuals or groups, as well as to compare disorders and discover factors that influence these abnormalities.

I. Introduction

Large-scale international imaging initiatives have increased the availability of brain imaging data worldwide. This has stimulated the development of powerful statistical tools to study brain diseases, such as normative models and generative models [1]. Normative modeling (NM) is a statistical technique that aims to calculate the normative distribution of a biological measure in a population and model its variation (centiles of variation), given explanatory or clinical variables such as age, sex, IQ, etc. As such, it can be considered a generative model of brain structure that learns from large-scale data; this supplies a powerful reference to gauge and track brain abnormalities and factors that protect the brain. NM is sensitive to individual differences offering metrics of abnormality that go beyond the standard case-control maps of group differences. This has sparked broader interest in NM because of its applications in personalized medicine.

NM has previously been applied in structural imaging studies to create lifespan trajectories. Rutherford et al. [2] recently proposed the Predictive Clinical Neuroscience toolkit (https://pcntoolkit.readthedocs.io) and used it to chart lifespan trajectories of structural brain metrics [3]. Bethlehem et al. [4] aggregated structural MRI scans across more than 100 primary studies, and created lifespan ‘brain charts’ from 101,457 human participants from birth to 100 years of age. Ge et al. [5] applied multivariable Fractional Polynomial Regression, warped Bayesian Linear Regression and HBR to map regional morphometric data from 37,407 healthy individuals (53.33% female; aged 3–90 years) collated from 86 international structural MRI datasets as part of the ENIGMA-Lifespan project, creating CentileBrain (https://centilebrain.org).

So far, we lack normative models for brain microstructure, which is altered in a range of degenerative, psychiatric and neurodevelopmental conditions; factors that influence the extent and timing of these anomalies are of great interest. DMRI is sensitive to the microstructural environment of the brain tissue and yields a rich set of metrics that are sensitive to a broad range of brain diseases. Building normative models of dMRI-derived metrics is an important aim for studying brain disease. Even so, dMRI metrics are influenced by several acquisition parameters, including the voxel size, number of diffusion gradient directions, and b-values [6]. This poses a serious challenge when attempting to estimate a normative or reference model for dMRI-derived metrics across multiple sites with different acquisition protocols. The other main source of multi-site variability comes from different sample characteristics, such as inclusion/exclusion criteria. Normative models should include data from multiple studies to model biological variation in a way that generalizes to populations internationally. Here, to gather enough dMRI data for NM, we pooled dMRI data from diverse international studies, including protocols with different voxel sizes, gradient sets, scanner vendors, and field strengths.

As noted by Bayer et al. [7], numerous mathematical approaches have been developed to model batch or site effects that contribute to variation in the data. The strategy we chose here for multi-site NM is a partial-pooling approach based on Hierarchical Bayesian Regression (HBR), proposed by Kia et al. for neuroimaging studies in neurology and psychiatry [8]. This approach differs from the complete pooling approach used in ComBat [9]. Complete pooling harmonizes the individual data by adjusting for multiplicative and additive batch effects and then feeding this corrected data as an input to the estimation of the reference normative model. NM with HBR adjusts the Z-scores instead of the input data points. In pilot work on multisite NM of dMRI, we showed that this approach could detect extreme deviations from the norm for subjects with neurogenetic disorders [10]. Thus, HBR applied to large-scale multi-site NM of dMRI-based brain metrics holds potential for clinical applications in psychiatry and neurology.

In this study, we built a reference model of DTI metrics across the lifespan (3–80 years) based on 51,830 subjects scanned in 18 large-scale neuroimaging studies. To illustrate the approach, we computed large-scale reference models for fractional anisotropy (FA) and mean diffusivity (MD) to detect WM abnormalities in Alzheimer’s disease (AlzD), mild cognitive impairment (MCI), Parkinson’s disease (PD), 22q11.2 deletion and duplication syndromes (22qDel & 22qDup, respectively). With this large-scale model that spans most of the human lifespan, we aimed to detect individual deviations from the reference model in subjects with these conditions at any age, offering a flexible framework suitable for precision medicine.

II. Methods

The following public datasets with a varied age distribution were included to cover the lifespan, including: ABCD [11], AOMIC [12], CAMCAN [13], CHBMP [14], CHCP [15], HCP-A & HCP-D [16], HCP-YA [17], NIH-Peds [18], PING [19], QTAB [20], QTIM [21], SLIM [22], and UKBB [23]. The reader is encouraged to consult the corresponding references for each dataset’s acquisition protocol. The clinical test datasets included: ADNI3 [24], OASIS3 [25], PPMI [26] and a 22q11.2 copy number variant (CNV) dataset (UCLA) [27]. The healthy controls of the latter four datasets were added to the pool of training data. Fig. 1 shows the age distributions and sample sizes of each study used for training.

Fig. 1. Age distribution for the 18 datasets we analyzed.

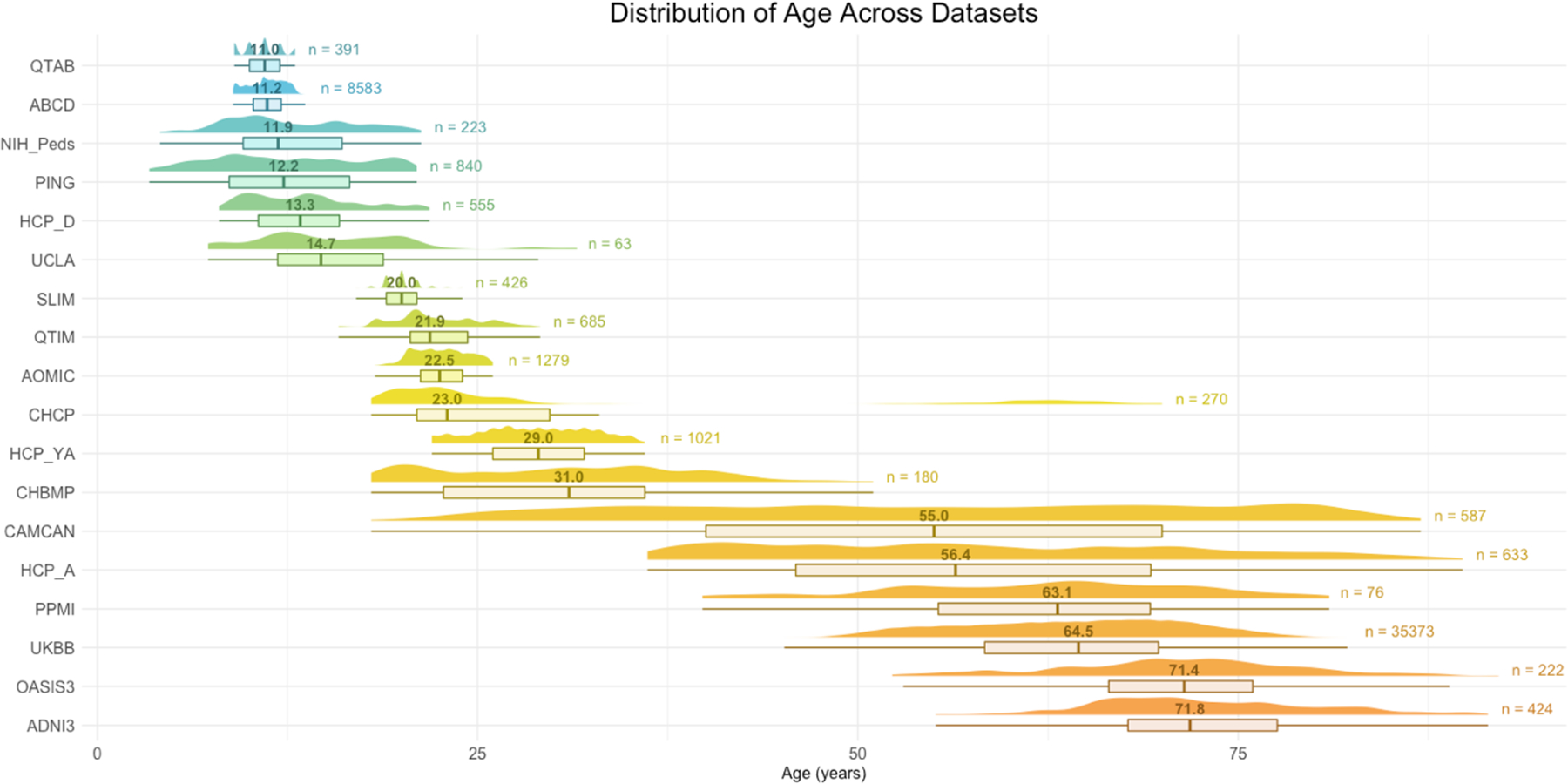
The number above the boxplot is the median age for each sample and to the right is the total number subjects used for training. For the clinical samples, only control subjects are shown here as the normative model is based on controls only.

Some datasets offered already preprocessed dMRI scans (HCP-YA, AOMIC), while others provided precomputed DTI maps (NIH-Peds, UKBB, ADNI3). The remaining datasets were preprocessed in-house. In all cases, preprocessing included correction for eddy currents, movement, and EPI-induced susceptibility distortions. For the datasets without precomputed DTI maps, FA and MD were computed with DIPY [28] or FSL [29] on the single shell or on the lowest shell available if multi-shell data were provided. All subjects’ FA maps were nonlinearly registered to the ENIGMA-FA template with ANTs [30]; these deformations were applied to the MD maps. Mean DTI metrics were extracted from 21 bilateral regions of interest (ROIs) from the Johns Hopkins University WM atlas (JHU-WM) [31] using the ENIGMA-DTI protocol [32].

A. JHU-WM ROIs

We use the following abbreviations for the ROIs studied: PCR=posterior corona radiata, CGH=cingulum of the hippocampus, CGC=cingulum of the cingulate gyrus, UNC=uncinate fasciculus, RLIC=retrolenticular part of internal capsule, SCR=superior corona radiata, ACR=anterior corona radiata, EC=external capsule, PLIC=posterior limb of internal capsule, GCC=genu, SS=sagittal stratum, ALIC=anterior limb of internal capsule, FXST=crus of the fornix/stria terminalis, BCC=body of corpus callosum, TAP=tapetum of the corpus callosum, SLF=superior longitudinal fasciculus, SFO=superior fronto-occipital fasciculus, SCC=splenium, FX=fornix, PTR=posterior thalamic radiation.

B. Normative Modeling with HBR

Although a thorough mathematical description of the HBR NM framework is beyond the scope of this paper, here we summarize the basic principle.

Let $X\in R^{n\times p}$ be a matrix of $n$ the number of subjects and $p$ clinical covariates. Here, we denote the dependent variable as $y\in R$. In its simplest form, NM assumes a Gaussian distribution over $y$, i.e., $y~N\left(\mu ,{\sigma }^2\right)$, and it aims to find a parametric or non-parametric form for $\mu$ and $\sigma$ given $\mathbf{X}$. Then, $\mu$ and $\sigma$ are respectively parameterized on $f_{\mu }\left(\mathbf{X},{\theta }_{\mu }\right)$ and $f_{\sigma }^{+}\left(\mathbf{X},{\theta }_{\sigma }\right)$, where ${\theta }_{\mu }$ and ${\theta }_{\sigma }$ are the parameters of $f_{\mu }$ and $f_{\sigma }^{+}.f_{\sigma }^{+}$ is a non-negative function that estimates the standard deviation of the noise. In a multi-site scenario, a separate set of model parameters could be estimated for each site, or batch, $i$, as follows:

$$y_i=f_{{\mu }_i}\left(\mathbf{X},{\theta }_{u_i}\right)+{ϵ}_{i}i\in \{1,\dots ,m\}$$ (1)

However, the assumption in HBR is that ${\theta }_{{\mu }_i}$ (and ${\theta }_{{\sigma }_i}$) across different batches come from the same joint prior distribution that functions as a regularizer and prevents overfitting of small batches. Similar to the no-pooling scenario, the parameters for $f_{\mu }$ and $f_{{\sigma }_i}^{+}$ are estimated separately for each batch. Then, in the NM framework, the deviations from the norm can be quantified as Z-scores for each subject in the $i$ th batch:

$$z_i=\frac{y_i-f_{{\mu }_i}\left({\mathbf{x}}_i,{\theta }_{{\mu }_i}\right)}{f_{{\sigma }_i}^{+}\left({\mathbf{x}}_i,{\theta }_{{\sigma }_i}\right)}$$ (2)

These Z-scores are further adjusted for additive and multiplicative batch effects using the estimated $f_{{\mu }_i}$ and $f_{{\sigma }_i}^{+}$ for each batch. The harmonization of Z-scores happens at this stage. The predictions of HBR for $f_{\mu }$ are not harmonized but the Z-scores are. Consequently, the model does not yield a set of “corrected” data, i.e., with the batch variability removed, as in ComBat. It instead preserves the sources of biological variability that correlate with the batch effects. Concordantly, the frequent statistical dependence in multi-site neuroimaging projects that occurs between age and site, caused by different inclusion criteria across cohorts, may be better tackled with HBR.

Here we used age and sex as covariates, and each DTI metric per ROI as the dependent variable. Thus, the inclusion criteria for the full sample were based on participants having age and sex information along with a dMRI scan. Importantly, we identified 32 dMRI acquisition protocols across all 18 datasets with different numbers of gradient directions, voxel sizes, b-values, etc., which affect the estimation of DTI parameters by inducing a strong site effect. Consequently, we chose the dMRI protocol as the “site” or batch variable for training the reference model. We used the PCN-toolkit package and Python 3.8 to fit NM with HBR [2].

Training and testing data sets were created with an 80% to 20% sample split stratifying the controls of each site. To achieve stability, we repeated the same procedure 10 times. Z-scores were re-calculated on each split of the test set and the clinical cases as well, measuring their deviations from the estimated reference distribution. We calculated probabilities of abnormality $(\mathrm{P}(\mathrm{z}))$ from the Z-scores for the controls and the clinical samples:

$$\mathrm{P}(z)=2\left(1-\frac{1}{\sqrt{2\pi }}{\int }_{-\mathrm{\infty }}^{\left|z\right|}{e}^{-t^2/2}dt\right)$$ (3)

ROI-wise areas under the ROC curves (AUCs) were calculated to determine the classification accuracy of the computed deviations, using a binary threshold on the Z-scores. Subsequently, we performed permutation tests with 1,000 random samples to derive permutation p-values for each DTI metric per ROI, and applied a false discovery rate (FDR) correction on each DTI metric separately across ROIs to identify those that showed significant group differences. The ROIs that showed significance in 9 out of the 10 experimental iterations were retained [3, 8]. For each clinical group, i.e., AlzD, MCI, PD, 22qDel and 22qDup, we summarized the individual deviations within each group by first separating them into positive and negative deviations, counting how many subjects had an extreme deviation (defined as $\mathrm{Z}>2$ for positive deviations, $\mathrm{Z}<-2$ for negative deviations) at a given ROI, and then dividing by the group size.

III. Results

Results are summarized in Fig. 2-A for FA and Fig. 2-B for MD, where we show the proportion of subjects of the clinical samples with positive and negative extreme deviations ($\mathrm{Z}>\left|2\right|$) . The displayed ROIs are those with an AUC>0.5 that were significant after FDR correction. In AlzD, the best performances were found in the CGH for both FA (AUC=0.68) and MD (AUC=0.71). In MCI, the best performance was observed in the BCC for MD (AUC=0.58), and no significant results were found for FA. In PD, the best performance was found in the ALIC for FA (AUC=0.59) and in the SFO for MD (AUC=0.59). In 22qDel, the SCC had the best performance for FA (AUC=0.64) and the PCR for MD (AUC=0.75). In 22qDup, it was the UNC for FA (AUC=0.69), and there were no significant results for MD.

Fig. 2.

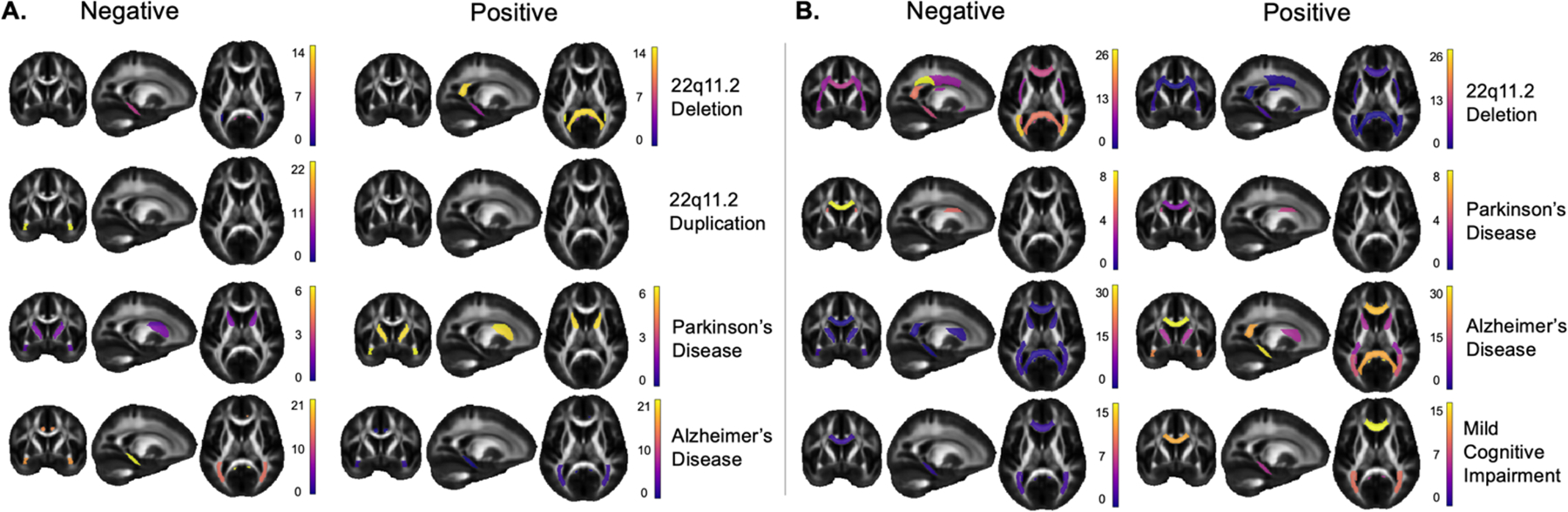
A) Fractional anisotropy (FA) results: proportion of extreme negative deviations on the left and positive extreme deviations on the right. Color bars show the proportion of subjects with extreme deviations per ROI. B) Mean diffusivity (MD) results: proportion of extreme negative deviations on the left and positive extreme deviations on the right. Color bars show the proportion of subjects with extreme deviations per ROI.

In general, we found extreme deviations ($\mathrm{Z}>\left|2\right|$) in both directions for AlzD, MCI, PD, and 22qDel. Our results show that the highest proportions of deviations are in the direction that has been previously reported in case-control studies for the 5 clinical conditions. For instance, lower FA and higher MD have been reported in AlzD and MCI, which was found here, where up to 20% of participants showed higher FA in the CGH and lower MD in the CGH, GCC, SCC, ACR and PCR. Interestingly, for all brain diseases, a smaller proportion of subjects showed extreme deviations in the opposite directions than previously reported in case-control studies, which is counterintuitive but nevertheless deserves more attention.

IV. Discussion

From the largest sample to date, we created well-defined reference models for the brain’s WM microstructure to quantify variability across the lifespan. We used HBR NM to infer the distributional properties of two widely-used DTI metrics in the brain’s WM based on datasets spanning a wide age range. By mapping the normal range of variation for FA and MD, we were able to detect patterns of deviations from this range in AlzD, MCI, PD, 22qDel and 22qDup. The HBR NM method may offer transdiagnostic clinical value, revealing different patterns of abnormalities in the WM across different brain diseases. Unlike group differences in case versus control analyses, NM offers individual-level profiles of anomalies, accepting that not all individuals with the same disease deviate in the same brain regions and not all disorders have the same characteristic patterns.

The current study is to our knowledge the first and largest study adapting nonlinear HBR theory to DTI metrics showing its potential for use in studies of a variety of psychiatric and neurologic conditions. The ability to create maps of the extent and magnitude of individual-level deviations can provide complimentary information to the group effects captured in case control studies.

As most large neuroimaging studies aggregate data from multiple sites, including existing datasets that target specific age ranges, there is an unavoidable sampling bias where certain sites contribute data to only part of the age range. Importantly, the ENIGMA-DTI protocol used in this study was not adjusted for early childhood scans (3–7 years) so the model should be interpreted cautiously if used on new data in this age range.

It is crucially important to test new open-source medical imaging algorithms on new data modalities such as dMRI, and in novel contexts (rare genetic variants, PD, AlzD and MCI), to offer a roadmap to generate rigorous, reproducible findings. By adapting normative models from structural MRI to dMRI, we offer a benchmark for merging diverse international data into a single normative model and comparing future datasets to the reference data. Lastly, this study is limited to only FA and MD, which are known to fail to model the crossing fibers in the WM. Future studies will include a richer set of dMRI measures, including multicompartmental models (e.g., NODDI) that are better suited to describe the brain’s microstructure.