Abstract
Adaptations in muscle physiology due to long-term physical training have been monitored using various methods: ranging from invasive techniques, such as biopsy, to less invasive approaches, such as electromyography (EMG), to various quantitative magnetic resonance imaging (qMRI) parameters. Typically, these latter parameters are assessed immediately after exercise. In contrast, this work assesses such adaptations in a set of qMRI parameters obtained at rest in the lumbar spine muscles of volunteers. To this end, we developed a multiparametric measurement protocol to extract quantitative values of (water) T2, fat fraction, T1, and Intra Voxel Incoherent Motion (IVIM) diffusion parameters in the lumbar back muscle. The protocol was applied to 31 healthy subjects divided into three differently trained cohorts: two groups of athletes (endurance athletes and powerlifters) and a control group with a sedentary lifestyle. Significant differences in muscle water T2, fat fraction, and pseudo-diffusion coefficient linked to microcirculatory blood flow in muscle tissue were found between the trained and untrained cohorts. At the same time, diffusion coefficients (resolved along different directions) provided additional differentiation between the two groups of athletes. Specifically, the strength-trained athletes showed lower axial and higher radial diffusion components compared to the endurance-trained cohort, which may indicate muscle hypertrophy. In conclusion, utilizing multiparametric information revealed new insights into the potential of quantitative MR parameters to detect and quantify long-term effects associated with training in differently trained cohorts, even at rest.
Keywords: qMRI, training, lumbar back muscle, diffusion, IVIM
1 Introduction
Physical activity and muscle training have several positive effects, such as improving cardiovascular health (Pinckard et al., 2019), increasing muscle resistance to fatigue (Nystoriak and Bhatnagar, 2018), and reducing the risk of developing diseases such as type II diabetes (Neufer et al., 2015) or colorectal cancer (Samad et al., 2005). The fact that consistent physical activity modifies skeletal muscle morphology is widely accepted (Flück et al., 2019), but assessing and quantifying these modifications usually requires invasive techniques such as muscle biopsies. Biopsy-based studies have demonstrated significant adaptations of muscle tissue to long-term physical activity, including changes in muscle fiber type composition and size (Andersen and Aagaard, 2010; Meijer et al., 2015). They have also successfully shown distinct effects of different training regimens on metabolism- and contraction-related cellular parameters (Terzis et al., 2010; Flück et al., 2019).
A prominent non-invasive tool for studying the activation of muscle tissue is electromyography (EMG). EMG records the electrical activity that leads to muscle contraction (Mills, 2005) and has been shown to aid in both diagnosis and the study of muscle function, although caution should be exercised in interpreting it in terms of muscle force or timing of contraction (Roberts and Gabaldón, 2008). A recent surface electromyography study observed a significant difference in muscle activation in subjects with different exercise routines (Schönau and Anders, 2023). In this study, both endurance athletes and controls performed better than strength athletes in a 10-minute back muscle endurance test at a load of 50% of upper body weight.
Possible long-term effects associated with regular training, detectable by EMG or biopsy, are less well-researched with quantitative magnetic resonance imaging (qMRI). There are only a few MRI-based studies on this topic (Le Rumeur et al., 1994; Sun et al., 2018; Berry et al., 2020; Marth et al., 2022), each generally focusing on only a few parameters, but highlighting the possible impact of exercise-induced muscle damage, affecting the transverse relaxation time T2 and significant changes in the fat fraction between the trained and untrained cohorts (Emanuelsson et al., 2022).
T2 relaxation time is a well-established parameter in MRI, frequently used for evaluating muscle tissues. It is important to distinguish water (muscle) T2 and global T2. Global T2 includes signals from both muscle and fat without differentiation. Water T2 has been shown to increase after exercise, and the origin of this phenomenon has been linked to an accumulation of osmolytes due to increased fluid influx (Patten et al., 2003; Cagnie et al., 2011). Apparent diffusion coefficients (ADC) have also been shown to increase after exercise (Hiepe et al., 2013; Kolmer et al., 2023), which is thought to be due to increased fluid in muscles during and after a strenuous exercise session. Other studies using Intravoxel Incoherent Motion (IVIM) MRI sequences have also demonstrated increased microcirculatory blood flow after exercise (Nguyen et al., 2016; Federau et al., 2020; Englund et al., 2022).
Two other MRI parameters that have been used to characterize muscle tissue morphology are fat fraction and T1 relaxation time. Increased fat fraction has been associated with reduced power output per muscle unit and with low back pain (Hildebrandt et al., 2017; Schlaeger et al., 2019). The level of fat replacement of muscle tissue can be quantitatively assessed by MRI, exploiting the chemical shift between the proton signals of fat and water. Furthermore, changes in T1 immediately after exercise have been associated with increased blood perfusion and tissue temperature (Fleckenstein et al., 1988; de Sousa et al., 2011), but the origin of this phenomenon is not fully understood.
Most of the qMRI literature on the effect of exercise on skeletal muscle has focused on measuring changes in some quantitative MRI parameters, such as T2 and diffusion, immediately after a strenuous exercise session (Cagnie et al., 2011; Hiepe et al., 2013). However, long-term effects associated with regular physical activity on qMRI parameters appear to be relatively understudied (Berry et al., 2020; Keller et al., 2020).
To bridge this gap, we developed a multi-parametric protocol to comprehensively characterize back muscle morphology and to investigate whether long-term physical activity and type of training are associated and detectable in changes of qMRI parameters. This protocol included well-established parameters, such as muscle water T2 and fat fraction, which have been used before to characterize skeletal muscle composition (even at rest), and less well-studied parameters such as T1, diffusion (Damon et al., 2002; Sinha et al., 2006; Karampinos et al., 2010) and perfusion-related parameters (Filli et al., 2015). Diffusion parameters have been shown to be sensitive to microstructural changes such as muscle fiber dispersion, organisation and size which might aid in the differentiation of the impact of different training regimes on the skeletal muscle tissue. Additionally, physical activity is associated with vascular adaptation which might influence perfusion values even at rest (Green et al., 2012; Welsch et al., 2013).
The protocol was applied to the muscles of the lumbar spine (specifically the area between L4 and L5) rather than the more commonly investigated skeletal muscles of the calf and thigh. This choice was made because the lumbar paraspinal muscles are increasingly being linked to nonspecific low back pain, which is one of the most common causes of disability worldwide (Balagué et al., 2012). The exact causes behind this condition are not yet fully understood and there is no consensus on the precise role of paraspinal muscles on nonspecific low back pain (Ranger et al., 2017; Hodges et al., 2021). This may be due to the fact that traditional clinical MRI examinations only allow qualitative morphological evaluations, while quantitative results have the potential to assess the underlying tissue function (Sollmann et al., 2022). Furthermore, physical activity has been shown to be a viable treatment, but there is still debate about which type of physical activity is most beneficial (Shipton, 2018). Quantitatively evaluating the long-term effects associated with training in healthy cohorts and at rest using the proposed protocol may pave the way for treatment monitoring in low back pain.
In this study, we hypothesize that while parameters like water T2 and fat fraction can distinguish between trained and untrained groups even at rest, a deeper analysis involving diffusion and perfusion coefficients is necessary to discern the impacts of various training regimens on both the skeletal muscle composition and structure.
2 Materials and methods
2.1 Participants
Three cohorts of male subjects were studied: Endurance athletes (long-distance runners and cyclists, n = 10), strength athletes (powerlifters, n = 11), and a control group (n = 10) with a non-athletic lifestyle. All subjects were between 20 and 31 years of age, average age and BMI per cohort are detailed in Table 1. The institutional ethics committee approved the study. All participants provided written informed consent. Athletes were recruited through advertisements in local sports clubs and gyms. They were enrolled into the study if they trained at least four times per week (training session duration of at least 1 h) and had been training for at least the previous 3 years. The sedentary control group, recruited from the local university student population through advertisements placed in university canteens, was required to have no regular participation in physical activities such as regular sport or any kind of deliberate physical training and a mostly sedentary occupation without intense physical activity. Adherence to these criteria, as well as the absence of back pain in all participants, was self-reported. Subjects underwent MRI examinations in supine position with the vendor’s spine coil in a 3T Magnetom Prisma fit scanner (Siemens Healthineers, Erlangen, Germany).
TABLE 1.
Summary of the ages and BMI of the analyzed volunteers. Values are given as mean ± standard deviation for each cohort. The ages across the groups showed no significant statistical differences, while the BMI of the strength training cohort was significantly different from the other two cohorts.
| Cohort | Age [years] | BMI [kg/m2] |
|---|---|---|
| Control | 29 3 | 23 2 |
| Endurance | 25 3 | 21 1 |
| Strength | 26 2 | 28 2 |
2.2 MRI protocol
The MRI protocol included sequences to determine relaxation parameters (i.e., water T2 and T1), fat fraction, and IVIM parameter values. Quantitative water T2 values were determined using a turbo spin echo (TSE) sequence with 28 echo times ranging from 7 ms to 218 ms, while the T1 relaxation time constants were determined using a variable flip angle (VFA) gradient echo sequence (Christensen et al., 1974) with five different flip angles (5°, 11°, 18°, 24°, 32°). For accurate VFA-based T1 determination, especially at higher field strengths and in areas where the RF signal is attenuated (e.g., lower lumbar and abdominal regions), correction of the B1-field is essential, which was performed here by acquiring an additional B1 calibration scan using the Bloch-Siegert method (Sacolick et al., 2010). The in-plane spatial resolution was (1.5 × 1.5) mm2 for all sequences, and the slice thickness was 3 mm (except for the TSE sequence, which used a slice thickness of 6 mm).
Diffusion-weighted images (DWI) were acquired with a multi-slice spin-echo EPI (echo planar imaging) sequence with TR/TE = 1,600/63 ms using four averages and three orthogonal directions of diffusion encoding aligned with the right-handed RAS system (each direction was repeated twice with opposite polarities). For each direction, the following 19 b-values were used: 0, 5, 15, 20, 30, 40, 45, 55, 60, 70, 75, 90, 105, 120, 135, 150, 300, 450, 600 s/mm2, with particular emphasis placed on acquiring low b-values as they have been shown to aid in IVIM based quantification (Ye et al., 2019). The resolution for the DWI data was (2.3 2.3 8) mm3. Spectral Attenuated Inversion Recovery (SPAIR) fat saturation was used.
All images (from L4 to L5) were acquired in axial orientation. The muscles included in the field of view were multifidus (MF), erector spinae (ES), psoas major, and quadratus lumborum. However, the latter two muscles could not be evaluated consistently in all subjects due to artifacts caused by respiration and bowel motion and were excluded from the analysis (cf. section 1.3 of the Supplementary Material). The total acquisition time was 43 min. All relevant acquisition parameters can be found in Table 2. MRI scans were performed at rest, at least 48 h after the last exercise session, to exclude exercise-related parameter changes.
TABLE 2.
Parameters of the MRI protocol. TR stands for repetition time, TE for echo time and TA for acquisition time. VFA GRE is a variable flip angle gradient echo sequence, TSE for turbo spin echo and finally EPI for echo planar imaging.
| VFA GRE | B1 map | TSE | Diffusion EPI | |
|---|---|---|---|---|
| TR [ms] | 16 | 20 | 5,000 | 1,600 |
| TE [ms] | 2.4 | 1.76 | 7.8–218.4 | 63 |
| Voxel [mm3] | 1.5 1.5 × 3 | 1.5 1.5 × 3 | 1.5 1.5 × 6 | 2.3 2.3 × 8 |
| FOV [mm3] | 380 285 × 3 | 380 285 × 3 | 380 285 × 6 | 300 187 × 8 |
| Averages | - | - | - | 4 |
| Saturation bands | - | - | yes | - |
| Slices | 40 | 40 | 20 | 10 |
| TA | 15 min | 40 s | 16 min | 12 min |
2.3 MRI data processing and analysis
Regions of interest (ROIs) were manually drawn to segment the multifidus and erector spinae muscles based on apparent diffusion coefficient (ADC) maps for each subject, avoiding fascia, connective tissue and subcutaneous fat. Since there were no significant differences between the left and right sides in any participants, the voxels from the quantitative maps (created through voxel-wise fitting) were pooled to calculate the reported averages.
The water T2, fat fraction and T1 maps were calculated by fitting the expected physical signal model to the measured signals. For T2 quantification, extended phase graphs (EPG) (Santini et al., 2021) were used to remove the signal contributions from intra-muscular fat. EPG allows the simulation of a spin system response to an arbitrary MRI sequence and enables the retrieval of accurate T2 values in multicompartment voxels containing lipids and muscle tissue (Marty et al., 2016). It is worth noting that the EPG method also returns fat fraction maps, which were used for fat fraction quantification and comparison between the cohorts. For T1 quantification, the values of the input flip angles were corrected using the B1 maps before fitting (Sacolick et al., 2010) using the code available at MedPhysJena/b1_corrected_t1_vfa.
Preprocessing of the IVIM diffusion data included denoising (using Mrtrix3 (Veraart et al., 2016b; Veraart et al., 2016a; Tournier et al., 2019)), averaging the repetitions, and geometric averaging the opposite polarities of the diffusion gradients to correct cross-terms between the imaging and diffusion gradients (Neeman et al., 1991). No corrections were made for susceptibility-induced distortions or eddy currents.
A scalar IVIM model from Equation 1 was fitted to each gradient encoding direction independently using DIPY (Garyfallidis et al., 2014), see Appendix A1 for details. For the IVIM model, the following signal equation was used
| (1) |
where j indices denote the directions of the applied diffusion gradients (i.e., x/AP, y/LR, or z/IS). and are the signal intensities for the ith b-value and b = 0, respectively, is the perfusion fraction, is the scalar pseudo-diffusion coefficient, and is the diffusion coefficient, associated with the jth gradient encoding direction. In each subject and each ROI, values of the perfusion fraction and the pseudo-diffusion coefficient, obtained from different gradient directions, were not significantly different. Thus, the three corresponding maps of , as well as were averaged, yielding a set of 6 maps per subject: S 0 , f, D * , D x , D y , and D z . Furthermore, D x and D y were additionally averaged to form D xy , hereafter referred to as the radial diffusion coefficient, while D z was reported as and referred to as the axial diffusion coefficient.
It's important to note that the diffusion coefficients D z and D xy do not inherently represent quantitative parameters of the muscle fibers, as radial and axial diffusivities do, and they may be influenced by the muscle fiber orientation. However, neither the full rank-2 diffusion tensor nor its eigenvectors could be reconstructed from the three orthogonal diffusion gradient directions. Yet, we believe that, given the characteristic geometry of the muscle fibers, one of the three gradient directions (specifically z/IS) approximately aligns with the fiber orientation, while the other two are roughly perpendicular. Therefore, we propose considering these diffusion coefficients as a rough approximation of the aforementioned quantitative parameters.
Differences between the averaged values extracted from ROIs in the control, endurance, and strength cohorts for T1, water T2, fat fraction, and all IVIM parameters, as well as the age and BMI of the subjects, were tested in Python (version 3.12) using a non-parametric Kruskal–Wallis test (Kruskal and Wallis, 1952) part of SciPy (Virtanen et al., 2020) version 1.91. If the Kruskal–Wallis test indicated significance, Dunn’s post hoc pairwise comparisons were performed (Dunn, 1961) with scikit-posthocs (Terpilowski, 2019) version 0.8.1. Statistical significance was considered at p ≤ 0.05. The p-values reported in the results are from Dunn’s post hoc comparisons, and all other p-values can be found in the Supplementary Material.
3 Results
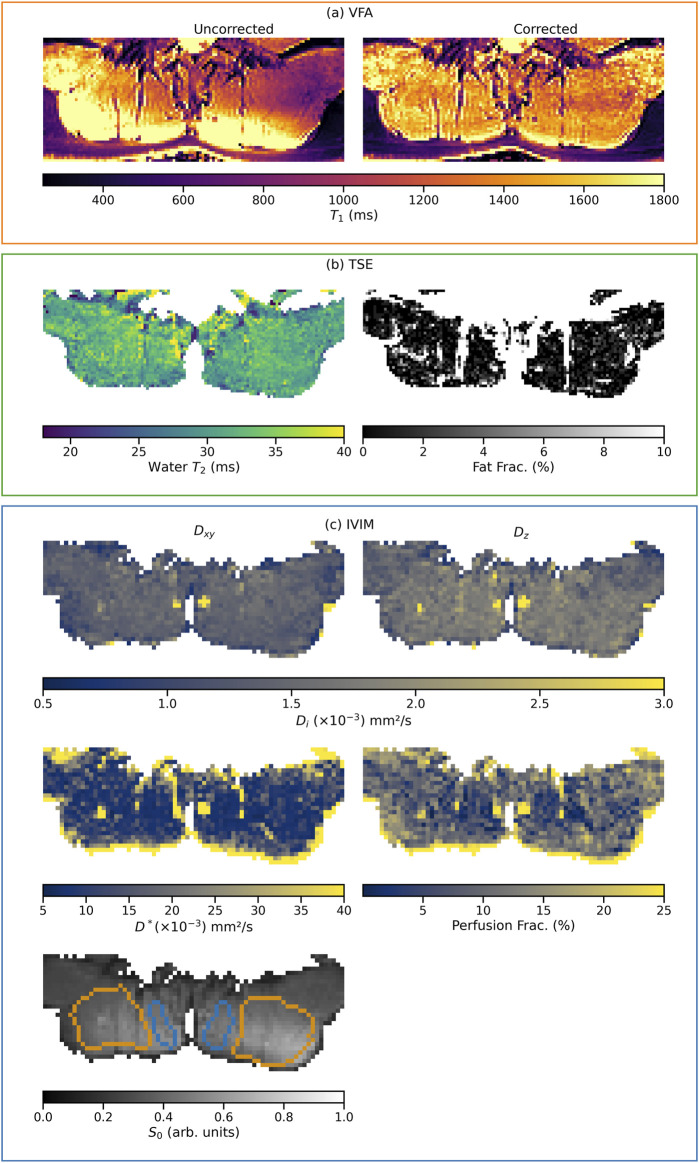
Figure 1 shows exemplary parameter maps from a single subject for all analyzed qMRI parameters of the proposed multi-parametric MR protocol, grouped by acquisition sequence (corresponding maps for subjects of the two other cohorts analyzed in this work are available in section 1.4 of the Supplementary Material). Additionally, the ROIs used in this subject are outlined on the S 0 image.
FIGURE 1.
Example parameter maps from one subject of the endurance cohort. The grouping of the maps, indicated by the frame color, represents the acquisition from which they originate (VFA, TSE, or IVIM). Maps sharing a color bar are windowed identically. In the corrected T1 relaxation time map, the successful B1-field inhomogeneity correction is clearly visible compared to the uncorrected map (A). Section (B) shows the water T2 and fat fraction maps extracted from the EPG. Section (C) shows the maps of the diffusion coefficients , D z , the pseudo-diffusion coefficient D * , and the perfusion fraction f. Additionally, the ROIs used for quantitative analysis are outlined on top of the map of S 0 (multifidus in blue and erector spinae in orange).
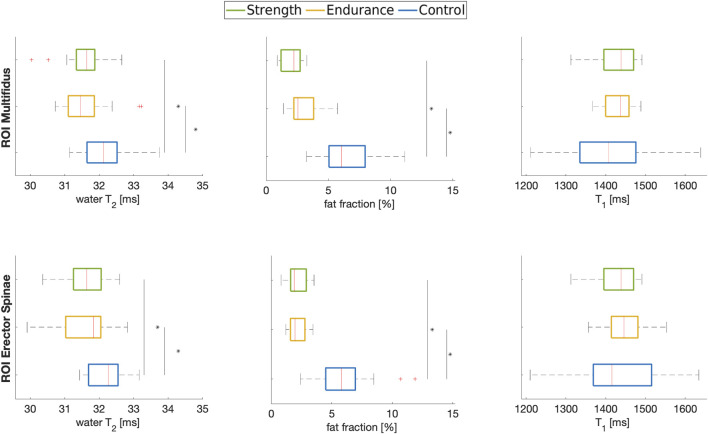
Figures 2, 3 summarize the results of the quantitative ROI analyses for both muscles and all cohorts. Specifically, Figure 2 includes the transverse relaxation parameters water T2, the fat fraction (both calculated using the EPG approach) and the longitudinal relaxation parameter T1. For both multifidus and erector spinae muscles, control subjects had significantly higher water T2 values (p = 0.012 for the comparison endurance athletes vs. controls for multifidus and p = 0.018 for erector spinae; p = 0.025 for the comparison strength athletes vs. controls for multifidus and p = 0.017 for erector spinae). Both athlete cohorts had significantly lower fat fractions compared to the control group, with the strength cohort showing particularly low fat fractions in the multifidus. However, even after implementing B1 correction, which removed large inhomogeneities in the T1 map, as shown in the top left section (a) of Figure 1, no significant difference in T1 relaxation times was found between the cohorts. The mean values of all quantified parameters for each group are shown in Tables 3, 4. Additionally, fat fraction maps were also obtained calculating the ratio of fat to the combined signal of fat and water in separately acquired clinically available 2-point Dixon sequence (Dixon, 1984). The two methods reveal the same differences between the cohorts (i.e., athletes’ fat fraction is significantly lower). The 2-point Dixon sequence parameters and fat fraction results are shown in Table 1a and 2a of the Supplementary Material (section 1.2).
FIGURE 2.
Boxplots of water T2, fat fraction and T1 in the multifidus (top row) and erector spinae (bottom row) muscles of the three cohorts analyzed in this work. * indicates significance at p < 0.05 between indicated cohorts.
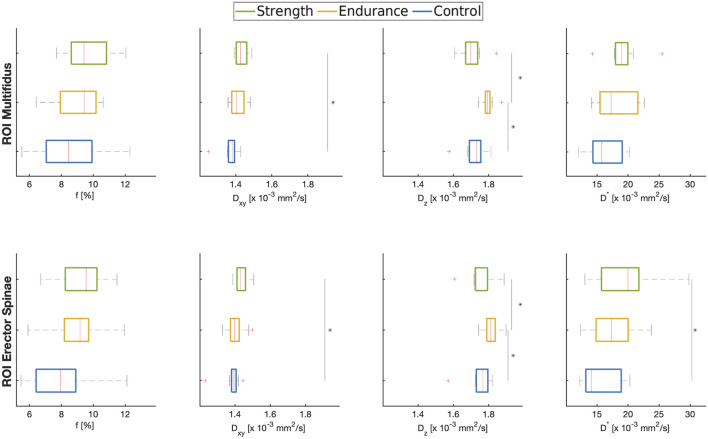
FIGURE 3.
Boxplots of ROI-averaged f, , D z , and D* in the multifidus (top row) and erector spinae (bottom row) muscles of the three cohorts analyzed in this work. * indicates significance at p < 0.05 between indicated cohorts.
TABLE 3.
Summary of the values of water T2, fat fraction and T1 extracted using the MRI protocol. Values are given as mean ± standard deviation for each cohort. MF—M. multifidus; ES—M. erector spinae.
| Cohort | Water T2 (ms) MF | Water T2 (ms) ES | Fat fraction EPG (%) MF | Fat fraction EPG (%) ES | T1 (ms) MF | T1 (ms) ES |
|---|---|---|---|---|---|---|
| Control | 32.1 ± 0.7 | 32.1 ± 0.5 | 7 ± 3 | 6 ± 2 | 1,400 ± 100 | 1,400 ± 120 |
| Endurance | 31.7 ± 0.7 | 31.6 ± 0.8 | 2.9 ± 1.2 | 2.1 ± 0.7 | 1,430 ± 40 | 1,440 ± 60 |
| Strength | 31.5 ± 0.6 | 31.6 ± 0.6 | 2.0 ± 0.8 | 2.1 ± 0.9 | 1,420 ± 50 | 1,430 ± 70 |
TABLE 4.
Summary of the different parameters extracted using the MRI protocol. Values are given as mean ± standard deviation for each cohort. MF—M. multifidus; ES—M. erector spinae.
| Cohort | MF | ES | ( mm/s2) MF | ( mm/s2) ES | ( mm/s2) MF | ( mm/s2) ES | ( mm/s2) MF | ( mm/s2) ES |
|---|---|---|---|---|---|---|---|---|
| Control | 8 ± 2 | 7.8 ± 1.9 | 1.37 ± 0.04 | 1.38 ± 0.05 | 1.72 ± 0.06 | 1.75 ± 0.08 | 16 ± 3 | 15 ± 3 |
| Endurance | 9.0 ± 1.4 | 8.9 ± 1.7 | 1.41 ± 0.04 | 1.40 ± 0.05 | 1.79 ± 0.03 | 1.81 ± 0.04 | 17 ± 3 | 17 ± 4 |
| Strength | 9.7 ± 1.5 | 9.5 ± 1.8 | 1.43 ± 0.03 | 1.43 ± 0.03 | 1.70 ± 0.06 | 1.75 ± 0.07 | 19 ± 3 | 20 ± 5 |
Figure 3 shows the estimated means of f, and as well as .The mean perfusion fraction in both training cohorts (f ≈ 9%) was slightly higher than in controls (f ≈ 7–8%). This trend was present in both muscles, although it wasn’t statistically significant.
The radial diffusion coefficient tends to be higher in the strength training cohort than in the controls and the endurance athletes, with the difference between the strength cohort and the controls being statistically significant (p = 0.001 for multifidus and p = 0.011 for erector spinae). The axial diffusion coefficient, on the other hand, shows different trends in the two athlete cohorts compared to the controls: the endurance cohort shows a higher value of Dz (p = 0.001 for multifidus and p = 0.026 for erector spinae) compared to the strength cohort and to the control group (p = 0.024 and p = 0.044 for multifidus and erector spinae, respectively).
The pseudo-diffusion coefficient D* was also higher for the athlete cohorts, with significant differences between the strength cohort and the control group (p = 0.02 for erector spinae).
4 Discussion
Among the numerous musculoskeletal studies using MRI, only a limited number of similar studies conducted at rest, exists. Still, they have examined only selected parameters at a time, focused only on athlete cohorts without including a control group (Marth et al., 2022), or investigated solely a single trained group (Sun et al., 2018; Berry et al., 2020; Keller et al., 2020) without including a differently trained cohort. Based on the synopsis and analysis of the multiparametric MRI protocol used in this work, our results suggest that although the water T2 and fat fraction could distinguish between trained and untrained cohorts, only the addition of the IVIM-based diffusion coefficients helped to reveal differences between the two cohorts of athletes.
The observation of lower water T2 values in the athletes is consistent with the findings of Le Rumeur et al. (1994), Sun et al. (2018), but contradicts those of Keller et al. (2020). However, it is important to note that all these studies assessed global T2 values. Sun et al. hypothesize that the lower T2 values in athletes are due to a higher concentration of macromolecules, which increase the bound water component, thus shortening T2. This hypothesis might further relate to the diffusion results presented in this work. However, it should be emphasized that all these results were obtained from leg skeletal muscles, which are characterized by a smaller fat fraction (compared to back muscles) and more directly influenced by movements, including walking to the MRI examinations. In contrast, the T2 values for the multifidus and erector spinae muscles reported in other studies for healthy controls are typically higher than those measured in this work (D’hooge et al., 2013; Huang et al., 2020). This discrepancy is likely because those studies did not account for the signal contribution from the fat fraction in their measurement of global T2 values.
The higher fat fraction observed in the control cohort aligns with the work of Emanuelsson et al. (2022) who evaluated the multifidus and erector spinae as a single ROI. The fat fraction maps were derived as a byproduct of the EPG T2 fitting process. Correction for inaccuracies in the slice profile (a well-known source of errors in multi-echo SE sequences) was also included in the EPG T2 fitting (Santini et al., 2021).
The T1 relaxation time in our study aligns with previously reported values (Han et al., 2003; Gold et al., 2004). However, as mentioned, no differences in T1 relaxation time were found between the three groups. The control group showed a slightly (although not significantly) shorter T1 value, potentially due to a higher fat fraction, since fat has a notably shorter T1 relaxation time compared to muscle. Unlike EPG-based T2 fitting, the VFA-based quantification method retrieves only a global T1 value (without being able to distinguish signal contribution from muscle water and fat).
Analysis of the IVIM parameters showed that both athlete cohorts tended to have higher perfusion fraction f values, consistent with previous results in leg muscles (Okamoto et al., 2012) and suggesting increased capillary density and perfusion as a long-term effect associated with training. Notably, the perfusion fraction in the strength cohort appears to be consistently higher, which may be a consequence of the targeted repeated exercises that powerlifters perform with the lumbar back muscle. Interestingly, the endurance cohort also shows a higher value of (when compared to the control group). Although this result is not significant, it suggests a possible effect of non-targeted training on perfusion and appears to agree with Hoier and Hellsten (2014).
The two diffusion coefficients paint a more nuanced picture of different effects in the various cohorts and muscles. Specifically, while shows an increasing trend that is most pronounced in the strength-training group, shows opposite signs in the two athlete cohorts. The axial diffusion coefficient ( ) is consistently higher than the radial diffusion coefficient, which aligns with the expected natural orientation of muscle fibers (Damon et al., 2002). In general, DWI is sensitive to microstructural alterations and adaptations in muscle tissue (Tan et al., 2022), although the full extent of how various muscle features affect DWI is not yet fully understood. Flück et al. (2019) performed a thorough analysis of very similar cohorts, but focused on biopsies of one muscle group in the thigh (vastus lateralis). They reported a higher myofibrillar volume density and a larger cross-sectional area of muscle fibers in their powerlifter cohort. Monte-Carlo simulations have revealed that muscle fiber diameter has the greatest influence on diffusion anisotropy and mean diffusivity (Berry et al., 2018). Thus, it could be speculated that the muscle hypertrophy observed by Flück et al. (2019) in the strength-training cohort is due to larger muscle fiber diameters, contributing to the higher value of radial diffusion compared to the control group and the endurance cohort. Similarly, the lower axial diffusion coefficient in the strength cohort could be attributed to a higher macromolecular fraction (also due to hypertrophy), a factor not present in the endurance cohort (Mazzoli et al., 2021).
Measurements on capillary phantoms have linked the pseudo-diffusion coefficient to blood velocity (Cho et al., 2012; Schneider et al., 2019), and non-MRI-based studies have shown that the effect of training leads to an increase in vascular velocity and blood flow in both endurance and powerlifting athlete cohorts (Green et al., 2012; Welsch et al., 2013). Thus, it could be speculated that this is reflected in the significantly higher values for D * in the athlete cohorts of this study. In the Supplementary Material (section 1.1, Figure 1), a further split of the pseudo-diffusion coefficient along the axial and radial directions is shown, with a higher than , consistent with (Haas and Nwadozi, 2015) who showed that capillaries are predominantly oriented along the direction of the muscle fiber. Finally, no significant correlations were found between the all the investigated parameters (apart from the expected positive correlation between f and D * ).
4.1 Limitations
Our study has several limitations: Only male subjects were analyzed, and the size of each cohort was relatively small, which impairs statistical power. Furthermore, the subjects were all measured at the same time of the day and had to refrain from training for 48 h before the measurements. While several different quantitative MRI studies in muscles at rest have used different rest periods before scanning, ranging from 6 h (Marth et al., 2022) to 24 h (Sun et al., 2018), the 48-hour rest interval chosen for this protocol was the most conservative approach that was still feasible given the athletes’ demanding training schedules. It is worth noting that although two studies (Maeo et al., 2017; Lyu et al., 2021), including one involving animal models, suggest that the effect of strenuous exercise could influence qMRI parameters for up to 72 h post-exercise, such a long rest period was not feasible for the athlete cohorts involved in our study.
The diffusion gradient scheme in our DWI acquisition was insufficient for full diffusion tensor reconstruction, necessitating the use of diffusion coefficients D z and D xy . The use of these coefficients to approximate the axial and radial diffusivities relied on assumptions about the orientation of the muscle fibers, which meant that fiber dispersion could influence the results. While we do not have the data to quantify such influence, it may be noted that this assumption may be more accurate in the case of erector spinae compared to multifidus due to the differences in fiber orientation of each muscle. Therefore it is recommended that future studies include additional diffusion directions to enable the reconstruction of the full diffusion tensor, thus allowing for a more accurate analysis.
All regions of interest were drawn by hand, with the aim of excluding muscle-fat replacements, which are commonly present in the back muscles. Nevertheless, partial volume effects may have affected some voxels, especially in DWI images due to the low spatial resolution in the inferior-superior (IS) direction.
Finally, while training may primarily explain the cohort differences observed by qMRI in this study, other important factors such as diet/supplement intake, which is particularly prevalent among young athletes (Farup et al., 2014; Jovanov et al., 2019), were not considered in this work. More comprehensive research is needed to clearly differentiate between these two factors.
5 Conclusion and outlook
This study focused on the development of a comprehensive protocol based on a variety of parameters, including water T2, fat fraction, T1 and IVIM-based diffusion parameters. Application of this protocol to a group of athletes revealed significant differences in muscle water T2 and fat fraction which we believe is a valuable contribution to the growing (and at times conflicting) qMRI results associated with long-term effects of exercise in skeletal muscles. Furthermore, the reported differences in IVIM parameters may indicate long-term effects associated with different types of training, potentially reflecting underlying microstructural changes. However, it is crucial for future implementations of the DWI protocol to include additional directions to effectively disentangle the influence of muscle fiber direction and dispersion, which was not achievable with the current protocol. Given that T1 mapping, carefully corrected for possible B1 contamination, appears to provide little insight into the effects of training, it may be interesting for future research to abandon the VFA approach used in this protocol and employ more advanced methods, such as the recently proposed MR-fingerprinting water T1 method (Marty and Carlier, 2020), which could help disentangle the different signal contributions or highlight potential differences between the cohorts, or more advanced diffusion models of microstructure (e.g., NODDI or HARDI, as shown in the preliminary results of Adluru et al. (2017)). Alternatively, future research efforts could focus on correlating the investigated parameters with functional parameters (such as EMG) or exploring additional parameters such as T1ρ, which are significantly influenced by macromolecular concentration and may be related to intervertebral disc degeneration, which is also implicated in non-specific low back pain. Finally, the ability of the proposed protocol to capture adaptations at rest may offer new perspectives in the evaluation of changes in skeletal muscle associated with training and may aid in the treatment monitoring of nonspecific low back pain patients who cannot undergo examinations after a strenuous exercise session.
Appendix A1
DIPY, an open-source python-based project aimed at the analysis and visualization of DWI data (https://dipy.org/index.html) implements a version of a variable projection (VarPro) (Golub and Pereyra, 1973) approach by treating the signal fitting in each voxel as a sequence of three optimization problems: first, the global optimum with respect to D * and D x,y,z is sought using a differential evolution algorithm (non-convex) and then used in a convex linear regression fitting of S 0 and f; the obtained values are then refined jointly using non-linear least squares (Farooq et al., 2016; Fadnavis et al., 2019). Note that this approach processes each voxel independently, without leveraging spatial regularization. Additionally, all acquired volumes were used at every step, without splitting b-values.
Funding Statement
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by a graduate scholarship from the Friedrich-Schiller-University Jena and the state of Thuringia (Landesgraduiertenstipendium) (to MM), the Competence Center for Interdisciplinary Prevention (KIP) at the Friedrich Schiller University Jena, the German Professional Association for Statutory Accident Insurance and Prevention in the Foodstuffs Industry and the Catering Trade (BGN) (projects 1.1.7.22 & 1.1.7.23) and the German Research Foundation (Deutsche Forschungsgemeinschaft; KR 4783/2-1). We acknowledge support by the German Research Foundation Projekt-Nr. 512648189 and the Open Access Publication Fund of the Thueringer Universitaets- und Landesbibliothek Jena.
Data availability statement
The datasets presented in this article are not readily available because they are available upon reasonable request to the corresponding author. Requests to access the datasets should be directed to marta.maggioni@uni-jena.de.
Ethics statement
The studies involving humans were approved by Ethik-Kommission der Friedrich-Schiller-Universität Jena. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
MM: Conceptualization, Formal Analysis, Investigation, Methodology, Visualization, Writing–original draft, Writing–review and editing. RS: Formal Analysis, Visualization, Writing–original draft, Writing–review and editing. MK: Conceptualization, Resources, Supervision, Writing–original draft, Writing–review and editing. DG: Methodology, Writing–original draft, Writing–review and editing. JR: Funding acquisition, Project administration, Supervision, Writing–original draft, Writing–review and editing.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2024.1408244/full#supplementary-material
References
- Adluru N., Kijowski R., Liu F. (2017). Improved muscle microstructure analysis with diffusion weighted imaging and advanced tissue modeling. Proc. Int. Soc. Magn. Reson. Med. 88. [Google Scholar]
- Andersen J. L., Aagaard P. (2010). Effects of strength training on muscle fiber types and size; consequences for athletes training for high-intensity sport. Scand. J. Med. Sci. Sports 20, 32–38. 10.1111/j.1600-0838.2010.01196.x [DOI] [PubMed] [Google Scholar]
- Balagué F., Mannion A. F., Pellisé F., Cedraschi C. (2012). Non-specific low back pain. Lancet 379, 482–491. 10.1016/S0140-6736(11)60610-7 [DOI] [PubMed] [Google Scholar]
- Berry D. B., Regner B., Galinsky V., Ward S. R., Frank L. R. (2018). Relationships between tissue microstructure and the diffusion tensor in simulated skeletal muscle. Magn. Reson. Med. 80, 317–329. 10.1002/mrm.26993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berry D. B., Rodriguez-Soto A. E., Englund E. K., Shahidi B., Parra C., Frank L. R., et al. (2020). Multiparametric MRI characterization of level dependent differences in lumbar muscle size, quality, and microstructure. JOR Spine 3, e1079. 10.1002/jsp2.1079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cagnie B., Elliott J., O’Leary S., D’Hooge R., Dickx N., Danneels L. (2011). Muscle functional MRI as an imaging tool to evaluate muscle activity. J. Orthop. Sports Phys. Ther. 41, 896–903. 10.2519/jospt.2011.3586 [DOI] [PubMed] [Google Scholar]
- Cho G. Y., Kim S., Jensen J. H., Storey P., Sodickson D. K., Sigmund E. E. (2012). A versatile flow phantom for intravoxel incoherent motion MRI. Magn. Reson. Med. 67, 1710–1720. 10.1002/mrm.23193 [DOI] [PubMed] [Google Scholar]
- Christensen K. A., Grant D. M., Schulman E. M., Walling C. (1974). Optimal determination of relaxation times of fourier transform nuclear magnetic resonance. Determination of spin-lattice relaxation times in chemically polarized species. J. Phys. Chem. 78, 1971–1977. 10.1021/j100612a022 [DOI] [Google Scholar]
- Damon B. M., Ding Z., Anderson A. W., Freyer A. S., Gore J. C. (2002). Validation of diffusion tensor MRI-based muscle fiber tracking. Magn. Reson. Med. 48, 97–104. 10.1002/mrm.10198 [DOI] [PubMed] [Google Scholar]
- de Sousa P. L., Vignaud A., Fleury S., Carlier P. G. (2011). Fast monitoring of T1, T2, and relative proton density (M0) changes in skeletal muscles using an IR-TrueFISP sequence. J. Magn. Reson. Imaging 33, 921–930. 10.1002/jmri.22511 [DOI] [PubMed] [Google Scholar]
- D’hooge R., Cagnie B., Crombez G., Vanderstraeten G., Achten E., Danneels L. (2013). Lumbar muscle dysfunction during remission of unilateral recurrent nonspecific low-back pain: evaluation with muscle functional MRI. Clin. J. Pain 29, 187–194. 10.1097/AJP.0b013e31824ed170 [DOI] [PubMed] [Google Scholar]
- Dixon W. T. (1984). Simple proton spectroscopic imaging. Radiology 153, 189–194. 10.1148/radiology.153.1.6089263 [DOI] [PubMed] [Google Scholar]
- Dunn O. J. (1961). Multiple comparisons among means. J. Am. Stat. Assoc. 56, 52–64. 10.1080/01621459.1961.10482090 [DOI] [Google Scholar]
- Emanuelsson E. B., Berry D. B., Reitzner S. M., Arif M., Mardinoglu A., Gustafsson T., et al. (2022). MRI characterization of skeletal muscle size and fatty infiltration in long‐term trained and untrained individuals. Physiol. Rep. 10, e15398. 10.14814/phy2.15398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Englund E. K., Berry D. B., Behun J. J., Ward S. R., Frank L. R., Shahidi B. (2022). IVIM imaging of paraspinal muscles following moderate and high-intensity exercise in healthy individuals. Front. Rehabil. Sci. 3, 910068. 10.3389/fresc.2022.910068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fadnavis S., Reisert M., Farooq H., Afzali M., Hu C., Amirbekian B., et al. (2019). MicroLearn: framework for machine learning, reconstruction, optimization and microstructure modeling. Proc. Int. Soc. Magn. Reson. Med. 3563. [Google Scholar]
- Farooq H., Xu J., Nam J. W., Keefe D. F., Yacoub E., Georgiou T., et al. (2016). Microstructure imaging of crossing (MIX) white matter fibers from diffusion MRI. Sci. Rep. 6, 38927. 10.1038/srep38927 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farup J., Rahbek S. K., Vendelbo M. H., Matzon A., Hindhede J., Bejder A., et al. (2014). Whey protein hydrolysate augments tendon and muscle hypertrophy independent of resistance exercise contraction mode. Scand. J. Med. Sci. Sports 24, 788–798. 10.1111/sms.12083 [DOI] [PubMed] [Google Scholar]
- Federau C., Kroismayr D., Dyer L., Farshad M., Pfirrmann C. (2020). Demonstration of asymmetric muscle perfusion of the back after exercise in patients with adolescent idiopathic scoliosis using intravoxel incoherent motion (IVIM) MRI. NMR Biomed. 33, e4194. 10.1002/nbm.4194 [DOI] [PubMed] [Google Scholar]
- Filli L., Boss A., Wurnig M. C., Kenkel D., Andreisek G., Guggenberger R. (2015). Dynamic intravoxel incoherent motion imaging of skeletal muscle at rest and after exercise. NMR Biomed. 28, 240–246. 10.1002/nbm.3245 [DOI] [PubMed] [Google Scholar]
- Fleckenstein J., Canby R., Parkey R., Peshock R. (1988). Acute effects of exercise on MR imaging of skeletal muscle in normal volunteers. Am. J. Roentgenol. 151, 231–237. 10.2214/ajr.151.2.231 [DOI] [PubMed] [Google Scholar]
- Flück M., Kramer M., Fitze D. P., Kasper S., Franchi M. V., Valdivieso P. (2019). Cellular aspects of muscle specialization demonstrate genotype – phenotype interaction effects in athletes. Front. Physiol. 10, 526. 10.3389/fphys.2019.00526 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garyfallidis E., Brett M., Amirbekian B., Rokem A., Van Der Walt S., Descoteaux M., et al. (2014). Dipy, a library for the analysis of diffusion MRI data. Front. Neuroinformatics 8, 8. 10.3389/fninf.2014.00008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gold G. E., Han E., Stainsby J., Wright G., Brittain J., Beaulieu C. (2004). Musculoskeletal MRI at 3.0 T: relaxation times and image contrast. Am. J. Roentgenol. 183, 343–351. 10.2214/ajr.183.2.1830343 [DOI] [PubMed] [Google Scholar]
- Golub G. H., Pereyra V. (1973). The differentiation of pseudo-inverses and nonlinear least squares problems whose variables separate. SIAM J. Numer. Anal. 10, 413–432. 10.1137/0710036 [DOI] [Google Scholar]
- Green D. J., Spence A., Rowley N., Thijssen D. H. J., Naylor L. H. (2012). Vascular adaptation in athletes: is there an “athlete’s artery”. Exp. Physiol. 97, 295–304. 10.1113/expphysiol.2011.058826 [DOI] [PubMed] [Google Scholar]
- Haas T. L., Nwadozi E. (2015). Regulation of skeletal muscle capillary growth in exercise and disease. Appl. Physiol. Nutr. Metab. Physiol. Appl. Nutr. Metab. 40, 1221–1232. 10.1139/apnm-2015-0336 [DOI] [PubMed] [Google Scholar]
- Han E., Gold G., Stainsby J., Wright G., Beaulieu C., Brittain J. (2003). In-Vivo T1 and T2 measurements of muskuloskeletal tissue at 3T and 1.5T. Proc. Intl. Soc. Mag. Reson. Med. 11. [Google Scholar]
- Hiepe P., Güllmar D., Gussew A., R R., Reichenbach J. (2013). Improved IVIM image quantitation of exercised lower back muscles by principle component analysis. Proc. Int. Soc. Magn. Reson. Med. 3491. [Google Scholar]
- Hildebrandt M., Fankhauser G., Meichtry A., Luomajoki H. (2017). Correlation between lumbar dysfunction and fat infiltration in lumbar multifidus muscles in patients with low back pain. BMC Musculoskelet. Disord. 18, 12. 10.1186/s12891-016-1376-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodges P. W., Bailey J. F., Fortin M., Battié M. C. (2021). Paraspinal muscle imaging measurements for common spinal disorders: review and consensus-based recommendations from the ISSLS degenerative spinal phenotypes group. Eur. Spine J. 30, 3428–3441. 10.1007/s00586-021-06990-2 [DOI] [PubMed] [Google Scholar]
- Hoier B., Hellsten Y. (2014). Exercise-induced capillary growth in human skeletal muscle and the dynamics of VEGF. Microcirculation 21, 301–314. 10.1111/micc.12117 [DOI] [PubMed] [Google Scholar]
- Huang Y.-L., Zhou J.-L., Jiang Y.-M., Zhang Z.-G., Zhao W., Han D., et al. (2020). Assessment of lumbar paraspinal muscle activation using fMRI BOLD imaging and T2 mapping. Quant. Imaging Med. Surg. 10, 106–115. 10.21037/qims.2019.10.20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jovanov P., Đorđić V., Obradović B., Barak O., Pezo L., Marić A., et al. (2019). Prevalence, knowledge and attitudes towards using sports supplements among young athletes. J. Int. Soc. Sports Nutr. 16, 27. 10.1186/s12970-019-0294-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karampinos D. C., King K. F., Sutton B. P., Georgiadis J. G. (2010). Intravoxel partially coherent motion technique: characterization of the anisotropy of skeletal muscle microvasculature. J. Magn. Reson. Imaging 31, 942–953. 10.1002/jmri.22100 [DOI] [PubMed] [Google Scholar]
- Keller S., Yamamura J., Sedlacik J., Wang Z. J., Gebert P., Starekova J., et al. (2020). Diffusion tensor imaging combined with T2 mapping to quantify changes in the skeletal muscle associated with training and endurance exercise in competitive triathletes. Eur. Radiol. 30, 2830–2842. 10.1007/s00330-019-06576-z [DOI] [PubMed] [Google Scholar]
- Kolmer F., Bierry G., Willaume T. (2023). Exercise-related leg muscle signal changes: assessment using diffusion-weighted MRI. Eur. Radiol. Exp. 7, 10. 10.1186/s41747-023-00323-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruskal W. H., Wallis W. A. (1952). Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 47, 583–621. 10.1080/01621459.1952.10483441 [DOI] [Google Scholar]
- Le Rumeur E., Carré F., Bernard A. M., Bansard J. Y., Rochcongar P., De Certaines J. D. (1994). Multiparametric classification of muscle T1 and T2 relaxation times determined by magnetic resonance imaging. The effects of dynamic exercise in trained and untrained subjects. Br. J. Radiol. 67, 150–156. 10.1259/0007-1285-67-794-150 [DOI] [PubMed] [Google Scholar]
- Lyu X., Gao Y., Liu Q., Zhao H., Zhou H., Pan S. (2021). Exercise-induced muscle damage: multi-parametric MRI quantitative assessment. BMC Musculoskelet. Disord. 22, 239. 10.1186/s12891-021-04085-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maeo S., Ando Y., Kanehisa H., Kawakami Y. (2017). Localization of damage in the human leg muscles induced by downhill running. Sci. Rep. 7, 5769. 10.1038/s41598-017-06129-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marth A. A., Auer T. A., Bertalan G., Gebert P., Geisel D., Hamm B., et al. (2022). Low back pain in adolescent elite rowers and its association to skeletal muscle changes detected by quantitative magnetic resonance imaging research square. Available at: https://www.researchsquare.com/article/rs-1369489/v1 (Accessed August 19, 2022). [DOI] [PubMed]
- Marty B., Baudin P.-Y., Reyngoudt H., Azzabou N., Araujo E. C. A., Carlier P. G., et al. (2016). Simultaneous muscle water T2 and fat fraction mapping using transverse relaxometry with stimulated echo compensation. NMR Biomed. 29, 431–443. 10.1002/nbm.3459 [DOI] [PubMed] [Google Scholar]
- Marty B., Carlier P. G. (2020). MR fingerprinting for water T1 and fat fraction quantification in fat infiltrated skeletal muscles. Magn. Reson. Med. 83, 621–634. 10.1002/mrm.27960 [DOI] [PubMed] [Google Scholar]
- Mazzoli V., Rubin E., Barbieri M., Schmidt A., Watkins L., Chaudhary A., et al. (2021). “Muscle hypertrophy in resistance training assessed with Diffusion Tensor Imaging,” in Proc. Int. Soc. Magn. Reson. Med., London, England, UK, 7-12 May 2022, 0668. 10.58530/2022/0668 [DOI] [Google Scholar]
- Meijer J. P., Jaspers R. T., Rittweger J., Seynnes O. R., Kamandulis S., Brazaitis M., et al. (2015). Single muscle fibre contractile properties differ between body-builders, power athletes and control subjects. Exp. Physiol. 100, 1331–1341. 10.1113/EP085267 [DOI] [PubMed] [Google Scholar]
- Mills K. R. (2005). The basics of electromyography. J. Neurol. Neurosurg. Psychiatry 76, ii32–ii35. 10.1136/jnnp.2005.069211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neeman M., Freyer J. P., Sillerud L. O. (1991). A simple method for obtaining cross-term-free images for diffusion anisotropy studies in NMR microimaging. Magn. Reson. Med. 21, 138–143. 10.1002/mrm.1910210117 [DOI] [PubMed] [Google Scholar]
- Neufer P. D., Bamman M. M., Muoio D. M., Bouchard C., Cooper D. M., Goodpaster B. H., et al. (2015). Understanding the cellular and molecular mechanisms of physical activity-induced health benefits. Cell Metab. 22, 4–11. 10.1016/j.cmet.2015.05.011 [DOI] [PubMed] [Google Scholar]
- Nguyen A., Ledoux J.-B., Omoumi P., Becce F., Forget J., Federau C. (2016). Application of intravoxel incoherent motion perfusion imaging to shoulder muscles after a lift-off test of varying duration. NMR Biomed. 29, 66–73. 10.1002/nbm.3449 [DOI] [PubMed] [Google Scholar]
- Nystoriak M. A., Bhatnagar A. (2018). Cardiovascular effects and benefits of exercise. Front. Cardiovasc. Med. 5, 135. 10.3389/fcvm.2018.00135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okamoto Y., Mori S., Kujiraoka Y., Nasu K., Hirano Y., Minami M. (2012). Diffusion property differences of the lower leg musculature between athletes and non-athletes using 1.5T MRI. Magma N. Y. N. 25, 277–284. 10.1007/s10334-011-0294-3 [DOI] [PubMed] [Google Scholar]
- Patten C., Meyer R. A., Fleckenstein J. L. (2003). T2 mapping of muscle. Semin. Musculoskelet. Radiol. 7, 297–305. 10.1055/s-2004-815677 [DOI] [PubMed] [Google Scholar]
- Pinckard K., Baskin K. K., Stanford K. I. (2019). Effects of exercise to improve cardiovascular health. Front. Cardiovasc. Med. 6, 69. 10.3389/fcvm.2019.00069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranger T. A., Cicuttini F. M., Jensen T. S., Peiris W. L., Hussain S. M., Fairley J., et al. (2017). Are the size and composition of the paraspinal muscles associated with low back pain? A systematic review. Spine J. Off. J. North Am. Spine Soc. 17, 1729–1748. 10.1016/j.spinee.2017.07.002 [DOI] [PubMed] [Google Scholar]
- Roberts T. J., Gabaldón A. M. (2008). Interpreting muscle function from EMG: lessons learned from direct measurements of muscle force. Integr. Comp. Biol. 48, 312–320. 10.1093/icb/icn056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sacolick L. I., Wiesinger F., Hancu I., Vogel M. W. (2010). B1 mapping by Bloch-Siegert shift. Magn. Reson. Med. 63, 1315–1322. 10.1002/mrm.22357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samad A. K. A., Taylor R. S., Marshall T., Chapman M. a. S. (2005). A meta-analysis of the association of physical activity with reduced risk of colorectal cancer. Colorectal Dis. 7, 204–213. 10.1111/j.1463-1318.2005.00747.x [DOI] [PubMed] [Google Scholar]
- Santini F., Deligianni X., Paoletti M., Solazzo F., Weigel M., de Sousa P. L., et al. (2021). Fast open-source toolkit for water T2 mapping in the presence of fat from multi-echo spin-echo acquisitions for muscle MRI. Front. Neurol. 12, 630387. 10.3389/fneur.2021.630387 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlaeger S., Inhuber S., Rohrmeier A., Dieckmeyer M., Freitag F., Klupp E., et al. (2019). Association of paraspinal muscle water-fat MRI-based measurements with isometric strength measurements. Eur. Radiol. 29, 599–608. 10.1007/s00330-018-5631-8 [DOI] [PubMed] [Google Scholar]
- Schneider M. J., Gaass T., Ricke J., Dinkel J., Dietrich O. (2019). Assessment of intravoxel incoherent motion MRI with an artificial capillary network: analysis of biexponential and phase‐distribution models. Magn. Reson. Med. 82, 1373–1384. 10.1002/mrm.27816 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schönau T., Anders C. (2023). EMG amplitude-force relationship of lumbar back muscles during isometric submaximal tasks in healthy inactive, endurance and strength-trained subjects. J. Funct. Morphol. Kinesiol. 8, 29. 10.3390/jfmk8010029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shipton E. A. (2018). Physical therapy approaches in the treatment of low back pain. Pain Ther. 7, 127–137. 10.1007/s40122-018-0105-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha S., Sinha U., Edgerton V. R. (2006). In vivo diffusion tensor imaging of the human calf muscle. J. Magn. Reson. Imaging 24, 182–190. 10.1002/jmri.20593 [DOI] [PubMed] [Google Scholar]
- Sollmann N., Bonnheim N. B., Joseph G. B., Chachad R., Zhou J., Akkaya Z., et al. (2022). Paraspinal muscle in chronic low back pain: comparison between standard parameters and chemical shift encoding-based water–fat MRI. J. Magn. Reson. Imaging 56, 1600–1608. 10.1002/jmri.28145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H., Xu M.-T., Wang X.-Q., Wang M.-H., Wang B.-H., Wang F.-Z., et al. (2018). Comparison thigh skeletal muscles between snowboarding halfpipe athletes and healthy volunteers using quantitative multi-parameter magnetic resonance imaging at rest. Chin. Med. J. (Engl.) 131, 1045–1050. 10.4103/0366-6999.230740 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan E. T., Zochowski K. C., Sneag D. B. (2022). Diffusion MRI fiber diameter for muscle denervation assessment. Quant. Imaging Med. Surg. 12, 80–94. 10.21037/qims-21-313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terpilowski M. A. (2019). scikit-posthocs: pairwise multiple comparison tests in Python. J. Open Source Softw. 4, 1169. 10.21105/joss.01169 [DOI] [Google Scholar]
- Terzis G., Spengos K., Kavouras S., Manta P., Georgiadis G. (2010). Muscle fibre type composition and body composition in hammer throwers. J. Sports Sci. Med. 9, 104–109. [PMC free article] [PubMed] [Google Scholar]
- Tournier J.-D., Smith R., Raffelt D., Tabbara R., Dhollander T., Pietsch M., et al. (2019). MRtrix3: a fast, flexible and open software framework for medical image processing and visualisation. NeuroImage 202, 116137. 10.1016/j.neuroimage.2019.116137 [DOI] [PubMed] [Google Scholar]
- Veraart J., Fieremans E., Novikov D. S. (2016a). Diffusion MRI noise mapping using random matrix theory. Magn. Reson. Med. 76, 1582–1593. 10.1002/mrm.26059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J., Novikov D. S., Christiaens D., Ades-Aron B., Sijbers J., Fieremans E. (2016b). Denoising of diffusion MRI using random matrix theory. NeuroImage 142, 394–406. 10.1016/j.neuroimage.2016.08.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Virtanen P., Gommers R., Oliphant T. E., Haberland M., Reddy T., Cournapeau D., et al. (2020). SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272. 10.1038/s41592-019-0686-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welsch M. A., Blalock P., Credeur D. P., Parish T. R. (2013). Comparison of brachial artery vasoreactivity in elite power athletes and age-matched controls. PLoS ONE 8, e54718. 10.1371/journal.pone.0054718 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye C., Xu D., Qin Y., Wang L., Wang R., Li W., et al. (2019). Estimation of intravoxel incoherent motion parameters using low b-values. PLOS ONE 14, e0211911. 10.1371/journal.pone.0211911 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets presented in this article are not readily available because they are available upon reasonable request to the corresponding author. Requests to access the datasets should be directed to marta.maggioni@uni-jena.de.