Dynamic interface printing

Abstract

Additive manufacturing is an expanding multidisciplinary field encompassing applications including medical devices¹, aerospace components², microfabrication strategies^3,4 and artificial organs⁵. Among additive manufacturing approaches, light-based printing technologies, including two-photon polymerization⁶, projection micro stereolithography^7,8 and volumetric printing^9–14, have garnered significant attention due to their speed, resolution or potential applications for biofabrication. Here we introduce dynamic interface printing, a new 3D printing approach that leverages an acoustically modulated, constrained air–liquid boundary to rapidly generate centimetre-scale 3D structures within tens of seconds. Unlike volumetric approaches, this process eliminates the need for intricate feedback systems, specialized chemistry or complex optics while maintaining rapid printing speeds. We demonstrate the versatility of this technique across a broad array of materials and intricate geometries, including those that would be impossible to print with conventional layer-by-layer methods. In doing so, we demonstrate the rapid fabrication of complex structures in situ, overprinting, structural parallelization and biofabrication utility. Moreover, we show that the formation of surface waves at the air–liquid boundary enables enhanced mass transport, improves material flexibility and permits 3D particle patterning. We, therefore, anticipate that this approach will be invaluable for applications where high-resolution, scalable throughput and biocompatible printing is required.

Dynamic interface printing is a new form of 3D printing that leverages an acoustically modulated, constrained air–liquid boundary to rapidly generate centimetre-scale 3D structures within tens of seconds.

Main

Rapid 3D printing, in which whole parts are created in seconds to minutes rather than hours, is increasingly being recognized as an enabling technology for a range of bioprinting, prototyping and manufacturing applications^15–18. Conventional optical-based printing approaches, such as stereolithography, use light to cure materials one layer at a time. Such approaches have advantages in terms of resolution and geometric fidelity. However, the need to continually reset the part’s position between layers to enable the flow of uncured resin imposes restrictions on printing speed, material composition and throughput.

Recently, volumetric printing approaches have been used to rapidly manufacture centimetre-scale constructs. Computed axial lithography^9,12 involves rotating a photopolymer-filled vial while exposing it to a sequence of telecentric projections from various azimuthal angles so that the cumulative light intersections create the target object. As this process depends on local oxygen depletion to constrain polymerization, the degree of curing is highly sensitive to both the polymerization dose and the material composition. Although computational corrections can partially mitigate these effects¹⁹, they impose limitations for resins and bioinks in these systems. Other recent methods, such as xolography¹⁰ or light sheet printing²⁰, apply dual-step photochemistry, where polymerization is initiated by two wavelengths—one from a light sheet and the other from an orthogonal projection—that converge simultaneously to create the desired object. Although such volumetric approaches permit the rapid fabrication of free-floating isotropic structures, they are limited by the requirement for specialist optical systems or material formulations. Specifically, the volumetric resolution is innately coupled to the material transparency, which precludes or constrains the use of many additives, such as cells, granular materials and dyes. Oxygen can also be used as a free-radical quencher in conventional bottom-up stereolithography to inhibit polymerization at the printing interface. For instance, continuous liquid interface production^21,22 uses an oxygen-permeable membrane as the fabrication interface, which creates a polymerization dead zone where material can be replenished continuously. In this approach, however, the printed structure is progressively extracted from a shallow liquid reservoir, posing difficulties for soft materials like hydrogels^18,19, which often exhibit structural instability when removed from a liquid suspension.

In this work, we present a rapid three-dimensional (3D) printing technique in which an object is generated at the boundary of an acoustically driven, constrained air–liquid interface, which facilitates the rapid creation of arbitrary supportless structures without specialized chemistry or optical feedback systems. This approach is compatible with a range of materials, including soft and biologically relevant hydrogels, at speeds suitable for high-viability tissue engineering, scalable manufacturing and rapid prototyping.

Dynamic interface printing

Dynamic interface printing (DIP) uses a hollow print head that is open at the bottom and sealed with a transparent glass window at the top. Submerging the print head in a liquid prepolymer solution traps air within it. An air–liquid meniscus forms at the print head’s end. This meniscus serves as the print interface where structures are polymerized by visible light (λ = 405 nm) transmitted from above through the glass window (Fig. 1a and Supplementary Fig. 1). Patterned cross sections, which conform to the meniscus, are delivered using a projection system with an in-plane resolution of 15.1 µm and variable irradiance levels (0–270 mW cm⁻²). Adjusting the air pressure inside the print head allows control of the meniscus position and curvature so that the print interface can made coplanar with the focal plane. Once aligned, two-dimensional (2D) projections that map to 3D regions of the desired object are sequentially projected axially through the print head onto the meniscus. By raising the print head relative to the print container, the entire object is built continuously in a matter of seconds.

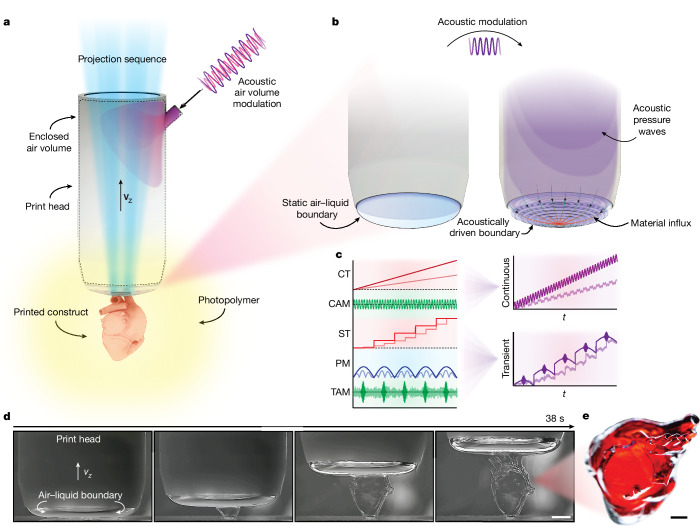
Fig. 1. Schematic illustration of DIP.

a, An air–liquid boundary forms at the base of a partially submerged print head. The boundary acts as a print interface in which patterned projections are used to locally solidify the photopolymer. b, Acoustic manipulation of the internal air volume in the print head promotes enhanced material influx through capillary-driven waves. c, In continuous mode (top right), the global location of the air–liquid interface(s) depends on continuous translation (CT) of the print head and constant acoustic modulation (CAM). In transient mode (bottom right), the location of the interface depends on stepped translation (ST), internal pressure modulation (PM) and transient acoustic modulation (TAM). d, Time-lapse photographs of the printing process for a heart geometry, demonstrating rapid fabrication of centimetre-scale constructs in less than 40 s. e, Printed heart geometry as shown in d, dyed red to improve visualization. Scale bars, 5 mm (d), 2 mm (e).

Unique to DIP is the ability to dynamically regulate the pressure within the print head, thereby allowing control of the shape and position of the meniscus during printing. Although this modulation can be fixed, which results in a static meniscus, the interface can also be modulated acoustically across a range of amplitudes and frequencies to form capillary-gravity waves (Fig. 1b). The precise position of the meniscus at any given moment is determined by the superposition of the print head’s vertical position, the static air pressure within the print head, and the amplitude and frequency of the acoustic modulation. This oscillatory actuation can be activated either continuously (Fig. 1c, top right) or transiently between projections (Fig. 1c, bottom right).

By localizing the optics and acoustic modulation to the print head, DIP is inherently container-agnostic and as such does not impose constraints on the shape or optical properties of the printing vessel, unlike other high-throughput approaches^9,10,14,17. DIP provides high fabrication rates by using capillary-gravity waves at the print interface to drive mass transport, so that high-resolution structures can be rapidly formed (Fig. 1d,e and Supplementary Video 1). Here, we demonstrate how this modality can be used to bolster the fabrication rate, enhance material processing ranges, and enable 3D particle patterning and overprinting capabilities. With this approach, we demonstrate the fabrication of a wide variety of centimetre-scale objects in tens of seconds.

Convex slicing

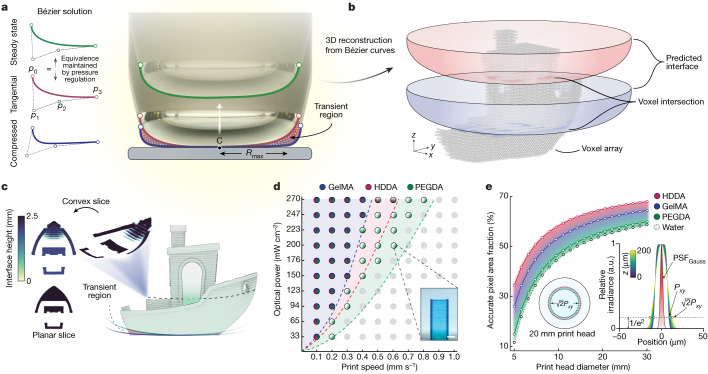
As with other light-based printing techniques, a 3D digital model of the desired geometry must first be translated into a series of images to be sequentially displayed by the projection system. However, unlike standard stereolithography, which uses a planar print interface, DIP features a curved meniscus. This requires a series of images that conform to the interface’s profile, representing 3D regions of the object. Each print begins with the interface being compressed against the base of the print volume to form a thin fluid film whose maximum size is dictated by the part’s dimensions. As the print advances, the compressed profile recedes until its centre is tangential to the base of the container. After this transient region, the interface shape can be calculated using the Young–Laplace equation. To predict the interface shape during initial compression and the subsequent transient region, we first employ Bézier curves^23,24 to solve the steady-state Young–Laplace equation, which provides an approximation of the uncompressed interface profile. The intermediate compressed regions are subsequently approximated by maintaining volume equivalency under a uniaxial deformation (Fig. 2a and Supplementary Fig. 4a). By using a cylindrical print head, the 3D shape of the convex interface can be computed from the 2D Bézier solution by revolving the half-profile about the print head’s central axis (Supplementary Fig. 4b,c). The projection sequence delivered to the interface is calculated by slicing a Cartesian voxel array of the input geometry with the corresponding 3D Bézier surface for each point in time (Fig. 2b). This slicing scheme ensures that 2D projections incident on the meniscus result in the correct 3D object for all intermediate interface locations (Fig. 2c and Supplementary Fig. 5).

Fig. 2. Characterization of the DIP system.

a, Images of the air–liquid interface profile formed at the base of the print head under the compressed, tangential and steady-state modes. Bézier curves were used to predict the shape of the interface during printing for each of the interface modes. b, The convex-slicing scheme was determined by first revolving the Bézier half-profile about the central axis and computing the voxel-wise intersection. c, Convex optimized projections extend in three dimensions and follow the boundary curvature for each interface mode. d, Print parameter space (n = 3) showing the optical power and print speed pairs for GelMA (blue), HDDA (red) and PEGDA (green). Inset, example of the rectangular test structure used to assess the parameter space. Scale bar, 2 mm. e, Accurate pixel area fraction for increasing print-head size for HDDA (red), GelMA (blue), PEGDA (green) and water (grey dashed). Left inset, variability of the area fraction for the 20 mm print head, dependent on material formulation. Right inset, simulated deviation of the pixel size based on Gaussian beam theory for a range of z values, compared to the Gaussian point spread function of the optical system, PSF_Gauss. a.u., arbitrary units.

Source Data

DIP characterization

Beyond high-throughput manufacturing, DIP is advantageous for creating biological models due to its rapid printing rate and minimal shear along the air–liquid interface in comparison to other light- and extrusion-based bioprinting techniques²⁵. Here, we create structures not only in hard acrylates, such as 1,6-hexanediol diacrylate (HDDA), but also in common biologically relevant materials such as poly(ethylene glycol) diacrylate (PEGDA) and gelatin methacryloyl (GelMA). To demonstrate and characterize the ability to print across several material types, we evaluated a parameter space that quantifies the achievable print speed as a function of the optical power (Fig. 2d). Although the maximum print speed for a resin depends on the photo-initiator concentration, monomer functionalization, material viscosity and optical power, here we use common formulations for ease of comparison. For instance, the relatively low concentrations of the photo-initiator lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP; at most 0.3%) that we used here have been previously shown to be biocompatible²⁶. We realized linear print rates greater than 700 µm s⁻¹ for a PEGDA hydrogel with an optical dose of 270 mW cm⁻². Notably, lower optical powers (for example, 30–50 mW cm⁻²) more appropriate for biofabrication still enabled high-speed printing of centimetre-scale constructs in tens of seconds.

As the print interface is inherently curved, mapping a planar projection to its surface results in defocusing of the image near the boundary of the print head. The magnitude of defocusing is primarily contingent on material properties that impact the capillary length and the material contact angle with the print head. If a uniform projection resolution is critical, a theoretical constraint can be applied to evaluate the usable fraction of the meniscus. This is achieved by ensuring that for a given pixel, the in-plane resolution $P_{\text{FP}}$ does not exceed $\sqrt{2}{P}_{\text{FP}}$ when mapped to the interface. A theoretical analysis using Gaussian beam theory (Supplementary Fig. 6) was used to predict the equivalent defocused pixel size (point spread function) at a location z above the focal plane. By coupling this with the Bézier solution of the interface profile for a given material formulation, the fractional area of the interface that maintains $P_{xy}\le \sqrt{2}{P}_{\text{FP}}$ was found (Fig. 2e). For the same material properties, smaller print heads achieve a lower accurate pixel area fraction due to the ratio of the capillary length to the print head’s diameter. Conversely, for larger print heads, the fraction of the diameter dominated by the capillary length decreases and the print interface transitions towards a free surface. Similarly, materials with a lower surface tension or a higher density exhibit shorter capillary lengths, resulting in a higher pixel area fraction.

Acoustic modulation

A core feature of DIP enabled by the air–liquid boundary is the ability to vibrate the print interface by acoustic modulation. These vibrations can be used either to improve the light-based printing process or to add another patterning degree of freedom for the 3D printed constructs. The interface modes depend on the chosen print-head shape, frequency, amplitude and the position of the interface relative to the underlying structure. To improve light-based printing, acoustic modulation creates capillary-gravity waves at the air–liquid interface, which produce streaming flows in the underlying fluid (Fig. 3b) that ultimately augment the achievable print speeds and fidelity due to the enhanced material transport. To excite the interface, we employed a new method that modulates the enclosed print-head volume above the meniscus (Fig. 3a and Supplementary Fig. 1c,d). This not only maintains the container-agnostic benefit of DIP but also largely eliminates the inherent coupling between the pressure field and the shape of the material container^27,28. Moreover, capillary-gravity waves generated at the print interface decay quickly, thus enabling a highly controlled combination of different acoustic signals during a single print (Supplementary Figs. 7, 22 and 25).

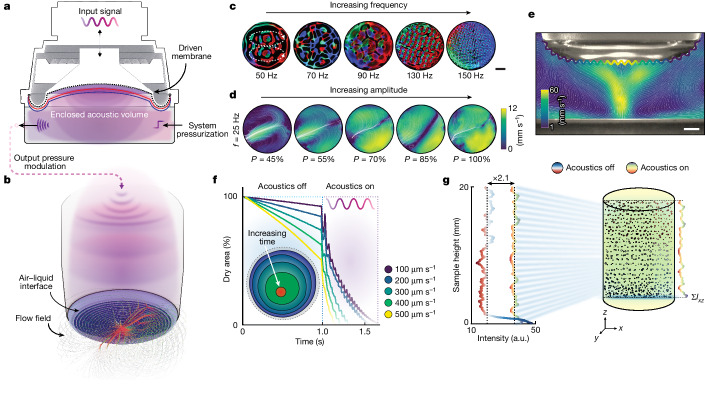
Fig. 3. Acoustic modulation in DIP.

a, Schematic illustration of the device used to acoustically modulate the air volume. b, Illustration of DIP with acoustic modulation. Capillary-gravity waves that form on the free surface of the print head result in flow fields that extend in three dimensions. c, Multi-coloured light is scattered from the air–liquid interface during acoustic excitation. d, PIV normal to the interface at 25 Hz for increasing amplitude. e, PIV perpendicular to the interface at 40 Hz and maximum amplitude, demonstrating the formation of high-velocity jetting flows. In d,e, the colour bars show average velocity (mm s⁻¹). f, Effect of acoustic actuation on material inflow below the interface for a 25 mm print head $\left(f=50\text{Hz},A=0.40\right)$. Inset, example time-series of a material inflow boundary during the wetting process. Coloured circles (blue to red) and black contours indicate the impending material boundary as a function of increasing time. g, Effect of acoustic stimulation on cellular sedimentation (n = 3). The cellular density (optical intensity, I_xz) is plotted over the height of a 10 mm circular pillar containing encapsulated 17 µm particles. Scale bars, 5 mm (c), 2.5 mm (e).

Source Data

To illustrate the range of possible wave modes on the print interface, a ring of multi-coloured LEDs was mounted within the print head to reflect surface permutations as the frequency was increased (Fig. 3c). At low frequencies, monochromatic modes with increasing azimuthal numbers formed²⁹, whereas at higher frequencies, N-fold rotationally symmetric waves were generated³⁰. These wave modes generated flows both tangentially and normal to the air–liquid interface. Particle image velocimetry (PIV) and computational fluid dynamics simulations (Supplementary Figs. 8–11, 20, 21 and 23–25 and Supplementary Videos 2 and 3) were used to quantify the fluid transport. A stationary print head under a low-amplitude excitation generated fluid velocities exceeding 10 mm s⁻¹, both at the interface and within the bulk fluid (Fig. 3d,e). Compared to situations where the flow is along a horizontally flat interface³¹, in our case, the curvature of the interface promoted secondary streaming effects, which further enhanced mass transport³² (Supplementary Figs. 10 and 25). When surface excitation is combined with print-head translation, as when printing, the average fluid velocities ranged from 17 mm s⁻¹ $\left(v_z=100{\mathrm{\mu }\mathrm{m}\mathrm{s}}^{-1}\right)$ to 45 mm s⁻¹ $\left(v_z=500{\mathrm{\mu }\mathrm{m}\mathrm{s}}^{-1}\right)$ (Fig. 3f). Notably, this trend held for higher viscosities, where interface excitation significantly bolstered the material influx, independent of viscosity (Supplementary Figs. 11 and 12). In conjunction with the object topology, this transport heuristic is used within our slicing software to predict and adapt the printing speed based on the fluidic path length, which, in some cases, led to a further (approximately 60%) reduction in the total print time (Supplementary Fig. 13).

Aside from improving process throughput, acoustic modulation reduces heterogeneity in structures comprising granular additives, such as those containing cells, which often sediment during printing. Volumetric printing approaches^12,16,33,34 often rely on high-viscosity prepolymer solutions or those that undergo thermal gelation (for example, GelMA) to minimize this effect. For thermally gelated materials, the print container and suspended cells need to be cooled before use. Therefore, although the print time for these parts is short, the total time required to cool, print and rewarm these structures to remove unpolymerized material results in workflow times essentially comparable with existing digital light projection (DLP) processes. Here we illustrate how acoustic modulation can mitigate sedimentation by actively mixing the fluid during printing (Fig. 3g and Supplementary Fig. 15). Additionally, the use of acoustics during printing promotes further focusing of suspensions to below the interface and results in a twofold increase in encapsulation efficiency, compared to structures printed without. This enhancement, combined with improvements in structural isotropy, reduces the total number of granular additives or cells required to create dense scaffolds.

DIP capabilities

Previous approaches, such as top-down stereolithography³⁵, that rely on unconstrained air–liquid interfaces suffer from mass transport and material film uniformity, limiting throughput. Although minimizing the fluidic path length can reduce this (Supplementary Figs. 13, 23 and 24), doing so imposes significant geometric constraints on what can be printed. To further capture the dynamics of DIP that would otherwise be challenging to investigate experimentally, we simulated the printing behaviour in contrast to other established air–liquid modalities (Supplementary Figs. 22–24). For a 15-mm-diameter print head, on increasing the structural diameter (D_S = 4–14 mm) in these simulations, DIP achieved approximately ×4 higher flow velocities compared to top-down stereolithography (Supplementary Fig. 25). When further incorporating acoustic modulation, the fluid velocities increased approximately ×10. To practically demonstrate the improvement that interface modulation has on mass transport, we printed a series of thick fluidic manifolds containing several independent fluid pathways (Fig. 4a–c and Supplementary Fig. 28). Next, to investigate the effect of interface curvature on the accurate pixel area fraction, we used a small 10-mm-diameter print head to fabricate a series of micro-lattice structures and pillar arrays in HDDA. Attempting to print a structure whose edges exceeded $\sqrt{2}{P}_{\mathit{xy}}$ without convex slicing resulted in regions at the periphery that were distorted and poorly adhered due to curvature-induced defocusing and convex-planar mismatch (Fig. 4d). Conversely, by using convex slicing and matching the print field of view to that predicted by the accurate area fraction, an array of uniform pillars was created with features ranging from approximately 30 to 100 µm (Fig. 4e).

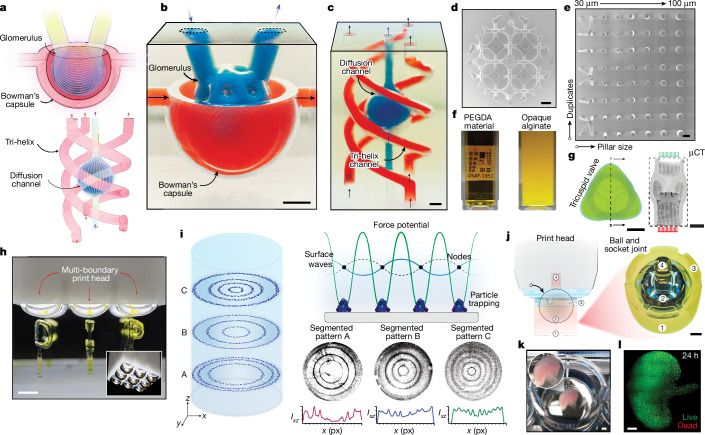
Fig. 4. DIP capabilities.

a, Illustration of Bowman’s capsule and tri-helix model. b, Printed model of Bowman’s capsule showing the glomerulus. These were injected with red and blue dye. The print time was approximately 2 min. c, Tri-helix structure perfused with red and blue dye. d, Stitched top-down scanning electron microscope image of a Kelvin lattice printed with a 10 mm print head. Object field of view corresponds to a diameter of approximately $1.5\sqrt{2}{P}_{xy}$ for HDDA. e, Stitched top-down helium-ion microscopy image of an equal height micropillar array printed with HDDA. Some pillars were distorted by surface tension during drying due to the high aspect ratio of the structures. f, Comparison of the opacities of the PEGDA (transparent) and alginate (opaque) hydrogel materials when imaged against a standard US Air Force test target in a 10 mm cuvette. g, Top-down image of a tricuspid valve printed with an alginate bioink and corresponding micro computed tomography cross section (μCT). h, Print head with several independent air–liquid interfaces used to create a 3 × 3 array of the letters ‘DIP’. i, Three-dimensional patterning based on standing surface waves. Suspended particles were trapped in nodal locations depending on the driving frequency, as shown in segmented patterns A–C. The corresponding intensity profile of the image section is shown below each patterned region. j, Multiple-step overprinting of a ball-and-socket joint. k, Kidney-shaped model containing 7.2 million cells per millilitre printed in situ in a 12-well plate. l, Stitched and deconvolved fluorescence image of k after 24 h showing that high cell viability was maintained through the printing process. Scale bars, 100 µm (e), 1 mm (c,d), 2 mm (b,g,j,k,l), 4 mm (h).

Source Data

DIP further enables the fabrication of structures from partially occluded or completely opaque materials. For example, hydrogels containing a high population of cells are often opaque in appearance due to the refractive index mismatch between their components³⁶. In volumetric printing, light must travel unobstructed through the volume, therefore index matching between the base and cellular materials is crucial^33,37. Although this can be partially overcome computationally³⁷, in our case, light transmission is confined to a thin region at the air–liquid interface, minimizing the scattering and photo-absorbing effects of suspended materials. To highlight this, we created a norbornene-functionalized sodium alginate in which the opacity was increased by pH until it completely occluded a US Air Force test target (Fig. 4f). Despite this material being completely opaque, a 10-mm-tall alginate tricuspid valve was fabricated in 33 s. This valve had 300-µm-thick internal leaflets when imaged with micro computed tomography (Fig. 4g). Further control, modulation and spatial distribution of several print interfaces can be achieved through arbitrary design of the print-head geometry. As an example, we built a print head with a 3 × 3 array of individual surfaces and used it to fabricate in parallel the letters ‘DIP’ (Fig. 4h and Supplementary Video 5). The effective amplitude and frequency of a constrained surface(s) (and by extension the resulting flow profile) can also be modulated by careful design, sizing and arrangement of holes at the print-head extent.

Thus far, we have shown how the production of travelling capillary-gravity waves can be used to augment mass transport³⁸. However, by forming standing waves at the liquid–air interface, suspended materials can also be spatially patterned. By momentarily stopping the printing process above the current layer, retracting the interface within the print head and applying an acoustic excitation, a hydrodynamic potential field at the top surface of the underlying structure can be formed. The potential field causes particles to migrate from regions of high to low potential energy. The resulting interactions cause particles to aggregate at nodal positions (Supplementary Fig. 26), contingent on the frequency and nodal locations of the standing wave^39,40. Although mechanical and hydrodynamic nodal patterning has previously been realized^41–44, these approaches are inherently constrained to two dimensions or at fixed nodal locations⁴⁵. However, by combining acoustic patterning with light-based printing, we demonstrate the formation of modular 3D particle arrangements contingent on various frequency and amplitude combinations (Fig. 4i). As these patterns are ultimately coupled to the print-head shape—we used axisymmetric print heads to produce concentric arrangements—the pattern complexity can be increased by adapting the cross-sectional profile of the print head. Future implementations could leverage this advantage to engineer optimized boundary shapes to produce desired acoustic fields^42,46. However, further work will be needed to understand and efficiently predict the complex hydrodynamic interaction with the underlying topology. Beyond the modulation features of DIP, the permeable air–liquid interface permits solid parts to traverse the printing interface, enabling direct in situ overprinting of multi-material or multi-component structures. To illustrate this, we created a ball-and-socket joint (Fig. 4j) by first printing the socket housing, followed by the insertion of a 10 mm ball bearing, and finally printing the socket cap and rod over and onto the ball.

To investigate our premise that DIP provides a unique advantage for soft materials (Supplementary Figs. 14 and 27), we sought to evaluate its potential as a biofabrication tool. As light has to pass through only the air–liquid interface into the photopolymer, as with other free-surface approaches³⁵, the optical properties and container shape pose less of a constraint compared to alternative approaches that require light to be partially^21,22 or completely^9,14 transmitted through the build volume. However, note that in our case, the structural height is limited by the ratio of the total container volume to the displaced volume of the print head to avoid material overflow during insertion. Therefore, future implementations could use fluidic paths to gradually inject material(s) during the duration of printing to mitigate this limitation. As the print head can move freely in three dimensions, sequential fabrication can be readily achieved (Supplementary Fig. 16a). Moreover, various material densities can be combined as fabrication platforms (Supplementary Fig. 17). This permits not only the printing of several structures in the same container but also the sequential in situ production of structures in several volumes (such as a well plate; Supplementary Video 4), each of which could contain various cell types, materials or geometries. As a preliminary assessment of the viability of this technique for generating cell-laden, biologically relevant constructs, we printed a simplified kidney-shaped hydrogel structure using human embryonic kidney 293-F cells at a density of 7.2 × 10⁶ cells per millilitre directly in a 12-well plate (Fig. 4k). The construct was imaged by fluorescence microscopy after 24 h, which demonstrated its low process cytotoxicity and high cell viability (approximately 93%) (Fig. 4l and Supplementary Fig. 18).

Discussion and future perspectives

We have demonstrated volumetric fabrication rates of the order of 10⁴ mm³ min⁻¹, which exceeds that of other high-speed printing processes, including computed axial lithography^9,14 and xolography¹⁰, without the need for specialist photochemistries or optical feedback mechanisms. This is enabled by surface-tension-mediated printing and further enhanced by an acoustically driven flow across the print interface. Coupled with the ability to multiplex print heads containing a greater number of individual interfaces, there is an opportunity to scale the throughput of this system, potentially permitting simultaneous fabrication across an entire multi-well plate. The permeable print interface we present here offers controllable manipulation and excitation during printing, along with the ability to overprint, configure mass transport and achieve 3D patterning. It is foreseeable that further modalities or applications of DIP could be developed in the future, including putting acoustically driven transport systems directly onto the print head⁴⁷ or applying sequential multi-material switching from within. Aside from further characterization and prediction of the parameter space for acoustic patterning, future investigations could explore more complex patterning strategies by modelling and taking advantage of the underlying structure⁴⁸ or by engineering the print-head boundary topology to produce desired acoustic fields^42,47. A further extension to higher numerical apertures⁴⁹ could facilitate rapid microscale fabrication without the cost associated with two-photon systems^50,51.

We envision that DIP will offer significant advances for biofabrication due to its ability to rapidly print high-resolution constructs in soft, biologically relevant materials without necessitating thermal gelation or imposing constraints on the optical characteristics of the prepolymer solution. Additionally, the capability to position the print interface in three dimensions allows the in situ fabrication into multi-well plates, underscoring the future potential for high-throughput biofabrication. Furthermore, the encapsulation enhancement and spatial localization presented here could also promote the patterning of several cell types with denser and more interspersed cell–cell connections, which is crucial for cellular functionality in many tissue constructs^52,53. Moreover, further investigations into the limits of both light and acoustic pattern formation, such as stiffness gradients created by greyscale exposure or growth factor gradients achieved through acoustic patterning of loaded nanoparticles, will be crucial to establishing its value for biofabrication.

Herein, we present a rapid and conceptually elegant printing approach that relies on the formation of a constrained and acoustically modulated air–liquid interface. We demonstrate a multifunctional, high-throughput approach that has unique benefits for the fabrication of soft and biologically relevant materials. We, therefore, posit that DIP is best used when high-speed, high-resolution and in situ fabrication is required of 3D structures.

Methods

3D printer assembly

Version 1

The DIP system components were mounted on two orthogonal optical breadboards to ensure precise alignment of the vertical and horizontal components (Supplementary Information section 1 and Supplementary Fig. 2a). Cross-sectional images were captured using a high-power projection module (LRS-WQ, Visitech) with a resolution of 2,560 × 1,600 pixels and a pixel size of 15.1 μm. The projection module and print head were positioned in the z direction using a 100 mm linear stage (MOX-02-100, Optics Focus) affixed to the vertical breadboard. The position of the air–liquid interface was controlled by a 50 ml syringe connected to the print head with a silicone tube and pressurized using a 50 mm linear stage (MOX-02-50, Optics Focus). Two further linear stages (MOX-02-100, Optics Focus) enabled precise positioning of the cuvette or well plate for sequential or multi-step printing. Motion control was managed using a commercially available 3D printer control board (BIGTREETECH, SKR 3) with a custom DB9 breakout board. Orthogonal videos of the printing process were captured with a 4K CCD camera (AmScope, HD408) equipped with a 16 mm lens (Raspberry Pi, RPI-16MM-LENS).

Version 2

A second system iteration was developed for in situ imaging, with modifications to allow the printing container to move relative to a stationary probe (Supplementary Fig. 3). The system incorporated a custom CoreXY motion system and a NEMA 23 ball-screw linear stage to translate the entire CoreXY stage relative to the stationary print head. In situ imaging was facilitated by a blue reflective dichroic mirror (35-519, Edmund Optics) and a 50:50 beam splitter for illumination (43-359, Edmund Optics). Illumination was provided either coaxially or with a custom well-plate holder with a red collimated backlight. To maintain physiological temperatures and sterility during printing, the motion components and print head were enclosed within a custom heated chamber. Sterility was maintained by continuous HEPA filtration during printing, surface sanitization with 70% ethanol and sterilization with UV-C before use.

Print head

In this study, the size of the print head was tailored contingent upon the desired dimensions of the resin container. For almost all configurations, we used axisymmetric cylindrical print heads to simplify the computation of the interface shape, although other (arbitrarily shaped) print-head boundary contours were feasible as demonstrated. For more complex print-head topologies resulting in complex interface shapes, numerical methods such as Surface Evolver⁵⁴ or SE-FIT⁵⁵ can be used. Here, we used print heads ranging from 30 to 5 mm. An object’s extent in the x and y directions was limited by the projector’s total field of view at the focal plane. Additionally, an object’s height was limited by the length of the print head, which was intrinsically coupled to the projection focal length and the ratio of the container volume to the volume displaced by the print head. For our set-up, the total submergible print-head length was approximately 70 mm. Note that much taller structures are conceptually feasible by submerging the projection and illumination optics or by increasing the working distance of the projection system. The print head was fabricated using a commercial 3D printing system (Form 3+, Formlabs). The print heads have an SM2 threaded insert, which allows us to quickly interchange print heads in version 2 of the system. A glass window was clamped between a gasket and the top of the print head to maintain an airtight enclosed volume while facilitating the transmission of light down its centre (Supplementary Fig. 1a,b). The print head also included an internal channel to enable gas to be delivered into the print-head cavity through the syringe system and acoustic modulation device. This port was used to either maintain or modulate the shape of the air–liquid interface during printing.

Acoustic modulation device

Acoustic modulation of the air–liquid interface was achieved by direct volume manipulation of the air volume within the print head. Conceptually, the approach was straightforward. The set-up consisted of a 3 inch 15 W voice coil driver (Techbrands, AS3034) affixed to an enclosed 3D printed manifold containing an inlet and outlet port (Fig. 3a and Supplementary Information section 2 and Supplementary Fig. 1c,d). The voice coil was driven by a commercially available amplifier (Adafruit, MAX9744) using the supplied auxiliary port, with specified waveforms sent by the MATLAB GUI. The frequency ranged between 1 and 500 Hz when possible, with fixed or transient frequency or amplitude switching. By specifying a waveform for each degree of freedom, it was straightforward to synchronize the acoustic modulation with the remainder of the motion, optical and pressure control (Fig. 1c).

Material composition and preparation

PEGDA materials

Various concentrations of PEGDA were used in this study, ranging from 10% to 100% w/v. For each formulation, we followed the same protocol. The required weight fraction of PEGDA M_n 700 (455008, Sigma) was dissolved in the corresponding volume fraction of 40 °C deionized water (excluding 100% w/v) and thoroughly mixed for 10 min. Subsequently, 0.035 w/w% of tartrazine (T0388, Sigma) and 0.25% w/w of LAP (900889, Sigma) were added to the mixture and stirred until complete dissolution. The materials were then stored in light-safe Falcon tubes until required.

HDDA material

A solution of 500 mg of phenylbis(2,4,6-trimethylbenzoyl) phosphine oxide (511447, Sigma) and 50 g of 1,6-hexanediol diacrylate (246816, Sigma) was prepared by warming the mixture to 40 °C and stirring for 30 min. To control the resolution in the z direction, the photo-absorber Sudan I (103624, Sigma) was added in various quantities ranging from 0 to 0.04% w/w. The materials were then stored in light-safe Falcon tubes until required.

GelMA material

GelMA was synthesized following a previously reported protocol⁵⁶, yielding a degree of substitution of 93% (confirmed by nuclear magnetic resonance). A 10% w/v GelMA solution was prepared by dissolving 1 g of GelMA in 10 ml of cell culture media (Freestyle 293 Expression Medium, Thermofisher) preheated to 37 °C. After complete dissolution of the GelMA, 3.5 mg of tartrazine and 25 mg of LAP were added to the solution, which was maintained at 37 °C until complete dissolution. The mixture was sterilized by passing it through a 0.22 µm sterile filter within a biosafety cabinet and subsequently stored in refrigerated light-safe Falcon tubes until required.

Alginate material

Norbornene-functionalized sodium alginate was synthesized based on a previously reported protocol⁵⁷. In short, 10 g of sodium alginate were dissolved in 500 ml of 0.1 M 2-(N-morpholino) ethane-sulfonic acid buffer (145224-94-8, Research Organics) and fixed to pH 5.0. Then, 9.67 g of 1-ethyl-3-(3-dimethylaminopropyl) carbodiimide•HCl, 2.90 g of N-hydroxysuccinimide and 3.11 ml of 5-norbornene-2-methylamine were added. The pH was fixed at 7.5 with 1 M NaOH. The reaction was carried out at room temperature for 20 h. The mixture was dialysed against water for 5 d before lyophilization. The degree of norbornene functionalization was determined to be 16.2% by ¹H nuclear magnetic resonance. A 7% w/v sodium alginate solution was prepared by dissolving 1 g of the sodium alginate in 14.29 ml of phosphate-buffered saline solution. Next, 5 mg of tartrazine, 36 mg of LAP and 122.7 µl of 2,2′-(ethylenedioxy)diethanethiol were dissolved in 5.59 ml of phosphate-buffered saline, added to the sodium alginate solution and mixed until it was homogeneous. The pH was adjusted with 1 M NaOH until the solution was visibly opaque.

Diurethane dimethacrylate (UDMA) support material

A solution of 50 mg of phenylbis(2,4,6-trimethylbenzoyl) phosphine oxide (511447, Sigma) and 5 g of diurethane dimethacrylate (436909, Sigma) was prepared by warming the mixture to 45 °C and stirring for 30 min. To remove trapped air bubbles, the mixture was transferred to a light-safe Falcon tube and centrifuged at 4,000 rpm for 10 min to remove residual air bubbles.

Cell printing

Human embryonic kidney 293-F cells (Freestyle 293-F, Thermo Fisher) were used in a preliminary determination of the cell viability of the DIP 3D printing system. In this work, a cell solution with 7.2 million cells per millilitre was used for both the model of the kidney and the cell-viability measurements. To determine cell viability, a thin 500 µm wall (5 mm × 0.5 mm × 10 mm) was printed to minimize the effect of cell death due to insufficient media diffusion, which was imaged using a live/dead viability/toxicity kit (L3224, Invitrogen). Three structures were printed (n = 3), and measurements were taken after 24 h to determine the preliminary viability of the technique. Cell viability was determined at three locations for each sample (s = 3), with the total viability being an average of all collection points (Supplementary Fig. 18).

To create the cell-loaded bioink, the GelMA solution was warmed to 37 °C followed by the resuspension of cells into the solution. The solution was passed through a cell strainer (0877123, Thermo Fisher) and stored in a water bath at 37 °C when not in use. The printing process involved pipetting approximately 3 ml of the GelMA ink into a single well of a 12-well plate and lowering the print head into the well. During each print, acoustic modulation (50 Hz, P = 0.3) was used to homogenize the suspension and mitigate cell settling. As the printed wall had a high aspect ratio and low contact area, a relatively slow print velocity of V_z = 150 µm s⁻¹ was used to mitigate unwanted detachment. This resulted in an object creation time of approximately 30 s.

Data preprocessing, printing and postprocessing

Three-dimensional design models of Bowman’s capsule, a tri-helix structure and a Kelvin cell were created using nTop. Tricuspid, heart and buckyball models were downloaded from Thingiverse.com. For each geometry, the STL file was extracted and sliced using Chitubox into a stack of PNG images. As the frame rate of the HDMI signal was limited to 120 frames per second (fps), we commonly used projection frame rates that matched the acoustic driving frequencies to minimize motion blurring. The object was discretized into a voxel array according to the desired linear print speed and frame rate. The layer height (L_h) was determined as $L_{\mathrm{h}}=v_z/f$, where v_z is the linear print speed and f is the acoustic excitation frequency, which matched the projection frequency. The image stack was further corrected using the convex-slicing algorithm to produce a secondary optimized image stack, with the sequence being sent to the projector over HDMI using Psychtoolbox-3 (ref. ⁵⁸). The print sequence started by moving the print head to a defined distance above the print surface (or high-density material). The interface was then automatically brought coplanar with the image plane contingent on the selected print head. The MATLAB GUI was operated by first sending a signal to turn on the LED module and subsequently controlling the location of the air–liquid interface by modulating the pressure, acoustic driving and translation location. The optical power of the projection module was automatically set depending on the selected print velocity using the parameter space matrix. For prints made with HDDA, the printed structures were removed from the print volume and washed with isopropyl alcohol. For soft structures made from PEGDA and GelMA, the excess material was gently removed using a pipette (and recycled if PEGDA) and resuspended in deionized water or cell culture media to remove unpolymerized material. If required, the structures were fluidically detached from the bottom of the container and stored in an appropriate solution.

Convex-slicing algorithm

The developed convex-slicing algorithm aims to correct for geometrical discretization differences between a traditionally flat construction surface and the curved surface used in this work. A detailed explanation of the convex-slicing process is given in the Supplementary Information. However, the main components will be briefly restated here. First, the general shape of the interface was determined by the Young–Laplace equation, $\mathrm{\Delta }p=-\gamma \nabla \cdot \widehat{n}$, which describes the Laplace pressure difference ($\mathrm{\Delta }p$) sustained across a gas–liquid boundary dependent on the material surface tension ($\gamma$) and surface normal ($\hat{n}$). Here, we used axisymmetric print containers such that $\hat{n}$ can easily be found by substituting the general expressions for principal curvatures. The capillary length $l=\sqrt{\gamma /\rho g}$, where γ is the material surface tension, ρ is the material density and g is the acceleration due to gravity, was used to normalize the radial and vertical coordinates of the interface as $x=r/l$ and $y=z/l$. The resulting ordinary differential equation for the interface shape was $\frac{y^{″}}{{\left(1+{\left(y^{\prime }\right)}^2\right)}^{3/2}}+\frac{y^{\prime }}{x{\left(1+{\left(y^{\prime }\right)}^2\right)}^{1/2}}-y=0$.

This equation can be readily solved using numerical integration with appropriate boundary conditions (Supplementary Information section 4). However, using this method would require numerical integration for the steady-state case, and moreover, we would need to solve each intermediate state during compression with the associated boundary conditions. We, instead, opted to approximate the solution using cubic Bézier curves for the steady-state case and approximating the compressed profiles by geometrically deforming the Bézier curve while ensuring volume equivalency (Supplementary Information section 7). This is computationally faster given the large number of intermediate surfaces within the transient region. To convert the 2D Bézier solution into a 3D surface, the half-profile was revolved about the print head’s central z axis (Supplementary Information section 5). This produced a sequence of surfaces starting at the compressed state and transitioning to the steady-state interface profile. The corresponding convex projection(s) were determined by minimizing the Euclidean distance between the Cartesian voxel grid and the surface arrays (Supplementary Information section 6). Reconstruction accuracy was validated by ‘replaying’ the projections over an empty voxel array and computing the Jaccard index between the reconstructed voxel array and the input voxel array (Supplementary Information sections 8 and 9).

Optical modelling

To determine our theoretical optical model (Supplementary Information section 10), we employed a similar approach to Behroodi et al.⁵⁹, who modelled the in-plane resolution as the spatial convolution of the point spread function ($\mathrm{PSF}\left(x,y\right)$) and the micro-mirror spatial arrangement ($f(x,y)$), where $f\left(x,y\right)\ast \mathrm{PSF}\left(x,y\right)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }f\left({\tau }_1,{\tau }_2\right)\cdot \mathrm{PSF}\left(x-{\tau }_1,y-{\tau }_2\right)\mathrm{d}{\tau }_1\mathrm{d}{\tau }_2$, and τ₁ and τ₂ represent spatial shifts, summed over all possible displacements, during convolution. To determine the effective delivered energy and depth of cure across the meniscus, a ray incident on the meniscus was decomposed into reflective and transmissive components, described by a transmissive efficiency η, dependent on the relative angle and refractive index mismatch $\eta (n_1,n_2,\hat{\mathbf{u}},\hat{\mathbf{n}})$. Here, n₁ and n₂ represent the refractive index of the air and liquid, respectively, and $\hat{\mathbf{u}}$ is the normal vector at a given point on the meniscus’s surface. The energy intensity along the transmissive vector ${\gamma }_z$ was approximated as a material-dependent Beer–Lambert decay $\mathcal{H}\left({\mathit{\gamma }}_x,{\mathit{\gamma }}_y,{\mathit{\gamma }}_z\right)=\eta \left(n_1,n_2,\widehat{\mathbf{u}},\widehat{\mathbf{n}}\right)\cdot \widehat{\mathbf{E}}\exp \left(\frac{-{\mathit{\gamma }}_z}{{\epsilon }_{\mathrm{d}}\left[D\right]+{\epsilon }_{\mathrm{i}}\left[S\right]}\right)$ (Supplementary Information section 11), where, ε_d and ε_i are molar absorption coefficients of the photoinitiator and the light absorber, respectively, and D and S are the concentrations of the photoinitiator and light absorber of the photopolymer resin, respectively. As the interface is curved, the effective resolution is spatially dependent on the local height of the meniscus relative to the focal plane. For each pixel at the focal plane, we mapped its local coordinate to the corresponding coordinate on the meniscus surface, resulting in a contour map of the effective pixel size across the interface. This map was used to theoretically predict the accurate area fraction the contingent on print head’s size and material properties (Supplementary Information section 12).

Acoustically driven flow

Analytical solution

To understand the formation of acoustically driven capillary-gravity waves, we used many established analytical approaches that describe the induced velocity and secondary streaming effects³² created by the meniscus (Supplementary Information sections 13–15). This analysis, therefore, establishes the velocity scaling laws for capillary-gravity waves dependent on the dominance of capillary- or gravity-driven effects. The dispersion relation for capillary waves, ${\omega }^2=\frac{\gamma }{\rho }{k}^3+\mathit{gk}$, relates the wave frequency (ω) to the wavenumber (k). We, therefore, show that ${\left(\lambda /l_{\mathrm{cap}}\right)}^2$ is a unitless quantity that relates the dominance of surface tension and acoustic parameters on the flow magnitude (Supplementary Information section 14). Here, l_cap denotes the capillary length of the material. Thus, the flow velocity U scales as $U\propto \frac{h_0^2\rho g\varphi }{\lambda \mu }$ for $\left(\lambda /l_{\mathrm{cap}}\right)>1$ and $U\propto \frac{h_0^2\gamma \varphi }{{\lambda }^3\mu }$ for $\left(\lambda /l_{\mathrm{cap}}\right)<1$, where, h₀, ϕ and μ represent the surface perturbation, wave amplitude and viscosity, respectively. Supplementary Fig. 19 shows the effect of material and acoustic parameters on velocity scaling.

Experimental investigation

PIV was employed to understand the 3D flow field produced below the air–liquid boundary under acoustic excitation. A high-speed camera (Kron Technologies, Chronos 1.4 Camera) was used to capture footage of 20–50 µm poly(methyl methacrylate) particles during excitation, both normal and orthogonal to the air–liquid boundary. Particle tracing and velocity reconstruction were performed on the captured video sequences using PIVLab (ref. ⁶⁰) for MATLAB. The exact parameters and methodology used can be found in Supplementary Information section 18. The velocity profiles for top-down and side are shown in Fig. 3c–e and Supplementary Figs. 8 and 9.

Interface restabilization

To determine the transient interface restabilization in the bulk flow, high-speed photography under a uniform backlight was captured at 5,000 fps (Supplementary Fig. 7). Restabilization was determined by segmenting the meniscus edge and tracking the minimum y pixel location of the video stream during excitation and subsequent stabilization. The interface settling time was determined by applying an exponential criterion set at 1/e² of the starting amplitude.

Image analysis of the material influx rate

The material influx rate with and without acoustic excitation was determined by filling a glass cuvette with materials doped with black dye to prevent light transmission. The cuvette was placed on top of a red backlight, such that when the air–liquid boundary formed against the base of the cuvette, the transmitted light was observed by a CCD (Supplementary Information section 19). The material influx rate was measured by raising the air–liquid boundary with and without acoustic excitation and tracking the influx of dyed material, which occluded the backlight transmission (Fig. 3f and Supplementary Information section 20 and Supplementary Fig. 11).

Print parameter space

To identify the ideal parameter space for DIP, a range of print speed and optical dose combinations were tested using three materials: PEGDA, GelMA and HDDA. For each combination, triplicate (n = 3) structures with dimensions of 5 × 5 × 15 mm³ were printed, with successful outcomes being defined by the presence of a sharply delineated structure and a smooth surface finish. Structures that did not meet these requirements, either because they were only partially resolved or because no structure had been produced, were removed from the parameter map. Generally, the print-speed parameter space was not only constrained by the optical dosage but also by the rate at which new material can ‘wet’ the interface. Inadequate wetting typically caused the interface to fluidically ‘pin’ to the underlying structure as the polymerization rate exceeded the mass transport of new material.

Microscopy

Micro computed tomography

Micro computed tomography images were acquired using a Phoenix Nanotom M scanner (Waygate Technologies, voxel size of 10 µm³, 90 kV tube voltage, 200 µA tube current and 8 min scan time). For hydrogel samples, the structures were briefly dried with tissue paper and mounted into a Falcon tube for imaging. For hard materials such as HDDA, the structures were placed on a plastic cap to provide good contrast between the printed structure and the supporting medium. An STL surface mesh was extracted and imported into Keyshot 11 (Keyshot, Luxion) to render the final micro computed tomography representation.

Fluorescence microscopy

Fluorescence microscopy images were captured using a Zeiss Axio Observer Z1 (Zeiss) using either a ×4 or a ×10 objective. For constructs that were larger than the objective’s field of view, the images were stitched within the Zeiss Zen software to create a large-format image. Once the fluorescence images were acquired, cell-counting was performed on each live/dead image pair using a custom MATLAB script.

Scanning electron microscopy

Scanning electron microscope images were acquired on a FlexSEM 1000 (Hitachi High Technologies). Printed structures on glass slides were mounted directly on the microscope stage with no further sample preparation. The samples did not have a conductive coating applied. The electron microscope was operated in variable-pressure mode at 50 Pa. Images were acquired with a 15 keV beam using the ultra-variable detector. To cover the field of view needed for the large structures, the working distance was typically 40–50 mm, and several images were collected in a tiled manner and stitched together in postprocessing.

Helium-ion microscopy images

Helium-ion microscopy images were acquired with a Zeiss NanoFab using a helium source. During imaging, the flood gun was used to actively neutralize the surface, thus removing the need for a conductive coating. All structures were imaged using an accelerating voltage of 30 kV, a beam current of between 1 and 2 pA, and a field of view of 1,100 µm. Structures were printed directly onto a silanized glass slide and were mounted on the stage using the integrated mounting clips. To facilitate the capture of structures larger than the field of view, several images were taken and later stitched using ImageJ/Fiji.

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at 10.1038/s41586-024-08077-6.

Author contributions

C.V. and D.J.C. conceptualized the technique. C.V., M.H. and D.J.C. developed the experimental design. C.V. and M.H. developed the printing system and associated code. K.K. developed the numerical simulations. C.V., P.S., D.J.S., M.M., D.E.H., A.J.B., D.R.N. and L.M.C.A. conducted the material development and characterization. C.V. wrote the paper with input from M.H., D.J.C., E.M.K. and A.R. All authors reviewed and edited the manuscript and supplementary materials.

Peer review

Peer review information

Nature thanks Christophe Moser and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Data availability

The data that support the findings of this study are available within the paper and Supplementary Information. Further data, simulations, images, videos and 3D models that further support the findings of this study are available at Zenodo (10.5281/zenodo.13340723)⁶¹. Source data are provided with this paper.

Code availability

The code used in this study, including the core-slicing algorithm, optical model and associated scripts, is available at Zenodo (10.5281/zenodo.13340723)⁶¹.

Competing interests

C.V., M.H. and D.J.C. have submitted Australian provisional patents (nos. 2023901976 and 2024900764) held/submitted by the University of Melbourne, which cover DIP of 3D structures.

Supplementary information

The online version contains supplementary material available at 10.1038/s41586-024-08077-6.