Fiber Microstructure Quantile (FMQ) Regression: A Novel Statistical Approach for Analyzing White Matter Bundles from Periphery to Core

Abstract

The structural connections of the brain’s white matter are critical for brain function. Diffusion MRI tractography enables the in-vivo reconstruction of white matter fiber bundles and the study of their relationship to covariates of interest, such as neurobehavioral or clinical factors. In this work, we introduce Fiber Microstructure Quantile (FMQ) Regression, a new statistical approach for studying the association between white matter fiber bundles and scalar factors (e.g., cognitive scores). Our approach analyzes tissue microstructure measures based on quantile-specific bundle regions. These regions are defined according to the quantiles of fractional anisotropy (FA) from the periphery to the core of a population fiber bundle, which pools all individuals’ bundles. To investigate how fiber bundle tissue microstructure relates to covariates of interest, we employ the statistical technique of quantile regression. Unlike ordinary regression, which only models a conditional mean, quantile regression models the conditional quantiles of a response variable. This enables the proposed analysis, where a quantile regression is fitted for each quantile-specific bundle region. To demonstrate FMQ Regression, we perform an illustrative study in a large healthy young adult tractography dataset derived from the Human Connectome Project-Young Adult (HCP-YA), focusing on particular bundles expected to relate to particular aspects of cognition and motor function. Importantly, our analysis considers sex-specific effects in brain-behavior associations. In comparison with a traditional method, Automated Fiber Quantification (AFQ), which enables FA analysis in regions defined along the trajectory of a bundle, our results suggest that FMQ Regression is much more powerful for detecting brain-behavior associations. Importantly, FMQ Regression finds significant brain-behavior associations in multiple bundles, including findings unique to males or to females. In both males and females, language performance is significantly associated with FA in the left arcuate fasciculus, with stronger associations in the bundle’s periphery. In males only, memory performance is significantly associated with FA in the left uncinate fasciculus, particularly in intermediate regions of the bundle. In females only, motor performance is significantly associated with FA in the left and right corticospinal tracts, with a slightly lower relationship at the bundle periphery and a slightly higher relationship toward the bundle core. No significant relationships are found between executive function and cingulum bundle FA. Our study demonstrates that FMQ Regression is a powerful statistical approach that can provide insight into associations from bundle periphery to bundle core. Our results also identify several brain-behavior relationships unique to males or to females, highlighting the importance of considering sex differences in future research.

1. Introduction

The white matter plays a critical role in brain function, serving as the brain’s communication infrastructure that is essential for the proper functioning of various cognitive domains (Fields 2008). Diffusion magnetic resonance imaging (dMRI) is an advanced imaging technique that can measure the diffusion process of water molecules and facilitate the investigation of the white matter. dMRI tractography is a three-dimensional reconstruction technique to reconstruct white matter fiber bundles using data collected by dMRI (P. J. Basser et al. 2000). Many large white matter fiber bundles have a long history of anatomical study and are classically defined (e.g. the arcuate fasciculus and the corticospinal tract). Recent machine learning methods can use dMRI tractography to efficiently identify white matter fiber bundles of individuals (Wasserthal, Neher, and Maier-Hein 2018; Garyfallidis et al. 2012; F. Zhang et al. 2018). The fiber bundles obtained from tractography enable the quantitative study of the brain’s white matter anatomy (F. Zhang et al. 2022) and its associations with scalar factors, such as those describing individual cognition or behavior (e.g., language, memory, executive function, or motor) (Zekelman et al. 2022), or those describing diseases or disorders (Kruper et al. 2023; Damatac et al. 2022).

Analyzing the association between fiber bundles and scalar factors requires summary data derived from fiber bundles. One popular quantity for fiber bundle analysis is fractional anisotropy (FA), a scalar value between zero and one that describes the degree of anisotropy of a diffusion process and relates to the geometry and health of the tissue (Peter J. Basser and Pierpaoli 2011). The FA mean within the fiber bundle has been widely used due to its parsimony (Zekelman et al. 2022; F. Zhang et al. 2022; Ciccarelli et al. 2003; Bozzali et al. 2002; Schilling et al. 2023). More sophisticated summary data can provide profiles that describe the values of FA along fiber bundles (Yeatman et al. 2012; L. J. O’Donnell, Westin, and Golby 2009; Chandio et al. 2020; Colby et al. 2012; Corouge et al. 2006). For example, the Automated Fiber Quantification (AFQ) method produces an FA profile along a fiber bundle (Yeatman et al. 2012). This popular method has enabled clinical research applications (Sarica et al. 2017; Johnson et al. 2022; Schilling, Archer, et al. 2022; Kruper et al. 2024, 2023).

The above summary data has limitations in analyzing the associations between fiber bundles and scalar factors. The FA mean overlooks the known microstructural variations of FA within a fiber bundle due to factors such as crossing or fanning white matter geometry and axons entering and leaving the bundle (L. J. O’Donnell, Westin, and Golby 2009; Colby et al. 2012; D. K. Jones et al. 2013; Schilling, Tax, et al. 2022; Jeurissen et al. 2013; Derek K. Jones 2010). Methods such as AFQ analyze FA at each cross-sectional location along the bundle profile (Chandio et al. 2020; Yeatman et al. 2012), which causes challenges in capturing the microstructural variations in the cross-section of the bundle, such as those due to axons crossing, entering, or leaving the bundle. It is also challenging to align bundle profiles across subjects in the presence of anatomical variability in bundle size and shape.

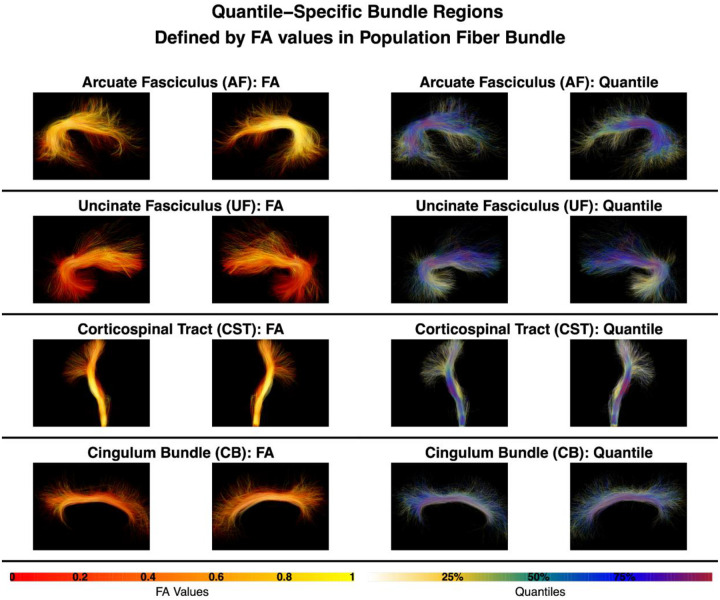
In our paper, we are motivated to address the aforementioned limitations. Our methodology is built on a population fiber bundle (L. O’Donnell and Westin 2005; Chenot et al. 2019; F. Zhang et al. 2018; Elias et al. 2024) that pools all individuals’ fiber bundles. We use the quantiles of FA within the population fiber bundle to define regions that we call quantile-specific bundle regions. As can be observed in Figure 1, the quantile-specific bundle regions finely subdivide the bundle and generally range from the central portion of a fiber bundle with higher FA (i.e., the bundle core) to more peripherally located regions of a fiber bundle with lower FA (i.e., the bundle periphery).

Figure 1:

The population fiber bundles studied in this paper are the Arcuate Fasciculus (AF), Uncinate Fasciculus (UF), Corticospinal Tract (CST), and Cingulum Bundle (CB), shown here in both the left and right hemispheres. In each row, the two left images show fiber tracts (right and left hemispheres) colored by FA values, and the two right images show the corresponding quantiles on the fiber tracts. In this way, the FA values define quantile-specific bundle regions. At the bottom of the figure, we provide the color bars for FA values and quantiles.

Quantile regression, a popular statistical technique, enables the investigation of FA in quantile-specific bundle regions, providing insights into the association of microstructure with scalar factors. Unlike ordinary regression that uses least squares to model the association between the conditional mean of the response variable and the independent variables, quantile regression models the association using the conditional quantiles of the response variable (Koenker et al. 2020). In our proposed approach, the conditional quantiles of the response variable are the quantiles of FA within the population fiber bundle, and the independent variables are the scalar factors. We call our proposed approach Fiber Microstructure Quantile (FMQ) Regression. While quantile regression has been successfully applied in many fields, including genetics and environmental science (Koenker et al. 2020), the proposed FMQ Regression is the first paper to use quantile regression to perform microstructural white matter analysis. To demonstrate its performance, we provide an illustrative study investigating sex-specific effects in brain-behavior associations using a large dataset.

In the rest of the paper, we first introduce the dataset for our illustrative study. We further present our proposed method in Section 2. Section 3 provides the results of our illustrative study using our methodology and other methods. Section 4 discusses the results of our illustrative study and the differences between methods and provides conclusions.

2. Methods

In this section, we first describe the tractography dataset used to illustrate the proposed method (Section 2.1). Then, in Section 2.2, we describe the FMQ Regression method that employs fiber tract data and quantile regression for population-based inference. Next, in Section 2.3, we describe two popular current methods that are used for comparison. Finally, in Section 2.4, we describe the statistical estimates resulting from the three compared methods and the approach for results visualization.

2.1. HCP-YA Dataset for Illustrative Study

To demonstrate our proposed approach, we perform an illustrative study based on a large tractography dataset, focusing on specific tracts expected to relate to particular aspects of motor function and cognition as described in a recent review (Forkel et al. 2022). We use dMRI and scalar factors (i.e., neurobehavioral assessments of language, memory, executive function, and motor performance) from the Human Connectome Project-Young Adult (HCP-YA), a comprehensive multimodal dataset acquired from healthy young adults (Van Essen et al. 2013) that provides minimally processed dMRI (Glasser et al. 2013). We use tractography data previously computed for a cohort of 809 HCP-YA participants published in (Zekelman et al. 2022). The study dataset comprises 809 participants, with 382 males and 427 females. Their ages range from 22 to 36 years, with an average age of 28.6. Brief details about data acquisition and processing follow. The HCP-YA dataset (Glasser et al. 2013) was acquired using three shells (b = 1000, 2000, and 3000 s/mm²), with TE/TR = 89.5/5520 ms and an isotropic voxel size of 1.25 mm³. The b = 3000 shell consisting of 90 gradient directions and all b = 0 scans was extracted to reduce computation time while providing high angular resolution for tractography (F. Zhang et al. 2018). Whole brain tractography was computed by applying a two-tensor Unscented Kalman Filter (UKF) method (Reddy and Rathi 2016), which is effective at reconstructing white matter tracts across various dMRI acquisitions and the lifespan (F. Zhang et al. 2018) with advantages for reconstructing anatomical somatotopy (He et al. 2023). UKF tractography used a two-tensor model to account for crossing fibers (Vos, Viergever, and Leemans 2013; Farquharson et al. 2013) and provided fiber-bundle-specific microstructural measures from the first tensor, which modeled the tract being traced (Reddy and Rathi 2016). White matter tracts were identified for each subject using the white matter analysis machine learning approach that can robustly identify white matter tracts across the human lifespan, health conditions including brain tumors, and different image acquisitions (F. Zhang et al. 2018; Cetin-Karayumak et al. 2024) with high test-retest reproducibility (F. Zhang et al. 2019).

In our illustrative study, we investigate the arcuate fasciculus (AF), uncinate fasciculus (UF), cingulum (CB), and corticospinal tract (CST). These four white matter tracts of interest are investigated in each subject’s left and right hemispheres. Each fiber tract contains a collection of streamlines representing the pathway of a particular white matter connection. Each streamline is composed of a sequence of points (streamline points) and their associated FA values. In this paper, we use FA as a primary measure for tract analysis, though the methods we propose are equally applicable to other microstructure or imaging data measured within fiber tracts, e.g., mean diffusivity (MD) (P. J. Basser 1995), or neurite orientation dispersion and density imaging (NODDI) (H. Zhang et al. 2012; Daducci et al. 2015).

We assess the relationship between the FA of each fiber tract and selected scalar factors, as summarized in Table 1. We study the associations of the AF, UF, CB, and CST with scalar factors of language, memory, executive function, and motor, respectively. Our choices of fiber tracts and corresponding scalar factors follow a recent review of fiber tracts and potentially associated neuro-behavioral functions in health and disease based on the existing literature (Forkel et al. 2022). In our work, the scalar factors are assessments from the NIH Toolbox, the state-of-the-art for neurobehavioral measurement (Hodes et al. 2013). These include the NIH Toolbox Oral Reading Recognition Test (Gershon et al. 2014), Picture Vocabulary Test (Gershon et al. 2014), Picture Sequence Memory Test (Loring et al. 2019), List Sorting Working Memory Test (Tulsky et al. 2014), Dimensional Change Card Sort Test (Zelazo et al. 2014), Flanker Inhibitory Control and Attention Test (Zelazo et al. 2014), 2-minute Walk Endurance Test (Reuben et al. 2013), and 4-Meter Walk Gait Speed Test (Reuben et al. 2013).

Table 1:

Input data for the illustrative study includes fiber tracts, corresponding neurobehavioral functions following a recent review, and scalar factors from the NIH Toolbox. We include an abbreviated name for each scalar factor.

Fiber Tract	Neuro-behavioral Function	Scalar Factor
Arcuate Fasciculus (AF)	Language	Picture Vocabulary Test (PicVocab)
		Oral Reading Recognition Test (ReadEng)
Uncinate Fasciculus (UF)	Memory	Picture Sequence Memory Test (PicSort)
		List Sorting Working Memory Test (ListSort)
Corticospinal Tract (CST)	Motor	Walk Endurance Test (Endurance)
		4-Meter Walk Gait Speed Test (GaitSpeed)
Cingulum Bundle (CB)	Executive function	Dimensional Change Card Sort Test (CardSort)
		Flanker Inhibitory Control and Attention Test (Flanker)

2.2. Key Steps in FMQ Regression

2.2.1. Step 1: Population Fiber Bundle Construction.

To construct a population fiber bundle, first the bundle and its FA values must be identified in all subjects in the population. This can be achieved using methods such as virtual dissection (Catani et al. 2002) or automatic segmentation (F. Zhang et al. 2018; Vázquez et al. 2020; Garyfallidis et al. 2018). The resulting individual fiber bundles have different numbers of streamlines, and their shapes and lengths are not the same due to factors such as anatomical variability and neural plasticity. Constructing a population fiber bundle, which contains the amalgamated streamlines among all individuals within a cohort (L. O’Donnell and Westin 2005; L. J. O’Donnell et al. 2012; Chenot et al. 2019; Elias et al. 2024), is the first step in microstructural inference using FMQ. Population fiber tracts studied in this paper are given in Figure 1. The statistical inference and the following anatomical interpretations rely on the constructed population fiber bundle.

We use the notation i ∈ {1,2,…, I} to denote an individual, where I is the total number of individuals. For a certain fiber tract, we randomly select K streamlines from each individual’s fiber tract (i.e., sampled fiber tract) to ensure each individual’s fiber tract has equal “weight” in constructing the population fiber bundle. We use Y_i = [Y_i1, …, Y_ipi] to denote the microstructure measures (FA values) of each individual, where p_i is the number of streamline points of the i-th individual’s sampled fiber tract. We construct the population fiber tract by assembling individuals’ fiber tracts together. The assembled data thus is a population fiber bundle with FA values ([Y₁, …,Y_I]).

In our HCP-YA illustrative study, the total number of individuals is I = 809. For each individual, we randomly select K = 2000 streamlines (Wasserthal et al. 2019) for each individual’s fiber bundle. Therefore, p_i is determined by the individual’s sampled fiber tract.

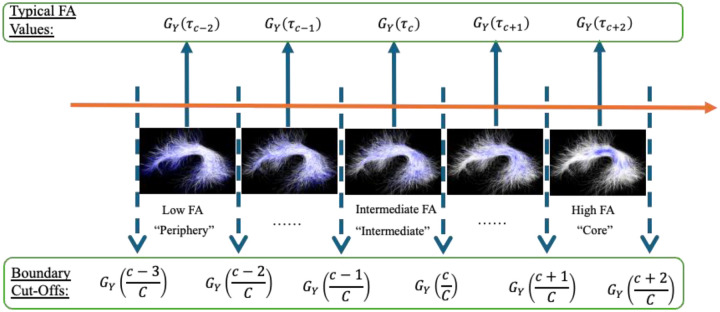
2.2.2. Step 2: Quantile-Specific Bundle Region Creation

In this step, we provide a data-driven approach to create quantile-specific bundle regions defined by the FA values in the population fiber bundle. Let G_Y(τ) be the τ-th quantile of the population fiber bundle’s FA values ([Y₁, …, Y_I]). By using the values of G_Y(c/C) for c ∈ {1,…, C – 1}, as cut-off values (the dashed lines in Figure 2), we can create C quantile-specific bundle regions ranging from bundle periphery to bundle core (Figure 2), and each quantile-specific bundle region has the same number of streamline points. We define ${\tau }_c=\left(\frac{c-1}{C}+\frac{c}{C}\right)/2$ for c ∈ {1,…, C – 1}. For each quantile-specific bundle region c ∈ {1,… , C}, the value G_Y(τ_c) is defined as the typical FA value since it is the middle value between the boundary cut-offs (see blue arrows in Figure 2). The typical FA value indicates the representative FA value in the quantile-specific bundle region and is used as the dependent variable in the regression model introduced in Section 2.2.3.

Figure 2:

Graphical illustration of the population FA distribution sorted along the orange arrow from low to high FA (e.g., bundle periphery, to intermediate bundle regions, to bundle core). C quantile-specific bundle regions are defined based on the values of G_Y(c/C) for c ∈ {1,…,C − 1}, as boundary cut-off values (the dashed lines). The upper and lower cut-off values give the range of FA within each quantile-specific bundle region. The value of G_Y(τ_c) is defined as the typical FA value in each region since it is the middle value between the boundary cut-offs. AF left is used as an illustrative example, where quantile-specific bundle regions are shown in blue.

In our HCP-YA illustrative study, we choose C = 100, and thus the studied quantiles range from 0.5% to 99.5%. This choice of 100 corresponds to the default number of subdivisions in the AFQ method and is chosen for fair comparison (Yeatman et al. 2012)

2.2.3. Step 3: Statistical Inference using Quantile Regression

In this section, we describe how to quantify the association between a typical FA value in a quantile-specific bundle region and a scalar factor. The relationship between the typical FA value and scalar factors is given as G_Y(τ_c) = X_iβ(τ_c) where X_i is a covariate vector of an individual i containing the scalar factor. In the illustrative study of the HCP-YA data, we give the covariate vector of the regression model as $X_i=\left[I_{\mathit{\text{Femal}}{e}_i}+I_{\mathit{\text{Mal}}{e}_i}+Ag{e}_i\times I_{\mathit{\text{Femal}}{e}_i}+Ag{e}_i\times I_{\mathit{\text{Mal}}{e}_i}+\mathit{\text{Scala}}{r}_i\times I_{\mathit{\text{Femal}}{e}_i}+\mathit{\text{Scala}}{r}_i\times I_{\mathit{\text{Mal}}{e}_i}\right]$. In the covariate vector, $I_{\mathit{\text{Femal}}{e}_i}$ and $I_{\mathit{\text{Mal}}{e}_i}$ are indicator variables that equal 1 if the individual i is a female or a male, respectively. Age_i and Scalar_i are the values of the individual’s age and scalar factor, respectively. Without loss of generality, the scalar factor is scaled into the range between 0 and 1. This scaling step allows direct comparison of the magnitudes of the regression coefficients of different scalar factors. In this regression model, the intercepts and regression coefficients are computed for both males and females. The regression coefficient associated with the assessment, β(τ_c), is used to quantify the effect of the scalar factor on the typical FA value of each quantile-specific bundle region.

The most conventional and fastest approach to estimating the coefficient vector is defined as follows,

$$\widehat{\beta }\left({\tau }_c\right)={\mathit{\text{argmin}}}_{\beta \left({\tau }_c\right)}{\sum }_{i=1}^I{\sum }_{p=1}^{p_i}{\rho }_{{\tau }_c}\left(Y_{ip}-X_i\beta \left({\tau }_c\right)\right),$$

where ${\rho }_{{\tau }_c}\left(a\right)=a\left({\tau }_c-I\left[a<0\right]\right)$ is the check function and I[e] is the indicator function for event of e. By giving asymmetric weights to positive and negative values, the check function is a loss function to estimate β(τ_c), making X_iβ(τ_c) as close to the τ_c-th quantile of [Y₁, …, Y_I], as possible. This estimator pools all FA values from all the individuals but does not consider the possible effect of between-individual variations. This estimator has been proven to be asymptotically consistent under certain conditions (Parente and Santos Silva 2016):

$$\sqrt{N}\left(\widehat{\beta }\left({\tau }_c\right)-{\beta }_0\left({\tau }_c\right)\right)\to N\left(0,\Omega \left({\tau }_c\right)\right)\text{as}N\to \infty$$

In other words, a large sample size of individuals (N) produces an estimator that better converges to the true regression coefficient values, i.e., β₀(τ_c). The asymptotic covariance matrix Ω(τ_c) = B(τ_c)⁻¹A(τ_c)B(τ_c)⁻¹ allows us to make valid statistical inferences to account for between-individual variations, providing valid uncertainties of regression coefficient estimates. Furthermore, Ω(τ_c) = B(τ_c)⁻¹A(τ_c)B(τ_c)⁻¹ is feasible to be estimated using the data, denoted as $\widehat{\Omega }\left({\tau }_c\right)$; thus, we can avoid the computationally expensive bootstrap for obtaining the covariance of the estimate. The estimators for A(τ_c) and B(τ_c) that were derived (see Section 2.2 Parente and Santos Silva 2016). The Z-scores and adjusted p-values for the regression coefficient associated with a scalar factor are reported as the principal results. False Discovery Rate (FDR) correction is applied to adjust p-values over the quantile-specific bundle regions for each scalar factor. We reject the null hypothesis if the corresponding p-value is smaller than 0.05. The Z-scores pool regression coefficient estimates’ magnitudes and uncertainties; thus, they are used as the primary quantities to describe the effects of scalar factors.

2.3. Alternative Methods to be Compared

In this section, we provide alternative methods to be compared to our proposed method. We use the FA mean and AFQ tract profile as quantities or profiles measured from the fiber tract, and we build regression models based on these. The names of the two compared regression methods are FA Mean Regression (Section 2.3.1) and AFQ Regression (Section 2.3.2).

2.3.1. FA Mean Regression

In FA Mean Regression, the fiber tract FA mean is the response of the regression models. The fiber tract FA mean is a value averaging all the FA values over streamline points within a fiber tract (L. J. O’Donnell and Westin 2007; Zekelman et al. 2022). FA Mean Regression is the simplest method that uses the FA mean as an imaging biomarker. Simplicity makes it easy to use, but the detailed information on the microstructure within the tract is aggregated. The regression model is defined as M_i = X_iβ + є_i; є_i ~ N(0, σ²), where the tract FA mean is expressed as M_i. In the regression, the covariate vector X_i is the same as in Section 2.2.3. The regression coefficient associated with each scalar factor quantifies the magnitude of effects on the FA mean M_i. The T-scores and p-values for the regression coefficient associated with a scalar factor are reported as the principal results. The p-values here are not corrected since there is no multiple comparison. We reject the null hypothesis if the corresponding p-value is smaller than 0.05. The T-scores that pool regression coefficient estimates’ magnitudes and uncertainties are used as the primary quantities to describe the effects of scalar factors.

2.3.2. AFQ Regression

In AFQ Regression, FA values within the AFQ tract profile are the responses of regression models. The AFQ method (Yeatman et al. 2012) implemented in the dipy software (Garyfallidis et al. 2014) automatically computes the profile, which consists of mean FA values at sequential locations along a fiber tract. The AFQ tract profile of FA is individual-specific. While the fiber tracts are different between individuals, the L locations along a fiber tract can be matched across individuals, given their relative positions. We use T_il to denote the mean FA value of an individual i at a location l. We set up a linear regression as $T_{il}=X_i{\beta }_l+{\in }_{il};{\in }_{il}~N\left(0,{\sigma }_l^2\right)$ In the regression, the covariate vector X_i is the same as in Section 2.2.3. The regression coefficients associated with scalar factors quantify their effects on the FA at the location l. We set L = 100, which is the default convention for AFQ (Yeatman et al. 2012), following the tutorial instructions on the website¹. This setting also makes it comparable to our FMQ Regression. The T-scores and adjusted p-values for the regression coefficient associated with a scalar factor are reported as the principal results. False Discovery Rate (FDR) correction is applied to adjust p-values over the locations along a bundle for each scalar factor. We reject the null hypothesis if the corresponding p-value is smaller than 0.05. Similarly, the T-scores that pool regression coefficient estimates’ magnitudes and uncertainties are used as the primary quantities to describe the effects of scalar factors.

3. Results

In this section, we first summarize the overall results of the illustrative study based on all three methods. Because the selected fiber tracts are potentially associated with the corresponding neurobehavioral functions (Forkel et al. 2022), we expect that many of the associations that we study in this paper should be of statistical significance. Therefore, we first assess the overall sensitivity of the compared regression approaches. Table 2 provides the statistical significance of regression coefficients for all the associations that we investigate. In the table, an association where there is at least one significant regression coefficient is labeled with an asterisk. For most of the experiments, the results show that the FA Mean Regression and FMQ Regression are equally powerful methods for identifying significance, while the AFQ Regression is not a powerful method comparatively.

Table 2.

The statistical significance of regression coefficients related to the scalar factors for all the associations that we investigate. An association where there is at least one significant regression coefficient will be labeled with an asterisk. Significant negative associations are noted as (Neg).

Figure	Fiber Tract	Neuro-behavioral Function	Scalar Factor	Gender	FA Mean Regression		AFQ Regression		FMQ Regression
					LHem	RHem	LHem	RHem	LHem	RHem
Figures 3–4	Arcuate Fasciculus (AF)	Language	PicVocab	Female	*		*		*	*
				Male	*				*
			ReadEng	Female	*
				Male	*				*
Figures 5–6	Uncinate Fasciculus (UF)	Memory	PicSort	Female				* (Neg)
				Male	*				*
			ListSort	Female
				Male	*				*
Figures 7–8	Cortico-spinal Tract (CST)	Motor	Endurance	Female		*
				Male
			GaitSpeed	Female	*	*		*	*	*
				Male
Figures 9–10	Cingulum Bundle (CB)	Executive function	CardSort	Female
				Male
			Flanker	Female
				Male

Next, we provide more detailed insight into the overall results in Table 2 by providing visualizations of the bundle experiments in Figures 3–10. The visualizations include the values of T-scores and Z-scores and how they relate to the anatomy of the studied bundles. In these figures, differences can be observed in the results of the two most statistically powerful methods, FA Mean Regression and FMQ Regression. While these two methods are similarly powerful in identifying associations (Table 2), the proposed FMQ Regression additionally provides the Z-scores from the periphery to the core of each bundle in both males and females (Figures 3–10). FMQ Regression therefore provides additional insight into potential anatomical underpinnings of brain-behavior associations and their differences related to sex. It can also be observed that the AFQ Regression is less powerful in identifying associations.

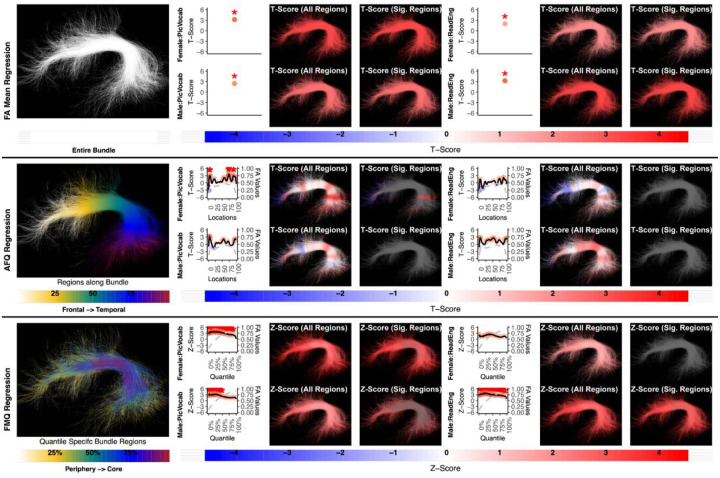
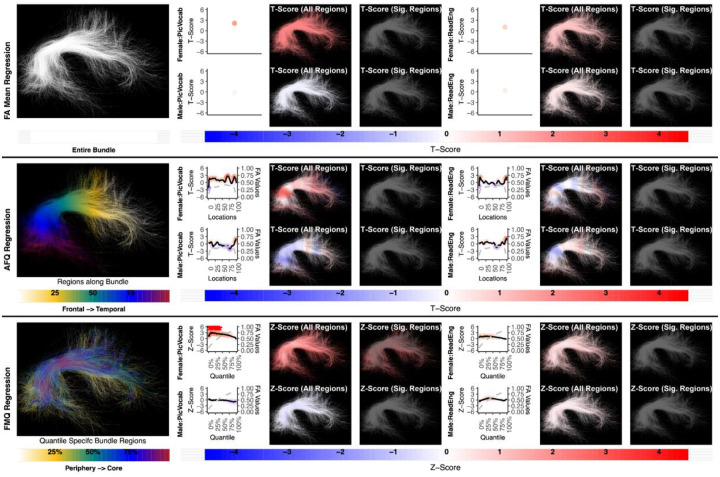
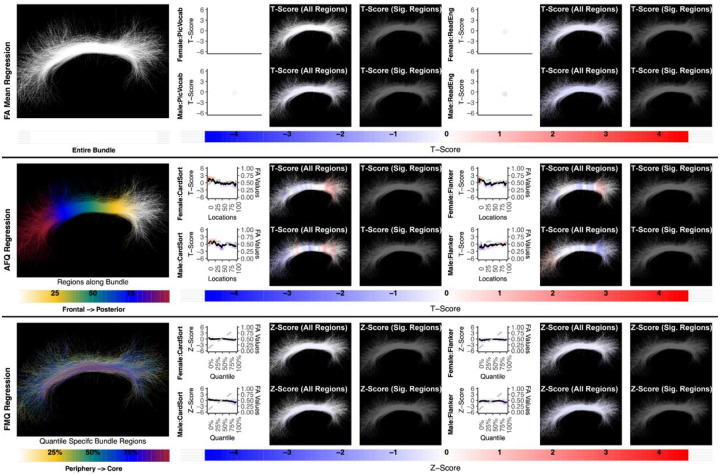
Figure 3:

Regression results for three methods studying the association between AF left and language performance. FA Mean Regression identifies a significant association in PicVocab and ReadEng for males and females; AFQ Regression identifies a significant association in PicVocab in females; FMQ Regression identifies a significant association in PicVocab for males and females and ReadEng for males. Studied bundle regions are shown at left. For each experiment, plots of Z- or T-scores (solid line) and FA (dashed line) are provided, with red asterisks indicating FDR-corrected statistical significance. Visualizations of Z- and T-scores are provided.

Figure 10:

The association between CB right and executive function performance. None of the methods identify a statistically significant association. Studied bundle regions are shown at left. For each experiment, plots of Z- or T-scores (solid line) and FA (dashed line) are provided, with red asterisks indicating FDR-corrected statistical significance. Studied bundle regions are shown at left. For each experiment, plots of Z- or T-scores (solid line) and FA (dashed line) are provided, with red asterisks indicating FDR-corrected statistical significance. Visualizations of Z- and T-scores are provided.

Here we give more detail about the specific quantiles that are significant when using FMQ Regression. First, we summarize the left AF (Figure 3). Significant associations are identified for PicVocab within the left AF. In females, the quantiles from 0.5% to 90.5% are significant, covering the peripheral, intermediate, and near-core bundle regions. In males, the significant quantiles range from 0.5% to 49.5%, including peripheral and intermediate bundle regions. Additionally, FMQ Regression identifies significant associations within the left AF for ReadEng (Figure 3) for males, with significant quantiles from 0.5% to 95.5%, encompassing almost all bundle regions. Next, we summarize the right AF (Figure 4). Significant associations are identified for PicVocab within the right AF in females between quantiles 4.5% and 40.5%, covering peripheral and intermediate bundle regions. Next, we summarize the left UF (Figure 5). FMQ Regression also identifies significant associations within the left UF for PicSeq (Figure 5) for males, where quantiles 16.5% to 91.5% are significant, including near-peripheral, intermediate, and near-core bundle regions. Another significant association is observed within the left UF for ListSort (Figure 5) in males between quantiles 54.5% and 80.5%, covering the intermediate and near-core bundle regions. Finally, we summarize the left and right CST (Figures 7 and 8). FMQ Regression identifies significant associations within the left CST for GaitSpeed (Figure 7) in females, with quantiles ranging from 2.5% to 99.5%, covering almost all bundle regions from periphery to core. Similarly, FMQ Regression identifies significant associations within the right CST for GaitSpeed in females across quantiles 0.5% to 99.5%, again covering almost all bundle regions.

Figure 4:

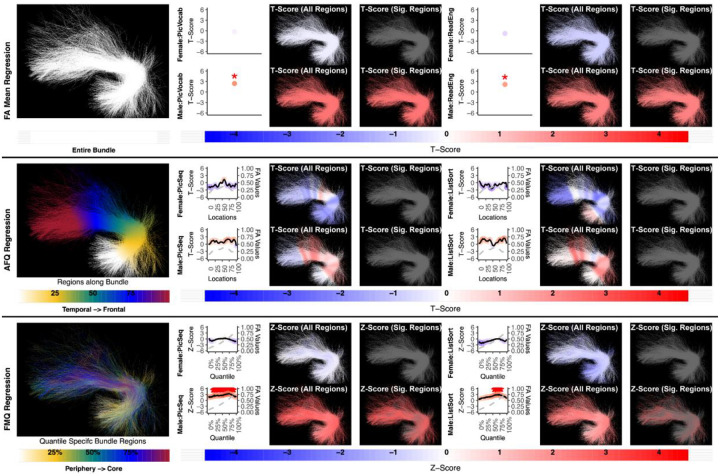
The association between AF right and language performance. FMQ Regression identifies a significant association in PicVocab for females. FA Mean Regression and AFQ Regression do not identify any statistically significant association. Studied bundle regions are shown at left. For each experiment, plots of Z- or T-scores (solid line) and FA (dashed line) are provided, with red asterisks indicating FDR-corrected statistical significance. Visualizations of Z- and T-scores are provided.

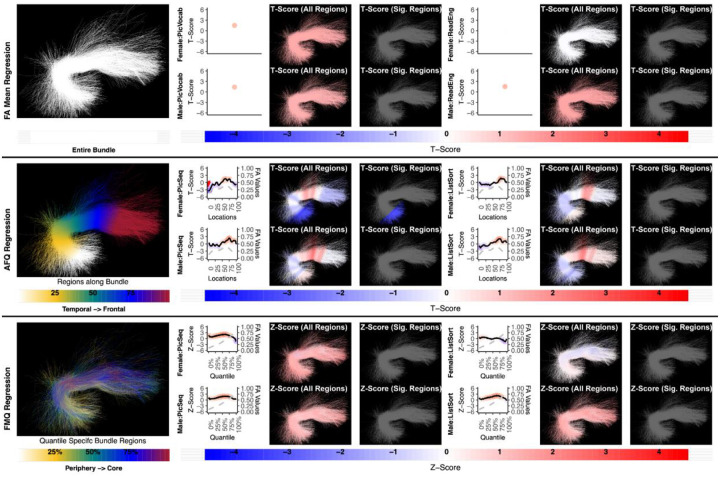
Figure 5:

The association between UF left and memory performance. Both FA Mean Regression and FMQ Regression identify significant associations in PicSeq and ListSort for males. AFQ Regression does not identify any statistically significant association. Studied bundle regions are shown at left. For each experiment, plots of Z- or T-scores (solid line) and FA (dashed line) are provided, with red asterisks indicating FDR-corrected statistical significance. Visualizations of Z- and T-scores are provided.

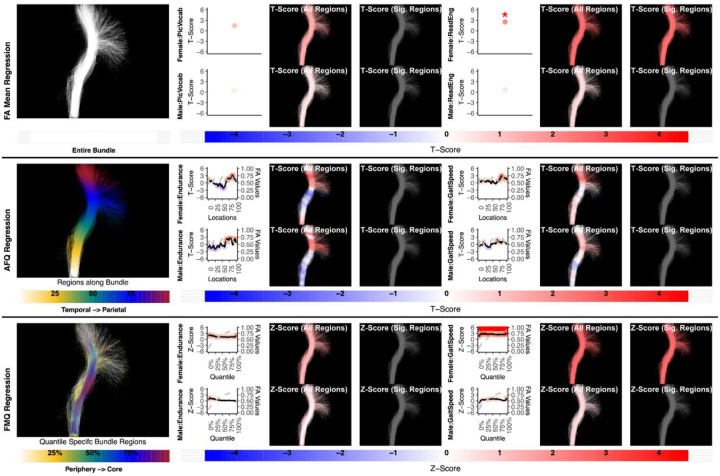
Figure 7:

The association between CST left and motor performance. Both FA Mean Regression and FMQ Regression identify significant associations in GaitSpeed for females. AFQ Regression does not identify any statistically significant association. Studied bundle regions are shown at left. For each experiment, plots of Z- or T-scores (solid line) and FA (dashed line) are provided, with red asterisks indicating FDR-corrected statistical significance. Visualizations of Z- and T-scores are provided.

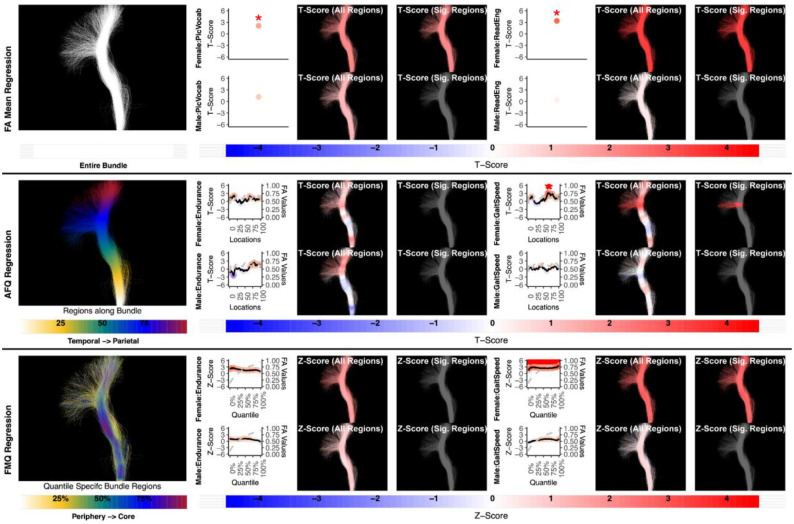
Figure 8:

The association between CST right and motor performance. FA Mean Regression, AFQ Regression, and FMQ Regression identify significant associations in GaitSpeed for females. FA Mean Regression identifies a significant association in Endurance in females. Studied bundle regions are shown at left. Studied bundle regions are shown at left. For each experiment, plots of Z- or T-scores (solid line) and FA (dashed line) are provided, with red asterisks indicating FDR-corrected statistical significance. Visualizations of Z- and T-scores are provided.

4. Discussion

4.1. Methodological Contribution

In this paper, we propose a new statistical approach, FMQ Regression, for the analysis of brain fiber tract data, and we compare results to two other popular methods from the literature. We apply these methods to an illustrative study motivated by a recent review paper that describes neurobehavioral functions associated with fiber tracts in health and disease (Forkel et al. 2022). Thus, we had expected that the associations that we study in this paper would be of statistical significance. Therefore, we suggest that a method that can better identify the significance should be considered a better method. From this perspective, we make several observations. The proposed FMQ Regression generally outperforms the compared methods and produces several significant results. Our FMQ Regression results include significant findings in bundle cores (e.g., male UF bundle core FA associates with two memory performance assessments) as well as bundle peripheries (e.g., female AF periphery FA associates with PicVocab). These results motivate the potential importance of analyzing FA based on quantile-specific bundle regions, which tend to occupy regions from bundle periphery to bundle core.

In comparison with the traditional AFQ Regression strategy, a popular alternative microstructural analysis tool, our results suggest that FMQ Regression is much more powerful. For example, FMQ identifies significant associations in AF, CST, and UF, while the other two methods fail to achieve equivalent power. While FMQ Regression and AFQ Regression are both methods that provide microstructural inference, the two methods have essential differences. One difference is that they provide different approaches for region-specific analysis: bundle periphery to bundle core versus along the bundle. Another difference between the methods is that the quantile-specific bundle regions are defined in a population-based fashion, while the AFQ profile is defined in an individual-specific fashion, followed by matching across subjects. The quantile-specific bundle regions thus have the potential to reduce the effect of subject-specific sources of variability that affect the AFQ profile, such as bundle anatomical variability in shape or length, as well as FA variability in each bundle region within and across subjects. Other works have mentioned limited statistical power when using the AFQ method, which was attributed to the challenge of multiple comparisons (Richie-Halford et al. 2021). Approaches such as data reduction via feature selection (Richie-Halford et al. 2021) and suprathreshold cluster analyses (L. J. O’Donnell, Westin, and Golby 2009) have been proposed to reduce challenges resulting from multiple comparisons along a fiber bundle. In contrast, we note that our proposed FMQ approach has relatively high statistical power, even when using a large number of quantile-specific regions and multiple comparison adjustments. This advantage of FMQ may relate to the population-based aspect of our approach that effectively captures variations of the data. As detecting brain-behavior associations is widely understood to be a challenging problem in neuroimaging (Marek et al. 2022; Gratton, Nelson, and Gordon 2022), new methods that can enable more powerful analysis can be a welcome addition to our toolbox.

In comparison with the traditional FA Mean Regression, the proposed FMQ Regression is similarly powerful while providing additional potential insight into associated anatomical regions (i.e., bundle core versus periphery). In Table 2, it can be seen that one significant association found by FMQ Regression was not identified by FA Mean Regression, while two significant associations identified by FA Mean Regression were not found by FMQ Regression. This suggests that the techniques are complementary, where some localized effects may be missed by the FA Mean Regression (as is well known in the literature (L. J. O’Donnell, Westin, and Golby 2009; Colby et al. 2012)), while some global or whole-bundle effects may be more sensitively detected by the FA Mean Regression. Overall, the fact that the significant findings were generally consistent across the FMQ and Mean FA Regression methods, across multiple NIH toolbox measures (e.g., of language function), and across hemispheres (e.g., bilateral female CST effects), suggests the robustness of the proposed FMQ Regression.

Our FMQ Regression is different from other fiber tract data analyses using the quantile regression technique (Lv et al. 2021; Ryan et al. 2022). In contrast to our approach, the previous works (Lv et al. 2021; Ryan et al. 2022) rely on the FA mean of the entire fiber tract and investigate the association between the conditional quantile of the FA mean and covariates of interest.

4.2. Neuroscience Findings

In the following paragraphs, we briefly discuss our current findings in each fiber tract in relation to the literature.

Consistent with many reports of associations between the left, but not right, AF and language performance in healthy individuals (Zekelman et al. 2022; Yeatman et al. 2011), the proposed FMQ Regression identified a statistically significant association in the left AF in both males and females. However, in females only, the FMQ Regression (and not the FA mean or AFQ methods) identified a statistically significant association with PicVocab in the bundle periphery and intermediate bundle regions of the right AF. This is of interest for further investigation and could potentially relate to known sex differences in AF, such as its greater symmetry in females (Thiebaut de Schotten et al. 2011). Interestingly, our significant findings relating the left AF FA to language performance spanned many quantiles of FA but never included the maximum FA bundle “core” regions (i.e. the highest quantiles near 100% were never significant, as shown in Figure 3). In fact, the relationships between AF microstructure (FA) and two assessments of language are stronger in the periphery and decrease toward the core of the bundle in both males and females. This observation may potentially represent a challenge for uncovering brain-behavior language associations using TBSS (tract-based spatial statistics), a method that focuses only on maximum-FA voxels thought to represent bundle cores (Smith et al. 2006). For example, a recent investigation studied 6 different language assessments using TBSS and found only one association of FA in the left superior longitudinal fasciculus, which includes the AF (Houston et al. 2019). Converging evidence from our recent geometric machine learning work also identified peripheral regions of AF, including regions of the gray-white matter interface, to be most predictive of individual performance on language assessments (Chen et al. 2024). This is in line with recent work investigating the shape of the white matter association tracts (including AF), which shows that the peripheral regions where bundles originate and terminate in the cortex have a large degree of inter-individual variability and are therefore a good descriptor of inter-individual differences in white matter structure (Yeh 2020).

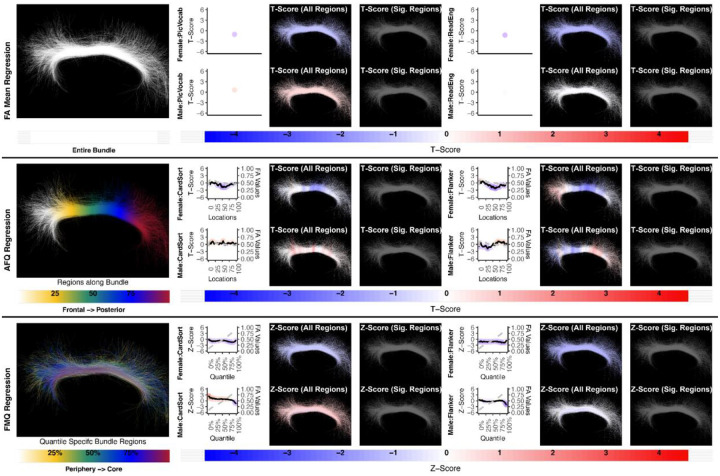
Consistent with a handful of other studies of UF in healthy individuals (Mabbott et al. 2009; Schaeffer et al. 2014), the proposed FMQ Regression identified a statistically significant association between left UF FA and memory performance (Figure 5). However, in the present study, this effect was observed only in males (in intermediate and near-core bundle regions). This finding motivates the importance of studying sex effects in the relationship between brain microstructure and individual functional performance.

While it is well understood that the CST subserves motor function (Welniarz, Dusart, and Roze 2017) and is left-lateralized (Thiebaut de Schotten et al. 2011), most existing studies of FA and motor function have been performed in patients with diminished function. However, a recent study in healthy young adults showed that CST FA was bilaterally associated with corticospinal excitability, a transcranial magnetic stimulation measure of individual function (Betti et al. 2022). Our finding that CST FA is associated with motor functional performance (GaitSpeed) bilaterally, and only in females, further motivates the need to study tract microstructure and its relationship to human brain functional performance in both males and females, as well as in healthy individuals (Fig. 7–8).

We report negative results (no significance) for the relationship between CB FA and measures of executive function (CardSort and Flanker) in healthy young adults using all compared regression methods (Fig. 9–10). A recent review on white matter tracts and executive function suggests a role for CB, especially in inhibition; however, the supporting neuroimaging studies include aging and neuropsychiatric populations, not healthy individuals (Ribeiro et al. 2024). Our results do not contradict the potential role of CB in executive function in healthy young adults; our findings merely indicate that CB FA microstructure does not relate to executive function performance in the study population. In this study we focused on the superior part of the CB, excluding the temporal portion of the bundle, because individual streamlines generally do not trace the entire trajectory of the CB. This is in part because axons enter and leave the CB along its entire length (D. K. Jones et al. 2013; Heilbronner and Haber 2014). In addition, the superior part of the cingulum more closely correlates with attention and executive function, whereas the temporal cingulum is associated with episodic memory (Metzler-Baddeley et al. 2012; Kantarci et al. 2011).

Figure 9:

The association between CB left and executive function performance. None of the methods identify a statistically significant association. Studied bundle regions are shown at left. For each experiment, plots of Z- or T-scores (solid line) and FA (dashed line) are provided, with red asterisks indicating FDR-corrected statistical significance. Studied bundle regions are shown at left. For each experiment, plots of Z- or T-scores (solid line) and FA (dashed line) are provided, with red asterisks indicating FDR-corrected statistical significance. Visualizations of Z- and T-scores are provided.

4.3. Neuroanatomical Discussion

In this paper, we have proposed analyzing white matter bundles in dMRI using regions that are defined using quantiles of FA, with the result that the quantile-specific regions are approximately defined from the bundle periphery to the bundle core. Neuroanatomical research demonstrates that for many bundles, axons enter and leave the bundle along its course (Yakovlev and Locke 1961; Morris, Pandya, and Petrides 1999; Mufson and Pandya 1984; Schmahmann and Pandya 2009; Petrides and Pandya 2007; Heilbronner and Haber 2014). As these axons leave the bundle, they curve and necessarily intersect and cross axons from other bundles closer to their cortical or subcortical targets. This intersection will lead to a lower FA (Derek K. Jones 2010). In the current study, these regions of lower FA are located toward the ends of the tract as the streamlines fan out as a spray of fibers and traverse the periphery of other fiber bundles (Makris et al. 1997). In addition, these regions of lower FA in peripheral locations are also observed along the length of the fiber, which corresponds to anatomical studies of the cingulum bundle that show that axons enter or leave the tract along its course (Yakovlev and Locke 1961; Mufson and Pandya 1984).

4.3. Limitations

Potential limitations of the present study, including suggested future work to address limitations, are as follows. In this work, we demonstrated the estimation of C = 100 sets of coefficients for all the quantile-specific bundle regions. Future work may investigate other numbers of quantile-specific bundle regions by varying C. From the computational perspective, our method requires a large streamline dataset sampled from all subject fiber bundles under study in the population. Future work may investigate optimizing the amount of input data needed to obtain results in very large datasets. In this study we have described quantile locations as bundle core, intermediate bundle regions, or bundle periphery regions, with accompanying visualizations to provide more detail. However, it can be observed that not all fiber bundles are completely included in the field of view (FOV) of a dMRI scan, which can make the periphery-core interpretation more nuanced. For instance, the high-FA “core” region of the CST can be observed to continue inferiorly in the brainstem, which extends outside of the FOV. Another consideration is the potential presence of somatotopic or functional subdivisions of a fiber bundle. For instance, future work could separately study associations of individual bundles within the CST, e.g., those originating in trunk, leg, hand, and face motor cortical regions (He et al. 2023), or bundles representing subdivisions within the AF (Fernández-Miranda et al. 2015). In this initial paper describing the proposed FMQ Regression method, we have performed a testbed study of selected white matter fiber bundles, where we studied one selected microstructure measure (FA) and multiple selected neurobehavioral measures. In future work, it will be interesting to extend and apply the proposed FMQ approach to perform studies of additional datasets, fiber bundles, microstructure measures, and scalar factors of interest, potentially leading to deeper insights into the brain’s structural-functional relationships.

5. Conclusion

We have proposed FMQ Regression, a novel quantile regression methodology for studying white matter bundles in the brain. We find that analyzing FA using quantile-specific bundle regions, which tend to define regions from bundle periphery to bundle core, is much more powerful than a traditional AFQ method that spatially subdivides bundles along their lengths. Our results suggest that FMQ Regression is a powerful tool for studying brain-behavior associations using white matter tractography data.

Figure 6:

The association between UF right and memory performance. AFQ Regression identifies a negative significant association in PicSeq for males. Other methods do not identify any statistically significant association. Studied bundle regions are shown at left. Studied bundle regions are shown at left. For each experiment, plots of Z- or T-scores (solid line) and FA (dashed line) are provided, with red asterisks indicating FDR-corrected statistical significance. Visualizations of Z- and T-scores are provided.

Data and Code Availability

This study utilized publicly available data from HCP-YA (https://www.humanconnectome.org/study/hcp-young-adult/overview). Data can be accessed via data use agreements. Upon acceptance, code for the FMQ Regression will be provided at https://github.com/SlicerDMRI/FMQRegression.