Skip to main content
NCBI home page
Biochemical Journal logoLink to Biochemical Journal
. 1985 Oct 1;231(1):65–74. doi: 10.1042/bj2310065

Analysis of progress curves for a highly concentrated Michaelian enzyme in the presence or absence of product inhibition.

N Kellershohn, M Laurent
PMCID: PMC1152704  PMID: 4062893

Abstract

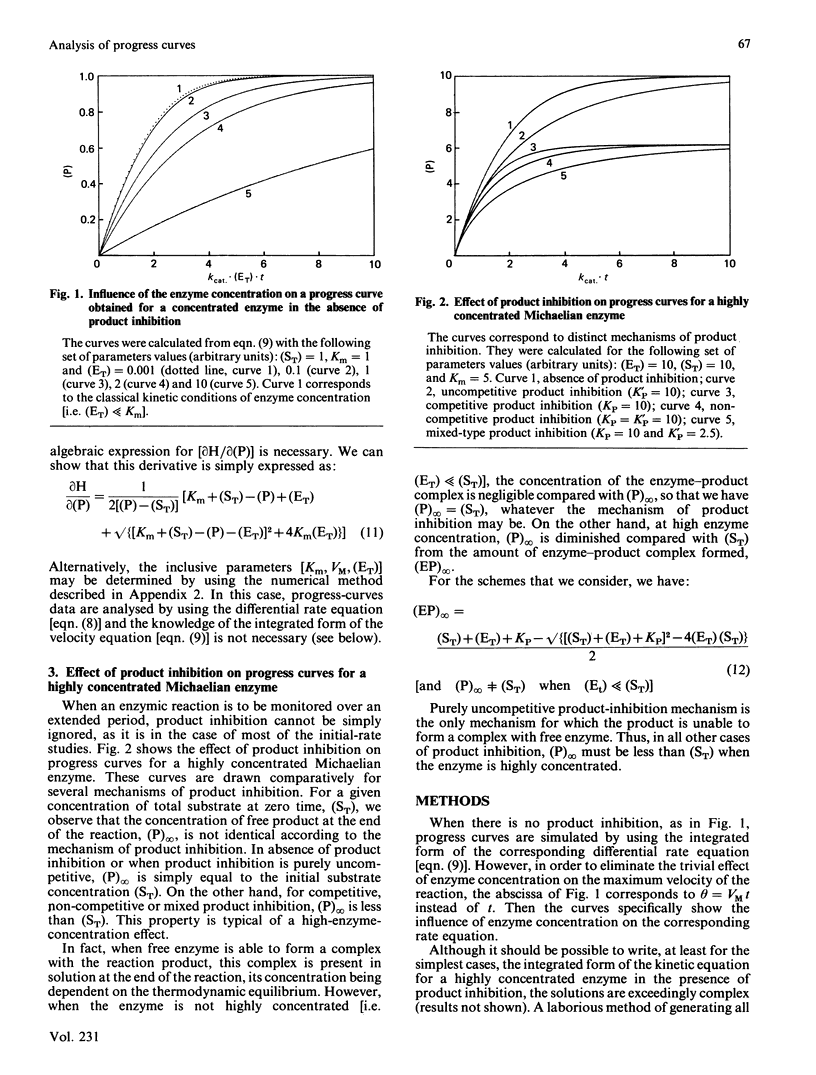
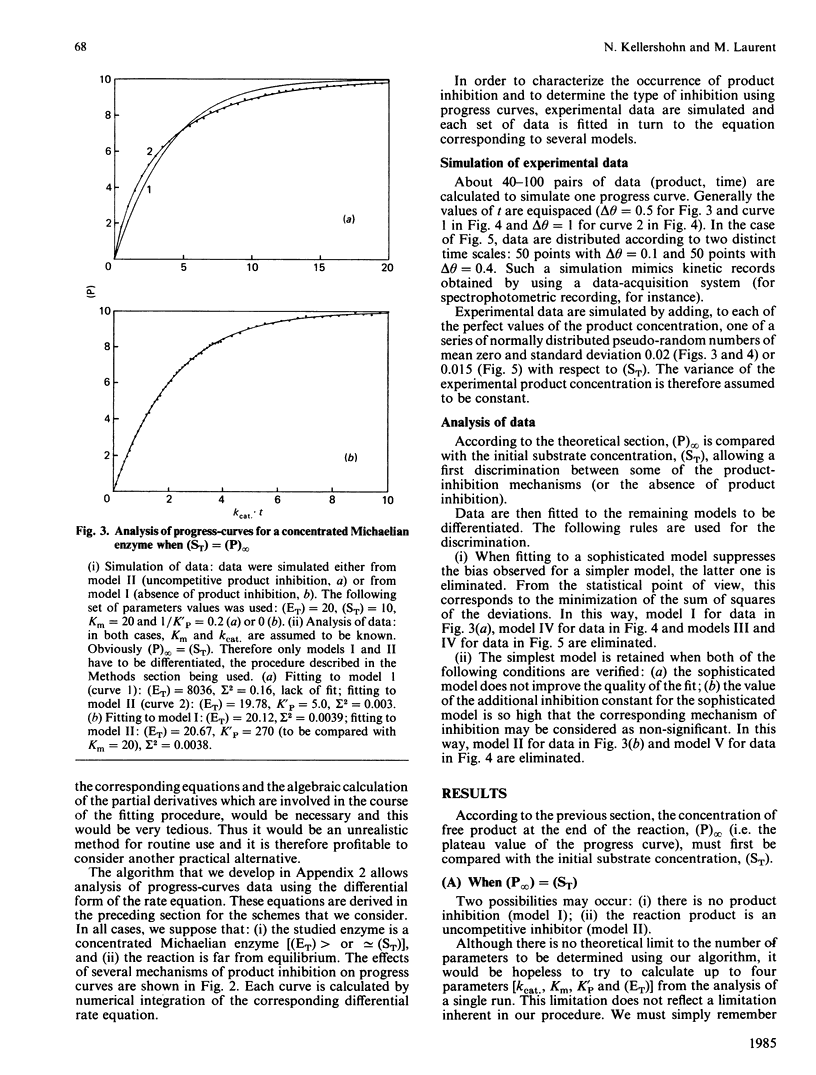
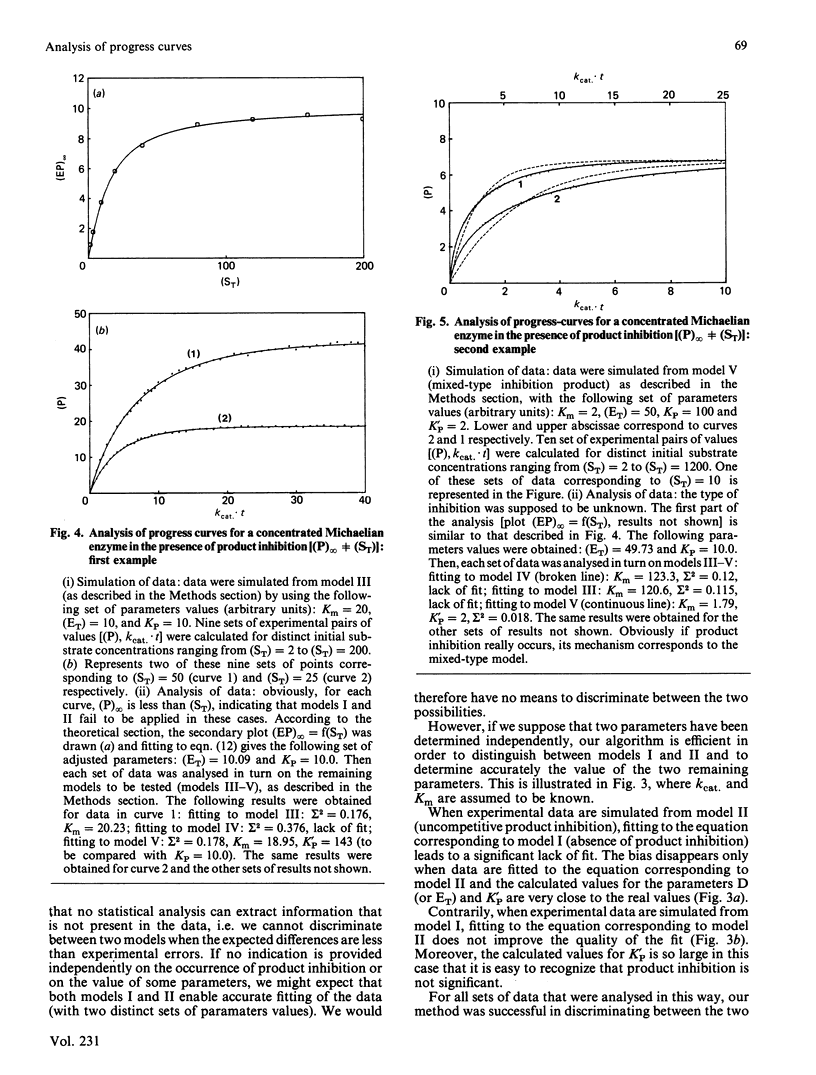
Methods are given for analysing the time course of an enzyme-catalysed reaction when the concentration of the enzyme itself is high, a situation which is often found in vivo. (1) The integrated form of the kinetic equation for a concentrated Michaelian enzyme in absence of product inhibition is given. Parameters are shown to be calculated easily using non-linear fitting procedures. (2) A general algorithm to analyse progress-curve data in more complex cases (i.e. when the analytical form of the integrated rate equation is not known or is exceedingly complex) is proposed. This algorithm may be used for any enzyme mechanism for which the differential form of the kinetic equation may be written analytically. We show that the method allows differentiation between the main types of product inhibition which may occur in the case of a highly concentrated Michaelian enzyme.

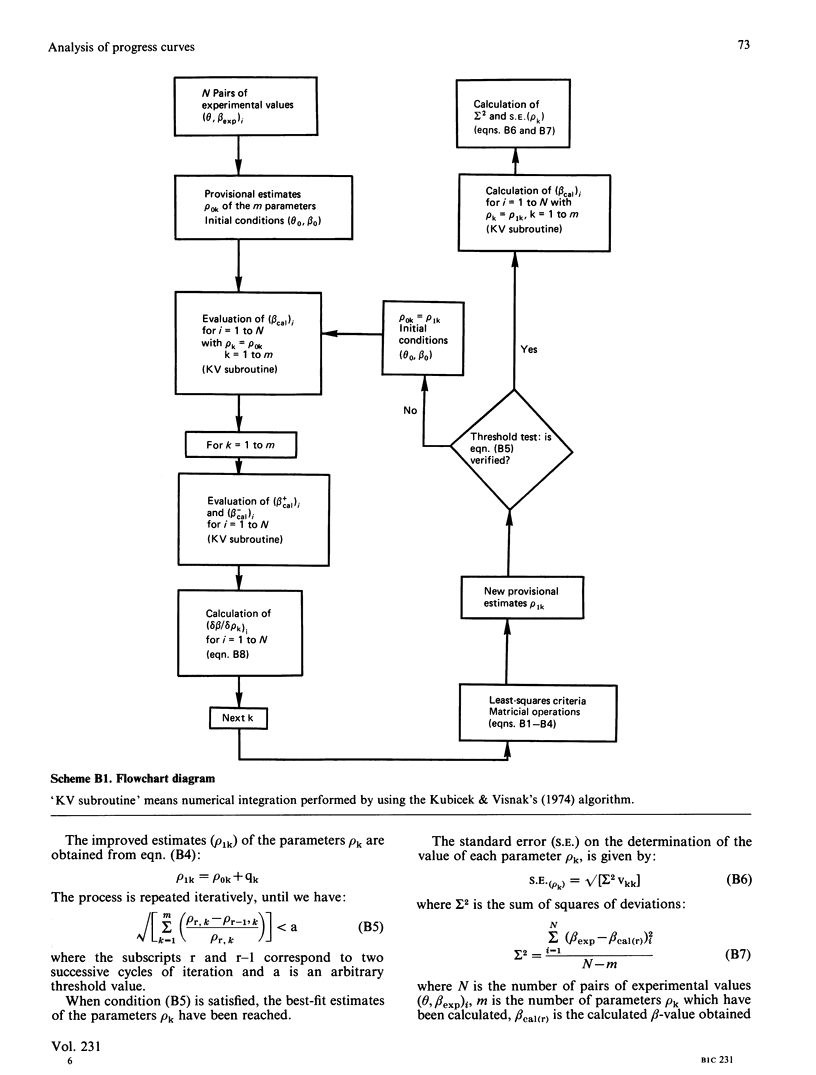
Full text

PDF
63

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Cleland W. W. The statistical analysis of enzyme kinetic data. Adv Enzymol Relat Areas Mol Biol. 1967;29:1–32. doi: 10.1002/9780470122747.ch1. [DOI] [PubMed] [Google Scholar]
  2. Fernley H. N. Statistical estimations in enzyme kinetics. The integrated Michaelis equation. Eur J Biochem. 1974 Apr 1;43(2):377–378. doi: 10.1111/j.1432-1033.1974.tb03423.x. [DOI] [PubMed] [Google Scholar]
  3. Garfinkel D., Marbach C. B., Shapiro N. Z. Stiff differential equations. Annu Rev Biophys Bioeng. 1977;6:525–542. doi: 10.1146/annurev.bb.06.060177.002521. [DOI] [PubMed] [Google Scholar]
  4. Halfman C. J., Marcus F. A method for determining kinetic parameters at high enzyme concentrations. Biochem J. 1982 Apr 1;203(1):339–342. doi: 10.1042/bj2030339. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Laurent M., Kellershohn N. Apparent co-operativity for highly concentrated Michaelian and allosteric enzymes. J Mol Biol. 1984 Apr 15;174(3):543–555. doi: 10.1016/0022-2836(84)90335-8. [DOI] [PubMed] [Google Scholar]
  6. MONOD J., COHEN-BAZIRE G., COHN M. Sur la biosynthèse de la beta-galactosidase (lactase) chez Escherichia coli; la spécificité de l'induction. Biochim Biophys Acta. 1951 Nov;7(4):585–599. doi: 10.1016/0006-3002(51)90072-8. [DOI] [PubMed] [Google Scholar]
  7. Nimmo I. A., Atkins G. L. Methods for fitting equations with two or more non-linear parameters. Biochem J. 1976 Aug 1;157(2):489–492. doi: 10.1042/bj1570489. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Penverne B., Hervé G. In situ behavior of the pyrimidine pathway enzymes in Saccharomyces cerevisiae. I. Catalytic and regulatory properties of aspartate transcarbamylase. Arch Biochem Biophys. 1983 Sep;225(2):562–575. doi: 10.1016/0003-9861(83)90068-1. [DOI] [PubMed] [Google Scholar]
  9. Reeves R. E., Sols A. Regulation of Escherichia coli phosphofructokinase in situ. Biochem Biophys Res Commun. 1973 Jan 23;50(2):459–466. doi: 10.1016/0006-291x(73)90862-0. [DOI] [PubMed] [Google Scholar]
  10. Sawula R. V., Suzuki I. Effect of enzyme concentration on the kinetics of D-lactate dehydrogenase from Aerobacter aerogenes. Biochem Biophys Res Commun. 1970 Sep 10;40(5):1096–1101. doi: 10.1016/0006-291x(70)90907-1. [DOI] [PubMed] [Google Scholar]
  11. Schwert G. W. Use of integrated rate equations in estimating the kinetic constants of enzyme-catalyzed reactions. J Biol Chem. 1969 Mar 10;244(5):1278–1284. [PubMed] [Google Scholar]
  12. Weitzman P. D. Behaviour of enzymes at high concentration. Use of permeabilised cells in the study of enzyme activity and its regulation. FEBS Lett. 1973 Jun 1;32(2):247–250. doi: 10.1016/0014-5793(73)80843-9. [DOI] [PubMed] [Google Scholar]

Articles from Biochemical Journal are provided here courtesy of The Biochemical Society

RESOURCES