A universal hippocampal memory code across animals and environments

Abstract

How learning is affected by context is a fundamental question of neuroscience, as the ability to generalize learning to different contexts is necessary for navigating the world. An example of swift contextual generalization is observed in conditioning tasks, where performance is quickly generalized from one context to another. A key question in identifying the neural substrate underlying this ability is how the hippocampus (HPC) represents task-related stimuli across different environments, given that HPC cells exhibit place-specific activity that changes across contexts (remapping). In this study, we used calcium imaging to monitor hippocampal neuron activity as rats performed a conditioning task across multiple spatial contexts. We investigated whether hippocampal cells, which encode both spatial locations (place cells) and task-related information, could maintain their task representation even when their spatial encoding remapped in a new spatial context. To assess the consistency of task representations, we used advanced dimensionality reduction techniques combined with machine learning to develop manifold representations of population level HPC activity. The results showed that task-related neural representations remained stable even as place cell representations of spatial context changed, thus demonstrating similar embedding geometries of neural representations of the task across different spatial contexts. Notably, these patterns were not only consistent within the same animal across different contexts but also significantly similar across different animals, suggesting a standardized neural encoding or ‘neural syntax’ in the hippocampus. These findings bridge a critical gap between memory and navigation research, revealing how the hippocampus maintains cognitive consistency across different spatial environments. These findings also suggest that hippocampal function is governed by a neural framework shared between animals, an observation that may have broad implications for understanding memory, learning, and related cognitive processes. Looking ahead, this work opens new avenues for exploring the fundamental principles underlying hippocampal encoding strategies.

Introduction

How can learning can be generalized across contexts as well as remaining localized to one context? This question is fundamental to both neuroscience and philosophy^1–4. Deficits in generalization or inappropriate generalization are hallmarks of many disorders, including autism^5,6, schizophrenia^7,8, and post-traumatic stress disorder^9,10. In spite of their importance, many questions related to generalization remain to be answered.

The hippocampus (HPC) is important for learning, memory, and navigation, and damage to this region can disrupt contextual learning^11–17. Many aspects of context, including an animal’s spatial location and the presence of local and distal cues, can be represented by ‘place cells’ in the HPC^18–22. The activity of many HPC cells therefore changes drastically in different environments (i.e. place cells remap), even when a task can be generalized across these different contexts^23–25. A major open question is if and how representations of task-relevant stimuli, which are also found in the HPC^26–31, can be maintained against the background of remapped place cells. A further question is whether different animals solve this problem using the same, or similar, neural strategies.

Until recently, the neural mechanisms behind contextual learning have been challenging to investigate due to the need for tracking large numbers of cells across various environments and learning stages— tasks which were unachievable prior to the development of calcium imaging^32–37. The use of calcium imaging in this study has allowed for a detailed exploration of hippocampal neuron dynamics, bridging previous gaps between studies of hippocampal cognitive maps and the hippocampal bases of memory and learning. The traditional separation between memory and navigation fields of HPC research is thus in the process of narrowing^38,39.

This research addresses two fundamental questions of learning and memory. The first question pertains to the persistence of learning across varying contexts. The modulation of hippocampal cells by spatial variables results in substantial changes to cell activity in different environments^24,25,40,41; how can conditioning-related neural representations remain stable amid such remapping? The second question is the extent to which neural representations in the hippocampus are invariant and consistent, not only within an individual across diverse contexts, but across different individuals; is there a standardized neural encoding or ‘neural syntax’ in the for learning and memory in the hippocampus? A commonality of encoding across animals would imply that the functionality of the HPC is informed not solely by individual experiences but also by a standardized framework of neural algorithms. Such a finding would provide key insights into the underlying neural mechanisms that govern learning and memory, helping to identify specific brain circuits and algorithms that drive behavior.

To answer these questions, we trained rats on an HPC-dependent conditioning task which is rapidly generalized between spatial contexts^42,43. We examined the same task in disparate contexts and looked for changes in a representation of spatial location provided by a population of place cells while the representation of the task features remains unchanged. We found that the representations of the conditioning task were maintained as the animal generalized learning from one environment to another, even as the representation of place changed. Surprisingly, we also found that the neural representation of the task was consistent across animals.

This study demonstrates that despite the well-known phenomenon of place cell remapping^24,25,40,41, there exists a stable population-level neural representation of task features that persists across diverse environments. These representations also show consistency across different individuals, indicating a standardized neural encoding or ‘neural syntax’ for the conditioning task within the hippocampus. This novel finding suggests the existence of a universal coding mechanism for associative learning in the hippocampus, a principle that could reorient our approach to studying memory and could challenge our current understanding of cognitive processes.

Results

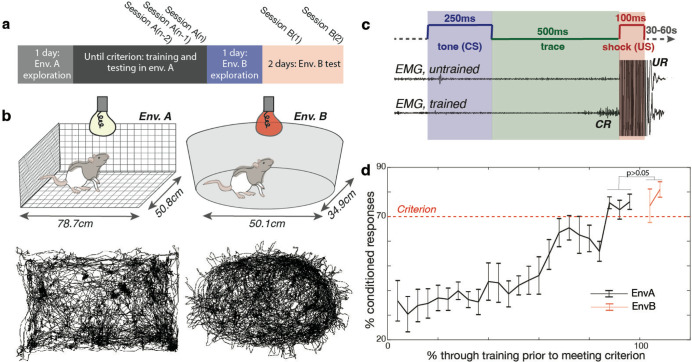
We trained a cohort of 5 freely moving rats in a conditioning task in one of two distinct environments, labeled A and B; the rats had been previously familiarized with the environment by the time the training began (Fig. 1a, Fig. S1). Environment A was an unscented rectangular enclosure with wire floor and walls, and white lighting; environment B was a scented ovular enclosure with white solid floor and walls, and red lighting (Fig. 1b). Both environments were located at the same spot in the room relative to external cues (see Methods); animals could see external cues out of the top of both environments, as well as out of the sides of environment A (animals also reared often, allowing them to see out of the sides of environment B). During training sessions, we recorded cellular activity in the hippocampal CA1 region via miniscopes, using Gcamp8m for calcium imaging (CaImg). To perform data analysis, we used both calcium events and calcium traces (see Methods), as indicated when applicable.

Fig 1. Experimental training paradigm and results.

a. Animals explored environment A for one session before undergoing eyeblink conditioning until they reached the learning criterion. Criterion was defined as achieving 70% conditioned responses (CRs) in 50 trials across three consecutive training sessions (A(n-2), A(n−1), and A(n)) or averaging over 70% CRs across the previous four training sessions. After meeting the criterion in environment A, animals were allowed one session of exploration in environment B, followed by two test sessions of trace eyeblink conditioning (B(1) and B(2)) in environment B.

b. (Top) Schematics of environments A and B. Environment A is a rectangular enclosure with wire walls, floor, and ceiling, lit with white light, and unscented. Environment B is oval-shaped with solid white floors and walls, without a ceiling, lit with red light, and scented with clove oil. Both environments provided distal cues visible from the top and sides. (Bottom) Animal trajectories in environments A and B during a single session, extracted using DeepLabCut.

c. Trace eyeblink conditioning (tEBC) paradigm. A 250 ms tone (conditioned stimulus, CS) was followed by a 500 ms trace interval, then a 100 ms eyelid shock (unconditioned stimulus, US). Eyelid activity was recorded using an EMG electrode implanted above the eye. Untrained animals only blinked in response to the US (unconditioned response, UR); trained animals began blinking during the trace interval after the CS and before the US (conditioned response, CR).

d. Performance of animals (n=5) in the tEBC task. Animals learned tEBC while freely moving in environment A and successfully transferred this learning to environment B. The dotted line indicates the performance criterion. No significant difference was found between performance in the criterion sessions in environment A (mean 74.75 ± 6.49%) and the test sessions in environment B (mean 77.70 ± 11.68%; two-tailed t-test, t(24) = −0.83, p > 0.05). Error bars represent standard error.

Animals easily transfer a conditioning task across environments

During the initial phase of our study, freely-moving rats (Fig. 1b) underwent training for trace eyeblink conditioning (tEBC) (Fig. S2), a hippocampus-dependent classical conditioning task that serves as a robust model for associative memory formation^44–47. This paradigm involves presenting a 250ms conditioned stimulus (CS, in the form of a tone) followed by a 500ms trace interval, followed by the 100ms presentation of an unconditioned stimulus (US, an eyelid shock) (Fig. 1c). Both shock and blinking were recorded with wires inserted into the muscle of the eyelid (see Methods). As rats were trained, they exhibited a conditioned blink (CR) to the tone. Animals were considered to have learned the task after reaching criterion (70% CRs in 50 trials) on three consecutive training sessions (termed ‘criterion sessions’) or when the previous four training sessions averaged over 70% (in this instance, only the final three of those sessions were considered ‘criterion sessions’) (Fig. 1d). There was substantial variability in the number of sessions it took to learn the task, for an average of 20±4.2 training sessions (note: number of sessions always includes criterion sessions). The two rats that learned the fastest reached criterion in 14 sessions, and the rat that learned the slowest reached criterion after 24 sessions (Fig. S2). After reaching criterion, the rats were introduced to environment B, where their ability to perform tEBC was assessed over a two-day period (one session per day). Comparative analysis revealed no significant difference in performance (measured in % CRs) between the criterion sessions in environment A and the testing phase in environment B (mean in environment A criterion sessions was 74.75±6.49, mean in environment B test sessions was 77.70±11.68, two tailed t-test(24)=−0.83, p>0.05) (Fig. 1d), indicating the successful transfer of tEBC learning to a new environment.

Calcium imaging (CaImg) enabled the longitudinal monitoring of the same hippocampal cells over multiple sessions in both environments. For criterion and testing sessions, we observed an average of 459.85±265.31 cells per session per animal, with no significant difference between the number of cells recorded in environment A and environment B (two-tailed t-test(24)= −0.56, p>0.05) On average, 132±95 cells were present in both the last criterion session in A and the first testing session in B. This was not a significantly different numbers of cells that were present, on average, in both the semi-final session in A, session A(n−1), and the final session in A, session A(n) (155±115 cells).

Hippocampal place cell representations differ across environments

To identify place cells, we compared actual mutual information (MI) to MI computed after bootstrapping circularly shifted position data 500 times. A cell was deemed a place cell if its MI was above the 95^th percentile of null provided by the bootstrapped MI scores. Using this 95% cutoff, on average, 9.3%±4.2% of cells across criterion sessions in A and testing sessions in B qualified as place cells. There was not a significant difference between the percent of cells that qualified as place cells in environment A and environment B (average in environment A was 8.1%±3.3%, average in environment B was 11.1%±4.9%, two-tailed t-test t(23) =−1.9, p>0.05) (Fig. 2a, Fig. S3). The average mutual information scores across all criterion and testing sessions was 1.08±0.18, with no difference in average MI between environments (environment A mean MI was 1.08±0.17, environment B mean MI was 1.08±0.21, two-tailed t-test t(4805)= −0.5, p>0.05). (See methods for more detailed analysis).

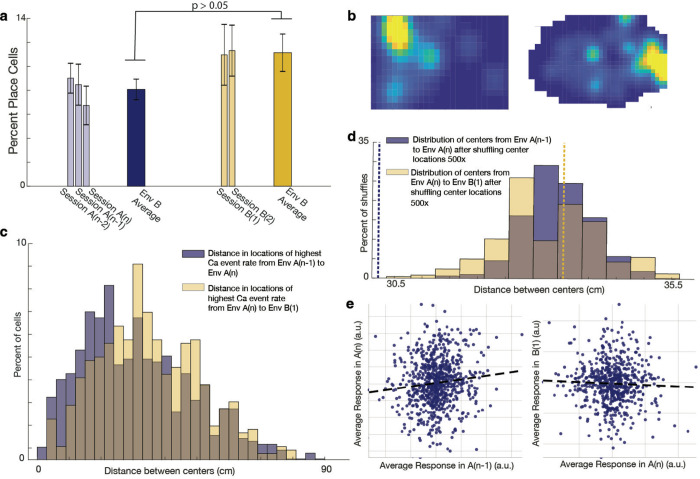
Fig 2. Place cells remap between environment A and environment B.

a. Percent of place cells during criterion sessions in environment A and test sessions in environment B. Light-colored bars represent averages within individual sessions, and dark-colored bars represent overall averages in environments A and B. Overlaid bars indicate standard deviation. On average, 9.3% ± 4.2% of cells were classified as place cells. There was no significant difference in the percentage of place cells between environments A and B (average in environment A: 8.1% ± 3.3%; average in environment B: 11.1% ± 4.9%; two-tailed t-test, t(23) = −1.9, p > 0.05).

b. Example activity map of a specific single cell in environments A and B. Yellow indicates the highest firing rates. This cell exhibited remapping between environments, showing different place fields relative to external cues in the two contexts.

c. Distribution of distances between place field centers (determined by the highest calcium event rate), comparing sessions A(n) and A(n−1) versus sessions A(n) and B(1). Place field centers shifted significantly more when the animal was moved to environment B compared to shifts between two consecutive sessions in environment A (Wilcoxon rank sum test, p = 0.002; two-sided t-test, t(1430) = −2.5, p = 0.01; two-sample Kolmogorov-Smirnov test, p = 3.6 × 10). The brown shaded area represents the overlap between distance histograms.

d. Distribution of the median distance between place field centers after shuffling center locations 500 times. The actual median value for session A(n) to A(n−1) was smaller than all shuffled medians (p = 0, dashed blue line), while the median for session A(n) to B(1) was greater than or equal to 56% of shuffled medians (p = 0.56, dashed yellow line). The brown shaded area represents the overlap between shuffled distributions.

e. Population vector correlation (PVC) based on calcium events for sessions A(n−1), A(n), and B(1). A significant positive correlation was found between sessions A(n−1) and A(n) for cells present in both sessions (p = 0.0023, r = 0.11). In contrast, there was no significant correlation between sessions A(n) and B(1) for shared cells (p > 0.05, r = −0.04). These findings suggest that calcium event patterns are significantly similar between sessions A(n−1) and A(n) but not between session A(n) and B(1). Dashed lines represent lines of best fit. (a.u. = arbitrary units).

Our analysis revealed that individual hippocampal (HPC) cells exhibited distinct spatial representations for environments A and B, altering their configurations of place cells and place fields relative to distal cues — a process known as ‘place cell remapping’ (Fig. 2b). We confirmed this remapping through several approaches. First, we quantified the shift in the location of highest calcium event rate (putative place field centers) by comparing their distances on the last two criterion sessions in environment A (sessions A(n−1) and A(n)) to the shift observed when transitioning from environment A on session n to environment B on session 1 (the centers of both environments were aligned, see methods). The data indicated a significantly greater change in these putative place field centers when the animals transitioned from A to B than when remaining within environment A (medians tested with Wilcoxon rank sum test p=0.002, means tested with double sided t-test t(1430)= −2.5, p=0.01, distributions tested with two-sample Kolmogorov-Smirnov (KS) test, p=3.6*10⁻⁴) (Fig. 2c). Second, to compensate for any differences in environment size, we also compared the distances between field centers to the distances expected if all centers were shuffled 100 times, and found that the median distance between field centers when comparing session A(n) to session A(n−1) was less than all median shuffled values (p=0), while the median distance between field centers when comparing session A(n) to session B(1) was greater or equal than 56% of shuffled values (p=0.56) (Fig. 2d). Third, accounting for the fact that cells may have multiple place fields, we computed the population vector correlation (PVC^40,48,49, see methods) using calcium events for sessions A(n−1), A(n), and B(1). When using cells that appeared in both sessions A(n−1) and A(n), we found a significant positive correlation when computing the PVC for these two sessions (p = 0.0023, r = 0.11). Conversely, when using cells that appeared in both sessions A(n) and B(1), we found no correlation (p>0.05, r=−0.04). This result indicates significantly similar calcium event patterns between sessions A(n−1) and session A(n), with no significant similarity in patterns between session A(n) and B(1). (Fig. 2e).

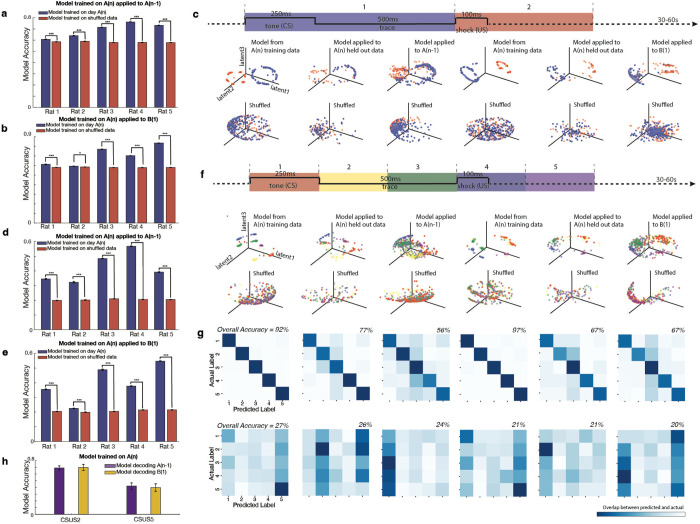
We then used a machine learning algorithm to determine the variation in neural embeddings between environments A and B. To do this, we applied the CEBRA algorithm⁵⁰ to calcium trace imaging data labelled with spatial coordinates from environment A, session A(n) (all were trained on 75% of data with 25% held out for verification). The choice of CEBRA was motivated by its efficacy and interpretability in decoding neural activity patterns when compared to alternative methods such as PCA⁵¹ and Isomap⁵² (see Methods for additional details). We then tested this model’s ability to decode the animals’ position in environment A and environment B when applied to neural data not used for training. The results showed that the model, when run 500 times, predicted the positions in session A(n−1) with significantly greater accuracy than what would be expected by chance; the null was constructed as determined when compared to a model trained on shuffled position data and also run 500x. (All double sided t-tests, for each rat: rat1: t(998): −34.3 p=5.0*10⁻¹⁷¹, rat2: t(998): −72.5 p=0, rat3: t(998)= −1.96 p=0.05, rat4: t(998): −53.7 p=2.6*10⁻²⁹⁹, rat5: t(998): −20.0 p=4.1*10⁻⁷⁵) (Fig. 3a–b). In contrast, when a model trained on data from A(n) was applied to environment B, the model’s predictions were significantly below the accuracy of a model trained on shuffled position data, implying that the place cell coding across environments A and B are actually more different than would be expected by chance (all double sided t-tests, for each rat: rat1: t(998):84.1 p=0, rat2: t(998):18.8 p=7.4*10⁻⁶⁸, rat3: t(998)=74.7 p=0, rat4: t(998):13.1 p=2.0*10⁻³⁶, rat5: t(998):154.4 p=0) (Fig. 3c–d). Collectively, these findings suggest a significant remapping of place cells when transitioning between environments, and also that the neural embeddings for place coding in individual rats change when the animal switches contexts.

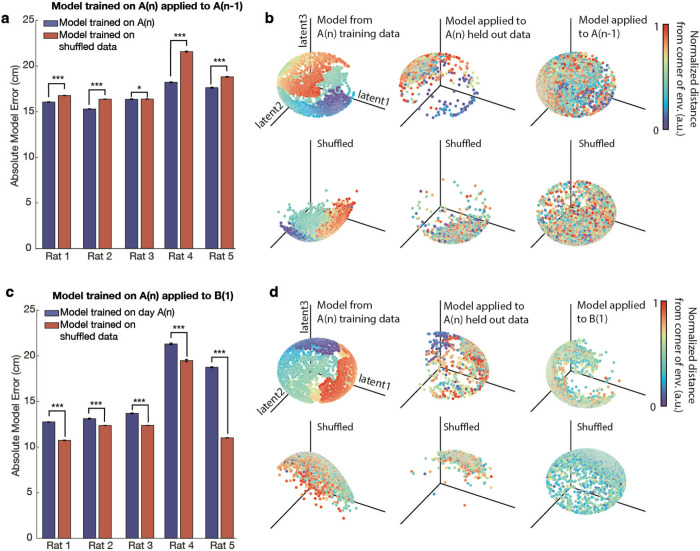
Fig. 3. A model trained in environment A can decode positions within environment A but not in environment B.

a. A model trained on calcium trace and position data from session A(n), using cells present in both A(n) and A(n−1), predicted positions in environment A(n−1) with significantly greater accuracy than that of a model trained on shuffled position data. The model was run 500 times, and the accuracy of predictions was assessed. The model trained on actual data significantly outperformed the shuffled model across rats (double-sided t-tests: Rat 1: t(998) = −34.3, p = 5.0 × 10⁻¹⁷¹; Rat 2: t(998) = −72.5, p = 0; Rat 3: t(998) = −1.96, p = 0.05; Rat 4: t(998) = −53.7, p = 2.6 × 10⁻²⁹⁹; Rat 5: t(998) = −20.0, p = 4.1 × 10⁻⁷⁵). Error bars represent standard error. A single asterisk (*) indicates p ≤ 0.05, and three asterisks (***) indicate p < 10⁻⁷⁴.

b. (Top row) Visualization of model performance for decoding animal position in environment A(n). Left: The trained model demonstrated on the training data from session A(n). Middle: The same model applied to held-out trace data (25%) from session A(n). Right: The model applied to predict animal position in session A(n−1). (Bottom row) The same models trained on shuffled position data. Shown here is the model for Rat 4, where the model trained on real data significantly outperformed model trained on shuffled data for decoding position in session A(n−1) (500 simulations, t(998) = −53.7, p = 2.6 × 10⁻²⁹⁹). For visualization purposes, distance from the corner of the environment is plotted using normalized values in arbitrary units [a.u.].

c. A model trained on data from session A(n), using cells present in both A(n) and B(1), was applied to environment B(1). The model’s predictions were significantly less accurate than those of a model trained on shuffled position data (double-sided t-tests: Rat 1: t(998) = 84.1, p = 0; Rat 2: t(998) = 18.8, p = 7.4 × 10⁻⁶⁸; Rat 3: t(998) = 74.7, p = 0; Rat 4: t(998) = 13.1, p = 2.0 × 10⁻³⁶; Rat 5: t(998) = 154.4, p = 0). Error bars represent standard error. Three asterisks (***) indicate p < 10⁻³⁵.

d. (Top row) Model trained on position and calcium trace data from session A(n), using cells present in both A(n) and B(1). Left: The model demonstrated on the training data from session A(n). Middle: The same model applied to held-out trace data (25%) from session A(n). Right: The model applied to predict the animal position in session B(1). (Bottom row) The same models trained on shuffled position data. Shown here is the model for Rat 4, where the shuffled model performed significantly better than the model trained on session A(n) for decoding position in session B(1) (500 simulations, t(998) = 13.1, p = 2.0 × 10⁻³⁶). For visualization purposes, distance from the corner of the environment is plotted using normalized values in arbitrary units [a.u.].

The hippocampus represents the conditioning task in both environments, and representations of the conditioning task are not spatial representations

We then investigated whether conditioning related data was represented equally in both environments A and B. It was obvious on visual inspection that individual cells varied their calcium event rate (Fig. 4a) and calcium trace (Fig. 4b) during the conditioning periods. To quantify this variation, we devised the metric ‘CSUS mutual information’ (CSUS-MI), analogous to spatial mutual information; this enabled us to assess the extent of task-related information captured by the calcium activity of each cell. We calculated the CSUS-MI for each cell and benchmarked it against a control distribution generated by shuffling CS and US periods and recalculating the MI 500 times. Using calcium event data, we found that 10.7±4.9% of cells held significant CSUS information related to whether the animal was in a CS or US period (termed CSUS-MI2 as the conditioning period was divided into 2 bins; see Methods) (Fig. S4a). An even stronger relationship was noted if using calcium traces: 19.9±8.2 percent of cells contained significant information related to whether the animal was in a CS or US period (Fig. S4a). Importantly, neither of these MI metrics were significantly different between environments A and B (double sided t-tests, using calcium events, t(23)=0.48, p>0.05, using calcium traces, t(23)= −0.52, p>0.05).

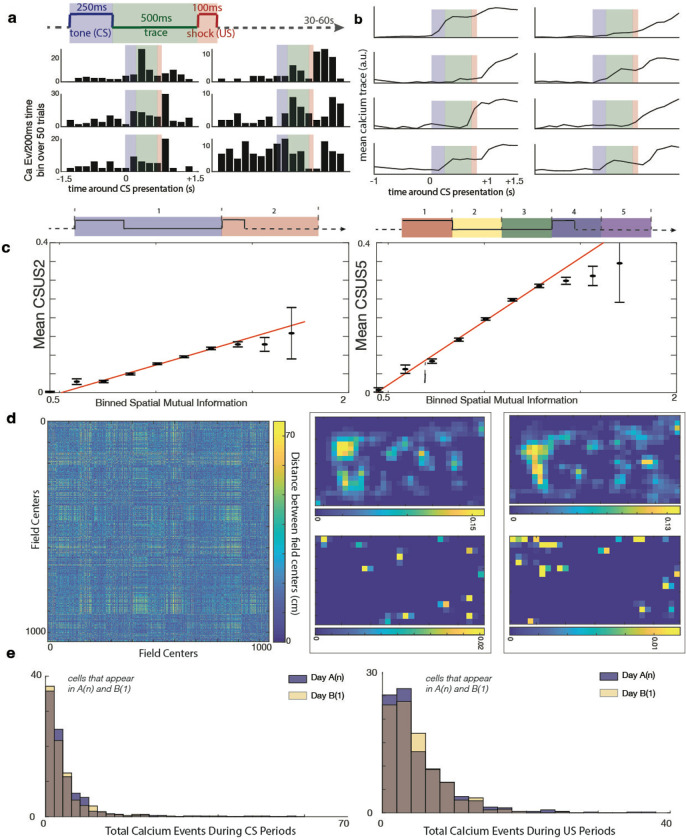
Figure 4. Identifying CS and US modulation in individual cells.

a. Peristimulus time histograms (PSTHs) of six example cells responding to the CS, US, and/or trace period. Bars represent calcium events summed across 50 trials. The shaded regions indicate different stimulus periods: blue (CS), green (trace), and red (US).

b. Mean calcium traces of eight example cells in response to the CS, US, and/or trace period, averaged across 50 trials. Shaded regions are consistent with panel a (a.u. = arbitrary units).

c. Scatter plots illustrating the significant positive correlation between spatial mutual information (MI) and CSUS mutual information (MI). Data points represent binned observations with error bars showing standard errors. The solid red line represents the best fit from a linear regression analysis of the original unbinned dataset. Left: CSUS-MI2 (r² = 0.04, p = 2.1 × 10⁻¹⁰⁴). Right: CSUS-MI5 (r² = 0.09, p = 1.7 × 10⁻²³⁷).

d. Mosaic plots showing the odds ratios for cells modulated by spatial and/or CSUS information. Cells were classified as significantly modulated if their mutual information exceeded 95% of shuffled values. Left: Cells with significant spatial modulation had a 1.35 times higher chance of being significantly modulated by CSUS-MI2 compared to cells without spatial modulation (Fisher’s exact test, p = 0.001). Right: Similar results for CSUS-MI5, where cells with significant spatial modulation had a 1.27 times higher chance of being significantly modulated by CSUS-MI5 (Fisher’s exact test, p = 0.002).

e. Place field remapping during conditioning and non-conditioning periods. (Left) Heat map comparing the spatial distances between place field centers during conditioning (e.g., during CS/US trials) versus non-conditioning periods (e.g., intertrial intervals). Color represents the absolute difference in distances between field centers: regions with minimal color variation (blue) suggest similar place field centers between the two conditions, while more yellow areas represent significant differences in distance (Mantel statistic = 534.58, p > 0.05). (Right) Example of two cells showing spatial calcium activity. Top: Heat maps showing calcium event rates during periods of movement but not conditioning (e.g., intertrial intervals). Bottom: Calcium event rates during CS/US conditioning periods. Dark blue signifies the lowest event rate, and yellow represents the highest event rate. These results show that calcium events during trials are not confined to a cell’s place field.

f. Distribution of calcium events during CS (left) and US (right) periods in sessions A(n) (blue) and B(1) (yellow). No significant difference was observed in hippocampal firing during the CS (left) or US (right) periods between environments A and B (CS: two-tailed t-test, t(1174) = 0.68, p > 0.05; US: two-tailed t-test, t(1174) = 1.20, p > 0.05; KS tests, p > 0.05 for both comparisons).

We then extended this analysis to determine if calcium events or traces of individual cells contained information about what temporal segment portion of the conditioning task the animal was in. To do this, we divided the CSUS period into 5 equal sized bins, computed CSUS-MI using these bins (termed CSUS-MI5, see methods), then compared these mutual information values to the controls provided by shuffled data. Using calcium event data, we found that 15.5±7.8% of cells contained this information, compared to 10.0±7.8% of cells when we calculated the MI using trace information (Fig. S4b). Again, neither of these mutual information metrics were significantly different between environments A and B (double sided t-tests, using calcium event data, t(23)= −0.32, using calcium trace data, t(23)= −1.1, p>0.05). There was not a significant difference in CSUS-MI2 values when comparing values in session A(n) to session A(n−1), versus comparing values in session A(n) to session B(1) (Wilcoxon rank sum test p>0.05, double sided t-test, t(1431)=0.86, p>0.05). In contrast, there was a small but significant difference in CSUS-MI5 when comparing session A(n) to session A(n−1) versus comparing A(n) to session B(1) (Wilcoxon rank sum test p=0.049, double sided t-test, t(1431)=−2.2, p=0.03) (Fig. S4c).Collectively, these results demonstrate that the conditioning task is represented in both environments A and B, and that the percentage of cells representing the conditioning task was not different between the two environments.

We then examined the overlap between cells that contained spatial information and those with CSUS information, identifying a significant positive correlation between spatial MI and CSUS-MI2 (linear regression, r² = 0.04, p=2.1*10⁻¹⁰⁴) and spatial MI and CSUS-MI5 (linear regression, r² = 0.09, p=1.7*10⁻²³⁷; note that the statistics have been computed for unbinned data but the graph presents binned data for visualization purposes due to the large number of points) (Fig. 4c). Further analysis revealed that cells with significant spatial modulation had a significantly higher likelihood of being significantly modulated by CSUS compared to cells without spatial modulation: 1.35 times higher chance of having significant spatial MI if the cell has a significant CSUS-MI2 (Fisher’s exact test, p=0.001) and 1.27 times higher chance if the cell has a significant CSUS-MI5 (Fisher’s exact test, p=0.002). We then inquired whether the calcium events that occurred during conditioning periods were confined to the ‘firing’ fields of place cells. We thus calculated the average location of calcium events during conditioning periods versus the average location during periods of movement that were not conditioning periods. We analyzed this data using the Mantel test, which statistically evaluates the correlation between two distance matrices to determine if the spatial patterns they represent are significantly related. Across all sessions, we found a Mantel statistic of 534.58; we compared this statistic to the result of 10,000 shuffles to determine the statistic was not significant (p>0.05); i.e. the spatial firing patterns during conditioning periods are not generally similar to those that occur during non-conditioning periods (Fig. 4d). In other words, the spatial distribution of firing during conditioning differs fundamentally from that during non-conditioning periods, a result which would not be expected if conditioning related responses were restricted to the cells’ place fields

We next assessed the consistency of task representation across environments. When we compared cells that appeared in both sessions A(n) and B(1), there was no difference in cell responses to either CS or US (double sided t-tests for CS: t(1174) = 0.68 p>0.05 and ks test p>0.05, for US: t(1174) = 1.20 p>0.05, and ks-test p>0.05) (Fig. 4e).

Conditioning task representations are consistent across environments

We then trained a CEBRA model using calcium imaging data and time-stamped CS/US periods from environment A, using only cells that were recorded in both environment A and B. We then used this trained model to decode if the animal was in a CS or US period during an additional session in environment A, as well as in environment B. All models successfully decoded CS and US periods the additional session in environment A, as compared to shuffled data (all double sided t-tests, for each rat: rat1: t(998):6.7 p=2.5*10⁻¹¹, rat2: t(998):16.1 p=7.4*10⁻⁵², rat3: t(998)=83.5 p=0, rat4: t(998):80.1 p=0, rat5: t(998):61.0 p=0) (Fig. 5a,c). All five models significantly outperformed chance level in environment B as determined by shuffled data (all double sided t-tests, for each rat: rat1: t(998):10.4 p=2.6*10⁻²⁴, rat2: t(998):2.7 p=7.6*10⁻³, rat3: t(998)=75.3 p=0, rat4: t(998):63.7 p=0, rat5: t(998):106.3 p=0) (Fig. 5b–c).

Fig. 5. A model trained in environment A can decode CS and US periods in both environment A and B at above chance levels, including fine-grained temporal decoding.

a. A CEBRA model was trained using calcium imaging data and time-stamped CS/US periods from environment A, using only cells that were recorded in both environments A and B. The model was used to decode whether the animal was in a CS or US period in another session in environment A; all models successfully decoded these periods compared to shuffled data (all double-sided t-tests: Rat 1: t(998) = 6.7, p = 2.5 × 10⁻¹¹; Rat 2: t(998) = 16.1, p = 7.4 × 10⁻⁵²; Rat 3: t(998) = 83.5, p = 0; Rat 4: t(998) = 80.1, p = 0; Rat 5: t(998) = 61.0, p = 0). Bars indicate standard error; significance denoted as ***p < 10⁻¹⁰.

b. The same models from panel a were now applied to environment B; they significantly outperformed chance level (all double-sided t-tests: Rat 1: t(998) = 10.4, p = 2.6 × 10⁻²⁴; Rat 2: t(998) = 2.7, p = 7.6 × 10⁻³; Rat 3: t(998) = 75.3, p = 0; Rat 4: t(998) = 63.7, p = 0; Rat 5: t(998) = 106.3, p = 0). Error bars represent standard error, *p < 10⁻³, ***p < 10⁻¹⁰.

c. (Top row) A CEBRA model trained on CS/US periods, divided into two time bins (data from Rat 4). For the top first three graphs, the model was trained using position and calcium trace data from session A(n), using cells present in both A(n) and A(n−1). First graph: The trained model applied to training data from session A(n). Second graph: The model applied to decode CS/US periods from held-out data (25%) from session A(n). Third graph: The model applied to session A(n−1). For the top last three graphs, the model was trained using position and calcium trace data from session A(n), using cells present in both A(n) and B(1). Fourth graph: The trained model applied to training data from session A(n). Fifth graph: The model applied to decode CS/US periods from held-out data (25%) from session A(n). Sixth graph: The model applied to session B(1). (Bottom row) The same model trained on shuffled data. The model trained on data from session A(n) significantly outperformed the model trained on shuffled data in decoding both session A(n−1) and session B(1) (double-sided t-tests, t(998) = 83.5, p = 0, and t(998) = 75.3, p = 0, respectively).

d. A CEBRA model was trained on data from environment A to decode temporal order within the CS, trace, and US periods split into five divisions, applied to an alternate session in environment A (session A(n−1)). The model significantly outperformed chance (all double-sided t-tests for accuracy: Rat 1: t(998) = 41.5, p = 3.3 × 10⁻²²⁰; Rat 2: t(998) = 28.7, p = 7.8 × 10⁻¹³³; Rat 3: t(998) = 122.6, p = 0; Rat 4: t(998) = 118.5, p = 0; Rat 5: t(998) = 62.6, p = 0). Bars indicate standard error; significance denoted as ***p < 10⁻¹⁰.

e. The same five models from panel d were now applied to environment B and outperformed models trained on shuffled data in decoding the temporal aspects of the CS/US periods, indicating that fine-grained temporal encoding is stable across environments (all double-sided t-tests for accuracy: Rat 1: t(998) = 55.1, p = 4.9 × 10⁻³⁰⁵; Rat 2: t(998) = 9.3, p = 1.1 × 10⁻¹⁹; Rat 3: t(998) = 71.4, p = 0; Rat 4: t(998) = 62.6, p = 0; Rat 5: t(998) = 106.2, p = 0). Bars indicate standard error; significance denoted as ***p < 10⁻¹⁰.

f. Same analysis as in panel c, but for a CEBRA model trained on CS/US periods split into five time bins. Top: The five divisions of the conditioning period are shown. Data from Rat 3 show that the model trained on session A(n) outperformed models trained on shuffled data when decoding both session A(n−1) and session B(1) (double-sided t-tests, t(998) = 88.9, p = 0, and t(998) = 71.4, p = 0, respectively).

g. Confusion matrices displaying CEBRA decoding of five CS/US time bins, as shown in panel f. Top row: Models trained on data from session A(n). Bottom row: Models trained on shuffled data. Darker colors along the diagonal indicate higher model accuracy.

h. Model accuracy for decoding sessions A(n−1) and B(1) using a model trained on data from session A(n) with CSUS2 and CSUS5 divisions. For both CSUS2 and CSUS5, a model trained in session A(n) decoded session B(1) with accuracy similar to that achieved when decoding session A(n−1) (CSUS2: double-sided t-test, t(8) = −0.13, p > 0.05; CSUS5: t(8) = 0.32, p > 0.05). Bars represent standard error

We then trained an additional model on data from environment A during session A(n)to ascertain whether it could decode the temporal order within the conditioning period (CSUS5), both in an alternate session in environment A (session A(n−1)) and in environment B (session B(1)). After being trained on session A(n), all models were able to decode environment A(n−1) well better than chance levels (all double sided t-tests for accuracy, for each rat: rat1: t(998):41.5 p=3.3*10⁻²²⁰, rat2: t(998):28.7 p=7.8*10⁻¹³³, rat3: t(998)=122.6 p=0, rat4: t(998):118.5 p=0, rat5: t(998):62.6 p=0) (Fig. 5d,f,g). Remarkably, our results for decoding environment B(1) showed that temporal aspects of CS/US temporal order were decodable across environments, suggesting that a refined level of task encoding is stable across both environments (all double sided t-tests for accuracy, for each rat: rat1: t(998):55.1 p=4.9*10⁻³⁰⁵, rat2: t(998):9.3 p=1.1*10⁻¹⁹, rat3: t(998)=71.4 p=0, rat4: t(998):62.6 p=0, rat5: t(998):106.2 p=0; results were also significant compared to those for shuffled data for precision, recall, F1 score, and area under the receiver operating characteristic curve, data not shown, see Methods) (Fig. 5e–g).

Remarkably, for both CSUS2 and CSUS5, the model trained on session A(n) was no less accurate decoding session B(1) than it was decoding session A(n−1) (double sided t-tests, for CSUS2 t(8)=−0.13, p>0.05, for CSUS5, t(8)=0.32, p>0.05) (Fig. 5h).

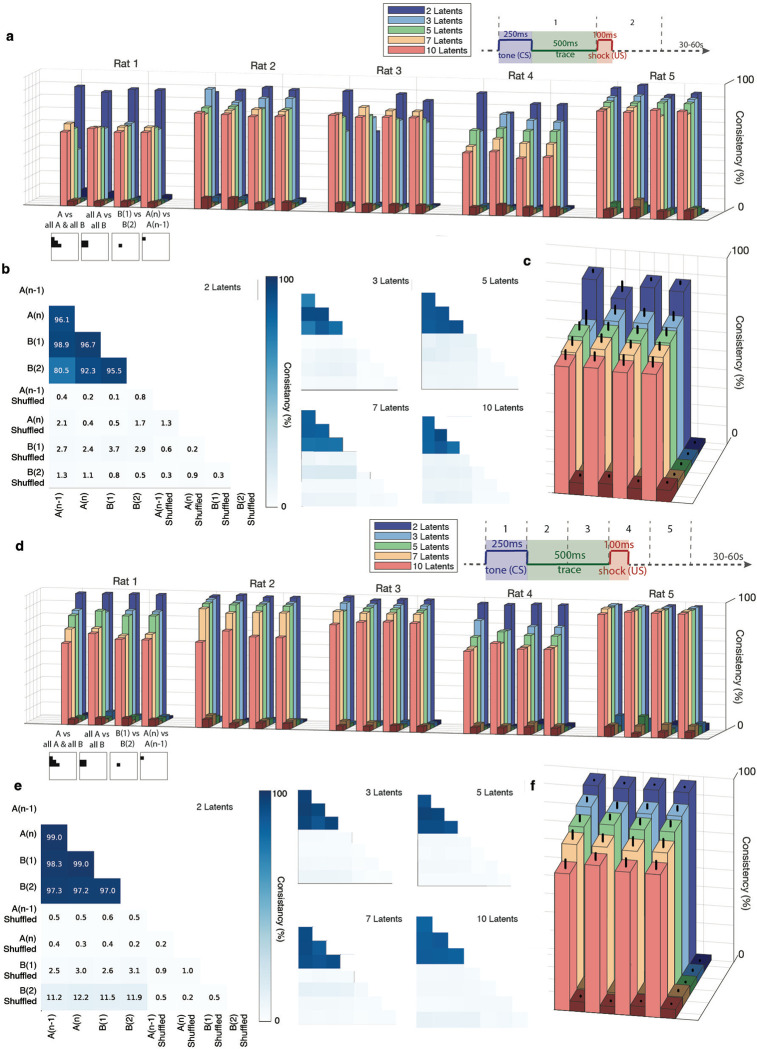
We then used CEBRA to analyze the embedding geometries of cell representations during CS/US periods in both environments. First, we examined the embedding geometries for the conditioning task divided into CS and US periods (CSUS2), for 2, 3, 5, 7, and 10 latents. We compared sessions A(n−1), A(n), B(1), and B(2) to each other, as well as shuffled versions of each session.

For all 5 rats, the geometries displayed a high and significant degree of similarity as compared to the shuffled control. This significance was maintained when examining up to 10 latents, the largest number of latents we utilized (averaging results from all animals, all double sided t-tests, for 2 latents all comparisons were p<1*10⁻⁵, for 3 latents p<1*10⁻⁴, for 5 latents p<1*10⁻⁵, for 7 latents p<1*10⁻⁵, and for 10 latents p<1*10⁻⁴) (Fig. 6a–c). This high degree of similarity was maintained when the CS/US periods were divided into 5 segments (CSUS5, (all double sided t-tests, for 2 latents all comparisons were p<1*10⁻¹², for 3 latents p<1*10⁻⁷, for 5 latents p<1*10⁻⁶, for 7 latents p<1*10⁻⁵, and for 10 latents p<1*10⁻⁵) (Fig. 6d–f).

Fig 6. High consistency in neural representations between environments A and B.

a. Consistency scores for each rat, calculated with 2, 3, 5, 7, and 10 latents. Lighter bars represent consistency percentage for actual data, while adjacent darker bars represent consistency for shuffled data. The schematic below the x-axis illustrates the data sets included in each comparison (for position and labelling of data sets see figure 6b). For the CSUS2 division of conditioning periods (split into CS and US components), all five rats show significantly higher consistency between environments A and B in the actual data compared to shuffled data. This consistency remains significant with up to 10 latents.

b. Example consistency measurements from Rat 5 for CSUS2 with 2, 3, 5, 7, and 10 latents.

c. Average consistency scores across all rats for CSUS2. The figure legend follows the format of panel a. Bars represent standard error. Consistency scores for actual data versus shuffled data were significantly different across all latent dimensions (all double-sided t-tests: 2 latents, p < 1 × 10⁻⁵; 3 latents, p < 1 × 10⁻⁴; 5 latents, p < 1 × 10⁻⁵; 7 latents, p < 1 × 10⁻⁵; 10 latents, p < 1 × 10⁻⁴).

d. Consistency scores for each rat, as in panel a, but for CSUS5, where the conditioning period is divided into five time bins. All five rats show significantly higher consistency between environments A and B in the actual data compared to shuffled data; this is maintained across latents for up to 10.

e. Example consistency measurements from Rat 3 for CSUS5 with 2, 3, 5, 7, and 10 latents.

f. Average consistency scores across all rats for CSUS5. The figure legend matches that of panel c. Bars represent standard error. Significant differences between actual and shuffled data were observed for all latent dimensions (all double-sided t-tests: 2 latents, p < 1 × 10⁻¹²; 3 latents, p < 1 × 10⁻⁷; 5 latents, p < 1 × 10⁻⁶; 7 latents, p < 1 × 10⁻⁵; 10 latents, p < 1 × 10⁻⁵).

These highly significant similarity signifies that the neural representations of the task were consistent between environments A and B.

Conditioning task representations are consistent across animals

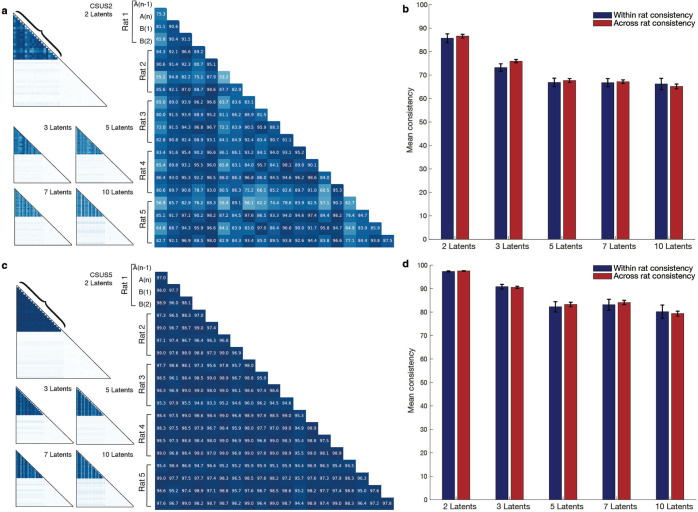
Considering the similarity between representations of the task in environments A and B, we wondered if there was a universal, inter-animal, representation of the conditioning task. To answer this question, we investigated if there were coding similarities of the conditioning task across subjects. For each animal, we developed a unique model based on calcium signal patterns and the structure of the conditioning task. We then calculated a similarity score among all animal-specific models. We observed a markedly significant consistency across these trained models compared to those trained on shuffled data. Notably, this consistency was apparent in models trained to differentiate between CS and US periods, as well as in more granular models that recognized five discrete time segments during CS presentation, the trace interval, and US delivery (akin to the models in Figures 6d–g). When the conditioning period is divided into 2 periods (CSUS2), the similarity across animal models is not significantly different than the similarity between models in one animal for all tested number of latents (2 latents: ttest(188) = −0.45 p>0.05, 3 latents: ttest(188) = −1.57 p>0.05, 5 latents: ttest(188) = −0.40 p>0.05, 7 latents: ttest(188) = −0.22, p>0.05, 10 latents: ttest(188) = 0.40, p>0.05) (Fig. 7a–b). This relationship also holds when the conditioning period is divided into 5 periods (CSUS5): the similarity across animal models is not significantly different than the similarity between models in one animal (2 latents: ttest(188) = −0.79 p>0.05, 3 latents: ttest(188) = 0.25 p>0.05, 5 latents: ttest(188) = −0.42 p>0.05, 7 latents: ttest(188) = 0.70, p>0.05, 10 latents: ttest(188) = 0.30, p>0.05) (Fig. 7c–d).

Figure 7. High degree of consistency between the conditioning representations across animals.

a. Consistency across animals for CSUS2 with 2, 3, 5, 7, and 10 latents. The larger graph highlights the bracketed area from the graph with two latents.

b. Conditioning period is divided into 2 time bins (CSUS2): the similarity between models across animals is not significantly different from the similarity between models for an individual animal, regardless of the number of latents (2 latents: t(188) = −0.45, p > 0.05; 3 latents: t(188) = −1.57, p > 0.05; 5 latents: t(188) = −0.40, p > 0.05; 7 latents: t(188) = −0.22, p > 0.05; 10 latents: t(188) = 0.40, p > 0.05). Error bars represent standard error.

c. Consistency across animals for CSUS5 with 2, 3, 5, 7, and 10 latents. The larger graph highlights the bracketed area from the graph with two latents.

d. Conditioning period is divided into 5 time bins (CSUS5); the similarity across animal models remains comparable to that for within-animal models, regardless of the number of latents (2 latents: t(188) = −0.79, p > 0.05; 3 latents: t(188) = 0.25, p > 0.05; 5 latents: t(188) = −0.42, p > 0.05; 7 latents: t(188) = 0.70, p > 0.05; 10 latents: t(188) = 0.30, p > 0.05). Error bars represent standard error.

Discussion

Our study provides significant insights into hippocampal function, as it demonstrates that the hippocampus not only responds to environmental change with changes in neural coding but also maintains consistent task-related information across varying contexts. These mechanisms underpin cognitive flexibility and the ability to apply learned behaviors in new situations. Below we will discuss this interplay between variability and consistency of representations through several theoretical lenses, including predictive coding and cognitive mapping theories, while exploring the stability of these processes within and across subjects.

Task abstraction across environments

A critical aspect of our study highlights that the hippocampus retains stable task representations, such as those required for eyeblink conditioning, despite variations in environmental contexts. This ability to generalize learned tasks across different settings supports models that posit a cognitive map that extends beyond simple spatial navigation, such as the Tolman-Eichenbaum Machine’s (TEM)⁵³. According to this model, “spatial” maps integrate task-related information and enable the hippocampus to utilize learned behaviors in novel environments that share cognitive demands but differ in sensory or environmental specifics. This flexible functionality exemplifies the hippocampus’ role in abstracting and applying learned knowledge, a hallmark of high-dimensional cognitive mapping. This integrated framework facilitates the adaptation of learned behaviors across diverse contexts, an essential capability for navigating both physical and abstract environments.

Our findings further reveal that the hippocampus abstracts task-related information from the surrounding sensory environment and suggests that the hippocampus connects experiences across different contexts by recognizing underlying similarities; these features help generalize learning and adjust behavior. Our results thus support the TEM’s perspective that the hippocampus can encode higher-order, abstract information crucial for task execution. The ability to detach task representation from immediate sensory inputs allows for a generalized version of learned information^54–56, enhancing the hippocampus’s utility in supporting the organism’s application of learned skills and behaviors in new albeit similar situations^55,56. This capacity for abstraction is indicative of a sophisticated neural coding mechanism and of an adaptable and extensive cognitive mapping system, as it provides a buffer against potential interference that could arise from the myriad of sensory stimuli an organism encounters. By maintaining a conceptual, generalized version of learned information, the hippocampus supports the organism’s ability to apply learned skills and behaviors in new situations that share underlying similarities with previous experiences but differ in sensory or contextual details.

Pattern Separation vs. Completion

Evidence from various areas of neuroscience has led to the development of a theory of HPC function holding that the HPC treats states that involve equivalent actions or relationships such as similar tasks as equivalent, resulting in learning that is easily transferred between environments^{53–55,57,58}. This theory contrasts with the theory that the HPC acts primarily to perform competitive “pattern separation”^59–63. The prevailing theory as well as the cellular and systems level bases for contextual memory remain to be elucidated. In our study, the distinct coding of different environments by hippocampal place cells provides evidence for pattern separation: the hippocampus differentiates between distinct contexts. This separation reduces interference between memories, allowing for more accurate recall based on specific environmental cues. On the other hand, consistent decoding of the eyeblink task across different environments suggests pattern completion. This process allows the hippocampus to reconstruct a complete memory or learned response from partial or generalized cues, enabling the execution of the learned task even when contextual details change.

Our results complement previous work that identifies the HPC as both a pattern completer and a pattern separator. Studies have demonstrated that place cells can differentially represent the same environment when task demands change^61,64,65, yet show similar firing patterns when locations have similar task demands⁶⁶. In more recent work⁶⁷, rats were exposed to two distinct environments while performing variations of the same task: approaching object A in the first environment and object B in the second; the study revealed anticorrelated hippocampal firing patterns for events in the two contexts. This suggests that the hippocampus encodes context-specific associations between items and locations, rather than just specific behavior. This study underscored the role of the hippocampus in robust pattern separation when environments differ but require similar behaviors, showing that even minor task variations can lead to significant neuronal pattern separation⁶⁷. In contrast, our study used a task that remained identical across both environments and found consistent hippocampal population-level task representations in both contexts. This consistency likely reflects that the task could be generalized between environments, without necessitating the hippocampus to differentiate between task demands. Therefore, the hippocampus seems to balance pattern separation and completion based on how similar or distinct task demands are across different contexts.

Non-spatial hippocampal representations

There is ongoing debate about whether hippocampal pyramidal cells encode both spatial and non-spatial aspects of a context^39,68,69. Our findings show that responses to the conditioning task were independent of place field location, with a fraction of the recorded individual cells found able to represent both spatial location and the conditioning task (Fig. 4). This contrasts with studies where conditioning responses were more closely tied to specific spatial locations^70,71. The difference likely stems from task design: in previous studies, spatially contingent rewards or freezing behavior after a shock made location highly salient, by associating the place where the shock occurred with the aversive event. In our experiment, spatial position was irrelevant; this allowed pyramidal cells to encode task-relevant features independent of location. This finding aligns with previous work showing that hippocampal cells often respond to non-spatial aspects like sensory cues or task demands, particularly in non-spatial tasks^19,72–74.

The discovery that population level patterns in the hippocampus are organized into manifolds provides an elegant solution to the problem of single cells representing both spatial coordinates and task features. Previous hippocampal work has described distinct encoding for spatial location along the center stem of a T maze vs accumulation of evidence for a left-right turning decision at the end of this branch through two distinct, orthogonal directions in a two-dimensional neural manifold⁷⁵. Other brain regions, such as the prefrontal cortex and cingulate cortex, appear to use a similar orthogonal coding strategy^76–78; this strategy has also emerged in neural network simulations of a context-dependent classification task⁷⁹.

Intra-Subject and Inter-Subject Consistency

The stability of neural representations within subjects across different testing sessions indicates that once hippocampal circuits are trained, their functional architecture remains remarkably consistent, even in varying contexts. This intra-subject consistency supports theories suggesting that neural circuits are not just reactive but possess a robust, predefined role in processing and responding to specific stimuli^80,81. Furthermore, the observation of similar neural encoding patterns across different animals performing the same task suggests a species specific, possibly evolutionary conserved, neural code^80,81. These findings highlight a generalized neural processing strategy that may have been shaped by natural selection to optimize cognitive and behavioral responses across environmental challenges faced by a species. Such a generalized coding strategy may be indicative of evolutionary pressures that have favored neural mechanisms promoting cognitive flexibility and rapid adaptation to environmental challenges^82–84.

The results of our study highlight the preservation of hippocampal task encoding across different contexts and species; this presents a surprising parallel to recent findings in motor cortex^85,86 and insular cortex⁸⁷. Motor functions, especially those fundamental to survival and interaction with the physical environment, are expected to exhibit conserved neural dynamics due to their innate and reflexive nature; motor tasks typically involve stereotyped and predictable patterns of behavior that are essential for immediate responses and interactions with the environment^88–91. Similarly, the motivational states preserved across animals in the insular cortex are those central to basic biological needs, such as thirst and hunger. These states and tasks are often highly conserved across individuals because they rely on well-established neural circuits that perform specific, crucial functions necessary for survival^89,91–95.

In contrast, hippocampal tasks involve complex cognitive processes that include memory, learning, and spatial navigation; these require a higher degree of cognitive flexibility^83,96–98. and are generally influenced by individual experiences (and, at the species level, specific ecological and evolutionary pressures)^99–103. Therefore, the conservation of hippocampal task encoding across different individuals, as observed in our study, challenges these traditional views and suggests a deeper, possibly adaptive significance to these cognitive functions.

The surprising conservation of the neural representation of tasks within the hippocampus suggests that certain aspects of cognitive mapping and memory processing might be as evolutionarily essential as motor functions. This conservation might reflect universal cognitive strategies that are critical for survival across a range of environmental contexts, providing individuals within a species with the ability to adapt behavior based on past experiences and anticipated future conditions. Such a mechanism would not only enhance an organism’s ability to navigate complex environments but also facilitate learning and decision-making across generational timescales.

Conclusion

The consistent decoding of eyeblink conditioning tasks across different environmental contexts indicates that the hippocampus can maintain a stable representation of task-specific information irrespective of the external sensory environment. This suggests an advanced capability for abstract cognitive mapping, where the hippocampus constructs and utilizes cognitive maps not only for physical locations but also for abstract tasks and concepts, allowing for effective application in varying contexts. These findings expand our understanding of how memories are formed, stored, and retrieved. They suggest that memories are not just static recollections of past events but dynamic and adaptable representations that can be applied to new situations.

Methods

LEAD CONTACT AND MATERIALS AVAILABILITY

Questions and requests for information should be directed to and will be fulfilled by the Lead Contact, Hannah Wirtshafter (hsw@northwestern.edu). This study did not generate new unique reagents. The data that support the findings of this study are available from the corresponding author.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All procedures were performed within Northwestern Institutional Animal Care and Use Committee and NIH guidelines. Five male Long Evans rats (275–325 g) were sourced from Charles River Laboratories, injected with AAV9-GCaMP8m, implanted with a 2-mm GRIN lens, and trained and tested on eyeblink conditioning in two apparatuses (Fig. 1). Animals were individually housed in an animal facility with a 12/12 h light/dark cycle.

METHOD DETAILS

GCaMP7c injection, lens implantation, EMG implantation

GCaMP8 injection and lens implantation were completed as reported in Wirtshafter and Disterhoft, 2022 and Wirtshafter and Disterhoft, 2023^1,2. Briefly, rats were anesthetized with isoflurane (induction 4%, maintenance 1–2%) and a craniotomy was performed at stereotaxic coordinates Bregma AP −4.00mm, ML 3.00mm. 0.06uL of GCaMP8m (obtained from AddGene, packaged AAV9 of pGP-AAV-syn-jGCaMP8m-WPRE, lot v175525, titer 1.3E+13 GC/mL) was injected over 12 minutes (approximate coordinates Bregma AP −4.00mm, ML 3mm, DV 2.95mm relative to skull); then the syringe was raised 0.2mm and an additional 0.6ul of GCaMP7 was injected. We repeated this process once more and at slightly different coordinates in the craniotomy hole, resulting in 4 total injections.

We then aspirated tissue from the craniotomy site using a vacuum pump and 25 gauge needle. Tissue was aspirated up to and including the horizontal striations of the corpus collosum. A 2mm GRIN lens (obtained from Go!Foton, CLH lens, 2.00mm diameter, 0.448 pitch, working distance 0.30mm, 550nm wavelength) was then inserted into the craniotomy hole and cemented in place using dental acrylic. Animals were given buprenorphine (0.05mg/kg) and 20mL saline, taken off anesthesia, and allowed to recover in a clean cage placed upon a heat pad.

Six to eight weeks after surgery, animals were again anesthetized with isoflurane and checked for GCaMP expression. If expression was seen, baseplates were attached using UV-curing epoxy and dental acrylic. Electrode implantation to record obicularis oculi electromyographic (EMG) activity occurred in the same surgery as baseplate attachment, as described previously^3,4. Briefly, a connector containing 5 wires was cemented on the front of the animal’s head: 4 wires were implanted directly above the eye in the surrounding muscle (2 for recording, 2 for electrical stimulation). An additional wire was attached to a connector attached to a ground screw located above the cerebellum; this screw was implanted during lens implantation surgery.

Behavioral environment and training

Two behavioral apparatuses were used in these experiments: Environment A was a 78.7cm × 50.8cm unscented rectangular enclosure with wire floor and walls and white lighting. Environment B was a 50.1cm × 34.9cm scented (with two dabs of clove essential oil on opposite walls) ovular enclosure with white solid floor and walls, and red lighting. Both environments were located at the same spot in the room relative to external cues (see Figures 1b and S1).

A tether containing a plug to relay the EMG activity and to deliver a shock to the rat’s eye was attached to a the eyeblink connector on the rat’s head. The miniscope was plugged into the cemented baseplate. The miniscope and EMG cords were all attached to a commutator for ease of animal movement.

The CS was a 250ms, 85dB free-field tone (5ms rise-fall time). The US was a 100ms shock directed to the left eye. Shock amount varied per session per animal and was calibrated, if needed, at the end of a training session for the next session’s training. Shock level was deemed appropriate when a shock was met with a firm shake of the animal’s head.

The trace interval was 500ms and the intertrial interval (ITI) was randomized between 30s and 60s, with a 45s average. EMG signal output was amplified (5000×) and filtered (100 Hz to 5 kHz), then digitized at 3 kHz and stored by computer.

A conditioned response (CR) was identified as an increase in integrated EMG activity that exceeded the baseline mean amplitude by more than four standard deviations, sustained for a minimum duration of 15ms. Baseline mean amplitude was calculated during the 500ms preceding CS onset. Additionally, the response had to commence at least 50ms after the conditioned stimulus (CS) onset and before the unconditioned stimulus (US) onset.

The animal’s first exposure to each environment was a 38min exploration session, in which the animal was able to freely move and explore the environment without any conditioning (Figure 1a). Animals were then trained in one environment per session, with no more than one session per day, and were considered to have learned the task after reaching criterion (70% CRs in 50 trials) on three consecutive training sessions (termed ‘criterion sessions’) or when the previous four training sessions averaged over 70% (in this instance, only the final three of those sessions were considered ‘criterion sessions’). Following the last session in environment A, the animal was given an exploratory session in environment B. The session after that, the animal was tested on eye blink conditioning in environment B, using the same parameters as used in environment A.

Calcium imaging

Calcium imaging was completed as reported in Wirtshafter and Disterhoft, 2022 and Wirtshafter and Disterhoft, 2023^1,2. Briefly, calcium imaging was done using UCLA V4 Miniscopes^5,6, assembled with two 3mm diameter, 6mm FL achromat lens used in the objective module and one 4mm diameter, 10mm FL achromat lens used in the emission module.

QUANTIFICATION AND STATISTICAL ANALYSIS

Means are presented as mean+-standard deviation. All analysis code is available at https://github.com/hsw28/ca_imaging and https://github.com/hsw28/Hannahs-CEBRAs. Code to create specific figures is also available at the former github repository.

Position and speed analysis

Position was sampled by an overhead camera at 30Hz. Position tracking was done post-recording using DeepLabCut⁷. Position was then converted from pixels to cm. Position was smoothed using a Gaussian filter with standard deviation of 2cm. Speed was calculated by taking the hypotenuse of the coordinates one before and after the time of interest.

Video pre-processing and cell identification

Video pre-processing and cell identification were performed as reported in Wirtshafter and Disterhoft, 2022 and Wirtshafter and Disterhoft, 2023^1,2. In brief, videos were recorded with Miniscope software at 15frames/second. Video processing was done using CIATAH software⁸. Videos were down sampled in space and normalized by subtracting the mean value of each frame from the frame. Each frame was then normalized using a bandpass FFT filter (70–100cycles/pixel) and motion corrected to a using TurboReg⁹. Videos were then converted to relative florescence (dF/F₀); F₀ was the mean over the entire video.

Cells were automatically identified using CIATAH⁸ using CNMF-E¹⁰. Images were filtered with a gaussian kernel of width 2 pixels and neuron diameter was set at a pixel size of 8. The threshold for merging neurons was set at a calcium trace correlation of 0.65; neurons were merged if their distances were smaller than 4 pixels and they had highly correlated spatial shapes (correlation>0.8) and small temporal correlations (correlation <0.4).

In vivo calcium imaging involves detecting changes in intracellular calcium levels, which serve as proxies for neuronal activity. Calcium events refer to transient increases in calcium concentration above a threshold level; these crossings putatively correspond to spikes in neuronal firing. These events typically appear as peaks in the data and indicate an active response from the neuron. Calcium traces are continuous recordings of calcium levels over time. Thus, calcium events highlight specific neuronal activations, while calcium traces provide a full temporal picture of these activations together with baseline activity.

All cells identified using CNMF-E were then scored as neurons or not by a human scorer. Scoring was also done within CIATAH software in a Matlab GUI. Scoring was done while visualizing and considering a calcium activity trace, average waveform, a montage of the candidate cell’s Ca2+ events, and a maximum projection of all cells on which the candidate cell was highlighted. The relative fluorescence (ΔF/F₀) local maxima of each identified cell were considered calcium event times.

Cell cross registration across sessions and within session

Validation and registration were completed as documented in Wirtshafter and Disterhoft². Briefly, videos underwent five rounds of registration using Turboreg image rotation⁹ with the CIATAH software^8,11. Background noise, axons, and dendrites were removed using an image binarization threshold of 40% of the images’ maximum value. Cells were matched across sessions using a distance threshold of a maximum of five pixels, with a minimum 2-D correlation coefficient of 0.5. Sessions were aligned to session A(n), the last session in environment A.

Place cell identification and computing spatial mutual information

Place cells were identified using mutual information computed when the animals were running at speeds greater than or equal to 4cm/s. MI was computed for all cells; there was no calcium event rate criterion for included cells. To be considered significant, the computed mutual information (MI) must be greater than 95% of MI scores computed 500 times from shuffled positions¹². To compute the MI for each cell, the training environments were divided into 2.5cm × 2.5cm bins. The calcium event rate of each cell and the occupancy of the animal were found for each bin. Rate and occupancy were smoothed with a Gaussian kernel with filter width of 3cm and Sigma of 0.5cm. Mutual information was computed during periods of movement as follows^2,12,13:

$$\mathrm{p}=\frac{{\mathrm{P}}_{\mathrm{s}}}{{\mathrm{P}}_{\mathrm{o}}}$$

$${\mathrm{M}}_{\mathrm{s}}=\sum {\mathrm{P}}_{\mathrm{s}}$$

$${\mathrm{M}}_{\mathrm{o}}=\sum {\mathrm{P}}_{\mathrm{o}}$$

$$\mathrm{M}\mathrm{I}=\sum \mathrm{p}\mathrm{*}{\mathrm{l}\mathrm{o}\mathrm{g}}_2\left(\frac{\mathrm{p}}{{\mathrm{M}}_{\mathrm{s}}\mathrm{*}{\mathrm{M}}_{\mathrm{o}}}\right)$$

where:

${\mathrm{P}}_{\mathrm{s}}=$ calcium event probability in each bin

${\mathrm{P}}_{\mathrm{o}}=$ occupancy probability at each bin

Mutual information using calcium traces was computed as above, except instead of ${\mathrm{P}}_{\mathrm{s}}$ being calcium event probability per bin, the value of ${\mathrm{P}}_{\mathrm{s}}$ was the average value of calcium trace in the bin.

We computed MI using both calcium events and calcium trace data. There was no significant difference between the number of place cells detected using calcium event data and calcium trace data, (paired t-test t(24)=1.01, p>0.05). Note that all place cell and place field measurements are presented with conditioning periods included, as the animal was frequently moving during conditioning periods. We also computed results while excluding conditioning periods and found no significant differences.

Computing CSUS mutual information

The computation of CSUS mutual information was very similarly to that for spatial mutual information. A 1.3 second period beginning at the start of the CS tone was either divided into 2 bins (CSUS-MI2) or 5 bins (CSUS-MI5) (Fig. 3c–3d). Mutual information was then computed using the following:

$$\mathrm{p}=\frac{{\mathrm{P}}_{\mathrm{s}}}{{\mathrm{P}}_{\mathrm{o}}}$$

$${\mathrm{M}}_{\mathrm{s}}=\sum {\mathrm{P}}_{\mathrm{s}}$$

$${\mathrm{M}}_{\mathrm{o}}=\sum {\mathrm{P}}_{\mathrm{o}}$$

$$\mathrm{M}\mathrm{I}=\sum \mathrm{p}\mathrm{*}{\mathrm{l}\mathrm{o}\mathrm{g}}_2\left(\frac{\mathrm{p}}{{\mathrm{M}}_{\mathrm{s}}\mathrm{*}{\mathrm{M}}_{\mathrm{o}}}\right)$$

Where:

${\mathrm{P}}_{\mathrm{s}}=$ calcium event probability in each CSUS bin

${\mathrm{P}}_{\mathrm{o}}=$ probability of individual CSUS occuring out of all CSUS bins

Mutual information using calcium traces was computed as above, except that ${\mathrm{P}}_{\mathrm{s}}$ did not represent the calcium event probability per bin, but the average value of calcium trace within the bin.

Remapping quantification

The place cell center was defined as the occupancy-normalized location with maximum number of calcium events while the animal was moving at 5cm/s or faster. Position was binned into 2.5cm square bins. The place cell centers at environments A and B, as well as at environment A across days and at environment B across days, were used to align each environment across days, as well as to align environment A to environment B.

Population vector correlation was calculated between two environments using calcium event data. Neurons present in both datasets (such as sessions A(n) and A(n−1), or A(n) and B(1)) were identified and their calcium event times were converted to rates using 0.75 second binning. These firing rates were then normalized using z-score normalization across each neuron’s activity across time. The mean calcium event rate for each neuron in each environment was then computed. The correlation among population vectors of firing rates in the two environments was cpmputed:

$$populationvectorcorrelation=\frac{{\sum }_{i=1}^N\left(r_{\left\{i,A\right\}}-\overline{{\left\{r\right\}}_A}\right)\left(r_{\left\{i,B\right\}}-{\overline{\left\{r\right\}}}_B\right)}{\sqrt{{\sum }_{i=1}^N{\left(r_{\left\{i,A\right\}}-\overline{{\left\{r\right\}}_A}\right)}^2}\sqrt{{\sum }_{i=1}^N{\left(r_{\left\{i,B\right\}}-{\overline{\left\{r\right\}}}_B\right)}^2}}$$

Where:

$r_{\{i,A\}}$ and $r_{\{i,B\}}=$ firing rates of neuron $i$ in environments $\mathrm{A}$ and $\mathrm{B}$

${\overline{\left\{r\right\}}}_A$ and ${\overline{\left\{r\right\}}}_B=$ mean firing rates across neurons in environments $\mathrm{A}$ and $\mathrm{B}$

The factors in the denominator correspond to the standard deviation of the components of each population vector relative to their mean, computed in each environment.

Use of CEBRA versus alternative methods

We explored multiple different methods before settling on the use of CEBRA for this study. A short summary of each tested method can be found below:

• Principal Component Analysis (PCA)¹⁴: Principal component analysis (PCA) is a statistical method used to reduce the dimensionality of data while retaining as much variability as possible. This linear technique identifies the axes (principal components) in the dataset that maximize variance. The first principal component explains the most variance, the second explains the second most, and so on. Principal components are combinations of original features and may not always have clear or intuitive meanings. In agreement with previous hippocampal data¹⁵, PCA required upwards of 15–25 components to capture 95% of the variance of the data. In addition, across and within all sessions and representations (spatial and task representations), the manifolds spanned by the largest PCs remained highly similar, with small principal angles in pairwise comparisons. This similarity in the orientation of the leading subspaces suggested that PCA did not distinguish between spatial or behavioral components of the task (Figure S5).

• Independent Component Analysis (ICA)¹⁶: Independent Component Analysis (ICA) is a computational technique used to separate a multivariate signal into additive, independent components. ICA operates under the assumption that observed data are linear mixtures of underlying, independent sources. It aims to find a linear transformation that maximizes the statistical independence of the estimated components. We found that ICA embeddings were unstable throughout the length of the recordings, and also did not clearly map onto behavioral states (Figure S6).

• Isomap¹⁷: Isomap is a manifold learning technique that seeks to capture the intrinsic geometric structure of data. Isomap is useful when linear methods like PCA cannot capture the intrinsic structure of the data, as it preserves the geodesic (curved) distances in the reduced dimensionality space. Unlike linear methods such as PCA, Isomap can capture nonlinear relationships in the data. Interestingly, using Isomap, only about 5 neural modes were required to achieve a residual variance of 5–10%. However, the embedding shape did not relate to any discernable property of neural data or behavior (Figure S7). Dimensionality reduction was achieved, but the resulting representations were not interpretable (Figure S7).

• MIND^15,18: MIND is a decoding method designed for integrating multiple data modalities to predict various features, particularly sensory and motor functions. MIND uses recurrent neural networks whose hidden variables provide a memory mechanism for remembering previous inputs; this approach is particularly apt for the analysis of time series data such as neural recordings. While MIND was very robust at distinguishing the different environments, it was not equipped to handle relatively short signals separated in time, such as the conditioning trials separated by intertrial intervals. Our analyses using MIND resulted in poor and unstable embeddings that could not be analyzed (Figure S8).

CEBRA¹⁹ was chosen for this project for its ability to capture nonlinear relationships in the data and to create stable embeddings over short and long time periods. Additionally, spatial separations of components were well isolated and correlated well with observed behaviors.

Use of CEBRA for position decoding

Optimal parameters for decoding the position of each animal from neural activity were determined using an extensive grid search across learning rate, temperature, and number of iterations (Figure S9). Models created to compare different sessions, such as a model trained on data from session A(n) used to decode session B(1), were only trained on cells that occurred in both sessions. Models were trained on spike traces of these cells, labeled with the animal’s (X,Y) position. In all cases, 75% of data was used to train the model while 25% of data was held out for verification. All models were run 500 times. Optimal embeddings were determined based on the minimum median absolute error between the predicted and true positions. The optimal parameters for each rat are as follows:

	Rat 1	Rat 2	Rat 3	Rat 4	Rat 5
Model Architecture	‘Offset10-model’
Batch size	512
Learning rate	5.5*10−5	6.625*10−4	5.5*10−4	1.0*10−3	1.0*10−3
Temperature mode	‘Auto’
Minimum temperature	No minimum	1.5	0.95	1.0*10−9	No minimum
Output dimensions (# of latents)	3
Max iterations	25000	8000	26500	30000	18000
Distance	‘Cosine’
Conditional	‘Time delta’
Number of hidden units	32
Time offsets	1

The number of output dimensions was chosen based on the fewest number of dimensions under which all 5 models consistently outperformed shuffled data for both position and conditioning decoding (Figure S10–12).

Use of CEBRA for conditioning decoding

As in position decoding, the optimal parameters for decoding conditioning were determined for each animal using an extensive grid search across learning rate, temperature, and number of iterations (Figure S11). Models created to compare different sessions of neural activity, such as a model trained on data from session A(n) used to decode session B(1), were only trained on cells that occurred in both sessions. Models were trained on spike traces of these cells, with labels corresponding to the CSUS bin during which the signal occurred (either one out of 2 bins or out of 5 bins, see Figures 3c–d). In all cases, 75% of data was used to train the model while 25% of data was held out for verification. All models were run 500 times. Optimal embeddings were determined based on the percent of correctly binned time points. The optimal parameters for each rat are as follows:

	Rat 1	Rat 2	Rat 3	Rat 4	Rat 5
Model Architecture	‘Offset10-model’
Batch size	512
Learning rate	3.5*10−3	7.0*10−3	3.5*10−3	7.5*10−3	9.5*10−3
Temperature mode	‘Constant’	‘Constant’	‘Auto’	‘Constant’	‘Constant’
Minimum temperature	2.33	1.75	1.67	1.67	2.66
Output dimensions (# of latents)	3
Max iterations	50000	7500	20000	18000	25000
Distance	‘Euclidian’	‘Cosine’	‘Cosine’	‘Euclidian’	‘Cosine’
Conditional	‘Time delta’
Number of hidden units	32
Time offsets	1

The number of output dimension was chosen based on the fewest number of dimensions under which all 5 models consistently outperformed shuffled data for both position and conditioning decoding (Figure S10–12). The parameters listed above were used for decoding into 2 or 5 bins, including the use of 3 output dimensions (# of latents).

The accuracy of results was computed from the entries in the confusion matrix:

$$Accuracy=\frac{\mathit{Sum}\mathit{of}\mathit{number}\mathit{of}\mathit{diagonal}\mathit{(correct)}\mathit{elements}}{\mathit{Sum}\mathit{of}\mathit{number}\mathit{of}\mathit{total}\mathit{elements}}$$

Precision was calculated for each class $i$, $1\le i\le n$, where $n$ is the number of classes:

$${\mathit{Precision}}_i=\frac{\left(T{P}_i\right)}{T{P}_i+F{P}_i}$$

where:

$$TP=truepositives$$

$$FP=falsepositives$$

The global precision is given by the average:

$$\mathit{Precision}=\frac{1}{n}\sum _{i=1}^n{\mathit{Precision}}_i$$

Recall, also known as sensitivity, was calculated for each class $i,1\le i\le n$, where $n$ is the number of classes:

$${\mathit{Recall}}_i=\frac{\left(T{P}_i\right)}{T{P}_i+F{N}_i}$$

where:

$$TP=truepositives$$

$$FN=falsenegatives$$

The global recall is given by the average:

$$\mathit{Recall}=\frac{1}{n}\sum _{i=1}^n{\mathit{Recall}}_i$$

The $\mathrm{F}1$ score was calculated for each class $i$, $1\le i\le n$, where $n$ is the number of classes:

$$F{1}_i=2\mathrm{*}\frac{{\mathit{Precision}}_i\mathrm{*}{\mathit{Recall}}_i}{{\mathit{Precision}}_i+{\mathit{Recall}}_i}$$

The global $\mathrm{F}1$ score is given by the average:

$$F1=\frac{1}{n}\sum _{i=1}^{n}F{1}_i$$

The area under the receiver operating characteristic (ROC) curve was calculated for each class $i,1\le i\le n$, where $n$ is the number of classes:

$$AU{C}_i=\mathit{roc\_auc\_score}\left(y_{\mathit{true-bin}}[:,i],y_{\mathit{pred-prob}}[:,i]\right)$$

The global value is given by the average:

$$\mathit{ROC}AUC=\frac{1}{n}\sum _{i=1}^{n}AU{C}_i$$

where:

$$y_{\mathit{true-bin}}=\mathit{binarized}\mathit{true}\mathit{labels}$$

$$y_{\mathit{pred-prob}}=\mathit{predicted}\mathit{probabilities}\mathit{for}\mathit{each}\mathit{class}$$

Model consistency

Model consistency was computed using a built-in CEBRA function which relies on the function ‘sklearn.metrics.consistency_score’²⁰. The function compares the embeddings from different models by calculating pairwise consistency scores. This comparison involves measuring the similarity of the embeddings using statistical metrics; i.e. this metric calculates how similar a model’s labels are for similar instances in the data set.

To determine consistency between environments and across animals, the data was fit to each model 20 times. The model with the lowest loss was selected and compared to other models with the lowest loss. Models were created using each individual animal’s optimal parameters (see above).