Ultrasonic chemical synthesis of zinc-manganese ferrites with improved magnetic properties

Highlights

• •Zinc-Manganese spinel ferrites nanoparticles were synthesized using sonochemical synthesis method.
• •The more mixed was the phase, the more stable it was.
• •Improved magnetic properties were due to a systematic ionic movement that promote super-exchange interactions.

Abstract

Zinc-Manganese spinel ferrites (Zn_1-xMn_xFe₂O₄) are nowadays very attractive magnetic materials for cancer diagnostic and therapy. With the help of intense ultrasonic waves, sonochemical synthesis method was used to prepare stoichiometric and chemically homogenous nanoparticles by varying the manganese content. The crystal structure along with the size and shape of the as-prepared nanoparticles were described using XRD, TEM and FT-IR techniques, while cations distribution was carefully investigated using XPS and Mössbauer spectroscopic techniques and supported with density functional theory calculations. The crystal structure study revealed the presence of a pure single cubic spinel phase, where the unit-cell and the size were observed to decrease as the manganese incorporation was increased with clear indication of cationic redistribution and degree of inversion variations. Due to the very small variation of the total energy between different configurations, the probability of formation of a mixed phase was found to be very high in such a way that the more mixed was the phase, the more stable it was. A relevant fact was the noticed quasi-systematic ionic exchange made possible by the very short reaction times and high energy offered by the ultrasonic waves. For manganese concentrations up to 60%, the systematic ionic process started by incorporating manganese ions into octahedral sites and pushing iron ions to migrate and replace those of zinc in tetrahedral sites. Such an ionic movement was of central importance for the improvement of the magnetic properties due to the establishment of super-exchange interactions. Such an ionic engineering should definitely open the way to promising applications in biomedical imaging.

1. Introduction

Due to their unique properties such as low coercivity [1], high value of initial permeability [2], high saturation magnetization [3], low power loss [4] and high magnetic induction [5], Zinc-Manganese (Zn-Mn) spinel ferrites have received a great attention as new highly effective magnetic media for cancer diagnostic and therapy [6], [7] Nevertheless, all these properties remain highly dependent on the occupancy of certain specific crystallographic sites which are distributed across a relatively complex atomic arrangement. In effect, the spinel structure, known as AB₂O₄, possesses a cubic lattice that includes 8 tetrahedral (A) and 16 octahedral (B) occupied sites. To consider the site occupancy feature, the spinel ferrite structure can be described as [M²⁺_1-δ Fe³⁺_δ]^A [M²⁺_δ Fe³⁺_2-δ]^B O₄, where metal (M) and ferric ions occupy A and B sites as a function of the inversion degree δ. In a normal (or direct) spinel (δ = 0), all of the M cations are in A sites, while in an inverse spinel (δ = 1) they occupy the B sites. When 0 < δ < 1, that is; metal and ferric ions occupying both A and B sites, the spinel ferrite is mixed. The magnetic properties of Zn-Mn spinel ferrites are therefore largely dependent on the Zn and Mn cations distribution, between the A and B sites, since the net magnetization of the lattice is given as the disparity in magnetization values between the B- and A-sublattices as a result of the occurrence of super-exchange interactions [8].

A series of methods have enabled the synthesis of Zn-Mn spinel ferrite nanoparticles, such as ball milling [9], co-precipitation [10], sol–gel [11], hydrothermal [12], thermal decomposition [13] and micro emulsion [14] Although all of these methods have demonstrated a reasonable control of the nanoparticles size and dispersion, they nevertheless suffer from controlling the occupancy of tetrahedral and octahedral sites due to their long reaction time, and the use of large doses of surfactant and complex molecules [15] In this sense, the sonochemical route [16], or ultrasonic cavitation chemistry, can be considered as an alternative synthesis method due to its safety, low-cost technology and environmental friendliness. Thanks to favorable thermodynamic conditions (not provided in the silent modes mentioned above), in terms of temperature (about 5000 K), pressure (20 MPa) and rapid cooling rates (about 10¹⁰ K/s) [17], [18], nanoparticles can be easily and quickly obtained and modified using ultrasonic irradiation based on chemical reactions in aqueous solutions. In addition, recent ultrasonic treatment was also reported to be an effective method for size refinement and dispersion of nanoparticles during their synthesis process [19] One can therefore take benefit from these conditions to provoke a fast reaction and thereafter fine tune the tetrahedral and octahedral site-occupancy to promote the A-B super-exchange interaction and consequently improve the magnetic properties of the as-synthesized ferrites.

Our approach in the present investigation consisted in reducing, as far as possible, the value of the magnetic moment of the A-sublattices by maintaining the Zn²⁺ ions (nonmagnetic) in the A-sites, on one hand, and pushing Fe³⁺ ions to migrate towards tetrahedral sites to create the desired Fe-O-Fe super-exchange interaction, on the other. Experimentally speaking, the strategy was to synthesize the zinc ferrite (ZnFe₂O₄) first, into which manganese will progressively be added to obtain Zn-Mn spinel ferrites, or Zn_1-xMn_xFe₂O₄, where x is the added Mn concentration. The ZnFe₂O₄ structure, x  = 0, is a paramagnetic [20] normal spinel ((Zn²⁺)^A[Fe₂³⁺]^BO₄²⁻) with efficient application in hyperthermia [21], [22] In such a structure, Zn²⁺ is preferably located in A sites due to its affinity for sp³ bonding with oxygen anions. While for x  = 1, MnFe₂O₄ is likely to adopt a mixed spinel structure [23], the magnetic moment of which was shown to decrease with increasing the inversion degree [24], [25] The challenge would then be to find the right balance in terms of Mn addition allowing the best magnetic performances.

In the present study, sonochemical method was used to provide optimal conditions for the synthesis of stoichiometric and chemically homogenous Zn_1−xMn_xFe₂O₄ nanoparticles (0 ≤ x ≤ 1). Mn incorporation was varied and cations distribution was followed and controlled at low temperatures in a very short processing time. The effect of such an “ionic engineering” on the structure, morphology and site occupancy on magnetic properties was respectively investigated by using X-Ray Diffraction (XRD), Transmission Electron Microscopy (TEM), Fourier Transform Infrared spectroscopy (FT-IR), X-ray Photoelectron Spectroscopy (XPS), Mössbauer spectroscopy and Superconducting QUantum Interference Device (SQUID) magnetometry.

2. Methods

2.1. Materials

Presently, commercial precursors and analytical grade chemicals were used. The reagents Manganese (II) chloride [MnCl₂·2H₂O], Zinc chloride [ZnCl₂·2H₂O], Ferric chloride [FeCl₃·6H₂O] and Potassium Hydroxide [KOH], from Sigma-Aldrich, were used to synthesize all our powders.

2.2. Sonochemical synthesis

In sonochemical synthesis, intense ultrasonic waves produce cavities that facilitate oxidation, reduction, dissolution, decomposition and hydrolysis phenomena at different stages of the synthesis [26] On this basis, a series of Zn_1-xMn_xFe₂O₄ samples were prepared by adding a fraction “x” of [MnCl₂·2H₂O] to the initially prepared [ZnCl₂·2H₂O] solution. The Mn concentration denoted as “x” was varied as 0.0, 0.2, 0.4, 0.8 and 1.0. Then, [ZnCl₂·2H₂O, MnCl₂·2H₂O] and [FeCl₃·6H₂O] were added in 2 separate beakers containing 10 mL of deionized water each, and stirred on a magnetic stirrer at room temperature for 20 min. These two solutions were mixed in a different beaker, and stirred for an additional 10 min. A base solution was prepared by adding 8.41 g of KOH in 50 mL of deionized water and stirred for 10 min. The reaction mixture was then put in a Branson Ultrasonic system (water bath mode) then exposed to ultrasonic waves (frequency: 40 kHz, power: 110 W) for 45 min. During ultrasonic irradiation, these precursors generate their respective ions while water decomposes into hydrogen ions (H⁺) and hydroxyl radicals (OH⁻) due to the high temperatures and pressures generated locally by cavitation bubbles. These free radicals combine to produce H₂ and H₂O₂, and consequently provide a highly oxidant medium [27] thereby forming the corresponding oxides (Fe₃O₄, ZnO, and Mn₃O₄). These oxides further oxidize under the influence of ultrasound to form precipitates that were centrifuged, washed with ultra-pure water five-to-six times and dried in air then annealed at 500 °C for one hour.

2.3. Characterization

The crystalline structure of as-prepared Zn_1-xMn_xFe₂O₄ nanoparticles with different Mn concentrations was investigated with X-Ray Diffraction (XRD) technique using Panalytical Expert Pro X-ray Diffractometer. The octahedral and tetrahedral vibrational modes were identified by Fourier Transform Infrared (FT-IR) using a PerkinElmer Spectrophotometer. The morphology of the Zn_1-xMn_xFe₂O₄ nanoparticles was investigated by Transmission Electron Microscopy (TEM) using a TALOS electron microscope operated at 200  kV accelerating voltage. A detailed site-occupancy study was first carried out using a constant-acceleration spectrometer with a ⁵⁷Co(Rh) was used to obtain Iron-57 (Fe⁵⁷) Mössbauer spectra at room temperature. The absorbers were made of a mixture (around 40 mg cm⁻²) of powders with boron nitride, while α-iron foil was used for calibration. The measurements were carried out in the velocity ranges of ± 4 mm/s, then fitted with three Lorentzian doublets (Fullham program). This first site-occupancy study was then further explored with X-ray photoelectron spectroscopy (XPS) in an ultrahigh vacuum (UHV) system equipped with an hemispherical electron analyzer (RESOLVE 120 MCD5). A dual anode X-ray source (aluminum Kα hν = 1486.6 eV) was used. Both survey and high-resolution spectra were recorded using the constant pass energy mode (100 and 20 eV respectively). Finally, magnetic measurements were conducted on dried powders introduced into standard capsules using a Quantum Design MPMS VSM SQUID magnetometer. Zero Field Cooled (ZFC) measurements were performed as follows: the samples were initially cooled down to 4 K with no magnetic field, and the magnetization was recorded under 100 mT while the temperature was increased to 350 K. For the Field Cooled (FC) measurements, the temperature was set to 350 K, the field was set to 100 mT, and the magnetization was recorded while cooling down the samples to 4 K.

2.4. DFT calculation

Density Functional Theory (DFT) was performed in all our computational simulations with the help of the Quantum ESPRESSO package (v.7.2) [28] We utilized the Perdew-Burke-Ernzerhof (PBESOL) exchange–correlation functional within the framework of the Generalized Gradient Approximation (GGA), incorporating an effective Hubbard coefficient (U) of 5.5 eV to better account for electron–electron interactions within the d-orbitals of the transition metal ions [29] The core and valence electron interactions were treated using the Projected Augmented Wave (PAW) pseudopotential method [30] with configurations as follows: Mn ([Ar] 4 s², 3d⁵), Fe ([Ar] 4 s², 3d⁶), Zn ([Ar] 4 s², 3d¹⁰), and O ([He] 2 s², 2p⁴). The kinetic energy cut-off for wave functions was set to 60 Ry, whereas for charge density, a cut-off of 400 Ry was chosen. Structural relaxations were conducted until the forces acting on the atoms were below 0.02 eV/Å. Additionally, convergence of the total energy was achieved to within 10⁻⁷ Ry, ensuring the accuracy of the optimized geometries. The Brillouin zone integrations during structural optimizations were performed with a 6 × 6 × 6 Monkhorst-Pack k-points grid.

3. Results and discussion

3.1. Microstructure and morphology

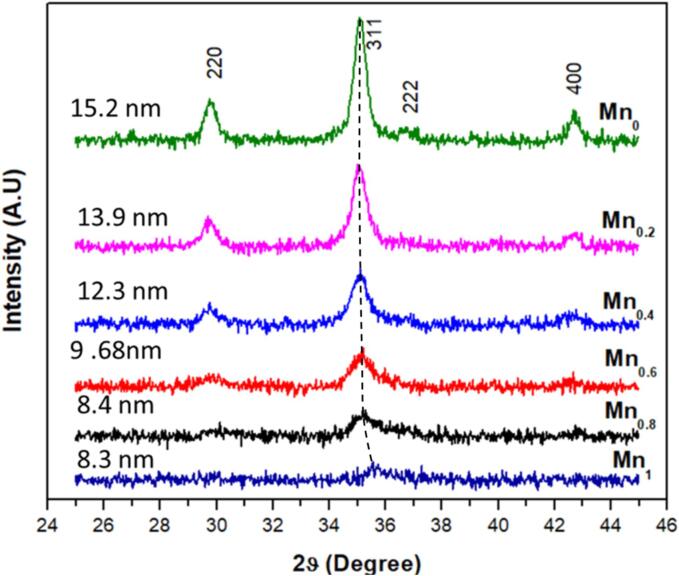
XRD technique was first used to study the crystal structure the as-prepared Zn_1-xMn_xFe₂O₄ powders, as depicted in Fig. 1. The observed diffraction peaks correspond to those of a single phase crystallized in the cubic spinel structure. In the case of x-Mn = 0, the powder diffraction diagram is in full agreement with that of the ZnFe₂O₄ crystal structure (JCPDS card 01–077-0011, Fd-3 m space group). These peaks were indexed as (2 2 0), (3 1 1), (2 2 2) and (4 0 0) planes, the broadening of which is attributed to the nanocrystalline nature of the as-prepared powders.

Fig. 1.

XRD patterns of the as-prepared Zn_1-xMn_xFe₂O₄ nanoparticles as a function the x-Mn concentration. The dashed line is a guide for the eye.

The lattice parameter “a” of the as-synthesized nanoparticles were determined using the following relation: $\mathit{a}={\mathit{d}}_{\mathit{h}\mathit{k}\mathit{l}}\times \sqrt{({\mathit{h}}^2+{\mathit{k}}^2+{\mathit{l}}^2)}$ and listed in Table 1, where d_hkl corresponds to the lattice spacing and (h,k,l) to their corresponding Miller indices. The d_hkl values were deduced from the Bragg formula d_hkl = λ/2.sin(θ). It can be noticed that the lattice parameter “a” of sonochemically prepared Zn_1-xMn_xFe₂O₄ nanoparticles showed a substantial decrease as the x-Mn concentration increased. The origin of such a decrease is directly linked to differences in ionic radii. Replacement of Zn²⁺ ions (a radius of 0.74 Å) with those of Mn²⁺ (a much lower radius 0.67 Å) should generally provoke a decrease in the interionic distances causing a shrinkage of the lattice parameter. This effect is expected to be very pronounced at high Mn concentration due to the establishment of a mixed spinel structure where magnetic (Mn²⁺, Fe³⁺) and nonmagnetic (Zn²⁺) ions are randomly placed. A behavior that is similar to the role of the inversion degree in Mn ferrites [31], where increasing the degree of inversion was seen to systematically decrease the lattice parameter.

Table 1.

Lattice parameters and Crystallite sizes of the as-prepared Zn_1-xMn_xFe₂O₄ nanoparticles.

x	Lattice Parameter a (Å)	XRD Crystallite size D (nm) (±0.1 nm)	TEM mean particles size (nm) (±0.1 nm)
0.0	8.469(1)	15.2	15.9
0.2	8.466(1)	13.1	14.0
0.4	8.457(1)	12.1	12.9
0.6	8.445(1)	9.6	10.8
0.8	8.399(1)	8.9	10.1
1.0	8.354(1)	7.1	7.9

The average crystallite size of the as-prepared Zn_1-xMn_xFe₂O₄ spinel ferrite nanoparticles was evaluated by using the Scherrer formula [32]: $\mathit{D}=\frac{\mathrm{K}\mathrm{\lambda }}{\mathrm{\beta }\mathrm{c}\mathrm{o}\mathrm{s}\theta }$ where K equals to 0.9, λ is the X-ray wavelength, β is the full width at half maximum of the considered (311) diffraction peak, and θ is the diffraction angle. The average crystallite sizes for all x-Mn concentrations were summarized in Table 1. At first glance, it should be noted that the intensity of the selected diffraction peak decreased drastically with increasing x-Mn concentration, which suggests a substantial decrease in the size of the crystallites. This could suggest that a longer sonication time [33] is probably needed to energetically activate the formation of larger Mn-rich Zn_1-xMn_xFe₂O₄ nanoparticles. This finding clearly demonstrates the influence of ultrasound on the nucleation and growth process of the ferrite nanoparticles. Let recall that in the present investigation, power and ultrasonic-time conditions were optimized to produce Mn-free ferrites (i.e. ZnFe₂O₄) in order to preserve the normal spinel structure. The Mn incorporation is, somehow, supposed to slowdown the nanoparticles growth and to obstruct their aggregation. Due to the surface energy of the particles, there will be a tension force at the edge of the contact surface leading to a competition between the surface energy and the ultrasonic force that is at the origin of the nanoparticles size control [34].

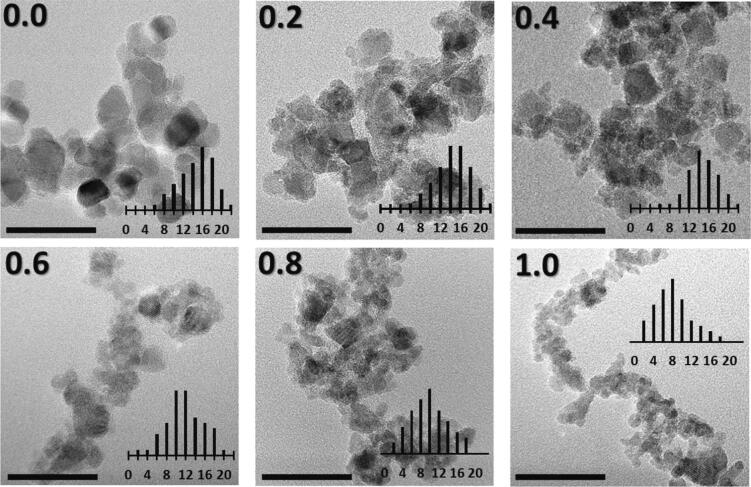
Fig. 2 shows a series of TEM images corresponding to Zn_1-xMn_xFe₂O₄ as-prepared nanoparticles (x = 0.0, 0.2, 0.4, 0.6, 0.8 and 1.0). In terms of morphology, ZnFe₂O₄ (x = 0.0) exhibit large and facetted nanoparticles. Increasing the x-Mn concentration seemed to affect the shape towards the formation of a quasi-spherical one. In addition, increasing the x-Mn concentration provoked a decrease in the crystallites size as can clearly be deduced from size distribution analyses (see diagrams in the insets and Table 1), which is in good agreement with the above XRD findings.

Fig. 2.

TEM images of Zn_1-xMn_xFe₂O₄ nanoparticles for x  = 0.0, 0.2, 0.4, 0.6, 0.8 and 1.0, along with the respective size distribution in “nm”. The scale-bar in the images corresponds to 50 nm, while the x-scale unit in particle size distribution is “nm”.

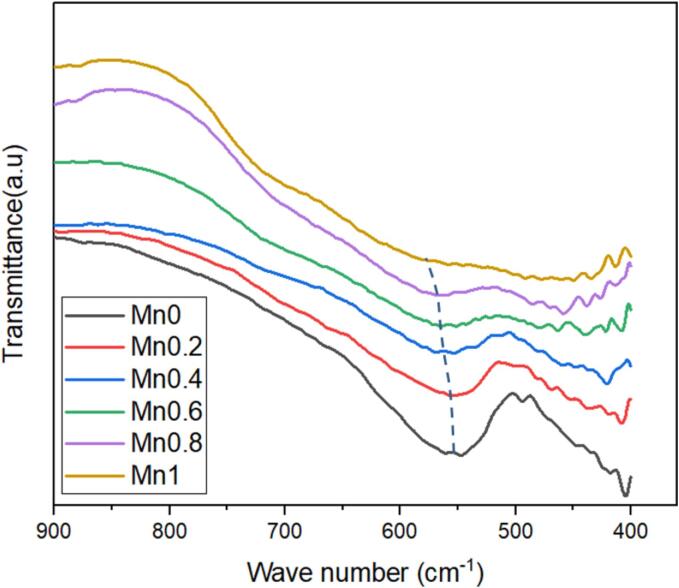
Fig. 3 depicts the FT-IR spectra of Zn_1-xMn_xFe₂O₄ nanoparticles. As shown, the transmittance spectra were recorded in the wavenumber range of 390 to 900 cm⁻¹. It is observable in Fig. 3 that the prominent vibrational mode frequencies lie in the range of 400–450 cm⁻¹ and 500–600 cm⁻¹, which respectively are assigned to the stretching in the interstitial octahedral (B) and tetrahedral (A) sub-lattices. The values of these vibrational mode frequencies, reported in Table 2, are seen to shift towards higher frequencies along with increasing substitution of Mn²⁺ ions. This shift provides a clear indication of cationic redistribution after the incorporation of Mn²⁺ ions into the zinc ferrite spinel matrix. These cationic redistribution is investigated in the following section using site sensitive techniques.

Fig. 3.

FT-IR spectra of sonochemically synthesized Zn_1-xMn_xFe₂O₄ nanoparticles. The dashed line is a guide for the eye.

Table 2.

Values of Infrared vibrational A- and B-sites mode frequencies as a function of x-Mn concentration.

x	Absorption band in A site (cm−1)	Absorption band in B site (cm−1)
0.0	549.3	404.9
0.2	554.1	407.5
0.4	559.0	421.2
0.6	562.2	439.9
0.8	570.6	458.6
1.0	574.4	−

3.2. Cation distribution and site occupancy

In the following section, a detailed investigation on the site occupancy was performed on 0.4-Mn and 0.6-Mn samples using Mössbauer and XPS spectroscopies, then supported with theoretical DFT studies. Our attention was mainly focused on these two samples since they are positioned in the middle-range of Mn concentrations where the site occupancy preferences would determine the overall magnetic properties.

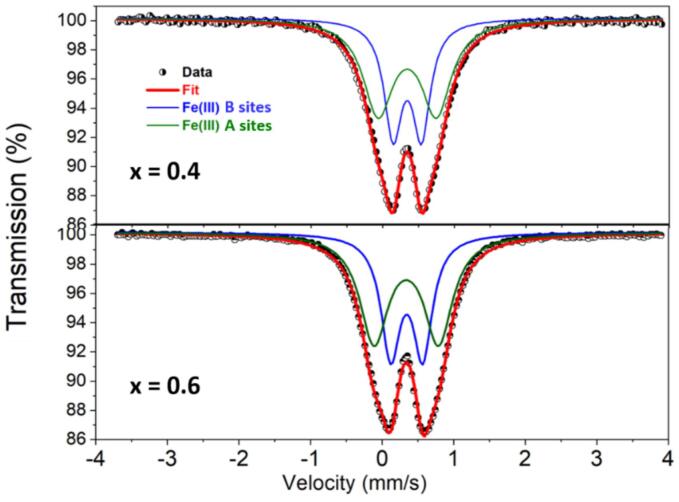
To investigate and assess the oxidation states of iron atoms in our powders, ⁵⁷Fe Mössbauer spectroscopy was carried out at room temperature. The obtained spectra for x  = 0.4 and 0.6 are depicted in Fig. 4. Their corresponding Mössbauer parameters are summarized in Table 3. The Mössbauer spectra showed no signs of magnetic splitting, which demonstrates the paramagnetic nature of the Zn_1-xMn_xFe₂O₄ nanoparticles (x = 0.4 and 0.6) at room temperature. This result confirms the absence of any super magnetic iron oxide-based impurity. The experimental data corresponds to an asymmetric doublet that can be fitted by using two doublets. Indeed, a good quality fit of the Mössbauer spectra was obtained by using two doublets attributed to Fe³⁺components. This result indicates the presence of two different environments of Fe³⁺ ions in the Zn_1-xMn_xFe₂O₄ structure. The obtained values of isomer shift imply that the high-spin Fe³⁺ ions occupy A and B sites in accordance with previous studies [35], [36] The relative areas of the sub-spectra were used to determine the Fe ions fraction in A- and B-sites by assuming that the recoilless fraction is the same for the two sites [37] For x  = 0.6 sample; Fe³⁺ ions located in B sites were estimated to be around 58 % and remaining 42 % are in A sites. This result is a signature of a significant Fe ions migration from B to A sites during Mn ions incorporation. In addition, the higher areas of the Mössbauer peaks in the x  = 0.6 sample is also an indication of a randomly placed of Fe³⁺ and Zn²⁺ ions at A and B sites. With the increase of the Mn ratio in Zn_1-xMn_xFe₂O₄ nanoparticles from x  = 0.4 to x  = 0.6, the values of the quadrupole splitting of Fe³⁺ increases in A sites (from 0.30 to 0.32 mm/s) and in B sites (from 0.80 to 0.89 mm/s) which is an indication of the strong asymmetric nature of the local environment.

Fig. 4.

The Mössbauer spectra recorded at room temperature of as-synthesized Zn_1-xMn_xFe₂O₄ nanoparticles for x  = 0.4 and x  = 0.6.

Table 3.

The Mössbauer data deduced from measurements in Fig. 4.

		x = 0.4	x = 0.6
Fe3+ − site A	δ (mm/s)	0.34 (1)	0.34 (1)
	Δ(mm/s)	0.39 (1)	0.44 (1)
	Γ(mm/s)	0.30 (1)	0.32 (1)
	Area (%)	42 (1)	42 (1)
Fe3+ − site B	δ (mm/s)	0.34 (1)	0.34 (1)
	Δ(mm/s)	0.81 (1)	0.89 (1)
	Γ(mm/s)	0.50 (1)	0.48 (1)
	Area (%)	58 (1)	58 (1)

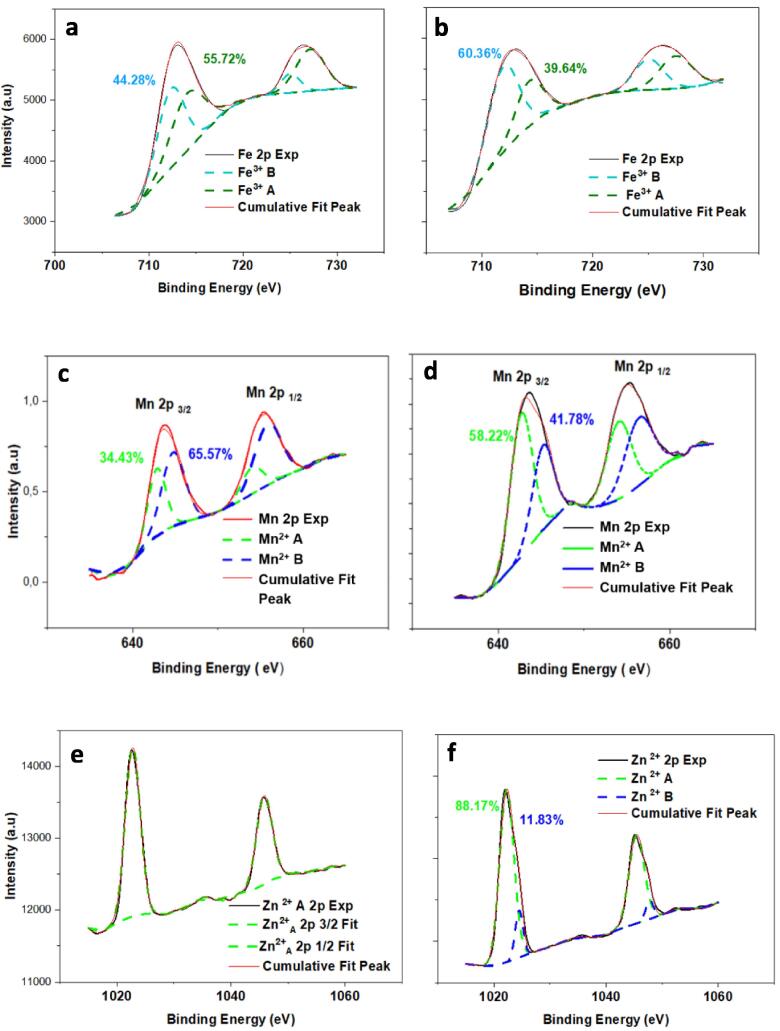
The XPS Fe-2p, Mn-2p, Zn-2p lines of the x  = 0.4 and x  = 0.6 samples are shown in Fig. 5, the data of which were regrouped in Table 4. As can be observed, the Zn-Mn ferrites signal varies as a function of the x-Mn content, which strongly indicates a re-distribution of cations. In terms of oxidation states, our findings revealed the existence of Mn²⁺, Zn²⁺ and Fe³⁺ ionic states within our samples, in accordance with previously reported valence and oxidation analyses [38], [39] Fe³⁺ and Mn²⁺ ions were seen to be located in both sites, A and B, in agreement with our Mössbauer findings. It can be seen from Fig. 5a, x  = 0.4, that Fe-2p^3/2 and Fe-2p^1/2 asymmetric peaks are composing the Fe-2p signal with binding energies at 712.8 and 726.5 eV, respectively, and the doublet spacing is around 13.7 eV in agreement with previous reports [40] For the Fe-2p^3/2 peak, the two contributions at about 712.5 and 714.8 eV were attributed to Fe³⁺ cations in octahedral and tetrahedral sites, respectively. Those corresponding to the x  = 0.6 sample (Fig. 5b) are slightly shifted due to a change in the chemical environment, as Fe³⁺ is more present in octahedral sites as compared to its proportions in the x  = 0.4 sample. This finding is in great accordance with the above Mössbauer results. In the case of Mn signal, Fig. 5c (x = 0.4) showed two asymmetric peaks located around 644.2 and 655.5 eV that correspond to Mn-2p^3/2 and Mn-2p^1/2, respectively. The Mn-2p^3/2 can be deconvoluted into two contributions and the binding energies are 642.8 and 644.9 eV that were attributed to the Mn²⁺ cations with tetrahedral and octahedral occupancies, respectively. Those corresponding to x  = 0.6 sample (Fig. 5d) show that Mn²⁺ is less present in octahedral sites as compared to those in tetrahedral ones. The spectrum and fitting results of Zn-2p in x  = 0.4 sample are presented in Fig. 5e. Zn-2p is composed of two asymmetric peaks located around 1023.1 and 1044.9 eV that correspond to Zn-2p^3/2 and Zn-2p^1/2, respectively. Obviously, these peaks only consist of a single site occupancy for Zn²⁺ that is tetrahedral. With increasing Mn incorporation, (x = 0.6 sample) a slight contribution from Zn²⁺ occupying octahedral sites is clearly evidenced. The Zn-2p^3/2 splits into two peaks centered at 1022.5 and 1024.9 eV, which is ascribed to the zinc cations occupying tetrahedral and octahedral sites, respectively, consistently with reported studies [41], [42] This behavior likely indicates that Mn²⁺ and Zn²⁺ ions are progressively occupying both A and B sites leaving behind a mixed spinel, which has also been confirmed by previous EXAFS [43] and neutron diffraction [44] studies where it was demonstrated that Mn²⁺ ions only start occupying the tetrahedral sites up to a Mn concentration close to x  = 0.6.

Fig. 5.

The XPS spectra corresponding to the as-synthesized Zn_1-xMn_xFe₂O₄ nanoparticles for x  = 0.4 (a, c, e) and x  = 0.6 (b, d, f).

Table 4.

XPS data as deduced from measurements in Fig. 5.

		x-Mn = 0.4	x-Mn = 0.6
Fe3+ (%)	A- sites	55.72	39.64
	B- sites	44.28	60.36
Mn2+ (%)	A- sites	34.43	85.22
	B- sites	65.57	41.78
Zn2+ (%)	A- sites	100.00	88.17
	B- sites	0.00	11.83

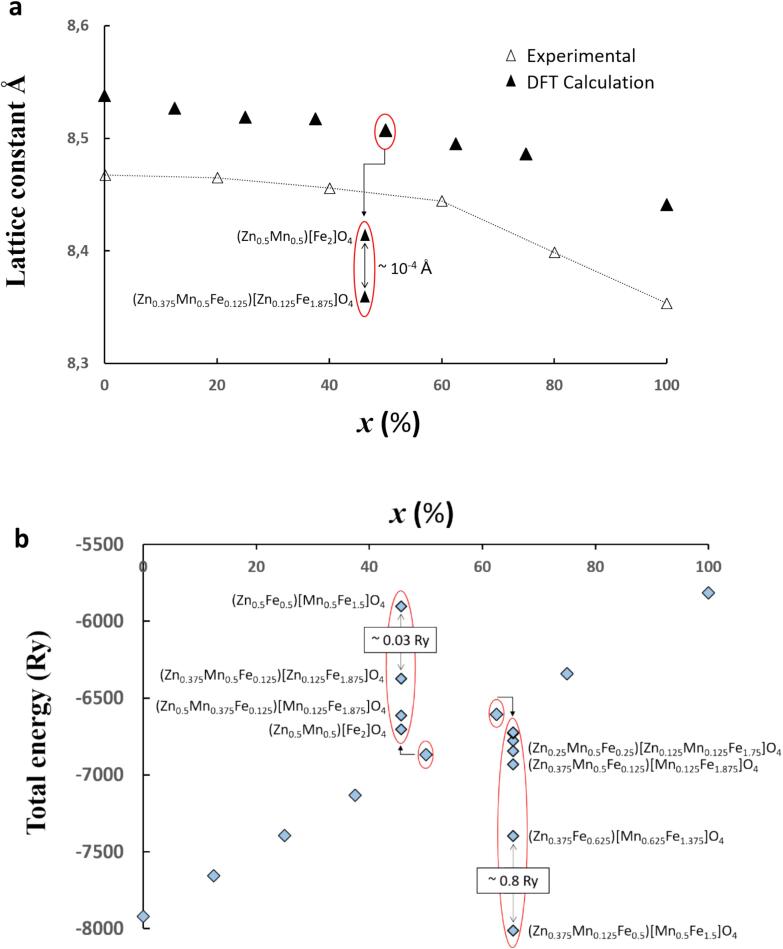
According to our XPS and Mössbauer results, it turned out that the crystallographic nature of the Zn_1-xMn_xFe₂O₄ nanoparticles was revealed to be of mixed spinel type whatever the incorporated quantity of Mn. In order to support our experimental data, we performed a series of theoretical DFT studies on Zn_1-xMn_xFe₂O₄ as a function the Mn content (x) and also a function of the inversion degree. First, calculation of the lattice parameter “a” as a function of the Mn content (x) and as a function of the inversion degree is illustrated in Fig. 6a. Our experimental XRD data (from Fig. 1) were also added for comparison. Interestingly, the trend of the later seems to perfectly match the one obtained from theoretical calculations, which is a strong indication of the validity of our approach. Furthermore, although the increase of the inversion degree seemed to decrease the lattice parameter, such a decrease was noticed to be quasi-negligible (less that 10^-4Å) in the case of x  = 0.5, for instance. A similar remark was also noticed in other values of “x”. Regarding the total energy of each system (illustrated in Fig. 6b), our theoretical calculations showed that the normal spinel type of ZnFe₂O₄ is the most stable phase. When incorporating Mn in the crystal structure of ZnFe₂O₄, the calculated total energy was observed to increase as a function of the Mn content. Again, differences in the calculated total energies as a function of the degree of inversion were found to be very small. An example is illustrated for x  = 0.5 where much less than 0.03 Ry was registered between two configurations (inset of Fig. 6b). In general, the more mixed is the phase, the more stable it is. For concentrations x  ≤ 0.4, the less energetic systems were those where Zn ions are only in A sites and Mn and Fe ions are occupying both sites, A and B, which is very consistent with our XPS findings for x  = 0.4. Due to the very small variation of the total energy between different configurations, one can deduce that the probability of formation of a mixed phase is very high. In addition, Zn migration towards B sites was seen to be viable only for x  ≥ 0.5. For x  = 0.6 for instance, Zn migration towards B sites was observed to be likely to occur, a result that explains well the occurrence of Zn²⁺ ions in B sites in our XPS results (Fig. 5f). Regarding the site preference issue, our calculations seemed to indicate that Mn²⁺ ions relatively prefer to occupy B sites up to x  ≤ 0.5, then A sites for higher Mn contents, which is likely indicative of an ion-exchange characterized by a migration of Fe³⁺ ions towards A sites to replace Zn²⁺ ions. Over a certain threshold in terms of Mn²⁺ ions incorporation, close to the one in x  = 0.6 sample, Mn²⁺ ions showed a preference to occupy A sites which logically should slowdown the migration of Fe³⁺ ions towards A sites. This tendency was seen to be accompanied by a migration of Zn²⁺ ions towards the B sites.

Fig. 6.

(a) Comparison of experimental and calculated lattice parameters as a function of x-Mn concentration. The role of the degree of inversion is highlighted at x  = 50 %, red ellipse, where parentheses and brackets denote sites A and B, respectively. (b) Calculated total energy of ZnMn ferrites as a function of x-Mn concentration. The role of the degree of inversion is highlighted at x  = 50 % and x  = 60 %, red ellipses, where parentheses and brackets denote sites A and B, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.3. Magnetic properties

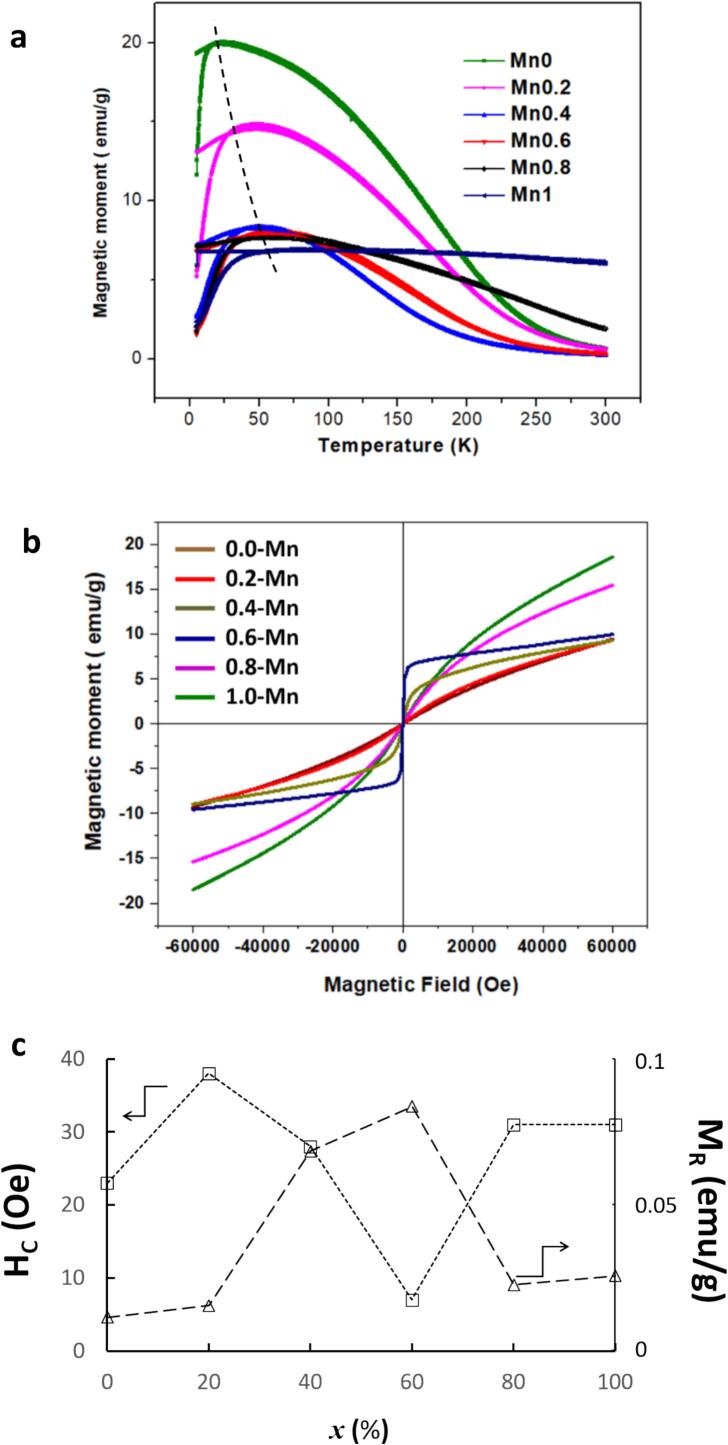
Magnetic hysteresis loops along with ZFC/FC vs temperature curves were measured in order to study the magnetic properties of the as-synthesized Zn_1-xMn_xFe₂O₄ nanoparticles. The measurement of the magnetization as a function of temperature, which provide information on the mean blocking temperature and particle size distribution [45], is illustrated in Fig. 7a. From the FC-ZFC curves it is observed that all samples transit from a blocked state to a superparamagnetic one at a blocking temperature T_B, which is different for each sample. The less Mn is incorporated, the lower the T_B. In a typical “two states” model, the ZFC curve is characterized by a maximum at T_B where the magnetic particles are supposed to be either fully blocked or fully superparamagnetic [46] However, given the stochastic nature of the thermally induced switching, the blocked/superparamagnetic transition will have a certain width that depends on the nanoparticles size-dispersion [47], [48], the contribution of which is expected to affect the shape of the curve [49], [45] In Fig. 7a, up to x  = 0.6, samples exhibit a curvature in the ZFC curve and a hump in the FC curve, which are indicative of the occurrence of high anisotropy [50] However, for x  ≥ 0.8, the flat nature of the FC curve and the broadening in the ZFC curve suggest a low anisotropy. Nevertheless, the shapes of all ZFC/FC curves are typical for magnetic nanoparticles with a broad size distribution [51], where T_B is seen to increase with decreasing the particles size. Such an increase in T_B might be the result of a magnetic interaction among particles due the increase in the nanoparticles concentration [52].

Fig. 7.

(a) FC-ZFC curves corresponding to the as-synthesized Zn_1-xMn_xFe₂O₄ nanoparticles. The dashed line indicates the evolution of the blocking temperature T_B (b) Magnetic hysteresis curves for as-synthesized Zn_1-xMn_xFe₂O₄ nanoparticles.

The variation of magnetization as a function of magnetic field (plotted in Fig. 7b) was recorded at room temperature (300 K) for all Zn_1-xMn_xFe₂O₄ samples (x = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0), while coercive field (H_C) and remanent magnetization (M_R) values evolution is reported in Table 5. The ZnFe₂O₄ (x = 0) sample is understandably quasi-paramagnetic, while all the samples become superparamagnetic with increasing x-Mn substitution. With increased incorporation of Mn²⁺ ions into the Zn ferrite structure (up to 0.4 ≤ x ≤ 0.6), a saturation magnetization was clearly obtained along with the lowest H_C and the highest M_R values. The observed magnetization at saturation in sample x  = 0.6 (Ms ∼ 10 emu/g) is in fact comparable with those reported in the literature (18 emu/g [53], 12 emu/g [54], [55]), but substantially higher than that of nanosized Zn-Mn particles synthesized by the sol–gel combustion method (5 emu/g) [56] The squareness ratio [57] (Mr/Ms) for such a sample was almost zero (∼ 0.0078) which suggests that the Zn_0.4Mn_0.6Fe₂O₄ compound might prove to be a promising candidate as a magnetic fluid to be used in biomedical imaging [58] Further increase of Mn²⁺, x  ≥ 0.8, the difficulty in aligning the very small nanoparticles is clearly seen, resulting in low M_R and high H_C values.

Table 5.

As-extracted values of M_S, M_R and H_C from hysteresis loops of Fig. 7b as a function of Mn concentration (x).

x-Mn	MS (emu/g)	MR (emu/g)	HC (Oe)
0.0	2.0	0.007	23.1
0.2	2.5	0.011	37.9
0.4	6.5	0.063	27.8
0.6	9.5	0.078	7.1
0.8	6.1	0.018	31.2
1.0	7.5	0.021	31.3

To recapitulate, in the Zn ferrite structure (x = 0), the spinel is normal and nonmagnetic Zn²⁺ ions occupy the A sites while Fe³⁺ ions occupy B sites with anti-parallel moments. No A-B interactions occur while that of B-B between Fe³⁺ ions is very weak making the ferrite paramagnetic. Up to a Mn concentration of x  = 0.6, the sudden increase in saturation magnetization is very obvious. Such an increase is actually caused by the incorporation of Mn²⁺ ions at the expense of Zn²⁺ ions giving rise to a change in the distribution of cations favorable to a super-exchange creation. Indeed, due to the observed migration of Fe³⁺ ions towards the tetrahedral A sites, an activation of the Fe³⁺–O^2––Fe³⁺ super-exchange interaction occurred, which results in the observed large magnetizations. In fact, an Fe³⁺ ion at a given A site and its nearest Fe³⁺ neighbors at B sites form a sort of cluster in which each Fe³⁺(B) spin is coupled with the Fe³⁺(A) spin by an A-B interaction, which is much stronger than B-B ones [59] With further incorporation of Mn²⁺ ions (x ≥ 0.8), the total net magnetic moment decreases, indicating that the magnetic moments at A and B sites are in opposite directions and somewhat cancel each other out. Thus, as the Mn content increases, the mixed nature of Zn_1-xMn_xFe₂O₄ spinel structure is altering, or even weakening, the super-exchange interaction between Fe³⁺–O^2––Fe³⁺ ions, and the B spins are no longer rigidly aligned parallel to the few remaining A spins. This increase in the inversion degree, combined with the very small size of the nanoparticles, is most probably responsible for the further decrease in magnetization.

4. Conclusions

In the present study, the sonochemical method was used to prepare Zn_1−xMn_xFe₂O₄ (0 ≤ x ≤ 1) nanoparticles with improved magnetic properties. The incorporation of Mn²⁺ was investigated by a variety of techniques such as XRD, TEM, FT-IR, Mössbauer and XPS. The crystalline phase of the as-prepared nanoparticles was found to be that of spinel-type ferrite crystallized in the cubic structure. As the incorporation of Mn increased, the shape of these nanoparticles was seen to vary from cubic to spherical forms, where fine analyses of the lattice parameter showed a substantial decrease. This decrease was due to the differences in the Zn²⁺ and Mn²⁺ ionic radii. In terms of cation distribution and site occupancy, spectroscopic analyses and theoretical DFT calculations showed that the more mixed the phase, the more stable it was. Quasi-systematic ionic movements were made possible by the very short reaction times and high energy offered by intense ultrasonic waves. A kind of rapid stabilization of the phase was observed upon introduction of Mn. The latter first occupied the Fe B-sites and pushed it to migrate towards the A-sites to fill the lack of Zn. The best magnetic performances were obtained at Mn incorporation thresholds between 50 % and 60 %, thanks to the accentuation of super-exchange interactions and a very low squarness ratio (M_R/M_S), which is very promising for applications in biomedical imaging. When these thresholds were exceeded, the stabilization of the structure required, on the one hand, that the Mn²⁺ ions occupied both sites, A and B, which forced the Zn to migrate towards octahedral sites. On the other hand, these ionic movements also caused a slowdown in the migration of Fe³⁺ ions towards the tetrahedral sites, thus reducing the much sought-after super-exchange effect. These two phenomena were therefore at the origin of the observed degradation of magnetic performances.

CRediT authorship contribution statement

Wafaa Azouzi: Investigation. Ikram Boulahya: Investigation. Jerome Robert: Investigation. Ahmed Essyed: Investigation. Abdelfattah Mahmoud: Investigation. Ahmed Al Shami: Investigation. Dris Ihiawakrim: Investigation. Hicham Labrim: Supervision. Mohammed Benaissa: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.