Federated difference-in-differences with multiple time periods in DataSHIELD

Summary

Difference-in-differences (DID) is a key tool for causal impact evaluation but faces challenges when applied to sensitive data restricted by privacy regulations. Obtaining consent can shrink sample sizes and reduce statistical power, limiting the analysis’s effectiveness. Federated learning addresses these issues by sharing aggregated statistics rather than individual data, though advanced federated DID software is limited. We developed a federated version of the Callaway and Sant’Anna difference-in-differences (CSDID), integrated into the DataSHIELD platform, adhering to stringent privacy protocols. Our approach reproduces key estimates and standard errors while preserving confidentiality. Using simulated and real-world data from a malaria intervention in Mozambique, we demonstrate that federated estimates increase sample sizes, reduce estimation uncertainty, and enable analyses when data owners cannot share treated or untreated group data. Our work contributes to facilitating the evaluation of policy interventions or treatments across centers and borders.

Graphical abstract

Highlights

• •Federated CSDID enables privacy-preserving causal analysis across data owners
• •R package extends DataSHIELD for federated causal impact analysis in sensitive datasets
• •Case study shows federated CSDID’s utility in evaluating policy effects on education

Health informatics; Computer science; Machine learning

Introduction

The difference-in-differences (DID) method is a widely used quasi-experimental approach for evaluating treatment effects, especially in the absence of experimental design in policy or treatment implementation. Originally introduced by Ashenfelter¹ to estimate the impact of job training programs on earnings, and later popularized by Card and Krueger² in their analysis of minimum wage effects, DID has since found broad applications. These include fields such as finance,^3,4 clinical research,^5,6 epidemiology,^7,8 and economics.^9,10 Examples of the use of DID for the evaluation of public health policies are Miller and Wherry⁶ who utilized DID to assess the impact of Medicaid expansions under the Affordable Care Act on health outcomes, insurance coverage, and health care use among low-income adults across states in the USA. Similarly, Galiani et al.⁵ applied DID to evaluate the effects of water privatization in Argentina during the 1990s. By comparing municipalities that privatized their water services with those that did not, they found a significant reduction in child mortality, particularly in the poorest areas, attributing the reduction to improvements in water quality.

Recent advances have addressed continuous treatment effects,¹¹ variations in treatment timing,^12,13 and varying effects across multiple periods.¹³ The Callaway and Sant’Anna¹³ method is available in R¹⁴ and Stata,¹⁵ referred to as CSDID (Callaway and Sant’Anna difference-in-differences). The most critical assumption in DID applications is the parallel trends assumption, which states that without treatment, the difference in outcomes between the treatment and control groups remains constant over time. For classical DID methods, this assumption must hold both unconditionally and conditionally on the covariates. Since time-varying covariates, like age, can influence the outcome differently across groups, this requirement is especially restrictive in the unconditional case. The CSDID estimator relaxes this requirement by only requiring the parallel trends assumption to hold conditionally on the covariates, providing greater flexibility and robustness in the presence of complex treatment and outcome relationships. Furthermore, the CSDID naturally accounts for variations in treatment timing (staggered DID) and treatment effect sizes over time, whereas traditional approaches assume constant effect sizes. CSDID has been applied to various policy evaluations. Mark and Wu¹⁶ investigated the impact of federal funding for comprehensive sex education on US teen birth rates, finding a reduction of over 3% using county-level data. Schulz and Rode¹⁷ studied the effect of public charging infrastructure on electric vehicle adoption in Norway, showing a significant increase in local ownership rates. However, the use of CSDID with sensitive individual-level data, such as patient data or student’s test performances, remains limited.

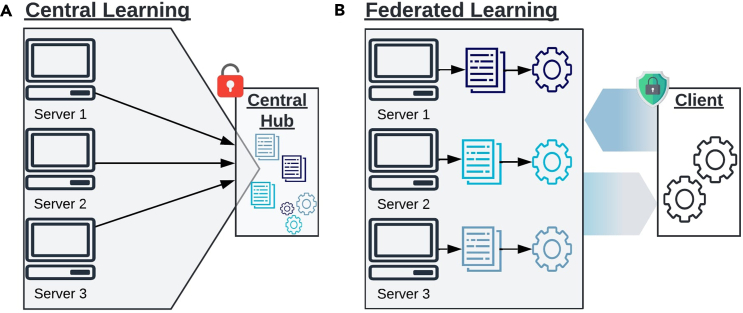
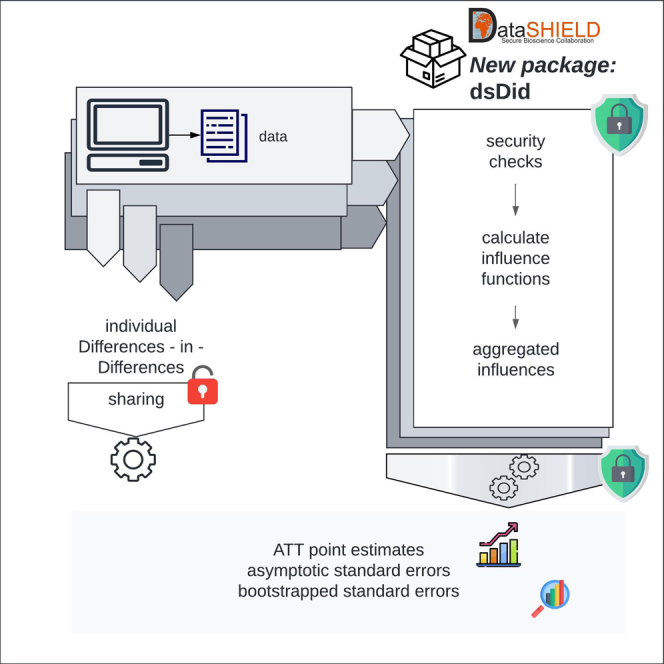
In cases involving sensitive individual-level data, sharing is restricted by research ethics and additional legal frameworks like the General Data Protection Regulation (GDPR).¹⁸ This restriction poses 3 major limitations to the analysis as follows. (1) Obtaining consent from all potential participants is challenging yielding reduced sample sizes. (2) Public health policies often vary regionally, and some entities, like schools or regional governments, may only have data for treated or untreated individuals. If these data cannot be shared, the CSDID cannot be used in these cases as either no treatment or no control group is available for estimating the treatment effect. (3) According to GDPR, the consent of the individuals or their legal representatives must be obtained before grades are processed. Students with poorer performance may withhold consent due to privacy concerns, introducing selection bias and limiting CSDID’s utility with central learning (Figure 1A). Federated learning¹⁹ addresses these limitations by enabling multiple data owners to collaborate while iteratively sharing only summary statistics, facilitating joint model training with larger sample sizes and preserving privacy (Figure 1B). It yields parameter estimates with convergence properties identical to central learning, often matching centrally stored data estimates. For CSDID, federated learning can reduce selection bias by mitigating privacy concerns, as data remain with the local institution. This might make students more willing to participate, thereby also increasing sample sizes and enhancing statistical power. Furthermore, in the case where schools or regional governments only have data for either treated or untreated records, the schools or regional governments can act as individual servers without sharing the data while enabling the federated CSDID analysis. Federated learning has been successfully applied in various biomedical studies,^20,21,22 but its application to student test performance data has not been explored.

Figure 1.

Learning paradigma

(A) Explanation of central learning. In central learning, models are trained at one central hub (analyst). All servers (data owners) send their data to the central hub, granting the analyst full access to individual-level information without preserving data privacy.

(B) Explanation of federated learning. In federated learning, model updates are computed locally at the servers, and only aggregated information is sent to the analyst (client). The locally aggregated information is then further aggregated to compute overall model parameter updates, which are sent back to the servers. This iterative process continues until a convergence criterion is met, ensuring efficient and privacy-preserving collaboration between servers and the analyst. This figure has been designed using resources from Flaticon.com.

We derived a federated learning algorithm of the CSDID approach and developed a computational package in DataSHIELD. DataSHIELD²³ is a well-established toolbox for federated learning, implemented in the statistical computing language R.²⁴ It is widely used in the biomedical community, including projects like the European Union’s Horizon 2020 ORCHESTRA project and unCover.²⁵ Although DataSHIELD supports many biomedical analysis tools, such as Survival Analysis²⁶ and deep Boltzmann Machines,²⁷ a tool for CSDID was previously missing. Our federated tool can obtain exact federated treatment effects, asymptotic standard errors, and distributional equivalent bootstrapped standard errors, comparable to the non-federated implementation.¹⁴ Our software incorporates standard DataSHIELD security measures, such as validity checks on the minimum non-zero counts of observational units and the maximum number of parameters in a regression. Additionally, we have included further security measures tailored to CSDID to prevent attacks as described by Huth et al.²⁸ These measures ensure that computations are secure and confidential, protecting sensitive data from unauthorized access or use.

In the remainder of this paper, we outline the fundamentals of DataSHIELD, explain the federated algorithm, detail the additional security measures implemented in our software, and demonstrate its application through a simulation study. Additionally, we present a case study examining the impact of a malaria elimination initiative on school outcomes, previously analyzed in a non-federated setup.²⁹

Results

DataSHIELD provides federated infrastructure

DataSHIELD^30,31 is an advanced distributed learning ecosystem that utilizes federated learning and federated meta-analysis to enable secure and collaborative data analysis across multiple data owners without sharing individual-level data. This approach maintains high statistical power by leveraging larger sample sizes while ensuring data privacy. DataSHIELD’s federated algorithms operate through a client-server structure (Figure 1B): client-side packages run on the analyst’s machine, and server-side packages are installed on the data owner’s machines. Server-side functions aggregate data locally, detect disclosure risks such as small sample sizes, and send non-disclosive information to the analyst to update parameters or compute overall aggregated statistics.

The dsBase package³² is the core of the DataSHIELD system, offering a wide range of functionalities, including summary statistics computation and generalized linear models (GLMs). Additionally, user-written packages extend DataSHIELD’s capabilities, such as restricted Boltzmann machines,²⁷ Omics analysis,³³ and mediation methods.³⁴ Our implementation in DataSHIELD enhances this framework by providing a robust tool for evaluating causal impact and treatment effects through the federated version of the CSDID. It is designed to minimize information transfer between the client side and server side, reducing both data leakage risks and communication overhead. Our software package consists of a client-side³⁵ and a server-side³⁶ R package. The server-side package can be accessed through the client-side package that uses Opal³⁷ for communication.

Privacy-preserving point estimates are obtained using federated averaging

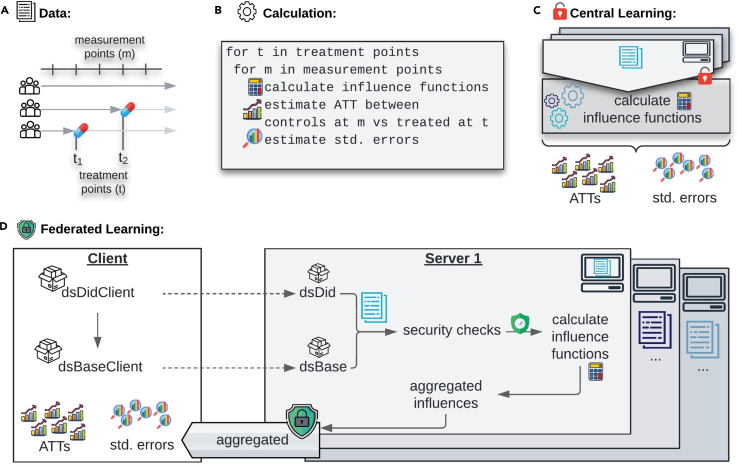
We present the methodology for computing federated point estimates of the average treatment effect on the treated (ATT). For clarity and consistency, we adopt the notation from Callaway and Sant’Anna.¹³

A dataset suitable for the CSDID analysis comprises multiple evaluation periods $t$ and treatment periods $g$ (Figure 2A). An ATT and its standard error are computed for each combination of $t$ and $g$ (Figure 2B) using appropriate control and treatment groups. As the control group, we can use either never-treated or not-yet-treated individuals. While this choice affects the specific individuals used to compute the counterfactual, it does not alter the overall methodology. Therefore, we illustrate the algorithm using never-treated individuals as the control group. Within the package, there are three methods to compute the ATT: the doubly robust (DR) approach, inverse-probability weighting (IPW), and the outcome regression (OR) approach. However, since the IPW and OR approaches are nested within the DR approach, federations are analogs. Thus, detailing the federation of the DR approach suffices.

Figure 2.

Federated implementation

(A) Visualization of data structure. The data have a panel structure with many observations per individual and varying treatment timing.

(B) High-level algorithm of the CSDID. For each combination of evaluation period and treatment period, an ATT and its standard error are computed using the influence function of each individual.

(C) CSDID for central learning. In central learning, the data are all at one server such that the sample analogs can be computed directly.

(D) CSDID for federated learning. The analysis is initialized by using functions from the client side package dsDidClient that calls the dsDid package on the server sides using opal. During the local computations of the influence functions on the server sides, security checks are enforced in order to guarantee data privacy. The server-side influences are aggregated on each server and only the aggregated information is sent to the client side at which ATTs and standard errors are computed. This figure has been designed using resources from Flaticon.com.

The non-federated DR ATT is defined as the expectation of the difference in outcome between the treated and the control group, weighted by the probability of receiving treatment. It is given, as described in Callaway and Sant’Anna,¹³ by the following equation:

$$ATT\left(g,t;\delta \right)={\mathbb{E}}^{\left(1\right)}\left[\left(\frac{G_g}{{\mathbb{E}}^{\left(2\right)}\left[G_g\right]}-\frac{\frac{p_g\left(X\right)C}{1-p_g\left(X\right)}}{{\mathbb{E}}^{\left(3\right)}\left[\frac{p_g\left(X\right)C}{1-p_g\left(X\right)}\right]}\right)\left(Y_t-Y_{g-\delta -1}-m_{g,t,\delta }\left(X\right)\right)\right]\text{,}$$ (Equation 1)

where expectations are donated with a superscript for referencing purposes. Further variables are defined as follows: $\delta$ is the number of anticipation periods in which individuals know about the upcoming treatment, $G_g$ is a binary variable indicating treatment status in period $g$, $C$ is a binary variable indicating membership in the never-treated control group, $Y_t$ is the outcome variable in period $t$, and $X$ is a matrix of pre-treatment covariates. The term $m_{g,t,\delta }\left(X\right)=\mathbb{E}\left[Y_t-Y_{g-\delta -1}|X,C=1\right]$ is the expected difference in outcome of the control group and $p_g\left(X\right)=\mathbb{E}\left[G_g|X,G_g+C=1\right]$ is the probability of receiving treatment in period $g$ given pre-treatment covariates and treatment status.

To estimate the ATT, the expectations in (1) are replaced by their corresponding sample analogs, which we subsequently denote by hat variables. In the case of central learning,¹⁴ the data are shared and stored centrally (Figure 2C) allowing all information $\left(Y_t,Y_{g-\delta -1},X,G_g,C\right)$ to be available for directly computing the sample analogs of all expectations. However, in the federated setting, the data remain on the server sides to avoid sharing sensitive information. Initially, the servers (but not the client) have access to their individual data $\left(Y_t,Y_{g-\delta -1},X,G_g,C\right)$. Thus, the sample analogs ${\hat{\mathbb{E}}}^{\left(2\right)},{\hat{\mathbb{E}}}^{\left(3\right)},{\hat{p}}_g\left(X\right)$, and ${\hat{m}}_{g,t,\delta }\left(X\right)$ can be computed by the client using federated means and federated GLMs (Figure 2D) via dsBase. For the federated means, only server-aggregated means need to be shared and for the federated GLMs iterative gradient sharing is used to obtain GLM parameter estimates. These parameters and means are then sent to the servers to compute the sample analog of the term inside the expectation of ${\hat{\mathbb{E}}}^{\left(1\right)}$ locally. These local influences can be aggregated using a federated mean in order to compute ${\hat{\mathbb{E}}}^{\left(1\right)}$ on the client-side. A more detailed description of the computation of the federated sample analogs, federated influence functions as well as a description of the federated standard error algorithms is given in the method details section.

Additional privacy-enhancing measures increase security

Our package adheres to DataSHIELD’s data security standards and the highest security standards as per recent assessments, ensuring all function outputs comply with the disclosure settings configured in Opal.³⁷ These measures include, inter alia, preventing the subsetting of data frames if the subset does not meet the minimum row requirement and prohibiting aggregations with fewer objects than the specified threshold determined by the data hosting institution. Given that CSDID subsets individuals for each treatment period and a fixed evaluation period (Figure 2B), servers with low sample sizes may not meet DataSHIELD’s security requirements and, therefore, cannot participate in computing the ATT for those periods. To address this, our package automatically checks in advance which servers have sufficient observations for the respective periods and excludes only those servers for the respective computations. This ensures that treatment effect estimations use larger sample sizes from the remaining servers, improving accuracy and efficiency while maintaining data security and privacy.

Additionally, when performing federated estimation of the influence functions, it is necessary to append columns to a matrix (ds.AppendInfluence). However, this process enables malicious clients to append arbitrary columns to a matrix and therefore the creation of known linearly independent matrices that can cause data leakage of all data points.²⁸ To mitigate this risk, we implement a strategy of row-wise shuffling of data frames and matrices after appending columns. This maintains the integrity of results through ID column matching while protecting against data leakage attacks.

Using globally summarized quantities, such as global means, on the server sides requires data transmission from the client. However, unrestricted data transmission can facilitate data leakage attacks. As a countermeasure, we process all data sent to the server immediately, ensuring it is not stored. For data that must be stored, the client is limited to sending a single number at a time to prevent attacks. Sending known numbers to the servers raises the potential threat of data leakage if the client is able to concatenate multiple known single numbers into different linearly independent vectors.²⁸ Therefore, it is not recommended to use this package with ds.cbind and ds.rbind from DataSHIELD’s base package,³² which can be disabled in Opal to enhance data privacy. However, the use of these two functions is in general, regardless of the federated CSDID package, not recommended because of the aforementioned attack strategy.

The method details section provides further details on the specific functions and the security measures implemented to protect the data privacy.

Federated estimates preserve privacy and equal central learning estimates

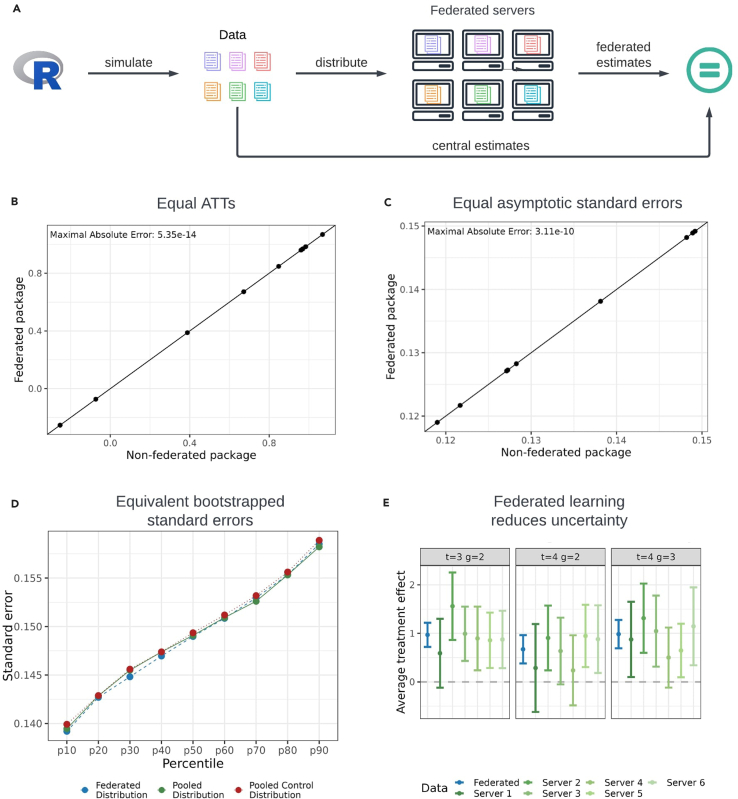
To validate our package, we used a simulated dataset generated with the non-federated R package and compared our federated implementation to the central learning. Specifically, we compared point estimates of the ATT, asymptotic standard errors, and bootstrapped standard errors. Additionally, we assessed the reduction of uncertainty achieved by the federated model compared to study-level analysis, where each data owner analyzes only their local dataset.

We simulated a dataset of 801 individuals with observations at four time periods, randomly allocated across six servers (Figure 3). Note that if all servers have sufficient data to meet the DataSHIELD security requirements for participation, the number of servers will only influence the results up to machine precision due to differences in the order of mathematical operations. This is the case as the federated operations used to compute the CSDID, e.g., means and regressions, do not depend on the number of servers. We have provided the equivalence results from 2 up to 18 servers within the supplementary material (Figure S6). Three servers contained 134 individuals (536 observations each), and three contained 133 individuals (532 observations each). Individuals were either never treated or treated in period two, three, or four. The total dataset comprises 222 individuals who are never treated, 168 individuals treated in period two, 195 individuals treated in period three, and 216 individuals treated in period four. Detailed information on the sample sizes, both pooled and per server, for treated and untreated individuals, as well as information on the data generating process, is provided in the STAR Methods section (data generation of the simulated data). All observations for an individual were stored on one server, reflecting the realistic scenario where different data providers, such as hospitals or schools, do not share data on the same individual. Our main results used the DR estimator with not-yet-treated individuals as the control group. Qualitatively equivalent results for the IPW and OR methods and other control groups are presented in the supplemental information.

Figure 3.

Similarity of federated and central estimation for the DR estimate with not-yet-treated individuals as the control group

(A) Simulation setup. The federated setup involved 6 servers. Three servers had 134 (536) individuals (observations), and three had 133 (532) individuals (observations). Individuals were either never treated or treated in period two or three, with all observations of an individual on one server.

(B) Equality of central and federated point estimates. The x axis shows central (non-federated) estimates,¹⁴ while the y axis shows federated estimates. The 45° line indicates equal results when aligned.

(C) Equality of central and federated asymptotic standard errors. The x axis shows central asymptotic standard errors, and the y axis shows federated standard errors. The 45° line is shown for reference.

(D) Comparison of bootstrapped standard errors. Percentiles of the distribution function compare the distribution of federated (blue) and central (green) bootstrapped standard errors. Two central learning distributions establish reference differences, with 500 bootstrapped standard errors analyzed.

(E) Treatment effect estimates. Point estimates (dots) and 95% confidence intervals for post-treatment periods are shown. Federated package estimates are in blue; estimates from one server are in green. This figure has been designed using resources from Flaticon.com.

We further investigated the scalability of our approach by increasing the number of individuals and comparing it to the pooled CSDID approach implemented in Callaway and Sant’Anna.¹⁴ To do this, we simulated 50 datasets for each specified number of individuals, ranging from 801 to 15,954, and applied both the pooled and federated estimation methods. The number of individuals in the simulation is determined by the specified number of observations (counting multiple data points per individual) within the simulation framework (ranging from 10,000 to 20,000). Both approaches demonstrated linear scalability with feasible computation times, even for large datasets. Notably, the longest recorded time for the federated algorithm with 15,954 individuals was approximately 95 s. The pooled approach, benefiting from the absence of client-server latencies and the ability to process all data simultaneously with minimal communication overhead, was even faster, with a longest recorded estimation time of around 1.8 s. Detailed results are given within Figure S7.

The federated package successfully reproduced the average treatment effect and asymptotic standard errors up to numerical precision. The maximal absolute error for the ATT is $5.35\mathrm{e}-14$ (Figure 3B) and for the asymptotic standard errors it is $3.11\mathrm{e}-10$ (Figure 3C). For the federated bootstrapped standard errors, we relied on inspecting the percentiles of the distributions to evaluate empirical validity, as statistical tests could only reject the null hypothesis of equal distributions, not that they are unequal. Reasoning for this limitation of statistical tests is provided in the method details section. We used a Monte Carlo simulation, repeating the bootstrap computation 500 times for both federated and central settings. Empirical distributions were generated, and the difference between two central learning distributions served as a benchmark for comparison. The distribution percentiles (Figure 3D) show the same pattern. The mean absolute percentile error, defined by the mean of the absolute difference between the federated and the pooled estimates, is $2.64\mathrm{e}-04$, whereas it is $2.98\mathrm{e}-04$ for the difference between the pooled control and the control distribution suggesting that the federated and central learning bootstrapped standard errors are distributional equivalent.

We also examined the impact of the federated implementation on the estimation of the overall treatment effect compared to study-level analysis. By observing the point estimates and 95% confidence intervals, with standard errors obtained from the multiplier bootstrap (Figure 3E), we found that (1) study-level point estimates fluctuated around the federated and central learning point estimate and (2) increased uncertainty in the study-level DR estimates was reflected in wider confidence intervals. The study-level point estimates fluctuated around the federated estimate since the federated simulated data are independent and identically distributed (i.i.d.) in individuals and we allocated the simulated individuals randomly to the servers. Therefore, the server data are also i.i.d, and thus, the point estimates of the study-level analysis fluctuate around the federated estimate. This i.i.d. case is the most favorable scenario for study-level analysis; point estimates will deviate more from the federated estimate in non-i.i.d. settings. The increased size of the confidence intervals reflects reduced sample sizes, resulting in more uncertainty and potentially failing to reject the null hypothesis of no treatment effect in study-level cases where it could be rejected in the federated case. The federated setup yields estimates with lower uncertainty, enhancing the detection of true treatment effects.

Federated learning enables CSDID analysis in cases when central learning fails

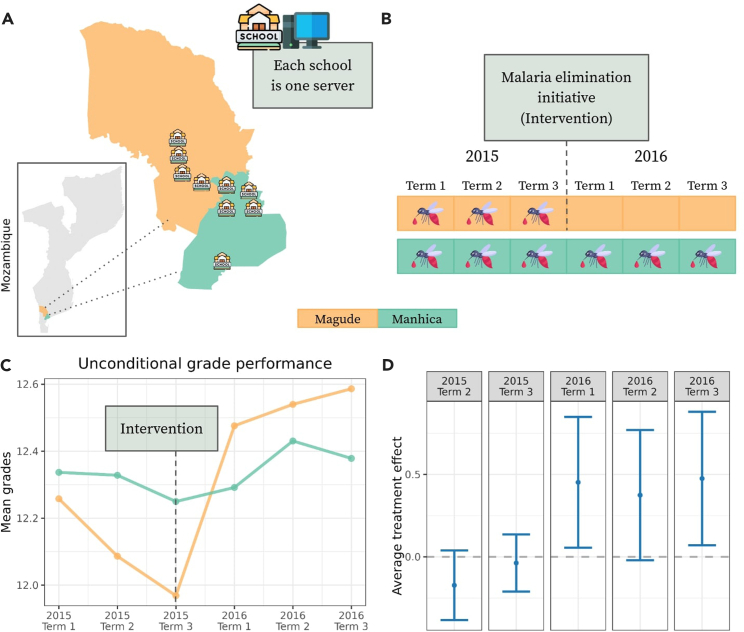
To test the effectiveness of our federated framework in a real-world scenario, we studied the impact of malaria interventions on school outcomes in Mozambique. In 2015, a malaria elimination initiative was implemented in Magude (Figures 4A and 4B) as a quasi-experiment to estimate its impact on selected primary school outcomes. Data were collected from nine schools in two districts of Mozambique. These data were initially analyzed using a regression DID approach,²⁹ which required data sharing agreements for data transfer to analysts. For our analysis, we conducted a complete case analysis with the CSDID, including data from 1,044 individuals with observations available for the three school terms of 2015 and 2016 (Figure 4B). Sample statistics for each school are provided in Table S2 in the supplementary. Student’s performance, as defined in Cirera et al.,²⁹ is measured by the grade point average across several subjects: natural sciences, social sciences, mathematics, music, physical education, Portuguese (language), and visual education. Each subject is graded on a scale from 0 to 20.

Figure 4.

Federated learning enables estimation of DR estimates

(A) The districts of Magude and Manhiça in Mozambique and the location of the 9 schools.

(B) The timeline of the malaria elimination initiative that was launched in Magude before the term 1 in 2016.

(C) Unconditional means of the mean grades in Magude and Manhiça, respectively. The means are estimated as sample averages over the observations (mean grades of students) of the individuals in the respective districts at the respective time.

(D) The subplot presents point estimates (depicted as dots) and 95% confidence intervals of the estimated federated treatment effects for all periods. This figure has been designed using resources from Flaticon.com.

In our federated setup, each of the nine schools hosted their own server, simulating that student data never left the school premises (Figure 4A). Consequently, the schools in Magude (four schools) only had data on treated individuals from 2015, while the schools in Manhiça (five schools) only had data on control group individuals. This separation would make it impossible to estimate non-federated local CSDID average treatment effects without sharing the data with a central hub.

Inspecting the unconditional means, computed in a federated manner, we observed that before the malaria elimination initiative, Magude (the treated district) had a lower grade average compared to Manhiça (Figure 4C). After the initiative, student performance in Magude improved significantly, whereas the improvement in Manhiça was comparatively moderate. To test the hypothesis of the malaria intervention’s effect, we ran the federated CSDID with age and gender as covariates to control for potential confounders (Figure 4D). The results revealed significant differences (at the 95% confidence level) in the first and third terms of 2016, while the estimate for the second term was close to the boundary of significance. Our findings align with those reported by Cirera et al.,²⁹ who, using a regression DID approach, assumed a constant ATT for the 2016 terms and found it to be approximately 0.241. In contrast, our analysis reveals varying ATTs for the 2016 terms: around 0.45 for term 1, 0.37 for term 2, and 0.47 for term 3. These effects are statistically significantly different from zero for the first and third terms, supporting the hypothesis that the malaria elimination initiative positively impacted average grade performance. Additionally, our results show no significant pre-intervention effects, further validating the assumption made by Cirera et al.²⁹ that there was no pre-intervention improvement.

Discussion

The use of federated learning has emerged as a promising approach to minimize exposure of private information, minimizing the need for central data storage and to increase sample sizes when dealing with sensitive data. However, the availability of tools for causal analysis within this context has been limited. To address this gap and make such methods accessible to the research community, we developed a federated version of the DID estimator proposed by Callaway and Sant’Anna¹³ and implemented it in the federated learning platform DataSHIELD using the statistical programming language R. Our federated package covers many functionalities of the CSDID R package.¹⁴ These include different estimation methods, such as doubly robust, inverse probability weighted, and OR-based ATTs. Users can choose between asymptotic and bootstrapped standard errors, select the control group from either all never-treated individuals or all not-yet-treated individuals, and include anticipation periods in their analysis. Additionally, it allows for the estimation of treatment effects when treatment and control groups are only available mutually exclusively to single data owners. Our results demonstrate that the proposed federated version of the CSDID estimator can be implemented while preserving the original estimates, asymptotic standard errors, and distributional equivalent bootstrapped standard errors. Additionally, federated learning reduces uncertainty and allows estimation in scenarios where treated and untreated individuals are separated across data owners. We have ensured that standard DataSHIELD security measures are in place to protect data privacy and have further enhanced security with additional measures.

We specifically chose the Callaway and Sant’Anna estimator due to its high relevance and flexibility. This estimator accommodates multiple time periods for treatments and evaluations, incorporates different types of control groups, and offers various estimators and simultaneous confidence bands via bootstrapped standard errors. Moreover, it requires the parallel trend assumption to hold only after conditioning on covariates, relaxing the assumption of the classical regression DID where the parallel trend must hold unconditionally. In this context, unconditional parallel trends do not allow for time-varying covariates that might affect the control group and the treatment group differently over time, which the CSDID can account for. Future work on federated causal impact analysis could explore estimating treatment effects from repeated cross-sections in the context of CSDID, as implemented in Callaway and Sant’Anna,¹⁴ or synthetic control methods that have gained traction in recent years.^38,39

Our federated version of the CSDID fills a gap in the availability of tools for causal analysis in federated learning. While other functionalities in DataSHIELD, such as linear regression, theoretically enable the estimation of treatment effects using fixed effects regression or even classical DID methods, our tool is the first to offer a user-friendly approach for estimating treatment effects in the presence of complex dependency structures. Our tool highlights the potential of using federated learning for privacy-preserving causal analysis in settings with sensitive data, while maintaining high levels of data security through standard and additional measures implemented within DataSHIELD. In situations where data cannot be shared with practitioners, our tool assists in analyzing these data, enabling the estimation of average treatment effects without compromising privacy. For data that would typically require data-sharing agreements, our tool streamlines the process by reducing the need for such agreements, thus accelerating analysis.

While offering privacy through the DataSHIELD security measures and tailored CSDID privacy measures, our software does not provide a mathematically founded way of privacy, such as differential privacy. We chose not to include differential privacy at this stage to maintain seamless integration with the existing DataSHIELD ecosystem, where the implemented functions, such as means and GLMs, do not currently support differential privacy. Regarding potential vulnerabilities, a malicious analyst could attempt to exploit information shared between data owners and the analyst, such as means or gradients coming from the training of GLMs. Attacks using mean values could be successful if arbitrary subsetting is allowed; however, DataSHIELD includes security measures, such as a threshold for minimal data size, trying to minimize the risk of such exploitation. This threshold is customizable by each data owner. For gradient sharing in GLMs, a similar threshold can be set, determining the ratio of data size to the number of parameters. Additionally for the linear model case, the gradients’ invariance to orthonormal transformations of the output vector and feature matrix adds another layer of complexity for a potential attacker.

The use of federated DID introduces key ethical considerations in handling sensitive data spanning out from the current academic debate. Ensuring that individual privacy is protected without compromising the quality of analysis reflects a commitment to ethical research practices. By preventing the direct sharing of sensitive data, our approach aligns with ethical standards that prioritize the confidentiality and autonomy of individuals, particularly in domains like healthcare where data misuse can have significant ethical and social consequences.

Limitations of the study

This study has four main limitations. The first significant limitation, shared with the non-federated method, is the necessity to bin the time points of individual records into discrete events to apply the CSDID. This binning process can lead to a loss of precise information regarding treatment timings, especially with non-equidistant observations. Splitting these bins further often results in a loss of statistical power, as separate regressions are required for each bin. However, the federated learning approach can alleviate this issue by incorporating data from multiple sources, thereby increasing the number of available data points within each bin. With more data in each bin, it becomes possible in some cases to achieve finer-grained binning, as the larger sample size allows certain bins to be split without sacrificing statistical power. This increased granularity helps to preserve more of the original timing information, thereby reducing the potential loss associated with the binning process. Second, the use of this software package is naturally limited to users familiar with the statistical programming language R²⁴. Moreover, it requires the establishment of a client-server infrastructure. This setup can be challenging for users without extensive technical experience. Nevertheless, the DataSHIELD platform provides comprehensive tutorials for R and community support, which can assist users in overcoming these technical hurdles and adapting to the process more efficiently. A comprehensive starting point is the DataSHIELD Get Started guide (https://www.datashield.org/help/get-started). A link to the Zenodo resources for this paper, including the codes that can serve as an example to build on, can be found within the STAR Methods of this paper. Third, in order to use the DataSHIELD infrastructure and our package, the data need to be harmonized. While this is the case for the ordinary CSDID as well, this can be particularly challenging to coordinate across multiple institutions. However, data collection protocols that are set up in advance can help to speed up this process. Fourth, one notable concern is the potential introduction of bias when certain servers are unable to participate in the computation of the ATT due to insufficient data sizes. This issue can become particularly problematic if there are strong server-specific effects, such as regional differences. In such cases, the exclusion of certain servers could skew the overall results, leading to biased conclusions. However, if the sample sizes are too low for participation, the impact of the excluded data points on the estimates is rather limited, which means that this problem could also arise in a non-federated estimation scenario, if privacy regulations permitted such an approach. It is important for future work to explore methods to mitigate these biases, possibly by ensuring a balanced participation across all servers from the beginning.

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Jan Hasenauer (jan.hasenauer@uni-bonn.de).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• •This paper analyses data in the example of the CSDID. Use of the Mozambique school data requires a data sharing agreement between your institution and the Centro de Investigação em Saúde de Manhiça as it contains privacy sensitive information. All of the data used for the simulation study is made available via Zenodo. It can be accessed via this link: Zenodo: https://doi.org/10.5281/zenodo.11565570.
• •All original code has been deposited at Zenodo and is publicly available under the link Zenodo: https://doi.org/10.5281/zenodo.11565570. This includes the Client- and the Server-side packages, the simulated data, files for the plot replication, the code for the malaria analysis. Additionally, it includes the scripts for the replication of the sensitivity analysis over number of individuals and over the number of servers. After publication, the latest update of the packages can be found on GitHub via https://github.com/datashield/dsBaseClient and https://github.com/manuhuth/dsDid.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Acknowledgments

This study was funded by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) under Germany’s Excellence Strategy (EXC 2047 - 390685813 and EXC 2151 - 390873048) and under the project IDs 432325352—SFB 1454 and 458597554—SEPAN, the University of Bonn (via the Schlegel Professorship of JH), the Helmholtz Association - Munich School for Data Science (MUDS), and the ORCHESTRA project. The ORCHESTRA project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement no 101016167. The views expressed in this paper are the sole responsibility of the authors and the Commission is not responsible for any use that may be made of the information it contains. The funders had no role in the study design, data collection, data analyses, data interpretation, writing, or submission of this manuscript.

Author contributions

M.H. developed the federation of the algorithms. M.H. and C.A.G, implemented the software packages in R. L.C., E.S., and F.S. collected the data for the study in Mozambique. M.H. and L.S. visualized the results. J.H and E.S. conceptualized the study. M.H., E.S., and J.H. wrote the manuscript. All authors read and approved the final manuscript.

The icons for the figures were created by Freepik, Flat Icons, Roundicons, Smashicons, and smashingstocks from www.flaticon.com.

Declaration of interests

The authors declare no competing interests.

Declaration of generative AI and AI-assisted technologies in the writing process

During the preparation of this work the authors used ChatGPT4 in order to improve the readability and language of the manuscript. After using ChatGPT4, the authors reviewed and edited the content as needed and take full responsibility for the content of the published article.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Code for mathematical modeling, analysis and visualization used in the manuscript	This paper	https://doi.org/10.5281/zenodo.11565570
Simulated data	This paper	https://doi.org/10.5281/zenodo.11565570
Software and algorithms
R version 4.3.2	R Core Team	https://www.r-project.org/
dsDiDClient (R package)	Zenodo/GitHub	https://doi.org/10.5281/zenodo.11565570 or https://github.com/manuhuth/dsDidClient
dsDiD (R package)	Zenodo/GitHub	https://doi.org/10.5281/zenodo.11565570 or https://github.com/manuhuth/dsDid
dsBaseClient (R package)	Github	https://github.com/datashield/dsBaseClient
dsBase (R package)	Github	https://github.com/datashield/dsBase

Experimental model and study participant details

This study focuses on primary school children aged 6 to 12 years, initially examined in Cirera et al.²⁹ As outlined in Cirera et al.,²⁹ the participants were selected from five public schools in Magude and four in Manhica, Mozambique. Schools were chosen using a probability proportional to size sampling method, favoring larger schools. The selection data were provided by the Mozambique Ministry of Education, with the number of schools determined by resource constraints.

All students enrolled during 2015 and 2016 were included in the study, with a total of 1,044 participants. Of these, 47.99% were male, and 52.01% were female. In Manhica, there were 794 participants (46.10% male), and in Magude, there were 250 participants (54% male). A chi-square test for independence revealed a significant difference in the biological sex distribution between the districts (p-value = 0.0349), indicating a lack of independence between the number of males and females in Manhica and Magude.

The mean age of participants in Manhica was 9.67 years, while in Magude it was 9.5 years. A t-test comparing these means did not show a significant difference (p-value = 0.2821). To address potential biases related to biological sex and age, both of these factors were included as covariates in the regression analysis, as stated in the results section.

District	Biological Sex (% Male)	Age (Mean +- SD)
Manhica	794 (46.10%)	9.67 ± 2.22
Magude	250 (54.00%)	9.50 ± 2.20
p-value	0.0349	0.2821
test	${\chi }^2$-test	t-test

The study was conducted following ethical guidelines, with oversight from the appropriate institutional review boards. Permission was obtained to ensure the welfare of all participants, and the influence of biological sex and age on the results was carefully considered and controlled for in the analysis.

Method details

List of DataSHIELD client-side functions

We list all functions that are used within the DataSHIELD framework for the client-side³⁵ and explain their functionalities. The main function is ds.did which computes treatment effects and standard errors and calls the other client-side functions while being executed.

• (1)ds.did: Calculates the average treatment effect of the treated, standard errors, and pre-tests for the parallel trend assumption.
• (2)ds.addColumnOnes: Adds a column of ones to a dataframe on the server side.
• (3)ds.appendInfluence: Appends influence to a specified column for given IDs and periods in a dataframe on the server side.
• (4)ds.computeMatrixCrossproduct: Computes the cross product of a matrix on the server side.
• (5)ds.computeOdds: Computes odds using propensity scores for a given dataset and outcome variable.
• (6)ds.createEmptyIdMatrix: Creates an empty matrix with unique identifiers from a dataframe on the server side.
• (7)ds.enoughIndividuals: Checks if enough individuals in a dataframe have a specified value in a specified column on the server side.
• (8)ds.generateNotYetTreated: Generates a dataframe of untreated individuals based on given variables on the server side.
• (9)ds.multiplierBootstrap: Performs multiplier bootstrap on a given influence matrix on the server side.
• (10)ds.multiplyMatrixMatrix: Multiplies two matrices and assigns the result to a new object on the server side.
• (11)ds.multiplyMatrixScalar: Multiplies a matrix and a scalar, then assigns the result to a new object on the server side.
• (12)ds.recode: Creates a new object and replaces entries of a vector.
• (13)ds.sendToServer: Sends a single number to the server side.
• (14)ds.subsetDf: Subsets a dataframe based on a specified variable and value.

Federated sample analogs for point estimates

In more detail, the computations are

• (1)${\hat{\mathbb{E}}}^{\left(2\right)}(·)$: The client computes the sample mean of the variable $G_g$ indicating if an individual has been treated in period $g$ using a federated mean (ds.mean from dsBaseClient). The aggregate mean is then sent back to the servers (ds.SendToServer) for further analysis and processing.
• (2)${\hat{p}}_g\left(x\right)$: The client computes the parameter estimates (ds.glm from dsBaseClient), denoted by $\hat{\pi }$, of a logistic regression model using a federated GLM with the individuals that have been treated in period $g$ or are never treated

$$p_g\left(x\right)=\frac{1}{1+\exp \left(-{\pi }_0-x^T\pi \right)}$$ (Equation 2)

The estimated parameters, $\hat{\pi }$, are then sent to the servers where they are immediately processed to compute the estimated probability of treatment, ${\hat{p}}_g\left(X\right)$, using 2 (ds.genProp). If no covariates are used, the probability of treatment can be directly computed using a federated mean of the variable indicating treatment $G_g$ (ds.mean).

• (1)${\hat{\mathbb{E}}}^{\left(3\right)}(·)$: With the knowledge of the estimated probability of treatment, ${\hat{p}}_g\left(X\right)$, from step 2 and the binary variable indicating if the individual is part of the never-treated group, $C$, the mean of the expected value, ${\hat{\mathbb{E}}}^{\left(3\right)}(·)$, can be computed using a federated mean (ds.mean).
• (2)${\hat{m}}_{g,t,\delta }$: The client computes the parameter estimates $\hat{\beta }$ (ds.glm) of a linear regression model using the individuals that have never been treated and the ones that are treated in $g$. The linear regression model is represented by

$$m_{g,t,\delta }\left(x\right)={\beta }_0+x^T\beta \text{,}$$ (Equation 3)

which relates the expected difference in the outcome of the control group and the covariates $X$. Subsequently, the client sends the estimated parameters $\hat{\beta }$ to the servers, where they are immediately processed to compute ${\hat{m}}_{g,t,\delta }$ by 3 (ds.multiplyMatrixMatrix). If no covariates are used, the client can directly compute ${\hat{m}}_{g,t,\delta }$ by taking the federated mean of $Y_t-Y_{g-\delta -1}$ (ds.mean).

• (1)${\hat{\mathbb{E}}}^{\left(1\right)}(·)$: Finally, the client computes the expectation ${\hat{\mathbb{E}}}^{\left(1\right)}(·)$ by using a federated mean (ds.mean) of all the known quantities and parameters. This expectation represents the point estimate of the average treatment effect of the treated $\widehat{ATT}\left(g,t;\delta \right)$.

Federated computations of influence functions

The influence function, denoted as ${\psi }_{g,t,\delta }\left(W_i,{\beta }_{g,t,\delta }\right)$, measures the impact that each individual has on the estimated treatment effect ${\widehat{ATT}}_{t\ge g-\delta }$. The collection of these influence functions ${\widehat{ATT}}_{t\ge g-\delta }$ is then used to compute (approximate) the variance of ${\widehat{ATT}}_{t\ge g-\delta }$ through the multiplier bootstrap method or asymptotic standard errors. In this section, we demonstrate the federation of the influence function for the DR estimate using the never-treated individuals as the control group. To maintain consistency with the notation used in,¹³ we adhere closely to the notation used in that paper throughout this section. It is also worth noting that, following,¹³ the parameters $\beta ,\pi$ used to estimate $m_{g,t,\delta }\left(X\right),p_g\left(X\right)$ are included in this section.

The theoretical influence function ${\psi }_{g,t,\delta }\left(W_i,{\beta }_{g,t,\delta }\right)$, as defined in,¹³

$${\psi }_{g,t,\delta }\left(W_i,{\beta }_{g,t,\delta }\right)={\psi }_{g,t,\delta }^{treat}\left(W_i,{\beta }_{g,t,\delta }\right)-{\psi }_{g,t,\delta }^{comp}\left(W_i,{\beta }_{g,t,\delta },{\pi }_g\right)-{\psi }_{g,t,\delta }^{est}\left(W_i,{\beta }_{g,t,\delta },{\pi }_g\right)\text{.}$$ (Equation 4)

quantifies the effect of each individual on the treatment estimate ${\widehat{ATT}}_{t\ge g-\delta }$. We will show in the following how this influence function can be estimated on the server sides in a federated manner using sample analogs, denoted by hat variables.

The components of the estimated influence function are given by¹³

$$\begin{array}{l}{\hat{\psi }}_{g,t,\delta }^{treat}\left(W_i,{\beta }_{g,t,\delta }\right)={\widehat{w_g}}^{treat}\left({\beta }_{g,t,\delta }\right)\left(Y_t-Y_{g-\delta -1}-{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)\right)-{\widehat{w_g}}^{treat}\left({\beta }_{g,t,\delta }\right)\hat{\mathbb{E}}\left({\widehat{w_g}}^{treat}\left({\beta }_{g,t,\delta }\right)\left(Y_t-Y_{g-\delta -1}-{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)\right)\right)\\ {\hat{\psi }}_{g,t,\delta }^{comp}\left(W_i,{\beta }_{g,t,\delta },{\pi }_g\right)={\widehat{w_g}}^{comp}\left({\pi }_g\right)[\left(Y_t-Y_{g-\delta -1}-{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)\right)\\ -{\widehat{w_g}}^{comp}\left({\pi }_g\right)\hat{\mathbb{E}}\left({\widehat{w_g}}^{comp}\left({\pi }_g\right)\left(Y_t-Y_{g-\delta -1}-{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)\right)\right)]\\ {\hat{\psi }}_{g,t}^{est}\left(W_i,{\beta }_{g,t,\delta }\right)={\hat{l}}_{g,t}^{or}{\left({\beta }_{g,t,\delta }\right)}^T{\hat{M}}_{g,\delta }^1+{\hat{l}}_g^{ps}{\left({\beta }_{g,t,\delta }\right)}^T{\hat{M}}_{g,\delta }^2\text{,}\end{array}$$ (Equation 5)

where $W_i$ is the collection of all individual information about $Y,X$, and $C$. The weights are defined as ${\widehat{w_g}}^{treat}\left({\beta }_{g,t,\delta }\right)=\frac{G_g}{\hat{\mathbb{E}}\left(G_g\right)}$ and

${\widehat{w_g}}^{comp}\left({\pi }_g\right)=\frac{p_g\left(X;{\pi }_g\right)C}{1-p_g\left(X;{\pi }_g\right)}/\hat{\mathbb{E}}\left(\frac{p_g\left(X;{\pi }_g\right)C}{1-p_g\left(X;{\pi }_g\right)}\right)$ and the asymptotic linear representations of the regression estimator for the outcome evaluation of the comparison group and the generalized propensity score are

$$\begin{array}{l}{\hat{l}}_{g,t}^{or}=\left[\left(Y_t-Y_{g-\delta -1}-{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)\right)◦X\right]{\left(X^{T}X\right)}^{-1}\\ {\hat{l}}_g^{ps}=\left[\left(G_g-p_g\left(X;{\pi }_g\right)\right)◦X\right]H_g^{ps}\text{,}\end{array}$$ (Equation 6)

where $a·B$ defines a columnwise Hadarmad product between the vector $a\in {\mathbb{R}}^n$ and the matrix $B\in {\mathbb{R}}^{n\times k}$. $H_g^{ps}$ is the hessian obtained from the regression on $p_g\left(X;{\pi }_g\right)$.

$$\begin{array}{l}{\hat{M}}_{g,\delta }^1=\hat{\mathbb{E}}\left[\left({\widehat{w_g}}^{treat}\left({\beta }_{g,t,\delta }\right)-{\widehat{w_g}}^{comp}\left({\pi }_g\right)\right)◦X\right]\\ {\hat{M}}_{g,\delta }^2=\hat{\mathbb{E}}\left[{\widehat{w_g}}^{comp}\left({\pi }_g\right)\left(Y_t-Y_{g-\delta -1}-{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)\right)◦X\right]-\hat{\mathbb{E}}\left[{\left({\widehat{w_g}}^{comp}\left({\pi }_g\right)\right)}^2\left(Y_t-Y_{g-\delta -1}-{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)\right)◦X\right]\end{array}$$ (Equation 7)

where ${\pi }_g$ is the analog of $\pi$ in Equation 2 and ${\beta }_{g,t,\delta }$ is the analog of $\beta$ in Equation 3.

To compute the influence function in a federated manner, the sample analogs of the theoretical influence function must be computed on the client side. Specifically, the client must compute ${\hat{\psi }}_{g,t,\delta }^{treat}\left(W_i,{\beta }_{g,t,\delta }\right)$, ${\hat{\psi }}_{g,t,\delta }^{comp}\left(W_i,\beta g,t,\delta ,{\pi }_g\right)$, and ${\hat{\psi }}_{g,t,\delta }^{est}\left(W_i,{\beta }_{g,t,\delta },{\pi }_g\right)$ using the individual data available on the servers. These sample analogs will be used to estimate the noise-corrupted influence function ${\psi }_{g,t,\delta }^{\ast }\left(W_i,{\beta }_{g,t,}\right)$.

• (1)${\hat{\psi }}_{g,t,\delta }^{treat}\left(W_i,{\beta }_{g,t,\delta }\right)$: $Y_t,Y_{g-\delta -1},{\widehat{w_g}}^{treat}\left({\beta }_{g,t,\delta }\right)$, and ${\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)$ are known from the federated point estimate computations on the server side. ${\widehat{w_g}}^{treat}\left({\beta }_{g,t,\delta }\right)\left(Y_t-Y_{g-\delta -1}-{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)\right)$ can therefore be computed on the client side (ds.make from dsBaseClient). Subsequently, the federated expectation can be returned to the client side (ds.mean) and be sent back to the server side (ds.SendToServer). Finally, ${\hat{\psi }}_{g,t,\delta }^{treat}\left(W_i,{\beta }_{g,t,\delta }\right)$ can be computed on the server side (ds.make).
• (2)${\hat{\psi }}_{g,t,\delta }^{comp}\left(W_i,{\beta }_{g,t,\delta },{\pi }_g\right)$: Analogsly to ${\hat{\psi }}_{g,t,\delta }^{treat}\left(W_i,{\beta }_{g,t,\delta }\right)$ using ${\widehat{w_g}}^{comp}\left({\pi }_g\right)$ instead of δ${\widehat{w_g}}^{treat}\left({\beta }_{g,t,}\right)$.
• (3)
  ${\hat{\psi }}_{g,t}^{est}\left(W_i,{\beta }_{g,t,\delta }\right)$: ${\hat{l}}_{g,t}^{or},{\hat{l}}_g^{ps},{\hat{M}}_{g,\delta }^1$, and ${\hat{M}}_{g,\delta }^2$ are unknown to the server side after the federated point estimate computations.

  • (a)
    ${\hat{l}}_{g,t}^{or}$: $Y_t,Y_{g-\delta -1},{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)$, and $X$ are known from the federated point estimate computations on the server side. $\left(X^{T}X\right)$ can be computed via a federated aggregation (ds.computeMatrixCrossproduct) and be sent to the client side, where its inverse ${\left(X^{T}X\right)}^{-1}$ is computed and send to the servers. Subsequently, ${\hat{l}}_{g,t}^{or}$ can be computed on the server side (ds.multiplyMatrixMatrix).
  • (b)
    ${\hat{M}}_{g,\delta }^1$: ${\widehat{w_g}}^{treat}\left({\beta }_{g,t,\delta }\right),{\beta }_{g,t,\delta },X$ and ${\widehat{w_g}}^{comp}\left({\pi }_g\right))$, are known to the server side from the federated point estimate computations. Such that $\left({\widehat{w_g}}^{treat}\left({\beta }_{g,t,\delta }\right)-{\widehat{w_g}}^{comp}\left({\pi }_g\right)\right)°X$ can be computed on the server side (ds.make) and the expectation can be estimated on the client side using a federated mean (ds.mean). The federated mean is subsequently send back to the servers (ds.sendToServer).
  • (c)
    ${\hat{l}}_g^{ps}$: $Y_t,Y_{g-\delta -1},{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)$, and $X$ are known from the federated point estimate computations on the server side such that $G_g-\left(p_g\left(X;{\pi }_g\right)\right)◦X$ can be computed on the server side (ds.make). $\left(H_g^{ps}\right)$ can be sent to the server side where it is immediately multiplied to compute ${\hat{l}}_g^{ps}$ on the server side (ds.multiplyMatrixMatrix).
  • (d)
    ${\hat{M}}_{g,\delta }^2$: ${\widehat{w_g}}^{comp}\left({\pi }_g\right),Y_t,Y_{g-\delta -1},{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)$ and $X$, are known to the server side from the federated point estimate computations. ${\widehat{w_g}}^{comp}\left({\pi }_g\right)\left(Y_t-Y_{g-\delta -1}-{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)\right)X$ and ${\left({\widehat{w_g}}^{comp}\left({\pi }_g\right)\right)}^2\left(Y_t-Y_{g-\delta -1}-{\hat{m}}_{g,t,\delta }\left(X;{\beta }_{g,t,\delta }\right)\right)◦X$ can therefore be computed on the server side (ds.make). The expectations can be returned to the client side using a federated mean (ds.mean). The means are subsequently send back to the servers (ds.sendToServer).

${\hat{l}}_{g,t}^{or},{\hat{l}}_g^{ps},{\hat{M}}_{g,\delta }^1$ and ${\hat{M}}_{g,\delta }^2$ are now known to the server side. ${\hat{l}}_{g,t}^{or}{\left({\beta }_{g,t,\delta }\right)}^T{\hat{M}}_{g,\delta }^1$ and ${\hat{l}}_g^{ps}{\left({\beta }_{g,t,\delta }\right)}^T{\hat{M}}_{g,\delta }^2$ can therefore be computed on the servers

(ds.multiplyMatrixMatrix). Subsequently, ${\hat{\psi }}_{g,t}^{est}\left(W_i,{\beta }_{g,t,\delta }\right)$ can be computed on the server sides (ds.make).

Knowing ${\hat{\psi }}_{g,t,\delta }^{treat}\left(W_i,{\beta }_{g,t,\delta }\right),{\hat{\psi }}_{g,t,\delta }^{comp}\left(W_i,{\beta }_{g,t,\delta },{\pi }_g\right)$ and ${\hat{\psi }}_{g,t,\delta }^{est}\left(W_i,{\beta }_{g,t,\delta },{\pi }_g\right)$ on the server sides, ${\hat{\psi }}_{g,t,\delta }^{\ast }$ can be computed on the server sides (ds.make).

Federated asymptotic variance-covariance matrix

In this subsection, we will demonstrate the estimation of the asymptotic variance-covariance matrix of the average treatment effect’s estimates in a federated setting.

The asymptotic distribution of the ATT is defined in¹³ as

$$\sqrt{n}\left({\widehat{ATT}}_{t\ge g-\delta }-AT{T}_{t\ge g-\delta }\right)\stackrel{d}{\sim }\mathcal{N}\left(0,\mathbb{E}\left[{\mathrm{\Psi }}_{t\ge g-\delta }\left(W\right){\mathrm{\Psi }}_{t\ge g-\delta }{\left(W\right)}^T\right]\right)\text{,}$$ (Equation 8)

where $AT{T}_{t\ge g-\delta }$ is the collection of $ATT\left(g,t;\delta \right)$ with $t\ge g-\delta$ and ${\mathrm{\Psi }}_{t\ge g-\delta }\left(W\right)$ is the collection of relevant influence functions ${\psi }_{g,t,\delta }$.

In order to estimate $\mathbb{E}\left[{\mathrm{\Psi }}_{t\ge g-\delta }\left(W\right){\mathrm{\Psi }}_{t\ge g-\delta }{\left(W\right)}^T\right]$, we use the sample analog ${\hat{\mathrm{\Psi }}}_{t\ge g-\delta }{\left(W\right)}^T{\hat{\mathrm{\Psi }}}_{t\ge g-\delta }\left(W\right)$, where the number of rows in the matrix ${\hat{\mathrm{\Psi }}}_{t\ge g-\delta }\left(W\right)$ corresponds to the total number of individuals and each column represents a combination of treatment periods $g$ and treatment evaluation periods $t$. The federated matrix product is computed using (ds.computeMatrixCrossproduct), which we explain more detail within the section federated matrix product with its transpose.

Federated multiplier bootstrap

The multiplier bootstrap allows computations of (clustered) standard errors. Callaway and Sant’Anna¹³ define one draw of the multiplier bootstrap as

$${\widehat{ATT}}_{t\ge g-\delta }^{\left(b\right)}={\widehat{ATT}}_{t\ge g-\delta }+{\mathbb{E}}_n\left[V·{\hat{\mathrm{\Psi }}}_{t\ge g-\delta }\left(W\right)\right]\text{,}$$ (Equation 9)

where ${\hat{\mathrm{\Psi }}}_{t\ge g-\delta }\left(W\right)$ is the sample analog of ${\mathrm{\Psi }}_{t\ge g-\delta }\left(W\right)$ and ${\mathbb{E}}_n\left(a\right)$ is the expectation over the components of a vector $a$. $V$ is a random variable with $P\left(V=1-\frac{\sqrt{5}+1}{2}\right)=\frac{\sqrt{5}+1}{2\sqrt{5}}$ and $P\left(V=\frac{\sqrt{5}+1}{2}\right)=1-\frac{\sqrt{5}+1}{2\sqrt{5}}$. We subsequently show that the multiplier bootstrap can be federated using an example with $s$ servers. By running the computations on each server (ds.multiplierBootstrap) and aggregating the results via a federated mean (ds.mean), the client can, due to the randomness of $V$, not exactly reproduce the results but obtain the same results qualitatively. Let ${\hat{\mathrm{\Psi }}}_{t\ge g-\delta }{\left(W\right)}^{\left(k\right)}$ be the estimated influence matrix and $v^{\left(k\right)}$ be the vector or observations drawn from $V$ on server $k$, such that

$$\begin{array}{cc}{\hat{\mathbb{E}}}_n\left[V·{\hat{\mathrm{\Psi }}}_{t\ge g-\delta }\left(W\right)\right]& ={\hat{\mathbb{E}}}_n\left(\begin{array}{c}{v}^{\left(1\right)}·{\hat{\mathrm{\Psi }}}_{t\ge g-\delta }{\left(W\right)}^{\left(1\right)}\\ ⋮\\ v^{\left(s\right)}·{\hat{\mathrm{\Psi }}}_{t\ge g-\delta }{\left(W\right)}^{\left(s\right)}\end{array}\right)\end{array}$$ (Equation 10)

The multiplier bootstrap can be run on each server (ds.multiplierBootstrap) and multiplied by the server side sample size in order to compute each row of the matrix on the right hand-side of 10 on the respective servers. The client subsequently returns an estimate of the expectation using (ds.mean). The variance-covariance matrix of the average treatment effect’s estimate can finally be estimated with $B$ bootstrap draws $\frac{1}{B-1}{\sum }_{b=1}{\widehat{ATT}}_{t\ge g-\delta }^{\left(b\right)}{\left({\widehat{ATT}}_{t\ge g-\delta }^{\left(b\right)}\right)}^T$.

Federated matrix product with its transpose

To compute asymptotic standard errors, the matrix product of the transposed data and itself must be returned to the client side. This allows for the calculation of the asymptotic linear representation, denoted ${\hat{l}}_{g,t}^{or}$, of the OR in Equation 7. In our package, this is done via the function ds.computeMatrixCrossproduct. Let $Z^{\left(i\right)}=\left(\begin{array}{ccc}{z}_1^{\left(i\right)}& \dots & z_p^{\left(i\right)}\end{array}\right)\in {\mathbb{R}}^{n\times p}$, for $i=1,2,\dots ,s$, be data matrices of $s$ different servers such that the full data $Z$ is given, without loss of generality, by

$$\begin{array}{c}Z=\left(\begin{array}{ccc}{z}_1^{\left(1\right)}& \dots & z_p^{\left(1\right)}\\ z_1^{\left(2\right)}& \dots & z_p^{\left(2\right)}\\ ⋮& ⋮& ⋮\\ z_1^{\left(s\right)}& \dots & z_p^{\left(s\right)}\end{array}\right)=\left(\begin{array}{c}{Z}^{\left(1\right)}\\ Z^{\left(2\right)}\\ ⋮\\ Z^{\left(s\right)}\end{array}\right)\end{array}$$ (Equation 11)

The matrix product of it’s transpose is therefore given by

$$Z^{T}Z={\left(\begin{array}{c}{Z}^{\left(1\right)}\\ Z^{\left(2\right)}\\ ⋮\\ Z^{\left(s\right)}\end{array}\right)}^T\left(\begin{array}{c}{Z}^{\left(1\right)}\\ Z^{\left(2\right)}\\ ⋮\\ Z^{\left(s\right)}\end{array}\right)=\left(\begin{array}{ccc}{Z}^{\left(1\right)T}{Z}^{\left(2\right)T}& \dots & Z^{\left(s\right)T}\end{array}\right)\left(\begin{array}{c}{Z}^{\left(1\right)}\\ Z^{\left(2\right)}\\ ⋮\\ Z^{\left(s\right)}\end{array}\right)=\sum _{i=1}^s{Z}^{\left(i\right)T}{Z}^{\left(i\right)}\text{.}$$ (Equation 12)

The multiplication of the server-side data with its transposed $Z^{\left(i\right)T}{Z}^{\left(i\right)}$ can be computed on each server and returned to the client side if it contains at least as enough different entries as allowed by the data providers via DataSHIELDS disclosure settings (default is 5). Knowing all $Z^{\left(i\right)T}{Z}^{\left(i\right)}$ on the client side, the sum can subsequently be computed on the client side to obtain $Z^{T}Z$.

Federated column appending of influence functions

While iterating over the treatment periods $g$ and the treatment impact periods $t$, the data frames are subsetted with respect to the individuals who are either treated in $g$ or in the control group. On the client side, the influence function is computed for these subsetted individuals. To apply the clustered multiplier bootstrap, however, the influence function must be sent back to the server side after each iteration of $g$ and $t$. Since the individuals change every iteration, simply appending the influences column-wise is not possible. Therefore, we create a data frame filled with zeros and one column indicating the ID of the individuals, which is known to the server. However, appending a full vector, even though the vector is stored on ther server side, poses a data security problem as it allows for the Covariance-Based Attack Algorithm described in Huth et al.²⁸ To address this, the rows of the data frame are randomly shuffled after each iteration.

To enhance understanding, we present a simplified example utilizing 4 individuals, two treatment periods $g=1,2$, and two treatment impact periods $t=3,4$. We assume that individual ${\text{id}}_1$ is treated in $g=1$, individual ${\text{id}}_3$ is treated in $g=2$, and individuals ${\text{id}}_2$ and ${\text{id}}_4$ are never treated. The initialized data frame ${\mathcal{F}}_0$ would be given by

$${\mathcal{F}}_0=\left(\begin{array}{ccccc}id& {\hat{\psi }}_{1,3}& {\hat{\psi }}_{2,3}& {\hat{\psi }}_{1,4}& {\hat{\psi }}_{2,4}\\ {id}_1& 0& 0& 0& 0\\ {id}_2& 0& 0& 0& 0\\ {id}_3& 0& 0& 0& 0\\ {id}_4& 0& 0& 0& 0\end{array}\right)$$ (Equation 13)

At the first iteration, the server stores the ID vector $v_{1,3}={\left(\begin{array}{ccc}\text{id}1& \text{id}2& \text{id}4\end{array}\right)}^T$ of the individuals used in this run. The server computes the influence vector $w_{1,3}={\left(\begin{array}{ccc}3& -1& 2\end{array}\right)}^T$. On the server, the ID vector and the influence vector are matched component-wise to create the matrix $\left(\begin{array}{cc}{v}_{1,3}& w_{1,3}\end{array}\right)$. In the next step, the relevant IDs in the first column of ${\mathcal{F}}_0$ are replaced with the corresponding values from $w_{1,3}$, and the matrix is subsequently shuffled row-wise

$${\mathcal{F}}_1=\left(\begin{array}{ccccc}id& {\hat{\psi }}_{1,3}& {\hat{\psi }}_{2,3}& {\hat{\psi }}_{1,4}& {\hat{\psi }}_{2,4}\\ {id}_4& 2& 0& 0& 0\\ {id}_2& -1& 0& 0& 0\\ {id}_3& 0& 0& 0& 0\\ {id}_1& 3& 0& 0& 0\end{array}\right)$$ (Equation 14)

This procedure is repeated for all combinations of $t$ and $g$ such that the final data frame is, depending on the random shuffling, given by

$${\mathcal{F}}_4=\left(\begin{array}{ccccc}id& {\hat{\psi }}_{1,3}& {\hat{\psi }}_{2,3}& {\hat{\psi }}_{1,4}& {\hat{\psi }}_{2,4}\\ {id}_2& -1& 1& 3& -2\\ {id}_4& 2& 4& 1& 2\\ {id}_1& 3& 0& 2& 0\\ {id}_3& 0& 2& 0& -1\end{array}\right)$$ (Equation 15)

By implementing this method, it is possible to append the influence functions in a privacy-preserving manner.

Verifying the validity of the federated multiplier bootstrap

Our package implements a federated version of the multiplier bootstrap to obtain standard errors. To assess the empirical validity of this federated bootstrap method, we must determine whether the standard errors it produces are equivalent to those generated by a pooled bootstrap. However, direct comparison of these two sets of standard errors is complicated by the inherent randomness of the bootstrap process. To address this challenge, we employ Monte Carlo simulations to generate empirical distributions for both the federated and pooled bootstrapped standard errors. The objective is to assess whether these distributions are derived from the same underlying distribution. In a statistical testing context, this would traditionally involve testing the null hypothesis that the two distributions are unequal. However, existing tests, such as the Kolmogorov-Smirnov test, only allow for testing the null hypothesis that the two distributions are equal. Generally, tests for distributional equivalence operate under the null hypothesis $H_0:F_x=F_y$, where $F_x$ and $F_y$ represent the distribution functions of the two distributions. The outcomes of such tests are typically evaluated based on the test statistic $s$ under $H_0$, with a rejection region ${\mathcal{R}}_{\alpha }$ determined by the chosen significance level $\alpha$. Two possible outcomes emerge: (i) if $s\in {\mathcal{R}}_{\alpha }$, $H_0$ is rejected, indicating evidence against equivalence; (ii) if $s\notin {\mathcal{R}}_{\alpha }$, $H_0$ is not rejected, meaning no evidence against equivalence is found. However, it is crucial to note that a lack of rejection does not constitute evidence for inequality. As a result, such tests with a null hypothesis of distributional equivalence cannot rigorously confirm equivalence; they can only reject it. Given these limitations, we opted not to use a formal statistical test. Instead, we compared the percentiles of each distribution. For this evaluation, we repeated the bootstrap computation 500 times using both the pooled and federated algorithms, resulting in an empirical distribution of bootstrapped standard errors for each method. Additionally, we performed the same process for the pooled implementation of the Callaway and Sant’Anna package to create a reference distribution. Since the two pooled distributions are guaranteed to originate from the same underlying distribution, the differences between these distributions served as for visual inspection.

Data generation of the simulated data

For simulating the data, we used the build_sim_dataset function from the did package¹⁴ to create the dataset and the reset.sim function to simulate the parameters. The simulation follows a linear model-like approach, producing a metric outcome variable. This includes time- and group-varying fixed effects, covariates, treatment effects, and a noise term. Further details on the simulation can be found in the function descriptions and the did starting tutorial.⁴⁰ The full code is available within our Zenodo repository https://doi.org/10.5281/zenodo.11565570.

Quantification and statistical analysis

The statistical details of the statistical analyses, including sample sizes and confidence levels used for confidence interval calculations, are outlined in the respective figure descriptions corresponding to specific subplots.

Published: October 9, 2024