Abstract
Strong relationships exist between sprint cycling torque and isometric mid‐thigh pull (IMTP) force production at one timepoint; however, the relationships between the changes in these measures following a training period are not well understood. Accordingly, this study examined the relationships in the changes of sprint cycling torque and IMTP force following six‐weeks of sprint cycling and resistance training performed by strength‐trained novice cyclists (n = 14). Cycling power, cadence, torque and IMTP force (Peak force [PF]/torque, average and peak rate of force/torque development [RFD/RTD], and RFD/RTD from 0 to 100 ms and 0–200 ms) were assessed before and after training. Training consisted of three resistance and three sprint cycling sessions per week. Training resulted in improvements in IMTP PF (13.1%) and RFD measures (23.7%–32.5%), cycling absolute (10.7%) and relative (10.5%) peak power, peak torque (11.7%) and RTD measures (27.9%–56.7%). Strong‐to‐very strong relationships were observed between cycling torque and IMTP force measures pre‐ (r = 0.57–0.84; p < 0.05) and post‐training (r = 0.63–0.87; p < 0.05), but no relationship (p > 0.05) existed between training‐induced changes in cycling torque and IMTP force. Divergent training‐induced changes in sprint cycling torque and IMTP force indicate that these measures assess distinct neuromuscular attributes. Training‐induced changes in IMTP force are not indicative of training‐induced changes in sprint cycling torque.
Keywords: performance, strength, testing, training
Highlights
Six weeks of resistance and sprint cycling training resulted in improvements in isometric mid‐thigh pull (IMTP) peak force (13.1%) and rate of force development measures (23.7%–32.5%), cycling absolute (10.7%) and relative (10.5%) peak power, peak torque (11.7%), and rate of torque development measures (27.9%–56.7%) in strength‐trained novice cyclists.
No significant relationships were observed between the training‐induced changes in IMTP force measures and sprint cycling torque measures following training.
No significant relationships were observed between the training‐induced changes in cycling peak power and changes in cycling torque, IMTP force, back squat and trap bar deadlift with three repetition maximum.
1. INTRODUCTION
The magnitude and rate at which a cyclist can apply force to the pedal to produce bicycle crank torque are important factors influencing mechanical power production and sprint cycling performance (Gardner et al., 2007; Watsford et al., 2010). Maximal torque (T peak) production is important in overcoming inertia to accelerate the bicycle, while the crank rate of torque development (RTD) is critical given the limited time available for torque production when cycling at moderate‐to‐high cadences. For instance, when pedalling at cadences of 110 revolutions per minute (rpm) or higher, the time available for muscular force production during the pedal downstroke can be less than the 300 ms needed to produce T peak in important lower limb muscles such as the knee extensors during an explosive maximal voluntary isometric contraction protocol (Aagaard et al., 2002). Accordingly, a greater crank RTD early (i.e., first 100 ms) in the pedal downstroke will result in a steeper torque rise and thus greater impulse, which will increase mean crank power and bicycle speed.
Sprint cyclists typically dedicate a substantial amount of time to resistance training to increase muscle strength in order to increase RTD and peak power output (PPO) (Dorel, 2018; Kordi, Folland, Goodall, Menzies, et al., 2020). Accordingly, valid and sensitive measures to assess changes in parameters of neuromuscular function are of importance to our understanding of sprint cycling performance. Cyclist neuromuscular function is commonly assessed using cycle‐ and gym‐based measures (Connolly et al., 2023; Kordi, Folland, Goodall, Menzies, et al., 2020; Vercoe & McGuigan, 2018). On the bicycle, a torque‐velocity test allows the valid and reliable delineation of a cyclist's torque‐ or power‐cadence profile (Dorel, 2018; Wackwitz et al., 2021). While recent technological advancements in power meter technology allows for reliable cycling RTD measurement (Connolly et al., 2022), little is known about the training‐induced changes in this measure. In the gym, physical qualities such as maximal strength can be assessed using repetition maximum (RM) testing in movements such as squat or deadlift, whereas rate of force development (RFD) and PF are commonly assessed using isometric testing, such as the IMTP (Guppy et al., 2018).
Strength measurements (PF/torque, RFD/RTD and weight lifted) are typically evaluated across a range of gym and field assessments (e.g., IMTP, 3RM and sprint cycling). Knowledge of the relationship between training‐induced changes in these measures is important in understanding which neuromuscular factors are indicative of changes in cycling performance. Previous studies reported strong‐to‐very strong relationships between PF/torque (Vercoe & McGuigan, 2018, r = 0.89–0.93, p < 0.05; Connolly et al., 2023, ρ = 0.76, p < 0.01), early and late RFD/RTD (from 0 to 100 ms and 0–200 ms, respectively) and peak RFD/RTD (Connolly et al., 2023; r or ρ = 0.61–0.70; <0.05) produced during an IMTP and sprint cycling at one timepoint. However, an isolated relationship does not imply a causal relationship, and therefore, it is currently unclear whether the training‐induced changes in these qualities are related. Findings from our earlier work (Connolly et al., 2023) revealed differences in the underpinning neuromuscular function measures related to IMTP RFD and sprint cycling torque, indicating a possible diverging response to training. Indeed, previous research provides conflicting evidence around the training‐induced changes in neuromuscular function from strength assessments and cycling. For instance, Rønnestad et al. (2010) reported that an experimental group of 11 well‐trained cyclists increased isometric half‐squat PF by 21.2 ± 4.9% (p < 0.01) and cycling P max by 9.4 ± 2.9% (p < 0.01) following a 12‐week intervention of endurance cycling and lower body heavy strength training. In contrast, Kordi, Folland, Goodall, Menzies, et al. (2020) observed a moderate relationship (r = 0.42–0.47; p < 0.05) between the training‐induced changes in knee extension late RTD (150–200 ms) and cycling P max following a 6‐week isometric cycling specific strength intervention in 24 elite track sprint cyclists. Given this, future research is warranted to determine the relationship between training‐induced changes in strength assessment and cycling neuromuscular function.
To this end, the aims of the present study were to investigate: (i) the extent that sprint cycling torque and IMTP force measures change following training; and (ii) the relationship between training‐induced changes in sprint cycling torque, cycling power, IMTP force and 3RM measures. Based on our earlier findings (Connolly et al., 2023), it was hypothesised that the training‐induced changes in IMTP force and sprint cycling torque would not be related. Further, based on previous findings (Kordi, Folland, Goodall, Menzies, et al., 2020), we also hypothesised that the training‐induced changes in sprint cycling torque measures and cycling PPO would be related.
2. MATERIALS AND METHODS
2.1. Participants
Fourteen recreationally active (as defined by McKay et al., 2022) individuals (mean ± SD; n = 8 males, age 28 ± 5 years, height 181.6 ± 9.6 cm, body mass 83.9 ± 13.2 kg, 3RM back squat 113 ± 17 kg, relative 3RM back squat 1.4 ± 0.4 kg.kg−1; n = 6 females, age 30 ± 8 years, height 170.0 ± 4.8 cm, body mass 67.3 ± 3.9 kg, 3RM back squat 74 ± 15 kg, relative 3RM back squat 1.1 ± 0.2 kg.kg−1) who were strength‐trained (group strength training experience; 2.3 ± 1.6 years, group habitual training 5.3 ± 2.6 h.wk−1) and novice cyclists, volunteered for this study. Participants were required to have more than six months of strength‐training experience and should be completing a minimum of two 1‐h strength sessions per week to be included. Participants were also required to have completed an average of less than 2‐h cycling per week for the past 12 months. A medical questionnaire confirmed that participants had no adverse cardiovascular or musculoskeletal risk factors. Before the commencement of the study, participants provided written informed consent. Ethics approval was provided by the host institution's Ethics Committee.
2.2. Experimental overview
A single‐group, longitudinal (pre‐test/post‐test) study design was employed to determine the effects of a 6‐week training program consisting of sprint cycling (Table S1) and resistance training (Figure S1). Prior to (pre‐testing; 6 ± 3 days) and following (post‐testing; 3 ± 1 day) the 6‐week training programme, participants completed an IMTP and sprint cycling testing protocol (described below), with each protocol separated by 30‐min passive rest. All participants performed a familiarisation session within seven days of pre‐testing, where each protocol was performed in a randomised order and anthropometric data (height and body mass) were collected. Protocol order was kept consistent from pre‐to post‐training testing for each participant. Participants body mass was also collected on arrival at pre‐ and post‐testing. Pre‐ and post‐testing sessions were completed at the same time of the day (±1 h) to avoid diurnal fluctuations in performance (Teo et al., 2011). For all testing sessions, participants were requested to refrain from ingesting stimulants or depressants for 12 h, strenuous exercise for 36 h, and to arrive 3 h post‐prandial in a well‐hydrated state. Participants were requested to refrain from performing any additional resistance‐type or high‐intensity training for the duration of the study (confirmed verbally post‐study).
2.3. 6‐Week training programme
Within each week of the programme, participants were prescribed three ergometer sprint cycle sessions (Table S1) and three gym‐based resistance training sessions (Figure S1). The aims of the resistance training program were to develop lower and upper body maximal strength and RFD capabilities. The aims of the cycling program were to develop all areas of the cycling power‐ and torque‐cadence relationships. All training sessions were supervised by the lead researcher.
Training program sprint cycle sessions commenced with a 15‐min standardised warm‐up. Training program sprint cycle sessions were performed on an ergometer (Wattbike Ltd), fitted with clipless pedals. Participants were fitted with cycling shoes (Shimano RP1, Sakai City, Japan) and instructed to “attack the effort as fast and as hard as possible” for all sprints, with strong verbal encouragement provided throughout (Kordi, Folland, Goodall, Menzies, et al., 2020).
Participants commenced training program gym sessions with a warm‐up and plyometrics (Figure S1). Participants were prescribed a bilateral, compound, multi‐joint key lift (back squat and trap bar deadlift), a secondary key exercise (hip thrusts and dynamic mid‐thigh clean pull), a unilateral exercise (box step up, rear foot elevated split squat and barbell lunge press), as well as supplementary exercises. The key lifts consisted of 3 sets of 5 repetitions, with a 2–3‐s descent, a maximal mobilisation of the load in the concentric phase, and 3–5‐min recovery between sets. Participants were instructed to perform the concentric phase of all key lifts “as fast and as hard as possible”. To determine dynamic lower‐body strength, back squat 3RM was assessed during resistance session one on weeks 1 and 6 of the training programme. Trap bar deadlift 3RM was assessed during resistance session two on weeks 1 and 6 of the training program. Each 3RM testing session was preceded by at least 36‐h rest and replicated the protocol of Darrall‐Jones et al. (2015). The 3RM data on week one were used for loading prescriptions for key lifts for the remainder of the program (Munro & Haff, 2018).
2.4. Isometric Mid‐Thigh Pull (IMTP)
Before the maximal IMTP testing, participants performed a standardised warm‐up (Guppy et al., 2022). Following 2 min of passive rest, participants were placed in a posture and bar position corresponding to the start of the second pull of the power clean (Haff et al., 1997) with hip and knee angles of 146 ± 4° and 142 ± 3°, respectively. Participants then performed one set of five 1‐s and one set of five 5‐s IMTP trials, with a 1‐min passive rest between trials and a 10‐min passive rest between sets. Set order was randomised during the familiarisation session and then standardised throughout. Participants were instructed to complete each trial “as fast and as hard as possible” for the 1‐s trials, and as “hard and as fast as possible” for the 5‐s trials (Guppy et al., 2022). The equipment used, standardisation of the set‐up (i.e., joint angles, bar height, hand grip width, foot position), individual trial countdown, implementation of the pull and in‐session trial exclusion criteria replicated the methods described previously by Guppy et al. (2022).
No filtering was applied to the force‐time data during analysis (Dos’Santos et al., 2018). All collected force‐time curves were analyzed using custom software (LabVIEW, Version 14.0, National Instruments). Force onset was defined as “the last peak/trough before the signal deflects away from baseline noise” (Tillin et al., 2010) and identified manually using previously outlined methods (Guppy et al., 2021). Peak force (PF) was defined as the maximum force in each trial minus the participants' body mass. Peak RFD (RFDpeak) was the fastest RFD during any 20‐ms sampling window (Haff et al., 2015). Early and late RFD (or RTD for the cycling protocol below) were defined as RFD in the time bands 0–100 ms (RFD0‐100) and 0–200 ms (RFD0‐200), respectively, with both calculated as the quotient of the changes in force and time. Average RFD (RFDavg) was calculated as the change in force from force onset to PF divided by the time elapsed (Haff et al., 2015). In accordance with previous recommendations, data for all RFD variables were derived from the 1‐s IMTP, while PF was derived from the 5‐s IMTP (Guppy et al., 2022). Once processed, the means of the 3 “best trials” within each set in each testing session were used for statistical analysis. The definitions for “best trials” replicated Connolly et al. (2023).
2.5. Sprint cycle protocol (pre‐ and post‐programme testing)
Cycling performance tests were performed on a Velotron cycle ergometer (Dynafit Pro Velotron; RacerMate), which was fitted with clipless pedals. Ergometer dimensions were adjusted to a comfortable position for each participant during familiarisation and were standardised throughout. Participants wore cycling shoes (Shimano RP1) fitted with cleats. The ergometer was fitted with 172.5 mm Infocrank powermeter cranks (Verve Cycling, Perth, Australia) that measured left and right crank torques independently. Once‐per‐revolution power, cadence and torque measurements (256 Hz analogue‐digital conversion rate) were recorded via customised Infocrank data logger software (Infocrank, Australia) and stored on a mobile phone (Sony Experia Z3 Compact). The warm‐up and main set were controlled by Velotron Coaching and Wingate software (RacerMate Inc), respectively.
The sprint cycle protocol commenced with participants performing a standardised 15‐min warm‐up. After 5‐min passive rest, participants performed three 5‐s sprints initiated from stationary starts against external resistances of 0.2, 0.4, and 0.6 Nm.kg−1 and two 5‐s sprints initiated from rolling starts (20‐s lead in) with an initial cadence of ∼80 rpm and external resistances of 0.0 and 0.2 Nm.kg−1. All sprints were separated by 5 min of passive rest. Sprints were conducted in a randomised order during familiarisation and were standardised throughout. Vigorous verbal encouragement was provided throughout each sprint, where participants were requested to remain seated and keep their hands on the dropped portion of the handlebars. For all stationary start sprints, the crank starting position of the lead sprint leg was standardised at 90° (0° = Top dead center) using a wooden block as this position was easiest to standardise. The lead sprint leg was self‐selected by the participants during familiarisation and was standardised throughout.
All collected torque, power and cadence data were downloaded and processed using Microsoft Excel 2010 (Microsoft Excel, 2010). All RTD measurements were calculated using the average of downstrokes 2 and 3 from the 0.6 Nm.kg−1 sprint replicating the methods of Connolly et al. (2022). The definition for torque onset and the calculation of RTD0‐100, RTD0‐200, RTDavg and RTDpeak mirrored that which was used in the IMTP protocol. Once individual downstrokes were processed, RTD measures were averaged for downstrokes 2 and 3.
The maximum torque produced within the subset of all downstrokes in all sprints in each testing session (i.e., pre‐ and post‐testing) was recorded as the peak torque (T peak). The observed (i.e., actual) peak cadence (RPMpeak) and PPO were the highest observed cadence and power in all sprints in each testing sessions (Table 1). In addition, power‐cadence (P‐C) and torque‐cadence (T‐C) relationships were developed using the mean torque values for each pedal stroke and the cadence and power data using the processing methods described by Connolly et al. (2023). The T‐C and P‐C relationships were established by fitting linear and third‐order polynomial regressions, respectively (Connolly et al., 2023; Wackwitz et al., 2021). The y‐intercept was set at zero for the P‐C relationship. The apex of the P‐C relationship was interpolated to derive theoretical peak power (P max) and cadence at P max (i.e., optimal cadence; RPMopt). Theoretical maximal torque (T 0) and maximal cadence (RPMmax) were the extrapolated y‐ and x‐intercepts of the torque‐cadence relationship. Individual P‐C and T‐C relationships were modelled from 19.5 ± 2.5 (mean ± SD) data points and had an r 2 equal to 0.997 ± 0.003 and 0.983 ± 0.014, respectively.
TABLE 1.
Pre‐ and post‐sprint cycling, isometric mid‐thigh pull (IMTP) and three repetition maximum (3RM) testing values in strength‐trained novice cyclists.
| Protocol | Measure | Pre (Week 1 for 3RM) | Post (Week 6 for 3RM) | % change | p‐value | Hedge's effect size (95%CI) |
|---|---|---|---|---|---|---|
| Cycling | PPO (W) | 1071 ± 250 | 1186 ± 246 | 10.7 | <0.01 | 0.45 (−0.30–1.20) |
| PPO:BM (W/kg) | 13.9 ± 2.3 | 15.4 ± 2.0 | 10.5 | <0.01 | 0.68 (−0.09–1.44) | |
| RPMpeak (rpm) | 185 ± 15 | 192 ± 14 | 4.3 | <0.01 | 0.47 (−0.28–1.22) | |
| Tpeak (Nm) | 207.1 ± 37.8 | 231.4 ± 35.1 | 11.7 | <0.01 | 0.65 (−0.11–1.41) | |
| RTD0‐100 (Nm.s−1) | 291.2 ± 111.4 | 456.4 ± 171.9 | 56.7 | <0.01 | 1.11 (0.31–1.90) | |
| RTD0‐200 (Nm.s−1) | 522.9 ± 176.9 | 716.1 ± 224.7 | 36.9 | <0.01 | 0.93 (0.15–1.71) | |
| RTDavg (Nm.s−1) | 507.0 ± 151.9 | 657.5 ± 186.3 | 29.7 | <0.01 | 0.86 (0.09–1.63) | |
| RTDpeak (Nm.s−1) | 864.9 ± 252.0 | 1106.2 ± 296.2 | 27.9 | <0.01 | 0.85 (0.08–1.63) | |
| T 0 (Nm) | 165.2 ± 25.0 | 182.0 ± 29.2 | 10.2 | <0.01 | 0.60 (−0.16–1.36) | |
| P max (W) | 1066.6 ± 255.4 | 1171.9 ± 265.7 | 9.9 | <0.01 | 0.39 (−0.36–1.14) | |
| RPMmax (rpm) | 232.2 ± 19.4 | 234.1 ± 19.1 | 0.8 | 0.44 | 0.10 (−0.65–0.84) | |
| RPMopt (rpm) | 118 ± 10 | 119 ± 9 | 0.8 | 0.77 | 0.10 (−0.64–0.84) | |
| IMTP | Peak force (N) | 1811.7 ± 573.6 | 2049.8 ± 608.4 | 13.1 | <0.01 | 0.39 (−0.36–1.14) |
| RFD0‐100 (N.s−1) | 3303.4 ± 1862.0 | 4246.6 ± 1828.5 | 28.6 | <0.01 | 0.50 (−0.26–1.25) | |
| RFD0‐200 (N.s−1) | 2786.7 ± 1146.9 | 3520.1 ± 1179.2 | 26.3 | <0.01 | 0.61 (−0.15–1.37) | |
| RFDavg (N.s−1) | 2852.5 ± 1465.4 | 3778.8 ± 2364.0 | 32.5 | 0.02 | 0.46 (−0.29–1.21) | |
| RFDpeak (N.s−1) | 11,344.2 ± 5608.7 | 14,030.1 ± 6419.9 | 23.7 | <0.01 | 0.35 (−0.40–1.09) | |
| 3RM | Back squat (kg) | 96 ± 25 | 108 ± 25 | 12.5 | <0.01 | 0.47 (−0.28–1.22) |
| Trap bar deadlift (kg) | 106 ± 35 | 119 ± 36 | 12.3 | <0.01 | 0.36 (−0.39–1.10) |
Note: Pre‐ and post‐values expressed as mean ± SD (n = 14). Hedge's effect size presented with 95% confidence intervals (CI).
Abbreviations: P max, theoretical peak power; PPO, observed peak power output; PPO:BM, PPO relative to body mass; RFD/RTD0‐100 and RFD/RTD0‐200, rate of force/torque development from 0 to 100 ms and 0–200 ms; RFD/RTDavg, average rate of force/torque development; RFD/RTDpeak, peak rate of force/torque development; RPMmax, theoretical peak cadence; RPMopt, theoretical optimal cadence; RPMpeak, observed peak cadence; T 0, theoretical peak torque; Tpeak, observed peak torque.
Statistical significance set at p < 0.05.
2.6. Statistical analysis
Descriptive statistics are reported as mean ± SD (Table 1). A linear mixed‐effect model using the R package (version 4.0.2, R Core Team, 2020) lme4 (Bates et al., 2015) was used to determine whether differences existed between pre‐ and post‐test IMTP, sprint cycling and 3RM variables. Accordingly, fixed effects were gender and timepoint, whereas participants were a random effect. Pairwise comparisons were performed using R emmeans package (Lenth, 2020). Visual inspection of the residual plots using R easystats performance package (Lüdecke et al., 2021) confirmed that linear modelling assumptions were met. Statistical significance was accepted at p < 0.05. Hedge's effect sizes (g) were calculated (with 95% confidence intervals) in a custom script (Hedges & Olkin, 1985) with bias corrected (Table 1) to estimate the magnitude of performance change and interpreted as trivial (<0.2), small (0.21–0.60), moderate (0.61–1.20), large (1.21–2.0), very large (2.1–4.0) and extremely large (>4.0) (Hopkins et al., 2009). Pearson's product–moment correlations (r) were computed in Prism GraphPad (Version 9.2.0) and used to examine the relationship between the following: (i) IMTP force and sprint cycling torque pre‐ and post‐training (Figure 1); (ii) the training‐induced change in IMTP force and cycling torque (Figure 2); and (iii) the training‐induced change in cycling PPO and P max with cycling torque, IMTP force and 3RM (Table 2). The Hopkins‐modified Cohen's scale was used to describe the relationships as follows: <0.1, trivial; 0.1–0.3, small (weak); 0.3–0.5, moderate; 0.5–0.7, large (strong); 0.7–0.9, very large (very strong); and >0.9, almost perfect (Hopkins et al., 2009).
FIGURE 1.
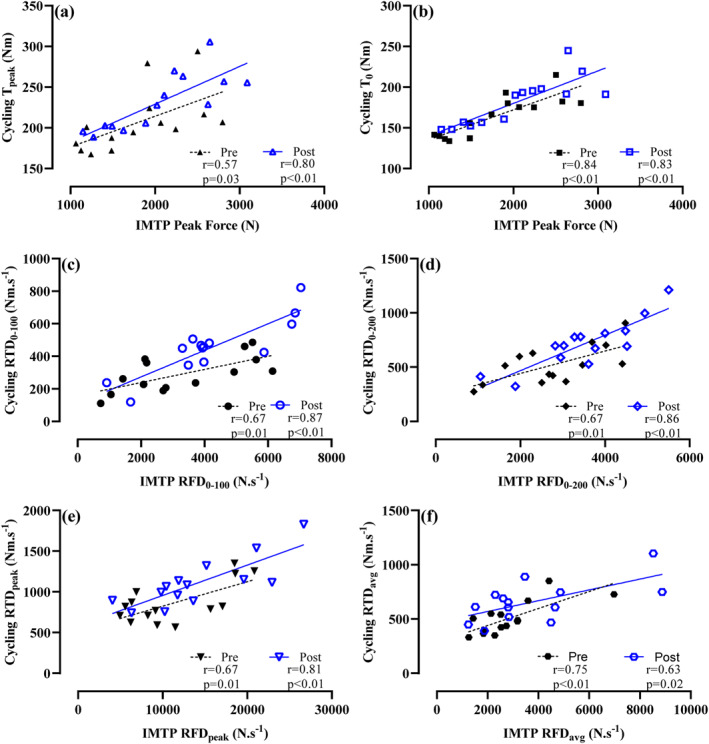
Pearson's correlation coefficients (r) between isometric mid‐thigh pull (IMTP) force and sprint cycling torque measures pre‐ and post‐training program. (A) Observed cycling peak torque (Tpeak) and IMTP peak force, (B) theoretical cycling peak torque (T 0) and IMTP peak force, (C) rate of force/torque development (RFD/RTD) from 0 to 100 ms (RFD/RTD0‐100), (D) RFD/RTD from 0 to 200 ms (RFD/RTD0‐200), (E) peak RFD/RTD (RFD/RTDpeak) and (F) average RFD/RTD (RTDavg).
FIGURE 2.
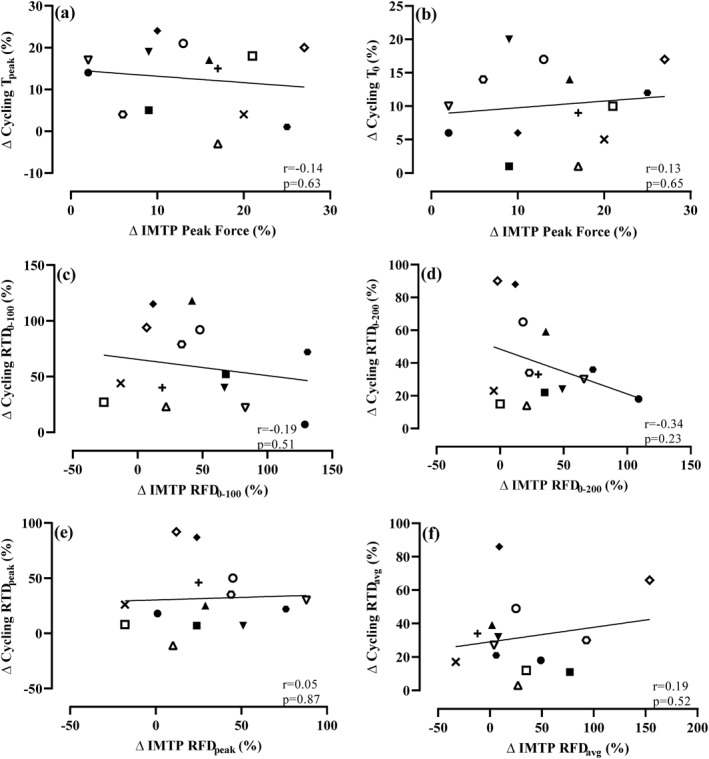
Pearson's correlation coefficients (r) between the relative change (Δ) in cycling torque measures and relative change in isometric mid‐thigh pull (IMTP) force measures pre‐to post‐training. (A) Observed cycling peak torque (Tpeak) and IMTP peak force, (B) theoretical cycling peak torque (T 0) and IMTP peak force, (C) rate of force/torque development (RFD/RTD) from 0 to 100 ms (RFD/RTD0‐100), (D) RFD/RTD from 0 to 200 ms (RFD/RTD0‐200), (E) peak RFD/RTD (RFD/RTDpeak) and (F) average RFD/RTD (RTDavg). Each participant is represented by a specific symbol shape in graphs a‐f.
TABLE 2.
Relationships between training‐induced changes in cycle power output and various test measures in strength‐trained novice cyclists.
| Predictor variable | PPO | P max | ||
|---|---|---|---|---|
| p | r | p | r | |
| Cycling Tpeak (Nm) | 0.38 | 0.25 | 0.34 | 0.27 |
| Cycling RPMpeak (rpm) | 0.27 | 0.32 | 0.11 | 0.44 |
| Cycling T 0 (Nm) | 0.10 | 0.46 | 0.07 | 0.50 |
| Cycling RTD0‐100 (Nm.s−1) | 0.59 | 0.16 | 0.45 | 0.22 |
| Cycling RTD0‐200 (Nm.s−1) | 0.84 | 0.06 | 0.58 | 0.16 |
| Cycling RTDavg (Nm.s−1) | 0.88 | −0.05 | 0.87 | 0.05 |
| Cycling RTDpeak (Nm.s−1) | 0.94 | −0.02 | 0.99 | −0.001 |
| IMTP peak force (N) | 0.43 | 0.23 | 0.48 | 0.21 |
| IMTP RFD0‐100 (N.s−1) | 0.59 | −0.16 | 0.62 | −0.15 |
| IMTP RFD0‐200 (N.s−1) | 0.33 | −0.28 | 0.30 | −0.30 |
| IMTP RFDavg (N.s−1) | 0.74 | 0.10 | 0.82 | 0.07 |
| IMTP RFDpeak (N.s−1) | 0.92 | 0.03 | 0.77 | 0.09 |
| 3RM back squat (kg) | 0.84 | −0.06 | 0.56 | −0.17 |
| 3RM trap bar deadlift (kg) | 0.38 | −0.25 | 0.37 | −0.26 |
Note: r, Pearson's correlation coefficients
Abbreviations: P max, cycling theoretical peak power; PPO, cycling observed peak power output; RFD/RTD0‐100 and RFD/RTD0‐200, rate of force/torque development from 0 to 100 ms and 0–200 ms; RFD/RTDavg, average rate of force/torque development; RFD/RTDpeak, peak rate of force/torque development; RPMpeak, cycling observed peak cadence; T 0, cycling theoretical peak torque; Tpeak, cycling observed peak torque.
Statistical significance set at p < 0.05.
3. RESULTS
Training resulted in significant improvements in all cycling power and torque measures, cycling RPMpeak, all IMTP force measures, and both 3RM measures in week 6 of the training program (p < 0.05; Table 1). No significant differences were observed in cycling RPMmax and RPMopt following training (p > 0.05; Table 1).
Strong‐to‐very strong positive relationships were observed between IMTP forces and cycling torque measures both pre‐ and post‐training (Figure 1). No significant relationships were observed between the training‐induced changes in IMTP force measures and sprint cycling torque measures following training (Figure 2). No significant relationships were observed between the training‐induced change in PPO or P max and the change in cycling torque, IMTP force and 3RM (Table 2).
4. DISCUSSION
The aims of the present study were to investigate: (i) the extent that sprint cycling torque and IMTP force measures change following training; and (ii) the relationship between the training‐induced changes in sprint cycling torque, cycling power (PPO/P max), IMTP force and 3RM measures. The following findings were observed: (1) significant training‐induced increases in cycling PPO (10.7%), T 0 (10.2%), RTD (27.9%–56.7%), IMTP PF (13.1%) and RFD (23.7%–32.5%); (2) no significant relationships between the training‐induced changes in IMTP force and sprint cycling torque; and (3) no significant relationships between the training‐induced changes in cycling PPO or P max and changes in IMTP force, cycling torque and 3RM measures. The divergent training‐induced changes in these assessments indicate that these tests are affected by different underpinning mechanisms, likely providing information on different aspects of neuromuscular function when measured following a period of training.
The present study indicates that as little as 6 weeks of resistance and sprint cycling training results in substantial improvements in cycling performance in strength‐trained novice cyclists. Indeed, the observed 10.7% increase in cycling PPO in the present study is greater than the 6.7% increase achieved following a 3‐month talent development sprint cycling program with developmental cyclists (Tofari et al., 2017), or the 3.0% increase following 6‐week of cycling specific isometric‐training stimulus in world‐class sprint cyclists (Kordi, Folland, Goodall, Menzies, et al., 2020). The steep improvement curve in cycling measures in the present study is not unexpected given that the participants were starting from a low experience base in cycling. The improvements in the present study (Table 1) align with previous research reporting improvements in RFD/RTD in as little as 2–6 weeks training, as well as research reporting the torque component of PPO to be more trainable than the cadence component (Dorel, 2018; Douglas et al., 2021; Kordi, Folland, Goodall, Menzies, et al., 2020). Training‐induced changes in torque may be attributable to neural adaptations, such as increased motor unit recruitment, rate of coding and synchronisation; or peripheral adaptations, such as increased muscle cross‐sectional area or increased pennation angle (Andersen & Aagaard, 2006; Andersen et al., 2010; Douglas et al., 2021; Kordi, Folland, Goodall, Haralabidis, et al., 2020; Maffiuletti et al., 2016). The present data indicate that, in the current population, an emphasis should be placed on systematically developing strength as substantial increases in torque (and PPO/Pmax) can be achieved in a relatively short period of time. However, it is noteworthy that our study design also included low torque/high cadence efforts with the goal of improving limits to the power–cadence relationship. As such it is plausible that such high cadence training also contributed to the improvements in power observed and should also be considered within a structured training program (Dorel, 2018; Douglas et al., 2021).
As hypothesised, we did not observe a relationship between the training‐induced changes in IMTP force and sprint cycling torque measures. In the present study, group percentage increases were greater in IMTP PF (13.1%) compared to sprint cycling Tpeak (11.7%) and T0 (10.2%), while most cycling RTD measures increased by a greater percentage (27.9%–56.7%) compared to IMTP RFD (23.7%–32.5%). The greater group percentage increases in IMTP compared to cycling peak values may be surprising given the participants had more experience in strength training than cycling. However, only 1 participant had previous experience at completing the IMTP, so the groups were relatively novice in this exercise, and improvement may be expected after 6 weeks of targeted training. The divergent training‐induced changes in the present study are likely due to differences in the underpinning mechanisms associated with the production of IMTP force and sprint cycling torque. Indeed, our earlier work (Connolly et al., 2023) showed a stronger relationship between peripheral neuromuscular function mechanisms and cycling torque and between central neuromuscular function mechanisms and IMTP force. Other reasons for divergent training‐induced changes in IMTP force and sprint cycling torque include differences in the muscle activation strategies and motor unit recruitment in isometric and dynamic actions (Murphy & Wilson, 1996), or the absence of the stretch‐shortening cycle in isometric actions (in contrast to dynamic action) (Wilson et al., 1991), in addition to musculoskeletal stiffness providing a greater contribution to force production within isometric compared to dynamic tasks (James et al., 2023; Wilson et al., 1994). The results of the present study indicate that while there is a level of transferability in an individual's ability to rapidly produce IMTP force and sprint cycling torque at a single timepoint, these measures change at a different rate in response to training in strength‐trained novice cyclists. From an applied perspective, these results emphasise why it is important that cross‐sectional relationships are not assumed to hold true when examined longitudinally following training (James et al., 2023).
Findings from the present study contrast our second hypothesis of a relationship between the training‐induced changes in cycling P max, cycling torque, IMTP force or 3RM measures. While previous research (Dorel, 2018; Dorel et al., 2005; Douglas et al., 2021; Kordi et al., 2017) highlights the importance of strength capacities for sprint cycling power production, our data show that the strength measures assessed here (cycling torque, IMTP force, 3RM) do not change at the same rate as cycling PPO or P max after a short training period in strength‐trained novice cyclists. The assessed strength measures may be useful to a practitioner interested in the progression of strength; however, our results indicate that these strength changes may not be transferable or related to cycling power changes following a short (e.g., 6 weeks) training intervention in the current population. The divergent changes in strength measures and PPO/P max in the current study agree with a previous study in well‐trained endurance cyclists (Rønnestad et al., 2010), but contradicts findings in world‐class cyclists (Kordi, Folland, Goodall, Menzies, et al., 2020), where a moderate relationship (r = 0.42–0.47; p < 0.05) between the training‐induced changes in knee extension late RTD (150–200 ms) and cycling P max were observed following a 6‐week isometric cycling specific intervention. The differences in study results mentioned above may be explained in part by the experience level of the cyclists and the differences in the assessments used.
As with any investigation, there are limitations to our work that should be considered. Firstly, we acknowledge that the training background of the participants in the present study will have influenced the findings, and therefore, our results are applicable specifically to individuals who are strength‐trained novice cyclists. By recruiting individuals with more experience in strength than cycling, we increased the likelihood of seeing a divergent adaptation in the strength and cycling assessments, and therefore, increased the likelihood of determining the relationship between force and torque measures (or not). Next, we acknowledge that the small sample size for the present study may have affected the relationships presented. Further research is needed to ascertain whether relationships in the present study are similar in other populations such as strength‐trained, sprint cyclists. Finally, we are aware that several measures such as cycling P max normalised by the frontal area, or 15‐s to 30‐s cycling PPO have a strong relationship with specific event measures (such as the flying 200‐m velocity) or with event specific durations of 15–30 s (Dorel et al., 2005; Ferguson et al., 2023). However, the present study was not designed to examine the factors that may be correlated with performance. Instead, we investigated the factors that may be correlated with RFD/RTD. We acknowledge that future research should investigate the factors that may be correlated with performance.
5. CONCLUSION
In conclusion, training resulted in substantial increases in cycling power and torque measures in strength‐trained novice cyclists. The increase in cycling power was mediated by increases in cycling torque, IMTP force and 3RM; however, these measures did not change at the same rate. Our results indicate no relationship between the training‐induced changes in IMTP force and sprint cycling torque following six weeks of training in strength‐trained novice cyclists. These data suggest that training‐induced changes in IMTP and 3RM are not indicative of training‐induced changes in sprint cycling in this population. The divergent training‐induced changes in these assessments suggest that these tests are potentially affected by different underpinning mechanisms, likely providing information on different aspects of neuromuscular function when measured following training.
CONFLICT OF INTEREST STATEMENT
The authors report there are no competing interests to declare.
Supporting information
Supporting Information S1
Supporting Information S2
ACKNOWLEDGEMENTS
The authors would like to sincerely thank the participants and the research support team for their commitment to this study. Shannon Connolly was supported by an Australian Government Research Training Programme Scholarship and a Western Australian Institute of Sport High Performance Research Center Scholarship.
Open access publishing facilitated by Edith Cowan University, as part of the Wiley ‐ Edith Cowan University agreement via the Council of Australian University Librarians.
DATA AVAILABILITY STATEMENT
The authors confirm that the data supporting the findings of this study are available within the article.
REFERENCES
- Aagaard, Per , Simonsen Erik B., Andersen Jesper L., Magnusson Peter, and Dyhre‐Poulsen Poul. 2002. “Increased Rate of Force Development and Neural Drive of Human Skeletal Muscle Following Resistance Training.” Journal of Applied Physiology 93(4): 1318–1326. 10.1152/japplphysiol.00283.2002. [DOI] [PubMed] [Google Scholar]
- Andersen, Lars L. , and Aagaard Per. 2006. “Influence of Maximal Muscle Strength and Intrinsic Muscle Contractile Properties on Contractile Rate of Force Development.” European Journal of Applied Physiology 96(1): 46–52. 10.1007/s00421-005-0070-z. [DOI] [PubMed] [Google Scholar]
- Andersen, L. L. , Andersen J. L., Zebis M. K., and Aagaard P.. 2010. “Early and Late Rate of Force Development: Differential Adaptive Responses to Resistance Training?” Scandinavian Journal of Medicine & Science in Sports 20(1): e162–e169. 10.1111/j.1600-0838.2009.00933.x. [DOI] [PubMed] [Google Scholar]
- Bates, Douglas , Mächler Martin, Bolker Ben, and Walker Steve. 2015. “Fitting Linear Mixed‐Effects Models Using Lme4.” Journal of Statistical Software 67(1): 1–48. 10.18637/jss.v067.i01. [DOI] [Google Scholar]
- Connolly, Shannon , Peeling Peter, Binnie Martyn J., Goods Paul S. R., Blazevich Anthony J., Timmerman Wouter P., and Abbiss Chris R.. 2022. “Assessing the Rate of Torque Development in Sprint Cycling: a Methodological Study.” European Journal of Sport Science 13(6): 1–11. 10.1080/17461391.2022.2079425. [DOI] [PubMed] [Google Scholar]
- Connolly, Shannon , Peeling Peter, Binnie Martyn J., Goods Paul S. R., Latella Christopher, Taylor Janet L., Blazevich Anthony J., Timmerman Wouter P., and Abbiss Chris R.. 2023. “Sprint Cycling Rate of Torque Development Associates with Strength Measurement in Trained Cyclists.” European Journal of Applied Physiology 123(6): 1215–1227. 10.1007/s00421-023-05143-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darrall‐Jones, Joshua D. , Jones Ben, and Till Kevin. 2015. “Anthropometric and Physical Profiles of English Academy Rugby Union Players.” The Journal of Strength & Conditioning Research 29(8): 2086–2096. 10.1519/JSC.0000000000000872. [DOI] [PubMed] [Google Scholar]
- Dorel, S. 2018. “Maximal Force‐Velocity and Power‐Velocity Characteristics in Cycling: Assessment and Relevance.” In Biomechanics of. Testing and Training: Innovative Concepts and Simple Field Methods, edited by Morin J. B. and Samozino P.. 10.1007/978-3-319-05633-3_2. [DOI] [Google Scholar]
- Dorel, S. , Hautier C. A., Rambaud O., Rouffet D., Van Praagh E., Lacour J. R., and Bourdin M.. 2005. “Torque and Power‐Velocity Relationships in Cycling: Relevance to Track Sprint Performance in World‐Class Cyclists.” International Journal of Sports Medicine 26(9): 739–746. 10.1055/s-2004-830493. [DOI] [PubMed] [Google Scholar]
- Dos'Santos, Thomas , Lake Jason, Jones Paul A., and Comfort Paul. 2018. “Effect of Low‐Pass Filtering on Isometric Mid‐thigh Pull Kinetics.” The Journal of Strength & Conditioning Research 32(4): 983–989. 10.1519/JSC.0000000000002473. [DOI] [PubMed] [Google Scholar]
- Douglas, Jamie , Ross Angus, and Martin James C.. 2021. “Maximal Muscular Power: Lessons from Sprint Cycling.” Sports Medicine 7(1): 48. 10.1186/s40798-021-00341-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson, Hamish , Harnish Chris, Klich Sebastian, Michalik Kamil, Dunst Anna Katharina, Zhou Tony, and Chase J. Geoffrey. 2023. “Power‐duration Relationship Comparison in Competition Sprint Cyclists from 1‐s to 20‐min. Sprint Performance Is More Than Just Peak Power.” PLoS One 18(5): e0280658. 10.1371/journal.pone.0280658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner, A. Scott , Martin James C., Martin David T., Barras Martin, and Jenkins David G.. 2007. “Maximal Torque‐ and Power‐Pedaling Rate Relationships for Elite Sprint Cyclists in Laboratory and Field Tests.” European Journal of Applied Physiology 101(3): 287–292. 10.1007/s00421-007-0498-4. [DOI] [PubMed] [Google Scholar]
- Guppy, S. , Brady, C. , Comfort, P. , Haff, G. (2018). The Isometric Mid‐thigh Pull: A Review and Methodology ‐ Part 1. Professional Strength & Conditioning, 51: 13–19. [Google Scholar]
- Guppy, S. , Kotani Y., Claire B., Connolly S., Comfort P., and Haff G. G.. 2022. “The Reliability and Magnitude of Time‐dependent Force‐Time Characteristics during the Isometric Midthigh Pull Are Affected by Both Testing Protocol and Analysis Choices.” The Journal of Strength & Conditioning Research 1(5): 1191–1199. 10.1519/JSC.0000000000004229. [DOI] [PubMed] [Google Scholar]
- Guppy, Stuart N. , Brady Claire J., Kotani Yosuke, Connolly Shannon, Comfort Paul, Lake Jason P., and Haff G. Gregory. 2021. “A Comparison of Manual and Automatic Force‐Onset Identification Methodologies and Their Effect on Force‐Time Characteristics in the Isometric Midthigh Pull.” Sports Biomechanics: 1–18. 10.1080/14763141.2021.1974532. [DOI] [PubMed] [Google Scholar]
- Haff, G. Gregory , Ruben Ryan P., Lider Joshua, Twine Corey, and Cormie Prue. 2015. “A Comparison of Methods for Determining the Rate of Force Development during Isometric Midthigh Clean Pulls.” The Journal of Strength & Conditioning Research 29(2): 386–395. 10.1519/JSC.0000000000000705. [DOI] [PubMed] [Google Scholar]
- Haff, G. Gregory , Stone Michael, O'Bryant Harold S., Harman Everett, Dinan Chris, Johnson Robert, and Han Ki‐Hoon. 1997. “Force‐time Dependent Characteristics of Dynamic and Isometric Muscle Actions.” The Journal of Strength & Conditioning Research 11(4): 269–272. . [DOI] [Google Scholar]
- Hedges, L. V. , and Olkin I.. 1985. “Estimation of a Single Effect Size: Parametric and Nonparametric Methods.” In Statistical Methods for Meta‐Analysis, 75–106. Academic Press. 10.1016/B978-0-08-057065-5.50010-5. [DOI] [Google Scholar]
- Hopkins, William G. , Marshall Stephen W., Batterham Alan M., and Hanin Juri. 2009. “Progressive Statistics for Studies in Sports Medicine and Exercise Science.” Medicine & Science in Sports & Exercise 41(1): 3–13. 10.1249/MSS.0b013e31818cb278. [DOI] [PubMed] [Google Scholar]
- James, Lachlan P. , Weakley Jonathon, Comfort Paul, and Huynh Minh. 2023. “The Relationship between Isometric and Dynamic Strength Following Resistance Training: A Systematic Review, Meta‐Analysis, and Level of Agreement.” International Journal of Sports Physiology and Performance 23: 1–11: Epub ahead of print. PMID: 37741636. 10.1123/ijspp.2023-0066. [DOI] [PubMed] [Google Scholar]
- Kordi, Mehdi , Folland Jonathan, Goodall Stuart, Haralabidis Nicos, Maden‐Wilkinson Tom, Sarika Patel Tejal, Leeder Jonathan, Barratt Paul, and Howatson Glyn. 2020. “Mechanical and Morphological Determinants of Peak Power Output in Elite Cyclists.” Scandinavian Journal of Medicine & Science in Sports 30(2): 227–237. 10.1111/sms.13570. [DOI] [PubMed] [Google Scholar]
- Kordi, Mehdi , Folland Jonathan P., Goodall Stuart, Menzies Campbell, Patel Tejal Sarika, Evans Martin, Thomas Kevin, and Howatson Glyn. 2020. “Cycling‐specific Isometric Resistance Training Improves Peak Power Output in Elite Sprint Cyclists.” Scandinavian Journal of Medicine & Science in Sports 30(9): 1594–1604. 10.1111/sms.13742. [DOI] [PubMed] [Google Scholar]
- Kordi, Mehdi , Goodall Stuart, Barratt Paul, Rowley Nicola, Leeder Jonathan, and Howatson Glyn. 2017. “Relation between Peak Power Output in Sprint Cycling and Maximum Voluntary Isometric Torque Production.” Journal of Electromyography and Kinesiology 35: 95–99. 10.1016/j.jelekin.2017.06.003. [DOI] [PubMed] [Google Scholar]
- Lenth, R. 2020. “Emmeans: Estimated Marginal Means, Aka Least‐Squares Means.” R package version 1.5.3. https://cran.r‐project.org/package=emmeans. [Google Scholar]
- Lüdecke, Daniel , Ben‐Shachar Mattan, Patil Indrajeet, Waggoner Philip, and Makowski Dominique. 2021. “Performance: An R Package for Assessment, Comparison and Testing of Statistical Models.” Journal of Open Source Software 6(60): 3139. 10.21105/joss.03139. [DOI] [Google Scholar]
- Maffiuletti, Nicola A. , Aagaard Per, Blazevich Anthony J., Folland Jonathan, Tillin Neale, and Duchateau Jacques. 2016. “Rate of Force Development: Physiological and Methodological Considerations.” European Journal of Applied Physiology 116(6): 1091–1116. 10.1007/s00421-016-3346-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKay, Alannah K. A. , Stellingwerff Trent, Smith Ella S., Martin David T., Mujika Iñigo, Goosey‐Tolfrey Vicky L., Sheppard Jeremy, and Burke Louise M.. 2022. “Defining Training and Performance Caliber: A Participant Classification Framework.” International Journal of Sports Physiology and Performance 17(2): 317–331. 10.1123/ijspp.2021-0451. [DOI] [PubMed] [Google Scholar]
- Munro, L. A. , and Haff G. G.. 2018. “Sprint Cycling.” In Handbook of Strength and Conditioning: Sport‐specific Programming for High Performance, edited by Turner A., 506–525. Routledge. https://test.routledgehandbooks.com/doi/10.4324/9781315542393‐28. [Google Scholar]
- Murphy, Aron J. , and Wilson Greg J.. 1996. “Poor Correlations between Isometric Tests and Dynamic Performance: Relationship to Muscle Activation.” European Journal of Applied Physiology and Occupational Physiology 73(3–4): 353–357. 10.1007/BF02425498. [DOI] [PubMed] [Google Scholar]
- Rønnestad, Bent R. , Hansen Ernst Albin, and Raastad Truls. 2010. “Effect of Heavy Strength Training on Thigh Muscle Cross‐Sectional Area, Performance Determinants, and Performance in Well‐Trained Cyclists.” European Journal of Applied Physiology 108(5): 965–975. 10.1007/s00421-009-1307-z. [DOI] [PubMed] [Google Scholar]
- Teo, Weipeng , McGuigan Michael R., and Newton Michael J.. 2011. “The Effects of Circadian Rhythmicity of Salivary Cortisol and Testosterone on Maximal Isometric Force, Maximal Dynamic Force, and Power Output.” The Journal of Strength & Conditioning Research 25(6): 1538–1545. 10.1519/JSC.0b013e3181da77b0. [DOI] [PubMed] [Google Scholar]
- Tillin, Neale A. , Jimenez‐Reyes Pedro, Pain Matthew T. G., and Folland Jonathan P.. 2010. “Neuromuscular Performance of Explosive Power Athletes versus Untrained Individuals.” Medicine & Science in Sports & Exercise 42(4): 781–790. 10.1249/MSS.0b013e3181be9c7e. [DOI] [PubMed] [Google Scholar]
- Tofari, Paul J. , Cormack Stuart J., Ebert Tammie R., Gardner A. Scott, and Kemp Justin G.. 2017. “Comparison of Ergometer‐ and Track‐Based Testing in Junior Track‐Sprint Cyclists. Implications for Talent Identification and Development.” Journal of Sports Sciences 35(19): 1947–1953. 10.1080/02640414.2016.1243795. [DOI] [PubMed] [Google Scholar]
- Vercoe, J. , and McGuigan M. R.. 2018. “Relationship between Strength and Power Production Capacities in Trained Sprint Track Cyclists.” Kinesiology 50(1): 96–101. [Google Scholar]
- Wackwitz, Thomas A. , Minahan Clare L., King Trish, Du Plessis Chantelle, Andrews Mark H., and Bellinger Phillip M.. 2021. “Quantification of Maximal Power Output in Well‐Trained Cyclists.” Journal of Sports Sciences 39(1): 84–90. 10.1080/02640414.2020.1805251. [DOI] [PubMed] [Google Scholar]
- Watsford, Mark , Ditroilo Massimiliano, Fernández‐Peña Eneko, D'amen Giancarlo, and Lucertini Francesco. 2010. “Muscle Stiffness and Rate of Torque Development during Sprint Cycling.” Medicine & Science in Sports & Exercise 42(7): 1324–1332. 10.1249/MSS.0b013e3181ce509d. [DOI] [PubMed] [Google Scholar]
- Wilson, G. J. , Murphy A. J., and Pryor J. F.. 1994. “Musculotendinous Stiffness: its Relationship to Eccentric, Isometric, and Concentric Performance.” Journal of Applied Physiology 76(6): 2714–2719. 10.1152/jappl.1994.76.6.2714. [DOI] [PubMed] [Google Scholar]
- Wilson, G. J. , Wood G. A., and Elliott B. C.. 1991. “Optimal Stiffness of Series Elastic Component in a Stretch‐Shorten Cycle Activity.” Journal of Applied Physiology 0(2): 825–833. 10.1152/jappl.1991.70.2.825. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information S1
Supporting Information S2
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.


