Abstract
Purpose:
Recently, there has been rapid development in model-informed drug development, which has the potential to reduce animal experiments and accelerate drug discovery. Physiologically based pharmacokinetic (PBPK) and machine learning (ML) models are commonly used in early drug discovery to predict drug properties. However, basic PBPK models require a large number of molecule-specific inputs from in vitro experiments, which hinders the efficiency and accuracy of these models. To address this issue, this paper introduces a new computational platform that combines ML and PBPK models. The platform predicts molecule PK profiles with high accuracy and without the need for experimental data.
Methods:
This study developed a whole-body PBPK model and ML models of plasma protein fraction unbound (), Caco-2 cell permeability, and total plasma clearance to predict the PK of small molecules after intravenous administration. Pharmacokinetic profiles were simulated using a “bottom-up” PBPK modeling approach with ML inputs. Additionally, 40 compounds were used to evaluate the platform’s accuracy.
Results:
Results showed that the ML-PBPK model predicted the area under the concentration-time curve (AUC) with 65.0 accuracy within a 2-fold range, which was higher than using in vitro inputs with 47.5 accuracy.
Conclusion:
The ML-PBPK model platform provides high accuracy in prediction and reduces the number of experiments and time required compared to traditional PBPK approaches. The platform successfully predicts human PK parameters without in vitro and in vivo experiments and can potentially guide early drug discovery and development.
Supplementary Information
The online version contains supplementary material available at 10.1007/s11095-024-03725-y.
Keywords: ADME prediction, Mechanistic modeling, Machine learning, PBPK
Introduction
Pharmacokinetics (PK) is a critical aspect of drug development, as it describes the absorption, distribution, metabolism, and excretion(ADME) of compounds in the body. During preclinical stages, lead compounds undergo evaluation for their PK properties through in vitro and in vivo animal experiments. The results of these evaluations can be used to rank compounds or optimize their structures based on the correlation between their physicochemical and PK properties. Moreover, these in vitro and animal PK results can be leveraged to predict human PK phenomena and guide clinical trial design through allometric scaling, compartment models, or PBPK models.
In contrast to traditional PK models with allometric scaling, PBPK models have the ability to predict drug concentrations in plasma and various tissues without the need for animal experiments. As a result, the application of PBPK models has significantly increased in drug discovery and development over the past few years [1]. Three approaches are commonly used in PBPK model prediction, including “top-down,” “middle-out,” and “bottom-up.” The top-down approach relies predominantly on observed clinical data, while the middle-out approach combines both in vitro and vivo information to determine unknown or uncertain parameters of the model [2]. The bottom-up approach, in particular, offers the potential to minimize or replace animal PK studies, as it relies solely on in vitro data for drug-related input parameters. However, IMI-Oral Biopharmaceutics Tools projects show limitations of a “bottom-up” approach in human PK predictions, with only half of the area Under the Concentration-Time Curve (AUC) predictions being within a 2-fold prediction error [3]. This accuracy may be affected by errors in in-vitro experiments or the accuracy of clearance prediction using in vitro hepatic systems. Such limitations may be overcome by using ML models to predict physicochemical properties directly from structures.
Drug-specific input parameters, such as , intrinsic hepatic clearance, and volume of distribution (), have been well predicted using in silico models. Previously, Doha combined in vitro and ML inputs with a minimal PBPK model and evaluated 240 compounds in rats. ML inputs with fup, LogD, and CL showed only 36.1 of systemic plasma AUC within a 2-fold prediction error [4]. Vector Group then developed a high-accuracy machine learning-integrated modeling platform, a whole-body PBPK model with an optimized Vdss prediction method [5].
Several studies have been conducted to optimize the calculation methods of Vdss to improve the accuracy of PBPK predictions. However, it is important to note that clearance also plays a significant role in PK prediction. Clearance, which determines the rate of drug elimination from the body, occurs in the liver, kidney, and bile. Early drug discovery focuses primarily on liver metabolism using in vitro experiments in hepatocytes or microsomes. As a result, several PBPK models only consider hepatic clearance from the in vitro to in vivo exploration (IVIVE) approach. This approach may result in the misprediction of clearance due to the exclusion of certain renal or bile elimination processes. Bowman has reported underprediction of clearance from the IVIVE method, with a 42.2 error rate within a 2-fold margin of error in the microsome system [6]. This highlights the need for total clearance to improve the accuracy of PBPK modeling in the early discovery stage.
In our study, we have developed a rapid ML-PBPK model platform that enables the simulation of human PK from compound structures. , Caco-2 cell permeability, and total plasma clearance for humans were predicted using ML models. These predicted results were then used as input parameters for a whole-body PBPK model encompassing 14 tissues. The prediction accuracy of the platform was evaluated for 40 drugs PK profiles in humans to define its applicability for use in early discovery and clinical phases.
Materials and Methods
Data Collection
The human model relies on two data sources: the Watanabe study, which provides data for 2139 compounds, and the Votano study [7, 8], which provides data for 808 compounds. Overlaps between the two datasets were checked, and compounds were removed if two records had values greater than a 2-fold difference. Compounds with values that differed by less than 2-fold were kept from Watanabe’s study due to having more significant figures. Caco-2 cell permeability data for 6083 compounds were collected from public sources [9–11]. The human CLt model used intravenous PK parameters from Lombardo’s study [12]. Compounds were removed if they had duplicates or invalid SMILES, a molecular weight greater than 900 Da, or where CL was none. Additionally, 40 molecules that overlapped with the experimental data were removed. Finally, we created three datasets: containing 2292 compounds, Caco-2 containing 6083 compounds, and CLt containing 1215 compounds.
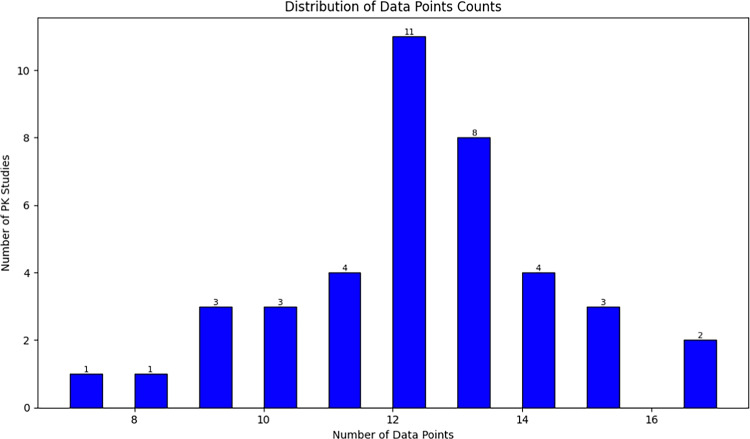
The human plasma PK data for the 40 tests in Table I were extracted from previously published papers in supplementary. All PK data were digitized using the free online tool WebPlotDigitizer [13]. Figure 1 presents the statistics regarding number of PK studies and data points for which PK data were collected.
Table 1.
Drug-specific Input Parameters from in vitro Experiments and Prediction
| Drug | LogP | pKa | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Acetaminophen | 0.91 | 9.46(a) | 0.52 | 0.34 | 1.04 | 100 | 19.2 | 12.0 | 0.30 | 0.40 |
| Alprazolam | 3.02 | 5.01(b) | 0.29 | 0.17 | 0.78 | 25.5 | 51.7 | 1.37 | 0.04 | 0.12 |
| Amitriptyline | 4.81 | 9.76(b) | 0.07 | 0.07 | 0.86 | 54.7 | 23.1 | 14.6 | 0.37 | 0.78 |
| Atenolol | 0.43 | 9.67(b) | 0.94 | 0.58 | 1.12 | 1.60 | 1.00 | 12.0 | 0.15 | 0.36 |
| Betaxolol | 2.54 | 9.67(b) | 0.22 | 0.36 | 1.03 | 53.9 | 44.8 | 19.0 | 0.20 | 0.52 |
| Bosentan | 4.94 | 5.8(a) | 0.04 | 0.07 | 0.55 | 1.05 | 21.0 | 12.0 | 0.13 | 0.18 |
| Caffeine | −0.07 | 0(n) | 0.64 | 0.46 | 1.00 | 40.1 | 33.6 | 0.33 | 0.08 | 0.11 |
| Chlorpromazine | 5.40 | 9.40(b) | 0.06 | 0.06 | 1.19 | 17.8 | 10.5 | 49.6 | 0.96 | 0.65 |
| Cimetidine | −0.11 | 6.91(b) | 0.78 | 0.76 | 0.97 | 4.48 | 3.00 | 8.56 | 0.49 | 0.57 |
| Clozapine | 3.40 | 7.35(b) | 0.06 | 0.04 | 0.81 | 30.7 | 31.5 | 13.7 | 0.15 | 0.32 |
| Desipramine | 3.90 | 10.01(b) | 0.16 | 0.14 | 0.93 | 29.5 | 14.5 | 19.7 | 0.66 | 0.86 |
| Dexamethasone | 1.68 | 12.42(a) | 0.198 | 0.25 | 0.93 | 15.0 | 16.5 | 8.56 | 0.20 | 0.39 |
| Diazepam | 2.82 | 3.4(b) | 0.02 | 0.05 | 0.81 | 41.0 | 50.1 | 1.88 | 0.02 | 0.04 |
| Diclofenac | 4.26 | 4(a) | 0.01 | 0.004 | 0.60 | 20.2 | 39.8 | 177 | 0.21 | 0.13 |
| Diltiazem | 2.73 | 12.86(a)-8.18(b) | 0.18 | 0.15 | 0.99 | 38.7 | 20.2 | 26.5 | 0.78 | 0.65 |
| Furosemide | 1.75 | 4.25(a) | 0.01 | 0.13 | 0.90 | 1.60 | 1.60 | 25.7 | 0.10 | 0.06 |
| Ibuprofen | 3.97 | 5.53(a) | 0.006 | 0.05 | 0.55 | 48.1 | 46.2 | 30.0 | 0.05 | 0.07 |
| Imipramine | 4.28 | 9.2(b) | 0.08 | 0.12 | 0.99 | 30.0 | 13.2 | 27.4 | 0.78 | 0.88 |
| Ketoprofen | 3.10 | 4.45(a) | 0.008 | 0.01 | 1.09 | 40.3 | 48.3 | 6.93 | 0.10 | 0.04 |
| Lidocaine | 2.84 | 7.75(b) | 0.33 | 0.28 | 0.74 | 18.5 | 21.5 | 15.9 | 0.96 | 0.65 |
| Methylprednisolone | 1.80 | 0(n) | 0.23 | 0.17 | 0.88 | 9.59 | 11.8 | 24.0 | 0.37 | 0.35 |
| Metoprolol | 1.76 | 9.67(b) | 0.88 | 0.61 | 1.15 | 34.2 | 12.3 | 3.68 | 0.78 | 0.58 |
| Midazolam | 2.90 | 6.19(b) | 0.02 | 0.04 | 0.68 | 39.8 | 42.6 | 302 | 0.32 | 0.11 |
| Montelukast | 8.49 | 4.40(a)-3.12(b) | 0.002 | 0.003 | 0.55 | 76.0 | 5.20 | 96.3 | 0.04 | 0.15 |
| Morphine | 0.89 | 8.21(b) | 0.65 | 0.57 | 1.00 | 6.27 | 10.2 | 64.6 | 1.56 | 1.23 |
| Nadolol | 0.81 | 9.76(b) | 0.14 | 0.65 | 1.00 | 1.17 | 2.90 | 17.1 | 0.17 | 0.33 |
| Naloxone | 1.67 | 10.07(a)-7.84(b) | 0.54 | 0.49 | 1.43 | 21.5 | 21.9 | 12.0 | 1.38 | 1.18 |
| Naproxen | 3.18 | 4.15(a) | 0.002 | 0.01 | 0.51 | 52.8 | 41.9 | 18.0 | 0.004 | 0.02 |
| Nifedipine | 2.20 | 0(n) | 0.04 | 0.04 | 0.74 | 42.0 | 29.0 | 82.2 | 0.44 | 0.81 |
| Omeprazole | 2.23 | 4.47(b)-9.29(a) | 0.05 | 0.03 | 0.61 | 54.8 | 12.4 | 15.4 | 0.50 | 0.17 |
| Ondansetron | 2.80 | 7.34(b) | 0.27 | 0.24 | 0.79 | 110 | 107 | 2.57 | 0.35 | 0.20 |
| Prazosin | 1.30 | 6.54(b) | 0.06 | 0.15 | 0.70 | 7.72 | 10.8 | 6.93 | 0.28 | 0.25 |
| Propranolol | 2.58 | 9.67(b) | 0.13 | 0.17 | 0.89 | 45.0 | 31.8 | 18.8 | 0.72 | 0.56 |
| Ranitidine | 0.20 | 7.8(b) | 0.95 | 0.59 | 1.00 | 4.45 | 0.70 | 3 | 0.58 | 0.34 |
| Quinidine | 2.51 | 9.05(b) | 0.26 | 0.09 | 1.02 | 21.0 | 5.70 | 21.4 | 0.24 | 0.43 |
| Sildenafil | 1.87 | 11.14(a)-5.59(b) | 0.04 | 0.06 | 0.81 | 55.0 | 43.9 | 51.4 | 0.54 | 0.49 |
| Theophylline | −0.02 | 8.81(a) | 0.61 | 0.34 | 0.92 | 44.1 | 14.5 | 2.65 | 0.05 | 0.19 |
| Triazolam | 3.63 | 4.26(b) | 0.10 | 0.16 | 0.62 | 28.0 | 29.9 | 43.5 | 0.18 | 0.11 |
| Verapamil | 3.79 | 8.92(b) | 0.09 | 0.14 | 0.817 | 9.02 | 4.30 | 122 | 1.08 | 0.58 |
| Vinorelbine | 4.80 | 8.66(b) | 0.87 | 0.09 | 0.58 | 1.30 | 2.90 | 108 | 1.20 | 0.47 |
a=acid,b=base, n=neutral
pr=predicted, ob=observed. Experimental Plasma protein fraction unbound from Lombardo et al. [12, 14]
Experimental Blood: Plasma ratio obtained from previous studies [15, 16]
Experimental Caco-2 cell permeability (cm/s) obtained from previous publications [17–19]
Experimental Intrinsic hepatic clearance (ml/min/kg) from literature [14, 20, 21]
Total plasma clearance (L/hr/kg) for drugs obtained from Lombardo et al. [12]
Fig. 1.
The statistics regarding number of PK studies and data points.
ML Model Building
Compounds SMILES were standardized using the ChEMBL standardizer [22]. Three different methods (RDKit, Mordred, and PaDEL-Descriptors) were used to calculate descriptors [23]. These methods generated molecular physicochemical properties for each molecule, resulting in 1826 (Mordred), 1444 (PaDEL), and 208 (RDKit) features used for model construction.
The datasets were split into training, validation, and test sets using random selection at an 8:1:1 ratio. Features with variance values less than 0.05 or those with the same information and a correlation coefficient higher than 0.9 were removed. The Boruta Algorithm [24] was also used to select significant features in a given data set.
Four common approaches to molecular property prediction were used to build , Caco-2, and CLt prediction models. These approaches [25, 26] included Support Vector Machine Regression (SVR), Random Forest (RF), XGBoost (XGB), and Gradient Boost Machine (GBM). In contrast to traditional chemical descriptors, message-passing neural networks (MPNNs) have exhibited advancements in molecular modeling and property prediction. MPNNs are a group of graph convolutional neural networks (GCNs) variants that can learn and aggregate local information of molecules through iterative message-passing iterations. Recently, Yang et al. [27] have proposed a directed MPNN (D-MPNN) and built the open-source package Chemprop for implementation of D-MPNN. D-MPNN constructs a learned molecular representation by operating on the graph structure of the molecule and passing a message through the edge-dependent neural network. In this study, D-MPNN builds the model based on different datasets and uses RDKit descriptors incorporated into D-MPNN to further improve performance.
The hyperparameters of the regression models were optimized with Bayesian optimization search. Five-fold cross-validation was used to check the stability and predictive ability of the model. Additionally, the performance of the regression models was assessed by the coefficient of determination () and root-mean-square error (RMSE).
PBPK Model Building
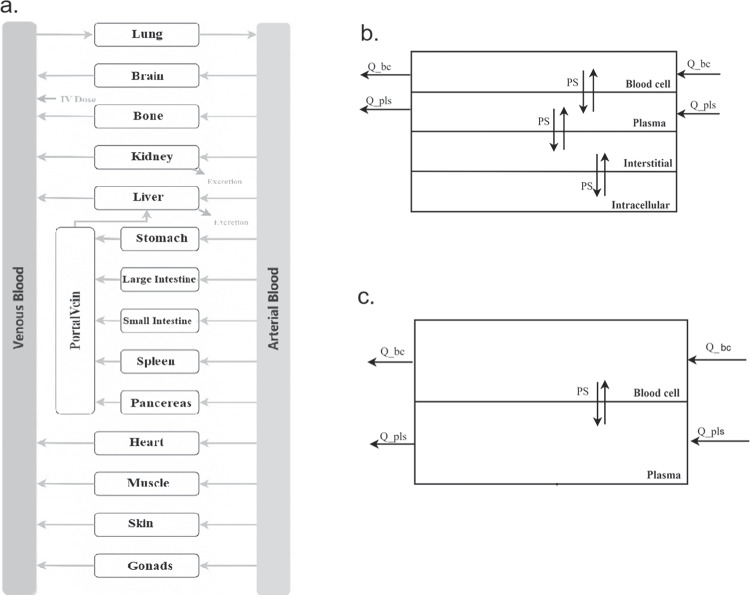
Figure 2a shows the compartment model for each tissue, which includes plasma, blood cells, interstitial space, and intracellular space, as previously discussed by Kawai [28].
Fig. 2.
Structure of the whole-body PBPK model (a). Each tissue is divided into blood cells, plasma, interstitial and intracellular spaces (b), and each blood vessel only has vascular compartments (c). Details of the model is presented in the method section.
Molecules move between adjacent compartments through passive diffusion and connect to the circulatory system through blood flow. The passive diffusion rate of drugs in each tissue was calculated by multiplying the cell permeability (P) by a tissue compartment surface area (SA) [29]. The cell permeability rate of tissues was assumed to be the same and was obtained through the Caco-2 cell system in this PBPK model. Figure 2c illustrates the structure of blood vessels, which comprises only plasma and blood cells.
In the ML-PBPK model, three key parameters, fup, caco-2 cell permeability, and CLt, were taken from predictions by ML models, and systemic drug elimination was assumed to occur in venous blood plasma through CLt. On the other hand, in the in vitro input model, a PBPK model using in vitro inputs, all in vitro parameters were taken from experiments. Specifically, elimination processes include hepatic clearance from microsomes or Hepatocytes stability experiments using the IVIVE method and renal clearance as glomerular filtration rate. The differential equations for venous blood vessels are described below as Eqs. 1 and 2. Where parameters are expressed as Q (blood flow), PSA (permeability-surface area), K (partition coefficient), CL (plasma clearance); bc and pls represent the blood cell and plasma compartment, and C is drug concentration in specific compartment. The equations for arterial blood and the portal vein are the same as for venous blood, except for the elimination process.
| 1 |
| 2 |
All physiological parameters were adapted from literature [30–32], including tissue volumes, blood flow rates, surface areas, tissue compositions, and tissue pH. Tissue partition coefficients (Kp) and blood: plasma ratio (BP) were calculated based on the Rowland-Roger method [33]. Drug physicochemical properties such as LogP, molecular weight, and pKa values were predicted from structure using ChemAxon. In vitro parameters such as , BP, Caco-2 cell permeability and intrinsic hepatic clearance were obtained from previous publications [14, 18, 34]. Physicochemical inputs for the ML-PBPK model simulation were predicted by ML models.
When administered intravenously in a short time, such as a bolus, the maximum concentration () in venous plasma is often reported to over-predict compared to the clinical PK profiles. Prediction errors may be due to the different sampling sites, as clinical samples are usually taken from a peripheral vein in the arm [35]. To avoid this, the plasma concentration profile in peripheral blood was chosen to evaluate prediction accuracy with observed PK.
Prediction Performance Assessment
PBPK models were used to simulate concentration-time profiles of tested drugs. Inputs for the models included machine learning and in vitro experimental data. Python was used for model development, and the matplotlib package was used to generate figures.
To evaluate the predicted PK data’s accuracy, non-compartmental analyses were conducted. This involved calculating important parameters such as half-life (), area under the curve (), clearance (CL), and volume of distribution at steady-state () using specific equations. and area under the moment curve () were calculated using the linear-trapezoidal method. The elimination rate constant () was calculated using the linear regression method. Mean residence time (MRT) was calculated by AUMC/AUC.
| 3 |
| 4 |
| 5 |
| 6 |
The accuracy of the predicted PK data was measured by calculating the average fold error (AFE) for each PK parameter Eq. 7. The total number of testing molecules was represented by n. This metric was used to evaluate the overall prediction accuracy of the model. Additionally, the prediction accuracy of the model was assessed by determining the percentage of prediction error within a 2-fold range for each PK parameter.
| 7 |
Results
ML models
Five ML methods were used to construct models for predicting human , Caco-2 cell permeability, and CLt. These methods included SVR, RF, XGB, GBM, and D-MPNN. A series of models were built for each parameter using different training sets. Table II presents the statistical evaluation results of the ML models in training and testing.
Table 2.
Statistics Results of ML Model of Human , Caco-2 cell Permeability and CLt
| Parameter | Method | ||||
|---|---|---|---|---|---|
| SVM | 0.672 | 0.408 | 0.662 | 0.427 | |
| RF | 0.605 | 0.447 | 0.626 | 0.439 | |
| XGB | 0.673 | 0.407 | 0.663 | 0.416 | |
| GBM | 0.664 | 0.412 | 0.690 | 0.399 | |
| DMPNN | 0.920 | 0.203 | 0.899 | 0.223 | |
| Caco-2 | SVM | 0.568 | 0.519 | 0.569 | 0.527 |
| RF | 0.497 | 0.561 | 0.499 | 0.568 | |
| XGB | 0.554 | 0.528 | 0.570 | 0.526 | |
| GBM | 0.550 | 0.530 | 0.552 | 0.537 | |
| DMPNN | 0.950 | 0.177 | 0.877 | 0.271 | |
| CLt | SVM | 0.308 | 0.542 | 0.277 | 0.504 |
| RF | 0.255 | 0.563 | 0.238 | 0.517 | |
| XGB | 0.295 | 0.548 | 0.278 | 0.503 | |
| GBM | 0.295 | 0.548 | 0.278 | 0.503 | |
| DMPNN | 0.678 | 0.362 | 0.546 | 0.411 |
The D-MPNN models outperformed the other models for all three parameters (Fig. 3). For predicting human , the D-MPNN model achieved an of 0.92 for an independent training set of 2292 compounds and predicted 77.5 (31/40) of the test set within a 2-fold prediction error. The D-MPNN model exhibited the highest value of 0.95 for the human Caco-2 training set, compared to the GBM model with an of 0.55. Additionally, the D-MPNN model demonstrated the best predictive ability for human CLt compared to the other models, with 67.5 of the 40 testing compounds predicted within a 2-fold prediction error.
Fig. 3.
Plots of the observed and predicted , Caco-2 cell permeability and CLt of the training set and the test set of the D-MPNN models. The dashed line indicates the line of unity (x=y).
Overall, the best models were used to predict the human , Caco-2 cell permeability, and CLt of the forty compounds. These predicted results were then used as inputs in PBPK models.
PBPK Models
For PBPK model with in-vitro inputs, the physicochemical properties are obtained from experimental values reported in literature, such as Caco-2, and the metabolism is based on LMS. On the other hand, for ML inputs, the physicochemical properties including metabolism clearance are predicted entirely using ML models.
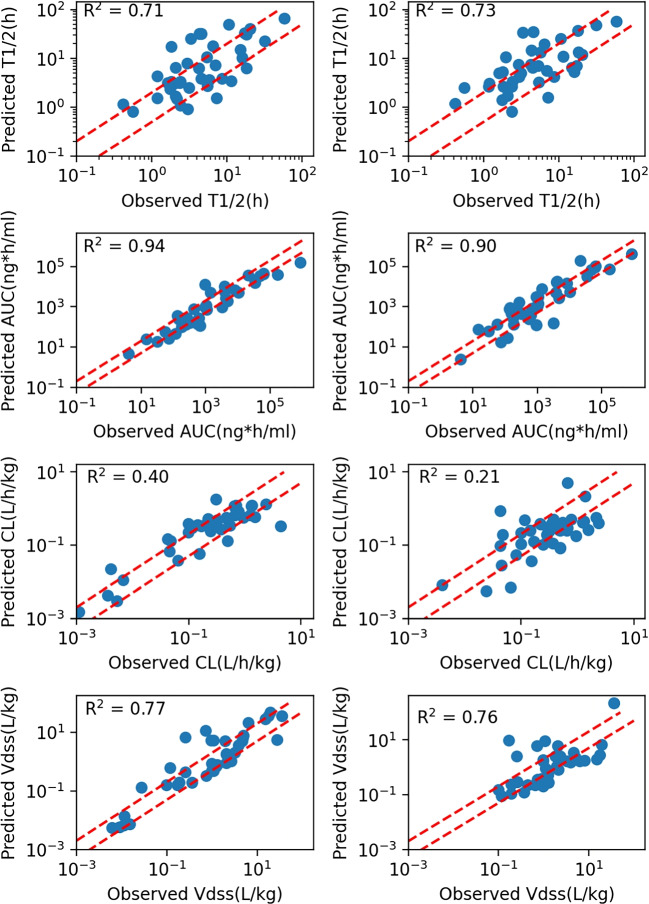
Figure 4 compares predicted and observed PK parameters for 40 compounds in humans. A table with details on the prediction accuracy of each drug is in the supplementary. All parameters exhibit a good correlation between observed and simulated values, except for CL. Pearson correlation coefficient values () range from 0.6-0.9. Prediction accuracy of is 65 (26/40), with slightly better performance in the ML-PBPK model compared to the in vitro inputs model, which had 47.5 (19/40) within 2-fold error (Table III).
Fig. 4.
Scatter plots are shown comparision of the predictions and observations for PK parameters after IV dosing in humans using ML inputs (left) and in vitro inputs (right). Two red dashed lines represent±two-fold errors. were the Pearson correlation coefficient values.
Table 3.
Prediction Accuracy of PK Parameters
| PK parameter | Method | AFE | AAFE | 2FE | 3FE |
|---|---|---|---|---|---|
| in vitro | 1.42 | 2.12 | 47.5 | 80.0 | |
| ML | 1.36 | 2.18 | 55.0 | 75.0 | |
| in vitro | 1.36 | 2.59 | 47.5 | 62.5 | |
| ML | 0.81 | 2.00 | 65.0 | 82.5 | |
| CL(L/h/kg) | in vitro | 0.74 | 2.59 | 47.5 | 62.5 |
| ML | 1.23 | 2.00 | 65.0 | 82.5 | |
| (L/kg) | in vitro | 0.80 | 2.80 | 37.5 | 70.0 |
| ML | 1.25 | 2.12 | 57.5 | 80.0 |
Average fold-error (Eq. 7)
Absolute Average Fold Error (AAFE) is calculated as follows:
where is the predicted value, is the observed value, and is the total number of predictions
Fold Error (FE) is defined as:
The percentage of prediction FE within 2 fold (%2FE) is calculated as:
The percentage of prediction FE within 3 fold (%3FE) is calculated as:
The ML-PBPK model showed relatively good results for CL prediction, with AAFEs of 2.00 and 2.59 and values of 0.4 and 0.21 respectively, compared to the in vitro inputs model. The predicted/observed ratios of PK parameters show a narrow range with ML inputs (Supplementary Figure 1), indicating a good agreement between predicted and observed values. Both models showed over- or under-predicted values of CL, with median predicted/observed ratios of 1.37 and 0.68. However, drugs extensively excreted in their unchanged form in urine and with elimination rates higher than normal GFR showed better prediction results with ML inputs, such as Vinorelbine.
The results of in the ML-PBPK model were similar to those of the in vitro inputs model, as the same tissue partition coefficient calculation method was chosen. describes the overall drug distribution in plasma and tissues. In the PBPK model mechanism, drug-related parameters such as , cell permeability, and Kp values affect drug distribution into tissues. Since the Kp values for tissues were the same in both the ML-PBPK and in vitro inputs models, comparable values indicate that ML prediction of and Caco-2 cell permeability was able to replace experimental values without compromising accuracy.
The ML-PBPK model was also more efficient than the in vitro inputs model, with a runtime of only 10 seconds per simulation compared to the few days it may take to collect experimental data and perform model simulations. Overall, the ML-PBPK model was found to be a fast platform that accurately predicts human PK profiles in plasma and tissues.
Discussion
The development of PBPK models has been a significant advancement in pharmacology. Initially, in vitro data were used to create these models to predict animal and human PK. However, the accuracy of PBPK models and the integrity of input parameters were limited because these measurements did not fully capture the complexity of the human body. As a result, there has been growing interest in developing PBPK models that incorporate inputs without experiments.
The integration of machine learning (ML) with traditional physiologically based pharmacokinetic (PBPK) models has been a focus of early research efforts aimed at minimizing the need for experimental data in model development [26]. The research includes using absorption (ka), elimination (CLint), distribution (Vss) parameters or physicochemical property parameters predicted based on ML as inputs to predict the in vivo exposure of oral drugs through a simplified PBPK model. Since the model only considers plasma, absorption tissues and elimination tissues, it may not meet the prediction needs that are more relevant to the target tissues for some drug effects or toxicities. Moreover, the literature has often adopted the intrinsic hepatic clearance rate for the prediction of metabolic parameters. While the reported test set demonstrates favorable outcomes, the variability in prediction accuracy when extrapolating from intrinsic hepatic clearance to whole-body hepatic serum clearance cannot be overlooked. To mitigate this discrepancy, our approach considers the use of in vivo hepatic serum clearance as an input parameter. Furthermore, the significance of unbound drug fraction () on model predictions, particularly for clearance, has been substantiated by several studies [36, 37]. It is also recognized that fup influences drug distribution; however, for drugs with high protein binding, the precision of empirical measurements diminishes. Consequently, ML has also been deployed to predict this parameter. Previous literature has also focused on improving the prediction of tissue distribution coefficients or the impact of liver clearance on PK simulation. In a study conducted by Murad, a machine learning model was used to predict , showing that 58 of predictions were within a 2-fold error [38]. The Miljkovic team used machine learning to predict PK parameters directly from structure, and 48.5 of their predictions in the test set were within a 2-fold error [39]. Although the ML predictions for have been promising, and some studies have directly used this parameter as an input for PBPK modeling, it must be noted that represents the overall drug distribution volume, inclusive of plasma and tissues, and does not delineate the specific distribution within tissues. Therefore, our study continues to employ the Rodgers and Rowland (RR) method to calculate drug distribution across various tissues, taking into account the specific composition of each tissue. Following the optimization methods previously mentioned, our model demonstrated improved predictive capabilities for the 40 testing compounds. We achieved the accuracies within a two-fold prediction error of 55, 65, 65, and 57.5 for , AUC, CL and respectively.
This study further showed the power of machine learning in predicting relevant parameters that may involve complex physiological processes and hard to be accurately measured by in vitro experiments. A large dataset of drug properties was used to develop ML models that predict , Caco-2 cell permeability, and total plasma clearance of drugs. These ML prediction values were then used as inputs for the PBPK models.
We have implemented the Deep Message Passing Neural Network (D-MPNN) for the prediction of input parameters of drugs, achieving superior performance compared to traditional machine learning approaches such as Support Vector Regression (SVR), Random Forest (RF), XGBoost (XGB), and Gradient Boost Machine (GBM). The superior performance of the D-MPNN in predicting ADMET properties of small molecular compounds in contrast to other traditional ML methods can be attributed as follows:
Structure-awareness: D-MPNN uses a graph-based representation of molecules, capturing the relationships between atoms and chemical bonds within the molecular structure. This may enable the model to understand the structural and chemical context of the molecule, which is crucial for predicting ADMET properties.
End-to-end learning: D-MPNN is an end-to-end model that learns to predict target properties directly from molecular structures without the need for manual feature engineering. This allows the model to automatically discover relevant features and patterns in the data.
Message passing mechanism: The D-MPNN architecture uses multiple rounds of message passing to update atom representations. This process enables the model to capture both local and global chemical environments, which are essential for accurately predicting ADMET properties.
These factors may enable the model to capture more relevant chemical information and make more accurate predictions.
Results on 40 drugs showed that the ML-PBPK model predicts human PK parameters with higher accuracy than the in vitro inputs model, and most of the compounds have prediction errors within 2 or 3-fold. Especially, compounds with extensive renal clearance have an average fold error (AFE) of 0.94 compared to the in vitro inputs model of 1.28. In addition, each PK prediction in general was completed within seconds on a machine with the ML-PK model, showing a higher efficiency without compromising accuracy compared to in vitro inputs model.
The PBPK model is a four-compartment permeability-limited model used to predict the distribution of drugs in various tissues. It assumes that the drug’s membrane permeability into different tissues is equal to the value measured in vitro using Caco-2 cells. The LogP values of the tested compounds range from -0.11 to 8.49, and the fup values range from 0.002 to 0.95.Based on the results of 40 molecules, the PBPK model tends to underestimate the tissue distribution volume for highly lipophilic and highly permeable drugs, such as Desipramine and Imipramine. However, the model fails to effectively predict tissue distribution coefficients for extremely lipophilic molecules with a LogP value exceeding 5, like Montelukast. In these cases, the calculation method for tissue distribution coefficients based on in vitro inputs leads to an overestimation of Vd for these compounds.The main difference between the in vitro and ML models lies in the input parameter for the elimination process. The in vitro model, which is based on microsomal experimental data and predicted using the IVIVE method, significantly underestimates the clearance for drugs like Cimetidine, Prazosin, and Metoprolol, which are eliminated primarily through renal clearance or are substrates of uptake transporters (such as OCTs). Moreover, the in vitro model also underestimates CL for drugs with high plasma protein binding, which have difficulty entering the elimination tissue according to the modeling assumption. On the other hand, the ML model significantly improves the prediction accuracy for this class of molecules.
This study showed how ML methods could improve PK prediction by predicting relevant physicochemical parameters. Future improvements on data quantity and quality that are used to train ML models worth more work. For example, using data from GI organoids may help us train better models to aid the PK prediction for drugs with oral administration. In this study, we predicted total clearance for PK prediction. With more data, we may have separate models for distinct clearance routes, e.g., separate models for hepatic and renal clearance, that provides more information in drug reaserch and development. Thus development of better models as our understanding of deep learning progresses is another valuable direction for future work.
Conclusions
We evaluated the accuracy of our developed ML-PBPK model platform on 40 compounds by comparing the accuracy of in vitro inputs and ML prediction inputs. The commonly used IVIVE method has limitations in predicting hepatic clearance, and there is a limited experimental exploration of clearance pathways outside the liver in the early stages of drug discovery. As drug clearance is crucial for PK prediction, we used an ML model to predict total human plasma clearance as inputs into the PBPK model for predicting drug concentrations in plasma and tissues. This method was able to guide the development and prioritization of lead compounds based on molecular structure for PK prediction before in vitro experiments. In the future, the accuracy of the ML-PBPK model can be further improved or optimized for specific molecular structures by expanding the training set. Methods such as graph-based multi-task learning, pre-trained models, and model ensembles will be employed to improve accuracy. Furthermore, studying the interpretability of the prediction results is also essential.
Supplementary Information
Below is the link to the electronic supplementary material.
Declarations
Conflict of Interest
The authors have no relevant financial or non-financial interests to disclose.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Poggesi I, Snoeys J, Van Peer A. The successes and failures of physiologically based pharmacokinetic modeling: there is room for improvement. Expert Opinion on Drug Metabolism & Toxicology. 2014;10(5):631–5. 10.1517/17425255.2014.888058. Accessed 2023-06-12. [DOI] [PubMed]
- 2.Tylutki Z, Polak S, Wiśniowska B. Top-down, Bottom-up and Middle-out Strategies for Drug Cardiac Safety Assessment via Modeling and Simulations. Current Pharmacology Reports. 2016;2(4):171–7. 10.1007/s40495-016-0060-3. Accessed 2023-06-13. [DOI] [PMC free article] [PubMed]
- 3....Ahmad A, Pepin X, Aarons L, Wang Y, Darwich AS, Wood JM, Tannergren C, Karlsson E, Patterson C, Thörn H, Ruston L, Mattinson A, Carlert S, Berg S, Murphy D, Engman H, Laru J, Barker R, Flanagan T, Abrahamsson B, Budhdeo S, Franek F, Moir A, Hanisch G, Pathak SM, Turner D, Jamei M, Brown J, Good D, Vaidhyanathan S, Jackson C, Nicolas O, Beilles S, Nguefack JF, Louit G, Henrion L, Ollier C, Boulu L, Xu C, Heimbach T, Ren X, Lin W, Nguyen-Trung AT, Zhang J, He H, Wu F, Bolger MB, Mullin JM, Van Osdol B, Szeto K, Korjamo T, Pappinen S, Tuunainen J, Zhu W, Xia B, Daublain P, Wong S, Varma MVS, Modi S, Schäfer KJ, Schmid K, Lloyd R, Patel A, Tistaert C, Bevernage J, Nguyen MA, Lindley D, Carr R, Rostami-Hodjegan A. IMI-Oral biopharmaceutics tools project-Evaluation of bottom-up PBPK prediction success part 4: Prediction accuracy and software comparisons with improved data and modelling strategies. Eur J Pharm Biopharm. 2020;156:50–63. 10.1016/j.ejpb.2020.08.006. Accessed 2023-06-12. [DOI] [PubMed]
- 4.Naga D, Parrott N, Ecker GF, Olivares-Morales A. Evaluation of the Success of High-Throughput Physiologically Based Pharmacokinetic (HT-PBPK) Modeling Predictions to Inform Early Drug Discovery. Mol Pharm. 2022;19(7):2203–16. 10.1021/acs.molpharmaceut.2c00040. Accessed 2023-06-12. [DOI] [PMC free article] [PubMed]
- 5.Antontsev V, Jagarapu A, Bundey Y, Hou H, Khotimchenko M, Walsh J, Varshney J. A hybrid modeling approach for assessing mechanistic models of small molecule partitioning in vivo using a machine learning-integrated modeling platform. Sci Rep. 2021;11(1):11143. 10.1038/s41598-021-90637-1. Accessed 2023-06-12. [DOI] [PMC free article] [PubMed]
- 6.Bowman CM, Benet LZ. In Vitro-In Vivo Extrapolation and Hepatic Clearance-Dependent Underprediction. J Pharm Sci. 2019;108(7):2500–4. 10.1016/j.xphs.2019.02.009. Accessed 2023-06-12. [DOI] [PMC free article] [PubMed]
- 7.Watanabe R, Esaki T, Kawashima H, Natsume-Kitatani Y, Nagao C, Ohashi R, Mizuguchi K. Predicting Fraction Unbound in Human Plasma from Chemical Structure: Improved Accuracy in the Low Value Ranges. Mol Pharm. 2018;15(11):5302–11. 10.1021/acs.molpharmaceut.8b00785. Accessed 2023-06-13. [DOI] [PubMed]
- 8.Votano JR, Parham M, Hall LM, Hall LH, Kier LB, Oloff S, Tropsha A. QSAR Modeling of Human Serum Protein Binding with Several Modeling Techniques Utilizing Structure-Information Representation. J Med Chem. 2006;49(24):7169–81. 10.1021/jm051245v. Accessed 2023-06-13. [DOI] [PubMed]
- 9.Orwat MJ, Qiao JX, He K, Rendina AR, Luettgen JM, Rossi KA, Xin B, Knabb RM, Wexler RR, Lam PYS, Pinto DJP. Orally bioavailable factor Xa inhibitors containing alpha-substituted gem-dimethyl P4 moieties. Bioorganic & Medicinal Chemistry Letters. 2014;24(15):3341–5. 10.1016/j.bmcl.2014.05.101. Accessed 2023-07-17. [DOI] [PubMed]
-
10.Kotoku M, Maeba T, Fujioka S, Yokota M, Seki N, Ito K, Suwa Y, Ikenogami T, Hirata K, Hase Y, Katsuda Y, Miyagawa N, Arita K, Asahina K, Noguchi M, Nomura A, Doi S, Adachi T, Crowe P, Tao H, Thacher S, Hashimoto H, Suzuki T, Shiozaki M. Discovery of Second Generation ROR
 Inhibitors Composed of an Azole Scaffold. Journal of Medicinal Chemistry. 2019;62(5):2837–2842. 10.1021/acs.jmedchem.8b01567 . Accessed 2023-07-17. [DOI] [PubMed]
Inhibitors Composed of an Azole Scaffold. Journal of Medicinal Chemistry. 2019;62(5):2837–2842. 10.1021/acs.jmedchem.8b01567 . Accessed 2023-07-17. [DOI] [PubMed] - 11.Ernst JT, Thompson PA, Nilewski C, Sprengeler PA, Sperry S, Packard G, Michels T, Xiang A, Tran C, Wegerski CJ, Eam B, Young NP, Fish S, Chen J, Howard H, Staunton J, Molter J, Clarine J, Nevarez A, Chiang GG, Appleman JR, Webster KR, Reich SH. Design of Development Candidate eFT226, a First in Class Inhibitor of Eukaryotic Initiation Factor 4A RNA Helicase. J Med Chem. 2020;63(11):5879–955. 10.1021/acs.jmedchem.0c00182. Accessed 2023-07-17. [DOI] [PubMed]
- 12.Lombardo F, Berellini G, Obach RS. Trend Analysis of a Database of Intravenous Pharmacokinetic Parameters in Humans for 1352 Drug Compounds. Drug Metab Dispos. 2018;46(11):1466–77. 10.1124/dmd.118.082966. [DOI] [PubMed]
- 13.WebPlotDigitizer. 2023. https://apps.automeris.io/wpd/.
- 14.Sohlenius-Sternbeck AK, Afzelius L, Prusis P, Neelissen J, Hoogstraate J, Johansson J, Floby E, Bengtsson A, Gissberg O, Sternbeck J, Petersson C. Evaluation of the human prediction of clearance from hepatocyte and microsome intrinsic clearance for 52 drug compounds. Xenobiotica. 2010;40(9):637–49. 10.3109/00498254.2010.500407. Accessed 2023-06-14. [DOI] [PubMed]
- 15.Mamada H, Iwamoto K, Nomura Y, Uesawa Y. Predicting blood-to-plasma concentration ratios of drugs from chemical structures and volumes of distribution in humans. Mol Diversity. 2021;25(3):1261–70. 10.1007/s11030-021-10186-7. Accessed 2023-09-26. [DOI] [PMC free article] [PubMed]
- 16.Murad N, Pasikanti KK, Madej BD, Minnich A, McComas JM, Crouch S, Polli JW, Weber AD. Predicting Volume of Distribution in Humans: Performance of In Silico Methods for a Large Set of Structurally Diverse Clinical Compounds. Drug Metab Dispos. 2021;49(2):169–78. 10.1124/dmd.120.000202. Accessed 2023-09-26. [DOI] [PMC free article] [PubMed]
- 17.Pham-The H, González-Álvarez I, Bermejo M, Garrigues T, Le-Thi-Thu H, Cabrera-Pérez MA. The use of rule-based and qspr approaches in adme profiling: A case study on caco-2 permeability. Mol Inf. 2013;32(5–6):459–79. 10.1002/minf.201200166. Accessed 2023-09-26. [DOI] [PubMed]
- 18.O’Hagan S, Kell DB. The apparent permeabilities of Caco-2 cells to marketed drugs: magnitude, and independence from both biophysical properties and endogenite similarities. PeerJ. 2015;3:1405. 10.7717/peerj.1405. Accessed 2023-06-12. [DOI] [PMC free article] [PubMed]
- 19.Bittermann K, Goss KU. Predicting apparent passive permeability of Caco-2 and MDCK cell-monolayers: A mechanistic model. PLoS ONE. 2017;12(12):0190319. 10.1371/journal.pone.0190319. Accessed 2023-09-26. [DOI] [PMC free article] [PubMed]
- 20.Hallifax D, Foster JA, Houston JB. Prediction of Human Metabolic Clearance from In Vitro Systems: Retrospective Analysis and Prospective View. Pharm Res. 2010;27(10):2150–61. 10.1007/s11095-010-0218-3. Accessed 2023-09-26. [DOI] [PubMed]
- 21.Williamson B, Harlfinger S, McGinnity DF. Evaluation of the Disconnect between Hepatocyte and Microsome Intrinsic Clearance and In Vitro In Vivo Extrapolation Performance. Drug Metab Dispos. 2020;48(11):1137–46. 10.1124/dmd.120.000131. Accessed 2023-09-26. [DOI] [PubMed]
- 22.Bento AP, Hersey A, Felix E, Landrum G, Gaulton A, Atkinson F, Bellis LJ, Veij MD, Leach AR. An Open Source Chemical Structure Curation Pipeline Using RDKit. J Cheminform. 2020;12:51. 10.1186/s13321-020-00456-1. [DOI] [PMC free article] [PubMed]
- 23.Yap CW. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J Comput Chem. 2011;32(7):1466–74. 10.1002/jcc.21707. [DOI] [PubMed]
- 24.Kursa MB, Rudnicki RW. Feature Selection with the Boruta Package. Journal of Statistical Software. 2010;36(11):1–13. 10.18637/jss.v036.i11.
- 25.Wang Y, Liu H, Fan Y, Chen X, Yang Y, Zhu L, Zhao J, Chen Y, Zhang Y. In silico prediction of human intravenous pharmacokinetic parameters with improved accuracy. J Chem Inf Model. 2019;59(9):3968–80. 10.1021/acs.jcim.9b00300. [DOI] [PubMed]
- 26.Chou WC, Lin Z. Machine learning and artificial intelligence in physiologically based pharmacokinetic modeling. Toxicol Sci. 2023;191(1):1–14. 10.1093/toxsci/kfac101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yang K, Swanson K, Jin W, Coley C, Eiden P, Gao H, Guzman-Perez A, Hopper T, Kelley B, Mathea M, Palmer A, Settels V, Jaakkola T, Jensen K, Barzilay R. Analyzing Learned Molecular Representations for Property Prediction. J Chem Inf Model. 2019;59(8):3370–88. 10.1021/acs.jcim.9b00237. [DOI] [PMC free article] [PubMed]
- 28.Kawai R, Lemaire M, Steimer JL, Bruelisauer A, Niederberger W, Rowland M. Physiologically based pharmacokinetic study on a cyclosporin derivative, SDZ IMM 125. J Pharmacokinet Biopharm. 1994;22(5):327–65. 10.1007/BF02353860. Accessed 2023-06-12. [DOI] [PubMed]
- 29.Burt HJ, Neuhoff S, Almond L, Gaohua L, Harwood MD, Jamei M, Rostami-Hodjegan A, Tucker GT, Rowland-Yeo K. Metformin and cimetidine: Physiologically based pharmacokinetic modelling to investigate transporter mediated drug-drug interactions. Eur J Pharm Sci. 2016;88:70–82. 10.1016/j.ejps.2016.03.020. Accessed 2023-09-26. [DOI] [PubMed]
- 30.Valentin J. Basic anatomical and physiological data for use in radiological protection: reference values. A report of age-and gender-related differences in the anatomical and physiological characteristics of reference individuals. ICRP Publication 89. Annals of the ICRP. 2002;32(3–4):5–265. [PubMed]
- 31.Deurenberg P, Weststrate JA, Seidell JC. Body mass index as a measure of body fatness: age- and sex-specific prediction formulas. Br J Nutr. 1991;65(2):105–14. 10.1079/BJN19910073. Accessed 2023-06-12. [DOI] [PubMed]
- 32.Pilari S, Gaub T, Block M, Görlitz L. Development of Physiologically Based Organ Models to Evaluate the Pharmacokinetics of Drugs in the Testes and the Thyroid Gland: Development of Physiologically Based Organ Models. CPT: Pharmacometrics & Systems Pharmacology. 2017;6(8):532–542. 10.1002/psp4.12205 . Accessed 2023-06-12. [DOI] [PMC free article] [PubMed]
- 33.Rodgers T, Leahy D, Rowland M. Physiologically Based Pharmacokinetic Modeling 1: Predicting the Tissue Distribution of Moderate-to-Strong Bases. J Pharm Sci. 2005;94(6):1259–76. 10.1002/jps.20322. Accessed 2023-06-13. [DOI] [PubMed]
- 34.Sohlenius-Sternbeck AK, Terelius Y. Evaluation of ADMET Predictor in Early Discovery Drug Metabolism and Pharmacokinetics Project Work. Drug Metab Dispos. 2022;50(2):95–104. 10.1124/dmd.121.000552. Accessed 2023-06-14. [DOI] [PubMed]
- 35.Musther H, Gill KL, Chetty M, Rostami-Hodjegan A, Rowland M, Jamei M. Are Physiologically Based Pharmacokinetic Models Reporting the Right Cmax? Central Venous Versus Peripheral Sampling Site. AAPS J. 2015;17(5):1268–79. 10.1208/s12248-015-9796-7. Accessed 2023-06-12. [DOI] [PMC free article] [PubMed]
- 36.Kamiya Y, al. In silico prediction of input parameters for simplified physiologically based pharmacokinetic models for estimating plasma, liver, and kidney exposures in rats after oral doses of 246 disparate chemicals. Chem. Res. Toxicol. 2021;34:507–513. 10.1021/acs.chemrestox.0c00457. [DOI] [PubMed]
- 37.Habiballah S, Reisfeld B. Adapting physiologically-based pharmacokinetic models for machine learning applications. Sci Rep. 2023;13:14934. 10.1038/s41598-023-14487-4. [DOI] [PMC free article] [PubMed]
- 38.Murad N, Pasikanti KK, Madej DB, Minnich A, McComas MJ, Crouch S, Polli WJ, Weber DA. Predicting Volume of Distribution in Humans: Performance of In Silico Methods for a Large Set of Structurally Diverse Clinical Compounds. 2021;49(2):169–278. 10.1124/dmd.120.000202. [DOI] [PMC free article] [PubMed]
- 39.Miljkovic F, Martinsson A, Obrezanova O, Williamson B, Johnson M, Sykes A, Bender A, Greene N. Machine Learning Models for Human In Vivo Pharmacokinetic Parameters with In-House Validation. Mol Pharm. 2021;18(12):4520–30. 10.1021/acs.molpharmaceut.1c00718. [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.