Abstract
In the current work, an innovative nondominated sorting colliding bodies optimization (NSCBO) technique is introduced to tackle multiobjective optimal power flow (MOOPF) challenges within electrical power networks. This method offers a means to generate a diverse array of nondominated solutions in a single iteration by including the nondominated (ND) sorting process and the concept of crowding distance. Additionally, it utilizes a spread indicator to archive the latest nondominated solutions. In the NSCBO method, the mass of each colliding body is determined by its nondominated rank rather than relying on objective function information. Moreover, a fuzzy decision-making strategy is employed to identify a suitable solution from the set of ND solutions. To showcase the scalability and viability of the NSCBO method, experiments are conducted on IEEE 30-bus, considering both bi- and tri-objective models. Comparative analysis with existing methods from recent literature demonstrates the efficacy of the NSCBO technique in handling constraints and deriving nondominated solutions for MOOPF problems.
Keywords: Colliding bodies optimization, Heuristic technique, Objective optimization, Emission pollution, Total production cost
Subject terms: Energy grids and networks, Power distribution
Introduction
The concept of Optimal Power Flow (OPF) developed by Dommel and Tinney in 1960 holds paramount importance in power system operation and control. The objective of OPF is to identify optimal control variable setups that minimize a selected function while adhering to a series of equality and inequality restrictions1. Initially, traditional approaches such as linear programming (LP)2and Newton’s method3were employed to address OPF problems. However, these methods face challenges in dealing with nonlinear objective functions and constraints. To overcome these limitations and achieve near-optimal solutions for various optimization challenges4–6, several heuristic techniques have been developed. namely, differential evolution (DE)7–10, genetic algorithm11, particle swarm optimization12, artificial bee colony (ABC)13, harmony search (HS)14, gravitational search algorithm (GSA)15,16, pathfinder algorithm (PA)17, imperialist competitive algorithm (ICA)18, firefly19, Cascaded fuzzy system20,21, Wavelet-Oriented22,23, stud krill herd24, and machine learning25methods have been devised to address multiobjective OPF challenges through algorithmic approaches. In7introduced enhanced self-adaptive DE with Mixed Crossover (ESDE-MC) algorithm for MOOPF problems, targeting production costs, emissions, L-index, and power loss minimization. It combines eigenvector and binomial crossovers with adaptive parameter adjustment. Simulation results demonstrate the algorithm’s effectiveness for MOOPF problems. In8, introduced a multi-objective optimization (MOO) approach for solving the MOOPF problem with improved computational efficiency. By reducing the number of load flows using sensitivities and heuristics, the approach accelerates the solution process while addressing fuel cost, loss, and L index minimization. Tested on the IEEE 30-bus system, it outperforms NSGA-II and can be implemented with various evolutionary algorithms. In10, the multi-objective adaptive guided differential evolution (MOAGDE) algorithm addressed MOO by enhancing exploration and exploitation compared to single-objective algorithms. It utilizes non-dominated sorting and crowding distance for optimal Pareto solutions, validated against the CEC 2020 benchmark suite. Applied to the multi-objective AC optimal power flow (MO-ACOPF) problem with renewable energy sources, the algorithm demonstrated superior performance on the IEEE 30-bus system. In11presented the Non-dominated Sorting GA II (NSGA-II), which addressed key criticisms of existing MOEAs by offering a fast non-dominated sorting approach with O(MN²) complexity. It features a selection operator that optimally combines parent and offspring populations and modifies dominance for constrained problems. Simulation results show that NSGA-II achieves superior solution spread and convergence to the true Pareto-optimal front compared to other elitist MOEAs. In12proposed a hybrid PSO-Salp swarm optimization (SSO) method for solving the OPF problem, optimizing generation cost, emissions, power loss, and voltage stability. Tested on 18 case studies, the algorithm demonstrates superior performance and robustness. Sensitivity analysis confirms its reliability against parameter variations. In13presented an efficient method for solving the MOOPF problem using ABC algorithm to optimize control variables. It addresses various multi objective functions, including fuel costs, power loss, and emissions, for highly constrained nonlinear optimization. In14presented a multi-objective harmony search (MOHS) algorithm for solving the MOOPF problem as a nonlinear constrained multi-objective optimization task. It utilized fast elitist non-dominated sorting and crowding distance techniques to manage the Pareto optimal front, along with a fuzzy mechanism for selecting compromise solutions. The article15presented the GSA, inspired by swarm behaviors, for solving MOOPF problems. GSA, based on Newton’s laws of gravity and motion, utilizes searcher agents to optimize objectives like fuel cost, active power loss, and voltage deviation. The algorithm is tested on a standard 26-bus system and the IEEE 118-bus system, addressing various combinations of these objectives. Results demonstrate that GSA outperforms other optimization techniques in convergence speed and global search capability. In16introduced the non-dominated sorting MO opposition-based GSA (NSMOOGSA) for solving single and MOOPF problems. The algorithm utilizes oppositional learning to enhance population improvement and convergence speed. It effectively manages the Pareto optimal front through non-dominated sorting with crowding distance. Tested on the IEEE 30-bus power system, NSMOOGSA demonstrates significant potential in minimizing conflicting objectives. In17, presented the MOOPF problem, focusing on generation cost, emissions, real power loss, and voltage deviation while integrating wind, solar, and tidal energy sources. The proposed multi-objective pathfinder algorithm (MOPFA) effectively optimizes these objectives in the IEEE-30 test system, yielding a well-distributed Pareto front and diverse solutions. In18, introduced the Gaussian Bare-bones MO Imperialist Competitive Algorithm (GBICA) and its Modified version (MGBICA) for optimal electric power planning, focusing on OPF and Optimal Reactive Power Dispatch (ORPD) problems. These problems are formulated as nonlinear constrained multi-objective optimization challenges. Evaluated on IEEE 30-bus and IEEE 57-bus test systems, the proposed algorithms show superior performance compared to existing methods. GBICA and MGBICA effectively address multi-objective electric power planning issues. In19presented an improved Firefly Algorithm (IFA) combined with extremal optimization (EO), called IFA-EO, to overcome slow convergence and local optima issues in traditional FA. The method features a hybrid attraction model for better exploration and exploitation, an adaptive step size, and EO for enhanced local search. IFA-EO is tested on three parameter identification problems for photovoltaic models. In20, introduced a dynamic MOO algorithm (DMOA) enhanced by a cascaded fuzzy system (CFS) to improve knowledge transfer and mitigate negative transfer issues in evolutionary transfer optimization (ETO). It adaptively selects previous Pareto solutions and assigns soft labels based on convergence and diversity. The algorithm employs kernel mean matching (KMM) to enhance knowledge transfer efficiency. Extensive evaluations show that CFS-DMOA outperforms state-of-the-art ETO-based DMOAs. In21presents a multi-strategy adaptive selection-based DMOA (MSAS-DMOA) using non-inductive transfer learning for solving DMOPs. It improves knowledge transfer with kernel mean matching (KMM) and avoids conventional labeling. Tested on 14 DMOPs, it shows superior convergence and diversity. Ablation studies validate its ability to mitigate negative transfer. In22presented HWM2SFLA-PSO, a hybrid meta-heuristic algorithm for solving MOOPF problems with multi-fuel constraints and FACTS devices. It optimizes four objectives: total generation cost, emissions, real power transmission losses, and voltage deviation. Results show HWM2SFLA-PSO’s superior performance on IEEE test systems, demonstrating improved execution time and solution quality while avoiding local optima. In23 presented HRS-DMOA, a dynamic multiobjective optimization algorithm that responds to environmental changes using diversity, memory, and prediction-based strategies.
Colliding Bodies Optimization (CBO), an evolutionary technique developed by Kaveh offers a promising solution for continuous optimization problems26, drawing inspiration from the collision dynamics between two objectives. In CBO, independent variables are analogized as colliding bodies (CBs), where collisions between pairs of CBs lead to enhancements in their positions. Notably, CBO operates without requiring control parameters, making it easily implementable. Its efficacy has been demonstrated across various optimization problems27–29.
However, the conventional CBO method falls short when addressing multiobjective Optimal Power Flow (MOOPF) problems. Addressing this research gap, the authors’ contributions: to the current research paper are (i) an extension named nondominated sorting colliding bodies optimization (NSCBO) is proposed to tackle MOOPF problems, (ii) incorporating ND sorting and crowding distance concepts enables the proposed technique to produce a diverse set of ND solutions in a single trial, (iii) each CB’s mass is determined by its nondominated rank rather than objective function values, (iv) a spread indicator is utilized to store and update nondominated solutions in an external archive, (v) Using a fuzzy decision method helps in effectively choosing the most appropriate and optimal solution from a set of ND solutions. The scalability and efficiency of the developed NSCBO are validated on IEEE 30-bus, encompassing both bi and tri-objective functions. Furthermore, the obtained results are compared with those of existing techniques documented in contemporary literature.
The main challenges in the current work research are.
The conventional CBO technique faces difficulty in multi-objective optimization due to its single fitness value reliance, requiring adjustments to CB mass calculations for multiple conflicting objectives.
Ensuring a diverse set of non-dominated solutions can be challenging, necessitating effective crowding distance strategies and efficient archiving to avoid premature convergence.
Efficiently updating positions and velocities of colliding bodies while managing a scalable population is crucial, particularly for complex systems like the IEEE 30-bus.
The subsequent sections of the paper follow this structure: Section II outlines the OPF formulation, while Section III elaborates on the NSCBO method proposed to tackle the Multi-Objective Optimal Power Flow (MOOPF) challenge. Section IV exhibits the results obtained across different scenarios, and lastly, Section V encapsulates the conclusions drawn from the study.
Multiobjective optimal power flow formulation
Mathematically, The OPF issue may expressed as below12:
 |
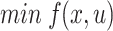1 |
 |
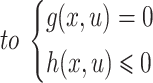2 |
where f indicates an objective;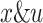 
indicates state and independent variables correspondingly. 
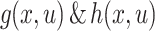denote equality and inequality constraints individually.
This study encompasses multiple objective functions, with the formulation of said functions and their associated constraints outlined below9:
Objective function models
Optimization of fuel cost (FC)
The fundamental objective function in OPF typically revolves around fuel cost and is expressed below9.
 |
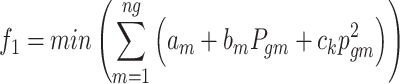3 |
Where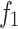 
denotes the minimization of fuel cost; 
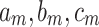indicates the cost coefficients of the 
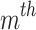generator; and 
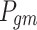indicates the real power of the 
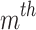generator.
Minimization of emission profile
The aggregate ton/h of atmospheric pollutants emitted, including sulfur and nitrogen oxides, from fossil fuel-fired units may expressed as below9:
 |
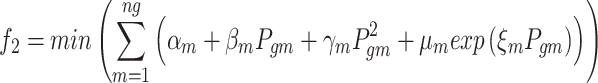4 |
where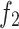 
indicates emission released from the thermal power plant; 
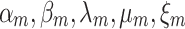denotes coefficients of 
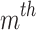the unit, and these values depend on factors such as boiler type, operational parameters, and the type of fuel being utilized.
Minimization of active power loss (APL)
Mathematically, the APL across all transmission lines may expressed as a total active power loss associated with each line and is given below:
 |
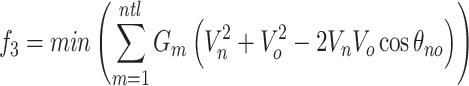5 |
Where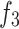 
symbolizes minimization of APL; 
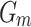represents the conductance of 
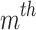the bus; 
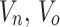signifies voltages of 
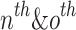buses individually.
Constraints
The multiobjective optimization optimal power flow (MOOPF) issue is constrained by a multitude of system requirements, including all the constraints, which may be given below:
Equality constraints
The equality constraints in OPF reflect the fundamental physical principles governing the power system. These constraints are articulated through the following equations:
 |
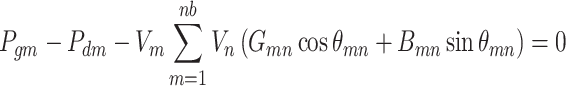6 |
 |
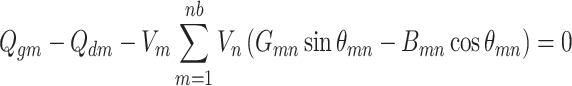7 |
where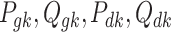 
signifies real and reactive power generations and loads at 
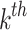bus respectively; 
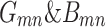indicates the conductance and susceptance among 
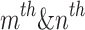buses individually.
Inequality constraints
The inequality constraints delineate the permissible range for variables, ensuring they remain within feasible limits as given as follows;
 |
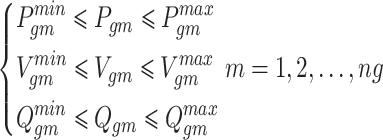8 |
where,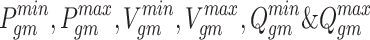 
signifies low and high values of real power, voltages, and reactive power limits of 
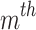generator respectively, 
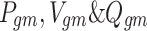symbolizes real power, voltage, and reactive power of 
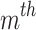generator respectively.
 |
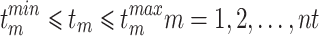9 |
 |
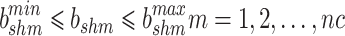10 |
 |
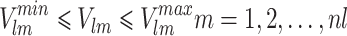11 |
 |
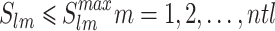12 |
where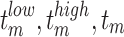 
symbolize low and high, transformer tap at 
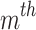transformer respectively; 
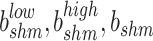, signifies the low, high, and susceptance value 
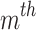shunt capacitor respectively; 
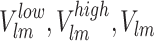, symbolizes low, high, and voltages at 
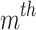load bus respectively; 
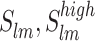denotes MVA flow and high MVA of 
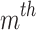line.
Non-dominated sorting colliding bodies optimization
Multiobjective optimization
Multiobjective optimization problems involve the concurrent minimization of multiple objective functions while adhering to a set of constraints.
 |
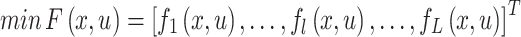13 |
 |
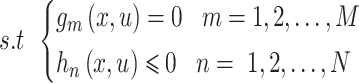14 |
where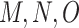 
indicate the count of objective functions, equality, and inequalities individually; The
Overview of colliding bodies optimization
Drawing inspiration from the interactions between objects in collision scenarios, Kaveh and Mahdavi introduced a novel evolutionary technique termed CBO in 201416. In CBO, the solution set of an optimization problem is metaphorically depicted as a colliding body characterized by specific mass and velocity. The efficacy of a solution is assessed based on its mass value and is calculated as follows:
 |
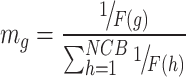15 |
where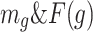 
denotes mass and fitness of 
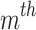CB. After arranging all CBs in ascending order and dividing them into two equal groups, the first half called stationary and the second half called moving groups, before the collision the velocities of the two said groups are expressed below:
 |
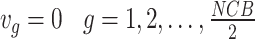16 |
 |
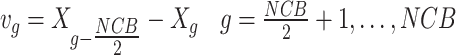17 |
where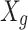 
denote position of 
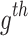CB. When the prompting CBs shadow the constant CBs and collisions happen between pairs of CBs, serving two resolves: (i) to adjust the stationary positions CBs for improved placement, and (ii) refining moving objects position. The CBs velocities later the impact is expressed below:
 |
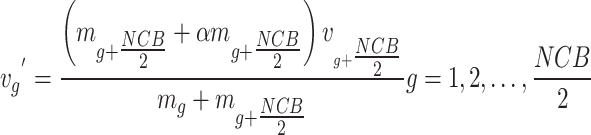18 |
 |
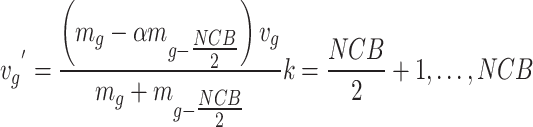19 |
where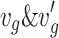 
indicates velocities of 
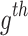CB prior and after collision; the coefficient of restitution, denoted by 
.
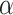Nondominated sorting colliding bodies optimization (NSCBO)
Here is the concept of NSCBO technique for addressing multiobjective OPF (MOOPF) issues. NSCBO initially adjusts the mass of CB to tackle MOOPF issues. Additionally, it employs an elite archive set to retain nondominated solutions attained during evolution. Ultimately, a fuzzy decision technique is utilized to derive the best compromise solution (BCS) from the archive set. The procedural steps for NSCBO technique to solve MOOPF issues are outlined as follows.
Initialization
In NSCBO, each CB is viewed as a solution that is arbitrarily generated in the initialization process. The entire feasible search space for the NSCBO technique, comprising colliding bodies, is combined and expressed below:
 |
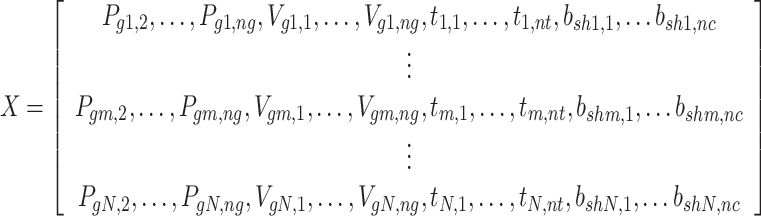20 |
Nondominated sorting process
In the NSCBO framework, the initialization of the CBs population follows Eq. (20). To categorize the CBs into distinct nondomination layers, a procedure for nondominated sorting is outlined as explained below:
-
Step 1:
Every CB result assesses all objectives and later determines two factors: (i) the domination count
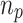, that dominates the given solution p, (ii) a 
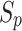solutions set dominated by the given one. In the initial ND front, all solutions have zero domination count. -
Step 2:
Solutions having zero domination count from the initial ND layer, identified as the Pareto optimal front with a rank of 1.
-
Step 3:
For every solution p with a domination count of zero, examine every one q of its dominant sets
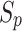and decrease their domination counts by one. If any member’s domination count reaches ‘0’ in this process, place it in the second nondomination layer and assign it a rank of 2. -
Step 4:
Following the same procedure for every CB of the second nondomination layer identifies subsequent nondomination layers. Repeat until all nondomination levels are established.
In selecting superior CBs, preference is given to those with lower ranks. When CBs share the same rank, those with greater crowding distances are retained within the current population. Hence, the NSCBO technique comprehensive search space necessitates the continuation of operations with a total of CBs.
Update an external archive
The Pareto dominance principle governs the updating of the archive set. If a specific CB in the search area is outperformed by any member of the archive, it is excluded from inclusion in the archive. Conversely, if an individual outperforms one or more members of the archive and is added to the archive cluster the outperformed CBs are eliminated. If the external members beat the extreme archive, the most densely populated region is selected for removal and a spread indicator is introduced to regulate the archive length30. Furthermore, the crowding distance procedure is applied to find the ranking of diverse layers, as elaborated as follows.
 |
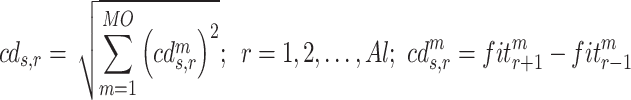21 |
 |
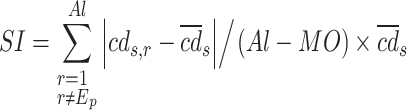22 |
where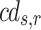 
denotes crowding distance, 
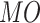expresses total number of objectives, 
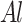is the elite external archive length, 
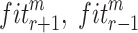are the 
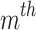fitness of 
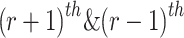points. SI indicates the spread indicator.
The definition of CB mass
Based on the literature, it is evident that the classical CBO technique is not suited for addressing MOOPF problems. This limitation arises from Eq. (15), where the mass of each colliding body (CB) signifies the fitness value of a single objective. However, MOOPF problems entail multiple objectives, necessitating a modification of CB masses to accommodate these conflicting objectives. The complexity of calculating mass for multiple objectives lies in the need to consider various fitness values simultaneously, which can introduce challenges in terms of normalization and aggregation. Specifically, each objective may have different scales and units, making direct comparisons difficult. To address this, the fitness values of all objectives must be normalized, requiring additional calculations to establish a common scale. Once normalized, these values are aggregated to determine the mass of each body, which adds further complexity to the process, as it involves finding a suitable method for combining the normalized values in a way that accurately reflects the trade-offs between the conflicting objectives. This aggregation process must be carefully designed to ensure that the resulting mass representation effectively captures the nuances of the multiobjective optimization problem, as outlined in30.
 |
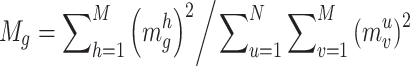23 |
 |
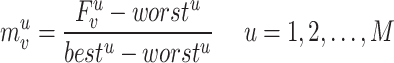24 |
where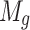 
shows mass of 
CB;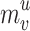 
denotes normalized fitness value; 
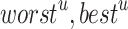indicate represent worst and best fitness values in all the CBs of 
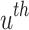objective.
Update positions of CBs with changed velocities
As a result of the updated velocities, all the CBs are adjusted as follows:
 |
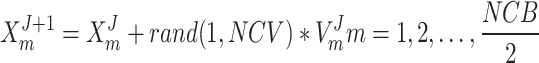25 |
 |
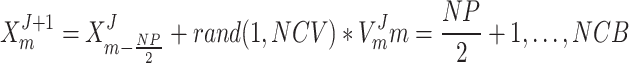26 |
where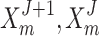 
indicate positions of 
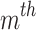CB in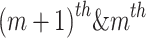 
iterations; and 
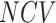denotes number of control variables.
Elite archive updating procedure
The upcoming generation’s CBs comprise the edge points of optimal solutions within the external archive, strategically positioned in the least congested region. As proposed in30, preserving elite CBs enhances performance and safeguards against losing valuable solutions. Consequently, a random selection of the percentage of CBs from the archive is incorporated into the CBs list. Subsequently, the total number of bodies is capped by eliminating the poorest colliding bodies, commencing from the preceding layer of the ND sporting bodies.
Fuzzy decision-making technique
In MOO with Pareto front issues, the objective is to identify solutions that are not dominated. In such problems, a solution is considered nondominated if improving one objective function can only be achieved by compromising another. Methodologies employed to tackle these problems vary in two key aspects: (i) the approach to generating the nondominated solution set, and (ii) the method of engagement with decision-makers, including the type of information provided such as trade-offs. Selecting the BCS from the trade-offs is crucial in the decision-making procedure. To end, a fuzzy decision procedure is utilized to attain an appropriate and optimal compromise solution from the non-dominated set. The determination of the membership function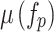 
is done independently by taking into account the lower and higher values of each objective, as well as the rate at which satisfaction increases as specified in30.
 |
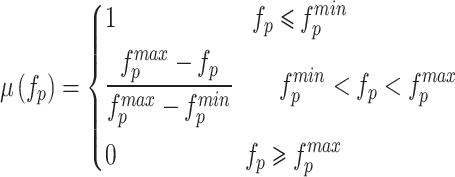27 |
The membership function values indicate the degree to which a nondominated solution satisfies the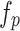 
objectives, measured on a scale of 0 to 1. Assessing the sum of membership function values 
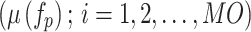across all objective functions allows for the evaluation of each solution’s effectiveness in meeting the objectives. The performance of every ND solution can be compared to others by normalizing its values relative to the total sum, as defined below:
 |
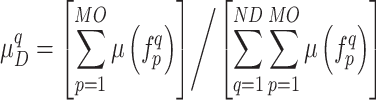28 |
where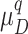 
indicates normalized membership function within a fuzzy set; The solution achieving the highest normalized membership 
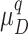within the fuzzy set 
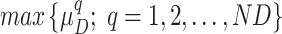should be selected as the BCS.
Sequential instructions NSCBO technique for multiobjective OPF issues
The computational structure of the proposed NSCBO approach, along with comprehensive procedural guidelines and the flowchart illustrated in Fig. 1, for addressing MOOPF problems, is outlined as follows:
Figure 1.
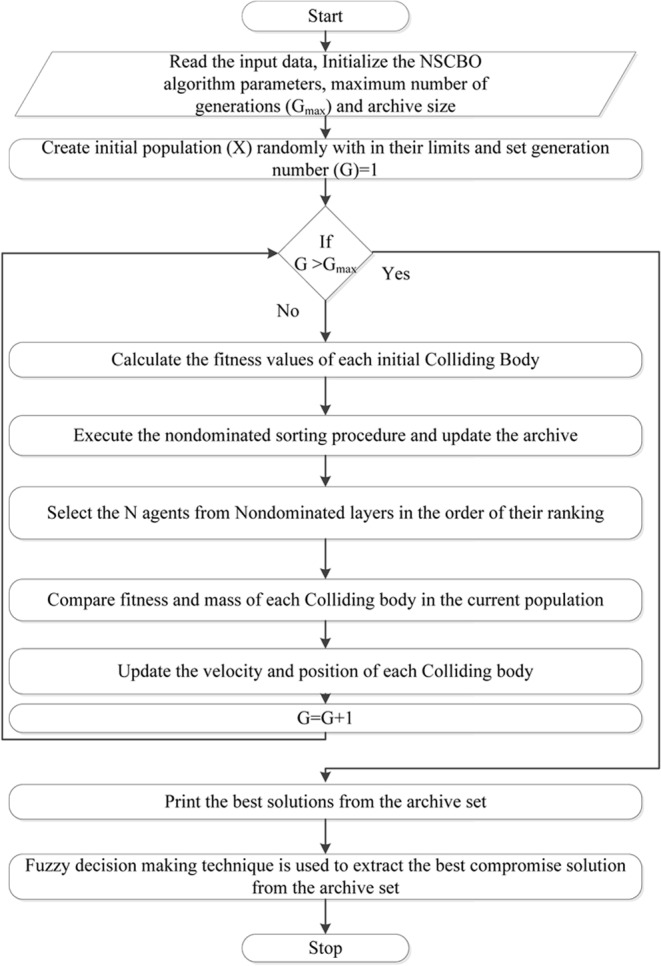
Flowchart of NSCBO approach for MOOPF problems.
-
Step 1.
Specify the NSCBO parameters, such as the number of CBs (NCB), archive size (A), and maximum iteration count (Imax).
-
Step 2.
Initialization: Generate each CB, indicating a potential solution of an objective function with CVs randomly generated.
-
Step 3.
Evaluate the fitness value of each CB is expressed below:
 |
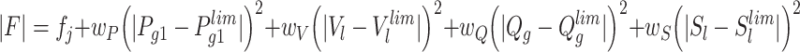29 |
-
Step 4.
Conduct the NS process and save all discovered nondominated CBs X into the archive set, then update it accordingly.
-
Step 5.
Determine the mass value of each CB. Arrange all CBs as described in Sect. 3.2. Evaluate the velocities of these groups before collision.
-
Step 6.
After the moving CBs trail the stationary CBs and a collision occurs among them, update the velocities of the CBs post-collision.
-
Step 7.
If the at-most generation has not been reached, return to Step 3; otherwise, display the ND solution in the external archive.
-
Step 8.
Utilize the fuzzy approach to extract the BCS from the ND solution set.
| Pseudocode for proposed NSCBO algorithm | |
|---|---|
| 1: | Assign the NSCBO parameters, namely NCB, archive set (A), and Imax |
| 2: | /////////////////////////Initialization ////////////////////////// |
| 3: | for each CB i = 1 to NCB |
| 4: | Initialize the position xi and velocity vi |
| 5: | Calculate the fitness each objective of every CB F_objective(xi) using Eq. (29) |
| 6: | Update the best CB in “A” non-dominated sorting procedure (see 3.3.2) |
| 7: | Calculate the crowding distance for find the ranking of diverse layers using Eqs. 21 & 22 |
| 8: | end for |
| 9: | While (k < I max) |
| 10: | For i = 1:NCB |
| 11: | Calculate the Mass of each CB using Eqs. 23 & 24 |
| 12: | Update the CB position using 28 & 29 |
| 13: | Calculate the fitness each objective of every CB F_objective(xi) using Eq. (29) |
| 14: | Update the best CB in “A” non-dominated sorting procedure (see 3.3.2) |
| 15: | Calculate the crowding distance for find the ranking of diverse layers using Eqs. 21 & 22 |
| 16: | End for |
| 17: | Next generation until stopping criteria is satisfied the end while |
| 18: | Find the BCS solution using Eqs. 27 & 28. |
Simulation results
To validate and assess the applicability of the developed NSCBO technique, conducted experiments on the IEEE 30-bus featuring two bi-objective issues: namely minimizing TFC & EP, minimizing TFC & APL, and one tri-objective issue involving the optimization of TFC, EP, and APL. The implementation utilized MATLAB 2023a on a PC equipped with a 2.2 GHz i3 core. The parameters for NSCBO included 60 CBs, a maximum of 200 iterations, and an archive set size of 20. Similarly, the reformulated multiobjective differential evolution (MODE) employed 60 chromosomes, a maximum of 200 iterations, an archive size of 20, a mutation rate of 0.6, and a crossover rate of 0.9. The IEEE 30-bus is equipped with 41 lines, 6 generators, 4 transformers, and 9 shunt reactors. It operates with a load of 283.4 MW and involves 24 variables. Voltage and transformer tap settings vary from 0.9 to 1.1 p.u., while shunt reactor values fall between 0 and 0.05 p.u. Bus and line specifications, along with fuel cost coefficients, were obtained from reference12. To showcase the effectiveness of the NSCBO technique, three distinct scenarios were analyzed.
Case 1: minimization of TFC and EP
Here, the objective is to minimize two conflicting objectives: TFC & EP, treated as a MOOPF issue. Figure 2 illustrates the best set of NDS achieved using the NSCBO technique, indicating its effective exploration of NDS within the search space. Employing a fuzzy decision-making approach, the BCS is determined from all NDS in the archive set. Table 1presents the best combination of CVs obtained for BCS with both MODE and NSCBO in Case 1, along with corresponding TFC, EP, and APL values. The results achieved with the other algorithms, including NSGA-II19, VEPSO19, NEKA14, Gaussian bare-bones ICA (GBICA)19, and modified GBICA (MGBICA)19, as well as MODE, as shown in Table 2. The analysis presented in Table 2 unequivocally showcases that, when contrasted with algorithms documented in existing literature, the NSCBO method consistently outperforms its counterparts by yielding the most optimal values.
Figure 2.
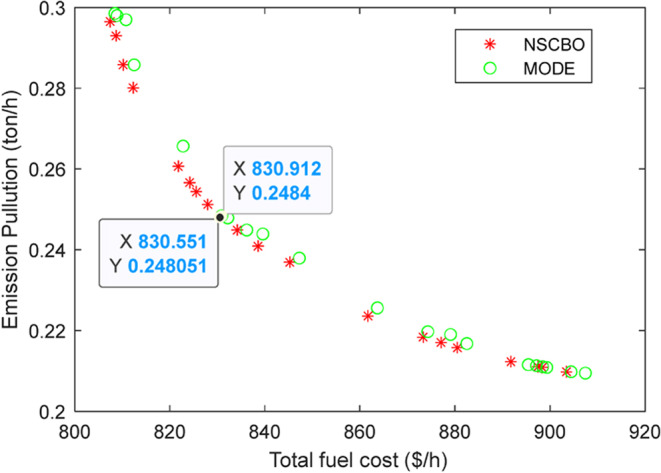
Pareto front attained in Case 1.
Table 1.
Optimal control variables of BCS were obtained in all cases.
| MODE | NSCBO | |||||
|---|---|---|---|---|---|---|
| Control variables | Case 1 | Case 2 | Case 3 | Case 1 | Case 2 | Case 3 |
| Pg1 (MW) | 117.6738 | 122.79 | 104.248 | 117.917 | 122.92 | 105.10 |
| Pg2 (MW) | 58.3414 | 52.121 | 54.7094 | 56.6998 | 52.494 | 58.886 |
| Pg5 (MW) | 27.1461 | 30.961 | 30.9903 | 25.9895 | 30.998 | 31.289 |
| Pg8 (MW) | 35.0000 | 35.000 | 35.0000 | 35.0000 | 35.000 | 35.000 |
| Pg11 (MW) | 25.7737 | 26.430 | 30.0000 | 27.3524 | 26.528 | 29.382 |
| Pg13 (MW) | 25.0592 | 21.313 | 33.1979 | 25.8268 | 20.681 | 28.458 |
| Vg1 (p.u.) | 1.0719 | 1.1000 | 1.0970 | 1.1000 | 1.0999 | 1.1000 |
| Vg2 (p.u.) | 1.0593 | 1.0912 | 1.0777 | 1.0871 | 1.0907 | 1.0847 |
| Vg5 (p.u.) | 1.0323 | 1.0685 | 1.0542 | 1.0555 | 1.0687 | 1.0644 |
| Vg8 (p.u.) | 1.0417 | 1.0781 | 1.0703 | 1.0692 | 1.0775 | 1.0832 |
| Vg11 (p.u.) | 1.0788 | 1.0974 | 1.0941 | 1.0999 | 1.0993 | 1.0895 |
| Vg13 (p.u.) | 1.0501 | 1.1000 | 1.0735 | 1.1000 | 1.1000 | 1.0918 |
| t6−9 (p.u.) | 1.0334 | 1.0399 | 1.0050 | 0.9583 | 1.0440 | 0.9722 |
| t6−10 (p.u.) | 0.9385 | 0.9243 | 1.0048 | 1.0031 | 0.9000 | 1.0446 |
| t4−12 (p.u.) | 0.9796 | 1.001 | 0.9844 | 1.0549 | 0.9784 | 1.0151 |
| t28−27 (p.u.) | 0.9753 | 0.9774 | 0.9866 | 0.9765 | 0.9652 | 0.9872 |
| bsh10 (p.u.) | 0.0126 | 0.0500 | 0.0150 | 0.0388 | 0.0500 | 0.0381 |
| bsh12 (p.u.) | 0.0190 | 0.0436 | 0.2379 | 0.0341 | 0.0498 | 0.0124 |
| bsh15 (p.u.) | 0.0393 | 0.0461 | 0.2235 | 0.0500 | 0.0471 | 0.0000 |
| bsh17 (p.u.) | 0.0488 | 0.0500 | 0.4190 | 0.0001 | 0.0491 | 0.0246 |
| bsh20 (p.u.) | 0.0385 | 0.0463 | 0.0366 | 0.0500 | 0.0385 | 0.0376 |
| bsh21 (p.u.) | 0.0500 | 0.0500 | 0.0094 | 0.0306 | 0.0500 | 0.0500 |
| bsh23 (p.u.) | 0.0257 | 0.0459 | 0.0423 | 0.0000 | 0.0245 | 0.0376 |
| bsh24 (p.u.) | 0.0498 | 0.0497 | 0.0325 | 0.0404 | 0.0500 | 0.0376 |
| bsh29 (p.u.) | 0.0247 | 0.0217 | 0.0500 | 0.0359 | 0.0233 | 0.0297 |
| TFC ($/h) | 830.9120 | 827.791 | 851.9996 | 830.551 | 827.54 | 847.17 |
| EP (ton/h) | 0.2486 | 0.2603 | 0.2300 | 0.2481 | 0.2540 | 0.2326 |
| APL (MW) | 5.5944 | 5.2312 | 4.7459 | 5.3860 | 5.2293 | 4.7238 |
Bold Values indicated that the results obtained by the proposed algorithm.
Table 2.
Comparison of BCS obtained in different cases with other methods.
| Different cases | Method | TFC ($/h) | EP (ton/h) | APL (MW) | Execution time (ET) (s) |
|---|---|---|---|---|---|
| Case 1 | MOMICA17 | 865.06 | 0.22 | - | - |
| PSO-SSO12 | 834.80 | 0.243 | - | - | |
| ESDE7 | 833.47 | 0.254 | - | - | |
| NSGA-II18 | 830.8 | 0.251 | - | - | |
| VEPSO18 | 830.95 | 0.253 | - | - | |
| MOEA/D-SF17 | 829.515 | 0.250 | |||
| NKEA18 | 830.85 | 0.249 | - | - | |
| GBICA18 | 830.85 | 0.248 | - | - | |
| MGBICA18 | 830.85 | 0.248 | - | - | |
| MODE | 830.9120 | 0.248 | - | 54.3 | |
| NSCBO | 830.55 | 0.248 | 5.3860 | 47.2 | |
| Case 2 | MOAGDE17 | 821.839 | - | 9.9646 | - |
| MOEA/D-SF17 | 881.01 | - | 4.144 | ||
| NSGA-II17 | 837.41 | - | 5.0397 | - | |
| MOHS14 | 832.67 | - | 5.3143 | - | |
| DE9 | 828.59 | - | 5.69 | - | |
| MOEA/D13 | 827.71 | - | 5.2556 | - | |
| PSO-SSO12 | 865.1 | - | 4.093 | - | |
| MOABC/D13 | 827.63 | - | 5.2451 | - | |
| MODE | 827.79 | - | 5.23 | 56.3 | |
| NSCBO | 827.54 | 0.254 | 5.2293 | 48.2 | |
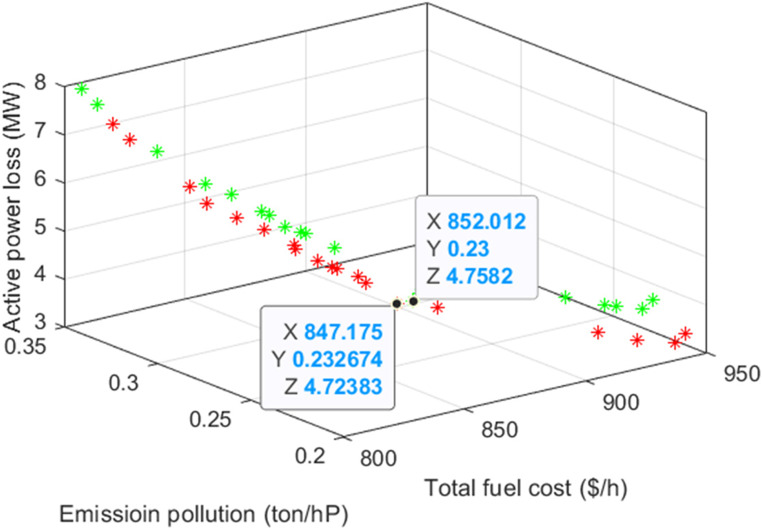
| Case 3 | MODE | 852.0118 | 0.2300 | 4.7502 | 71.23 |
| NSCBO | 847.1749 | 0.2326 | 4.7238 | 63.29 |
Bold Values indicated that the results obtained by the proposed algorithm.
Case 2: minimization of TFC and APL
In this context, we tackle the challenge of minimizing TFC while considering APL as an additional objective, forming a MOOPF problem. Figure 3 illustrates the nondominated solutions obtained using the NSCBO method, exposing a diverse collection of Pareto-optimal solutions that are evenly dispersed throughout the search space. Table 1presents the superior set of control variables, along with corresponding TFC, APL, and EP values attained with both MODE and NSCBO. These results are compared with various algorithms, including NSGA-II19, MOHSA13, MODE9, MOEA/D9, and MOABC/D12, as well as MODE methods, as detailed in Table 2. This analysis underscores the efficiency of the developed NSCBO technique to solve bi-objective issues, demonstrating its capability to generate high-quality solutions across multiple conflicting objectives.
Figure 3.
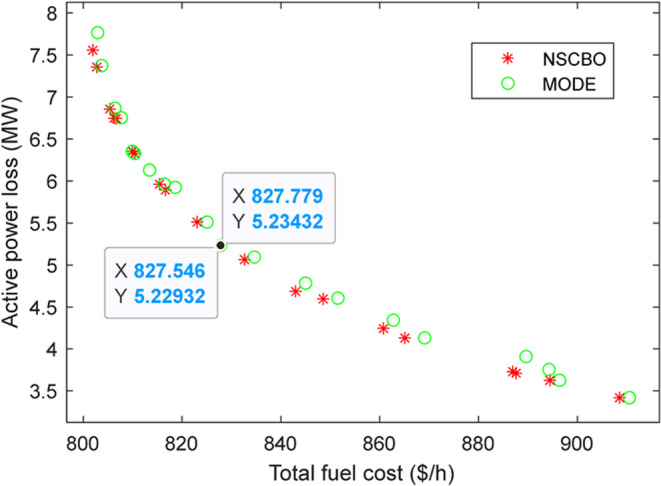
Pareto front attained in Case 2.
Case 3: minimization of TFC, EP, and APL
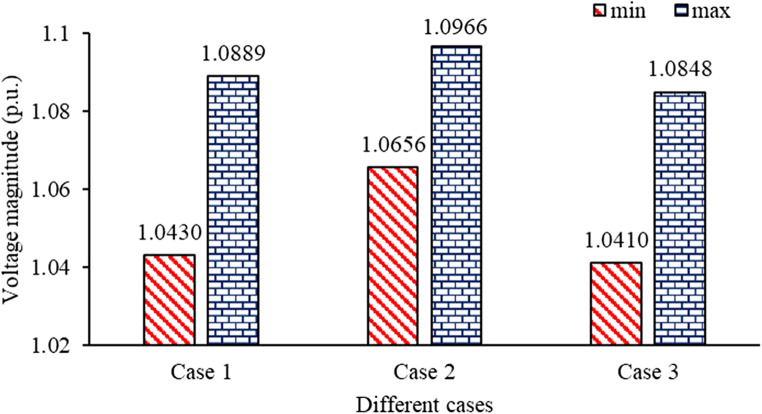
Here, addressed a MOOPF issue involving three challenging objectives: TFC, EP, and active APL. Figure 4 displays the nondominated solutions obtained through the NSCBO technique, demonstrating its ability to effectively distribute solutions across a wide range. The optimal set of CVs for this case, with corresponding TFC, EP, & APL values attained with both MODE and NSCBO, are presented in Table 1. Furthermore, Table 2 compared the optimal values of TFC, EP, APL, and execution time (ET) obtained with NSCBO against MODE. These results unequivocally show the superiority of the NSCBO method over MODE. Figure 5 illustrates the high and lower limits of load bus voltages achieved across all three cases, confirming the NSCBO technique’s adeptness in handling voltage constraints. Overall, the results substantiate the effectiveness of the proposed NSCBO technique in tackling MOOPF issues, showcasing its capability to generate high-quality solutions and effectively manage conflicting objectives.
Figure 4.
Pareto front obtained in Case 3.
Figure 5.
Minimum and maximum load bus voltages obtained in all cases.
Conclusions
In the current research, successfully developed and applied the nondominated sorting colliding bodies optimization (NSCBO) technique for the first time to address multiobjective optimal power flow (MOOPF) issues. The efficacy and reliability of the NSCBO technique were assessed using the IEEE 30-bus system, considering two bi-objectives: minimization of Total Fuel Cost (TFC) and Emission pollution (EP), optimization of TFC and Active Power Loss (APL), as well as one tri-objective involving the optimization of TFC, EP, and APL. The results achieved were compared with other techniques documented in the literature. Based on these comparisons, the developed NSCBO technique consistently yielded feasible and superior optimal solutions across all models when compared to other methods. The key differentiators of NSCBO, such as its unique approach to mass determination based on nondominated rank, normalization of fitness values across multiple objectives, and integration of crowding distance for diversity in solutions, were critical in achieving these outcomes. Additionally, the incorporation of fuzzy decision-making enhanced the robustness of the solution selection process, allowing for effective handling of uncertainties in the objectives. Therefore, that the NSCBO technique is an efficient and reliable approach to solving MOOPF issues. This study underscores the potential of NSCBO as a valuable tool in the field of power systems optimization, offering improved solutions and contributing to advancements in multiobjective optimization techniques. Given its demonstrated effectiveness, future work may focus on implementing the proposed NSCBO technique to tackle the multiobjective Combined Heat and Power Economic Dispatch (CHPED) problem, especially with the inclusion of renewable energy sources. This expansion of applications not only showcases the versatility of the NSCBO approach but also its potential to drive innovations in sustainable energy management and optimization methodologies.
Author contributions
All authos have contributed equally. All authors reviewed the manuscript.
Funding
The authors declare that no funds, grants or other support were received during the preparation of this manuscript.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Declarations
Ethical approval
The paper is not currently being considered for publication elsewhere.
Consent to participate
Not applicable.
Consent to publish
Not applicable.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Dommel, H. W. & Tinney, W. F. Optimal power flow solutions. IEEE Transc Power Apparat Syst.87, 1866–1876 (1968). [Google Scholar]
- 2.Scott, B. & Hobson, E. Power system security control calculations using linear programming- part I. IEEE Transc. Power Appart Syst.97 (5), 1713–1720 (1978). [Google Scholar]
- 3.Sun, D. I., Ashley, B., Brewer, B. & Tinney, W. F. Optimal powerflow by Newton appraoch. IEEE Transc Power Appart Syst.103 (10), 2864–2880 (1984). [Google Scholar]
- 4.Omar, A. A., AL-Smadi, M., Shaher, M. & Tasawar, H. Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method. Soft Comput.20 (8), 3283–3302 (2016). [Google Scholar]
- 5.Omar, A. A., AL-Smadi, M., Shaher, M. & Tasawar, H. Application of reproducing kernel algorithm for solving second-order, two-point fuzzy boundary value problems. Soft. Comput.21 (13), 7191–7206 (2017). [Google Scholar]
- 6.Omar, A. A. Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm-Volterra integrodifferential equations. Neural Comput. Appl.28 (7), 1591–1610 (2017). [Google Scholar]
- 7.Pulluri, H., Sharma, R. N. & Sharma, V. An enhanced self-adaptive differential evolution based solution methodology for multiobjective optimal power flow. Appl. Soft Comput.54, 229–245 (2017). [Google Scholar]
- 8.Surender Reddy, S. & Bijwe, P. R. Differential evolution-based efficient multi-objective optimal power flow. Neural Comput. Applic. 31, 509–522 (2019). [Google Scholar]
- 9.Abido, M. A. Al-Ali. Multiobjective optimal power flow using differential evolution. Arab. J. Sci. Eng.37, 991–1005 (2012). [Google Scholar]
- 10.uman, S., Akbel, M. & Kahraman, H. T. Development of the multi-objective adaptive guided diferential evolution and optimization of the MO-ACOPF for wind/PV/tidal energy sources. Appl. Sof Comput.112, 107814 (2021). [Google Scholar]
- 11.Deb, K., Agarwal, S., Pratap, A. & Merayivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transc Evol. Comput.6 (2), 182–197 (2002). [Google Scholar]
- 12.Ragab, A. E., Selim, F., Bachir, B. & bido, M. A. A novel multi-objective hybrid particle swarm and salp optimization algorithm for technical-economical environmental operation in power systems. Energy. 193, 116817 (2020). [Google Scholar]
- 13.Rezaei, M., Daryani, A. & Karami, M. Artificial bee colony algorithm for solving multiobjective optimal power flow problem. Int. J. Electr. Power Energy Syst.53, 219–230 (2013). [Google Scholar]
- 14.Sivasubramani, S. & Swarup, K. S. Multiobjective harmony search algorithm for optimal power flow problem. Int. J. Electr. Power Energy Syst.33, 745–752 (2011). [Google Scholar]
- 15.Aniruddha, B. & Provas, K. R. Solution of multi-objective optimal power flow using gravitational search algorithm. IET Gener Transm Distr. 6 (8), 751–763 (2012). [Google Scholar]
- 16.Arup, R. B. & Ajoy, K. C. Solution of optimal power flow using non dominated sorting multi objective opposition based gravitational search algorithm. Int. J. Electr. Power Energy Syst.64, 1237–1250 (2015). [Google Scholar]
- 17.Li, N. et al. Multi-objective pathfinder algorithm for multi-objective optimal power flow problem with random renewable energy sources: wind, photovoltaic and tidal. Sci. Rep.13, 10647 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ghasemi, M., Ghavidel, S., Ghanbarian, M. M. & Gitizadeh, M. Multiobjective optimal electric power planning in the power system using Gaussian bare-bones imperialist competitive algorithm. Inf. Sci.294, 286–304 (2015). [Google Scholar]
- 19.Chen, M. R., Yang, L. Q. & Zeng, G. Q. IFA-EO: an improved firefly algorithm hybridized with extremal optimization for continuous unconstrained optimization problems. Soft Comput.27 (6), 2943–2964 (2023). [Google Scholar]
- 20.Li, H., Wang, Z., Zeng, N., Wu, P. & Li, Y. Promoting objective knowledge transfer: a cascaded fuzzy system for solving dynamic Multiobjective optimization problems. in IEEE Trans. Fuzzy Syst., 10.1109/TFUZZ.2024.3443207
- 21.Li, H., Wang, Z., Lan, C., Wu, P. & Zeng, N. A novel dynamic multiobjective optimization algorithm with non-inductive transfer learning based on multi-strategy adaptive selection. IEEE Trans. Neural Netw. Learn. Syst.2810.1109/TNNLS.2023.3295461 (2023). [DOI] [PubMed]
- 22.Naderi, E., Mirzaei, L., Trimble, J. P. & Cantrell, D. A. multi-objective optimal power flow incorporating flexible alternating current transmission systems: application of a wavelet-oriented evolutionary algorithm. Electr. Power Compo Syst.52 (5), 766–795 (2023). [Google Scholar]
- 23.Li, H., Wang, Z., Lan, C., Wu, P. & Zeng, N. A novel dynamic multiobjective optimization algorithm with hierarchical response system. IEEE Trans. Comput. Social Syst.11 (2), 2494–2512 (2024). [DOI] [PubMed] [Google Scholar]
- 24.Pulluri, H., Naresh, R. & Sharma, V. A solution network based on stud krill herd algorithm for optimal power flow problems. Soft Comput.22 (1), 159–176 (2016). [Google Scholar]
- 25.Beibei, S. et al. Prediction of recurrent spontaneous abortion using evolutionary machine learning with joint self-adaptive sime mould algorithm. Comput. Biol. Med.148, 105885 (2022). [DOI] [PubMed] [Google Scholar]
- 26.Kaveh, A. & Mahdvi, V. R. Colliding bodies optimization: a novel meta-heuristic method. Comput. Struct.139, 8–27 (2014). [Google Scholar]
- 27.Pulluri, H., Naresh, R., Sharma, V. & Preeti Solving non-convex and non-linear optimal power flow problems using colliding bodies optimization, Proceedings of the 2nd international Conference on Recent Adnvances in Engineering and Computer Sciences (RAECS-2015), Chandighar, INDIA, pp. 1–6. (2015).
- 28.Pulluri, H., Naresh, R., Sharma, V. & Preeti A new colliding bodies optimization for solving optimal power flow problem in power system. Proceedings of the 6th International Conference on Power Systems (ICPS – 2016), New Delhi, INDIA, pp. 1–6. (2016).
- 29.Kaveh, A. & Mahdvi, V. R. Colliding bodies optimization method for optimum design of truss structures with continuous variables. Adv. Eng. Soft. 70, 1–12 (2014). [Google Scholar]
- 30.Gouthamkumar, N., Srinivasarao, B., Venkateswararao, B. & Narasimham, P. V. R.L. Nondominated sorting-based disruption in oppositional gravitational search algorithm for stochastic multiobjective short-term hydrothermal scheduling. Soft Comput.23 (16), 7229–7248 (2019). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.