Prediction of Femoral Bone Strength in the Presence of Tumors and Tumor-like Lesions Using Finite Element Analysis

Abstract

Background/Aim

Patients with bone tumors in their femurs are at risk of developing pathological fractures. Tumors with high fracture risk, especially fragile malignant lesions, are treated surgically. However, it is difficult to estimate bone strength based on clinical and radiographic findings. This study aimed to determine whether finite element analysis (FEA) provides useful information on the bone strength of femurs with tumors and tumor-like lesions.

Patients and Methods

Total femoral computed tomography (CT) data (slice thickness, 0.5 mm) were retrospectively obtained from 18 patients with femoral bone tumors. Three-dimensional FEA of femurs were developed using CT data. The virtual femoral head compression test and direct three-point bending test were performed on the femurs using FEA to predict bone strength and fracture location. The compression direction was parallel to the mechanical axis, whereas that of the three-point bending test was applied to the tumor itself.

Results

In the femoral head compression test using FEA, 13 out of 18 femurs with bone tumors fractured at the femoral head, while 14 out of 18 femurs fractured at the tumor site during the virtual direct three-point bending test. The median loads predicted using the femoral head compression test were significantly higher than those predicted by the direct three-point bending test.

Conclusion

The FEA results indicated that pathological fractures are unlikely to occur during normal walking. Direct external forces applied to the tumor body may lead to fractures.

Bone tumors are rare and comprise a wide range of histological types (1). It is essential to determine the appropriate treatment strategy, particularly in cases where a malignant tumor is suspected. However, certain complications, such as massive bleeding and malignant tumor contamination due to pathological fractures, are associated with fragile diseased bones (2).

The Mirel scoring system has been used to estimate the risk of fractures using X-ray images (3) and is reported to be highly sensitive but less specific (4). Additionally, there is a high risk of fracture if a bone defect invades an axial cortical part of >30 mm on computed tomography (CT) imaging, in which surgery should be performed for stabilization (5). When the ratio of circumferential cortical osteolytic lesions to the circumferential perimeter of the bone on CT imaging is >30%, orthopedic oncologists should consider surgical treatment (6). Finite-element analysis (FEA) based on CT imaging may also be an essential tool for calculating the risk of pathological fractures (7).

Many reports have discussed the bone strength of femurs with bone tumors using FEA; however, these articles mainly focused on metastatic bone disease (8,9). Previously, we evaluated bone strength using a rabbit femoral head compression test with FEA (10). However, to our knowledge, there are few similar experimental studies on the bone strength of not only bone tumors (benign, malignant, and metastatic tumors) but also tumor-like lesions using the human femoral head compression test and the direct three-point bending test using FEA. It is essential to assess the risk of pathological fractures in bone tumors and tumor-like lesions. Therefore, we hypothesized that FEA may provide useful information to orthopedic oncologists regarding the strength of bones with tumors.

Patients and Methods

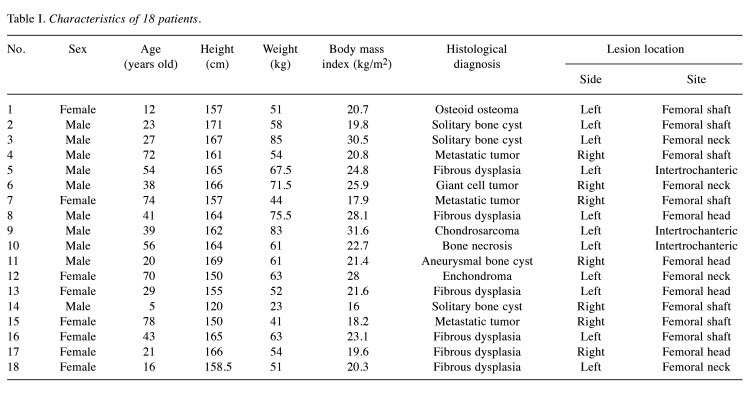
Data aggregation. We retrospectively investigated the clinical characteristics of 18 patients [10 men and eight women; median age at initial consultation: 38.5 years (interquartile range (IQR)=21.5-55.5 years)] with femoral bone lesions at the Department of Orthopedic Surgery (Osaka Metropolitan University Hospital) between December 2018 and March 2022. This study was approved by the Institutional Review Board of Osaka Metropolitan University Graduate School of Medicine and was conducted according to the ethical standards outlined in the Declaration of Helsinki (no. 4200). The subjects included in the study provided informed consent prior to their inclusion in the study.

Parameters. The following parameters were evaluated: sex, age, height, weight, body mass index (BMI), histological diagnosis, and lesion location.

Nonlinear FEA prediction. Axial CT scans of the entire femur were obtained using a single-slice helical scanner (Prospeed AI; GE Healthcare, London, UK) with a slice thickness of 0.5 mm. A calibration phantom (QRM-BDC; QRM, Möhrendorf, Germany) containing three hydroxyapatite rods (0, 100, and 200 mg/cm³) was used to test the specimens in water. Three-dimensional finite element (FE) models of the femurs were developed using CT data from Mechanical Finder version 9.0, standard edition (Research Center of Computational Mechanics, Inc., Tokyo, Japan), which reconstructs individual bone shapes and density distributions. All femoral trabecular bones and inner parts of the cortex were meshed using linear tetrahedral elements with a global edge length of 1.5 mm. The outer surface of the cortical bone was modeled using three nodal-point shell elements with a thickness of 0.3 mm. The CT value of each element was set as the average of the voxels contained in that element. The mechanical properties of each element were calculated in Hounsfield units (HU) (11). Previous studies on compression tests used Keller’s equation for FEA; therefore, the equation was also used in this study (12,13).

The following specific equations were used: Young’s modulus (E, MPa); E=0.001 (ρ=0); E=1,890 ρ1.92 (ρ<0); Yield stress (σ, MPa); σ=1.0×1,020 (ρ≤0.2); σ=284 ρ2.27 (ρ>0.2).

A previous study on a direct three-point bending test utilized Kayak’s equation for FEA; therefore, the following equation was also used (14): Young’s modulus (E, MPa); E=0.001 (ρ=0); E=33,900 ρ2.20 (0<ρ≤0.27); E=5,307 ρ+469 (0.27<ρ<0.6); E=10,200 ρ2.01 (0.6≤ρ); Yield stress (σ, MPa); σ=1.0×1,020 (ρ≤0.2); σ=137 ρ1.88 (0.2<ρ<0.317); σ=114ρ1.72 (0.317≤ρ).

Modulus values <0.01 MPa were designated as 0.01 Mpa, whereas those >20 Gpa were designated as 20 Gpa (14). The Young’s modulus and yield stress of the shell element were calculated assuming a CT value of 1,000 HU. The Drucker–Prager equivalent criterion was adopted for the element yield (15). The tensile yield stress was assumed to be 0.8 times the compressive yield stress, in agreement with a previous study (16). The Poisson coefficient for each element was set to 0.3 (13).

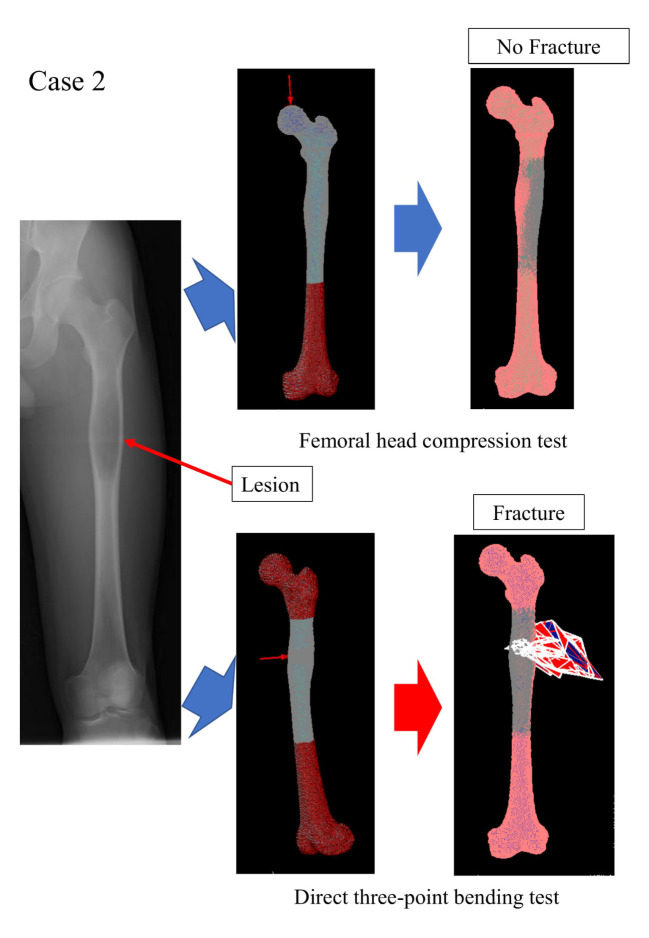
To simulate real mechanical testing, the FEA model was created as identical as possible to the mechanical test (Figure 1). The FE-predicted fracture load was defined as the load at which the displacement increases sharply.

Figure 1.

Representative case (Case 2, Table I). Virtual femoral head compression test and direct three-point bending test using finite element analysis (FEA).

However, owing to the material characteristics of each lesion, it is impossible to use a single definition for all lytic lesions (17). In our study, bone lesions were defined as empty cavities with an elastic modulus of zero.

Statistical analysis. The Mann–Whitney U-test was performed to compare the two groups in terms of the FE-predicted fracture load (in Newtons). Statistical analyses were performed using the IBM SPSS Statistics (SPSS 26.0, IBM, Corp., Armonk, NY, USA) and Excel statistical software packages (Ekuseru-Toukei 2015; Social Survey Research Information Co., Ltd., Tokyo, Japan). Statistical significance was set at p<0.05.

Results

Clinical information. The median height, weight, and BMI were 163 (IQR=157-165.8) cm, 59.5 (IQR=51.3-66.4) kg, and 21.5 (IQR=19.9-25.6) kg/m², respectively. Femoral bone lesions were located in the head, neck, intertrochanteric, and shaft of four, four, three, and seven patients, respectively (Table I); these were also situated on seven right and 11 left sides, respectively.

Table I. Characteristics of 18 patients.

Histological diagnoses. The histological classification of all 18 femoral bone lesion subtypes is shown in Table I. The most common subtypes identified in this study were fibrous dysplasia (six cases, 33.3%) and solitary bone cysts (three cases, 16.7%).

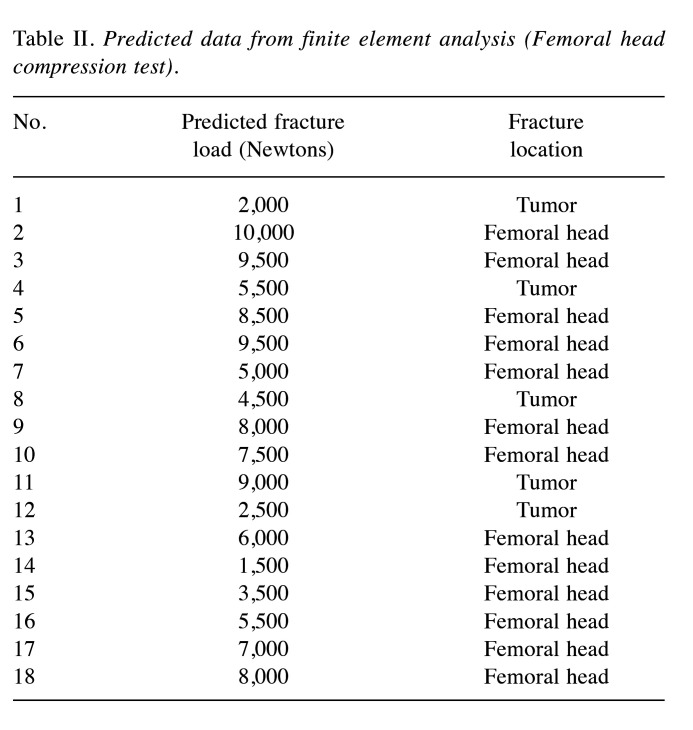
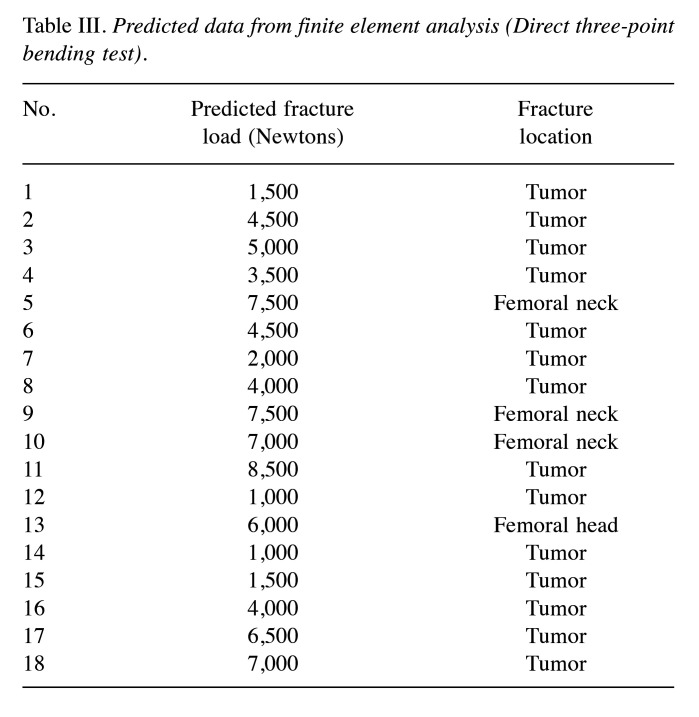
Nonlinear FEA prediction. The median FE-predicted fracture loads of the femoral head compression and direct three-point bending tests were 6,500 (4,625-8,375) and 4,500 (2,375-6,875) Newtons, respectively (Table II and Table III). Thirteen of the 18 femurs with bone tumors were fractured at the femoral head in the femoral head compression test using FEA, whereas 14 of the 18 femurs were fractured at the tumor site in the virtual direct three-point bending test (Table II and Table III). A representative FEA image of a solitary bone cyst in the femoral shaft (Case 2) is shown in Figure 1.

Table II. Predicted data from finite element analysis (Femoral head compression test).

Table III. Predicted data from finite element analysis (Direct three-point bending test).

The median loads predicted by the femoral head compression test were significantly higher than those predicted by the direct three-point bending test (p=0.049; Figure 2).

Figure 2.

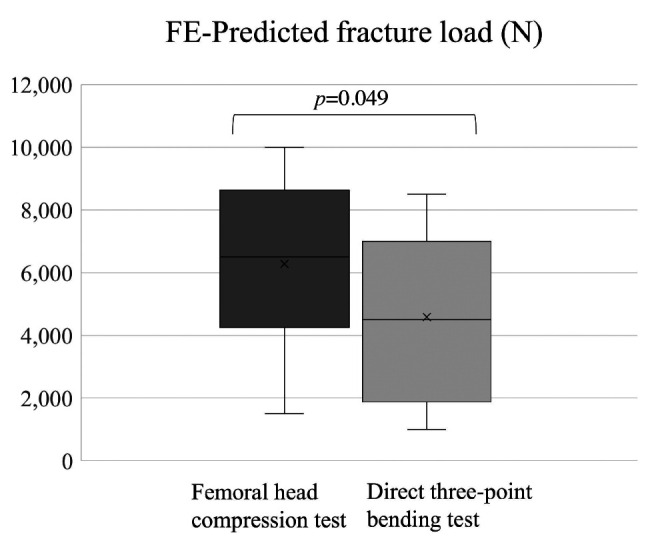
Finite element (FE)-predicted fracture load in femoral head compression test and direct three-point bending test.

Discussion

Numerous studies have already focused on FEA, an important tool that estimates the fracture loads of femurs with metastatic bone disease that does not only provide results consistent with those of biomechanical tests using fresh cadaver bone specimens but also determines whether prophylactic surgery is required (8,9). We previously demonstrated that the fragility of the affected bone might be associated with the width of the defect in a rabbit femoral head compression test using FEA (10). Nevertheless, we were not able to calculate the FE-predicted value of the human femur. In this study, we conducted a virtual human femoral head compression test and a direct three-point bending test using FEA to determine the risk of pathological fractures in bone tumors and tumor-like lesions.

We also planned to perform an FE-predicted femoral head compression test from the femoral head in the direction of the mechanical axis, as described in this study and a previous report (10). Although no consensus was reached regarding the privileged anatomical site of the femur during pathological fractures in patients, we estimated the numerical value using the compression test and the direct three-point bending test by FEA (Table I and Figure 1). Furthermore, the part of the femur anatomically fractured according to FEA was verified to be well correlated with the tumor location (Table II and Table III).

In terms of the fracture load predicted by the FEA, the femoral head compression test indicated that it was significantly higher than that predicted by the direct three-point bending test (Figure 2, p=0.049). Thirteen of the 18 femurs with bone tumors were fractured at the femoral head in the femoral head compression test, whereas 14 of the 18 femurs were fractured at the tumor site in the three-point bending test (Table II and Table III). Based on these results, fractures are unlikely to occur during normal walking, whereas direct external forces applied to the tumor body may lead to fractures. To our knowledge, this is the first study to provide interesting conclusions regarding the mechanisms of pathological fractures.

Pathological femoral fractures often lead to a low quality of life. Patients with primary or metastatic malignant bone tumors may undergo surgery for internal fixation or prostheses. Determining the risk of pathological fractures based on physical findings is difficult. Stress on the hip and knee varies for different types of activities, such as walking, standing, and sitting (18). Therefore, it is impossible to calculate the fracture risk value based on an individual patient’s weight using previous methods. However, in this study, using FEA, an accurate estimation of the stress on the femoral head as well as the tumor according to each patient’s weight and physical activity may result in good results in the prevention of fractures.

In a previous report, BMI was positively associated with bone density (19). Additionally, interaction terms for the relationship between BMI and age, as well as between BMI and sex, were not statistically significant (19). In this study, the median BMI was 21.5, which was not significantly associated with risk of fracture based on the results of a recent article (20).

In addition to the strengths of this study, we acknowledge several limitations. First, the number of patients enrolled in our study was small, and this was a retrospective study. Second, it was impossible to confirm the results of the actual experiments based on mechanical testing because only FEA using patient CT information was conducted. Third, only the results of the femoral head compression and three-point bending tests were used to verify the data. Torsion-testing data should be added to obtain more accurate results. Additionally, to confirm the mechanisms of fracture in patients, we must validate other loading conditions, such as walking, running, falling, and hip movements. Finally, owing to the material characteristics of each lesion, all the bone lesions were defined as empty cavities with an elastic modulus of zero, which is the most crucial limitation of this study.

Conclusion

This study assessed the prediction of bone strength in femoral bone tumors and tumor-like lesions using FEA. We verified that fractures are unlikely to occur during normal walking, whereas direct external forces applied to the tumor body may lead to fractures. These findings may be valuable for the treatment of patients with femoral bone tumors and tumor-like lesions. Further studies are required to determine whether the results of this study can be applied in clinical practice by investigating CT images of more patients with femoral bone tumors and conducting FEA.

Conflicts of Interest

The Author reports no conflicts of interest in relation to this work.

Authors’ Contributions

Tadashi Iwai designed this study and performed the statistical analysis. Tadashi Iwai prepared figures and tables. Tadashi Iwai wrote the original draft manuscript. Manabu Hoshi and Hiroaki Nakamura oversaw the study and revised the manuscript. All Authors reviewed the manuscript.

Acknowledgements

The Authors are very grateful for the invaluable support and various discussions with other members of the Department of Orthopedic Surgery.

Funding

There is no funding source.