A Physical Framework to Study the Effect of Magnetic Fields on the Spike-Time Coding

Abstract

A temporal neural code reliant on the pattern of spike times rather than spike rates offers a feasible mechanism for encoding information from weak periodic external stimuli, such as static or extremely low-frequency electromagnetic fields. Our model focuses on the influence of magnetic fields on neurotransmitter dynamics near the neuron membrane. Neurotransmitter binding to specific receptor sites on membrane proteins can regulate biochemical reactions. The duration a neurotransmitter spends in the bonded state serves as a metric for the magnetic field’s capacity as a chemical regulator. By initiating a physical analysis of ligand-receptor binding, utilizing the alpha function for synaptic conductance, and employing a modified version of Bell’s law, we quantified the impact of magnetic fields on the bond half-life time and, consequently, on postsynaptic spike timing.

Introduction

The existence of biological effects resulting from non-thermal exposure to static or extremely low frequency (ELF) magnetic fields is undeniable; however, it remains a topic of ongoing debate. Investigating the impact of electromagnetic (EM) fields on neuronal activity poses significant challenges. The biological effects triggered by electric or magnetic fields can be examined independently or in conjunction by applying an EM field. Numerous variables come into play, including the broad spectrum of frequencies, varying field strengths, signal waveform, signal duration, field application duration and the shape of the signal. Additionally, the development of experimental models presents considerable diversity, encompassing in vitro or in vivo studies involving animals or human volunteers. This diversity significantly complicates efforts to consolidate results into one or a few unified models.

Experimental data have progressively converged to identify the cell membrane as the primary target structure for the interaction of ELF electromagnetic fields with living organisms.^{1 -4} The cell membrane’s capacity to amplify biological signals has been elucidated through various physical models incorporating non-linear mechanisms.^{5 -8}

Moggia et al ⁹ present experimental studies aimed at establishing that among the various explanatory mechanisms involved in the interaction between biological membranes and external EM fields, ligand-receptor binding stands out as the pivotal process. While the Langevin-Lorentz model remains prevalent in the study of cell receptors,^10,11 there has been ongoing development and refinement of this model over the last two decades.

In recent years, numerous studies have utilized magnetic fields to modulate cell activity by targeting cell-surface receptors. An applied magnetic field has been shown to modify Notch receptors, initiating receptor signaling. ¹² For E-cadherin, low magnetic forces have been observed to cluster the molecule, thus initiating F-actin assembly. ¹³ A similar mechanism has been employed to mechanically deflect and activate inner ear hair cells by targeting membrane glycoproteins. ¹⁴ Magnetic field displacement of the hair bundle has been found to increase intracellular calcium, indicating the activation of the hair cells. ¹⁵ Magnetic activation of endogenous receptors has also been utilized to enhance stem cell differentiation. ¹⁶ Other studies have employed magnetic fields to investigate the role of mechanical force on neurons. Tay et al ¹⁷ cultured cortical neurons and discovered that, in the presence of a magnetic field, a mechanical force in the piconewton range was exerted on the neurons, increasing intracellular calcium by targeting membrane calcium channels. Magnetic fields have also been employed to regulate apoptosis. Cancer cells, expressing high levels of the DR4 death receptor, have shown clustering upon application of magnetic fields, subsequently activating caspase-8 and caspase-3, ultimately leading to cell death. ¹⁷

The synapse, also known as the synaptic cleft, refers to the space containing the extracellular fluid situated between the pre- and postsynaptic neurons. Its diminutive size, approximately 20 nm wide, facilitates effective neurotransmitter-receptor binding. Fast responses at these synapses are mediated by ligand-gated ion channels (LGICs). ¹⁸

The duration, amplitude, and frequency of synaptic responses are determined by the kinetics of channel opening, closing, and desensitization. Binding to LGICs entails a specific and reversible reaction, as it typically involves weak interactions (such as ionic bonds, Van der Waals forces, and hydrogen bonds) between the receptor and ligand.^2,19

Naundorf et al discovered that key features of spike initiation dynamics -such as the spike-time pattern- cannot be explained by the original Hodgkin-Huxley (HH) model. They analyzed the action potential dynamics in cortical neurons by in vivo, in vitro, and computational models ²⁰ ; and found that the spike onset was 10 times greater than the one predicted by the original HH model. Unlike the original HH model, in which the channel opening and closing are independent processes, they proposed a model based on the cooperative action of sodium channels.

While the Naundorf et al model elucidates spike onset characteristics not accounted for in the original HH model, more comprehensive explanations have emerged in recent years. In 2009, Colwell et al introduced a HH-type model incorporating a stochastic term attributed to background synaptic activity. They utilized the path integral formalism to derive an analytical formula that correlates onset speed with onset potential. ²¹

In the Colwell HH model, the dynamics of neuron membrane potential $(V$ ) are described as follows,

$$C_m\frac{dV}{dt}=I_{syn}-I_{Na}-I_K-I_L$$ (1)

$$I_{syn}=g_e\left(t\right)\left(V-E_e\right)+g_I\left(t\right)\left(V-E_I\right)$$ (2)

where the input current is implicitly included in equation (1) as an initial condition of the differential equation.

Background synaptic activity is modeled by assuming that synaptic conductance is stochastic, comprising excitatory conductance ( $g_e$ ) with a reversal potential $E_e$ and inhibitory conductance ( $g_I$ ) with a reversal potential $E_I$ . The conductances $g_e(t)$ and $g_I(t)$ are represented by white Gaussian noises, with noise diffusion coefficients $D_e$ and $D_I$ respectively. Colwell et al examined the correlation between voltage threshold variation and onset speed, enabling them to elucidate the findings of Naundorf et al.

The voltage threshold is defined as the membrane potential value at which $\frac{dV}{dt}=10\frac{mV}{ms}$ . As a result of stochastic synaptic background activity, a voltage distribution arises where the voltage threshold is attained. The action potential is triggered when $V$ reaches $V^{*}$ , where $V^{*}$ represents an unstable equilibrium of the aforementioned equation in the absence of noise. Below $V^{*}$ , the membrane potential returns to its resting state, while above $V^{*}$ , a spike can be initiated. Anastassiou et al have studied the problem of spike-timing control through external electromagnetic fields, we provide a more detailed explanation in the Supplemental Information section. Hence, in his model, the enhancement in coding properties stems from the stimulus input not arising from stochastic fluctuations but from a deterministic external field. Nonetheless, the model proposed by Anastassiou et al is purely phenomenological. Here, our aim is to establish a mechanistic model aligned with the one we will detail in subsequent sections, potentially enabling us to broaden the findings for studying temporal coding within local neural networks.

In this paper, we propose a modified HH model based on Colwell’s advancements. In our model, the noise term arises not only from a stochastic component but also from a deterministic one, which encompasses the synapse-induced magnetic field. We adjust the Bell equation, expressing the bond half-life time, to account for the dynamics of neurotransmitters. The paper is structured as follows: firstly, we introduce a physical framework to examine the influence of magnetic fields on biological dipoles under physiological conditions. Secondly, we establish a connection between ligand-receptor binding and the synapse-induced magnetic field, deriving the explicit solution for synaptic conductance. Finally, we analyze the variation in postsynaptic spike timing as a function of magnetic fields and the stability analysis of the solutions.

Methods

Ionic conductance properties and parameters

The ionic conductances, excluding the leakage current $g_L$ , which was assumed constant, are described by the following equations (3) to (4) for potassium conductance and (5) to (7) for sodium conductance,

$$g_K={\overline{g}}_K{n}^4,$$ (3)

$$\frac{dn}{dt}={\alpha }_n\left(1-n\right)-{\beta }_{n}n,$$ (4)

$$g_{Na}={\overline{g}}_{Na}{m}^{3}h,$$ (5)

$$\frac{dm}{dt}={\alpha }_m\left(1-m\right)-{\beta }_{m}m,$$ (6)

$$\frac{dh}{dt}={\alpha }_h\left(1-h\right)-{\beta }_{h}h,$$ (7)

where ${\alpha }_n,{\beta }_n,{\alpha }_m,{\beta }_m,{\alpha }_h$ and ${\beta }_h$ are free parameters and ${\overline{g}}_K$ and ${\overline{g}}_{Na}$ represent the maximum ionic conductances. The dimensionless variables $m,n$ and $h$ describe the open probability of ion channels (and thus the expected fraction of the full ionic conductance across the membrane at a given time and voltage), while the $\alpha$ and $\beta$ terms denote rate constants.

After selecting rate parameters $\alpha$ and $\beta$ for various clamped voltages, Hodgkin and Huxley empirically proposed functions capable of explaining the voltage dependency of these parameters, resulting in the following equations (8) to (9) for potassium conductance and (10) to (13) for sodium conductance,

$${\widehat{\alpha }}_n\left(V\right)=\frac{0.01\left(V+10\right)}{exp\left(\frac{V+10}{10}\right)-1},$$ (8)

$${\widehat{\beta }}_n\left(V\right)=0.125\exp \left(\frac{V}{80}\right),$$ (9)

$${\widehat{\alpha }}_m\left(V\right)=\frac{0.1\left(V+25\right)}{exp\left(\frac{V+25}{10}\right)-1},$$ (10)

$${\widehat{\beta }}_m\left(V\right)=4\exp \left(\frac{V}{18}\right),$$ (11)

$${\widehat{\alpha }}_h\left(V\right)=0.07\exp \left(\frac{V}{20}\right),$$ (12)

$${\widehat{\beta }}_h\left(V\right)=\frac{1}{exp\left(\frac{V+30}{10}\right)-1},$$ (13)

All HH’s conductance data were sourced from Marom and Abbott. ²² Given the absence of computers in 1952 for conducting numerical solutions, HH’s numerical algorithm was designed for manual calculations using the tools available at the time. The numerical method employed in this study is known as Euler’s method. ²³ All simulations using Euler’s method were performed using a contemporary implementation in MATLAB, ²⁴ equipped with metadata tags to facilitate adjustment of the $\alpha$ and $\beta$ parameters (equations (4), (6), and (7)) through a fitting algorithm. Similarly, the constants in equations (8) to (13) were replaced with free, externally adjustable variables as outlined in equations (14) to (19), thereby introducing 5 free parameters for the voltage-dependent potassium conductance $g_K$ and 9 free parameters for the voltage-dependent sodium conductance $g_{Na}$  .

When fitting the limited six-parameter form of the model (equations (4), (6), and (7)), the rate parameters ${\alpha }_n,{\beta }_n,{\alpha }_m,{\beta }_m,{\alpha }_h$ , and ${\beta }_h$ are defined by the protocol to be constants, which are set by the fitting algorithm. When fitting the full 14-parameter voltage-dependent model, these six rate parameters are in turn parametrized according to the following equations (14) to (15) for potassium conductance type and (16) to (19) for sodium conductance, with the 14 free parameters set by the fitting algorithm,

$${\alpha }_n(V)=\frac{k_{{\alpha }_{n}1}\left(V+k_{{\alpha }_{n}2}\right)}{exp\left(\frac{V+k_{{\alpha }_{n}2}}{k_{{\alpha }_{n}3}}\right)-1},$$ (14)

$${\beta }_n\left(V\right)=k_{{\beta }_{n}1}\exp \left(\frac{V}{k_{{\beta }_{n}2}}\right),$$ (15)

$${\alpha }_m(V)=\frac{k_{{\alpha }_{m}1}\left(V+k_{{\alpha }_{m}2}\right)}{exp\left(\frac{V+k_{{\alpha }_{m}2}}{k_{{\alpha }_{m}3}}\right)-1},$$ (16)

$${\beta }_m\left(V\right)=k_{{\beta }_{m}1}\exp \left(\frac{V}{k_{{\beta }_{m}2}}\right),$$ (17)

$${\alpha }_h\left(V\right)=k_{{\alpha }_{h}1}\exp \left(\frac{V}{k_{{\alpha }_{h}2}}\right),$$ (18)

$${\beta }_h(V)=\frac{1}{exp\left(\frac{V+k_{{\beta }_{h}1}}{k_{{\beta }_{h}2}}\right)+1},$$ (19)

$k_{{\alpha }_{n}1},k_{{\alpha }_{n}2},k_{{\alpha }_{n}3},k_{{\beta }_{n}1},k_{{\beta }_{n}2},k_{{\alpha }_{m}1},k_{{\alpha }_{m}2},k_{{\alpha }_{m}3},k_{{\beta }_{m}1},k_{{\beta }_{m}2},k_{{\alpha }_{h}1},k_{{\alpha }_{h}2},k_{{\beta }_{h}1}$ , and $k_{{\beta }_{h}2}$ are free parameters.

Membrane potential properties and parameters

All membrane potential data were sourced from Marom and Abbott. ²² The voltage differential between the cell’s interior and the synapse influences both the excitatory synaptic response (EPSP) and spike generation. Under resting conditions, a neuron typically maintains a membrane potential of approximately $-65\mathrm{mV}$ (ranging from $-60$ to $-70\mathrm{mV}$ ), with the interior of the cell being negatively charged relative to the external environment (ie, $V_{t=0}=V_R=V_{in}-V_{out}=-65\mathrm{mV}$ ).

The membrane potential of the neuron is contingent upon the disparate concentrations of $K^{+}$ and $N{a}^{+}$ ions on either side of the membrane, as well as the varying membrane permeability to these ions, with $K^{+}$ exhibiting significantly higher permeability.

Potassium ions ( $K^{+}$ ) are predominantly concentrated within the cell’s interior, with a concentration reaching approximately 150 mM ( ${\left[K^{+}\right]}_i$ ), while outside the cell (  ${\left[K^{+}\right]}_e$ ), it typically remains around 4 to 5 mM. By employing the Nernst equation, we can calculate the equilibrium potential of the equivalent electrochemical cell,

$$E_K=\frac{k_{B}T}{zF}Ln\frac{{\left[K^{+}\right]}_i}{{\left[K^{+}\right]}_e}$$ (20)

Here, $k_B$ represents the Boltzmann constant, $T$ denotes the absolute temperature, $F$ stands for the Faraday constant, and $z$ signifies the number of electrons transferred in the electrochemical reduction reaction (which is $+1$ ). At the mentioned physiological concentrations, $E_k$ is approximately $-90\mathrm{mV}$ .

Conversely, $N{a}^{+}$ ions have an internal concentration of $5-10\mathrm{mM}$ and an external concentration of $140\mathrm{mM}$ , resulting in an equilibrium potential $E_{Na}$ of approximately $+50\mathrm{mV}$ . $K^{+}$ and $N{a}^{+}$ ions possess opposing electrochemical gradients, with the gradient for $K^{+}$ ions driving outward currents (positive current) from the cell, while that for $N{a}^{+}$ ions pushes them from the external to the internal cell space (negative current). The significantly higher membrane permeability to $K^{+}$ ions maintains the membrane potential at a depolarization level equivalent to the equilibrium potential for $K^{+}$ ( $-90\mathrm{mV}$ ). Sodium-potassium channels act as electrical pumps for the neuron membrane.

The neuron expends metabolic energy to uphold the membrane voltage at a less depolarized level of $-65\mathrm{mV}$ . This function is carried out by biochemical electrogenic pumps that transport $K^{+}$ ions from the external to the internal cell space and $N{a}^{+}$ ions in the opposite direction, against their electrochemical gradients. These pumps, known as $N{a}^{+}$ / $K^{+}$ pumps, rely on the ATP biochemical conversion of energy and establish the resting membrane potential (a potential where the net current crossing the membrane is $0A$ ) at $V(t)=V_R=-65\mathrm{mV}$ . At this level, the voltage-dependent conductance for $N{a}^{+}$ and $K^{+}$ ions ( $G_{Na}$ and $G_K$ , respectively) is inactivated ( $0\mathrm{S}$ ), and the resistance to these ions can be considered infinite (factoring in the pump action), resulting in respective currents of are 0 A ( $I_{Na}=I_K=0$ in equation (1)). $G_{Na}$ and $G_K$ undergo rapid increases for membrane potentials depolarized to almost $+10\mathrm{mV}$ , which can be deemed an activation threshold value ( $V_{th}$ = $V_r+10\mathrm{mV}=-65+10=-55\mathrm{mV}$ ).

At the threshold level ( $V_{th}=-55\mathrm{mV}$ ), there is a rapid membrane depolarization triggered by a negative net current resulting from the swift inward movement of $N{a}^{+}$ ions. This is attributed to the significantly higher driving force at this potential level for this ion. Specifically, the ionic current can be represented as $I_{ion}$ = $G_{ion}(V\left(t\right)-E_{ion}$ , where the driving forces generating the respective $N{a}^{+}$ and $K^{+}$ currents are calculated as follows: $V\left(t\right)-E_{Na}=-55\mathrm{mV}-\left(+50mV\right)=-105\mathrm{mV}$ ; $V\left(t\right)-E_K=-55\mathrm{mV}-\left(-90mV\right)=+35\mathrm{mV}$ .

The negative, inward total current not only governs the rapid rise phase of the spike but also contributes to the synaptic current. This current initiates depolarization of the membrane potential, reaching and often surpassing $0\mathrm{mV}$ , leading to overshooting potentials of $+20$ , $+30\mathrm{mV}$ at the spike peak. As the membrane potential $(V\left(t\right))$ enters positive territory, the driving force on $N{a}^{+}$ ions diminishes while that on $K^{+}$ ions increases. The net current definitively reverses direction at the spike peak ( $+20$ , $+30\mathrm{mV}$ ), and the membrane begins repolarization as the $K^{+}$ ion battery approaches the ion equilibrium potential ( $-90\mathrm{mV}$ ). This repolarization is facilitated by the rapid inactivation of $N{a}^{+}$ conductance ( $G_{Na}$ returning swiftly to $0\mathrm{S}$ ). Subsequently, the energy-dependent work of the $N{a}^{+}$ / $K^{+}$ pump restores the resting potential value ( $V_r=-65\mathrm{mV}$ ), completing the spike cycle. The membrane dynamics, encompassing both spike and synaptic activity, can be likened to an electrical circuit operating in accordance with the aforementioned parameters and following the dynamics outlined in the HH model.

The sole distinction, from an electrical standpoint, between synaptic response and spike generation lies in the driving force behind the synaptic current. Unlike spike generation, where the driving force stems from the disparity between membrane voltage and the ion-specific equilibrium potential, excitatory receptors (primarily AMPA receptors) constitute nonspecific ionic channels. Consequently, the net current is determined by the synaptic conductance (dependent on neurotransmitter-receptor binding) and a nonspecific synaptic equilibrium potential, typically around $-10\mathrm{mV}$ . This signifies that membrane potentials exceeding $-10\mathrm{mV}$ result in inward currents (negative and depolarizing), while those below produce outward currents (repolarizing), primarily due to outward flow of $K^{+}$ ions from the cell. This framework offers a straightforward explanation for the dynamics of neuron membrane voltage.

Physical Derivation of the Model

Electric dipole moment of neurotransmitters under physiological conditions

Finite electric dipoles typically consist of two-point charges of equal magnitude: a negative charge ( $-q$ ) and a positive charge ( $q$ ), with the relative position vector $\overrightarrow{d}$ extending from the first to the second. Therefore, we define the electric dipole moment as follows, ²⁵

$$\overrightarrow{p}=q\cdot \overrightarrow{d}$$ (21)

The point dipole moment is obtained in the limit as $q\to \infty$ and $d\to 0$ . Thus, the expressions in equation (24) can be derived directly from Tsang, ²⁶

$$\overrightarrow{p}=\widehat{k}\underset{0}{\overset{\pi }{{\displaystyle \int }}}\underset{0}{\overset{2\pi }{{\displaystyle \int }}}{a}^2\sin \theta d\theta d\phi {\rho }_{0}co{s}^2\theta =\widehat{k}\frac{4\pi a^3{\rho }_0}{3}$$ (22)

here, $a$ represents the radius of the electric dipole, assuming the dipole as a spherical particle, and ${\rho }_0$ denotes the surface charge density.

Sivasankar et al ²⁷ determined the value of ${\rho }_0$ for neurotransmitters under physiological conditions and obtained an average value of $12.5\frac{mC}{m^2}$ (range $1-20$ ). Assuming a neurotransmitter size of $a$ = $3\stackrel{\circ }{A}$ (and ${\rho }_0=12.5\frac{mC}{m^2}$ ), ²⁸ we obtain a dipole moment ( $p$ ) value of $1.979\cdot {10}^{-30}m\cdot C$ . Antosiewicz and Porschke ²⁹ determined the dipole moment ( $p$ ) value for neurotransmitters in aqueous solution at physiological pH and obtained a range of variation of $\left(1-10\right)\cdot {10}^{-30}m\cdot C$ . ³⁰

Dynamics of electric dipoles in magnetic fields

A current element $Idl$ immersed in a magnetic field $B$ will experience a force $dF$ given by, ³¹

$$dF=I\times Bdl$$ (23)

The current $I$ in equation (26) is attributed to electrons moving within the medium and is referred to as conduction current. We can adapt equation (23) to explicitly address charges moving in free space, constituting what is known as a convection current. A charge $q$ moving with velocity $v$ is equivalent to a current element $Idl=qv$ , thus we obtain,

$$F=qv\times B(24)$$ (24)

When a charged particle encounters a static field at right angles, it undergoes a force known as the Lorentz force, which alters the particle’s motion into uniform circular motion around the magnetic field lines. According to Newton’s second law, the radial force acting on the particle is $F_r=m\cdot a_r=q\cdot v_{\perp }\cdot B$ , where $v_{\perp }=v\cdot sin\theta$ represents the velocity component perpendicular to the magnetic field. The radial or centripetal acceleration is given by $a_r=\frac{{v_{\perp }}^2}{r}=w^2\cdot r$ , where $r$ is the radius of the circle and $w$ is the angular velocity of the charged particle orbiting with mass $m$ . The parallel component of velocity, $v_{\parallel }=v\cdot cos\theta$ , remains unaffected by the presence of $B$ . Therefore, when a particle enters a magnetic field at an angle to the magnetic field lines, it follows a helical path around the magnetic field lines, with $v_{\parallel }$ unchanged and $v_{\perp }$ causing the circular motion (Figure 1). ³²

Figure 1.

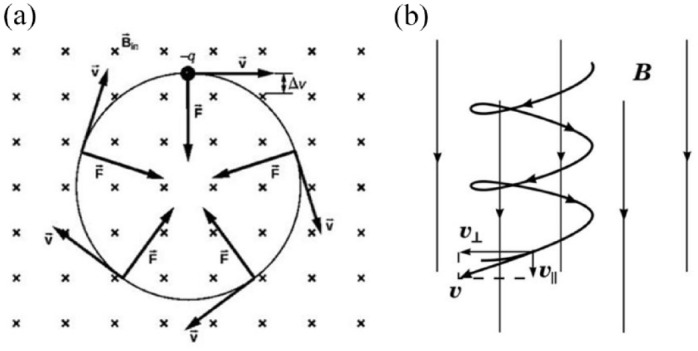
(a) Trajectories of charged particles in a magnetic field and (b) a charged particle with a velocity component parallel to a magnetic field and another perpendicular to it, moves in a helical path around the field lines.

The energy principle can be applied to derive force distributions. To develop a simple model for force density distribution, we require the expression for the force on an electric dipole in polarizable media, which can be derived from the Lorentz force law. The force on a stationary electric charge is governed by the Lorentz law with a frequency of zero. Considering two charges $q$ of opposite polarity separated by a vector distance $d$ , the total force on the dipole is the sum of the forces acting on the individual charges.

$$f=qE$$ (25)

where $E$ is the electric field. The total force on the dipole is the sum of the forces acting on the individual charges, given by,

$$f=q\left[E\left(r+d\right)-E\left(r\right)\right]$$ (26)

Unless the electric field at the location $r+d$ of the positive charge differs from that at the location $r$ of the negative charge, the separate contributions cancel each other out. To derive an expression for the force on the dipole in the limit where the spacing $d$ of the charges is small compared to distances over which the field varies appreciably, equation (26) is expressed in Cartesian coordinates. The field at the positive charge is then expanded about the position of the negative charge. Thus, the $x$ component is,

$$\begin{array}{c}{f}_x=q\left[E_x\left(x+d_x,y+d_y,z+d_z\right)-E_x\left(x,y,z\right)\right]\\ =q\left[\begin{array}{l}{E}_x\left(x,y,z\right)+d_x\frac{\partial E_x}{\partial x}+d_y\frac{\partial E_y}{\partial y}+d_z\frac{\partial E_z}{\partial z}\\ +\dots -E_x\left(x,y,z\right)\end{array}\right]\end{array}$$ (27)

The first and last terms cancel each other out. In a more concise notation, this expression is thus represented as,

$$f_x=p\cdot \nabla E_x$$ (28)

where we have identified the dipole moment $p=qd$ . The other force components are derived similarly, with $y$ and $z$ taking the place of $x$ . These 3 components are then summarized in the vector expression,

$$f=p\cdot \nabla E$$ (29)

Time-scale hierarchy in complex systems

In dynamics involving far-from-equilibrium irreversible processes, the relax integrability function tends to converge toward stable asymptotic configurations. The relaxation time is contingent upon the dissipative process parameters operating at each level. Neuronal time scales exhibit dynamism, with a succession of relaxation times discernible, each succeeding level characterized by an increase in magnitude^33,34:

1. Microsecond scale, associated with the rearrangement of ionic concentrations and reactive phenomena in tissue electrolytes.

2. Hundreds of microseconds scale, associated with the activation of sodium channels and subsequently with calcium channels involved in membrane excitation.

3. Millisecond scale, associated with the membrane time constant, pulse and stimulation duration, and electrochemical double layer polarization at the membrane-electrolyte interface.

4. Hundreds of milliseconds scale, associated with the mechanisms of activation and inactivation of membrane channels related to recovery phenomena.

5. Minute scale, involved in membrane adaptation phenomena (slow excitability variations dependent on ionic accumulation in regions where transport processes are disturbed).

The differences in the numerical order of characteristic relaxation times among hierarchical scales in dissipative systems often enable simplification of their description by applying 2 connecting scale principles. First, on a particular time scale, the variables of the higher time scale can be treated as constant parameters (as their relaxation times are significantly greater). Second, the variables of the lower time scale can be disregarded (as their relaxation times are much smaller). ³⁵

Suppose we have an electric dipole initially at rest within a static vertical magnetic field. The movement of the dipole depends on the EM field configuration, specifically on the electric potential $\left(V_e\right)$ generating the field, rather than the magnetic field itself, which remains constant. Zemped et al investigated the effect of small extracellular fields on spike-time variation. Although they did not propose an explanatory mechanism, they provided an experimental model to refute a potential explanation based on the resonant properties of neurons. ³⁶ In their studies, they applied magnetic fields in the millitesla (mT) range, and the voltage measurement was approximately 2 mV, with a range of 1 to 5 mV. We will use this value in the following calculation.

While the magnetic field may not be conservative, the EM field as a whole is conservative. Therefore, applying the principle of conservation of energy to a dipole positioned in a region of potential $V_e$ , the potential energy $\frac{p}{d}\cdot V_e$ is converted into kinetic energy.

$$\frac{1}{2}m{v_z}^2=q{V}_e\Rightarrow v_z=\sqrt{\frac{2q{V}_e}{m}}=\sqrt{\frac{2\frac{p}{d}{V}_e}{m}}$$ (30)

Taking $p=1.979\cdot {10}^{-30}m\cdot C$ ; $d=2\cdot a=2\cdot 3\cdot {10}^{-10}=6\cdot {10}^{-10}meters;m=6\cdot 023\cdot {10}^{-26}kg$ , $V_e=2mV$ and a synaptic cleft width of $20nm,$ we obtain a $v_z$ value of $14.491\frac{meters}{s}$ ³⁷ and a transit time of $1.38ns(1.38\cdot {10}^{-9}s)$ . ³⁸

Therefore, the electrical potential associated with extremely weak static magnetic fields induces temporal variations in neurotransmitter dynamics at a much lower time scale, from a hierarchical perspective, compared to what is typical in classical studies of chemical synapses. This suggests that the very weak synapse-induced magnetic fields may serve as fine control mechanisms in shaping the overall process of postsynaptic spike-time patterns.

Dynamics of hybrid multiscale systems: Combining deterministic and stochastic elements

Deterministic and stochastic hybrid systems no longer evolve with a deterministic trajectory in the parameter space, but rather with a certain probability distribution defined within that same space. A general formulation for these systems is based on nonlinear differential equations incorporating both a stochastic noise term, which models fluctuations, and a deterministic term.^39,40 The statistical properties of the noise completely define the system through its stochastic differential equation (SDE). This additive noise, resulting from fluctuation timescales and system response time, is typically assumed to have zero correlation time (white noise). Additionally, there may be an additional source of fluctuations arising from environmental influences, known as external noise.

The most common assumption regarding the stochastic term present in the SDE is that it follows a normal distribution, meaning it is Gaussian. In many systems, noise represents the influence of random factors whose cumulative effect, according to the central limit theorem, converges to a Gaussian distribution. White noise intensity is constant in the frequency-domain. Its correlation function is defined as follows, ⁴¹

$$\xi (t)\xi (t^{\prime })=2D\delta \left(t-t^{\prime }\right)$$ (31)

Here, the parameter $D$ represents the intensity of the noise. White noise represents the extreme case of a stochastic force evolving at an exceedingly rapid pace. From a physical standpoint, this indicates that the fluctuation time scale is significantly smaller compared to typical system response times. This heuristic approximation method is used to account for internal fluctuations and serves as a starting point for expanding the analysis to include external fluctuations in oscillating and excitable systems.

In a region of local instabilities in phase space induced by external stochastic influences, such as thermal motions or fluctuations in boundary conditions, a particle can be significantly affected by a deterministic force field. The existence of deterministic chaos is not a prerequisite for this phenomenon. If a deterministic force field is sufficiently strong and persistent, deviations from a stochastic trajectory can be profound, leading to predictable, even deterministic trajectories that are asymptotically stable. The outcome is noisy behavior that would not be observable without the influence of deterministic dynamics but cannot be sustained by deterministic dynamics alone.

The probability distribution $P(x,t)$ for systems with white noise follows a Fokker-Planck equation. Technically, white noise is a random signal where the values of the signal at 2 different times are not statistically correlated. However, white noise serves as an approximation of true noise, as real systems subjected to external fluctuations typically do not have a zero-correlation time. The most effective approach to address this issue is to model the random signal as an Ornstein-Uhlenbeck noise, which is a Gaussian noise characterized by a correlation function that decreases exponentially, expressed as, ⁴²

$$\xi (t)\xi (t^{\prime })=\frac{Dt}{\tau }{e}^{-\frac{\left|t-t^{\prime }\right|}{\tau }}$$ (32)

The parameters $D$ and $\tau$ represent the intensity and the noise correlation time, respectively. White noise corresponds to the limit as $\tau$ approaches zero.

Extended kinetics of the ligand-receptor bell model incorporating synaptic magnetic fields

The temporal evolution of the reversible chemical reaction between 2 reactants A and $B$ , forming the product $AB$ ( $A+B\iff AB$ ), can be described by the equation,

$$\frac{d[AB]}{dt}=k_{on}\left[A\right]\cdot \left[B\right]-k_{off}\left[AB\right]$$ (33)

Here, $\left[A\right]$ , $\left[B\right]$ , and $\left[AB\right]$ represent the concentrations of the reactants and product, respectively. $k_{on}$ and $k_{off}$ denote the association and dissociation rate constants, which govern the kinetics of the interaction. $k_{on}$ is influenced by the diffusive properties of the molecules and depends on factors such as distance and orientation. On the other hand, $k_{off}$ is linked to the bond half-life time, denoted as $\tau ={\left(k_{off}\right)}^{-1}$ , ⁴³ providing insights into the specificity and spontaneity of the reaction,

$$k_{off}=A\cdot e^{\frac{-\Delta G^0}{k_{B}T}}$$ (34)

In this equation, $A$ represents the Arrhenius constant, $k_B$ stands for the Boltzmann constant, $T$ denotes the absolute temperature, and $\Delta G^0$ represents the activation free energy of the reaction under standard conditions.

In our study, we introduce a theoretical model rooted in mechanics force fields theory to simulate the impact of magnetic forces on molecular interactions, particularly chemical bonds. When an external force is exerted, it alters the activation energy of the chemical reaction. The Bell model establishes a relationship between the magnitude of the force and the dissociation constant of the reaction, ⁴⁴

$$k_{off}\left(F\right)={\left(k_{off}\right)}_0\cdot e^{-\left(\frac{F\cdot x_{\beta }}{k_B\cdot T}\right)}$$ (35)

In the equation, $F$ represents the external force, ${\left(k_{off}\right)}_0$ denotes the equilibrium dissociation rate constant when the external force on the system is zero, and $x_{\beta }$ represents the activation energy of the chemical reaction. Rewriting the equation in terms of the bond half-life time,

$$\tau ={\tau }_0\cdot e^{\frac{F\cdot x_{\beta }}{k_B\cdot T}}$$ (36)

where ${\tau }_0={\left(k_{off}\right)}_0^{-1}$ . If we incorporate the typical parameters of LGIC-type binding into equation (39), ⁴⁵ we derive ${\tau }_0={10}^{-8}$ seg. In this context, we suggest employing a slightly adjusted version of the Bell equation that incorporates the synapse-induced magnetic field $B$ , expressed as,

$$\tau ={\tau }_0\cdot e^{\frac{B\cdot \frac{p}{d}}{k_B\cdot T}}$$ (37)

Here, $p$ and $d$ represent the dipole moment and the diameter of the neurotransmitter, respectively.

Neuron models that integrate alpha function conductance-based synapses

Synaptic noise acts as the primary origin of membrane potential fluctuations in neurons and plays a significant role in shaping their integrative behaviors, including synaptic conductance. Destexche and Rudolph-Lilith ⁴⁶ conducted a review of experimental synaptic noise measurements and formulated a model grounded in stochastic noise processes.

A common approach to estimating the alteration in conductance within the postsynaptic neuron is through the alpha function model. In numerous synapses, the progression of synaptic conductance undergoes a finite-duration phase. The alpha function delineates this phase of conductance progression as not infinitely rapid, implying it possesses a finite rise time,

$$g_s\left(t\right)=\frac{t}{\tau }{e}^{-\frac{t}{\tau }}$$ (38)

It is worth noting the similarity between equations (32) and (38), which validates the application of stochastic-deterministic noise theory to conductance-based synapses. Consequently, we can express the kinetics of synaptic conductance as follows,

$$g_{syn}={\overline{g}}_{syn}\cdot g_s\left(t\right)={\overline{g}}_{syn}\cdot \frac{t}{\tau }{e}^{-\frac{t}{\tau }}$$ (39)

Hence, we eventually deduce a membrane potential dynamics equation rooted in the Colwell HH model, integrating the synapse-induced magnetic field,

$$I_{syn}=g_{syn}\left(t\right)\left[V\left(t\right)-E_{syn}\right]$$ (40)

Here, $E_{syn}$ denotes the constant voltage source.

Figure 2 depicts the temporal progression of synaptic conductance ( $g_{syn}\left(t\right)$ ) for different magnitudes of $B$ .

Figure 2.

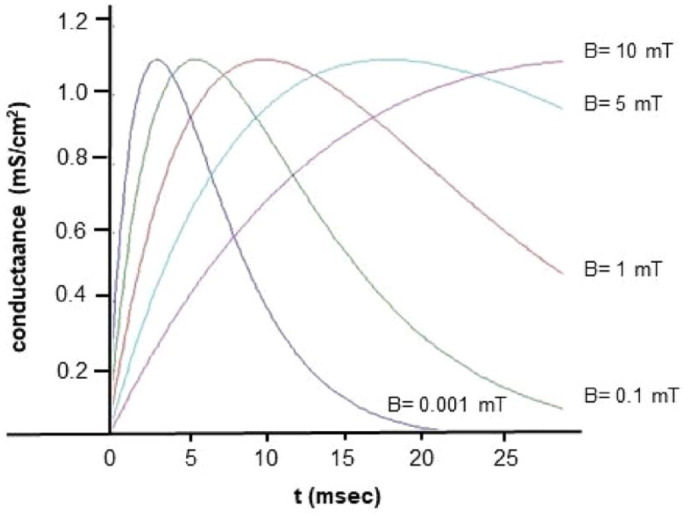
Synaptic conductance analytic solutions using the alpha-function model at different synapse magnetic field values ( $B$ ).

Results and Discussion

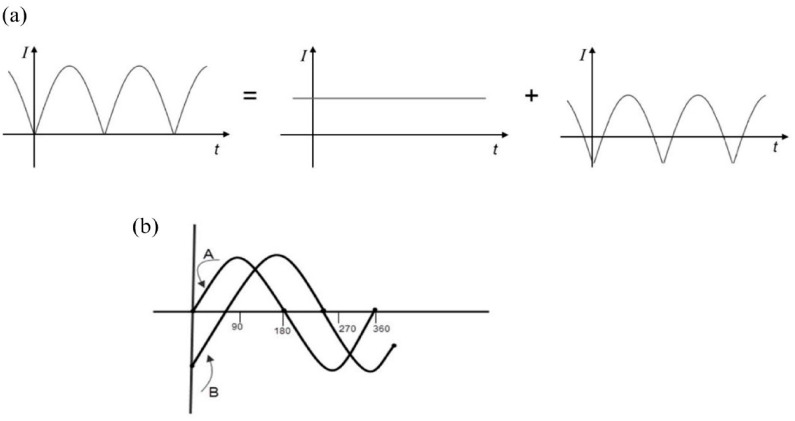
Cell membrane proteins can be arranged as a kind of electric amplifiers, such as is used in electronics. Every periodic current can be analyzed using Fourier series as a sum of a constant component (DC) and alternating components. These are entirely transformed by the transformer, all in the same ratio, while the DC component induces no voltage across the secondary. Consequently, the transformed voltage is, except for the transformation factor, identical to the initial voltage, minus its mean value—(Figure 3a)—(the transformed voltage has a zero-mean value).

Figure 3.

In (a), we can observe the decomposition of a rectified alternating current (primary current) into a direct current (untransformed) and a rectified alternating current with zero average offset. In (b), the phase shift of the intensity of a sinusoidal alternating current due to an external disturbance is presented, in this case, a magnetic field.

The phase shift $(\Delta \varphi )$ is contingent upon both the phase ( $\varphi$ ) and the magnitude of the disturbance. For extremely brief perturbations, $\Delta \varphi$ remains zero across the entire phase spectrum. This domain corresponds to the oscillation’s refractory zone, wherein no effect is observed regardless of the phase value of the applied disturbance. Beyond this zone, the disturbance consistently induces a phase shift, the magnitude of which hinges on the phase value. At the boundary between the refractory and sensitive zones, there exists a discontinuity in amplitude directly influenced by the intensity of the disturbance. This discontinuity underscores the excitability nature of the system.

From the perspective of alternating current circuit theory, it’s feasible to manipulate the phase of the resulting electric current (the initiation timing) by adjusting the amplitude of the sinusoidal potential at the moment $t=0$ when the circuit closes. Let’s consider a capacitor (cell membrane), initially in an open circuit, perturbed by a sinusoidal voltage $U=U_{0}sinwt$ at $t=0$ (corresponding to the periodic extracellular EM disturbance associated with the induced magnetic field). Initially, the current remains zero until the circuit is closed, and begins to rise as the capacitor charges. However, this represents a transient regime primarily due to the non-zero resistance of the capacitor (the duration of this transient regime is approximately of the order of RC, where R and C denote the resistance and capacitance of the capacitor). Subsequently, the steady state is achieved, where the current leads the voltage. In other words, the EM signal doesn’t manifest instantaneously but undergoes a transient phase (Figure 3b)).

A single excitatory synapse, such as a glutamatergic synapse, which accounts for nearly 90% of synapses in the cortex, generates a current ranging from 5 to 110 pA, with an average of 25 pA, and a maximal conductance of 700 to 1000 pS (ranging from 0 to 1000 pS). The reliability of a synapse to elicit or influence spikes depends not only on its conductance but also on its proximity to the spike initiation point, typically located near the soma where the axon emerges, and often distant from the synapse itself. At most, a single synapse produces 100 pA at the origin, with a local membrane potential variation of less than 3 to 5 mV, insufficient to surpass the threshold for firing. As the potential wave travels from the origin to the soma, where the spike is generated, these values decrease due to dendritic cable properties. Typically, a synaptic event occurring in the dendritic tree induces less than 0.5 mV in membrane potential, which, when added to the resting level, fails to reach the threshold. These observations lead to a significant conclusion: firing a spike necessitates the temporal integration of currents arriving from multiple synapses.

A post-synaptic current intensity of ${10}^{-10}A$ generates a magnetic field near the dendrite, at the external cranial base, of approximately ${10}^{-4}\mathrm{fT}(1\mathrm{fT}=1femtotesla={10}^{-15}Tesla)$ . Consequently, this field is undetectable, as current sensors typically necessitate a minimum field strength of $100\mathrm{fT}$ . To register this field with a sensor, a simultaneous contribution of 1 million post-synaptic currents would be required.

In a recent study, ⁴⁷ we explored the induced magnetic fields within living tissues. Our findings suggest that if we acknowledge the presence of off-diagonal terms in the synapse conductivity tensor, an exogenous EM field can indeed trigger a synapse magnetic field, thereby altering neurotransmitter dynamics.

Hence, the following question emerges: Could an exogenous EM field, generating a weak synapse magnetic field ( $10-100\mathrm{fT})$ , potentially modify the temporal patterns of postsynaptic action potentials? Presently, there is limited research exploring the connection between magnetic fields and synapses. Nevertheless, a few studies have investigated the impact of magnetic fields within the mT range on action potential patterns.^{48 -50}

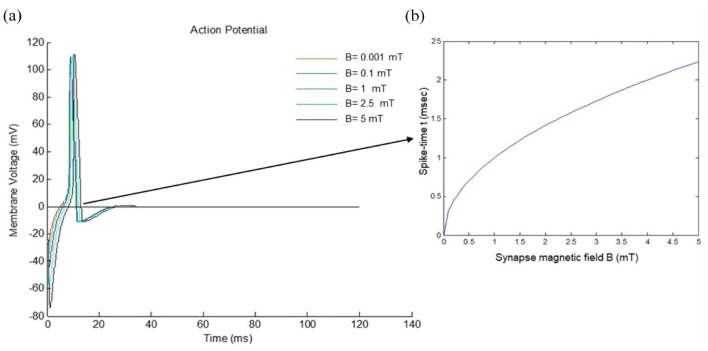
When applying a continuous input of 1  $\mu \mathrm{A}$ , while maintaining the remaining chemical-physical variables constant, but altering the magnetic field within the range of $0.001-5\mathrm{mT}$ , we observe a nonlinear variation in spike timing with increasing $B$ (Figure 4a)). Changes in spike timing directly correlate with fluctuations in bond half-life and, consequently, neurotransmitter dynamics. As a result, magnetic fields at the synapse induce a time-varying spike pattern (Figure 4b)). Additionally, we have modeled the scenario with a continuous input of 5  $\mu \mathrm{A}$ , considering magnetic field values ranging from $0.001-10\mathrm{mT}$ in Figure 5. As we may observe in Figure 4b the postsynaptic spike-time results are highly non-linear, resulting from a number of non-linear voltage dependent currents acting in context. Instead of instantiating these complexities, we focused on making the analysis of the results as simple as possible and relegated ourselves to establish the qualitative conclusions.

Figure 4.

Numerical simulation of the model with input driving current of 1  $\mu$ A and induced magnetic fields of 0.001, 0.1, 1, 2.5, and 5 mT. In (a) membrane voltaje time-variation. In (b) time-varying spike pattern.

Figure 5.

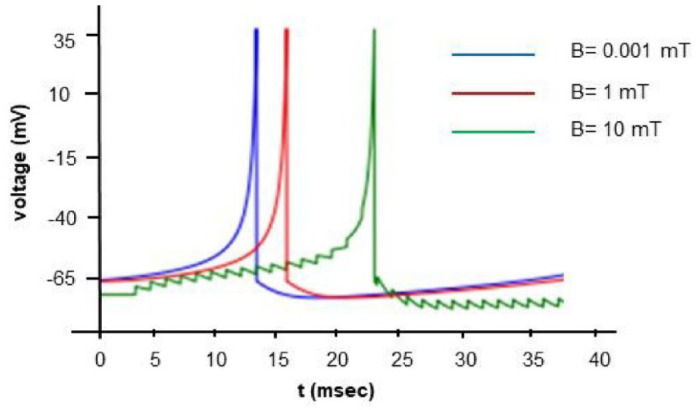
Numerical simulation of the model with input driving current of 5  $\mu$ A and induced magnetic fields of 0.001, 1, and 10 mT.

Anastassiou et al^51,52 investigated the impact of spatially inhomogeneous extracellular electromagnetic fields on neurons, specifically focusing on alterations in spike timing. They observed that extracellular magnetic fields, within the same order of magnitude as those utilized in our study, induced changes in somatic membrane potential of less than 0.5 mV under subthreshold conditions. Furthermore, they conducted simultaneous recordings from up to 4 patched neurons located proximally to each other. Their findings suggest that despite their small magnitude, these magnetic fields could significantly influence spike timing, aligning with the theoretical outcomes of our study.

We can analyze the stability of disturbances within the framework of stable oscillator theory. Figure 6 illustrates the phase shift among identical oscillators with matching periods, initially synchronized, upon application of a continuous current input of 100  $\mu \mathrm{A}$ , albeit with varying $B$ values. The spike trains could be represented like a sine wave, its amplitude is represented on vertical axis and time on horizontal axis. As we have previously discussed (Figure 3b), this process has an initial phase with highly unstable behavior (transient phase, varying in duration depending on the magnitude of the applied magnetic field) with many artifacts due to the large number of nonlinear equations involved. So, in Figure 6 we focused on the difference between the first spikes of the spike trains corresponding to the different applied magnetic fields $(\Delta \varphi )$ .

Figure 6.

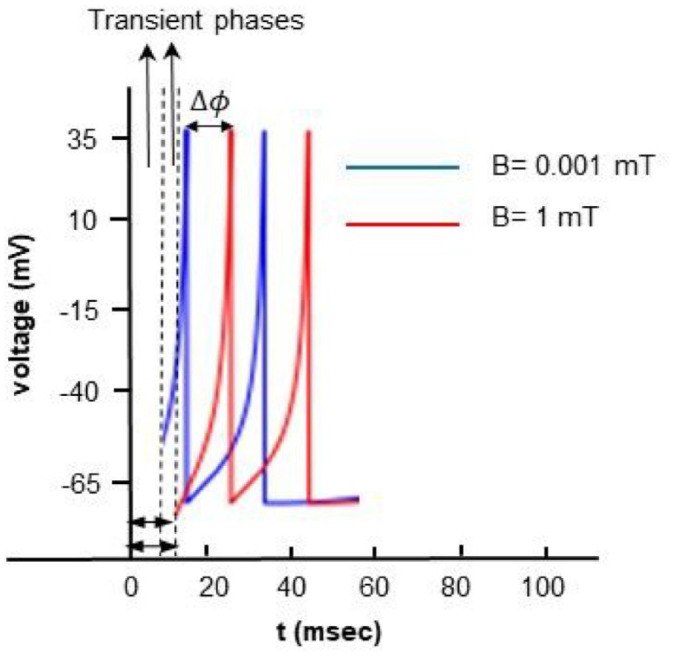
Numerical simulation of the model with input driving current of 100  $\mu$ A and induced magnetic fields of 0.001 and 1 mT.

Stability analysis of the spike-timing model based on bi-dimensional dynamic systems

Our modified HH model is a dynamic system consisting of the state variables $V,n,myh$ , governed by a 4-dimensional system of ordinary differential equations. This HH model can be reduced to a 2-dimensional model and still produce the same action potentials.

The system state is a 2-dimensional vector $(V,n)$ in the phase plane $R^2$ because the current exhibits instantaneous activation kinetics, such that its conductance can be considered maximal, $m_{\infty }$ , over most of the time interval. Activation kinetics for $n$ are much slower and therefore need to be defined by its derivative.

First, we need to establish the equilibrium points to study the nullclines of the state variables. A nullcline is the set of locations in the phase plane where the state variable is at rest. In this system, it would correspond to the conditions $\stackrel{.}{V}=0$ and $\stackrel{.}{n}=0$ .

The intersections of these nullclines will be the points where none of the state variables are changing, thus indicating membrane equilibrium. In Figure 7, we observe the cubic-shaped nullcline for $V$ in red and the sigmoid-shaped nullcline for $n$ in green. Their intersection is the equilibrium point for this model.

Figure 7.

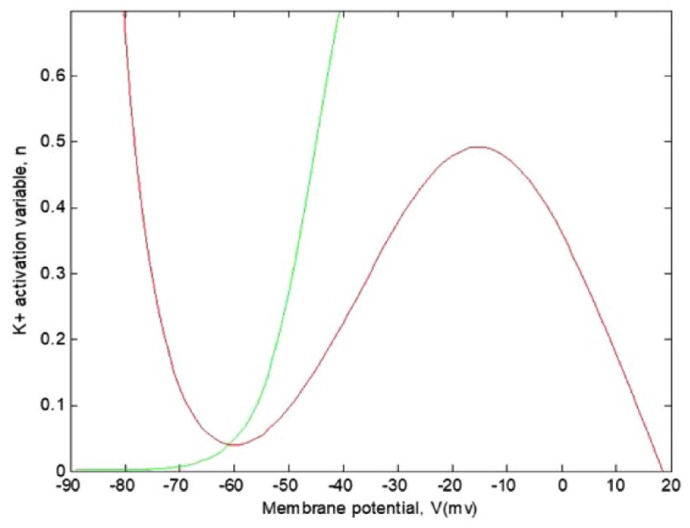
Representation of the nullclines of the model with $I=1pA$ and $B=0mT$ . The curves appear to have an equilibrium point approximately at $V=-62mV$ .

Unlike 1-dimensional systems, stability cannot be determined solely by the slope of the $\stackrel{.}{V}vsV.$ curve. Often, a local linear analysis can determine the stability of an equilibrium $(u_0,w_0)$ , in 2 dimensions. We know from linear algebra that 2 nullclines can be approximated by their linearizations near the equilibrium. We use the Jacobian matrix, $A$ , at the equilibrium to obtain the eigenvalues and eigenvectors.

Now we will analyze the stability of the equilibrium point of $I_{Na,p}+I_k$ (Figure 7), which was approximately at $V=-62mV$ . The partial derivatives required for the elements of the Jacobian matrix are as follows,

$$\frac{\partial \stackrel{.}{V}}{\partial V}=\frac{1}{C_m}\left(\begin{array}{l}-g_L-g_{Na}{m}_{\infty }\left(V\right)-\\ g_{Na}\left(V-E_{Na}\right)\left(-1\right)\\ {\left(1+exp\left(V_{\frac{1}{2}}-V\right)/k\right)}^{-2}\cdot \\ \left(exp\left(V_{\frac{1}{2}}-V\right)/k\right)\cdot \left(\frac{-1}{k}\right)-g_k\cdot n\end{array}\right),$$ (41)

$$\frac{\partial \stackrel{.}{V}}{\partial n}=-g_k\left(V-E_K\right),$$ (42)

$$\begin{array}{c}\frac{\partial \stackrel{.}{n}}{\partial V}=\frac{1}{{\tau }_V}{\left(1+exp\left(V_{\frac{1}{2}}-V\right)/k\right)}^{-2}\\ \left(exp\left(V_{\frac{1}{2}}-V\right)/k\right)\cdot \left(\frac{1}{k}\right)\end{array}$$ (43)

$$\frac{\partial \stackrel{.}{n}}{\partial n}=-\frac{1}{{\tau }_V}$$ (44)

The corresponding value of $n$ can be computed using the equilibrium value of $V$ in equation $(41)$ . The equilibrium coordinates are $\left(-62,0.032\right)$ The Jacobian matrix is as follows,

$$A=\left(\begin{array}{cc}-0,679& -280\\ 0,00625& -1\end{array}\right)$$ (45)

The trace of the matrix is $Tr\left(A\right)=-1,6779$ and the determinant $\left|A\right|=2,429$ . Finally, we can calculate the eigenvalues for this equilibrium point using $\frac{Tr\left(A\right)\pm \sqrt{{\left(Tr\left(A\right)\right)}^2-4\left|A\right|}}{2}$ . The eigenvalues for $V=-62$ are $-0,84\pm 1,31i$ . Since they have a negative real part, this corresponds to an equilibrium point with asymptotic stability; more precisely, to a stable spiral point.

Next, in Figure 8, we can observe trajectories in the phase plane with different initial values of continuous current inputs (1 and 10  $\mu \mathrm{A}$ ) but with different $B$ values (0.1, 1, 2, 5, and 10 mT), corresponding to the external magnetic field, while maintaining the same initial value for the potassium activation variable, $n$ . We can appreciate that all trajectories follow a subthreshold path toward equilibrium. We can see that this model does not have a fixed threshold for membrane potential. All action potentials shown are transient; they all return to equilibrium values.

Figure 8.

Representation of various action potential trajectories with different continuous current inputs and different $B$ values: (a) $I=1\mu \mathrm{A}$ and (b) $I=10\mu \mathrm{A}$ .

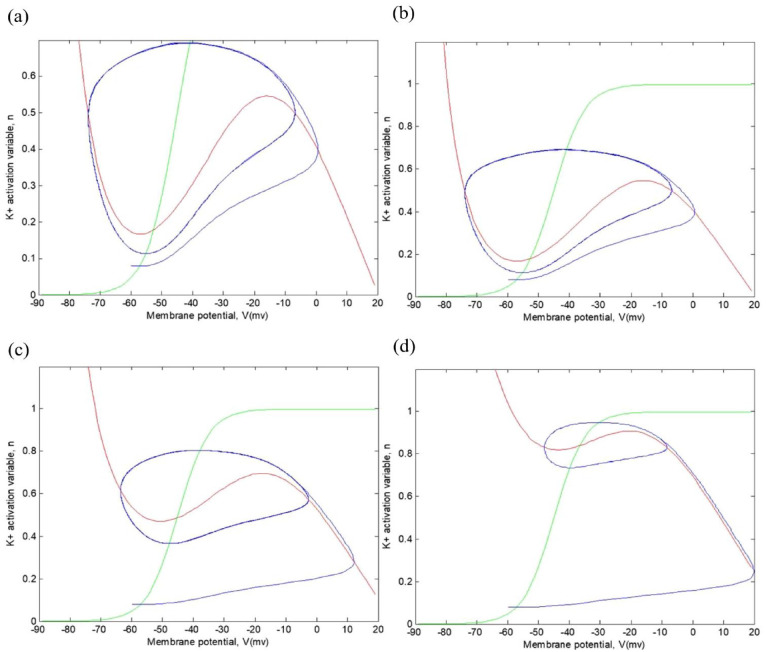
Figure 9 shows the emergence of the limit cycle between the values of $I=100-400$  μA, corresponding to an external magnetic field $B=5mT$ . Limits cycles exhibit repetitive patterns of stationary movement in contrast to critical points, which represent equilibrium states. By definition, a solution $\gamma (t)$ is called periodic with period $p$ when it satisfies $\gamma \left(t+p\right)=\gamma (t)$ , for all $t$ , but $\gamma \left(t+m\right)\ne \gamma (t)$ , when $m<p$ . In 2-dimensional linear systems, the only possible periodic trajectories are centers, where 2 purely imaginary eigenvalues appear. However, the center is not considered an ideal model for many cyclic processes due to its structurally unstable nature; any variation in the system parameters can alter its dynamic structure, changing its behavior. Nevertheless, nonlinearity can lead to stable cyclic behaviors that persist despite small changes in the system parameters. These are limit cycles, phenomena exclusively associated with nonlinear systems. Finally, note that in the caption of Figures 8 and 9, the lines with other colors correspond to the same lines as in Figure 7.

Figure 9.

Representation of various action potential trajectories with different continuous current inputs and $B$  = 5 mT: (a) $I=100\mu \mathrm{A}$ , (b) $I=200\mu \mathrm{A}$ , (c) $I=300\mu \mathrm{A}$ , and (d) $I=400\mu \mathrm{A}$ .

STDP, or Spike Timing-Dependent Plasticity, is a phenomenon whereby the precise timing of neuronal spikes influences both the direction and magnitude of synaptic strength alterations.^53,54 Often regarded as the fundamental learning rule governing synapses, STDP has undergone successive refinements to address predictive limitations. In proposing an alternative fundamental principle, we suggest that exogenous or endogenous EM fields induce changes in crucial biochemical intermediates, such as neurotransmitters, serving as more direct triggers of plasticity mechanisms. The modulation of chemical synapses by STDP is dictated by the temporal discrepancy between pre- and postsynaptic neuronal firing, essentially the synchronization between neurons. ⁵⁵ Concurrently, the magnetic coupling among neurons can enhance signal exchange and foster global synchronization within the neural network.^56,57

We have observed that the mechanism underlying the temporal information processing of a neuron is determined by a non-linear current-voltage relationship associated with the interactions between the exogenous EM field and certain proteins within the excitable membrane. Therefore, the variability of the spike timing of a neuron would be strongly influenced by extracellular EM fields in close proximity to a bifurcation point. However, we have demonstrated that within the range of $I=0-400\mu \mathrm{A}$ and $B=0-10mT$ , there exist equilibrium situations that would ensure precise control of the STDP mechanism.

Conclusions

Cognitive neuroscience has revealed a direct correlation between structural connections throughout the brain’s temporal hierarchical levels. Considering that all cognitive functions exhibit temporal characteristics, it is conceivable that the accurate estimation of transient alterations within specific temporal hierarchies is crucial for interpreting information from weak periodic endogenous or exogenous stimuli, such as static or extremely low-frequency magnetic fields. Thus, investigating the effects of magnetic fields on spike-time dynamics and their influence on other core cognitive functions may shed light on fundamental processes in typical cognition and their dysregulation in neuropsychological and mental disorders.

The EM field theory enables the determination of fields at the mesoscopic scale based on the morphological properties and bioelectrical tissue parameters at the microscopic scale. In this study, structural and functional intricacies are simplified by delineating 2 domains (internal and external neuron spaces), characterized by a set of interconnected fields governing the movement of charged particles within a magnetic field.

Estimating synaptic conductance for any noise correlation time remains an unresolved issue. While we outline a physical framework with simplifying assumptions to aid in understanding or predicting phenomena, obtaining data from experimental or quasi-experimental studies would be valuable and insightful.

We establish a connection between the STPD phenomenon and equations that depict the movement of neurotransmitters under an induced magnetic field. Our findings uncover the pivotal role of EM fields in governing the precise timing of pre- and postsynaptic spikes. This timing intricately shapes the outcomes of the STDP rule, while the propagation delay of neural signals significantly influences the connectivity patterns and dynamics of neural networks.^58,59

The macroscopic study of complex phenomena such as STPD is based on the application of constitutive equations to a supposedly continuous model subject to given constraints. These equations arise from the incorporation into conservation relationships (mass, momentum, energy. . .) of phenomenological laws known as kinetics, which connect the various currents therein (diffusion, chemical reaction rates, stresses, heat. . .) with corresponding state variables and their spatial derivatives (Fick’s law, chemical kinetics, Fourier’s law. . .).

In the particular case of STPD, the mechanisms generating instability are the autocatalytic transport of ions across excitable membranes in nerve cells or positive or negative feedback between neurons. Metabolic oscillations result from the control of enzyme activity, while oscillations in protein synthesis result from genetic regulation. The common point of biological rhythms in our study is that they have an exogenous origin. They possess all the properties of dissipative structures, in the sense that they exhibit a phenomenon of temporal self-organization under conditions of non-equilibrium. It is the internal regulatory mechanisms of biological systems that, through the bias of nonlinear kinetics, lead to instability phenomena associated with the emergence of periodic behaviors beyond the bifurcation point. In our case, within the physiological parameter range of intensity ( $I=0-400\mu \mathrm{A}$ ) and magnetic field ( $B=0-10mT$ ), the temporary dissipative structures (spike-timing) of action potentials associated with the STPD mechanism manifest rhythmic characteristics in the form of limit cycles around a stable steady state, resulting from nonlinear effects due to catalytic actions in associated chemical, physical, and biological processes.

Our approach to predicting timing changes in spike induced by magnetic fields can be extended to local neural networks. In fact, some authors consider extracellular EM field oscillations as a marker of neural network oscillations.^{60 -62} It is even suggested that information contained in the oscillations of endogenous extracellular potentials could provide particularly relevant insights into the temporal coding of network activity.^63,64 This offers promising prospects regarding potential therapies for pathological neural synchronization, such as in the case of Parkinson’s disease, for example. The results may suggest that, by appropriately choosing the delay time, a mechanism of control like STPD through locally applied external EM field to a neural subpopulation could suppress global neuron synchronization. The coupling mechanisms of network activity to exogenous EM field are not an alternative to classical approaches but complementary mechanisms that take into account the spatiotemporal characteristics of the involved EM field.

A fresh perspective on the macroscopic system, arguably one of the most debated topics in neuroscience research, emerges from examining the average synaptic activity time in neural networks through the lens of path integrals. This approach offers insights into the partial understanding of asymptotic behavior on a microscopic scale. In the long run, it becomes imperative to delve into the topological equations governing neural temporal hierarchical levels, an area where analytical findings are scarce. This poses an issue of exceptional interest, as theoretical conjectures supported by experimental evidence indicate that neural networks retain information over timescales corresponding to their anatomical hierarchy.