Machine learning and analytic hierarchy process integration for selecting a sustainable tractor

Abstract

Selecting the appropriate tractor for small-scale farms is a complex process due to the multitude of technical, environmental, and economic criteria that must be evaluated. This study addresses this challenge by integrating the Analytic Hierarchy Process (AHP) with machine learning (ML) to reduce the number of criteria and simplify the decision-making process. The research aims to determine the most relevant criteria aligned with sustainable development goals for selecting the right tractor, focusing on small farms in the Egyptian Delta. Four tractors, with horsepower ranging from 55 to 95, were evaluated based on inputs from forty-two governmental service providers in the study area. Initially, nine criteria were identified, encompassing key technical, environmental, and economic factors. These criteria were reduced to three—price, power, and maintenance costs by weights 0.142, 0.334, and 0.525, respectively—using Hierarchical Agglomerative Clustering with Euclidean distance. This reduction streamlined the selection process, making it more practical for farmers. Results show that the second tractor (T2), with a priority score of 0.326 and a normalized value of 33.4%, emerged as the optimal choice for small-scale farmers, outperforming the first tractor (T1) (28.7%) and third tractor (T3) (21%). Integrating AHP and ML simplifies tractor selection, ensuring sustainability, cost-efficiency, and operational effectiveness.

Introduction

The Sustainable Development Goals (SDGs), which comprise seventeen targets for the years 2015–2030, took the place of the eight Millennium Development Goals (MDGs) in September 2015 ¹. The Food and Agriculture Organization presented five principles for achieving sustainable development in the agricultural and food sectors². Among these goals is the role of smallholder farmers in the sustainability of agriculture¹. So, natural resource preservation and easier access are critical components of our efforts to guarantee the agriculture sector’s sustainability. According to the World Commission on Development and Environment, it’s also essential to fulfill the demands of future generations³. A substantial emphasis on agricultural mechanization is necessary to increase the productivity and efficiency of agricultural industry activities^4,5. Mechanizing agriculture can also increase output and reduce crop losses⁶. , cut back on emissions of greenhouse gases⁷and lower manufacturing expenses^8,9. The labor shortage is also a driver for using agricultural mechanization¹⁰. According to some academics, mechanization alternatives lead to advances in labor, land productivity, and environmental impact¹¹. The key to attaining sustainability in the agriculture industry is helping smallholder farmers select the right automation to maximize their financial and technological gains¹². Therefore, choosing appropriate mechanization, especially for tractor purchase or rental, is critical for small farms^13,14, increasing revenues and land productivity¹⁵. The agricultural tractors are considered the primary source of mechanical power for operating agricultural mechanization at different farm sizes^16,17.

One well-known method for selecting the best options is multi-criteria decision-making (MCDM)^14,18. MCDM is an important and multidisciplinary area of operations research that has grown in prominence recently. Multi-attribute and multi-objective decision-making are the two primary branches of this area¹⁹. Farmers use many criteria to choose the best tractor: brand, price, mechanical power, weight, and dimensions¹⁶. The tractor alternatives were compared by evaluation and weight of criteria to make the right decision²⁰. Selecting the appropriate tractor and related equipment necessitates more research. Choosing the wrong tractor might have expensive repercussions. Tractor power is considered the first criterion for selecting appropriate tractors. Gürsoy et al²¹. and Shorkpour & Asakreh²²applied the ability to perform agricultural operations. In addition, the gearbox, driving wheel, number of cylinders, tractor weight, number of gears, and rated engine speed were also used as tractor selection criteria²³. The economic aspects of tractor selection, such as price, were also studied through a study conducted by Multu²⁴. AHP is an MCDM instrument that considers both quantitative and qualitative factors. It is possible to establish the weights of the criteria objectively, using certain techniques that are not influenced by the decision-makers’ opinions, or subjectively, based on the decision-makers’ assessments of their significance. Many researchers have used AHP for various purposes, as shown in Table 1..

Table 1.

Chronological overview of AHP applications in various decision-making contexts

Author	Year	Application	Key Contribution
Tam and Tummala25	2001	Vendor selection in telecommunication systems	Demonstrated AHP’s advantage in achieving consensus and saving time in multi-criteria decision-making
Byun 26	2001	Car selection	Combined AHP with pairwise comparison and a five-point rating scale; applied group weights for consistency ratio
AlKhalil27	2002	Project delivery method selection	Developed a user-friendly AHP model for choosing the most suitable project delivery method
Kahraman et al.28	2003	Provider selection in a White Turkish factory	Used fuzzy AHP with triangular fuzzy numbers to prioritize providers and analyze the development process for comparisons
Yurdakul29	2004	Machine tool selection in manufacturing strategy	Integrated AHP with manufacturing strategy, focusing on investments in ML
Choughle and Ravi30	2005	Process planning in castings	Proposed an AHP-based nearest neighbor algorithm for case retrieval
Bol and Mohammed31	2005	Farm machinery selection	Developed a mathematical model for farm machinery selection
Ayag32	2007	ML technique selection	Combined AHP and simulation to choose the best ML techniques
Grisso et al.33	2009	Farm tractor selection	Used tractor test data to aid in selecting farm tractors
Osman34	2011	Farm machinery management optimization	Created a linear programming model to optimize farm machinery management
Ahadi and Gha-zanfar-Rad35	2011	Rolling stock supplier selection	Utilized AHP to choose the best rolling stock supplier
Kilincci and Onal36	2011	Provider selection based on customer satisfaction	Used fuzzy AHP to prioritize providers by satisfaction levels
Zhou37	2011	Neural networks and support vector machines integration	Introduced a method combining Particle Swarm Optimization (PSO) with neural networks and support vector machines
UmaDevi et al.38	2012	Vendor selection in supply chain management	Developed an AHP model to choose the best vendors, accounting for both quantitative and qualitative factors
Russo and Camanho 39	2015	Systematic literature review on AHP criteria	Reviewed thirty-three cases where AHP or fuzzy AHP was used to define and measure criteria weights
Amini and Asoodar17	2016	Tractor selection	Applied the AHP method to select the best tractor
García-Alcaraz et al.40	2016	Agricultural tractor evaluation	Suggested a hybrid AHP and TOPSIS method for evaluating agricultural tractors
Houshyar et al.41	2020	Agricultural machinery distribution in Iran	Evaluated machinery distribution using fuzzy AHP and constrained weight DEA methods
Hoose et al.42	2021	Select trailers for grain transportation.	Utilized AHP and Data Envelopment Analysis (DEA) techniques for selection process
Stofkova et al.43	2022	calculation and to set the proper order of criteria	Used the AHP method as essential for strategic managerial decision-making
Veisi et al.44	2022	Select a sustainable irrigation system	Used the AHP to select the irrigation system
Pant et al.45	2024	monitoring health management practices	Used AHP for ranking the best alternative for monitoring health management practices in a smart healthcare system
Present study	2024	Tractor selection	Integrates AHP with ML (Hierarchical Agglomerative Clustering) for criteria reduction and streamlining tractor selection

High-performance computer and big data technologies have given rise to ML, which has opened up new possibilities for data-intensive science in the multidisciplinary field of agri-technology⁴⁶. ML has been widely applied in many domains and applications in agriculture and energy⁴⁷. ML allows data processing with less computation and time. MCDM approaches are increasingly combined with ML to address complex decision-making problems across various industries. MCDM evaluates multiple options based on competing criteria, while ML enhances this process through advanced data analysis and pattern recognition. This combination is particularly effective in fields requiring large datasets and complex criteria, such as energy management, inventory optimization, and urban planning⁴⁸. Continual learning is necessary to ensure progress. ML is categorized into reinforcement, semi-supervised, supervised, and unsupervised learning⁴⁹. This study will use a hybrid approach combining AHP with ML methods to choose the best tractor for small farms in the Egyptian Delta, considering subjective and objective criteria for determining weights⁵⁰. Subjective criteria rely on decision-makers’ judgments⁵¹, while objective criteria weights are calculated using specific techniques without decision-maker influence^52,53.

This paper introduces several innovative contributions. First, it integrates the AHP with ML (Hierarchical Agglomerative Clustering) for criteria reduction and streamlining tractor selection—a novel approach not widely used in previous studies. The research reduces decision criteria from nine to three, making the process more accessible for small-scale farmers. It is one of the first studies to apply this methodology to small farms in Egypt’s Delta, addressing their operational and financial constraints. Additionally, the selection framework aligns with global sustainability goals by incorporating technical, environmental, and economic factors. The findings are empirically validated through input from forty-two governmental service providers, ensuring practical relevance.

Materials and methods

Research area

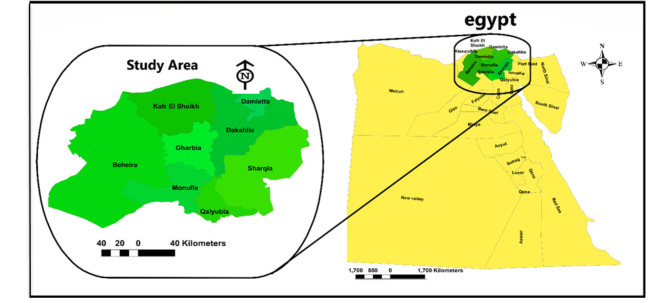
Delta region is located in the north of the Egyptian Republic. It is one of the largest deltas in the world, with a total area of about 240 km². It extends from the eastern side of Port Said until it reaches the western side as far as Alexandria. It was given this name due to its triangular shape. Delta was formed due to the accumulation of silt brought by the Nile River, which ended up in the Mediterranean Sea. Over time, due to the accumulation of silt and Nile riverbanks’ physical weathering and flood sedimentation for thousands of years, the Delta was formed when the Nile River was bifurcated into two branches. One of them is the eastern Damietta Branch and the western Rosetta Branch. The length of the Delta is about 160 km, and it begins on the southern side at Al-Qanater Al-Khayriyah, near the city of Cairo. The Egyptian Delta is famous for the fertility of its soil, which is always suitable for agriculture. The Egyptian Delta includes eight governorates, as shown in Fig. 1.

Fig. 1.

Study area (ArcGIS^®, Version 10.3.1.4959, License type: Advanced, Esri Inc.).

The Delta of Egypt is considered one of Egypt’s most important agricultural regions and a major source of agricultural production in Egypt. It is characterized by its fertile soil, which is suitable for cultivation at any time, and the availability of fresh water from the Nile River, which contributes to the cultivation of a wide range of crops such as rice, wheat, vegetables, fruits, etc. The area of agricultural land in the Delta exceeds 55% of the total agricultural area in Egypt. Small areas for agriculture prevail in the Delta.

Research methodology

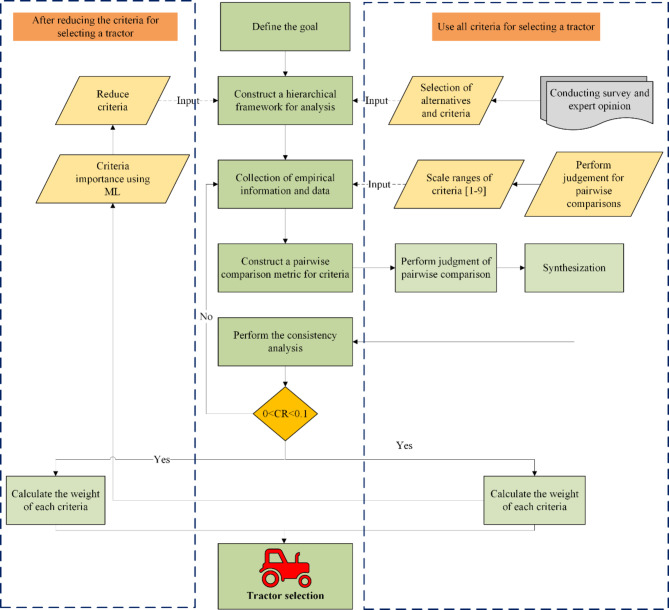
In general, hybrid techniques were used to select the appropriate tractor between the available tractors in the study area using more than one method. In this study, nine criteria were identified for tractor selection. Weight calculation methods were used to determine the importance of each criterion identified in the work. The AHP method for weight calculation was used, which uses assumptions from experts’ decisions, with ML techniques to reduce the criteria numbers and rank the alternatives according to the weight of selected criteria. The study focused on tractors category B (from 55 to 95 hp), which is common in farms less than two hectares and achieves most of the farm operations as results from farms survey. The category of tractors was selected according to the American Society of Agricultural Engineers (ASAE), depending on 3-point hitch specifications and power. The principles mentioned can be expanded and organized into a more detailed step-by-step process, illustrated in Fig. 2.

Fig. 2.

The AHP Flowchart with ML method.

Essentials of AHP

AHP is a valuable decision-support tool decision-makers (DMs) use to select or rank the most appropriate alternative or set of alternatives. It is widely recognized as a user-friendly tool for Multiple Criteria Analysis (MCA) and typically involves several stages⁵⁴. These stages include selecting decision options and evaluation criteria, collecting performance measures for the evaluation matrix, standardizing the measures to a common scale, assigning weights to the criteria, ranking or scoring the options, conducting sensitivity analysis, and ultimately making a decision. The DM defines the desired outcome as a goal, which serves as the target, indicating the preferred direction.

The AHP was selected for this study due to its proven effectiveness in handling qualitative and quantitative data, especially where expert judgment is required. AHP allows for subjective assessments through pairwise comparisons, which is crucial in agricultural decision-making where empirical data may be scarce. Its hierarchical structure breaks down complex problems into manageable components, facilitating a transparent decision-making process. AHP is particularly advantageous for integrating expert knowledge, ensuring the reliability of subjective inputs through consistency checks, and is widely accepted in agricultural machinery selection⁵⁵. It has been applied in various fields like alternative selection, planning, and optimization, and its flexibility allows for integration with methods like fuzzy logic, QFD, and linear programming^56–58. AHP is widely used for multiple criteria decision-making due to its simplicity and hierarchical approach, which supports the measurement and synthesis of various components¹⁷. As a well-established MCDM method, AHP provides objective mathematics and logic to address subjective preferences, making it ideal for tractor selection through a multi-level hierarchy of goals, criteria, and alternatives. The process involves building a preference matrix, ensuring consistency, and calculating criteria weights that sum to 100% ^59,60.

Expert participation: governmental service providers

The questionnaire used to evaluate the tractor selection criteria was distributed to forty-two governmental service providers in the Egyptian Delta. These governmental service providers have extensive experience in agricultural machinery, particularly tractors, as they are responsible for maintaining, operating, and managing tractors on small-scale farms. Their practical knowledge of tractor performance, operational costs, and maintenance requirements provided crucial insights into the decision-making process. The expertise of the service providers is particularly relevant for this study, as they work directly with small farmers and have firsthand knowledge of the challenges and needs related to tractor use in the region. By relying on their practical experience, the study ensured that the selected criteria reflect the real-world considerations of small-scale farming operations. The service providers survey was distributed among the Egyptian Delta governorates, and the criteria were defined. These criteria were technical parameters such as power, tank capacity, overall width, and weight of the tractor, as well as economic criteria such as price and environmental criteria such as fuel consumption at operating power, as shown in Table 2.

Table 2.

AHP goal and criteria description.

AHP model goals	Select the appropriate tractor for agricultural production in the small farms of the Egyptian Delta
Serial Number	Criterion	Attributes
C1	Power (HP)	Power is the power available at the flywheel of the engine
C2	Overall width (mm)	The width of the tractor from the outer wheels
C3	Tractor weight (kg)	The total weight of the tractor without any attachment
C4	Fuel consumption (L/h)	The fuel consumption in units of L/h, in the same forward speed and same conditions for all tractors
C5	Price (USD $)	The price in the same year and market
C6	Maintenance costs and spare parts	Evaluation of available spare parts and their cost
C7	Fuel tank capacity (L)	The capacity of the fuel tank with the same fuel type
C8	Agrotechnical clearance (mm)	The agrotechnical clearance effect on tractor operations
C9	least turning radius (m)	The least turning radius for the tractor on the head of the field

*Note: The criteria were evaluated by a panel of forty-two governmental service providers with extensive practical experience in tractor operation, maintenance, and selection for small-scale farms.

The criteria presented in Table 2were selected based on a combination of expert input and a thorough review of relevant literature in the field of agricultural machinery selection. Experts in agricultural engineering were consulted to ensure that the chosen criteria reflect the practical needs of small-scale farms in the Egyptian Delta, where factors such as price, power, and maintenance costs play a crucial role in tractor selection²⁴. Additionally, criteria such as tractor dimensions, fuel consumption, and operational weight were chosen due to their direct impact on the maneuverability and efficiency of tractors in small land areas. These criteria align with established principles in agricultural mechanization, which emphasize the need to select cost-effective and technically suitable machinery for the terrain and farm size. This combination of expert input and literature-backed criteria ensures that the evaluation process addresses small farms’ specific constraints while also reflecting broader trends in tractor selection methodologies⁶¹.

The alternative tractor was also defined from the farms’ survey and forty-two governmental service providers with expertise, skills, and knowledge in the field of agricultural engineering and spread on the Egyptian Delta governorate in addition to governorates statistics and the different alternative tractor was shown in Table 3.

Table 3.

The criteria and alternatives.

Criteria No.	First Tractor (T1)	Second Tractor (T3)	Third Tractor (T3)	Fourth Tractor (T4)
C1 (HP)	64	60	63	56
C2 (mm)	2010	2050	1970	1830
C3 (kg)	2710	2940	4800	2940
C4 (L/h)	7	10	9	7
C5 (USD $)	36,808	12,390	28,196	30,433
C6	4	5	3	4
C7 (L)	90	78	135	60
C8 (mm)	420	350	560	400
C9 (m)	3.6	3.5	3.9	3.5

In the AHP flowchart (Fig. 3), the initial step of the decision-making process involves formulating the decision problem as a hierarchical framework, where the top level represents the goal or objective. The middle levels entail identifying and selecting criteria and decomposing the problem into a systematic hierarchical structure, resulting in a model of decision alternatives. Once the hierarchical framework is established, pairwise comparison matrices are created using empirical information and data that reflect the judgments of decision-makers and experts regarding the relative importance of each indicator compared to others.

Fig. 3.

The overall AHP Model structure (AHP tree).

The intensity or level of significance of the contrasted criteria is expressed on a scale from one to nine. Concerning the other criteria, a value of one denotes “equal importance,” and a number of nine denotes “great importance.” Table 4. illustrates this approach. To make sure the findings are coherent, a consistency check is done. Decision makers should review and revise the pairwise comparisons if the consistency ratio rises beyond the threshold (10%). In order to ascertain the priority of criterion ratings and alternative performances, each comparison matrix is solved during the synthesis and prioritizing phase by computing an eigenvector value.

Table 4.

The scale of pairwise comparison

Numerical amount	9	7	5	3	1	2, 4, 6, 8
Preferences (oral judgment)	Extreme	Very Strong	Strong	Moderate	Equal	Intervals between strong preferences

Four alternatives of tractors with different power levels (55 to 95 hp) were selected for the appropriate tractor, which is common in small farms in Egypt with less than two hectares. Experts were asked to indicate the importance of each criterion within the specified range for each criterion, following Saaty’s scale (Table 4.), and these pairwise judgments were collected^59,60. The gathered information is then processed using the AHP method.

The AHP methodology involves determining the priority weights of a set of criteria or alternatives based on a square matrix of pairwise comparisons, denoted as A = [a_ij], which is positive. In an ideally consistent paired comparison judgment, the matrix is reciprocal, meaning a_ij = 1/a_ji for all ij = 1, 2, 3 … n.

The normalized weight of the i-th factor, w_i, can be calculated using Eq. (1):

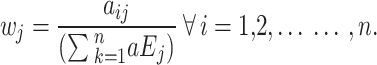1

A certain level of inconsistency is expected and tolerated since comparisons are subjective and based on personal preferences. Furthermore, individuals’ decisions and preferences can be intransitive and inconsistent, which may affect the calculation of the criteria eigenvector. To mitigate this, a consistency check is performed to validate the judgments and ensure the consistency of the calculated weighted values. The consistency ratio (CR) is a valuable feature of the AHP method⁶³ and is used to measure the level of consistency among the pairwise comparisons. The weights are considered consistent when the resulting CR is below 10% ⁵⁹. The CR is calculated as follows:

• i)First, the maximum eigenvalue 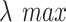of the matrix A is determined using Eq. (2):

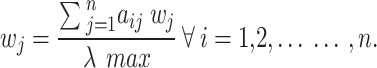2

• ii)The consistency index (CI) is calculated by Eq. (3):

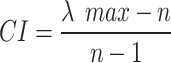3

• iii)Finally, Eq. (4) is used for estimating the CR:

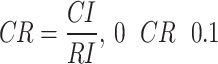4

Table 5 provides the consistency index (random index - RI) for randomly generated reciprocal matrices of various sizes from scales one to nine⁶⁴.

Table 5.

The random matrixes for incompatibility index.

Matrix order	1	2	3	4	5	6	7	8	9	10
RI	0.00	0.00	0.58	0.9	1.12	1.24	1.32	1.41	1.45	1.45

The consistency ratio (CR) is calculated as CR = CI/RI, where RI is a function of the matrix size. An acceptable limit for CR is CR < 0.01; otherwise, adjustments and revisions are needed. Another aspect of the hierarchy is synthesizing the judgments across the hierarchy to compute the overall priorities of alternatives relative to the goal. The weights are determined by aggregating the priority of each element according to a particular criterion with the weights assigned to that criterion.

The alternative comparisons in AHP

In the AHP, comparisons of alternatives involve pairwise comparisons of criteria and alternatives⁵⁹. This technique is widely used and requires comparing each unique pair of criteria and alternatives. Based on the measured values of the respective criteria (both objective and subjective), decision-makers make pairwise comparisons to achieve the research objective. These comparisons are used to determine criteria weights and performance scores for decision options. Various scaling systems can be employed, and in the AHP, decision-makers are asked to express their preference for one criterion/option over another on a nine-point scale.

Agglomerative hierarchical clustering

Three crucial issues must be considered when analyzing data for agglomerative hierarchical clustering. The visual inspection of the dendrograms was used to explain the clustering criteria for selecting the appropriate tractor⁶⁵.

1.  Selecting a distance measurement

2. Selecting the metric for linking

3. Establishing the number of clusters

The object’s pairwise distances are specified by distance metrics. To calculate the distances between the samples, square Euclidean distances were utilized. Transforming variable values as part of the data preprocessing yields average zero or Z scores and standard deviation. From zero (greater similarity) to twenty-five are the dendrogram similarity scales generated by the Origin 2024b algorithm (lower similarity). The similarities between the examined samples were shown on each restaurant’s dendrogram⁶⁶.

ML approach for criteria reduction

The significance of each criterion was assessed, and the most crucial ones were chosen using the hierarchical agglomerative clustering technique. Hierarchical clustering is an unsupervised ML algorithm that groups unlabeled datasets into clusters. The most common type of hierarchical clustering is agglomerative clustering, which groups objects into clusters based on similarity. The algorithm initially treats every object as a distinct cluster, which then gradually merges pairings of clusters until every object is combined into a single, sizable cluster. A dendrogram, or depiction resembling a tree, is produced by this technique. Three crucial issues must be considered when analyzing data for agglomerative hierarchical clustering: Selecting a distance measurement, selecting the metric for linking, and establishing the number of clusters. This study initially employed nine criteria, and the AHP approach was used to determine each criterion’s weight. The weights of those criteria were then used to determine the importance of each criterion and reduce those criteria using hierarchical agglomerative clustering.

The criteria reduction process employed in this study utilized hierarchical clustering, an effective unsupervised ML technique. Hierarchical clustering allows for grouping similar items based on their characteristics, facilitating the identification of the most relevant criteria for tractor selection. We used agglomerative hierarchical clustering to reduce the nine criteria to the three most important ones. For our analysis, we measured the similarity between the criteria using Euclidean distance, which quantifies the distance between pairs of criteria based on their attributes. This distance metric is particularly suitable for assessing criteria that can be expressed in continuous numerical forms. We applied Ward’s method for linkage, which is a strategy that minimizes the total within-cluster variance. This method effectively groups criteria in a way that preserves the integrity of their relationships, ensuring that the clusters formed are representative of the underlying data structure^67–69. To validate the reliability of the reduced criteria, we implemented a consistency check by calculating the Consistency Ratio (CR)⁷⁰. This ratio is critical in MCDM frameworks such as the AHP. Our analysis ensured that the CR remained below the threshold of 0.1, confirming that the pairwise comparisons used in determining the criteria weights were sufficiently consistent and reliable. Implementing these methodological steps strengthens the robustness of our criteria reduction process and enhances the overall reliability of the decision-making framework established in this study.

Results and discussion

Stage one: the pairwise comparison matrix analysis

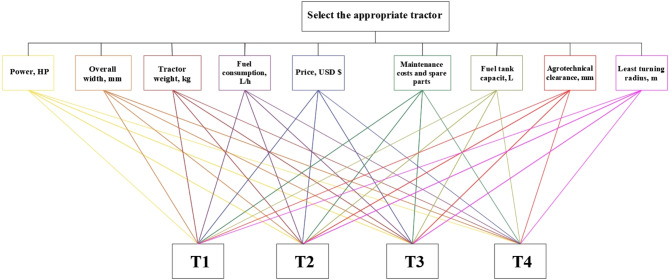
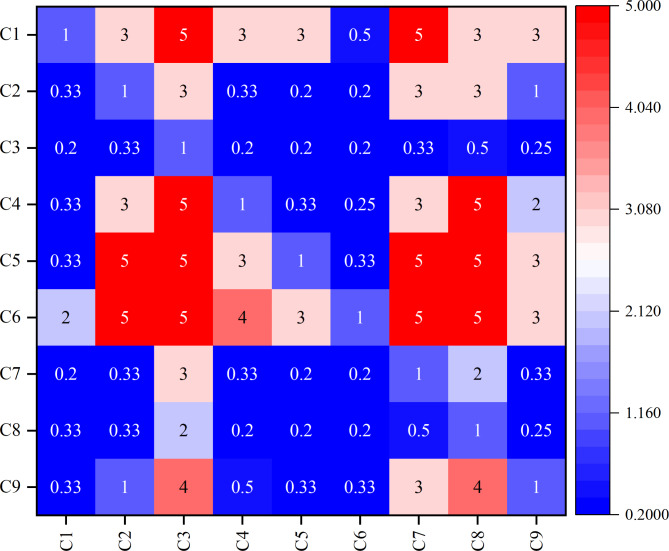
Analyzing the problem using a hierarchical framework with the criteria in the middle, the options at the bottom, and the ultimate aim at the top is the first step in the AHP. This study’s main objective is to find the ideal tractor for agricultural productivity on the small farms in the Egyptian Delta. At the summit of the analytical hierarchy was the overarching goal, “Select the suitable tractor.” The key elements for assessing the target are the following: agrotechnical clearance (C8), least turning radius, power (C1), overall width (C2), tractor weight (C3), fuel consumption (C4), price (C5), maintenance costs and spare parts (C6), fuel tank capacity (C7), fuel consumption (C6), and least turning radius (C9). Four alternative tractors (T1, T2, T3, and T4) are positioned at the bottom of the AHP model and evaluated for each criterion to achieve the aim. Using the AHP model, experts can break down complex problems into a hierarchy of goals, criteria, and options based on the decision-makers’ points of view. Figure 4 displays a comprehensive pairwise comparison heatmap with nine sets of paired comparisons.

Fig. 4.

Pairwise comparison matrix.

Decision-makers and academic experts examine the weights of the nine criteria. These results also assess the stability of tractor selection decisions when the criteria weights are altered⁴⁴. The analysis aims to select appropriate tractors for small plots of land in the Egyptian Delta. The results are expressed as integer values ranging from one (indicating equal importance) to nine (representing significantly different degrees of importance). A higher number indicates that the chosen criteria are considered more important compared to other criteria.

Stage two: criteria weight and synthesis of the AHP model analysis

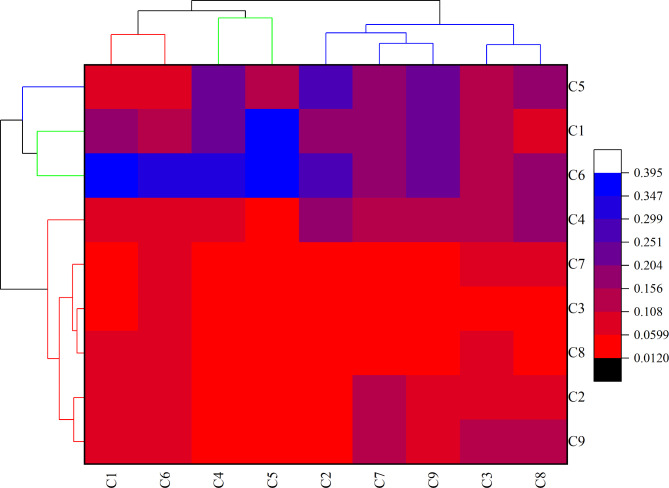
The hierarchical clustering Heatmap shows the relationship between the criteria in the matrix, as illustrated in Fig. 5. This shows the connection of all criteria used to select the appropriate tractor and their respective significance to each other. The normalized values between the criteria are expressed in different color shades, as shown in Fig. 5. The blue area indicates the high-effect criteria for selecting the appropriate tractor. In the main hierarchical clustering, the first high-effect cluster was between C1 and C6, and the second cluster was between C4 and C5. then, that hierarchical clustering was collected between C1, C6, C4, and C5. The blue color map confirmed the clustering value; the blue area indicates the high effect criteria for selecting the appropriate tractor.

Fig. 5.

A hierarchical clustering Heatmap analysis between nine criteria.

As in Eqs. (3 and 4), the aforementioned matrix’s consistency ratio (CR) is employed to look for differences. The number of criteria evaluated determines the experimental value of the random index. Table 6 displays the synthesis findings of the AHP model. The results showed that the highest-effect criteria for choosing a tractor are maintenance costs and spare parts (C6), with a weight factor of 0.2643, as shown in Table 6. These results agreed with those of Durczak et al⁷¹., who said that reliability, which is related to maintenance and failure rate, was the most important criterion. In another study, maintenance and repair costs were the main factors in the optimum selection for appreciating farm mechanization⁷².

Table 6.

Synthesis results of the AHP model.

Criteria	Criteria Weight	Weighted Sum Value	Average ʎmax
C1	0.1968	2.0859	10.6003
C2	0.0684	0.6579	9.6221
C3	0.0264	0.2508	9.5032
C4	0.1120	1.1121	9.9291
C5	0.1696	1.7788	10.4855
C6	0.2643	2.7342	10.3448
C7	0.0437	0.4077	9.3305
C8	0.0354	0.3284	9.2902
C9	0.0835	0.7961	9.5386
ʎmax			9.849373

Consistency index (C.I.) = 0.106172.

Consistency ratio (CR) = 0.073222 < 0.1 (Acceptable).

Stage three: identify high-impact criteria via ML

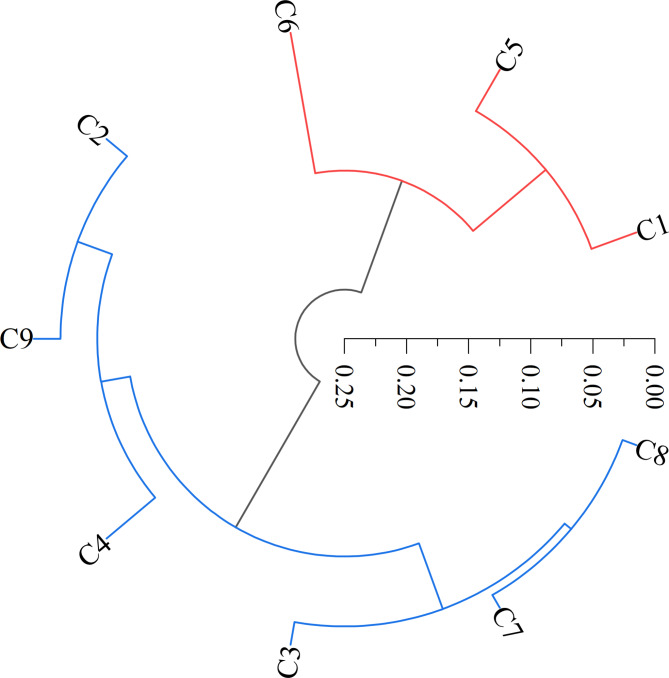
Figure 6 shows the dendrogram tree structure of all criteria. The Euclidean distances between the data points and the criteria are presented in the dendrogram plot. From the results obtained, it was found that three criteria are more important than others; the method was reused to pair using the three criteria obtained again. The obtained criteria are C1, C5, and C6.

Fig. 6.

The dendrogram of all criteria.

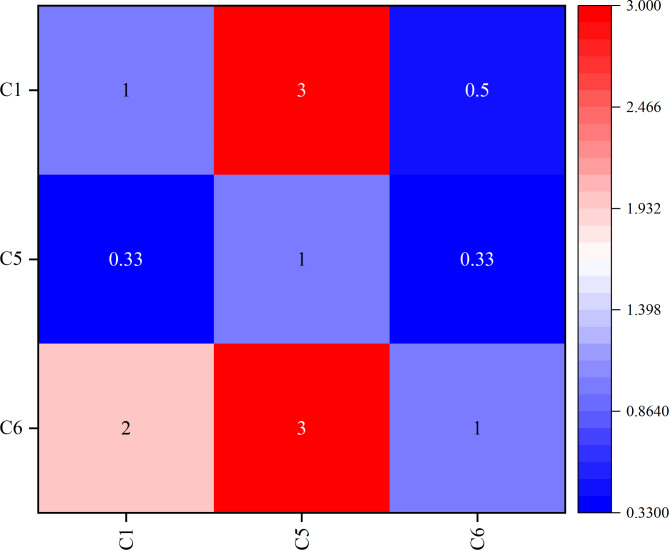
After applying the ML, the AHP pairwise comparison matrix was applied to calculate each weight of the criteria and the scale level for each indicator. A pairwise comparison is presented in Fig. 7.

Fig. 7.

Pairwise comparison matrix for three criteria.

The consistency ratio (CR) is computed for the matrix to ensure that the observations are accurate. We use Eqs. (3) and (4) to find differences. The amount of criteria that are reviewed determines the value of the random index, which is determined via experimentation. Table 7 shows the synthesis results of the AHP model.

Table 7.

The AHP model synthesis results for the three criteria.

Criteria	Criteria weight	Weighted sum value	Average ʎmax
C1	0.334	1.021	3.058366
C5	0.525	1.617	3.081683
C6	0.334	1.021	3.058366
ʎmax			3.053819

Consistency index (C.I) = 0.026909.

Consistency ratio (CR) = 0.046395 < 0.1 (Acceptable).

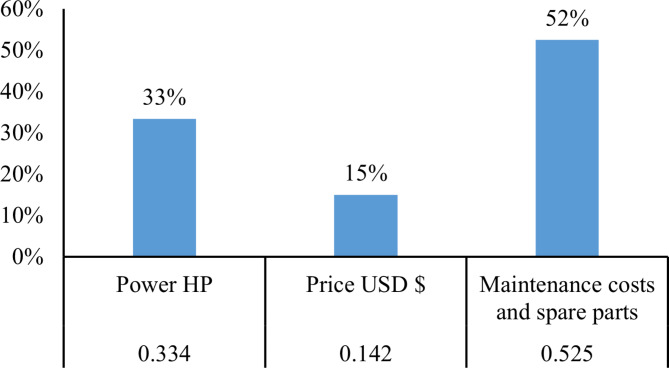
One benefit of using AHP is that it makes it simple to manage many criteria with different degrees of variance. Figure 8 illustrates the relationship between the three criteria in the matrix using a hierarchical clustering heatmap. Figure 8 displays the various color tones of the normalized values between the criteria. The criteria for choosing the right tractor with a high effect size are indicated in the blue region. In the primary hierarchical clustering, C1–C6 comprised the first high-effect cluster. Maintenance expenditures and spare components (C6) have a greater normalized weight of 0.524, or 52%, making them the highest-ranked criterion, according to AHP. The power criterion has the second-highest weight (0.334). Next, the remaining criteria were applied, which included price (0.142), as Fig. 9 illustrates.

Fig. 8.

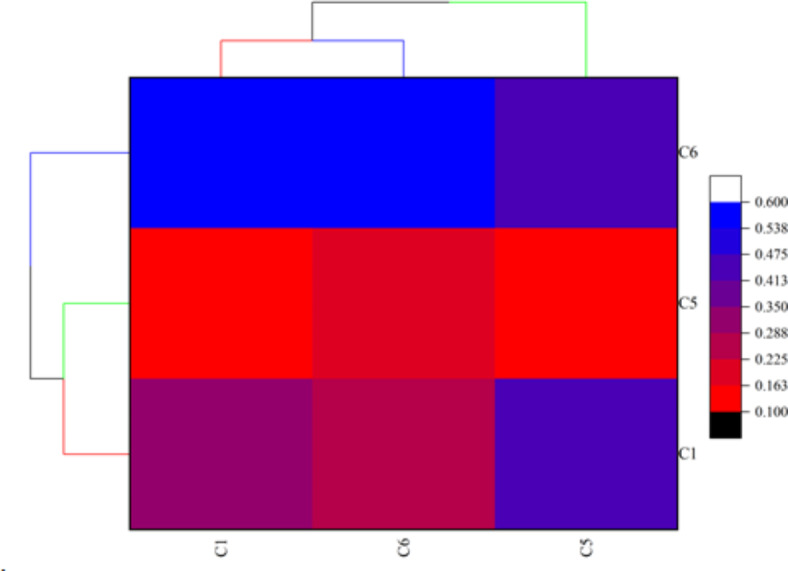
A hierarchical clustering Heatmap heatmap analysis between 4 three criteria.

Fig. 9.

The weight of different criteria.

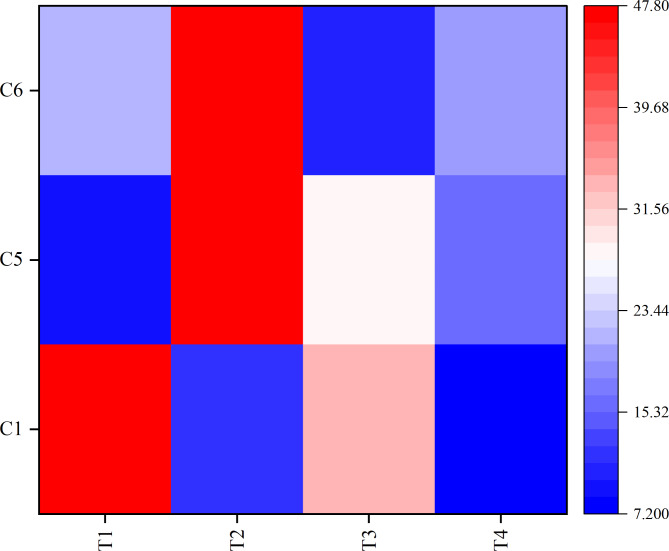
Stage four: paired comparison of tractors

Figure 10 show the heatmap performance of all selected tractors and their corresponding criterion. It’s clear that T2 has a high relationship with C6. The results of the comparison between different alternative tractors appropriate for small areas in the Egyptian Delta were the three large impact criteria in the purchase decision for maintenance costs and spare parts, power, and price. T2 ranked highest primarily due to its competitive pricing and lower maintenance costs, which are critical factors for small-scale farmers. The combination of high power also makes T2 particularly suitable for the terrain and operational needs of small farms in the Egyptian Delta. Farmers could utilize these findings to make more cost-effective purchasing decisions. The analysis revealed that T2 ranked highest among the evaluated tractors, primarily due to its strong performance across the three most important criteria: price, power, and maintenance costs. T2’s competitive pricing made it particularly appealing to small-scale farmers, for whom cost-efficiency is critical. In addition, the low maintenance costs associated with T2 further enhanced its attractiveness, as ongoing operational expenses are a significant concern for farmers in the Egyptian Delta. Another key factor contributing to T2’s superior ranking was its favorable power, which ensures efficient energy use and adaptability to the small and often challenging terrains typical of the region. This balance between power and weight allows T2 to perform a wide range of tasks without compromising fuel efficiency or operational speed, making it well-suited for small-scale farms requiring versatility in their machinery.

Fig. 10.

A hierarchical heatmap analysis between three criteria and alternative tractors.

Given these strengths, farmers can utilize T2 to improve productivity while minimizing both upfront costs and long-term maintenance expenses. The findings suggest that T2 offers a cost-effective solution for farmers aiming to optimize tractor performance in small, resource-limited farm settings. This combination of factors positions T2 as the most practical and efficient option for smallholders in the region.

Based on the AHP analysis, T2 had the highest average ranking among the selected tractors, with a percentage of 33.4%. T1 is ranked second and T3 as third, with normalized values of 28.7% and 21%, respectively, as shown in Fig. 11.

Fig. 11.

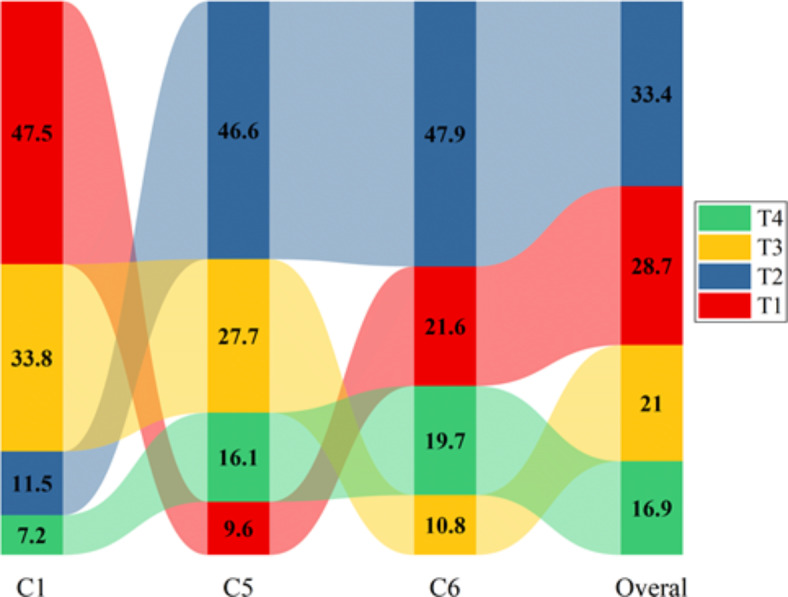
A comparison between alternative tractors under study.

Although environmental factors were initially considered in the criteria selection, the final prioritization focused on technical and economic factors that directly impact small farm operations in the Egyptian Delta. Given smallholders’ economic and technical challenges, criteria such as price, power, and maintenance costs were deemed to have the most immediate relevance. Nonetheless, the importance of environmental sustainability is fully acknowledged. Future studies will aim to integrate critical environmental metrics such as emissions and fuel efficiency into the decision-making framework. This approach will provide a more balanced evaluation that aligns with global sustainability goals and ensures that environmental considerations are adequately factored into tractor selection decisions.

While this study focuses on four tractor models commonly used in small farms in the Egyptian Delta, we acknowledge that this limits the generalizability of the findings. In future research, we aim to expand the number of tractor models and include other geographical regions to provide a broader application of the results.

While the relationships between tractor specifications, such as power, fuel tank capacity, and cost, may seem intuitive, using Multi-Criteria Decision-Making (MCDM) methods like AHP remains crucial for formalizing and quantifying these relationships in a structured manner. The selection of tractors for small farms involves multiple competing criteria—such as price, maintenance costs, power, and operational efficiency—that need to be evaluated simultaneously. Relying solely on intuition or direct correlations may overlook the trade-offs between these factors, leading to suboptimal decisions. MCDM methods allow for a systematic approach to weighting the importance of each criterion, enabling a more nuanced decision-making process. By assigning appropriate weights to factors based on their relevance to the specific farming context, AHP helps to capture the complexities of tractor selection, providing a decision framework that is both transparent and replicable. Therefore, despite the apparent direct relationships between some variables, MCDM methods are essential for ensuring that all relevant criteria are considered holistically⁷².

Conclusions

This study makes several notable contributions to the field of agricultural mechanization and decision-making for small-scale farms. First, it demonstrates the effective application of the AHP in the context of tractor selection, providing a structured, multi-criteria approach that simplifies decision-making for smallholders. Farmers are very confused when choosing agricultural tractors from among the available alternatives due to the many selection criteria for agricultural tractors, and the wrong choice of agricultural tractors may lead to problems, including disruption of agricultural operations or financial loss, etc. In order to select the best tractor among the options for small farms in the Egyptian Delta, this research combined the AHP with ML. The existing criteria were evaluated for significance based on experts’ opinions, and the results were then reviewed. Nine factors encompassing economic, environmental, and technical aspects were considered to meet the aims of sustainable development when selecting the tractor. Among the four agricultural tractors that small farms in the Egyptian Delta frequently utilize, ML technology was employed to narrow down the list of criteria to the three most crucial ones (from 55 to 95 horsepower). The results showed that the most important criterion for choosing agricultural tractors was the cost of spare parts by weight (0.525). After the criteria weighting process, the selected tractors were ranked, and T2 obtained the highest average ranking among the selected tractors, with a percentage of 33.4%, then T1, followed by T3, with percentage values of 28.7% and 21%, respectively.

In conclusion, integrating AHP and ML facilitates the appropriate selection of agricultural tractors when purchasing them. The current research method is recommended to be used to reduce the number of criteria used in selecting any agricultural machinery when purchasing it. While this study provides valuable insights into tractor selection for small farms, future research will incorporate emissions and fuel efficiency metrics to ensure a more holistic approach to sustainable tractor selection that aligns with global environmental goals. We suggest future research about application software using programming code that uses the MCDM calculation methods as the best tractor.

Author contributions

All authors wrote the original draft of the manuscript; M. A., Q. L. and H. S. used software; T. A., A. M., and M. R. data curation; All authors reviewed the manuscript.

Data availability

The manuscript data is available by the corresponding author through reasonable request.

Declarations

Conflict of interest

The authors declare no conflict of interest.