Exploring the inorganic perovskite materials Mg₃SbX₃ (Where, X=I, Br, Cl and F) through the perspective of density functional theory: Adjustment of physical characteristics as consequence of strain

Abstract

The solar technology industry has lately given inorganic perovskite materials an abundance of thought because of their unique optical, electrical and structural characteristics. Issues pertaining to lead (Pb) toxicity and instability require being referred to promptly, making lead-free atomically designed metal halide perovskites of foremost importance to the photovoltaic and optoelectronic industries. Perovskites, a class of inorganic metal halide semiconductors, have variant similarities with ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F). According to the space group Pm-3m ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) has a cubic perovskite crystal structure. Utilizing first-principles density-functional theory (FPDFT), The intention of this investigation is to analyze how strain and spin-orbit coupling (SOC) impact the structural, electrical, optical and mechanical features of the inorganic cubic perovskite of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F). At the point between R and Γ, the ${\text{Mg}}_3{\text{SbI}}_3,{\text{Mg}}_3{\text{SbBr}}_3,{\text{Mg}}_3{\text{SbCl}}_3$ molecule displays an indirect bandgap of 0.105 eV, 0.957 eV, 1.728 eV. At the Γ point, the ${\text{Mg}}_3{\text{SbF}}_3$ molecule displays a direct bandgap of 3.184 eV. The bandgaps of the ${\text{Mg}}_3{\text{SbI}}_3,{\text{Mg}}_3{\text{SbBr}}_3,{\text{Mg}}_3{\text{SbCl}}_3$ and ${\text{Mg}}_3{\text{SbF}}_3$ perovskites are 0.198 eV, 1.203 eV, 1.901 eV and 3.723 eV respectively, when considering the spin-orbital coupling (SOC) quantum influence. A wider bandgap is investigated for increasing compressive strain while a smaller bandgap is observed for increasing tensile strain. Apart from the elastic constants and anisotropic factors, other factors that are anticipated include Pugh's ratio, Poisson's ratio, bulk modulus and others. Isotropic, ductile and mechanically stable are the words that best describe these materials, according to the elastic property evaluations. In the photon energy range that is appropriate for solar cells, the dielectric constant spikes of ${\text{Mg}}_3{\text{SbX}}_3$ are found to be visible. Therefore, ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) perovskite is a good material to use in solar cells for managing light and producing electricity.

Graphical abstract

Highlights

• •The ${Mg}_3{SbX}_3$ (X = I, Br, Cl, F) compounds.
• •Mg₃SbF₃ shows direct bandgap.
• •Applying biaxial strains on these perovskites.
• •Tuning the physical properties by strain effect.

1. Introduction

Studies on organic-inorganic perovskites (OILHP) have recently skyrocketed due to its intriguing properties, such as minimal reflectivity, a fair bandgap, widespread availability, an incredible optical absorption capacity, and inexpensive production cost [[1], [2], [3]]. Researchers have started using perovskite materials because of their amazing characteristics [[4], [5], [6], [7], [8], [9]], even though CdTe, CIGS, Sb₂Se₃, FeSi₂ and CMTS solar cell arsenal have achieved great progress in the PV area [[10], [11], [12], [13], [14]]. To be more precise, Light absorption is enhanced in perovskite materials when the layer thickness is smaller than 1 μm, more so than other semiconductor-related substances [[15], [16], [17]]. Power conversion efficiency (PCE) for perovskite-like CsPbI₃ solar cells can reach 17.9 % [18] in 2022 without a hole transport layer (HTL) and 19.06 % [19] with one. Using OILHP as an association, solar cells acquired a PCE of 26.1 % in 2023 [20]. The evolution of perovskites has sped up in the last decade due to breakthroughs in their properties. A large amount of research has focused on inorganic perovskites that are composed of metal halides. Currently, there is significant concern about the OILHP's long-term durability. Humidity, wind, sunshine and temperature are just a few of the environmental variables that might drastically alter the long-term stability of these perovskites in an actual-life situation [19,[21], [22], [23]]. The upshot is that solving the transiency problem using these perovskites has grown increasingly difficult in recent times. According to earlier studies [24,25], switching out the organic cation in OILHP solar cells for an inorganic cation could resolve their heat instability and optical transiency issues. New inorganic halide perovskites outperform and outlast OILHP in terms of stability and effectiveness. Inorganic halide perovskites have almost the same band edge carrier peculiarity as the ones demonstrated by Zhu et al. [26]. The areas of solar technology, light-emitting diode (LED) technology, and semiconducting technology could benefit from inorganic cubic perovskites, which are presently being studied as direct bandgap components and possess a high optical absorption capacity [[27], [28], [29], [30]]. Inorganic halide perovskite components and solar cells made from them are anticipated to perform better than OILHP in addressing these difficulties. Power conversion efficiency (PCE) in solar cells is influenced by the bandgap of the active layer materials, which controls the amount of light absorbed and the carriers assembled. The Shockley-Queisser hypothesis implies that perovskite solar cells might accomplish a power conversion efficiency (PCE) of up to 33 % when the bandgap of the substance is set between 1.2 and 1.4 eV [31]. Inorganic lead halide perovskites are great for optoelectronic and photovoltaic usages, but their relatively large bandgap is a major drawback [32,33]. Therefore, there is an extreme need to tune the electronic bandgap using promising techniques to get the maximum PCE in ILHP solar cells. Numerous recent studies suggest that strain engineering and compositional size tampering are viable options to strengthen electrical bandgaps [[34], [35], [36], [37], [38], [39]]. Lead halide perovskites reveal band structure fragmentation and a decrease in bandgap of around 1 eV when the SOC effect is deliberated, as stated in a report [40]. Optical, electrical, and structurally exceptional A₃BX₃-type perovskite materials, including ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) perovskite, have recently garnered considerable interest in solar technology. Investigating this to determine its potential utility in solar cells and optoelectronics. The ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) perovskite, however, has not yet been the subject of adequate study. Therefore, thoroughly investigating ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) perovskites is of greatest significance.

Using density functional theory (DFT) methodology, the optical and electrical characteristics of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) are explored thoroughly in this article. The band structure and bandgap tuning process of ${\text{Mg}}_3{\text{SbX}}_3$ were thoroughly investigated. In addition, these studies determined ${\text{Mg}}_3{\text{SbX}}_3$'s loss function, dielectric function, Poisson's ratio, Bulk modulus, Pugh's ratio and absorption coefficient. By adjusting its optoelectronic features, the ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) material may be optimized for deployment in photovoltaic and optoelectronic technologies.

2. Computational details

The Perdew-Berke-Enzerhof (PBE) [41] and the FP-DFT with norm-conserving (NC) pseudopotential [[42], [43], [44]]. The perovskite structure of ${\text{Mg}}_3{\text{SbX}}_3$ was subjected to an exchange-correlation mechanism. The Quantum Espresso simulation software was supposed to produce the DFT [[45], [46], [47], [48]]. At the outset, the input data contained crystal shapes, lattice parameters, kinetic cut-off energy, and a grid of Brillouin zones. A kinetic energy cut-off of 30 Rydberg (Ry) and a charge density cut-off of 220 Rydberg (Ry) were established to optimize structures and enhance performance. A self-consistency function can be accomplished by adopting a convergence prerequisite of almost 10⁻⁶ a.u. and a maximum force tolerance of less than 0.01 eV/Å. The relaxation estimations used ∼10⁻³ a.u. as the ionic reduction force convergence threshold. The band structure and PDOS were calculated in the Brillion zone using the Monkhorst-Pack k-grid at 6 × 6 × 6. Organic halides have been identified employing functionals for the local density approximation (LDA) and the generalized gradient approximation (GGA). In this most current investigations, investigation have refrained from using corrected PBE functions for metals, even though there are methods to mitigate this problem [47,48]. Modifying the lattice parameter in this study at the same time also revealed that the biaxial strain level, in which tension and compression are both present, varies between −6% and +6 %, with 2 % increments. To find the strain, using this formula: $\mathrm{\epsilon }=\frac{{\mathrm{a}}_{\text{strained}}-{\mathrm{a}}_{\text{relaxed}}}{{\mathrm{a}}_{\text{relaxed}}}\times 100\%$. The values of $\mathrm{\epsilon }$ represent applied strain and range can fluctuate between −6% and +6 %, in increment of 2 %. ${\mathrm{a}}_{\text{relaxed}}$ denotes the optimal lattice constant and ${\mathrm{a}}_{\text{strained}}$ the strained one. Using a special formula to change the lattice parameter, ${\mathrm{a}}_{\text{strained}}$, so it could imitate biaxial compressive and tensile strain [49].

Samples of the Brillouin zone is collected for the purpose of assessing the optical features with a Monkhorst-Pack k-point grid that is Γ-centered and has dimensions of 6 × 6 × 6. Afterward, this finding determined the absorption peaks' energy range (in eV) by dissecting the intricate dielectric function. To find the dielectric function $\mathrm{\epsilon }\left(\mathrm{\omega }\right)$, just need to add the real and imaginary components of the complex dielectric function, which obtains.

$$\mathrm{\epsilon }\left(\mathrm{\omega }\right)={\mathrm{\epsilon }}_1\left(\mathrm{\omega }\right)+\mathrm{j}{\mathrm{\epsilon }}_2\left(\mathrm{\omega }\right)$$ (1)

3. Results and discussion

3.1. Structural properties

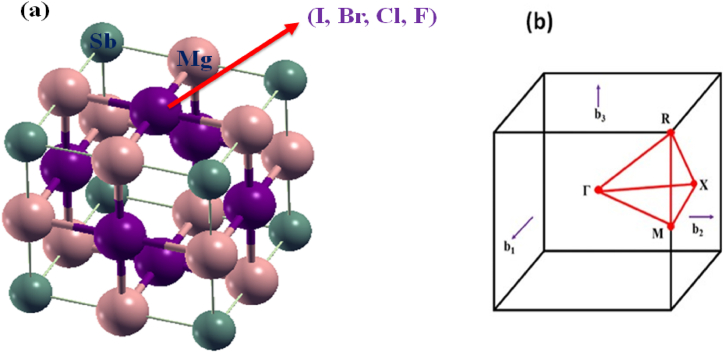
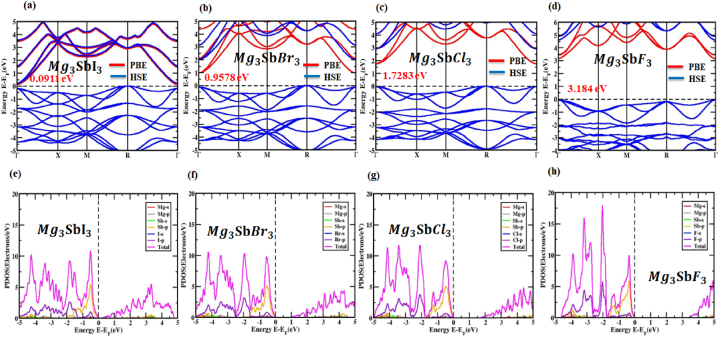
As previously mentioned, the periodic pattern of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) is the Pm-3m cubic foundation. Unit cells in buildings usually consist of seven atoms. An octahedral gap is filled with $\mathrm{X}$ atoms and the $\text{Mg}$ and $\text{Sb}$ atoms are organized in a face-centered cubic lattice in this material. The bond distances of ${\text{Mg}}_3{\text{SbI}}_3$ for $\text{Mg}$–$\text{Sb}$ and $\text{Mg}$–$\mathrm{I}$ is surveyed at 3.0060 $\mathrm{A}°$ and 3.0060 $\mathrm{A}°$, ${\text{Mg}}_3{\text{SbBr}}_3$ for $\text{Mg}$–$\text{Sb}$ and $\text{Mg}$–$\text{Br}$ is surveyed at 2.8609 $\mathrm{A}°$ and 2.8609 $\mathrm{A}°$ and ${\text{Mg}}_3{\text{SbCl}}_3$ for $\text{Mg}$–$\text{Sb}$ and $\text{Mg}$–$\text{Br}$ is surveyed at 2.7709 $\mathrm{A}°$ and 2.7709 $\mathrm{A}°$, respectively. The bond distances of ${\text{Mg}}_3{\text{SbF}}_3$ for $\text{Mg}$–$\text{Sb}$ and $\text{Mg}$–$\mathrm{F}$ are 2.5108 $\mathrm{A}°$ and 2.5108 $\mathrm{A}°$. To form $\text{SbMg}$₆ octahedra that share corners, six similar $\text{Mg}$²⁺ atoms are connected to $\text{Sb}$³⁻. There is no slanting between adjacent octahedra. The fractional coordinates of $\text{Sb}$ are (0,0,0), $\mathrm{X}$ is (0.5,0.5,0) and $\text{Mg}$ is (0,0.5,0). These coordinates follow the 1a, 3c and 3d Wyckoff sites, respectively. Fig. 1(a) illustrates the computation of structural properties and Fig. 1(b) illustrates the k-path of the first Brillouin zone (BZ) of ${\text{Mg}}_3{\text{SbX}}_3$ perovskite is required prior to calculate the different attributes of the material. Table 1 shows details about the structure that were derived from PBE, such as the lattice constant value (($\mathrm{A}°$) in Angstroms. After combining the entire quantity of energy with the lattice parameter, the most economically viable lattice constant for ${\text{Mg}}_3{\text{SbX}}_3$ was found. An estimated value of the lattice constant for ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$, ${\text{Mg}}_3{\text{SbCl}}_3$ and ${\text{Mg}}_3{\text{SbF}}_3$ compound is 6.01 $\mathrm{A}°$, 5.72 $\mathrm{A}°$, 5.54 $\mathrm{A}°$ and 5.02 $\mathrm{A}°$ [50]. Similarly, one can effectively test a building's durability using its conjunctive and production energies [6,51,52].

Fig. 1.

(a) The optimal structure of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) and (b) the k-path of the initial Brillouin zone for establishing its electronic band arrangement.

Table 1.

Investigated data and earlier DFT calculations were used to calculate the lattice constant and energy bandgap of ${\mathrm{M}\mathrm{g}}_3{\text{Sb}\mathrm{X}}_3$ (X = I, Br, Cl and F).

Structure	Lattice constant ($\mathrm{A}°$)		Bandgap Energy (eV)		Optical bandgap (eV)
	This work	Previous work	This work	Previous work	This work
Mg3SbI3	6.01	6.01 [50]	0.1057(PBE)	0.53(HSE) [50]	0.1213
			0.1921(HSE)	0.186(PBE) [77]
Mg3SbBr3	5.72	5.72 [50]	0.9578(PBE)	1.58(HSE) [50]	0.9630
			2.0178(HSE)	1.097(PBE) [77]
Mg3SbCl3	5.54	5.54 [50]	1.7283(PBE)	2.43(HSE) [50]	1.7243
			2.9183(HSE)	1.655(PBE) [77]
Mg3SbF3	5.02	5.02 [50]	3.184(PBE)	4.88(HSE) [50]	3.2019
			4.604(HSE)	3.460(PBE) [77]

We observe that the when the biaxial compression is applied then the lattice parameter and the volume of the material ${\text{Mg}}_3{\text{SbX}}_3$ is changing. When the compressive strain is increasing the lattice parameter value is decreasing, and for tensile strain increasing then lattice parameter value is increasing for ${\text{Mg}}_3{\text{SbX}}_3$ perovskite, that displayed in Fig. S1(a). Similarly, when the compressive strain is increasing the volume is decreasing, and for increasing tensile strain then volume value is also increasing, this illustrated in Fig. S1(b).

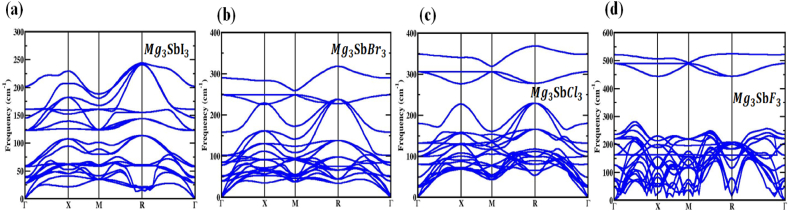
The association between momentum and phonon energy is described by using the term "phonon dispersion" when addressing phonons in a crystal lattice. As they traverse a material, phonons, which are quantized vibrations of its lattice, influence its mechanical and thermal attributes. During the phonon estimation, the lattice volume and atomic positions are entirely relaxed [53,54]. The initial Brillouin zone, along the high-symmetry domains Γ-X-M -R-Γ, shapes the phonon band of the ${\text{Mg}}_3{\text{SbX}}_3$ molecule. At unstaring Fig. 2, the dispersion mapping, must be analyzed to figure out the ongoing stability of the substance. This map validates that the evolving matrix excludes any negative frequencies for proximity. For different compressive and tensile strain of ${\text{Mg}}_3{\text{SbX}}_3$ structure is illustrated in Fig. S(2, 3, 4, 5), from this we observe that for compressive strain the material is stable and for tensile the material tens to unstable.

Fig. 2.

The Phonon band structure of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) compound, where there in strain is applied.

3.2. Charge density

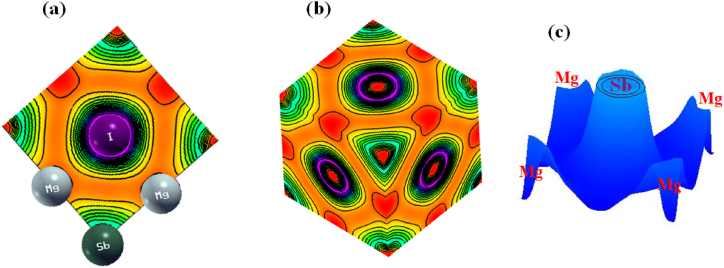
Electronic charge density analysis is a crucial component of electronic characteristic analysis. An easy way to visualize the relationship between the charge concentration in a structure's unit cell and the valence electrons' density is to use this feature. When studying molecular bonding, it is common practice to look at the total electronic charge density map. Atomic structures that make up illustrates density curve typically illustrate the role that orbital electrons play in the electrical features of atoms through the accumulation of charges. The differentiated color density map, which also considers the charge contributions of the elements, is subsequently employed to correlate the electronic DOS spectra of the individual elements. Fig. 3(a) shows a two-dimensional representation of the charge density in ${\text{Mg}}_3{\text{SbX}}_3$ with respect to the (200) crystallographic plane. The charge density is shown in Fig. 3(c) from an aerial view, or top-down perspective. Viewed from this angle, the distribution of charges surrounding atoms of different concentrations becomes readily apparent. From a three-dimensional viewpoint, the distribution of charges is shown in Fig. 3(b). Different colors are used to represent high and low intensity, respectively.

Fig. 3.

The distribution of electronic charges in ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) (a) A two-dimensional depiction of the (200) plane, (b) A three-dimensional viewpoint and (c) An aerial view.

The regular distribution of charges and the tendency for positively charged particles to congregate around the $\text{Mg}$ atom is both readily apparent. So many negative charges were surrounding the $\mathrm{X}$ atom. The charge density map makes it impossible to differentiate the $\text{Sb}$ atom from the $\text{Mg}$ atom due to the overlapping charges of the two atoms. This led to the formation of a covalent link between the ions $\text{Mg}$ and $\text{Sb.}$ The charge distribution map added to the evidence that the ions have formed an ionic connection since the $\mathrm{X}$ and $\text{Mg}$ ion charge patterns were found to be non-coincidental [18,55]. $\text{Mg}$ and $\text{Sb}$ ions form a weaker link through covalent bonding, however, the binding strength within the structural unit is enhanced by the ionic bonding approach. Contrarily, $\text{Sb}$ and $\mathrm{X}$ do not bond.

3.3. Electronic properties

The major factors that determine the electrical characteristics of a substance are its band structure, charge density and density of states (DOS) [56]. For ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) perovskite structures the high equipoise directions and electronic band attributes have been anticipated. An electronic band framework of the ${\text{Mg}}_3{\text{SbX}}_3$ framework is demonstrated in Fig. 4(a, b, c, d). Fermi levels have been set to zero in studies to facilitate the analysis of the bandgap value. The k-axis is taken for consideration alongside the Γ, X, M, R and Γ in the cubic structure. Fig. 4(a, b, c, d) reveals the conduction band minimum (CBM) and valence band maximum (VBM), which are located between the Γ and R points for the ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$, ${\text{Mg}}_3{\text{SbCl}}_3$ materials, indicating an indirect bandgap and at point Γ for the ${\text{Mg}}_3{\text{SbF}}_3$ compound, indicating a direct bandgap. This approach unveils the indirect bandgap structure of the ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$, ${\text{Mg}}_3{\text{SbCl}}_3$ materials, with estimated values of around 0.105 eV, 0.9578 eV and 1.7283 eV, respectively. The observed ${\text{Mg}}_3{\text{SbF}}_3$ material also has a direct bandgap, with an estimated value of about 3.184 eV, as shown by the function. In most cases, while evaluating the GGA approach, the norm of the bandgap is underestimated. The bandgap value is understated in the LDA + U and LDA techniques, respectively. This issue with bandgap estimates can be circumvented by the methods developed by the researchers, who have included the hybrid functional and the GW methodology. There are benefits and drawbacks to these methods, but overall, they work. In cases when the bandgap values predicted theoretically and those obtained investigation do not match, even using the GGA + U technique, the gap is only partially filled. The PBE approach yielded the expected results, and bandgap and band arrangement alterations caused by strain were determined to have no functional relationship, as determined by a recent findings by Nayak et al. [57]. As a result, it appears that the PBE/GGA mechanism is an excellent option for materials strain testing. Photovoltaic, optoelectronic and photothermal applications are best served by crystalline materials having a direct bandgap [[58], [59], [60], [61]].

Fig. 4.

(a, b, c, d) electronic band structure and. (e, f, g, h) partial density of states (PDOS) with the ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) arrangement PBE function without the presence of SOC.

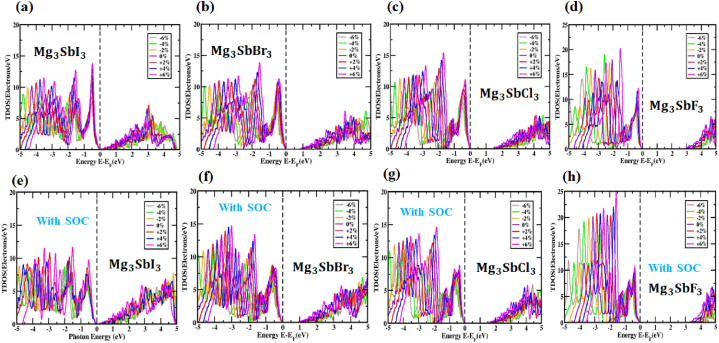
To comprehend the effects of specific atomic states on the bandgap energy in ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) structures, the partial density of states (PDOS) could be a useful tool. Fig. 4(e, f, g, h) displays the PDOS distribution for the ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$, ${\text{Mg}}_3{\text{SbCl}}_3$ structures in the energy fluctuation range of −5 to +5 eV and ${\text{Mg}}_3{\text{SbF}}_3$ structures in the energy fluctuation range of −4 to +6 eV. The hybridization of the $\text{Mg}$ and $\text{Sb}$ states in ${\text{Mg}}_3{\text{SbX}}_3$ with X (I, Br, Cl and F) extends over the full energy range, with the bandgap intact. Additional evidence that the main covalent bonds between $\text{Mg}$–$\mathrm{X}$ and $\text{Sb}$–$\mathrm{X}$ indeed exist is provided by this. ${\text{Mg}}_3{\text{SbX}}_3$ is where electron transfer from $\text{Mg}$, $\text{Sb}$ and $\mathrm{X}$ takes place because their atomic states are very different. Atoms of magnesium contributed essentially nothing close to the edge of the band because their states were so far from the Fermi level. Findings observed that the p orbitals of $\mathrm{X}$ and $\text{Mg}$ had a significant impact on the conduction band (CB) after studying ${\text{Mg}}_3{\text{SbX}}_3$ in its cubic grade, whereas the $\text{Sb}$-p orbital controlled the valence band (VB).

3.4. The effect of SOC on electronic structure

The impact of SOC on the electrical characteristics of the ${\text{Mg}}_3{\text{SbX}}_3$ perovskite was considered in these investigations by accounting for the SOC-containing Hamiltonian equation [62].

$${\mathrm{H}}_{\text{soc}}=\frac{\mathrm{ħ}}{4{\mathrm{m}}_0{\mathrm{c}}^2}(\overrightarrow{\mathrm{F}}\times \overrightarrow{\mathrm{p}})\cdot \overrightarrow{\mathrm{s}}\text{.}$$ (2)

The Hamiltonian operator for SOC is denoted as H_soc, where ħ is the reduced Planck's constant, p⃗ is the orbital angular momentum, F⃗ is the potential energy or force, ${\mathrm{m}}_0$ is the mass of free electrons and s⃗ is the spin angular momentum.

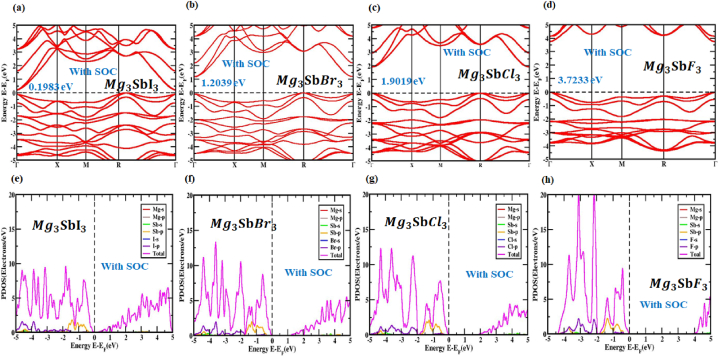
The amplitude of the relativistic effect and the relativistic impacts on the electronic structures of ${\text{Mg}}_3{\text{SbX}}_3$ perovskites that contain SOC were computed using the PBE functional technique in these findings, as well as on the effects of heavy elements $\text{Mg}$ and $\text{Sb}$. As seen in Fig. 5(a, b, c, d), the CBM and VBM locations were altered because of the profound impact of SOC on the conduction and valence band regions. The orbit's spin momentum is denoted by s and its angular momentum by l in this case. Between |l - s| and |l + s|, the total angular momentum, j, might fluctuate. Theoretically, molecular orbital s-orbitals have l = 0 and 1/2, p-orbitals have l = 1/2 and 3/2 and d-orbitals have l = 2 and 3/2 and 5/2. Each orbital is given a spin value between +1/2 and −1/2. It is clear from Fig. 5(a, b, c, d) that SOC is responsible for the discernible shift in the positions of the valence band and conduction band components. While the CBM shifted upwards close to the Fermi level, the VBM shifted downwards by a large margin. The direct bandgap of ${\text{Mg}}_3{\text{SbF}}_3$ is 3.723 eV, which is generated by the SOC impact and the indirect bandgap energy values of ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$ and ${\text{Mg}}_3{\text{SbCl}}_3$ are 0.198 eV, 1.203 eV and 1.901 eV, respectively. Table 2 displays the bandgap energies of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) perovskites that were affected by and those that were not affected by SOC. A better understanding of the band structure of cubic ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) was achieved by assessing the related PDOS with the SOC impact. As seen by the PDOS in Fig. 5(e, f, g, h), the preponderance of $\text{Mg}$ atoms do not follow a continuous trend when SOC is added. At high symmetry points, $\text{As}$-2p separates into two sections, j = 1/2 (in p) and j = 0 (in p), but the eventual band is unaffected by this SOC effect.

Fig. 5.

The electronic band arrangement (a, b, c, d) and PDOS (e, f, g, h) of the unstrained inorganic perovskite structure for the optimized ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) with SOC.

Table 2.

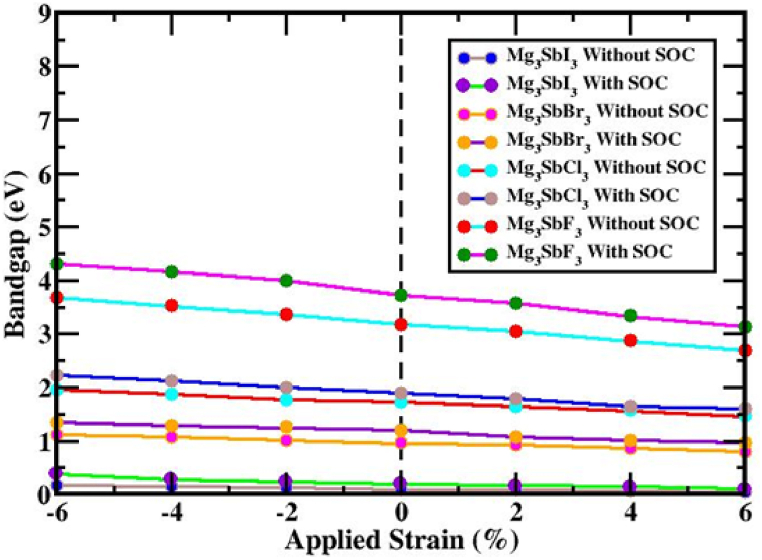
The bandgap of cubic ${\mathrm{M}\mathrm{g}}_3{\text{Sb}\mathrm{X}}_3$ (X = I, Br, Cl and F) perovskite under various compressive and tensile loads was computed.

Applied Strain (%)	Mg3SbI3				Mg3SbBr3				Mg3SbCl3				Mg3SbF3
	Compressive		Tensile		Compressive		Tensile		Compressive		Tensile		Compressive		Tensile
	Without SOC	With SOC	Without SOC	With SOC	Without SOC	With SOC	Without SOC	With SOC	Without SOC	With SOC	Without SOC	With SOC	Without SOC	With SOC	Without SOC	With SOC
0	0.105	0.198	0.105	0.198	0.957	1.203	0.957	1.203	1.728	1.901	1.728	1.901	3.184	3.723	3.184	3.723
2	0.126	0.237	0.084	0.170	1.010	1.253	0.918	1.066	1.775	2.001	1.649	1.784	3.360	3.997	3.044	3.570
4	0.141	0.281	0.058	0.148	1.072	1.275	0.860	1.003	1.880	2.128	1.568	1.642	3.521	4.156	2.871	3.333
6	0.171	0.387	0.044	0.102	1.119	1.345	0.809	0.961	1.963	2.22	1.464	1.607	3.679	4.309	2.689	3.134

3.5. Strain-induced electronic properties

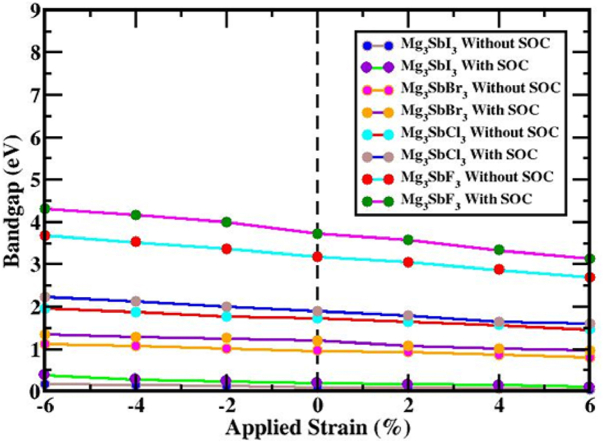
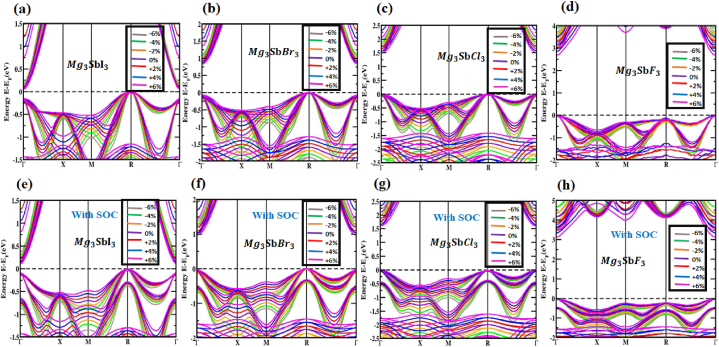
Before and after the strain was applied, in percentage terms, under tensile and compressive loads, respectively, this study investigated the ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) configuration and how spin-orbit coupling (SOC) affected it. Compression and tension strains can be measured with a 2 % increment, covering a range of −6% to +6 %. The valence band maximum (VBM) and conduction band minimum (CBM) of the ${\text{Mg}}_3{\text{SbX}}_3$ layout moved toward the Fermi energy spectrum under compressive strain (−6%–0 %), but they stayed at the R and Γ (Gamma)-point for the ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$ and ${\text{Mg}}_3{\text{SbCl}}_3$ compound, as well as the Γ-point for the ${\text{Mg}}_3{\text{SbF}}_3$ materials shows Fig. 6(a, b, c, d). A direct bandgap exists at the Γ-point despite the effects of the SOC and an indirect bandgap is established between the R and Γ points. The band configurations of the ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) framework, controlled by compressive strain and considering the influence of SOC, are shown in Fig. 6(e, f, g, h). Regardless of how it looked or how much attention it received from the SOC effect, orbital overlap strengthened the bonds between $\text{Mg}$, $\text{Sb}$ and $\mathrm{X}$. There was the formation of an indirect bandgap between the R and Γ points and a direct bandgap at the Γ point; this gap might be analyzed with or without SOC. Induced tensile strain spanning from 0 % to +6 % impacts the arrangement of the electrical bands of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) perovskite, as illustrated in Fig. 6(a, b, c, d). The band configurations in the ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) construction during tensile stress, incorporating the SOC effect, are also shown in Fig. 6(e, f, g, h). As the VBM and CBM diverge from the Fermi energy spectra, tensile strain is observed to cause a decrease in the bandgap. Both compressive and tensile strains impact the structure of the ${\text{Mg}}_3{\text{SbX}}_3$ which consequently impacts the structure of the electrical band. Fig. 7 and Table 2 detail the changes in bandgap for the ${\text{Mg}}_3{\text{SbX}}_3$ structure when compressed and exposed to strains ranging from −6 to +6 percent of the input strain, the bandgaps of ${\text{Mg}}_3{\text{SbI}}_3$ varied from 0.171 to 0.044 eV (except SOC) and 0.387 to 0.102 eV (including SOC); ${\text{Mg}}_3{\text{SbBr}}_3$ varied from 1.119 to 0.809 eV (except SOC) and 1.345 to 0.961 eV (with SOC); ${\text{Mg}}_3{\text{SbCl}}_3$ varied from 1.963 to 1.464 eV (except SOC) and 2.22 to 1.607 eV (including SOC); and ${\text{Mg}}_3{\text{SbF}}_3$ varied from 3.679 to 2.689 eV (except SOC) and 4.309 to 3.134 eV (together with SOC) respectively. The fact that the direct bandgap properties of ${\text{Mg}}_3{\text{SbF}}_3$ and the indirect bandgap properties of ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$ and ${\text{Mg}}_3{\text{SbCl}}_3$ stay unchanged over the entire applied strain limit is quite remarkable It implies that these structures might be possible to boost solar cell efficiency by using the Shockley-Queisser formula's stated principles.

Fig. 6.

The electronic bands of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) are calculated utilizing (a, b, c, d) compressive and tensile strains integrating without SOC effect and (e, f, g, h) compressive and tensile strains incorporating using SOC impact.

Fig. 7.

The energy bandgap of the ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) structure shifts when strain is applied in addition to the effects of both SOC and without SOC.

Additionally, the strain effort changes the number of ${\text{Mg}}_3{\text{SbX}}_3$ atoms engaged in the orbit. Fig. S6–9 show the PDOS for ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$ and ${\text{Mg}}_3{\text{SbCl}}_3$ and ${\text{Mg}}_3{\text{SbF}}_3$ under compressive and tensile stresses, respectively. The PDOS for ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$ and ${\text{Mg}}_3{\text{SbCl}}_3$ and ${\text{Mg}}_3{\text{SbF}}_3$ compound under SOC effect the compressive and tensile stresses are demonstrated in Fig. S10,11,12,13. As a result of the strain's cyclical variation between −6% and +6 %, the PDOS bonded to the $\mathrm{X}$ atom's 2p orbital moved into the valence band and settled below the Fermi level. The 3p orbitals of atoms have the greatest impact on the total DOS in the conduction band. The overall DOS impression changes from −6% to +6 % as the changed strain develops, although the 3p orbital of the $\text{Sb}$ atom remains unchanged, the occupied DOS is side structured in the conduction band. In conduction band space, the $\text{Sb}$ atom's 3p orbital has a significant impact on the total density of states (TDOS). With strain increments ranging from −6% to +6 %, taking the SOC impact into account improves TDOS's overall performance. When the influence of SOC is considered, the overall density of states (DOS) of the ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) material changes. In Fig. S6–9, the partial density of states (PDOS) without SOC effect in ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$ and ${\text{Mg}}_3{\text{SbCl}}_3$ and ${\text{Mg}}_3{\text{SbF}}_3$ material is about 7.82 electrons/eV, 8.77 electrons/eV, 10.10 electrons/eV and 14.09 electrons/eV at −6% strain to roughly 14.16 electrons/eV, 14.24 electrons/eV, 14.49 electrons/eV and 20.42 electrons/eV at +6 % strain. When the SOC influence is considered, as exhibited in Fig. S10,11,12,13 the partial density of states (PDOS) in ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$ and ${\text{Mg}}_3{\text{SbCl}}_3$ and ${\text{Mg}}_3{\text{SbF}}_3$ material changes from about 8.31 electrons/eV, 9.71 electrons/eV, 10.63 electrons/eV and 17.87 electrons/eV at −6% strain to roughly 11.82 electrons/eV, 14.70 electrons/eV, 14.74 electrons/eV and 25.41 electrons/eV at +6 % strain. Total density of states (TDOS) of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) under various biaxial compressive and tensile strain levels, the absence in Fig. 8(a, b, c, d) and presence in and Fig. 8(e, f, g, h) of SOC, and as impacted by SOC, in Fig. 8 exhibits the same data. By studying the TDOS, findings may have a better thinking of the impacts of the electrical band structure of ${\text{Mg}}_3{\text{SbX}}_3$. The material's bandgap and semiconductor nature are strongly supported by the fact that no DOS line is observed around the Fermi level. Earlier work by Nayak and colleagues [63,64] demonstrated that pressure modification significantly impacted the bandgap value and band arrangement of MoS₂. Using any exchange-correlation function yielded the same result. That is, regardless of the presence or absence of the SOC impact, compressive stresses ranging from 0 % to −6% cause the TDOS line to develop to the Fermi level, resulting in enhanced conductivity in ${\text{Mg}}_3{\text{SbX}}_3$ materials. As a result, the electrical conducting properties of ${\text{Mg}}_3{\text{SbX}}_3$ substances decrease due to the TDOS line, which is independent of the SOC effect. When applied tensile strain between 0 and +6 %, the Fermi level is violated by the SOC. Numerous studies on the bandgap and band framework of the ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) materials led to the anticipated shift in the bandgap. Materials ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) show enhanced conductivity when compressed under stresses that vary from 0 % to −6%, irrespective of the presence or absence of SOC influence. This leads to the TDOS line evolving in the direction of the Fermi level. Therefore, the conductivity of ${\text{Mg}}_3{\text{SbX}}_3$ materials decrease because of the TDOS line, which under tensile tensions between 0 % and +6 %, deviates from the Fermi level, regardless of the SOC effect. A complete investigation of the band configuration and DOS of the ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) materials were expected to result in a modification to the bandgap.

Fig. 8.

The TDOS values of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) in various strains without (a, b, c, d) and with SOC consequence (e, f, g, h) are nearly at Fermi levels.

3.6. Optical properties

The dielectric function, absorption coefficient, and electron loss function are all parts of a material's optical property study. The material's suitability for use in optoelectronic and photovoltaic applications can be determined by these qualities. One way to make optical materials work better is to use thermodynamic biaxial strain. Modifying the material's lattice parameter improves its performance and alters its optical characteristics. This work investigates the extensional and optical characteristics of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) subjected to compressive (0 % to −6%) and tensile (0 % to +6 %) stresses. Improved material performance may be possible because of the study's discovery of improved optical properties under various strains.

Equation (1) determines the dielectric function of a compound, denoted as $\mathrm{\epsilon }$ (ω), by combining the two elements. The real element, represented as ${\mathrm{\epsilon }}_1$ (ω) is the first component and the imaginary part, represented as ${\mathrm{\epsilon }}_2$ (ω) is the second. The Kramers-Kronig conversion [65] can be employed to ascertain the dielectric property's imaginary part and the motion matrix's components can be evaluated to determine the real part. The portions of the motion matrix were applied to simultaneously ascertain the imaginary dielectric operation. By using the critical section of the dielectric function ${\mathrm{\epsilon }}_1$ (ω) and Equation (3), one may ascertain the EELF and absorption rate of the ${\text{Mg}}_3{\text{SbX}}_3$ perovskite material [61,66].

$${\mathrm{\epsilon }}_1\left(\omega \right)=1+\frac{2}{\mathrm{\pi }}\mathrm{P}\underset{0}{\overset{\infty }{\int }}\frac{{\mathrm{\epsilon }}_2\left({\mathrm{\omega }}^{\prime }\right){\mathrm{\omega }}^{\prime }}{{\mathrm{\omega }}^{\prime 2}-{\mathrm{\omega }}^2}\mathrm{d}\omega$$ (3)

for situations in which P is a perfect prime.

Obtaining the hypothetical dielectric function ${\epsilon }_2$ (ω) from Equation (4) [67,68].

$${\epsilon }_2\left(\omega \right)=\frac{V{e}^2}{2\pi \mathrm{\hslash }{m}^2{\omega }^2}\times \int d^{3}k\sum {\left|⟨{\phi }_c\left|p\right|{\phi }_v⟩\right|}^2\delta (E_c-E_v-\mathrm{\hslash }\omega )$$ (4)

with p representing momentum, V unit cell volume, ℏ compact Planck's constant and ${\phi }_c$ and ${\phi }_v$ representing valence and conduction bands matching wave functions, respectively.

The absorption coefficient α(ω) can be calculated by integrating the real and imaginary parts of the dielectric component. Using Equation (5) [60,61] to obtain a rough estimate of the absorption coefficient.

$$\alpha \left(\omega \right)=\frac{\surd 2\omega }{c}{[\sqrt{{{\epsilon }_1\left(\omega \right)}^2+{{\epsilon }_2\left(\omega \right)}^2}–{\epsilon }_1\left(\omega \right)]}^{1/2}$$ (5)

The speed of light is represented by the symbol C.

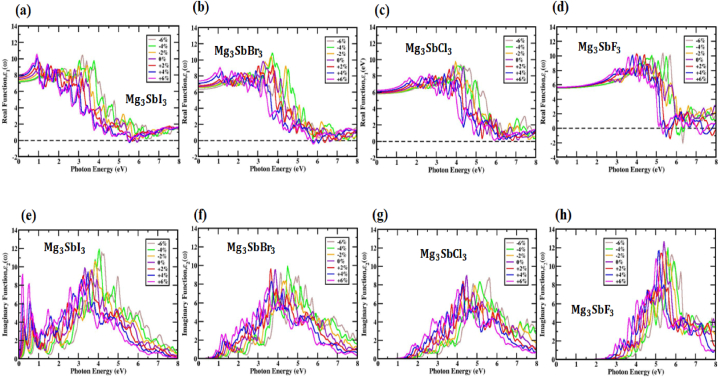
Using the actual component of the dielectric constant, investigators can investigate the effects of polarization and diffraction on ${Mg}_3{SbX}_3$ [42,69]. See Fig. 9(a, b, c, d) and Fig. S14(a, b, c, d) for the actual and strain-induced degradation of the dielectric permittivity of unstrained ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F). The dielectric function values are shown on the graphs for photon energies up to 8.02 eV for ${Mg}_3{SbI}_3$, 7.38 eV for ${Mg}_3{SbBr}_3$, 6.22 eV for ${Mg}_3{SbCl}_3$ and 5.66 eV for ${Mg}_3{SbF}_3$ are illustrated in Fig. 9(a, b, c, d). By determining the material's real dielectric coefficient, one can learn about its polarization and diffusion effects. The greatest frequency at which the dielectric distribution is zero is its most salient feature, that is represented as ${\epsilon }_1$ (0). An important portion of the ${\epsilon }_1$ (ω) component, this number shows how electronic influences affect the real part of the dielectric constant. Fig. S14(a, b, c, d) illustrates that the cubical values of the square roots of ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$ are 7.25 eV, 6.75 eV, 5.90 eV and 5.59 eV, respectively. The material's ${\epsilon }_1$ (0) value starts to increase from its initial value, reaches its maximum during optical excitation, and then suddenly drops. The material's exceptional light absorption in this spectral band is demonstrated by this reaction. The material possesses characteristics like semiconductors and exhibits a high refractive index, as demonstrated by the positive values of ${\epsilon }_1$ (ω) for unstrained ${Mg}_3{SbX}_3$. Biaxial strain was used to move the real component dielectric constant maxima of the ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) perovskite. Changes in strain-dependent optical characteristics of ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) are displayed in Table 3. This occurs because of applied strain. Because we observe that when compressive strain increases the lattice parameter value is decreasing alongside the distance between Mg-Sb atom also decreasing. In contrast when tensile strain increases the lattice parameter value is increasing alongside distance between Mg-Sb atom also increasing. For increasing atomic distance, the volume of the material also increases and for decreasing atomic distance, the volume of the material is also decreasing. All things considered, materials with smaller bandgaps tend to have more pronounced dielectric constant peaks than those with wider ones.

Fig. 9.

For strained ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) the real component of the dielectric function fluctuates as a function of photon energy of (a, b, c, d). For strained ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F), The dielectric function's imaginary component varies with photon energy of (e, f, g, h).

Table 3.

Changes in strain-dependent optical characteristics of ${\mathrm{M}\mathrm{g}}_3{\text{Sb}\mathrm{X}}_3$ (X = I, Br, Cl and F).

Applied Strain (%)		−6	−4	−2	0	+2	+4	+6
The static dielectric constant ɛ1(0)	Mg3SbI3	7.13	7.20	7.36	7.50	7.69	7.85	8.02
	Mg3SbBr3	6.32	6.54	6.58	6.68	6.79	7.11	7.38
	Mg3SbCl3	5.80	5.82	5.85	5.90	5.98	6.08	6.22
	Mg3SbF3	5.53	5.54	5.58	5.59	5.61	5.62	5.66
Location of maximum point ɛ2(ω) (eV)	Mg3SbI3	4.20	4.04	3.83	3.31	3.26	3.16	3.09
	Mg3SbBr3	4.88	4.48	4.40	3.90	3.66	3.63	3.48
	Mg3SbCl3	5.61	4.13	4.89	4.50	4.28	4.23	4.03
	Mg3SbF3	5.81	5.61	5.53	5.40	5.27	5.17	5.00
Energy of maximum absorption peak (eV)	Mg3SbI3	6.09	6.01	5.93	5.84	5.64	5.24	4.93
	Mg3SbBr3	7.28	6.90	6.58	6.25	5.93	5.65	5.43
	Mg3SbCl3	8.12	8.01	7.83	7.65	6.52	6.16	5.81
	Mg3SbF3	9.75	9.27	8.33	7.94	7.62	7.30	7.03
Peak location of loss function (eV)	Mg3SbI3	10.9	10.46	10.09	9.61	9.26	8.79	8.48
	Mg3SbBr3	11.75	11.30	10.75	10.32	9.91	9.52	9.03
	Mg3SbCl3	12.42	11.91	11.38	10.85	10.42	9.95	9.50
	Mg3SbF3	13.32	12.73	12.18	11.69	11.22	10.81	10.38

The redshift toward lower photon energies and a bigger dielectric constant peak are consequent to the bandgap lowering under decreasing compressive strain in the ${Mg}_3{SbX}_3$ perovskite structure.

Under various relaxation and strain states, the handling of the imaginary component, ${\epsilon }_2$ (ω) of the dielectric function is shown in Fig. S14 (e, f, g, h) and Fig. 9(e, f, g, h). One should be familiar with the imaginary part of the dielectric function if one wishes to understand how unbiased charge excitations generate optical absorption and how much energy a crystal structure can store. Using the imaginary dielectric function ${\epsilon }_2$ (ω), the electronic bandgap surrounding the Fermi level, and the energy of inter-band transitions can be obtained. A material's optical properties, such as its reflectance and absorption, can be gleaned from the data. The ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$ ${\epsilon }_2$ (ω) peaks are most pronounced at optical positions of 10.16, 9.62, 9.24 and 12.65, respectively, indicating that the absorption photons have energies of approximately 3.31 eV, 3.90 eV, 4.50 eV and 5.40 eV, as shown in Fig. S14 (e, f, g, h). In Fig. 9(e, f, g, h), as stress is applied, the expansion of the imaginary part of the dielectric coefficient becomes apparent. Theoretical peak absorption rates govern the transition of carriers between the valence and conduction bands. Alterations to the bandgap and lattice parameter cause the peaks to move. The imaginary peaks undergo a blue-shift under compressive tension, signifying an increase in energy. Conversely, assuming tensile strain circumstances, the peaks undergo a red-shift, signifying a drop in energy. Results suggest that the properties of the ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) compound may be adjusted by adjusting its absorption spectra area using either compressive or tensile strain. Beyond 9.55 eV, 10.22 eV, 10.67 eV and 11.45 eV for ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$, there is no dielectric with an imaginary component. The material appears to be optically transparent with minimal absorption, as ${\epsilon }_2$ (ω) does not exist at photon energies over 11.45 eV.

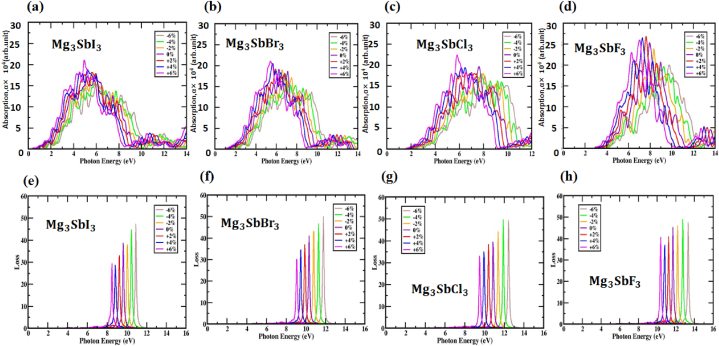
An essential characteristic of the compound ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) is its absorption coefficient, that represent the amount of light that the components in the compound receive at different wavelengths. The structure of the absorption parameter for ${Mg}_3{SbX}_3$ is identical to the imaginary portion of the dielectric element in all configurations. A larger absorption coefficient is commonly observed in this region since most of the sun's radiation occurs within the electromagnetic spectrum's variable range. The absorption parameter of the ${Mg}_3{SbX}_3$ perovskite material when subjected to biaxial strain and when not is shown in Fig. S15(a, b, c, d) and Fig. 10(a, b, c, d) as a function of photon energy, conversely. Under tensile strain, the absorption peak of ${Mg}_3{SbX}_3$ increases, but it drops under compressive strain.

Fig. 10.

The absorption fluctuates with photon energy for strained (a, b, c, d) ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F). The loss function of (e, f, g, h) strained ${\text{Mg}}_3{\text{SbX}}_3$ (X = I, Br, Cl and F) and its dependency on photon energy.

While the unstrained material is significantly more absorbent in the visible spectrum, the compressed structure of ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) is less so. As the tensile strain increases, the visible range absorption coefficient ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) gets better. Solar cell applications rely on this quality. Despite this, as compressive strain increases, the visible-light absorption coefficient of ${Mg}_3{SbX}_3$ drops. Optimizing the absorption coefficient is of utmost importance for developing photovoltaic devices with ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) perovskites. Potentially, it might make these devices more efficient, leading to potentially superior solar cells in the long run.

The "electron loss function" quantifies the amount of energy that an electron undergoes a net loss while navigating a dielectric. "When electrons flow through a dielectric substrate, some of their energy is lost. This is called the "electron loss function." Power loss occurs due to the emission of photons with energies beyond the bandgap of the material, as seen by the peak in the L(ω) plot in Fig. S15(e, f, g, h) for ${Mg}_3{SbX}_3$. One can find the electron loss function, L(ω), by using the provided formula (6) [67].

$$L\left(\omega \right)=\frac{{\epsilon }_2\left(\omega \right)}{{\epsilon }_1^2\left(\omega \right)+{\epsilon }_2^2\left(\omega \right)}$$ (6)

The energy range for ${Mg}_3{SbI}_3$, between 9.05 and 10.32 eV, for ${Mg}_3{SbBr}_3$ between 9.66 and 11.02 eV for ${Mg}_3{SbCl}_3$ between 10.15 and 11.62 eV and for ${Mg}_3{SbF}_3$ between 11.16 and 12.36 eV is ideal for the L(ω) peaks is shown in Fig. S15(e, f, g, h). The loss function peaks at 9.61 eV, 10.32 eV, 10.85 eV and 11.69 eV respectively, when this studies investigates ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$. As demonstrated by the lowest peak value, this layer may efficiently absorb optical photon spectra and infrared spectra. For photon energies up to 11.83 eV, 12.81 eV, 13.55 eV and 14.42 eV, respectively, the strain-applied in ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$ substances do elicit a loss function are demonstrated in Fig. 10(e, f, g, h). The energy losses of ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) may be estimated using several biaxial compressive and tensile strain situations, as expressed in Fig. 10(e, f, g, h). Based on the findings, a higher compressive strain is indicative of a higher photon energy for the ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ structures and a lower photon energy for the ${Mg}_3{SbF}_3$ structure. Increases in tensile strain are indicative of reductions in photon energy and optical loss. ${Mg}_3{SbX}_3$ greatly affects how well these materials function in general; thus, it is important to take them into account when designing and optimizing them for use.

3.7. Mechanical properties

Rigid materials rely heavily on their elastic constant, which expresses the stability and rigidity of the material. A crystal's biaxial strain resistance can be accurately measured by its elastic constant. Understanding the impact of stress on the elastic constants of these ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) structures is crucial for grasping their mechanical properties. Three notable elastic constants, C₁₁, C₁₂, and C₄₄, were observed in the ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) structure in this density-functional theory investigation that utilized an alternate halide ratio. The conversion of a material's C₁₂-C₄₄ value to a parameter known as Cauchy pressure allows one to study its ductile and flexible qualities. To determine the mechanical stability of materials such as ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$, one of the common methods is:

C₁₁ > 0, C₄₄ > 0, C₁₁ + 2C₁₂ > 0, C₁₁ − C₁₂ > 0

Only materials with a positive Cauchy pressure are considered ductile. The classic formula, Pugh's ratio [[70], [71], [72], [73], [74], [75]], was proposed by Pugh et al. for the purpose of distinguishing between brittle and hard components.

$$B_H=\frac{B_V+B_R}{2}$$ (7)

$$G_H=\frac{G_V+G_R}{2}$$ (8)

$$\vartheta =\frac{\left(3B-2G\right)}{2\left(3B+G\right)}$$ (9)

The ratio of the shear modulus ($G_H$) to the bulk modulus ($B_H$), measured in units of 1.75, is an important parameter. The material is considered ductile if the ratio is more than 1.75 and fragile if it is lower than 1.75. Based on the calculated values, the compounds ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$ are ductile. The use of Poisson's ratio ($\vartheta$) is one method for differentiating ductile from cracked materials. Table 4, Table 5, Table 6, Table: 7 shows the B/G and $\vartheta$ values. One further thing to remember is that $\vartheta$ is bigger for ductile materials than for fragile ones, which is 0.26 or smaller. Because $\vartheta$ is greater than 0.26, the structures ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) are ductile materials. The bulk modulus describes a material's stiffness and flexibility. The Shear Modulus may measure how much a material will bend plastically in response to stress. Shear modulus and Poison's ratio decrease, respectively, when applying tensile strain increasing. On the other hand, shear modulus and Poison's ratio increase, respectively, when applying compressive strain increases. The Pugh's ratio and Poisson's ratio are calculated and displayed in Table 4, Table 5, Table 6, Table: 7, which shows higher ductile nature in compressive strain compared to tensile strain. As a result, this material can be considered extremely useful for real-life applications and the manufacture of technical equipment.

Table 4.

Cubic ${\mathrm{M}\mathrm{g}}_3{\text{Sb}\mathrm{I}}_3$ perovskite's mechanical and elastic characteristics as determined under various compressive and tensile strains.

Strain (%)	C11	C12	C44	C12- C44	${\mathrm{B}}_{\mathrm{H}}$ (GPa)	${\mathrm{G}}_{\mathrm{H}}$ (GPa)	E (GPa)	B/G	$\mathrm{\vartheta }$
−6	114.4	37.1	23.7	13.4	66.2	30.3	77.2	2.18	0.320
−4	88.7	31.8	21.6	10.2	54.1	25.7	64.7	2.10	0.315
−2	67.7	29.5	19.6	9.9	44.2	21.6	53.4	2.04	0.298
0	62.7	28.4	19.1	9.3	41.9	20.6	50.9	2.03	0.289
+2	63.3	27.6	18.8	8.8	38.2	19.7	51.3	1.93	0.284
+4	47.4	25.6	17.5	8.1	34.6	18.3	42.1	1.89	0.281
+6	34.4	23.5	16.2	7.3	28.5	15.3	34.2	1.86	0.276

Table 5.

Cubic ${\mathrm{M}\mathrm{g}}_3{\text{SbB}\mathrm{r}}_3$ perovskite's mechanical and elastic characteristics as determined under various compressive and tensile strains.

Strain (%)	C11	C12	C44	C12- C44	${\mathrm{B}}_{\mathrm{H}}$ (GPa)	${\mathrm{G}}_{\mathrm{H}}$ (GPa)	E (GPa)	B/G	$\mathrm{\vartheta }$
−6	123.6	37.4	25.6	11.8	69.5	33.0	83.6	2.10	0.325
−4	94.9	35.3	23.7	11.6	57.8	28.2	70.4	2.04	0.314
−2	73.4	33.2	22.1	11.1	51.9	26.3	59.5	1.97	0.304
0	68.6	32.2	21.6	10.6	44.7	23.3	56.9	1.91	0.298
+2	67.0	29.6	21.2	8.4	41.7	22.1	56.1	1.88	0.284
+4	52.7	28.0	20.3	7.7	37.2	20.1	48.1	1.85	0.280
+6	37.2	27.3	19.8	7.5	30.6	16.7	38.6	1.83	0.274

Table 6.

cubic ${\mathrm{M}\mathrm{g}}_3{\text{SbC}\mathrm{l}}_3$ perovskite's mechanical and elastic characteristics as determined under various compressive and tensile strains.

Strain (%)	C11	C12	C44	C12- C44	${\mathrm{B}}_{\mathrm{H}}$ (GPa)	${\mathrm{G}}_{\mathrm{H}}$ (GPa)	E (GPa)	B/G	$\mathrm{\vartheta }$
−6	130.5	38.0	27.1	10.9	72.2	35.1	88.7	2.056	0.320
−4	103.6	34.5	25.4	9.1	60.6	30.4	76.0	1.993	0.315
−2	77.7	32.8	23.9	8.9	53.2	27.1	63.9	1.963	0.308
0	73.9	31.9	23.6	8.3	45.4	25.2	61.5	1.920	0.297
+2	75.7	31.2	23.8	7.4	46.9	24.8	62.8	1.891	0.289
+4	57.4	29.6	22.4	7.2	40.9	22.1	52.8	1.850	0.281
+6	40.9	27.9	21.1	6.8	33.8	18.6	42.8	1.817	0.273

Table: 7.

Cubic ${\mathrm{M}\mathrm{g}}_3{\text{Sb}\mathrm{F}}_3$ perovskite's mechanical and elastic characteristics as determined under various compressive and tensile strains.

Strain (%)	C11	C12	C44	C12- C44	${\mathrm{B}}_{\mathrm{H}}$ (GPa)	${\mathrm{G}}_{\mathrm{H}}$ (GPa)	E (GPa)	B/G	$\mathrm{\vartheta }$
−6	89.1	34.8	20.4	14.4	77.69	38.2	171.2	2.034	1.237
−4	76.2	33.3	19.6	13.7	60.45	30.5	95.7	1.982	0.794
−2	72.1	32.0	19.1	12.9	56.58	29.5	110.7	1.918	0.815
0	68.2	30.1	18.5	11.3	50.08	26.6	92.3	1.883	0.735
+2	53.2	28.3	17.6	10.7	43.16	23.5	79.5	1.837	0.686
+4	48.4	26.9	17.1	9.8	36.56	20.1	86.1	1.819	0.711
+6	44.8	25.4	16.7	8.7	32.91	18.4	83.0	1.789	0.696

3.8. Thermal properties

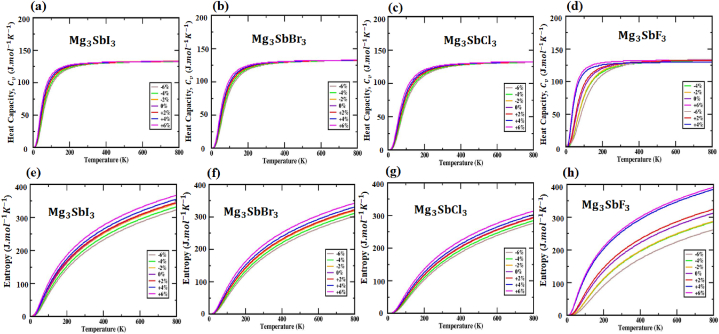
A quasi-harmonic Debye approximation is required for high-pressure and high-temperature thermal property investigations. Applying this constant estimate to the total energy as a function of the primitive cell volume (E-V) is one approach to determining the structural variables at T = 0 and P = 0. Per the generally acknowledged thermodynamic correlations, the macroscopic characteristics are thereafter described in terms of T. Estimating thermal characteristics from 0 to 800 K using the quasi-harmonic method is also very precise. The thermal effect is shown by the heat capacity $C_v$, which is represented in Fig. 11(a, b, c, d). Dulong and Petit set thresholds and the $C_v$ is getting close to them. The values for ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$ at a constant volume are as follows: 133 ${J.mol}^{-1}{K}^{-1}$ for ${Mg}_3{AsI}_3$, 132.2 ${J.mol}^{-1}{K}^{-1}$ for ${Mg}_3{AsBr}_3$, 132 ${J.mol}^{-1}{K}^{-1}$ ${Mg}_3{AsCl}_3$, 130 ${J.mol}^{-1}{K}^{-1}$ for ${Mg}_3{AsF}_3$. It is directly proportional to $T^3$ that the $C_v$ increases when temperatures are low. Nevertheless, in the past, extensive investigational testing over extended periods of time was necessary to ascertain the heat potential, which is determined by the dynamics of atomic movements at intermediate temperatures [71,76]. As depicted in Fig. 10(a, b, c, d), the $C_v$ changes when the strain of ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) varies at a specific temperature. Fig. 10(e, f, g, h) shows the temperature variability of the ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) material from 0 K to 800 K. At 800K, the best thermal entropy for the ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F) structure is observed. Despite the presence of strain variations, studies observe that entropy varies and find that it increases with temperature. Fig. 11(e, f, g, h) displays as the entropy changes for different compressive and tensile strains. The highest entropy is observed at 800K temperature, and the entropy of ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$ is 345 ${J.mol}^{-1}{K}^{-1}$, 322 ${J.mol}^{-1}{K}^{-1}$, 294 ${J.mol}^{-1}{K}^{-1}$, 392 ${J.mol}^{-1}{K}^{-1}$ when the strains are not applied. With strain increasing from 0 % to +6 %, the thermal entropy peaks at 367 ${J.mol}^{-1}{K}^{-1}$, 342 ${J.mol}^{-1}{K}^{-1}\text{,}$ 313 ${J.mol}^{-1}{K}^{-1}$ and 392 ${J.mol}^{-1}{K}^{-1}$. The values that are lowest at −6% strain, which is 323 ${J.mol}^{-1}{K}^{-1}$, 302 ${J.mol}^{-1}{K}^{-1}$, 276 ${J.mol}^{-1}{K}^{-1}$, 262 ${J.mol}^{-1}{K}^{-1}$ for ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$ materials.

Fig. 11.

The heat capacity of the ${\text{Mg}}_3{\text{AsX}}_3$ (X = I, Br, Cl and F) structures against temperature is plotted in (a, b, c, d). The ${\text{Mg}}_3{\text{AsX}}_3$ (X = I, Br, Cl and F) structures' entropy as a function of temperature are shown in (e, f, g, h).

4. Conclusion

Utilizing first-principles density-functional theory (DFT) calculations, this study investigated the electrical, optical and structural characteristics of the inorganic compound ${Mg}_3{SbX}_3$ (X = I, Br, Cl and F). The optimal structure is shown by the estimated lattice value of 6.01 $A°$, 5.72 $A°$, 5.54 $A°$, and 5.02 $A°$ for ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${Mg}_3{SbCl}_3$ and ${Mg}_3{SbF}_3$. The indirect bandgap value of the ${Mg}_3{SbI}_3$, ${Mg}_3{SbBr}_3$, ${M\mathrm{g}}_3{\text{SbCl}}_3$ is 0.105 eV, 0.957 eV, 1.728 eV and the direct bandgap value of ${\text{Mg}}_3{\text{SbF}}_3$ structure is settled on to be 3.184 eV. The electronic indirect bandgap of ${\text{Mg}}_3{\text{SbI}}_3$, ${\text{Mg}}_3{\text{SbBr}}_3$, ${\text{Mg}}_3{\text{SbCl}}_3$ and the direct bandgap of ${\text{Mg}}_3{\text{SbF}}_3$ is shifted to 0.198 eV, 1.203 eV, 1.901 eV and 3.723 eV when the SOC effect is considered. With or without the SOC effect, a reduction in bandgap appears with increasing tensile strain. Bandgap, on the other hand, grows larger with increasing induced compressive strain. Throughout this investigation we observe that the system is stable and different properties including its dielectric function, light absorption, loss these are suitable and display absorption peaks near the UV to the visible spectrum, with a blue-shift and a red-shift occurring simultaneously. This result suggests that the electrical and optical strain dependent characteristics of ${\text{Mg}}_3{\text{SbX}}_3$ that have been investigated here may soon find use in the manufacturing of optoelectronics and solar cells.

CRediT authorship contribution statement

I.K. Gusral Ghosh Apurba: Writing – original draft, Visualization, Investigation, Formal analysis, Data curation. Md. Rasidul Islam: Writing – review & editing, Validation, Supervision, Methodology, Investigation, Data curation, Conceptualization. Md. Shizer Rahman: Writing – original draft, Visualization, Methodology, Formal analysis, Data curation. Md. Ferdous Rahman: Writing – review & editing, Validation, Software, Resources, Methodology. Sohail Ahmad: Writing – review & editing, Validation, Resources, Funding acquisition.

Data availability

Data can be shared by corresponding authors upon reasonable request.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.