An improved finite set model predictive control of SRM drive based on a voltage vectors strategy for low torque ripple

Abstract

The robust rotor structure and fault-tolerance characteristics of the Switched Reluctance Motors (SRMs) are the best choice for next-generation Electric Vehicle (EV) applications. This machine has few restraints like high torque and flux ripples. However, the existing Model Predictive Control (MPC) using multiple control objectives and maximum sectors in the switching table results in high torque ripples due to the improper sector partition, Voltage Vectors (VVs) and weight factor (K₁) selection. This paper proposes a Finite Set-Model Predictive Control (FS-MPC) for an analytical model of a non-linearity SRM machine to analyze the torque ripple performance. The proposed VVs are derived using sector partition based on the rotor position. The control is designed as a single cost function with the weighting factor contributing to smooth torque by selecting optimal control signals. Simulation studies and experiments with a four-phase 8/6 SRM drive verifies the enhanced FS-MPC for real-time implementation. The dynamic speed and ripple values of SRM Drives are measured using a mixed signal oscilloscope and the sensor probes. The laboratory outcomes calculate the analytical equations to validate the findings. The calculated value of torque ripple is 9 % through this FS-MPC. The study reveals that the proposed method is well suited for torque ripple reduction than flux ripples.

1. Introduction

1.1. Background

EV development in the transportation sector demands high performance, reliability, power, torque density and, most importantly, a reduction in the overall cost of vehicles. In Refs. [1,2], the main subsystem parts of EVs are electrical drives, batteries, power electronics converters, control techniques, materials, and other electrical and mechanical components that use non-earth materials. At [3] present, the Permanent Magnet (PM) motor and the Induction Motor (IM) are used in EVs to achieve overall better performance in all aspects. However, the PM motor uses non-earth magnet material neodymium samarium iron boron, and IM uses copper, which has low availability and comes too expensive. In Refs. [4,5] Fig. 1, the EV motor has a few drawbacks, such as fault-tolerant, demagnetization, losses, reduction in efficiency at high speed, power factor, and field weakening operation. Therefore [6], high cost and low availability reason, researchers, the automotive industry, and the government have initiated alternate solutions to reduce PM usage. In Ref. [7], research and development in the powertrain sector focus on high performance, power density, and low cost instead of using magnet or copper motors to replace special machines such as wound synchronous field motors and SRM.

Fig. 1.

Finite element analysis 8/6 SRM for 2.2 kW for analytical approximation model.

In [8,9], SRM uses magnet-free, low-cost silicon material in the stator and rotor pole, representing simple construction, minimum fabrication cost, and robustness. In Ref. [10], SRM is driven by a special power electronics converter that helps improve performance and operate smoothly. In Refs. [11,12], the double salient structure of SRM has many advantages of high fault-tolerant capability, high temperature, high speed, and no demagnetization effect compared to PM and IM. Although [13,14] SRMs have a few drawbacks, such as high commutation, conduction torque ripple, high acoustic noise, medium torque density, and vibration. Thus [15,16], technology development in power semiconductor devices, advanced control techniques, design optimization, and digital power processors can mitigate the main challenges in SRM drive for EVs. The Researchers used different conventional control techniques to (a) minimize the SRM drive drawbacks and (b) improve the performance to compete with the IM and PM motors. Moreover [17,18], conventional control techniques have the following challenges: (a) adoption of the non-linear behaviour of motor constraints for tuning, (b) computational complexity, (c) requires high memory space, (d) requires high offline data and (e) unable to control dynamic response, switch turn on and turn off mechanism. Furthermore [19], existing control techniques adopted for SRM drives are [20] Torque Sharing Function (TSF), Current Profiling method (CP) [24], vector control [23,25], direct instantaneous torque/force control (DITC/DIFC) [22], sliding mode control (SMC), iterative control techniques, and [21] intelligent control techniques (fuzzy, neural network, adaptive neuro-fuzzy inference system). In Ref. [26], TSF needs high computational time and a predefined function. The SMC-based neural or fuzzy logic model proposed was computationally intensive. In Ref. [27], the SRM stator phase requires independent excitation, but the sequential excitation of the phase winding in the DTC procedure needs to be balanced.

1.2. Motivation

Predictive Control (PC) has the main advantage over conventional controllers as it can handle nonlinearities and constraints. However [28,29], conventional PC techniques such as generalized PC, deadbeat PC, and hysteresis-based PC are used in an effective manner to focus on single control objectives. However, it is difficult to control multiple objectives. In recent trends, Model Predictive Control (MPC) has classified as continuous and finite control sets, including nested cost functions for multiple objective drive applications. Only a few papers are used in MPC techniques to implement in the SRM drive for torque ripple analysis. The SRM has highly nonlinear behaviour, especially the relationship of self-inductance with the current magnitude and rotor position. The back EMF characteristics are also nonlinear, in addition to rotor speed and self-inductance. Therefore, accurate information on the motor characteristics is essential in order to implement the MPC in the SRM to predict the future state. Few methods were adopted to obtain the motor characteristics, using predefined look-up tables and analytical models which may cause prediction errors in the MPC. Therefore, the finite-element method is typically used to obtain motor characteristics in real-time implementation. In few literatures, MPC is primarily used for current control in SRM drives that implement a current predictive control with a fixed switching frequency. Predictive current control-based approach has been proposed in Ref. [30]. Some of the applications need less ripple torque and less noise which can be attained by the predictive current control approach [31]. When it comes to model predictive control of SRM, the variation and uncertainties in inductance and other parameters needs to be controlled [31]. For the low-speed applications of SRM, it necessitates the need of torque ripple reduction with minimized switching frequence and copper loss [32,33]. In the dynamic operation and due to the dynamic behaviour of conventional MPC control, the reference current and phase current values are dynamically changed, and it will not achieve the constant value. This creates the back EMF that restricts the four-quadrant operation of SRM. This needs to be reduced for the effective operation [34]. The MPC has specially developed with the individual constraints to optimize the different power enhancing weight factors in four phase SRM [35]. Along with this, the multiple objective function gives cost function for MPC control [36]. In Refs. [37,38], MPTC and MPFC techniques developed six sectors partition with 9 VVs instead of 27 VVs, 12 sectors with 12 VVs select candidate VVs for three-phase SRM, which increase the system computational burden time and torque ripple also high. In Ref. [39], MPC designed for three-phase SRM, which includes all 27 VVs for the torque production phase, creates a high torque ripple. The existing FS-MPC for SRM suffers a large torque ripple and flux ripple due to inaccurate calculation of self-inductance, and improper selection of sector partition with rotor position, which includes one phase conduction, overlap conduction period, and number of VVs selection for control signals. The literature still needs to address this problem [49].

The main contribution of this paper is to propose an enhanced FS-MPC implemented in the SRM drive non-linear flux linkage characteristics behavioural approach for effective torque ripple control techniques. The initial focus was on designing low power ratings, later machine modelling was obtained through electromagnetic analysis to determine the rotor position, flux linkage, phase current, and torque curve lookup tables. The non-linear inductance phase profile, rate of change of phase current, estimation of flux, and torque are essential parameters for MPC. Table 1 shows the concise literature survey on conventional controller techniques switching state, inner loop control strategy, and modelling approach of SRM drive with proposed FS-MPC, respectively. This research mainly focuses on torque ripple and flux ripple reduction.

Table 1.

Concise literature survey on predictive control techniques.

Topology	Adopted techniques	Switching state	Modelling approach	Key challenges	Ref
Conventional MPC control techniques for 8/6 SRM	HCC (Hysteresis current control)	Hysteresis band	Model-free	Torque ripple and flux ripple reduction	[40]
	PI-PWM (Proportional Integral)	PI- regulator	Various		[41]
	Delta modulation	Hysteresis band	Model-free		[42]
	Back emf compensation	PI- regulator	Various		[43]
	CCS (Continuous control set)	Continuous CF	Analytical/static map		[44]
	HPC (Hysteresis predictive control)	Hysteresis band	Analytical/static map		[45]
	GPC (Generalized predictive control)	Continuous CF	Transfer function		[46]
	Current profiling techniques	Direct calculation	Analytical/static map		[[47], [48]]
Enhanced FS- MPC 8/6 SRM	Discrete function/static maps using a discrete cost function	Four quadrant operations, torque ripple reduction, and improving drive performance analysis.			–

The major contribution of the FS-MPC method is given as follows.

• •The mathematical model of non-linearity 4-phase 8/6 SRM is built utilizing the appropriate parameter values, such as flux linkage, rotor position, which were acquired using finite element analysis with JMAG.
• •The improved FS-MPC is designed for a non-linearity 4-phase 8/6 SRM drive by eliminating the flux linkage calculation, splitting the SRM's electric cycles into eight sectors depending on rotor position, and determining the active voltage vectors (VVs) for operation.
• •To regulate the motor torque, the switching table is proposed based on the torque estimation, prediction, and cost function.
• •The process to select the VVs based on cost function is shown in the flowchart. It's evident from the results that the level of torque reduction is 9 % for the proposed FS-MPC under different speed conditions compared to existing MPC techniques.

This paper is organized as follows: Section II discusses the dynamic mathematical modelling of the four-phase SRM Drive. It also includes a four-phase asymmetric half-bridge converter. A finite set model predictive controller employed a novel switching state VVs which is effectively managed from the existing method is proposed in section III. The simulation and hardware prototype results for the proposed model and the existing MPC results are elaborated in section IV. The last section comprises the results, discussion and conclusion of the proposed work.Table 2

Table 2.

The dynamic model of SRM.

Stator Resistance	Inertia	Friction	Flux Linkage	Aligned Inductance	Unaligned Inductance	Prediction Horizon	Sampling Time
(Ω)	(kg.m2)	(N.m. s)	(Wb)	(mH)	(mH)	(unit)	(Seconds)
0.837	0.08	0.0065	0.174	4	0.55	1	1 × 10−4

2. Dynamic model of SRM

2.1. Modelling on SRM

The dynamic mathematical model of an 8/6 SRM is an important requirement to implement the proposed MPC techniques. The SRM exhibits double salient pole nonlinear behavior and is a multivariable system. Considering that the SRM has four phases and neglecting factors such as mutual inductance, voltage drops across switches, hysteresis, and eddy current, the 1-phase voltage equation of the SRM drive system [37] is expressed as equation (1)

$$V=i\times R_s+\frac{d\lambda \left(\theta ,i\right)}{dt}$$ (1)

Where flux linkage (λ), rotor position (ө), stator phase current (i), and stator resistance (R_s), respectively. Generally, the function of flux linkage correlated between phase current and rotor position, as expressed in equation (2).

$$V=i\times R_s+\frac{\partial \lambda }{\partial \theta }\frac{d\theta }{dt}+\frac{\partial \lambda }{\partial i}\frac{di}{dt}$$ (2)

The optimized geometry of 2.2 kW SRM performance analysis was carried out using JMAG to measure and validate the aligned inductance, unaligned inductance, and middle aligned. The nonlinear operation of flux linkage condition on the phase winding current and the rotor position is collected of three components: alignment, unalignment, and middle aligned performance to apply the analytical model [37] to calculate the phase current as equation (3)

$$\frac{di}{dt}=\frac{1}{\frac{\partial \lambda }{\partial i}}\left(v-R_{s}i-\frac{\partial \lambda }{\partial \theta }\omega \right)$$ (3)

where ω is angular speed. The look up table (LUT) is developed with respect to stator phase current changes and rotor position λ (ө, i). Similarly, the stator phase current changes and the rotor position. The instantaneous torque can be calculated directly from an mathematical model of co-energy.

The developed electromagnetic torque [38] for a single phase is expressed as equation (4)

$$T_{ph}\left(i_{,}\theta \right)=\frac{\partial w_c}{\partial \theta }$$ (4)

Where w_c = co-energy expressed as equation (5)

$$w_c={\int }_0^i\lambda \left(i,\theta \right)di$$ (5)

According to the laws of mechanics [38], total torque developed is expressed as equation (6)

$$T_e=\sum T_{ph}\left(i,\theta \right)=j\frac{d\omega }{dt}+B\omega +T_L$$ (6)

Where T_e, T_L, T_ph, j, B, and ω are the electromagnetic torque, load torque, phase torque, moment of inertia, damping coefficient, and rotor speed, respectively.

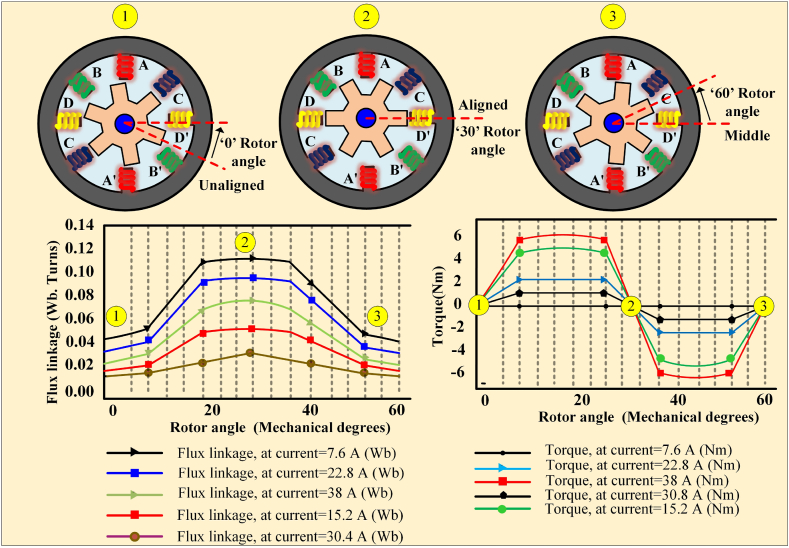
The magnetic flux linkage characteristics are obtained from FEA, as shown in Fig. 2. It is observed that the unsaturated inductance value is smallest under the unaligned position compared to the value obtained during the aligned position. Also, it is evident that the curve is linear at the beginning under an aligned position and slowly gets saturated. So, it is vital to find the current value to get a linear curve to evaluate the required phase torque.

Fig. 2.

Flux linkage characteristics.

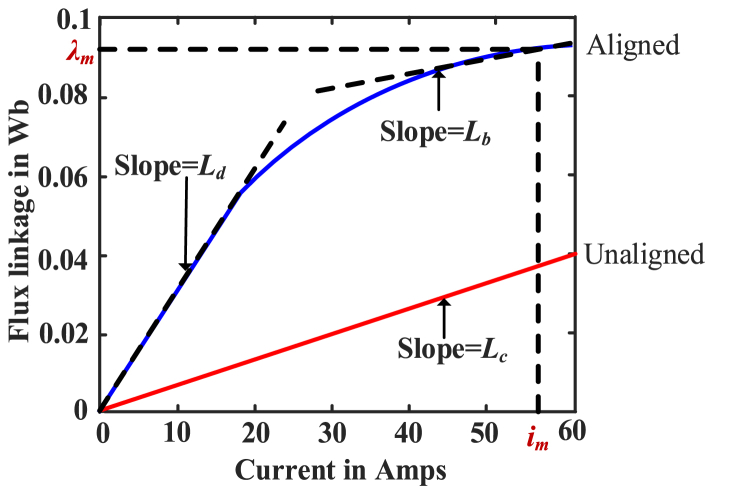
Let the magnetization characteristics of the 8/6 SRM flux linkage and torque modelling [26] equation be expressed as equation (7) and equation (8)

$$\lambda \left(i,\theta \right)=L_{c}i+\left[L_{b}i+A\left(1-e^{-Bi}\right)-L_{c}i\right]f\left(\theta \right)$$ (7)

$$T_{ph}=\left[\frac{L_b-L_c}{2}{i}^2+Ai-\frac{A}{B}\left(1-e^{-Bi}\right)\right]f^{\prime }\left(\theta \right)$$ (8)

The magnetization curve of SRM inductance characteristics [38] considers L_b as saturated inductance at the aligned position, L_c as an inductance in the unaligned position, and L_d as saturation inductance in the aligned position, respectively.

Where the values of A and B are expressed as equation (9)

$$\begin{array}{c}A={\lambda }_m-L_b{i}_m\\ \begin{array}{c}B=\left(L_d-L_b\right)/\left({\lambda }_m-L_b{i}_m\right)\\ f\left(\theta \right)=\left(2N_r^2/{\pi }^3\right){\theta }^3-\left(2N_r^2/{\pi }^2\right){\theta }^2+1\end{array}\end{array}]$$ (9)

Where N_r is a number of rotor poles, A and B are chosen constant in terms of rated current (I_m) with respect to corresponding flux linkage, and f(ө) denotes the magnetization curves intermediate positions are obtained interpolation between two external curves.

The dynamics of the 4-phase SRM has been summed as the differential equations as given in equation (10)

$$\begin{array}{c}\frac{di}{dt}=\frac{1}{\frac{\partial {\lambda }_p}{\partial i}}\left(v-R_{s}i-\frac{\partial {\lambda }_p}{\partial \theta }\omega \right),\left[p=1,2,3,4\right]\\ \frac{d\omega }{dt}=\frac{1}{j}\left[T_e-T_L-B\omega \right]\\ \frac{d\theta }{dt}=\omega ,{\theta }_p=\theta -\left(p-1\right)\pi /3\end{array}]$$ (10)

The mathematical validation model of SRM has been modelled using these equations and the modelling has been done in the MATLAB/Simulink® based on the parameters given in table 2.

2.2. Model of asymmetric half Bridge(AHB) converter

There are eight start pole windings in the 4-phase SRM, and they are powered by separate, unidirectional phase controls: AA', BB', CC', and DD'.

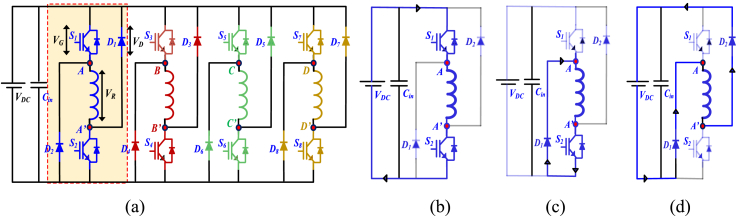
The 4-phase 8/6 AHB converter the following components such as; eight switches (S₁, S₂, S₃ … S₈), power diodes (D₁, D₂, D₃ … D₈), and DC link voltage (V_DC) is split by a capacitor (C_in) maintain constant voltage as shown in Fig. 3 (a).

Fig. 3.

SRM (a) Construction of converter (b) Phase 1 - Magnetization (c) Phase 2 - Freewheeling (d) Phase 3 - Demagnetization.

The designed converter has been operated in three different modes as given in Table 3.

Table 3.

Control signals of Phase A switching (P = 1,2,3,4) [26].

Mode of operation	S1	S2	D1	D2
Mode 1	1	1	0	0
Mode 2 (S1-D1)	1	0	1	0
Mode 2 (S2-D2)	0	1	0	1
Mode 3	0	0	1	1

AHB converter has three different modes of operation states, as listed in Table 3. In phase A, switching signals (S₁, S₂) are operated based on the three modes of operation (magnetization, freewheeling, demagnetization). The strategy of current flow from DC link voltage is depicted in Fig. 3. (b)–(d). In total, there are 81 different possible switching states. Therefore, control signals (V_k) are obtained for each switch with proper gate signals generated through the controller. However, independent control of phase winding improves the fault-tolerant capability of the machine and increases overall system performance using this configuration.

The converter has three unique operating modes, as given in Table 3.In phase A, the switching signals (S1, S2) are regulated using three operating modes: magnetization is the first mode freewheeling is the second mode, and demagnetization is the third mode. Fig. 3(b)–(d) show the flow of current from the DC link voltage in different modes. Overall, there are 81 different switching combinations. As a consequence, control signals (Vk) are triggered for each switch, and the controller provides the required gate signals. This configuration enables separate control of the phase windings, increasing the machine's fault tolerance and overall system performance.

3. Model predictive control

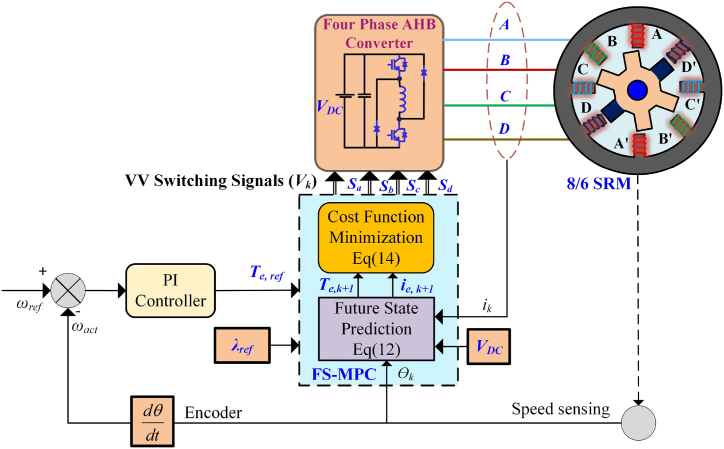
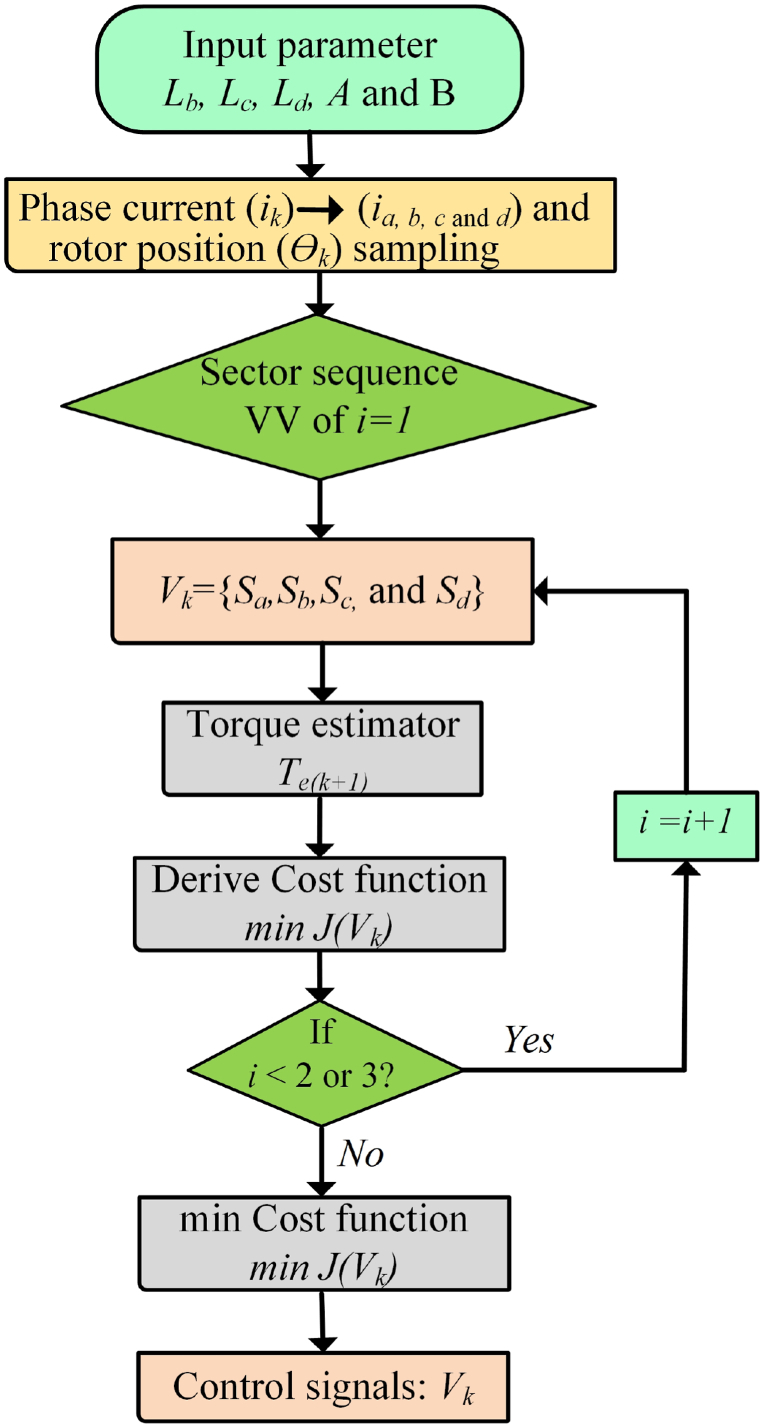
The functional block diagram of the proposed MPC control method for SRM is shown in Fig. 4. The derived voltage vectors for the proposed MPC control and its corresponding switching pulses are represent the different switching states. Initially the rotor position is detected by the flux. The phase flux and current at any time can be estimated using the phase current and the rotor position. The effective VVs are chosen by the multi objective function which adds the cost function to it. The cost function utilizes the reference torque and the current of the motor operating state at any instant.

Fig. 4.

Proposed controller functional diagram.

3.1. Selection of VVs

The proposed converter topology operated in three different modes that represented as 1, 0, −1. A DC link voltage has been provided across the windings of 4-phased SRM. The applied DC link voltage in these three modes of operation can be expressed as equation (11)

$$\begin{array}{c}\text{Mode}1,V_{p,1}=V_{DC}-2V_G-V_{R,L}\\ \text{Mode}2,V_{p,0}=-\left(V_D+V_G+V_{R,L}\right)\\ \text{Mode}3,V_{p,-1}=-\left(V_{DC}+2V_D+V_{R,L}\right)\end{array}]$$ (11)

Where V_G, V_D, and V_R are, voltage drop across switches, diodes and resistors respectively.

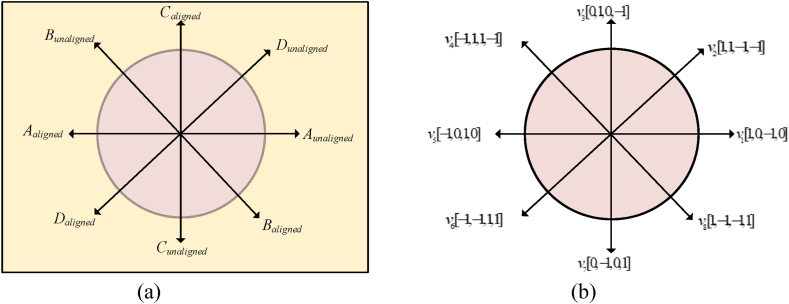
The 4-phase switching state is 3⁴ = 81 VVs. But, applying 81 different VVs generated V_k to SRM, calculates the torque evaluation and prediction at any instant requires more time for the execution of algorithm also it necessitates the need of system with higher configuration. The above problem is the main drawback for FS-MPC to adopt SRM drive in the automotive industry applications. Therefore, the conventional model used different switching tables derived from sector partition based on the rotor position that selects the active VVs. In this mode, the minimal quantity of active VVs decreases the computational load duration of the proposed FS-MPC. Furthermore, the use of VVs in sectors results in a reduction in inductance, leading to the generation of negative torque by the SRM. To mitigate the adverse torque, the overall quantity of functional VVs may be decreased. Consequently, the suggested MPC employs effective VVs state 81 to 8 active VVs, as shown in Fig. 5(a). Take 8/6 SRM as an example; the conduction sequence is A-B-C-D, with the stator phase windings stimulated in that order. The four-phase SRM can be divided into eight sectors, and the electrical angular period is 45°($\frac{2\pi }{N_r}$), as shown in Fig. 5(b). The switching table derived for conventional MPC is listed in Table 4. Consequently, this method may produce significant torque ripple at low and medium velocities while reducing computational load time.

Fig. 5.

The proposed rotor positions (a) eight sectors, (b) eight VVs.

Table 4.

Conventional switching table.

Switching state	Sec 1	Sec 2	Sec 3	Sec 4
Position	$\left[0°,15°\right]$	$\left[15°,30°\right]$	$\left[30°,45°\right]$	$\left[45°+60°\right]$
Ph-A	1,0,-1	1,0,-1	−1	−1
Ph-B	−1	1,0,-1	1,0,-1	−1
Ph-C	−1	−1	1,0,-1	1,0,-1
Ph-D	1,0,-1	−1	−1	1,0,-1

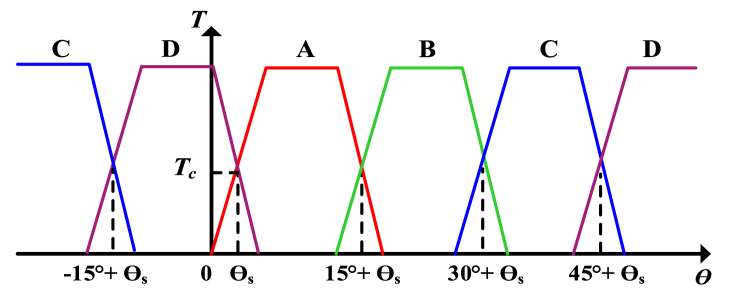
In Fig. 6, the commutation of each phase sequence order and rotor position, Phase A from $\theta s$ to 15°+ $\theta s$, Phase B from 15°+ $\theta s$ to 30°+ $\theta s$, Phase C from 30°+ $\theta s$ to 45°+ $\theta s$ and phase D from 45°+ $\theta s$ to $\theta s\text{,}$ are shown respectively.

Fig. 6.

Torque contributions of a four-phase 8/6 pole SRM.

The switching table proposed MPC is given in Table 5. The enhanced switching states for the 8/6 switched reluctance motor, where θs denotes the position of the stator pole coinciding with the rotor pole. Table 5 defines the eight sectors (N1 to N8), with an example in sector 1, where the position ranges from 0 to θ1 in Phase A, characterized by an unaligned position and a minimal derivative of inductance. In this circumstance, the switch state is designated as "0″ and "1". In the same location, the derivative of the inductance for Phase D is significantly elevated, resulting in the generation of positive torque in this phase; hence, the switch state is configured as “1”, “0”, and “-1”. Consequently, Phases B and C are demagnetized to “-1”. Correspondingly, the derivative inductance of each sector, the aligned position, and the demagnetization of phases are enumerated in Table 5. The proposed model used 4 active VVs instead of 8 VVs. This model effectively reducing the torque ripple and contribute to obtain smooth torque in the transition operation.

• •One phase controls the torque in single-phase conduction (per sector). Therefore, in this interval, there are only three switching states: 1, 0, and −1. Two switching vectors are produced by combining the switching states of each phase.
• •The torque of two neighbouring phases is regulated. Eight switching vectors are produced through the combination of the switching states of two neighbouring phases.

Table 5.

Selection of four-phase proposed switching table.

Switching state	Position $\left[{\theta }_A\right]$	P-A	P-B	P-C	P-D
Sector 1	$\left[0°,{\theta }_1\right]$	1,0	−1	−1	1,0,-1
Sector 2	$\left[{\theta }_1,15°\right]$	1,0,-1	−1	−1	0,-1
Sector 3	$\left[15°,15°+{\theta }_1\right]$	1,0,-1	1,0	−1	−1
Sector 4	$\left[15°+{\theta }_1,30°\right]$	0,-1	1,0,-1	−1	−1
Sector 5	$\left[30°,30°+{\theta }_1\right]$	−1	1,0,-1	1,0	−1
Sector 6	$\left[30°+{\theta }_1,45°\right]$	−1	0,-1	1,0,-1	−1
Sector 7	$\left[45°,45°+{\theta }_1\right]$	−1	−1	1,0,-1	1,0
Sector 8	$\left[45°+{\theta }_1,60°\right]$	−1	−1	0,-1	1,0,-1

The proposed model is applied for high or low phase SRM (example.,6/4,10/8,18/12.) then only to change the sector re-organized and select active VVs.

Fig. 6 illustrates the active VVs that are applied to the SRM phases to control, and by rotor position selecting these VVs with the proposed switching state are presented in Table 5. The proposed selected active VVs that lead to smoother transitions in the rotor position (example., In sector from the rotor position $\mathit{\theta }$₁–15°+ $\mathit{\theta }$_1, torque production is achieved by energizing the phase A windings to align the rotor poles with the stator poles, choosing active VVs as V₁ and V₅) Similarly, other rotor positions15°+ $\mathit{\theta }$₁–30°+ $\mathit{\theta }$_1, 30°+ $\mathit{\theta }$₁–45°+ $\mathit{\theta }$_1, and 45°+ $\mathit{\theta }$₁ to $\mathit{\theta }$₁ choosing active VVs are (V₂ V₆, V₃ V₇, and V₄ V₈) produce smooth torque at entire operations. The exact process was applied to eight sectors with respect to rotor position, respectively.

3.2. Derivation of torque and cost function

The torque and current with relate to the minimum error are the basic parameters for defining the objective function of proposed MPC control. As a result, the torque and current are approximated using (9 and 10), and the forecast value may be represented as equation (12).

$$\begin{array}{c}{T}_{ph,k+1}=\left[\frac{L_b-L_c}{2}{i_{k+1}}^2+A{i}_{k+1}-\frac{A}{B}\left(1-e^{-B{i}_{k+1}}\right)\right]f^{\prime }\left({\theta }_{k+1}\right)\\ T_{e,k+1}=\sum T_{ph,k+1}\\ \begin{array}{c}{i}_{e,k+1}=i_k+\frac{T_s}{\frac{d\lambda }{d{i}_k}}\left(V_{k+1}-R_s{i}_k-\frac{d\lambda }{d{\theta }_k}{\omega }_k\right)\\ {\theta }_{k+1}={\theta }_k+{\omega }_k{T}_s\\ {\lambda }_{s,k+1}=L_c{i}_{k+1}+\left[L_b{i}_{k+1}+A\left(1-e^{-B{i}_{k+1}}\right)-L_c{i}_{k+1}\right]f\left({\theta }_{k+1}\right)\end{array}\end{array}]$$ (12)

Initially, the sensors measure the phase current and rotor position. The magnitude of flux linkage, vector, and angle can be calculated using the phase current and voltage. The cost function then reduces the error and finds the optimum VVs [37,38], which is expressed as equation (13).

$$\begin{array}{c}\min J\left(V_k\right)={\left(T_{e,k+1}-T_{e,ref}\right)}^2+{\kappa }_1\left({\lambda }_{s,p+1}-{\lambda }_{s,ref}\right)\\ s.t.V_k\in \left\{S_a,S_b,S_c,\text{and}{S}_d\right\}\end{array}]$$ (13)

Where, J represents the cost function, k1 denotes the weighting factors chosen in relation to control objectives such as flux linkage deviance and reference, while k+1 signifies the discrete-time constant. The 4-phase switching states are chosen by the best active large and small VVs. The magnitude of reference flux is set to be constant, and reference torque is determined using a PI controller. Nonetheless, the cost function (13) illustrates the total torque estimation and flux monitoring performance, respectively. By effectively utilizing VVs in a proposed control strategy, SRM can achieve a substantial reduction in torque ripple, leading to smoother and more reliable motor operation. During different phases of SRM operation, the optimal VVs are selected based on the rotor position at each sector, as listed in Table 5. The proposed control approaches dynamically adjust VVs based on the motor state, and torque ripple is minimized across a wide range of operating conditions and avoid the complexity of system control objective. Therefore, the proposed model cost function incorporates two terms for control objectives. The first term of the control objective represents torque, and the second term represents stator current. In these conditions, torque production is smoother, increasing stability at phase energization and transition period. Finally, the proposed model cost function is expressed as equation (14)

$$\begin{array}{c}\min J\left(V_k\right)={\left(T_{e,k+1}-T_{e,ref}\right)}^2+{\kappa }_1\sum i_{k+1}^2\\ s.t.V_k\in \left\{S_a,S_b,S_c,\text{and}{S}_d\right\}\end{array}]$$ (14)

The cost function weighting factor(K₁ = 0.05) is selected to balance the torque and current to produce the control signal (V_k), which helps to evaluate and measure the rotor position, DC-link voltage and currents of each phase corresponding to the current state.

The weighting factor (K₁ = 0.05) was carefully selected based on comprehensive analysis and testing, demonstrating its efficacy in balancing the conflicting objectives of minimizing current and maintaining desired torque levels in SRM drives. This choice directly contributes to improved system efficiency, stability, and overall performance.

The proposed Model Predictive Control (MPC) is carried out on the MATLAB/Simulink platform to ascertain future instantaneous torque values using a minimized cost function, shown in Fig. 7. The outer speed control loop is conducted at each sample interval, whereas the MPC loop directly regulates the output variables for every potential state. Consequently, the optimum switching state will be implemented in the subsequent sample period. The following section discusses the simulation findings.

Fig. 7.

Flowchart of proposed FS-MPC.

4. Results and discussion

4.1. Simulation results

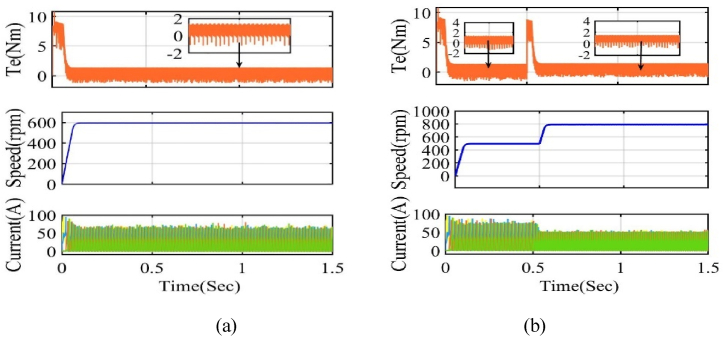
The 8/6 SRM with a 2.2 kW rating is designed using the JMAG simulation tool, incorporating flux linkage, torque, and rotor position profiles. The optimized machine model parameters have been developed and integrated into the proposed MPC framework in MATLAB/Simulink. These parameters were rigorously tested under various operating conditions. The results of both static and dynamic characteristics and the comprehensive analysis of the SRM performance are presented in this section. The MPC model yields a prediction of torque and flux linkage with minimal error, as demonstrated by the comparison. Thus, the waveform results and ripples are achieved successfully by the minimization of the MPC cost function error. The proposed MPC model, simulated in MATLAB/Simulink, operates at a reference speed of 1500 rpm and reference torque of 5 Nm for all operating conditions.

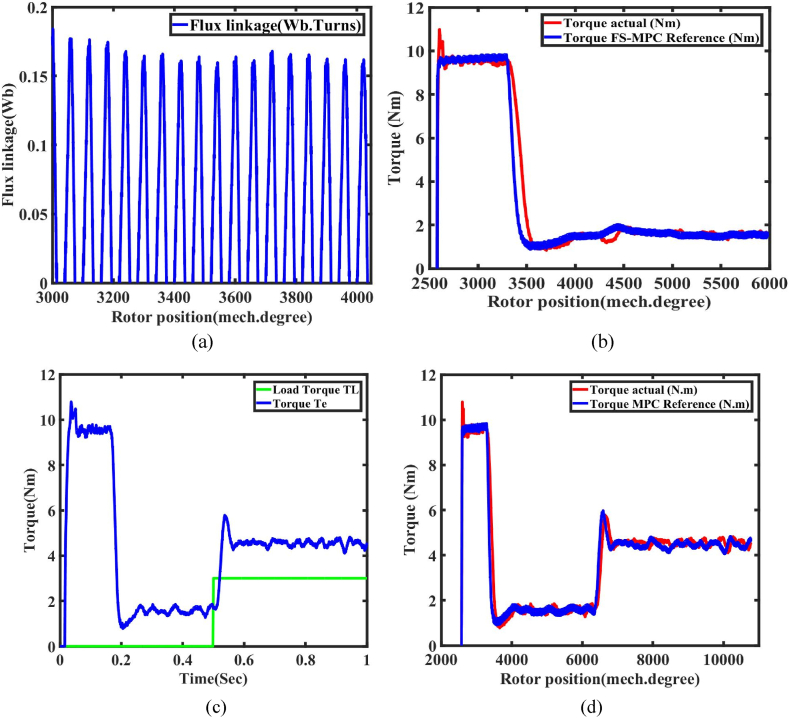
The flux linkage value, shown in Fig. 8(a), is measured at 0.174 Wb relative to the rotor location in both aligned and unaligned configurations. Fig. 8(b) depicts the load and actual torque attained with minimum positional error, across a speed range of 2500 rpm–6000 rpm. Throughout the simulation, a uniform sampling interval of 10μs and a fixed switching frequency of 10 KHz were maintained. The reference speed was established at 1500 rpm, and the actual speed was attained with a negligible error duration of 0.2 s.

Fig. 8.

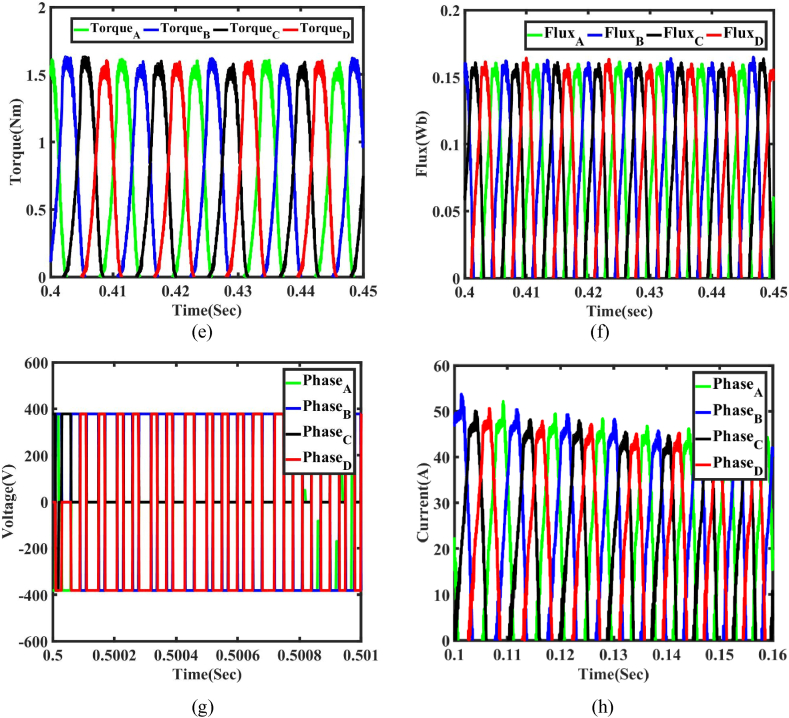
Simulation result of the closed-loop control with MPC at 1500 rpm reference speed. (a) Flux linkage variation at constant speed operation. (b) Actual and reference torque prediction with respect to rotor position (c) Simulation result of torque deviation with load torque (d) Load given at 0.5s (e) Torque at steady state (f) Four phase flux (g) DC link voltage (h) Phase current.

The instantaneous torque attains a peak of 10 Nm, but the load torque remains at 3 Nm throughout the 0.5 step response, as seen in Fig. 8 (c). The load torque escalates from the base torque to 6 Nm within 0.5 s, and the speed response is precise, shown in Fig. 8 (d). The proportional-integral control is achieved by reducing the speed error at 0.2 s by the optimization of Kp and Ki parameters. Upon attaining the aligned position, the phase current persists for a lengthy period, establishing a steady state for electromagnetic torque and flux throughout all four phases, shown in Fig. 8(e) and (f). The DC link voltage of the four-phase AHB converter is 380 V, with phase currents sustained at 50 A, shown in Fig. 8(g) and (h).

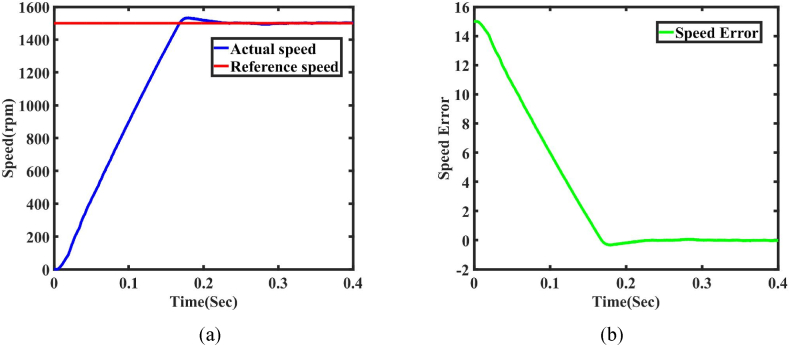
The PI control reference speed is maintained at 1500 rpm, and the actual speed reaches 0.17s, as shown in Fig. 9 (a). The speed error becomes zero at 0.17s, providing a reference torque of 2 Nm, as shown in Fig. 9 (b).

Fig. 9.

Simulation result of the closed-loop control with MPC at 1500 rpm reference speed (a) Actual speed response at 0.2 s with respect to reference speed. (b) reference speed and error settled minimum at 0.2 s.

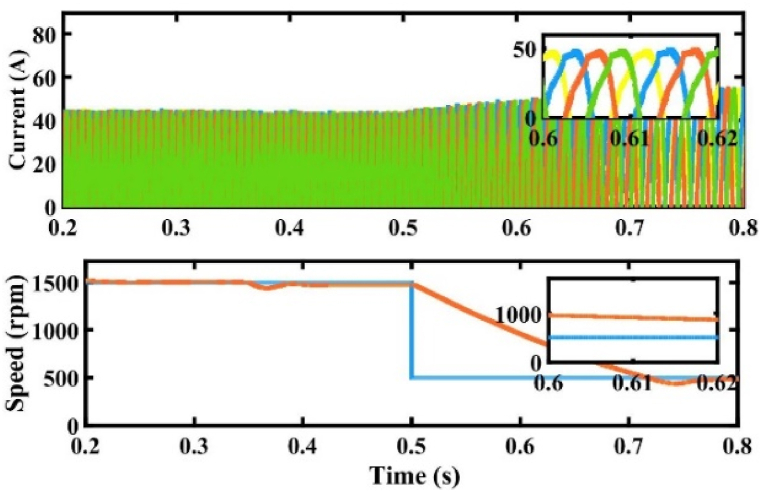
In the steady state condition, reference speed maintains at 1500 rpm concerning initial time to 1s. Hence, dynamic conditions operate at different speeds with accelerations of 1500 rpm–500 rpm, as depicted in Fig. 10. Further, investigate the effectiveness of the proposed method for the below base speed of 1000 rpm and reference torque of 5 Nm.

Fig. 10.

Simulation results of speed response from 1500 rpm to 500 rpm at 0.5 s.

The time analysis of various performances is addressed. The proposed MPC for the SRM drive reduces the time needed to anticipate and choose the best switching state. The computational duration rises because of the evaluation of the load model and cost function, which is performed eighty-one times for various VV choices.

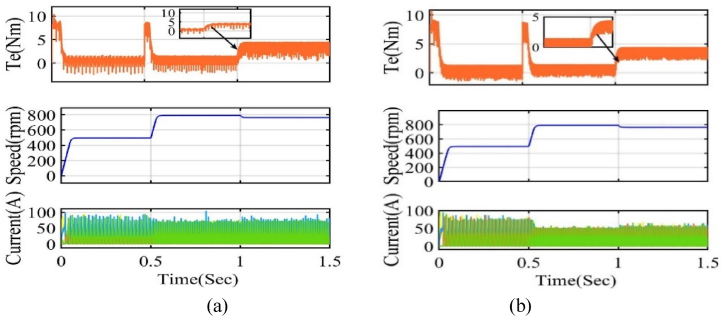
Fig. 11 shows the simulation results of the whole speed response for both traditional MPC and the suggested MPC. The traditional MPC exhibits constant, dynamic, and load response activities, characterized by significant torque ripple, as seen in the waveform shown in Fig. 11 (a). Likewise, the same circumstance pertains to the suggested model, and it is noted that the SRM at steady-state velocity generates less torque ripple in comparison to the standard MPC, shown in Fig. 11 (b). The application of a 3 Nm load response at 1 s yields a rapid dynamic response while preserving consistent torque ripple with smooth fluctuation. Consequently, the steady-state response of the proposed model at 600 rpm diminishes the torque ripple, as seen in Fig. 12 (a). On raising the speed from 500 rpm to 800 rpm, the torque ripple progressively diminished and attained a saturated value, shown in Fig. 12 (b). The findings indicate that the suggested Model Predictive Control (MPC) generates lower torque ripples compared to traditional control methods.

Fig. 11.

Simulation results of dynamic speed response (a) Conventional MPC (b) Proposed FS-MPC.

Fig. 12.

Simulation results for proposed FS-MPC speed response (a) Steady state 600 rpm (b) 500 rpm–800 rpm.

4.1.1. Hardware Realization and experimental results

Fig. 13 shows the experimental configuration for the SRM drive test. A prototype of the 8/6 SRM, integrated with load, speed, and torque sensors, is affixed next to the motor and linked to the AHB converter. The AHB converter has an input DC link voltage of 380V and a rated current of 20A. The hall sensor transmits rotor position data to the controller, the torque sensor detects torque signals, and the current sensor senses current signals. Furthermore, all these signals are transmitted to the real-time control prototyping WAVECT (WCU300) box, which operates in real-time mode. The torque ripple value is quantified by standard deviation, expressed as equation (15)

$$T_r=\frac{T_M-T_m}{T_{av}}\ast 100\%$$ (15)

Where T_r represents torque ripple, T_m represents minimum torque, T_M represents maximum torque, and T_av represents average torque.

Fig. 13.

Experimental set-up for 8/6 SRM-AHB with proposed MPC.

The parameters configured for the SRM drive are detailed in Table 6. An electrically powered electrodynamometer is interfaced with the SRM to perform tests across various load conditions. Speed measurement can be accomplished through the use of an encoder. The waveforms were captured using six-channel oscilloscopes with a bandwidth of 200 MHz, and the corresponding data and screenshots were recorded.

Table 6.

Experimental setup details.

Experimental setup	Specifications
SRM	8/6, 2.2 kW,400V
MSO	Tektronix MSO44 4-BW-200
AHB	8 Power MOSFET, 8 Power Diode
GW Current Probe	GW INSTEK GCP300
Controller	WAVECT (WCU300)
GW Voltage Probe	GW INSTEK GDP050

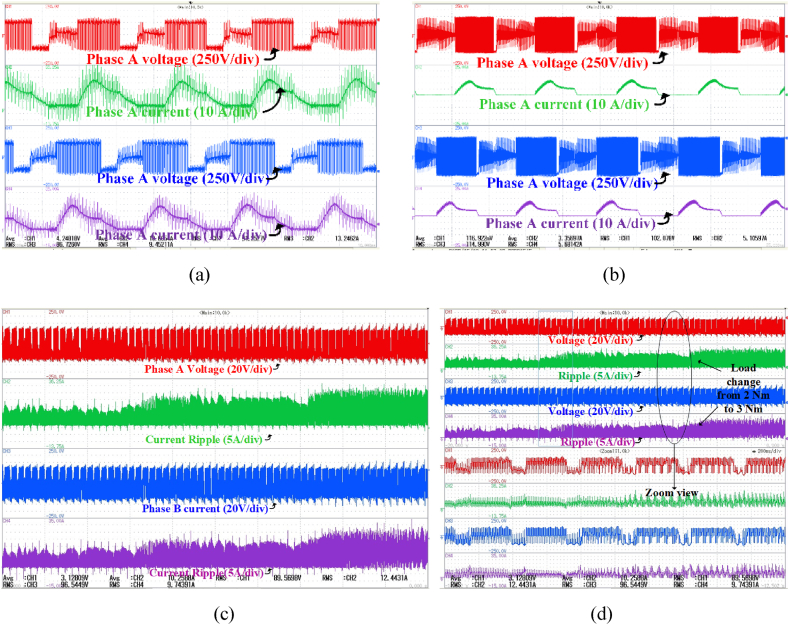
The hardware configuration for SRM-MPC was used to investigate various operating situations to analyze the responses of speed, torque, and flux ripple. An autotransformer was used to control the voltage supply to the AHB converter at the nominal operating voltage. The experimental configuration and measuring apparatus are enumerated in Table 6. The experimental findings demonstrate the phase currents and voltages, both in steady state and dynamic state (forward and reverse), as well as the load response of the effective implementation of FS-MPC drive SRM.

Fig. 14 (a) shows the current output of conventional method observed from the experimental validation. Phase Current of the proposed method is shown in Fig. 14(b). The ripples and the torque variation in the experimental validation is shown in Fig. 14(c) and (d). The findings indicate that the suggested model sustains a 380 V DC connection voltage and a 50 A phase current. The phase current of FS-MPC exhibits a reduced current ripple in comparison to the MPC system. The phase current directly affects the phase torque. The flux and torque ripple of the two-phase system at steady-state performance, as well as during dynamic load torque variations from 2 Nm to 3 Nm, have been experimentally validated.

Fig. 14.

Results of experimental validation (a) Current output of conventional method (b) Phase Current of proposed method (c) Ripples from the proposed method (d) Torque variation from 2 Nm to 3Nm.

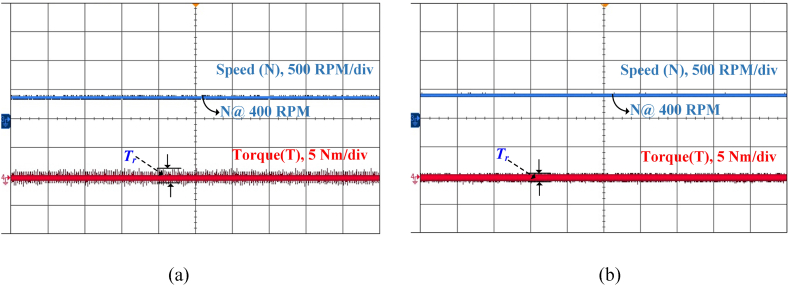
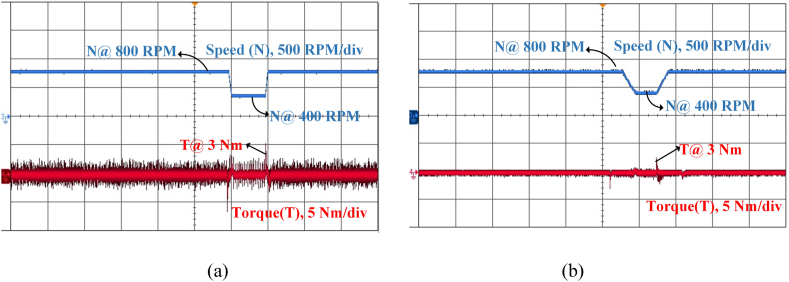
The steady-state speed response of 400 rpm for both conventional and suggested MPC is shown in Fig. 15(a) and (b), respectively. The waveforms indicate that the proposed MPC approach reduces torque ripples and spikes.

Fig. 15.

FS-MPC SRM drive steady state torque and speed at 400 rpm (a) Conventional (b) Proposed (Time axis: 1 s/div).

The proposed FS-MPC shows in Table 7, a computational time of 0.5 ms per iteration, significantly lower than the conventional MPC (1.5 ms). The proposed method uses 10 KB of memory, substantially lower than the conventional MPC, indicating a balanced use of computational resources while maintaining efficiency. The converges in 3 iterations, faster than the standard MPC (7 iterations). This faster convergence speed highlights the effectiveness of the optimized cost function in achieving desired control outcomes more rapidly.

Table 7.

Quantitative comparison results.

Control Techniques	Computational time (ms)	Memory usage (KB)	Convergence speed (iterations)
Conventional MPC	1.5	15	7
Proposed FS-MPC	0.5	10	3

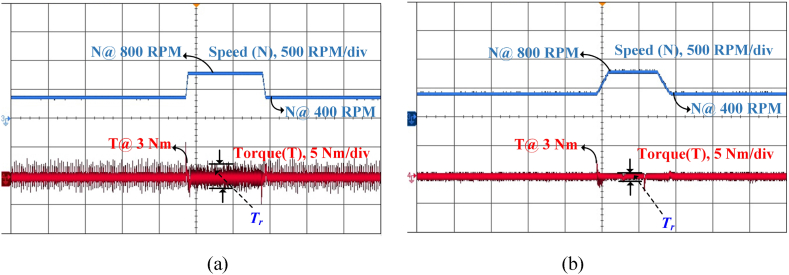
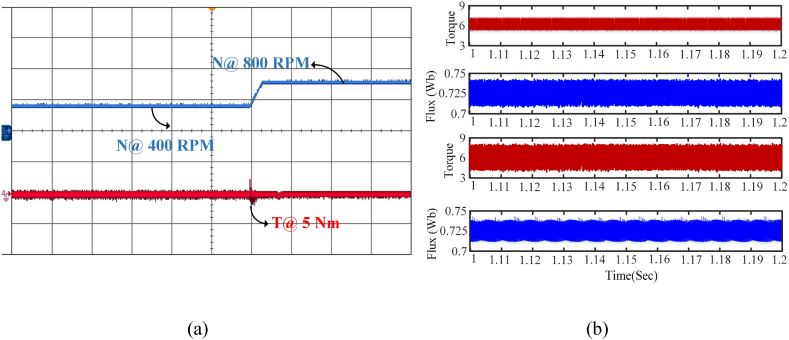
Fig. 16 shows the dynamic speed response of the forward operation for both the standard and suggested MPC. The speed response is initially sustained at 400 rpm under steady-state circumstances, with a torque value of 3 Nm. The speed increases in forward acceleration from 400 rpm to 800 rpm, with torque reaching 8 Nm. Correspondingly, the rotational speed decreases from 800 rpm to 400 rpm during forward deceleration, while the torque attains a value of 3 Nm. Under forward situations, the acceleration response from 400 rpm to 800 rpm generates less torque ripple compared to the usual scheme, as seen in Fig. 16(a) and (b). During the deceleration from 800 rpm to 400 rpm, it is noticed that the suggested MPC approach exhibits less torque ripples in comparison to the traditional scheme. The speed reverse reaction from 800 to 400 rpm for both conventional and suggested methods is shown in Fig. 17(a) and (b). The waveform analysis indicates that the suggested model generates reduced torque ripple in comparison to traditional methods, as shown in Table 7. The MPC controller's speed responses, seen in Fig. 18 (a), exhibit more rapid dynamic changes at full load circumstances, with the requisite load torque sustained at 8Nm. The dynamic load response exhibits a rapid and seamless shift between 1s and 1.2s, with a speed response of 800 rpm. Fig. 18 (b) indicates that the flux and torque ripples are measured at steady-state low and medium speeds, with a minimum duration of 1–1.2 s. It is noticed that at a speed of 400 rpm, torque and flux ripples are more pronounced compared to the reaction at 800 rpm. Consequently, the results indicate that the SRM generates significant torque ripple at low speeds and little torque ripple at high speeds. The performance evaluation of the traditional and new MPC schemes for SRM is shown in Table 8. The torque and flux ripples are computed with the standard deviation approach.

Fig. 16.

FS- MPC SRM drive dynamic forward speed from 400 to 800 rpm (a) Conventional (b) Proposed (Time axis: 1 s/div).

Fig. 17.

FS-MPC SRM drives dynamic reverse speed from 800 to 400 rpm (a) Conventional (b) Proposed (Time axis: 1 s/div).

Fig. 18.

Experimental result of the MPC-SRM drive (a) Load response at full load (b) Torque and flux ripple at steady state (speed medium and low) speed operation. (Time axis: 1 s/div).

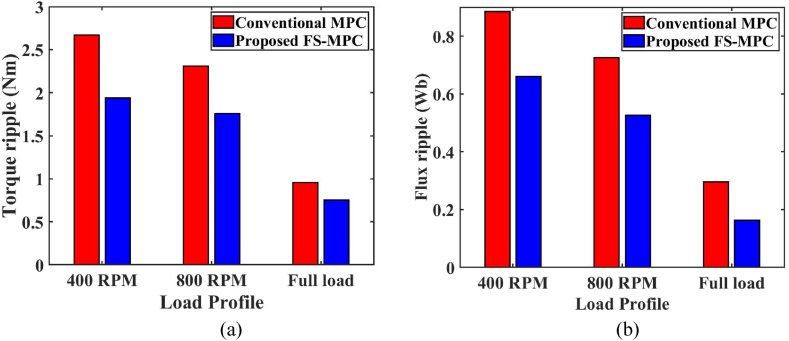
Table 8.

Result comparison.

Speed	400 rpm	800 rpm	Full load
Conventional MPC
Flux ripple (Wb)	0.875	0.715	0.296
Torque ripple (Nm), Tr	2.61	2.31	0.941
Proposed FS- MPC
Flux ripple (Wb)	0.661	0.527	0.163
Torque ripple (Nm), Tr	1.82	1.72	0.742

Table 7 presents a comparative performance study of the SRM drive using the standard MPC approach vs the proposed FS-MPC technique. The computed torque ripple value is 9 % using this FS-MPC, which is lower than the torque ripples reported in the literature at 20.12 % [28] and 21.35 % [31] using standard Model Predictive Control (MPC) methods. The torque ripple comparison between the proposed and traditional Model Predictive Control (MPC) at steady-state speeds of 400 rpm, 800 rpm, and at full load conditions of 8 Nm is shown in Fig. 19.

Fig. 19.

Result comparison (a) Torque ripple (b) Flux ripple.

The overall outcomes and discussions justify the proposed MPC methodologies against traditional MPC, specifically in mitigating low torque and flux ripples at both steady-state and dynamic speed settings (low and medium). Furthermore, load step alterations at full load circumstances in SRM drives diminish torque ripple and demonstrate rapid dynamic speed response. The proposed Model Predictive Control approach has a minimal error cost function goal that aids in diminishing torque and flux ripples. The proposed MPC is regarded as one of the most effective solutions for mitigating torque ripple in Switched Reluctance Motor (SRM) drive systems. It demonstrates efficacy in rapid dynamic speed response throughout both low and medium speed ranges, as well as a decrease in torque and flux ripples of the SRM Drive.

Compared with other classical methods: The proposed FS-MPC approach is compared with various traditional control methods in Table 9. In Ref. [30], the continuous control set-MPC approach used in SRM drive exhibits nonlinear behavior in control goal estimation, prolonged prediction time, and a rising cost function, resulting in a complicated and expensive controller. In Ref. [44], the model predictive current control employs a singular cost function, and the purpose of the hysteresis loop reduces complexity within a single prediction time frame; nevertheless, the phases augment switching variables, resulting in increased complexity and extended calculation time for the algorithm. In Ref. [28], the Model Predictive Torque Control (MPTC), which assesses two or three control voltage vectors (CVVs) throughout each control period, efficiently reduces torque ripple; but, it necessitates torque estimate from two rotor locations, hence increasing the complexity of the controller. In Refs. [22,25], traditional DTC methods necessitated two hysteresis loops for the measurement of torque or flux. Additionally, rotor position-current-torque characteristics are required to construct a look-up table, leading to significant torque ripple and time-intensive flux linkage calculations.

Table 9.

Compared to other existing control techniques.

	Dynamic response	Torque ripple	Number of VVs	Controller	Modulator required	Torque estimation	Ref
CCS-MPC	Complex	Medium	9	Multiple cost function	Yes	Polynomials	[30]
MPCC	Medium	Medium	9	1 Hysteresis loop 1 Cost function	No	Look up table	[[37], [50]]
MPTC	Complex	Low	2	2 Hysteresis loop 1 cost function	No	Composite function	[28]
DTC-SMC	Complex	Medium	6	1 Hysteresis loop External torque	No	Look up tables	[22]
Classical DTC	Medium	Medium	4	2 Hysteresis loop	No	Look up tables	[25]
Proposed Method	Medium	Low	9	1 cost function	No	Composite function	–

5. Conclusion

The proposed FS-MPC approaches for the 8/6 SRM, developed in MATLAB/Simulink, are verified by simulation results demonstrating reduced torque and flux ripple. The suggested FS-MPC system optimally determines the voltage vector according to the error levels of the output cost function. The controller was assessed and examined in both constant and dynamic speed operational modes. The performance of FS-MPC is critically analyzed and appraised. Furthermore, experimental outcomes are juxtaposed with modelling findings at varying operating speeds to assess torque and flux ripples. The achieved decrease in torque ripple is 9 % using this FS-MPC. Consequently, the non-linear characteristics of the MPC algorithm design are well aligned with the SRM drive system. The suggested FS-MPC algorithm, owing to its simplicity and reduction of ripple, is suitable for use in electric car applications. The analysis indicates that the proposed approach is more effective for reducing torque ripple than for mitigating flux ripples.

CRediT authorship contribution statement

Deepak Mohanraj: Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. Devakirubakaran S: Visualization, Validation, Resources, Investigation, Data curation, Conceptualization. Praveen Kumar Balachandran: Writing – review & editing, Supervision, Project administration, Investigation, Funding acquisition, Formal analysis.

Data and code availability statement

No data was used for the research described in the article.

Declaration of competing interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:Corresponding author (Praveen Kumar Balachandran) currently holds the Associate Editor position in Heliyon, Energy. If there are other authors, they declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.