Abstract
We explore ocean circulation on a rotating icy moon driven by temperature gradients imposed at its upper surface due to the suppression of the freezing point of water with pressure, as might be induced by ice thickness variations on Enceladus. Using high-resolution simulations, we find that eddies dominate the circulation and arise from baroclinic instability, analogous to Earth’s weather systems. Multiple alternating jets, resembling those of Jupiter’s atmosphere, are sustained by these baroclinic eddies. We establish a theoretical model of the stratification and circulation and present scaling laws for the magnitude of the meridional heat transport. These are tested against numerical simulations. Through identification of key nondimensional numbers, our simplified model is applied to other icy moons. We conclude that baroclinic instability is central to the general circulation of icy moons.
Baroclinic eddies, analogous to weather systems on Earth, are ubiquitous in the ocean of icy moons.
INTRODUCTION
Enceladus has a global subsurface ocean (1, 2) with active physical and chemical processes occurring within it. Observations of water jets emanating from the south pole of Enceladus reveal the presence of several chemical compounds that come from its ocean interior, including liquid water, sodium salts, carbon dioxide, methane, and macromolecular organic compounds (3–6). Evidence of ongoing hydrothermal activity on Enceladus is also emerging, indicative of habitability (7, 8). It is therefore important to understand the ocean circulation on Enceladus and its role in physical transport of properties such as heat and chemical tracers.
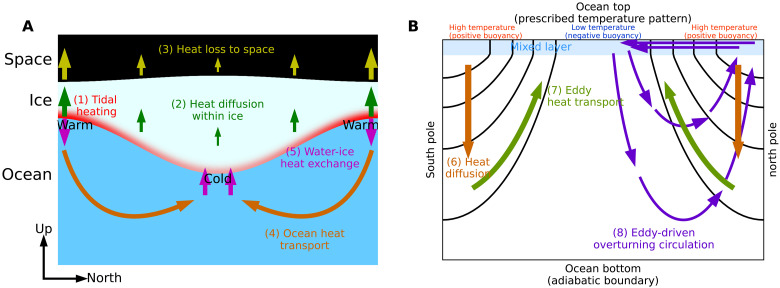
Ocean circulation on icy moons is often envisioned as a rotating body of water heated from the bottom (9–11). However, heat and salinity fluxes from the ice at its upper boundary can also drive ocean circulation (12–16), if ice thickness variations are substantial, which has been confirmed by shape and gravity measurements collected by Cassini (17). Enceladus, for example, is known to have an ice shell whose thickness varies by as much as its mean depth on moving from the equator where the ice is thick to the pole where it is thin (18–20). The resulting temperature variations beneath the Enceladean ice shell, due to the dependence of freezing point on pressure stemming from the Clausius-Clapeyron relation, are likely to be at least an order of magnitude greater than the temperature contrast induced by bottom heating (15, 21). As a result, the ocean just beneath the ice is warm at the poles and cold at the equator, as sketched in Fig. 1.
Fig. 1. Schema of the energy budget of the ice shell and ocean circulation on an icy moon driven from the upper boundary.
In the absence of abyssal heat sources, the following processes contribute: (1) tidal heating in the ice shell, (2) heat diffusion within the ice, (3) heat loss to space, (4) ocean heat transport, and (5) water-ice heat exchange. In (A), the temperature difference between the water-ice interface and the very top of the ice induces outward diffusion of heat, which is ultimately lost to space. Ocean circulation is induced by freezing point temperature variations at the ice-ocean interface, which make the poles warm because the ice is thin there, relative to the equator where it is thick. The ocean therefore carries heat from the poles to the equator. The resulting heat exchange between the ice and the ocean tends to smooth out ice shell geometry variations. In (B), the ocean circulation is driven by a prescribed top temperature variation. Black lines represent temperature surfaces, here synonymous with isotherms because salinity plays no role. The top temperature is higher over the poles and lower at the equator. This pole-to-equator temperature gradient is diffused down vertically into the ocean [process (6)], supporting zonal currents that spawn baroclinic eddies. The eddies flux heat down the temperature gradient [process (7), eddy heat transport]. This eddy transport can be equivalently viewed as an overturning circulation sinking at the equator and rising near the poles [marked as (8), eddy-driven overturning circulation, shown only in the Northern Hemisphere]. There is a balance between eddy transport of heat (7) [or equivalently, the overturning circulation (8)] and vertical diffusion of heat (6). Note that here we have assumed that the buoyancy of seawater depends only on temperature and that the thermal expansion coefficient is positive. The temperature and circulation patterns in (B) are inspired by previous works (14, 15).
Salinity strongly affects the thermal expansion coefficient of water and the salt flux associated with freezing and melting. Both influence the strength and direction of ocean circulation (15). Depending on whether the ocean salinity is greater or smaller than 20 g kg−1 (10, 15, 22, 23), the ocean of Enceladus can be categorized as in either “high-salinity” or “low-salinity” regimes. In the former, water expands upon warming, so that both the temperature and salinity forcing from ice creates high-density water at the equator, which then sinks. In contrast, in the low-salinity scenario, water contracts upon warming. Temperature-induced density anomalies dominate those due to salinity, making polar waters denser. As a result, the overturning circulation reverses. In the absence of direct observational constraints, the salinity of the ocean on Enceladus can be anywhere between 2 and 40 g kg−1 (23), and thus it remains unclear if the high-salinity or low-salinity regime is the most relevant. In this study, we focus on the high-salinity regime. Moreover, for simplicity, we also ignore spatial variations of salinity.
In Earth’s ocean, the action of the wind leads to Ekman pumping, which perturbs the density field in the interior (24). On an icy moon, in contrast, there are no winds acting and so the upper boundary condition must be drawn down into the interior through a different mechanism. Vertical mixing due to ocean tides and small-scale processes (25–27) likely diffuses the upper boundary condition into the interior. In addition, spatial variations of ice-ocean stresses due to tides, eddies, and mean flows can also induce Ekman pumping even in the absence of surface wind stress.
Once a meridional density gradient is established in the interior of the ocean, baroclinic eddies—a hydrodynamical instability of ocean currents in thermal wind balance—may grow. Because the ocean of Enceladus has a small Rossby number (between ∼10−6 and ∼10−4) (11, 28), gravity acting on sloping buoyancy surfaces is balanced by the tilting over of planetary vorticity by the vertical shear of zonal currents, as expressed in the thermal wind relationship. Expectedly, as to be demonstrated by numerical simulations here, such zonal flows are baroclinically unstable (16), creating a vigorous eddy field that is dynamically similar to baroclinic weather systems observed in Earth’s atmosphere and ocean. These eddies turn out to be the primary agent of meridional heat transport from the (warm) polar regions to the (cold) equatorial regions and thus play a central role in the energy budget of Enceladus (Fig. 1). The main focus of our study is to highlight the role of ocean weather systems on Enceladus and their contribution to setting up the stratification, depth of penetration, and pattern of ocean currents in the equilibrium state. The framework that we will use has much in common with those developed to describe the Antarctic Circumpolar Current of Earth’s ocean (29, 30).
We use eddy-resolving simulations of an ocean circulation configured in an idealized setting appropriate to Enceladus. The circulation is energized by diffusing down into its interior meridional temperature gradients prescribed at its upper surface. The meridional temperature gradients result in baroclinic instability. As a result, baroclinic eddies, which are dynamically exactly analogous to weather systems in Earth’s atmosphere, are generated and become the dominant agency of energy transfer. These eddies induce down-gradient heat flux in the ocean, which transport heat from high latitudes (warm) to low latitudes (cold). The physical transport by these eddies can be represented with an eddy-driven meridional overturning circulation, and this overturning circulation, together with vertical diffusion, becomes the main mechanism of tracer transport. The strength of such transport is controlled by the balance between vertical heat diffusion, which energizes eddies by diffusing the meridional temperature gradient from the top boundary into the ocean interior, and downward-gradient eddy heat flux, smoothing out the meridional temperature gradients. On the basis of this idea, a theoretical model and scaling laws are used to interpret our simulations expanding on the prior Lobo2021 model (14). Our simulations show that Lobo2021’s choice of eddy diffusivity coefficient, which was motivated by Earth’s ocean dynamics, is not appropriate to Enceladus resulting in them overestimating the strength of overturning circulation and underestimating the penetration depth of the thermocline by several orders of magnitude. Implications of our study for the oceans on other icy moons are also discussed.
RESULTS
Modeling framework
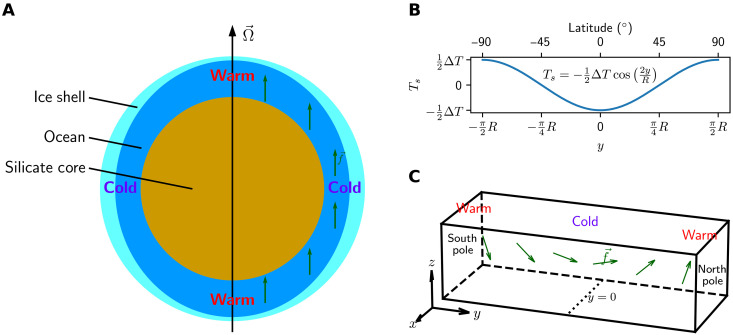
We consider flow in a Cartesian box configured to represent flow in a spherical shell, as set out in Fig. 2. Flow is energized through a lateral temperature gradient chosen to have a cosine meridional profile with amplitude ΔT (see Fig. 2B) imposed at its upper boundary. This is diffused down into the interior as a rate determined by κ. The two key external parameters of our study are ΔT and κ. The bottom is insulating. Here, no attempt is made to represent the dynamical effect of possible fluid-depth variations associated with the nonconstant ice shell thickness.
Fig. 2. An idealized model for the ocean of an icy moon.
(A) Diagram of an icy moon, the ice shell of which is thin at the poles and thick at the equator. The nonuniform ice shell induces a temperature gradient at the top of the ocean. We use a cosine temperature profile, as shown in (B), to represent this top temperature forcing in our numerical simulations. Here, ΔT is the pole-to-equator temperature difference, and Ts is the top temperature. (C) Setup of our numerical simulations. We use a cuboid to represent the ocean; in Cartesian coordinates, the x, y, and z directions point eastward, northward, and upward, respectively. The green arrows in (A) and (C) show the Coriolis parameters at different locations.
The extent of the box in the eastward x, northward y, and vertical z directions is [0, Lx], [−πR, πR], and [−H,0] respectively. Here, Lx = 102 km; R, the radius of the moon, is 252 km; and H, the depth of the ocean, is 30 km. The western (x = 0) and eastern (x = Lx) boundaries are periodic. We set rotation rate Ω = 5.3 × 10−5 s−1 and gravity g to 0.1 m2 s−1. All the above parameters are appropriate to Enceladus (17, 19, 31, 32).
We use a model known as Oceananigans (33), coded in Julia and running on graphics processing units (GPUs), which solves the rotating, nonhydrostatic equations for a Boussinesq fluid in a cube at a very high resolution. Despite using a Cartesian framework, as described in (11), we can nevertheless represent the dynamics of a deep, rotating fluid in spherical geometry using equations that capture the change with latitude of the angle between the rotation vector and gravity. Derivations of such equations was pioneered by Grimshaw (34), who wrote down a nontraditional β plane set for a fluid on a rotating planet in which the vertical component of the Coriolis parameter was allowed to vary in the horizontal, while the horizontal component (set to zero on the traditional β plane) was kept constant. Dellar (35) advanced Grimshaw’s work by using Hamilton’s principle to derive a nontraditional set in which both components of Coriolis are allowed to vary in latitude, without sacrificing conservation properties. In the Supplementary Materials, we write out the equations inspired by Dellar’s work used here.
The Coriolis parameter is chosen to mimic that in a spherical shell (green arrows in Fig. 2) and is given by
| (1) |
This form guarantees that the angle between g and f is as it is on a rotating sphere and that f is nondivergent, ensuring conservation of potential vorticity (PV) in adiabatic, inviscid flow.
The tangent cylinder—a cylinder whose axis is parallel to the moon’s rotation vector with sides tangent to the inner core—separates the ocean into two dynamically distinct regions (10, 11, 13, 16). In our Cartesian framework, the tangent cylinder is a curved surface (Fig. 2C), which is tangent to the ocean bottom at the equator, normal to the bottom at the poles, and parallel to f everywhere in between.
We adopt a highly idealized equation of state in which the buoyancy depends only on temperature through a thermal expansion coefficient, α, which is assumed to be constant and positive, appropriate if the ocean has a salinity greater than 20 g kg−1 (10, 15, 22). The buoyancy, b = −g δρ/ρref, where δρ is the density anomaly related to temperature, T, by a linear equation of state
| (2) |
and Tref is a reference temperature. We use a constant thermal expansion coefficient, α, of 1.67 × 10−4 K−1 in all simulations.
The appropriate value of the thermal diffusivity κ is highly uncertain but will likely be much larger than the molecular value of water because here it represents mixing by turbulent processes. We adopt a range of values. The minimum κ used is 1 × 10−3 m2 s−1. This has been used in previous studies (16, 36) and inferred from a scaling for vertical diffusivity appropriate to Earth’s ocean (37) assuming a dissipation rate in the ocean of Enceladus (26). The maximum diffusivity used here is 0.1 m2 s−1. Although larger values could be considered, they are inconsistent with energy constraints on Enceladus, as described later in Implications for Enceladus.
We run two groups of experiments. One uses a constant ΔT = 0.1 K and various κ’s of 1 × 10−3, 3 × 10−3, 1 × 10−2, 3 × 10−2, and 1 × 10−1 m2 s−1. The other group uses a constant κ = 1 × 10−3 m2 s−1 and various ΔT’s of 0.025, 0.05, 0.1, and 0.4 K. All simulations are run out until equilibrium is established and the last 10,000 rotation periods are used for diagnostic purposes.
Phenomenology of the reference solution
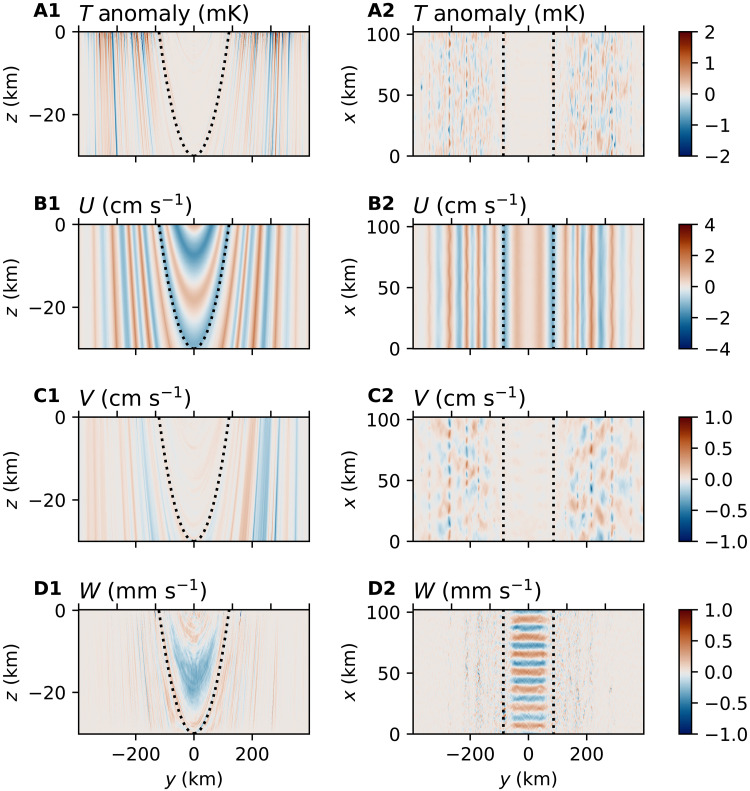
Turbulence, eddies, and zonal flows dominate the ocean circulation in all our experiments. The instantaneous velocity field of the reference solution, with ΔT = 0.1 K and a vertical diffusivity of κ = 1 × 10−3 m2 s−1, is shown in Fig. 3 and is typical of the kind of solutions we obtain. The zonal flow U comprises very many alternating jets at all latitudes, which are mostly aligned with the rotation axis (Fig. 3, B1 and C1), indicating the dominance of the barotropic component. We decompose the U field into the barotopic component, which is invariant along the rotation axis, and the remaining baroclinic component (fig. S1). The baroclinic component is one order of magnitude weaker than the barotropic component as the weak damping in our model allows energy to accumulate in the system as barotropic jets. Thermal wind balance is manifested by the correspondence between the baroclinic U field and the T field. A similar flow field has been found in previous studies with three-dimensional (3D) configurations (11, 16, 38). It is markedly different from the patterns of flow seen in 2D systems, in which geostrophic turbulence induced by baroclinic instability or convection cannot exist and lateral heat transport primarily occurs along the boundaries (15, 36). When the zonal dimension is resolved, baroclinic turbulence plays the dominant role in transporting heat and angular momentum, the latter giving rise to jets as is evident in Fig. 3B1. This is in accord with 3D simulations forced through interaction with the ice (16) and/or bottom heating (9, 11, 13, 38).
Fig. 3. Zonal jets and baroclinic eddies in the reference simulation.
The column on the left shows the instantaneous (A1) temperature anomaly, (B1) zonal velocity, (C1) meridional velocity, and (D1) vertical velocity along a zonal cross section. Here, the anomaly is defined as the instantaneous departure from the zonal mean. The column on the right (A2 to D2) shows the same fields on a horizontal cross section, which is at the depth of 15 km, halfway down the water column. The black dotted lines represent the tangent cylinders.
The zonal jets are almost aligned with the planetary rotation axis instead of the direction of gravity, as expected by the Taylor-Proudman theorem, which pertains in the limit that the buoyancy frequency (N) is much smaller than the rotation frequency (measured by the Coriolis parameter, f). When N/f << 1, vortex tubes tend to align with the direction of the rotation axis. This is the case in our simulations and will also likely be true on Enceladus provided that the buoyancy gradient induced by the salinity gradient is not so strong that the buoyancy forcing at the top creates a strong stratification near the poles, making N larger than f. However, this seems unlikely to happen because the buoyancy gradient due to salinity is estimated to be of the same order as that due to temperature (15). In our reference simulation, N/f is of order 10−1, a consequence of the large depth of the ocean and the smallness of the imposed temperature gradient.
Baroclinic eddies are most clearly evident in the latitude-longitude plot of the temperature anomaly (Fig. 3, A2 and D2). The characteristic length of these eddies is several kilometers and, as discussed below, well matched with the Rossby deformation radius. Baroclinic eddies predominate at mid-to-high latitudes (inside the tangent cylinder), whereas roll-like structures dominate in equatorial regions (outside the tangent cylinder), as can be seen in Fig. 3 (D1 and D2). These rolls are a prominent feature of the solutions presented in a previous study that simulates ocean convection driven by bottom heating on Enceladus (11). Because the temperature is almost uniform outside the tangent cylinder, the heat transport due to rolls is rather weak and is not our focus here.
Scale of jets and eddies
The lateral scale of the jets might be expected to depend on the Rhines scale because the inverse cascade of 2D eddy energy will be arrested by the β effect (39). This theory has been used to successfully explain jet widths in previous studies (11, 40). Following their method, the Rhines scale is defined as
| (3) |
where U is the peak zonal velocity of the jet, θ is the latitude of the jet, and β is the topographic β parameters
| (4) |
where h is the length of the Taylor column measured parallel to the rotation axis and s is the axial distance between the Taylor column and the rotational axis.
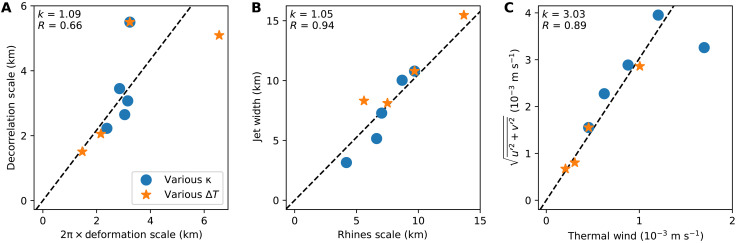
In fig. S2A, we show the instantaneous zonal-mean zonal velocity at mid-depth in the ocean as a function of latitude. Every local maximum of u2 represents the center of the corresponding jet (marked by orange circles), flanked by minima (marked by red dashed lines); the width of the jet is defined as the latitudinal distance between neighboring local minima of u2 (marked by red dashed lines) divided by π (11, 40). We find that jet widths match well with the Rhines scales in middle and high latitudes in all our experiments: Figure 4A shows that median values of the Rhines scales and jet widths in each simulation lie on a straight line. We use the median values because the jet width can vary by a factor of 5 or more across latitudes in a particular simulation (fig. S2), and thus the median better captures the whole sample than the arithmetic mean.
Fig. 4. Observed eddy scale, jet scales, and eddy velocities measured against the Rossby deformation, Rhines scales, and thermal wind.
(A) Relation between the eddy scale and the Rossby deformation. (B) Relation between the median values of the jet widths and the Rhines scales among all simulations. (C) u′ and v′ represent velocity anomalies from the time-mean zonal-mean u and v velocities, respectively, and thermal wind is αgDΔT/(2RΩ), where D is the vertical penetration depth (see the section An idealized model for the temperature distribution for definitions). We use different colors to represent different simulations [see the subpanel in (A)]. The dashed line, whose slope is shown in the upper right corner, represents the best linear fit in each panel.
The size of the eddies might be expected to scale with the Rossby deformation radii, LR, or perhaps Lβ if there is a strong inverse cascade. Linear theory would suggest that the eddies are energized by baroclinic instability at the LR scale with a wavelength of order of 2πLR. To investigate, the Rossby deformation radius is calculated using the mean vertical temperature profile, , between the latitudes of 90°S and 72.5°S. We find the gravity wave speed, ci, for the ith baroclinic mode, ϕi, by solving the eigenvalue problem
| (5) |
where is the buoyancy frequency. The Rossby deformation radius is
| (6) |
where c1 the gravity speed of the first baroclinic mode. We compute the decorrelation scale of relative vorticity to quantify the size of the eddies. We first calculate the autocorrelation of relative vorticity, ζ = ∂xv−∂yu, in the zonal direction and then average it in space from 90°S to 72°S. The decorrelation scale is defined as the distance at which the autocorrelation drops to one-half. Figure 4B shows a satisfying relationship between the Rossby deformation radii and the decorrelation scale.
Last, it should be noted that the Rhines scale and the deformation radius are also linearly related to one another. As can be seen from inspection of Fig. 3, the eddy scale and the jet scale are close to one another with a typical eddy roughly filling the space between the jets.
The central role of baroclinic eddies
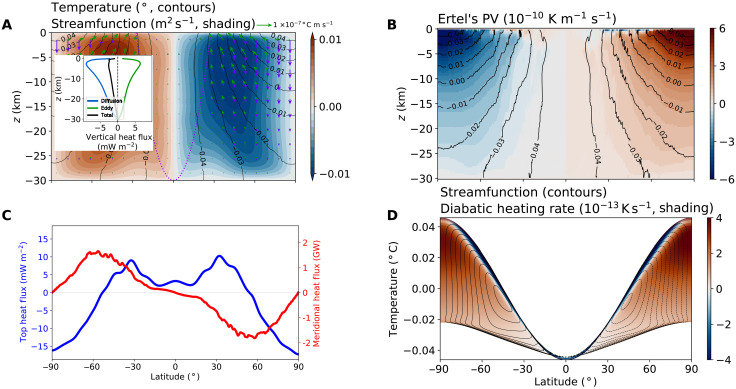
In the reference simulation, the zonal-mean temperature pattern features (i) uniform temperature in equatorial regions, (ii) stable stratification over the pole, and (iii) a pole-to-equator temperature gradient in the interior ocean, which decays with depth (see Fig. 5A). The minimum temperature is found at the equator, where surface cold water sinks into the abyss. As a result, the temperature is almost vertically uniform at the equator, and the stratification is close to neutral. Over the poles, in contrast, the seawater temperature is higher than elsewhere, so the stratification is stable and vertical diffusive heat transport is found. Because the interior of the ocean has a lower temperature compared to the surface at the poles, the diffusive heat flux is directed downward, as shown by the purple arrows in Fig. 5A. A pole-to-equator temperature gradient in the interior ocean forms due to the imposed temperature gradient at the top boundary being diffused downward into the interior.
Fig. 5. Plots of temperature, streamfunction, Ertel’s PV, and heat transport in the reference simulation.
(A) Zonal, time-averaged temperature (contours), eddy-driven overturning circulation (shading, defined in eq. S1), diffusive heat flux (purple arrows), and eddy heat transport (green arrows). The purple dotted line marks the tangent cylinder. The subpanel shows the horizontally averaged vertical heat flux. (B) Instantaneous Ertel PV defined by (∇ T) ⋅ (f + ∇ × u) along a zonal section. The contours show the instantaneous temperature at an interval at 0.01 K. (C) Vertical heat flux at the top of the ocean (blue) and the meridional heat transport (red). (D) Streamfunction (contours) and diabatic heating rate (shading) in temperature/latitude coordinates. The meridional heat flux is scaled to the circumference of the moon by multiplying by a factor of πR/Lx, where R is the radius of the icy moon and Lx is the domain size in the x direction.
The meridional temperature gradient in the ocean is in thermal wind balance and is baroclinically unstable, resulting in eddying motions. The Charney-Stern theorem (41) states that a change in the sign of the Ertel PV gradient is required for instability to occur. This criterion is satisfied, as can be seen by inspection of the PV field in our reference simulation. In Fig. 5B, the Ertel PV gradients in the interior and close to the top boundary are of opposite sign. The Ertel PV gradient is positive in the interior of the ocean, largely due to the gradient of planetary vorticity. In the generalized PV definition (42), a top PV sheet is introduced from a temperature gradient at the top boundary, and the direction of the Bretherton PV gradient within it is opposite to (the same as) the gradient of temperature at the top in the Northern (Southern) Hemisphere, thus satisfying the Charney-Stern criterion.
One important effect of baroclinic eddies is that they flux heat down-gradient from higher latitudes to lower latitudes. Because the weak mean overturning flow is not effective in heat transfer, eddy heat transport dominates. Vertical integration of the meridional component of eddy heat flux is shown in Fig. 5C and peaks at 4 kW m−1. At equilibrium, the convergence of this heat transport must be equal to the vertical heat flux at the water-ice interface, as shown in Fig. 5C. Thus, over the poles, heat is transferred from the ice shell to the ocean; in mid-latitudes, it is transferred from the ocean to the ice shell. Because cooling (heating) results in thickening (thinning) of the ice shell, ocean heat transport tends to homogenize ice shell thickness variations, as first proposed in a terrestrial setting (43). At low latitudes, the strength of the heat flux at the water-ice interface is relatively weak, possibly due to the weak temperature gradient there.
Importance of vertical diffusion of heat
Vertical mixing is essential to energize oceans forced by a surface temperature gradient (44, 45) because it enables that gradient to be diffused down into the ocean interior. This downward diffusive heat flux (purple arrows in Fig. 5A) balances the upward heat transport due to baroclinic eddies (green arrows in Fig. 5A), as shown by the subpanel in Fig. 5A. While baroclinic eddies arise due to the horizontal temperature gradient in the ocean interior, it is vertical diffusion that maintains that interior gradient sustaining baroclinic activity. From an energetic point of view, it can also be shown that it is vertical diffusion rather than the heat flux from the ice that energizes ocean circulation (28, 44).
In our simulations, the diffusion coefficient is larger than its molecular value by several orders of magnitude. Diffusion of heat can be a result of both molecular and turbulent/eddy diffusion. Diffusion by turbulent scales in Earth’s atmosphere and ocean is the rate-limiting mixing process. Turbulence is generated by many processes, including tidal processes exciting inertia-gravity waves, convective instability caused by heating and cooling and/or freezing/melting, flow over topography, and baroclinic instability of the large-scale flow and its turbulent cascade. All these processes can be expected to be at work on icy moons. Here, in our numerical simulations, we attempt to resolve the baroclinic eddy scales but perhaps not its turbulent cascade. We therefore interpret κ to represent the net effect of mixing by all smaller scales.
The linkage between diffusion and meridional heat transport can be clearly seen by considering the budget of temperature variance, T2. If we multiply Eq. 34, the governing equation for T in our simulations, by T, take the time average and integrate over the domain, at equilibrium, we obtain
| (7) |
where Ttop is the prescribed top temperature and is the time-mean vertically integrated meridional temperature flux due to diffusive and advective processes
| (8) |
The left-hand side of Eq. 7 is the flux of heat directed down the large-scale gradient, which is balanced by explicit diffusive processes acting on temperature gradients represented by κ on the right-hand side. This clearly demonstrates that the large-scale eddy heat flux is directed down-gradient and tends to zero when κ tends to zero. It shows the important role of vertical diffusion in the temperature variance budget and therefore large-scale meridional heat transport.
At low latitudes, convection dominates vertical transport, as is to be expected when the ocean is forced by a lateral temperature gradient from above (44, 45). Between 30°S and 30°N, the stratification is unstable under the top boundary (see fig. S3 in the Supplementary Materials), resulting in convection and near-vertical isotherms there. Convection transports heat upward, which is balanced by downward heat diffusion at higher latitudes. Thus, vertical diffusion remains essential for energizing ocean circulation (44, 45).
Overturning circulation
Eddies drive a pole-to-equator overturning circulation in each hemisphere (Fig. 5A and the schematic in Fig. 1B). Sinking occurs at low latitudes where water is cold, while upwelling happens at high latitudes where it is warm. We discuss how we diagnose the streamfunction in the Supplementary Materials.
The cross-isotherm component of the overturning balances diabatic heating, which includes a contribution from diffusion () and the parameterized heat exchange with the ice shell, as well as the convergence of the residual fluxes. Diffusive heating is the dominant term in the ocean interior and leads to a circulation that crosses isotherms. This can be seen most clearly by plotting Ψ⋆ in temperature-latitude coordinates (Fig. 5D). At low latitudes, where diffusive heating is weak, Ψ⋆ contours mostly follow surfaces. Near the upper boundary, strong diabatic cooling associated with heat exchange with the ice causes Ψ⋆ contours to cross temperature surfaces.
When the skew heat flux (which is the component of eddy heat transport that are parallel to the isotherms; see the Supplementary Materials for definition) becomes the dominant mechanism of meridional heat transport, the total heat transport is proportional to the product of the maximum streamfunction and the meridional temperature gradient
| (9) |
where Ψ⋆ is the maximum of the Ψ⋆ pattern. The predicted heat transport agrees well with numerical simulations (Fig. 6).
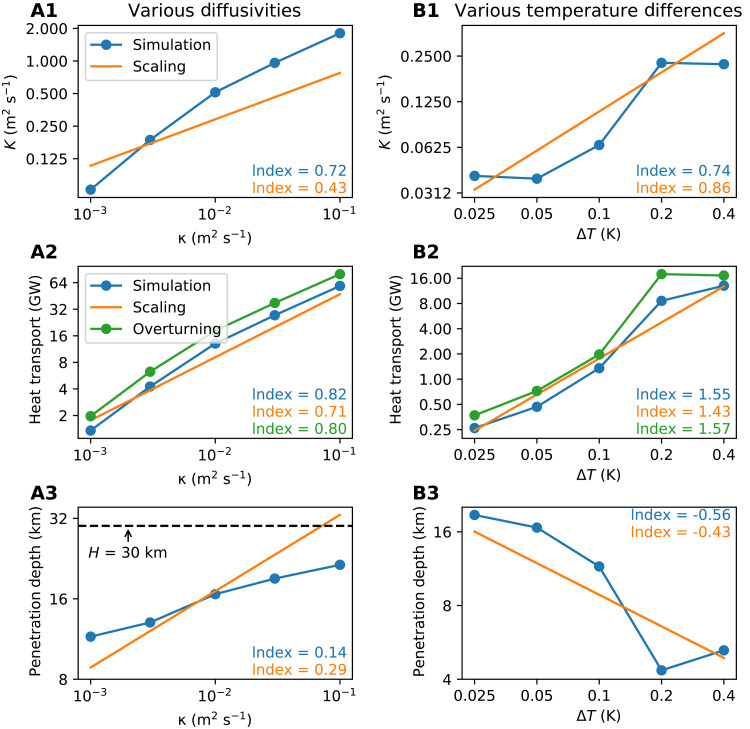
Fig. 6. Measures of key flow parameters in two groups of simulations compared to predictions from scaling.
The left column shows the (A1) eddy heat transport coefficient K, (A2) meridional heat transport, and (A3) penetration depth in calculations in which the vertical diffusivity, κ, is varied; the right column (B1 to B3) shows the same but when the prescribed temperature difference is varied. Theoretical predictions are made from Eqs. 23, 24, and 25. The overturning [green lines in (A2) and (B2)] represents the meridional heat transport calculated from streamfunction (Eq. 9). The index for the best power fit for each curve is shown in every panel with the corresponding color.
An idealized model for the temperature distribution
As can be seen from Fig. 5A, the direction of vector eddy heat transport in the meridional plane by baroclinic eddies in the interior of our solution is directed along temperature surfaces, as described, for example, in the Antarctic Circumpolar Current of Earth’s ocean (29). This motivates a separation between skew fluxes and residual fluxes (discussed in the Supplementary Materials). In our control simulation, the residual fluxes turn out to be small compared to the skew fluxes in most of the ocean, as we expected (fig. S4). The vertical integral of is several times larger than that of as can be seen in fig. S4. Residual fluxes are small in the ocean interior because diabatic processes are weak there on the timescale/length scale of eddies. Thus, fluid parcels are constrained to move along isotherms (here T surface). This does not contradict our statement that diffusion is a central part of the large-scale ocean heat balance because eddy processes have a much shorter timescale (tens of days) than that of the large-scale thermal structure (hundreds of years). It should be noted that residual fluxes become more important as diffusivity is increased. In simulations using κ = 0.1 m2 s−1, the strength of residual flux fluxes is comparable to that of skew fluxes.
When the T surfaces tilt, the meridional heat transport will naturally be associated with a vertical component. At equilibrium, this vertical, upward eddy heat transport must balance the downward diffusive heat flux (16, 36). This allows us to construct a simple model (which we call the K-κ model) to predict the interior temperature distribution, in which K represents the eddy heat transport and κ is the explicit vertical diffusion. The resulting framework has much in common with idealized models of the stratification and overturning circulation in the Southern Ocean (29, 30), which were applied to Enceladus in Lobo2021.
At equilibrium, the Reynolds-averaged temperature equation is, neglecting advection by the mean
| (10) |
where κ is the vertical heat diffusivity. The horizontal component of the eddy heat flux is directed down-gradient (equatorward) (Fig. 5C), and so, as is commonly assumed in dynamical meteorology and oceanography, we liken the eddy heat flux to a mixing process and express it thus
| (11) |
where K is a lateral mixing coefficient of temperature associated with baroclinic eddies. Although our simulations and previous studies show that K will varies spatially (13, 16), for simplicity, here we use a single value for K although we will allow it to vary between simulations.
We can connect the vertical component of eddy heat flux to its horizontal component by assuming it to be a skew flux, thus
| (12) |
where s is the slope of the mean temperature surfaces
| (13) |
The residual fluxes are small in the ocean interior (fig. S4) and are therefore not considered in this simple model.
Combining Eqs. 11, 12, and 13 enables us to write Eq. 10 as
| (14) |
where J(A, B) = (∂yA)(∂zB)−(∂zA)(∂yB), where the streamfunction for the residual overturning circulation is given by
| (15) |
Such an expression for Ψ⋆ has been widely used in studies of terrestrial (46, 47) and Enceladean (14, 16) ocean circulation. This eddy-driven circulation, depicted in Fig. 1B, draws cold water upward, balancing heat being diffused down from the surface.
Equation 14 was the model used in Lobo2021 to study the circulation of Enceladus for prescribed values of K and κ. It was solved using a method of characteristics that has been used for modeling the Southern Ocean (29). Here, we take a different approach and rewrite Eq. 14 using temperature as a vertical coordinate by noting that (i) the slope of isotherms, s, can be expressed as ∂yz in temperature coordinates and (ii) can be interpreted as the gradient of Ψ⋆ in the direction along the local isotherms and so also expressed in temperature coordinates. As derived in the Supplementary Materials, Eq. 14 can be written as
| (16) |
where z is a function of y and T. We see that the depth of isotherms are diffused horizontally by K and vertically by κ, having their origin at the top. This is simpler than Eq. 14 with a direct physical interpretation. However, the boundary conditions are more complicated: The shape of the domain, the collection of all possible (y, T), is now nonrectangular because temperature varies at the upper boundary. Although this complicates the solution for the interior temperature distribution, it allows us to readily derive scaling laws for the penetration depth of surface temperature anomalies. Moreover, one great advantage of Eq. 16 is that it can be readily solved numerically.
The depth of penetration, D, of ocean circulation is closely linked to the slope of temperature surfaces, thus
| (17) |
where we have assumed that the horizontal length scale is the radius of the moon R, as can be seen in Fig. 2; s, in Eq. 17, can be understood as the average slope (dz/dy for constant ) for a given isotherm. Note the slope actually takes on a large range of values from almost infinite at low latitudes to close to zero near the poles.
Outside of the strong convective regions at the low latitudes, the vertical heat budget is a balance between diffusion and eddy heat flux
| (18) |
This can be combined with Eq. 13 to yield
| (19) |
Substituting back into Eq. 17 gives a scaling for the depth of penetration D
| (20) |
Equations 19 and 20 indicate that the isotherm slope and the depth to which surface warm water penetrates are determined by the ratio of κ to K. This can be understood as follows: Vertical diffusion at higher latitudes brings heat into the ocean, making isotherms steeper (increasing s), while baroclinic eddies try to flatten temperature surfaces (decreasing s). The ratio of κ to K controls the relative efficiency of these two processes, and thereby the equilibrium slopes. This is directly analogous to the models of the Antarctic Circumpolar Current (29): There, the wind curl pumped the surface boundary conditions into the interior, rather than mixing processes, but a balance with lateral eddy mixing, as here, determined the equilibrium slope.
Note that Eq. 19 is only applicable when D given by Eq. 17 is smaller than the ocean depth H. When D > H, a different scaling pertains (16). Later, we will see that this scenario is very unlikely for Enceladus.
In the K-κ model, the strength of the ocean circulation, obtained by combining Eq. 19 with Eq. 15 is given by
| (21) |
This is exactly the same relationship obtained for the strength of the lower cell driven by mixing and eddies around Antarctica in Earth’s ocean (30).
Scaling for the eddy diffusivity K and ocean heat transport
A scaling for K enables a prediction of ocean heat transport with the K-κ model for a given diapycnal mixing rate κ. This scaling (16), inspired by geostrophic turbulence theory (48, 49), uses mixing length theory (24) and assumes that K can be expressed as the product of a characteristic eddy length le and eddy speed ve. We have noted that our eddy length covaries with the deformation radius LR (Eq. 6 and Fig. 4). When vertical diffusion does not dominate, ve will scale with the thermal wind speed UTW ≡ αgDΔT/(Rf), as shown in Fig. 4C. This suggests that
| (22) |
where is the buoyancy frequency. The penetration depth D is given by Eq. 20. On substituting into Eq. 22, we obtain the κv-limit scaling presented in (16)
| (23) |
where CK is a constant. Fitting to our numerical simulations, we find that the best fit is CK = 0.0692.
Equation 23 suggests that K increases with ΔT and κ. This is expected because the baroclinic eddies are energized from the horizontal temperature gradient. Also, the maintenance of the horizontal temperature gradient in the ocean interior requires vertical diffusion.
Last, combining our K-κ model (Eqs. 15 and 19) with the scaling for K (Eq. 23), we obtain the following expressions for penetration depth and the meridional energy flux
| (24) |
| (25) |
where CD and CF are constants. Again, fitting to our simulations, we find that CD = 1.39 and CF = 0.435 (Fig. 6). This formula is identical to the κv-limit scaling given by a previous study (16).
Test of theory against numerical solutions
To test the K-κ model against numerical solutions, we need to determine if (i) Eq. 16 (or equivalently, Eq. 14) correctly predicts the temperature patterns in our numerical simulations; (ii) the interplay of K and κ determines the penetration depth of surface temperature anomaly D and the strength of the ocean circulation, Ψ⋆, following Eqs. 20 and 21; and (iii) the eddy diffusivity K and the meridional heat transport can be predicted using Kscaling from Eq. 23 and Fheat from Eq. 25, respectively.
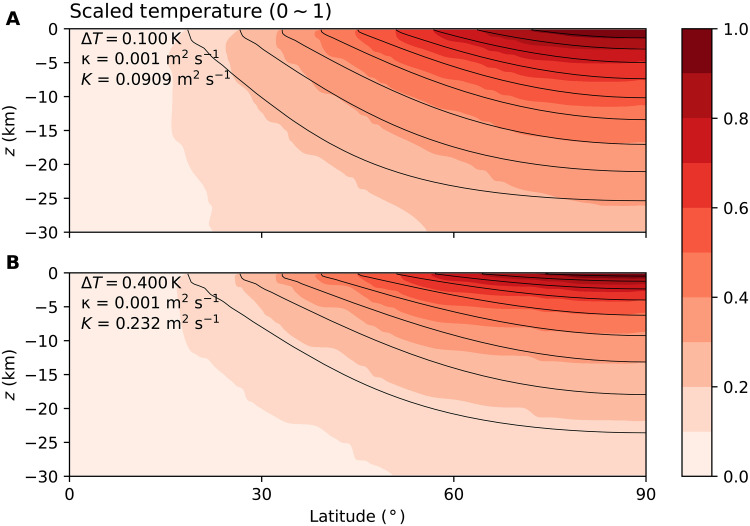
First, as can be seen from Fig. 7, solutions of Eq. 16 well match the equilibrium state of our numerical model. To obtain these solutions, boundary conditions are set as follows: Over northern and southern boundaries, is set to zero, consistent with the adiabatic boundary condition prescribed in the high-resolution simulations. At the bottom, the temperature is assumed to be the minimum temperature prescribed at the water-ice interface. This is reasonable because we observe that the coldest prescribed temperature occupies the abyssal ocean (Fig. 5A). Also, to obtain a solution of Eq. 16, we linearized it by replacing ∂Tz with {H/[Ts(y)−Ts(0)]}, set by top-to-bottom temperature difference at a given latitude. This approximation prevents us from capturing the top-amplified structure of stratification (∂Tz). However, despite these assumptions, the solution is still able to capture the broad temperature patterns found in the numerical simulations (see Fig. 7). We also notice that the temperature patterns in the numerical simulations (Figs. 5A and 7) contain perturbations due to the baroclinic component of the zonal velocity pattern, which is in thermal wind balance (fig. S1).
Fig. 7. Solutions of the K-κ model compared with that from our explicit, eddy-resolving model at equilibrium.
(A and B) For each of our eddying simulations, we diagnose K and then solve for the temperature distribution for the appropriate κ/K value.
Second, we demonstrate that Eqs. 19 and 21 capture the isotherm slope s and the magnitude of the ocean circulation Ψ⋆ in our simulations. To diagnose s, we replace it by D/R following Eq. 17 and define the penetration depth, D, based on the vertical profile of the vertical temperature gradient, , at the poles. Starting from the surface, where is a maximum, the depth at which drops to 1/e (e = 2.71828…) of its maximum value is taken as a measure of D.
Third, to see if the scaling laws for penetration depth (Eq. 24) and meridional heat transport (Eq. 25) capture the numerical results, we overlay the scaling predictions on Fig. 8 using green markers. The predictions given by scaling laws (green markers) are well aligned with numerical simulations (orange crosses).
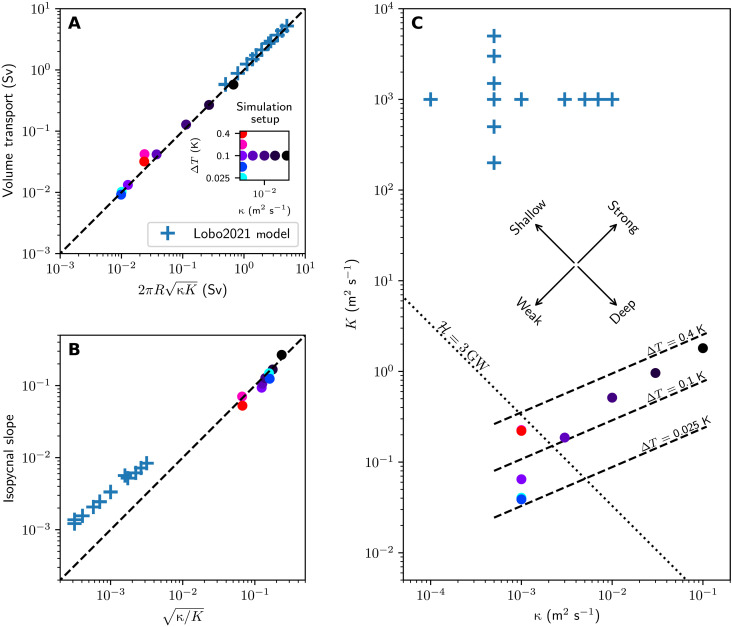
Fig. 8. Ocean circulation characteristics as a function of our two key parameters, κ and K.
Theory predicts the strength of the eddy-driven overturning circulation as and that the isotherm slope is . (A) Volume transport versus these predictions in our simulations (points, similar to Fig. 4) and calculations in the Lobo2021 model (14) (blue crosses). (B) Isopycnal slopes. In our simulations, isopycnals are identical to isotherms. (C) Comparison of the parameter space of (κ, K) in our simulations to those assumed in the Lobo2021 model (14). The four arrows indicate how changes in κ and K affect the strength and the depth of the eddy-driven overturning circulation. Dashed lines indicate how K depends on κ and the prescribed temperature difference at the top, ΔT. The values of K used in the Lobo2021 model (14) are roughly three orders of magnitude larger than our simulations suggest, resulting in overturning circulations that are too strong and too shallow.
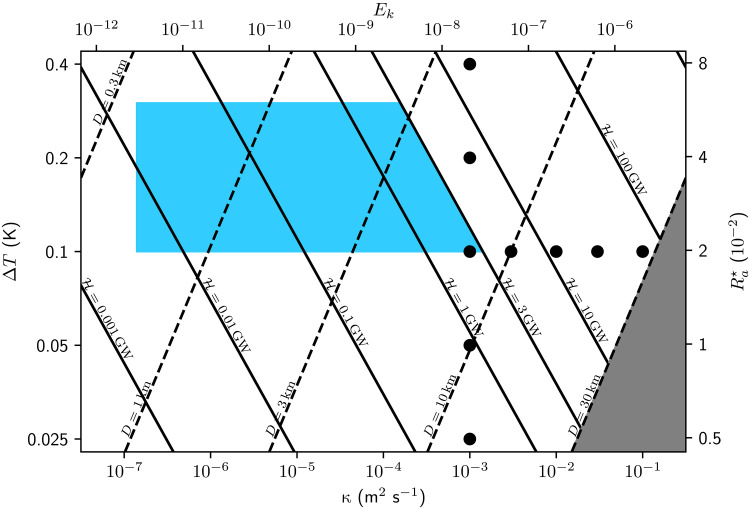
Equation 24 slightly overestimates the penetration depth D when the prediction approaches the full ocean depth H. This is expected because, as D → H, the ocean enters the so-called D-limit scenario described in a previous study (16), in which vertical diffusion is strong enough to carry the top boundary condition all the way down to the ocean bottom. Figure 9 marks the D-limit with gray shading and shows that none of our simulations are in this regime (some simulations may be arguably in the transient zone between the two regimes).
Fig. 9. Dynamical parameter space for Enceladus.
The black points represent our simulations; the blue blocks represent the possible position of Enceladus in this space. The minimum value of κ on Enceladus is assumed to be 1.4 × 10−7m2 s−1. This is the estimated molecular diffusivity (9), but tidal mixing will likely produce much elevated values. The solid lines show the parameters for the corresponding meridional heat flux predicted by Eq. 26. Because the ocean heat transport is unlikely larger than 3 GW, the diffusivity must be smaller than ∼10−3m2 s−1. Ek and are defined in Eqs. 28 and 30, respectively.
We also present the isotherm slope and the volume transport from Lobo2021 (14) in the same plots (Fig. 8, A and B) using blue plus markers. Evidently, the K-κ model, specifically Eqs. 15 and 19, also matches the results by Lobo2021. This is not unexpected given the similarity between our model and theirs. However, as can be seen from Fig. 8C, the κ and K values chosen in the Lobo2021 model are in a very different parameter regime than suggested by our numerical solutions.
Implications for Enceladus
The pole-to-equator ice shell thickness variation (17–20) creates a meridional temperature difference at the top of Enceladus’ ocean, which will drive ocean circulation and meridional heat transport. The ocean circulation forced by a buoyancy gradient at the top in the oceans of icy moons was first studied using a box model (12) or in a zonally symmetric configuration (15, 36). A zonally symmetric model accounts for an overturning circulation and qualitatively capture associated features Ψ⋆. However, because of the lack of the zonal dimension, baroclinic eddies are not present. This, consequently, leads to an underestimate of the meridional heat transport, especially when the ocean is strongly baroclinically unstable. Moreover, the dynamic features that appear in 3D configurations are drastically different from those in zonally symmetric configurations: Multiple jets and associated overturning circulation cells form rather than the single overturning circulation of the 2D model. Such differences have been noted in previous studies (13, 16).
The pole-to-equator temperature difference on Enceladus is perhaps of order 0.1 to 0.2 K, which can induce a substantial meridional heat transport. Substituting such a temperature difference and Enceladus parameters (g, R, and Ω) into Eq. 25 (16), the meridional heat transport on Enceladus is
| (26) |
The relation between κ and ΔT is plotted in Fig. 9, assuming α = 1.67 × 10−4 K−1. The blue shaded area in Fig. 9 marks the possible parameters of Enceladus by requiring the meridional heat transport to be <3 GW, the amount of heat that can be lost through the equatorial (30°S to 30°N) ice shell (19, 50). If this is exceeded, then the equatorial ice shell would melt, which, together with likely poleward ice flow (51, 50), would eventually smooth out ice thickness variations (15, 16, 36). Such a heat budget constraint can also be used to place an upper limit on the vertical diffusivity of between ∼10−3 m2 s−1, depending on the assumed value of the thermal expansion coefficient α, which is a function of ocean salinity (15) and the pole-to-equator temperature difference ΔT.
Furthermore, a pole-to-equator temperature difference can potentially strongly modify convective upward heat transport powered by possible bottom heating. Given that the meridional temperature gradient (0.1 K) is likely much greater than the simulated vertical temperature gradient induced by a bottom heating of 40 mW/m2 (11, 52), the heating pattern at the seafloor may be substantially altered by the time it is delivered to the ice. This mechanism is different from the imprint of bottom heating patterns due to bottom convection (9–11, 38, 53). This may draw into question, for example, the scenario in which a poleward-amplified heating pattern emanating from the seafloor can sustain the poleward-thinning ice geometry on Enceladus (54).
To put our work in context, in Fig. 8, we also present some results inferred from the Lobo2021 model (14). Our K-κ model shows that the ratio of κ to K controls the depth of the circulation (panel B), while the product of κ and K controls the strength of overturning circulation (panel A). The major difference between our work and that of Lobo2021 is that K is estimated using scaling laws (Eq. 23), which is then validated using high-resolution numerical experiments, rather than, as in Lobo2021, being prescribed at terrestrial values. Our calculations suggest that K should be of order ∼0.1 m2 s−1, which is three to four orders of magnitude smaller than assumed in (14)—Fig. 8C. As a result, Lobo2021’s overturning circulation is two orders of magnitude too shallow (panel B) and two orders of magnitude too strong (panel A). Last, as noted earlier, the energy budget of the ice shell of Enceladus puts an upper bound on the strength of ocean heat transport and thereby the residual circulation. This limit is marked by the dotted line in Fig. 8C. The parameter space explored by Lobo2021 would result in a heat transport orders of magnitude greater than the 3-GW limit due to the assumption of a very large K, even for the smallest κ assumed. If this were true, then ice shell thickness variations would be quickly smoothed out.
Application to other icy moons
The idea that ice thickness variation drives an ocean circulation can be applied to other icy moons, which may have a pole-to-equator temperature gradient beneath an ice shell of variable thickness. Although a substantial ice shell thickness variation has been found on Enceladus, similar unevenness of the ice shell may not exist on Europa or Titan. The upper limit of the pole-to-equator ice thickness variation on Europa is perhaps of order 10 km (55). Because of Europa’s large size and hence strong gravity (36, 16), the meridional heat transport in the ocean could be as large as 2.4 GW even if the vertical diffusivity is as low as 1.6 × 10−7 m2 s−1, the molecular value (9). Here, we assume that cw = 4 × 103 J kg−1 K−1, ρw = 1 × 103 kg m−3, α = 2 × 10−4 K−1, R = 1561 km, and Ω = 2.1 × 10−5 s−1 (9). The rate that the freezing point varies with pressure is set to −7.5 × 10−8 K Pa−1. Furthermore, spatial variations in tidal heating on Titan can possibly induce ice shell thickness variations, which is an explanation to the surface topography (56). The resulting lateral ice thickness variation can be several kilometers. Because Titan has an even larger size and an even slower rotation rate than Europa (9), ocean heat transport may be even more efficient in removing thickness variations in the overlying ice shell. In the future, Europa Clipper (57) will be able to better constrain the ice thickness profile of Europa, and JUICE (JUpiter ICy moons Explorer) (58) may be able to reveal the ice geometry on Ganymede and Callisto. The sustainability of a specific ice thickness profile will lead to a constraint on ocean heat transport, which can then perhaps be used to infer subsurface ocean properties, such as vertical diffusivity, using our scaling law.
The scaling laws (Eqs. 23, 24, and 25) and heat budget can also be written in a dimensionless form. This can simplify determining if the scaling law is applicable to the regime in question. Physical parameters involved are (i) the radius of the moon, R; (ii) the rotational rate, Ω; (iii) the depth of the ocean, H; (iv) the diffusivity, κ; (v) the viscosity, ν; and (vi) the buoyancy forcing, Δb. Buckingham’s Π theorem tells us that four nondimensional numbers can be constructed
| (27) |
| (28) |
| (29) |
| (30) |
Here, χ is the nondimensional depth of the ocean; Ek is the Ekman number to represent the strength of diffusion relative to rotation; Pr is the Prandtl number, and it is set to unity in this study; and is the slantwise Rayleigh number (59). Note that the slantwise Rayleigh number does not depend on a poorly constrained diffusivity or viscosity, in analogy with the natural Rossby number, (11). Figure 9 shows Ek and in the upper x axis and the right y axis, respectively. Although our scalings have been tested within the parameter space of our simulations, it is yet to be confirmed if they are applicable beyond this space. However, on the basis of the principles of geostrophic turbulence theory (48, 49), we expect our scalings to hold as long as and Ek are sufficiently small.
DISCUSSION
We have explored how ocean circulation can be induced on an icy moon when forced by a temperature variation at the top, which is diffused down into the interior. Our main findings are as follows:
1) Eddies play a dominant role in ocean dynamics and heat/tracer transport. The Eulerian-mean meridional overturning circulation is much weaker than that associated with eddies in terms of strength and associated heat transport.
2) Eddies are generated by a baroclinic instability of the thermal wind. The Charney-Stern theorem, a necessary condition for baroclinic instability, is satisfied, with the meridional gradient of PV having different signs above and below the thermocline.
3) Heat is diffused downward over the poles and then fluxed equatorward and upward along the isotherms by baroclinic eddies. It is eventually deposited underneath the equatorial ice shell. The balance between diffusion and eddies allows us to construct a K-κ model, from which temperature patterns can be computed given the vertical diffusivity, κ, and the horizontal eddy heat transport coefficient, K. The temperature patterns match well with our numerical simulations. The equilibrium isotherm slope and the strength of the eddy-driven overturning circulation can also be written as a function of κ and K. A comparison with the Lobo2021 model (14) is made.
4) Scaling laws for K, the penetration depth, and the meridional heat transport (Eqs. 23, 24, and 25) given by a previous study (16) are tested against numerical simulations.
5) If a larger vertical diffusivity is assumed, we find (i) a larger horizontal eddy diffusivity, (ii) a stronger horizontal heat transport, and (iii) an increased penetration depth of the boundary conditions into the interior.
6) Increased top temperature difference results in (i) a larger horizontal eddy heat transfer coefficient, (ii) a stronger horizontal heat transport, (iii) a smaller penetration depth of the temperature variation, and (iv) a potentially flatter ice shell if the ice geometry is close to equilibrium, as in (16).
In our study, only temperature forcing from the ice shell is considered and the density variation contributed by salinity gradient induced by freezing/melting is neglected. In reality, the total buoyancy gradient between the equator and the pole depends strongly on the mean salinity of the ocean S0 because it controls both thermal expansion coefficient and the salinity change due to melting or freezing (15). However, we can include the salinity factor by replacing αΔT with (αΔT−βΔS), where β is the haline contraction coefficient and ΔS is the pole-to-equator salinity difference. The thermal expansion coefficient α can also be changed depending on the assumed S0.
Barotropic flows are strong in our simulations. Therefore, barotropic or mixed barotropic-baroclinic instability might also be present and generate eddies along with baroclinic instability. Our focus is on baroclinic instability here because it ultimately energizes ocean circulation and is central to understanding the overturning circulation.
Last, our simulations do not represent the topography of the water-ice interface. The absence of topography may also affect ocean circulation and its baroclinic instability, especially when κ is small and the penetration depth D is shallow. The effects of the top topography on the ocean circulation should be investigated in future work.
MATERIALS AND METHODS
Governing equations and boundary conditions
The three-component velocity, u = (u, v, w), and the temperature, T, are the prognostic fields in simulations. Because we use the Boussinesq approximation, velocity is nondivergent everywhere
| (31) |
The momentum equation is
| (32) |
where f is the Coriolis parameter in vector form; P is the pressure divided by the reference density; b is the buoyancy, which is later given by Eq. 33; and k is the unit vector in the z direction; ν∇2u is the viscosity term, and ν is the viscosity. The value of ν is set to κ, the diffusion coefficient, in all simulations.
The inclusion of Coriolis effects is given careful consideration, as described in the main body of the text to take account of the deep ocean and nontraditional Coriolis terms.
We use a highly idealized equation of state. The buoyancy, b, is a linear function of temperature, T
| (33) |
where Tref, the reference temperature, is 0°C; α, the thermal expansion coefficient, is 1.67 × 10−4 K−1; and g, the gravity in the ocean, is 0.1 m s−1. This idealized equation of state (Eq. 33) neglects the contribution of the variation of salinity to the density and also assumes that the salinity is high enough to suppress the abnormal thermal expansion.
The equation for the evolution of temperature is
| (34) |
where κ is the diffusivity; δtop = exp (z/d0) and d0 = 50 m; τ is the relaxation time; and Ttop(y) is the prescribed top temperature pattern as a function of y. In all simulations, τ is small enough to relax temperature near the top of the ocean to the prescribed value.
The bottom (z = −H), northern [y = (π/2)R], and southern [y = −(π/2)R] boundaries are adiabatic. Although the bottom heating can be an important driver of the ocean (9–11), it is not included because we focus on the ocean circulation forced by a top temperature gradient in the paper. We use the no-slip boundary condition for the bottom, top, northern, and southern boundaries.
Numerical techniques
We use Oceananigans.jl (33), a state-of-the-art ocean general circulation model that runs fast on GPUs, for all numerical simulations. Powered by advanced GPUs, our simulations use a high resolution of 300 m in all x, y, and z directions, which is smaller than the Rossby deformation radii in all simulations and enables resolving baroclinic eddies. The velocity and the temperature fields are discretized using a staggered Arakawa C-grid (60). The advection terms in Eqs. 32 and 34 are calculated with a fifth-order WENO (weighted essentially nonoscillatory advection) scheme (61). The integration over time is performed with a third-order Runge-Kutta method designed for 3D incompressible flows (62). A nonhydrostatic solver is used.
All of our simulations have reached the equilibrium following this criterion: The relative difference between the amplitudes of the horizontally averaged diffusive heat flux and eddy heat transport needs to be within 15% at every depth.
Acknowledgments
We thank A. Ramadhan of MIT for helping setting up the numerical model and P. O’Gorman and G. Flierl of MIT for helpful discussion.
Funding: This work was supported in part by the NASA Astrobiology Grant 80NSSC19K1427 “Exploring Ocean Worlds.”
Author contributions: Y.Z., W.K., and J.M. designed the simulations. Y.Z. performed the simulations and conducted the analyses. All authors wrote the manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. The data used in this article are available in Dryad: https://datadryad.org/stash/share/Vqma77fBUqcvYo2INyOXtbEueFczocGcyv-bh9aBd1I.
Supplementary Materials
This PDF file includes:
Supplementary Text
Figs. S1 to S4
REFERENCES AND NOTES
- 1.Iess L., Stevenson D. J., Parisi M., Hemingway D., Jacobson R. A., Lunine J. I., Nimmo F., Armstrong J. W., Asmar S. W., Ducci M., Tortora P., The gravity field and interior structure of Enceladus. Science 344, 78–80 (2014). [DOI] [PubMed] [Google Scholar]
- 2.Thomas P., Tajeddine R., Tiscareno M., Burns J. A., Joseph J., Loredo T. J., Helfenstein P., Porco C., Enceladus’s measured physical libration requires a global subsurface ocean. Icarus 264, 37–47 (2016). [Google Scholar]
- 3.Waite J. H. Jr., Combi M. R., Ip W.-H., Cravens T. E., McNutt R. L., Kasprzak W., Yelle R., Luhmann J., Niemann H., Gell D., Magee B., Fletcher G., Lunine J., Tseng W.-L., Cassini ion and neutral mass spectrometer: Enceladus plume composition and structure. Science 311, 1419–1422 (2006). [DOI] [PubMed] [Google Scholar]
- 4.Postberg F., Kempf S., Schmidt J., Brilliantov N., Beinsen A., Abel B., Buck U., Srama R., Sodium salts in E-ring ice grains from an ocean below the surface of Enceladus. Nature 459, 1098–1101 (2009). [DOI] [PubMed] [Google Scholar]
- 5.Postberg F., Khawaja N., Abel B., Choblet G., Glein C. R., Gudipati M. S., Henderson B. L., Hsu H.-W., Kempf S., Klenner F., Moragas-Klostermeyer G., Magee B., Nölle L., Perry M., Reviol R., Schmidt J., Srama R., Stolz F., Tobie G., Trieloff M., Waite J. H., Macromolecular organic compounds from the depths of Enceladus. Nature 558, 564–568 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Taubner R.-S., Pappenreiter P., Zwicker J., Smrzka D., Pruckner C., Kolar P., Bernacchi S., Seifert A. H., Krajete A., Bach W., Peckmann J., Paulik C., Firneis M. G., Schleper C., Rittmann S. K.-M. R., Biological methane production under putative Enceladus-like conditions. Nat. Commun. 9, 748 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hsu H.-W., Postberg F., Sekine Y., Shibuya T., Kempf S., Horányi M., Juhász A., Altobelli N., Suzuki K., Masaki Y., Kuwatani T., Tachibana S., Sirono S.-i., Moragas-Klostermeyer G., Srama R., Ongoing hydrothermal activities within Enceladus. Nature 519, 207–210 (2015). [DOI] [PubMed] [Google Scholar]
- 8.Waite J. H., Glein C. R., Perryman R. S., Teolis B. D., Magee B. A., Miller G., Grimes J., Perry M. E., Miller K. E., Bouquet A., Lunine J. I., Brockwell T., Bolton S. J., Cassini finds molecular hydrogen in the Enceladus plume: Evidence for hydrothermal processes. Science 356, 155–159 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Soderlund K. M., Ocean dynamics of outer solar system satellites. Geophys. Res. Lett. 46, 8700–8710 (2019). [Google Scholar]
- 10.Zeng Y., Jansen M. F., Ocean circulation on Enceladus with a high-versus low-salinity ocean. Planet. Sci. J. 2, 151 (2021). [Google Scholar]
- 11.Bire S., Kang W., Ramadhan A., Campin J.-M., Marshall J., Exploring ocean circulation on icy moons heated from below. J. Geophys. Res. Planets 127, e2021JE007025 (2022). [Google Scholar]
- 12.Zhu P., Manucharyan G. E., Thompson A. F., Goodman J. C., Vance S. D., The influence of meridional ice transport on Europa’s ocean stratification and heat content. Geophys. Res. Lett. 44, 5969–5977 (2017). [Google Scholar]
- 13.Ashkenazy Y., Tziperman E., Dynamic Europa ocean shows transient taylor columns and convection driven by ice melting and salinity. Nat. Commun. 12, 6376 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lobo A. H., Thompson A. F., Vance S. D., Tharimena S., A pole-to-equator ocean overturning circulation on Enceladus. Nat. Geosci. 14, 185–189 (2021). [Google Scholar]
- 15.Kang W., Mittal T., Bire S., Campin J.-M., Marshall J., How does salinity shape ocean circulation and ice geometry on Enceladus and other icy satellites? Sci. Adv. 8, eabm4665 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kang W., Different ice-shell geometries on Europa and Enceladus due to their different sizes: Impacts of ocean heat trans. Astrophys. J. 934, 116 (2022). [Google Scholar]
- 17.Hemingway D. J., Mittal T., Enceladus’s ice shell structure as a window on internal heat production. Icarus 332, 111–131 (2019). [Google Scholar]
- 18.Čadek O., Tobie G., Van Hoolst T., Massé M., Choblet G., Lefèvre A., Mitri G., Baland R.-M., Běhounková M., Bourgeois O., Trinh A., Enceladus’s internal ocean and ice shell constrained from Cassini gravity, shape, and libration data. Geophys. Res. Lett. 43, 5653–5660 (2016). [Google Scholar]
- 19.Tajeddine R., Soderlund K. M., Thomas P. C., Helfenstein P., Hedman M. M., Burns J. A., Schenk P. M., True polar wander of Enceladus from topographic data. Icarus 295, 46–60 (2017). [Google Scholar]
- 20.W. McKinnon, P. Schenk, AGU Fall Meeting Abstracts (AGU, 2021), vol. 2021, pp. P35C–2141. [Google Scholar]
- 21.Kang W., Bire S., Marshall J., The role of ocean circulation in driving hemispheric symmetry breaking of the ice shell of Enceladus. Earth Planet. Sci. Lett. 599, 117845 (2022). [Google Scholar]
- 22.Bire S., Mittal T., Kang W., Ramadhan A., Tuckman P. J., German C. R., Thurnherr A. M., Marshall J., Divergent behavior of hydrothermal plumes in fresh versus salty icy ocean worlds. J. Geophys. Res. Planets 128, e2023JE007740 (2023). [Google Scholar]
- 23.Zeng Y., Jansen M. F., The effect of salinity on ocean circulation and ice–ocean interaction on Enceladus. Planet. Sci. J. 5, 13 (2024). [Google Scholar]
- 24.G. K. Vallis, Atmospheric and Oceanic Fluid Dynamics (Cambridge Univ. Press, 2017). [Google Scholar]
- 25.Chen E. M. A., Nimmo F., Glatzmaier G. A., Tidal heating in icy satellite oceans. Icarus 229, 11–30 (2014). [Google Scholar]
- 26.Rekier J., Trinh A., Triana S., Dehant V., Internal energy dissipation in Enceladus’s subsurface ocean from tides and libration and the role of inertial waves. J. Geophys. Res. Planets 124, 2198–2212 (2019). [Google Scholar]
- 27.Rovira-Navarro M., Matsuyama I., Hay H. C. C., Thin-shell tidal dynamics of ocean worlds. Planet. Sci. J. 4, 23 (2023). [Google Scholar]
- 28.Jansen M. F., Kang W., Kite E. S., Zeng Y., Energetic constraints on ocean circulations of icy ocean worlds. Planet. Sci. J. 4, 117 (2023). [Google Scholar]
- 29.Marshall J., Radko T., Residual-mean solutions for the Antarctic Circumpolar Current and its associated overturning circulation. J. Phys. Oceanogr. 33, 2341–2354 (2003). [Google Scholar]
- 30.Ito T., Marshall J., Control of lower-limb overturning circulation in the Southern Ocean by diapycnal mixing and mesoscale eddy transfer. J. Phys. Oceanogr. 38, 2832–2845 (2008). [Google Scholar]
- 31.Nimmo F., Bills B., Thomas P., Geophysical implications of the long-wavelength topography of the Saturnian satellites. J. Geophys. Res. Planets 116, 2011JE003835 (2011). [Google Scholar]
- 32.Vance S. D., Panning M. P., Stähler S., Cammarano F., Bills B. G., Tobie G., Kamata S., Kedar S., Sotin C., Pike W. T., Lorenz R., Huang H.-H., Jackson J. M., Banerdt B., Geophysical investigations of habitability in ice-covered ocean worlds. J. Geophys. Res. Planets 123, 180–205 (2018). [Google Scholar]
- 33.Ramadhan A., Wagner G., Hill C., Campin J.-M., Churavy V., Besard T., Souza A., Edelman A., Ferrari R., Marshall J., Oceananigans.jl: Fast and friendly geophysical fluid dynamics on GPUs. J. Open Source Softw. 5, 02018 (2020). [Google Scholar]
- 34.Grimshaw R. H. J., A note on the β-plane approximation. Tellus 27, 351–357 (1975). [Google Scholar]
- 35.Dellar P. J., Variations on a beta-plane: Derivation of non-traditional beta-plane equations from hamilton’s principle on a sphere. J. Fluid Mech. 674, 174–195 (2011). [Google Scholar]
- 36.Kang W., Jansen M., On icy ocean worlds, size controls ice shell geometry. Astrophys. J. 935, 103 (2022). [Google Scholar]
- 37.Wunsch C., Ferrari R., Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314 (2004). [Google Scholar]
- 38.Soderlund K., Schmidt B., Wicht J., Blankenship D., Ocean-driven heating of Europa’s icy shell at low latitudes. Nat. Geosci. 7, 16–19 (2014). [Google Scholar]
- 39.Rhines P. B., Waves and turbulence on a beta-plane. J. Fluid Mech. 69, 417–443 (1975). [Google Scholar]
- 40.Heimpel M., Aurnou J., Turbulent convection in rapidly rotating spherical shells: A model for equatorial and high latitude jets on jupiter and saturn. Icarus 187, 540–557 (2007). [Google Scholar]
- 41.Charney J. G., Stern M. E., On the stability of internal baroclinic jets in a rotating atmosphere. J. Atmos. Sci. 19, 159–172 (1962). [Google Scholar]
- 42.Bretherton F. P., Critical layer instability in baroclinic flows. Q. J. R. Meteorol. Soc. 92, 325–334 (1966). [Google Scholar]
- 43.Lewis E., Perkin R., Ice pumps and their rates. J. Geophys. Res. 91, 11756–11762 (1986). [Google Scholar]
- 44.Paparella F., Young W., Horizontal convection is non-turbulent. J. Fluid Mech. 466, 205–214 (2002). [Google Scholar]
- 45.Whitehead J., Flows in horizontal thermohaline convection with differential diffusion. Geophys. Astrophys. Fluid Dyn. 115, 473–498 (2021). [Google Scholar]
- 46.Karsten R., Jones H., Marshall J., The role of eddy transfer in setting the stratification and transport of a circumpolar current. J. Phys. Oceanogr. 32, 39–54 (2002). [Google Scholar]
- 47.Plumb R. A., Ferrari R., Transformed Eulerian-mean theory. Part I: Nonquasigeostrophic theory for eddies on a zonal-mean flow. J. Phys. Oceanogr. 35, 165–174 (2005). [Google Scholar]
- 48.Held I. M., Larichev V. D., A scaling theory for horizontally homogeneous, baroclinically unstable flow on a beta plane. J. Atmos. Sci. 53, 946–952 (1996). [Google Scholar]
- 49.Jansen M., Ferrari R., Equilibration of an atmosphere by adiabatic eddy fluxes. J. Atmos. Sci. 70, 2948–2962 (2013). [Google Scholar]
- 50.Kang W., Flierl G., Spontaneous formation of geysers at only one pole on Enceladus’s ice shell. Proc. Natl. Acad. Sci. U.S.A. 117, 14764–14768 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ashkenazy Y., Sayag R., Tziperman E., Dynamics of the global meridional ice flow of Europa’s icy shell. Nat. Astron. 2, 43–49 (2018). [Google Scholar]
- 52.Gastine T., Wicht J., Aubert J., Scaling regimes in spherical shell rotating convection. J. Fluid Mech. 808, 690–732 (2016). [Google Scholar]
- 53.Amit H., Choblet G., Tobie G., Terra-Nova F., Čadek O., Bouffard M., Cooling patterns in rotating thin spherical shells—Application to Titan’s subsurface ocean. Icarus 338, 113509 (2020). [Google Scholar]
- 54.Čadek O., Souček O., Běhounková M., Choblet G., Tobie G., Hron J., Long-term stability of Enceladus’ uneven ice shell. Icarus 319, 476–484 (2019). [Google Scholar]
- 55.Nimmo F., Thomas P., Pappalardo R., Moore W., The global shape of Europa: Constraints on lateral shell thickness variations. Icarus 191, 183–192 (2007). [Google Scholar]
- 56.Nimmo F., Bills B., Shell thickness variations and the long-wavelength topography of Titan. Icarus 208, 896–904 (2010). [Google Scholar]
- 57.Phillips C. B., Pappalardo R. T., Europa Clipper mission concept: Exploring Jupiter’s ocean moon. Eos 95, 165–167 (2014). [Google Scholar]
- 58.Grasset O., Dougherty M., Coustenis A., Bunce E., Erd C., Titov D., Blanc M., Coates A., Drossart P., Fletcher L., Hussmann H., Jaumann R., Krupp N., Lebreton J.-P., Prieto-Ballesteros O., Tortora P., Tosi F., Van Hoolst T., JUpiter ICy moons Explorer (JUICE): An ESA mission to orbit Ganymede and to characterise the Jupiter system. Planet. Space Sci. 78, 1–21 (2013). [Google Scholar]
- 59.Christensen U. R., Zonal flow driven by strongly supercritical convection in rotating spherical shells. J. Fluid Mech. 470, 115–133 (2002). [Google Scholar]
- 60.Arakawa A., Lamb V. R., Computational design of the basic dynamical processes of the UCLA general circulation model. Methods Comput. Phys. 17, 173–265 (1977). [Google Scholar]
- 61.Shu C.-W., High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Rev. 51, 82–126 (2009). [Google Scholar]
- 62.Le H., Moin P., An improvement of fractional step methods for the incompressible Navier-Stokes equations. J. Comput. Phys. 92, 369–379 (1991). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S4