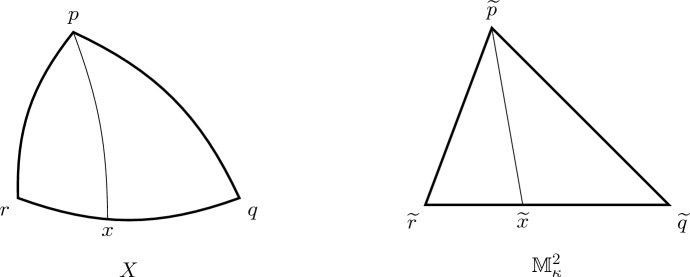Abstract
Persistence diagrams are objects that play a central role in topological data analysis. In the present article, we investigate the local and global geometric properties of spaces of persistence diagrams. In order to do this, we construct a family of functors , , that assign, to each metric pair (X, A), a pointed metric space . Moreover, we show that is sequentially continuous with respect to the Gromov–Hausdorff convergence of metric pairs, and we prove that preserves several useful metric properties, such as completeness and separability, for , and geodesicity and non-negative curvature in the sense of Alexandrov, for . For the latter case, we describe the metric of the space of directions at the empty diagram. We also show that the Fréchet mean set of a Borel probability measure on , , with finite second moment and compact support is non-empty. As an application of our geometric framework, we prove that the space of Euclidean persistence diagrams, , and , has infinite covering, Hausdorff, asymptotic, Assouad, and Assouad–Nagata dimensions.
Keywords: Alexandrov spaces, Asymptotic dimension, Metric pairs, Gromov–Hausdorff convergence, Persistence diagram, Fré chet mean set
Introduction
After first appearing in the pioneering work of Edelsbrunner et al. (2000), in recent years, persistent homology has become an important tool in the analysis of scientific datasets, covering a wide range of applications (Adcock et al. 2014; Buchet et al. 2018; Edelsbrunner and Harer 2008; Kovacev-Nikolic et al. 2016; Munch 2013; Cássio 2015; Zhu 2013) and playing a central role in topological data analysis.
In Zomorodian and Carlsson (2005), Carlsson and Zomorodian introduced persistence modules indexed by the natural numbers as the algebraic objects underlying persistent homology. The successful application of persistent homology in data analysis is, to a great extent, due to the notion of persistence diagrams. These were introduced by Cohen-Steiner, Edelsbrunner, and Harer as equivalent representations for persistence modules indexed by the positive real numbers (Cohen-Steiner et al. 2007). More precisely, a persistence diagram is a multiset of points , where and . Persistence diagrams are objects that, in a certain sense, are easier to visualize than persistence modules. Moreover, the set of persistence diagrams supports a family of metrics, called p-Wasserstein metrics, parametrized by (see Cohen-Steiner et al. 2010), with the metric corresponding to also known as the bottleneck distance. We will denote by , where is the diagonal of , the metric space defined by the set of persistence diagrams that arise in persistent homology equipped with the p-Wasserstein metric.
Several authors have extensively studied the geometry and topology of the spaces . For instance, Mileyko et al. (2011) examined the completeness, separability, and compactness of subsets of the space with the p-Wasserstein metric, . Turner et al. (2014) showed that is an (infinite dimensional) Alexandrov space with non-negative curvature. The results in Mileyko et al. (2011) imply the existence of Fréchet means for certain probability distributions on . For , the results in Turner et al. (2014) imply the convergence of certain algorithms used to find Fréchet means of finite sets in . Turner (2020) studied further statistical properties, such as the median of finite sets in , and its relation to the mean. All these results are crucially based on the presence of the p-Wasserstein metric and, when p=2, on the Alexandrov space structure.
Our contributions
Motivated by the preceding considerations, we develop a general framework for the geometric study of generalized spaces of persistence diagrams. To the best of our knowledge, the present article is the first attempt to systematically analyze the geometric properties of such spaces. Our departure point is the existence of a family of functors , (resp. ), from the category of metric pairs equipped with relative Lipschitz maps into the category of pointed metric spaces equipped with pointed Lipschitz maps (resp. the category of pointed pseudometric spaces equipped with pointed Lipschitz maps), which assign to each metric pair (X, A), where X is a metric space and is a closed and non-empty subset, a space of persistence diagrams . In particular, for , where is the diagonal of , we recover the spaces , that arise in persistent homology, equipped with the p-Wasserstein distance. These spaces were studied in Mileyko et al. (2011), Turner et al. (2014). Bubenik and Elchesen studied such functors from an algebraic point of view in Bubenik and Elchesen (2022). Here, we disregard the algebraic structure and focus on the behavior of several basic topological, metric, and geometric properties and invariants under the functors . When and for , the resulting spaces , that we call from now on spaces of Euclidean persistence diagrams, can be considered as the parameter spaces for rectangle persistent modules. These modules arise in the context of multiparameter persistent homology and have been investigated by several authors (see, for example, Bjerkevik 2021; Botnan et al. 2022; Cochoy and Oudot 2020; Skryzalin and Carlsson 2017).
Our aim is twofold: first, to show that many basic results useful in statistical analysis on spaces of Euclidean persistence diagrams hold for the generalized persistence diagram spaces , and, second, to study the intrinsic geometry of such spaces, which is of interest in its own right. As an application of our framework, we show that different notions of dimension are infinite for spaces the spaces of Euclidean diagrams .
Given that each metric pair (X, A) gives rise to a pointed metric space , it is natural to ask whether some form of continuity holds with respect to (X, A). To address this question, we introduce the Gromov–Hausdorff convergence of metric pairs, a mild generalization of the usual Gromov–Hausdorff convergence of pointed metric spaces (see Definition 3.1), and obtain our first main result.
Theorem A
The functor , , is sequentially continuous with respect to the Gromov–Hausdorff convergence of metric pairs if and only if .
One may think of Theorem A as providing formal justification for using persistence diagrams calculated by computers in applications. Since computers have finite precision, such diagrams are elements of a discrete space that approximates the ideal space of persistence diagrams in the Gromov–Hausdorff sense. Theorem A ensures that this approximation is continuous. In particular, a small perturbation of the space of parameters (X, A) (which is in the Euclidean case) will result in a small perturbation in the corresponding space of persistence diagrams.
Our second main result is the invariance of several basic metric properties under , , generalizing results in Mileyko et al. (2011), Turner et al. (2014) for spaces of Euclidean persistence diagrams. These properties include completeness and geodesicity (which we require of Alexandrov spaces), as well as non-negative curvature when .
Theorem B
Let and let . Then the following assertions hold:
If X is complete, then is complete.
If X is separable, then is separable.
If X is a proper geodesic space, then is a geodesic space.
If X is a proper Alexandrov space with non-negative curvature, then is an Alexandrov space with non-negative curvature.
One may show that is complete if and only if X/A is complete for any (see Che et al. (2024)). The behavior of is substantially different to that of , . Indeed, Theorem B fails for , as shown in Che et al. (2024).
The functor allows us to carry over, with some minor modifications, the Euclidean proofs of completeness and separability in Mileyko et al. (2011) to prove items (1) and (2) in Theorem B. Items (3) and (4) generalize the corresponding Euclidean results in Turner et al. (2014), asserting that the spaces , , are geodesic and that is an Alexandrov space of non-negative curvature. Our proofs differ from those in Turner et al. (2014) and rely on a characterization of geodesics in persistence diagram spaces originally obtained by Chowdhury in Chowdhury (2019) in the Euclidean case.
Motivated by results in Turner et al. (2014) on the Alexandrov space , we analyze the infinitesimal geometry of Alexandrov spaces arising via Theorem B (4) at their distinguished point, the empty diagram . The infinitesimal structure of an Alexandrov space at a point is captured by the space of directions, which is itself a metric space and corresponds to the unit tangent sphere in the case of Riemannian manifolds.
First, we show that the space of directions at has diameter at most (Proposition 6.1). Second, we show that directions in corresponding to finite diagrams are dense in (Proposition 6.2). Finally, we use this to obtain an explicit description of the metric structure of . These results are new, even in the case of Euclidean persistence diagrams.
Theorem C
The space of persistence diagrams at has diameter at most and directions in corresponding to finite diagrams are dense in . Moreover, consider elements in given by geodesics and joining with , where and are geodesics in X joining points in A with a and , respectively. Then
where d is the metric on X, is the 2-Wasserstein metric, and ranges over all bijections between subsets and of points in and , respectively, such that for all .
In , persistence diagrams in a neighborhood of the empty diagram may be thought of as coming from noise. Thus, the space of directions at the empty diagram may be interpreted as directions coming from noise. Theorem C implies that the geometry at the empty diagram is singular, as directions at this point make an angle of at most . In particular, the infinitesimal geometry is not Euclidean. Hence, embedding noisy sets of persistence diagrams into a Hilbert space might require large metric distortions. This might be of relevance in the vectorization of sets of persistence diagrams where noise might be present, which in turn plays a role in applying machine learning to such sets (see, for example, Bubenik 2015; Carrière and Bauer 2019; Kusano et al. 2017).
A further advantage of the metric pair framework is that it yields the existence of Fréchet mean sets for certain classes of probability measures on generalized spaces of persistence diagrams, as shown in Mileyko et al. (2011) in the Euclidean case. The elements of Fréchet mean sets (which, a priori, may be empty) are also called barycenters (see, for example, Afsari 2011) and may be interpreted as centers of mass of the given probability measure. In the case of the spaces , we may interpret a finite collection of persistence diagrams as a measure on with finite support. An element of the corresponding Fréchet mean set then may be interpreted as an average of the diagrams determining the measure. For the spaces , we have the following result.
Theorem D
Let be a Borel probability measure on , . Then the following assertions hold:
If has finite second moment and compact support, then the Fréchet mean set of is non-empty.
If is tight and has rate of decay at infinity , then the Fréchet mean set of is non-empty.
The proof of this theorem follows along the lines of the proofs of the corresponding Euclidean statements in Mileyko et al. (2011), and hinges on the fact, easily shown, that the characterization of totally bounded subsets of spaces of Euclidean persistence diagrams given in Mileyko et al. (2011) also holds in the setting of metric pairs (see Proposition A.11).
As mentioned above, our constructions include, as a special case, spaces of Euclidean persistence diagrams, such as the classical space . Our fourth main result shows that different notions of dimension for this space are all infinite. We let .
Theorem E
The space , and , has infinite covering, Hausdorff, asymptotic, Assouad, and Assouad–Nagata dimension.
It is known that every metric space of finite asymptotic dimension admits a coarse embedding into some Hilbert space (see Roe 2003, Example 11.5). The spaces , , do not admit such embeddings (see Bubenik and Wagner 2020, Theorem 21; Wagner 2021, Theorem 3.2). Hence, their asymptotic dimension is infinite (cf. Bubenik and Wagner 2020, Corollary 27). These observations, along with Theorem E, immediately imply the following.
Corollary F
The space , , has infinite asymptotic dimension.
Our analysis also shows that other spaces of Euclidean persistence diagrams appearing in topological data analysis, such as and , have infinite asymptotic dimension as well (see Sect. 7 for precise definitions). One may think of these spaces as parameter spaces for persistence rectangles in multidimensional persistent homology (Bjerkevik 2021; Skryzalin and Carlsson 2017). We point out that the proof of Theorem E is based on different arguments to those in Bubenik and Wagner (2020), Wagner (2021) and provides a unified approach for all . The crucial point in our proof is the general observation that, if a metric pair (X, A) contains a curve whose distance to A grows linearly, then has infinite asymptotic dimension (see Proposition 7.3). We point out that our arguments to prove Theorem E can be used to prove an analogous result for the spaces of persistence diagrams with finitely (but arbitrarily) many points equipped with the p-Wasserstein distance, , as defined, for example, in Bubenik and Elchesen (2022). Thus, all such spaces have infinite Hausdorff, covering, asymptotic, Assouad, and Assouad–Nagata dimensions (see Corollary 7.7).
Note that Theorem B (4) provides a systematic way of constructing examples of Alexandrov spaces of non-negative curvature. In particular, by Theorem E, the space is an infinite-dimensional Alexandrov space. In contrast to the finite-dimensional case, where every Alexandrov space is proper, there are few results about infinite-dimensional Alexandrov spaces in the literature (see, for example, Plaut 2002, Sect. 13, and more recently, Mitsuishi 2010; Yokota 2012, 2014). Technical difficulties occur that do not arise in finite dimensions (see, for example, Halbeisen 2000), and a more thorough understanding of the infinite-dimensional case is lacking.
Related work
Different generalizations of persistence diagrams have appeared in the persistent homology literature, as well as their corresponding spaces of persistence diagrams. In Patel (2018), Patel generalizes persistent diagram invariants of persistence modules to cases where the invariants are associated to functors from a poset P to a symmetric monoidal category. In Kim and Mémoli (2021), Kim and Mémoli define the notion of rank invariant for functors with indices in an arbitrary poset, which allows defining persistence diagrams for any persistence module F over a poset regardless of whether F is interval-decomposable or not. In Divol and Lacombe (2021), Divol and Lacombe considered a persistence diagram as a discrete measure, expressing the distance between persistence diagrams as an optimal transport problem. In this context, the authors introduced Radon measures supported on the upper half plane, generalizing the notion of persistence diagrams, and studied the geometric and topological properties of spaces of Radon measures. Bubenik and Elchesen considered a functor in Bubenik and Elchesen (2022), which sends metric pairs to free commutative pointed metric monoids and studied many algebraic properties of such a functor.
In Bubenik and Hartsock (2024), which followed the first version of the present article, Bubenik and Hartsock studied topological and geometric properties of spaces of persistence diagrams and also considered the setting of pairs (X, A). To address the existence of optimal matchings and geodesics, non-negative curvature in the sense of Alexandrov, and the Hausdorff and asymptotic dimension of spaces of persistence diagrams, Bubenik and Hartsock require the set to be distance minimizing, i.e., for all , there exists such that . This property holds when X is proper and A is closed, which we assume in items (3) and (4) of Theorem B. The authors of Bubenik and Hartsock (2024) also show that has infinite asymptotic dimension when X is geodesic and proper, X/A is unbounded, and A is distance minimizing. The spaces of Euclidean persistence diagrams on points equipped with the p-Wasserstein distance, , have finite asymptotic dimension and therefore admit a coarse embedding into a Hilbert space (see Mitra and Virk 2021). On the other hand, the space of Euclidean persistence diagrams on finitely many points equipped with the bottleneck distance has infinite asymptotic dimension (Bubenik and Hartsock 2024, Corollary 27) and cannot be coarsely embedded into a Hilbert space (see Mitra and Virk 2021, Theorem 4.3). Bubenik and Hartsock have extended these results to metric pairs in Bubenik and Hartsock (2024). Carrière and Bauer have studied the Assouad dimension and bi-Lipschitz embeddings of spaces of finite persistence diagrams in Carrière and Bauer (2019). More recently, Bate et al. (2024) have shown that the space of persistence barcodes with at most m-points can be bi-Lipschitz embedded into . They point out that their results also hold for generalized persistence diagrams as considered in the present article whenever , , and is a proper, open subset of .
With respect to Fréchet means of probability measures defined on the spaces of persistence diagrams, Divol and Lacombe in Divol and Lacombe (2021) investigated the existence of such Fréchet means for probability measures defined on the space of persistence measures in equipped with the optimal partial transport, which in particular contain the spaces . Our results, although more particular in the hypotheses that we impose on the probability measures considered, are more general with respect to the spaces they are defined on.
Organization
Our article is organized as follows. In Sect. 2, we present the background on metric pairs, metric monoids, and Alexandrov spaces, and introduce the functor . In Sect. 3, we define Gromov–Hausdorff convergence for metric pairs and prove Theorem A. The proofs of items (1) and (2) in Theorem B and of Theorem D follow, with minor modifications, along the same lines as those for the corresponding statements in the Euclidean case. For the sake of completeness, we have included a full treatment of these results in Appendix A. In Sect. 4, we analyze the geodesicity of the spaces and prove item (3) of Theorem B. In Sect. 5, we analyze the existence of lower curvature bounds for our spaces of persistence diagrams and prove item (4) of Theorem B. In Sect. 6, we make some remarks about their local structure. Finally, in Sect. 7 we specialize our constructions to the spaces of Euclidean persistence diagrams, which include the classical space of persistence diagrams, and prove Theorem E (cf. Corollary 7.5).
Preliminaries
In this section, we collect preliminary material that we will use in the rest of the article and prove some elementary results on the spaces of persistence diagrams. Our primary reference for metric geometry will be Burago et al. (2001).
Metric pairs
Let X be a set. A map is a metric on X if d is symmetric, satisfies the triangle inequality, and is definite, i.e. if and only if . A pseudometric space is defined similarly; while keeping the other properties, and still requiring that for all , we allow for points x, y in X with and , in which case d is a pseudometric. We obtain extended metric and extended pseudometric spaces if we allow for d to take the value . Note that when d is a pseudometric, points at distance zero from each other give a partition of X, and d induces a metric in the corresponding quotient set.
Let , be two extended pseudometric spaces. A Lipschitz map with Lipschitz constant C is a map such that for all and .
Definition 2.1
Let denote the category of metric pairs, whose objects, , are pairs (X, A) such that is a metric space and is closed and non-empty, and whose morphisms, , are relative Lipschitz maps, i.e. Lipschitz maps such that . When A is a point, we will talk about pointed metric spaces and pointed Lipschitz maps, i.e. Lipschitz maps such that . We will denote the category of pointed metric spaces by . Similarly, we define the category of pointed pseudometric spaces, whose objects , are pairs such that D is a pseudometric space and is a point in D. The morphisms of are pointed Lipschitz maps.
Commutative metric monoids and spaces of persistence diagrams
Some of the definitions and results in this subsection may be found in Bubenik and Elchesen (2022), Bubenik and Elchesen (2022). For completeness, we provide full proofs of all the statements. We will denote multisets by using two curly brackets and will usually denote persistence diagrams by Greek letters.
Let (X, d) be a metric space and fix . We define the space on X as the set of countable multisets of elements of X equipped with the p-Wasserstein pseudometric , which is given by
| 2.1 |
if , and
| 2.2 |
if , where ranges over all bijections between and in . Here, by convention, we set , that is, we have whenever and do not have the same cardinality.
The function defines an extended pseudometric in , since it is clearly non-negative, symmetric, and the triangle inequality may be proved as follows: if have the same cardinality and and are bijections, then is also a bijection and, if , then
Taking the infimum over bijections and we get the claim. If the cardinalities of are not the same, the inequality is trivial, since both sides or just the right-hand side would be infinite. For the argument is analogous and easier.
Given two multisets and , we define their sum to be their disjoint union. We can make into a commutative monoid with monoid operation given by taking sums of multisets, and with identity the empty multiset. It is easy to check that is (left-)contractive, that is, for all .
From now on, let . Given , we write if there exist such that . It is easy to verify that defines an equivalence relation on such that, if and , then , i.e. is a congruence relation on (see, for example, Hungerford 1974, p. 27). We denote by the quotient set . Given , we write for the equivalence class of in . Note that if and only if , that is, and share the same points with the same multiplicities outside A. The monoid operation on induces a monoid operation on by defining as the congruence class corresponding to .
The function on induces a non-negative function defined by
| 2.3 |
Note that is also contractive, that is, for all .
Definition 2.2
The space of p-persistence diagrams on the pair (X, A), denoted by , is the set of all such that .
Lemma 2.3
If is a finite multiset, then .
Proof
Let be a multiset of cardinality . Since is non-empty, we can pick an element , and so there exists a multiset of cardinality k. Therefore, there exists a bijection between the finite multisets and , implying that .
Lemma 2.4
The following assertions hold:
If , then the function is an extended pseudometric on and a pseudometric on .
If , then the function is an extended metric on and a metric on .
Proof
We will first show that , , is an extended pseudometric. We will then show that, for , the function is an extended metric.
It is clear that, for all , the function is symmetric, non-negative, and for all . The triangle inequality follows from the facts that is commutative and that is contractive. More precisely, fix , and let . By the definition of , there exist such that and . Using the commutativity of , the contractivity of , and the triangle inequality for , we get
Our choice of was arbitrary, implying that , as required. Hence, is an extended pseudometric on . By the triangle inequality, is a pseudometric on . Indeed, if , then . This completes the proof of part (1).
Now, we prove part (2). Fix and let be multisets such that . It then follows that there exists a point which appears in and with different multiplicities (which includes the case when it has multiplicity 0 in one of the diagrams and positive multiplicity in the other). Without loss of generality, suppose that u appears with higher multiplicity in . Now let . Observe that since, otherwise, there would be a sequence of points in converging to u in X, which in turn would imply that . Let be such that for all , which exists since and is open in X. We set . Now, for any , if is a bijection, then must map some copy of to a point with , implying that . By taking the infimum over all , it follows that , as required. This shows that is an extended metric on . The triangle inequality implies, as in part (1), that is a metric on . This completes the proof of part (2).
For , the metric is the p-Wasserstein metric. The following example shows that, for , the function is not a metric, only a pseudometric.
Example 2.5
Let (X, A) be a metric pair such that there exists a sequence of different points which converges to some and for all . Then the multisets and induce diagrams such that and as can be seen considering the sequence of bijections given by
Thus is a pseudometric space but not a metric space.
From now on, unless stated otherwise, we will only consider metric pairs (X, A) where X is a metric space. Also, for the sake of simplicity, we will treat elements in as multisets, with the understanding that whenever we do so we are actually dealing with representatives of such elements in . Thus, for instance, we will consider things like for or bijections for , meaning there are representatives and and a bijection . We point out that the constructions discussed above can be carried out for extended pseudometric spaces with straightforward adjustments.
Given two metric pairs (X, A) and (Y, B), their disjoint union is the space . We can form the extended pseudometric space , where , and for all and . The following result is an immediate consequence of the definition of the space .
Proposition 2.6
If (X, A) and (Y, B) are metric pairs, then
where denotes the space endowed with the metric
if , and
if .
Proof
It is clear that for any , we can write with and . Therefore, given , we have
if , and
if .
Remark 2.7
Note that, if we allow (X, A) and (Y, B) to be extended metric pairs, then the disjoint union with the metric defines a coproduct in the category of extended metric pairs whose objects are extended metric pairs and whose morphisms are relative Lipschitz maps (cf. Definition 2.1).
Definition 2.8
Given a metric pair (X, A), and a relative map (i.e. such that ), we define a pointed map as follows. Given a persistence diagram , we let
| 2.4 |
We now define the functor , which we will study in the remaining sections.
Proposition 2.9
Consider the map .
If , then is a functor from the category of metric pairs equipped with relative Lipschitz maps to the category of pointed pseudometric spaces with pointed Lipschitz maps.
If , then is a functor from the category of metric pairs equipped with relative Lipschitz maps to the category of pointed metric spaces with pointed Lipschitz maps.
Proof
Consider a C-Lipschitz relative map , i.e. holds for all for some . We will prove that the pointed map , defined in (2.4), restricts to a C-Lipschitz map .
First, given a p-diagram, we need to prove that . For any , we have
for any choice . Since this choice is arbitrary,
Now consider two diagrams . Observe that, if is a bijection, then it induces a bijection given by whenever for some . Therefore
Since is an arbitrary bijection, we get that
Thus, is C-Lipschitz.
Now consider two relative Lipschitz maps and . Let . Then
Thus, .
Finally, if is the identity map, it is clear that is also the identity map. Thus, defines a functor.
Remark 2.10
Note that we could have proved that defines a functor on the category of metric spaces equipped with isometries or even bi-Lipschitz maps. However, Proposition 2.9 is more general.
Remark 2.11
Proposition 2.9 implies that, if (X, A) is a metric pair and is an action of a group G on (X, A) via relative bi-Lipschitz maps, then we get an action of G on given by
Observe that the Lipschitz constant of the bi-Lipschitz maps in the group action is preserved by the functor . Hence, if G acts by relative isometries on (X, A) (i.e., by isometries such that ) then so does the induced action on .
Remark 2.12
We point out that is, in fact, a functor from to , the category of commutative pointed metric monoids (see Bubenik and Elchesen 2022). In this case, given a map , the induced map is a monoid homomorphism. Composing the functor with the forgetful functor one obtains the map to . In this work we consider this last composition, since we are mainly focused on the metric properties of the spaces , and leave the study of the algebraic properties of the monoids for future work.
Consider now the quotient metric space X/A, namely, the quotient space induced by the partition endowed with the metric given by
for any (cf. Munkres 2000, Ch. 2, Sect. 22 and Burago et al. 2001, Definition 3.1.12). It follows from (Bubenik and Elchesen 2022, Remark 4.14 and Lemma 4.24) that and are isometrically isomorphic. We have the following commutative diagrams of functors. For ,  and, for ,
and, for ,  both given by
both given by 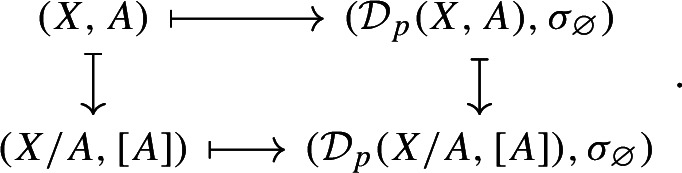 Observe that the map is a natural isomorphism. Therefore, diagrams (2.6) and (2.5) show that the functor factors through the quotient functor and the functor for .
Observe that the map is a natural isomorphism. Therefore, diagrams (2.6) and (2.5) show that the functor factors through the quotient functor and the functor for .
Remark 2.13
Note that we also have the following commutative diagrams of functors. For ,  and, for ,
and, for ,  both given by
both given by 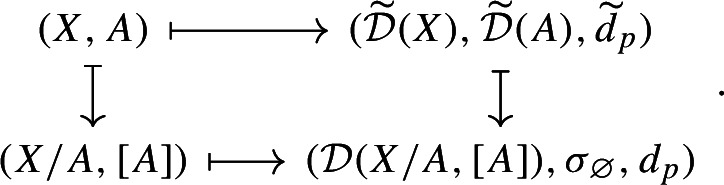 here the categories , , and consist of extended (pseudo)metric pairs and pointed (pseudo)metric spaces respectively.
here the categories , , and consist of extended (pseudo)metric pairs and pointed (pseudo)metric spaces respectively.
Remark 2.14
Observe that the subspace of consisting of diagrams with finitely many points can be identified, as a set, with the infinite symmetric product of the pointed space (X/A, [A]) (see Hatcher 2002, p. 282, for the relevant definitions). These two spaces, however, might not be homeomorphic in general, as the infinite symmetric product is not metrizable unless A is open in X (see, for instance, Wofsey 2015).
Alexandrov spaces
Let X be a metric space. The length of a continuous path is given by
where the supremum is taken over all finite partitions of the interval [a, b]. A geodesic space is a metric space X where for any there is a shortest path (or minimizing geodesic) between , i.e. a path such that
| 2.5 |
In general, a path , where J is an interval, is said to be geodesic if each has a neighborhood such that is a shortest path between any two of its points.
We will also consider the model spaces given by
Definition 2.15
A geodesic triangle in X consists of three points and three minimizing geodesics between those points. A comparison triangle for in is a geodesic triangle in such that
Definition 2.16
We say that X is an Alexandrov space with curvature bounded below by k if X is complete, geodesic and can be covered with open sets with the following property (cf. Fig. 1):
-
(T)For any geodesic triangle contained in one of these open sets, any comparison triangle in and any point , the corresponding point such that satisfies
Fig. 1.
The condition for a complete geodesic metric space X to be an Alexandrov space with curvature . Here, the curves [pq], [qr], [rp], [px], , , , are geodesics, and the length of [pq] (respectively, [rp], [qx], [xr]) is equal to the length of (respectively, , , ). Condition (T) then says that the length of is not greater than the length of [px]
By Toponogov’s Globalization Theorem, if X is an Alexandrov space with curvature bounded below by k, then property (T) above holds for any geodesic triangle in X (see, for example, Plaut 2002, Sect. 3.4). Well-known examples of Alexandrov spaces include complete Riemannian n-manifolds with a uniform lower sectional curvature bound, orbit spaces of such manifolds by an effective, isometric action of a compact Lie group, and, in infinite dimension, Hilbert spaces. The latter are instances of infinite-dimensional Alexandrov spaces of non-negative curvature.
The angle between two minimizing geodesics [pq], [pr] in an Alexandrov space X is defined as
Geodesics that make an angle zero determine an equivalence class called tangent direction. The set of tangent directions at a point is denoted by . When equipped with the angle distance , the set is a metric space. Note that the metric space may fail to be complete, as one can see by considering directions at a point in the boundary of the unit disc D in the Euclidean plane, D being an Alexandrov space of non-negative curvature. The completion of is called the space of directions of X at p, and is denoted by . Note that in a complete, finite-dimensional Riemannian manifold with sectional curvature uniformly bounded below, the space of directions at any point is isometric to the unit sphere in the tangent space to the manifold at the given point. For further basic results on Alexandrov geometry, we refer the reader to Burago et al. (2001), Burago et al. (1992), Plaut (2002).
We conclude this section by briefly recalling the definition of the Hausdorff dimension of a metric space (see Burago et al. 2001, Sect. 1.7, for further details). One may show that the Hausdorff dimension of an Alexandrov space is an integer or infinite (see Burago et al. 2001, Corollary 10.8.21 and Exercise 10.8.22).
Let X be a metric space and denote the diameter of a subset by . For any and any , let
where is a countable covering of X by sets of diameter less than . Note that if no such covering exists, then . The -dimensional Hausdorff measure of X is given by
where is a normalization constant such that, if is an integer n, the n-dimensional Hausdorff measure of the unit cube in n-dimensional Euclidean space is 1. This is achieved by letting be the Lebesgue measure of the unit ball in . As its name indicates, the Hausdorff measure is a measure on the Borel -algebra of X. One may show that there exists such that for all and for all . We then define the Hausdorff dimension of X, denoted by , to be . Thus,
Gromov–Hausdorff convergence and sequential continuity
In this section, we investigate the continuity of the functors and defined in the preceding section. Since , , takes values in , the category of pointed metric spaces, while takes values in , the category of pointed pseudometric spaces, we will consider each case separately. As both and are defined on , the category of metric pairs, we will first define a notion of Gromov–Hausdorff convergence of metric pairs (X, A). We do this in such a way that when A is a point, our definition implies the usual pointed Gromov–Hausdorff convergence of pointed metric spaces (see Burago et al. 2001, Definition 8.1.1 and Herron 2016; cf. Jansen 2017, Definition 2.1 for the case of proper metric spaces; see also Definition 3.4 below). After showing that is sequentially continuous with respect to the Gromov–Hausdorff convergence of metric pairs, and that , , is not always sequentially continuous, we will prove the sequential continuity of with respect to the Gromov–Hausdorff convergence of metric pairs on and pointed Gromov–Hausdorff convergence of pseudometric spaces on .
Definition 3.1
(Gromov–Hausdorff convergence for metric pairs) A sequence of metric pairs converges in the Gromov–Hausdorff topology to a metric pair (X, A) if there exist sequences and of positive numbers with , , and -approximations from to for each , i.e. maps satisfying the following three conditions:
for any ;
, where stands for the Hausdorff distance in X;
.
We will denote the Gromov–Hausdorff convergence of metric pairs by and the pointed Gromov–Hausdorff convergence by .
With Definition 3.1 in hand, we now show that the functor is continuous, while is not necessarily continuous when .
Proposition 3.2
The quotient functor , given by , is sequentially continuous with respect to the Gromov–Hausdorff convergence of metric pairs.
Proof
We will prove that, if there exist sequences and of positive numbers with , and -approximations from to , then there exist -approximations from to . For ease of notation, we will omit the subindices in the metric which indicate the corresponding metric space.
Let be an -approximation from to in the sense of Definition 3.1. Then, for any , , we have
which implies
| 3.1 |
Moreover, for any and , we have
and, since , this yields
| 3.2 |
Combining inequalities (3.1) and (3.2), we get
Now, for each i, define by
We will prove that is a -approximation from to . Indeed, consider . Then and therefore
If and , then
A similar inequality is obtained when and . When both and , we get
In any case, we see that the distortion of is , which is item xm(1) in Definition 3.1.
For item (2) in Definition 3.1, we simply observe that by definition of they are pointed maps.
Finally, we see that for we have , so given that is an -approximation from to there exists such that . Therefore,
Thus . This gives item (3) in Definition 3.1.
Example 3.3
(with is not sequentially continuous) Let and set . Then . Observe that for , the space is unbounded. Indeed, if is the diagram that contains a single point, 1/i, with multiplicity n, then as .
Now, let be the empty diagram and suppose, for the sake of contradiction, that there exist -approximations for some and . Then
for all . However, we have , implying that
| 3.3 |
for all . As and as , inequality (3.3) contradicts the fact that is unbounded for each i.
Finally, we turn our attention to the functor . Recall, from Sect. 2, that takes values in , the category of pointed pseudometric spaces. Thus, to discuss the continuity of , we must first define a notion of Gromov–Hausdorff convergence for pointed pseudometric spaces. We define this convergence in direct analogy to pointed Gromov–Hausdorff convergence of pointed metric spaces.
Definition 3.4
(Gromov–Hausdorff convergence for pointed pseudometric spaces) A sequence of pointed pseudometric spaces converges in the Gromov–Hausdorff topology to a pointed pseudometric space if there exist sequences and of positive numbers with , , and -approximations from to for each , i.e. maps satisfying the following three conditions:
for any ;
;
.
As for metric spaces, we will also denote the Gromov–Hausdorff convergence of pseudometric pairs by .
Given a pseudometric space D, we will denote by the metric quotient , where if and only if . We also denote sometimes by the image of under the metric quotient. The following proposition shows that pointed Gromov–Hausdorff convergence of pseudometric spaces induces pointed Gromov–Hausdorff convergence of the corresponding metric quotients.
Proposition 3.5
Let , be pointed pseudometric spaces and let , be the canonical metric identifications. Then the following assertions hold:
If , then .
If , then .
Proof
For each i, consider such that for all and similarly. These maps exist due to the axiom of choice. Let be -approximations from to . Define as
for any . Then is a -approximation from to . Indeed,
Also
Moreover, if then . Then there is some with such that . Therefore,
This proves item (1).
Conversely, given an -approximation from to , we can define as
for any . Then is an -approximation from to . Indeed,
Moreover
Finally, if then there exists such that and , or equivalently, . This proves item (2).
In particular, if we consider the following commutative diagram 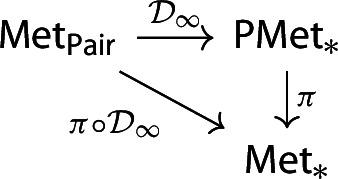 where is the canonical metric identification functor, then is continous if and only if is continuous.
where is the canonical metric identification functor, then is continous if and only if is continuous.
We will now show that, if , then .
Proposition 3.6
The functor is sequentially continuous with respect to the Gromov–Hausdorff convergence of metric pairs.
Proof
Let , , , and be -approximations from to . We can define a map as
We will prove that is a -approximation from to .
Let . We now show that, for any bijection , there exists a bijection such that
| 3.4 |
and, conversely, that for any bijection , there exists a bijection such that inequality (3.4) holds.
Indeed, let be a bijection, and let and be such that . We set , where, given any , we set if , and we set to be a point such that if . In the latter case, such a choice is possible by item (2) in Definition 3.1. In particular, in either case we have . Up to changing representatives of and in , this completely defines a bijection , and we have
by item (1) in Definition 3.1 and the triangle inequality. Taking the supremum over all yields inequality (3.4).
Conversely, let be a bijection, and let and be such that . We define a bijection by setting , where, given any (viewed as an element in the multiset or ), we set to be such that if z is defined as for some , and such that and otherwise. In the latter case, we must have and hence such a choice is possible by item (2) in Definition 3.1. Similarly as above, we can then show that , and hence (3.4) holds with and .
Therefore, for any , we have
On the other hand, by definition, we have that
Finally, if , then for any , and since is an -approximation from to , we know that there is some such that . Hence, the diagram given by
satisfies and , so we conclude that .
Thus, is a -approximation from to .
Proof of Theorem A
The result follows from Proposition 3.6 and Example 3.3.
Remark 3.7
Note that we have only shown that is sequentially continuous. To show continuity, we must first introduce topologies on , , and compatible with the definitions of Gromov–Hausdorff convergence on each of these categories. Herron has done this for in Herron (2016). The arguments in Herron (2016) may be generalized to and , allowing to show the continuity of . This has been carried out in Ahumada Gómez and Che (2023).
Geodesicity
In this section, we show that the functor , with , preserves the property of being a geodesic space and, in the case and assuming X is a proper geodesic space, we characterize geodesics in the space . This section adapts the work of Chowdhury (2019) to the context of general metric pairs.
The following two lemmas are generalizations of Chowdhury (2019, Lemmas 17 and 18) and the proofs are similar. For a general metric pair (X, A) where X is assumed to be proper, points in X always have a closest point in A. Here, however, as opposed to Chowdhury (2019), such a point is not necessarily unique.
Lemma 4.1
Let . Let be diagrams, be a sequence of bijections such that as . Then the following assertions hold:
If , are such that , then there exists such that for all .
If , are such that , then .
Proof
Since and , there is some such that . Since for sufficiently large k, the conclusion follows.
For the sake of contradiction, if , then and for sufficiently large k, where . This contradicts the fact that as .
Lemma 4.2
Let and assume X is a proper metric space. Let , and let be a sequence of bijections such that as . Then there exists a subsequence and a limiting bijection such that pointwise as and .
Proof
Since , for each point the sequence consists of a bounded set of points in X and at most countably many points in A. In particular, thanks to Lemma 4.1 and the fact that X is proper, and using a diagonal argument, we can assume that for each , the sequence is eventually constant equal to some point or it is convergent to some point such that . In any case, we can define as
By mapping enough points in A to all the points in that were not matched with points in , we get the required bijection .
Corollary 4.3
(Existence of optimal bijections) Let and assume X is a proper space, then for any there exists an optimal bijection , i.e. .
Definition 4.4
A convex combination in is a path such that there exist an optimal bijection and a family of geodesics in X such that joins x with for each and for each . Sometimes we also write to indicate is the convex combination with associated optimal bijection and family of geodesics .
With this definition in hand, the proof of geodesicity follows along the lines of Chowdhury (2019, Corollary 19).
Proposition 4.5
Let . If X is a proper geodesic space, then is a geodesic space.
Proof
Let be diagrams, be an optimal bijection as in Corollary 4.3 and let be some convex combination. Then is a geodesic joining and . Indeed, if we consider the bijection given by , then
Therefore is a geodesic from to .
Non-negative curvature
In this section, we prove that the functor preserves non-negative curvature in the sense of Definition 2.16 (cf. Turner et al. 2014, Theorem 2.5; Chowdhury 2019, Theorems 10 and 11). On the other hand, it is known that the functor does not preserve the non-negative curvature for (see Turner 2020). Also, does not preserve upper curvature bounds in the sense of CAT spaces for any p (cf. Turner et al. 2014, Proposition 2.4; Turner 2020, Proposition 2.4). Whether the functor preserves strictly negative lower curvature bounds remains an open question. Additionally, observe that we cannot use the usual -norm in to get lower curvature bounds on any space of persistence diagrams, as the following result shows.
Proposition 5.1
The space is not an Alexandrov space for any when is endowed with the metric .
Proof
For , the space is only a pseudometric space, so it cannot be an Alexandrov space. Suppose now that . Consider the points , and , and let for . We may check that for all , implying that for each there will be a geodesic between and such that has only one point for all t. Such geodesics are precisely paths of the form , where is a geodesic between and . But for each we can pick so that . This implies that, for instance, for but not for , implying that there is a branching of geodesics at the point , which cannot happen in an Alexandrov space.
We will use the following lemma, which does not require any curvature assumptions, to prove this section’s main result.
Lemma 5.2
Let be a geodesic. Let , , be optimal bijections. Then is an optimal bijection and, for all , x is a midpoint between and .
Proof
By the triangle inequality, it is clear that
holds for all . Therefore,
Thus,
and
for all . In particular, is an optimal bijection between and , and x is a midpoint between and for all .
Proposition 5.3
Let . If X is a proper Alexandrov space with non-negative curvature, then, is also an Alexandrov space with non-negative curvature.
Proof
Since X is an Alexandrov space, it is complete and geodesic. Thus, by Theorem A.1, the space is complete, and, since X is assumed to be proper, Proposition 4.5 implies that is geodesic. Now we must show that has non-negative curvature.
Let be diagrams and be a geodesic from to . We want to show that the inequality
holds. This inequality characterizes non-negative curvature (see, for example, Ohta 2012, Sect. 2.1).
Let , , be optimal bijections, and define . From the formula for the distance in we observe that the following inequalities hold:
Now, since , we have that
for all . Therefore, thanks to Lemma 5.2,
Lemma 5.2 implies the following corollary, which one can use to give an alternative proof of Proposition 5.3 along the lines of the proof for the Euclidean case in Turner et al. (2014).
Corollary 5.4
Let and assume X is a proper geodesic space. Then every geodesic in is a convex combination.
Proof
This argument closely follows the proofs of Theorems 10 and 11 in Chowdhury (2019). We repeat some of the constructions for the convenience of the reader.
Let be a geodesic. We first claim there exists a sequence of convex combinations such that for each and
Indeed, given , we define and as follows. For each consider optimal bijections . By Lemma 5.2,
is an optimal bijection. Moreover, Lemma 5.2 implies that, for each , there is some geodesic joining with which has x as its midpoint. This way, starting from some point and following the bijections , we construct a geodesic joining x with .
Now, thanks to Lemma 4.2, there is a subsequence of which pointwise converges to some optimal bijection . Moreover, we can extract a further subsequence such that, for fixed dyadic rationals and , the sequence of bijections induced by pointwise converge as well. By Arzelà–Ascoli theorem and a applying one more diagonal argument, we may assume that for each the sequence uniformly converges to some geodesic joining x with . By the continuity of and it easily follows that for each .
Remark 5.5
We note that cannot in general be an Alexandrov space with curvature bounded below by for any . To see this, let (X, A) be a metric pair, where X is proper and geodesic. For , let and let be a constant speed geodesic with and of minimal length, i.e. of length ; such exists since X is proper and A is closed. Suppose that
| 5.1 |
For , let . It follows from (5.1) that for , and therefore .
It is then easy to see that the path , where
is a constant speed geodesic in from to . But it is then easy to verify, again using (5.1), that
where . In particular, it follows that the geodesic triangle in formed by geodesics , and is isometric to the geodesic triangle in with vertices , and . It follows that cannot be -Alexandrov for any .
The condition (5.1) is not hard to achieve: it can be achieved whenever X is a connected Riemannian manifold of dimension and , for instance. Indeed, in that case, if then (5.1) is satisfied for any with , where are distinct elements and . On the other hand, if then since X is connected of dimension , and so we may pick in such a way that for any i and any , where is a fixed element. It then follows that for each i. Since , we may do this in such a way that the angle between and at a is when ; but then, as a consequence of the Rauch comparison theorem, (5.1) will be satisfied whenever is chosen small enough.
Remark 5.6
Let X be an Alexandrov space and let be a convex subset, i.e. such that any geodesic joining any two points in K remains inside K (cf. Burago et al. 2001, p. 90). It is a direct consequence of the definition that K is also an Alexandrov space with the same lower curvature bound as X. In particular, if with X an Alexandrov space of non-negative curvature, and is a convex subset with , then is an Alexandrov space of non-negative curvature.
Proof of Theorem B
The result follows from Theorem A.1, Propositions A.7, 4.5, and 5.3.
Spaces of directions: the local geometry of noise
In this section we prove some metric properties of the space of directions at the empty diagram for with X an Alexandrov space with non-negative curvature. As mentioned in the introduction, the space of directions at the empty diagram in could be interpreted as controlling the local geometry of small noise perturbations.
Proposition 6.1
The space of directions has diameter at most
Proof
Consider . We can always consider a bijection such that for every different from A and for every different from A. Thus, by definition of the distance function , we have
Therefore,
i.e. . This immediately implies the result.
Proposition 6.2
Directions in corresponding to diagrams with finitely many points are dense in .
Proof
Consider an arbitrary diagram and an enumeration of its points. We can define a sequence of finite diagrams given by
Let be a minimizing geodesic joining with the empty diagram . By Corollary 5.4, we know that is a convex combination, i.e. for some optimal bijection and some collection of geodesics such that joins with . Let be the restricted convex combination between and . Then the inclusion induces a bijection between the corresponding diagrams, which in turn implies that
Thus, using the definition of the angle between geodesics in an Alexandrov space (see, for example, Burago et al. 2001, Definition 3.6.26) and the law of cosines, we get that
and the last quotient converges to 1. Thus, converges to 0. This way, we can conclude that the set of directions in induced by finite diagrams can approximate any geodesic direction, and since is the metric completion of that set, the result follows.
We can calculate explicitly the angle between any two directions at determined by finite diagrams, as the following result show.
Lemma 6.3
Let and be two diagrams with finitely many points, and let be geodesics joining to , respectively, so that and for some geodesics joining to and to , respectively. Then
where ranges over all bijections between subsets and of points in and , respectively, such that for all .
Proof
For each , let be a bijection realizing the distance . Then there exists a bijection between subsets and of points in and , respectively, such that for and and such that matches all the other points of to A. Moreover, by the construction we have
for all (where ), implying that for all when s and t are small enough (which we will assume from now on).
Now we can compute that
and therefore
| 6.1 |
where and . Moreover, note that since minimizes , the bijection maximizes the right hand side of (6.1). It follows that
| 6.2 |
where ranges over all bijections between subsets and of points in and , respectively, such that for all . Since and each has finitely many points, there are only finitely many such bijections , allowing one to swap the limit and the maximum on the last line of (6.2). The result follows.
Proof of Theorem C
Propositions 6.1 and 6.2 correspond to the first two assertions in Theorem C. Using Lemma 6.3 and the density of the directions in corresponding to diagrams with finitely many points yields the third assertion in the theorem.
Dimension of spaces of Euclidean persistence diagrams
In this section, we analyze some aspects of the global geometry of the spaces of Euclidean persistence diagrams. We denote such spaces by , and , where we let (and for simplicity we write ) and is endowed with the Euclidean metric. The investigation of the geometric properties of the spaces , where the metric in is induced by the -norm in , was carried out in Mileyko et al. (2011). In Turner et al. (2014), the authors showed that , where has the Euclidean metric, is an Alexandrov space of non-negative curvature.
We will also consider the sets
and
which are convex subsets of the Euclidean space . In particular, the space , is the classical space of persistence diagrams which arises in persistent homology, is also an Alexandrov space of non-negative curvature (cf. Remark 5.6). The interest in studying the spaces when is motivated by the fact that the subspaces can be thought of as the parameter spaces of a family of n-dimensional persistence modules, namely, persistent rectangles (cf. Bjerkevik 2021, Theorem 4.3; Skryzalin and Carlsson 2017, Lemma 1).
As an application of our geometric results, we now show that the asymptotic dimension of , , and is also infinite, for any . It may be feasible to also obtain these results by extending the work of Mitra and Virk in Mitra and Virk (2021), where they consider spaces of persistence diagrams with finitely many points in . The asymptotic dimension, introduced by Gromov in the context of finitely generated groups (see Gromov 1991), is a large scale geometric version of the covering dimension. For an introduction to this invariant, we refer the reader to Bell (2017), Bell and Dranishnikov (2008), Piotr (2012), Roe (2003).
Definition 7.1
(cf. Piotr 2012, Definition 2.2.1) Let be a cover of a metric space X. Given , the R-multiplicity of is the smallest integer n such that, for every , the ball B(x, R) intersects at most n elements of . The asymptotic dimension of X, which we denote by , is the smallest non-negative integer n such that, for every , there exists a uniformly bounded cover with R-multiplicity . If no such integer exists, we let .
The following lemma should be compared with (Mitra and Virk 2021, Lemma 3.2), where the authors compute the asymptotic dimension of spaces of persistence diagrams with n points.
Lemma 7.2
The asymptotic dimension of , , is infinite.
Proof
Consider the subspace consisting of diagrams with points. As a set, can be identified with the quotient , where the symmetric group acts by permutations of coordinates. Consider two diagrams and in , where and . We then claim that
| 7.1 |
Indeed, by regarding and as atomic measures in with the same total mass, and applying the classical theory of optimal transport in dimension one, the monotone map induces an optimal bijection between and . See for example (Santambrogio 2015, Theorem 2.9). But this implies that the metric on agrees with the quotient metric on , where denotes the metric. This implies that the inclusion into is isometric.
Finally, we claim that the asymptotic dimension of is N. Indeed, equipped with the metric is a quotient of an action of on by isometries, and is a quotient of an action of on by isometries. As and are proper, it follows by Kasprowski (2017, Theorem 1.1) that the asymptotic dimensions of , and are the same. Thus the asymptotic dimension of is N, as claimed. As is an isometric subspace of for each N, it follows that has infinite asymptotic dimension, as required.
Proposition 7.3
Let and let . Suppose that there exists a C-bi-Lipschitz map such that and such that for all . Then , , has infinite asymptotic dimension.
Proof
Note that f induces a map of pairs , and therefore a map
We will show that is a C-bi-Lipschitz equivalence onto its image. The result will then follow from Lemma 7.2. By Proposition 2.9, the map is C-Lipschitz. Now, let be a bijection realizing the distance , and note that for some bijection , where for and . Given any , we then have
since f is C-bi-Lipschitz. Furthermore, if , then we have
and, if , we have
It follows that
in any case, and therefore
Hence is C-bi-Lipschitz, as required.
Before proving the next result, we recall the definition of covering dimension.
Definition 7.4
(cf. Munkres 2000, Chapter 8) Let be an open cover of a metric space X. The order of is the smallest number n for which each point belongs to at most n elements in . The covering dimension of X is the minimum number n (if it exists) such that any finite open cover of X has a refinement of order .
Corollary 7.5
The spaces , and , for , have infinite Hausdorff, covering and asymptotic dimensions.
Proof
For each , the map defined by
is an isometric (and so -bi-Lipshitz) embedding such that and . Hence, by Proposition 7.3, has infinite asymptotic dimension.
To see that has infinite covering and Hausdorff dimensions, observe that the same argument in the end the proof of Lemma 7.2, shows that the covering and Hausdorff dimensions of is infinite. Since , we conclude that also has infinite covering and Hausdorff dimensions.
Putting the results in this section together yields the proof of our article’s last main result. Before proceeding, recall that the Assouad dimension of a metric space X, when infinite, yields an obstruction to bi-Lipschitz embedding X into a finite-dimensional Euclidean space (see Jonathan 2021 for a detailed discussion of this dimension and related results). More precisely, if X has a bi-Lipschitz embedding into some finite-dimensional Euclidean space, then X must have finite Assouad dimension (see Jonathan 2021, Ch. 13). The Assouad–Nagata dimension, which Assouad introduced in Assouad (1982), may be thought of as a variant of the asymptotic dimension (see Lang and Schlichenmaier 2005 for basic properties of this dimension).
Proof of Theorem E
The result for the Hausdorff, covering, and asymptotic dimensions follows from Corollary 7.5. Both the Hausdorff and covering dimensions are lower bounds for the Assouad dimension (see Jonathan 2021), while the asymptotic dimension is a lower bound for the Assouad–Nagata dimension (see Lang and Schlichenmaier 2005). Therefore, these dimensions are also infinite.
Remark 7.6
Recall that the Hausdorff dimension of an Alexandrov space must be either an integer or infinite (see Sect. 2). Using this fact, we can give an alternative proof that , , has infinite Hausdorff dimension. Indeed, the space is not locally compact, since one can always construct sequences of points in arbitrarily small balls around with no convergent subsequence (cf. Mileyko et al. 2011, Example 16). Since an Alexandrov space of finite Hausdorff dimension must be locally compact (see Burago et al. 2001, Theorem 10.8.1), the Hausdorff dimension of must be infinite.
We point out that our arguments to prove Lemma 7.2, Proposition 7.3, and Corollary 7.5 can be used to prove analogous results for the spaces of persistence diagrams with finitely (but arbitrarily) many points, , as defined, for example, in Bubenik and Elchesen (2022). Thus, all such spaces also have infinite Hausdorff, covering, asymptotic Assouad, and Assouad–Nagata dimensions.
Corollary 7.7
The space , and , has infinite covering, Hausdorff, asymptotic, Assouad, and Assouad–Nagata dimension.
Acknowledgements
Luis Guijarro and Ingrid Amaranta Membrillo Solis would like to thank the Department of Mathematical Sciences at Durham University for its hospitality while part of this paper was written. Fernando Galaz-García would like to thank Marvin Karsunky for his help at the initial stages of this project. The authors would like to thank Samir Chowdhury, Tristan Madeleine, and Motiejus Valiunas for their helpful comments on a previous version of this article. Finally, the authors would also like to thank one of the referees for their detailed comments on the manuscript and suggestions on how to improve some of our results in Sect. 7, leding to the strengthened statement of Theorem E.
Completeness, separability, and Fréchet means
Completeness and separability
In this subsection we will show that completeness and separability are both preserved by the functor , , as well as the existence of Fréchet means for probability measures with compact support or with rate of decay at infinity bounded below by . The proofs in this section follow almost verbatim the arguments in Mileyko et al. (2011, Sect. 3.1) for the properties of the classical spaces of persistence diagrams (i.e. when and in our notation). We include these arguments in our more general setting for the sake of completeness. Also, we will assume throughout this section that , since the results do not hold in the case (see Che et al. 2024).
We first prove completeness of . This proof will follow by putting together a series of lemmas.
Theorem A.1
Let . If X is complete, then is complete.
Let be a Cauchy sequence in . Let the multiplicity of , denoted by , be the number of points of outside A and, for , let be the function defined by
We call the -upper part of . We define in a similar way the -lower part of by letting be given by
Compare with the definition of and in Mileyko et al. (2011, Sect. 3.1). Observe that, in general, we cannot define the persistence of points in X with respect to A as usual (i.e. the difference between the coordinates of the point). However, we can take the distance to A as the notion of persistence, which in the case of the classical space of persistence diagrams (either with the norm or in ) is some multiple of the distance to the diagonal . This will affect the computations in this and the following two sections.
Since the -upper part of any diagram has finite multiplicity for arbitrary , it is reasonable to consider the convergence of the -upper parts of the diagrams .
Lemma A.2
Let . There exist and , such that, for all , there exists an such that whenever .
Proof of Lemma 4.2
For with , let and let . Since is a Cauchy sequence, is bounded and this directly implies that . Also, if , then which means that and . Therefore, the limits and exist and, moreover, there exists a such that and whenever . Now suppose that . Fix and let . Let and be two subsequences of such that and . Since is a Cauchy sequence, there exists such that for all . By assumption, , which implies that, for any bijection , there is a point such that and . This means that , leading to , which is a contradiction. We then set .
Given , let and .
Lemma A.3
For any , the sequence is a Cauchy sequence in .
Proof of Lemma 4.3
Let be as in Lemma A.2 and let . By Lemma A.2, there is an such that, for all , there is no point with . Let and let . If we increase N so that for all , then there exists a bijection such that
which implies that . Therefore,
The following lemma shows that the sequence converges for arbitrary .
Lemma A.4
For any , there is a diagram such that , hence and . Moreover, if , we have .
Proof of Lemma 4.4
Let , , and let be such that for all . Let and choose a subsequence such that and for . Let be a bijection realizing the p-Wasserstein distance between and , which, by our choice of , maps points outside A to points outside A. Let be points outside A in and let be sequences such that , for , and . By the choice of our diagram subsequence, we get that each is a Cauchy sequence and we denote the corresponding limits by (here we are using the fact that X is complete). Let be the diagram whose points outside A are exactly , where the multiplicity of each is the number of sequences whose limit is .
For , we choose such that, for all , we have and , for . It follows that
.
Hence, is the unique limit of and does not depend on the choice of bijections , subsequences , or .
Finally, let . Then points such that have . Repeating the above argument with such that , and , for , where ,, and such that leads to the last statement.
Lemma A.5
Let . Then and .
Proof of Lemma 4.5
Let and (big enough) such that . Then
for some constant , since is a Cauchy sequence. Since the right-hand side of the preceding equation is independent of , we get .
Finally, note that
The last step in the proof of the completeness of is the following lemma.
Lemma A.6
For each , there exists an such that, for all and , we have and, therefore, .
Proof of Lemma 4.6
Suppose there is an such that, for all , there exists with . Let be a sequence of positive values monotonically decreasing to 0. Since , we have and we find a subsequence such that . Let and choose such that , for all . Now, pick such that for all . This implies that
.
For let be a bijection such that . Then also .
Since , we can pick such that for all . If we now take such that , we see that
,
with . Now let be a bijection such that
and also points are getting mapped to A. Then, for , we have
Therefore, if , we have that , which is a contradiction.
The triangle inequality together with the aforementioned lemmas finally gives us Theorem A.1.
Let us now prove the separability of .
Proposition A.7
Let . If X is separable, then is separable.
Proof of Proposition 4.7
Let S be a countable dense subset of X and let be the set of persistence diagrams with finite total multiplicity and with points in S, that is,
Let . Then, for each , we can find such that . Then, we have . Since is dense in , we can find such that . Then, , which implies that is dense.
Note that , where . Each can be embedded into , thus it is countable. Hence, is countable.
Remark A.8
In Bubenik and Elchesen (2022), the authors consider completions of spaces of persistence diagrams in the more general context of pairs (X, A) with X an extended pseudometric space (i.e. a space in which the distance between points could also be zero or infinite). They define as the set of countable persistence diagrams such that, up to removing a finite subdiagram, have finite p-persistence. Let denote the quotient set obtained by collapsing A to a point and let be the extended metric space obtained by identifying points with zero distance. Proposition 6.16 in Bubenik and Elchesen (2022) (cf. 5th Theorem on page 350 of Bubenik and Hartsock 2024) asserts that is complete if and only if is complete, where is the metric on on X/A given by . In our context, X is a metric space in the usual sense and, therefore, . Thus, one may obtain an alternative characterization of the completeness of our via Proposition 6.16 in Bubenik and Elchesen (2022).
Fréchet means
We now consider the existence of Fréchet means for probability measures on . Following the arguments in Mileyko et al. (2011, Sect. 3.2), we will establish a characterization of totally bounded sets in the space of persistence diagrams , (see Proposition A.11), which is the main ingredient in Mileyko et al. (2011) to prove the existence of Fréchet mean sets for probability measures with compact support. Before carrying on, we make the following elementary observation.
Proposition A.9
If and , then is not totally bounded. In particular, is not compact.
Proof
Fix and consider the sequence of diagrams such that . Then , which is not bounded.
The following definition adapts Definitions 17, 18 and 20 from Mileyko et al. (2011) to our setting.
Definition A.10
Let and let .
The set S is birth-death bounded if the set is bounded.
The set S is off-diagonally birth-death bounded if, for all , the set is birth-death bounded.
The set S is uniform if, for all , there exists such that for all .
These conditions allow us to characterize totally bounded subsets of the space of diagrams, i.e. subsets such that, for each , there exists a finite collection of open balls in of radius whose union contains S. The proof of Proposition A.11 is a slight modification of that of Mileyko et al. (2011, Theorem 21). Observe again that our definition for the objects and differs slightly from that in Mileyko et al. (2011) due to our different definition for the persistence of points.
Recall that a metric space X is proper if it satisfies the Heine–Borel property, i.e. if every closed and bounded subset of X is compact (equivalently, if every closed ball in X is compact). Note that every proper metric space is complete.
Proposition A.11
Let with X a proper metric space. Then, a set is totally bounded if and only if it is bounded, off-diagonally birth-death bounded, and uniform.
Proof
First, we prove the “if” statement. Assume then that is totally bounded. Then, in particular, S is bounded. Now, let , take , and let , for , be a collection of balls of radius which cover S. For each we can find a ball such that for with , and for all with . Let C be a ball containing . Also, we can find such that for .
Let us prove that S is off-diagonally birth-death bounded. We will proceed by contradiction. Suppose that and there is an such that and , where is the ball concentric with C and with radius equal to the radius of C plus . Then, for any bijection , we have , which implies that . This contradicts the assumption that and implies that is birth-death bounded since, for all and all , we have proved that .
To prove that S is uniform, we also proceed by contradiction. Suppose that and . Consider a bijection and let and be maximal subdiagrams of such that for and for . If , then
where denotes the subdiagram of which coincides with the image of under . Since and do not have common points outside A and is the union of and , we have
Thus, if , then
Note also that if , then . Therefore,
Thus, for any bijection we have
Therefore, , which contradicts our assumption that . Consequently,
for all , which implies that S is uniform.
We now prove the “only if” statement. Assume that is bounded, off-diagonally birth-death bounded, and uniform. Given , let be such that for all . Take a ball such that, for all and all , we have . Since S is bounded, we can also find a constant such that for all . On the other hand, since C is a bounded subset of a proper complete space, C is also totally bounded and we can find points such that, for any , we have for some . Let be the diagram consisting of points with , each with multiplicity M and let with be all subdiagrams of . If , we can find and a bijection such that
Let be the extension of to obtained by mapping the points in to A. Then,
Therefore, and we conclude that S is totally bounded.
We now recall the definition of Fréchet mean set of probability measures on a metric space and state it in our setting.
Definition A.12
Given a Borel probability measure on , the quantity
is the Fréchet variance of and the Fréchet mean set of , denoted by is the set of points in that realize , i.e.
We also recall the definitions of various concepts mentioned in Theorem D.
Definition A.13
Let be a Borel probability measure on .
- We say that has finite second moment if
for any . The support of is the smallest closed subset S of such that .
We say that is tight if, for any , there is a compact subset such that .
- We say that has rate of decay at infinity q if for some (and hence for all) there exist and such that, for all ,
The following lemma is essential for the proof of Theorem D(1) and is an analog of Lemma 23 in Mileyko et al. (2011). We include the proof with the necessary modifications for the reader’s convenience.
Lemma A.14
Let be a finite Borel measure on with finite second moment and compact support , and let be a bounded sequence which is not off-diagonally birth-death bounded or uniform. Further, let and be bounds on S and , respectively, that is, for all and for all . Then there exists (depending only on ), a subsequence , and subdiagrams such that
where
With these preliminaries in hand, the proof of Theorem D now follows as in the Euclidean case (see Mileyko et al. 2011, Theorems 24 and 28). We include the proof of item (1), as it is brief, and indicate the necessary steps to prove item (2), referring to Mileyko et al. (2011) for further details.
Proof of Lemma 5.6
First, consider the case when is not off-diagonally birth-death bounded. Fix . Then there exists such that, for any and , there is and satisfying and . Take and choose such that for all we have for . Set . Let be a subsequence of such that each contains a point x with and , and let be the subdiagram of obtained by removing all such points x. Take and let be a bijection such that
Note that
Hence, for any such that , we have
since we can take to be sufficiently small. Thus, for with and it follows that, for any such that and , we have
Let be the bijection obtained from by pairing points such that and to the diagonal. Then
| A.1 |
which implies, after applying the inequalities in the proof of Mileyko et al. (2011, Lemma 23), that
| A.2 |
where
Therefore, after taking infimum with respect to and integrating with respect to on both sides in inequality (A.2), we obtain
This proves the lemma in the case where is not off-diagonally birth-death bounded.
Suppose now that is not uniform. Let be such that, for any and , there exists such that . If necessary, decrease the from the previous case so that and choose such that for all . Take and such that, for all , we have and for . Define as . Note that f is a continuous, monotonically increasing function and , . Set , and . Let be a subsequence of such that , , and let . Take and let be a bijection such that
Let be the bijection obtained from by pairing points in to the diagonal. For convenience, let
Note that
Thus,
Consequently,
for any . Thus,
Also,
We then have
Thus, we have arrived at inequality (A.1), and we may finish the argument as in the previous case. This finishes the proof of the lemma.
Proof of Theorem D
For the proof of item (1), let be the support of and let be a sequence such that .
We will proceed by contradiction. Suppose that is not bounded and let
Then is not bounded either. In particular,
which is absurd. Thus, is bounded.
Assume now that is not off-diagonally birth-death bounded or it is not uniform. Then, by Lemma A.14, there exist a subsequence and subdiagrams such that
Taking the infimum over k, we get that
which is a contradiction. This finishes the proof of item (1).
To prove item (2), one first proves an analog of Mileyko et al. (2011, Lemma 27), with minor modifications necessary to adapt the Euclidean proof to the general setting of . This lemma then implies the result, in a similar fashion as in the proof of Mileyko et al. (2011, Theorem 28).
Author Contributions
All authors contributed equally to the manuscript.
Funding
M.C. was funded by CONACYT Doctoral Scholarship No. 769708. F.G.G. was funded in part by research grants MTM2017-85934-C3-2-P from the Ministerio de Economía y Competitividad de España (MINECO) and PID2021-124195NB-C32 from the Ministerio de Ciencia e Innovación (MICINN). L.G. was funded in part by research grants MTM2017-85934-C3-2-P from the Ministerio de Economía y Competitividad de España (MINECO), PID2021-124195NB-C32 from the Ministerio de Ciencia e Innovación (MICINN), QUAMAP - Quasiconformal Methods in Analysis and Applications (ERC grant 834728), and by ICMAT Severo Ochoa project CEX2019-000904-S (MINECO). I.A.M.S. was funded by the Leverhulme Trust (grant RPG-2019-055).
Data availability
Not applicable.
Declarations
Conflict of interest
The authors do not have any conflict of interest.
Ethical approval
Not applicable.
Footnotes
M. Che: Supported by CONACYT Doctoral Scholarship No. 769708.
F. Galaz-García, L. Guijarro: Supported in part by research grants MTM2017–85934–C3–2–P from the Ministerio de Economía y Competitividad de España (MINECO) and PID2021-124195NB-C32 from the Ministerio de Ciencia e Innovación (MICINN).
L. Guijarro: Supported in part by QUAMAP - Quasiconformal Methods in Analysis and Applications (ERC grant 834728), and by ICMAT Severo Ochoa project CEX2019-000904-S (MINECO).
I. Membrillo: Supported by the Leverhulme Trust (grant RPG-2019-055).
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Adcock, A., Rubin, D., Carlsson, G.: Classification of hepatic lesions using the matching metric. Comput. Vis. Image Underst. 121, 36–42 (2014) [Google Scholar]
-
Afsari, B.: Riemannian
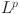 center of mass: existence, uniqueness, and convexity. Proc. Am. Math. Soc. 139(2), 655–673 (2011) [Google Scholar]
center of mass: existence, uniqueness, and convexity. Proc. Am. Math. Soc. 139(2), 655–673 (2011) [Google Scholar] - Ahumada Gómez, A., Che, M.: Gromov-Hausdorff convergence of metric pairs and metric tuples. Differential Geom. Appl. 94, 102135 (2024) [Google Scholar]
- Assouad, P.: Sur la distance de Nagata. C. R. Acad. Sci. Paris Sér. I Math 294(1), 31–34 (1982) [Google Scholar]
-
Bate, D., Garcia Pulido, A.L.: Bi-Lipschitz embeddings of the space of unordered
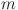 -tuples with a partial transportation metric. Math. Ann. (2024). 10.1007/s00208-024-02831-x [DOI] [PMC free article] [PubMed]
-tuples with a partial transportation metric. Math. Ann. (2024). 10.1007/s00208-024-02831-x [DOI] [PMC free article] [PubMed] - Bell, G.: Asymptotic Dimension, Office Hours with a Geometric Group Theorist, pp. 219–236. Princeton Univ. Press, Princeton, NJ (2017) [Google Scholar]
- Bell, G., Dranishnikov, A.: Asymptotic dimension. Topol. Appl. 155(12), 1265–1296 (2008) [Google Scholar]
- Bjerkevik, H.B.: On the stability of interval decomposable persistence modules. Discrete Comput. Geom. 66(1), 92–121 (2021) [Google Scholar]
- Botnan, M.B., Lebovici, V., Oudot, S.: On rectangle-decomposable 2-parameter persistence modules. Discrete Comput. Geom. 68, 1–24 (2022) [Google Scholar]
- Bubenik, P.: Statistical topological data analysis using persistence landscapes. J. Mach. Learn. Res. 16, 77–102 (2015) [Google Scholar]
- Bubenik, P., Elchesen, A.: Universality of persistence diagrams and the bottleneck and Wasserstein distances. Comput. Geom. 105/106, 101882 (2022) [Google Scholar]
- Bubenik, P., Elchesen, A.: Virtual persistence diagrams, signed measures, Wasserstein distances, and Banach spaces. J. Appl. Comput. Topol. 6(4), 429–474 (2022) [Google Scholar]
- Bubenik, P., Hartsock, I.: Topological and metric properties of spaces of generalized persistence diagrams. J. Appl. Comput. Topol. 8, 347–399 (2024) [Google Scholar]
- Bubenik, P., Wagner, A.: Embeddings of persistence diagrams into Hilbert spaces. J. Appl. Comput. Topol. 4(3), 339–351 (2020) [Google Scholar]
- Buchet, M., Hiraoka, Y., Obayashi, I.: Persistent homology and materials informatics. Nanoinformatics 75–95 (2018)
- Burago, Y., Gromov, M., Perel’man, G.: A. D. Aleksandrov spaces with curvatures bounded below. Uspekhi Mat. Nauk 47(2(284)), 3–51 (1992) [Google Scholar]
- Burago, D., Burago, Y., Ivanov, S.: A Course in Metric Geometry. Graduate Studies in Mathematics, vol. 33. American Mathematical Society, Providence, RI (2001) [Google Scholar]
- Carrière, M., Bauer, U.: On the metric distortion of embedding persistence diagrams into separable hilbert spaces. In: 35th International Symposium on Computational Geometry (SoCG 2019) (Dagstuhl, Germany) (Gill Barequet and Yusu Wang, eds.), Leibniz International Proceedings in Informatics (LIPIcs), vol. 129, Schloss Dagstuhl – Leibniz-Zentrum für Informatik, pp. 21:1–21:15 (2019)
- Cássio, M.M., de Mello, R.F.: Persistent homology for time series and spatial data clustering. Expert Syst. Appl. 42(15–16), 6026–6038 (2015) [Google Scholar]
- Che, M., Galaz-García, F., Guijarro, L., Membrillo Solis, I., Valiunas, M.: Basic metric geometry of the bottleneck distance. Proc. Am. Math. Soc. 152(8), 3575–3591 (2024) [Google Scholar]
- Chowdhury, S.: Geodesics in Persistence Diagram Space. arXiv:1905.10820 (2019)
- Cochoy, J., Oudot, S.: Decomposition of exact pfd persistence bimodules. Discrete Comput. Geom. 63(2), 255–293 (2020) [Google Scholar]
- Cohen-Steiner, D., Edelsbrunner, H., Harer, J.: Stability of persistence diagrams. Discrete Comput. Geom. 37(1), 103–120 (2007) [Google Scholar]
-
Cohen-Steiner, D., Edelsbrunner, H., Harer, J., Mileyko, Y.: Lipschitz functions have
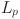 -stable persistence. Found. Comput. Math. 10(2), 127–139 (2010) [Google Scholar]
-stable persistence. Found. Comput. Math. 10(2), 127–139 (2010) [Google Scholar] - Divol, V., Lacombe, T.: Understanding the topology and the geometry of the space of persistence diagrams via optimal partial transport. J. Appl. Comput. Topol. 5(1), 1–53 (2021) [Google Scholar]
- Edelsbrunner, H., Letscher, D., Zomorodian, A.: Topological persistence and simplification. In: 41st Annual Symposium on Foundations of Computer Science, vol. 2000, pp. 454–463. IEEE Comput. Soc. Press, Los Alamitos, CA (2000)
- Edelsbrunner, H., Harer, J.: Persistent Homology–A Survey, Surveys on Discrete and Computational geometry. Contemp. Math., vol. 453, pp. 257–282. Amer. Math. Soc., Providence, RI (2008) [Google Scholar]
- Gromov, M.: Asymptotic invariants of infinite groups, Geometric group theory, vol. 2 Sussex. London Math. Soc. Lecture Note Ser., vol. 182, pp. 1–295. Cambridge Univ. Press, Cambridge (1991)
- Halbeisen, S.: On tangent cones of Alexandrov spaces with curvature bounded below. Manuscr. Math. 103(2), 169–182 (2000) [Google Scholar]
- Hatcher, A.: Algebraic Topology. Cambridge University Press, Cambridge (2002) [Google Scholar]
- Herron, D.A.: Gromov-Hausdorff distance for pointed metric spaces. J. Anal. 24(1), 1–38 (2016) [Google Scholar]
- Hungerford, T.W.: Algebra, Graduate Texts in Mathematics, vol. 73. Springer, New York-Berlin (1980). Reprint of the 1974 original
- Jansen, D.: Notes on Pointed Gromov–Hausdorff Convergence. arXiv:1703.09595 (2017)
- Jonathan, M.: Persistent Homology–A Survey. Surveys on Discrete and Computational geometry, vol. 222. Cambridge University Press, Cambridge (2021) [Google Scholar]
- Kasprowski, D.: The asymptotic dimension of quotients by finite groups. Proc. Am. Math. Soc. 145(6), 2383–2389 (2017) [Google Scholar]
- Kim, W., Mémoli, F.: Generalized persistence diagrams for persistence modules over posets. J. Appl. Comput. Topol. 5(4), 533–581 (2021) [Google Scholar]
- Kovacev-Nikolic, V., Bubenik, P., Nikolić, D., Heo, G.: Using persistent homology and dynamical distances to analyze protein binding. Stat. Appl. Genet. Mol. Biol. 15(1), 19–38 (2016) [DOI] [PubMed] [Google Scholar]
- Kusano, G., Fukumizu, K., Hiraoka, Y.: Kernel method for persistence diagrams via kernel embedding and weight factor. J. Mach. Learn. Res. 18, 189 (2017) [Google Scholar]
- Lang, U., Schlichenmaier, T.: Nagata dimension, quasisymmetric embeddings, and Lipschitz extensions. Int. Math. Res. Not. 58, 3625–3655 (2005) [Google Scholar]
- Mileyko, Y., Mukherjee, S., Harer, J.: Probability measures on the space of persistence diagrams. Inverse Probl. 27(12), 124007 (2011) [Google Scholar]
-
Mitra, A., Virk, Ž: The space of persistence diagrams on
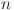 points coarsely embeds into Hilbert space. Proc. Am. Math. Soc. 149(6), 2693–2703 (2021) [Google Scholar]
points coarsely embeds into Hilbert space. Proc. Am. Math. Soc. 149(6), 2693–2703 (2021) [Google Scholar] - Mitsuishi, A.: A splitting theorem for infinite dimensional Alexandrov spaces with nonnegative curvature and its applications. Geom. Dedic. 144, 101–114 (2010) [Google Scholar]
- Munch, E.: Applications of Persistent Homology to Time Varying Systems, Ph.D. thesis, Duke University (2013)
- Munkres, J.R.: Topology, 2nd edn. Prentice Hall Inc, Upper Saddle River, NJ (2000) [Google Scholar]
- Ohta, S.: Barycenters in Alexandrov spaces of curvature bounded below. Adv. Geom. 12(4), 571–587 (2012) [Google Scholar]
- Patel, A.: Generalized persistence diagrams. J. Appl. Comput. Topol. 1(3–4), 397–419 (2018) [Google Scholar]
- Piotr, W.: Nowak and Guoliang Yu, Large scale geometry. EMS Textbooks in Mathematics, European Mathematical Society, Zürich (2012) [Google Scholar]
- Plaut, C.: Metric Spaces of Curvature
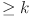 , Handbook of Geometric Topology, pp. 819–898 (2002)
, Handbook of Geometric Topology, pp. 819–898 (2002) - Roe, J.: Lectures on Coarse Geometry. University Lecture Series, vol. 31. American Mathematical Society, Providence, RI (2003) [Google Scholar]
- Santambrogio, F.: Optimal Transport for Applied Mathematicians. Calculus of Variations, PDEs, and Modeling, Prog. Nonlinear Differ. Equ. Appl., vol. 87. Birkhäuser/Springer, Cham (2015)
- Skryzalin, J., Carlsson, G.: Numeric invariants from multidimensional persistence. J. Appl. Comput. Topol. 1(1), 89–119 (2017) [Google Scholar]
- Turner, K.: Medians of populations of persistence diagrams. Homol. Homotopy Appl. 22(1), 255–282 (2020) [Google Scholar]
- Turner, K., Mileyko, Y., Mukherjee, S., Harer, J.: Fréchet means for distributions of persistence diagrams. Discrete Comput. Geom. 52(1), 44–70 (2014) [Google Scholar]
-
Wagner, A.: Nonembeddability of persistence diagrams with
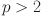 Wasserstein metric. Proc. Am. Math. Soc. 149(6), 2673–2677 (2021) [Google Scholar]
Wasserstein metric. Proc. Am. Math. Soc. 149(6), 2673–2677 (2021) [Google Scholar] - Wofsey, E.: The metrizability of symmetric products of metric spaces, MathOverflow (version: 2015-01-16) (2015)
- Yokota, T.: A rigidity theorem in Alexandrov spaces with lower curvature bound. Math. Ann. 353(2), 305–331 (2012) [Google Scholar]
- Yokota, T.: On the spread of positively curved Alexandrov spaces. Math. Z. 277(1–2), 293–304 (2014) [Google Scholar]
- Zhu, X.: Persistent homology: an introduction and a new text representation for natural language processing. In: Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, pp. 1953–1959 (2013)
- Zomorodian, A., Carlsson, G.: Computing persistent homology. Discrete Comput. Geom. 33(2), 249–274 (2005) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Not applicable.